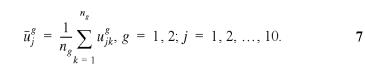Abstract
The Z curve is a three-dimensional space curve constituting the unique representation of a given DNA sequence in the sense that each can be uniquely reconstructed from the other. Based on the Z curve, a new protein coding gene-finding algorithm specific for the yeast genome at better than 95% accuracy has been proposed. Six cross-validation tests were performed to confirm the above accuracy. Using the new algorithm, the number of protein coding genes in the yeast genome is re-estimated. The estimate is based on the assumption that the unknown genes have similar statistical properties to the known genes. It is found that the number of protein coding genes in the 16 yeast chromosomes is ≤5645, significantly smaller than the 5800–6000 which is widely accepted, and much larger than the 4800 estimated by another group recently. The mitochondrial genes were not included into the above estimate. A codingness index called the YZ score (YZ Œ [0,1]) is proposed to recognize protein coding genes in the yeast genome. Among the ORFs annotated in the MIPS (Munich Information Centre for Protein Sequences) database, those recognized as non-coding by the present algorithm are listed in this paper in detail. The criterion for a coding or non-coding ORF is simply decided by YZ > 0.5 or YZ < 0.5, respectively. The YZ scores for all the ORFs annotated in the MIPS database have been calculated and are available on request by sending email to the corresponding author.
INTRODUCTION
An important problem in the study of the yeast genome is whether an ORF longer than a threshold is a true protein coding gene or not. Traditionally, the codingness of an ORF or a fragment of DNA sequence was described using the Codon Bias Index (CBI) (1) or the Codon Adaptation Index (CAI) (2). Although these indices were used widely (3), the coding properties of a coding sequence are not sufficiently reflected by them. For example, some ORFs shorter than 150 codons with CAI < 0.11 have identified phenotypes (4). The analysis of the entire yeast genome created the need for a more accurate codingness index. It is the aim of this paper to propose a new gene-finding algorithm at better than 95% accuracy. Based on the algorithm, a new index called the YZ score is proposed, which is used to reflect the codingness of an ORF or a fragment of DNA sequence. The YZ score is not meant to replace CBI or CAI, rather, to act as a complement to these already widely used indices.
The methodology adopted here is based on the Z curve theory of DNA sequences (5–7). Although most computational biologists are not aware of the technique term Z curve, it is a powerful tool for visualizing and analyzing DNA sequences. The Z curves method has been applied with some success to areas such as distinguishing between genes with and without introns (8), and recognizing coding sequences in the human genome (9). It is hoped that the Z curves method will become a convenient tool for genome analysis.
Using the new gene-finding algorithm, we re-estimate the number of protein coding genes in 16 yeast chromosomes. To our surprise, the number of genes estimated here is ≤5645, significantly less than the 5800–6000 widely accepted (10–12), and significantly greater than the 4800 estimated recently by another group (4).
DATABASES AND METHODS
The database
The Saccharomyces cerevisiae genome DNA sequences were obtained from a CD-ROM distributed from MIPS, the Munich Information Centre for Protein Sequences, Release 1997. The newest data for classification of ORFs in the yeast genome were downloaded from http://speedy.mips.biochem.mpg.de Release September 27, 1999.
The Z curve
The Z curve is a three-dimensional space curve constituting the unique representation of a given DNA sequence in the sense that for the curve and sequence each can be uniquely reconstructed from the other. We present briefly the method of the Z curve as follows. Consider a DNA sequence read from the 5′ to the 3′-end with N bases. Inspect the sequence one base at a time, beginning from the first base. Let the number of the inspecting steps be denoted by n, i.e., n = 1, 2, …, N. In the nth step, count the cumulative numbers of the bases A, C, G and T, occurring in the subsequence from the first to the nth base in the DNA sequence inspected. Denoting the cumulative occurring numbers of the bases A, C, G and T in the above subsequence by An, Cn, Gn and Tn, respectively, we defined the Z curve in the following. The Z curve consists of a series of nodes Pn, where n = 1, 2, …, N, whose coordinates are denoted by xn, yn and zn. It was shown (6,7) that 
where A0 = C0 = G0 = T0 = 0 and hence x0 = y0 = z0 = 0. The connection of the nodes P0 (P0 = 0), P1, P2, …, until PN one by one sequentially by straight lines is called the Z curve for the DNA sequences inspected. To clarify the biological implication of the Z curve defined, using the normalized equation An + Cn + Gn + Tn = n we rewrite equation 1 as
where R, Y, M, K, W and S represent the bases of purine, pyrimidine, amino, keto, weak hydrogen bonds and strong hydrogen bonds, respectively, according to the Recommendation 1984 by the NC-IUB (13). The Z curve defined above is a three-dimensional space curve, having three independent components, i.e., xn, yn and zn. Each has a clear biological meaning. The component xn displays the distribution of bases of the purine/pyrimidine (A or G/C or T) types along the sequence. When the number of the purine bases in the subsequence from the first to the nth base is greater than that of the pyrimidine bases, xn > 0, otherwise xn < 0. Similarly, the component yn displays the distribution of bases of the amino/keto (A or C/G or T) types along the sequence. When the number of the amino bases in the subsequence from the first to the nth base is greater than that of the keto bases, yn > 0, otherwise, yn < 0. Finally, the component zn displays the distribution of bases of the weak H-bond/strong H-bond (A or T/G or C) types along the sequence. When the number of the weak H-bond bases in the subsequence from the first to the nth base is greater than that of the strong H-bond bases, zn > 0, otherwise, zn < 0. In summary, the Z curve is the unique representation for a given DNA sequence in a three-dimensional space and each can be uniquely reconstructed from the other (6,7). Therefore, any DNA sequence is uniquely and completely described by the three distributions, i.e., those of the bases of purine/pyrimidine, amino/keto and weak/strong H-bonds, respectively. The Z curve offers an intuitive and convenient approach to study DNA sequences. By viewing the Z curve, some overall and local features of the sequence can be detected in a perceivable way. Furthermore, a new methodology has been derived from the Z curve by which DNA sequences can be studied geometrically.
The phase-specific Z curve
Most gene-finding algorithms are based on the differences of statistical properties between DNA sequences in coding and non-coding regions. The distributions of bases among the three phases in one strand of a DNA double helix are heterogeneous in the coding region, whereas uniform in the non-coding regions, (e.g. 5). This fact constitutes the basis of the present gene-finding algorithm. The Z curve for the subsequence in an ORF with bases at positions 1, 4, 7, …, forms a phase-specific curve. We call this curve the phase-1 Z curve. Similarly, the Z curves with bases at positions 2, 5, 8, …, and 3, 6, 9, ..., are called the phase-2 and phase-3 Z curves, respectively. For an ORF sequence, the phase-1, -2 and -3 Z curves describe the distributions of bases at first, second and third codon positions, respectively. For each phase-specific Z curve there are three components, as for the ordinary Z curve. The three components of the phase-1 Z curve are denoted by xn(1), yn(1) and zn(1), respectively, and xn(2), yn(2), zn(2), xn(3), yn(3) and zn(3) are defined similarly.
To simplify the later calculation, each component curve of a phase-specific Z curve listed above (e.g., xn(1) ~ n) is approximately described by a straight line. Consequently, we have
where kx(1), ky(1), kz(1), kx(2), ky(2), kz(2), kx(3), ky(3) and kz(3) are the slopes for the straight lines. For simplicity, they are calculated as follows
where M = N/3, and N is the length of the ORF. According to the property of the Z curve, the slopes of the straight lines defined in equation 4 are determined by the average base composition of the corresponding sequences associated with the curve. For example, given kx(1), ky(1) and kz(1), the base composition of the subsequence in an ORF with bases at positions 1, 4, 7, …, can be calculated (6,7). Therefore, slopes are statistical quantities describing the basic features of the sequence concerned. The approximation expressed in equations 3 and 4 is simple and effective. Of course, it is possible to fit Z curves by using more complicated functions, rather than straight lines.
The Fisher discriminant algorithm in a 10-dimensional space
Each ORF (or an intergenic DNA sequence) is described by a point or a vector in a 10-dimensional (10-D) space spanned by u1, u2, …, u10. They are defined by
where a, c, g and t are the average occurrence frequencies of bases A, C, G and T in the DNA sequence studied. That is, a = AN/N, c = CN/N, g = GN/N and t = TN/N, where AN, CN, GN and TN are the occurrence numbers of bases A, C, G and T, respectively, in the sequence, and N is the total length of the sequence. The variable u10 was found to be a useful statistical quantity for the analysis of DNA sequences (5). Obviously, the minimum of u10 is equal to 1/4, if, and only if, a = c = g = t = 1/4. Usually the value of u10 in the coding region is smaller than that in the non-coding region.
To complete the protein coding gene-finding algorithm, we need two groups of samples. One is a set of the positive samples corresponding to the true protein coding genes; another is a set of the negative samples corresponding to the intergenic sequences. The number of samples in each group should be identical. The two groups of samples form the training set used in the Fisher discrinimant algorithm. The Fisher linear discriminant equation in this case represents a super-plane in the 10-D space, described by a vector c which has 10 components c1, c2, … and c10. The determination of c is extremely simple in the case of two groups of samples, such as the case studied here. Group 1 (denoted by g = 1) corresponds to coding samples; whereas group 2 (denoted by g = 2) corresponds to non-coding samples. Denoted by ujkg the jth component of the 10-D vector defined in equation 5 of the kth sample in the g group, where g = 1, 2; j = 1, 2, …., 10; and k = 1, 2, …, ng(n1 = n2, i.e., the numbers of samples in both groups are identical), we calculate the geometrical center vector Ug for each group
where ‘T’ indicates the transpose of a matrix, and
Denoting by S = (sij) the sum of the covariance matrices of two groups, we have
The vector c is simply determined by the following equation
where S–1 is the inverse of the matrix S. See the detailed explanation on these equations in Mardia et al. (14). The vector c is not unique in the sense that c multiplied by a constant is still acceptable. Without losing generality we choose the constant such that │c│2 = 1. Based on the data in the training set, an appropriate threshold c0 is determined to make the coding/non-coding decision. The threshold c0 is uniquely determined by letting the false negative rate and the false positive rate be identical. Once the vector c and the threshold c0 are obtained, the decision of coding/non-coding for each ORF in the test set is simply performed by the criterion of c·u > c0 / c·u < c0, where c = (c1, c2, …, c10)T and u = (u1, u2, …, u10)T.
The YZ score for an ORF or a fragment of DNA sequence
The criterion of c·u > c0 / c·u < c0 for making the decision of coding/non-coding can be rewritten as F(u) > 0 / F(u) < 0, where F(u) = c·u – c0. Let the maximum and minimum of F(u), calculated based on the data in the training set, be denoted by Fmax and Fmin, respectively. Furthermore, let Fmax+ and Fmax– be the quantities a little bit larger and smaller than Fmax and Fmin, respectively. Define the YZ score (Yeast, Z curve)
Then the criterion to make the decision of coding/non-coding simply becomes YZ > F0 / YZ < F0, where
Choose Fmax+ = 0.30 and Fmin– = –0.30 such that F0 = 0.50. The criterion to make the decision of coding/non-coding clearly becomes YZ > 0.5 / YZ < 0.5. In some rare cases, the YZ scores calculated for some practical samples may be <0 or >1. In the former case, let the YZ score be equal to 0, whereas in the latter case, let the YZ score be equal to 1. Consequently, for any u, YZ Œ [0,1].
RESULTS AND DISCUSSION
Six-fold cross-validation tests
To test the new algorithm, six-fold cross-validation tests are performed. In the version of MIPS database, Release September 27, 1999, the ORFs were classified into six classes, in which the first class consists of 3199 entries corresponding to the known proteins. Excluding the protein coding genes from the mitochondria and those containing introns, 2958 protein coding genes of the first class residing at the 16 yeast chromosomes remain. The number of the mitochondrial genes available at present is too limited to perform a statistical study. They are thus excluded from the present study. Randomly divide the 2958 genes into two unequal parts, in which the larger part consists of 1958 genes, and the smaller consists of 1000 genes. The former serves as a training set used to find the Fisher coefficients; whereas the latter serves as a test set used to test the accuracy of the algorithm.
As mentioned above, both the training and test sets should be accompanied by the counterparts of negative samples. We have randomly selected about 6000 intergenic sequences with length longer than 300 bp from the 16 yeast chromosomes, and each of them starts with ATG and ends with one of the stop codons. The detailed procedure to select the intergenic sequences is described as follows. For each of the 16 yeast chromosomes:
(i) Find the number and locations of the ORFs annotated in the MIPS database and denote the number of ORFs by K.
(ii) Calculate the length for each of the (K–1) DNA sequences between any two adjoining ORFs. Ignore sequences where the length is <300 bp.
(iii) For all sequences ≥300 bp, starting from the first base, search for the first ‘ATG’ codon encountered along the sequence. In the downstream direction, starting from the 101st codon beginning from ATG, search for the first stop codon encountered. Then the DNA sequence starting from ATG and ending with one of the stop codons is regarded as one candidate for the intergenic sequences. Note that this is not an ORF because there often may be several stop codons within it. Continue to search for more intergenic sequences in the downsteam direction until no more can be found in the remaining sequence.
(iv) Repeat step (iii) for each of the six phases in the sequence. The possible numbers of such sequences are quite large. Randomly select about 6000 such sequences from the 16 yeast chromosomes as the intergenic sequences used for complementing the Fisher algorithm. A computer program has been written to do this job. We should point out that the lengths of the intergenic sequences thus obtained are roughly equal to the ORF lengths, but not identical. Because the present algorithm is based on the difference of the base composition between coding and non-coding sequences, the non-identity of the lengths between the two kinds of sequences does not seem to be a major problem. When the lengths of both kinds of sequences are >300 bp, the calculated results of base composition are not usually sensitive to small variations in sequence length.
Randomly select 1958 and 1000 intergenic sequences from the 6000 sequences, which form the training and test sets of negative samples, respectively. In summary, the training set consists of 1958 positive samples (true genes) and 1958 negative samples (intergenic sequences). The test set consists of 1000 positive samples (true genes) and 1000 negative samples (intergenic sequences). Using the sequences in the training sets, the Fisher coefficients c0, c1, c2, … and c10 are determined. Using the Fisher coefficients just obtained, the accuracy of the gene-finding algorithm is calculated based on the test set.
Repeating the above procedure three times, we have performed 3-fold cross-validation tests. The sensitivity, specificity and accuracy of each test are listed in Table 1. As can be seen, all three quantities obtained are >95%.
Table 1. The accuracy of the gene-recognition algorithm for three different test sets.
| Test set | 1 | 2 | 3 |
|---|---|---|---|
| Sensitivity (%) |
95.2 |
96.3 |
95.7 |
| Specificity (%) |
95.2 |
95.3 |
96.1 |
| Accuracya (%) | 95.2 | 95.8 | 95.9 |
aAccuracy is defined as the average of the sensitivity and specificity.
There are 223 intron-containing genes of the 1st class in the MIPS database. These ORFs are used as an independent test set to perform another 3-fold cross-validation test. Consequently, the accuracy (defined as the sensitivity) is always >95% for each of the above three tests.
We now discuss the definitions of accuracy, sensitivity and specificity, which are used to evaluate the performance of the algorithm. The notations used here are the same as those used by Burset and Guigo (15). Using TP and FN to denote the number of coding ORFs that have been predicted as coding and non-coding, respectively, we define the sensitivity sn as
That is, sn is the proportion of coding ORFs that have been correctly predicted as coding. Similarly, using TN and FP to denote the number of intergenic sequences that have been predicted as non-coding and coding, respectively, we define the specificity sp as
That is, sp is the proportion of intergenic sequences that have been correctly predicted as non-coding. The accuracy is defined as the average of sn and sp.
The definition of sp in equation 13 may cause problems in recognizing genes along the genomic DNA sequence. Because the frequency of non-coding nucleotides is generally much larger than that of coding ones, TN >> FP, and therefore sp tends towards 1. To solve this problem, instead of using the definition of sp in equation 13, one used the refined definition (15,16):
However, in the present study, the test set consists of 1000 coding ORFs and 1000 intergenic sequences, respectively, and it is therefore appropriate to use sp as defined in equation 13, rather than in equation 14.
The final Fisher coefficients
The 2958 positive samples (true genes) are merged together as a new training set. The 2958 negative samples are selected randomly from the 6000 intergenic sequences mentioned above. The random selection is repeated three times. Consequently, we have three experiments. For each experiment the positive samples are identical, whereas the negative samples are different each time. Calculating the Fisher coefficients for each experiment, the results are listed in Table 2. The final Fisher coefficients are obtained by simply averaging the corresponding values for the three experiments, which are listed in the last column of Table 2. The Fisher coefficients c0 ~ c10 make an internally consistent set. Averaging with coefficients from several experiments may break the internal consistency. However, since the variations of coefficients for different experiments are considerably small, as shown in Table 2, the problem is not severe. On the other hand, the Fisher super-plane in the 10-D space is described by the equation c·u – c0 = 0. To take advantage of each experiment, averaging the coefficients allows to adjust the position and orientation of the super-plane slightly.
Table 2. Fisher coefficients for three different training sets and their averages.
| Set | 1 | 2 | 3 | Average |
|---|---|---|---|---|
| c0 | 1.759 × 10–1 | 1.626 × 10–1 | 1.685 × 10–1 | 1.690 × 10–1 |
| c1 | 2.797 × 10–1 | 3.131 × 10–1 | 2.964 × 10–1 | 2.964 × 10–1 |
| c2 | –3.365 × 10–2 | –3.626 × 10–2 | –4.625 × 10–2 | –3.872 × 10–2 |
| c3 | –1.582 × 10–1 | –1.831 × 10–1 | –1.769 × 10–1 | –1.727 × 10–1 |
| c4 | –9.574 × 10–2 | –1.112 × 10–1 | –1.032 × 10–1 | –1.034 × 10–1 |
| c5 | 2.180 × 10–1 | 2.481 × 10–1 | 2.430 × 10–1 | 2.364 × 10–1 |
| c6 | 1.039 × 10–1 | 1.154 × 10–1 | 1.147 × 10–1 | 1.113 × 10–1 |
| c7 | –7.364 × 10–2 | –8.997 × 10–2 | –8.574 × 10–2 | –8.312 × 10–2 |
| c8 | –6.173 × 10–2 | –6.487 × 10–2 | –6.394 × 10–2 | –6.351 × 10–2 |
| c9 | 8.564 × 10–3 | 7.111 × 10–3 | –1.091 × 10–3 | 4.860 × 10–3 |
| c10 | –8.876 × 10–1 | –8.609 × 10–1 | –8.695 × 10–1 | –8.727 × 10–1 |
Apply the algorithm to recognize yeast genes
As mentioned above, in the version of the MIPS database, Release September 27, 1999, the ORFs were classified into six classes, which consist of 3199, 248, 869, 789, 805 and 447 entries, respectively. They correspond to known proteins (1st class), strong similarity to known proteins (2nd class), similarity or weak similarity to known proteins (3rd class), similarity to unknown proteins (4th class), no similarity (5th class) and questionable ORFs (6th class), respectively. Using the final Fisher coefficients and the criterion of c·u > c0 / c·u < c0 for making the decision of coding/non-coding, we re-recognize the nuclear genes from the ORFs in the 2nd ~ 6th classes in the MIPS database. The detailed results are listed in Tables 3 and 4, for the non-coding ORFs in the 2nd ~ 5th classes and the 6th class, respectively, in which the names of non-coding ORFs are clearly indicated. As shown in Table 3, 434 ORFs of the 2nd ~ 5th classes in the MIPS database are recognized as non-coding. Similarly in Table 4, 340 ORFs of the 6th class are recognized as non-coding. However, due to the limited sensitivity (95%) and specificity (95%) achieved, statistically, 119 of the 434 ORFs listed in Table 3 and four of the 340 ORFs listed in Table 4 (see calculations below), are actually coding genes. We cannot identify which 119 of the 434 or which four of the 340 ORFs are coding genes at present, unless the sensitivity and specificity are further increased.
Table 3. The 434 ORFs of the 2nd ~ 5th classes in the MIPS database, which are recognized as non-coding.
| YAL004w | YDL228c | YFR012w | YIR044c | YLR283w | YNR075w |
| YAL008w | YDL248w | YFR035c | YJL003w | YLR296w | YNR077c |
| YAL018c | YDR010c | YFR042w | YJL027c | YLR311c | YOL002c |
| YAL034c | YDR015c | YFR054c | YJL028w | YLR312c | YOL003c |
| YAL064w | YDR018c | YFR057w | YJL064w | YLR365w | YOL038c-a |
| YAL066w | YDR024w | YGL006w-a | YJL077c | YLR366w | YOL048c |
| YAR030c | YDR029w | YGL010w | YJL091c | YLR376c | YOL053w |
| YAR040c | YDR042c | YGL015c | YJL097w | YLR381w | YOL072w |
| YAR047c | YDR065w | YGL041c | YJL108c | YLR394w | YOL079w |
| YAR053w | YDR084c | YGL054c | YJL118w | YLR400w | YOL101c |
| YAR060c | YDR102c | YGL084c | YJL136w-a | YLR402w | YOL107w |
| YAR061w | YDR107c | YGL085w | YJL147c | YLR404w | YOL118c |
| YAR064w | YDR115w | YGL104c | YJL170c | YLR414c | YOL129w |
| YAR068w | YDR119w | YGL160w | YJL193w | YLR416c | YOL160w |
| YAR070c | YDR126w | YGL186c | YJL215c | YLR463c | YOL162w |
| YBL009w | YDR131c | YGL188c | YJR013w | YML047c | YOL163w |
| YBL044w | YDR179w-a | YGL226w | YJR023c | YML084w | YOR015w |
| YBL048w | YDR210w | YGL260w | YJR036c | YML090w | YOR024w |
| YBL049w | YDR215c | YGL263w | YJR044c | YML107c | YOR029w |
| YBL071c | YDR249c | YGR016w | YJR116w | YML122c | YOR044w |
| YBL089w | YDR274c | YGR023w | YJR120w | YML132w | YOR053w |
| YBL091c-a | YDR278c | YGR026w | YJR136c | YMR003w | YOR068c |
| YBL108w | YDR302w | YGR101w | YJR157w | YMR007w | YOR072w |
| YBL109w | YDR307w | YGR110w | YJR161c | YMR010w | YOR080w |
| YBL112c | YDR319c | YGR131w | YJR162c | YMR040w | YOR175c |
| YBR004c | YDR344c | YGR141w | YKL008c | YMR057c | YOR183w |
| YBR016w | YDR350c | YGR149w | YKL031w | YMR082c | YOR268c |
| YBR022w | YDR366c | YGR168c | YKL033w-a | YMR088c | YOR292c |
| YBR027c | YDR384c | YGR203w | YKL037w | YMR101c | YOR301w |
| YBR058c-a | YDR396w | YGR225w | YKL044w | YMR103c | YOR314w |
| YBR085c-a | YDR411c | YGR268c | YKL051w | YMR119w | YOR343c |
| YBR096w | YDR413c | YGR284c | YKL097c | YMR122c | YOR350c |
| YBR099c | YDR438w | YGR290w | YKL102c | YMR141c | YOR364w |
| YBR126w-a | YDR459c | YGR291c | YKL158w | YMR151w | YOR365c |
| YBR141c | YDR492w | YGR293c | YKL162c | YMR155w | YOR376w |
| YBR144c | YDR504c | YGR295c | YKL219w | YMR158w | YOR392w |
| YBR147w | YDR524c | YHL005c | YKL221w | YMR187c | YPL041c |
| YBR157c | YDR524w-a | YHL037c | YKL223w | YMR221c | YPL056c |
| YBR168w | YDR525w | YHL041w | YKL225w | YMR245w | YPL066w |
| YBR183w | YDR525w-a | YHL042w | YKR030w | YMR252c | YPL087w |
| YBR209w | YDR543c | YHL044w | YKR032w | YMR254c | YPL103c |
| YBR210w | YDR544c | YHL045w | YKR051w | YMR306w | YPL123c |
| YBR220c | YEL004w | YHL048w | YKR073c | YMR320w | YPL162c |
| YBR292c | YEL008w | YHR035w | YLL005c | YMR324c | YPL165c |
| YBR293w | YEL010w | YHR067w | YLL023c | YMR326c | YPL189w |
| YBR300c | YEL014c | YHR095w | YLL030c | YNL017c | YPL200w |
| YBR302c | YEL033w | YHR130c | YLL037w | YNL038w | YPL244c |
| YCL001w-a | YEL035c | YHR139c-a | YLL042c | YNL065w | YPL246c |
| YCL002c | YEL045c | YHR142w | YLL051c | YNL109w | YPL264c |
| YCL056c | YEL059w | YHR162w | YLL059c | YNL122c | YPR012w |
| YCL057c-a | YEL067c | YHR173c | YLR010c | YNL143c | YPR014c |
| YCL058c | YER044c | YHR181w | YLR023c | YNL146w | YPR064w |
| YCL075w | YER046w | YHR212c | YLR036c | YNL150w | YPR071w |
| YCR001w | YER048w-a | YHR214w-a | YLR046c | YNL156c | YPR094w |
| YCR006c | YER050c | YHR217c | YLR047c | YNL174w | YPR096c |
| YCR022c | YER066c-a | YHR218w-a | YLR050c | YNL176c | YPR100w |
| YCR025c | YER072w | YIL012w | YLR064w | YNL179c | YPR114w |
| YCR043c | YER091c-a | YIL025c | YLR111w | YNL203c | YPR151c |
| YCR062w | YER097w | YIL029c | YLR112w | YNL211c | YPR153w |
| YCR063w | YER113c | YIL040w | YLR122c | YNL255c | YPR170c |
| YCR085w | YER135c | YIL054w | YLR124w | YNL269w | YPR170w-a |
| YCR087c-a | YER140w | YIL058w | YLR145w | YNL303w | YPR195c |
| YCR102w-a | YER172c-a | YIL088c | YLR151c | YNL305c | YPR203w |
| YCR103c | YER184c | YIL089w | YLR156w | YNL320w | YBL059w* |
| YDL015c | YER188c-a | YIL090w | YLR159w | YNL324w | YDL012c* |
| YDL027c | YFL015c | YIL152w | YLR161w | YNL326c | YDR367w* |
| YDL054c | YFL019c | YIL174w | YLR162w | YNL336w | YDR535c* |
| YDL119c | YFL021c-a | YIL175w | YLR164w | YNL337w | YMR292w* |
| YDL123w | YFL040w | YIR020c | YLR184w | YNL338w | YOL047c* |
| YDL162c | YFL062w | YIR020c-a | YLR204w | YNR020c | |
| YDL196w | YFL063w | YIR020w-b | YLR246w | YNR056c | |
| YDL199c | YFL065c | YIR040c | YLR255c | YNR059w | |
| YDL206w | YFL068w | YIR043c | YLR264c-a | YNR062c |
Of the 434 ORFs listed, 428 are intronless and six are intron-containing (marked with *). Note that of the 434 ORFs listed, statistically, 119 actually code for proteins. Unfortunately, we cannot identify them at present due to the limited recognition accuracy achieved.
Table 4. The 340 ORFs of the 6th class in the MIPS database, which are recognized as non-coding.
| YAL034c-b | YDR112w | YGL182c | YJL142c | YLR379w | YOL150c |
| YAL042c-a | YDR114c | YGL193c | YJL150w | YLR428c | YOR041c |
| YAL056c-a | YDR133c | YGL204c | YJL152w | YLR434c | YOR082c |
| YBL012c | YDR136c | YGL214w | YJL169w | YLR444c | YOR102w |
| YBL053w | YDR149c | YGL217c | YJL175w | YLR458w | YOR121c |
| YBL062w | YDR154c | YGL218w | YJL182c | YLR465c | YOR146w |
| YBL065w | YDR157w | YGR011w | YJL202c | YML009w-a | YOR169c |
| YBL070c | YDR187c | YGR018c | YJL211c | YML012c-a | YOR170w |
| YBL073w | YDR199w | YGR025w | YJL220w | YML031c-a | YOR199w |
| YBL077w | YDR203w | YGR039w | YJR018w | YML034c-a | YOR200w |
| YBL094c | YDR220c | YGR045c | YJR020w | YML047w-a | YOR218c |
| YBL107w-a | YDR230w | YGR051c | YJR038c | YML057c-a | YOR225w |
| YBR051w | YDR241w | YGR064w | YJR071w | YML089c | YOR235w |
| YBR064w | YDR269c | YGR069w | YJR087w | YML094c-a | YOR248w |
| YBR089w | YDR290w | YGR073c | YJR128w | YML099w-a | YOR263c |
| YBR109w-a | YDR355c | YGR107w | YJR146w | YML116w-a | YOR277c |
| YBR113w | YDR360w | YGR114c | YKL030w | YMR046w-a | YOR282w |
| YBR116c | YDR401w | YGR115c | YKL036c | YMR052c-a | YOR300w |
| YBR124w | YDR426c | YGR122c-a | YKL053w | YMR075c-a | YOR309c |
| YBR178w | YDR431w | YGR137w | YKL076c | YMR086c-a | YOR325w |
| YBR206w | YDR442w | YGR139w | YKL083w | YMR119w-a | YOR331c |
| YBR224w | YDR445c | YGR151c | YKL111c | YMR135w-a | YOR333c |
| YBR226c | YDR455c | YGR164w | YKL115c | YMR153c-a | YOR345c |
| YBR266c | YDR467c | YGR176w | YKL118w | YMR158c-b | YOR379c |
| YBR277c | YDR509w | YGR182c | YKL123w | YMR158w-a | YPL025c |
| YCL006c | YDR521w | YGR219w | YKL131w | YMR172c-a | YPL034w |
| YCL023c | YDR526c | YGR228w | YKL136w | YMR193c-a | YPL035c |
| YCL041c | YEL075w-a | YGR259c | YKL147c | YMR290w-a | YPL044c |
| YCL042w | YER006c-a | YGR265w | YKL153w | YMR304c-a | YPL073c |
| YCL065w | YER046w-a | YHL002c-a | YKL162c-a | YMR306c-a | YPL102c |
| YCR018c-a | YER067c-a | YHL006w-a | YKL169c | YMR316c-a | YPL114w |
| YCR041w | YER084w | YHL030w-a | YKL202w | YNL013c | YPL185w |
| YCR049c | YER119c-a | YHL046w-a | YKR033c | YNL028w | YPL205c |
| YCR064c | YER145c-a | YHR049c-a | YKR047w | YNL089c | YPL238c |
| YCR087w | YER148w-a | YHR056w-a | YLL020c | YNL105w | YPL251w |
| YDL009c | YER165c-a | YHR063w-a | YLR101c | YNL114c | YPL261c |
| YDL016c | YER181c | YHR070c-a | YLR123c | YNL120c | YPR038w |
| YDL026w | YFL012w-a | YHR125w | YLR140w | YNL170w | YPR039w |
| YDL032w | YFL013w-a | YHR145c | YLR169w | YNL171c | YPR044c |
| YDL034w | YFL032w | YIL060w | YLR171w | YNL184c | YPR050c |
| YDL041w | YFR036w-a | YIL066w-a | YLR198c | YNL198c | YPR053c |
| YDL050c | YFR056c | YIL068w-a | YLR217w | YNL205c | YPR077c |
| YDL062w | YGL024w | YIL071w-a | YLR230w | YNL226w | YPR087w |
| YDL068w | YGL042c | YIL100c-a | YLR232w | YNL228w | YPR092w |
| YDL071c | YGL052w | YIL156w-a | YLR252w | YNL235c | YPR099c |
| YDL094c | YGL072c | YIL163c | YLR261c | YNL266w | YPR126c |
| YDL151c | YGL074c | YIL171w-a | YLR269c | YNL276c | YPR130c |
| YDL152w | YGL088w | YIR017w-a | YLR279w | YNL296w | YPR136c |
| YDL158c | YGL102c | YIR023c-a | YLR280c | YNR005c | YPR142c |
| YDL172c | YGL109w | YJL009w | YLR282c | YNR025c | YPR146c |
| YDL187c | YGL118c | YJL015c | YLR294c | YOL013w-a | YPR150w |
| YDL221w | YGL132w | YJL022w | YLR302c | YOL013w-a | YPR177c |
| YDR008c | YGL149w | YJL032w | YLR317w | YOL035c | YBR090c* |
| YDR034c-a | YGL152c | YJL067w | YLR322w | YOL037c | YER014c-a* |
| YDR048c | YGL165c | YJL086c | YLR334c | YOL099c | YLR202c* |
| YDR053w | YGL168w | YJL120w | YLR339c | YOL106w | |
| YDR094w | YGL177w | YJL135w | YLR358c | YOL134c |
Of the 340 ORFs listed, 337 are intronless and three are intron-containing (marked with *). Note that of the 340 ORFs listed, statistically, four actually code for proteins. Unfortunately, we cannot identify them at present due to the limited recognition accuracy achieved.
The four quantities TP, TN, FP and FN mentioned above can be calculated, based on the sensitivity, specificity and the gene-recognition result obtained. The calculation for recognizing genes of the 2nd ~ 5th class ORFs in the MIPS database should be performed first. The total number of ORFs to be recognized is 2710, of which 2276 and 434 are recognized as coding and non-coding, respectively. We have a set of four equations as follows: TP/(TP + FN) = 0.95; TN/(TN + FP) = 0.95; TP + FP = 2276 and TN + FN = 434. Solving the above set of equations, we find TP ≈ 2259; TN ≈ 315; FP ≈ 17 and FN ≈ 119. The number of real coding ORFs should be equal to TP + FN ≈ 2378. Of the 434 ORFs recognized as non-coding, statistically, 119 (FN) are actually coding. Next, the calculation for the 6th class ORFs in the MIPS database should be performed. The total number of ORFs to be recognized is 439, of which 99 and 340 are recognized as coding and non-coding, respectively. In this case, the set of four equations consists of: TP/(TP + FN) = 0.95; TN/(TN + FP) = 0.95; TP + FP = 99 and TN + FN = 340. Solving this set of equations, we find TP ≈ 81; TN ≈ 336; FP ≈ 18 and FN ≈ 4. The number of real coding ORFs should be equal to TP + FN ≈ 86. Of the 340 ORFs recognized as non-coding, statistically, four (FN) are actually coding.
Based on the above results, we re-estimate the number of protein coding genes in the 16 yeast chromosomes. The total number should be equal to the number of intronless genes in the 1st class (2958) + the number of intron-containing genes in the 1st class (223) + the number of coding ORFs in the 2nd ~ 5th classes (including intronless and intron-containing genes) recognized by the present algorithm (2378) + the number of coding ORFs in the 6th class (including intronless and intron-containing genes) recognized by the present algorithm (86). The final result is 5645. Considering the fact that the actually sensitivity and specificity are >95% (see Table 1), the above estimate should be considered as an upper limit. Note that the above number (5645) does not include the mitochondrial genes. The estimate that the total number of the nuclear protein coding genes in the yeast genome is ≤5645 conflicts with the previous estimate of 5800–6000 genes (10–12).
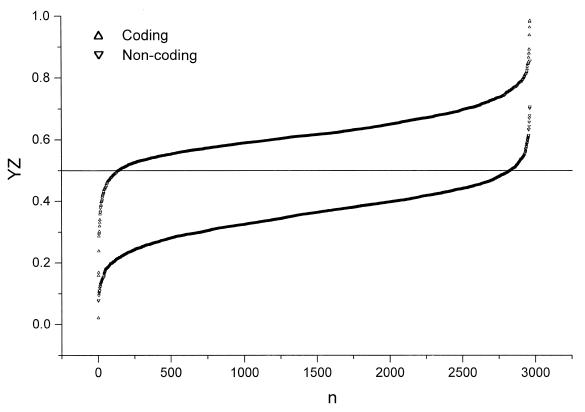
The YZ score for each ORF annotated in the MIPS database is calculated. The distribution of the YZ scores for the 2958 genes classified as ORFs of the 1st class in the MIPS database is shown in Figure 1. Here the y-axis indicates the YZ scores, whereas the x-axis indicates the rank number of ORFs, arranged according to the increasing order of the YZ scores. For comparison, the YZ scores for 2958 negative samples (intergenic sequences) are also calculated. The corresponding plot is also shown in Figure 1. As can be seen, for most genes the points are situated above the threshold 0.5, denoted by a horizontal line, whereas for most intergenic sequences the points are situated below the threshold 0.5. This fact demonstrates the accuracy of the new algorithm in distinguishing between the two kinds of DNA sequences. Furthermore, the curves clearly displaying the above two distributions are shown in Figure 2. Both distribution curves are well fitted by normal distributions with a small overlapping area between them. For comparison, the curve displaying the distribution of YZ scores calculated for the 2669 ORFs of the 2nd ~ 5th classes in the MIPS database is also shown. This curve is also well fitted by a normal distribution. As can be seen, the third normal distribution curve is in between the former two, indicating that a fraction of the ORFs of the 2nd ~ 5th classes are actually non-coding. This observation is in agreement with the data listed in Table 3.
Figure 1.
Distribution of the YZ scores for the 2958 protein coding genes of the 1st class in the MIPS database. Here the y-axis indicates the YZ scores, whereas the x-axis indicates the rank number of ORFs, arranged according to the increasing order of the YZ scores. For comparison, the YZ scores for 2958 negative samples (intergenic sequences) are also calculated and the corresponding curve is shown here. As can be seen, for most genes the points are situated above the threshold 0.5, denoted by a horizontal line, whereas for most intergenic sequences the points are situated below the threshold 0.5. This fact demonstrates the accuracy of the new algorithm in distinguishing between the two kinds of DNA sequences.
Figure 2.
Distribution curves showing the YZ score distributions for 2958 genes and 2958 intergenic sequences in the yeast genome, respectively. Here the x-axis indicates the YZ score, whereas the y-axis indicates the probability of the genes or intergenic sequences with the YZ score annotated on the x-axis. Both curves are well fitted by normal distributions with a small overlapping area between them. For comparison, the distribution curve showing the YZ score distribution calculated for the ORFs of the 2nd ~ 5th classes in the MIPS database, is also shown. This curve is also well fitted by a normal distribution. Note that the third normal distribution curve is in between the former two, indicating that a fraction of the ORFs of the 2nd ~ 5th classes are actually non-coding.
On the mystery of orphan ORFs
There are more than 7000 ORFs longer than 300 bp in the yeast genome (4). For some of them, known as orphan ORFs (17,18), neither their function nor homology is known. With the increase in known genes, more orphans should be found to have homologous relationships with the known genes and, as a result, the number of orphans should decrease. In fact, this is not the case. This paradox was deemed as a mystery of orphans (17,18). However, the results presented in this paper give some insight into the problem. According to the classification of ORFs in the MIPS database, orphans are mainly assigned to the 5th class (no similarity) and the 6th class (questionable, including no similarity to other ORFs). As can be seen from Table 5, of the 805 ORFs in the 5th class, 193 (24%) are non-coding. Furthermore, of the 439 ORFs in the 6th class, 340 (77%) are non-coding. In other words, more than 500 orphans or partially overlapping ORFs are actually not protein-coding genes. After removing these ORFs from the list of orphans in the MIPS database, there remain some real orphans which may be true protein-coding genes whose functions and homology need to be explored.
Table 5. The percentages of non-coding ORFs of the 2nd ~ 6th classes recognized by the present algorithm, over the total numbers of ORFs in the classes.
| Class | 2 | 3 | 4 | 5 | 6 |
| Total ORFs | 248 | 869 | 789(1)a | 805 | 447(8)a |
| Percentage of non-coding ORFs | 19/248 = 7.7% | 85/869 = 9.8% | 137/788 = 17.4% | 193/805 = 24.0% | 340/439 = 77.4% |
aFigures in parentheses indicate the numbers of mitochondrial ORFs in this class.
We should emphasise that the present work is based on an assumption that has not been clearly elucidated previously. The claim of <5% error is valid only when all of the unknown genes have the same statistical properties as the known genes. As pointed out by an anonymous referee, this obviously will not be the case, especially for the ORFs in the 6th class. Some genes tend to have low expression levels and many of them will only express in extreme conditions. Since they are under-represented in the training sample (i.e., in the ORFs of the 1st class), they would mostly be predicted to be non-coding. One would not be surprised if many of the ‘non-coding’ ORFs predicted in Table 4 later turn out to be coding. Therefore, based on this consideration, the predictive error for the ORFs in the 6th class would be >5%. We remind readers that the results listed in Table 4 should be referred to with caution.
It will be very interesting to see if most or many ORFs listed in Table 4 will be experimentally verified to be functional genes in the future. If the answer is yes, we have to say that the DNA sequences coding for these genes have different statistical properties with those coding for genes of the 1st class in the MIPS database. Alternatively, if the answer is no, the statistical properties for both the 1st and 6th class ORFs should be similar. To avoid the inherently circular argument, we have compared the distributions of bases at the first and second codon positions for the 1st and 6th class ORFs in the MIPS database with those of other species, specifically human, Escherichia coli, etc. One cannot simply compare the base distributions at the third codon position between different species, because the distributions are species-dependent (19). Consequently, we have found that the distributions of bases at the first and second codon positions for the 1st class ORFs in the MIPS database of the yeast genome show considerable similarity to those of genes for other species. In contrast, the distributions of bases at the first and second codon positions for the 6th class ORFs are not only remarkably different from those of the 1st class ORFs, but are also remarkably different from those of genes from other species. It is thought that the distributions of DNA bases at the first and second codon positions reflect the need for native folding of proteins (19). Based on this consideration, it is unlikely that most or many ORFs listed in Table 4 code for proteins.
Acknowledgments
ACKNOWLEDGEMENTS
Stimulating discussions with Ren Zhang are acknowledged. We are grateful to both referees for their comments, which were very useful in improving the paper. The present study was supported in part by the 973 Project grant G1999075606 of China.
REFERENCES
- 1.Bennetzen J.L. and Benjamin,D.H. (1982) J. Biol. Chem., 257, 3026–3031. [PubMed] [Google Scholar]
- 2.Sharp P.M. and Li,W.-H. (1987) Nucleic Acids Res., 15, 1281–1295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Dujon B., Alexandraki,D., Andre,B., Ansorge,W., Baladron,V., Ballesta,J.P., Banrevi,A., Bolle,P.A., Bolotin-Fukuhara,M., Bossier,P. et al. (1994) Nature, 369, 371–378. [DOI] [PubMed] [Google Scholar]
- 4.Mackiewicz P., Kowalczuk,M., Gierlik,A., Dudek,M.R. and Cebrat,S. (1999) Nucleic Acids Res., 27, 3503–3509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zhang C.-T. and Zhang,R.(1991) Nucleic Acids Res., 19, 6313–6317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zhang R. and Zhang,C.-T. (1994) J. Biomol. Struct. Dyn., 11, 767–782. [DOI] [PubMed] [Google Scholar]
- 7.Zhang C.-T. (1997) J. Theor. Biol., 187, 297–306. [DOI] [PubMed] [Google Scholar]
- 8.Zhang C.-T., Lin,Z.-S., Yan,M. and Zhang,R. (1998) J. Theor. Biol., 192, 467–473. [DOI] [PubMed] [Google Scholar]
- 9.Yan M., Lin,Z.-S. and Zhang,C.-T. (1998) Bioinformatics, 14, 685–690. [DOI] [PubMed] [Google Scholar]
- 10.Goffeau A., Barrel,B.G., Bussey,H., Davis,R.W., Dujon,B., Feldmann,H., Galibert,F., Hoheisel,J.D., Jacq,C., Johnston,M., Louis,E.J., Mewes,H.W., Murakami,Y., Philippsen,P., Tettlin,H. and Oliver,S.G. (1996) Science, 274, 546. [DOI] [PubMed] [Google Scholar]
- 11.Winzeler E.A. and Davis,R.W. (1997) Curr. Opin. Genet. Dev., 7, 771–776. [DOI] [PubMed] [Google Scholar]
- 12.Mewes H.W., Albermann,K., Bahr,M., Frishman,D., Gleissner,A., Hani,J., Heumann,K., Kleine,K., Maierl,A., Oliver,S.G., Pfeiffer,F. and Zollner,A. (1997) Nature, 387 (Suppl.), 7–8. [DOI] [PubMed] [Google Scholar]
- 13.Cornish-Bowden A. (1985) Nucleic Acids Res., 13, 3021–3030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Mardia K.V., Kent,J.T. and Bibby,J.M. (1979) Multivariate Analysis. Academic Press, London, UK.
- 15.Burset M. and Guigo,R. (1996) Genomics, 34, 353–367. [DOI] [PubMed] [Google Scholar]
- 16.Burge C. and Karlin,S. (1997) J. Mol. Biol., 268, 78–94. [DOI] [PubMed] [Google Scholar]
- 17.Casari G., de Druvar,A., Sander,C. and Schneider,R. (1996) Trends Genet., 12, 244–255. [DOI] [PubMed] [Google Scholar]
- 18.Dujon B. (1996) Trends Genet., 12, 263–270. [DOI] [PubMed] [Google Scholar]
- 19.Zhang C.-T. and Chou,K.C. (1994) J. Mol. Biol., 238, 1–8. [DOI] [PubMed] [Google Scholar]