Abstract
Family-based association methods such as the transmission/disequilibrium test (TDT) have become very popular during the past few years, often being preferred to case-control studies because family-based approaches avoid the difficulties of ascertainment of appropriate populations of cases and controls for case-control studies. Significant TDT results indicate both linkage and allelic association. However, significant TDT results are often interpreted as implying tight linkage of marker and disease locus, and we shall argue here that, in general, this interpretation is not justified.
There has been considerable recent interest in the possibility of localization of loci contributing to disease predisposition, by using their allelic association with marker loci. This could be done by population-based association studies, but the difficulties in the ascertainment of appropriate populations of cases and controls—and, in particular, concerns about the effect of population stratification on such studies—have contributed to a growing interest in the use of family-based association tests (e.g., see Risch and Merikangas 1996; Curnow et al. 1998; Schaid 1998). These tests have the attractive property of testing the compound null hypothesis of no linkage or no association. A significant result thus suggests both population association with the disease and linkage of the locus under study to a disease locus. When considered as tests of linkage, these tests therefore have the nominal false-positive rate even in the presence of population stratification; indeed, population stratification is often seen as beneficial for these tests, since it increases the allelic association present and, thus, the power to detect linkage (Ewens and Spielman 1995; Kaplan et al. 1998).
However, it is common to interpret a significant result from a family-based association test as implying tight linkage between the locus under study and a disease locus—for instance, in the analysis of candidate loci—by arguing that, if this were not so, recombination would have eroded any initial association between the loci. This is probably true if the initial association is purely due to shared ancestry, unless the mutation is very recent (Kruglyak 1999; but also see Ott 2000); but it may not be true in the presence of population stratification, for example. We argue here that this implies that significant results from family-based association tests may be due to a combination of association and loose linkage; this has important implications both for the analysis of data by use of family-based association tests and for the ongoing debate about the relative advantages of family-based and population association studies.
We shall concentrate on perhaps the best known family-based association test, the transmission/disequilibrium test (TDT) of Spielman et al. (1993), but our general conclusions are valid for any family-based association test, such as the extended TDT (ETDT [Sham and Curtis 1995]) and the score tests introduced by Schaid (1996). We consider a sample of N families, each with a single affected child, in which all individuals have been genotyped at a marker locus with alleles M1 and M2 and in which the parental alleles transmitted to the affected child are recorded as shown in table 1.
Table 1.
Types of Transmission
|
Result When Nontransmitted Allele Is |
||
| Transmitted Allele | M1 | M2 |
| M1 | n11 | n12 |
| M2 | n21 | n22 |
The TDT statistic is then (n12-n21)2/(n12+n21). We shall assume that there is a disease locus with alleles D1 and D2 located at recombination fraction θ from this marker. Since only parents heterozygous at the marker locus contribute to the TDT statistic, the properties of the test for given parameter values and a fixed number of heterozygous parents are determined by the probability that a heterozygous parent transmits an M1 allele to the affected child, which we denote by “τ.”
Let γC be the proportion of M1M2 parents of affected children who are D1D2 heterozygotes with the M1 and D1 alleles in coupling phase—that is, on the same chromosome—and let τC be the probability that such a parent transmits an M1 allele to the affected child. Similarly, let γR be the proportion of M1M2 parents of affected children who are D1D2 heterozygotes with the M1 and D1 alleles in repulsion phase—that is, on different chromosomes—and let τC be the probability that such a parent transmits an M1 allele to the affected child. The two marker alleles carried by parents homozygous at the disease locus are equally likely to be transmitted, so we see that τ=.5(1-γC-γR)+τCγC+τRγR. Consider a coupling-phase parent who transmits a D1 allele: such a parent also will transmit an M1 allele, unless a recombination event occurs. Similarly, transmission of a D2 allele will imply transmission of an M2 allele unless a recombination event occurs. Thus, if the probability that a D1 allele is transmitted from a D1D2 parent to an affected child is ρ, we have τC=(1-θ)ρ+θ(1-ρ) and, by an identical argument, τR=(1-θ)(1-ρ)+θρ. Putting all this together gives
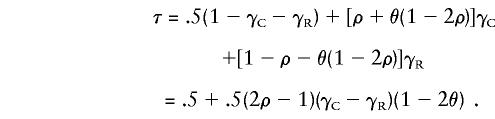 |
Here, ρ is dependent on the disease model and the disease-allele frequencies, whereas γC and γR depend on the association between marker and disease, in addition to being dependent on the disease model and disease-allele frequencies, but neither ρ, γC, nor γR depends on θ. Since our primary interest here is in θ, we replace the nuisance parameters ρ, γC, and γR by a single parameter, η=.5(2ρ-1)(γC-γR), describing the association between marker and disease, and so τ=.5+η(1-2θ). Note that, since τ is a probability and thus τ∈[0,1] for all θ∈[0,.5], we must have η⩽.5 also. A value of η=.5 would be given, for example, by a recessive disease with no phenocopies and complete association between marker and disease alleles, since, then, ρ=1, γC=1, and γR=0. Less-extreme disease models or incomplete association between marker and disease alleles will give lower values of η and, therefore, lower values of τ.
If the disease model is multiplicative at the marker locus—that is, the risk of an individual getting the disease is the product of the contributions to risk for the individual’s alleles—alleles are transmitted from the two parents in the family independently, and so the probabilities given here will apply to any individual with the appropriate genotype. For other disease models, parental transmissions are not independent (Bickeböller and Clerget-Darpoux 1995), and therefore the probability, for example, of an M1M2 individual transmitting the M1 allele depends on the allele transmitted from the other parent. The marginal probabilities given above are still correct, but now they represent an averaging over possible partners for the individual under consideration. We mention this point here solely for the sake of completeness: it does not affect the remainder of our argument.
A contour plot for τ is given, for η∈[0,.5] and θ∈[0,.5], in figure 1. It is clear from figure 1, together with the expressions for τ above, that the same transmission probabilities can arise from a number of different values of η and θ. In particular, strong association and loose linkage will be indistinguishable from weak association and tight linkage; in fact, we can see from figure 1 that, for a given η, we get very similar values for τ, with both θ=0 and, for example, θ=.1. It follows that we cannot infer tight linkage from significant TDT results unless there is other evidence to suggest that the possibility of association and loose linkage can be excluded. This is perhaps best seen in figure 2, which shows the power of the TDT as a function of the recombination fraction θ and parameter η, for a sample of 50 heterozygous parents and a significance level of 5%. Similar results are obtained for other combinations of parameter values.
Figure 1.
Contour plot of the probability that a heterozygous parent transmits an M1 allele to the affected child, τ, against recombination fraction θ and η, a measure of association between disease and marker.
Figure 2.
Power of TDT against recombination fraction θ and η, a measure of association between disease and marker
It would therefore seem sensible to consider the possibility that a marker is loosely linked with a disease locus but that, because of population stratification, for instance, sufficient association exists to give significant TDT results. The importance of population stratification as a mechanism for the generation of allelic associations has been much debated. However, it is clear that population stratification is a potential cause of association between marker alleles and disease, and this is often given as the motivation for using a family-based rather than a case-control design. Associations arise where marker-allele frequencies and disease prevalence vary among population subgroups. Often the difference in prevalence is assumed to be due to variation, in some environmental factor, between the population subgroups, but this is not of relevance here; neither are we concerned with variations in prevalence that are due to variation in allele frequency at disease loci unlinked to the marker under study. We are concerned solely with associations due to variation in allele frequency at disease loci loosely linked to the marker. To determine the frequency of such associations, we would need to make assumptions both about the influence of the disease loci and about the association between marker and disease locus. Here we merely note that population stratification can give rise to substantial allelic associations: for example, Chakraborty and Weiss (1988) found that recent admixture can give high levels of association in loci up to 10 cM apart, and Pritchard and Rosenberg (1999) relied on associations between unlinked marker loci as a method of detection of population stratification. More information on the distribution of allelic association due to population structure would be most helpful, given the current interest in the use of family-based association tests for fine-scale mapping.
We have concentrated on the TDT statistic, but our remarks apply equally to any other family-based association test, including multiallelic extensions such as the ETDT (Sham and Curtis 1995) and the score tests introduced by Schaid (1996). For multiallelic marker loci, the association and linkage parameters determining the table of transmission probabilities are no longer completely confounded as in the diallelic case discussed above: in principle, it would be possible to estimate θ and the allelic-association parameters from this table by maximization of an appropriate likelihood. In practice, however, the likelihood is very flat with respect to θ, and so it remains virtually impossible to distinguish, solely on the basis of such data, between tight and loose linkage. Such a difficulty is also relevant in the application of Bayesian approaches to the problem, since the flatness of the likelihood with respect to θ will tend to make the resulting posterior distribution highly sensitive to the prior distribution used. It is, of course, possible to estimate θ if a number of markers have been typed in the region of interest and an appropriate multipoint method (e.g., see McPeek and Strahs 1999) is used, because multipoint methods rely on modeling the erosion, over a number of generations, of association by recombination. However, these methods are reliant on the detection, over a small chromosomal region, of an association pattern characteristic of the presence of a disease locus and, therefore, also are affected by population stratification, although to what extent is as yet unclear. Any population-history information that is available will be valuable in the assessment of the possible impact of population stratification on association-based methods, whether these are multipoint or single point.
In summary, we cannot distinguish, using family-based association tests alone, strong association and loose linkage from weak association and tight linkage. Thus, for example, a significant result at a candidate locus may be due to relatively loose linkage of that locus to a disease locus, rather than confirming the direct influence of the candidate on the disease. This can easily be seen by noting that, to test for linkage, all family-based association tests rely on recombinations occurring in a single generation and, therefore, are incapable of distinguishing between tight and loose linkage. However, this point does not seem to be widely appreciated at present.
References
- Bickeböller H, Clerget-Darpoux F (1995) Statistical properties of the allelic and genotypic transmission/disequilibrium test for multiallelic markers. Genet Epidemiol 12:577–582 [DOI] [PubMed] [Google Scholar]
- Chakraborty R, Weiss KM (1988) Admixture as a tool for finding linked genes and detecting that difference from allelic association between loci. Proc Natl Acad Sci USA 85:3071–3074 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Curnow RN, Morris AP, Whittaker JC (1998) Locating genes involved in human diseases. Appl Stat 47:63–76 [Google Scholar]
- Ewens WJ, Spielman RS (1995) The transmission/disequilibrium test: history, subdivision, and admixture. Am J Hum Genet 57:455–464 [PMC free article] [PubMed] [Google Scholar]
- Kaplan NL, Martin ER, Morris RW, Weir BS (1998) Marker selection for the transmission/disequilibrium test, in recently admixed populations. Am J Hum Genet 62:703–712 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruglyak L (1999) Prospects for whole-genome linkage disequilibrium mapping of common disease genes. Nat Genet 22:139–144 [DOI] [PubMed] [Google Scholar]
- McPeek MS, Strahs A (1999) Assessment of linkage disequilibrium by the decay of haplotype sharing with application to fine scale genetic mapping. Am J Hum Genet 65:858–875 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ott J (2000) Predicting the range of linkage disequilibrium. Proc Natl Acad Sci USA 97:2–3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard JK, Rosenberg NA (1999) Use of unlinked markers to detect population stratification in association studies. Am J Hum Genet 65:220–228 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Risch N, Merikangas K (1996) The future of genetic studies of complex human diseases. Science 273:1516–1517 [DOI] [PubMed] [Google Scholar]
- Schaid DJ (1996) General score tests for associations of genetic markers with disease using cases and their parents. Genet Epidemiol 13:423–449 [DOI] [PubMed] [Google Scholar]
- ——— (1998) Transmission disequilibrium, family controls, and great expectations. Am J Hum Genet 63:935–942 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sham PC, Curtis D (1995) An extended transmission/disequilibrium test (TDT) for multi-allele marker loci. Ann Hum Genet 59:323–336 [DOI] [PubMed] [Google Scholar]
- Spielman RS, McGinnis RE, Ewens WJ (1993) Transmission test for linkage disequilibrium: the insulin gene region and insulin-dependent diabetes mellitus (IDDM). Am J Hum Genet 52:506–516 [PMC free article] [PubMed] [Google Scholar]




