Abstract
Single particle tracking is a powerful tool for probing the organization and dynamics of the plasma membrane constituents. We used this technique to study the μ-opioid receptor belonging to the large family of the G-protein-coupled receptors involved with other partners in a signal transduction pathway. The specific labeling of the receptor coupled to a T7-tag at its N-terminus, stably expressed in fibroblastic cells, was achieved by colloidal gold coupled to a monoclonal anti T7-tag antibody. The lateral movements of the particles were followed by nanovideomicroscopy at 40 ms time resolution during 2 min with a spatial precision of 15 nm. The receptors were found to have either a slow or directed diffusion mode (10%) or a walking confined diffusion mode (90%) composed of a long-term random diffusion and a short-term confined diffusion, and corresponding to a diffusion confined within a domain that itself diffuses. The results indicate that the confinement is due to an effective harmonic potential generated by long-range attraction between the membrane proteins. A simple model for interacting membrane proteins diffusion is proposed that explains the variations with the domain size of the short-term and long-term diffusion coefficients.
INTRODUCTION
The full understanding of the mechanism of the signal transduction mediated by the G-protein-coupled receptors still requires the unraveling of the dynamic organization of these multimolecular systems in cell membranes. To date, a large amount of information has been published regarding this question and evidence has now been accumulated for nonrandom distribution and collision of the receptors, protein G, and effectors. A compartmentation of the receptors and/or the other partners was suggested as accounting for the rapidity and specificity of signaling (Neubig, 1994; Ostrom et al., 2000), but experimental studies devoted to the question of the membrane organization and dynamics of the components of this signal transduction pathway are still very scarce.
Recently, the single particle tracking (SPT) technique was developed allowing observation of the movements of individual membrane proteins or lipids at the cell surface with nanometer spatial resolution (Saxton and Jacobson, 1997). A submicrometer particle (colloidal gold or fluorescent latex) is specifically attached to the molecule of interest. The displacement of the particle recorded by videomicroscopy exhibits the movement of the labeled molecule. Careful analysis of the trajectories is required to distinguish between the possible different modes of motion and can reveal submicroscopic or larger membrane structures. This method is certainly the most promising to address the question of the mechanism of membrane-associated functions (Jacobson et al., 1995; Cherry et al., 1998).
In the present study we address the question of the lateral diffusion of the receptor as part of the mechanism of the signal transduction mediated by G-protein-coupled receptors. The principal objectives of this work were, first, to characterize the movements of the receptor and identify an eventual compartmentation, and second, to give a simple physical interpretation for the observed behaviors leading to a consistent model for the membrane organization around the receptors. We chose to study the μ-opioid receptor, target of many analgesic drugs including opiates, as a complementary approach to the efforts in our laboratory directed to the global understanding of the signaling mechanisms of this receptor (Capeyrou et al., 1997; Lagane et al., 2000). Experiments were carried out on a μ-opioid receptor tagged with a T7 phage capsid protein at its amino-terminal extracellular domain allowing for the labeling by 40 nm gold colloids bearing T7-tag antibodies. The tagged receptors were tracked at the surface of normal rat kidney (NRK) fibroblast cells, chosen for their morphological characteristics suitable for single particle tracking experiments, where they were stably expressed and functional. We followed the movements of the receptors during 2 min with a 40 ms time resolution and a 15 nm spatial resolution. The μ-opioid receptors were found to exhibit two different classes of diffusion. A slow or directed diffusion mode and a mode superimposing a long-term random diffusion with a short-term confined diffusion consisting of a diffusion confined within a domain that itself diffuses, what we call the walking confined diffusion. A thorough statistical analysis of the trajectories supports the image that the confinement seen here is of dynamical nature and does not involve the presence of fences as invoked in the membrane skeleton fence model (Kusumi et al., 1993).
MATERIALS AND METHODS
Reagents
Bovine serum albumin (BSA) (fraction V, protease free) was from Sigma-Aldrich (St. Louis, MO). Antibiotics G418 sulfate, penicillin, streptomycin, and fetal calf serum were from Gibco BRL (France). Gold colloids 40 nm in diameter were supplied by British Biocell International (UK). The T7-tag monoclonal antibody was from Novagen (Madison,WI), and its dissociation constant Kd = 2 × 10−12 M as measured by surface plasmon resonance on a Biacore 3000. All chemicals used were of analytical grade.
Conjugation of the gold colloids
The preparation of gold colloids bearing a number of antibodies close to one was necessary for the SPT experiments. The minimal stabilizing concentrations of T7-tag antibody and BSA, required to stabilize the gold colloid suspension and to coat the colloids by one monolayer of protein, were determined as described previously (Goodman et al., 1981). These concentrations were found to be 2.6 μg/ml of antibody and 40 μg/ml of BSA for a 9 × 1010 particles/ml suspension of gold colloids in 2 mM glycine buffer at pH 8.5. The colloids used in the experiments were prepared by incubating the gold suspension with 1% and 99% of the minimal stabilizing concentrations of antibody and BSA, respectively. An aliquot of the gold colloids suspension was first resuspended in 2 mM glycine buffer, pH 8.5, and dispersed in a sonication bath before mixing with an identical volume of a solution containing the antibody and BSA in the same buffer. After incubation at 4°C for 1 h, the unbound antibody and BSA in excess were eliminated by two steps of consecutive centrifugation (20 min at 5000 × g, 4°C) and resuspension in glycine buffer. The suspension of conjugated colloids was then kept at 4°C and used within five days (monodispersity was checked by transmission electron microscopy). Making the hypothesis that the fraction of coated surface is equal to the fraction of the minimal stabilizing concentration for the antibody and BSA, and that the proportion of bound antibody relative to the total amount of antibody is equal to 1/3 as determined by protein assay for BSA at the minimal stabilizing concentration, the number of antibody molecules conjugated to each colloid in this condition was statistically less than two.
Cell culture
NRK-μ cell line, obtained by the stable transfection of NRK cells, have 20,600±1500 μ-opioid receptors per cell as determined by μ-specific agonist binding, and the receptors were shown to have appropriate pharmacological properties (manuscript in preparation). Cells were maintained in Dulbecco's modified Eagle's medium supplemented with 7% fetal calf serum, 100 IU/ml penicillin, 100 μg/ml streptomycin, 2 mM glutamine, and 0.4 mg/ml G418 sulfate. One or two days before the microscopic observations, cells were plated onto sterile 22 mm × 22 mm coverslips at a cell density yielding isolated or small groups of cells (120,000 cells for a 30 mm cell culture dish).
Labeling of the cells
The cells on the coverslip were carefully rinsed twice with 2 ml of phosphate-buffered saline (PBS), and 60 μl of the conjugated colloids, resuspended at least 12 h before in PBS, 1% BSA, and 10 mM Hepes, pH 7.6, were deposited on the coverslip, then kept on ice for 45 min. After incubation, the coverslip was inverted on a microscope glass slide coated with parafilm, including a hole of 10 mm diameter constituting an observation chamber of depth of around 120 μm. The preparation was sealed with fingernail polish and placed on the stage of the microscope. The duration of observation was limited to 30 min per preparation to guarantee that the cells do not exceed their survival time.
Three different tests of the specificity were made. The transfected NRK-μ cells were incubated with 100% BSA conjugated colloids and with antibody/BSA conjugated colloids in the presence of an excess of free antibody (factor of 1000). The wild-type NRK cells were incubated with antibody/BSA conjugated colloids.
Nanovideomicroscopy
Imaging of the colloids on the cells was in majority performed by video-enhanced differential interferential contrast microscopy at room temperature (22 ± 1°C) and additional observations were made at 37°C. The microscope (Axioplan II, Zeiss) was equipped with a condenser lens (NA = 0.9) and an oil-immersion ×63 objective (Plan-Neofluar, NA = 1.4). An additional 4× magnification was provided by an intermediate lens projecting the image on a CCD camera (C2400-75i, Hamamatsu). An image processor (Argus 20, Hamamatsu) allowed the real-time subtraction of the background and contrast enhancement. The processed image was recorded at video rate (25 frames/s) on a numerical videotape recorder (DSR30P, Sony) and further digitized by means of a workstation equipped with a real-time acquisition board (Intergraph workstation with 8 Go hard disk, DPS Hollywood acquisition board, and 18 Go SCSI-RAID hard disk, IEC, France).
Tracking of the colloids
Single particle tracking experiments have to be carried out not only on flat but also poorly contrasted regions of the cell to make the automatic detection of the gold colloids feasible. Thus, the perinuclear region was avoided because of its slope and the large quantity of organelles it contains. The lamellipodial regions were used for most experiments (∼90% of the video recordings) and some could be performed over the nucleus when it offered a flat portion of the plasma membrane with a low contrasted background. Before digitization the videotapes were viewed to eliminate the recordings performed on cells, which showed a visible retraction during the observation and which would have led to erroneous results.
The numerical images were analyzed using a home-made software written using Optimas (6.2 version, MediaCybernetics, Silver Spring, MD). The position of a colloid was determined from the pixel weighted center of gray of the dark portion of the colloid, the contour of which being automatically detected by a threshold function. For each sequence of images, a region of interest roughly centered on the tracked colloid was manually selected and the calculation was performed inside this region for each image of the sequence yielding to the trajectory of the tracked colloid.
To estimate the accuracy of our setup with respect to the determination of the particle position, we recorded a sequence of 12,000 images (8 min) of several colloids deposited on a coverslip and immobilized in a 15% polyacrylamide gel. The standard deviations of the colloids coordinates were found to increase with time indicating a limitation due to a thermomechanical instability of the microscope. Considering the size of the colloids (diameter 40 nm), an average standard deviation not exceeding 15 nm was satisfactory for our experiments on cells. This condition fixed the maximal duration of the recordings to 2 min (3000 images) for which the standard deviations σx = 6.5 nm and σy = 19 nm were found. Let us note that the use of the cross correlation method developed by Gelles et al. (1988), gave identical results. From the trajectories obtained for the immobilized colloids we determined, by fitting the corresponding mean-square displacement (MSD) versus time plot with the equation expected for random diffusion, i.e., MSD(t) = 4 Dt (Berg, 1983), the lower limit for the diffusion coefficient, which was found to be equal to 3 × 10−13 cm2/s.
Trajectory analysis
Once the trajectories had been determined from overall recordings, we considered only those that were more than 90% complete. The analysis of the trajectories relied on the calculation for each of the trajectories of the MSD as a function of the time interval nδt according to the equation (Qian et al., 1991; Kusumi et al., 1993):
 |
(1) |
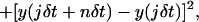 |
where δt is the time interval between two successive frames (δt = 40 ms), x(t) and y(t) are the colloid coordinates at time t, N is the total number of frames, and n is the number of time intervals. To maximize the precision in the long-range MSD, we restricted the calculation to intervals smaller than N/10 (Qian et al., 1991).
In addition to this standard MSD analysis, we also carried out the same analysis but on consecutive subintervals of single trajectories, to see if there was any evolution with the total time of the experiment.
Furthermore, the histograms of the displacements x (t + nδt) − x(t) and y(t + nδt) − y(t) were also constructed for various short time intervals nδt to establish the existence of any short time local equilibriation on these timescales.
FRAP measurements
Fluorescence recovery after photobleaching (FRAP) measurements were carried out at room temperature under conditions of constant incident light intensity and uniform disk illumination in an epifluorescence microscope (Lopez et al., 1988) equipped with an argon ion laser (488 nm). The radius of the bleached and observation area was 1.05 μm and the time of observation was ∼300 s.
RESULTS
Specific labeling of the μ-opioid receptor by gold colloids
The specificity of the receptor labeling was ensured by the use of a monoclonal antibody against the T7-tag at the N-terminal of the receptor as a link between the receptor and the colloidal gold probe. Increasing evidence suggests that the oligomerization of the G-protein-coupled receptors plays a role in the G-protein-coupled receptor signaling and regulation (Hébert and Bouvier, 1998; Overton and Blumer, 2000). Consequently it was important for our study to avoid as far as possible a multiple labeling, i.e., the possibility of tracking a probe attached to several receptors. So, we coated the gold colloids with statistically less than two antibody molecules per bead and stabilized the particles with one monolayer of BSA. Moreover, to limit the nonspecific binding of the coated colloids at the cell surface, BSA (1%) was added to the incubation buffer.
An evaluation of the specificity of the binding was performed by counting the gold colloids attached to the surface of the cells under various conditions. For each condition, the average number of fixed colloids per cell was calculated in duplicate by the examination of ∼50 cells per preparation. An average of nine particles conjugated with T7-tag antibody and BSA per cell were found on the transfected NRK-μ. The specific particle binding was inhibited in the presence of an excess of free antibody. In this case, it decreased close to the average level of 0.27 particle/cell found for the nonspecific binding conditions: BSA-coupled colloids on the NRK-μ and untransfected NRK cells as well as the antibody/BSA-coated colloids on the untransfected NRK cells (cf. Table 1). Thus, with a relative proportion of ≈3% of nonspecific binding, these results indicate a high specificity of the binding of the μ-opioid receptor with the antibody/BSA gold colloids.
TABLE 1.
Average number of colloids attached per cell on untransfected and NRK-μ cells for various coatings of the gold particles
| Average number of colloids bound per cell
|
|||
|---|---|---|---|
| Cells | Antibody/BSA gold | BSA gold | Antibody/BSA gold + excess free antibody |
| NRK | 0.30 | 0.30 | — |
| NRK-μ | 9.00 | 0.24 | 0.24 |
The average number of colloids bound to the NRK-μ cells is close to the lower limit of the values between 10 and 100 reported in other works (Sako and Kusumi, 1994; Sheets et al., 1997; Sako et al., 1998; Tomishige et al., 1998). An interesting comparison can be made with the results obtained by Sako and Kusumi (1994) for the transferrin receptor on untransfected NRK cells where the expression rate was found to be ∼200,000 sites per cell (value determined for human fibroblasts by Ward et al., 1982). In similar conditions of incubation and with 100% transferrin-coated colloids, the authors found ∼100 particles/cell. Considering that the expression level of the transferrin receptor is larger by a factor of ∼10 as compared to that of the μ-opioid receptor in the NRK-μ cells studied here and considering the differences in particle surface coverage by the transferrin and the T7-tag antibody, our findings are quite comparable.
Determination of different diffusional behaviors of the receptor
SPT data analysis, which consists of sorting and characterizing the various modes of motion, is a difficult task due to the lack of a priori knowledge of statistical fluctuations. This problem is made worse in case of limited duration or time resolution of the trajectories. To date, a universal analysis method is still lacking, and each laboratory uses a distinct method to classify the trajectories into different diffusion modes: normal, anomalous, directed, or confined (Saxton and Jacobson, 1997). Cherry and colleagues (Wilson et al., 1996; Smith et al., 1999) determined for each trajectory the best fit of the calculated MSD with the analytical expressions for the different diffusion modes. These authors also fitted the experimental histograms of the distance moved as a function of the time interval averaged over all tracks on a cell by standard forms for the probability distribution. Feder et al. (1996), classified the trajectories according to the anomalous diffusion exponent determined from the log-log plot of the MSD versus time. Two other analysis tools proceed by the evaluation of the deviation of the experimental data from a random diffusion behavior. One developed by Kusumi et al. (1993), allows for the classification of the complete trajectories between three modes: directed, random, and restricted diffusion. Another method that allows for the detection of temporary confinement, based on the theoretical work of Saxton (1993), was developed by Simson et al. (1995). In combination with the classification of the short-term trajectories by means of the shape of the MSD = f(t) plot, they used D (calculated from the initial slope of the MSD versus time plot) and certain characteristics derived from the radius gyration tensor for the analysis of long-term trajectories (Simson et al., 1998).
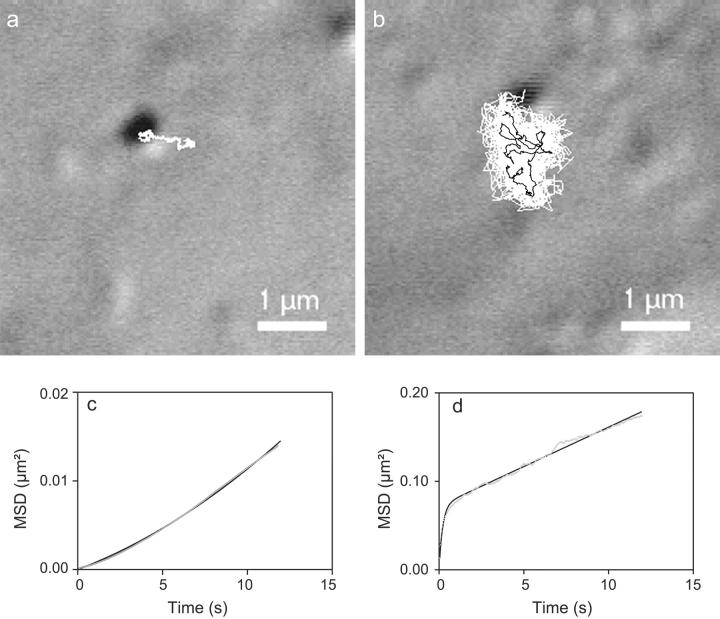
Our experimental data, consisting of trajectories of 2 min duration at 25 frames/s, contain potentially much information. So, before making the choice of a method of analysis, we proceeded with the examination of the trajectories and the associated MSD versus time plots. Two different types of movement could be clearly distinguished by the eye among the trajectories. Either the particles moved very slowly (Fig. 1 a) or they exhibited a rapid diffusion apparently restricted to a region of size of ∼1 μm (Fig. 1 b). The corresponding MSD versus time plots were also clearly different in shape. One set of plots showed straight or slightly curved lines as expected for simple or directed diffusion (Fig. 1 c). The other MSD versus time plots exhibited a tendency to a more or less complete saturation possibly due to the superposition of a short-term confined diffusion with a more or less efficient long-term random walk (Fig. 1 d). This statistical behavior can arise via different physical mechanisms; therefore it is necessary to carry out a further statistical analysis of the trajectories (beyond the MSD fit) to identify the most consistent scenario. Our subsequent analysis and modelization show that the minimal physical picture explaining this statistical behavior is that of a diffusion confined within a domain that itself diffuses. Shown in Fig. 1 b in black is the diffusive trajectory of the domain evaluated by time averaging the particle position over 4 s periods, during which the domain diffusion itself is negligible. We call this a walking confined diffusion, where “walking” refers to the macroscopic diffusion of the domain. To start with, to classify the statistical behavior of the various trajectories rigorously and extract the corresponding diffusional parameters, we systematically determined, by using a nonlinear least mean-square regression algorithm (Prism, Graphpad, San Diego, CA), which equation gave the best fit of the MSD versus time plots between
 |
(2) |
for a directed diffusion (Qian et al., 1991) where D is the diffusion coefficient and v the drift or transport velocity, and
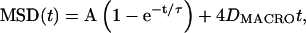 |
(3) |
the sum of the equations for a confined diffusion and a random walk where DMACRO is the long time diffusion coefficient. The first term in Eq. 3 is the generic form for a confined diffusion where the constants A and τ are determined by the mechanism of confinement (barriers, tether, or effective potential, …). However, A is the characteristic area of the confined region given by the equilibrium value of the squared distance r2 between two points on a trajectory in the interior of the domain separated by a time greater than τ, the equilibriation time:
 |
(4) |
where L is the characteristic length of the domain. If the transport inside the domain is dominated by a diffusion with a diffusion coefficient Dmicro, then
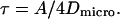 |
(5) |
FIGURE 1.
Video-enhanced differential interferential contrast images of gold colloids attached to the lamellipodial region of NRK-μ cells with the associated 2-min-long trajectories shown as an overlay (white line). Two types of movement were observed: (a) slow displacement and (b) apparently restricted rapid diffusion with the slow long-term component shown in black (see text). Below each image the corresponding mean-square displacement (MSD) versus time plot (gray line) is reported and its theoretical fit (black line) for the associated diffusion mode (c) slow or directed diffusion (see Eq. 2) and (d) walking confined diffusion (see Eq. 3).
As illustrated in Fig. 1, c and d, the quality of the fit was satisfactory (correlation coefficient r > 0.95) for slow or directed diffusion and walking confined diffusion MSD versus time plots. Let us point out that out of the 101 trajectories established from the video recordings, three trajectories clearly exhibited a transition from a walking confined diffusion mode to a slow or directed diffusion mode, and two trajectories had MSD versus time plots that could be well fitted only by the equation for an anomalous diffusion MSD(t) = 4Dtϕ with ϕ ∼0.7 (Bouchaud and Georges, 1990). Consequently, among the 96 retained trajectories, we found that 91% of the receptors exhibited the walking confined diffusion behavior whereas the 9% left had a slow or directed diffusion.
Statistical analysis of the trajectories according to Kusumi et al. (1993), was further performed to control for which trajectories one could effectively exclude the hypothesis of a simple random diffusion. We found that 100% of the trajectories that are correctly fitted by Eq. 3 (walking confined diffusion) clearly deviate from a random walk. Among the trajectories exhibiting directed or slow diffusion, 25% were distinguishable from random walks, hence classified as directed diffusion, whereas the remaining 75% were not (as expected, because the corresponding velocities determined were very small) and were thus classified as slow diffusion.
Microscopic diffusion coefficient
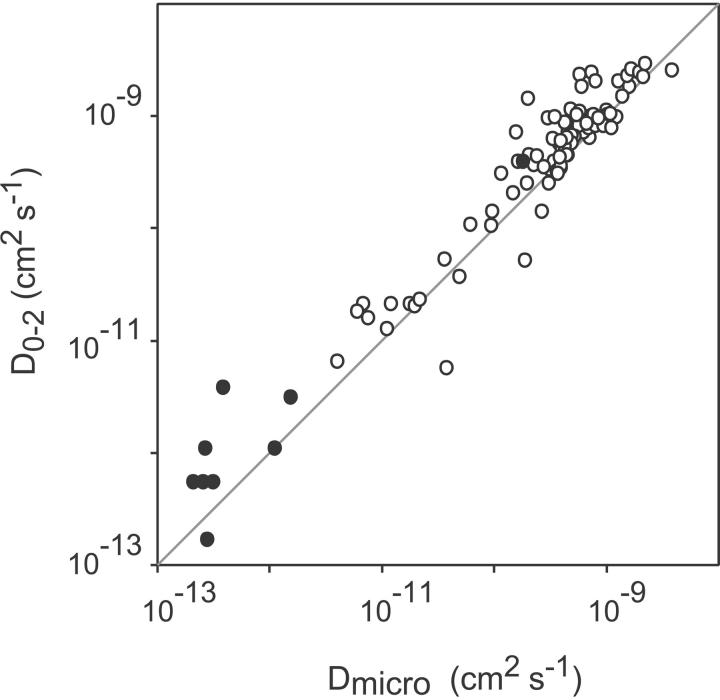
The microscopic diffusion coefficient Dmicro, which can be determined independently of the diffusion mode, characterizes the movement of the molecule of interest in its immediate neighborhood at a submicrometer scale. Its value depends on the composition of the local environment, the size of the intramembranous part of the molecule itself, and eventual extramembranous interaction (e.g., with the cytoskeleton). It is determined from the slope of the MSD versus time plot at the origin assuming that the slope is equal to 4Dmicrot. By zooming at the origin the MSD versus time plots, we observed that the majority of the plots exhibited a significant curvature after the second data point. So, in our investigation, the microscopic diffusion coefficient designated as D0-2 was obtained by fitting the first two points at δt and 2δt by a straight line extrapolating at 0 (cf. Fig. 2). For the slow or directed diffusion mode, the microscopic diffusion coefficient is equal to D, the diffusion coefficient of the random walk's contribution to Eq. 2, as the diffusion coefficient of a random walk is independent of the timescale. In the case of the walking confined diffusion mode, the microscopic diffusion coefficient is the diffusion rate of the receptors within the domains given by Dmicro in Eq. 5. The log-log plot of D0-2 as a function of D and Dmicro (Fig. 3) shows an excellent agreement over the whole range of values covering five decades, between D0-2 on the one hand and D and Dmicro on the other hand. This result strongly validates a posteriori the method (detailed in the precedent subsection) that we used to analyze and classify the trajectories.
FIGURE 2.
MSD versus time plot at short time interval showing the determination of D0-2, the microscopic diffusion coefficient. D0-2 is calculated from the slope of the straight line connecting 0–2δt using MSD(t) = 4D0-2t. For this experiment, D0-2 = 9.3 × 10−10 cm2/s.
FIGURE 3.
Plot of the microscopic diffusion coefficients D0-2 against Dmicro derived from the plot of the MSD versus time by the slope at the origin for D0-2 and by the fit with the theoretical expressions for Dmicro. The points are aligned on a straight line of slope 1 showing a good correlation between D0-2 and Dmicro for slow or directed diffusion (•) and walking confined diffusion (○).
Fig. 4 shows the histogram of the distribution of the microscopic diffusion coefficient D0-2. As indicated in the graph, the lowest values of D0-2, D0-2 < 5 × 10−12 cm2/s, characterize the receptors with a slow or directed diffusion mode (with the exception of one data point). The receptors exhibiting a walking confined diffusion mode have 5 × 10−12 ≤ D0-2 ≤ 4 × 10−9 cm2/s.
FIGURE 4.
Histogram showing the distribution of the microscopic diffusion coefficient D0–2. The dashed line separates the populations found in slow or directed diffusion (black bars) and walking confined diffusion modes (white bars).
Slow and directed diffusion modes
The fit by Eq. 2 of the MSD associated to the particles showing a slow or directed diffusion mode gave the following results:
 |
 |
where the error on v is the standard deviation. The small values of the diffusion coefficients and the range of magnitude of the velocity are quite comparable to those found for various proteins when they are attached to the cytoskeleton (Sheetz et al., 1989; de Brabander et al., 1991; Felsenfeld et al., 1996; Wilson et al., 1996; Sako et al., 1998). All the observations leading to a slow or directed diffusion mode have been made on the lamellipodial region of the cells, so the involvement of a binding to the cytoskeleton, which is known to have a rearward centripetal movement in these regions of fibroblasts (Wang, 1985) is the most reasonable interpretation for our results. In the absence of evidence for a direct binding between the receptor and the actin filaments, it is more likely that the receptors apparently linked to the cytoskeleton are located within clathrin-coated pits attached to the membrane skeleton (Gaidarov et al., 1999). The clathrin-coated pits have been clearly identified as the predominant pathway for the internalization of many G-protein-coupled receptors (Tsao and von Zastrow, 2000). Hence, the receptors exhibiting here the slow or directed diffusion mode are probably in course of internalization, which is undoubtedly extremely slow at the experimental temperature (Cao et al., 1998).
Walking confined diffusion mode
The receptors exhibiting a walking confined diffusion had MSD versus time plots well fitted by the sum of the equations for short-term confined and long-term random diffusion (Eqs. 3–5). Concerning the microscopic diffusion coefficient, the maximum of the distribution of the values is about 10−9 cm2/s (Fig. 4), close to the value measured by SPT of gold-labeled lipids on cell membranes: D ≈ 1.1–1.7 × 10−9 cm2/s (Lee et al., 1993). This is an indication that, in this case, the receptors are surrounded mainly by lipids, at least in the short term corresponding to the timescale of the measurement of D0-2. Indeed, in a dilute regime, with an average seven rings of lipids per protein, the lateral diffusion coefficient of bacteriorhodopsin within a lipid bilayer has been found of the same order as that of the lipids (Peters and Cherry, 1982).
The distribution of the values of the macroscopic diffusion coefficient DMACRO, which characterizes the apparent long-range diffusion of the domains, is bell-shaped with a mean value (close to that at the maximum of the distribution peak) of 1.3 ± 2.4 × 10−11 cm2/s (error is the standard deviation) (data not shown). To check for the consistency of this estimation of the macroscopic diffusion coefficient with that obtained by FRAP, we labeled the receptors using a fluorescein isothiocyanate-Fab fragment against the primary anti-T7 antibody. Due to the moderate expression rate of μ-opioid receptor in the NRK-μ cells, the fluorescence level was too low to run the experiments under proper conditions with our equipment. Thus, we used a Chinese hamster ovary μ-cell line expressing the same T7-tagged μ-opioid receptor at a higher rate (280,000 receptors per cell). A long-term diffusion with D = 5 ± 2 × 10−11 cm2/s was observed consistent with the SPT determination. Furthermore, these values are consistent with the macroscopic diffusion coefficient DMACRO = 3.3 × 10−11 cm2/s determined from the slope at long term of the average MSD versus time plot of long-term trajectories for the transferrin and α2-macroglobulin receptors in NRK cells (Sako and Kusumi, 1994).
The histogram of the distribution of the size of the domains determined for the receptors undergoing walking confined diffusion is shown in Fig. 5. The data are distributed over a broad range going from 0.02 to 0.55 μm with a mean size (±SD) of the domains equal to 0.15 ± 0.10 μm. Confined diffusion has been detected in many SPT experiments, and domain sizes have been determined for different proteins in various cell types. Interestingly, our findings can be compared to those obtained with a 40 nm gold labeling on fibroblastic cells (Simson et al., 1998; de Brabander et al., 1991; Sako and Kusumi, 1994). Taking into account the differences in the mode of determination of the domain size from one author to another, the values found ranging from 0.175 to 1 μm are compatible with those determined in the present study.
FIGURE 5.
Histogram showing the distribution of the characteristic domain size L: the average value of L is 0.15 ± 0.10 μm.
Both the microscopic and macroscopic diffusion coefficients were found to increase with increasing sizes of the domains. Taking the trajectories altogether, the log-log plot of the microscopic diffusion coefficient D0-2 as a function of the domain size L, as determined by the fit with Eq. 3 of the MSD of the complete trajectories, reveals a quadratic dependence of D0-2 on L : D0-2 ∼ L2 (Fig. 6). The variation of the macroscopic diffusion coefficient as a function of L reported as a log-log plot on Fig. 6 is also compatible with a quadratic dependence of DMACRO on L : DMACRO ∼ L2.
FIGURE 6.
Plots of the microscopic and macroscopic diffusion coefficients D0-2 and DMACRO against the characteristic domain size L. The two sets of points are both aligned on straight lines of slope 2 showing that D0-2 ∼ L2 and DMACRO ∼ L2.
Then the question was to determine the origin of the confinement for the walking confined diffusion trajectories. For this, we established for each trajectory the histograms of the distribution of x(t + nδt) − x(t) for nδt between 0–1 s and 0–4 s (Fig. 7). The lower time interval was chosen to be several times the equilibriation time τ (estimated from Eq. 5) to ensure that the equilibrium distribution is well sampled. The largest interval was determined (depending on the trajectory) by the time over which the distance diffused by the domain (with DMACRO) is significantly smaller than the domain size. The normalized histograms taken over these ranges of time intervals superimpose. This supports the hypothesis that the diffusion is composed of an equilibrated confined component within a domain, which itself diffuses with a diffusion coefficient DMACRO, which is at least an order of magnitude less than Dmicro. We found an excellent fit with a Gaussian probability distribution for these histograms (Fig. 7) and the standard deviations were comparable for each normalized histogram (a pure Brownian motion would lead to a significant broadening of the distribution with increasing time). Exactly the same behavior was found for the histograms for y with similar standard deviations to that for x. A Gaussian equilibrium distribution is compatible with the existence of a simple isotropic harmonic effective potential leading to the confinement of the receptor Veff(r) = ½Kr2, where K characterizes the strength of the attraction toward the center of the domain and is given by K = kBT/A, where A = 2L2 used in the fit of the MSD plots by Eq. 3.
FIGURE 7.
Histograms of x(t + nδt) – x(t) for nδt between 0–1 s (black circles) and 0–4 s (gray circles) showing a Gaussian equilibrium distribution within the domain (Gaussian fits of the distributions are drawn in solid lines). One sees that there is no broadening of the Gaussian between 0–1 to 0–4 s, showing that the domain itself does not diffuse significantly on these time scales and that the system is equilibrated within the domain at timescales greater than 1 s.
The appearance of a harmonic potential is natural from general physics arguments. The receptor is subject to a potential due to interactions with objects (e.g., proteins) in the membrane. In general, this potential will be complex and difficult to determine. However, the receptor will be localized about the minimum of this potential. Generically, a potential about its minimum is of quadratic form. As long as the fluctuations about this minimum are not too large, the histogram seen will be Gaussian.
Experiments at physiological temperature
To ensure that the results obtained at 22°C are relevant, we performed SPT experiments at 37°C (PBS being replaced by Dulbecco's modified Eagle's medium). The duration of the analyzed sequences was reduced to 10 s due to enhanced thermomechanical instabilities. About 50 trajectories obtained from eight tracked particles were analyzed. The general features of the results are the same: one population has a simple or directed diffusion; another population has a walking confined diffusion or simply confined diffusion (the long-term random walk is not systematically detected for 10 s trajectories). Interestingly, deviations of the diffusion coefficients values and domain sizes from their values at 22°C are observed:
For the simple or directed diffusion mode, the average of D ∼5 × 10−11 cm2/s is higher than at room temperature where D < 5 × 10−12 cm2/s. This result is consistent with the enhanced diffusion of the clathrin-coated pits linked to the cytoskeleton in which the receptors are presumably localized.
For the walking confined diffusion mode, the average Dmicro = 1.3 × 10−10 cm2/s and average L = 0.075 μm are lower by a ratio, Dmicro(37°C) = Dmicro(22°C)/10 and L(37°C) = L(22°C)/2, roughly consistent with Dmicro ∼ L2 as seen at 22°C. DMACRO instead is found unchanged, but its determination, due to the short duration of the observations, cannot be considered reliable. Such a variation of Dmicro could be due to interactions that do not take place at room temperature (with scaffolding proteins?…). Let us point out that for the confined diffusion, a tendency to a decrease of Dmicro with temperature can be noted also in Kusumi's studies of the transferrin receptor, which found Dmicro = 7 × 10−2 μm2/s at 37°C (Sako and Kusumi, 1994) and Dmicro = 12 × 10−2 μm2/s at 25°C (Sako and Kusumi, 1995).
DISCUSSION AND CONCLUSION
A simple model to explain the walking confined diffusion
We were able to deduce from our results that the receptors are subject to an effective potential that confines them and are therefore probably in interaction with other proteins. A natural framework to discuss the effect of protein interactions on self diffusion is the Brownian or Langevin model (Van Kampen, 2001). At scales larger than the range of the short-range repulsive interactions, the motion of a receptor or protein can be modeled by the Langevin equation (see Abney et al. (1989), and references therein)
 |
(6) |
where 1 ≤ i ≤ N is the particle index and α the spatial index (here in two dimensions one may write Xi1 = Xi and Xi2 = Yi). μ is the mobility of the particle measuring the linear response of the particle to an applied external force. The particles interact via an effective pairwise potential V for length scales above which Langevin equation is valid. The term η is Gaussian white noise such that  . The noise magnitude Dmicro and coupling of the long-range forces depend on the protein concentration.
. The noise magnitude Dmicro and coupling of the long-range forces depend on the protein concentration.
The Einstein or fluctuation dissipation relation (Van Kampen, 2001) gives: Dmicro = kBTμ.
If the interaction is attractive, the particle system will tend to stay clumped together. In other words, any given particle will be confined in a region about the center of mass of the system defined by
 |
(7) |
(when the spatial indices are omitted, the equation is to be taken as vectorial.)
The form of the pairwise potential leads to the equation for Xc
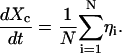 |
(8) |
Hence Xc undergoes pure diffusion and one finds
 |
(9) |
Hence if the local diffusion coefficient for a single protein is Dmicro, one expects that an assembly of such particles with attractive interactions diffuses with a macroscopic diffusion coefficient
 |
(10) |
On a smaller length scale, we must now address the evaluation of Dmicro and in particular its dependence on the protein concentration. The relation of protein self diffusion coefficient to the surrounding protein concentration is in general (except for very dilute almost ideal systems) an open question despite much theoretical work in this area (Scalettar and Abney, 1991). Here we present a simple heuristic argument in agreement with the few known experimental results on model membranes and also compatible with the findings of our experiments. If one assumes that the protein concentration is such that the self diffusion of proteins is dominated by pairwise interaction, the friction coefficient f (the inverse of μ) as a function of the protein concentration ρ should have the form
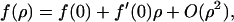 |
(11) |
where f(0) is the friction coefficient in the pure lipid membrane. If one assumes that this expansion is valid for large ρ, and that in the regime we are interested in the quadratic corrections are negligible, then we obtain
 |
(12) |
Now assuming that the second term in the denominator dominates, which means that pairwise protein interactions give the dominant contribution to the friction as compared to the lipid-protein interaction, we find
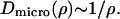 |
(13) |
The protein concentration is given by ρ = N/A, where N is the number of proteins in the region of confinement of effective area A. Thus we have
 |
(14) |
Making the basic assumption that a domain can vary in size—notably undergo contraction—whereas the proteins cannot leave the domain, that is to say that N remains constant, gives the dependence of Dmicro on A observed experimentally in this study.
Experimental data on lateral diffusion coefficient dependence on protein concentration are very scarce. However, we could test our simple model on the results of Peters and Cherry (1982) obtained for bacteriorhodopsin in lipid bilayers. A good fit of the variation of the protein diffusion coefficient as a function of the lipid/protein ratio was obtained for lipid/protein ratios superior to 30 (corresponding to two rings of lipids around the protein and hence where jamming effects should dominate).
The fact that we found a variation in the domain size from trajectory to trajectory suggested that the domain size itself may vary in time. To check this point, we examined the histograms of x(t + nδt) − x(t) and y(t + nδt) − y(t) for nδt between 0 and 1 s for the successive 5 s duration segments along the trajectories to detect any significant change in the fitted value of L (related to the halfwidth at half maximum of the distribution) between segments. We estimated a criterion for significant fluctuations to be where we found domain size variations by a factor of at least three. Fifteen trajectories exhibited such significant fluctuations of the domain size with time. Interestingly, the associated variation of D0-2(5 s) with L(5 s) measured in each successive 5 s segment followed the prediction above Eq. 14. We report in Fig. 8 one of the most instructive plots of D0-2(5 s) = f(L(5 s)) obtained for these trajectories.
FIGURE 8.
Plot of D0-2(5 s) as a function of L(5 s) extracted from a single trajectory over intervals of 5 s. The points are aligned on a straight line of slope 2 showing that D0-2(5 s) ∼L2(5 s).
Let us summarize the main points in the above arguments. The existence of a domain is due to the existence of long-range attractions between proteins. These attractions have the consequence that the collection of proteins diffuses as an ensemble with diffusion constant proportional to Dmicro/N. The short-range interactions between proteins determine the value of Dmicro as a function of local protein concentration. A simple argument and experimental evidence is compatible with Dmicro scales as 1/ρ. Assuming that the number of proteins in interaction within a domain is constant therefore explains fully the main experimental observations.
Ruling out other models
The observed apparent walk of the domains could rather be the signature of a “hopping” diffusion following the membrane-skeleton fence model proposed by Kusumi et al. (1993), based itself on earlier work on the red cell membrane (Sheetz, 1983; Tsuji et al., 1988). In this model, the authors suggested that the proteins are confined within compartments due to the collision of their cytoplasmic portion with the membrane skeleton network and that long-range diffusion occurs by successive jumps between adjacent compartments. Careful examination of the total of 87 trajectories we obtained in the walking confined diffusion mode allowed us to detect only a few jumps from one domain to another. To check this point more precisely, we plotted the “linear” trajectories x and y versus time (data not shown), which did not reveal more jumps.
More recently, a dynamic corral model was proposed for the regulation of the protein mobility by a stochastic gating mechanism of the corrals (Leitner et al., 2000). If it can describe the variation of DMACRO on L, it is insufficient to explain the behavior of Dmicro inasmuch as gating would lead to a Dmicro independent of the domain size (Gheber and Edidin, 1999).
So, at their present stage of development, the existing models of the dynamic organization of the cell membrane cannot explain our results.
CONCLUDING REMARKS
The most striking feature of our results is the demonstration that the diffusion of a membrane receptor can be confined inside a domain due to the existence of interactions between proteins in the absence of membranous or extramembranous fences. We were able to draw such conclusions from the detailed statistical analysis we performed of our SPT data, demonstrating the interest of going beyond a “simple” fit of the MSD versus time plots. We emphasize here that MSD fits alone do not allow one to distinguish between physically different microscopic models for the diffusion. The model we propose here is consistent with both the long time behavior of the trajectories (MSD measurements) and with their short time statistics (local equilibriation histograms). Moreover the numerical values obtained for the various fitting parameters are related in a simple way, which is also explained by our model.
Let us mention here that the results found in this paper support the ideas of Abney and Scalettar (1995), where membrane organization and heterogeneity are brought about by interprotein interactions rather than an imposed compartmentalization. Finally, the relevance of our model based on experiments performed at 22°C is confirmed by the consistency found with the measurements done at 37°C. Thus, a challenging question will be now to identify among all the possibilities, which are the interactions dominating the system and what is responsible for their regulation.
The recently suggested compartmentation of the G-protein-coupled receptors is confirmed by our data that show a confined diffusion component to the behavior of the receptor. However, a great deal of work is still needed to be able to establish the functional implication of such a behavior. In particular, the effect of the binding of a ligand on the diffusion properties will be very informative and is currently under study in our laboratory.
Acknowledgments
We are grateful to J.F. Tocanne for having initiated this project and for stimulating discussions. We thank D. Choquet for helpful advice during the setting up of the SPT device. The stably transfected NRK-μ cell line was established by M. Corbani and S. Ducasse.
This work was supported by the Nano-Objet Individuel program of the Centre National de la Recherche Scientifique and the Association pour la Recherche contre le Cancer.
References
- Abney, J. R., and B. E. Scalettar. 1995. Fluctuations and membrane heterogeneity. Biophys. Chem. 57:27–36. [DOI] [PubMed] [Google Scholar]
- Abney, J. R., B. E. Scalettar, and J. C. Owicki. 1989. Self diffusion of interacting membrane proteins. Biophys. J. 55:817–833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berg, H. C. 1983. Random Walks in Biology. Princeton University Press, Princeton, NJ. 5–12
- Bouchaud, J. P., and A. Georges. 1990. Anomalous diffusion in disordered media: statistical mechanisms, models and physical applications. Phys. Rep. 195:127–293. [Google Scholar]
- de Brabander, M., R. Nuydens, A. Ishihara, B. Holifield, K. Jacobson, and H. Geerts. 1991. Lateral diffusion and retrograde movements of individual cell surface components on single motile cells observed with nanovid microscopy. J. Cell Biol. 112:111–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao, T. T., R. W. Maysz, and M. von Zastrow. 1998. Regulated endocytosis of G-protein-coupled receptors by a biochemically and functionally distinct subpopulation of clathrin-coated pits. J. Biol. Chem. 273:24592–24602. [DOI] [PubMed] [Google Scholar]
- Capeyrou, R., J. Riond, M. Corbani, J. F. Lepage, B. Bertin, and L. J. Emorine. 1997. Agonist-induced signaling and trafficking of the μ-opioid receptor: role of serine and threonine residues in the third cytoplasmic loop and C-terminal domain. FEBS Lett. 415:200–205. [DOI] [PubMed] [Google Scholar]
- Cherry, R. J., P. R. Smith, I. E. G. Morrison, and N. Fernandez. 1998. Mobility of cell surface receptors: a re-evaluation. FEBS Lett. 430:88–91. [DOI] [PubMed]
- Feder, T. J., I. Brust-Mascher, J. P. Slattery, B. Baird, and W. W. Webb. 1996. Constrained diffusion or immobile fraction on cell surfaces: a new interpretation. Biophys. J. 70:2767–2773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felsenfeld, D. P., D. Choquet, and M. P. Sheetz. 1996. Ligand binding regulates the directed movement of b1 integrins on fibroblasts. Nature. 383:438–440. [DOI] [PubMed] [Google Scholar]
- Gaidarov, I., F. Santini, R. A. Warre, and J. H. Keen. 1999. Spatial control of coated-pit dynamics in living cells. Nat. Cell Biol. 1:1–7. [DOI] [PubMed] [Google Scholar]
- Gelles, J., B. J. Schnapp, and M. P. Sheetz. 1988. Tracking kinesin-driven movements with nanometer scale precision. Nature. 331:450–453. [DOI] [PubMed] [Google Scholar]
- Gheber, L. A., and M. Edidin. 1999. A model for membrane patchiness: lateral diffusion in the presence of barriers and vesicle traffic. Biophys. J. 77:3163–3175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodman, S. L., G. M. Hodges, L. K. Trejdosiewicz, and D. C. Livingston. 1981. Colloidal gold markers and probes for routine application in microscopy. J. Microsc. 123:201–213. [DOI] [PubMed] [Google Scholar]
- Hébert, T. E., and M. Bouvier. 1998. Structural and functional aspects of G-protein-coupled receptor oligomerization. Biochem. Cell Biol. 76:1–11. [DOI] [PubMed] [Google Scholar]
- Jacobson, K., E. D. Sheets, and R. Simson. 1995. Revisiting the fluid mosaic model of membranes. Science. 268:1441–1442. [DOI] [PubMed] [Google Scholar]
- Kusumi, A., Y. Sako, and M. Yamamoto. 1993. Confined lateral diffusion of membrane receptors as studied by single particle tracking (nanovid microscopy). Effects of calcium-induced differentiation in cultured epithelial cells. Biophys. J. 65:2021–2040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lagane, B., G. Gaibelet, E. Meilhoc, J. M. Masson, L. Cézanne, and A. Lopez. 2000. Role of sterols in modulating the human μ-opioid receptor function in Saccharomyces cerevisiae. J. Biol. Chem. 275:33197–33200. [DOI] [PubMed] [Google Scholar]
- Lee, G. M., F. Zhang, A. Ishihara, C. L. McNeil, and K. A. Jacobson. 1993. Pericellular matrix viscosity revealed by measuring the mobility of gold-tagged lipids. J. Cell Biol. 120:25–35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leitner, D. M., F. L. H. Brown, and K. R. Wilson. 2000. Regulation of protein mobility in cell membranes: a dynamic corral model. Biophys. J. 78:125–135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopez, A., L. Dupou, A. Altibelli, J. Trotard, and J. F. Tocanne. 1988. Fluorescence recovery after photobleaching (FRAP) experiments under conditions of uniform disk illumination. Biophys. J. 53:963–970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neubig, R. R. 1994. Membrane organization in G-protein mechanisms. FASEB J. 8:939–946. [DOI] [PubMed] [Google Scholar]
- Ostrom, R. S., S. R. Post, and P. A. Insel. 2000. Stoichiometry and compartmentation in G-protein-coupled receptor signaling: implications for therapeutic interventions involving Gs. J. Pharmacol. Exp. Ther. 294:407–412. [PubMed] [Google Scholar]
- Overton, M. C., and K. J. Blumer. 2000. G-protein-coupled receptors function as oligomers in vivo. Curr. Biol. 10:341–344. [DOI] [PubMed] [Google Scholar]
- Peters, R., and R. J. Cherry. 1982. Lateral and rotational diffusion of bacteriorhodopsin in lipid bilayers: experimental test of the Saffman-Delbrück equations. Proc. Natl. Acad. Sci. USA. 79:4317–4321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qian, H., M. P. Sheetz, and E. L. Elson. 1991. Single particle tracking. Analysis of diffusion and flow in two-dimensional systems. Biophys. J. 60:910–921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sako, Y., and A. Kusumi. 1994. Compartmentalized structure of the plasma membrane for receptor movements as revealed by a nanometer-level motion analysis. J. Cell Biol. 125:1251–1264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sako, Y., and A. Kusumi. 1995. Barriers for lateral diffusion of transferrin receptor in the plasma membrane as characterized by receptor dragging by laser tweezers: fence versus tether. J. Cell Biol. 129:1559–1574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sako, Y., A. Nagafuchi, S. Tsukita, M. Takeichi, and A. Kusumi. 1998. Cytoplasmic regulation of the movement of E-cadherin on the free cell surface as studied by optical tweezers and single particle tracking: corralling and tethering by the membrane skeleton. J. Cell Biol. 140:1227–1240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saxton, M. J. 1993. Lateral diffusion in an archipelago: single particle diffusion. Biophys. J. 64:1766–1780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saxton, M. J., and K. Jacobson. 1997. Single particle tracking: application to membrane dynamics. Annu. Rev. Biophys. Biomol. Struct. 26:373–399. [DOI] [PubMed] [Google Scholar]
- Scalettar, B. E., and J. R. Abney. 1991. Molecular crowding and protein diffusion in biological membranes. Comments Mol. Cell Biophys. 7:79–107. [Google Scholar]
- Sheets, E. D., G. M. Lee, R. Simson, and K. Jacobson. 1997. Transient confinement of a glycosylphosphatidylinositol-anchored protein in the plasma membrane. Biochemistry. 36:12449–12458. [DOI] [PubMed] [Google Scholar]
- Sheetz, M. P. 1983. Membrane skeletal dynamics: role in modulation of red cell deformability, mobility of transmembrane proteins, and shape. Semin. Hemattol. 20:175–188. [PubMed] [Google Scholar]
- Sheetz, M. P., S. Turney, H. Qian, and E. L. Elson. 1989. Nanometre-level analysis demonstrates that lipid flow does not drive membrane glycoprotein movements. Nature. 340:284–288. [DOI] [PubMed] [Google Scholar]
- Simson, R., E. D. Sheets, and K. Jacobson. 1995. Detection of temporary lateral confinement of membrane proteins using single-particle tracking analysis. Biophys. J. 69:989–993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simson, R., B. Yang, S. E. Moore, P. Doherty, F. S. Walsh, and K. A. Jacobson. 1998. Structural mosaicism on the submicron scale in the plasma membrane. Biophys. J. 74:297–308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith, P. R., I. E. G. Morrison, K. M. Wilson, N. Fernandez, and R. J. Cherry. 1999. Anomalous diffusion of major histocompatibility complex class I molecules on HeLa cells determined by single particle tracking. Biophys. J. 76:3331–3344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomishige, M., Y. Sako, and A. Kusumi. 1998. Regulation mechanism of the lateral diffusion of band 3 in erythrocyte membranes by membrane skeleton. J. Cell Biol. 142:989–1000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsao, P., and M. von Zastrow. 2000. Downregulation of G-protein-coupled receptors. Curr. Opin. Neurobiol. 10:365–369. [DOI] [PubMed] [Google Scholar]
- Tsuji, A., K. Kawasaki, S. Ohnishi, H. Merkle, and A. Kusumi. 1988. Regulation of band 3 mobilities in erythrocyte ghost membranes by protein association and cytoskeletal meshwork. Biochemistry. 27:7447–7452. [DOI] [PubMed] [Google Scholar]
- Van Kampen, N. G. 2001. Stochastic Processes in Physics and Chemistry. North-Holland, Amsterdam.
- Wang, Y. L. 1985. Exchange of actin subunits at the leading edge of living fibroblasts: possible role of treadmilling. J. Cell Biol. 101:597–602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ward, J. H., J. P. Kushner, and J. Kaplan. 1982. Transferrin receptors of human fibroblasts. Analysis of receptor properties and regulation. Biochem. J. 208:19–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson, K. M., I. E. G. Morrison, P. R. Smith, N. Fernandez, and R. J. Cherry. 1996. Single particle tracking of cell-surface HLA-DR molecules using R-phycoerythrin labeled monoclonal antibodies and fluorescence digital imaging. J. Cell Sci. 109:2101–2109. [DOI] [PubMed] [Google Scholar]