Abstract
The multivalent acidic phospholipid phosphatidylinositol 4,5-bisphosphate (PI(4,5)P2) plays a key role in many biological processes. Recent studies show that unstructured clusters of basic residues from a number of peripheral proteins can laterally sequester PI(4,5)P2 in membranes. Specifically, experiments suggest that the basic effector domain of the myristoylated alanine-rich C kinase substrate (MARCKS), or a peptide corresponding to this domain, MARCKS(151–175), sequesters several PI(4,5)P2 and that this sequestration is due to nonspecific electrostatic interactions. Here, we use the finite difference Poisson-Boltzmann method to test this hypothesis by calculating the electrostatic free energy of lateral sequestration of PI(4,5)P2 by membrane-adsorbed basic peptides: Lys-7, Lys-13, and FA-MARCKS(151–175), a peptide based on MARCKS(151–175). In agreement with experiments, we find that the electrostatic free energy becomes more favorable when: 1), Lys-13 and FA-MARCKS(151–175) sequester several PI(4,5)P2; 2), the linear charge density of the basic peptide increases; 3), the mol percent monovalent acidic lipid in the membrane decreases; and 4), the ionic strength of the solution decreases. In addition, the electrostatic sequestration free energy is in excess of the entropic penalty associated with localizing PI(4,5)P2. Our calculations, thus, provide a structural and quantitative description of the observed interaction of PI(4,5)P2 with membrane-adsorbed basic sequences.
INTRODUCTION
Phosphatidylinositol 4,5-bisphosphate (PI(4,5)P2 or PIP2) is the major poly-phosphoinositide in mammalian cells and exhibits a wide variety of functions related to its ability to interact with many different proteins: it plays key roles in the attachment of the cytoskeleton to the plasma membrane, membrane trafficking, and the activation of a diverse set of enzymes (De Camilli et al., 1996; Toker, 1998; Raucher et al., 2000; Cockcroft, 2000; Irvine, 2002; Martin, 2001; Payrastre et al., 2001; McLaughlin et al., 2002; Cantley, 2002; Yin and Janmey, 2003). It has been hypothesized that peripheral proteins that bind PIP2 at the surface of the plasma membrane may contribute to the regulation of PIP2 function by controlling its accessibility to other proteins (Laux et al., 2000; McLaughlin et al., 2002). Among the proteins that have been shown to interact with PIP2 is the myristoylated alanine-rich C kinase substrate (MARCKS), which uses a dramatic cluster of basic residues, termed its effector domain, to interact electrostatically with both monovalent acidic phospholipids and polyvalent phosphoinositides in the plasma membrane (Kim et al., 1994; McLaughlin and Aderem, 1995; Swierczynski and Blackshear, 1995; Laux et al., 2000; Wang et al., 2002). There are a number of other peripheral proteins that contain similar basic sequences that may be adsorbed to the plasma membrane surface (Wang et al., 2002); e.g., MacMARCKS (Blackshear, 1993), GAP43 (Laux et al., 2000), DAKAP200 (Rossi et al., 1999), and adducin (Matsuoka et al., 2000). All may be present in cells at high concentrations and could, therefore, potentially bind most of the cellular PIP2 (McLaughlin et al., 2002). Furthermore, all are protein kinase C (PKC) substrates, and PKC phosphorylation of serines within the basic regions of these proteins would result in the desorption of the basic clusters from the membrane surface and the subsequent release of PIP2. Indeed, recent studies show that MARCKS and peptides based on the basic effector domain of MARCKS, MARCKS(151–175), laterally sequester PIP2 and that the sequestration inhibits the hydrolysis of PIP2 by phospholipase C (PLC). Phosphorylation by PKC or binding of Ca2+/calmodulin displaces the effector domain from the membrane and releases the inhibition of PLC (Kim et al., 1994; Glaser et al., 1996; Arbuzova et al., 1998; Ohmori et al., 2000; Wang et al., 2001). Because PIP2 is a multivalent anionic lipid, its association with the membrane-adsorbed basic effector domain may be driven by electrostatic interactions (McLaughlin et al., 2002; Wang et al., 2002; Gambhir et al., 2004).
Recent experiments with a peptide based on the MARCKS effector domain, MARCKS(151–175), provide evidence that this may well be the case. Binding assays show that this peptide binds with high affinity to phospholipid vesicles containing PIP2 as the only acidic lipid (i.e., vesicles composed of PIP2 and phosphatidylcholine (PC); Wang et al., 2001, 2002; Rauch et al., 2002). In contrast to the PH domain of PLC-δ1, the peptide does not require PIP2 for membrane binding: it also binds with high affinity to membranes containing physiological concentrations of monovalent acidic lipids such as phosphatidylserine (PS) (i.e., to PC/PS vesicles). Spectroscopic techniques show that once the peptide is adsorbed to a PC/PS/PIP2 membrane, it laterally sequesters PIP2, even when the PS is present in excess of PIP2 (Gambhir et al., 2004). These experimental studies indicate that both the binding of peptides to PIP2-containing vesicles (i.e., PC/PIP2 vesicles) and the sequestration of PIP2 by membrane adsorbed basic peptides (i.e., on PC/PS/PIP2 vesicles) are driven by nonspecific electrostatic interactions: 1), increasing the ionic strength of the solution decreases the binding of basic peptides to PIP2-containing vesicles and abolishes sequestration; 2), PI(4,5)P2 and PI(3,4)P2 interact with basic peptides with the same affinity, indicating that the interactions are independent of the chemical nature of the phosphoinositide; 3), peptides comprised of the same number of Lys or Arg residues bind PIP2-containing membranes with the same affinity, indicating that the interactions are independent of the chemical nature of the basic residue as well; 4), peptides with high local positive charge density are able to sequester PIP2; and 5), a single peptide may laterally sequester several PIP2 simultaneously.
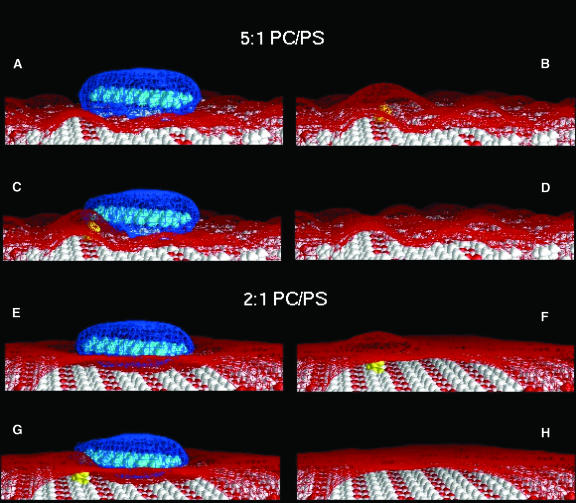
Because of the importance of membrane organization to many biological processes, it is of interest to understand how the membrane adsorption of basic sequences affects the electrostatic properties of membrane surfaces, which may consequently lead to lateral reorganization of PIP2 through an electrostatic mechanism. In this work, we provide a computational model for the sequestration of PIP2 by membrane-adsorbed basic peptides that is experimentally characterized in a companion paper (Gambhir et al., 2004). Our model, based on solutions to the Poisson-Boltzmann equation, explicitly tests the hypothesis that nonspecific electrostatic interactions are sufficient to drive the lateral accumulation of PIP2 by membrane-adsorbed basic sequences. Specifically, we use the finite difference Poisson-Boltzmann (FDPB) method (Davis and McCammon, 1990; Sharp and Honig, 1990b; Honig and Nicholls, 1995; Baker et al., 2001) with atomic models of PIP2, membranes and peptides (Fig. 1) to calculate the electrostatic free energy of laterally sequestering a PIP2 lipid from a region of “bulk” membrane (Fig. 1, A and B) to a region in the vicinity of a membrane-adsorbed basic peptide (Fig. 1, C and D). There are many examples of protein domains, e.g., PH, PX, FYVE, and ENTH domains, that contain basic regions that bind poly-phosphoinositides in a specific, 1:1 fashion (Lemmon, 2003). Here, we examine a different mode of PIP2 binding that is based on nonspecific interactions, which do not depend on structural detail and need not be 1:1. Rather, in this case, there may be a “many-to-one” interaction between several PIP2 lipids and one of many possible basic sequences (Wang et al., 2002; Rauch et al., 2002; Gambhir et al., 2004). Hence, establishing that nonspecific electrostatic interactions can provide enough energy to account for the experimentally observed partitioning supports the existence of a fundamentally different type of interaction between peripheral proteins and these important signaling lipids.
FIGURE 1.
The FDPB calculations of the electrostatic free energy of PIP2 sequestration, ΔGel(PIP2), are based on atomic-level models of the peptide/membrane system. The view is from above, looking down on an example of the peptide/membrane models used in our calculations. In the example illustrated here, the composition of the “bulk” membrane is 5:1 PC/PS. The peptide, Lys-13, is colored cyan, and the headgroups of PC, PS, and PIP2 are colored white, red, and yellow, respectively. Initially, membrane-adsorbed Lys-13 and PIP2 are infinitely far apart (A and B), and PIP2 is considered to be located in the bulk membrane phase, which contains ∼1 mol% PIP2. The arrow denotes the position to which the PIP2 will be sequestered. In the final state (C and D), PIP2 has moved, as suggested by the arrow in panels A and B, to a position adjacent to the membrane-adsorbed Lys-13 peptide. It is assumed that the presence of PIP2 does not affect the orientation of Lys-13 with respect to the membrane, i.e., in A and C, Lys-13 remains in its minimum electrostatic free-energy orientation as determined in the absence of PIP2. Panels A and B represent the initial state, and panels C and D represent the final state used in the calculation of ΔGel(PIP2) in Eq. 2.
Traditionally, the electrostatic properties of membrane systems have been described by smeared charge models based on Gouy-Chapman theory, which assumes that the charges due to both the acidic lipids and bound peptide are smeared uniformly over a planar membrane surface (McLaughlin, 1989). Previous experimental and theoretical work shows that “smeared charge” models have utility in providing quantitative descriptions when the shape and charge distribution of the molecules can be neglected (Kim et al., 1991; Heimburg and Marsh, 1996). However, simple smeared charge models are unable to describe the electrostatic properties of membrane surfaces that depend on localized effects produced by multivalent species, such as poly-phosphoinositides and clusters of basic residues on peptides and electrostatically polarized proteins. For example, our previous FDPB calculations on phospholipid bilayers with a high surface concentration of adsorbed basic peptides demonstrate that to describe the observed electrostatic properties of these systems, it is crucial to account for the molecular detail of the peptides (Murray et al., 1999). The FDPB method, through describing lipids and proteins in atomic detail, realistically depicts the complex electrostatic potential patterns that protein/membrane systems often produce as well as the desolvation effects that occur upon association of the interacting species. However, it makes a number of simplifying assumptions: 1), the solvent is represented as a dielectric continuum, i.e., a structureless aqueous phase; 2), the finite size of the salt ions as well as ion-ion correlation effects are ignored; and 3), the membrane and peptide are assumed to be static structures. A number of experimental approaches suggest that water molecules at the membrane surface may be treated in the continuum limit (reviewed in McLaughlin, 1989), and theoretical work has justified the assumptions related to salt ions for physiological conditions (Carnie and Torrie, 1984). By neglecting the dynamics of the systems we are studying, our models are not able to account for hydrogen bonding and other interactions that rely on structural detail. Hence, in terms of structural representation, it is intermediate between smeared charge models on the one hand, and molecular dynamics and Monte Carlo simulations on the other. Dynamical simulations are extremely valuable in depicting the short-time (< μs), detailed motions of lipids in a membrane environment (Pastor and Feller, 1996; Forrest and Sansom, 2000), but have been limited in their capacity to describe the electrostatic properties of membranes and protein/membrane systems (Tobias, 2001). The FDPB method has proved to be a reliable theoretical methodology for depicting the electrostatic free energies of interaction that occur in large, highly charged multicomponent systems, especially those involving high ionic strengths (Honig and Nicholls, 1995). Recently, an adaptive Poisson-Boltzmann (PB) solver has been developed (Baker et al., 2001) that allows for the calculation of the electrostatic properties of extremely large molecular assemblages (Elcock, 2002).
Several groups have modified smeared charge models to more realistically depict the charge distributions of membrane-adsorbing molecules and membrane surfaces (May et al., 2000, 2002; Haleva et al., 2004). These thermodynamic models predict that there is significant lateral redistribution of both monovalent and multivalent charged lipids in response to the membrane association of oppositely charged proteins. However, in this study, we assume, in agreement with the available experimental results, that monovalent acidic lipids are not appreciably sequestered by membrane-adsorbed basic peptides (Kleinschmidt and Marsh, 1997; Murray et al., 2002). As shown in Fig. 1, monovalent acidic lipids (red) remain distributed uniformly in the membrane, and only the redistribution of the biologically important PIP2 (yellow) is considered. Our computational models of the interactions of PIP2 and membrane-adsorbed basic peptides presented here, thus, provide insight into the lateral organization of these molecules by quantifying the role of electrostatics and by providing molecular models of the membrane-associated complexes.
METHODS
Finite difference Poisson-Boltzmann calculations: overview
Electrostatic potentials and free energies are obtained from a modified version of the DelPhi program (Gallagher and Sharp, 1998) that solves the nonlinear Poisson-Boltzmann equation for protein/membrane systems (Ben-Tal et al., 1996). DelPhi produces finite difference solutions to the Poisson-Boltzmann equation (the FDPB method) for a system where the solvent (plus 1:1 electrolyte, i.e., KCl) is described in terms of a bulk dielectric constant and mean concentrations of mobile ions, whereas large solutes (here, basic peptides) and lipids comprising the bilayer (e.g., PIP2) are described in terms of the coordinates of the individual atoms as well as their atomic radii and partial charges. The FDPB method has previously been shown to yield satisfactory agreement with experimental measurements of the binding of peptides and proteins to charged membranes (Ben-Tal et al., 1996, 1997; Murray et al., 1998, 2002; Arbuzova et al., 2000; Murray and Honig, 2002; Diraviyam et al., 2003).
In the calculations described in this work, each atom of a peptide/membrane system is assigned a radius and partial charge that is located at its nucleus. The molecular model is then mapped onto a three-dimensional cubic grid of l3 points, each of which represents a small region of the peptide, membrane, or solvent. The charges and radii used for the amino acids were taken from a CHARMM22 parameter set (Brooks et al., 1983); those used for the lipids are the ones described in Peitzsch et al. (1995) and were used in previous studies (Ben-Tal et al., 1996, 1997; Murray et al., 1998). The partial charges for PI(4,5)P2 were taken from similar functional groups from the CHARMM22 parameter set so that the net charge on the lipid headgroup is −4; it was assumed, in agreement with experimental evidence, that one of the oxygens in the phosphate group at position 5 of the inositol ring was protonated at physiological pH (McLaughlin et al., 2002). The molecular surfaces of the molecules are defined as the locus of points traced out by the inward facing surface of a spherical probe or radius 1.4 Å (the radius of a water molecule). Regions inside the molecular surfaces of the peptide and membrane are assigned a dielectric constant of 2 to account for electronic polarizability and those outside are assigned a dielectric constant of 80 (Sharp and Honig, 1990b). An ion exclusion layer is added to the solutes and extends 2 Å beyond the molecular surfaces (see, e.g., Fig. 3 of Ben-Tal et al., 1996). The nonlinear Poisson-Boltzmann equation is solved in the finite difference approximation, and the numerical calculation of the potential is iterated to convergence, which is defined as the point at which the electrostatic potential changes <10−4 kT/e between successive iterations. Electrostatic free energies are obtained from the calculated potentials (Sharp and Honig, 1990a).
FIGURE 3.
FDPB calculations suggest that the nonspecific electrostatic component of the sequestration of PIP2 from bulk membrane to positions within and around the imprint of a membrane-adsorbed basic peptide is significant. For each of the three peptides denoted, the black and gray bars represent the results for 2:1 and 5:1 PC/PS, respectively. The values plotted for 〈ΔGel(PIP2)〉 and ΔGS correspond to the mean of the Boltzmann factor-weighted averages calculated with the ΔGel(PIP2) values depicted in Fig. 2, and the error bars correspond to one standard deviation from the mean (see Methods for details). (A) The black and gray bars represent the average electrostatic free energy of sequestration, 〈ΔGel(PIP2)〉, and the white bars, above, represent the average free energy of PIP2 demixing, ΔGS, for the corresponding membrane containing 1 mol% PIP2. (B) The black and gray bars represent the average net energy, 〈ΔGel(PIP2)〉 + ΔGS.
Calculation of the electrostatic free energy of interaction of basic peptides with phospholipid membranes
The electrostatic free energy of interaction of a basic peptide associating with a phospholipid bilayer, ΔGel, is determined as the difference between the electrostatic free energy of the peptide docked at the surface of the membrane, Gel(P·M), and the electrostatic free energies of the peptide, Gel(P), and membrane, Gel(M), infinitely far apart, i.e., taken separately:
 |
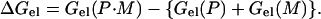(1) |
The electrostatic free energies in Eq. 1 are dependent on the size of the finite difference grid and the resolution or scale of the calculation through a grid-dependent electrostatic self-energy term due to the distribution of each partial charge onto the grid. To remove the self-energy contribution, it is necessary to ensure that the molecules and, thus, the fixed charges, have the same location on the grid in the initial and final states; this is true of the calculations with PIP2 described below. ΔGel was calculated as a function of the distance, R, of closest approach between the van der Waals surfaces of the peptide and membrane. These calculations defined the orientation of minimum electrostatic free energy for each of the basic peptides examined in this study.
Phosphatidylcholine (net charge of 0) and phosphatidylserine (net charge of −1) bilayers were built as described previously (Ben-Tal et al., 1996). The lipids were distributed uniformly in an hexagonal array and each lipid headgroup occupies an area of 68 Å2 in the plane of the membrane. Each leaflet of the bilayer contains 192 lipids so that the bilayers have lateral dimensions of ∼130 Å × 120 Å. The headgroup regions from the two opposing leaflets encompass ∼1/2 the thickness of the bilayer, which is 62 Å; in between resides the acyl chain portion of the lipids. It was assumed that the lipids change neither structure nor position upon interaction with a peptide. Previous work has shown that the membrane partitioning of a basic peptide that resides outside the polar envelope of the membrane, i.e., pentalysine, is independent of whether the membrane is in the liquid crystalline or gel phase, suggesting that the use of static bilayer models is appropriate for calculating the electrostatic free energy of their membrane interaction (Ben-Tal et al., 1996). Two types of PC/PS membranes were used in determining the electrostatic free energy of interaction of basic peptides with membranes: 5:1 and 2:1 PC/PS.
Three basic peptides were considered in this study: acetyl-Lys-7-amide, acetyl-Lys-13-amide, and acetyl-FA-MARCKS(151–175)-amide. FA-MARCKS(151–175) is a peptide based on the effector domain of MARCKS in which the five phenylalanines are replaced by alanine. It has the amino acid sequence: acetyl-KKKKKRASAKKSAKLSGASAKKNKK-amide. Experiments suggest that MARCKS(151–175) has an extended conformation both in solution and when associated with a membrane surface (Qin and Cafiso, 1996; Zhang et al., 2003). Due to electrostatic repulsions among the basic residues, Lys-13 and Lys-7 are expected to adopt extended conformations as well. The peptides were, therefore, built in extended form using the Insight/Biopolymer molecular modeling package (INSIGHT-II, Accelrys, San Diego, CA). To reduce atomic overlaps and to relax torsional and dihedral constraints, each peptide model was energy minimized using the Insight/Discover molecular modeling package (INSIGHT-II, Accelrys). The minimization consisted of 100 iterations with a conjugate gradient method in gas phase using the CVFF force field and neglecting electrostatic interactions. The minimization did not significantly alter the extended structure of the peptides. The Lys-7, Lys-13, and FA-MARCKS(151–175) peptide models have dimensions of 31 Å × 17 Å × 7 Å, 53 Å × 17 Å × 7 Å, and 97 Å × 18 Å × 7.5 Å and net charges of +7, +13, and +13, respectively. In the FDPB calculations, the plane of each peptide was kept parallel to the membrane surface and the vertical distance between the van der Waals surfaces of the peptide and membrane was varied. For the purpose of mapping the molecules onto the finite difference grid, the peptide was rotated about an axis perpendicular to the membrane surface such that the peptide has a diagonal orientation with respect to the grid to reduce the overall size of the system that needed to be considered. For example, by placing the peptide on a diagonal, the minimal size of a square that could accommodate a Lys-13 peptide was reduced from 53 to 42 Å2. The calculations were designed to determine the peptide orientation that produces close to the minimum free energy of electrostatic interaction with the membrane; this is the orientation considered throughout this study. Previous work has established that, for peripheral association, the electrostatic contribution to binding free energies is well described by consideration of the minimum free energy orientation alone (Ben-Tal et al., 1996, 1997; Murray et al., 1998; Arbuzova et al., 2000).
A sequence of focusing runs (Gilson et al., 1987) of increasing resolution was employed to calculate the electrostatic potentials. In the initial calculation, the peptide/membrane model encompassed a small percentage of the grid (∼10%) and the potentials at the boundary points of the grid are approximately zero; this procedure ensures that the system is electroneutral. The calculation of ΔGel for Lys-13 on a 2:1 PC/PS membrane in 0.1 M KCl employed focusing resolutions of 0.375, 0.75, 1.5, and 3.0 grid/A, each with a grid size of l3 = 2573. The precision in ΔGel is determined as the difference between the results obtained at the two highest resolution scales. This difference is much less than the value of the calculated free energy of interaction (<0.3 kcal/mol) for R > 1.5 Å and is ∼1–2 kcal/mol for R < 1.5 Å. Because the distance corresponding to the minimum electrostatic free energy is ∼2–2.5 Å, the orientations of minimum electrostatic free energy of interaction for the three peptides are well defined and reliable. The calculation of a full electrostatic free energy curve for Lys-13 on a 2:1 PC/PS membrane in 0.1 M KCl required 3 Gb of main memory and ∼80 h of CPU time on a Silicon Graphics Origin3400 (Mountain View, CA) with 500-MHz R14K processors. A tutorial on how to perform these calculations is available at our website: http://maat.med.cornell.edu/qnifft.html.
Basic peptides are placed in their minimum free-energy orientations at the surfaces of PC/PS membranes
Throughout this paper, we examine the electrostatic sequestration of PIP2 by three membrane-adsorbed basic peptides: Lys-7, Lys-13, and FA-MARCKS(151–175). We make the assumption that these peptides interact similarly with both PC/PS membranes and PC/PS membranes that contain PIP2, which is present at small concentrations (∼1%). In other words, it is assumed that the sequestration of PIP2 from “bulk” membrane to the vicinity of a membrane-adsorbed basic peptide does not change the membrane-associated state that the peptides are predicted to have in the absence of PIP2. In addition, in most of our calculations, we consider a single orientation of each peptide at the membrane surface, the orientation of minimum electrostatic free energy of interaction with pure PC/PS membranes as determined by the calculations described above. In all cases, the minimum electrostatic free energy of interaction occurred at distances, R, between the van der Waals surfaces of the peptide and membrane of ∼2.0–2.5 Å; throughout, we use R = 2.5 Å to depict the minimum free-energy orientation.
As shown in previous work on similar systems (Ben-Tal et al., 1996; Murray et al., 1998), a basic peptide experiences an increasing electrostatic attraction as it approaches the membrane surface from large distances. When the peptide is close to the membrane surface, the desolvation repulsion experienced by charged and polar groups on both the peptide and membrane dominates the electrostatic attraction. The balance of these two effects predicts that there is a minimum in the electrostatic interaction when the van der Waals surfaces of the peptide and membrane are separated by about the thickness of a layer of water (R ∼ 2.5 Å), i.e., when both molecules are essentially solvated. The exact location of these basic peptides has not been determined experimentally, but surface pressure measurements on monolayers show they do not penetrate the polar headgroup region, in contrast to peptides that contain both basic and aromatic residues. In all cases the minimum electrostatic free energy of interaction is predicted to be quite strong and ranges from −4 kcal/mol for Lys-7 and 5:1 PC/PS to −12 kcal/mol for Lys-13 and 2:1 PC/PS. In agreement with experiments (Ben-Tal et al., 1996), the electrostatic free energy of interaction becomes more favorable as the mol percent acidic lipid in the membrane increases and as both the number and density of basic residues in the peptide increases. An example of the minimum free-energy orientation of a peptide is depicted in Fig. 1 A where Lys-13 is docked parallel to and 2.5 Å above the surface of a 5:1 PC/PS membrane.
Calculation of the electrostatic free energy of the sequestration of a single PIP2 lipid by a membrane-adsorbed basic peptide
An example of the scheme followed for determining the electrostatic free energy of laterally sequestering a PIP2 from a region of bulk membrane to a region adjacent to or beneath a membrane-adsorbed basic peptide, ΔGel(PIP2), is illustrated in Fig. 1. The initial state of the system is composed of two equal-sized regions of membrane containing the same mol percent monovalent acidic lipid: one with a basic peptide (e.g., Lys-13) adsorbed to its surface (Gel(P·M); Fig. 1 A), and one with a single PIP2 lipid (Gel(PIP2·M); Fig. 1 B). Fig. 1, A and B, represent the situation in which PIP2 is “infinitely” far away from the membrane-adsorbed peptide. The final state of the system is also composed of two equal-sized regions of membrane containing the same mol percent monovalent acidic lipid: one with PIP2 in the vicinity of the membrane-adsorbed peptide (Gel(PIP2·P·M); Fig. 1 C), and one in the absence of PIP2 (Gel(M); Fig. 1 D). Fig. 1, C and D, represent the situation in which PIP2 is sequestered by the membrane-adsorbed basic peptide, leaving behind a region of bulk membrane. ΔGel(PIP2) is the difference between the electrostatic free energies of the models for the final state (Fig. 1, C and D) and the electrostatic free energies of the models for the initial state (Fig. 1, A and B) as determined by the FDPB method:
 |
(2) |
As described above for Eq. 1, it is necessary to ensure that the molecules remain in the same location on the finite difference grid in both the initial and final states to subtract out the grid-dependent electrostatic self-energy. ΔGel(PIP2) was calculated for many different locations of PIP2 with respect to the membrane-adsorbed peptides as illustrated in Fig. 2. The dependence of ΔGel(PIP2) on both the mol percent monovalent acidic lipid in the membrane (either 5:1 PC/PS or 2:1 PC/PS) and the ionic strength of the solution was calculated.
FIGURE 2.
FDPB calculations suggest that PIP2 can associate with a membrane-adsorbed basic peptide through nonspecific electrostatic interactions in many different ways. The view is from above, looking down on the membrane. The peptides, FA-MARCKS(151–175) (A and B), Lys-13 (C and D), and Lys-7 (E and F), are colored cyan. The ovals represent the positions of lipids in the membranes with respect to the peptides. Each number is the calculated electrostatic free energy, ΔGel(PIP2), in kcal/mol, for sequestering a PIP2 lipid from bulk membrane, either 2:1 PC/PS (A, C, and E) or 5:1 PC/PS (B, D, and F), to a given position, either adjacent to or beneath the peptide, as shown. The peptides are located in their minimum free-energy orientations determined in the absence of PIP2 (see Methods). The positions highlighted in bold are further investigated in subsequent figures.
Models for the Lys-7, Lys-13, and FA-MARCKS(151–175) peptides were built as described above. The peptides were docked at the surfaces of the PC/PS membranes in their minimum free-energy orientations determined in the absence of PIP2; i.e., it was assumed that the presence of PIP2 does not affect the membrane-associated states of the basic peptides. This assumption is reasonable because the minimum free-energy orientations of the peptides are similar for different mol percentages of PS and because we are modeling the experimental situation in which the basic peptides are bound to PC/PS vesicles that contain only a trace amount (e.g., 1 mol%) of PIP2. In addition, a search for the minimum electrostatic free energy of the peptide/PIP2/membrane system that accounts for the effect of PIP2 on the minimum free-energy orientation of the peptides for each of the conditions we examined would be computationally intractable due to technical considerations of the grid-dependent, electrostatic self-energy contribution (see discussions after Eqs. 1 and 2) and the computational expense of numerically solving the nonlinear PB equation (see below). Hence, except where noted, the basic peptides were parallel to and located at a distance R = 2.5 Å from the membrane surface.
Phospholipid membranes were constructed as described above except that a single PIP2 replaced a single PC or PS lipid to construct the membranes containing PIP2 (e.g., Fig. 1, B and C). We calculated ΔGel(PIP2) for most of the positions denoted schematically by ovals in Fig. 2, which, as illustrated, extend several lipid layers in the plane of the membrane beyond the imprint of the peptide on the membrane surface. To accurately calculate ΔGel(PIP2) and to fully account for the electrostatic interactions arising not only from the peptide but the surrounding lipid milieu, the membranes used in the calculations had to be large enough to extend several Debye lengths beyond the outermost lipid layers considered. This allowed each position denoted in Fig. 2 to be examined with sufficient bulk membrane surrounding the site of sequestration. For example, in the calculations of ΔGel(PIP2) with Lys-13, which is depicted in Fig. 1, we used membranes that contained 1400 lipids per leaflet. The smallest membrane required for our calculations should extend several Debye lengths (one Debye length is ∼10 Å in 0.1 M KCl) beyond the region of membrane encompassing all of the positions at which we calculate ΔGel(PIP2). In addition, we further increased the size of the membrane (by more than double) so that the computational grid would focus into the membrane at the two highest resolution scales to obtain good estimates for the electrostatic potential at the grid boundary. For Lys-13, this meant constructing membranes of 40 × 35 lipids per leaflet.
The coordinates for the PIP2 headgroup, Ins(1,4,5)P3 were taken from the experimentally determined structure of the Ins(1,4,5)P3-bound PH domain from PLC-δ1 (Ferguson et al., 1996; Protein Data Bank identifier 1mai). As stated above, the radii and partial charges for the headgroup were taken from similar functional groups from the CHARMM22 parameter set. To construct a full model for PIP2, Ins(1,4,5)P3 was docked onto the glycerol backbone and acyl chain region of a PC lipid. Because we are interested in the electrostatic properties of the membrane surface, structural details of the acyl chains of the lipids in our static membranes can be ignored. The net charge of PIP2 is −4. PIP2 was placed in a membrane at a particular position using the same procedure for building PC/PS membranes, as described above, so that the acyl chain region of the PIP2 lipid was aligned with the acyl chain region of the surrounding lipids. As the orientation of the PIP2 headgroup has not been determined experimentally, the PIP2 headgroup in our membrane models (yellow in Fig. 1) was placed on the lipid backbone in two limiting orientations. In the first orientation, the long dimension of the inositol ring was perpendicular to the membrane surface so that the PIP2 headgroup extends ∼4 Å beyond the van der Waals envelope of the PC/PS membrane. In the second orientation, the long dimension of the inositol ring was parallel to the membrane surface so that the PIP2 headgroup is within the van der Waals envelope of the PC/PS membrane. The latter orientation was used for calculations of ΔGel(PIP2) for positions beneath the membrane adsorbed peptides; PIP2 with the former orientation were sterically excluded from this region. The values of ΔGel(PIP2) calculated for a position adjacent to membrane-adsorbed Lys-13, illustrated in Fig. 1, are independent of the orientation, parallel or perpendicular to the membrane surface, of the PIP2 headgroup. In addition, we performed calculations in which the charge distribution on a PC lipid was adjusted so that the lipid had a net charge of −4. Calculations of the sequestration of this lipid, ΔGel(PC(z = −4)), to a position either adjacent to or beneath a membrane-adsorbed peptide differ from ΔGel(PIP2) by <−0.3 kcal/mol. These “control calculations” suggest that the calculated ΔGel(PIP2) is relatively insensitive to both the charge distribution and shape of the headgroup of PIP2, in agreement with the experimental evidence mentioned in the Introduction that suggests the sequestration is due to nonspecific electrostatic interactions.
As in the calculation of ΔGel (Eq. 1), a sequence of focusing runs was used to determine the electrostatic potentials on the finite difference grid from which the electrostatic free energies are derived. All values of ΔGel(PIP2) are precise to within 0.1 kcal/mol. The calculation of ΔGel(PIP2) for a single position in the vicinity of Lys-13, required a grid size of l3 = 2253, focusing resolutions of 0.3, 0.6, 1.2, and 2.4 grid/Å, and 2.2 h of CPU time on the SGI Origin3400. The calculation of ΔGel(PIP2) for a single position adjacent to FA-MARCKS(151–175), required a grid size of l3 = 2893, focusing resolutions of 0.3, 0.6, 1.2, and 2.4 grid/Å, and 6.3 h of CPU time on the Pittsburgh Supercomputing Center terascale computing system (PSC TCS), which contains 1-GHz Compaq Alphaserver ES45 (Palo Alto, CA) processors. The calculation of ΔGel(PIP2) for a single position beneath FA-MARCKS(151–175), required a grid size of l3 = 3373, focusing resolutions of 0.35, 0.7, 1.4, and 2.8 grid/Å, and 10.3 h of CPU time on the PSC TCS. Altogether, the production runs that produced the results in Fig. 2 alone required ∼1690 h or 70 days of CPU time.
Boltzmann-weighted averages of the electrostatic and entropic components to the sequestration of PIP2
We used the following relations to calculate the average electrostatic free energy of sequestration and the average entropic cost of PIP2 demixing:
 |
(3) |
 |
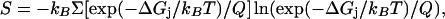(4) |
where Q = Σ(exp(−ΔGi/kBT) is the partition function, kB is the Boltzmann constant, T is the absolute temperature, ΔGj is the electrostatic free energy associated with PIP2 moving to position j in the membrane, and the sum is over all positions, j. Our standard state corresponds to a region of membrane which, on average, is occupied by one PIP2 in the absence of peptide. Therefore, when the membrane contains 1 mol% PIP2, we sum over 100 positions, and when the membrane contains 0.1 mol% PIP2, we sum over 1000 positions. The energetic and entropic costs for PIP2 sequestration by a membrane-adsorbed basic peptide are given by ΔGel = 〈ΔGel(PIP2)〉2−〈ΔGel(PIP2)〉1, and ΔGS = −T (S2 − S1), where 〈ΔGel(PIP2)〉1 and S1 are the average electrostatic free energy and entropy of PIP2 in the initial state, i.e., in the absence of peptide (Fig. 1 B), and 〈ΔGel(PIP2)〉2 and S2 are the average electrostatic free energy and entropy of PIP2 sequestration in the final state, i.e., in the presence of peptide (Fig. 1 C). In our model, we assume PC and PS are not redistributed, and hence there are no energy and entropy changes associated with these lipids. In the initial state, it is assumed for simplicity that ΔGj, the change in electrostatic free energy of PIP2 when it moves from one position in the bulk membrane to another, is 0, i.e., that all positions in the bulk membrane in the absence of peptide are of equal electrostatic free energy. In this case, Eq. 3 gives 〈ΔGel(PIP2)〉1 = 0 and Eq. 4 reduces to S1 = −kB ln(1/N), where N = 100 for 1% PIP2 and GS1 = −2.73 kcal/mol, and where N = 1000 for 0.1% PIP2 and GS1 = −4.09 kcal/mol. For the calculation of 〈ΔGel(PIP2)〉2 and S2 for the final state, the summations in Eqs. 3 and 4 are over the electrostatic free-energy values depicted in Fig. 2. However, the number of positions surrounding each peptide for which we calculate significant electrostatic free energy changes is less than the number of positions in our standard states, i.e., N = 100 and 1000. We assume that ΔGj = 0 for the required remaining positions and that PIP2 is essentially experiencing bulk membrane in the absence of peptide at these positions. The Boltzmann-weighted averages for the electrostatic free energy and entropic cost of PIP2 sequestration for the ΔGel(PIP2) values depicted in Fig. 2 are listed in Tables 1 and 2 for standard states corresponding to both 1% PIP2 and 0.1% PIP2.
TABLE 1.
Boltzmann-weighted averages of the entropic price for PIP2 demixing (ΔGS) and the electrostatic free energy of PIP2 sequestration (〈ΔGel(PIP2)〉) from Eqs. 3 and 4 and using the ΔGel(PIP2) values depicted in Fig. 2
| 2:1 PC/PS
|
5:1 PC/PS
|
|||||||
|---|---|---|---|---|---|---|---|---|
| GS2 | ΔGS | 〈ΔGel(PIP2)〉 | ΔGnet | GS2 | ΔGS | 〈ΔGel(PIP2)〉 | ΔGnet | |
| FA-MAR | −2.5 | +0.2 | −0.7 | −0.5 | −2.1 | +0.6 | −1.8 | −1.2 |
| Lys-13 | −2.0 | +0.7 | −2.0 | −1.3 | −1.5 | +1.2 | −3.8 | −2.6 |
| Lys-7 | −2.3 | +0.4 | −1.0 | −0.6 | −1.6 | +1.1 | −2.5 | −1.4 |
The membranes contain 1% PIP2. All units are kcal/mol. GS1 = −2.7 kcal/mol. ΔGS = GS2 − GS1. ΔGnet = ΔGS + 〈ΔGel(PIP2)〉.
TABLE 2.
Boltzmann-weighted averages of the entropic price for PIP2 demixing (ΔGS) and the electrostatic free energy of PIP2 sequestration (〈ΔGel(PIP2)〉) from Eqs. 3 and 4 and using the ΔGel(PIP2) values depicted in Fig. 2
| 2:1 PC/PS
|
5:1 PC/PS
|
|||||||
|---|---|---|---|---|---|---|---|---|
| GS2 | ΔGS | 〈ΔGel(PIP2)〉 | ΔGnet | GS2 | ΔGS | 〈ΔGel(PIP2)〉 | ΔGnet | |
| FA-MAR | −4.0 | +0.1 | −0.2 | −0.1 | −3.6 | +0.5 | −0.8 | −0.3 |
| Lys-13 | −3.5 | +0.6 | −0.9 | −0.3 | −2.0 | +2.1 | −3.4 | −1.3 |
| Lys-7 | −4.0 | +0.1 | −0.2 | −0.1 | −3.2 | +0.9 | −1.3 | −0.4 |
The membranes contain 0.1% PIP2. All units are kcal/mol. GS1 = −4.1 kcal/mol. ΔGS = GS2 − GS1. ΔGnet = ΔGS + 〈ΔGel(PIP2)〉.
Determination of the statistical significance of ΔGel(PIP2)
The free-energy values plotted in Fig. 3 and listed in Tables 1 and 2 are calculated from Boltzmann-weighted averages of the free-energy values determined from the calculations depicted in Fig. 2. We used the “bootstrap” method to determine the statistical significance of these values (Efron and Tibshirani, 1993). Simply put, the bootstrap is a method that uses data resampling to determine the trustworthiness of a statistic, in our case the Boltzmann-weighted average. The advantage of the bootstrap is that it leverages a limited data set to approximate the variability of a statistic about its unknown “true” value without making assumptions about the underlying distribution. The bootstrap calculates the statistic with M different subsamples. Each subsample is randomly drawn from the original data set with replacement, i.e., once a particular value is chosen, it is still included for selection in future draws. The result is then the mean and standard deviation of the M values for the statistic obtained from the M subsamples. For example, if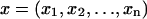 
is our original data set, with each xi corresponding to a different ΔGel(PIP2) value, then 
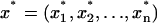is a bootstrap sample obtained by sampling x randomly with replacement. We, thus, generate a large number (M = 1000) of bootstrap samples 
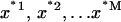, each consisting of n ΔGel(PIP2) values. For each subsample, we calculate the Boltzmann-weighted averages as given in Eqs. 3 and 4. The mean and standard deviation of the M = 1000 values are plotted in Fig. 3.
Calculation of the electrostatic free energy of the sequestration of multiple PIP2 lipids by a membrane-adsorbed basic peptide
Fig. 6 illustrates schematically the sequential sequestration of several PIP2 lipids by a membrane-adsorbed basic peptide. For example, as depicted in Fig. 6 B, the first PIP2 lipid is sequestered to position 1, a second PIP2 is then sequestered to position 2, and so on. The calculated electrostatic free energy of sequestering a PIP2 to position 1 from bulk membrane is given by ΔGel(PIP2) in Eq. 2. The presence of the first PIP2 is expected to affect (i.e., increase) the electrostatic sequestration energy of the second PIP2 relative to its sequestration in the absence of other PIP2. Hence, each subsequent PIP2 is considered in succession, and its electrostatic free energy of lateral sequestration is calculated in the presence of the PIP2 lipids that were previously sequestered to their corresponding positions. The electrostatic free energy of placing a second PIP2 at position 2 in the presence of a PIP2 already at position 1 (ΔGel(2(PIP2)) is determined from the electrostatic free energies of initial and final states that are correspondingly different from those depicted in Fig. 1 and used in Eq. 2. In this case, although the initial state of the system is still composed of two equal-sized regions of membrane containing the same mol percent monovalent acidic lipid, one region contains a basic peptide adsorbed to its surface with a PIP2 already sequestered at position 1 (Gel(PIP2·P·M)), and the other contains a single PIP2 lipid (Gel(PIP2·M)) in position 2. This represents the situation in which the second PIP2 is in bulk membrane, far away from the first PIP2 and the membrane-adsorbed peptide. The final state of the system is also composed of two equal-sized regions of membrane containing the same mol percent monovalent acidic lipid, however, one region has a PIP2 at position 2 in the vicinity of the membrane-adsorbed peptide with the first PIP2 already at position 1 (Gel(2(PIP2)·P·M)), and the other region contains no PIP2 (Gel(M)), as in Eq. 2. This represents the situation in which the second PIP2 is sequestered by the membrane-adsorbed basic peptide in the presence of the first PIP2, leaving behind a region of bulk membrane. ΔGel(2(PIP2) is the difference between the electrostatic free energies of the models for the final state and the electrostatic free energies of the models for the initial state as determined by the FDPB method:
 |
(5) |
FIGURE 6.
Representative configurations used in the calculation of the sequestration of multiple PIP2 lipids by membrane-adsorbed basic peptides: FA-MARCKS(151–175) (A), Lys-13 (B), and Lys-7 (C). The view is from above, looking down on the membrane. The scheme reflects the sequential partitioning of PIP2 lipids from bulk membrane to the positions labeled in the order given by the numbering. Illustrations representing the other configurations examined in this work are included with the supplementary material.
More generally, to calculate the electrostatic free energy of sequestration of the nth lipid to the vicinity of a membrane-adsorbed peptide when (n − 1) PIP2 are already sequestered, we use FDPB calculations and a scheme based on the following relationship:
 |
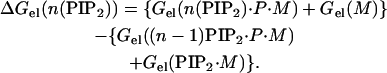(6) |
ΔGel(n(PIP2)) was calculated for many different configurations of PIP2 lipids with respect to the membrane-adsorbed peptides as illustrated in Fig. 6 and the supplementary material. Membranes with two surface concentrations of monovalent acidic phospholipid were considered (5:1 PC/PS and 2:1 PC/PS). We make the assumption that there is an infinite reservoir of PIP2, present at 1 or 0.1 mol%, so that when one or more PIP2 are bound, the number of PIP2 per area of membrane in the bulk does not change. Therefore, we estimate that the increase in the free-energy penalty associated with the entropy of lipid demixing in the presence of other PIP2 is small, and, hence, we approximate the change in free energy due to lipid demixing when n PIP2 are sequestered as n·ΔGS(PIP2) (see Tables 1–3).
TABLE 3.
Sequestration of multiple PIP2 lipids by membrane-adsorbed basic peptides for the configurations illustrated in Fig. 6
| Position
|
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Energy | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| FA-MARCKS | 2:1 PC/PS | ΔGel(PIP2) | −1.7 | −1.3 | −0.9 | −0.8 | −0.6 | −0.8 | −1.0 | −0.4 |
| ΔGel(nPIP2) | −1.7 | −0.4 | −0.9 | −0.4 | −0.5 | +0.1 | +0.6 | +0.5 | ||
| Σ ΔGel(nPIP2) | −2.6 | |||||||||
| ΔGS(nPIP2) | +0.2 | +0.2 | +0.2 | +0.2 | +0.2 | +0.2 | +0.2 | +0.2 | ||
| ΔGnet(nPIP2) | −1.5 | −0.2 | −0.7 | −0.2 | −0.3 | +0.3 | +0.8 | +0.7 | ||
| Σ ΔGnet(nPIP2) | −2.2 | |||||||||
| 5:1 PC/PS | ΔGel(PIP2) | −2.7 | −1.9 | −1.6 | −1.2 | −1.2 | −1.6 | −1.9 | −1.0 | |
| ΔGel(nPIP2) | −2.7 | −0.7 | −1.6 | −0.4 | −1.0 | 0 | +1.0 | +0.9 | ||
| Σ ΔGel(nPIP2) | −6.0 | |||||||||
| ΔGS(nPIP2) | +0.5 | +0.5 | +0.5 | +0.5 | +0.5 | +0.5 | +0.5 | +0.5 | ||
| ΔGnet(nPIP2) | −2.2 | −0.2 | −1.1 | +0.1 | −0.5 | +0.5 | +1.5 | +1.4 | ||
| Σ ΔGnet(nPIP2) | −3.3 | |||||||||
| Lys-13 | 2:1 PC/PS | ΔGel(PIP2) | −2.4 | −2.8 | −2.0 | −2.3 | −1.3 | −0.9 | −0.5 | – |
| ΔGel(nPIP2) | −2.4 | −2.1 | −1.0 | −0.5 | −0.4 | +0.5 | +1.1 | – | ||
| Σ ΔGel(nPIP2) | −5.5 | |||||||||
| ΔGS(nPIP2) | +0.7 | +0.7 | +0.7 | +0.7 | +0.7 | +0.7 | +0.7 | – | ||
| ΔGnet(nPIP2) | −1.7 | −1.4 | −0.3 | +0.2 | +0.3 | +1.2 | +1.8 | – | ||
| Σ ΔGnet(nPIP2) | −3.1 | |||||||||
| 5:1 PC/PS | ΔGel(PIP2) | −4.1 | −3.5 | −3.3 | −3.6 | −2.1 | −1.3 | −1.3 | – | |
| ΔGel(nPIP2) | −4.1 | −2.5 | −1.4 | −0.9 | −0.9 | +0.6 | +1.9 | – | ||
| Σ ΔGel(nPIP2) | −9.8 | |||||||||
| ΔGS(nPIP2) | +1.2 | +1.2 | +1.2 | +1.2 | +1.2 | +1.2 | +1.2 | – | ||
| ΔGnet(nPIP2) | −2.9 | −1.3 | −0.2 | +0.3 | +0.3 | +1.8 | +3.1 | – | ||
| Σ ΔGnet(nPIP2) | −4.2 | |||||||||
| Lys-7 | 2:1 PC/PS | ΔGel(PIP2) | −1.9 | −1.6 | −1.0 | −0.7 | −0.5 | – | – | – |
| ΔGel(nPIP2) | −1.9 | −0.8 | −0.4 | +0.5 | +1.0 | – | – | – | ||
| Σ ΔGel(nPIP2) | −2.7 | |||||||||
| ΔGS(nPIP2) | +0.4 | +0.4 | +0.4 | +0.4 | +0.4 | – | – | – | ||
| ΔGnet(nPIP2) | −1.5 | −0.4 | 0 | +0.9 | +1.4 | – | – | – | ||
| Σ ΔGnet(nPIP2) | −1.5 | |||||||||
| 5:1 PC/PS | ΔGel(PIP2) | −3.3 | −2.7 | −1.7 | −1.0 | −1.1 | – | – | – | |
| ΔGel(nPIP2) | −3.3 | −1.0 | −0.4 | +0.8 | +1.7 | – | – | – | ||
| Σ ΔGel(nPIP2) | −4.3 | |||||||||
| ΔGS(nPIP2) | +1.0 | +1.0 | +1.0 | +1.0 | +1.0 | – | – | – | ||
| ΔGnet(nPIP2) | −2.3 | 0 | +0.6 | +1.8 | +2.7 | – | – | – | ||
| Σ ΔGnet(nPIP2) | −2.3 | |||||||||
ΔGel(PIP2) is the electrostatic free energy of sequestrating a single PIP2, labeled in Fig. 6, in the absence of other PIP2 lipids (values are from Fig. 2). ΔGel(nPIP2) is the electrostatic free energy of sequestration of a PIP2 to position n, labeled in Fig. 6, in the presence of (n − 1) PIP2 at positions m < n (see Eq. 6). ΣΔGel(nPIP2) is the sum of ΔGel(nPIP2) values that are equal to or less than the cut-off energy of −0.6 kcal/mol (i.e., −1 kBT). ΔGS(nPIP2) is the free-energy penalty associated with localizing a PIP2 lipid to the nth position (see the Methods and the Results sections). ΔGnet(PIP2) = ΔGel(nPIP2) + ΔGS(nPIP2). ΣΔGnet(nPIP2) is the sum of ΔGnet(nPIP2) values that are equal to or less than the cut-off energy of −0.6 kcal/mol (i.e., −1 kBT). All units are in kcal/mol.
RESULTS
Nonspecific electrostatic interactions provide a driving force for the lateral sequestration of PIP2 by membrane-adsorbed basic peptides
We used the FDPB method to calculate the electrostatic free energy associated with moving a PIP2 to the vicinity of a membrane-adsorbed basic peptide, ΔGel(PIP2) (see Fig. 1). Through the use of atomic models, the calculations account for the shape and charge distribution of the interacting species and, consequently, the effect that PIP2 and the peptide have on each other's electrostatic potentials as well as the desolvation repulsion that may occur upon association. Fig. 1 illustrates a representative example of the peptide/membrane models used in the calculation of ΔGel(PIP2). Panels A and B depict the initial state of the system in which a basic peptide (Lys-13, cyan) that is docked at the surface of a 5:1 PC/PS membrane (PC, white; PS, red) in its minimum free-energy orientation (see Methods) and a PIP2 lipid (yellow) are infinitely far apart. Panels C and D depict the final state of the system in which the PIP2 is moved from “bulk” membrane to a position in the vicinity of the peptide, i.e., PIP2 is “sequestered” by the membrane-adsorbed basic peptide (denoted by the arrow in panels A and B). ΔGel(PIP2) is the difference of the electrostatic free energies of these final and initial states. Fig. 2 summarizes the results of many calculations, each of which corresponds to the sequestration of PIP2 to a different position in the membrane with respect to the peptide. The peptides (cyan) are located in their minimum free-energy orientations as determined for the corresponding PC/PS membrane (2:1 or 5:1). Lipid positions in the plane of the membrane are denoted schematically as ovals. Values for ΔGel(PIP2) are reported in kcal/mol at the locations to which a single PIP2 lipid is sequestered. Each value is precise to within 0.1 kcal/mol as judged by the difference in ΔGel(PIP2) for the two highest resolution scales from the focusing calculations (see Methods). As described in the sections below, our calculations support the hypothesis that nonspecific electrostatic interactions are a significant driving force for PIP2/peptide colocalization (McLaughlin et al., 2002; Wang et al., 2002; Haleva et al., 2004; Gambhir et al., 2004).
No effort was made to optimize ΔGel(PIP2) for the many calculations we performed (see Methods). Specifically, we assumed that both the orientation of the peptide with respect to the membrane and the distribution of PS are unaffected by the presence of PIP2. In the several cases we tested, it was possible to decrease ΔGel(PIP2) by up to 0.5 kcal/mol through optimizing the lateral distance between the membrane-adsorbed peptide and PIP2 by moving the peptide in a plane parallel to the membrane surface with respect to a specific position of PIP2, denoted schematically by an oval in Fig. 2. The vertical distance of the peptide from the membrane surface also affects ΔGel(PIP2); see Fig. 5, below.
FIGURE 5.
The electrostatic free energy of sequestration of PIP2 decreases as the distance between FA-MARCKS(151–175) and the membrane decreases. The position to which PIP2 is sequestered is shown as a bold black oval in panels A and B of Fig. 2. The calculations represented on the left were performed for the peptide FA-MARCKS(151–175) in its minimum electrostatic free-energy orientation for which the distance between the van der Waals surfaces of the peptide and membrane (R) is 2.5 Å. The calculations represented on the right were performed for R = 0 Å. The calculations examined three different lipid compositions in 0.1 M KCl: 2:1 PC/PS (black bars), 5:1 PC/PS (gray bars), and 1:0 PC/PS (white bars).
There are many energetically equivalent sites for PIP2 in the vicinity of a membrane-adsorbed basic peptide
As depicted in Fig. 2, ΔGel(PIP2) for many different positions with respect to a membrane-adsorbed peptide is significant, i.e., more favorable than thermal energy, which is ∼0.6 kcal/mol at T = 298 K. For example, in Fig. 2 D, which contains the results of calculations with Lys-13 on 5:1 PC/PS, ΔGel(PIP2) < −0.6 kcal/mol for at least 40 positions and <−2.0 kcal/mol for at least 20 positions. In this case, ΔGel(PIP2) is most negative for positions directly beneath the peptide (e.g., −4.4 kcal/mol), but is also significant (e.g., −0.9 kcal/mol) for positions even two lipid layers away from the imprint of the peptide on the membrane surface. This suggests that PIP2 can sample over 3000 Å2 of the surface of a 5:1 PC/PS membrane in the vicinity of an adsorbed Lys-13 peptide and experience a significant electrostatic attraction to the peptide. For all cases depicted in Fig. 2, the calculations suggest that nonspecific electrostatic interactions contribute to the recruitment of PIP2 to regions that contain a membrane-adsorbed peptide.
The electrostatic free energy of PIP2 sequestration is in excess of the entropic penalty for PIP2 localization
Because the electrostatic association of a PIP2 with a membrane-adsorbed peptide is not specific, i.e., there are many energetically equivalent ways in which PIP2 may interact with the peptide, the free energy loss due to lipid demixing upon the sequestration of a PIP2 from bulk membrane to a localized region, ΔGS, is expected to be relatively small. The Boltzmann-weighted averages of the electrostatic free energy of PIP2 sequestration and the free energy of PIP2 demixing for the six conditions illustrated in Fig. 2 are depicted in Tables 1 and 2 for membranes containing 1 mol% PIP2 (Table 1) and 0.1 mol% PIP2 (Table 2). As suggested by the values for ΔGel(PIP2) in Fig. 2, the entropic cost is greatest in those cases for which the electrostatic sequestration is most favorable. For example, for membranes containing 1 mol% PIP2, 〈ΔGel(PIP2)〉 = −3.8 kcal/mol and ΔGS = +1.2 kcal/mol for Lys-13 on 5:1 PC/PS, whereas 〈ΔGel(PIP2)〉 = −0.7 kcal/mol and ΔGS = +0.2 kcal/mol for FA-MARCKS(151–175) on 2:1 PC/PS. As depicted by the bar graph in Fig. 3 A, 〈ΔGel(PIP2)〉 (gray and black bars) is in significant excess of ΔGS (white bars) leading to a favorable net free energy (Fig. 3 B) for most conditions when the membrane contains 1 mol% PIP2. However, as depicted in Table 2 the entropic cost is a much greater proportion of the magnitude of the electrostatic sequestration free energy for membranes containing 0.1 mol% PIP2, and in this case, our calculations predict that PIP2 would be, at best, only weakly sequestered.
The electrostatic free energy of PIP2 sequestration depends on both the net charge and linear charge density of the peptide
Fig. 3 summarizes the data presented in Fig. 2. The Boltzmann factor-weighted averages of the free energies, i.e., 〈ΔGel(PIP2)〉 in Fig. 3 A and 〈ΔGel(PIP2)〉 + ΔGS in Fig. 3 B, were calculated for each of the conditions examined: three basic peptides and two membrane compositions. The mean values and errors depicted in Fig. 3 were determined statistically as described in Methods. Overall, considering either electrostatic interactions alone (Fig. 3 A) or both electrostatic and entropic contributions (Fig. 3 B), the PIP2 sequestration free energy is predicted to be most favorable for Lys-13 and similar in the cases of FA-MARCKS(151–175) and Lys-7. That Lys-13 is predicted to sequester PIP2 more strongly than FA-MARCKS(151–175) agrees with what is observed experimentally and suggests that the linear charge density of the peptide is an important determinant because both peptides have a net charge of +13 (Gambhir et al., 2004). Our calculations also predict that PIP2 is sequestered significantly more strongly by Lys-13 than Lys-7 and, hence, that the net charge of the peptide is also an important determinant. The experiments, however, indicate that PIP2 interacts strongly with both Lys-7 and Lys-13 (Gambhir et al., 2004). Possible reasons for this discrepancy are considered in the Discussion section.
The electrostatic free energy of PIP2 sequestration decreases as the net charge of the lipid becomes more negative
PIP2, in its fully unprotonated state, has a net charge of −5. Experiments indicate that, at pH 7.0, at least one proton is bound to the phosphate at either the 4 or 5 position of the inositiol ring (van Paridon et al., 1986). Hence, under physiological conditions, PIP2 may have a net charge between −3 and −5 (Toner et al., 1988; McLaughlin et al., 2002). For most of the calculations presented in this report, we assume that z = −4. However, our calculations predict that the electrostatic sequestration is sensitive to the net charge of PIP2. For example, for sequestration to the position demarcated by the bold blue oval in Fig. 2 D, PIP2 lipids with a valence of −3, −4, and −5 are predicted to have electrostatic sequestration free energies of −2.3, −3.5, and −4.4 kcal/mol, respectively. Thus, phosphoinositides with a higher negative charge, e.g., phosphatidylinositol 3,4,5-trisphosphate (PIP3), should be sequestered even more strongly than PIP2. On the other hand, the dependence on net charge is weaker for more peripheral positions: For the position demarcated by the bold black oval in Fig. 2 D, ΔGel(PIP2) decreases by only 0.8 kcal/mol when the net charge is decreased from −3 to −5. Importantly, PIP2 with z = −4 is sequestered to this same position significantly more strongly than PS (z = −1); ΔGel(PIP2) is −2.9 kcal/mol whereas ΔGel(PS) is only −1.0 kcal/mol.
The electrostatic free energy of PIP2 sequestration increases as the mol percent PS in the membrane increases
Fig. 2 presents ΔGel(PIP2) for each of the three peptides on both a 5:1 and 2:1 PC/PS membrane. Comparisons of panels A, C, and E with panels B, D, and F, respectively, show that ΔGel(PIP2) is consistently more favorable when the bulk membrane contains 5:1 PC/PS. This prediction agrees with experimental observations (see Figs. 7 B and 11 from Gambhir et al., 2004). Fig. 3 plots 〈ΔGel(PIP2)〉 and 〈ΔGel(PIP2)〉 + ΔGS for the calculations depicted in Fig. 2. The free energy of PIP2 sequestration decreases by ∼1 kcal/mol for all peptides when the mol percent PS in the membrane decreases from 33 (black bars) to 17 (gray bars). The basis for the difference in 〈ΔGel(PIP2)〉 as a function of membrane composition is considered in more detail in the Discussion section.
The electrostatic free energy of PIP2 sequestration increases as ionic strength of the aqueous phase increases
Fig. 4 depicts the ionic strength dependence of ΔGel(PIP2) for sequestration to the two positions in the vicinity of Lys-13 denoted by bold ovals in Fig. 2, C and D. As expected for an electrostatic interaction and in agreement with experiments (see Fig. 9 from Gambhir et al., 2004), ΔGel(PIP2) increases as the ionic strength increases. When [KCl] = 0.3 or 0.5 M, ΔGel(PIP2) is significantly less favorable than the values at [KCl] = 0.1 M.
FIGURE 4.
The electrostatic free energy of sequestration of PIP2 from bulk membrane to a position either adjacent to (circles) or beneath (squares) a membrane-adsorbed Lys-13 peptide increases as the ionic strength increases. The open and filled symbols represent calculations of ΔGel(PIP2) for 5:1 and 2:1 PC/PS, respectively. The two positions to which PIP2 was sequestered are represented by bold ovals in panels C and D of Fig. 2.
The electrostatic free energy of PIP2 sequestration decreases as the distance between peptide and membrane decreases
Recent spectroscopic studies reveal that the phenylalanine residues in a peptide based on the MARCKS effector domain, MARCKS(151–175), penetrate into the acyl chain region of phospholipid vesicles (Qin and Cafiso, 1996; Rauch et al., 2002; Zhang et al., 2003; Ellena et al., 2003). (The peptide we consider here, FA-MARCKS(151–175), has alanines in place of the phenylalanines and is not expected to appreciably penetrate the membrane interface.) We are unable to satisfactorily model the membrane interaction of MARCKS(151–175) with our static peptide and membrane models. However, we can roughly approximate the effect that MARCKS(151–175) has on the electrostatic properties of membranes by docking the FA-MARCKS(151–175) peptide at the surface of our bilayer models so that the van der Waals surfaces of peptide and membrane are just touching (R = 0 Å). Fig. 5 shows how ΔGel(PIP2) decreases as the distance between the peptide and membrane decreases. Specifically, the electrostatic free energy of sequestering PIP2 to a position adjacent to FA-MARCKS(151–175) (bold ovals in Fig. 2, A and B) decreases by 0.5–1.0 kcal/mol for 2:1, 5:1, and 1:0 PC/PS membranes when the distance between peptide and membrane decreases from 2.5 Å (the distance corresponding to the minimum electrostatic free-energy orientation of FA-MARCKS(151–175)) to 0 Å. This is consistent with the stronger sequestration of PIP2 by MARCKS(151–175) versus FA-MARCKS(151–175) observed experimentally (Gambhir et al., 2004). Localizing basic residues more closely to the membrane interface increases their positive potential profile due to a combination of image charge effects and a perturbation of the diffuse double layer, as explained in our companion paper (Gambhir et al., 2004), and, thus, provides a stronger electrostatic driving force for PIP2 sequestration.
The electrostatic free energy of PIP2 sequestration is strongly dependent on the solution of the nonlinear versus linear Poisson-Boltzmann equation
The linearized version of the Poisson-Boltzmann equation is applicable only when the electrostatic potentials are small compared to 1 kBT/e, i.e., for low fixed charge densities (McLaughlin, 1989; Sharp and Honig, 1990b; Misra and Honig, 1995). This is not the case for the systems we are examining here. As illustrated below in Fig. 8, the −1 kBT/e or −25 mV equipotential profiles of 2:1 PC/PS and 5:1 PC/PS in 0.1 M KCl extend appreciably into the aqueous phase. Furthermore, the basic peptides produce regions of strong positive potential. Hence, the concentration of monovalent ions is quite high in the vicinity of the peptide and membrane, which constitutes another regime, i.e., high ionic strength, in which the linear PB equation breaks down. When inappropriately applied, the linear theory predicts erroneously large electrostatic potentials. Previous work showed that solution of the full nonlinear PB equation is required to accurately reproduce the electrostatic equipotential profiles of membranes containing acidic phospholipids (Peitzsch et al., 1995). In addition, other computational work showed that the salt-dependent terms obtained from solutions to the nonlinear PB equation constitute ∼30% of the electrostatic free energy of interaction of a Lys-5 peptide with 2:1 PC/PS in 0.1 M KCl (Ben-Tal et al., 1996). Here, we find an even more dramatic effect: ΔGel(PIP2) is 5 kcal/mol more positive when the nonlinear versus the linear PB equation is solved, i.e., the linear PB treatment predicts much stronger sequestration. This large difference highlights the importance of solving the nonlinear PB equation for highly charged systems, which are often applicable in the modeling of biological systems (Honig and Nicholls, 1995), e.g., protein/membrane, protein/nucleic acid, and large multicomponent systems.
FIGURE 8.
Electrostatic properties of Lys-13/PIP2/membrane systems. Panels A–D depict the electrostatic equipotential profiles for the system shown in Fig. 1. Here, the view is from the side. Lys-13 is colored cyan and the PIP2 headgroup is colored yellow. The bulk membrane composition is 5:1 PC/PS, and [KCl] = 0.1 M. The electrostatic potentials were determined by solving the nonlinear Poisson-Boltzmann equation in the finite difference approximation on a computational grid of size 653 so that they may be visualized in GRASP (Nicholls et al., 1991). Blue and red meshes represent the +25 mV and −25 mV equipotential contours, respectively. Panels E–H are the same as A–D except that the bulk membrane composition is 2:1 PC/PS. Panels A and B (E and F) depict the initial state of the system, in which the membrane-adsorbed Lys-13 peptide and PIP2 are infinitely far apart, and panels C and D (G and H) depict the final state of the system, in which PIP2 has been moved to a position adjacent to Lys-13.
FA-MARCKS(151–175) and Lys-13 are predicted to sequester several PIP2 lipids
The calculations presented in this report along with evidence from complementary experiments (Wang et al., 2002; Rauch et al., 2002; Gambhir et al., 2004) indicate that the interaction of PIP2 with membrane-adsorbed basic peptides is nonspecific. As shown in Fig. 2, there are many different locations adjacent to the membrane-adsorbed peptide where PIP2 can gain significant electrostatic free energy. This implies that more than one PIP2 may be sequestered simultaneously. Indeed, there is good experimental evidence from EPR, centrifugation, kinetic, and fluorescence measurements that these peptides do sequester more than one PIP2 (Rauch et al., 2002; Wang et al., 2002; Gambhir et al., 2004). To quantify these interactions, we used models similar to those described above and the FDPB method to calculate how many PIP2 lipids FA-MARCKS(151–175), Lys-13, and Lys-7 can sequester through nonspecific electrostatic interactions. Our calculations are based on Eq. 6 and the scheme outlined in the Methods section and account for the sequential sequestration of increasing numbers of PIP2 lipids by membrane-adsorbed basic peptides. Fig. 6 schematically illustrates the positions to which PIP2 lipids are sequestered as well as the order of sequestration for one representative set of the many configurations we considered. Each configuration was generated by hand and chosen so that PIP2 lipids partition to energetically favorable positions as delineated in Fig. 2. Table 3 contains detailed results from calculations with models based on the configuration illustrated in Fig. 6, and Fig. 7 summarizes the results for these and many alternative configurations for which we performed calculations. Figures and tables analogous to Fig. 6 and Table 3 and that provide details related to the other configurations we examined are provided with the supplementary material.
FIGURE 7.
Membrane-adsorbed basic peptides can sequester multiple PIP2 lipids through nonspecific electrostatic interactions. The total free energy of sequestration and the number of PIP2 lipids sequestered are plotted for calculations based on electrostatic interactions alone (A and C), or for calculations based on both electrostatic and entropic components to the free energy (B and D). The values for the various energetic components are given in the supplementary material.
Our calculations show that the electrostatic free energy associated with sequestering a PIP2 to a position in the vicinity of a membrane-adsorbed basic peptide generally increases (becomes less favorable) in the presence of other PIP2 lipids relative to the values listed in Fig. 2, whose underlying calculations assume there are no other PIP2 present. For example, following the scheme in Fig. 6 B for Lys-13 and a 5:1 PC/PS membrane, Table 3 shows that ΔGel(PIP2) for position 1 is the same as for the corresponding position in Fig. 2 D, i.e., −4.1 kcal/mol. However, ΔGel(2PIP2), the electrostatic free energy of sequestering a PIP2 to position 2 of Fig. 6 B in the presence of a PIP2 already at position 1, is −2.5 kcal/mol, which is an increase of 1 kcal/mol from the value obtained in the absence of other PIP2 (see Fig. 2). ΔGel(3PIP2) is even less favorable than ΔGel(PIP2) for position 3 (−1.4 vs. −3.3 kcal/mol). As seen in Table 3 for a system containing Lys-13 and 5:1 PC/PS, the electrostatic sequestration free energy becomes repulsive after five PIP2 are sequestered, i.e., ΔGel(6PIP2) > 0. Furthermore, if we include the free-energy component due to lipid demixing, ΔGS (see Methods), then the free energy of sequestration becomes insignificant (i.e., of magnitude less than thermal energy, kBT ∼ 0.6 kcal/mol at T = 298 K) much sooner, after only an additional PIP2 is sequestered. Fig. 7, A and C, present the results based on electrostatics alone, whereas Fig. 7, B and D, incorporate the entropic contribution to the free energy due to PIP2 localization (see Methods for details).
Fig. 7 B summarizes our results based on calculations for five to 12 different configurations, such as those illustrated in Fig. 6, for each condition (basic peptide and membrane composition). The calculations predict a similar dependence of the sequestration free energy on the mol percent PS in the membrane as for the single PIP2 case (Fig. 3 B), i.e., that the sequestration free energy decreases as the mol percent PS decreases. In agreement with the available experimental data (Wang et al., 2002; Rauch et al., 2002; Gambhir et al., 2004), our calculations predict that a peptide with 13 basic residues (e.g., Lys-13, FA-MARCKS(151–175), MARCKS(151–175)) can sequester at least two PIP2, whereas Lys-7 is predicted to sequester only one PIP2 (Fig. 7 D). Hence, our calculations provide molecular models for the experimentally observed lateral organization of PIP2 and basic peptides at membrane surfaces.
DISCUSSION
In this study, we used computational models to describe how unstructured clusters of basic residues on membrane-associated proteins can laterally sequester biologically important multivalent lipids such as PIP2 and PIP3. The FDPB methodology is based on well-defined physical principles, and our implementation of the method incorporates atomic-level models of the interacting species (Honig and Nicholls, 1995; Gallagher and Sharp, 1998). We are, therefore, able to ascribe physical meaning to our computational results. Furthermore, the overall qualitative agreement of our calculations with experimental observations on simple model systems suggests that local, nonspecific electrostatic interactions do indeed constitute a significant driving force for the sequestration of PIP2 by membrane-adsorbed basic peptides. Specifically, our calculations provide models that describe how nonspecific electrostatic interactions may be of sufficient affinity to account for sequestration and how several PIP2 lipids may be sequestered by a single peptide.
In addition, our calculations predict, in agreement with experiment, that the sequestration free energy is more favorable when: 1), the linear charge density of the peptide is higher; 2), the mol percent monovalent acidic lipid, PS, in the membrane decreases; 3), the ionic strength of the solution decreases; and 4), the distance between the peptide and membrane surface decreases, which occurs when a peptide contains aromatic residues that penetrate the membrane interface as in the case of MARCKS(151–175). Although not tested experimentally, our calculations also predict that the sequestration free energy is more favorable when the net charge of the lipid is more negative (e.g., PIP3 versus PIP2). The physical basis of a number of these predictions is illustrated in Fig. 8, which depicts in quantitative detail the electrostatic properties of PIP2/peptide/membrane systems, such as that shown in Fig. 1 and used in our calculations.
Fig. 8 illustrates the electrostatic driving forces that contribute to the sequestration of PIP2 by membrane-adsorbed basic peptides. The negative electrostatic potential profiles of membranes containing physiological amounts of acidic phospholipids is significant: The −25 mV or −1 kT/e equipotential profiles above 5:1 (panel D) and 2:1 (panel H) PC/PS bilayers extend beyond the envelope of the polar headgroup region, and, as expected, the −25 mV profile is located farther from the surface for 2:1 PC/PS than for 5:1 PC/PS; in 0.1 M salt solution, the negative profile above 2:1 PC/PS is located about a Debye length (∼10 Å) from the membrane surface. As shown in panels A and E, basic peptides, such as Lys-13, interact strongly with PC/PS membranes: membrane adsorption of Lys-13 produces a highly localized region of positive potential in its vicinity. As suggested by panels C and G, PIP2, because of its high negative charge (z = −4), is preferentially attracted over PS (z = −1) to the positively charged peptide. As described in Methods, the electrostatic free energy of interaction of Lys-13 with PC/PS membranes is significantly more favorable when the membrane contains more PS, and this is manifested as a smaller positive potential profile (i.e., the +25 mV contour is closer to the peptide) for Lys-13 on 2:1 versus 5:1 PC/PS (compare panels A and E in Fig. 8). Because of the relatively depressed positive potential of Lys-13 on 2:1 PC/PS, the electrostatic attraction between PIP2 and the peptide is lower in this case. However, as suggested by panels B and F, the electrostatic free energy of a PIP2 in a membrane in the absence of peptide is higher for 2:1 PC/PS than 5:1 PC/PS because the potential produced by PS is more negative in the 2:1 PC/PS bilayer. Thus, there is a stronger electrostatic repulsive force driving PIP2 out of bulk membrane in the 2:1 PC/PS case. Nevertheless, as quantitated in Fig. 2, the model predicts a more favorable sequestration of PIP2 by Lys-13 when the membrane contains 5:1 rather than 2:1 PC/PS. This prediction agrees with the experimental results (Gambhir et al., 2004). Overall, Fig. 8 shows how unstructured clusters of basic residues on proteins can produce strong localized electrostatic potential profiles that can mediate lateral organization at membrane surfaces through nonspecific electrostatic interactions.
The thermodynamic models of May and Ben-Shaul (2003) and Haleva et al. (2004) account for the electrochemical equilibrium of all lipid species and are, therefore, self-consistent. These models are able to comprehensively explore the lipid composition of peptide/membrane systems and, thus, characterize parameters that may minimize the free energy of the system, e.g., the concentration of acidic lipids in the vicinity of the membrane-adsorbed peptide. Indeed, the model of Haleva et al. (2004) predicts that the surface density of both monovalent and polyvalent acidic lipids is enhanced in the region of the peptide and that the polyvalent lipid species is preferentially accumulated. In contrast, our model ignores any redistribution of monovalent acidic lipids and focuses only on the lateral partitioning of PIP2, though experimental studies suggest that neglecting PS sequestration is not unreasonable (Kleinschmidt and Marsh, 1997; Murray et al., 2002). (Surface pressure effects are taken into account explicitly by the replacement of a PC or PS lipid by a single PIP2 (see Fig. 1)). The thermodynamic models employ simplified representations of the molecules and may, thus, be limited in their capacity to accurately describe the electrostatic properties of peptide/membrane systems. For example, the model of Haleva et al. (2004) depicts the peptide as a large flat surface whose size is much greater than the Debye length so that the interaction between the peptide and lipids is driven principally by charge matching between the planes representing the peptide and membrane (Parsegian and Gingell, 1972). Nevertheless, this model is able to account for many of the experimental observations associated with PIP2 sequestration. The peptides in the model employed by May and Ben-Shaul (2003) are represented as charged spheres with a radius comparable to the length of the peptide, which is presumably a more realistic representation. However, their model does not include multivalent species. Although our calculations neglect the lateral redistribution of PC and PS lipids, they are based on atomic-level models of the interacting species (Fig. 1). Thus, there are advantages and disadvantages to each of the theoretical models.
As a consequence of the limitations of our model (see below), our calculations are unable to reproduce a number of features of the PIP2/peptide interactions observed experimentally. First, our calculations clearly predict that Lys-13 should sequester PIP2 more strongly than Lys-7 does (Figs. 2, 3, and 7), whereas experiments show that both these peptides sequester PIP2 very strongly (Gambhir et al., 2004). Second, our calculations underestimate the magnitude of the PIP2 sequestration free energy. For example, although our calculations predict that the electrostatic sequestration is strong enough to overcome the penalty of PIP2 demixing when the concentration of PIP2 in the membrane is 1 mol%, the entropy of lipid demixing when the membrane contains 0.1 mol% PIP2 is comparable to the electrostatic sequestration we predict for most cases (see Tables 1 and 2). This further suggests that our calculations underestimate ΔGel(PIP2). Our current approach will have to be modified to satisfactorily model the very interesting and potentially biologically relevant interaction between PIP2 and the MARCKS effector domain, which has been characterized experimentally in great detail (Wang et al., 2002; Rauch et al., 2002; Gambhir et al., 2004). A peptide based on the MARCKS effector domain has been shown to appreciably penetrate the membrane interface with its five phenylalanine residues reaching down to the acyl chain region of the membrane interior (Qin and Cafiso, 1996; Zhang et al., 2003; Ellena et al., 2003). The localization of positive charge within the polar headgroup region may have effects on the electrostatic properties of membranes distinct from those examined here.
Because our calculations are based on the use of static models for the interacting species, our analysis does not account for the effects of lipid motions and peptide orientational and conformational changes that may result in interactions that contribute to the sequestration free energy. In particular, because of the computational demands (see Methods), we were not able to optimize the peptide/PIP2 interactions nor to examine in detail the effect that the peptide and lipid may have on their relative orientations. Not surprisingly, though, we found that ΔGel(PIP2) decreased dramatically if we assumed that the placement of PIP2 in the vicinity of a membrane-adsorbed peptide was accompanied by the movement of several PS lipids out of this region. But because of the uncertainty of the lipid composition in the PIP2/peptide regions, we did not include these effects in our modeling. In addition, our calculations do not account for other energetic factors that may contribute to sequestration, e.g., nonpolar and hydrogen bonding interactions, and peptide penetration into the membrane interface. For example, because the peptide/PIP2 interactions are not optimized, the association of these molecules is relatively loose, and we find that the nonpolar contribution to sequestration, calculated as the product of a surface tension coefficient and the change in solvent accessible surface area of the interacting species, is negligible for our models. However, as described above in the context of Fig. 8, the models presented in this report provide insight into the basic mechanism underlying lateral sequestration.
Our calculations along with complementary experiments (Wang et al., 2002; Rauch et al., 2002; Gambhir et al., 2004) establish that the manner in which unstructured basic sequences interact with PIP2 is dramatically different from the way in which many structured lipid-binding domains, e.g., PH, FYVE, PX, and ENTH domains, interact with poly-phosphoinositides (Lemmon, 2003). Structural studies of these domains with bound ligand show that the interaction with lipid headgroups is highly specific and sensitive to structural and chemical detail. For example, the PH domain of PLC-δ1 binds specifically to PI(4,5)P2 over PI(3,4)P2 and monovalent acidic lipids such as PS. In addition, the binding of these structured domains to poly-phosphoinositides functions mainly to target proteins to membrane surfaces (Hurley and Meyer, 2001; Itoh and Takenawa, 2002). For example, the PH domains of PLC-δ1 targets this enzyme to the plasma membrane, which is enriched in PIP2. In contrast, unstructured basic sequences do not require PIP2 to anchor the protein to the membrane, but, as predicted theoretically and observed experimentally, will laterally sequester PIP2 when membrane bound. The electrostatic sequestration is predicted to serve a reversible buffering function for MARCKS: PIP2 lipids can be transiently protected from at least some proteins that bind, hydrolyze, or phosphorylate them when cells are in their resting state (e.g., electrostatic sequestration of PIP2 decreases the hydrolysis catalyzed by PLC). Signals that mediate the dissociation of the basic sequences from membranes, such as PKC phosphorylation of the effector domain of MARCKS or GAP43, would then provide free localized pools of PIP2 upon cellular stimulation (McLaughlin et al., 2002). PIP2 binds to clusters of basic/aromatic residues on several ion channels (Hilgemann et al., 2001; Runnels et al., 2002; Prescott and Julius, 2003), but the mechanism by which this binding activates or inhibits the channel is not known.
In addition, this sequestration mechanism may play a role in the organization and regulation of macromolecular complexes thought to function in signaling and vesicle trafficking pathways (Czech, 2000; Martin, 2001; Cantley, 2002; Yin and Janmey, 2003). The positive potential produced by membrane-adsorbed basic sequences, illustrated in Fig. 8, should provide a basin of attraction for other poly-valent acidic lipids, such as the important signaling lipid PI(3,4,5)P3, as well as for negatively charged proteins, such as Ca2+/calmodulin, which binds to the basic effector domain on MARCKS (Arbuzova et al., 1997) through additional short-range interactions (Yamauchi et al., 2003). In general, the electrostatic profile of the plasma membrane surface is expected to be quite complex and may produce driving forces for many types of lateral interactions.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Supplementary Material
Acknowledgments
The authors are grateful for fruitful discussions with Avinoam Ben-Shaul.
S.M. acknowledges the support of the National Institutes of Health (grant GM24971). D.M. acknowledges the support of the National Science Foundation (grant MCB0212362). The calculations were performed, in part, on the computers at the Pittsburgh Supercomputing Center (grant MCB020020P) and the Advanced Biomedical Computing Center (NCI, Frederick, MD).
References
- Arbuzova, A., D. Murray, and S. McLaughlin. 1998. MARCKS, membranes and calmodulin: kinetics of interaction. Biochim. Biophys. Acta. 1376:369–379. [DOI] [PubMed] [Google Scholar]
- Arbuzova, A., J. Wang, D. Murray, J. Jacob, D. S. Cafiso, and S. McLaughlin. 1997. MARCKS, membranes, and calmodulin: Kinetics of interaction. J. Biol. Chem. 272:27167–27177. [DOI] [PubMed] [Google Scholar]
- Arbuzova, A., L. Wang, J. Wang, G. Hangyas-Mihalyne, D. Murray, B. Honig, and S. McLaughlin. 2000. Membrane binding of peptides containing both basic and aromatic residues. Experimental studies with peptides corresponding to the scaffolding region of caveolin and the effector region of MARCKS. Biochemistry. 39:10330–10339. [DOI] [PubMed] [Google Scholar]
- Baker, N. A., D. Sept, M. J. Holst, and J. A. McCammon. 2001. Electrostatics of nanosystems: application to microtubules and the ribosome. Proc. Natl. Acad. Sci. USA. 98:10037–10041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ben-Tal, N., B. Honig, C. Miller, and S. McLaughlin. 1997. Electrostatic binding of proteins to membranes: theoretical prediction and experimental results with charybdotoxin and phospholipid vesicles. Biophys. J. 73:1717–1727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ben-Tal, N., B. Honig, R. M. Peitzsch, G. Denisov, and S. McLaughlin. 1996. Binding of small basic peptides to membranes containing acidic lipids: theoretical models and experimental results. Biophys. J. 71:561–575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blackshear, P. J. 1993. The MARCKS family of cellular protein kinase C substrates. J. Biol. Chem. 268:1501–1504. [PubMed] [Google Scholar]
- Brooks, B. R., R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan, and M. Karplus. 1983. CHARMM: a program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 4:187–217. [Google Scholar]
- Cantley, L. C. 2002. The phosphoinositide 3-kinase pathway. Science. 296:1655–1657. [DOI] [PubMed] [Google Scholar]
- Carnie, S. L., and G. M. Torrie. 1984. The statistical mechanics of the electrical double layer. In Advances in Chemical Physics. I. Prigogine and S. A. Rice, editors. John Wiley and Sons. New York. 141–253.
- Cockcroft, S. 2000. Biology of phosphoinositides. Oxford University Press, Oxford, UK.
- Czech, M. P. 2000. PIP2 and PIP3: complex roles at the cell surface. Cell. 100:603–606. [DOI] [PubMed] [Google Scholar]
- Davis, M. E., and J. A. McCammon. 1990. Electrostatics in biomolecular structure and dynamics. Chem. Rev. 90:509–521. [Google Scholar]
- De Camilli, P., S. D. Emr, P. S. McPherson, and P. Novick. 1996. Phosphoinositides as regulators in membrane traffic. Science. 271:1533–1539. [DOI] [PubMed] [Google Scholar]
- Diraviyam, K., R. Stahelin, W. Cho, and D. Murray. 2003. Computer modeling of the membrane interaction of FYVE domains. J. Mol. Biol. 328:721–736. [DOI] [PubMed] [Google Scholar]
- Efron, B., and R. Tibshirani. 1993. An Introduction to the Bootstrap. Chapman and Hall, New York.
- Elcock, A. H. 2002. Modeling supramolecular assemblages. Curr. Opin. Struct. Biol. 12:154–160. [DOI] [PubMed] [Google Scholar]
- Ellena, J. F., M. C. Burnitz, and D. S. Cafiso. 2003. Location of the myristoylated alanine-rich C-kinase substrate (MARCKS) effector domain in negatively charged phospholipid bicelles. Biophys. J. 85:2442–2448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferguson, K. M., M. A. Lemmon, J. Schlessinger, and P. B. Sigler. 1996. Structure of the high affinity complex of inositol trisphosphate with a phospholipase C pleckstrin homology domain. Cell. 83:1037–1046. [DOI] [PubMed] [Google Scholar]
- Forrest, L. R., and M. S. Sansom. 2000. Membrane simulations: bigger and better? Curr. Opin. Struct. Biol. 10:174–181. [DOI] [PubMed] [Google Scholar]
- Gallagher, K., and K. A. Sharp. 1998. Electrostatic contributions to heat capacity changes of DNA-ligand binding. Biophys. J. 75:769–776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gambhir, A., G. Mihaly, I. Zaitseva, D. Cafiso, J. Wang, D. Murray, S. Pentyala, S. O. Smith, and S. McLaughlin. 2004. Electrostatic sequestration of PIP2 on phospholipid membranes by basic/aromatic regions of proteins. Biophys. J. 86:2188–2207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilson, M. K., K. A. Sharp, and B. H. Honig. 1987. Calculating the electrostatic potential of molecules in solution: method and error assessment. J. Comput. Chem. 9:327–335. [Google Scholar]
- Glaser, M., S. Wanaski, C. A. Buser, V. Boguslavsky, W. Rashidzada, A. Morris, M. Rebecchi, S. F. Scarlata, L. W. Runnels, G. D. Prestwich, J. Chen, A. Aderem, J. Ahn, and S. McLaughlin. 1996. MARCKS produces reversible inhibition of phospholipase C by sequestering phosphatidylinositol 4,5-bisphosphate in lateral domains. J. Biol. Chem. 271:26187–26193. [DOI] [PubMed] [Google Scholar]
- Haleva, E., N. Ben-Tal, and H. Diamant. 2004. Increased concentration of polyvalent phospholipids in the adsorption domain of a charged protein. Biophys. J. 86:2165–2178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heimburg, T., and D. Marsh. 1996. Thermodynamics of the interaction of proteins with lipid membranes. In Biological Membranes. K. Merz, Jr. and B. Roux, editors. Birkhauser, Boston, MA. 405–64.
- Hilgemann, D. W., S. Feng, and C. Nasuhoglu. 2001. The Complex and Intriguing Lives of PI(4,5)P2 with Ion Channels and Transporters. STKE http://www.stke.org/cgi/content/full/OC_sigtrans; 2001/111/re19:1–8. [DOI] [PubMed]
- Honig, B. H., and A. Nicholls. 1995. Classical electrostatics in biology and chemistry. Science. 268:1144–1149. [DOI] [PubMed] [Google Scholar]
- Hurley, J. H., and T. Meyer. 2001. Subcellular targeting by membrane lipids. Curr. Opin. Cell Biol. 13:146–152. [DOI] [PubMed] [Google Scholar]
- Irvine, R. F. 2002. Nuclear lipid signaling. SciSTKE 150:1–12. [DOI] [PubMed] [Google Scholar]
- Itoh, T., and T. Takenawa. 2002. Phosphoinositide-binding domains. Functional units for temporal and spatial regulation of intracellular signaling. Cell. Signal. 14:733–743. [DOI] [PubMed] [Google Scholar]
- Kim, J., M. Mosior, L. A. Chung, H. Wu, and S. McLaughlin. 1991. Binding of peptides with basic residues to membranes containing acidic phospholipids. Biophys. J. 60:135–148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim, J., T. Shishido, X. Jiang, A. Aderem, and S. McLaughlin. 1994. Phosphorylation, high ionic strength, and calmodulin reverse the binding of MARCKS to phospholipid vesicles. J. Biol. Chem. 269:28214–28219. [PubMed] [Google Scholar]
- Kleinschmidt, J. H., and D. Marsh. 1997. Spin-label electron spin resonance studies on the interactions of lysine peptides with phospholipid membranes. Biophys. J. 73:2546–2555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laux, T., K. Fukami, M. Thelen, T. Golub, D. Frey, and P. Caroni. 2000. GAP43, MARCKS, CAP23 modulate PI(4,5)P2 at plasmalemmal rafts, and regulate cell cortex actin dynamics through a common mechanism. J. Cell Biol. 149:1455–1472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemmon, M. A. 2003. Phosphoinositide recognition domains. Traffic. 4:201–213. [DOI] [PubMed] [Google Scholar]
- Martin, T. F. 2001. PI(4,5)P2 regulation of surface membrane traffic. Curr. Opin. Cell Biol. 13:493–499. [DOI] [PubMed] [Google Scholar]
- Matsuoka, Y., X. Li, and V. Bennett. 2000. Adducin: structure, function and regulation. Cell. Mol. Life Sci. 57:884–895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- May, S., and A. Ben-Shaul. 2003. Membrane-macromolecule interactions and their structural consequences. In Planar Lipid Bilayers and Their Applications. H. T. Tien and A. Ottova-Leitmannova, editors. Elsevier Science. 315–346.
- May, S., D. Harries, and A. Ben-Shaul. 2000. Lipid demixing and protein-protein interactions in the adsorption of charged proteins on mixed membranes. Biophys. J. 79:1747–1760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- May, S., D. Harries, and A. Ben-Shaul. 2002. Macrioin-induced compositional instability of binary fluid membranes. Phys. Rev. Lett. 89:1–4. [DOI] [PubMed] [Google Scholar]
- McLaughlin, S. 1989. The electrostatic properties of membranes. Annu. Rev. Biophys. Biophys. Chem. 18:113–136. [DOI] [PubMed] [Google Scholar]
- McLaughlin, S., and A. Aderem. 1995. The myristoyl-electrostatic switch: a modulator of reversible protein-membrane interactions. Trends Biochem. Sci. 20:272–276. [DOI] [PubMed] [Google Scholar]
- McLaughlin, S., J. Wang, A. Gambhir, and D. Murray. 2002. PIP2 and proteins: interactions, organization and information flow. Annu. Rev. Biophys. Biomol. Struct. 31:151–175. [DOI] [PubMed] [Google Scholar]
- Misra, V., and B. Honig. 1995. On the magnitude of the electrostatic contribution to ligand-DNA interactions. Proc. Natl. Acad. Sci. USA. 92:4691–4695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray, D., A. Arbuzova, G. Mihaly, A. Ghambir, N. Ben-Tal, B. Honig, and S. McLaughlin. 1999. Electrostatic properties of membranes containing acidic lipids and adsorbed basic peptides: theory and experiment. Biophys. J. 77:3176–3188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray, D., A. Arbouzova, B. Honig, and S. McLaughlin. 2002. The role of electrostatic and nonpolar interactions in the association of peripheral proteins with membranes. In Current Topics in Membranes: Peptide-Lipid Interactions. S. A. Simon and T. J. McIntosh, editors. 278–309.
- Murray, D., L. Hermida-Matsumoto, C. A. Buser, J. Tsang, C. Sigal, N. Ben-Tal, B. Honig, M. D. Resh, and S. McLaughlin. 1998. Electrostatics and the membrane association of Src: theory and experiment. Biochemistry. 37:2145–2159. [DOI] [PubMed] [Google Scholar]
- Murray, D., and B. Honig. 2002. Electrostatic control of the membrane targeting of C2 domains. Mol. Cell. 9:145–154. [DOI] [PubMed] [Google Scholar]
- Nicholls, A., K. A. Sharp, and B. Honig. 1991. Protein folding and association: insights from the interfacial and thermodynamic proterties of hydrocarbon. Proteins. 11:281–296. [DOI] [PubMed] [Google Scholar]
- Ohmori, S., N. Sakai, Y. Shira, H. Yamamoto, E. Miyamoto, N. Shimizu, and N. Saito. 2000. Importance of protein kinase C targeting for the phosphorylation of its substrate, myristoylated alanine-rich C-kinase substrate. J. Biol. Chem. 275:26449–26457. [DOI] [PubMed] [Google Scholar]
- Parsegian, V. A., and D. Gingell. 1972. On the electrostatic interaction that occurs across a salt solution between two bodies bearing unequal charges. Biophys. J. 12:1192–1204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pastor, R. W., and S. E. Feller. 1996. Time scales of lipid dynamics and molecular dynamics. In Membrane Structure and Dynamics. K. M. Merz and B. Roux, editors. Birkhauser, Boston, MA. 3–29.
- Payrastre, B., K. Missy, S. Giuriato, S. Bodin, M. Plantavid, and M. Gratacap. 2001. Phosphoinositides: key players in cell signalling, in time and space. Cell. Signal. 13:377–387. [DOI] [PubMed] [Google Scholar]
- Peitzsch, R. M., M. Eisenberg, K. A. Sharp, and S. McLaughlin. 1995. Calculations of the electrostatic potential adjacent to model phospholipid bilayers. Biophys. J. 68:729–738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prescott, E. D., and D. Julius. 2003. A modular PIP2 binding site as a determinant of capsaicin receptor sensitivity. Science. 300:1284–1288. [DOI] [PubMed] [Google Scholar]
- Qin, Z., and D. S. Cafiso. 1996. Membrane structure of the protein kinase C and calmodulin binding domain of myristoylated alanine rich C kinase substrate determined by site-directed spin labeling. Biochemistry. 35:2917–2925. [DOI] [PubMed] [Google Scholar]
- Rauch, M. E., C. G. Ferguson, G. D. Prestwich, and D. Cafiso. 2002. Myristoylated alanine-rich C kinase Substrate (MARCKS) sequesters spin-labeled phosphatidylinositol-4,5-bisphosphate in lipid bilayers. J. Biol. Chem. 277:14068–14076. [DOI] [PubMed] [Google Scholar]
- Raucher, D., T. Stauffer, W. Chen, K. Shen, S. Guo, J. D. York, M. P. Sheetz, and T. Meyer. 2000. Phosphatidylinositol 4,5-bisphosphate functions as a second messenger that regulates cytoskeleton-plasma membrane adhesion. Cell. 100:221–228. [DOI] [PubMed] [Google Scholar]
- Rossi, E. A., H. Feng, and C. S. Rubin. 1999. Characterization of the targeting, binding, and phosphorylation site domains of an A kinase anchor protein and a myristoylated alanine-rich C kinase substrate-like analog that are encoded by a single gene. J. Biol. Chem. 274:27201–27210. [DOI] [PubMed] [Google Scholar]
- Runnels, L. W., L. Yue, and D. Clapham. 2002. The TRPM7 channel is inactivated by PIP2 hydrolysis. Nat. Cell Biol. 4:329–336. [DOI] [PubMed] [Google Scholar]
- Sharp, K. A., and B. H. Honig. 1990a. Calculating total electrostatic energies with the nonlinear Poisson-Boltzmann equation. J. Phys. Chem. 94:7684–7692. [Google Scholar]
- Sharp, K. A., and B. H. Honig. 1990b. Electrostatic interactions in macromolecules: theory and applications. Annu. Rev. Biophys. Biophys. Chem. 19:301–332. [DOI] [PubMed] [Google Scholar]
- Swierczynski, S. L., and P. J. Blackshear. 1995. Membrane association of the myristoylated alanine-rich C kinase substrate (MARCKS) protein. Mutational analysis provides evidence for complex interactions. J. Biol. Chem. 270:13436–13445. [DOI] [PubMed] [Google Scholar]
- Tobias, D. J. 2001. Electrostatic calculations: recent methodological advances and applications to membranes. Curr. Opin. Struct. Biol. 11:253–261. [DOI] [PubMed] [Google Scholar]
- Toker, A. 1998. The synthesis and cellular roles of phosphatidylinositol 4,5-bisphosphate. Curr. Opin. Cell Biol. 10:254–261. [DOI] [PubMed] [Google Scholar]
- Toner, M., G. Vaio, A. McLaughlin, and S. McLaughlin. 1988. Adsorption of cations to phosphatidylinositol 4,5-bisphosphate. Biochemistry. 27:7435–7443. [DOI] [PubMed] [Google Scholar]
- van Paridon, P. A., B. De Kruijff, R. Ouwerkerk, and K. W. Wirtz. 1986. Polyphosphoinositides undergo charge neutralization in the physiological pH range: a 31P-NMR study. Biochim. Biophys. Acta. 877:216–219. [DOI] [PubMed] [Google Scholar]
- Wang, J., A. Arbuzova, G. Hangyas-Mihalyne, and S. McLaughlin. 2001. The effector domain of myristoylated alanine-rich C kinase substrate (MARCKS) binds strongly to phosphatidylinositol 4,5-bisphosphate (PIP2). J. Biol. Chem. 276:5012–5019. [DOI] [PubMed] [Google Scholar]
- Wang, J., A. Gambhir, G. Hangyas-Mihalyne, D. Murray, U. Golebiewska, and S. McLaughlin. 2002. Lateral sequestration of phosphatidylinositol 4,5-bisphosphate by the basic effector domain of myristoylated alanine-rich C kinase substrate is due to nonspecific electrostatic interactions. J. Biol. Chem. 277:34401–34412. [DOI] [PubMed] [Google Scholar]
- Yamauchi, E., T. Nakatsu, M. Matsubara, H. Kato, and H. Taniguchi. 2003. Crystal structure of a MARCKS peptide containing the calmodulin-binding domain in complex with Ca2+-calmodulin. Nat. Struct. Biol. 10:226–231. [DOI] [PubMed] [Google Scholar]
- Yin, H. L., and P. A. Janmey. 2003. Phosphoinositide regulation of the actin cytoskeleton. Annu. Rev. Physiol. 65:761–789. [DOI] [PubMed] [Google Scholar]
- Zhang, W. E., S. Crocker, S. McLaughlin, and S. O. Smith. 2003. Binding of peptides with basic and aromatic residues to bilayer membranes: phenylalanine in the MARCKS effector domain penetrates into the hydrophobic core of the bilayer. J. Biol. Chem. 278:21459–21466. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.