Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Apr;86(4):2165–2178. doi: 10.1016/S0006-3495(04)74276-9

Increased Concentration of Polyvalent Phospholipids in the Adsorption Domain of a Charged Protein

Emir Haleva *, Nir Ben-Tal *, Haim Diamant †
PMCID: PMC1304068  PMID: 15041657

Abstract

We studied the adsorption of a charged protein onto an oppositely charged membrane, composed of mobile phospholipids of differing valence, using a statistical-thermodynamical approach. A two-block model was employed, one block corresponding to the protein-affected region on the membrane, referred to as the adsorption domain, and the other to the unaffected remainder of the membrane. We calculated the protein-induced lipid rearrangement in the adsorption domain as arising from the interplay between the electrostatic interactions in the system and the mixing entropy of the lipids. Equating the electrochemical potentials of the lipids in the two blocks yields an expression for the relations among the various lipid fractions in the adsorption domain, indicating a sensitive dependence of lipid fraction on valence. This expression is a result of the two-block picture but does not depend on further details of the protein-membrane interaction. We subsequently calculated the lipid fractions themselves using the Poisson-Boltzmann theory. We examined the dependence of lipid enrichment, i.e., the ratio between the lipid fractions inside and outside the adsorption domain, on various parameters such as ionic strength and lipid valence. Maximum enrichment was found for lipid valence in the range between −3 and −4 in physiological conditions. Our results are in qualitative agreement with recent experimental studies on the interactions between peptides having a domain of basic residues and membranes containing a small fraction of the polyvalent phosphatidylinositol 4,5-bisphosphate (PIP2). This study provides theoretical support for the suggestion that proteins adsorbed onto membranes through a cluster of basic residues may sequester PIP2 and other polyvalent lipids.

INTRODUCTION

Some membrane-associated proteins are known to bind to membranes nonspecifically through electrostatic interactions (Murray et al., 1997, 2002; Resh, 1999; McLaughlin et al., 2002). These interactions result from the attraction between a cluster of charged residues in the protein and the oppositely charged membrane lipids. As the charged protein approaches the membrane, it changes the local membrane composition in its vicinity. We refer to this protein-affected region on the membrane as the adsorption domain. The lateral fluidity of the membrane allows oppositely charged lipids to migrate toward the adsorption domain to minimize the interaction free energy. Evidence for such redistribution was reported in experimental (Heimburg et al., 1999; Rauch et al., 2002; Wang et al., 2002) and theoretical (Harries et al., 1998; May et al., 2000, 2002; Fleck et al., 2002) studies. Lipid redistribution was observed also in monolayers (Lee et al., 1994; Lee and McConnell, 1995) and bilayers (Groves et al., 1997, 1998) that were subjected to external electric fields.

Local changes in lipid concentration may have biological significance. For example, PIP2, a polyvalent phospholipid with valence in the range from −3 to −5 (Toner et al., 1988; McLaughlin et al., 2002; Rauch et al., 2002; Wang et al., 2002) participates in signal transduction (Czech, 2000; Payrastre et al., 2001; Simonsen et al., 2001). Its average fraction in plasma membranes is very low, ∼1%, and it is known to be concentrated in specific regions of the membrane (Liu et al., 1998; Stauffer et al., 1998). The PIP2 lipid serves as a substrate for phospholipase C (PLC), which cleaves it to two secondary messengers (Katan and Williams, 1997). Another component, the myristoylated alanine-rich C kinase substrate protein (MARCKS), containing an amino acid segment of 13 basic and no acidic residues (Blackshear, 1993; McLaughlin and Aderem 1995), is believed to form a PIP2 “reservoir” in its adsorption domain. As long as PIP2 is concentrated in the MARCKS adsorption domain, PLC is inhibited and cannot catalyze the PIP2 hydrolysis (Wang et al., 2001). It is assumed that upon demand, by phosphorylating the MARCKS effector segment, these lipids are freed for signaling (McLaughlin et al., 2002). Thus the capability of MARCKS to sequester PIP2 potentially affects intracellular signaling.

Lipids of various valences are attracted to the adsorption domain to different extents. This electrostatically induced enrichment is partially balanced by entropy effects that favor homogeneous lipid distribution. Theoretical studies of bilayers composed of neutral and monovalent lipids, where the lipid mobility was taken into account, showed that the formation of a charged lipid domain due to the adsorbed protein is energetically favorable and outweighs entropy effects (e.g., Heimburg et al., 1999; May et al., 2000). Recently, Fleck et al. (2002) presented a detailed formulation for the interactions between charged objects and a membrane composed of lipids of various valences. These studies demonstrate the importance of lipid redistribution in the thermodynamics of protein-membrane adsorption.

Based on the findings of these theoretical studies, we focus in this work on a simplified model for the redistribution of different-valence lipids in the adsorption domain of a charged protein. We start by deriving an expression that relates the fractions of the various lipids in the adsorption domain to their values in the unperturbed membrane. The general expression is restricted, however, to relations between concentrations of different lipids. To obtain the actual concentration values for each lipid type, we use the Poisson-Boltzmann (PB) theory (e.g., Andelman, 1995). The model is then applied to peptide segments, such as a polylysine chain, interacting with a membrane composed of uncharged, monovalent, and trivalent lipids, corresponding to zwiterionic PC, PS, and PIP2, respectively. Finally, the model is evaluated and the biological implications of its results are discussed.

MODEL

A schematic view of the protein-membrane system under study is provided in Fig. 1. In the model, the membrane is considered to be an infinite surface composed of k phospholipid species. Each phospholipid type i is ascribed a fraction (in the unperturbed membrane) φi and a fixed valence zi. (We do not consider pH-dependent dissociation of charged lipids, which was found to have a minor effect compared to lipid mobility; Fleck et al., 2002.) The indices i = 0 and i = 1 are assigned to neutral lipids (z0 = 0) and monovalent anionic ones (z1 = −1), respectively, which are always present in biological membranes. For simplicity, all phospholipids are ascribed the same headgroup area a. (In a more detailed model, one can treat different headgroup areas; Andelman et al., 1994.)

FIGURE 1.

FIGURE 1

Open in a new tab

Schematic view of the protein-membrane system. The protein region interacting with the membrane is modeled as a planar surface of charge density σp, hovering parallel to the membrane at a distance h. The unperturbed membrane is composed of various lipids, each having valence zi and area fraction φi. The interaction region on the membrane, the adsorption domain, has area A and lipid fractions ψi. The whole system is embedded in an ionic solution characterized by a dielectric constant ɛ, Debye screening length κ−1, and temperature T.

We assume that the adsorption domain is a “patch” of finite area A and uniform charge density σm, whose size is much larger than the Debye screening length of the solution κ−1, i.e., κ2A ≫ 1. The screening provided by the surrounding ionic solution ensures a cutoff for the effect of the adsorbed protein on the membrane, justifying the finite-area assumption. The uniform charge density, employed merely for simplicity, can be thought of as an effective or average domain charge density. We thus neglect effects related to charge discreteness. (This assumption becomes invalid in certain circumstances; we shall return to it in the Discussion.) The membrane outside the domain serves as a large reservoir, assumed to be unaffected by the protein. Thus, in this study (similar to the description of May et al., 2002) we regard the membrane as composed of two blocks, the protein-affected adsorption domain, with lipid fractions ψi, and the unaffected remainder of the membrane, with fractions φi. Both blocks are assumed to contain enough molecules to be considered, to a good approximation, as macroscopic phases. (A treatment of finite-size effects can be found in May et al., 2002.) The charge densities 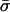Inline graphic and σm, in the protein-free and protein-bound regions, respectively, are defined as:

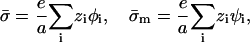graphic file with name M2.gif (1)

where e is the elementary charge.

The free energy per unit area of the bare (protein-free) membrane, F(0), is

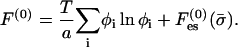graphic file with name M3.gif (2)

The first term is the mixing entropy contribution, where T is the temperature in energy units (taking the Boltzmann constant as unity). We neglect short-range, nonelectrostatic interactions between lipid molecules (May et al., 2002) except for excluded-volume effects. The second term accounts for the electrostatic contribution. Similarly, the free energy per unit area of the protein-bound domain, F, is

graphic file with name M4.gif (3)

where Fes accounts for the electrostatic interactions among the phospholipids and between them and the protein. Note that 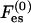Inline graphic and Fes are functions of φi and ψi, respectively, only via the charge densities Inline graphic and σm as defined in Eq. 1. These free energies can be calculated using various theories, e.g., the commonly used PB theory (see Appendix 2). However, at this stage of our formulation, we need not specify the expressions for Inline graphic and Fes at all.

The adsorption domain and the rest of the membrane are at thermodynamic equilibrium, thus the electrochemical potentials μi of each lipid type are equal in the two regions. In addition, the membrane incompressibility adds two constraints:

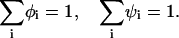graphic file with name M8.gif (4)

The electrochemical potential of phospholipid i in the protein-free membrane is

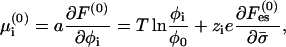graphic file with name M9.gif (5)

and similarly, in the adsorption domain,

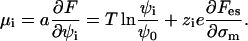graphic file with name M10.gif (6)

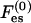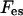In Eqs. 5 and 6 the dependencies on φ0 and ψ0 arise from the incompressibility constraint, Eq. 4. They can be viewed as partial surface pressures exerted by the uncharged species (i = 0) due to excluded-volume effects. (Their surface pressure is equal to −T ln φ0 and −T ln ψ0, respectively, in the bare membrane and in the adsorption domain.) We still have not specified explicit expressions for Inline graphic and Inline graphic. As a particular example, one may assume a mean electric potential (as in PB), having a value Ψ(0)(0) at the bare membrane, and then 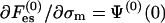Inline graphic. If, in addition, we set φ0 ≃ 1 (low membrane charge), then the familiar expression for the electrochemical potential is recovered, 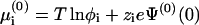Inline graphic (and similarly for μi). Note, however, that the validity of our formulation is more general than this specific example.

Equating 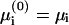Inline graphic we get

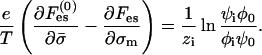graphic file with name M16.gif (7)

Importantly, the left-hand side of Eq. 7 is independent of i. We can therefore compare the right-hand side of the equation for a certain species i with the same expression for the monovalent species (i = 1). This gives a set of equations relating the enrichment ratios for the various lipids,

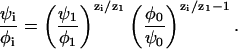graphic file with name M17.gif (8)

We refer to Eq. 8 as the “relative enrichment equation.” It is a set of (k − 2) equations for every i ≠ 0,1. The relative enrichment equation is one of the key results of this work. In the limit of low charge density, φ0,ψ0 ≃ 1, and assuming a mean electric potential having the values Ψ(0)(0) and Ψ(0) at the unperturbed membrane and the adsorption domain, respectively, Eq. 8 is directly related to a Boltzmann relation,

graphic file with name M18.gif (9)

As derived above, however, the applicability of Eq. 8 is more general; it is more accurate and is valid for highly charged membranes and beyond the mean-field approximation. In particular, Eq. 9 implies that the protein does not perturb the local concentration of the neutral lipid, ψ0/φ0 ≃ 1. Yet, as we shall see below, in the biologically relevant case, where the membrane contains a large fraction of monovalent lipid, the neutral lipid is significantly depleted from the adsorption domain. Hence, Eq. 8, rather than Eq. 9, will be used throughout our analysis.

In the absence of protein, the phospholipid composition would not change and both sides of Eq. 8 are trivially equal to 1. Another consequence of Eq. 8 is that perturbation of one lipid fraction necessarily entails perturbation in others. In cases where the charge density in the adsorption domain increases (in absolute value), 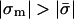Inline graphic, neutral phospholipids will be depleted from the domain to allow the entrance of charged ones, φ0/ψ0 > 1. The relative enrichment of lipid i, ψi/φi, is then at least that of the monovalent one raised to the power |zi|.

As an example, let us consider the binding of a basic protein to a membrane containing uncharged zwiterionic lipids (e.g., PC), monovalent lipids (e.g., PS), and trivalent ones (e.g., PIP2). According to Eq. 8, the polyvalent enrichment ratio will be stronger than that of the monovalent fraction by at least a power of zi/z1 = 3. This is a strong effect. If the monovalent concentration increases twofold, the trivalent concentration will increase by a factor of 23 = 8. Similarly, a slight decrease in the negative charge of the adsorption domain leads to a significant decrease in polyvalent fraction. This entropy-driven enhancement of high-valence ion concentration is an example of a more general phenomenon manifest, e.g., in the favorable accumulation of dissolved polyvalent ions near charged surfaces or polyelectrolytes (e.g., Rouzina and Bloomfield, 1996). Note again that the relative enrichment equation is independent of the specific expressions for 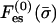Inline graphic and Fes(σm). It does not depend explicitly on details such as the distance between the protein and membrane, or the protein charge.

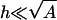Equation 8 provides us only with a relation between the different fractions ψi. To calculate the actual values of ψi we need to derive explicit expressions for the electrochemical potentials Inline graphic and μi. To this end, we must introduce details of the protein. It is treated, for simplicity, as a flat surface of uniform charge density σp located at a distance h parallel to the membrane (see Fig. 1). This schematic description may be relevant to proteins that have a flat cluster of basic residues facing the membrane at close proximity, whereas the rest of the charged residues are further away, screened by the ionic solution. We regard the protein-membrane distance h as an external parameter determined by other interactions (e.g., desolvation effects), which are not taken into account in our theory. We further assume that h is small enough (Inline graphic), such that the induced adsorption domain on the membrane and the interacting cluster on the protein can be taken to have roughly the same area A.

We apply the commonly used mean-field Poisson-Boltzmann (PB) theory (e.g., Andelman, 1995; Gilson, 1995; Honig and Nicholls, 1995) to calculate the electrochemical potentials 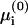Inline graphic and μi. The applicability of this theory to solutions containing polyvalent ions is questionable (e.g., Netz, 2001). However, in the systems discussed here the polyvalent ions (phospholipids) are restricted to the membrane and their mol fraction is much smaller than that of the monovalent lipids, in accord with biological conditions. The more mobile salt ions in the aqueous solution are assumed to be monovalent. Polyvalent ions thus enter the PB calculation merely as a (minor) contribution to the membrane surface charge. As such they should not induce strong correlations, and the PB theory should be applicable. (An exception, where the polyvalent lipid is the majority charge in the membrane and simple electrostatic models indeed seem to fail, will be presented in the Discussion.)

We derive 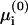Inline graphic and μi using three alternative levels of approximation, all of which are discussed in detail in Appendix 1. In presenting the three methods we wish to demonstrate that even a much simplified approach, involving minimum computation, still gives useful results. The nonlinear problem (NLPB) resulting from the PB theory can only be treated numerically. Subsequently, we examine a further approximation where the PB expressions are linearized. This approximation is valid when the electrostatic potential Ψ is much smaller than T/e everywhere (Andelman, 1995). Although this condition is not fulfilled in the relevant biological systems, the two derivations give similar results for reasons that are discussed in Appendix 1. The LPB approximation allows us to derive analytical expressions for μi, yet solutions for the various lipid fractions (i.e., for the equations 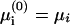Inline graphic) still cannot be obtained in closed form.

The fact that, in most relevant systems, the electrostatic interactions dominate over entropy effects (May et al., 2000) led us to examine one last approximation, in which the derivation is divided into two stages. In the first, we neglect entropy when equating 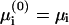Inline graphic. This implies that the electrostatic potential is uniform along the membrane (i.e., the membrane behaves as a perfect conductor). The resulting membrane charge density in the adsorption domain is

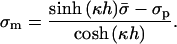graphic file with name M27.gif (10)

In the second stage, this value of σm is substituted in Eq. 1. Equations 1, 4, and 8 (the latter incorporating the effect of entropy) thus provide a closed set of k polynomial equations that can be easily solved for the k lipid fractions ψi. We refer to this scheme as the simplified linear Poisson-Boltzmann method (SLPB).

RESULTS

To study the effects of protein adsorption on a mixed membrane, we calculated the lipid fractions for several representative conditions. Our aim was to examine the redistribution of different-valence lipids in the adsorption domain of a membrane-adsorbed protein as a function of several parameters: protein-membrane distance, protein charge, and the valence of the most charged lipid species. Unless otherwise stated, we used physiological values for the Debye length (κ−1 = 10 Å), temperature (300 K), dielectric constant of water (ɛ = 80), and lipid headgroup area (a = 70 Å2). Throughout the text, the notation 69%/30%/1% uncharged/monovalent/polyvalent was used to describe the unperturbed membrane composition (φi values). For consistency, the results presented in this section were all obtained using the more elaborate NLPB method.

Enrichment as a function of protein-membrane distance

The enrichment ratio, ψi/φi, was calculated for the association of a charged protein with a membrane composed of 69% neutral (zwiterionic), 30% monovalent, and 1% trivalent lipids (in the absence of a protein). This implies an average charge density 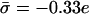Inline graphic per lipid headgroup area. We present the enrichment arising from a protein that is slightly more charged than the membrane, Inline graphic. (These values are typical to protein-membrane interactions, as demonstrated below.) Fig. 2 shows the enrichment ratios as a function of protein-membrane distance.

FIGURE 2.

FIGURE 2

Open in a new tab

Protein–membrane distance effect. Enrichment ratios (ψi/φi) of uncharged (dotted), monovalent (dashed), and trivalent (solid) lipid fractions in the adsorption domain of a protein as a function of the protein-membrane distance h, scaled by the Debye length κ−1. The unperturbed membrane contains 69%/30%/1% uncharged/monovalent/trivalent lipid fractions. The charge density of the protein is 1.3-fold that of the unperturbed membrane and of opposite sign. The inset shows the actual lipid fractions. Although quite similar in charge density to the membrane, the protein causes a marked change in lipid composition. Note the relatively large increase in the trivalent lipid fraction.

Far from the membrane (h ≫ κ−1) the protein charge is screened and its effect on the membrane is weak. As the charged protein approaches the membrane, oppositely charged lipids move into the adsorption domain whereas the neutral lipids are depleted from it. The choice of similar charge densities (in absolute value) for the protein and membrane leads to minor changes in the fractions of the abundant (neutral and monovalent) lipids, even at distances smaller than κ−1. Notably, the fraction of trivalent lipids changes by a much larger factor of ∼3. This result is a consequence of the exponential dependence of the enrichment on lipid valence as seen in Eq. 8.

The nonmonotonic behavior at small distances, shown in Fig. 2, is a delicate point that deserves further discussion. If the membrane charge density had a fixed value σm ≠ −σp, then, at a sufficiently short distance, the mutual attraction between the surfaces would turn into repulsion (Parsegian and Gingell, 1972). This is caused by the increased concentration of the salt ions, which are bound to remain in the confined volume between the protein and membrane to neutralize the system. In our case, however, the system has the additional freedom to change σm. As a result, the electrostatic contribution to the free energy of the protein-membrane interaction decreases monotonously with decreasing distance, i.e., the interaction is purely attractive (cf. Fig. 11). (The effect of charge mobility on the interaction between two membranes has been studied in detail recently; Russ et al., 2003.) As long as the two objects are not too close, it may become favorable to overcharge the membrane and gain attraction energy. This is what happens in the system of Fig. 2 for κh < 1. For example, at κh = 0.5, we find 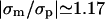Inline graphic. In such a case of overcharging, as the distance is further reduced, the osmotic pressure of the salt ions at short distances causes the membrane to decrease its charge density to lower the energetic penalty of further compression (Fig. 2 in the range κh ≲ 0.5). At contact (κh = 0) we have σm = −σp, such that the system is neutral without mobile ions. Thus, the ability to redistribute the lipids allows the system to avoid high concentration of ions in the solution.

FIGURE 11.

FIGURE 11

Open in a new tab

Contribution from electrostatics and entropy within the smeared charge model to the free energy of peptide–membrane interaction. Free energy in units of T as a function of the peptide–membrane distance. The curves correspond to FA-MARCKS(151–175) and membrane compositions of 69%/30%/1% (solid), 77%/18%/5% (dash-dotted), 72%/17%/1% (dashed), and 90%/10%/0% (dotted). The vertical dotted line indicates a distance of κh = 0.3. The presented contribution to the free energy decreases monotonously with distance. The solid and dash-dotted curves correspond to membranes of very different lipid compositions but of the same charge density, −0.33 e/a).

Effect of protein charge

In Fig. 3 we present the enrichment ratios (ψi/φi) of the different lipid species as a function of the protein charge density for a given protein-membrane distance and membrane composition. As expected, when the protein is highly charged, the adsorption domain is strongly enriched with oppositely charged lipids. On the other hand, at low protein charge, depletion of charged lipids is observed. Remarkably, in both cases, the trivalent species exhibits a much stronger effect than the monovalent one. This is again a consequence of the sensitive dependence of the enrichment ratio on lipid valence (Eq. 8). In between the strongly charged and weakly charged limits, there is a value of σp for which the membrane is unperturbed (see arrow in Fig. 3). This point does not correspond to 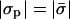Inline graphic, as might have been expected. As discussed in the previous subsection, for a nonzero protein-membrane distance the membrane may become overcharged. As a result, this special point where ψi/φi = 1 is obtained for 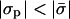Inline graphic. For example, for the parameters of Fig. 3 it occurs at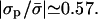 Inline graphic

FIGURE 3.

FIGURE 3

Open in a new tab

Protein charge effect. Enrichment ratios (ψi/φi) of the uncharged (dotted), monovalent (dashed), and trivalent (solid) lipids in the adsorption domain of a protein as a function of its charge density (in units of elementary charge per 1000 Å2). The inset shows the actual lipid fractions. The unperturbed membrane contains 69%/30%/1% uncharged/monovalent/trivalent lipid fractions, corresponding to 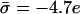Inline graphic per 1000 Å2 and the protein-membrane distance is κh = 0.3. The enrichment in charged lipids increases with protein charge. The arrow indicates the σp value for which the membrane is unperturbed.

Effect of lipid valence

Equation 8 implies that, the higher the valence |z2| of the lipid, the stronger its enrichment, ψ2/φ2, relative to that of the monovalent species, ψ1/φ1. This does not imply that ψ2/φ2 per se (not relative to ψ1/φ1) increases monotonously with |z2|. In fact, there is a competition between two opposing effects. The first, which is entropy driven, favors charging of the adsorption domain by high-valence lipids to minimize the perturbation of membrane composition. On the other hand, from simple stoichiometry, only a small concentration of a high-valence lipid is needed to attain a given membrane charge density. The competition should result in a maximum of ψ2/φ2 at a certain value of valence 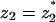Inline graphic. This is confirmed in Fig. 4, where we present ψ2/φ2 as a function of z2 for a wide range of protein charge densities. (To obtain smoother curves we calculated ψ2/φ2 also for artificial, noninteger values of z2.) For high protein charge, where electrostatic interactions are strong, the entropy effect is negligible and 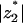Inline graphic is small; for unphysically high protein charge Inline graphic eventually tends to |z1| = 1. At low protein charge, entropy dominates and Inline graphic increases.

FIGURE 4.

FIGURE 4

Open in a new tab

Valence effect. The enrichment ratio of polyvalent lipids (ψ2/φ2) in the adsorption domain of a protein as a function of the lipid valence z2. The different curves correspond to different protein charges, the number on each curve indicating the number of elementary charges per 1000 Å2. Maximum enrichment is marked by a box. The unperturbed membrane composition and protein-membrane distance are the same as in Fig. 3.

As seen in Fig. 4, Inline graphic does not drastically change with protein charge. For reasonable, physiological charge densities (σp of up to ∼10 e/1000 Å2) we find Inline graphic. Thus, lipid enrichment due to the adsorption of an oppositely charged protein will be most effective for a certain lipid valence which, within our idealized model assumptions, seems to be in the range between −3 and −4.

APPLICATION TO PEPTIDE-MEMBRANE INTERACTIONS

In this section we compare the qualitative results of our model with recent experimental studies of the lateral sequestration of the polyvalent lipid PIP2 by adsorbed basic peptides. It should be borne in mind that our simple model can only provide an approximate description of such systems. Treating the interaction region of the peptide as a large flat surface is a particularly severe simplification. We return to this and other weaknesses of the model in the Discussion below.

We focus on two peptides for which there are available experimental data: FA-MARCKS(151–175) and a polylysine chain of 13 residues, (Lys)13. The former corresponds to the basic effector segment of the MARCKS protein, where five alanine residues were substituted for the original phenylalanine ones (Gambhir et al., 2004; Wang et al., 2004). We avoid dealing with the MARCKS peptide, because experiments indicate that its hydrophobic phenylalanine residues pull the peptide into the membrane such that its backbone penetrates the membrane (Qin and Cafiso, 1996; Zhang et al., 2003). This kind of interaction is expected to be sensitive to specific molecular details, which are not encompassed by our model.

To apply the model, we need an estimate for the area of the peptide that interacts with the membrane to determine the peptide charge density. In addition, this area is assumed to be equal to that of the adsorption domain, A (Fig. 1). We built extended peptides (MOE software 2002, Chemical Computing Group, Montreal, Quebec, Canada), similar to the ones used by Wang et al. (2004). We then defined the effective peptide area as the area of its projected backbone plus an envelope of width κ−1 around it. (This somewhat arbitrary definition will be further examined at the end of this section.) Dividing the number of charged residues in the peptide by this area, we got the estimates σp ≃ 13 e/2120 Å2 and 13 e/1060 Å2 for FA-MARCKS(151–175) and (Lys)13, respectively. Note that for these calculated areas and typical peptide–membrane distances h of a few angstroms, the basic assumption of the model, 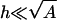Inline graphic, is well satisfied.

We used these estimated σp values to produce Fig. 5, plotting the trivalent lipid fraction in the adsorption domain of each peptide as a function of its distance from the membrane. In accordance with experiments (Gambhir et al., 2004), we took the unperturbed membrane composition to be: φ0 = 82% (corresponding to the uncharged zwiterionic PC lipid), φ1 = 17% (monovalent PS), and φ2 = 1% (trivalent PIP2). Fig. 5 shows that the PIP2 fraction rises to 18% in the (Lys)13 adsorption domain, whereas only 6% PIP2 is obtained in the case of FA-MARCKS(151–175). This is caused by the higher charge density of (Lys)13, roughly double that of FA-MARCKS(151–175). However, FA-MARCKS(151–175) has twice the effective area of (Lys)13; thus, if we examine the average number of PIP2 molecules per peptide adsorption domain, N2, the difference is less significant—whereas N2 ∼ 2.7 for (Lys)13 at κh ≲ 0.3, for FA-MARCKS(151–175) at the same distance N2 ∼ 1.8. (The value of κh ≈ 0.3 corresponds to h ≈ 3 Å at 100 mM salt, which is the approximate peptide-membrane distance; Ben-Tal et al., 1996; Murray et al., 2002. Consequences of this small value will be addressed in the Discussion below.)

FIGURE 5.

FIGURE 5

Open in a new tab

Comparison between lipid rearrangement induced by FA-MARCKS(151–175) and (Lys)13. Trivalent lipid fraction in the adsorption domain of the FA-MARCKS(151–175) (dashed) and (Lys)13 (solid) peptides as a function of their distance from the membrane. The unperturbed membrane is composed of 82%/17%/1% uncharged/monovalent/trivalent lipid fractions. The enrichment caused by (Lys)13 is much stronger than that achieved by FA-MARCKS(151–175) due to its higher (roughly double) charge density.

Next, we examined the dependence of the trivalent lipid (PIP2) fraction in the adsorption domain on φ1, the monovalent lipid fraction in the unperturbed membrane. Fig. 6 presents the results obtained for FA-MARCKS(151–175) and (Lys)13 at various distances. The smaller the value of φ1, the stronger the enrichment in trivalent lipids. When there is a little amount of monovalent lipids, the membrane charge density induced by the peptide-membrane interaction is attained primarily by the trivalent species. Therefore, at φ1 = 0, the enrichment in trivalent lipid is maximum. At that limit, the number of PIP2 molecules per adsorption domain can be simply approximated (at short distances) as the number of charges on the peptide divided by the lipid valence, N2 ≈ |Aσp/(z2e)|. (In practice, however, this example of the polyvalent lipid being the majority charge is problematic, as will be presented in the Discussion.) Fig. 6 shows that, under physiological conditions of 30% monovalent lipid fraction and only 1% PIP2, both peptides sequester PIP2—roughly one molecule per FA-MARCKS(151–175) peptide and approximately two molecules per (Lys)13 peptide. This result is in qualitative agreement with experiments (Gambhir et al., 2004), where (Lys)13 was found to attract PIP2 more strongly than FA-MARCKS(151–175).

FIGURE 6.

FIGURE 6

Open in a new tab

Effect of monovalent lipid concentration. Trivalent lipid fraction (left ordinate) and number (right ordinate) in the adsorption domain of (A) FA-MARCKS(151–175) and (B) (Lys)13 peptides as a function of the peptide–membrane distance. Different curves correspond to membranes of different lipid compositions: 69%/30%/1% (solid), 72%/17%/1% (dashed), and 99%/0%/1% (dotted). The enrichment in the polyvalent lipid increases with decreasing monovalent-lipid fraction.

To emphasize the strong sequestration of the trivalent lipid, consider the case of a 73%/17%/0 PC/PS/PIP2 membrane interacting with (Lys)13. At a short distance the peptide charge will be neutralized by ∼13 PS molecules. For a 72%/17%/1% membrane, as shown by the dashed curve in Fig. 6, there are roughly two to three sequestered PIP2 lipids per (Lys)13, providing six to nine elementary charges. Thus, introducing 1% PIP2 into a membrane of 17% PS leads to replacement of about one half of the PS lipids in the adsorption domain by PIP2. Indication of such an exchange of PS for PIP2 upon addition of a small amount of PIP2 was found in a recent experiment (S. McLaughlin, personal communication).

Interestingly, the concentration, on average, of about two PIP2 molecules per (Lys)13 would not be possible if PIP2 were of much different valence. Fig. 7 shows the average number of PIP2 molecules per adsorption domain of both peptides as a function of the PIP2 hypothetical valence. Similar to the results shown in Fig. 4, we find a nonmonotonic behavior as a function of valence with a maximum at 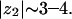Inline graphic It is stressed again that, in view of our simplified model, one should pay more attention to the existence of a competition mechanism, leading to an optimum valence, than to the exact value obtained for that valence.

FIGURE 7.

FIGURE 7

Open in a new tab

Effect of hypothetical PIP2 valence on sequestration. Average number of polyvalent lipids per adsorption domain of FA-MARCKS(151–175) and (Lys)13 as a function of PIP2 valence. Concentration is a maximum for |z2| ∼ 3–4. Both calculations were performed using a membrane composition of 69%/30%/1% uncharged/monovalent/polyvalent lipid fractions in the unperturbed membrane, and a peptide–membrane distance of κh = 0.3.

In Fig. 8 we show the dependence of the trivalent lipid fraction in the adsorption domain on its value in the unperturbed membrane. As expected, ψ2 increases with φ2. This calculation shows that one needs φ2 ≳ 1% to get an average stoichiometry of 1:1 between FA-MARCKS(151–175) and PIP2. As we have seen above, (Lys)13 sequesters PIP2 more effectively. Hence, as demonstrated in Fig. 8, a φ2 value of only 0.1% is sufficient to obtain a 1:1 (Lys)13:PIP2 ratio. That is, (Lys)13 can sequester an appreciable amount of PIP2 even when the membrane contains 300-fold more PS lipids than PIP2. This value is in very good agreement, perhaps fortuitously, with the measurements of Gambhir et al. (2004).

FIGURE 8.

FIGURE 8

Open in a new tab

Effect of φ2 on enrichment. Trivalent lipid fraction (left ordinate) and average number (right ordinate) in the adsorption domain of (A) FA-MARCKS(151–175) and (B) (Lys)13 peptides as a function of the peptide–membrane distance. The two curves correspond to membrane compositions of 69%/30%/1% PC/PS/PIP2 (solid) and 69.9%/30%/0.1% PC/PS/PIP2 (dashed).

Finally, we examined the dependence of the PIP2 enrichment on the ionic strength, i.e., the concentration of mobile salt ions in the solution, n0. This parameter enters into the model through the Debye screening length κ−1, which both scales the distance h and affects the amplitude of the electrostatic potential (see, e.g., Eq. 21 in Appendix 1). Fig. 9 shows that ψ2 decreases with ionic strength. This is a result of the increased screening of the electrostatic attraction between the membrane and protein. The changes are not dramatic up to quite high n0 values. The reason is the very close proximity of the two objects (3 Å) for which κh < 1 in the entire n0 range examined.

FIGURE 9.

FIGURE 9

Open in a new tab

Ionic strength effect. Trivalent lipid fraction in the adsorption domain of FA-MARCKS(151–175) (dashed) and (Lys)13 (solid) peptides as a function of salt concentration. The two curves for each peptide were calculated using membrane compositions of 69%/30%/1% (upper), and 82%/17%/1% (lower). A peptide–membrane distance of h = 3 Å was used.

Effect of approximated peptide size

As discussed above, we define the effective area of the peptide as the area of its projected backbone plus an envelope of width κ−1 around it. This definition, however, is somewhat arbitrary. We therefore examine the effect of relaxing the effective-area definition on the values obtained for N2.

Fig. 10 shows the average number of trivalent lipids N2 per adsorption domain of a 20-amino-acid-long peptide for a range of 1/A values extending to ±50% of our original estimate. In this range the alteration in N2 is limited to ±1 lipid molecules.

FIGURE 10.

FIGURE 10

Open in a new tab

Dependence of polyvalent lipid number on estimated peptide area. Average number of trivalent lipids (N2) as a function of the inverse area of the adsorption domain 1/A. A is also taken as the effective peptide area. The arrow marks the 1/A value according to the definition used throughout this study. Results were obtained for a 10 (dotted), 15 (dashed), and 20 (solid) charged residues in a 20-amino-acid-long peptide interacting with a 69%/30%/1% uncharged/monovalent/trivalent membrane at a distance of κh = 0.3.

Interaction free energy

From the Poisson-Boltzmann theory, as applied to our model, we can calculate the contribution to the free energy of peptide-membrane association coming from electrostatics and entropy. The derivation is given in Appendix 2. The results for the case of FA-MARCKS(151–175) interacting with a membrane of different compositions are presented in Fig. 11. Some of these compositions have also been studied by Gambhir et al. (2004) and Wang et al. (2004). It should be recalled that our model does not take into account repulsive interactions, such as the Born desolvation effect (see Wang et al., 2004). Lipid demixing effects are included in the model, so the local membrane charge density may change due to the peptide. As a result, the electrostatic free energy in our model decreases monotonously as FA-MARCKS(151–175) approaches the membrane. To get the total free energy of association, one ought to add a repulsive interaction at short distances (not included in our model), that would yield a free-energy minimum at a distance of a few angstroms (see, e.g., Wang et al., 2004). Thus, the free-energy values presented in Fig. 11 are probably more negative than the actual binding free energy. More detailed models provide values for the total binding free energy that are roughly one-half the contribution presented here (Wang et al., 2004).

As expected, electrostatic attraction between the peptide and the membrane is proportional to the charge density of the membrane (Fig. 11). The interaction free energy is not sensitive to the specific lipid composition of the membrane, but rather to its average charge density. This result stems from the minor contribution of mixing entropy to the free energy (fourth term in Eq. 23) and the approximate behavior of the membrane in our model as a surface of constant electric potential, which is determined by the average charge density Inline graphic (May et al., 2000). The calculated contribution to the free energy, therefore, is mainly the work required to bring a charged object (protein) into such a potential, regardless of the lipid redistribution. This may also be the reason why finite difference Poisson-Boltzmann (FDPB) calculations (e.g., Ben-Tal et al., 1996; Murray et al., 2002), although ignoring lipid redistribution, often give a good estimate of the binding free energy.

DISCUSSION

Model evaluation

A simplified theoretical model for the effect of an adsorbed charged protein on the distribution of phospholipids in the membrane has been presented. One of the key theoretical results is the relative enrichment equation, Eq. 8, relating the concentrations of various lipid species in the adsorption domain. It should be emphasized that this result is almost model independent. Within a two-block picture, it should hold for any protein-membrane system governed by electrostatics, regardless of particular details of the protein, the strength of the electrostatic interactions, and the validity of a mean-field (Poisson-Boltzmann) assumption. The main physical effect described by this relation is the sensitivity of lipid enrichment to valence, i.e., the increased concentration of polyvalent lipids compared to that of monovalent ones in the adsorption domain.

We have demonstrated how simple Poisson-Boltzmann calculations can be added to Eq. 8 to obtain further details of the membranal interaction region. In most of the biologically relevant cases, including the peptides discussed here, the peptide-membrane distance h is of the order of a few angstroms only (Ben-Tal et al., 1996, 1997; Murray et al., 2001, 2002). In the context of our model, the elaborate Poisson-Boltzmann theory is unnecessary for such a thin water layer between the two charged objects. Nevertheless, it should be recalled that, at any rate, our calculations converge to the correct membrane charge density at small h due to charge neutrality, σm = −σp (cf. Fig. 12 in Appendix 1).

FIGURE 12.

FIGURE 12

Open in a new tab

Comparison of the different computational methods. Trivalent lipid fraction in the adsorption domain of a highly charged protein (σp = 13 e/1000 Å) as a function of the protein-membrane distance. Results were obtained using three methods: nonlinear Poisson-Boltzmann (solid curve), linear Poisson-Boltzmann (dashed curve), and the simplified linear Poisson-Boltzmann (dotted curve). At distances κh < 0.3, where the membrane approaches charge matching, the three methods differ by <10%. The unperturbed membrane composition is the same as in Fig. 3.

The model is focused on the qualitative behavior of electrostatically dominated protein-membrane systems. Our description of the protein-membrane interaction is evidently crude, as it omits the molecular details of this complex system; see the atomistic description used in the companion report of Wang et al. (2004). Thus, effects related to charge discreteness and three-dimensional structure are ignored. Such effects, for example, may play an important role in the membrane adsorption of the MARCKS protein, whose backbone is believed to penetrate the membrane (Zhang et al., 2003) and whose charges are not evenly spaced. Furthermore, we considered only electrostatic and entropy effects while neglecting other interactions (e.g., desolvation). The model is not intended to reproduce such data as the total binding free energy or the optimum protein-membrane distance (e.g., Ben-Tal et al., 1996; Arbuzova et al., 2000). Similarly, the values that have been obtained for the various lipid concentrations should be regarded as rough estimates.

Treating a peptide as a large, flat, uniformly charged surface is probably the gravest simplification of the model, deserving further discussion. The assumption of flatness may be applicable to proteins interacting with the membrane through such effector regions as those described in Wang et al. (2004) and Gambhir et al. (2004). The assumption regarding the lateral extent of the peptide is reasonable in cases where the peptide-membrane distance h is much smaller than both lateral dimensions. For example, in the case of the FA-MARCKS(151–175) discussed above, we estimated the peptide surface area facing the membrane as a rectangle of dimensions 106 Å × 20 Å. The smaller lateral dimension is still significantly larger than the typical value of h ∼ 3 Å. In addition, the fact that this smaller lateral dimension (∼20 Å) is comparable to the screening length may lead, in principle, to significant finite-size effects. Yet, as already noted above, because of the small value of h in the relevant systems, the charge density in the adsorption domain should become insensitive to these details and be determined, to a good approximation, merely by charge neutrality.

The small value of h, on the other hand, raises a difficulty with respect to the smeared-charge simplification. Because h is similar to or smaller than the typical distance between charged groups on the peptide, neglecting charge discreteness is clearly questionable. Spreading the charges of the lipid headgroups evenly over the membrane is problematic as well. Nonetheless, several recent experiments might help us indicate the limits of validity of models based on smeared electrostatics, such as ours. The affinity of FA-MARCKS(151–175) to PC:PS membranes was found to depend linearly on PS fraction (Murray et al., 1999). Adding a small amount of PIP2 to such membranes, having a significant PS fraction, did not change the binding significantly (S. McLaughlin, personal communication). These two observations are in line with simple electrostatic considerations. However, the binding affinity of the same peptide to a membrane of relatively low charge density, composed of 99:1 PC:PIP2, is surprisingly large—similar to that of a 5:1 PC:PS membrane—even though the membrane charge densities in the two cases differ by a factor of ∼5 (Wang et al., 2002). Clearly, the latter observation cannot be accounted for by smeared electrostatics. We therefore believe that our model gives reliable results regarding lipid redistribution only in cases where the membrane has a high “background” charge density, i.e., a large fraction of monovalent lipid, which is the biologically relevant case. For such membranes, as discussed in the previous section, the model predictions are in qualitative agreement with available experiments.

Apart from these assumptions, the model contains another implicit simplification, namely, that all the electric field lines are contained within the aqueous spacing between the membrane and protein. This commonly used assumption is strictly correct in the limit where the objects are either infinitely thick or of a vanishing dielectric constant. As will be reported elsewhere, we find that this approximation is, in fact, still good for objects of ɛ = 2 and thickness as small as one-third the Debye length.

On the positive side, the simplified model presented here provides new insights into lipid redistribution caused by protein adsorption. Although most of the results presented in this work were obtained using a numerical solution of the nonlinear Poisson-Boltzmann equation, we have demonstrated how one can get the same qualitative results using a much simpler calculation, the SLPB method, involving merely a set of polynomial equations (see Appendix 1). Such a scheme may serve as a better starting point for more detailed numerical calculations, e.g., FDPB (Honig et al., 1993). In most of the current FDPB calculations, a predefined membrane composition identical to that of the bare membrane is used (Ben-Tal et al., 1996, 1997; Murray et al., 1999; Wang et al., 2004). This arbitrary description of the adsorption domain may be improved if one uses a preliminary analysis of the type presented here to produce an approximate lipid configuration.

Future extensions of this work may include phenomena such as elastic deformation of the membrane (Dan et al., 1993; May, 2000), adsorption of multiple proteins (May et al., 2000, 2002), nonuniform charge density in the adsorption domain (May et al., 2000), and acid dissociation at different pH values (Fleck et al., 2002).

Biological implications

ENTH, FYVE, PX, and other membrane-association domains use predefined stereochemistry to recognize poly-phosphoinositides (McLaughlin et al., 2002; Lemmon, 2003). These domains, which are commonly found in proteins involved in intracellular signaling, bind tightly to the poly-phosphoinositides, often via ion pairs, anchoring the protein firmly and irreversibly to membrane surfaces. The binding specificity is reflected in the evolutionary conservation across the homologous domains comprising the family; usually the amino acid residues that mediate the poly-phosphoinositides binding are strictly conserved and can often serve as sequence signatures to recognize these domains using sequence analysis tools.

Here we dealt with a much less specific, and often reversible, mode of membrane recognition via a cluster of basic residues on the membrane-facing region of the protein. These residues interact electrostatically with acidic lipids in the adsorption domain on the bilayer surface. Our model showed that in such cases membrane association induces a preference for polyvalent lipids such as PIP2 to sequester in the adsorption domain. The number of sequestered polyvalent lipids may be regulated by the charge density and size of the membrane-interaction region on the protein. This result supports the suggestion, advocated in the accompanying papers (Gambhir et al., 2004; Wang et al., 2004), that membrane-associated proteins such as adducin (Matsuoka et al., 2000), DAKAP200 (Rossi et al., 1999), GAP43 (Laux et al., 2000), MARCKS (Wang et al., 2002), and MacMARCKS (Blackshear, 1993), which contain a cluster of basic residues, may create a reservoir of PIP2 molecules in their adsorption domain (McLaughlin et al., 2002). It may further imply that the membrane-interaction region of such proteins does not have to be strictly conserved evolutionarily; it should only preserve a specific charge density, as in C2 domains (Murray and Honig, 2002). This speculation, naturally, needs to be checked in future studies.

We found that, when all other parameters are held fixed, there is an optimum value of lipid valence that yields maximum enrichment in the adsorption domain (Figs. 4 and 7). This value, resulting from a competition between entropy and stoichiometry, is found to be at reasonable valence values (e.g., 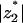Inline graphic = 3–4 in the examples above). Thus, if in a certain biological scenario there is a need to increase the local concentration of a phospholipid by electrostatic interactions, a polyvalent lipid of valence larger than 1 but not too large (say, ∼−3) would be advantageous. The valence of PIP2, considered to be between −3 and −5 (Toner et al., 1988; McLaughlin et al., 2002; Rauch et al., 2002; Wang et al., 2002) appears to be in line with this criterion.

Assuming a certain valence for PIP2 and a certain distance for peptide association with the membrane, our model enables the derivation of a set of approximate rules relating the number of basic residues on the peptide to the average number of sequestered PIP2 molecules per peptide. For example, assuming a trivalent PIP2 and association distance of ∼3 Å, under physiological conditions, each segment of seven consecutive lysine residues of an adsorbed poly-lysine peptide such as (Lys)13 (Fig. 6 B) would sequester on the average approximately one PIP2 molecule when the membrane composition is 69%/30%/1% uncharged/monovalent/trivalent, and roughly one-and-a-half PIP2 molecules when the membrane composition is 82%/17%/1%. These results are in good agreement with the detailed calculations reported in the companion report of Wang et al. (2004).

Acknowledgments

We thank S. McLaughlin and D. Murray for providing us with draft copies of their papers before submission, and we are grateful to S. McLaughlin for comments on the manuscript and for valuable discussions. We benefited from discussions with D. Andelman, Y. Burak, M. Gutman, and M. Kozlov.

H.D. acknowledges support from the Israeli Council of Higher Education (Alon Fellowship).

APPENDIX 1: METHODS FOR CALCULATING LIPID CONCENTRATIONS

In this section we present the method for calculating the values of ψi. We present three levels of approximation and compare their results.

In thermodynamic equilibrium the electrochemical potentials of each lipid species in the protein-free membrane and in the protein adsorption domain should be equal, Inline graphic. Within a mean-field approximation, this condition can be written as

graphic file with name M46.gif (11)

where Ψ(0)(0) is the mean electrostatic potential at the bare membrane, and Ψ(0) its value at the adsorption domain. Equation 11 is actually a set of (k − 1) equations for every species i ≠ 0. The incompressibility condition, ∑iψi = 1, closes a set of k equations for the k unknown ψi. To solve these equations we need the surface potentials Ψ(0)(0) and Ψ(0). We derive them using the Poisson-Boltzmann theory. Note that Ψ(0) depends on the variables ψi that determine the charge density of the adsorption domain, σm.

Nonlinear Poisson-Boltzmann

To find the surface potentials we need to solve the Poisson-Boltzmann equation,

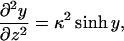graphic file with name M47.gif (12)

with the appropriate boundary conditions. In Eq. 12 y is the local dimensionless potential at a distance z from the membrane, y(z) ≡ eΨ(z)/T. Note that this equation holds only for salt comprised of monovalent ions.

For the bare membrane the boundary conditions are

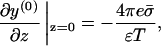graphic file with name M48.gif (13)

and vanishing of the field at z → ∞. This problem, of a single charged plate in an electrolyte, is analytically solvable in closed form (Andelman, 1995). The result is

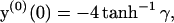graphic file with name M49.gif (14)

where γ is the positive root of the quadratic equation 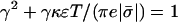Inline graphic. (We have assumed the membrane to be negatively charged.)

For the protein-membrane system, the boundary conditions are

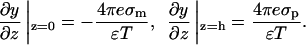graphic file with name M51.gif (15)

Integrating the Poisson-Boltzmann equation (Eq. 12) once while applying both boundary conditions, we get

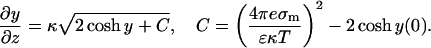graphic file with name M52.gif (16)
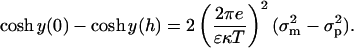graphic file with name M53.gif (17)

We then integrate Eq. 16 to get

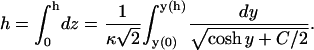graphic file with name M54.gif (18)

Equations 17 and 18 are solved numerically for the two unknowns y(0) and y(h), the surface potentials of the membrane and protein. Finally, the values of y(0) and y(0)(0) (Eq. 14) are used in Eq. 11 to calculate the values of ψi.

Linear Poisson-Boltzmann

The LPB approximation holds when the electrostatic interactions are weak compared to T, y ≪ 1. (In fact, the systems relevant to our study are far from this limit; cf. Fig. 11.) In this limit we can linearize the Poisson-Boltzmann equation (Eq. 12),

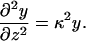graphic file with name M55.gif (19)

The surface potential of the unperturbed membrane then takes the form (Evans and Wennerstrom, 1994),

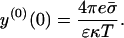graphic file with name M56.gif (20)

For the protein-membrane system we integrate Eq. 19 twice while applying the boundary conditions (Eq. 15) to obtain (Parsegian and Gingell, 1972)

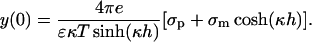graphic file with name M57.gif (21)

The potential values of Eqs. 20 and 21 are then used in Eq. 11 to calculate the ψi values.

Simplified linear Poisson-Boltzmann

In this further approximation the entropy is neglected in 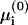Inline graphic and μi, and we are left with a uniform surface potential y(0) = y(0)(0). Note that the entropy contribution is not necessarily small compared to T. The strong enrichment in trivalent lipid, as demonstrated in Figs. 3 and 12, entails an entropy penalty of a few T. Yet, it is still much smaller than the electrostatic contribution, which amounts to tens of T (cf. Fig. 11).

Within the LPB approximation we can equate Eqs. 20 and 21 to obtain the charge density in the adsorption domain in closed form as given in Eq. 10 (May et al., 2000). Substituting σm in Eq. 1 yields a set of k equations, Eqs. 1, 4, and 8, which are easily solved for the k lipid fractions ψi.

Comparison of the methods

Here we compare the NLPB, LPB, and SLPB calculation methods for a specific example. In the limit of weak electrostatic interactions compared to the thermal energy T the LPB method should coincide with the NLPB one. To highlight the difference between the methods we therefore chose as an example a highly charged protein (σp = 13 e/1000 Å2). The trivalent lipid fractions in the adsorption domain, as calculated using the three methods, are plotted in Fig. 12. For both long and short distances all three curves match. In the long distance limit (κh ≫ 1), the protein-membrane interaction is weak and the linearization of the Poisson-Boltzmann equation is valid. At very short distances the membrane, as described by all three methods, is forced by charge neutrality to match the charge density of the protein (in opposite sign). In the intermediate range the methods differ, yet because of the two constraints at κh ≪ 1 and κh ≫ 1 the differences are mild. It is noteworthy that at distances κh ≲ 0.3 (typical to protein-membrane adsorption), the calculated ψi values obtained using the three methods differ by <10%, and the difference in magnitude between the charge densities of the protein and membrane are also <10%.

APPENDIX 2: FREE-ENERGY CALCULATION

In this appendix we calculate the free energy of protein-membrane interaction as arising from our model. It should be recalled that what is presented here is not the total binding free energy but only the contributions due to simple electrostatics and entropy. In particular, because charges are allowed to redistribute in the membrane, the interaction is purely attractive and the free energy decreases monotonously with distance, reaching its minimum at h = 0. This should be contrasted with the FDPB calculations (e.g., Ben-Tal et al., 1996; Wang et al., 2004), which take desolvation into account and yield a free-energy minimum at a finite distance.

The general form of the free energy per unit area within a mean-field approximation is

graphic file with name M59.gif (22)

The first term in Eq. 22 is the energy associated with the mean electric field. The second term corresponds to the interaction of the mobile ions with the field, where n+ and n− are the local concentrations of the monovalent positive and negative ions. The second integral accounts for the ideal entropy of mixing of the mobile ions and their contact with ion reservoirs having chemical potentials μ+ and μ−. The last four terms correspond to the surface energy of the membrane and protein, including mixing entropy of the lipids and electrostatic interactions.

Setting the variations of F with respect to n+, n−, and Ψ to zero, one properly recovers the Boltzmann relations for the mobile ions, the Poisson equation, and, hence, also the Poisson-Boltzmann equation. Using these results along with Eq. 16, and changing the integration variable from z to y, we obtain the following simplified expression for the free energy:

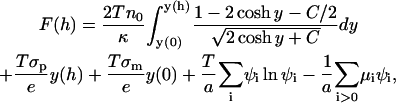graphic file with name M60.gif (23)

where the constant C was defined in Eq. 16. We can now use the values obtained for y(0), y(h), μi, and ψi, as described in Appendix 1, to calculate the free energy of interaction F(h).

References

  1. Andelman, D., M. M. Kozlov, and W. Helfrich. 1994. Phase transitions between vesicles and micelles driven by competing curvatures. Europhys. Lett. 25:231–236. [Google Scholar]
  2. Andelman, D. 1995. Electrostatic properties of membranes: the Poisson Boltzmann theory. In Structure and Dynamics of Membranes, 2nd Ed, Vol 1B. R. Lipowsky and E. Sackmann, editors. Elsevier, Amsterdam, The Netherlands. 603–642.
  3. Arbuzova, A., L. Wang, J. Wang, G. Hangyas-Mihalyne, D. Murray, B. Honig, and S. McLaughlin. 2000. Membrane binding of peptides containing both basic and aromatic residues. Experimental studies with peptides corresponding to the scaffolding region of caveolin and the effector region of MARCKS. Biochemistry. 39:10330–10339. [DOI] [PubMed] [Google Scholar]
  4. Ben-Tal, N., B. Honig, R. M. Peitzsch, G. Denisov, and S. McLaughlin. 1996. Binding of small basic peptides to membranes containing acidic lipids: theoretical models and experimental results. Biophys. J. 71:561–575. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Ben-Tal, N., B. Honig, C. Miller, and S. McLaughlin. 1997. Electrostatic binding of proteins to membranes. Theoretical predictions and experimental results with charybdotoxin and phospholipid vesicles. Biophys. J. 73:1717–1727. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Blackshear, P. J. 1993. The MARCKS family of cellular protein kinase C substrates. J. Biol. Chem. 268:1501–1504. [PubMed] [Google Scholar]
  7. Czech, M. P. 2000. PIP2 and PIP3: complex roles at the cell surface. Cell. 100:603–606. [DOI] [PubMed] [Google Scholar]
  8. Dan, N., P. Pincus, and S. A. Safran. 1993. Membrane-induced interactions between inclusions. Langmuir. 9:2768–2771. [Google Scholar]
  9. Evans, D. F., and H. Wennerstrom. 1994. The Colloidal Domain, Where Physics, Chemistry, Biology, and Technology Meet, 2nd Ed. VCH Publishers, New York.
  10. Fleck, C., R. R. Netz, and H. H. von Grünberg. 2002. Poisson-Boltzmann theory for membranes with mobile charged lipids and the pH-dependent interaction of a DNA molecule with a membrane. Biophys. J. 82:76–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Gambhir, A., G. Hangyás-Mihályné, I. Zaitseva, D. Cafiso, J. Wang, D. Murray, S. Pentyala, S. Smith, and S. McLaughlin. 2004. Electrostatic sequestration of PIP2 on phospholipid membranes by basic/aromatic regions of proteins. Biophys. J. 86:2188–2207. [DOI] [PMC free article] [PubMed]
  12. Gilson, M. K. 1995. Theory of electrostatic interactions in macromolecules. Curr. Opin. Struct. Biol. 5:216–223. [DOI] [PubMed] [Google Scholar]
  13. Groves, J. T., S. G. Boxer, and H. M. McConnell. 1997. Electric field-induced reorganization of two-component supported bilayer membranes. Proc. Natl. Acad. Sci. USA. 94:13390–13395. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Groves, J. T., S. G. Boxer, and H. M. McConnell. 1998. Electric field-induced critical demixing in lipid bilayer membranes. Proc. Natl. Acad. Sci. USA. 95:935–938. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Harries, D., S. May, W. M. Gelbart, and A. Ben-Shaul. 1998. Structure, stability, and thermodynamics of lamellar DNA-lipid complexes. Biophys. J. 75:159–173. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Heimburg, T., B. Angerstein, and D. Marsh. 1999. Binding of peripheral proteins to mixed lipid membranes: effect of lipid demixing upon binding. Biophys. J. 76:2575–2586. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Honig, B., K. Sharp, and A. Suei-Yang. 1993. Macroscopic models of aqueous solutions: biological and chemical applications. J. Phys. Chem. 97:1101–1109. [Google Scholar]
  18. Honig, B., and A. Nicholls. 1995. Classical electrostatics in biology and chemistry. Science. 268:1144–1149. [DOI] [PubMed] [Google Scholar]
  19. Katan, M., and R. L. Williams. 1997. Phosphoinositide-specific phospholipase C: structural basis for catalysis and regulatory interactions. Semin. Cell Dev. Biol. 8:287–296. [DOI] [PubMed] [Google Scholar]
  20. Laux, T., K. Fukami, M. Thelen, T. Golub, D. Frey, and P. Caroni. 2000. GAP43, MARCKS, and CAP23 modulate PI(4,5)P(2) at plasmalemmal rafts, and regulate cell cortex actin dynamics through a common mechanism. J. Cell Biol. 149:1455–1472. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Lee, K. Y. C., J. F. Klinger, and H. M. McConnell. 1994. Electric-field-induced concentration gradients in lipid monolayers. Science. 263:655–658. [DOI] [PubMed] [Google Scholar]
  22. Lee, K. Y. C., and H. M. McConnell. 1995. Effect of electric-field gradients on lipid monolayer membranes. Biophys. J. 68:1740–1751. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Lemmon, M. A. 2003. Phosphoinositide recognition domains. Traffic. 4:201–213. [DOI] [PubMed] [Google Scholar]
  24. Liu, Y., L. Casey, and L. J. Pike. 1998. Compartmentalization of phosphatidlyinositol 4,5- bisphosphate in low-density membrane domains in the absence of caveolin. Biochem. Biophys. Res. Commun. 245:684–690. [DOI] [PubMed] [Google Scholar]
  25. Matsuoka, Y., X. Li, and V. Bennett. 2000. Adducin: structure, function and regulation. Cell. Mol. Life Sci. 57:884–895. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. May, S. 2000. Theories on structural perturbations of lipid bilayers. Curr. Opin. Coll. Interface Sci. 5:244–249. [Google Scholar]
  27. May, S., D. Harries, and A. Ben-Shaul. 2000. Lipid demixing and protein–protein interactions in the adsorption of charged proteins on mixed membranes. Biophys. J. 79:1747–1760. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. May, S., D. Harries, and A. Ben-Shaul. 2002. Macroion-induced compositional instability of binary fluid membranes. Phys. Rev. Lett. 89:268102. [DOI] [PubMed] [Google Scholar]
  29. McLaughlin, S., and A. Aderem. 1995. The myristoyl-electrostatic switch: a modulator of reversible protein-membrane interactions. Trends Biochem. Sci. 20:272–276. [DOI] [PubMed] [Google Scholar]
  30. McLaughlin, S., J. Wang, A. Gambhir, and D. Murray. 2002. PIP2 and proteins: interactions, organization, and information flow. Annu. Rev. Biophys. Biomol. Struct. 31:151–175. [DOI] [PubMed] [Google Scholar]
  31. Murray, D., N. Ben-Tal, B. Honig, and S. McLaughlin. 1997. Electrostatic interaction of myristoylated proteins with membranes: simple physics, complicated biology. Structure. 5:985–989. [DOI] [PubMed] [Google Scholar]
  32. Murray, D., A. Arbuzova, G. Hangyas-Mihalyne, A. Gambhir, N. Ben-Tal, B. Honig, and S. McLaughlin. 1999. Electrostatic properties of membranes containing acidic lipids and adsorbed basic peptides: theory and experiment. Biophys. J. 77:3176–3188. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Murray, D., S. McLaughlin, and B. Honig. 2001. The role of electrostatic interactions in the regulation of the membrane association of G protein beta gamma heterodimers. J. Biol. Chem. 276:45153–45159. [DOI] [PubMed] [Google Scholar]
  34. Murray, D., A. Arbuzova, B. Honig, and S. McLaughlin. 2002. The role of electrostatic and nonpolar interactions in the association of peripheral proteins with membranes. Curr. Top. Membr. 52:271–302. [Google Scholar]
  35. Murray, D., and B. Honig. 2002. Electrostatic control of the membrane targeting of C2 domains. Mol. Cell. 9:145–154. [DOI] [PubMed] [Google Scholar]
  36. Netz, R. R. 2001. Electrostatistics of counter-ions at and between planar charged walls: from Poisson-Boltzmann to the strong-coupling theory. Eur. Phys. J. E. 5:557–574. [Google Scholar]
  37. Parsegian, V. A., and D. Gingell. 1972. On the electrostatic interaction across a salt solution between two bodies bearing unequal charges. Biophys. J. 12:1192–1204. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Payrastre, B., K. Missy, S. Giuriato, S. Bodin, M. Plantavid, and M. Gratacap. 2001. Phosphoinositides: key players in cell signalling, in time and space. Cell. Signal. 13:377–387. [DOI] [PubMed] [Google Scholar]
  39. Qin, Z. and D. S. Cafiso. 1996. Membrane structure of protein kinase C and calmodulin binding domain of myristoylated alanine rich C kinase substrate determined by site-directed spin labeling. Biochemistry. 35:2917–2925. [DOI] [PubMed] [Google Scholar]
  40. Rauch, M. E., C. G. Ferguson, G. D. Prestwich, and D. Cafiso. 2002. Myristoylated alanine-rich C kinase substrate (MARCKS) sequesters spin-labeled phosphatidylinositol 4,5-bisphosphate in lipid bilayers. J. Biol. Chem. 277:14068–14076. [DOI] [PubMed] [Google Scholar]
  41. Resh, M. D. 1999. Fatty acylation of proteins: new insights into membrane targeting of myristoylated and palmitoylated proteins. Biochim. Biophys. Acta. 1451:1–16. [DOI] [PubMed] [Google Scholar]
  42. Rossi, E. A., Z. Li, H. Feng, and C. S. Rubin. 1999. Characterization of the targeting, binding, and phosphorylation site domains of an A kinase anchor protein and a myristoylated alanine-rich C kinase substrate-like analog that are encoded by a single gene. J. Biol. Chem. 274:27201–27210. [DOI] [PubMed] [Google Scholar]
  43. Rouzina, I., and V. A. Bloomfield. 1996. Competitive electrostatic binding of charged ligands to polyelectrolytes: planar and cylindrical geometries. J. Phys. Chem. 100:4292–4304. [DOI] [PubMed] [Google Scholar]
  44. Russ, C., T. Heimburg, and H. H. von Grünberg. 2003. The effect of lipid demixing on the electrostatic interaction of planar membranes across a salt solution. Biophys. J. 84:3730–3742. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Simonsen, A., A. E. Wurmser, S. D. Emr, and H. Stenmark. 2001. The role of phosphoinositides in membrane transport. Curr. Opin. Cell Biol. 13:485–492. [DOI] [PubMed] [Google Scholar]
  46. Stauffer, T. P., S. Ahn, and T. Meyer. 1998. Receptor-induced transient reduction in plasma membrane PtdIns(4,5)P2 concentration monitored in living cells. Curr. Biol. 8:343–346. [DOI] [PubMed] [Google Scholar]
  47. Toner, M., G. Vaio, A. McLaughlin, and S. McLaughlin. 1988. Adsorption of cations to phosphotidylinsitol 4,5-bisphosphate. Biochemistry. 27:7435–7443. [DOI] [PubMed] [Google Scholar]
  48. Wang, J., A. Arbuzova, G. Hangyas-Mihalyne, and S. McLaughlin. 2001. The effector domain of myristoylated alanine-rich C kinase substrate binds strongly to phosphatidylinositol 4,5-bisphosphate. J. Biol. Chem. 276:5012–5019. [DOI] [PubMed] [Google Scholar]
  49. Wang, J., A. Gambhir, G. Hangyas-Mihalyne, D. Murray, U. Golebiewska, and S. McLaughlin. 2002. Lateral sequestration of phosphatidylinositol 4,5-bisphosphate by the basic effector domain of myristoylated alanine-rich C kinase substrate is due to nonspecific electrostatic interactions. J. Biol. Chem. 277:34401–34412. [DOI] [PubMed] [Google Scholar]
  50. Wang, J., A. Gambhir, S. McLaughlin, and D. Murray. 2004. Computational model for the electrostatic sequestration of PI(4,5)P2 by membrane-adsorbed basic peptides. Biophys. J. 86:1969–1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Zhang, W., E. Crocker, S. McLaughlin, and S. O. Smith. 2003. Binding of peptides with basic and aromatic residues to bilayer membranes: phenylalanine in the myristoylated alanine-rich C kinase substrate effector domain penetrates into the hydrophobic core of the bilayer. J. Biol. Chem. 278:21459–21466. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES