Abstract
Mechanical folding trajectories for polyproteins starting from initially stretched conformations generated by single-molecule atomic force microscopy experiments [Fernandez, J. M. & Li, H. (2004) Science 303, 1674–1678] show that refolding, monitored by the end-to-end distance, occurs in distinct multiple stages. To clarify the molecular nature of folding starting from stretched conformations, we have probed the folding dynamics, upon force quench, for the single I27 domain from the muscle protein titin by using a Cα-Go model. Upon temperature quench, collapse and folding of I27 are synchronous. In contrast, refolding from stretched initial structures not only increases the folding and collapse time scales but also decouples the two kinetic processes. The increase in the folding times is associated primarily with the stretched state to compact random coil transition. Surprisingly, force quench does not alter the nature of the refolding kinetics, but merely increases the height of the free-energy folding barrier. Force quench refolding times scale as  , where Δxf ≈ 0.6 nm is the location of the average transition state along the reaction coordinate given by end-to-end distance. We predict that τF and the folding mechanism can be dramatically altered by the initial and/or final values of force. The implications of our results for design and analysis of experiments are discussed.
, where Δxf ≈ 0.6 nm is the location of the average transition state along the reaction coordinate given by end-to-end distance. We predict that τF and the folding mechanism can be dramatically altered by the initial and/or final values of force. The implications of our results for design and analysis of experiments are discussed.
Keywords: temperature-denatured ensemble, force-denatured ensemble, temperature quench, mechanical proteins
An ongoing challenge in molecular biology is to decipher the folding routes of biomolecules and map the underlying energy landscape. Major advances in theory, simulations, and ensemble experiments have resulted in a better understanding of how proteins and RNA molecules fold (1–3). In conventional experiments, folding (unfolding) is triggered by decreasing (increasing) concentration of denaturants or temperature. Under folding conditions, biomolecules traverse the energy landscape from the high-entropy unfolded states to a low-entropy native basin of attraction (NBA). Because the initial conformations in the unfolded basin of attraction are difficult to characterize and their fluctuations are averaged out in ensemble experiments, unambiguous description of the folding mechanisms remains a challenge.
Recently, mechanical force (f) has been used as a variable to prepare well defined initial states of RNA and proteins (4–7). Besides the intrinsic interest in folding, f is a natural variable in several mechanosensitive processes. For example, a newly synthesized polypeptide chain may be subject to an equilibrium force f ≈ 10 pN as it exits the tunnel in the ribosome (8). Similarly, the domains of the muscle protein titin have evolved to withstand cycles of stretching and force release (9). Using f to unfold proteins, Fernandez and Li (6) showed that refolding can be initiated starting from stretched conformations and quenching the force to a low constant value, fq, at which the NBA is preferably populated. The mechanical folding experiments probe, at a single-molecule level, the dynamics of transition from a stretched low-entropy state to the low-entropy NBA. The force-quench method was used to obtain mechanical folding trajectories for tandem constructs of poly ubiquitin (Ub). Although the interpretation of the data is not straightforward (see below), the folding trajectories reveal several interesting features: (i) The approach to the NBA from the stretched state occurs in multiple stages when monitored by the time dependence of the end-to-end distance of the poly Ub construct. The initial stage of refolding appears to be continuous. Individual atomic force microscopy trajectories demonstrate significant dynamic heterogeneity. (ii) The force-quench refolding time scales as  , where
, where  is the folding time in the absence of force, fq is the quench force, T is the temperature, and Δxf is the average location of the transition state. The direct observation of single molecule collapse offers an unprecedented glimpse not only into the energy landscape of proteins, but into the relationship between folding and collapse of polypeptide chains.
is the folding time in the absence of force, fq is the quench force, T is the temperature, and Δxf is the average location of the transition state. The direct observation of single molecule collapse offers an unprecedented glimpse not only into the energy landscape of proteins, but into the relationship between folding and collapse of polypeptide chains.
The poly Ub construct makes it difficult to decipher the nature of refolding of a monomeric protein. The dynamics of a particular Ub module may be influenced by the covalent linkage to other Ub domains, which collectively act as entropic springs just as the handles do in the mechanical unfolding of RNA molecules (5). To ascertain that the Fernandez and Li experiments (6) describe the refolding dynamics of individual domains and to establish the generality of those results, we have undertaken force-quench simulations of I27 by using a Cα-Go model. We chose I27, one of the domains in the large muscle protein titin, because there have been extensive forced-unfolding studies on this system (10–12). More importantly, because I27 is subject to mechanical stress under physiological conditions (9), it is instructive to compare folding initiated by temperature and force quenches.
At a fixed temperature, force-quench refolding mechanism must depend on the initial stretching force, fI, fq, and the equilibrium temperature-dependent critical force fc above which the native state becomes unstable. Both fI and fq can be experimentally controlled, whereas fc is an intrinsic sequence-dependent property. From general theoretical considerations we expect that the refolding pathways and time scales should depend on the dimensionless variables fI/fc and fc/fq. For a fixed fI, the depth of quench Δfq = (fc – fq)/fc determines the folding times. Conversely, if fq is fixed, then τF is a function of ΔfI = (fI – fc)/fc. Large deviations from temperature-quench refolding are expected when ΔfI > 1. These arguments show that force-quench refolding can be altered either by changing the initial conditions by varying fI or by modifying fq.
To probe the molecular details of force-quench refolding, we use coarse-grained protein models (13), which have been successful in protein folding studies (14–16). The results are as follows: (i) Upon force quench, I27 refolds to the NBA from a stretched state in multiple stages. The initial stage involves a rapid transition from a stretched state to an ensemble of metastable random coil (RC) conformations, RCf, that retains the “memory” of the initial stretched state. (ii) The folding pathways initiated from stretched conformations differ substantially from those observed for temperature-quench refolding. In particular, the collapse and folding processes that are synchronous under temperature quench occur on a different time scale when folding is initiated by force quench (3). Force-quench refolding time for I27 monomer  shows the same dependence on fq as for poly Ub (6). Thus, for a fixed fI, the refolding free-energy barrier grows linearly with fq (4). Just as in the Fernandez and Li experiments (6), the I27 simulations correspond to ΔfI > 1. To probe the effect of varying ΔfI on refolding, we carried out extensive simulations of a model β-barrel protein that also includes non-native interactions. For a fixed fq, refolding times depend dramatically on the initial conditions, i.e., fI.
shows the same dependence on fq as for poly Ub (6). Thus, for a fixed fI, the refolding free-energy barrier grows linearly with fq (4). Just as in the Fernandez and Li experiments (6), the I27 simulations correspond to ΔfI > 1. To probe the effect of varying ΔfI on refolding, we carried out extensive simulations of a model β-barrel protein that also includes non-native interactions. For a fixed fq, refolding times depend dramatically on the initial conditions, i.e., fI.
Methods
Coarse-Grained Model for I27. The conformation of a polypeptide chain in a coarse-grained representation is specified by a set of coordinates 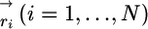 of the Cα-carbon atoms, where N is the number of amino acids. The energy of a conformation for the Cα-Go model is (14)
of the Cα-carbon atoms, where N is the number of amino acids. The energy of a conformation for the Cα-Go model is (14)
 |
[1] |
where ri, θi, and φi are the bond length between i and i – 1 residues, the bond angle between (i – 1, i) and (i, i + 1) bonds, and the dihedral angle around the ith bond, respectively. The distance between residues i and j is rij. Subscript 0 and superscripts NC and NNC refer to native conformation and native and non-native contacts, respectively. The values of the parameters are Kr = 250 kcal/(mol·Å2), Kθ = 50 kcal/(mol·rad2),  ,
, 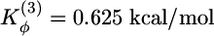 , ε = 1.25 kcal/mol, and C = 4 Å. The unit of f in our model is ≈23 pN. Beads i and j form a contact in the native state, if rij ≤ dc = 0.6 nm. A contact between i and j in an arbitrary conformation exists if rij ≤ 1.2 dc. The native conformation of I27 (Protein Data Bank ID code 1TIT) has 86 native Cα – Cα contacts.
, ε = 1.25 kcal/mol, and C = 4 Å. The unit of f in our model is ≈23 pN. Beads i and j form a contact in the native state, if rij ≤ dc = 0.6 nm. A contact between i and j in an arbitrary conformation exists if rij ≤ 1.2 dc. The native conformation of I27 (Protein Data Bank ID code 1TIT) has 86 native Cα – Cα contacts.
Simulations. The folding dynamics is obtained by integrating the Langevin equations of motion by using the corrector-predictor algorithm (17). In the presence of a constant f and assuming a rapid alignment of the end-to-end vector  along the force direction, the total energy of the polypeptide is Ef = E – fR.We calculated f-dependent thermodynamic quantities by using a version of the multiple histogram method, in which both temperature T and f are varied (18).
along the force direction, the total energy of the polypeptide is Ef = E – fR.We calculated f-dependent thermodynamic quantities by using a version of the multiple histogram method, in which both temperature T and f are varied (18).
Results
Force-Quench Refolding Occurs in Steps. The equilibrium f – T phase diagram shows that when f exceeds fc = 43 pN at Ts = 0.85 TF (TF is a folding transition temperature at f = 0), I27 unfolds (M.S.L., unpublished work). The calculated value of fc is in approximate agreement with the estimate (fc ≈ 30 pN) by Li et al. (19) based on nonequilibrium atomic force microscopy experiments. Given the simplicity of the model and the crude methods used to estimate fc in the atomic force microscopy experiments (19), the semiquantitative agreement validates the use of the Go model. To follow the dynamics of approach to the NBA we initially prepared stretched structures by applying a constant f = 87 pN (ΔfI ≈ 2). A molecule is stretched, if R ≥ 0.85 L, where L = 30.4 nm is the contour length of I27. Starting from force-denatured ensemble (FDE) conformations, we quenched the force to fq < fc. The refolding dynamics is monitored for 100 molecules by following the time dependence of the number of native contacts Q(t), the end-to-end distance R(t), and the radius of gyration Rg(t).
Refolding trajectories upon force quench show considerable heterogeneity (Fig. 1). Different molecules traverse distinct routes in the FDE → NBA transition. The reduction in R for the fq = 0 case occurs in multiple steps (Fig. 1 a and b). At very short times (t ≲ 30 ns) R decreases continuously from 25 nm to ≈10 nm (stage 1, Fig. 1a). R fluctuates ≈10 nm (stage 2) until a transition to R ≈ 5 nm occurs around t ≈ 50 ns (stage 3). In this refolding trajectory the molecule fluctuates in the compact state (stage 4, R ≃ 5 nm, Rg ≃ 2.5 nm, Q ≃ 30 nm) until the NBA is reached around t ≃ 200 ns. At t > 200 ns the fluctuations in R are considerably reduced (Fig. 1a). Surprisingly, the observed multistep reduction in R is masked in the time course of Rg, which changes continuously from the initial value of 7.5 nm to 1.3 nm in the NBA. The acquisition of the native structure, as measured by Q, also occurs in steps from the initial value of Q ≈ 0 until the NBA is reached. Although another trajectory for fq = 0 quench (Fig. 1b) can be similarly interpreted, it is clear that there are significant variations in the lifetimes of the transient intermediates and in the time scales of transition between them. There is no “typical” trajectory, which implies that refolding pathways are heterogeneous.
Fig. 1.
FDE refolding of I27 domain monitored for individual molecules at the quench forces fq = 0(a and b) and fq = 0.06 fc (c and d). The time dependences of the end-to-end distance R(t), the radius of gyration Rg(t), and the number of native contacts Q(t) are shown in black, red, and green, respectively. The final points in the plots correspond to the first passage time to the NBA. All panels show that FDE refolding occurs in multiple steps (as indicated in a and c) characterized by varying chain extension, size, and native content. Dramatic differences between refolding trajectories suggest a heterogeneity of folding pathways.
The pathway diversity is also evident when fq > 0 (Fig. 1 c and d). Although the decrease in R occurs in steps as for fq = 0, the nature of intermediates sampled en route to the NBA is different. In Fig. 1c, there is a rapid reduction in R to ≈10 nm (stage 1) followed by a further decrease to R ≈ 5 nm on longer times (stage 3). Another trajectory (Fig. 1d) shows that the residence time of the R ≈ 10 nm intermediate is ≈300 ns (≈2/3 of the first passage time to the NBA). The number of native contacts reveals these differences even more dramatically. In both cases, there are three distinct metastable intermediates that are sampled. Their Q values are different (Fig. 1 c and d), which shows that molecules sample distinct regions of the energy landscape even though the starting conformations are similar. It is interesting that even though R(t) and Q(t) reflect the stepwise acquisition of structure, Rg(t) in all cases decreases more continuously, thus masking the presence of any barriers to folding.
Collapse and Folding Occur on Distinct Time Scales upon Force Quench. The time dependence of 〈R(t) 〉, 〈Rg(t) 〉, and 〈Q(t) 〉 that monitors the relaxation to the NBA from the FDE shows a spectrum of time scales (Fig. 2). Upon force quench to fq the initial event is the entropically driven transition from the stretched FDE state to a RC-like state (RCf). The time dependencies of probes of collapse and folding are well described by using a sum of two exponentials. When fq = 0 (Fig. 2), the FDE → RCf transition takes place on a time scale of  and corresponds to a drastic contraction of the dimensions of the polypeptide chain. The amplitudes in the two exponential fits indicate that on
and corresponds to a drastic contraction of the dimensions of the polypeptide chain. The amplitudes in the two exponential fits indicate that on  〈R(t) 〉 decreases by about two-thirds of the total variation during refolding, whereas 〈Rg(t) 〉 decreases by ≈75%. The second kinetic stage results in a further reduction of 〈R(t) 〉 by ≈30% on a time scale
〈R(t) 〉 decreases by about two-thirds of the total variation during refolding, whereas 〈Rg(t) 〉 decreases by ≈75%. The second kinetic stage results in a further reduction of 〈R(t) 〉 by ≈30% on a time scale 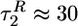 , whereas collapse, monitored by 〈Rg(t) 〉, takes place on a significantly longer time scale (
, whereas collapse, monitored by 〈Rg(t) 〉, takes place on a significantly longer time scale ( ). This difference shows that the overall chain collapse is more complex than the reduction of the end-to-end distance. The decrease in 〈Rg 〉 is followed by the acquisition of the native interactions. The formation of native interactions, 〈Q(t) 〉, also occurs in two kinetic stages with the time scales
). This difference shows that the overall chain collapse is more complex than the reduction of the end-to-end distance. The decrease in 〈Rg 〉 is followed by the acquisition of the native interactions. The formation of native interactions, 〈Q(t) 〉, also occurs in two kinetic stages with the time scales  and
and  . Only 20% of native contacts are formed during the first fast kinetic stage, whereas the majority (80%) are formed after the final chain collapse.
. Only 20% of native contacts are formed during the first fast kinetic stage, whereas the majority (80%) are formed after the final chain collapse.
Fig. 2.
Kinetics of I27 FDE (in gray) and TDE (in black) refolding monitored by the end-to-end distance 〈R(t) 〉, the radius of gyration 〈Rg(t) 〉, and the number of native contacts 〈Q(t) 〉. Smooth curves represent multiexponential fits to these probes (see text for the time scales, amplitudes, and other details). Angular brackets indicate averages over individual trajectories. Compared with TDE folding, collapse and folding occur on different time scales and are markedly slower when folding commences from FDE.
The plots of various time scales, describing the transition from FDE to NBA, as a function of fq (Fig. 3) show no apparent dependence of time scales 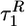 and
and  on fq. We rationalize this surprising finding by noting that the entropic force (fe) needed to stretch the protein is much greater than the maximum value of the quench force (
on fq. We rationalize this surprising finding by noting that the entropic force (fe) needed to stretch the protein is much greater than the maximum value of the quench force ( ). From the worm-like chain model we find that fe ≈ 100 pN for stretching Ig27 to 0.85 L. Because
). From the worm-like chain model we find that fe ≈ 100 pN for stretching Ig27 to 0.85 L. Because 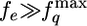 the initial compaction of the polypeptide chain that is driven by the magnitude of fe is not sensitive to the small fq values. In contrast, the collapse time scales,
the initial compaction of the polypeptide chain that is driven by the magnitude of fe is not sensitive to the small fq values. In contrast, the collapse time scales,  and
and  , and the folding time scale τF increase exponentially with f. For example,
, and the folding time scale τF increase exponentially with f. For example,  , at fq ≈ 0.13 fc ≈ 6 pN, increases 3-fold as compared with fq = 0. For all values of fq,
, at fq ≈ 0.13 fc ≈ 6 pN, increases 3-fold as compared with fq = 0. For all values of fq,  and
and 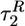 are smaller than τF, which implies that chain collapse occurs before the acquisition of the native state.
are smaller than τF, which implies that chain collapse occurs before the acquisition of the native state.
Fig. 3.
Dependence of various time scales on fq extracted from the multiexponential fits of collapse and folding probes. • and ○ correspond to the burst-phase kinetic time scales 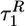 and
and  in the time dependence of the end-to-end distance 〈R(t) 〉 and the radius of gyration 〈Rg(t) 〉, respectively. ▵ and □ represent the second time scales
in the time dependence of the end-to-end distance 〈R(t) 〉 and the radius of gyration 〈Rg(t) 〉, respectively. ▵ and □ represent the second time scales  and
and 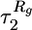 for these functions, respectively. ⋄ denote the folding times τF, which are calculated as averages of the first passage times to the NBA. The time scales
for these functions, respectively. ⋄ denote the folding times τF, which are calculated as averages of the first passage times to the NBA. The time scales 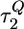 extracted from the exponential fits of 〈Q(t) 〉 are similar to τF. All time scales, except for those associated with the burst phase, grow exponentially with fq. A lag between folding and collapse time scales is evident at all values of quench force fq. (Inset) The fit of the dependence log(τF) vs. fq by using the linear function log(τF) =–0.054 +6.77(fq/fc). Using the Bell-like model (Eq. 2) we obtain fcΔxf/kBT = 6.77, therefore Δxf ≈ 0.6 nm.
extracted from the exponential fits of 〈Q(t) 〉 are similar to τF. All time scales, except for those associated with the burst phase, grow exponentially with fq. A lag between folding and collapse time scales is evident at all values of quench force fq. (Inset) The fit of the dependence log(τF) vs. fq by using the linear function log(τF) =–0.054 +6.77(fq/fc). Using the Bell-like model (Eq. 2) we obtain fcΔxf/kBT = 6.77, therefore Δxf ≈ 0.6 nm.
Ensemble of Initial Unfolded Structures Determines the Folding Pathways. A RC-like temperature-denatured ensemble (TDE) is generated by increasing temperature. Upon temperature quench the folding transition starts from a high-entropy TDE state to a low-entropy folded (NBA) state. In contrast, in FDE refolding, the low-entropy NBA is reached from a low-entropy stretched state with the initial rapid kinetic stage being the FDE → RCf transition. If the relaxation of tension along the chain is rapid compared with protein conformational changes, then the ensemble of transiently populated coil conformations upon force-quench RCf must be distinct from the TDE. The transiently populated metastable RC state RCf at T < TF is under tension when fq > 0. These physical arguments suggest that FDE refolding pathways and time scales must be different from those observed for TDE refolding (Fig. 4).
Fig. 4.
Conceptual differences in FDE and TDE refolding pathways. The mechanically stretched state in the FDE has a low conformational entropy. Upon force quench it rapidly contracts to a RCf ensemble, in which the memory of stretched state still persists. The RCf → RC (≈TDE) transition is associated with local equilibration in the RC ensemble. Both transitions are entropically driven as entropy reaches a maximum in RC. As the FDE folding pathway passes through the RC, it begins to resemble the TDE pathway. The transition RC → NBA involves a progressive loss in entropy in both pathways.
When refolding is initiated by a temperature quench, 〈R(t) 〉 decreases exponentially with a single characteristic time scale τ R = 8 ns (Fig. 2). In contrast, 〈Rg(t) 〉 and 〈Q(t) 〉 show two-stage kinetics. Their double exponential fits indicate that the first kinetic (“burst”) stage coincides with the contraction of the end-to-end distance (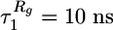 and
and  ). During this initial stage, the chain dimensions are reduced by ≈50%, and ≈25% of native contacts are formed. The final collapse and folding take place on a much longer time scale (
). During this initial stage, the chain dimensions are reduced by ≈50%, and ≈25% of native contacts are formed. The final collapse and folding take place on a much longer time scale ( ). This stage is associated with the formation of the bulk of the native interactions (75%) and further compaction of the chain by ≈50%. The data show that collapse and folding starting with the TDE conformations are effectively synchronous.
). This stage is associated with the formation of the bulk of the native interactions (75%) and further compaction of the chain by ≈50%. The data show that collapse and folding starting with the TDE conformations are effectively synchronous.
In contrast to TDE folding, 〈R(t) 〉 in FDE refolding shows a two-stage relaxation (Fig. 2). The radius of gyration and the number of native contacts also follow a two-stage kinetics as for TDE. However, FDE time scales,  and
and  , increase by 30% and 50%, respectively (Fig. 2). The folding time τF shows a similar increase (from
, increase by 30% and 50%, respectively (Fig. 2). The folding time τF shows a similar increase (from 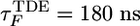 to
to  ). More importantly, collapse and folding are no longer synchronous (Figs. 2 and 3) when folding is initiated from FDE.
). More importantly, collapse and folding are no longer synchronous (Figs. 2 and 3) when folding is initiated from FDE.
Physics of Refolding Is Not Model Dependent. To ascertain that the qualitative results for the I27 Go model are not model dependent, we performed the force-quench refolding simulations by using the four-strand β-barrel model sequence S1 (20). This model differs from I27 in two important aspects. First, the energy function of S1 includes non-native interactions that are neglected in the I27 model. Second, the native topology of S1 is a β-barrel, which is simpler than the β-sandwich structure of I27. The S1 simulations (for details see Supporting Text and Figs. 6 and 7, which are published as supporting information on the PNAS web site) were performed under the conditions similar to those used for I27. All structural probes, which monitor TDE refolding, show a concerted collapse and folding on a single time scale of ≈85 ns. When folding is initiated with FDE conformations (fq = 0), we observe an additional rapid relaxation, corresponding to contraction of the initially fully stretched conformations to partially stretched RCf, whose average dimensions are about double that of TDE. In addition, the time scale for reaching the NBA increases by a factor of two. Surprisingly, the final collapse time scales in TDE and FDE refolding are nearly the same. Therefore, folding and collapse occur on distinct time scales upon the change in initial conformations. Hence, the findings for S1 and I27 are in qualitative agreement.
From the results for S1 and I27, we surmise that the qualitative differences between folding initiated by temperature or force quenches are primarily related to the variations in the nature of the metastable RCf and the thermally equilibrated TDE (Fig. 4). It is the memory of the initially stretched conformation that makes the RCf ensemble sampled along FDE refolding pathways different from the TDE. By shifting the FDE plots by Δt to the left, we find that the distribution of conformations in the FDE pathway approaches TDE if Δt ≈ 50 ns (Fig. 5). The striking agreement between FDE and TDE refolding plots upon Δt shift suggests that folding begins only after RCf conformations start to “resemble” the TDE RC conformations. Subsequently, both kinetic processes are similar. The delay in FDE folding compared with collapse is primarily caused by the time required for RCf conformations to equilibrate among the ensemble of coil-like structures. The time scale for local equilibration of RCf is surprisingly long ( ). The long time needed to reach local equilibrium in RCf, after which folding begins, explains the increase in τF for FDE folding as compared with that for TDE. This finding also shows that folding strongly depends on the starting point on the energy landscape.
). The long time needed to reach local equilibrium in RCf, after which folding begins, explains the increase in τF for FDE folding as compared with that for TDE. This finding also shows that folding strongly depends on the starting point on the energy landscape.
Fig. 5.
FDE (in gray) and TDE (in black) folding pathways for the β-barrel S1 model are compared by using the end-to-end distance 〈R(t) 〉 and the number of native contacts 〈Qi(t) 〉 formed by an individual β-strand i(= 1,...,4). The coincidence between FDE and TDE curves upon shifting the FDE data by Δt = 50 ns to the left suggests that FDE folding pathway becomes similar to TDE pathway in 50 ns after folding initiation. Within 50 ns, the polypeptide chain contracts and equilibrates in the RC ensemble (Fig. 4). L and Qi,0 are, respectively, the contour length and the number of contacts formed by the β-strand i in a native state. 〈R(t) 〉 and 〈Qi(t) 〉 are averaged over 200 trajectories. (Inset) The dependence of the folding time τF on the average end-to-end distance R in the FDE shows that folding is progressively slower as the FDE becomes more extended. The FDE conformations are prepared by pulling the NBA structures at a constant speed of 6 × 104 μm/s.
To further probe the dependence of force quench τF on the initial conditions, we prepared distinct FDEs by stretching S1 to a different values of the initial end-to-end distance, R. This procedure is equivalent to varying fI albeit in a nonlinear manner. In accord with the physical picture in Fig. 4. we find that, at fq = 0, τF changes dramatically with R (Fig. 5 Inset). Thus, initial conditions, which can be readily manipulated in laser optical tweezer or atomic force microscopy experiments by altering fI, determine the refolding mechanism and time scales.
Collapse and Refolding Times for I27 Depend Exponentially on fq. We obtained the fq-dependent refolding time τF from the distributions of first passage times computed by using 50–100 trajectories for each value of fq. When fq = 0, we find that 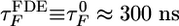 , which is ≈60% more than the TDE refolding time at Ts = 0.85 TF. When fq > 0, the refolding times obey the relation
, which is ≈60% more than the TDE refolding time at Ts = 0.85 TF. When fq > 0, the refolding times obey the relation
 |
[2] |
where Δxf is the average location of the folding transition-state ensemble (Fig. 3 Inset). From the linear fit of log(τF) as a function of fq by using Eq. 2 we get Δxf ≈ 0.6 nm for I27 at Ts = 0.85 TF. In the force-quench experiments R can be treated as a suitable reaction coordinate in the FDE → NBA transition (6). The dependence of τF on fq can be written as τF ≈ exp(yΔGUFΔxf/XUFkBT), where ΔGUF is the equilibrium free energy of stability of the NBA with respect to the unfolded states, y = fq/fc, and XUF is the distance between the NBA and the unfolded states. In force-quench experiments, the search for the transition-state ensemble occurs among the ensemble of unfolded states. With this interpretation, a Tanford-like parameter can be written as β ≈Δxf/ΔXUF ≈ 0.2 for I27, where ΔXUF ≈ a(N3/5 – N1/3). Fernandez and Li (6) found that the mean relaxation time for poly Ub also obeys Eq. 2 with Δxf ≃ 0.8 nm, which implies that β for Ub is also likely to be close to the NBA. Given the simplicity of our model and the differences in the topology of I27 (β-sandwich protein) and Ub (α/β protein), the agreement in Δxf suggests that the native states of these proteins might be “brittle,” i.e., once the extension exceeds a small value the structure unravels. A similar conclusion follows from the steered molecular dynamics simulations of mechanical β-sandwich proteins (12).
Discussion and Conclusions
Force-quench experiments offer a potential of initiating biomolecular refolding starting from arbitrary initial values of the end-to-end distance, R (6). Fernandez and Li (6) generated mechanical folding trajectories from the regions of free energy landscape that cannot be accessed in conventional experiments. In this work, we have used coarse-grained models for the β-sandwich protein I27 and β-barrel to probe refolding from the ensemble of stretched structures. The implications of our findings are discussed below.
The refolding pathways are heterogeneous, with the approach to NBA occurring in distinct stages. The longer refolding times in FDE simulations compared with TDE refolding are caused by the reduction in the rate of formation of low-energy compact structures. Similar to poly Ub, several long-lived intermediates with varying values of R and Q are sampled en route to the NBA. These results for a monomeric I27 are in qualitative accord with the conclusions drawn from mechanical folding trajectories for poly Ub (6).
The nature of the ensemble of initial states determines the collapse and folding pathways. When the protein is fully extended, the entropy of the stretched state is dramatically lower than that of TDE conformations. Refolding from FDE effectively starts from extended conformations (Rg ≈ N), whereas TDE refolding begins from the ensemble of conformations with a mean Rg ≈ N0.6. The folding initiated with FDE differs from TDE folding in two aspects. First, the stretched polypeptide chain must initially contract to the ensemble of conformations with the dimensions approximately similar to TDE RCs. Second, FDE leads to the delay in the formation of native interactions, because chain must not only contract, but also “equilibrate” within a RC ensemble. Therefore, when folding begins from stretched state, the collapse and folding occur on distinct time scales. In contrast, when TDE is used, collapse and folding often occur in concert for two-state folders.
Force-quench experiments on poly Ub (6) and the present study on monomeric proteins show that the fq-dependent refolding time obeys Eq. 2. However, the value of τF extrapolated to fq = 0 is larger than that obtained by conventional experiments. Fernandez and Li (6) obtained  for ubiquitin, whereas the folding time from ensemble experiments
for ubiquitin, whereas the folding time from ensemble experiments  (21). Our results show that the difference between the two experimental values is caused by the vastly different initial conditions, from which refolding is initiated. In the transition from the stretched state to the NBA, a large free-energy cost is involved in burying substantial surface area
(21). Our results show that the difference between the two experimental values is caused by the vastly different initial conditions, from which refolding is initiated. In the transition from the stretched state to the NBA, a large free-energy cost is involved in burying substantial surface area  . In contrast, the NBA is accessed from TDE by much smaller conformational fluctuations. The discrepancy between
. In contrast, the NBA is accessed from TDE by much smaller conformational fluctuations. The discrepancy between  and
and  should decrease, if fI does not fully stretch the polypeptide chain (Fig. 5 Inset).
should decrease, if fI does not fully stretch the polypeptide chain (Fig. 5 Inset).
In the Fernandez and Li experiments (6), fI is fixed (ΔfI ≈ 3) and fq is varied, which affects the free energies of the folded and unfolded states. The linear increase in the free-energy barrier to folding, which is consistent with the Bell-type model (22), is caused by the stabilization of the RCf states with increasing fq. The presence of free-energy barrier to folding is consistent with theoretical (23, 24) predictions and simulation results (25) that show that equilibrium-force unfolding is a first-order transition. On the other hand, if fq is fixed and fI is varied, then we expect 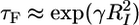 , where γ is an effective surface tension. This finding suggests that the shape of the dependence of τF on fI should approximately resemble the equilibrium force-extension curve (Fig. 5 Inset). These arguments show that force-quench refolding with fixed fI and varying fq is qualitatively different from folding with fq fixed and differing fI values. This inherent asymmetry can be exploited to map the free-energy landscape of proteins.
, where γ is an effective surface tension. This finding suggests that the shape of the dependence of τF on fI should approximately resemble the equilibrium force-extension curve (Fig. 5 Inset). These arguments show that force-quench refolding with fixed fI and varying fq is qualitatively different from folding with fq fixed and differing fI values. This inherent asymmetry can be exploited to map the free-energy landscape of proteins.
It is not straightforward to infer the nature of monomeric protein folding from mechanical folding trajectories of polyprotein constructs. The folding of the ith domain may be influenced by the neighboring domains that act as “flexible” linkers. Resolution of folding trajectories of a single domain requires that the spring constant of a linker kL > kP, where kP is a measure of the “softness” of a protein. This requirement may not be satisfied in polypeptide constructs. Therefore, it is preferable to use stiff linkers that sandwich the monomeric protein just as was done in the mechanical unfolding of RNAs (5). Computational studies of force-quench refolding of RNA hairpins with linkers show that relaxation dynamics of the hairpin and the linkers is additive (C. Hyeon and D.T., unpublished work). This finding implies that by varying separately the mechanical properties of the linker and the linker-biomolecule-linker constructs the refolding dynamics of the monomeric protein can be directly monitored.
The major limitation of the present study is the use of the coarse-grained models. For more realistic models, the difference between the time scales of TDE and FDE folding is likely to grow (6). Because the physics of the transition from stretched states to the native conformation is generic (Fig. 4), we propose that the qualitative aspects of force-quench refolding explored here should be valid for other single-domain proteins.
Supplementary Material
Acknowledgments
D.T. thanks Chanbong Hyeon for useful discussions. This work was supported by National Science Foundation Grant CHE 05-14056, Komitet Badañ Naukowych Grant IP03B01827, National Science Council (Taiwan) Grants NSC 93-2112-M-001-027 and NSC 94-2119-M-002-001, and Academia Sinica (Taiwan) Grant AS-92-TP-A09.
Author contributions: D.K.K. and D.T. designed research; M.S.L., C.-K.H., and D.K.K. performed research; C.-K.H. contributed new reagents/analytic tools; M.S.L., D.K.K., and D.T. analyzed data; and M.S.L., D.K.K., and D.T. wrote the paper.
Conflict of interest statement: No conflicts declared.
This paper was submitted directly (Track II) to the PNAS office. J.M.F. is a guest editor invited by the Editorial Board.
Abbreviations: NBA, native basin of attraction; Ub, ubiquitin; RC, random coil; FDE, force-denatured ensemble; TDE, temperature-denatured ensemble.
References
- 1.Onuchic, J. N. & Wolynes, P. G. (2004) Curr. Opin. Struct. Biol. 14, 70–75. [DOI] [PubMed] [Google Scholar]
- 2.Eaton, W., Munoz, V., Thompson, P., Henry, E. & Hofrichter, J. (1998) Acc. Chem. Res. 31, 745–753. [Google Scholar]
- 3.Thirumalai, D. & Hyeon, C. (2005) Biochemistry 44, 4957–4970. [DOI] [PubMed] [Google Scholar]
- 4.Fisher, T. E., Oberhauser, A. F., Carrion-Vazquez, M., Marszalek, P. E. & Fernandez, J. M. (1999) Trends Biochem. Sci. 24, 379–384. [DOI] [PubMed] [Google Scholar]
- 5.Liphardt, J., Onoa, B., Smith, S. B., Tinoco, I., Jr., & Bustamante, C. (2001) Science 292, 733–737. [DOI] [PubMed] [Google Scholar]
- 6.Fernandez, J. M. & Li, H. (2004) Science 303, 1674–1678. [DOI] [PubMed] [Google Scholar]
- 7.Tinoco, I. (2004) Annu. Rev. Phys. Chem. 33, 363–385. [Google Scholar]
- 8.Klimov, D. K., Newfield, D. & Thirumalai, D. (2002) Proc. Natl. Acad. Sci. USA 99, 8019–8024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Erickson, H. P. (1997) Science 276, 1090–1093. [DOI] [PubMed] [Google Scholar]
- 10.Rief, M., Gautel, M., Oesterhelt, F., Fernandez, J. & Gaub, H. E. (1997) Science 276, 1109–1112. [DOI] [PubMed] [Google Scholar]
- 11.Fisher, T. E., Marszalek, P. E. & Fernandez, J. M. (2000) Nat. Struct. Biol. 7, 719–724. [DOI] [PubMed] [Google Scholar]
- 12.Lu, H. & Schulten, K. (2000) Biophys. J. 79, 51–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Thirumalai, D. & Klimov, D. K. (1999) Curr. Opin. Struct. Biol. 9, 197–207. [DOI] [PubMed] [Google Scholar]
- 14.Clementi, C., Nymeyer, H. & Onuchic, J. N. (2000) J. Mol. Biol. 298, 937–953. [DOI] [PubMed] [Google Scholar]
- 15.Shea, J.-E., Onuchic, J. N. & Brooks, C. L., III (1999) Proc. Natl. Acad. Sci. USA 96, 12512–12517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Klimov, D. K. & Thirumalai, D. (2000) Proc. Natl. Acad. Sci. USA 97, 2544–2549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Allen, M. P. & Tildesley, D. (1987) Computer Simulations of Liquids (Clarendon, Oxford).
- 18.Klimov, D. K. & Thirumalai, D. (2001) J. Phys. Chem. B 105, 6648–6654. [Google Scholar]
- 19.Li, H., Linke, W. A., Oberhauser, A. F., Carrion-Vasquez, M., Kerkvliet, J. G., Lu, H., Marszalek, P. E. & Fernandez, J. M. (2002) Nature 418, 998–1002. [DOI] [PubMed] [Google Scholar]
- 20.Klimov, D. K. & Thirumalai, D. (2000) Proc. Natl. Acad. Sci. USA 97, 7254–7259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Khorasanizadeh, S., Peters, I. D., Butt, T. R. & Roder, H. (1993) Biochemistry 32, 7054–7063. [DOI] [PubMed] [Google Scholar]
- 22.Bell, G. I. (1978) Science 200, 618–627. [DOI] [PubMed] [Google Scholar]
- 23.Halperin, A. & Zhulina, E. B. (1991) Eur. Phys. Lett. 15, 417–421. [Google Scholar]
- 24.Geissler, P. L. & Shakhnovich, E. I. (2002) Macromolecules 35, 4429–4436. [Google Scholar]
- 25.Klimov, D. K. & Thirumalai, D. (1999) Proc. Natl. Acad. Sci. USA 96, 6166–6170. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.







