Abstract
Quantitative characterization of protein interactions under physiological conditions is vital for systems biology. Fluorescence photobleaching/activation experiments of GFP-tagged proteins are frequently used for this purpose, but robust analysis methods to extract physicochemical parameters from such data are lacking. Here, we implemented a reaction-diffusion model to determine the contributions of protein interaction and diffusion on fluorescence redistribution. The model was validated and applied to five chromatin-interacting proteins probed by photoactivation in living cells. We found that very transient interactions are common for chromatin proteins. Their observed mobility was limited by the amount of free protein available for diffusion but not by the short residence time of the bound proteins. Individual proteins thus locally scan chromatin for binding sites, rather than diffusing globally before rebinding at random nuclear positions. By taking the real cellular geometry and the inhomogeneous distribution of binding sites into account, our model provides a general framework to analyze the mobility of fluorescently tagged factors. Furthermore, it defines the experimental limitations of fluorescence perturbation experiments and highlights the need for complementary methods to measure transient biochemical interactions in living cells.
INTRODUCTION
Since the first studies on nuclear protein dynamics (1–4), a large number of studies have shown that the majority of nuclear proteins examined so far are highly dynamic: they diffuse rapidly in the nucleoplasm and typically show a fast exchange with their binding sites (e.g., (5–8)). This dynamic behavior is thought to have a major role in chromatin organization and plasticity, and in regulation of gene expression. Conceptually high dynamics have been interpreted as evidence that nuclear proteins find their specific binding sites by random three-dimensional diffusion and collision in the entire nuclear space. To model the interaction of nuclear proteins quantitatively for systems biology, methods to accurately determine their binding times under physiological conditions are needed.
Fluorescence recovery after photobleaching (FRAP), and more recently, photoactivation (PA) as well, have become methods of choice to visualize the dynamics of fluorescently tagged proteins in cells (9–11). These fluorescence perturbation methods offer the possibility to quantitatively characterize diffusive processes and kinetics of interactions with binding sites in a physiological context and can be readily performed on most commercial confocal laser scanning microscopes. By contrast, analyzing such experiments to extract physicochemical parameters of molecular mobility is nontrivial. Several analysis models have been developed, some to characterize diffusion alone (12–15), but most models were designed to characterize chemical interactions. However, fluorescence redistributions can be limited by interactions and diffusion, which, in principle, requires us to solve the complex problem of reaction-diffusion systems. Although this was done in some mostly theoretical studies (14,16–19) almost all biological studies have assumed that diffusion was not limiting the fluorescence recovery (6,20–22) and therefore neglected it to simplify the analysis. Many studies (for example, of nuclear proteins) assumed that if fluorescence redistribution was long compared to the case of freely diffusing molecules, diffusion could be neglected in the analysis (e.g., (23)). Unfortunately, this assumption is incorrect, because very transient interactions where diffusion is clearly limiting, can also lead to slow fluorescence redistributions—as was also noticed recently by others during the preparation of this article (18). In addition, all analysis methods we are aware of have ignored or largely simplified the cellular geometry, within which protein mobility occurs, and assumed a homogeneous distribution of binding sites. Although neglecting diffusion and ignoring cellular geometry and the distribution of binding sites can lead to wrong interpretations of fluorescence perturbation experiments, these assumptions that underlie widely used analysis methods are typically not validated in the biological literature.
The goal of this study was therefore to analyze the contribution of both diffusion and chemical interactions to the kinetics of fluorescence redistribution. To compare our data to previous studies, we used the well-studied case of chromatin interacting proteins. We used photoactivation of proteins tagged with photoactivatable GFP (PAGFP, (11)) to perturb steady-state distribution of fluorescence and followed its redistribution by standard fluorescence confocal microscopy. Analysis was performed by simulating the relaxation after perturbation with a reaction-diffusion model and fitting to the experimental data. Importantly, the model used the real geometry of the nucleus and took the inhomogeneous distribution of binding sites (in this case, chromatin) into account. We applied our method to the chromatin proteins guanine nucleotide exchange factor RCC1 (24), the histone methyltransferase SUV39H1, and its hyperactive mutant (25), and five isoforms of the linker histone H1 (26). All three types of proteins bind either to nucleosomes or DNA in general, without known sequence specificity. In contrast to previous studies, we found that diffusion limits the fluorescence redistribution for all of these proteins, and that with the exception of the hyperactive mutant of SUV39H1, the interaction was so transient that only the upper limit of its residence time and the fraction of unbound protein could be measured with standard fluorescence perturbation methods. Our method provides a new general framework to analyze the contribution of diffusion and interaction to fluorescence redistributions in the nucleus, and can be extended to other cellular compartments.
MATERIALS AND METHODS
DNA constructs, protein purification, cell lines, and cell culture
H2B-diHcRed was described in Gerlich et al. (27). β-galactosidase-diHcRed was made by fusing the entire coding sequence of β-galactosidase (28) 5′ to diHcRed (27), generating a LPDPPVAT linker between the two proteins. pEGFP-RCC1 was made by fusing the entire coding sequence of RCC1 (a generous gift from Iain Mattaj) 3′ to EGFP (Clontech Laboratories, Palo Alto, CA) generating a SGLRS linker between the two proteins. PAGFP-RCC1 was made by replacing the coding sequence of EGFP by PAGFP (11). H2B-PAGFP was made by fusing the entire coding sequence of H2B 5′ to PAGFP generating a DPP linker between the two proteins. PAGFP-hERα was made using EGFP-hERα (29) and replacing EGFP by PAGFP. H1.1, H1.2, H1.3, H1.4, and H1.5-PAGFP were made by fusing the entire coding sequence of the different H1 5′ to PAGFP generating the linker PGIHRPVAT between the proteins. PAGFP-SUV39H1 and PAGFP-SUV39H1-H320R were made by fusing the entire coding sequence of SUV39H1 and the mutant H320R (25) 3′ to PAGFP generating a YSDLEGGRDYKDDDDKGGR linker between the two proteins. EGFP-HP1β was made by fusing the entire coding sequence of HP1β (a generous gift from Howard Worman) 3′ to EGFP, generating a SGLRSLE linker between the two proteins.
Normal rat kidney (NRK) cells stably expressing H1.1-PAGFP, H1.2-PAGFP, H1.3-PAGFP, H1.4-PAGFP, H1.5-PAGFP, PAGFP-SUV39H1, H2B-PAGFP, and H2B-diHcRed were selected according to standard protocols and maintained in DMEM/10% FCS/0.5 mg/ml G418. Transfections were done using FuGene 6 (Roche, Mannheim, Germany). PAGFP-RCC1, PAGFP-hERα, and PAGFP-SUV39H1-H320R were transiently transfected and experiments were performed 24 h or 48 h after transfection for PAGFP-RCC1and PAGFP-hERα, and one week after transfection in the case of PAGFP-SUV39H1-H320R. PAGFP-hERα photoactivation was performed in the presence of 10 nM of β-estradiol (Sigma, Taufkirchen, Germany).
For microscopy, cells were cultured in No. 1 LabTekII chambered cover glasses (Nalge Nunc International, Naperville, IL) and maintained at 37°C on the microscope as described (30). In all experiments either H2B-DiHcRed or β-galactosidase-diHcRed were used as nuclear reference for image alignment.
PAGFP-RCC1 was histidine-tagged and purified on a nickel-agarose column (Qiagen, Valencia, CA). It was immobilized in a 30% acrylamide gel cast between a coverslip and a microscope slide to test photoactivation settings.
Photoactivation and three-dimensional imaging
Photoactivation experiments were performed on a Zeiss LSM 510 or a LSM 510 Meta (Carl Zeiss, Jena, Germany). PAGFP was photoactivated using a 80-mW Kr, 413-nm laser (Coherent, Dieburg, Germany) on the LSM 510 or a 20-mW, 405-nm laser diode (Point Source, Hamble, UK) on the LSM 510 Meta and observed at 488 nm. The 488-nm laser line was used at low power to prevent any residual photobleaching or photoactivation. A 40× PlanApochromat IRIS NA 1.0 oil objective (Zeiss) was used and the pinhole was wide-open to ensure imaging the entire nucleus. All images were 128 × 128 pixels to allow short frame acquisition times (100 ms). For all experiments, half of the nucleus was photoactivated and the whole nucleus was imaged. In the case of PAGFP alone, the cytoplasmic pool of protein was photoactivated and subsequently photobleached to prevent any contribution from the cytoplasm to the measurements. The experiment was then performed within the next 30 s on the nucleus to minimize the equilibration between nucleus and cytoplasm. H2B-PAGFP was imaged using an autofocus and tracking macro as described (31).
Simulations in three dimensions were performed starting from stacks of confocal sections of real nuclei with 0.3*0.3*0.35 μm3 (xyz) voxel sizes.
Image segmentation, alignment, and quantitation
Segmentation of three-dimensional stacks and quantitation of fluorescence intensities for the simulation were performed using in-house developed plugins for ImageJ (http://rsb.info.nih.gov/ij/). Photoactivation sequences were aligned as follows: first, each sequence was aligned using the nuclear diHcRed signal using a registration plug-in on ImageJ (http://bigwww.epfl.ch/thevenaz/turboreg/); then the same transformation was applied on the PAGFP signal using a in-house modified version of the plugin.
Quantitation for data fitting was performed with the LSM 2.8 software using an in-house developed macro to measure and format the fluorescence intensities for simulation and parameter optimization. Background was subtracted and intensities were normalized to the total intensity. Typically, nuclei were divided in six regions distributed along the main fluorescence redistribution direction, covering the whole nucleus.
Quantitation of fluorescence recovery was performed with ImageJ. Fluorescence of a bleached or a nonphotoactivated region was background-subtracted and normalized to the total intensity, also background-subtracted. This measurement was then normalized to 0 for the image taken right after photobleaching or photoactivation and to 100 for the steady-state distribution of fluorescence, yielding a direct readout of the percentage of recovery.
Computer simulation and curve fitting
Partial differential equations were simulated numerically using a finite difference approach. The following equation,
 |
becomes, in finite differences in three dimensions,
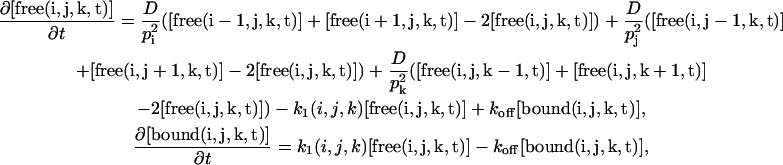 |
with pi, pj, and pk the spatial steps in the three dimensions and  and
and 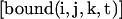 the local concentration of free and bound fluorescent proteins at the position (i,j,k) in the grid.
the local concentration of free and bound fluorescent proteins at the position (i,j,k) in the grid.
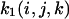 is
is with ist (i,j,k) the steady-state intensity at the position (i,j,k) in the grid and
with ist (i,j,k) the steady-state intensity at the position (i,j,k) in the grid and  the sum of all the ist (i,j,k) dividing by the number of grid elements that are inside the nucleus.In two dimensions, the equation becomes
the sum of all the ist (i,j,k) dividing by the number of grid elements that are inside the nucleus.In two dimensions, the equation becomes
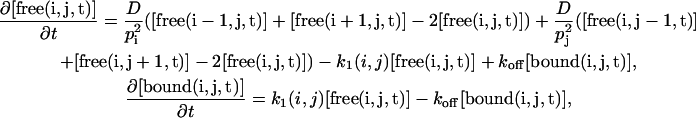 |
with pi and pj the spatial steps in the two dimensions. For our simulations, we chose pi = pj.
In three dimensions, the nucleus was subdivided in cuboids (Fig. 2 A), all of identical size with a typical side length of 0.3 μm (doubling the size did not significantly change the simulation result). As proteins were assumed not to cross the nuclear envelope, fluxes were fixed to zero across nuclear boundaries. The system of ordinary differential equations derived from the discretization was simulated and fitted to data using the solver Berkeley Madonna (www.berkeleymadonna.com). Initial conditions were measured from images taken right after photoactivation. Steady-state distributions of fluorescence were measured from images either before photoactivation at 413 or 405 nm or when the redistribution was complete at 488 nm. Integration was performed using a Runge-Kutta fourth-order algorithm with an adaptive step-size. The curve fit used the downhill simplex method. The six measured regions were fitted to the simulation except in the case of SUV39H1-H320R, where only two measured regions were fitted (see Results). Residuals were calculated by subtracting the fit from the data and normalizing it to the values of the fit at the end of the simulation.
FIGURE 2.
Modeling. (A) Finite difference approach of reaction-diffusion model. The nucleus, in this case an NRK cell expressing transiently PAGFP-SUV39H1, is discretized in cuboids (images). The reaction occurs in each cuboid (arrows “binding”) and exchange of free proteins occurs between the nearest-neighbors by diffusion (solid arrows). (B) Simulation of a photoactivation experiment in three dimensions starting from a cell transiently expressing PAGFP-SUV39H1. The three-dimensional sequence shows the simulated nucleus before perturbation (first image) and during fluorescence redistribution, from the top and the side (total intensity projection).
The simplified two-dimensional model, and potentially other unidentified systematic experimental errors, induced small but systematic deviation of the residuals from zero (see Supplementary Material, Fig. S3A), which makes the statistical analysis of the fit and of the confidence interval by classical methods not conclusive (data not shown). We therefore broadened this confidence interval by using an empirical cutoff at two times the square of the residuals obtained by the best fit (see one example in Supplementary Material, Fig. S3B).
RESULTS
A general reaction-diffusion model in the geometry of the nucleus
A simple experimental test for diffusion limited mobility: gradient smoothing
To characterize the interaction kinetics of proteins with chromatin by photoactivation and kinetic modeling, we first tested experimentally whether diffusion could be neglected by analyzing gradient shapes after photoactivation. If the intensity profile of the gradient changes during fluorescence redistribution, diffusion has to be modeled, otherwise it can be neglected (32). As expected, the highly mobile PAGFP alone expressed in normal rat kidney (NRK) cells, which should only diffuse, showed a smoothing gradient over time (Fig. 1 A). By contrast, the slowly exchanging core histone H2B (33) exhibited a completely constant intensity profile after normalization (Fig. 1 B). We then tested five dynamic chromatin interacting proteins tagged with (PA)GFP and expressed in NRK cells: RCC1, SUV39H1, and its hyperactive mutant, H1.1, estrogen receptor hERα, and heterochromatin protein 1 HP1β. For all five proteins, fluorescence gradients smoothed over time and diffusion therefore had to be taken into account to model the mobility of these proteins (see Fig. 1 C for RCC1, and Supplementary Material, Fig. S1, for the other proteins). Importantly, the timescale of fluorescence redistribution did not correlate with gradient smoothing. Chromatin interacting proteins that showed a change of gradient shape required between 2.8 s (SUV39H1) and 24.5 min (H1.1) for 80% fluorescence redistribution (Fig. 1 and Supplementary Material, Fig. S1, last image of each row). This clearly shows that the length of fluorescence redistribution cannot be used to determine if it is limited by diffusion or not.
FIGURE 1.
Test for diffusion-limited mobility NRK cells expressing PAGFP transiently (A), H2B-PAGFP stably (B), and PAGFP-RCC1 transiently (C). The first image of each dataset shows protein steady-state distribution in the nucleus imaged at 413 or 405 nm at low laser power before photoactivation. In all cases, half of the nucleus was photoactivated (open rectangle on second frame of each dataset). The last image represent 80% of fluorescence redistribution compared to steady state. To measure intensity profiles, each dataset was cropped using cropping regions like the one represented on the last frame of PAGFP. For each protein intensity, profiles were measured along the long axis of the nucleus, averaged along the short axis and normalized with the profile in steady state to generate fluorescence profiles for each time point. Plots display fluorescence intensity versus distance along the nucleus. The insets for PAGFP and H2B-PAGFP show the same profiles normalized between 0 and 1: note that whereas normalized profiles do not change for H2B-PAGFP, they become smoother for PAGFP and for PAGFP-RCC1. Scale bars: 5 μm.
A general three-dimensional reaction-diffusion model for chromatin interacting proteins
We therefore developed a model that included both diffusion and chemical interactions to simulate the fluorescence redistribution after photoactivation and fit the simulation to the experiments to determine the amount of bound protein, its residence time and, where possible, the diffusion coefficient of the unbound protein. The model was initially built in three dimensions based on the real geometry of the nucleus and distribution of chromatin of each observed cell.
We assumed that proteins are immobile when bound to chromatin, because chromatin does not show large-scale movements over 1 h in mammalian cells (34–36) and that free molecules can normally diffuse within the whole nucleus with a single diffusion coefficient D following Fick's second law,
 |
(1) |
where 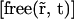 is the local concentration of unbound fluorescent molecules. We also assumed that chromatin occupies a negligible volume and that all binding sites are equally accessible. The interaction between proteins and chromatin was modeled as a simple first-order chemical reaction,
is the local concentration of unbound fluorescent molecules. We also assumed that chromatin occupies a negligible volume and that all binding sites are equally accessible. The interaction between proteins and chromatin was modeled as a simple first-order chemical reaction,
 |
(2) |
where free is the free protein, C is the free binding site on chromatin, bound is the bound protein, and kon and koff are the on- and off-rates of the interaction. Combining diffusion and interaction kinetics, changes in the local concentrations of fluorescent proteins during fluorescence redistribution can then be described by the partial differential equations of
 |
(3) |
It is important to note that photobleaching/activation perturbs the fluorescence only and is assumed not to modify the chemical interaction of fluorescent molecules. Therefore, the fluorescence perturbation does not affect the distribution of chemical species, seen independently of their fluorescent state. Therefore, as in our case chemical interactions can be considered to be in steady state over the whole experiment, the distribution of free binding sites  does not depend on time. Their spatial distribution is nevertheless not known, leading to an unknown parameter
does not depend on time. Their spatial distribution is nevertheless not known, leading to an unknown parameter 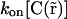 that depends on space. Nevertheless, we could show that this spatial dependency can be fully determined from the fluorescence distribution in steady state (see Appendix A), and that Eq. 3 can be rewritten by replacing
that depends on space. Nevertheless, we could show that this spatial dependency can be fully determined from the fluorescence distribution in steady state (see Appendix A), and that Eq. 3 can be rewritten by replacing  by a parameter
by a parameter 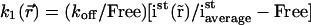 where
where  is the steady-state intensity distribution in space, proportional to the concentration of fluorescent protein (37),
is the steady-state intensity distribution in space, proportional to the concentration of fluorescent protein (37),  is the average steady-state intensity over the whole nucleus and Free is the global fraction of unbound proteins in steady state:
is the average steady-state intensity over the whole nucleus and Free is the global fraction of unbound proteins in steady state:
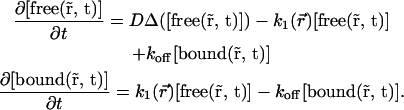 |
(4) |
Although Eq. 3 contains two parameters, D and koff, that are constant and one parameter, 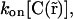 that depends on space, Eq. 4 has the major advantage of containing three parameters, D, koff, and Free that do not depend on space, and only requires the intensity distribution in steady state, which can easily be measured experimentally.
that depends on space, Eq. 4 has the major advantage of containing three parameters, D, koff, and Free that do not depend on space, and only requires the intensity distribution in steady state, which can easily be measured experimentally.
The reaction-diffusion Eq. 4 was simulated in silico using the real geometry of a nucleus and a typical distribution of chromatin interacting proteins (Fig. 2). As it cannot be solved analytically in such a complex geometry, it was solved numerically using a finite difference approach (Fig. 2 A; see also Materials and Methods, above). Initial conditions are needed for the free and bound fluorescent protein concentrations, but for chromatin proteins the resolution of light microscopy does not allow the discrimination between these two populations, and images just after photoactivation only provide their local sum  We thus further assumed that the ratio between free and bound fluorescent proteins after activation is the same as in steady state, which is correct either when the fluorescence perturbation (photoactivation/bleaching) is so fast that no significant free protein movement occurs during the perturbation, or when the interaction is so fast that local free and bound pools immediately equilibrate.
We thus further assumed that the ratio between free and bound fluorescent proteins after activation is the same as in steady state, which is correct either when the fluorescence perturbation (photoactivation/bleaching) is so fast that no significant free protein movement occurs during the perturbation, or when the interaction is so fast that local free and bound pools immediately equilibrate.
Two-dimensional simplification of the reaction-diffusion model
Most molecular kinetics are too fast to be imaged in three dimensions by acquiring z-stacks of images over time. We therefore performed all image acquisitions in two dimensions on a confocal laser scanning microscope with a wide-open pinhole and a low numerical aperture objective focused in the middle of the nucleus, such that the entire nuclear depth could be illuminated and detected (Fig. 3 A). To directly use this two-dimensional information, and to reduce the computing time, we then tested the validity of a two-dimensional model. In this simplified model we assumed that the steady-state concentration of free proteins was homogeneous and that the distribution of bound and free fluorescent proteins could be considered as two-dimensional (see Materials and Methods, above, for the finite difference equations), whereas, in fact, our two-dimensional observations correspond to the convolution of the reaction-diffusion process in three dimensions with the point-spread function (PSF) axially centered in the middle of the nucleus. To test the simplification we simulated a photoactivation experiment in three dimensions (Fig. 3 B, first row; see Supplementary Material 1 for the details of the procedure and (38) for the assumptions used), that we convolved radially, using the axial profile of Fig. 3 A to project in two dimensions and mimic our observation (Fig. 3 B, second row). We then tested the simplified model with these two-dimensional convolved images by fitting the six regions depicted on the figure (Fig. 3 B, second row, last frame) equally distributed in the direction of the fluorescence gradient. As can be seen on the plots, it can be fitted to the convolved images, and the fitted parameters are similar to the one used for the three-dimensional simulation. This shows that deconvolution of images is not necessary and that a two-dimensional model is sufficient to characterize protein dynamics. To statistically test the two-dimensional simplification and the influence of the real geometry, we simulated photoactivation in three dimensions in seven different nuclei, ignoring the convolution and assuming an homogeneous axial illumination in this case. The quality of the fit and the parameters were the same as when the PSF was considered. Starting from koff = 0.05 s−1, a low 1% free pool and a diffusion coefficient D of 29 μm2 s−1 in three dimensions, and keeping D = 29 μm2 s−1 in two dimensions, the two-dimensional fit gave koff = 0.051 s−1 ± 0.001 s−1 and a free pool of 1.04% ± 0.01%, with residual differences between the two- and three-dimensional simulations below 1%.
FIGURE 3.
Two-dimensional simplification. (A) PAGFP-RCC1 fixed in a 30% acrylamide gel was photoactivated in the red region using a 40× iris objective with a numerical aperture fixed to 1.0, seen from the top and the side. Scale bar: 5 μm. The longitudinal profile shows the average intensity of the profile generated by photoactivation in the confocal section where photoactivation was focused. The red curves correspond to a fit of half of this profile with the error function. The axial intensity profile corresponds to the profile of illumination in depth along the arrow of the image. (B) Simulation of a photoactivation experiment in three dimensions, using the depth profile from panel A and a Gaussian radial PSF for the photoactivation profile (first row, total intensity top and side projection), and two-dimensional observation of the simulation, using the same depth profile and radial PSF as for the photoactivation profile (second row). The first images of each row represent the steady-state distribution of fluorescence and the following represent the fluorescence redistribution. The first plot shows the average fluorescence intensity over time of the six regions depicted on the last images of the two-dimensional sequence (circles) and the fit using the simplified two-dimensional model (solid curves). The second plot represents the residuals, <1% for the six regions, between the three-dimensional simulations and the two-dimensional fit. (C) Three-dimensional simulation with a higher percentage of free proteins, starting from cell stably expressing PAGFP-SUV39H1 (first row). The second plot in the first row is a zoom of the early phase of the first plot and shows the diffusion of the initial free pool of fluorescent proteins. The amplitude of this early phase is related to the amount of free proteins. The late phase visible on the first plot corresponds mostly to the kinetics of the interaction. In this case, the same regions as in B cannot be well fitted with the two-dimensional simplified model (second row) with residuals reaching 25%, but it improves drastically (see solid curves and residuals of the third row) and parameters are close to the three-dimensional situation when one uses only the two regions depicted on the image of the third row. Scale bars: 5 μm.
We found only one particular case where the two-dimensional simplification is invalid, i.e., when the percentage of free fluorescent proteins is large and the dissociation of proteins from chromatin is slow compared to diffusion. This case represented in Fig. 3 C is characterized by an early phase of diffusion of free proteins when there is no significant contribution of the chemical interaction (Fig. 3 C, zoom of the early part of the plot), followed by a slower phase corresponding mostly to the dynamics of the interaction. The intensity amplitude of the early phase corresponds to the amount of free proteins, which fill the nonactivated half of the nucleus homogeneously according to the assumptions of the two-dimensional simplification (Fig. 3 C, second row, time 1.9 s). On the other hand, the three-dimensional simulation predicts an inhomogeneity due to the variable depth of the nucleus, which makes the two-dimensional simplification invalid when one tries to fit all the regions to the model (Fig. 3 C, plots of second row). Nevertheless we observed that when we fitted only the two regions depicted on the third row of Fig. 3 C, we could estimate the three parameters, D, free pool, and koff with good precision, with residual differences between three-dimensional simulation and two-dimensional fit below 1%. Starting from D = 29 μm2 s−1, Free = 50%, and koff = 0.020 s−1 in three dimensions, the two-dimensional fit gave D = 32 μm2 s−1 ± 1 μm2 s−1, Free = 52% ± 1%, and koff = 0.020 ± 0.001 s−1 for eight nuclei. In all other cases, the two-dimensional simplification was satisfactory for all nuclear regions. When the free pool is small enough, the amplitude of the first phase is too small to contribute to the fit, and when the interaction is fast enough, the first purely diffusive phase is no longer visible.
In conclusion, we could show that within the geometry of the nucleus of intact cells, a simplified two-dimensional reaction-diffusion model can globally describe the mobility of chromatin-interacting proteins with good precision. In cases where the free pool is high and the interaction slow compared to diffusion, the parameter estimation must be restricted to certain regions, but such cases are easy to identify before parameter estimation, as they show clear biphasic redistribution kinetics (see also the representative case of PAGFP-SUV39H1-H320R, below).
Calibration of nuclear viscosity
The model contains three parameters: the diffusion coefficient, the fraction of unbound proteins, and the dissociation rate or its inverse, the residence time of the interaction with chromatin. As can be seen on Fig. 4 A, PA experiments will not always allow us to identify all three parameters, because in some cases, different combinations of parameters fit the data equally well. In such cases, we calculated the diffusion coefficient independently from the model based on the molecular weight of the protein and the viscosity of the nucleoplasm. The apparent viscosity of the nucleoplasm was calibrated using PAGFP alone as an inert probe regarding binding interactions in the nucleus.
FIGURE 4.
Parameter identifiability. (A) Fit and residuals for Fig. 3 B starting from two different fixed diffusion coefficients. It should be noted that the fits are almost similar, showing that in such a case the diffusion constant has to be determined separately to be able to estimate the other parameters. (B) PAGFP photoactivation. The nucleus was photoactivated (open region, first image) and imaged over time (first row). The intensities of the six regions depicted on the last image were plotted over time (upper plot, circles) and fitted (solid curves). Residuals are below 6% (lower plot). The sequence on the second row is the simulation using the parameter from the fit. Scale bar: 5 μm.
Nucleoplasmic PAGFP diffusion was probed by photoactivating half of the nucleus and measuring its redistribution over time as described above (Fig. 4 B). The pure diffusion model Eq. 1 was simulated in two dimensions, using an empirical method proposed by Siggia et al. (39) that we validated for the nucleus the same way as in the previous section (see Supplementary Material 2 and Fig. S2 for details). Nuclear PAGFP photoactivation was performed on 67 nuclei. The example shown in Fig. 4 B shows that the fit is qualitatively very close to the data, with residuals below 6%. On average, we measured a two-dimensional diffusion coefficient of 40.6 μm2 s−1 ± 3.8 μm2 s−1. Given that the GFP diffusion coefficient in water is 87 μm2 s−1 at room temperature (40,41) and that water viscosity drops from 1.00 to 0.69 cP between 20°C and 37°C (42), we found the apparent viscosity of the nucleoplasm to be ∼3.1 times higher than water, consistent with the literature (43–45).
Knowing the apparent viscosity, the diffusion coefficient of chromatin-interacting proteins was then calculated from the mass of the protein, using the Stokes-Einstein relation,
 |
(5) |
D is the diffusion coefficient, k the Boltzmann constant, T the temperature, η the viscosity, and R the spherical radius of the molecule. We approximated the radius to be proportional to the cubic root of its mass, yielding
 |
(6) |
with mprotein as the molecular weight of the protein (Table 1). As all our proteins of interest were of similar size, their diffusion coefficient was estimated to ∼30 μm2s−1. This is only an approximation, which likely contributes an uncertainty of up to a factor of 2 in the diffusion coefficient.
TABLE 1.
Fit results
| Protein name | Molecular weight | Diffusion coefficient | Percentage of free proteins | Dissociation constant | n |
|---|---|---|---|---|---|
| PAGFP-RCC1 | 74 kDa | 30 μm2 s−1 imposed | 2.1% ± 0.6% | >0.15 s−1 | 19 |
| PAGFP-SUV39H1 | 77 kDa | 30 μm2 s−1 imposed | 36% ± 8% | >0.9 s−1 | 20 |
| PAGFP-SUV39H1-H320R | 77 kDa | 5.7 ± 1.6 μm2 s−1 fit* | 57% ± 17% | 5.1.10−3 ± 2.2.10−3 s−1 | 8 |
| H1.1-PAGFP | 50 kDa | 34 μm2 s−1 imposed | 0.09% ± 0.04% | >6e–3s−1 | 19 |
| H1.2-PAGFP | 49 kDa | 34 μm2 s−1 imposed | 0.08% ± 0.03% | 12 | |
| H1.3-PAGFP | 50 kDa | 34 μm2 s−1 imposed | 0.05% ± 0.02% | 10 | |
| H1.4-PAGFP | 50 kDa | 34 μm2 s−1 imposed | 0.04% ± 0.01% | 11 | |
| H1.5-PAGFP | 50 kDa | 34 μm2 s−1 imposed | 0.03% ± 0.01% | 13 |
Diffusion coefficients come from the fit unless the model could not estimate them, in which case they were imposed. When the lower limit of dissociation rate is given, it means that the actual value is not measurable experimentally. The value n is the number of nuclei investigated for each construct.
As the fitted diffusion coefficient is much lower than expected from the size of the protein, it can be interpreted as an apparent one, corresponding to an instantaneous reaction.
Measuring chromatin interactions with the model
We then applied the model to simulate photoactivation experiments of PAGFP fusion proteins to analyze the interactions of RCC1, SUV39H1, and its hyperactive mutant SUV39H1-H320R, and the five human isoforms of H1 with chromatin. We found two classes of behavior. The most common, instantaneous interaction with chromatin is illustrated in detail by PAGFP-RCC1. Despite large differences in the timescales of redistribution, the dynamics of SUV39H1 and H1 isoforms were extremely similar to that of RCC1. The second class of behavior, a noninstantaneous interaction with chromatin, is illustrated by the hyperactive mutant of SUV39H1.
PAGFP-RCC1 interacts instantaneously with chromatin and 2% of the protein pool is unbound in steady state
RCC1 interacts with the core histones H2A and H2B (24). FRAP experiments on GFP-RCC1 have already shown that its association with chromatin is dynamic: the half-time of recovery was found to be ∼2 s for a bleached spot in U2OS cells (46), and ∼10 s for a bleached stripe in tsBN2 (47), and one study fitted the recovery with a diffusive model with an apparent diffusion coefficient of 0.5 μm2 s−1 in 3T3 cells (48). We performed the experiment as described before for PAGFP alone, using transient expression of PAGFP-RCC1 in NRK cells (Fig. 5 A). The model using Eq. 4 was fitted to the measured intensities using D = 30 μm2 s−1 (Table 1), yielding as an initial set of parameters a dissociation rate koff of 2 s−1, i.e., a residence time of 0.5 s, and an unbound pool Free of 2.9%. The fit was qualitatively in good agreement with the data (Fig. 5 A) and residuals did not exceed 8% (Fig. 5 A and Supplementary Material, Fig. S3 A, for the details of the residuals).
FIGURE 5.
PAGFP-RCC1. The percentage of free molecules and only the lower limit of dissociation rate can be estimated. (A) Nucleus of NRK cell transiently expressing PAGFP-RCC1, acquired at 405 nm, low power, and 488 nm before photoactivation (first two images) and at 488 nm after activation (second row). The plots represent the average intensity over time of the regions depicted on the last image (circles) and the fit (solid curves, first plot), and the residuals (second plot). The simulation using the parameters from the fit is shown on the last image row. Scale bar: 5 μm. (B) Color-coded sum of the square of the residuals for different values of dissociation rates koff and percentage of free proteins. The black-cross fit on the parameter space corresponds to the fit in A. The regions with white boundaries correspond to the values of sum of residual squares that are less than the double of the one corresponding to the fit. (C) Same plots as in panel A, but using a instantaneous reaction model. Note that it is almost completely similar to panel A.
We then tested the certainty of the parameters for PAGFP-RCC1 by plotting the sum of the square of the differences between experimental data and simulation for different combinations of koff and Free. Fig. 5 B shows the importance of exploring parameter space in this manner: the dark-blue region represents the area of parameters that fit the data qualitatively well (see Supplementary Material, Fig. S3 B, for simulations with parameters of this area), and this region is infinite toward the high values of koff. By contrast, the percentage of free molecules could be identified as 2.9% ± 0.2% (white bounded region on Fig. 5 B) (could be up to 4.3%; isolated white bounded region on Fig. 5 B) and the lower limit of the dissociation rate koff could be determined as 0.4 s−1, i.e., a maximum residence time of 2.5 s (could be as low 0.2 s−1).
From the chemical point of view, this means that the interaction of PAGFP-RCC1 is too transient to be accurately measured by fluorescence perturbation methods such as PA/FRAP. At first glance, this is counterintuitive, as the fluorescence redistribution of PAGFP-RCC1 was very slow compared to PAGFP alone (compare Fig. 1, A and C, and Figs. 4 B and 5 A). The speed of redistribution of RCC1, however, does not reflect the length of the interaction but rather its affinity. The small fraction of free molecules, 2.9%, are very often trapped on their ubiquitous binding sites, and although they reside in the bound state for short times, they can therefore not diffuse efficiently over long distances and need long times to redistribute across the nucleus.
In such a case, the reaction-diffusion model Eq. 4 can be strongly simplified because the interaction can be considered as instantaneous. For homogeneously distributed binding sites, it has been shown that the model then becomes effectively diffusive (49), and also for an inhomogeneous distribution of binding sites we can rewrite the model to (Appendix B)
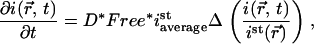 |
(7) |
with 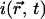 the local fluorescence intensity. For relatively homogeneous distributions of binding sites Eq. 7 is approximately a diffusive equation with an effective diffusion coefficient equal to the product of the diffusion coefficient with the percentage of free proteins, D*Free. Thus, the speed of redistribution depends only on the diffusion coefficient of the protein and on the percentage of protein available for diffusion in steady state, but not on the kinetics of the interaction. If the unbound fraction is low, the fluorescence redistribution is slow. Fig. 5 C shows a fit performed on the same data as on Fig. 5 A using Eq. 7. The residuals are as expected identical and the estimated fraction of free protein is very similar, 2.8%. It should be noted that this would lead to an effective diffusion coefficient of D*Free = 0.8 μm2 s−1, close to already published values (48), but the correct interpretation possible by the model is that 97% of RCC1 is bound to chromatin and that the interaction can be considered as instantaneous. The analysis was performed on 19 nuclei and led to an average percentage of free molecules of 2.1% ± 0.6% (Table 1), with the uncertainty linked to our estimation of the diffusion coefficient (see above).
the local fluorescence intensity. For relatively homogeneous distributions of binding sites Eq. 7 is approximately a diffusive equation with an effective diffusion coefficient equal to the product of the diffusion coefficient with the percentage of free proteins, D*Free. Thus, the speed of redistribution depends only on the diffusion coefficient of the protein and on the percentage of protein available for diffusion in steady state, but not on the kinetics of the interaction. If the unbound fraction is low, the fluorescence redistribution is slow. Fig. 5 C shows a fit performed on the same data as on Fig. 5 A using Eq. 7. The residuals are as expected identical and the estimated fraction of free protein is very similar, 2.8%. It should be noted that this would lead to an effective diffusion coefficient of D*Free = 0.8 μm2 s−1, close to already published values (48), but the correct interpretation possible by the model is that 97% of RCC1 is bound to chromatin and that the interaction can be considered as instantaneous. The analysis was performed on 19 nuclei and led to an average percentage of free molecules of 2.1% ± 0.6% (Table 1), with the uncertainty linked to our estimation of the diffusion coefficient (see above).
PAGFP-SUV39H1 interacts instantaneously with chromatin and 36% of the protein pool is unbound in steady state
SUV39H1 is a methyltransferase that specifically methylate lysine 9 of histone H3 (25), a key epigenetic modification involved in gene silencing. SUV39H1 binds to core histones without apparent preferences in vitro (50).
Photoactivation experiments to probe SUV39H1 interaction with chromatin were performed in NRK cells stably expressing PAGFP-SUV39H1. Models were simulated and fit to the data with a diffusion coefficient of 30 μm2 s−1. Fluorescence redistribution could be fit equally well by the reaction-diffusion model Eq. 4 (data not shown) and by the instantaneous reaction model Eq. 7 (Fig. 6, A–C). Thus, similar to PAGFP-RCC1, the percentage of free protein and only the lower limit of the dissociation rate could be determined. The analysis of 20 nuclei led to an average free protein pool of 36% ± 8% and a lower limit of dissociation rate of 0.9 s−1, i.e., a residence time of, at most, 1.1 s determined from the parameter space analysis (Fig. 6 B).
FIGURE 6.
PAGFP-SUV39H1 and H1.1PAGFP. Different timescales but same conclusions as for PAGFP-RCC1; only the lower limit of dissociation rate can be estimated. (A) Nucleus of an NRK cell stably expressing PAGFP-SUV39H1, acquired at 405 nm, low power, before activation (first image) and at 488 nm before and after activation of half of the nucleus (open region, second image). (B) Parameter space as in Fig. 5 B. (C) Instantaneous reaction model for PAGFP-SUV39H1, almost similar to a reaction-diffusion model (not shown). (D) NRK cell stably expressing H1.1-PAGFP. Images as in A. (E) The parameter space represents the sum of the squares of the residuals for different values of dissociation rates koff, the percentage of free proteins being fixed to the value given by the fit. The horizontal dashed line corresponds to the double of the minimum of this sum, giving the lower limit of dissociation rate 0.017 s−1 depicted on the plot. (F) Instantaneous reaction model for H1.1-PAGFP, similar to a reaction-diffusion model (not shown). Scale bars: 5 μm.
Five isoforms of H1-PAGFP interact instantaneously with chromatin and have <0.1% of unbound protein in steady state
Histones H1 are components of the nucleosomal subunits that play an important role in chromatin structure and function (26). The dynamics of some isoforms have already been investigated by FRAP (3,51), which gave a recovery in the range of 1 min for a small bleached spot, a time that was interpreted as the residence time.
We stably expressed five isoforms of H1-PAGFP, H1.1-5, in NRK cells. Models were simulated using a diffusion coefficient of 34 μm2 s−1. All isoforms showed very similar behavior, which is illustrated for H1.1-PAGFP in Fig. 6 D. The behavior of fluorescence redistribution is similar to PAGFP-RCC1 and PAGFP-SUV39H1. It could be fit by the reaction-diffusion model Eq. 4 (data not shown) as well as by the instantaneous reaction model Eq. 7 (Fig. 6 F), yielding an average fraction of free protein of 0.09% ± 0.04% (n = 19). Due to the stiffness of the reaction-diffusion model Eq. 4 with such a low percentage of unbound molecules, we could not explore parameter space as exhaustively as for PAGFP-RCC1 and PAGFP-SUV39H1 at reasonable computational cost. We therefore only plotted the sum of the residual squares for different values of dissociation rate koff, fixing the percentage of free proteins that best fit the data (Fig. 6 E). Because of the curved distribution of best-fitting koff values (see Figs. 5 B and 6 B), this procedure could lead to an underestimation of the lowest possible limit of koff of a factor of 2.9 for PAGFP-RCC1 and 2.4 for PAGFP-SUV39H1 (Supplementary Material, Fig. S4). Because the lower limit of koff is 0.017 s−1, according to the plot (Fig. 6 E), we can estimate it to 6*10−3 s−1—i.e., a residence time of no more than 170 s, with a correction factor of 2.7.
The results for the four other isoforms are summarized in Table 1. The percentages of free protein are all similar to H1.1-PAGFP and, as the levels of noise are comparable, the lower limits of the dissociation rate are also expected to be similar (see Discussion).
It should be noted that the model shows a complete recovery of fluorescence, contrary to what has been published for H1°-GFP and H1c-GFP (3). It should also be noted that our timescale of fluorescence redistribution is much longer than the published ones (3,51), notably because our photoactivated regions are much larger, which directly affects a diffusion-limited redistribution (see Discussion).
Hyperactive PAGFP-SUV39H1-H320R is bound for 200 s on chromatin
The hyperactive mutant of PAGFP-SUV39H1-H320R is mutated in the catalytic SET domain of the enzyme, unexpectedly resulting in an increase of activity (25). It was transiently expressed in NRK cells. Likely due to the toxicity of the mutant in living cells, only very low levels of expression could be observed, which explains the lower signal/noise ratio of the images compared to the other proteins studied here (Fig. 7). In contrast to the wild-type protein, most nuclei exhibited a high percentage of diffusive proteins that led to a fast early redistribution followed by a slower phase limited by the kinetics of the chemical interaction (Fig. 7, plots), as already mentioned for validation of the two-dimensional model. In this case, all three parameters of the reaction-diffusion model could be identified using the two regions depicted on the images of Fig. 7. The fit yielded an average diffusion coefficient of 5.7 μm2 s−1 ± 1.6 μm2 s−1, a percentage of free diffusive proteins of 57% ± 17% and a dissociation rate of 5.1*10−3 s−1 ± 2.2*10−3 s−1, i.e., a residence time of 196 s (n = 8).
FIGURE 7.
PAGFP-SUV39H1-H320R case. Free pool of 35% and residence time of 210 s. Nucleus of NRK cell stably expressing the hyperactive PAGFP-SUV39H1-H320R, acquired at 488 nm. Contrary to the other cases, the steady-state distribution was not measured at 405 nm as the signal was too low. The intensities of the two regions depicted on the last image are plotted (circles) and fitted (solid curves) as in Fig. 3 C. The second plot correspond to a zoom of the early part of the first plot.
The diffusion coefficient of 5.7 μm2 s−1 is nevertheless smaller than 30 μm2 s−1 expected from the size of the protein. The diffusion coefficient of the early redistribution, may therefore also correspond to an effective diffusion coefficient, reduced by a relatively large fraction of protein bound in an instantaneous interaction, like in the case of wild-type PAGFP-SUV39H1. The redistribution of fluorescence would then be due to two types of interactions: one fast, compared to diffusion that led to an apparent diffusive process at early times similar to the wild-type protein; and one slow, with a dissociation rate of 5.1*10−3 s−1 and a percentage of free proteins, i.e., proteins that are not bound in the second interaction, of 57%. To understand the estimated parameters in the context of two reactions, we wrote the reaction-diffusion equations for a model where the second interaction is a stabilization of the first:
 |
If the first interaction can be considered as instantaneous, then we can write the differential equations describing the system in a similar way to Eq. 4 (see Appendix C). The interpretation of the dissociation rate remains the same: it corresponds to koff2. What we call here the free pool of 57% is actually the ratio The fraction of free proteins regarding only the first reaction
The fraction of free proteins regarding only the first reaction  is the ratio of the apparent diffusion coefficient with the real D of the free proteins (see Appendix C), i.e., 19% assuming a diffusion coefficient of 30 μm2 s−1. The real fraction of free proteins,
is the ratio of the apparent diffusion coefficient with the real D of the free proteins (see Appendix C), i.e., 19% assuming a diffusion coefficient of 30 μm2 s−1. The real fraction of free proteins,  is therefore the product of these 19% with the apparent free pool of 57%, i.e., 11%.
is therefore the product of these 19% with the apparent free pool of 57%, i.e., 11%.
DISCUSSION
Comparison to other FRAP experiment and analysis methods
One of the main experimental approaches used to quantitatively characterize diffusion (12,52) and reactions limited by diffusion (18) consists in bleaching a small spot and analytically analyzing the fluorescence recovery in this spot. Compared to this classical FRAP approach, the method presented here requires more computational skills and more time, but offers several advantages. First, the theoretical analysis of the spot-bleaching technique has always assumed an infinite system, a questionable assumption as most cellular compartments are not very large compared to the bleached spot. By contrast, our method takes the complete geometry of the sample, including boundaries, into account. Moreover, the spot technique requires the size and shape of the bleaching intensity profile to be known (12), which requires nontrivial optical calibrations. Our method is independent of the geometry of bleaching/photoactivation, and does not require the characterization of the amount of bleaching, as in certain cases for the spot technique (12). Furthermore, spots are typically chosen small to make the rest of the sample infinite, as possible leading to noisy data. Here, we measure the intensity in the whole nucleus, offering a much better precision in model validation and parameter estimation. Finally, fluorescence distributions are typically considered as homogeneous in space to simplify the analysis, whereas here such simplification is not needed: the distributions of both bound and unbound molecules are taken into account, allowing higher precision and a convincing validation of the model.
Limits of residence times that can be measured by FRAP/PA
Three of the proteins we examined, RCC1, H1, and wild-type SUV39H1 illustrate that for generic chromatin-interacting proteins, the binding reaction can appear instantaneous in FRAP/PA experiments and that only a lower limit for koff can be determined from such experiments. Exploiting the possibility to do in silico experiments with our reaction-diffusion model, we wanted to generally test the dependence of the ability to identify the dissociation rate on the percentage of free proteins, which reflects the affinity of the interaction in steady state.
To this end, we used a simplified one-dimensional reaction-diffusion model with a homogeneous distribution of binding sites and a hypothetical protein with a diffusion coefficient of 30 μm2 s−1. For given percentages of free protein, we tested at what dissociation rate the reaction-diffusion model can no longer be discriminated from an instantaneous reaction model with a tolerance of 5% between the two models (see Supplementary Material 3 for details). Fig. 8 shows that the method has the best sensitivity for high dissociation rates if ∼30% of the protein is unbound, then dissociation rates up to ∼30 s−1— i.e., residence times as short as 33 ms can be identified. For amounts of free protein from 0 to 30%, the limit that can be estimated for the dissociation rate increases proportionally with the free fraction. For higher percentages of free proteins, the identifiable limit of dissociation rate decreases rapidly again with the free fraction, presumably because the contribution of the bound fraction to the fluorescence equilibration diminishes significantly. These in silico results are in good agreement with our experimental data on the instantaneous interactions of SUV39H1, RCC1, and H1.1 with chromatin. For all three proteins, the limit of the identifiable dissociation rate increased with the free fraction (Fig. 8, vertical lines).
FIGURE 8.
Estimation of dissociation rates. Experimental and theoretical limits. Positions of the different constructs on the diagram of fraction of free proteins versus dissociation rates. The curve between the shaded and the unshaded regions corresponds to the limit of dissociation rates that can be estimated, with a tolerance of 5%, determined from the comparison between reaction-diffusion and instantaneous reaction models. The shaded region corresponds to the space where the dissociation rate cannot be estimated. It should be noted that although the dissociation rates of H1.1-PAGFP, PAGFP-RCC1, and PAGFP-SUV39H1 cannot be determined, their limit is outside the shaded region, likely because this limit also takes into account data noise and systematic errors.
Thus, for cases where interactions appear instantaneous, FRAP/PA experiments are suitable to measure the amount of free protein but give limited information on the kinetics of the interaction. As illustrated over the parameter space in Fig. 8, combinations of dissociation rate and unbound fraction that can be physiologically expected can easily be found in the half-space, where koff cannot be identified. Thus there is clearly a need for complementary methods to measure transient biochemical interactions in living cells. Fluorescence correlation spectroscopy may be a good alternative to access this information as the timescales accessible by this technique are orders-of-magnitude shorter than with FRAP/PA.
General implications for the interpretation of FRAP and PA experiments
Slow redistribution does not mean stable interaction
Our study clearly shows that the analysis of FRAP and PA experiments to determine interaction parameters is not trivial. Simplifying the reaction-diffusion process that typically drives the mobility of nuclear proteins to a model where diffusion is ignored has been often used in recent studies (e.g., (6,21)), but may lead to wrong parameter values and biological interpretations if the simplification is not justified. It is clear from our data that a long timescale of redistribution compared to diffusion alone is not indicative of long-lived interaction, because an instantaneous interaction with a ubiquitous binding site can lead to any timescale of recovery depending on how small the unbound fraction of protein is. Such behavior can then be modeled by an instantaneous reaction equation limited by an apparent diffusion coefficient that can take any value below the real diffusion coefficient, depending on the free protein fraction available for diffusion. A long timescale of fluorescence recovery may correspond to a long-lived interaction, but it may also correspond to a very transient interaction with high affinity.
In this context, the number of free binding sites may influence the dynamics of fluorescence recovery. This could notably explain why the H1 isoform H1° becomes more dynamic when HMG proteins, which compete with H1 for the same binding sites, is microinjected into nuclei (53): the reduction in the number of binding sites for H1° could increase the amount of free H1°, leading to a faster fluorescence recovery; likely, however, without any change in association and dissociation kinetics.
Half-time of recovery is not a measure of residence times
It is also clear that the half-time of recovery that is typically measured in FRAP studies may not be related at all to the residence time of a protein on its binding site. In this study, the examples of RCC1, SUV39H1, and of the different H1 isoforms clearly illustrate this, because their residence time cannot be measured. Even in the case of SUV39H1-H320R, the half-time of recovery is not informative: since more than half of the proteins are considered as unbound and the dissociation rate is small, the early fast recovery will contribute to more than half of the complete recovery. Therefore the half-time of recovery will relate mostly to the early, diffusive part of the recovery curve, and not to the later part, which contains the information about the residence time.
Moreover, whereas kinetics of chemical reactions depend only on concentration changes over time, diffusive processes depend on both time and space. This means that half-times of recovery can strongly depend on the geometry of photobleaching/activation: for a purely diffusive process the characteristic time of diffusion is roughly proportional to the square of the spatial scale of fluorescence recovery. For example, bleaching a spot of ∼1 μm in diameter or bleaching half of a nucleus, ∼5 μm in diameter, will result in a 25-fold increase in half-time of recovery. This explains why published half-times of recovery can be so different for a given protein, e.g., GFP-RCC1 (46,47). Therefore the half-time of recovery that is typically measured in FRAP experiments should only be interpreted as a measurement of the dynamics of the protein and not as a residence time on a binding site or a diffusion coefficient, unless that is clearly justified. Moreover, in cases where diffusion is limiting fluorescence redistribution, half-times of fluorescence recovery can only be compared between identical experimental geometries.
On the other hand, trying to model fluorescence recovery by a diffusive process with popular analytical solutions (12) may also lead to misinterpretation of the results. This method only works for purely diffusive processes or when the interactions are very fast compared to diffusion, in which case it will yield an effective diffusion coefficient lowered by the fraction of unbound protein. It is not applicable in any other cases.
Deriving equilibrium dissociation constant and association rate in living cells
From the reaction-diffusion Eq. 3 it can be seen that kon cannot be estimated from photobleaching/activation without information on the concentration of free binding sites. Likewise the equilibrium dissociation constant KD, which is the product of Free/(1-Free) and the concentration of free binding sites, cannot be determined without the latter.
PAGFP-RCC1 interacts with histones, which in cells are assembled into nucleosomes, therefore
 |
where  is the concentration of free nucleosomes available for RCC1 binding. Here,
is the concentration of free nucleosomes available for RCC1 binding. Here,
 |
The amount of free nucleosomes available for RCC1 binding is nevertheless not known and cannot be estimated from our experiments as nucleosomes can be occupied by RCC1 tagged and untagged, as well as by many other nucleosome binding proteins, whose concentrations and affinities are unknown. We can therefore only estimate its upper limit, assuming that all nucleosomes are free. Given that a rat cell contains ∼6*109 basepairs of DNA and nucleosomes repeat at intervals of ∼200 basepairs, we can estimate that a rat cell contains ∼3*107 nucleosomes (54). As the nuclear volume is ∼0.7 pl, the total concentration of nucleosomes is ∼70 μM. If we assume one binding site per nucleosome, the dissociation constant KD is then smaller than 1.4 μM. The real value is the product of this upper limit by the fraction of free binding sites, a number difficult to estimate. It should be noticed that KD has been estimated to ∼5 nM in vitro (55), suggesting that only ∼0.5% of nucleosomes are available for RCC1 binding in steady state.
The case of H1 is very similar: as one linker histone H1 binds to one histone octamer, like RCC1, this leads to an upper limit for the dissociation constant KD of 70 nM. Like in the case of RCC1, the real dissociation constant is the product of this upper limit with the fraction of free histones. In vitro H1 binds nucleosomes with a KD of 7.4 nM (56), suggesting that ∼10% of nucleosomes are available for binding to H1 in steady state.
Implications for dynamics of protein-DNA interactions
The problem of specific protein-DNA recognition has been a challenging issue since 1970 when the Escherichia coli lac repressor was found to find its target at a much higher rate than predicted for a diffusion-controlled process (57). It was therefore suggested that more elaborate mechanisms than simple three-dimensional diffusional collisions should occur (58,59). Notably it has been proposed that proteins can interact with nonspecific sequences of DNA at low affinity and then diffuse along the DNA molecule in one dimension, restricting the volume which has to be searched by the protein and resulting in more efficient encounters with specific sites. Most FRAP studies on chromatin interacting proteins have been taken to suggest that the three-dimensional diffusional collision process was universal in living eukaryotic cells (60). The suggestion that chromatin interacting proteins can diffuse all over the nucleus before interacting with a binding site is in contradiction with the very high association rates found for the lac repressor. The interpretation of FRAP data was based on the assumption that diffusion does not limit fluorescence recovery, an assumption not validated in most studies. Here we could see that in the cases of RCC1, Suv39H1 and H1, this assumption is not valid. In the context of a three-dimensional reaction-diffusion model these individual proteins will therefore reassociate with a binding site in close proximity, which could be compatible with a one-dimensional diffusion along DNA molecules. Our present study shows that FRAP studies showing rapid nuclear protein mobilities do not provide per se grounds to rule out the one-dimensional diffusion hypothesis for eukaryotic cells. It might therefore be worth considering testing it with appropriate methods.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Supplementary Material
Acknowledgments
We thank Iain Mattaj for the kind gift of the RCC1 cDNA, Howard Worman for the kind gift of the HP1β cDNA, and Christine Ruckenbauer and Jan Michael Peters for the kind gift of GFP-SUV39H1 and GFP-SUV39H1-H320R. We also thank Werner Albig and Detlef Doenecke for the kind gift of the five H1 isoform cDNAs. J.E. acknowledges funding from the German Research Council (DFG grant No. EL 246/1-1 and grant No. EL 246/2-1/2).
APPENDIX A: REFORMULATION OF REACTION-DIFFUSION EQUATIONS USING STEADY-STATE FLUORESCENCE DISTRIBUTION
Equation 3 is the standard reaction-diffusion with immobile bound molecules:
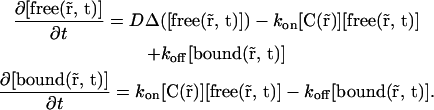 |
(8) |
Our goal was to modify the product  by using the spatial information we have in steady state to get parameters that do not depend on space anymore.
by using the spatial information we have in steady state to get parameters that do not depend on space anymore.
The steady-state intensity  is proportional to the sum of free and bound protein steady-state concentrations, with a proportionality coefficient A,
is proportional to the sum of free and bound protein steady-state concentrations, with a proportionality coefficient A,
 |
(9) |
where  represents concentrations in steady state. In such conditions, we have local chemical equilibrium of
represents concentrations in steady state. In such conditions, we have local chemical equilibrium of
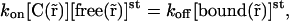 |
(10) |
and because of the expressions in Eq. 8 are equal to zero and because of Eq. 10, we have no gradients of free molecules:
 |
This means that  is actually a constant in space freest. One can therefore write Eq. 10 as
is actually a constant in space freest. One can therefore write Eq. 10 as
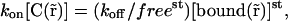 |
(11) |
or, using Eq. 9,
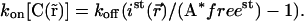 |
To get rid of the unknown proportionality coefficient A, we introduced a new parameter Free equal to the ratio of the total amount of free fluorescent molecules over the total amount of fluorescent molecules in the nucleus.
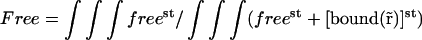 |
or
 |
with  representing the sum over the whole nuclear volume. By dividing both terms of the ratio by the nuclear volume we see that Free is also proportional to the ratio of the average amount of free molecules, which is freest because this is a constant, and the average of steady-state intensity
representing the sum over the whole nuclear volume. By dividing both terms of the ratio by the nuclear volume we see that Free is also proportional to the ratio of the average amount of free molecules, which is freest because this is a constant, and the average of steady-state intensity  :
:
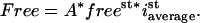 |
Eq. 11 then becomes
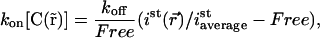 |
which we noted 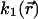 in the main text.
in the main text.  could be directly measured from images showing the steady-state distribution of fluorescent molecules.
could be directly measured from images showing the steady-state distribution of fluorescent molecules.  was determined by summing
was determined by summing 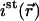 over the whole nucleus and dividing it by the nuclear volume.
over the whole nucleus and dividing it by the nuclear volume.
APPENDIX B: DIFFUSION-REACTION MODEL WITH INSTANTANEOUS REACTION
In such a case, the reaction-diffusion model,
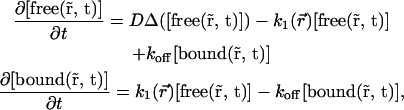 |
(12) |
can be simplified, because the fact that the reaction is instantaneous means that we always have chemical equilibrium even during the diffusion,
 |
(13) |
and therefore
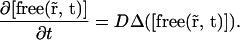 |
(14) |
Now the measured intensity 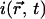 is proportional to the sum of the free and bound pool of proteins, with a coefficient of proportionality A,
is proportional to the sum of the free and bound pool of proteins, with a coefficient of proportionality A,
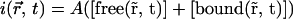 |
(15) |
or, using Eq. 13,
 |
(16) |
So from Eq. 12,
 |
(17) |
or
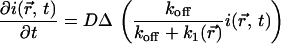 |
(18) |
Given that 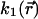 is defined as
is defined as
 |
(19) |
Eq. 18 can be rewritten as
 |
APPENDIX C: DIFFUSION-REACTION MODEL WITH A FIRST INSTANTANEOUS REACTION AND A SLOW STABILIZATION
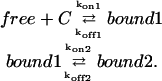 |
To simplify the writing of the equations, we consider here an homogeneous distribution of binding sites,
 |
(20) |
If the first interaction can be considered as instantaneous, then
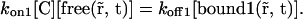 |
(21) |
The free pool of proteins seen in the case of PAGFP-SUV39H1 corresponds to proteins that are not stabilized, i.e. to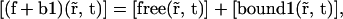 which is described by the sum of the two first equations of Eq. 20,
which is described by the sum of the two first equations of Eq. 20,
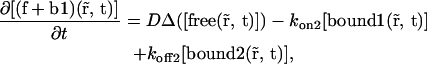 |
i.e., using Eq. 21,
 |
which is equivalent to the reaction-diffusion Eq. 4, by replacing 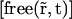 by
by 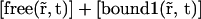 and the diffusion coefficient by an apparent one which is its product with the fraction of free proteins regarding only the first reaction:
and the diffusion coefficient by an apparent one which is its product with the fraction of free proteins regarding only the first reaction: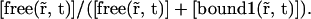
J. Beaudouin's present address is German Cancer Research center (DKFZ), Div. Theoretical Bioinformatics (B080), Im Neuenheimer Feld 580 (TP3), D-69120 Heidelberg, Germany.
References
- 1.Houtsmuller, A. B., S. Rademakers, A. L. Nigg, D. Hoogstraten, J. H. Hoeijmakers, and W. Vermeulen. 1999. Action of DNA repair endonuclease ERCC1/XPF in living cells. Science. 284:958–961. [DOI] [PubMed] [Google Scholar]
- 2.Phair, R. D., and T. Misteli. 2000. High mobility of proteins in the mammalian cell nucleus. Nature. 404:604–609. [DOI] [PubMed] [Google Scholar]
- 3.Misteli, T., A. Gunjan, R. Hock, M. Bustin, and D. T. Brown. 2000. Dynamic binding of histone H1 to chromatin in living cells. Nature. 408:877–881. [DOI] [PubMed] [Google Scholar]
- 4.McNally, J. G., W. G. Muller, D. Walker, R. Wolford, and G. L. Hager. 2000. The glucocorticoid receptor: rapid exchange with regulatory sites in living cells. Science. 287:1262–1265. [DOI] [PubMed] [Google Scholar]
- 5.Bubulya, P. A., and D. L. Spector. 2004. On the movements of nuclear components in living cells. Exp. Cell Res. 296:4–11. [DOI] [PubMed] [Google Scholar]
- 6.Phair, R. D., P. Scaffidi, C. Elbi, J. Vecerova, A. Dey, K. Ozato, D. T. Brown, G. Hager, M. Bustin, and T. Misteli. 2004. Global nature of dynamic protein-chromatin interactions in vivo: three-dimensional genome scanning and dynamic interaction networks of chromatin proteins. Mol. Cell. Biol. 24:6393–6402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Belmont, A. 2003. Dynamics of chromatin, proteins, and bodies within the cell nucleus. Curr. Opin. Cell Biol. 15:304–310. [DOI] [PubMed] [Google Scholar]
- 8.Hager, G. L., C. Elbi, and M. Becker. 2002. Protein dynamics in the nuclear compartment. Curr. Opin. Genet. Dev. 12:137–141. [DOI] [PubMed] [Google Scholar]
- 9.Phair, R. D., and T. Misteli. 2001. Kinetic modelling approaches to in vivo imaging. Nat. Rev. Mol. Cell Biol. 2:898–907. [DOI] [PubMed] [Google Scholar]
- 10.Lippincott-Schwartz, J., E. Snapp, and A. Kenworthy. 2001. Studying protein dynamics in living cells. Nat. Rev. Mol. Cell Biol. 2:444–456. [DOI] [PubMed] [Google Scholar]
- 11.Patterson, G. H., and J. Lippincott-Schwartz. 2002. A photoactivatable GFP for selective photolabeling of proteins and cells. Science. 297:1873–1877. [DOI] [PubMed] [Google Scholar]
- 12.Axelrod, D., D. E. Koppel, J. Schlessinger, E. Elson, and W. W. Webb. 1976. Mobility measurement by analysis of fluorescence photobleaching recovery kinetics. Biophys. J. 16:1055–1069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kaufman, E. N., and R. K. Jain. 1990. Quantification of transport and binding parameters using fluorescence recovery after photobleaching. Potential for in vivo applications. Biophys. J. 58:873–885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Berk, D. A., F. Yuan, M. Leunig, and R. K. Jain. 1993. Fluorescence photobleaching with spatial Fourier analysis: measurement of diffusion in light-scattering media. Biophys. J. 65:2428–2436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Tsay, T. T., and K. A. Jacobson. 1991. Spatial Fourier analysis of video photobleaching measurements. Principles and optimization. Biophys. J. 60:360–368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tardy, Y., J. L. McGrath, J. H. Hartwig, and C. F. Dewey. 1995. Interpreting photoactivated fluorescence microscopy measurements of steady-state actin dynamics. Biophys. J. 69:1674–1682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Coscoy, S., F. Waharte, A. Gautreau, M. Martin, D. Louvard, P. Mangeat, M. Arpin, and F. Amblard. 2002. Molecular analysis of microscopic ezrin dynamics by two-photon FRAP. Proc. Natl. Acad. Sci. USA. 99:12813–12818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Sprague, B. L., R. L. Pego, D. A. Stavreva, and J. G. McNally. 2004. Analysis of binding reactions by fluorescence recovery after photobleaching. Biophys. J. 86:3473–3495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Farla, P., R. Hersmus, B. Geverts, P. O. Mari, A. L. Nigg, H. J. Dubbink, J. Trapman, and A. B. Houtsmuller. 2004. The androgen receptor ligand-binding domain stabilizes DNA binding in living cells. J. Struct. Biol. 147:50–61. [DOI] [PubMed] [Google Scholar]
- 20.Bulinski, J. C., D. J. Odde, B. J. Howell, T. D. Salmon, and C. M. Waterman-Storer. 2001. Rapid dynamics of the microtubule binding of ensconsin in vivo. J. Cell Sci. 114:3885–3897. [DOI] [PubMed] [Google Scholar]
- 21.Dundr, M., U. Hoffmann-Rohrer, Q. Hu, I. Grummt, L. I. Rothblum, R. D. Phair, and T. Misteli. 2002. A kinetic framework for a mammalian RNA polymerase in vivo. Science. 298:1623–1626. [DOI] [PubMed] [Google Scholar]
- 22.Rabut, G., V. Doye, and J. Ellenberg. 2004. Mapping the dynamic organization of the nuclear pore complex inside single living cells. Nat. Cell Biol. 6:1114–1121. [DOI] [PubMed] [Google Scholar]
- 23.Phair, R. D., S. A. Gorski, and T. Misteli. 2004. Measurement of dynamic protein binding to chromatin in vivo, using photobleaching microscopy. Methods Enzymol. 375:393–414. [DOI] [PubMed] [Google Scholar]
- 24.Nemergut, M. E., C. A. Mizzen, T. Stukenberg, C. D. Allis, and I. G. Macara. 2001. Chromatin docking and exchange activity enhancement of RCC1 by histones H2A and H2B. Science. 292:1540–1543. [DOI] [PubMed] [Google Scholar]
- 25.Rea, S., F. Eisenhaber, D. O'Carroll, B. D. Strahl, Z. W. Sun, M. Schmid, S. Opravil, K. Mechtler, C. P. Ponting, C. D. Allis, and T. Jenuwein. 2000. Regulation of chromatin structure by site-specific histone H3 methyltransferases. Nature. 406:593–599. [DOI] [PubMed] [Google Scholar]
- 26.Brown, D. T. 2003. Histone H1 and the dynamic regulation of chromatin function. Biochem. Cell Biol. 81:221–227. [DOI] [PubMed] [Google Scholar]
- 27.Gerlich, D., J. Beaudouin, B. Kalbfuss, N. Daigle, R. Eils, and J. Ellenberg. 2003. Global chromosome positions are transmitted through mitosis in mammalian cells. Cell. 112:751–764. [DOI] [PubMed] [Google Scholar]
- 28.Verhoeyen, E., H. Hauser, and D. Wirth. 2001. Evaluation of retroviral vector design in defined chromosomal loci by FLP-mediated cassette replacement. Hum. Gene Ther. 12:933–944. [DOI] [PubMed] [Google Scholar]
- 29.Reid, G., M. Hübner, R. Métivier, H. Brand, S. Denger, D. Manu, J. Beaudouin, J. Ellenberg, and F. Gannon. 2003. Cyclic, proteasome-mediated turnover of unliganded and liganded ER-α on responsive promoters is an integral feature of estrogen signaling. Mol. Cell. 11:695–707. [DOI] [PubMed] [Google Scholar]
- 30.Gerlich, D., J. Beaudouin, M. Gebhard, J. Ellenberg, and R. Eils. 2001. Four-dimensional imaging and quantitative reconstruction to analyse complex spatiotemporal processes in live cells. Nat. Cell Biol. 3:852–855. [DOI] [PubMed] [Google Scholar]
- 31.Rabut, G., and J. Ellenberg. 2004. Automatic real-time three-dimensional cell tracking by fluorescence microscopy. J. Microsc. 216(Pt2):131–137. [DOI] [PubMed] [Google Scholar]
- 32.Bormann, G. B., and F. De Schutter. E. 2001. Computational Modeling of Genetic and Biochemical Networks. MIT Press, Cambridge, MA. 189–224.
- 33.Kimura, H., and P. R. Cook. 2001. Kinetics of core histones in living human cells: little exchange of H3 and H4 and some rapid exchange of H2B. J. Cell Biol. 153:1341–1353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Chubb, J. R., S. Boyle, P. Perry, and W. A. Bickmore. 2002. Chromatin motion is constrained by association with nuclear compartments in human cells. Curr. Biol. 12:439–445. [DOI] [PubMed] [Google Scholar]
- 35.Abney, J. R., B. Cutler, M. L. Fillbach, D. Axelrod, and B. A. Scalettar. 1997. Chromatin dynamics in interphase nuclei and its implications for nuclear structure. J. Cell Biol. 137:1459–1468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Gerlich, D., J. Mattes, and R. Eils. 2003. Quantitative motion analysis and visualization of cellular structures. Methods. 29:3–13. [DOI] [PubMed] [Google Scholar]
- 37.Fink, C., F. Morgan, and L. M. Loew. 1998. Intracellular fluorescent probe concentrations by confocal microscopy. Biophys. J. 75:1648–1658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Braeckmans, K., L. Peeters, N. N. Sanders, S. C. De Smedt, and J. Demeester. 2003. Three-dimensional fluorescence recovery after photobleaching with the confocal scanning laser microscope. Biophys. J. 85:2240–2252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Siggia, E. D., J. Lippincott-Schwartz, and S. Bekiranov. 2000. Diffusion in inhomogeneous media: theory and simulations applied to whole cell photobleach recovery. Biophys. J. 79:1761–1770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Swaminathan, R., C. P. Hoang, and A. S. Verkman. 1997. Photobleaching recovery and anisotropy decay of green fluorescent protein GFP-S65T in solution and cells: cytoplasmic viscosity probed by green fluorescent protein translational and rotational diffusion. Biophys. J. 72:1900–1907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Terry, B. R., E. K. Matthews, and J. Haseloff. 1995. Molecular characterisation of recombinant green fluorescent protein by fluorescence correlation microscopy. Biochem. Biophys. Res. Commun. 217:21–27. [DOI] [PubMed] [Google Scholar]
- 42.Franks, F. 1972. Water: A Comprehensive Treatise. Plenum Press, New York, London.
- 43.Seksek, O., J. Biwersi, and A. S. Verkman. 1997. Translational diffusion of macromolecule-sized solutes in cytoplasm and nucleus. J. Cell Biol. 138:131–142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wachsmuth, M., W. Waldeck, and J. Langowski. 2000. Anomalous diffusion of fluorescent probes inside living cell nuclei investigated by spatially resolved fluorescence correlation spectroscopy. J. Mol. Biol. 298:677–689. [DOI] [PubMed] [Google Scholar]
- 45.Lukacs, G. L., P. Haggie, O. Seksek, D. Lechardeur, N. Freedman, and A. S. Verkman. 2000. Size-dependent DNA mobility in cytoplasm and nucleus. J. Biol. Chem. 275:1625–1629. [DOI] [PubMed] [Google Scholar]
- 46.Hutchins, J. R., W. J. Moore, F. E. Hood, J. S. Wilson, P. D. Andrews, J. R. Swedlow, and P. R. Clarke. 2004. Phosphorylation regulates the dynamic interaction of RCC1 with chromosomes during mitosis. Curr. Biol. 14:1099–1104. [DOI] [PubMed] [Google Scholar]
- 47.Cushman, I., D. Stenoien, and M. S. Moore. 2004. The dynamic association of RCC1 with chromatin is modulated by RAN-dependent nuclear transport. Mol. Biol. Cell. 15:245–255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Li, H. Y., D. Wirtz, and Y. Zheng. 2003. A mechanism of coupling RCC1 mobility to RanGTP production on the chromatin in vivo. J. Cell Biol. 160:635–644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Crank, J. 1975. The Mathematics of Diffusion. Oxford University Press, Oxford, UK.
- 50.Lachner, M., D. O'Carroll, S. Rea, K. Mechtler, and T. Jenuwein. 2001. Methylation of histone H3 lysine 9 creates a binding site for HP1 proteins. Nature. 410:116–120. [DOI] [PubMed] [Google Scholar]
- 51.Lever, M. A., J. P. Th'ng, X. Sun, and M. J. Hendzel. 2000. Rapid exchange of histone H1.1 on chromatin in living human cells. Nature. 408:873–876. [DOI] [PubMed] [Google Scholar]
- 52.Soumpasis, D. M. 1983. Theoretical analysis of fluorescence photobleaching recovery experiments. Biophys. J. 41:95–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Catez, F., H. Yang, K. J. Tracey, R. Reeves, T. Misteli, and M. Bustin. 2004. Network of dynamic interactions between histone H1 and high-mobility-group proteins in chromatin. Mol. Cell. Biol. 24:4321–4328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Alberts, B. 1994. Molecular Biology of the Cell, 3rd Ed. Garland, New York.
- 55.Bilbao-Cortes, D., M. Hetzer, G. Langst, P. B. Becker, and I. W. Mattaj. 2002. RAN binds to chromatin by two distinct mechanisms. Curr. Biol. 12:1151–1156. [DOI] [PubMed] [Google Scholar]
- 56.Ura, K., K. Nightingale, and A. P. Wolffe. 1996. Differential association of HMG1 and linker histones B4 and H1 with dinucleosomal DNA: structural transitions and transcriptional repression. EMBO J. 15:4959–4969. [PMC free article] [PubMed] [Google Scholar]
- 57.Riggs, A. D., S. Bourgeois, and M. Cohn. 1970. The lac repressor-operator interaction. 3. Kinetic studies. J. Mol. Biol. 53:401–417. [DOI] [PubMed] [Google Scholar]
- 58.Halford, S. E., and J. F. Marko. 2004. How do site-specific DNA-binding proteins find their targets? Nucleic Acids Res. 32:3040–3052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.von Hippel, P. H., and O. G. Berg. 1989. Facilitated target location in biological systems. J. Biol. Chem. 264:675–678. [PubMed] [Google Scholar]
- 60.Misteli, T. 2001. Protein dynamics: implications for nuclear architecture and gene expression. Science. 291:843–847. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.










