Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2006 Oct 20;92(1):46–60. doi: 10.1529/biophysj.106.091934

Charge Delocalization in Proton Channels, I: The Aquaporin Channels and Proton Blockage

Hanning Chen *, Boaz Ilan *, Yujie Wu *, Fangqiang Zhu †, Klaus Schulten †, Gregory A Voth *
PMCID: PMC1697834  PMID: 17056733

Abstract

The explicit contribution to the free energy barrier and proton conductance from the delocalized nature of the excess proton is examined in aquaporin channels using an accurate all-atom molecular dynamics computer simulation model. In particular, the channel permeation free energy profiles are calculated and compared for both a delocalized (fully Grotthuss shuttling) proton and a classical (nonshuttling) hydronium ion along two aquaporin channels, Aqp1 and GlpF. To elucidate the effects of the bipolar field thought to arise from two α-helical macrodipoles on proton blockage, free energy profiles were also calculated for computational mutants of the two channels where the bipolar field was eliminated by artificially discharging the backbone atoms. Comparison of the free energy profiles between the proton and hydronium cases indicates that the magnitude of the free energy barrier and position of the barrier peak for the fully delocalized and shuttling proton are somewhat different from the case of the (localized) classical hydronium. The proton conductance through the two aquaporin channels is also estimated using Poisson-Nernst-Planck theory for both the Grotthuss shuttling excess proton and the classical hydronium cation.

INTRODUCTION

The concomitant conduction of water and exclusion of protons exhibited by the aquaporin family of membrane protein channels is a marvelous feat of Nature since proton transport (PT) is naturally mediated by water. Excess protons can, in principle, shuttle rapidly across networks of hydrogen bonds according to a Grotthuss-type mechanism and delocalize their charge (see Fig. 1) (1). This behavior translates in part into a mobility larger than that of any other cation, by fivefold in bulk water, and even more so along water-files of ion-conducting channels, such as in the gramicidin A channel, where the disparity is estimated at greater than 10-fold magnitude (2).

FIGURE 1.

FIGURE 1

Open in a new tab

A schematic figure of the Grotthuss proton shuttle and charge delocalization process through a short chain of water molecules (a so-called water-wire or proton-wire).

Several filtering properties are enhanced in aquaporins relative to archetypical ion channels such as gramicidin A, facilitating exclusion of other charged solutes besides protons, thus maintaining key electrochemical potentials across cell membranes. For one, aquaporin channels (Fig. 2) are relatively narrow, thereby excluding both large neutral solutes and small ions. Their pores are also lined by far fewer carbonyl groups, providing less efficient dehydration for ionic solutes while possibly also optimizing rapid water permeation (3). It is not clear, however, whether these features are sufficient by themselves to exclude protons. Protons are unique among charged solutes in that they experience the environment of the pore lining and width rather indirectly through the ordering of the embedded water-file; they are charge-delocalized and because of this, their effective radius is unclear. Experimental evidence suggests that, in principle, cation exclusion is achieved before proton exclusion (the companion article (4) examines such a proton-selective channel). Moreover, a study (5) of a model hydrophobic cylindrical channel displayed a greater than 10-fold enhancement of proton mobility with decreasing pore radius. The enhancement was ascribed to the formation of a one-dimensional water-wire as the pore radius was decreased to 2 Å, reflecting both changes in solvation structures and directional restriction in a statistical sense. These latter results (5) did not account for desolvation effects, as water molecules were included only along the channel interior.

FIGURE 2.

FIGURE 2

Open in a new tab

An equilibrium snapshot of the GlpF monomer. The highlighted water-file on the pathway is polarized about the ASN-PRO-ALA (NPA) signature motifs that are colored orange. The HB and HE helices are modeled as purple images. The residues that project their backbone carbonyl groups into the water pathway are colored green. The cytoplasmic exit is at the top. The figure was created with VMD software (65).

One aspect of understanding proton exclusion in aquaporins seems to be related in some way to the bipolar orientation of the embedded water-file about the Asn-Pro-Ala (NPA) motifs (Fig. 3), as initially conjectured by x-ray (6) and molecular dynamics (MD) simulation studies (7,8) based on hydrogen-bond patterns of the single water-file. The bipolar orientation has been suggested to be induced by the eight key pore-lining residues in the channel lumen (9). No matter what the origin of the bipolar water orientation, the same Grotthuss-type mechanism by which PT can proceed so rapidly would also allow protons to shuttle down the one-way Grotthuss pathways toward either end of the channel (Fig. 3). Several recent simulation studies (10–17) have calculated or estimated, in one way or another, the free energy profile or potential of mean force (PMF) along the pathway of PT for the aquaporin-1 (Aqp1) channel (11–13), and the Escherichia coli glycerol facilitator (GlpF) (14–16), a member of the aquaglyceroporins subfamily, which also conducts glycerol. All studies have observed the main free-energy barrier centered about the conserved NPA motifs, though with considerably differing magnitudes and interpretations.

FIGURE 3.

FIGURE 3

Open in a new tab

One proposed mechanism for proton exclusion: The positively charged excess proton is repelled through the desolvation penalty from the bulk water regions and the bipolar electrostatic field of the aquaporin matrix (thick arrows). Additionally the proton experiences opposing shuttling pathways along the bipolar directions. The role of Grotthuss shuttling and protonic charge delocalization is estimated in this work by examining the free-energy and self-diffusion profiles along the pathways of proton and classical hydronium transport.

Notably, we have recently employed the same computational methodology used in this article to explain (17) with good quantitative accuracy the role of selective mutations on the experimental proton conductance of the Aqp1 channel (18). That study provides key validation for the accuracy and reliability of our simulation methodology, which contains all primary physical features of this process, starting from the asymptotic bulk phase limit of the excess proton and then moving through the channel environment. The present approach may be compared and contrasted with various other computational methodologies that have been used to study the aquaporin proton blockage phenomenon (see the Appendix). In addition, the companion article (4) is devoted to the topic of a proton-selective channel, which provides additional insight into the proton charge delocalization effect and its rather subtle nature in the context of biomolecular channel environments.

Computational free energy (i.e., PMF) profiles deliver valuable structure-function relationships concerning selectivity mechanisms. Current experimental methodologies provide evidence that is more indirect; for example, mutagenic studies and estimates of the free energy barrier according to patch-clamp (2) experiments and through the Arrhenius plot for the proton conduction (19,20). The latter activation energy may be related to the overall effective ion permeation free energy barrier, given by the difference between the maximum of the barrier profile and the bulk limit just beyond the channel mouth, if an estimate of the activation entropy is also known. This quantity seems not to be experimentally available for PT through aquaporins since their proton conduction is practically undetectable. Thus, computational results can be especially valuable provided they are physically meaningful and quantitatively accurate (or at least semiquantitatively). The central objective of this article, as opposed to our prior articles on this aquaporin channels, is to explicitly study the role of Grotthuss charge delocalization in the aquaporin proton blockage mechanism using the computer simulation approach described above. Furthermore, the exact connection with the measured transport rate must, in principle, be established through a theoretical framework such as the Poisson-Nernst-Planck (21) accounting also for finite ion concentrations, frictional corrections, and recrossing events along the trans-membrane translocation pathway, the latter two being related to the diffusive behavior of the ion in the channel. This connection has also been made in the present article.

It is also important to clarify the role of the proton permeation PMF calculated in this work versus the so-called two-step “turn-hop” mechanism (14). While both the PMFs of the turn- and hop-steps are well defined, the interpretations and terminologies concerning these PMFs are not as clear. The former is a quantity reflecting the stability of the water-file orientational ordering and is defined by the free-energy profile as a function of the orientational order parameter of the water-file in absence of the excess proton. The latter (hop-step) is the explicit PMF of PT along the trans-membrane pathway, accounting for all possible water configurations (and orientations). Intuitively a higher PMF for the turn-step in aquaporin channels (bi- to unipolar) might be expected to be correlated with a higher PMF of PT. The relationship of the PMF for a turn-step (in the absence of an excess proton) to the actual permeation barrier for PT, however, is less clear.

As stated earlier, this article adds significant new results to our earlier preliminary study (16) by examining the effects of proton charge delocalization on the properties of PT to further characterize the role played by the electrostatic environment in the aquaporin channels in proton versus cation exclusion. Specifically, the PMF along the transport pathway of the Aqp1 and GlpF channels is calculated for both a delocalized (Grotthuss shuttling through water) excess proton, according to the all-atom second generation multistate empirical valence bond (MS-EVB2) molecular dynamics methodology (22), and for a localized (and therefore classical and non-Grotthuss shuttling) hydronium ion, represented by the reduction, or computational mutation, of the MS-EVB2 model into a single (classical hydronium) system. Since the classical hydronium does not have the possibility of Grotthuss shuttling, the excess protonic charge is localized to a single hydronium cation as opposed to the case of the fully Grotthuss shuttling and delocalizing excess proton in the MS-EVB2 model. The electrostatic effects of this localization are then calculated precisely as reflected in the permeation free energy barrier (PMF), something that obviously cannot be measured experimentally since the classical (nonshuttling) hydronium does not exist in Nature. In addition, the actual proton conductance for these two limiting cases is calculated for the first time for both aquaporin channels by utilizing Poisson-Nernst-Planck theory, which includes the significant differences between the diffusive properties of the two ions in the channel in addition to the differences in the ion permeation free energy profiles.

An effort has been made in this article to further clarify the origin of electrostatic bipolarity about the NPA motifs and the contribution of this part of the electrostatic environment to the proton permeation free energy profile. This issue is a rather subtle one because the approach to studying these effects involves reducing the charges on the opposing helices to zero in an effort to quantify their contribution to the proton permeation free energy barrier. This subtlety has two origins. The first is because electrostatics in proteins are everywhere and, in fact, it is a long-ranged and highly correlated interaction. This obvious aspect of the problem seems to be often overlooked in some arguments regarding the role of electrostatics versus other factors (e.g., Grotthuss shutting) in proton transport processes. Indeed, everything in a protein and its surrounding environment (solution phase or membrane-bound) is electrostatic, right down to the nuclei and the electrons. The second origin of the subtlety seems more concrete. When artificially reducing charges on amino acids to zero (e.g., in opposing helices such as the present case), the question arises as to whether the resulting artificial protein system should be relaxed or constrained. Clearly, it is no longer a real protein, so relaxing it (i.e., equilibrating it to its stable structure) does not really have any overlap with actual reality. In fact, since the goal is actually to try to understand the contribution of certain charged or polar groups to the free energy barrier in the real protein, it might make more sense to artificially constrain the mutated protein to its native structure (i.e., for the one having the charged, not uncharged, amino-acid groups). However, such constraints reduce the ability of the protein to fluctuate and elementary theories of charge transport show that fluctuations in the electrostatic field are essential for the charge to translocate (otherwise it is perfectly happy to stay where it is). So, despite reservations about these subtle issues, we have carried out free energy profile calculations of computationally mutated aquaporin channels that have removed the opposing helix charges, largely because this is a common practice. However, we are not certain of how meaningful such results may truly be, especially in light of our recent studies (17) confirming through direct comparison with experiment that the proton blockage in Aqp1 appears to come from multiple sources (most notably direct electrostatic interactions of the permeating proton with key residues and an electrostatic desolvation penalty from entrance of the proton into the constricted space of the channel). In light of these issues, It should therefore be stated that the primary goal of this article, i.e., to demonstrate the precise role of Grotthuss charge delocalization on the proton permeation free energy barriers of GlpF and Aqp1, is a much more clearly defined computational target since only the character of the permeating ion (proton) is being computationally mutated, as opposed to the features of its highly complex environment.

RESULTS

The MS-EVB computer simulation method utilized in the present work has been developed and applied over a number of years (23). This approach explicitly simulates PT in MD simulations using all-atom deterministic trajectories derived from the MS-EVB potential function, and it can accurately describe excess protons, including the Grotthuss mechanism, in aqueous (22–35) and biological environments (16,17,36–43). As stated earlier, the methodology has recently received important additional validation for aquaporins by virtue of its ability to accurately predict the effect of several experimental mutations on the proton conductance behavior in these channels (17). A comparison of the MS-EVB approach with other simulations of PT in aquaporin channels will also be presented at the end of this article in the Appendix. As an additional study to further demonstrate the accuracy and flexibility of the simulation methodology, the companion article (4) describes the case of the proton-selective LS2 channel, which is an interesting system in its own right relative to the aquaporin channels due to its proton selectivity.

Our main results, the PMFs of excess proton and classical hydronium permeation along the transport pathway of Aqp1 and GlpF, are depicted in Fig. 4, A and B, respectively. The PMF of the bulkier hydronium is more jagged, as expected, with minor peaks manifesting as shoulders in the proton PMF. However, due to the background desolvation penalty for charged solutes, the structural details are smoothed relative to the PMF of glycerol transport. There is a major barrier centered about the NPA motif and a secondary barrier about the selectivity filter (SF).

FIGURE 4.

FIGURE 4

Open in a new tab

The free energy profile (or potential of mean force, PMF) along the channel permeation pathway for fully Grotthuss shuttling proton (red), classical (non-Grotthuss shuttling) hydronium (blue), fully Grotthuss shuttling proton for NBC mutant (purple), and fully Grotthuss shuttling proton for the NBC_NPA mutant (green) is displayed in panels A and B for GlpF and Aqp1, respectively. The estimated errors bars for all PMFs are also shown. The profile of the pore radius (C) as calculated by the Hole2 program (52) is also depicted for Aqp1 (red) and for the wider GlpF (blue). Note the difference in free-energy scale between panels A and B.

Overall, the PMFs of the proton and the classical hydronium are rather similar for both channels, yet the two cations display quite different dynamics. For the GlpF, when placed to the right of the NPA motif, the classical hydronium ion has to overcome an ∼11 kcal/mol free energy barrier, ∼2 kcal/mol lower than the excess proton, to reach its first PMF peak centered at z ≈ 7.5 Å, then it is trapped at a ∼2 kcal/mol deep saddle point just before its 12 kcal/mol maximum PMF peak centered at the NPA motif. By contrast, the excess proton meets its 14 kcal/mol maximum directly without being trapped. When placed to the left of the SF, the classical hydronium has ∼3 kcal/mol lower energy barrier even though its PMF is not as smooth as the excess proton, and its chance to be trapped in the central part of the channel centered at z ≈ 0 is smaller than the excess proton. Since the free-energy barrier difference between the NPA motif and the SF domain is only ∼2.0 kcal/mol for both the classical hydronium and the excess proton, one might expect that the NPA motif and SF regions have comparable contributions in gating the ion transport in the GlpF channel. For the Aqp1, which is more hydrophobic than the GlpF, the classical hydronium has a 3 Å long free energy barrier platform from z ≈ 5.0 Å to z ≈ 2.0 Å with a maximum of ∼28 kcal/mol, which is approximate to the PMF peak observed for the excess proton centered at z ≈ 5.0 Å. Even though the PMF of the SF domain of the Aqp1 is a few kcal/mol higher than its counterpart in the GlpF channel due to its narrower pore radius, unlike the GlpF, the NPA motif of Aqp1 should dominate the ion transport gating because of the very large addition of free energy difference, ∼10 kcal/mol.

The comparable magnitudes of the barriers against proton and hydronium transport—the former actually higher by 2 kcal/mol for GlpF (Fig. 4)—seems rather surprising (see corresponding profiles in the companion article (4)). As shown for the LS2 channel in the companion article, the ability of an excess proton to delocalize its charge via the Grotthuss shuttling mechanism generally reduces its desolvation penalty, and in that case its permeation profile is lower than that of classical hydronium, and of simple cations, such as K+. However, a resolution to this apparent paradox can be proposed through an analogy with a person trying to climb a mountain pass while repeatedly sliding backward. The proton experiences the available shuttling pathways along the directions away from the NPA motif. The opposite pathways are unfavorable since the proton-induced ordering of the conducting water-file (bidirectional about the excess proton) is frustrated by the intrinsic bipolarity of the aquaporins with regard to the NPA motif. The latter effect is electrostatic in origin, although arguments about the origins of electrostatic effects are difficult, at best, given the long-range nature of such interactions. In Fig. 5 is shown the position-dependent diffusion coefficient for the excess proton and classical hydronium in the two channels.

The ordering frustration is depicted in Fig. 6 through the orientational order parameter of the embedded water-file, with regard to the classical hydronium and excess proton (in both GlpF and Aqp1), tethered at z = 7 Å and z = 10 Å. The water molecules between the tethered hydronium or proton and the cytoplasmic exit are strongly correlated, with their oxygen atoms pointing toward the hydronium or proton. The ordering extends to approximately the same range into the bulk for the hydronium, or proton positioned at both z = 7 Å and z = 10 Å. On the other hand, the water molecules between the excess proton and the NPA motifs are unsteady. This disorder is quantified by the standard deviation (SD) of the order parameter in Fig. 7, which exhibits appreciable peaks in this region, and more so for the delocalized excess proton than for the classical hydronium. The more flexible orientations are explained by the delocalization effects of the proton; not only does the instantaneous hydronium carry effective positive charge, but the nearby water molecules share the positive charge. Since the ordering of the conducting water file is induced by the competing hydronium or proton electrostatics with the bipolarity of the channel electric field, the orientation of the water molecules depends on the relative strength of these two effects. For all of the hydronium cases, with the exception of Aqp1 with z ≈ 10.0 Å, the strong hydronium electrostatics localization dominates the bipolarity, due to its complete charge localization. Thus, the water oxygen atoms point toward the hydronium. Since the NPA motif region of Aqp1 is narrower than the GlpF by ∼0.5 Å, a larger free energy barrier is observed in Aqp1 to move the proton through the channel. For the excess proton in the wider GlpF channel, the water bipolarity is more dominated by the proton electrostatics. Thus, the variation in the proton exclusion mechanisms exists between the classical hydronium and the excess proton, as well as the different aquaporin channels, GlpF and Aqp1, and the excess proton. The water molecules were also observed occasionally to form a double-file-like formation or just congregate slightly about the excess proton, manifesting the metastability of the ordering of the water-file in presence of the excess proton.

FIGURE 6.

FIGURE 6

Open in a new tab

The water orientational order parameter for the proton (shaded) and hydronium (solid) oxygen atom tethered at z = 7 Å (dashed curves) and z = 10 Å (solid curves) in (A) GlpF and (B) Aqp1. The orientational ordering is represented by the order parameter P1(z) = 〈cos(θ)〉, where θ is the angle between the membrane normal and the normalized water dipole vector.

FIGURE 7.

FIGURE 7

Open in a new tab

The standard deviations (SD) of the water orientational order parameter for the proton (solid) and hydronium (dashed) oxygen atom tethered at (A) z = 7 Å in GlpF, (B) z = 10 Å in GlpF, (C) z = 7 Å in Aqp1, and (D) z = 10 Å in Aqp1. The peaks of the SD about the location of the classical hydronium and excess proton are physically irrelevant.

The magnitude and shape of the hydronium PMF in GlpF (Fig. 4) is in reasonable agreement with electrostatic profiles of probe cations in GlpF (15). These electrostatic profiles (15) were calculated by the Poisson-Boltzmann equation and were depicted to increase only slightly with increasing cation radius and slightly more so about the SF. Approximations associated with the continuum electrostatic approach—particularly the neglect of the explicit representation of embedded water molecules—may, however, be too drastic, as has been demonstrated by a recent study of model ion channels (44). Additionally, the continuum PMFs seem to vary slightly more—further into the bulk region—relative to the PMF of the explicit hydronium. Although the excess proton is also positively charged, the underlying potential energy surface (PES) of the MS-EVB2 model is fundamentally different, accounting not only for explicit electrostatic interactions with the channel environment but also for the delocalized character of the excess proton (exemplified by the very different channel dynamics of the two cation species). It seems possible that the relatively high overall barrier to cation transport in aquaporins is a consequence of the mechanism required to exclude protons, and that the barrier about the SF would be sufficient to exclude other cations (3). This conjecture is supported by noting that the secondary barrier of the PMF of PT about the SF would have been reduced (11) had we incorporated the (computationally more demanding) acid-base MS-EVB2 model (24) to include protonation states of the conserved histidine residue (45) along the SF.

The overall barriers to PT through Aqp1, ∼28 kcal/mol, and GlpF, ∼14 kcal/mol (Fig. 4), are much higher than the corresponding barriers reported for the Q-HOP model: 6–7 kcal/mol in Aqp1 (11), and for the PM6 model, ∼4 kcal/mol in GlpF (14). The latter are also much lower than the electrostatic barriers for positive charge transport through Aqp1 and GlpF, as estimated by the hydronium profiles in Fig. 4 and by continuum (15) and other (12) electrostatic calculations. By comparison, the experimentally measured activation free-energy for PT through the gramicidin channel, which is considered a good proton conductor, is 4–6 kcal/mol (19), implying the PM6 and Q-HOP models may contain systematic errors (see the Appendix). They do capture some “soft-core” and delocalized aspects of the excess proton, but they fail to describe properly the barrier to PT. The free-energy barrier to PT in Aqp1 according to a simplified EVB calculation (12) combined with other approximations is, on the other hand, significantly larger and of a magnitude likely to also be sufficient for the exclusion of protons.

A dipolar field that could prevent proton entering the channel has been conjectured to arise from macrodipoles of two opposing α-helices, HB and HE (see Figs. 2 and 3). The effects of this field on proton blockage in aquaporin channels are rather unclear and controversial. To help clarify these issues, free energy profiles for proton permeation were calculated for both channels where the backbone atoms of the HB and HE helices were artificially discharged. These computational mutants are herein denoted as the NBC mutants, where the dipolar field was presumably eliminated. Our results demonstrate a significant (though not complete) drop of the overall barrier to PT from ∼14 kcal/mol to ∼7 kcal/mol for GlpF and from ∼28 kcal/mol to ∼12 kcal/mol for Aqp1. Furthermore, this mutation results in a shift of the position of the main barrier on the channel axis from the NPA region to the center of the bilayer (for Aqp1) or to selectivity filter (for GlpF). A visual examination finds that the pore water bipolarity disappeared in the NBC mutants in contrast to its presence in the wild-type channels. All these results, taken together, help confirm that the bipolar field arises from the α-helical macrodipoles, and it has a significant (though not complete) contribution to the main free energy barrier to proton permeation. Moreover, to examine the contributions of the terminal NPA domain to the macrodipoles, the free energy profiles for proton permeation for both channels were calculated for the NBC_NPA mutants that have the backbone atoms of the HB and HE helices artificially discharged, except for those of the NPA domains. The results reveal that the fully charged NPA residues only raises the barrier by ∼2 kcal/mol at the NPA region for both channels by comparing with the barriers of the NBC mutants. Thus, the bipolar field arises from the entire helices of HB and HE, rather than being primarily determined by the terminal NPA residues.

The PMF along the transport pathway of charged solutes through channel environments is sensitive to charge delocalization and dehydration patterns, as reported also in the companion article (4) for the proton-selective LS2 channel. This observation, as well as the sensitivity of electrostatic profiles of probe cations to mutagenic charge distributions in GlpF (15), calls into question a primary association of the mechanism of proton exclusion in aquaporins with the desolvation penalty (12); this penalty arises from the passage of ions through low-dielectric media, characteristic of protein channels in general. In the LS2 channel, (4) the overall free-energy barrier for K+ transport was calculated to be ∼11 kcal/mol as compared with ∼6 kcal/mol for PT, the former sufficiently high for exclusion of the bulkier K+ and the latter sufficiently low for passage of H+, in agreement with experiment (46). K+ exclusion is achieved mainly by dehydration of its first solvation shell. The free-energy profiles of K+ and H+ in LS2 were also observed to be qualitatively different from each other, with the peaks and troughs of the latter strongly correlated with minima and maxima along the pore radius profile, respectively, alluding to the effect of water ordering on the PES of PT (the pore radius profile of the LS2 channel undulates periodically between peaks of ∼2.2 Å and troughs of ∼1.5 Å with different characteristic hydration structures). The free-energy profile for H3O+ through LS2 is intermediate between that of K+ and H+, and qualitatively similar to the latter. The higher magnitude of the free-energy barrier to H3O+ relative to that of H+ makes sense physically for LS2 and for proton channels in general, highlighting the interesting opposite correspondence for aquaporin channels (Fig. 4). The lower magnitude of the free-energy of H3O+ relative to that of K+ for the LS2 channel also makes sense; the H3O+ represents a zero-order model of charge delocalization with the excess positive charge split equally among the three hydrogen atoms. The hydronium adopts hydration patterns similar to that of H+.

The Aqp1 channel, relative to GlpF, is narrower, more hydrophobic and stretched, and has a charge of +3 versus +1 for GlpF, which should account for the larger barriers against proton and hydronium transport. These differences manifest also through an accentuation of the nature of the Grotthuss pathway in Aqp1 as depicted by the profile of the average total number of EVB states included in the MS-EVB complex (Fig. 8 A) and the average amplitude of the largest EVB state (Fig. 8 B). The crests in the latter reflect localization and association of the excess proton primarily with a single water molecule, and are strongly correlated with peaks in the density profile of water molecules—in absence of the excess proton (Fig. 8 C). At the troughs, the proton is delocalized and is shared more evenly between its nearest-neighbor water molecules. Because of the larger change of the pore radius along the channel, the amplitude profile is qualitatively similar for GlpF and Aqp1 even though GlpF has stronger fluctuation than Aqp1. At z ≈ −2.0 Å, the average number of EVB states is the lowest (Fig. 8 A) due to spatial confinement. In this region the interaction of the water molecules with the pore-lining residues is enhanced considerably—relative to the self-interactions of the water molecules along the single-file (47)—and the excess proton appears to do little to perturb this hierarchy of interactions. At z ≈ 2.0 Å, Inline graphic, and Inline graphic, so the delocalized excess proton is shared by a Zundel complex. This suggests a somewhat different PT mechanism, which will be examined with more detail in the next section, than in the bulk and other part of the channel. To the right of the NPA motif and to the left of the SF, the envelope of the amplitude profile fluctuations at Inline graphic with z, which is slightly lower then the average bulk value of Inline graphic, corresponding to an Eigen cation, along with a more even population of the amplitudes of the second-to-fourth EVB states. The trough to the right of the NPA motif of the GlpF is quite deep—Inline graphic—reflecting a large contribution to the second largest EVB amplitude from the water molecule to the left of the excess proton with its oxygen atom pointing to the pivot hydronium (see Fig. 8). Unlike GlpF, the crest to the right of the NPA motif of the Aqp1 channel is comparatively high, up to Inline graphic, indicating a small contribution to the second largest EVB amplitude from the unsteady water molecule in the PT pathway. The results of the EVB amplitude analysis are consistent with the observation of the ordering of the conducting water file. For Wu et al. (4), the amplitude profile of the first EVB state of an excess proton through the LS2 channel undulates less sharply between troughs of Inline graphic and crests of Inline graphic. The crests are correlated with high densities of the oxygen atoms of the water molecules and the Ser side chains, as well as wider regions of the LS2 channel, and are more representative of an Eigen cation—the most probable proton hydration-structure in bulk water. On the other hand, the constriction region of the hourglass-shaped aquaporin channels narrows rather monotonically (Fig. 4 C), and the crests of the Inline graphic profile are correlated with the locations of the polar carbonyl groups (and their residing water molecule) and are more representative of a hydronium cation.

FIGURE 8.

FIGURE 8

Open in a new tab

The profiles of the average number of EVB states and the average amplitude of the first EVB state are depicted in panels A and B, respectively, for Aqp1 (solid) and GlpF (dashed). (C) Profiles of the amplitude of the first EVB state (solid) and the relative density of neat (oxygen) water (dashed) for the Aqp1 (solid) and GlpF (dashed) channels.

The z-dependent (channel axis) profile of the probability distribution of the first EVB amplitude, Inline graphic, for GlpF and Aqp1 is given by Fig. 9, A and B, respectively, and both are unimodal. The profile for GlpF is rather smooth and the variance is generally narrow, reflecting substantial translational ordering of the water-file and a small measure of available conduction pathways. The profile of Aqp1 is rather rough and the variance is generally wide, indicating the interruption of the ordering of the water-file along the PT pathways and of the various PT mechanisms. The probability distribution of Inline graphic in bulk water is, on the other hand, wider and bimodal with the global maximum corresponding to an Eigen cation and a shoulder corresponding to a Zundel cation (see discussion in the Appendix). The confinement therefore has the effect of inducing a single characteristic proton hydration-structure at most points along the channel axis (the distribution is a little more smeared at a few locations where the proton is more delocalized).

FIGURE 9.

FIGURE 9

Open in a new tab

The profile of the probability distribution of the largest EVB amplitude in (a) GlpF and (b) Aqp1. Hot colors correspond to high probabilities.

According to Kramer's theory (48) of diffusive barrier-crossing, transport rates for one-dimensional diffusive motion exponentially depend upon the free energy profile (PMF) F(z), but are only linearly proportional to the local diffusion coefficient D(z). For PT in inhomogenous systems such as the ion channels, the estimation of the position-dependent diffusion coefficient D(z) is important. This is due to the significance of D(z) in the evaluation of the maximum ion conductance by the Poisson-Nernst-Plank (PNP) electrodiffusion theory(49) when combined with F(z), and its importance in providing valuable information about the PT mechanism and dynamics in different environments. Following the earlier work of Berne et al. (50), Woolf and Roux (51), and Brewer and Voth (5), the D(z) of the classical hydronium and excess proton at both GlpF and Aqp1 are estimated and presented in Fig. 5. Generally, the excess proton has a much higher D(z) than the classical hydronium, sometimes even an order-of-magnitude larger, depending upon the pore radius and charge delocalization. This is due to the diffusion of the Grotthuss shuttling, wherein the excess proton does not necessarily require the slower displacement of the water molecules to move, as does the classical hydronium. For the similar pore radius, the stronger proton delocalization effect increases the diffusion coefficient in most cases. For example, to the right of the NPA motif of both GlpF and Aqp1, the crests of the D(z) profiles usually correspond to the troughs of the largest EVB amplitude profiles Inline graphic. On the other hand, the trough of the D(z) just right to the NPA motif can be explained by the formation of the unsteady water molecules. The high D(z), 6.0 Å2/ps of excess proton at Aqp1 z ≈ 2.0 Å results from the fast interconversion of the pivot EVB (hydronium) state between the two “quasi-degenerate” water molecules, sharing the excess proton almost equally.

FIGURE 5.

FIGURE 5

Open in a new tab

The profile of the position-dependent diffusion coefficient of the classical hydronium (solid) and Grotthuss shuttling excess proton (dashed) in (A) GlpF and (B) Aqp1.

The difference of D(z) between the classical hydronium and excess proton has greater significance when the pore radius becomes increasingly narrow. At the narrowest point of the SF, centered at z ≈ −2.0 Å, the classical hydronium has a value of D ≈ 0.1 Å2/ps and D ≈ 0.01 Å2/ps for GlpF and Aqp1, respectively, because in such a spatially confined region it is difficult for the relatively bulky classical hydronium to diffuse without the possibility of Grotthuss shuttling. Contrarily, the Grotthuss-shuttling excess proton has D ≈ 4.0 Å2/ps for GlpF, which is consistent with the results previously reported by Brewer and Voth (5) for the proton wires in channel environments when the pore radius of the channel is <2.0 Å. For Aqp1, with its pore radius of <1.0 Å, the excess proton diffusion constant is D ≈ 0.3 Å2/ps. With an extremely small pore radius in the latter case, the breaking of the hydrogen-bond water-wire network for Grotthuss shuttling becomes more likely, as does the slowing of the proton diffusion.

The maximum ion conductances are calculated by Eq. 7 as derived from the PNP electrodiffusion theory (49), and are summarized in Table 1. Since both classical hydronium and proton give similar results for the maximum ion conductance for both aquaporin channels, the overall electrostatic free energy barrier (whatever its origin) is likely the main feature in blocking the proton permeation. In GlpF, the higher diffusion rate of the Grotthuss shuttling excess proton relative to the classical hydronium may be compensated for by its somewhat higher free energy barrier at both the SF and the NPA motif. All of the four possible ion conductances are well below the range that can be accurately detected by current experiments, which is consistent with the fact that no experimental proton conductance results are yet available for either GlpF or Aqp1. Interestingly, a mutant of Aqp1, which does appear to conduct protons within other ions, has recently been reported (18), as mentioned earlier.

TABLE 1.

Maximum ion conductances

gmax (picoSiemens) GlpF Aqp1
Hydronium (8.3 ± 0.8) × 10−4 (1.7 ± 0.2) × 10−14
Proton (1.8 ± 0.2) × 10−4 (1.9 ± 0.4) × 10−14
Open in a new tab

DISCUSSION

Rapid water conduction in aquaporin channels appears to be correlated with the optimization of electrostatic variables governing charge exclusion (3,53,54). The barrier for positive charge transport along the Aqp1 channel is larger than that for GlpF, the latter displaying inferior water conduction (3). (GlpF conducts water less efficiently probably due to its design (6) as a glycerol facilitator; in addition, the cavity at its fourfold axis of symmetry (6) resembles the known structure of ion-conducting channels.) Nevertheless, the evidence suggests the high cation permeation free-energy barrier associated with the aquaporin family has also evolved to exclude excess protons. The central complicating feature of protons versus other cations is their ability to shuttle through water molecules and thus to delocalize their charge via the Grotthuss mechanism. The proton versus classical hydronium permeation pathways have therefore been characterized explicitly in this article for two members of the aquaporin family of trans-membrane protein channels. The aquaporin pathway is well defined and exhibits a translational ordering of the embedded water-file as induced by the electrostatic environment, including the hydrogen-bond interactions with the pore-lining carbonyl groups and other residues. On average, protons shuttle through an alteration of localized hydronium and delocalized Zundel configurations, with a transition to an Eigen-like configuration toward the pore exits. The signature of the amplitude profile is rather inhomogeneous, embodying features of the pore radius and hydrophobicity profiles and a measure of the bidirectionality of the transport pathways. The role of Grotthuss shuttling and proton delocalization has a significant effect on the diffusion behavior of the excess proton, but its channel permeation behavior is still dominated in both channels by the large free energy barriers in the SF and NPA regions of the free energy profile (PMF). The charge delocalization due to proton shuttling of the excess proton has a secondary effect on the free energy barrier in the case of the GlpF channel, which has a larger pore radius. As can be seen in the companion article on the LS2 channel, when the pore is larger the effects of Grotthuss shuttling and charge delocalization become more important because of the rather subtle electrostatics associated with this behavior. Interestingly, in the case of GlpF the free energy barrier is higher, not lower, for the fully Grotthuss shuttling proton relative to the classical hydronium, which may reflect an evolutionary feature in this channel to counteract the higher diffusion rate of the former cation relative to the latter. In Aqp1, on the other hand, the free energy barrier is substantially higher for both cations, so such subtle differences may be difficult to distinguish. It also seems evident that the bipolarity, as confirmed in this work, originates from the opposing macrodipoles of the HB and HE α-helices and has a significant (∼50%) contribution to the overall free energy barrier to proton permeation through both channels.

At a more general level, this study compliments an emerging picture from recent research in our group, which suggests that free-energy landscapes of PT through hydrated protein channels can be different, but interesting, in ways other than the corresponding landscapes for ion transport. This is due to the small effective radius and delocalized nature of the excess proton. Another example of this unique behavior is reported in the companion article for the LS2 channel (4).

Acknowledgments

We thank members of the Voth and Schulten groups, past and present, for stimulating discussions and for making this project possible. We thank Dr. Christian Burnham for calculating the results in Figs. 10 and 11, and also Prof. Bruce J. Berne for insightful comments during a presentation by B. Ilan at Columbia University.

G.A.V. gratefully acknowledges National Institutes of Health grant No. RO1-GM53148. K.S. acknowledges National Institutes of Health grants No. PHS 2 P41 RR05969 and R01 GM067887. We also gratefully acknowledge the National Center for Supercomputing Applications, the Pittsburgh Supercomputing Center, and the Arches Metacluster, administered by the Center for High Performance Computing at the University of Utah (provided by National Institutes of Health grant No. NCRR 1 S10 RR17214-01) for computational resources. This material is also based upon computational work supported by the National Science Foundation under the following programs: Partnerships for Advanced Computational Infrastructure, Distributed Terascale Facility, and Terascale Extensions: Enhancements to the Extensible Terascale Facility.

APPENDIX

Simulation protocol

We have adopted, for both GlpF and Aqp1, a reduced system consisting of one monomeric unit capped by slabs consisting of ∼1800 water molecules as depicted in Fig. 2. Initial configurations were taken from snapshots saved after several nanoseconds of equilibrium MD simulation of the membrane-embedded tetramer (7,55), with PDB entry codes given by 1FX8 (6) and 1J4N (56) for GlpF and Aqp1, respectively. All the α-carbon backbone atoms, except for those whose distance to any of the embedded water molecules was <6 Å, were tethered during the simulation to their initial positions; the absence of tethering along the immediate proton conduction pathway allows for modest structural reorganization due to its presence. The root mean-square fluctuations (RMSF) of the reduced system, with regard to the backbone configuration of the crystal structure, was observed to be in good qualitative agreement with the RMSF of the membrane-embedded tetramer system, with the backbone atoms aligned against the crystal structure. The tethering force constant, 2 kcal/(mole Å2), was determined by tuning the amplitudes of the RMSF of the reduced system to obtain a quantitative fit with the RMSF of the membrane-embedded tetramer system. The tethering procedure is justified on the grounds of the rigidity imparted by the monomers on one another. The approximation associated with a single monomer representation is justified because the immediate channel environment is the most relevant to the transport properties of the charged solute. Support for this approximation is provided by the negligible contributions to the electrostatic energy from the interaction of the single-file water molecules with the embedding membrane and neighboring protein monomers (53). Initial configurations along the channel-axis—for the free-energy calculations—were generated by saving snapshots from a 5 Å/ns cross-channel pulling trajectory of the classical hydronium, starting from a 100-ps preequilibrated configuration, with the backbone atoms frozen to preserve the same reference backbone configuration. Initial configurations for the excess proton were easily obtained by replacing the hydronium ion with a water molecule and an excess proton. Total electric neutrality was maintained by adding Cl− atoms, 2 and 4, respectively, for the GlpF and Aqp1 systems, and both the Cl− atoms and the cap water molecules were excluded from the missing membrane domain by a soft repulsive potential. Simulations were carried for the classical hydronium by the DL_POLY MD package (57) and for the excess proton by a modified version of DL_POLY, called DL_EVB, which incorporates the MS-EVB2 methodology with a new EVB state-searching algorithm that better conserves the total system energy. The protein was modeled by the AMBER force-field and water molecules were represented by the flexible TIP3P (58) model. The electrostatics were calculated by the smooth particle-mesh Ewald method and the cutoff radius for both the Lennard-Jones and Coulombic interactions was set to be 9.5 Å. A constant NVT ensemble with T = 308 K was generated by a Nosé-Hoover thermostat with a relaxation constant of 0.5 ps and a simulation time-step of 1.0 fs.

Proton transport simulation methodology

The MS-EVB method (22,23,25,26) calculates the PES of PT for a given nuclear configuration of the excess proton and the water molecules according to an empirical Hamiltonian with a restricted number of chemically motivated EVB states and a given functional form of the matrix elements, in the spirit of semiempirical electronic-structure methodologies. The EVB states consist of localized hydronium ions with a prefixed charge distribution, +0.5 for the hydrogens and −0.5 for the oxygen, and are constructed by an algorithm that associates the nonlocalized excess proton with water molecules according to the instantaneous hydrogen-bond topology. The diagonal elements of the Hamiltonian are represented by intra- and intermolecular interactions of a given hydronium state with all other atoms in the system, including the protein matrix and the remaining water molecules, according to standard Coulombic and Lennard-Jones expressions. The off-diagonal elements are constructed to reflect the charge exchange electrostatic interaction between pairs of EVB states—Zundel cations, 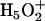Inline graphic—along with a damping factor accounting for unfavorable Zundel geometries (for example, when the O-O distance is large); they are parameterized (22,23,25,26) to reproduce the PES of protonated water-clusters according to high-level ab initio calculations, and have the effect of reducing the localization tendency of the hydronium states due to the polarization of the environment. The fitting observables consist of ab initio formation energies of stable cluster structures, the ab initio barrier profile for PT along the O-O distance of the Zundel cation, and the vibrational spectrum of several different cluster numbers. The MS-EVB2 model (22) is the second generation of the parameter set and state selection of algorithm for the MS-EVB methodology.

The MS-EVB model for the bulk water phase incorporates into the EVB Hamiltonian also interactions with water molecules outside the EVB complex of the hydronium states. While MS-EVB accounts for nontrivial and nonadditive effects (usually requiring ab initio level calculations) with increasing cluster number, such as the nonlinear elongation of O-O bonds and changes in hydration energies, it somewhat underestimates the experimental mobility of the excess proton in the bulk phase. This is attributed both to some degree of missing quantum effects of the nuclear motion such as tunneling and zero-point quantization, as well as the prepolarization of the flexible TIP3P model by which water molecules in the MS-EVB2 are represented. Nevertheless, contrary to the suggestion in Burykin and Warshel (13), the MS-EVB2 model has been extensively validated and applied in a variety of both aqueous and biomolecular contexts (22–43). It displays overall good agreement with experiment, with respect to both the dynamical and equilibrium properties of the excess proton, and moreover—concerning this study—protonated water-structures within narrow hydrated pores. This latter is more typical of small gas-phase protonated chains of water molecules, for which the model is quite accurate relative to other models that have been used (14,15) such as the PM6 model (see next subsection).

The empirical MS-EVB2 PES is calculated at each time step by diagonalizing the MS-EVB2 Hamiltonian matrix to determine the ground state solution. The nuclear degrees of freedom are propagated classically within the MD framework with the forces given by the Hellmann-Feynman theorem. The ground state MS-EVB vector, Inline graphic, reflects the delocalization of the excess charge over the hydrogen-bond network with weights given by the amplitudes, Inline graphic, of the different EVB states. The process of PT proceeds through the redistribution of these amplitudes at each time step, as well as through the propagation of the nuclear coordinates. The distribution of the first (largest) EVB amplitude, Inline graphic, in bulk water is bimodal (22,23,25,26), with a maximum at Inline graphic, corresponding to an Eigen cation, Inline graphic. The Zundel cation, with Inline graphic, is slightly less thermodynamically stable than the Eigen in bulk water, whereas it is the dominant structure along the single water-file formation of a model hydrophobic channel (5). The spatial position of the excess proton, with respect to which the PMF of PT is calculated, is defined to be the center of excess of charge (CEC) of the EVB complex (5,22),

graphic file with name M20.gif (1)

where ri(t) values are the center-of-charge vector of the hydronium in the ith MS-EVB2 state at time t. The (classical) hydronium ion is represented as a simple limit of the MS-EVB2 model corresponding to a single (1 × 1) diagonal element of the MS-EVB2 Hamiltonian. Throughout this article, the terms “proton” and “hydronium” stand for the CEC of the full MS-EVB2 model and the single state MS-EVB2 model (i.e., a classical hydronium cation), respectively.

Comparison to other simulation models

As stated earlier, a number of other computer modeling and simulation articles have appeared that are devoted to the issue of proton blockage by aquaporin channels (11–16). These articles, while all suggesting to explain the origin(s) of the blockage, actually contain rather different results, largely because four different modeling approaches have been employed. In this subsection, we will compare and contrast the methodology utilized in this article, and also in our preliminary communication (16), with those employed by other researchers.

To make reasonably conclusive statements regarding the free energy barrier of proton blockage in aquaporins, the full potential energy function for the process is required because the free energy F is directly related to the all-atom configurational integral of the Boltzmann factor exp(−V(x)/kBT), where x are all atomic coordinates of the system. The same is true for a constrained free energy, such as a potential of mean force (leading to the free energy barrier for PT through a proton channel). In an MD simulation, any free energy term can only be rigorously calculated using dynamics from deterministic (Newtonian) equations of motion subject to the proper ensemble constraints such as constant temperature, pressure, etc. When one replaces the all-atom, deterministic MD approach by other and more phenomenological approximations (e.g., dielectric continuum modeling, stochastic dynamics, etc.), it can lead to the introduction of uncontrolled errors in the simulation methodology. To be fair, if one has inadequate sampling in the MD simulation or an intrinsically inaccurate or incomplete potential energy function, here again one can introduce serious error, although these errors (simulation statistics, potential energy function refinement) can be more controllable.

It is with the above perspective that the differences between the present MD simulations, based on the MS-EVB methodology (22,23,25–43), and those of other articles on the topic of proton blockage by aquaporin channels (11–15), can be understood. However, none of the other computational studies have employed a deterministic MD simulation approach based on an accurate and validated underlying potential energy function having the required attributes to describe proton solvation and transport (as described above) across all regions of the problem, from the bulk aqueous phase to the channel interior. This is the likely reason why a variety of different results have been produced in these various studies.

In terms of the underlying computational methodology to study aquaporin proton blockage (and proton solvation and transport in general), our approach to this general problem (16,17,22,25–35,37–43) is to employ a single all-atom MD simulation methodology that includes explicit proton shuttling and charge delocalization in a deterministic MD fashion over all regions of the system, from the asymptotic bulk water regions to the interior of the protein channel. In other words, the present MD approach employs an underlying potential energy function, V(x), which describes as accurately as possible the physics of the delocalized excess proton within the all-atom protein and aqueous phase environments. This proton solvation and transport simulation methodology, although no doubt imperfect and likely to continually improve with time, has also been independently validated in a variety of different contexts (23). These latter results show that the general problem of proton solvation and transport can be a very complex and even subtle one, not easily lending itself to overly-approximate concepts and/or computational treatments. For example, although the electrostatic environment in the aquaporin channels has a critical role in defining the behavior of the proton transport barrier, some of the features of proton shuttling, such as charge localization and resonance stabilization in the proton wire, may be competing effects. They should therefore be fully and explicitly included in the MD simulation methodology to provide conclusive quantitative results, as has been done in the present work (and in the companion article (4), submitted in part as a counter-example to the aquaporin proton blockage story).

By contrast, the first simulation article to appear (11) on the topic of proton blockage by aquaporin channels utilized a stochastic hopping algorithm in an attempt to describe the Grotthuss proton shuttling process. While such algorithms are often useful, they are not deterministic (the dynamics are not directly derived from an underlying potential energy function as described above), and therefore it is difficult to associate a free energy profile with the underlying stochastic dynamics. Furthermore, a number of ad hoc assumptions in the stochastic dynamics, based on significantly reduced (few coordinate) descriptions of the problem, are generally made to define a basis for the proton hopping probability function (as it relates to the underlying dynamics of the environment). This function, even for bulk water, is very difficult to identify and justify from the actual dynamics of the proton hopping (34). For these reasons, it is perhaps not surprising that Nollert et al. (9) estimated a barrier to proton blockage, which is only slightly higher than the barrier to proton translocation in gramicidin A, which is considered to be a good proton conductor, thus providing an apparent contradiction in those simulation results.

With regard to the aquaporin proton blockage problem, Chakrabarti et al. (14,15) have employed the PM6 model for their potential energy function in their MD studies. This potential energy function can describe proton shuttling and charge delocalization, and it provides deterministic MD dynamics, so that in principle, a free energy profile for proton permeation might be calculated. The PM6 potential, however, appears to be highly inaccurate for proton solvation and transport in both liquid water and in protonated water wires. Fig. 10 shows the radial distribution function for bulk PM6 water compared to the experimental curve (59). The behavior of PM6 is that of a highly structured and glassy liquid, i.e., one that does not bear any resemblance to liquid water. Therefore, the PM6 model never provides an accurate asymptotic description of proton permeation through channels (at and beyond the channel mouth regions where it is in contact with bulk water). As such, the potential also cannot describe the possibly critical desolvation penalty associated with proton entrance into a channel. It is perhaps for this reason that Chakrabarti et al. (14,15) have attempted to bridge the PM6 free energy profile results from within the channel to dielectric continuum results at and near the channel mouths, even though such a bridging is not straightforward and may contain uncontrolled errors. In addition, within a proton channel there is the important process of proton hopping along the quasi-one-dimensional water wire, and here again the PM6 model appears to be highly inaccurate. Shown in Fig. 11 a is a small protonated water wire fragment for which the barrier to proton transfer was calculated at various fixed O-O distances in the central Zundel cation as shown, and Fig. 11 b shows the resulting proton transfer curves for the accurate ab initio, MS-EVB2, and PM6 data. As can be seen in the figure, for all O-O separations the PM6 model gives very large errors, some nearly as large as the overall barrier to proton blockage in aquaporins. In light of these results, it is not clear to what degree the results from the PM6 model for aquaporins and related systems can be viewed as being meaningful.

FIGURE 10.

FIGURE 10

Open in a new tab

Bulk water oxygen-oxygen radial distribution function for the PM6 model (dashed line) compared to the experimental curve (solid line). The PM6 model is seen to give a greatly overstructured glassy system.

FIGURE 11.

FIGURE 11

Open in a new tab

(a) A depiction of the protonated water wire segment and relevant coordinates used to test the accuracy of the PM6 and MS-EVB2 models. (b) Potential energy barriers for proton transfer in the internal Zundel cation of the water wire fragment shown in panel a, as a function of the oxygen-oxygen atom (O1-O2) distance on the central Zundel species. (Solid lines) Ab initio results. (Dashed lines) PM6 results. (Dot-dashed lines) MS-EVB2 results.

Warshel and co-workers have also adapted their empirical valence bond (EVB) method to study the proton translocation barrier in aquaporins (12,13). This approach, of course, bears the closest relationship to the present MS-EVB methodology. In their simpler EVB approach, a few (two or three) EVB states are used to model the proton transfer between water molecules and then somehow moved along the channel to reflect the shuttling. However, this approach by Warshel and co-workers does not appear to be dynamical, i.e., actual trajectories do not seem to be generated in deterministic fashion from an underlying potential energy function. This is to be contrasted with the present MS-EVB approach in which a large number of EVB states are continuously utilized to provide a continuous (within numerical error) potential energy function for deterministic MD trajectories and, hence, the free energy profile for proton permeation is calculated directly from the MS-EVB trajectories. The MS-EVB approach also includes the possibility of water diffusion so that the identity of the EVB states associated with the excess proton on those waters can continuously change while still providing a deterministic MD trajectory (23). Nevertheless, the simpler EVB approach of Warshel and co-workers does seem to reveal the dominant electrostatic barrier for the aquaporin channels (as also seen in the more complex MS-EVB simulations), so both approaches are in basic agreement on this aspect of the aquaporin proton blockage problem.

Free-energy sampling procedures

The PMFs in Fig. 4, A and B, of hydronium and proton permeation through the aquaporin channels were calculated by the umbrella sampling method with a harmonic biasing potential. The only difference lay in the tethering coordinate, which for the delocalized proton is the z-coordinate of the CEC (Eq. 1), and for the hydronium is the z-coordinate of its oxygen atom. We experimented with bin-widths of 0.5 Å, and spring constants of 5∼20 kcal/mol according to the umbrella overlap criteria between nearest-neighbor bins. The PMFs were calculated by the weighted histogram analysis method (60) (WHAM); a sufficiently large number of operational WHAM bins was applied, and sampling data corresponding to the same biasing potential was conjoined. The sampling density was taken to be at least 1.0 ns/Å to ensure full convergence and a meaningful comparison between the PMFs of hydronium and proton transport for each of the aquaporin channels. The convergence was verified visually by plotting the PMFs for different fractions of the overall sampling data. In addition, an error analysis was performed according to the block averaging method (61,62). This method splits the sampling data into two new sets according to the time series. The PMFs of the two newly generated data sets were then calculated by WHAM and superimposed by the least-square fitting with the PMF achieved by the full sampling data.

The SD was calculated at each point along the channel axis, according to

graphic file with name M21.gif (2)

where Fi(z) is the PMF at point z (with a vertical adjustment) of the ith data set. The SD for the four PMFs in this study was calculated by this block-averaging method. The SD was estimated on average along the channels to be ±0.4 kcal/mol for PT for hydronium in GlpF, ±0.3 kcal/mol for proton in GlpF, ±0.3 kcal/mol for hydronium in Aqp1, and ±0.4 kcal/mol for proton in Aqp1, as shown in Fig. 4.

Estimation of position-dependent diffusion coefficients

The position-dependent diffusion coefficients along the two aquaporin channels were estimated according to the Woolf-Roux equation (51) as recently simplified by Hummer (63),

graphic file with name M22.gif (3)

where 〈Q〉 is average of the reaction coordinate Q, var(Q) = 〈Q2〉 − 〈Q〉2 is the variance of the reaction coordinate, and τQ is the characteristic time of its autocorrelation function at the harmonic biasing window i according to

graphic file with name M23.gif (4)

with δQ(t) = Q(t) − 〈Q〉. Equations 3 and 4 are exact for an overdamped harmonic oscillator, but to fulfill this assumption a careful selection of magnitude of the spring constant is required such that the harmonic umbrella potential is strong enough to damp out any anharmonic forces. However, it is much weaker than the Langevin dynamics viscous friction. At times, it was difficult to obtain a converged estimate of the characteristic time within the 500-ps-long umbrella sampling trajectories because of the highly oscillatory resulting autocorrelation function, when applying the harmonic potential as used in calculating the PMFs and Eq. 4. If one assumes that the damping of the autocorrelation function of the reaction coordinate is due to different independent interaction modes, the autocorrelation function of the reaction coordinate can be expanded as the sum of a series of the exponential decays with different characteristic times τn (54),

graphic file with name M24.gif (5)

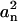where Inline graphic is the normalized coefficient that represents the contribution of mode i. Since the harmonic biasing potential was applied explicitly to effectively restrain the reaction coordinate, one may expect that the mode with the shortest characteristic time min(τn) corresponds to the harmonic biasing potential, and there min(τn) is the closest estimate of the characteristic time τ of Eq. 3. The fittings were performed with the simplex searching algorithm by the MatLab package (The MathWorks, Natick, MA) and it was found that a four-term expansion in Eq. 5 was adequate to provide the converged results in most cases. To justify this method of position-dependent diffusion coefficient estimation, its results were compared with those obtained from the Einstein relationship

graphic file with name M26.gif (6)

for three cases: respectively, the flexible TIP3P water model, the classical hydronium model used in MSEVB2, and the CEC of the MSEVB2 model. The results are summarized in Table 2.

TABLE 2.

Comparison of the Einstein relationship with the exponential fitting, for the estimation of position-dependent diffusion coefficient to the largest significant figure

D(Å2/ps) TIP3P (flexible) Hydronium Proton
Einstein relationship 0.35 0.2 0.4
Three-term fitting 0.31 0.4 0.4
Four-term fitting 0.32 0.3 0.4
Open in a new tab

Although the accurate estimation of position-dependent diffusion coefficients for inhomogeneous systems remains a challenging problem, the method utilized here seems to provide results that are reasonably consistent with the standard Einstein relationship. Further, slight error in the estimation of the position-dependent diffusion constants does not seem to be a critical flaw since the calculated ion channel conductance is largely dominated by the free energy profile in the case of high barriers.

Calculation of the maximum ion conductance

For a quasi-one-dimensional ion transport process, the maximum ion conductance gmax can be calculated according to

graphic file with name M27.gif (7)

where e is the elementary charge, kB is the Boltzmann constant, T is the temperature, L is the length of the pore region, D(Q) and F(Q) are, respectively, the diffusion coefficient and PMF as a function Q, and the bracket denotes spatial averaging over the length of the channel. For both the GlpF and Aqp1 channels, L = 30 Å is the range where the one-dimensional PMF is meaningful (|Q| ≤ 15 Å). Since the gmax exponentially depends on the free energy profile F(Q) but is only linearly proportional to the position-dependent diffusion coefficient D(Q), the error analysis of the uncertainty of gmax due to the error of F(Q) is performed using the Monte Carlo Bootstrap (64) method by randomly generating N sets of pseudo data for F(Q). At each point of Qi, the randomly generated F(Qi) has a normal distribution centered at F(Qi)wham and standard deviation σUMB(Qi), as previously achieved by WHAM and block average, respectively. A value of N = 106 was used in calculating the standard deviation of gmax of Table 1 to guarantee sufficient sampling. The resulting standard deviations of gmax are reasonable, only ∼20% off the average values. It is expected that the estimation of the D(Q), which is more crude, would lead to additional uncertainties of gmax. However, even in the worst scenario, the calculated gmax by the present method is still meaningful to an order of magnitude. It should be noted that Eq. 7 may overestimate the ion conductance compared with the experimental values because Eq. 7 accounts only for the contribution from the part inside the channel, and does not consider the energy barrier and diffusion restrictions for the ion to enter and exit the channel.

Boaz Ilan's present address is Dept. of Chemistry, Columbia University, 3000 Broadway, New York, NY 10027.

References

  • 1.Agmon, N. 1995. The Grotthuss mechanism. Chem. Phys. Lett. 244:456–462. [Google Scholar]
  • 2.Decoursey, T. E. 2003. Voltage-gated proton channels and other proton transfer pathways. Physiol. Rev. 83:475–579. [DOI] [PubMed] [Google Scholar]
  • 3.Agre, P., and D. Kozono. 2003. Aquaporin water channels: molecular mechanisms for human diseases. FEBS Lett. 555:72–78. [DOI] [PubMed] [Google Scholar]
  • 4.Wu, Y., B. Ilan, and G. A. Voth. 2005. Electrostatics and proton delocalization in proton channels. II. The minimalist synthetic LS2 channel and proton selectivity. Biophys. J. 92:61–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Brewer, M. L., U. W. Schmitt, and G. A. Voth. 2001. The formation and dynamics of proton wires in channel environments. Biophys. J. 80:1691–1702. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Fu, D., A. Libson, L. J. W. Miercke, C. Weitzman, P. Nollert, J. Krucinski, and R. M. Stroud. 2000. Structure of a glycerol-conducting channel and the basis for its selectivity. Science. 290:481–486. [DOI] [PubMed] [Google Scholar]
  • 7.Tajkhorshid, E., P. Nollert, M. Ø. Jensen, L. J. W. Miercke, J. O'Connell, R. M. Stroud, and K. Shulten. 2002. Control of the selectivity of the aquaporin water channel family by global orientational tuning. Science. 296:525–530. [DOI] [PubMed] [Google Scholar]
  • 8.Jensen, M. Ø., U. Röthlisberger, and C. Rovira. 2005. Hydroxide and proton migration in aquaporins. Biophys. J. 89:1744–1759. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Nollert, P., W. E. C. Harries, D. Fu, L. J. W. Miercke, and R. M. Stroud. 2001. Atomic structure of a glycerol channel and implications for substrated permeation in aqua(glycerol)porins. FEBS Lett. 504:112–117. [DOI] [PubMed] [Google Scholar]
  • 10.Yarnell, A. 2004. Blockage in the cell's waterway. Chem. Eng. News. 82:42–44. [Google Scholar]
  • 11.de Groot, B. L., T. Frigato, V. Helms, and H. Grubmueller. 2003. The mechanism of proton exclusion in aquaporin-1 water channel. J. Mol. Biol. 333:279–293. [DOI] [PubMed] [Google Scholar]
  • 12.Burykin, A., and A. Warshel. 2003. What really prevents proton transport through aquaporin? Charge self-energy versus proton wire proposals. Biophys. J. 85:3696–3706. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Burykin, A., and A. Warshel. 2004. On the origin of the electrostatic barrier for proton transport in aquaporin. FEBS Lett. 570:41–46. [DOI] [PubMed] [Google Scholar]
  • 14.Chakrabarti, N., E. Tajkhorshid, B. Roux, and R. Pomes. 2004. Molecular basis of proton blockage in aquaporins. Structure. 12:1–20. [DOI] [PubMed] [Google Scholar]
  • 15.Chakrabarti, N., B. Roux, and R. Pomes. 2004. Structural determinants of proton blockage in aquaporins. J. Mol. Biol. 343:493–510. [DOI] [PubMed] [Google Scholar]
  • 16.Ilan, B., E. Tajkhorshid, K. Shulten, and G. A. Voth. 2004. The mechanism of proton exclusion in aquaporin channels. Proteins Struct. Funct. Bioinform. 55:223–228. [DOI] [PubMed] [Google Scholar]
  • 17.Chen, H., Y. Wu, and G. A. Voth. 2006. Origins of proton transport behavior from selectivity domain mutations of the aquaporin-1 channel. Biophys. J. 90:L73–L75. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Beitz, E., B. Wu, L. M. Holm, J. E. Schultz, and T. Zeuthen. 2006. Point mutations in the aromatic/arginine region in aquaporin 1 allow passage of urea, glycerol, ammonia, and protons. Proc. Natl. Acad. Sci. USA. 103:269–274. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Chernyshev, A., and S. Cukierman. 2002. Thermodynamic view of activation energies or proton transfer in various gramicidin A channels. Biophys. J. 82:182–192. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Berry, R. S., S. A. Rice, and J. Ross. 2000. Physical Chemistry. Oxford University Press, New York.
  • 21.Mamonov, A. B., R. D. Coalson, A. Nitzan, and M. G. Kurnikova. 2003. The role of the dielectric barrier in narrow biological channels: a novel composite approach to modeling single-channel currents. Biophys. J. 84:3646–3661. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Day, T. J. F., A. V. Soudackov, M. Cuma, U. W. Schmitt, and G. A. Voth. 2002. A second generation multistate empirical valence bond model for proton transport in aqueous systems. J. Chem. Phys. 117:5839–5849. [Google Scholar]
  • 23.Voth, G. A. 2006. Computer simulation of proton solvation and transport in aqueous and biomolecular systems. Acc. Chem. Res. 39:143–150. [DOI] [PubMed] [Google Scholar]
  • 24.Cuma, M., U. W. Schmitt, and G. A. Voth. 2001. Multi-state empirical valence bond model for weak acid dissociation in aqueous solution. J. Phys. Chem. A. 105:187–199. [Google Scholar]
  • 25.Schmitt, U. W., and G. A. Voth. 1999. The computer simulation of proton transport in water. J. Chem. Phys. 111:9361–9381. [Google Scholar]
  • 26.Schmitt, U. W., and G. A. Voth. 1998. A multi-state empirical valence bond model for proton transport in water. J. Phys. Chem. B. 102:5547–5551. [Google Scholar]
  • 27.Lobaugh, J., and G. A. Voth. 1996. The quantum dynamics of an excess proton in water. J. Chem. Phys. 104:2056–2069. [Google Scholar]
  • 28.Schmitt, U. W., and G. A. Voth. 1999. Quantum properties of the excess proton in liquid water. Israel J. Chem. 39:483–492. [Google Scholar]
  • 29.Cuma, M., U. W. Schmitt, and G. A. Voth. 2000. A multi-state empirical valence bond model for acid-base chemistry in aqueous solution. Chem. Phys. 258:187. [Google Scholar]
  • 30.Schmitt, U. W., and G. A. Voth. 2000. The isotope substitution effect on the hydrated proton. Chem. Phys. Lett. 329:36–41. [Google Scholar]
  • 31.Day, T. J. F., U. W. Schmitt, and G. A. Voth. 2000. The mechanism of hydrated proton transport in water. J. Am. Chem. Soc. 122:12027–12028. [Google Scholar]
  • 32.Kim, J., U. W. Schmitt, J. A. Grüetzmacher, G. A. Voth, and N. F. Scherer. 2002. The vibrational spectrum of the hydrated proton: comparison of experiment, simulation, and normal mode analysis. J. Chem. Phys. 116:737–746. [Google Scholar]
  • 33.Petersen, M. K., S. S. Iyengar, T. J. F. Day, and G. A. Voth. 2004. The hydrated proton at the water liquid/vapor interface. J. Phys. Chem. B. 108:14804–14806. [Google Scholar]
  • 34.Lapid, H., N. Agmon, M. K. Petersen, and G. A. Voth. 2004. A bond-order analysis of the mechanism for hydrated proton mobility in liquid water. J. Chem. Phys. 122:014506. [DOI] [PubMed] [Google Scholar]
  • 35.Wang, F., and G. A. Voth. 2005. A linear-scaling self-consistent generalization of the multi-state empirical valence bond model for multiple excess protons in aqueous systems. J. Chem. Phys. 122:144105. [DOI] [PubMed] [Google Scholar]
  • 36.Xu, J., and G. A. Voth. 2006. Free energy profiles for H+ conduction in the D-pathway of cytochrome c oxidase: a study of the wild-type and N98D mutant enzymes. Biochim. Biophys. Acta. 1757:852–859. [DOI] [PubMed] [Google Scholar]
  • 37.Xu, J., and G. A. Voth. 2005. Computer simulation of explicit proton translocation in cytochrome c oxidase: the D-pathway. Proc. Natl. Acad. Sci. USA. 102:6795–6800. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Smondyrev, M., and G. A. Voth. 2002. Molecular dynamics simulation of proton transport near the surface of a phospholipid membrane. Biophys. J. 82:1460–1468. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.Smondyrev, M., and G. A. Voth. 2002. Molecular dynamics simulation of proton transport through the influenza A virus M2 channel. Biophys. J. 83:1987–1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 40.Wu, Y., and G. A. Voth. 2003. A computer simulation study of the hydrated proton in a synthetic proton channel. Biophys. J. 85:864–875. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Wu, Y., and G. A. Voth. 2003. Computational studies of proton transport through the M2 channel. FEBS Lett. 552:23–27. [DOI] [PubMed] [Google Scholar]
  • 42.Voth, G. A. 2003. The computer simulation of proton transport in biomolecular systems. Front. Biosci. 8:1384–1397. [DOI] [PubMed] [Google Scholar]
  • 43.Tepper, H. L., and G. A. Voth. 2005. Protons may leak through pure lipid bilayers via a concerted mechanism. Biophys. J. 88:3095–3108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 44.Beckstein, O., K. Tai, and M. S. Sansom. 2004. Not ions alone: barriers to ion permeation in nanopores and channels. J. Am. Chem. Soc. 126:14694–14695. [DOI] [PubMed] [Google Scholar]
  • 45.Németh-Cahalan, K. L., K. Kalman, and J. E. Hall. 2004. Molecular basis of pH and Ca2+ regulation of aquaporin water permeability. J. Gen. Physiol. 123:573–580. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 46.Lear, J. D., Z. R. Wasserman, and W. F. DeGrado. 1998. Synthetic amphiphilic peptide models for protein ion channels. Science. 240:1177–1181. [DOI] [PubMed] [Google Scholar]
  • 47.Jensen, M. Ø., E. Tajkhorshid, and K. Schulten. 2003. Electrostatic tuning of permeation and selectivity in aquaporin water channels. Biophys. J. 85:2884–2899. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 48.Kramers, H. A. 1940. Computational studies of membrane channels. Phys. 7:284–304. [Google Scholar]
  • 49.Levitt, D. 1991. General continuum theory for multiion channel. I. Theory. Biophys. J. 59:271–277. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 50.Berne, B. J., M. Borkovec, and J. E. Straub. 1988. Classical and modern methods in reaction rate theory. J. Phys. Chem. 92:3711–3725. [Google Scholar]
  • 51.Woolf, T. B., and B. Roux. 1994. Conformational flexibility of O-phosphorylcholine and O-phosphorylethanolamine: a molecular dynamics study of solvation effects. J. Am. Chem. Soc. 116:5916–5926. [Google Scholar]
  • 52.Smart, O., J. M. Goodfellow, and B. A. Wallace. 1993. The pore dimensions of gramicidin A. Biophys. J. 65:2455–2460. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 53.Finkelstein, A. 1987. Water Movement Through Lipid Bilayers, Pores and Plasma Membranes. Wiley, New York. [DOI] [PubMed]
  • 54.Pohl, P., S. M. Saparov, M. J. Borgnia, and P. Agre. 2001. Highly selective water channel activity measured by voltage clamp: analysis of planar lipid bilayers reconstituted with purified AqpZ. Proc. Natl. Acad. Sci. USA. 98:9624–9629. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 55.Fangqiang, Z., E. Tajkhorshid, and K. Schulten. 2004. Theory and simulation of water permeation in aquaporin-1. Biophys. J. 86:50–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 56.Sui, H., B. G. Han, J. K. Lee, P. Walian, and B. K. Jap. 2001. Structural basis of water-specific transport through the AQP1 water channel. Nature. 414:872–878. [DOI] [PubMed] [Google Scholar]
  • 57.Smith, W., and T. R. Forester. The DL-POLY Molecular Simulation Package. In CCLRC. Daresbury Laboratory, Daresbury, Warrington, England.
  • 58.Jorgensen, W. L., J. Chandrasekhar, J. D. Madura, R. W. Impey, and M. L. Klein. 1983. Comparison of simple potential functions for simulation liquid water. J. Chem. Phys. 79:926–935. [Google Scholar]
  • 59.Soper, A. K. 2000. The radial distribution functions of water and ice from 220 to 673 K and at pressures up to 400 MPa. Chem. Phys. 258:121–137. [Google Scholar]
  • 60.Kumar, S., D. Bouzida, R. H. Swendsen, P. A. Kollman, and J. M. Rosenberg. 1992. The weighted histogram analysis method for free-energy calculations. J. Comput. Chem. 13:1011–1021. [Google Scholar]
  • 61.Park, S., F. Khalili-Araghi, E. Tajkhorshid, and K. Schulten. 2003. Free energy calculation from steered molecular dynamics simulations using Jarzynski's equality. J. Chem. Phys. 199:3559–3566. [Google Scholar]
  • 62.Hummer, G. 2001. Fast-growth thermodynamic integration: error and efficiency analysis J. Chem. Phys. 114:7330–7337. [Google Scholar]
  • 63.Hummer, G. 2005. Position-dependent diffusion coefficients and free energies from Bayesian analysis of equilibrium and replica molecular systems. N. J. Phys. 7:34–47. [Google Scholar]
  • 64.Manly, B. F. J. 1998. Randomization, Bootstrap and Monte Carlo Methods in Biology. Chapman and Hall, London.
  • 65.Humphrey, W., A. Dalke, and K. Schulten. 1996. VMD—visual molecular dynamics. J. Mol. Graph. 14:33–38. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES