Abstract
There has been emerging interest whether plasma membrane constituents are moving according to free Brownian motion or hop diffusion. In the latter model, lipids, lipid-anchored proteins, and transmembrane proteins would be transiently confined to periodic corrals in the cell membrane, which are structured by the underlying membrane skeleton. Because this model is based exclusively on results provided by one experimental strategy—high-resolution single particle tracking—we attempted in this study to confirm or amend it using a complementary technique. We developed a novel strategy that employs single molecule fluorescence microscopy to detect confinements to free diffusion of CD59—a GPI-anchored protein—in the plasma membrane of living T24 (ECV) cells. With this method, minimum invasive labeling via fluorescent Fab fragments was sufficient to measure the lateral motion of individual protein molecules on a millisecond timescale, yielding a positional accuracy down to 22 nm. Although no hop diffusion was directly observable, based on a full analytical description our results provide upper boundaries for confinement size and strength.
INTRODUCTION
The cellular plasma membrane has shifted into the spotlight of cell biologists because it represents the major regulatory platform for the initiation of early signaling events. Signal transmission is generally enabled by a sequence of tightly regulated protein interactions, which trigger intracellular second messenger release. A comprehensive model of early signaling events therefore requires understanding the physical principles that mediate and affect interactions between proteins in the plasma membrane. Currently, the concepts are as indecisive as can be: a majority of researchers has accepted the view that small lipid domains—so-called lipid rafts—should segregate membrane proteins into two exclusive fractions: a raft fraction comprising basically signaling molecules, and a nonraft fraction including, e.g., the majority of transmembrane proteins (1–3). However, a growing number of scientists have articulated their skepticism (4,5) based on new experimental insights into potential artifacts associated with the original supporting studies (6).
An additional aspect has been recently introduced into the field, when the mobility of various membrane constituents has been measured in unprecedented detail: although there was evidence for years that transmembrane proteins interact with the membrane skeleton underlying the cytosolic leaflet of the cellular plasma membrane (7), single particle tracking at 25 μs time resolution revealed that even the diffusion of gold-labeled phospholipids or lipid-anchored proteins in the exoplasmic leaflet was affected by the membrane skeleton (8,9); transient confinement to periodic corrals with a size ranging from 32 to 230 nm for different cell types has been detected (9). This model of hop diffusion appeared attractive because it provides an elegant explanation for the observed increase in the apparent viscosity of the plasma membrane compared to artificial lipid bilayers (10–12). Because confinement of probes without direct contact to the confining elements was difficult to interpret, lipid rafts were suggested as the most promising transmitting elements. The residence time of a lipid within a corral would then correlate with the lifetime of the metastable raft itself, which the probe lipid is part of; based on these studies, lifetimes of only a millisecond or less are frequently attributed to rafts (13). However, these studies are also prone to errors: it has been found that gold labeling affects the motion of the diffusing probe in studies on model membranes (14) and cell membranes (15). The reason might be the size of the gold label that exceeds the size of the probe molecule severalfold as well as potential cross-linking of probe molecules by the gold particle that is coated with an antiprobe reagent.
Here, we investigated the mobility of CD59—a GPI-anchored protein—in the plasma membrane of living T24 (ECV) cells using single molecule microscopy. By employing minimum invasive labeling via fluorescent Fab fragments the recorded single molecule trajectories closely reflect the movement of an unlabeled protein. To sense confinement zones at the reported size of 120 nm (9), we dramatically improved the resolution in space and time of state of the art single molecule imaging devices down to 22 nm and 1 ms, respectively. For appropriate data interpretation, we derived an analytical approximation describing the time dependence of mean square displacements for diffusing molecules impeded by an infinite array of partially permeable barriers.
THEORY
Analytical approximation for hop diffusion
To quantitatively characterize hop diffusion, we derived an analytical approximation for the according mean square displacement (see Table 1 for list of abbreviations). Diffusion within impermeable square corrals of size L can be described by the mean square displacement  with Dmicro the short-range diffusion constant of the molecule within the confined area (
with Dmicro the short-range diffusion constant of the molecule within the confined area ( ); f has been calculated by Powles et al., yielding
); f has been calculated by Powles et al., yielding  (16). Its asymptotic behavior for long time-lags is given by
(16). Its asymptotic behavior for long time-lags is given by  .
.
TABLE 1.
Summary of abbreviations used in the Theory section
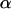 |
Apparent fraction of fully confined motion in hop diffusion |
| CO | Confinement offset, corrected for localization errors |
| COcorr | Confinement offset, corrected for localization precision and illumination time effects |
| COreal | Measured confinement offset |
| Dmacro | Macroscopic diffusion constant |
| Dmicro | Microscopic diffusion constant |
| Δ | Effect of localization precision on MSD |
| f | MSD for totally confined diffusion according to Powles et al. (16) |
| L | Size of square corral |
| MSD | Mean square displacement |
| MSDreal | Measured mean square displacement |
| σx, σy, σxy | Localization precision in x- and y-direction (assumed to be equal) |
| σCO | Error of CO |
 |
Error of COcorr |
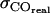 |
Error of COreal |
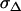 |
Error of Δ |
 |
Error of Dmacro |
| tdel | Time delay |
| till | Illumination time |
 |
Normalized illumination time |
| tlag | Time-lag |
| τ | Residence time of a confined molecule |
| τmicro | Residence time of a freely diffusing molecule in a corral of size L |
 |
Confinement strength; normalized residence time of a confined molecule |
If the corrals have a nonzero permeability, a molecule can escape and hop from corral to corral. For long observation times, the molecule appears to diffuse freely with a macroscopic diffusion constant  , where
, where  describes the residence time within a corral. MSD increases with increasing time-lag and converges to
describes the residence time within a corral. MSD increases with increasing time-lag and converges to
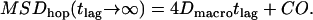 |
(1) |
In this scenario, the confinement offset CO contains the information about the size of the confinement zones. Considering scaling invariance, 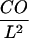 can be regarded as a sole function of the dimensionless variable
can be regarded as a sole function of the dimensionless variable  .
. 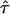 sets the residence time of a confined molecule,
sets the residence time of a confined molecule,  , in relation to the time a freely diffusing molecule would stay in the same region; per definition
, in relation to the time a freely diffusing molecule would stay in the same region; per definition  . As a rule of thumb,
. As a rule of thumb, 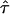 can be interpreted as the confinement strength. In general, partially permeable corrals will lead to a decrease in the offset, which will vanish when the barriers are totally removed.
can be interpreted as the confinement strength. In general, partially permeable corrals will lead to a decrease in the offset, which will vanish when the barriers are totally removed.
In the following we derive an analytical approximation for MSDhop (supplemental Fig. 1, Supplementary Material). For this, we estimate the distance a molecule moves between two independent observations separated by the time-lag tlag, characterized by the start position  and the end position
and the end position 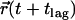 . Let us begin with an impermeable corral, and introduce weak permeability. The physical origin may be a single gate in the corral boundary. Whenever the molecule hits the gate, it will escape the corral with probability 1. Let us further characterize the trajectory of the molecule by time-averaging its positions within each visited corral, yielding in particular the average starting position
. Let us begin with an impermeable corral, and introduce weak permeability. The physical origin may be a single gate in the corral boundary. Whenever the molecule hits the gate, it will escape the corral with probability 1. Let us further characterize the trajectory of the molecule by time-averaging its positions within each visited corral, yielding in particular the average starting position  and end position
and end position 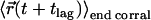 . In this scenario of quasiimpermeable boundaries, the time-averaged positions lie in the corral center. In the limit
. In this scenario of quasiimpermeable boundaries, the time-averaged positions lie in the corral center. In the limit  , the time-dependent component of the mean square displacement is given by the movement of the average position yielding
, the time-dependent component of the mean square displacement is given by the movement of the average position yielding 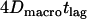 . The actual position of the molecule within the domain at the time point of the observation will deviate from
. The actual position of the molecule within the domain at the time point of the observation will deviate from 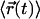 by
by  ; according to Powles et al. (16), the distance is given by
; according to Powles et al. (16), the distance is given by  . Noting that this additional distance has to be considered for both the start and end position of the molecule, we estimate
. Noting that this additional distance has to be considered for both the start and end position of the molecule, we estimate 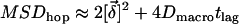 .
.
FIGURE 1.
Principle of the analysis. (A) The mean square displacement as a function of the time-lag is shown for confined diffusion simulated using Monte Carlo algorithms. Simulations for 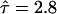 , 7.6, and 31 are shown as circles, dots, and stars, respectively. The full lines are drawn according to Eq. 2. The asymptotic behavior of MSD for short (long) time-lags defines the microscopic (macroscopic) diffusion constant Dmicro (Dmacro). The intersection of the asymptote for long time-lags (dashed line) with the y axis defines the confinement offset CO. (B)
, 7.6, and 31 are shown as circles, dots, and stars, respectively. The full lines are drawn according to Eq. 2. The asymptotic behavior of MSD for short (long) time-lags defines the microscopic (macroscopic) diffusion constant Dmicro (Dmacro). The intersection of the asymptote for long time-lags (dashed line) with the y axis defines the confinement offset CO. (B)  increases with increasing confinement strength
increases with increasing confinement strength  and approximates 1/3. (C) Monte Carlo simulation of positional averaging due to totally confined diffusion during illumination. Trajectories of various lengths were simulated for random walk in impermeable corrals (
and approximates 1/3. (C) Monte Carlo simulation of positional averaging due to totally confined diffusion during illumination. Trajectories of various lengths were simulated for random walk in impermeable corrals ( 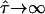 ). For each trajectory, the average position was determined, and its square distance from an independent second trajectory of the same length
). For each trajectory, the average position was determined, and its square distance from an independent second trajectory of the same length 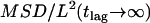 was calculated (20,000 trajectories). The plot shows this value as a function of
was calculated (20,000 trajectories). The plot shows this value as a function of 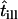 , which is specified by the trajectory length. The full line shows the derived correction term
, which is specified by the trajectory length. The full line shows the derived correction term 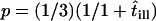 .
.
When we increase the permeability of the corral boundary, a significant fraction 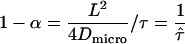 of the molecular motion will mediate the transition to the adjacent corral. This fraction is characterized by free diffusion with diffusion constant
of the molecular motion will mediate the transition to the adjacent corral. This fraction is characterized by free diffusion with diffusion constant 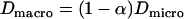 and therefore does not contribute to the confinement offset. The remaining fraction
and therefore does not contribute to the confinement offset. The remaining fraction  of the trajectory will experience no transitions, and is therefore described by totally confined diffusion. We account for the contributions of the two fractions by the modification
of the trajectory will experience no transitions, and is therefore described by totally confined diffusion. We account for the contributions of the two fractions by the modification 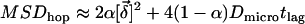 .
.
Moreover, due to fractions of free diffusion in the trajectory the apparent extension of the observable corrals is reduced. We can estimate the area portion of the free diffusion subfraction by  . In the remaining area
. In the remaining area  the random walker experiences full confinement. The total movement of a random walker in partially permeable corrals is therefore well approximated by
the random walker experiences full confinement. The total movement of a random walker in partially permeable corrals is therefore well approximated by 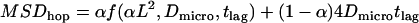 .
.
This equation provides an analytical approximation for hop diffusion in square corrals; its agreement with Monte Carlo simulations for different values of 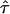 is shown in Fig. 1 A. The asymptotic behavior for short time-lags
is shown in Fig. 1 A. The asymptotic behavior for short time-lags  approximates unbounded motion. For long time-lags, we find
approximates unbounded motion. For long time-lags, we find  , which converges to
, which converges to 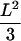 for
for  (Fig. 1 B). It has to be noted that for finite
(Fig. 1 B). It has to be noted that for finite 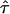 the shape of the fully confined subsections may deviate from a perfect square; however, the deviations are quantitatively negligible in the context of this study.
the shape of the fully confined subsections may deviate from a perfect square; however, the deviations are quantitatively negligible in the context of this study.
In addition, movements of the molecule during the illumination time affect the results. For free Brownian motion with diffusion constant Dmacro, a negative contribution to the offset 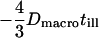 has to be taken into account (17). For hop diffusion, a qualitative estimate (18) and a quantitative approximation (19) have been given in the literature, which we extend here by a more general analytical expression. The following heuristic argument assumes that even for impermeable barriers a confined molecule shows free diffusion, although only for a short period of time
has to be taken into account (17). For hop diffusion, a qualitative estimate (18) and a quantitative approximation (19) have been given in the literature, which we extend here by a more general analytical expression. The following heuristic argument assumes that even for impermeable barriers a confined molecule shows free diffusion, although only for a short period of time 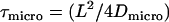 , i.e., with the probability
, i.e., with the probability  ,
, 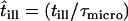 no effects due to confined molecular movements during the illumination time are observable. On the contrary, with a probability 1 − p the molecular motion collapses to the center of the confinement region, which reduces the respective mean square displacement to zero. This approach provides a valid approximation in the parameter range of our experiments, as tested by Monte Carlo simulations (Fig. 1 C). Considering all above contributions, a total mean square displacement for hop diffusion
no effects due to confined molecular movements during the illumination time are observable. On the contrary, with a probability 1 − p the molecular motion collapses to the center of the confinement region, which reduces the respective mean square displacement to zero. This approach provides a valid approximation in the parameter range of our experiments, as tested by Monte Carlo simulations (Fig. 1 C). Considering all above contributions, a total mean square displacement for hop diffusion
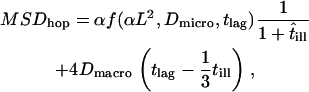 |
(2) |
is derived.
Assuming rapid free Brownian motion inside the corrals (Dmicro ∼ 10 μm2/s), recording of the full time course of MSD represents a challenging task, as the initial rising phase would occur at  . Still, the asymptotic behavior of MSD with
. Still, the asymptotic behavior of MSD with  contains information about confined diffusion due to an additional offset CO (Eq. 1 and Fig. 1):
contains information about confined diffusion due to an additional offset CO (Eq. 1 and Fig. 1):
 |
(3) |
In an experimental realization, the nonzero localization precision has to be further taken into account by
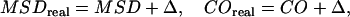 |
(4) |
with 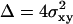 ,
,  denoting localization precision, i.e., the standard deviation in a data set of positions from consecutive images of a single immobile molecule.
denoting localization precision, i.e., the standard deviation in a data set of positions from consecutive images of a single immobile molecule.
Error analysis
For error propagation analysis, we accounted for contributions due to errors in determination of the confinement offset 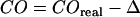 ,
,  , and of the macroscopic diffusion constant Dmacro,
, and of the macroscopic diffusion constant Dmacro,  (for illustration, see Supplemental Fig. 2, Supplementary Material). First, the confinement offset was corrected for illumination time effects,
(for illustration, see Supplemental Fig. 2, Supplementary Material). First, the confinement offset was corrected for illumination time effects,  . Using Gaussian error propagation analysis according to
. Using Gaussian error propagation analysis according to 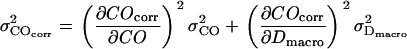 the expected error is given by
the expected error is given by
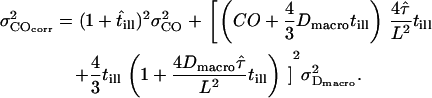 |
FIGURE 2.
Determination of the saturation intensity for Alexa647-labeled antibodies. Fluorescent antibodies were immobilized to glass coverslips, and the fluorescence signal, N, was measured as a function of the excitation intensity I. The saturation intensity IS was determined according to  , yielding IS = 19 kW/cm2.
, yielding IS = 19 kW/cm2.
For Fig. 10, we determined the parameter duplet  , which yields consistency with the measured values
, which yields consistency with the measured values 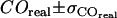 ,
,  ,
, 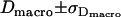 in a one-σ-range:
in a one-σ-range: 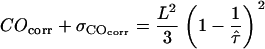 . Note that both COcorr and
. Note that both COcorr and  are functions of L and
are functions of L and 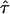 .
.
FIGURE 10.
Estimation of a “forbidden region” in two-dimensional parameter space  . Based on Gaussian error propagation theory, we estimated for all experimental realizations the maximum values of the duplet
. Based on Gaussian error propagation theory, we estimated for all experimental realizations the maximum values of the duplet  , which would be consistent with the experimental data in a one-sigma interval. All data shown in Table 2 were included and plotted according to the specified color code. See text for a detailed interpretation of this figure.
, which would be consistent with the experimental data in a one-sigma interval. All data shown in Table 2 were included and plotted according to the specified color code. See text for a detailed interpretation of this figure.
MATERIALS AND METHODS
Reagents
The CD59 monoclonal antibody MEM-43/5 was kindly provided by Vaclav Horejsi, Institute of Molecular Genetics, Prague, Czech Republic. Fab fragments were produced by standard papain digestion of the monoclonal antibody in the presence of 2-mercaptoethanol, followed by iodoacetamide for stopping the reaction. For labeling, the sample was treated with AlexaFlour 647 (Molecular Probes, Eugene, OR). Labeled Fabs were purified from the sample by gel filtration on a Superdex 200/30 HR column (Amersham Biosciences, Uppsala, Sweden). As shown in supplemental Fig. 3 A (top) (Supplementary Material), in our setup the Fabs eluted between 27 and 31 min in comparison to low molecular digestion products (elution time >32 min) and the intact monoclonal antibody (21–25 min; supplemental Fig. 3 A, bottom). The purity of the isolated Fabs was further assessed by SDS-PAGE (supplemental Fig. 3 B); the specificity was analyzed in comparison to the untreated intact monoclonal antibody using a panel of positive and negative cells lines including Jurkat T cells that are CD59 positive and a clone of the myeloid cell line U973 that is CD59 negative (supplemental Fig. 3 C). The 30-nm fluorescent latex spheres were obtained from Molecular Probes.
FIGURE 3.
Test experiment on artificially moved 30-nm latex spheres immobilized to a glass coverslip. The stage was moved sinusoidally with a xy-piezo with an amplitude of L = 200 nm at a frequency of 10 Hz. Trajectories of individual beads were recorded at tlag = 50 ms, and the MSD was calculated. The lower value originates from the in-phase movement of the stage with the illumination protocol, resulting in a return of the particles to its start position after 100 ms; it therefore specifies the localization precision. The maximum value is given by the average square distance of two arbitrary points in a sine wave, 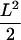 . We find here L = 170 nm, which agrees well with the applied setting.
. We find here L = 170 nm, which agrees well with the applied setting.
Cell culture
ECV-304(T-24) cells (DSMZ No. ACC 310) were maintained in monolayer cultures with RPMI 1640 medium (with L-glutamine, without phenol red; PAA-Laboratories, Linz, Austria) supplemented with 10% fetal calf serum (PAA-Laboratories), 1% penicillin-streptomycin, and 1% 1 M Hepes buffer (N-2-hydroxyethylpiperazine-N′2-ethane-sulfonic acid) and incubated at 37°C in a 5% CO2 atmosphere. Confluent cells were harvested with trypsin/EDTA (PAA-Laboratories) and diluted to 30 mm petri dishes at least 24 h before measurements.
Microscopy
Experiments were performed on a modified epi-fluorescence microscope (Axiovert 200, Zeiss, Germany), which was equipped with a temperature control system (POCmini Zeiss). Samples were illuminated via the epiport through a 100× NA = 1.4 Plan-Apochromat objective (Zeiss) using the 647-nm line of a Kr+-ion laser (Innova, Coherent, Santa Clara, CA) at high excitation intensities of up to I = 44 kW/cm2. Still, a substantial gain in signal  has been achieved due to the high saturation intensity Is = 19 kW/cm2 for Alexa647 (Fig. 2). An acousto-optic modulator (Isomet, 1205C) was used to achieve exact timing of the laser illumination till. After filtering (holographic notch plus 647.1 nm, Kaiser Optical Systems, Ann Arbor MI; custom dichroic, Chroma, Brattleboro, VT), images were recorded on a back-illuminated liquid nitrogen cooled charge-coupled device (CCD) camera (Micro Max 1300-PB, Roper Scientific, Trenton, NJ). Short delays between two images were enabled by operating the camera in kinetics mode; upon illumination, individual images within a time sequence were transferred into a masked region of the chip. In this mode, the time delay tdelay between two consecutive images is only limited by the parallel shift time of tp = 6 μs and the number of rows per image nrow according to
has been achieved due to the high saturation intensity Is = 19 kW/cm2 for Alexa647 (Fig. 2). An acousto-optic modulator (Isomet, 1205C) was used to achieve exact timing of the laser illumination till. After filtering (holographic notch plus 647.1 nm, Kaiser Optical Systems, Ann Arbor MI; custom dichroic, Chroma, Brattleboro, VT), images were recorded on a back-illuminated liquid nitrogen cooled charge-coupled device (CCD) camera (Micro Max 1300-PB, Roper Scientific, Trenton, NJ). Short delays between two images were enabled by operating the camera in kinetics mode; upon illumination, individual images within a time sequence were transferred into a masked region of the chip. In this mode, the time delay tdelay between two consecutive images is only limited by the parallel shift time of tp = 6 μs and the number of rows per image nrow according to 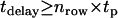 . Consecutive images were recorded with the following parameter settings: (till = 50 μs; tdelay = 0.45 ms), (0.65 ms; 0.4 ms), (0.3 ms; 0.7 ms), (0.3 ms, 14.7 ms), (1 ms, 49 ms), (1 ms, 100 ms). All experiments were performed in Dulbecco's phosphate buffered saline (PBS) (PAA-Laboratories).
. Consecutive images were recorded with the following parameter settings: (till = 50 μs; tdelay = 0.45 ms), (0.65 ms; 0.4 ms), (0.3 ms; 0.7 ms), (0.3 ms, 14.7 ms), (1 ms, 49 ms), (1 ms, 100 ms). All experiments were performed in Dulbecco's phosphate buffered saline (PBS) (PAA-Laboratories).
Data analysis
Images were analyzed using in-house algorithms implemented in MATLAB (MathWorks, Natick, MA). Individual diffraction limited signals were selected and fitted with a Gaussian intensity profile, yielding the single molecule position  with an accuracy
with an accuracy  . Single molecule trajectories were reconstructed according to previous studies (20), and the mean square displacement
. Single molecule trajectories were reconstructed according to previous studies (20), and the mean square displacement 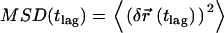 ,
, 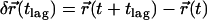 was calculated as a function of the time lag
was calculated as a function of the time lag  .
.
In Figs. 3, 4, 7, and 8 error bars indicate errors of the mean 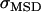 . To estimate the errors of the confinement offset
. To estimate the errors of the confinement offset  and the diffusion constant
and the diffusion constant  , Gaussian distributed values specified by the mean (MSD) and error of the mean (
, Gaussian distributed values specified by the mean (MSD) and error of the mean (  ) of the measured data were fitted with Eq. 1. The deviation of the individual fit results obtained from multiple fits yield appropriate predictions of the errors
) of the measured data were fitted with Eq. 1. The deviation of the individual fit results obtained from multiple fits yield appropriate predictions of the errors  ,
, 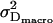 .
.
FIGURE 4.
Localization precision for single molecules. T24(ECV) cells were stained with fluorescent antibody to CD59, fixed with methanol/acetone (1:1), flushed with PBS, and single molecule trajectories were recorded for all applied experimental conditions. Here, an experiment is shown with till = 0.65 ms, tdelay = 0.4 ms. A linear fit yields an offset 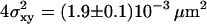 , concomitant to a localization precision
, concomitant to a localization precision  .
.
FIGURE 7.
MSD as a function of the time-lag for Fab-labeled CD59 in T24(ECV) cells. Each dot represents the mean value of >100 individual square displacement steps, recorded on 10–20 different cells. All data are corrected for the localization precision 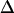 according to Eq. 4. (A) The movement of single CD59 molecules labeled with fluorescent Fab fragments was recorded with till = 0.3 ms (till = 0.65 ms) and tdelay = 0.7 ms (tdelay = 0.4 ms) at 37°C (20°C). The data were fitted by a linear increase according to Eq. 1, yielding a diffusion constant
according to Eq. 4. (A) The movement of single CD59 molecules labeled with fluorescent Fab fragments was recorded with till = 0.3 ms (till = 0.65 ms) and tdelay = 0.7 ms (tdelay = 0.4 ms) at 37°C (20°C). The data were fitted by a linear increase according to Eq. 1, yielding a diffusion constant  (
(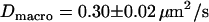 ) and a concomitant confinement offset
) and a concomitant confinement offset 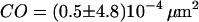 (
(  ) for experiments performed at 37°C shown as open circles (20°C shown as solid circles). (B) To test for confinement on larger length scales, experiments were repeated using time-lags of 15 ms (circles), 50 ms (squares), and 101 ms (stars). A fit based on the model of anomalous diffusion according to
) for experiments performed at 37°C shown as open circles (20°C shown as solid circles). (B) To test for confinement on larger length scales, experiments were repeated using time-lags of 15 ms (circles), 50 ms (squares), and 101 ms (stars). A fit based on the model of anomalous diffusion according to 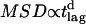 reveals an anomalous diffusion coefficient d = 0.93.
reveals an anomalous diffusion coefficient d = 0.93.
FIGURE 8.
MSD as a function of the time-lag for full Ab-labeled CD59 in T24(ECV) cells. To induce dimerization of CD59, cells were labeled with a fluorescent full antibody. Experiments were performed at 20°C (A) and 37°C (B), yielding  ,
, 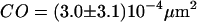 and
and 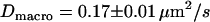 ,
,  , respectively. In experiment A (B), the illumination was set to till = 50 μs (till = 0.65 ms); trajectories were recorded with a time-lag of 0.5 ms (1.05 ms).
, respectively. In experiment A (B), the illumination was set to till = 50 μs (till = 0.65 ms); trajectories were recorded with a time-lag of 0.5 ms (1.05 ms).
Monte Carlo simulations of hop diffusion
Five-hundred trajectories consisting of 15 steps, each generated from 300 substeps, were simulated for hop diffusion in an infinite meshwork of periodic, partially permeable barriers. Simulations were performed in the following way: when the molecule hits a barrier a number n is generated at random between 0 and 1, and compared to a predefined escape probability η. If n < η, the barrier is crossed; if not, the molecule remains at its previous position. Simulated trajectories were analyzed in the same way as original data, i.e., the MSD was calculated as a function of tlag.
Test measurements
We tested if the system is sensitive enough to resolve minute movements. Latex spheres (30 nm) were immobilized to a glass slide, which was moved periodically along one dimension with an amplitude L = 200 nm and a frequency of 10 Hz by using a piezo-driven stage (Physik Instrumente, Karlsruhe, Germany). Fig. 3 shows MSD as a function of the time-lag recorded with 50-ms time resolution: as expected, MSD alternates between the minimum square distance specified by the localization precision, and the maximum square distance of  for the applied sine-wave. The measured value L = 170 nm just slightly deviates from the set amplitude (15% error).
for the applied sine-wave. The measured value L = 170 nm just slightly deviates from the set amplitude (15% error).
RESULTS
The fact that single molecules can be localized with subpixel precision beyond the diffraction limits of light microscopy has enabled a manyfold of applications, in which the structure of biomolecules or biomolecular assemblies was studied on the submicrometer length scale (21–24). A key demand for confinement analysis is precise knowledge of the intrinsic errors in position determination, 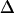 . We therefore calibrated our system by measuring the localization precision for all experimental conditions used in the further experiments. Cells were labeled with a fluorescent antibody to CD59, fixed, and single molecule trajectories were recorded and analyzed (Fig. 4). Within experimental errors, MSD was found to be constant when plotted as a function of the time-lag. From the offset of the curves,
. We therefore calibrated our system by measuring the localization precision for all experimental conditions used in the further experiments. Cells were labeled with a fluorescent antibody to CD59, fixed, and single molecule trajectories were recorded and analyzed (Fig. 4). Within experimental errors, MSD was found to be constant when plotted as a function of the time-lag. From the offset of the curves, 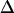 was calculated according to Eq. 4. We determined the localization precision under various illumination conditions, and plotted
was calculated according to Eq. 4. We determined the localization precision under various illumination conditions, and plotted 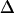 as a function of the average number of counts detected from a single molecule (Fig. 5). The expected proportionality (25,26) was confirmed quantitatively and used to correct all further experimental results according to
as a function of the average number of counts detected from a single molecule (Fig. 5). The expected proportionality (25,26) was confirmed quantitatively and used to correct all further experimental results according to  .
.
FIGURE 5.
Localization precision  for single CD59 molecules as a function of the signal brightness N, determined according to Fig. 4. The three data points indicate experiments performed at till = 0.05 ms (full antibody), till = 0.65 ms (Fab fragment) and till = 1.5 ms (Fab fragment). A theoretical derivation for the localization precision derived in Thompson et al. (26) was calculated using the measured values for the background noise, the width of the point spread function, the molecular brightness N, and the known pixel size of 200 nm (line), which perfectly describes the measured localization precision.
for single CD59 molecules as a function of the signal brightness N, determined according to Fig. 4. The three data points indicate experiments performed at till = 0.05 ms (full antibody), till = 0.65 ms (Fab fragment) and till = 1.5 ms (Fab fragment). A theoretical derivation for the localization precision derived in Thompson et al. (26) was calculated using the measured values for the background noise, the width of the point spread function, the molecular brightness N, and the known pixel size of 200 nm (line), which perfectly describes the measured localization precision.
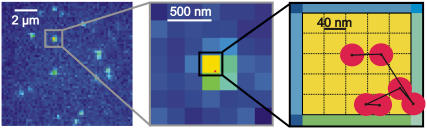
Fig. 6 shows typical raw data for CD59 molecules moving in the plasma membrane of living T24 (ECV) cells. Before the experiment, cells were stained with a low concentration of Alexa647-labeled Fab-fragments to CD59; thereby, only a minority fraction of cellular CD59 was observable. In general, surface densities of ∼1 fluorescent CD59 molecule per 10 μm2 were adjusted throughout our studies. An image sequence was recorded with tdelay = 0.4 ms and till = 0.65 ms, and the position of individual molecules was determined on each image by fitting with a two-dimensional Gaussian profile. At the highest magnification shown, the trajectory of a single CD59 molecule is plotted as overlay (red points); due to the high temporal resolution, the total recorded molecular motion remains within one pixel of 200 nm. In this experiment, an average number of 340 counts per molecule was obtained, concomitant with a localization precision of 22 nm, indicated by the radius of the circles. The length of the trajectory of six observations was representative throughout our study.
FIGURE 6.
Movement of single fluorescently labeled CD59 molecules in a living T24(ECV) cell, shown in different magnifications. By fitting a two-dimensional Gaussian distribution to the intensity profile the actual single molecule positions were determined, exemplified here for one selected molecule; its trajectory over six consecutive images is shown in red, with the localization precision of 22 nm being indicated by the radius of the circle. Due to the short time-lag tlag = 1 ms, the trajectory hardly exceeds one pixel.
We first analyzed data recorded at 20°C at the bottom membrane of the cells (Fig. 7 A; see also Table 2). The mean square displacement increases linearly with the time-lag, as expected for free Brownian motion. A fit according to Eq. 1 yields a diffusion constant D = 0.30 ± 0.02 μm2/s. No saturation or offset of the curve can be observed within the error bars (  ). Similarly, no saturation or offset has been detected when measurements were performed at the top membrane, or at 37°C. However, as expected, the latter measurement revealed a higher diffusion constant D = 0.46 ± 0.05 μm2/s (Fig. 7 A). We conclude that on a length scale of
). Similarly, no saturation or offset has been detected when measurements were performed at the top membrane, or at 37°C. However, as expected, the latter measurement revealed a higher diffusion constant D = 0.46 ± 0.05 μm2/s (Fig. 7 A). We conclude that on a length scale of  the membrane protein diffuses freely; if confinement regions exist, they are either too large or too small to be detected directly in this plot.
the membrane protein diffuses freely; if confinement regions exist, they are either too large or too small to be detected directly in this plot.
TABLE 2.
Summary of all experimental results obtained in this study
| T | till | CO | Dmacro | N | Color | |
|---|---|---|---|---|---|---|
| Fab-fragment | 37°C | 0.30 ms |  |
 |
150 | Green |
| Fab-fragment | 20°C | 0.65 ms | 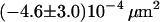 |
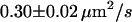 |
118 | Black |
| Full Ab | 37°C | 0.65 ms | 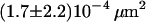 |
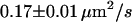 |
132 | Red |
| Full Ab | 20°C | 0.65 ms | 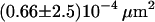 |
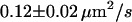 |
142 | Cyan |
| Full Ab | 20°C | 0.05 ms |  |
 |
191 | Blue |
To test for larger confinements, we repeated the experiments at longer time-lags of tlag = 15 ms, 50 ms, and 101 ms (Fig. 7 B). MSD was found to increase slightly sublinear with time-lag, an effect that had been observed frequently for membrane proteins (27). Anomalous subdiffusion is generally ascribed to molecular crowding and transient binding (28–30), and can be described by  , with d the anomalous diffusion exponent. The measured value
, with d the anomalous diffusion exponent. The measured value 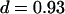 is close to unity, showing that the mobility over long timescales was decreasing only slightly. For the applied conditions there is no indication for confinement of CD59 to regions with a size
is close to unity, showing that the mobility over long timescales was decreasing only slightly. For the applied conditions there is no indication for confinement of CD59 to regions with a size  .
.
We next tested whether confinements could be introduced by transient cross-linking of two CD59 molecules. We therefore repeated the above experiments using the full antibody to CD59. This antibody had the additional advantage that it could be labeled with on average more than one Alexa647 molecule without losing its binding affinity. We made use of this advantage by reducing the illumination time to 50 μs; during such short illuminations, the molecules are practically immobile, which allows for determining the correct position without influences due to positional averaging according to Eq. 3. Fig. 8 shows the results of the analysis: although the diffusion constant is decreased to D = 0.11 ± 0.03 μm2/s at 20°C (D = 0.17 ± 0.01 μm2/s at 37°C) due to the motion of a larger object in the plasma membrane (31), no significant offset was detected.
It could still be possible that only a fraction of molecules undergoes confined diffusion, which is masked by the majority of nonconfined molecules. We therefore investigated the statistics of the diffusion process by measuring the probability distribution P(δr2, tlag) of individual square displacement steps; this function specifies the probability that a particle starting at the origin will be found within a circle of radius δr at time tlag. Although for free Brownian motion of a single component a monoexponential function is expected according to 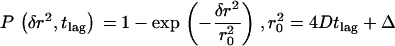 , components with a different mobility would contribute as additional fractions with different characteristic diffusion lengths r0 (20). Fig. 9 shows the according distribution of the data displayed in Fig. 7 A, 37°C: no indication for additional components was found. In addition, all other recorded data could be fitted perfectly with a monoexponential function (supplemental Figs. 4 and 5 and data not shown).
, components with a different mobility would contribute as additional fractions with different characteristic diffusion lengths r0 (20). Fig. 9 shows the according distribution of the data displayed in Fig. 7 A, 37°C: no indication for additional components was found. In addition, all other recorded data could be fitted perfectly with a monoexponential function (supplemental Figs. 4 and 5 and data not shown).
FIGURE 9.
Probability analysis of square displacements δr2. The cumulative probability distribution of δr2 was plotted for the data shown in Fig. 7 A (37°C, tlag = 1 ms) and fitted by a monoexponential function  describing free Brownian motion (20). No significant deviations were detectable. An expectation value
describing free Brownian motion (20). No significant deviations were detectable. An expectation value 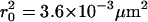 was calculated.
was calculated.
DISCUSSION
In this study, we addressed the question whether confinements restrict the Brownian motion of CD59—a GPI-anchored protein—in the plasma membrane of living T24(ECV) cells. From photobleaching experiments reported in the literature, we know that this molecule is diffusing freely on length scales >1.4 μm (32). However, it has been shown recently that the movement of gold-labeled lipids or lipid-anchored proteins in the exoplasmic leaflet of the cellular plasma membrane is hindered by immobile periodic structures, which confine the diffusing membrane constituents to corrals with a size of ∼120 nm (8,9). It was the aim of this study, to confirm or amend the results of those experiments with a complementary method under less invasive conditions.
We used fluorescent Fab fragments to CD59 for labeling, and recorded the trajectories of single protein molecules at maximum resolution in space and time. To achieve best localization precision, the signal brightness had to be maximized. Increasing the illumination time for this purpose, however, was impracticable since residual movements during illumination would have strongly affected the shape of the recorded trajectories, resulting in an underestimation of confinement sizes (18). We therefore selected a dye with high extinction coefficient ɛ = 220,000 M−1 cm−1 at 647 nm and high saturation intensity  , which can be rapidly cycled between ground state and excited state. Using Alexa647 and employing a high excitation intensity I = 44 kW/cm2, on average 340 photons have been detected from a single molecule during an illumination time of only 0.6 ms. In addition to signal brightness, the image pixelation and background noise define the precision for localizing single molecules (25,26): for optimum performance, a pixel-size equal to the standard-deviation of the point-spread function of 200 nm was selected (33). Finally, by choosing long wavelength excitation autofluorescence background could be dramatically reduced; for till = 0.6 ms, a background noise b = 6 counts was measured. The precise value of the localization precision was determined from single molecule trajectories recorded on fixed cells for different illumination times; it was in excellent agreement with theoretical predictions (26). Experiments have been performed at settings in a range of 22 nm < σxy < 30 nm.
, which can be rapidly cycled between ground state and excited state. Using Alexa647 and employing a high excitation intensity I = 44 kW/cm2, on average 340 photons have been detected from a single molecule during an illumination time of only 0.6 ms. In addition to signal brightness, the image pixelation and background noise define the precision for localizing single molecules (25,26): for optimum performance, a pixel-size equal to the standard-deviation of the point-spread function of 200 nm was selected (33). Finally, by choosing long wavelength excitation autofluorescence background could be dramatically reduced; for till = 0.6 ms, a background noise b = 6 counts was measured. The precise value of the localization precision was determined from single molecule trajectories recorded on fixed cells for different illumination times; it was in excellent agreement with theoretical predictions (26). Experiments have been performed at settings in a range of 22 nm < σxy < 30 nm.
Single molecule observations are terminated by photobleaching, which sets a limit to the length of individual trajectories (34). The application of reducing agents to increase the stability of fluorophores was not feasible here, as such reagents are toxic to cells. We therefore did not attempt to image confined diffusion directly at the single molecule level, but to detect its fundamental consequence: an increase in average jump distances due to the hypothetical rapid random walk within a corral—here termed confinement offset CO—which adds up to the macroscopically observed slow diffusion. A similar consequence has been recently suggested as promising observable for analyzing confined diffusion using fluorescence correlation spectroscopy (35,36). On the millisecond timescale the confinement offset solely depends on the corral size L and the confinement strength  ; an analytical approximation has been derived as basis for estimating the confinement strength. Maximum sensitivity of the assay is obtained at high frame rates, where the contribution of CO to the observed jump distances becomes large compared to the macroscopic slow diffusion. We therefore employed the kinetics mode of the CCD camera to record images at acquisition rates of up to 1000 frames per second.
; an analytical approximation has been derived as basis for estimating the confinement strength. Maximum sensitivity of the assay is obtained at high frame rates, where the contribution of CO to the observed jump distances becomes large compared to the macroscopic slow diffusion. We therefore employed the kinetics mode of the CCD camera to record images at acquisition rates of up to 1000 frames per second.
Let us assume corrals of 120 nm size as reported for T24(ECV) cells by single particle tracking (9). Within the bounded region, CD59 shall move rapidly with a diffusion constant of Dmicro = 8 μm2/s (9); in this case, the particle would diffuse freely for a time 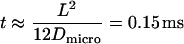 , too fast to be resolved with single molecule methods. For the experiment shown in Fig. 7 (37°C), however, according to Eq. 3 we would expect a confinement offset
, too fast to be resolved with single molecule methods. For the experiment shown in Fig. 7 (37°C), however, according to Eq. 3 we would expect a confinement offset  , which was not detected here (
, which was not detected here ( ). Even more so, variation of the temperature or usage of full antibodies to induce dimerization had no significant effects on the confinement offset (see Table 2).
). Even more so, variation of the temperature or usage of full antibodies to induce dimerization had no significant effects on the confinement offset (see Table 2).
The resolution of single molecule microscopy reaches its limits in the presented study. Residual errors in determination of CO might mask the effect of periodic permeable barriers. To provide an unambiguous conclusion, we performed an error analysis based on the analytical description of hop diffusion (Fig. 10). Apparently, the value of CO depends both on L and 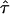 , which can be regarded as the only unknowns in the model (Eq. 3). In particular, for small values of
, which can be regarded as the only unknowns in the model (Eq. 3). In particular, for small values of 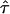 CO would reduce to zero, which renders a precise measurement of the confinement size in this parameter regime difficult and prone to errors. In contrast, high values of
CO would reduce to zero, which renders a precise measurement of the confinement size in this parameter regime difficult and prone to errors. In contrast, high values of 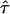 are concomitant with high values of the hypothetical microscopic diffusion constant Dmicro; in this regime, results are sensitive to positional averaging effects according to Eqs. 2 and 3. It is therefore not possible to determine L and
are concomitant with high values of the hypothetical microscopic diffusion constant Dmicro; in this regime, results are sensitive to positional averaging effects according to Eqs. 2 and 3. It is therefore not possible to determine L and 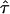 independently by this method. However, we can provide an upper boundary for the parameter duplet
independently by this method. However, we can provide an upper boundary for the parameter duplet  by accounting for all potential sources of errors. As described in the error analysis section, we first estimated the error of each measured parameter (
by accounting for all potential sources of errors. As described in the error analysis section, we first estimated the error of each measured parameter (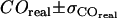 ,
, 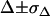 ,
, 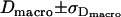 ), calculated via Gaussian error propagation analysis
), calculated via Gaussian error propagation analysis  as a function of L and
as a function of L and  , and compared this value with the expected confinement offset
, and compared this value with the expected confinement offset 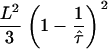 ; the equality
; the equality 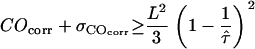 therefore defines a region bounded by the maximum values of the duplet
therefore defines a region bounded by the maximum values of the duplet 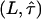 , which are consistent with the data within a one-sigma confidence limit (84% accuracy). For each experimental realization (variation of temperature, illumination time, full antibody versus Fab fragment) we determined the maximum values of the duplet
, which are consistent with the data within a one-sigma confidence limit (84% accuracy). For each experimental realization (variation of temperature, illumination time, full antibody versus Fab fragment) we determined the maximum values of the duplet 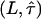 , which would yield consistency between the measured data and the hypothesis of square confinement regions in the plasma membrane (Fig. 10). In other words, the lower left region of the plot bounded by the set of curves represents the parameter range, in which confinement regions cannot be excluded within the one-sigma confidence limit. It has to be noted that for each data a second duplet
, which would yield consistency between the measured data and the hypothesis of square confinement regions in the plasma membrane (Fig. 10). In other words, the lower left region of the plot bounded by the set of curves represents the parameter range, in which confinement regions cannot be excluded within the one-sigma confidence limit. It has to be noted that for each data a second duplet 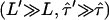 exists that provides a solution to the equation
exists that provides a solution to the equation 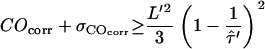 . However, this duplet specifies a lower boundary to
. However, this duplet specifies a lower boundary to 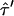 , yielding unrealistically high values of Dmicro and has thus not been taken into further account.
, yielding unrealistically high values of Dmicro and has thus not been taken into further account.
For large values of L the curves approach 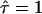 , which is equivalent to unconfined diffusion; in other words, the existence of large but highly permeable corrals would be in agreement with the data. This is not unexpected, as with
, which is equivalent to unconfined diffusion; in other words, the existence of large but highly permeable corrals would be in agreement with the data. This is not unexpected, as with 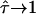 deviations of MSD from a linear increase vanish. In contrast, high values of
deviations of MSD from a linear increase vanish. In contrast, high values of 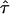 are concomitant with the extreme case of strong confinement, which directly provide an estimate for the maximum value of L consistent with the data. The spread within the curve set reflects the different limitations of the applied conditions: e.g., although achieving highest localization precision using long illumination times, positional averaging due to residual motion during the illumination renders this data less strict. This effect can be observed when comparing the blue curve representing experiments at till = 50 μs with the remaining curves recorded at 10 times longer illuminations. At till = 50 μs, diffusion during illumination hardly affects the observed confinement offset, therefore the curve is rather flat for small values of L.
are concomitant with the extreme case of strong confinement, which directly provide an estimate for the maximum value of L consistent with the data. The spread within the curve set reflects the different limitations of the applied conditions: e.g., although achieving highest localization precision using long illumination times, positional averaging due to residual motion during the illumination renders this data less strict. This effect can be observed when comparing the blue curve representing experiments at till = 50 μs with the remaining curves recorded at 10 times longer illuminations. At till = 50 μs, diffusion during illumination hardly affects the observed confinement offset, therefore the curve is rather flat for small values of L.
The presented analysis has been based on a homogenous population of molecules moving in a perfectly periodic meshwork of barriers. Let us estimate the consequences of deviations from this model. One might speculate that not all molecules were confined, with a large number of freely diffusing molecules masking the confinement effect. This scenario, however, is not supported by our data, as statistical analysis did not indicate any additional component with a distinct diffusion behavior (Fig. 9). Moreover, the expected high value of Dmicro ∼ 8 μm2/s would be inconsistent with the measured Dmacro = 0.46 μm2/s. Let us next assume corrals to be not perfectly periodic, with considerable variations in size. A distribution of L values would yield an average MSD according to  , with p(L2)dL2 the probability of finding a domain with area in an interval [L2, L2 + dL2]. Since
, with p(L2)dL2 the probability of finding a domain with area in an interval [L2, L2 + dL2]. Since  , analysis of the data would yield a proper estimate of the average domain area, but a too large estimate of the domain size, resulting even in an overestimation of L. Monte Carlo simulations performed on domains with broad size-distributions corroborate the interpretation (data not shown).
, analysis of the data would yield a proper estimate of the average domain area, but a too large estimate of the domain size, resulting even in an overestimation of L. Monte Carlo simulations performed on domains with broad size-distributions corroborate the interpretation (data not shown).
We can interpret the obtained results in two different ways: first, strong confinements with 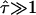 exist in T24(ECV) cells, however, with a size much smaller than reported in the literature (9). In this scenario, our data provide strong evidence that such corrals have to be smaller than ∼60 nm, at 20°C even smaller than 40 nm. We want to point out, however, that there is no report in the literature for the existence of confinements in T24(ECV) cells with such a size, rendering this scenario rather speculative. Second, periodic restrictions to the free Brownian motion of CD59 in T24(ECV) cells exist with the reported value of L = 120 nm (9), but have a low confinement strength
exist in T24(ECV) cells, however, with a size much smaller than reported in the literature (9). In this scenario, our data provide strong evidence that such corrals have to be smaller than ∼60 nm, at 20°C even smaller than 40 nm. We want to point out, however, that there is no report in the literature for the existence of confinements in T24(ECV) cells with such a size, rendering this scenario rather speculative. Second, periodic restrictions to the free Brownian motion of CD59 in T24(ECV) cells exist with the reported value of L = 120 nm (9), but have a low confinement strength 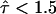 . In this case, the barriers are hardly sensed by the moving molecule, leading to no significant decrease of Dmacro compared to Dmicro.
. In this case, the barriers are hardly sensed by the moving molecule, leading to no significant decrease of Dmacro compared to Dmicro.
In conclusion, our data clearly indicate that the motion of the GPI-anchored protein CD59 is not restricted by periodic cytoskeletal barriers. At this point, it is difficult to reason why the presented approach did not yield the same results as previous studies performed with larger particles as labels. It seems as if gold labeling leads to an exaggerated confinement strength, maybe due to its ability to transiently bind specifically or unspecifically to other membrane proteins. Single particle tracking of gold-labeled membrane constituents may still provide a proper method to probe diffusion barriers; however, our results show that the single molecule hop frequency and concomitantly the confinement strength cannot be directly inferred from single particle tracking studies.
SUPPLEMENTARY MATERIAL
An online supplement can be found by visiting BJ Online at http://www.biophysj.org.
Acknowledgments
We are grateful to Vaclav Horejsi for providing mAbs.
This work was supported by the Austrian Science Fund (FWF), project Nos. P15053, P15025, and Y250-B10, the Competence Center for Biomolecular Research-Vienna, and the GEN-AU project of the Austrian Federal Ministry for Education, Science and Culture.
Abbreviations used: CO, confinement offset; D, diffusion constant;  , localization precision; GPI, glycosylphosphatidylinositol; L, confinement size; MSD, mean square displacement;
, localization precision; GPI, glycosylphosphatidylinositol; L, confinement size; MSD, mean square displacement; 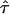 , confinement strength; till, illumination time.
, confinement strength; till, illumination time.
References
- 1.Sharma, P., R. Varma, R.C. Sarasij, Ira, K. Gousset, G. Krishnamoorthy, M. Rao, and S. Mayor. 2004. Nanoscale organization of multiple GPI-anchored proteins in living cell membranes. Cell 116:577–589. [DOI] [PubMed] [Google Scholar]
- 2.Simons, K., and E. Ikonen. 1997. Functional rafts in cell membranes. Nature. 387:569–572. [DOI] [PubMed] [Google Scholar]
- 3.Vereb, G., J. Szollosi, J. Matko, P. Nagy, T. Farkas, L. Vigh, L. Matyus, T. A. Waldmann, and S. Damjanovich. 2003. Dynamic, yet structured: the cell membrane three decades after the Singer-Nicolson model. Proc. Natl. Acad. Sci. USA. 100:8053–8058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Munro, S. 2003. Lipid rafts: elusive or illusive? Cell. 115:377–388. [DOI] [PubMed] [Google Scholar]
- 5.Douglass, A. D., and R. D. Vale. 2005. Single-molecule microscopy reveals plasma membrane microdomains created by protein-protein networks that exclude or trap signaling molecules in T cells. Cell. 121:937–950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Heerklotz, H. 2002. Triton promotes domain formation in lipid raft mixtures. Biophys. J. 83:2693–2701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Saxton, M. J., and K. Jacobson. 1997. Single-particle tracking: applications to membrane dynamics. Annu. Rev. Biophys. Biomol. Struct. 26:373–399. [DOI] [PubMed] [Google Scholar]
- 8.Fujiwara, T., K. Ritchie, H. Murakoshi, K. Jacobson, and A. Kusumi. 2002. Phospholipids undergo hop diffusion in compartmentalized cell membrane. J. Cell Biol. 157:1071–1081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Murase, K., T. Fujiwara, Y. Umemura, K. Suzuki, R. Iino, H. Yamashita, M. Saito, H. Murakoshi, K. Ritchie, and A. Kusumi. 2004. Ultrafine membrane compartments for molecular diffusion as revealed by single molecule techniques. Biophys. J. 86:4075–4093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Schlessinger, J., D. Axelrod, D. E. Koppel, W. W. Webb, and E. L. Elson. 1977. Lateral transport of a lipid probe and labeled proteins on a cell membrane. Science. 195:307–309. [DOI] [PubMed] [Google Scholar]
- 11.Kusumi, A., C. Nakada, K. Ritchie, K. Murase, K. Suzuki, H. Murakoshi, R. S. Kasai, J. Kondo, and T. Fujiwara. 2005. Paradigm shift of the plasma membrane concept from the two-dimensional continuum fluid to the partitioned fluid: high-speed single-molecule tracking of membrane molecules. Annu. Rev. Biophys. Biomol. Struct. 34:351–378. [DOI] [PubMed] [Google Scholar]
- 12.Fahey, P. F., D. E. Koppel, L. S. Barak, D. E. Wolf, E. L. Elson, and W. W. Webb. 1977. Lateral diffusion in planar lipid bilayers. Science. 195:305–306. [DOI] [PubMed] [Google Scholar]
- 13.Kusumi, A., I. Koyama-Honda, and K. Suzuki. 2004. Molecular dynamics and interactions for creation of stimulation-induced stabilized rafts from small unstable steady-state rafts. Traffic. 5:213–230. [DOI] [PubMed] [Google Scholar]
- 14.Lee, G. M., A. Ishihara, and K. A. Jacobson. 1991. Direct observation of Brownian motion of lipids in a membrane. Proc. Natl. Acad. Sci. USA. 88:6274–6278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Tomishige, M., and A. Kusumi. 1999. Compartmentalization of the erythrocyte membrane by the membrane skeleton: intercompartmental hop diffusion of band 3. Mol. Biol. Cell. 10:2475–2479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Powles, J. G., M. J. D. Mallett, G. Rickayzen, and W. A. B. Evans. 1992. Exact analytic solutions for diffusion impeded by an infinite array of partially permeable barriers. Proc. R. Soc. London. 436:391–403. [Google Scholar]
- 17.Goulian, M., and S. M. Simon. 2000. Tracking single proteins within cells. Biophys. J. 79:2188–2198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ritchie, K., X. Y. Shan, J. Kondo, K. Iwasawa, T. Fujiwara, and A. Kusumi. 2005. Detection of non-Brownian diffusion in the cell membrane in single molecule tracking. Biophys. J. 88:2266–2277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Destainville, N., and L. Salome. 2006. Quantification and correction of systematic errors due to detector time-averaging in single-molecule tracking experiments. Biophys. J. 90:L17–L19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Schütz, G. J., H. Schindler, and T. Schmidt. 1997. Single-molecule microscopy on model membranes reveals anomalous diffusion. Biophys. J. 73:1073–1080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lommerse, P. H., B. E. Snaar-Jagalska, H. P. Spaink, and T. Schmidt. 2005. Single-molecule diffusion measurements of H-Ras at the plasma membrane of live cells reveal microdomain localization upon activation. J. Cell Sci. 118:1799–1809. [DOI] [PubMed] [Google Scholar]
- 22.Schütz, G. J., G. Kada, V. P. Pastushenko, and H. Schindler. 2000. Properties of lipid microdomains in a muscle cell membrane visualized by single molecule microscopy. EMBO J. 19:892–901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yildiz, A., J. N. Forkey, S. A. McKinney, T. Ha, Y. E. Goldman, and P. R. Selvin. 2003. Myosin V walks hand-over-hand: single fluorophore imaging with 1.5-nm localization. Science. 300:2061–2065. [DOI] [PubMed] [Google Scholar]
- 24.Betzig, E., G. H. Patterson, R. Sougrat, O. W. Lindwasser, S. Olenych, J. S. Bonifacino, M. W. Davidson, J. Lippincott-Schwartz, and H. F. Hess. 2006. Imaging intracellular fluorescent proteins at nanometer resolution. Science. 313:1642–1645. [DOI] [PubMed] [Google Scholar]
- 25.Bobroff, N. 1986. Position measurement with a resolution and noise-limited instrument. Rev. Sci. Instrum. 57:1152–1157. [Google Scholar]
- 26.Thompson, R. E., D. R. Larson, and W. W. Webb. 2002. Precise nanometer localization analysis for individual fluorescent probes. Biophys. J. 82:2775–2783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Feder, T. J., I. Brust-Mascher, J. P. Slattery, B. Baird, and W. W. Webb. 1996. Constrained diffusion or immobile fraction on cell surfaces: a new interpretation. Biophys. J. 70:2767–2773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bouchaud, J. P., and A. Georges. 1988. The physical mechanisms of anomalous diffusion. In Disorder and Mixing. E. Guyon, editor. Kluwer Academic Publishers, Dordrecht, The Netherlands. 19–29.
- 29.Saxton, M. J. 1994. Anomalous diffusion due to obstacles: a Monte Carlo study. Biophys. J. 66:394–401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Saxton, M. J. 1996. Anomalous diffusion due to binding: a Monte Carlo study. Biophys. J. 70:1250–1262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zhang, F., W. G. Schmidt, Y. Hou, A. F. Williams, and K. Jacobson. 1992. Spontaneous incorporation of the glycosyl-phosphatidylinositol-linked protein Thy-1 into cell membranes. Proc. Natl. Acad. Sci. USA. 89:5231–5235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kenworthy, A. K., B. J. Nichols, C. L. Remmert, G. M. Hendrix, M. Kumar, J. Zimmerberg, and J. Lippincott-Schwartz. 2004. Dynamics of putative raft-associated proteins at the cell surface. J. Cell Biol. 165:735–746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Schütz, G. J., V. P. Pastushenko, H. J. Gruber, H.-G. Knaus, B. Pragl, and H. Schindler. 2000. 3D imaging of individual ion channels in live cells at 40 nm resolution. Single Mol. 1:25–31. [Google Scholar]
- 34.Füreder-Kitzmüller, E., J. Hesse, A. Ebner, H. J. Gruber, and G. J. Schütz. 2005. Non-exponential bleaching of single bioconjugated Cy5 molecules. Chem. Phys. Lett. 404:13–18. [Google Scholar]
- 35.Wawrezinieck, L., H. Rigneault, D. Marguet, and P. F. Lenne. 2005. Fluorescence correlation spectroscopy diffusion laws to probe the submicron cell membrane organization. Biophys. J. 89:4029–4042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Lenne, P. F., L. Wawrezinieck, F. Conchonaud, O. Wurtz, A. Boned, X. J. Guo, H. Rigneault, H. T. He, and D. Marguet. 2006. Dynamic molecular confinement in the plasma membrane by microdomains and the cytoskeleton meshwork. EMBO J. 25:3245–3256. [DOI] [PMC free article] [PubMed] [Google Scholar]