Abstract
There is empirical evidence that genotypes differ not only in mean, but also in environmental variance of the traits they affect. Genetic heterogeneity of environmental variance may indicate genetic differences in environmental sensitivity. The aim of this study was to develop a general framework for prediction of breeding values and selection responses in mean and environmental variance with genetic heterogeneity of environmental variance. Both means and environmental variances were treated as heritable traits. Breeding values and selection responses were predicted with little bias using linear, quadratic, and cubic regression on individual phenotype or using linear regression on the mean and within-family variance of a group of relatives. A measure of heritability was proposed for environmental variance to standardize results in the literature and to facilitate comparisons to “conventional” traits. Genetic heterogeneity of environmental variance can be considered as a trait with a low heritability. Although a large amount of information is necessary to accurately estimate breeding values for environmental variance, response in environmental variance can be substantial, even with mass selection. The methods developed allow use of the well-known selection index framework to evaluate breeding strategies and effects of natural selection that simultaneously change the mean and the variance.
THE standard genetic model in quantitative genetics is that phenotype P is the sum of genotype G and environment E: 
(Falconer and Mackay 1996). The phenotypic variance can be written as 
, assuming no covariance between G and E. This model allows for genetic differences in mean (G), with a genetic variance 
. For different genotypes, environmental variances (
) are assumed to be constant. On the basis of analysis of field data and laboratory (selection) experiments, there is, however, some empirical evidence that genotypes differ in 
.
Several studies have been carried out to quantify genetic differences in environmental variance in field data. SanCristobal-Gaudy et al. (2001), Sorensen and Waagepetersen (2003), and Ros et al. (2004) explicitly modeled genetic differences in environmental variance and found substantial genetic variance in environmental variance for litter size in sheep, litter size in pigs, and body weight in snails, respectively. Van Vleck (1968) and Clay et al. (1979), in analysis of milk yield in dairy cattle, and Rowe et al. (2006), in analysis of body weight in broiler chickens, found large differences between sires in phenotypic variance within progeny groups. In these studies, it was not possible to distinguish whether these differences were due to heterogeneity of environmental variance, genetic variance, or both.
Several selection experiments have been carried out to investigate whether phenotypic variance can be changed by selection. Phenotypic variance changed in some selection experiments with Drosophila melanogaster and Tribolium castaneum (Rendel et al. 1966; Kaufman et al. 1977; Cardin and Minvielle 1986), while it did not in an experiment with mice (Falconer and Robertson 1956). In these experiments, it was not always clear whether the response in variance was due to a change in environmental variance, genetic variance, or both.
Mackay and Lyman (2005) derived 300 isofemale lines of Drosophila and computed the coefficient of variation (CV) for environmental variance within each homozygous line, effectively a clone, and within crosses of each line with another inbred line. They found highly significant genetic variance in the CV and in environmental variance between lines. Homozygotes had higher environmental variance, in agreement with findings of Robertson and Reeve (1952). This study is probably the cleanest known example of showing genetic variance in environmental variance because the design allowed repetition of genotypes.
In livestock and plant breeding, uniformity of end product is an important topic. In meat type animals, for instance, uniformity has economic benefits because excessive variability in carcass weight or conformation is penalized by slaughterhouses. Hohenboken (1985) reviewed the potential of mating systems (crossing, inbreeding) and breeding schemes to change variability. To evaluate breeding strategies, methods to predict responses to selection for uniformity are necessary. SanCristobal-Gaudy et al. (1998) derived prediction equations and SanCristobal-Gaudy et al. (2001) evaluated different selection indices using Monte Carlo simulation when the aim was to select for an optimum phenotype and thereby decrease the variance around the optimum (canalizing selection). Sorensen and Waagepetersen (2003) evaluated response to selection using an index including the mean and the variance of multiple records of an individual and Ros et al. (2004) discussed the use of a restricted index aiming at decreasing the environmental variance, while maintaining the mean. Hill and Zhang (2004) derived simple equations to predict response to directional mass selection with genetic heterogeneity of environmental variance. In general, these prediction equations can be used only in special cases. A general framework to predict responses in mean and variance is lacking.
The objective of the present study was to develop a general framework for prediction of breeding values and responses to selection with genetic heterogeneity of environmental variance. Responses to selection were predicted for different forms of selection based on a single phenotype, as well as selection on a mean or variance of a group of relatives. Furthermore, a measure of heritability of environmental variance was developed, enabling a direct comparison between selection to change the environmental variance of a trait and the well established framework of selection to change its mean.
DERIVATION AND EVALUATION OF EXPRESSIONS
In this section, the model incorporating genetic heterogeneity of environmental variance is defined and the framework for prediction is explained. Prediction of breeding values and selection responses based on a single phenotype and a group of relatives are then considered, in each case using Monte Carlo simulation to investigate the relationships between true breeding values and phenotypic information. Using these observations, multiple-regression equations are derived for one generation of selection and their goodness of fit is evaluated by simulation. Finally, a measure of heritability for environmental variance is proposed.
Genetic model and framework for prediction
The classical model, in the absence of dominance and epistasis, 
(Falconer and Mackay 1996), is extended to include an additive genetic effect for the environmental variance,
 |
(1) |
(Hill and Zhang 2004), where μ and 
are, respectively, the mean trait value and the mean environmental variance of the population, 
and 
are, respectively, the breeding value for the mean and environmental variance, and χ is a standard normal deviate for the environmental effect. It is assumed that 
and 
are the sum of the effects at an infinite number of loci each with small additive effects and follow a multivariate normal distribution 
, where A is the additive genetic relationship matrix,
 |
is the additive genetic variance in 
, 
is the additive genetic variance in 
, 
, and 
is the additive genetic correlation between 
and 
. The term χ is normally distributed 
and is scaled by 
to obtain the environmental effect. The notation is listed in Table 1.
TABLE 1.
Notation used
| P, μ, Am, Av | Phenotype, mean, breeding values for mean and environmental variance |
| χ, MS | Standard normal deviate, Mendelian sampling term |
 ,  ,  , C
|
Genetic variance in mean and environmental variance, genetic correlation between  and  , genetic variance–covariance matrix |
 , 
|
Mean environmental and phenotypic variances |
 ,  , 
|
Mean P, P2, and P3 of selected animals |
 ,  ,  , n
|
Mean phenotype of relatives, mean phenotype squared, mean squared phenotype of relatives, number of relatives |
 , 
|
Within-family variance, log-transformed within-family variance |
 , 
|
Additive genetic relationships between animal j and the group of relatives and between animals within the group of relatives |
| a, x | Vectors of breeding values  and  and of phenotypic information |
P, G,  , 
|
Variance–covariance matrix of x, covariance matrix between x and a, vectors with 
|
 ,  , L
|
P- and G-matrices with  , scalar matrix |
B,  , 
|
Matrix with regression coefficients, vectors with 
|
| i, x, p, z | Selection intensity, truncation point, selected proportion, ordinate of standard normal distribution |
 ,  , 
|
Response in  and  , accuracy of 
|
 ,  , 
|
Heritability of mean and environmental variance, evolvability of environmental variance |
 ,  , 
|
Environmental variance, breeding value for environmental variance, and genetic variance in environmental variance for the exponential genetic model |
The genetic model in Equation 1 does not allow for random environmental effects on the magnitude of the environmental variance, because without repeated measurements on each individual these cannot be separated from the usual random environmental effects. With repeated measurements on each individual, these environmental effects on environmental variance become equivalent to permanent environmental effects (e.g., SanCristobal-Gaudy et al. 1998; Sorensen and Waagepetersen 2003).
To predict the breeding values 
and 
and selection responses 
and 
, multiple regression was used. Selection index theory is essentially an application of multiple regression (Hazel 1943). Multiple regression gives the best linear prediction (BLP), which is equal to best linear unbiased prediction (BLUP) when fixed effects are known without error (Henderson 1984). When variables are multivariate normally distributed, regressions are linear and homoscedastic (Lynch and Walsh 1998). Although the distribution of P deviates slightly from normality with genetic heterogeneity of environmental variance (
), P, 
, and 
follow an approximately multivariate normal distribution for values of 
observed in the literature (e.g., SanCristobal-Gaudy et al. 2001; Sorensen and Waagepetersen 2003; Ros et al. 2004; Rowe et al. 2006), justifying the use of multiple regression.
Multiple regression with selection on a single phenotype
Monte Carlo simulation:
Monte Carlo simulation was used to investigate the relationships between 
and 
with P, with the objective to decide which order of fit would be required for accurate prediction and then to evaluate the fit of predictions on the basis of multiple regressions. Fifty replicates with one phenotypic observation on each of 500,000 unrelated animals in each replicate were generated according to the genetic model in Equation 1, assuming 
. The breeding values 
and 
and the environmental effect χ were randomly drawn from 
and scaled by their corresponding standard deviations. When the genetic correlation between 
and 
was nonzero, 
was sampled given the expected value based on 
with variance 
. Expected breeding values were calculated as the mean 
and 
within successive intervals of 0.01 units of P (
) and averaged over replicates. Expected selection responses to directional mass selection were calculated as the mean 
and 
of all selected animals having 
and averaged over replicates, where x is the truncation point. The selected proportion was assumed to be the same in both sexes.
Breeding value estimation:
Figure 1, A and B, presents, respectively, the expectation of 
given P and the expectation of 
given P2 when 
, obtained by simulation. These show that the relationship between 
and P is almost linear and that the relationship between 
and P2 is also almost linear (quadratic in P). Therefore, 
roughly predicts 
and regression on 
roughly predicts 
. As a consequence of genetic heterogeneity of environmental variance, the distribution of P is slightly leptokurtic and is slightly skewed when 
. By fitting curves to the simulation results, it was found that regression on 
explained most of the residual nonlinearity and skewness when 
. Moments of P of higher order did not improve the fit and were therefore not considered in the rest of this study.
Figure 1.—
Expected 
(A) and 
(B) as a function of P and P2, respectively (
; 
; 
; 
; 
).
On the basis of this curve fitting, breeding values were predicted using multiple regression on the first through third order of P,
 |
(2) |
where
 |
 |
 |
and
 |
Elements of P and G were derived using the higher-order moments of the normal distribution (e.g., Stuart and Ord 1994) and standard variance–covariance rules (see appendix a). Elements in these matrices were verified with Monte Carlo simulation.
Evaluation of predictions:
Predictions of Equation 2 were close to the expectations obtained from Monte Carlo simulation when 
, as could be expected from the almost linear relationships shown in Figure 1, A and B (
). For 
, Figure 2A shows that 
is approximately linear in P, with a slope close to 
, for P within two standard deviations (SD) of its mean, but becomes curvilinear for extreme P. The predicted 
using the full model with multiple regressions on P, P2, and P3 fitted well to the expectations obtained from Monte Carlo simulation (
) and, in contrast to multiple regressions on only P and P2, also explained the nonlinearity in the extremes.
Figure 2.—
Expected (MC) and predicted breeding values 
(A) and 
(B) based on a single phenotype as a function of phenotype using the full model with multiple regression on P, P2, and P3 (MR3) or the reduced model with multiple regression on P and P2 (MR2) (
; 
; 
; 
; 
).
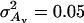Figure 2B shows that the relationship between 
and P is highly curvilinear for 
, with higher 
for more extreme P. As for 
, the predicted 
using the full model with multiple regressions on P, P2, and P3 fitted well to the expectation from Monte Carlo simulation (
). The use of only P and P2 was adequate only within 2 SD of the mean, but was biased for extreme P.
Response to mass selection:
Response to selection (
) is predicted as 
, where b is the regression coefficient of the breeding value on the selection criterion, and S is the selection differential in units of the selection criterion (e.g., phenotype) (Falconer and Mackay 1996). With homogenous environmental variance and directional mass selection, 
and 
, where i is the selection intensity, and 
is the breeders' equation (Falconer and Mackay 1996; Lynch and Walsh 1998). With genetic heterogeneity of environmental variance, directional mass selection leads to responses in mean and variance (Hill and Zhang 2004). To predict this, Equation 2 can be rewritten as 
, giving
 |
(3) |
where 
, 
, and 
are the respective means for the selected animals.
Directional selection:
With directional selection by truncation, 
, where 
for normally distributed observations, z is the height of the standardized normal at the truncation point x, and p is the selected proportion (Falconer and Mackay 1996; Lynch and Walsh 1998). 
and 
were calculated by integration assuming that P is normally distributed, which is approximately the case for observed values of 
in the literature:
 |
(4a) |
 |
(4b) |
The predicted response to directional mass selection is thus
 |
(5) |
The term 
is similar to the term 
derived by Hill and Zhang (2004), who calculated the probability of selection by using a Taylor series approximation, where the factor 
appears here in the B-matrix, assuming that 
and 
is small. Equation 5 can be rewritten using the regression coefficients in B and ignoring the terms involving P3, which were not included by Hill and Zhang (2004),
 |
(6) |
 |
(7) |
where 
. When 
and 
are close to zero, Equations 6 and 7 approach 
and 
, which are Equations 10 and 11 of Hill and Zhang (2004). Differences arise when 
is substantially different from zero, as the covariance between P and P2 was ignored by Hill and Zhang.
Stabilizing and disruptive selection:
Stabilizing and disruptive selection can be considered as selecting the animals with low or high P2, respectively (Falconer and Mackay 1996). Assuming that selection is by truncation, selection differentials 
for P2 can be obtained from Equation 4a and selection differentials for P and P3 are zero for these types of selection when P is normally distributed. With stabilizing selection by truncation, animals only in the middle of the distribution are selected, giving a selection differential
 |
(8a) |
where 
and 
are, respectively, the selection intensity and truncation point corresponding to 
, the proportion of animals culled on one side of the distribution. With disruptive selection by truncation, the extreme animals in both tails of the distribution are selected, giving a selection differential
 |
(8b) |
where 
, the proportion of animals selected on one side of the distribution. The standardized selection differentials 
for directional, stabilizing, and disruptive selection are in Table 2.
TABLE 2.
Standardized selection differentials of 
for directional, stabilizing, and disruptive selection by truncation on a normal distribution corrected for the expectation of P2 (= 1) for different selected proportions (p)
| Selected proportion (p)
|
|||||||
|---|---|---|---|---|---|---|---|
| Type of selection | 0.80 | 0.40 | 0.20 | 0.10 | 0.05 | 0.01 | 0.001 |
| Directional | −0.29 | 0.24 | 1.18 | 2.25 | 3.39 | 6.20 | 10.41 |
| Stabilizing | −0.56 | −0.91 | −0.98 | −0.99 | −1.00 | −1.00 | −1.00 |
| Disruptive | 0.24 | 1.18 | 2.25 | 3.39 | 4.58 | 7.45 | 11.70 |
Evaluation of predictions with directional mass selection:
The predictions of Equation 5 [multiple regressions (MR) 3] and Equations 6 and 7 (MR2) and those of the Hill–Zhang (HZ) model (Hill and Zhang 2004) are compared in Table 3 with the observed responses obtained from Monte Carlo (MC) simulation, for different values of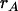 
and selected proportions. Multiple regressions on P, P2, and P3 (MR3) predicted the responses well, with prediction errors <5% when the selected proportion was at least 5% (prediction error relative to 
with 
, 
, 
). Prediction errors were on average smaller for MR3 than for MR2, although occasionally larger. They were also on average slightly smaller for MR2 than for the Hill–Zhang model, especially with 
, because in the latter the covariance between P and P2 was not accounted for in calculation of the regression coefficients. Prediction errors using MR were mainly due to poor prediction of selection differentials because of deviations from normality and thus increased with decreasing selected proportion as the tails of the distribution were most affected (results not shown). When 
increased to 0.10 or 0.15, which reflects the upper range of estimates in the literature (e.g., SanCristobal-Gaudy et al. 2001; Ros et al. 2004), prediction errors increased up to 10–20% (prediction error relative to 
with 
, 
, 
), especially with selected proportion of 1% (results not shown). Increasing 
increases deviations from normality in P, but it seems that the multiple-regression framework is robust against these relatively small deviations from normality, except when the selected proportion is very small. It can be concluded that MR3 is the preferred method for predicting responses in 
and 
with directional mass selection, having prediction errors <5% when at least 5% are selected.
TABLE 3.
Response to directional mass selection in Am (ΔAm) and Av (ΔAv) for different values rA and selected proportions comparing predictions [as prediction errors (predicted minus observed)] with observed responses obtained from Monte Carlo simulation (MC)
 : |
 : |
||||||
|---|---|---|---|---|---|---|---|
| Selected proportion (%)
|
Selected proportion (%)
|
||||||
 |
Method | 20 | 5 | 1 | 20 | 5 | 1 |
| −0.5 | MCa | 0.410 | 0.547 | 0.630 | −0.059 | −0.037 | 0.004 |
| MR3b | 0.004 | 0.025 | 0.049 | 0.001 | 0.002 | 0.016 | |
| MR2b | 0.006 | 0.061 | 0.150 | 0.000 | −0.020 | −0.045 | |
| HZb | −0.026 | −0.032 | −0.020 | 0.003 | −0.004 | −0.013 | |
| 0 | MCa | 0.422 | 0.597 | 0.740 | 0.031 | 0.082 | 0.137 |
| MR3b | 0.002 | 0.002 | −0.011 | −0.004 | −0.003 | 0.007 | |
| MR2b | −0.002 | 0.021 | 0.059 | −0.004 | −0.003 | 0.007 | |
| HZb | −0.002 | 0.021 | 0.059 | −0.002 | 0.003 | 0.018 | |
| 0.5 | MCa | 0.434 | 0.638 | 0.820 | 0.110 | 0.183 | 0.254 |
| MR3b | −0.002 | −0.021 | −0.060 | −0.002 | −0.008 | −0.020 | |
| MR2b | −0.011 | −0.010 | −0.004 | −0.008 | −0.001 | 0.013 | |
| HZb | 0.022 | 0.085 | 0.169 | 0.005 | 0.028 | 0.064 | |
Observed responses obtained from MC simulation: 
; 
; 
; 
.
Predictions: MR3, multiple regressions on P, P2, and P3 (see Equation 5); MR2, multiple regressions on P and P2 (see Equations 6 and 7); HZ, prediction based on Hill and Zhang (2004).
Multiple regression with selection based on a group of relatives
Monte Carlo simulation:
In animal breeding sires are often selected on performance of their half-sib progeny. Monte Carlo simulation was used to investigate relationships between the 
and 
of the sires and statistics on phenotypes of their progeny and then to evaluate the fit of predictions on the basis of multiple regressions. Fifty replicates were generated of 500,000 unrelated sires each with 10 or 100 half-sib progeny or of 50,000 unrelated sires each with 1000 or 10,000 half-sib progeny. Data were simulated according to the genetic model in Equation 1. The breeding values of sires (
and 
) and unrelated random-mated dams (
and 
) were randomly sampled with variance 
or 
, respectively. For each progeny, the Mendelian sampling terms 
and 
were randomly sampled with variance 
and 
, respectively, to give breeding values for each progeny (
and 
):
 |
When the genetic correlation between 
and 
was nonzero, breeding values 
and Mendelian sampling terms 
were sampled given their expected value based on 
or 
and with variance 
or 
, respectively. For each progeny, the environmental effect χ was randomly sampled and scaled with its standard deviation.
Expected breeding values of sires were calculated as the mean 
and 
within successive intervals of 0.01 SD units of progeny mean 
or log-transformed within-family variance [
] and averaged over replicates. Expected genetic selection differentials of directional selection on 
were calculated as the mean 
and 
of all selected sires with 
and averaged over replicates.
Breeding value estimation:
When there is an observation on only a single phenotype, there is no independent information available on the mean and variance of the genotype, although P and P2 provide point estimates. When phenotypes of a group of relatives each having the same relationship to an individual are available (e.g., progeny), statistics such as 
, 
, and 
can be used to predict its 
and 
. Here 
is the mean phenotype and 
is the mean P2 of the relatives, 
is the within-family variance, and n is the number of relatives within the group. With large n, 
becomes the main predictor of 
, but otherwise 
contains additional information because animals with a high 
have a higher probability of having a very high or low 
. This is similar to directional mass selection and the term 
therefore plays an equivalent role to P2. Although the Monte Carlo simulation was based on sires with half-sib progeny, the prediction of breeding values generalizes to any group of relatives with the same relationship. The multiple-regression equation can be represented as
 |
(9) |
where 
is the additive genetic relationship between relatives within the family,
 |
 |
and 
is the relationship of relatives to individual j. Elements in the P- and G-matrices, derived in appendix a, were verified with Monte Carlo simulation for the case of sires with half-sib progeny.
Log-transformation of var W:
In multiple regression linearity is assumed and is typically satisfied if the explanatory variables are normally distributed. Because variances of normally distributed variates are 
- distributed, the distribution of 
is not normal. As the number of relatives increases, 
approaches a normal distribution, but the convergence is slow (Stuart and Ord 1994). The relationship between 
and 
is therefore nonlinear if there are a finite number of relatives (see Figure 3B), and also the sampling variance of 
increases with its mean. A logarithmic transformation of 
seems a logical choice to reduce both the nonnormality of 
and the positive relationship between the mean and its sampling variance. When using 
instead of 
, the elements in the P- and G-matrices involving 
were transformed using a first-order Taylor series approximation (Lynch and Walsh 1998). The matrices 
and 
involving 
were calculated, respectively, as 
and 
, where 
with 
based on a first-order Taylor series approximation. The quantity 
was calculated using a second-order Taylor series approximation (Lynch and Walsh 1998): 
, replacing 
in Equation 9.
Figure 3.—
Expected (MC) and predicted 
as a function of the standardized mean phenotype of half-sib progeny (A) and expected and predicted 
as a function of 
(B) using either 
(MR linear) or 
(MR log) in multiple regression (
; 
; 
; 
; 
; number of half-sib progeny/sire = 100).
Evaluation of predictions:
Predictions of Equation 9, which holds for any group of relatives with the same relationship, were evaluated for the case of sires with half-sib progeny. The expected and predicted values of 
are shown as a function of the standardized 
of 100 half-sib progeny in Figure 3A for 
. 
is linear in standardized 
with a slope of 
. The predicted 
fitted well the expectation from Monte Carlo simulation (
) and the predictions using 
or 
did not differ if 
.
Figure 3B shows that the relationship between 
and 
is curvilinear for the case of 100 half-sib progeny when 
. The predicted 
using untransformed 
(MR linear) overestimated 
for extreme values of 
, whereas predicted 
using log-transformed 
(MR log) was curvilinear in 
and fitted well the expectation from Monte Carlo simulation (
).
As the bias in 
was largest with extreme values of 
, the bias in 
at 2 SD from the mean 
predicted by multiple regression using either 
or 
was computed for different values of 
and numbers of progeny per sire (Table 4). Multiple regression on 
was seen to overestimate, but on 
to underestimate, 
. The bias using 
was negligible when the number of progeny was 100, but increased when the number of progeny was small (10) or large (10,000). The bias with 
was negligible with 10,000 progeny, as could be expected from the slow convergence of a 
-distribution to a normal distribution, and was small with a few progeny. Note that a higher degree of symmetry between the expected 
at −2 and 2 SD of the mean 
corresponded with a smaller bias in 
with 
. The value of log-transformation of 
thus depends on the number of progeny per sire.
TABLE 4.
The expectation of Av and bias in Âv at 
using either var W or ln(var W) in multiple regression for different values of 
and numbers of half-sib progeny per sire
χ (=  )
|
|||||||
|---|---|---|---|---|---|---|---|
Bias in  ( )
| |||||||
|
|
|
|||||
 |
No. of progeny | −2 | 2 | −2 | 2 | −2 | 2 |
| 0.01 | 10 | −0.016 | 0.032 | −0.001 | 0.000 | 0.007 | 0.009 |
| 100 | −0.066 | 0.076 | −0.004 | −0.003 | 0.004 | 0.005 | |
| 1,000 | −0.155 | 0.155 | −0.009 | −0.007 | −0.001 | 0.001 | |
| 10,000 | −0.187 | 0.198 | −0.001 | −0.004 | 0.007 | 0.004 | |
| 0.05 | 10 | −0.084 | 0.133 | −0.011 | −0.018 | 0.024 | 0.025 |
| 100 | −0.286 | 0.283 | −0.042 | −0.042 | −0.003 | 0.000 | |
| 1,000 | −0.392 | 0.436 | −0.014 | −0.023 | 0.025 | 0.018 | |
| 10,000 | −0.407 | 0.484 | −0.002 | −0.002 | 0.037 | 0.040 | |
| 0.10 | 10 | −0.173 | 0.234 | −0.039 | −0.054 | 0.030 | 0.031 |
| 100 | −0.467 | 0.475 | −0.072 | −0.081 | 0.005 | 0.004 | |
| 1,000 | −0.556 | 0.658 | −0.025 | −0.035 | 0.053 | 0.049 | |
| 10,000 | −0.569 | 0.710 | −0.017 | −0.004 | 0.060 | 0.080 | |
; 
; 
; 
.
Response to directional selection on family mean:
With the common procedure in livestock breeding to directionally select animals by truncation on the mean (
) of relatives, e.g., progeny, information on the within-family variance (
) is ignored. As for mass selection, if there is genetic heterogeneity of environmental variance, animals with a higher 
would have a higher probability of selection when the selected proportion is <50%, diminishing as the number of relatives increases. If 
and 
are uncorrelated, the response in 
is proportional to the selection differential 
,
 |
(10) |
where
 |
(11) |
There is therefore no selection pressure on 
with an infinite number of relatives (Equation 11), as suggested by Hill and Zhang (2004) using a different argument.
Response in 
and 
with selection on 
can be generalized as
 |
(12) |
To compute (12), 
was not included in the information vector x because selection is solely on 
. For infinitely many relatives, Equation 12 can be rewritten as 
, which is the corresponding standard breeders' equation, and 
, showing that response in 
then becomes solely a correlated response to selection on 
.
Evaluation of predictions:
Table 5 shows predicted responses (Equation 12) in 
and 
when selecting on the mean of half-sib progeny (
) in comparison to observed responses from Monte Carlo simulation. In general, these agreed well, although prediction errors were slightly higher when 
, especially with high selection intensity. As expected, the response in 
increased with more progeny (higher accuracy of selection) and lower selected proportion (higher selection intensity). The response in 
was small, becoming negligible with 100 progeny/sire when 
, but was, however, substantial when 
, basically as a correlated response to selection on the mean. Response in 
increased nonlinearly with increasing selection intensity, similar to directional mass selection, but to a lesser extent. In conclusion, responses in 
and 
to selection on 
can be predicted accurately using multiple regression.
TABLE 5.
Response to selection on mean of half-sib progeny (
) in Am (ΔAm) and Av (ΔAv) for different values of rA, different numbers of progeny/sire, and different selected proportions comparing predictions (MR) [as prediction errors (predicted minus observed)] with observed responses obtained from Monte Carlo simulation (MC)
 : |
 : |
|||||||
|---|---|---|---|---|---|---|---|---|
| Selected proportion (%)
|
Selected proportion (%)
|
|||||||
 |
No. of progeny | Method | 20 | 5 | 1 | 20 | 5 | 1 |
| −0.5 | 10 | MC | 0.517 | 0.759 | 0.976 | −0.099 | −0.134 | −0.160 |
| MR | 0.005 | 0.021 | 0.044 | −0.001 | −0.005 | −0.012 | ||
| 100 | MC | 0.724 | 1.071 | 1.386 | −0.146 | −0.215 | −0.275 | |
| MR | 0.003 | 0.006 | 0.011 | −0.001 | −0.001 | −0.003 | ||
| 0 | 10 | MC | 0.513 | 0.752 | 0.968 | 0.009 | 0.025 | 0.045 |
| MR | 0.000 | 0.004 | 0.009 | 0.000 | 0.000 | 0.001 | ||
| 100 | MC | 0.723 | 1.068 | 1.379 | 0.002 | 0.005 | 0.009 | |
| MR | 0.000 | −0.002 | −0.002 | 0.000 | 0.000 | 0.000 | ||
| 0.5 | 10 | MC | 0.512 | 0.749 | 0.963 | 0.111 | 0.171 | 0.227 |
| MR | −0.006 | −0.015 | −0.026 | −0.002 | −0.003 | −0.003 | ||
| 100 | MC | 0.721 | 1.061 | 1.368 | 0.149 | 0.220 | 0.286 | |
| MR | −0.002 | −0.005 | −0.010 | 0.000 | −0.001 | −0.002 | ||
; 
; 
; 
.
Defining a measure of heritability for environmental variance at the phenotypic level
Heritability (
) is a central parameter in quantitative genetics (Falconer and Mackay 1996; Lynch and Walsh 1998). For standardization of results of analysis of genetic heterogeneity of environmental heterogeneity in field data and for making comparisons to “conventional” traits easier, it would be helpful to define a measure of heritability (
) for environmental variance at the phenotypic level. Heritability equals the regression coefficient of the breeding value A on the phenotype P. Here we propose a definition of 
, which equals the genetic variance in environmental variance as a proportion of the variance of P2. This definition is equal to the regression of 
on P2, where 
and 
, and 
is therefore
 |
(13) |
Alternatively, 
could be defined at the level of environmental variance, which equals one in Equation 1. On the basis of single phenotypic records, the environmental variance of a genotype is, however, not estimable. The measure of heritability in Equation 13 is directly related to single squared phenotypic records and as such is the natural analogy of the classical heritability of the mean (
), which can be used in prediction of response to mass selection when 
.
Under the assumption of 
and making use of Equation 13, Equation 9 can be greatly simplified when selecting on information of a group of relatives, for example, half-sib progeny. When 
, 
reduces to 
because 
, so the multiple regression for 
can be simplified by regressing solely on 
. The accuracy of 
can then be derived as
 |
(14) |
where 
and 
are columns of B and G corresponding to 
. The resulting expression is exactly the same as that for accuracy of 
(Cameron 1997), except that h2 is replaced by 
. To investigate the effect of assuming 
, the accuracy of 
predicted with Equation 14 was compared to that predicted using Equation 9 and Monte Carlo simulation when 
(Table 6). In general, accuracies were slightly underestimated by Equation 14, increasingly so with greater 
(
), whereas the ones of Equation 9 were close to those from simulation. It seems that 
can be used as a first approximation in standard prediction equations when 
, but predictions should be interpreted with caution.
TABLE 6.
Realized (MC) and predicted accuracy of Âv for different numbers of half-sib progeny per sire and 
using either the exact prediction (MR exact) or the approximate prediction (MR approx)
| No. of progeny
|
||||||
|---|---|---|---|---|---|---|
| 10
|
100
|
|||||
 |
MC | MR exact | MR approx | MC | MR exact | MR approx |
Accuracy 
| ||||||
| 0 | 0.235 | 0.235 | 0.235 | 0.607 | 0.607 | 0.607 |
| 0.1 | 0.236 | 0.236 | 0.235 | 0.615 | 0.615 | 0.607 |
| 0.3 | 0.243 | 0.244 | 0.235 | 0.633 | 0.633 | 0.607 |
| 0.6 | 0.251 | 0.260 | 0.235 | 0.648 | 0.663 | 0.607 |
The exact prediction with multiple regression: 
, where 
and 
are columns of B and G. The approximate prediction (Equation 14): 
, where 
and with assumption 
. 
; 
; 
; 
.
EXAMPLES OF CHANGING ENVIRONMENTAL VARIANCE BY SELECTION
In the previous section the focus was mainly on evaluating the goodness of fit of multiple-regression predictions with Monte Carlo simulation, but the results also show the effects of selection on environmental variance. For example, the response in 
with directional mass selection increased nonlinearly with increasing selection intensity (Table 3), and environmental variance increased unless 
. The response in 
was, however, negligible with directional selection on a half-sib progeny mean when 
(Table 5), but was substantial when 
, due to a correlated response.
We now use the formulas (Equations 2, 3, and 9) to assess the effects of selection strategies aimed at changing the environmental variance, taking values of 
between 0.01 and 0.10. These correspond to a low 
but are large relative to 
, indicating a genetic coefficient of variation between 14 and 45%, higher than that for standard quantitative traits (Houle 1992). As expected, the accuracy of 
increased with 
(Table 7). The accuracy was low when using information only on own phenotype or a small number of progeny, but increased with number of relatives, especially with half-sib progeny, and when 
. With 1000 half-sib progeny, the accuracy was >0.90, unless 
.
TABLE 7.
Predicted accuracy of Âv based on a single phenotype or different numbers of full-sibs or half-sib progeny for different values of 
and rA
 : |
 : |
||||||
|---|---|---|---|---|---|---|---|
|
|
||||||
| Information | No. of progeny | 0.01 | 0.05 | 0.10 | 0.01 | 0.05 | 0.10 |
Predicted accuracy 
|
|||||||
| Phenotype | — | 0.070 | 0.152 | 0.209 | 0.279 | 0.299 | 0.319 |
| Full-sibs | 10 | 0.123 | 0.252 | 0.327 | 0.299 | 0.348 | 0.388 |
| 50 | 0.267 | 0.468 | 0.544 | 0.394 | 0.505 | 0.560 | |
| 100 | 0.355 | 0.553 | 0.610 | 0.442 | 0.570 | 0.617 | |
| Half-sib | 10 | 0.115 | 0.244 | 0.325 | 0.346 | 0.386 | 0.424 |
| Progeny | 50 | 0.257 | 0.499 | 0.618 | 0.490 | 0.597 | 0.671 |
| 100 | 0.353 | 0.633 | 0.745 | 0.545 | 0.693 | 0.772 | |
| 1000 | 0.768 | 0.933 | 0.962 | 0.798 | 0.936 | 0.963 | |
; 
; 
.
Table 8 shows the predicted response in 
for directional, stabilizing, and disruptive selection based on phenotype (Equation 3, selection differentials from Table 2, neglecting the terms involving P3) and for directional downward selection on 
based on 100 half-sib progeny assuming 
[calculated as 
, where 
). Predictions were close to observed responses in Monte Carlo simulation. For all selection strategies, responses in 
increased with 
due to a higher accuracy and a higher genetic variance in itself.
TABLE 8.
Predicted response in Av (ΔAv) for directional (up/down), stabilizing, and disruptive selection based on phenotype and downward directional selection on 
based on 100 half-sib progeny for different values of 
and selected proportions
 : |
|||||
|---|---|---|---|---|---|
| |||||
| Selection criterion | Selection type | Selected proportion | 0.010 | 0.050 | 0.100 |
| Phenotype | Directional | 0.20 | 0.006 | 0.027 | 0.051 |
| 0.10 | 0.011 | 0.052 | 0.098 | ||
| 0.05 | 0.017 | 0.079 | 0.148 | ||
| 0.01 | 0.031 | 0.144 | 0.270 | ||
| Stabilizing | 0.20 | −0.005 | −0.023 | −0.043 | |
| 0.10 | −0.005 | −0.023 | −0.043 | ||
| 0.05 | −0.005 | −0.023 | −0.043 | ||
| 0.01 | −0.005 | −0.023 | −0.043 | ||
| Disruptive | 0.20 | 0.011 | 0.052 | 0.098 | |
| 0.10 | 0.017 | 0.079 | 0.148 | ||
| 0.05 | 0.023 | 0.107 | 0.199 | ||
| 0.01 | 0.037 | 0.173 | 0.324 | ||
 progeny |
Directional down | 0.20 | −0.049 | −0.198 | −0.330 |
| 0.10 | −0.062 | −0.249 | −0.413 | ||
| 0.05 | −0.073 | −0.292 | −0.486 | ||
| 0.01 | −0.094 | −0.377 | −0.628 | ||
; 
; 
; 
, equal selection differentials in both sexes.
With directional and disruptive selection on phenotype, the predicted response in 
was positive and environmental variance increased substantially and nonlinearly with selection intensity. Disruptive selection gave a slightly larger response because the selection intensity in each tail of the distribution of P was higher. With stabilizing selection on phenotype, the response in 
was negative but small, even when the selection was intense because selection differentials remain small and were nearly constant (Table 2). With directional downward selection on 
based on 100 half-sib progeny, response in 
was negative and environmental variance decreased substantially, which in an agricultural context would imply increased uniformity of end product. Responses increased linearly with selection intensity and became large, especially with 
. When the best 5% of the sires are selected on 
and dams are selected at random with 
, the environmental variance would be 0.554 in the next generation, which is only 79.1% of that in the current generation! In conclusion, a large number of progeny is necessary to predict 
with high accuracy, but responses in 
can be large relative to the environmental variance in the current generation.
DISCUSSION
A multiple-regression framework has been developed to predict breeding values and selection responses in mean and variance for mass selection and selection between families in the presence of genetic heterogeneity of environmental variance. The model of Hill and Zhang (2004) has been refined for directional mass selection and extended to stabilizing and disruptive selection based on phenotype and to between-family selection. The phenotypic variance increases nonlinearly with selection intensity under directional mass selection when 
. It increases even more with disruptive selection, but decreases only slightly with stabilizing selection, which is in agreement with results of Gavrilets and Hastings (1994) and Wagner et al. (1997). With selection on family mean, phenotypic variance is expected to change little unless 
, but with selection on within-family variance, response in phenotypic variance may be large providing 
, even though a large number of relatives is necessary to estimate 
accurately.
Methodology:
Comparison of genetic models:
Different genetic models to account for genetic heterogeneity of environmental variance appear in the literature, basically either additive effects both at the level of the mean and at the level of the environmental variance (Hill and Zhang 2004; Zhang and Hill 2005; this study) or additive effects on the mean and an exponential model for the environmental variance (SanCristobal-Gaudy et al. 1998, 2001; Sorensen and Waagepetersen 2003; Ros et al. 2004). In the exponential model
 |
(15) |
where 
is the environmental variance when 
, and 
is the individual's breeding value for environmental variance in the exponential model, such that environmental variances are multiplicative on the observed scale and additive on a log-scale. (Note that 
in the notation of SanCristobal-Gaudy et al. 1998.) The distribution of true variances (not variance estimates) is unknown in practice and cannot help in guiding whether the additive model or the exponential model better reflects the real world. Clearly, each model has specific (dis)advantages. The exponential model has tractable properties so it is easier to use in data analysis; for example, the environmental variance can never become negative, whereas in the additive model the term 
is defined only when 
. The additive model, however, fits nicely in quantitative genetic theory, leading to better properties for deterministic predictions of selection response. A disadvantage of the exponential model is that the average environmental variance in the population is 
, so there is no full separation of the mean environmental variance and the genetic variance in environmental variance, and 
has to be known to interpret 
.
Fortunately, the models are sufficiently similar that their genetic parameters can be interconverted. The breeding values for environmental variance can be converted by equating the expectations of the second central moments of the environmental effects (see appendix b):
 |
(16) |
[a first-order Taylor series approximation of Equation 16 is 
, illustrating the factor 
between breeding values and the correction for the difference between 
and 
]. The genetic variances can be converted by equating the fourth central moments of the environmental effects:
 |
(17) |
(a first-order Taylor series approximation of Equation 17 is 
, showing a factor 
between genetic variances and a correction for the difference between 
and 
). Thus results obtained using the exponential model in data analysis could be converted using Equations 16 and 17 to the additive model and the deterministic equations derived in this study used to predict selection responses. Gavrilets and Hastings (1994) and Wagner et al. (1997) adopted slightly different multiplicative models to deal with genetic heterogeneity of environmental variance, but these are in essence very similar to the exponential model.
Multiple-regression framework:
In this study, a multiple-regression framework was used to predict breeding values and selection responses. Prediction equations were derived for incorporating phenotypic information of only one type, individual or family statistics, but the method can easily be extended to situations where phenotypic information is available from different kinds of relatives. For the common situation of optimal weighting of own performance and family information, most of the necessary elements in the prediction equation either have been derived here or can be derived straightforwardly using the same methods. Furthermore, the regression structure enables prediction of responses in mean and variance with different selection strategies using the classical selection index theory and extension to give optimal changes in mean and variance via a selection index (Hazel 1943). The framework presented can be used only for prediction of selection response after one generation of selection; due to buildup of gametic phase disequilibrium, genetic variance would decrease with directional selection, lowering selection responses (Bulmer 1971). Furthermore, gametic phase disequilibrium induces an unfavorable covariance between the additive genetic effects for mean and environmental variance, counteracting desired changes in mean and variance (Hill and Zhang 2004). Inclusion of the Bulmer effect was beyond the scope of this article, but could be implemented (Hill and Zhang 2004, 2005).
In the multiple-regression framework fixed effects are assumed to be known without error, but in practice they are estimated from the data, thereby reducing accuracy and selection response. Therefore, results in this study should be interpreted using an effective number of observations, which is lower than the actual number of observations. To predict breeding values in the presence of fixed effects on mean (e.g., herd effect) and variance (e.g., heterogeneity of variance between herds, environments with different stress levels), a model with genetically structured environmental variance can be used (SanCristobal-Gaudy et al. 1998; Sorensen and Waagepetersen 2003). Modeling of environmental heterogeneity of variance (e.g., between herds) has been reviewed by Foulley and Quaas (1995) and Hill (2004). To predict selection responses with genetic heterogeneity of environmental variance in environments differing in mean environmental variance (e.g., herds, stress levels), the present framework can be used by adjusting 
.
A disadvantage of the multiple-regression framework is that it relies on the assumption that the explanatory variables (x) are linearly related to the dependent variables (y), which is ensured when x and y are bivariate normally distributed. As a consequence, results may not be robust against deviations from normality, particularly when higher-order terms such as P3 are included in predictions. The multiple-regression framework was, however, robust against small deviations from normality induced by genetic heterogeneity of environmental variance. SanCristobal-Gaudy et al. (1998) and Sorensen and Waagepetersen (2003) also assumed multivariate normality in predictions of selection responses, but their approaches were more flexible in allowing for other distributions. Their approaches were not very different from those in this study, but some expressions were much more complex due to the use of the exponential model.
Multiple-regression methods would be useful to study the evolution of phenotypic variance in natural populations, to further develop analyses of Zhang and Hill (2005). Selection for reduced environmental variance could result in environmental canalization, a phenomenon of long-standing interest (e.g., Waddington 1942, 1960; reviews in Scharloo 1991, Debat and David 2001, and Flatt 2005). On the basis of our predictions, stabilizing selection cannot cause environmental canalization of traits within a few generations, but may do so eventually. With long-term canalizing selection, the question arises whether the limit of environmental variance is zero, whereas most quantitative traits in nature under stabilizing selection still exhibit environmental variance (e.g., Wagner et al. 1997). We know little about how levels of environmental variation are determined and maintained in nature in the face of stabilizing selection. Different mechanisms have been proposed (e.g., Wagner et al. 1997), such as introducing a cost for homogeneity or canalization (Zhang and Hill 2005). To further investigate long-term effects of natural selection on environmental variance, the current framework can be extended to include the effects of gametic phase disequilibrium, inbreeding, and mutation, analogous to effects of selection on the mean of traits.
Evidence for genetic heterogeneity of environmental variance:
Although the tools for evaluating breeding strategies to change the mean and the size of environmental variance are now available, the whole exercise would just be a theoretical game if 
. As reviewed in the Introduction, there is empirical evidence that genotypes differ in environmental variance, but it is not abundant. To compare results of different studies analyzing field data we use Equation 17, because some are based on the exponential genetic model (SanCristobal-Gaudy et al. 1998, 2001; Sorensen and Waagepetersen 2003; Ros et al. 2004) and some on the additive genetic model (Rowe et al. 2006). The measure of heritability (
) developed in this study (Equation 13) and the genetic coefficient of variation for environmental variance 
, denoted “evolvability” (Houle 1992), are used to compare results from different studies (Table 9). Heritabilities of environmental variance were low, in the range 0.02–0.05 as used in this study, and GCVE's were large, in the range of 0.30–0.58 (excluding 0). Note that 
is close to 
. The low values of 
show that a large amount of information is necessary to estimate 
accurately, but the high values of 
show that there is substantial opportunity for genetic change.
TABLE 9.
Comparison of literature estimates of genetic variance in environmental variance
| Source | Trait |  |
 b
|
 c
|
 d
|
|---|---|---|---|---|---|
| SanCristobal-Gaudy et al. (1998) | Fat/protein goat milk | 0.000 | 0.000 | 0.000 | 0.000 |
| pH pig | 0.150 | 1.2E-04 | 0.039 | 0.402 | |
| SanCristobal-Gaudy et al. (2001) | Litter size sheep | 0.230 | 0.057 | 0.048 | 0.509 |
| Sorensen and Waagepetersen (2003)a | Litter size pigs | 0.090 | 4.291 | 0.026 | 0.307 |
| Ros et al. (2004)a | Body weight (g) snails | 0.290 | 0.368 | 0.017 | 0.580 |
| Rowe et al. (2006) | Body weight (kg) broiler ♂ | 0.086 | 8460 | 0.029 | 0.299 |
| Body weight (kg) broiler ♀ | 0.096 | 5310 | 0.031 | 0.318 |
Models included permanent environmental variance; environmental variance was taken from their model 1 estimates.
Equation 17: 
.
= heritability of environmental variance.
, a measure of evolvability (Houle 1992).
Other evidence of the existence of genetic heterogeneity of environmental variance can come from selection experiments. With genetic heterogeneity of environmental variance, environmental variance would decrease with stabilizing selection and increase with disruptive selection. In most studies (e.g., Rendel et al. 1966; Cardin and Minvielle 1986), however, only changes in phenotypic variance are reported, which are not separated into changes in genetic and environmental variance. Interpretation of any selection experiment is complicated by possible changes in genetic variance due to gene frequency change, which cannot be predicted from simple base population parameters. Under infinitesimal model assumptions, effects of gene frequency change can be ignored and those due to gametic phase disequilibrium can be predicted. Due to negative gametic phase disequilibrium, genetic variance is expected to decrease with stabilizing selection and increase with disruptive selection (Bulmer 1971). In agreement with this expectation, Kaufman et al. (1977) found substantial decreases in genetic and environmental variance with stabilizing selection in T. castaneum and Scharloo et al. (1972) observed substantial increases in genetic and environmental variance with disruptive selection in D. melanogaster, indicating a substantial genetic variance in environmental variance. Sorensen and Hill (1983), however, found large increases only in genetic variance with disruptive selection in D. melanogaster.
Even though some studies analyzing field data or selection experiments show existence of genetic heterogeneity of environmental variance, it could still be due to statistical artifacts, e.g., due to confounding genetic and environmental effects on variance or violation of the infinitesimal model assumption. If genetic heterogeneity of environmental variance is a truly biological phenomenon, it could be due to scaling, genetic variance in environmental sensitivity, or a combination of both. Traits seem to have a rather constant CV, even when the mean changes dramatically due to selection (Hill and Bünger 2004). A constant CV would require a correlation of unity between mean and standard deviation, which has not been found in analysis of field data (Sorensen and Waagepetersen 2003; Ros et al. 2004; Rowe et al. 2006). Genetic heterogeneity of environmental variance can arise from genetic differences in environmental sensitivity (Falconer and Mackay 1996; Lynch and Walsh 1998). When genotypes perform under variable environmental conditions, which are unknown to the researcher, genetic differences in response to environmental conditions may be observed as genetic heterogeneity of environmental variance.
Genetic heterogeneity of environmental variance is a complicated phenomenon and there is not yet abundant evidence of its existence. The results in this study may help in understanding the consequences of genetic heterogeneity of environmental variance on phenotypes and the methods can help in designing selection experiments and in evaluating breeding strategies or the effects of natural selection that change both the mean and the variance. Genetic heterogeneity of environmental variance may indeed be exploited to breed more “robust” or “stable” genotypes.
Acknowledgments
H.M. thanks Johan van Arendonk, Bart Ducro, and Roel Veerkamp for valuable comments on earlier versions of the manuscript. We thank Ian White for statistical advice. European Animal Disease Genomics Network of Excellence for Animal Health and Food Safety is acknowledged for financial support to a visit of H.M. to Edinburgh and the Biotechnology and Biological Sciences Research Council for research support to W.G.H.
APPENDIX A: DERIVATION OF ELEMENTS IN THE P- AND G-MATRICES
Selection on a single phenotype:
The elements in the P- and G-matrices were derived as follows, using the Roman E to denote expectation and the italic E to denote the environmental deviation 
and noting that 
:
 |
 |
Similarly 
, 
, and 
.
Selection based on a group of relatives:
 |
 |
 |
 |
 |
 |
 |
 |
 |
where k, l, m, and n are different relatives within the family.
 |
 |
 |
and similarly 
, 
, and 
.
APPENDIX B: SIMILARITIES BETWEEN EXPONENTIAL AND ADDITIVE GENETIC MODELS
The breeding values for environmental variance were converted from the exponential model (Equation 15) to the additive model (Equation 1) by equating the second central moments of the environmental effects of both models resulting in Equation 16:
 |
The genetic variance in environmental variance was converted from the exponential model to the additive model by equating the fourth central moments of the environmental effects of both models resulting in Equation 17 (e.g., Stuart and Ord 1994):
 |
References
- Bulmer, M. G., 1971. The effect of selection on genetic variability. Am. Nat. 105: 201–211. [Google Scholar]
- Cameron, N. D., 1997. Selection Indices and Prediction of Genetic Merit in Animal Breeding. CAB International, Wallingford, UK.
- Cardin, S., and F. Minvielle, 1986. Selection on phenotypic variation of pupa weight in Tribolium castaneum. Can. J. Genet. Cytol. 28: 856–861. [Google Scholar]
- Clay, J. S., W. E. Vinson and J. M. White, 1979. Heterogeneity of daughter variances of sires for milk yield. J. Dairy Sci. 62: 985–989. [Google Scholar]
- Debat, V., and P. David, 2001. Mapping phenotypes: canalization, plasticity and developmental stability. Trends Ecol. Evol. 16: 555–561. [Google Scholar]
- Falconer, D. S., and T. F. C. Mackay, 1996. Introduction to Quantitative Genetics. Pearson Education Limited, Essex, UK.
- Falconer, D. S., and A. Robertson, 1956. Selection for environmental variability of body size in mice. Z. Indukt. Abstammungs-Vererbungsl. 87: 385–391. [DOI] [PubMed] [Google Scholar]
- Flatt, T., 2005. The evolutionary genetics of canalization. Q. Rev. Biol. 80: 287–316. [DOI] [PubMed] [Google Scholar]
- Foulley, F. L., and R. L. Quaas, 1995. Heterogeneous variances in Gaussian linear mixed models. Genet. Sel. Evol. 27: 211–228. [Google Scholar]
- Gavrilets, S., and A. Hastings, 1994. A quantitative-genetic model for selection on developmental noise. Evolution 48: 1478–1486. [DOI] [PubMed] [Google Scholar]
- Hazel, L. N., 1943. The genetic basis for constructing selection indexes. Genetics 28: 476–490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henderson, C. R., 1984. Applications of Linear Models in Animal Breeding. University of Guelph, Guelph, Ontario, Canada.
- Hill, W. G., 2004. Heterogeneity of genetic and environmental variance of quantitative traits. J. Ind. Soc. Agric. Stat. 57: 49–63. [Google Scholar]
- Hill, W. G., and L. Bünger, 2004. Inferences on the genetics of quantitative traits from long-term selection in laboratory and domestic animals. Plant Breed. Rev. 24(2): 169–210. [Google Scholar]
- Hill, W. G., and X. S. Zhang, 2004. Effects of phenotypic variability of directional selection arising through genetic differences in residual variability. Genet. Res. 83: 121–132. [DOI] [PubMed] [Google Scholar]
- Hill, W. G., and X. S. Zhang, 2005 Erratum Hill and Zhang (2004). Genet. Res. 86: 160. [Google Scholar]
- Hohenboken, W. D., 1985. The manipulation of variation in quantitative traits: a review of possible genetic strategies. J. Anim. Sci. 60: 101–110. [Google Scholar]
- Houle, D., 1992. Comparing evolvability and variability of quantitative traits. Genetics 130: 195–204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufman, P. K., F. D. Enfield and R. E. Comstock, 1977. Stabilizing selection for pupa weight in Tribolium castaneum. Genetics 87: 327–341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch, M., and B. Walsh, 1998. Genetics and Analysis of Quantitative Traits. Sinauer Associates, Sunderland, MA.
- Mackay, T. F. C., and R. F. Lyman, 2005. Drosophila bristles and the nature of quantitative genetic variation. Philos. Trans. R. Soc. B. 360: 1513–1527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rendel, J. M., B. L. Sheldon and D. E. Finlay, 1966. Selection for canalization of the scute phenotype. II. Am. Nat. 100: 13–31. [Google Scholar]
- Robertson, F. W., and E. C. R. Reeve, 1952. Heterozygosity, environmental variation and heterosis. Nature 170: 286. [DOI] [PubMed] [Google Scholar]
- Ros, M., D. Sorensen, R. Waagepetersen, M. Dupont-Nivet, M. SanCristobal et al., 2004. Evidence for genetic control of adult weight plasticity in the snail helix aspersa. Genetics 168: 2089–2097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rowe, S. J., I. M. S. White, S. Avendano and W. G. Hill, 2006. Genetic heterogeneity of residual variance in broiler chickens. Genet. Sel. Evol. 38: 617–635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- SanCristobal-Gaudy, M., J. M. Elsen, L. Bodin and C. Chevalet, 1998. Prediction of the response to a selection for canalisation of a continuous trait in animal breeding. Genet. Sel. Evol. 30: 423–451. [Google Scholar]
- SanCristobal-Gaudy, M., L. Bodin, J. M. Elsen and C. Chevalet, 2001. Genetic components of litter size variability in sheep. Genet. Sel. Evol. 33: 249–271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scharloo, W., 1991. Canalization: genetic and developmental aspects. Annu. Rev. Ecol. Syst. 22: 65–93. [Google Scholar]
- Scharloo, W., A. Zweep, K. A. Schuitema and J. G. Wijnstra, 1972. Stabilizing and disruptive selection on a mutant character in Drosophila. IV. Selection on sensitivity to temperature. Genetics 71: 551–566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sorensen, D., and R. Waagepetersen, 2003. Normal linear models with genetically structured residual variance heterogeneity: a case study. Genet. Res. 82: 207–222. [DOI] [PubMed] [Google Scholar]
- Sorensen, D. A., and W. G. Hill, 1983. Effects of disruptive selection on genetic variance. Theor. Appl. Genet. 65: 173–180. [DOI] [PubMed] [Google Scholar]
- Stuart, A., and J. K. Ord, 1994. Kendall's Advanced Theory of Statistics: Distribution Theory. Arnold, London.
- Van Vleck, L. D., 1968. Variation of milk records within paternal-sib groups. J. Dairy Sci. 51: 1465–1470. [Google Scholar]
- Waddington, C. H., 1942. Canalization of development and the inheritance of acquired characters. Nature 150: 563–565. [Google Scholar]
- Waddington, C. H., 1960. Experiments on canalizing selection. Genet. Res. 1: 140–150. [Google Scholar]
- Wagner, G. P., G. Booth and H. Bagheri-Chaichian, 1997. A population genetic theory of canalization. Evolution 51: 329–347. [DOI] [PubMed] [Google Scholar]
- Zhang, X. S., and W. G. Hill, 2005. Evolution of the environmental component of the phenotypic variance: stabilizing selection in changing environments and the cost of homogeneity. Evolution 59: 1237–1244. [PubMed] [Google Scholar]