Abstract
The kinetics of the dark-adapted salamander rod photocurrent response to flashes producing from 10 to 105 photoisomerizations (Φ) were investigated in normal Ringer's solution, and in a choline solution that clamps calcium near its resting level. For saturating intensities ranging from ∼102 to 104 Φ, the recovery phases of the responses in choline were nearly invariant in form. Responses in Ringer's were similarly invariant for saturating intensities from ∼103 to 104 Φ. In both solutions, recoveries to flashes in these intensity ranges translated on the time axis a constant amount (τc) per e-fold increment in flash intensity, and exhibited exponentially decaying “tail phases” with time constant τc. The difference in recovery half-times for responses in choline and Ringer's to the same saturating flash was 5–7 s. Above ∼104 Φ, recoveries in both solutions were systematically slower, and translation invariance broke down. Theoretical analysis of the translation-invariant responses established that τc must represent the time constant of inactivation of the disc-associated cascade intermediate (R*, G*, or PDE*) having the longest lifetime, and that the cGMP hydrolysis and cGMP-channel activation reactions are such as to conserve this time constant. Theoretical analysis also demonstrated that the 5–7-s shift in recovery half-times between responses in Ringer's and in choline is largely (4–6 s) accounted for by the calcium-dependent activation of guanylyl cyclase, with the residual (1–2 s) likely caused by an effect of calcium on an intermediate with a nondominant time constant. Analytical expressions for the dim-flash response in calcium clamp and Ringer's are derived, and it is shown that the difference in the responses under the two conditions can be accounted for quantitatively by cyclase activation. Application of these expressions yields an estimate of the calcium buffering capacity of the rod at rest of ∼20, much lower than previous estimates.
Keywords: G-protein cascade, signal transduction, photoreceptors, calcium, guanylyl cyclase
introduction
Many G-protein receptor-coupled signal transduction systems comprise a reaction chain linking two or more enzymes; the G-protein cascade of the vertebrate rod is one of the most thoroughly investigated mechanisms of this class. Physiologically realistic models of the rod phototransduction G-protein cascade have been shown to provide quantitative accounts of the activation phases of the photoresponses of rods to flashes over many decades of intensity (Lamb and Pugh, 1992; Pugh and Lamb, 1993; Kraft et al., 1993; Breton et al., 1994; Hood and Birch, 1994; Cideciyan and Jacobson, 1996; Lyubarsky and Pugh, 1996; Smith and Lamb, 1997).
Accounts of the recovery phases of photoresponses have not yet progressed to the same degree as those of activation, despite a wealth of information available about biochemical mechanisms that inactivate or downregulate the different steps of the transduction cascade. Among the reasons for the slower progress in the development of a full account of photoresponse recoveries are the co-occurrence in situ of the various biochemical inactivation mechanisms, the high concentrations of reactants in situ (which cannot be achieved in vitro), and the complexity of the dynamic changes in Ca2+ i that accompany light responses and modulate the inactivation biochemistry.
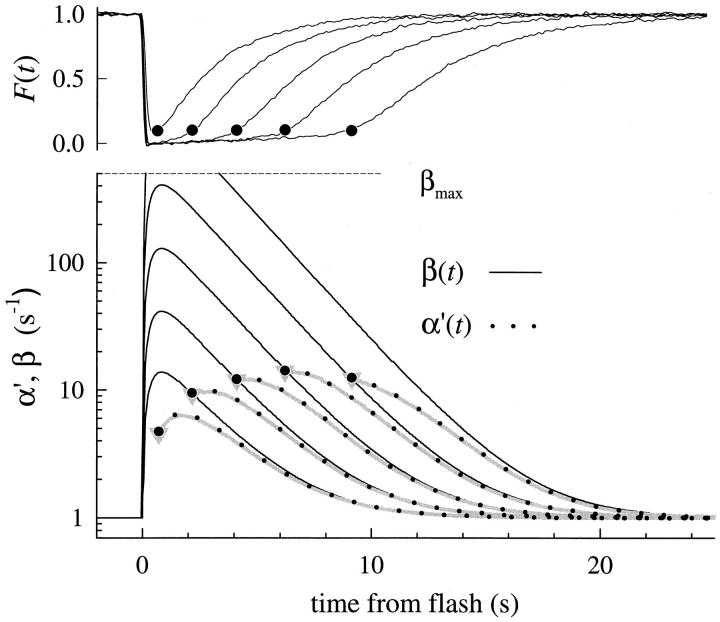
Photoresponse recoveries of intact salamander rods to saturating flashes exhibit a striking kinetic feature that we believe provides a key for unlocking the door to understanding inactivation in situ: over an intensity range that can exceed 100 fold, rod response recoveries to saturating flashes translate on the time axis with a characteristic linear increment (τc) per e-fold increase in flash intensities. Such translatory behavior of photoresponses suggests that recovery is “dominated” by a single biochemical mechanism that inactivates exponentially with the time constant τc (Baylor et al., 1974; Adelson, 1982a , 1982b ; Pepperberg et al., 1992).
In a previous investigation (Lyubarsky et al., 1996), we made an unexpected observation: salamander rod photoresponses to saturating flashes measured under conditions that maintain Ca2+ i near its resting level were delayed in their recovery by a constant amount of time (typically 5–7 s, depending on the individual rod) relative to those measured in Ringer's, over a substantial range of intensity. Thus, the “dominant time constant” (τc) was statistically the same, whether Ca2+ i was clamped to rest, or free to decline to a low level during the period of response saturation. The focus of that previous investigation was on characterizing the method of clamping Ca2+ i, and on measuring τc under Ca2+ i clamp and with Ca2+ i varying freely.
The theoretical goal of this investigation was to provide a rigorous foundation for the concept of a dominant time constant of inactivation, and for interpreting its apparent lack of calcium dependence in the presence of the large effect of declining Ca2+ i on overall recovery time. The empirical goals were to examine response recoveries for obedience to the law that we show to define a dominant time constant, and to analyze the contributions of different mechanisms underlying the speed-up of recoveries in Ringer's relative to those in calcium clamp. To achieve these goals, we have done the following. First, we have examined the complete form of the response recoveries in clamped Ca2+ i and in Ringer's, determining the extent to which the recoveries to saturating flashes are invariant in shape. Previous experimental protocols have precluded an examination of the complete form of the recoveries in clamped Ca2+ i over an adequately wide range of times and intensities. Second, based on the observation that the recoveries are invariant in form for saturating flashes producing up to ∼10,000 photoisomerizations, we derive and illustrate several general theoretical results not previously formalized; these mathematical theorems provide a rigorous basis for interpreting results presented here and elsewhere by others. Third, we quantify the contributions of two non–mutually exclusive explanations of the 5–7-s time shift between recoveries to single saturating flashes in clamped Ca2+ i and Ringer's (see Fig. 1): (a) calcium-dependent guanylyl cyclase activation, as characterized by Hodgkin and Nunn (1988); (b) calcium-dependent gain-control, as described by Lagnado and Baylor (1994), Murnick and Lamb (1996), Gray-Keller and Detwiler (1996), and Matthews (1996, 1997).
Figure 1.
A schematic representation of the rod transduction cascade. Table I identifies the variables and parameters. The notation is that used in previous papers (see for example Pugh and Lamb, 1993; Lyubarsky et al., 1996). The arrows at right point to sites in the cascade at which calcium is known or has been hypothesized to affect photoresponse recoveries, based on results of biochemical and physiological experiments. These sites are (1) R* inactivation kinetics, via the calcium-binding protein recoverin; (2) R* catalytic gain; (3) guanylyl cyclase activity.
methods
General Experimental
The experimental methods employed for preparing isolated salamander rods, and for recording and analyzing their electrical responses have been reported (Cobbs and Pugh, 1987; Lyubarsky et al., 1996). For all the experiments whose data are reported here, the circulating currents of rods were recorded by means of suction electrodes into which the rod inner segment was drawn; the outer segment was continually superfused, either with a standard Ringer's solution or by rapid exchange with a test solution.
Calcium Clamping
We made use of recent work showing that Ca2+ i in the outer segments of salamander rods can be maintained near its resting (dark) level by exposing the outer segment to an isotonic choline solution containing very low Ca2+ (Matthews, 1995; Lyubarsky et al., 1996). In most of our previous experiments, we employed a “0-Ca2+ choline” solution, which, while keeping Ca2+ i near its resting level, allows Ca2+ i to decline slowly in the dark (Lyubarsky et al., 1996; see Figs. 4 and 6); we will report some results and analyses of four rods whose responses were recorded in 0-Ca2+ choline. In the present investigation, which reports new data from 19 rods, for calcium clamping we employed exclusively a choline solution containing an estimated 2.3 nM Ca2+. This latter concentration of Ca2+ o is in equilibrium with the measured resting concentration in salamander rods, Ca2+ i = 400 nM (Lagnado et al., 1992), and the membrane potential, −67 mV, estimated for the condition in which the outer segment is exposed to a nonpermeant solution while the inner segment is maintained in normal Ringer's (Lyubarsky et al., 1996). While a jump in the dark from Ringer's into choline solution containing 2.3 nM Ca2+ o yields a circulating current whose initial magnitude (∼10 pA) is diminished ∼50% relative to that (∼20 pA) in 0-Ca2+ choline, 2.3 nM Ca2+ o serves to maintain a stable circulating current in the dark, allowing the recovery kinetics under calcium clamp to be examined over time intervals up to 40 s or more, as required for examination of the response recovery phase to bright flashes.
Figure 4.
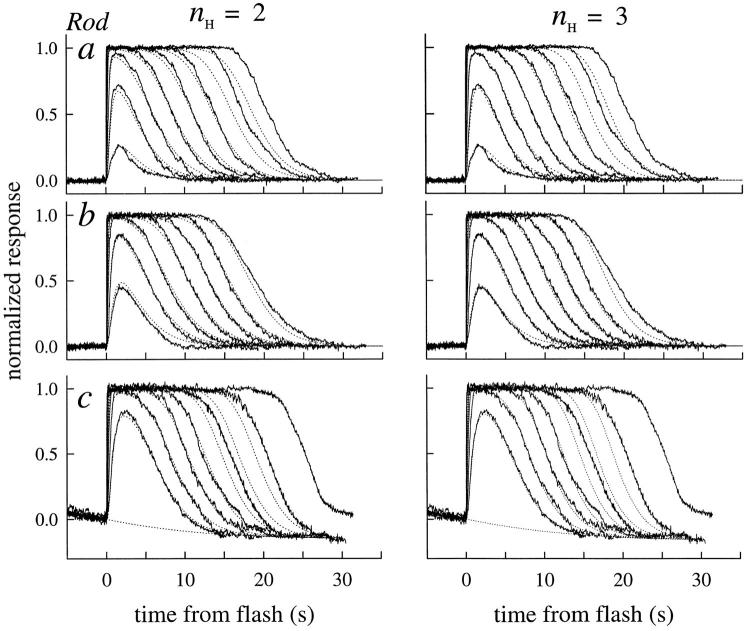
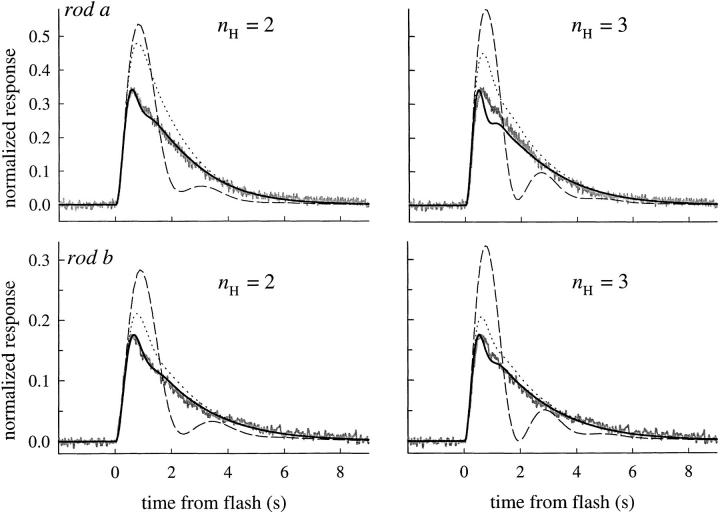
Averaged photoresponses of three rods (noisy traces) obtained under calcium clamp, fitted with a model (dotted traces) in which the disc-associated reactions are characterized as a linear cascade having two inactivation time constants (Eq. 5). The larger of the two time constants, τc, was estimated initially from analysis of the recovery half-times as in Fig. 5 A (i.e., by application of theorem 1), with small variations (∼5%) allowed to optimize the fittings. The lesser time constant τnd was estimated from the fitting; its value was strongly constrained by the time to peak of the subsaturating responses, though also affected somewhat by the value of βdark, as expected from theorem 5. The value of βdark was varied between 0.8 and 1.2 to optimize the fittings: the final values were 1.1, 0.8, and 0.8 s−1. The fittings were done with the Hill coefficient n H = 2 (left), and also with n H = 3 (right). Holding the value of n H at either 2 or 3 had negligible effect on the estimates of τnd (as expected from theorems 2–3), or on the amplification constant, A (Table II). Such invariance of A is expected from previous work (Lamb and Pugh, 1992). Rods a and b are typical in their parameter values. In contrast, rod c was unusual in being about three times more light-sensitive (without having an unusually large value of A); however, the estimate of τnd for this rod was about three times greater than the average. The “undershoot” of current after the responses of rod c was modeled by continual activation of cyclase at rate 0.017/n H s−1 (Lyubarsky et al., 1996, Eq. 12). The unusual features of the rod suggest that it may have had a higher Ca2+ i in Ringer's than the other rods.
Figure 6.
Recovery templates and tail phase data obtained in choline of eight different rods; letter labels correspond to those used in Table II to identify the rods. (top) The noisy traces are the recovery templates of the rods obtained by averaging the responses in choline to saturating flashes up to Φ = 10,000, as illustrated in Fig. 2. The thicker gray curves lying behind the template traces are the theoretical recovery template forms generated with the model, as in Fig. 4; the parameter values characterizing these theoretical templates are reported in Table II (the value of n H used was 3). The dotted trace is a first-order exponential, fitted to the tail phase of the template data trace, beginning at the point (∼0.2) marked with a filled circle; the exponentials were fitted with the simplex fitting algorithm in the MatLab™ software package. The values of the time constants τtail for the exponentials are reported in Table II. (bottom) The data traces and fitted exponentials are replotted in semilog coordinates; the traces are truncated at a normalized amplitude of ∼0.03–0.04, corresponding to an absolute magnitude of 0.3–0.4 pA (the amplitude of saturated responses under these conditions in choline is ∼10–11 pA; see Fig. 2).
Because of intrinsic variability between rods, one would not expect 2.3 nM Ca2+ o (or any particular value) to be in equilibrium for all rods whose outer segments are exposed to choline. In fact, we observe increases or decreases in the circulating current of some rods of up to 20% between 10 s after the jump into choline (when we deliver our first flash) and 45 s (the greatest time at which we deliver a second saturating flash and terminate the exposure to the choline). A 20% increase in circulating current corresponds to a change of <10% in [cGMP], assuming a Hill coefficient of at least 2 for activation of the cGMP channels, and to a change of <5% in Ca2+ i, assuming the cooperativity coefficient for calcium dependence of cyclase activity is also ∼2 (Koutalos et al., 1995a ). A 20% increase in circulating current is also only 0.09 of the average 3.2-fold (220%) increase in circulating current that occurs when the cGMP concentration is strongly elevated before the jump into choline (Lyubarsky et al., 1996).
Stimuli
Stimuli were monochromatic (500 nm, 8 nm full width at half-maximum), circularly polarized light flashes, generated via one of two optical channels: (a) a tungsten/halogen source illuminating a grating monochromator, followed by a shutter; (b) a xenon flashlamp (flash duration, 20 μs) filtered with an interference filter. Intensities are reported in photoisomerizations (symbolized by Φ), obtained by multiplying the physically measured energy density (photons μm−2) of the flash at the image plane by an estimated outer segment collecting area of 18 μm2. For all new response family data reported here, one of two flash series was used: Φ = 47, 150, 470, 1,500, 4,700, 1.5 × 104, 4.7 × 104 (10-ms flashes); Φ = 23, 94, 300, 940, 3,000, 9,400, 3 × 104, 9.4 × 104 (20-ms flashes); the Φ = 23 flash was not used in all experiments. In general, we avoided flashes of intensity lower than Φ = 47 because of the low amplitude (<2 pA) they evoke in choline (necessitating extra superfusion cycles for reliable data), and because of the focus in this investigation on responses to saturating flashes. Flashes of higher intensities than listed above were generated with the flashlamp channel as needed (for example, to produce strongly saturated responses in choline immediately before the return to Ringer's solution).
Theorems and Model Calculations
The principal theoretical results of this paper are analytical in nature and are cast as “theorems.” Our concept of a theorem is that of a relatively short proposition about well defined variables and quantities, a proposition that can be established by formal reasoning. The theorems are important for providing the context for the presentation of our findings, and thus are given together with the empirical results. However, grasp of the proofs of the theorems is not necessary to understand our conclusions, and so the proofs have been placed in i, where they are available for interested readers. Several of the theorems involve straightforward applications of linear systems theory (e.g., Jaeger, 1966); they have been included, nonetheless, so that readers not familiar with this branch of mathematics may have a self-contained framework for understanding all the theoretical results.
To illustrate certain theoretical results and estimate critical parameters of the rod phototransduction cascade, we employ a computational model developed to characterize responses in clamped-Ca2+ i condition, and written in the MatLab™ programming language (Lyubarsky et al., 1996). The model is generalized here to apply to responses of dark-adapted rods in Ringer's solution, in which Ca2+ i is free to vary. Details of the model calculations will be given as needed in the text, or in ii.
results
The general framework and notation adopted for the variables and parameters describing the reactions of the rod G-protein cascade have been presented previously (Lamb and Pugh, 1992; Pugh and Lamb, 1993; Lyubarsky et al., 1996), and thus are summarized in an abbreviated manner in Table I and in Fig. 1.
Table I.
Variables and Parameters of Phototransduction
| Symbol | Unit | Interpretation | ||
|---|---|---|---|---|
| Φ | #‡ | Number of photoisomerizations per rod per flash | ||
| R *(t) | # | Number of activated rhodopsins per rod at time t | ||
| G *(t) | # | Number of free, activated G-proteins per rod at time t | ||
| E *(t) | # | Number of activated PDE catalytic subunits per rod at time t | ||
| cG(t) | μM | Concentration of free cGMP in the outer segment | ||
| F(t) | # | Normalized circulating current at time t | ||
| νRP | s−1 | Rate of production of E*s per R* | ||
| τR | s | Time constant for first-order inactivation of R* catalytic activity | ||
| τE | s | Time constant for first-order inactivation of G*–E* complex | ||
| α(t) | μM s−1 | Rate of synthesis of cGMP by guanylyl cyclase | ||
| αdark | μM s−1 | Dark rate of cGMP synthesis | ||
| βsub | s−1 | Rate constant of cGMP hydrolysis by single PDE catalytic subunit | ||
| β(t) | s−1 | Rate “constant” of PDE activity in outer segment | ||
| βdark | s−1 | Rate constant of cGMP hydrolysis in the dark | ||
| cG dark | μM | Resting cytoplasmic concentration of cGMP | ||
| n H | # | Hill coefficient of the cGMP-activated channels in situ | ||
| A | s−2 | Amplification constant; equal to vRPβsub n H |
Numerical range of variables and values for parameters are as given in Lyubarsky et al. (1996; Table I), unless otherwise specified in the text. Note that E
has been used to represent PDE
*.
Dimensionless variable or parameter.
Recovery Translation Invariance
Fig. 2 illustrates the experimental protocol used to obtain response families of rods with Ca2+ i clamped near its resting value. The figure shows three repeated superfusion cycles in which the rod was stimulated first in Ringer's, and then in choline with a test flash producing 3,000 photoisomerizations. To insure that the rod was always in an identical state upon each exposure to choline, a “conditioning flash” of 9,400 photoisomerizations was delivered in Ringer's 40 s before the jump into choline. Unlike the protocol followed in previous calcium-clamping experiments in which a second, saturating flash was delivered at a fixed time after the jump into choline (Fain et al., 1989; Lyubarsky et al., 1996), in the experiments reported here, the timing of the second flash in choline was varied with the intensity of the first flash in such a way as to allow the full recovery to be followed in choline.
Figure 2.
Protocol used for measuring photoresponses in Ringer's and calcium-clamping choline solution. As illustrated in the inset at right, the inner segment of the rod is held in a suction pipette containing normal Ringer's, while the outer segment is fully exposed to a test solution, which is either Ringer's or isotonic choline containing 2.3 nM Ca2+. At the beginning of each cycle, the rod was exposed to the test flash, in this case producing Φ = 3,000 photoisomerizations; the rod was then exposed to a standard flash, Φ = 9,400, and 40 s later the outer segment was jumped into choline. At 10 s after the jump into choline, the test flash was again delivered and, after an appropriate period (which depended on the test flash intensity), given a standard saturating flash and returned to Ringer's. The junction current produced by the jump to choline has been subtracted from the raw records (see Lyubarsky et al., 1996, Fig. 1). The entire cycle was completed three times for flashes spanning the intensity range from Φ = 94 to 94,000. Over the 2.5-h time period required for the recording, the circulating current declined ∼10–15%; the photocurrent traces were normalized before averaging for additional analysis. In addition, the circulating current recovery after the initial test flash in choline increased ∼10% over the time course of recording from its magnitude at the time of the first flash, as indicated by the dashed line. Before averaging the photocurrents, a correction for this effect was applied by dividing the overall circulating current (at each time point) by the current course represented by the dashed line. (The line drawing of the rod was made from a videotape record of the experiment, obtained with infrared viewing equipment.)
Fig. 3 illustrates response families of the rod of Fig. 2 for saturating flashes, obtained in choline (Fig. 3 A) and in Ringer's (Fig. 3 B), and for a second rod (Fig. 3, C and D). The responses are plotted in a nonconventional manner: only the response to the most intense flash is plotted correctly with respect to the time axis; all other responses were translated to coincide at the point of 50% recovery. Here it can be seen that the recovery phases of the responses in Ca2+ i clamp (Fig. 3, A and C) are nearly identical in shape. The responses in Ringer's (Fig. 3, B and D) are also quite similar to one another, though clearly less so than those obtained in choline.
Figure 3.
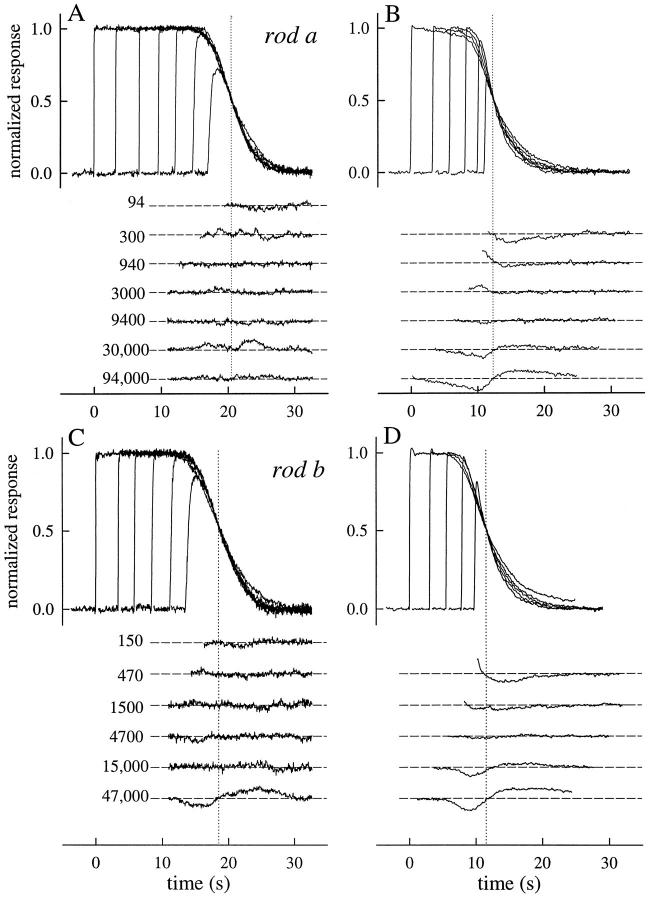
Experimental results examining Recovery Translation Invariance for two rods. A and B show photoresponses collected from the rod of Fig. 2 (rod a); C and D show photoresponses collected from a second (rod b). In the upper part of each panel, the responses are shown translated on the time axis to coincide with the point of 50% recovery, which is indicated by a dotted vertical line; in the lower part of each panel a template recovery shape has been subtracted from each trace; the template was made by averaging the three responses in the midrange of intensities (940– 9,400) that have the most closely identical shapes. For rod a, the template curve was essentially identical to the responses to the flash Φ = 9,400; for rod b, the template curve was most closely similar to the responses to the flash Φ = 4,700. The responses of rod a are the averages of three individual responses to each intensity; those of the rod b to two flashes. The flashes delivered to rod a were 20 ms in duration; those to rod b were 10 ms. Full obedience to RTI (Eq. 1) requires not only that the recovery shapes be identical, but also that the spacing between the activation phases in the upper part of each panel be uniform.
Another way to examine the shape invariance of the recoveries is illustrated in the lower half of each of the four panels (Fig. 3). Here we have taken the average of the traces in each case most closely similar in form (see legend), and then, with smoothing created an empirical template recovery shape; the template was subtracted from each of the individual traces and the residuals were plotted. For the responses in choline, shape invariance is again seen to hold well for flashes that produce up to 15,000–20,000 photoisomerizations. Above 20,000 photoisomerizations, systematic changes in recovery form are observed, most notably for the responses in Ringer's.
Fig. 3 also serves to illustrate another feature of the recoveries: geometric increases in flash intensity give rise to linear increments in recovery time. This feature is revealed by the approximately constant spacing of the rising phases of the translated responses.
The experiment illustrated in Fig. 3 was completed on eight rods, with similar results. (Summary data from all the rods will be reported in Table II, and also in Figs. 6 and 9, below.) We return to consideration of the deviations from shape invariance later. Our immediate goal is explicating the theoretical implications of the shape-invariant recovery behavior.
Table II.
Parameters of Activation and Inactivation
| Rod | Figures | A | Calcium clamp | ΔT 0.5 | Ringer's | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| τc | τtail | Number | τnd | τc | τtail | Number | α′ F = 0.1 | |||||||||||||||
| s−2 | s | s | s | s | s | s | s−1 | |||||||||||||||
| a | 2–12 | 0.10 | 2.1 | 2.4 | 14 | 0.39 | 7.7 | 2.3 | 2.6 | 28 | 10.2 ± 1.8 | |||||||||||
| b | 4–6, 9–12 | 0.09 | 2.2 | 2.2 | 21 | 0.35 | 7.0 | 2.3 | 2.8 | 37 | 7.8 ± 0.9 | |||||||||||
| c | 4–6, 9–12 | 0.10 | 1.9 | 1.7 | 6 | 1.2 | 6.7 | 2.6 | 2.6 | 9 | 9.7 ± 2.4 | |||||||||||
| d | 5, 6, 9–12 | 0.12 | 2.2 | 2.3 | 6 | 0.40 | 7.8 | 2.1 | 2.2 | 11 | 11.2 ± 1.9 | |||||||||||
| e | 5, 6, 9–12 | 0.12 | 1.9 | 1.8 | 4 | 0.38 | 6.3 | 2.0 | 2.2 | 24 | 9.8 ± 1.4 | |||||||||||
| f | 5, 6, 9–12 | 0.23 (0.10)* | 1.6 | 1.6 | 24 | 0.35 | 5.7 | 1.6 | 1.6 | 7 | 15.7 ± 3.0 | |||||||||||
| g | 5, 6, 9–12 | 0.08 | 1.7 | 1.4 | 7 | 0.20 | 4.0 | 1.5 | 1.4 | 9 | 4.6 ± 0.6 | |||||||||||
| h | 5, 6, 9–12 | 0.08 | 1.7 | 1.4 | 10 | 0.45 | 5.5 | 1.6 | 2.0 | 34 | 12.8 ± 4.6 | |||||||||||
| i | 10–13 | 0.06 (0.11)* | 2.5 | — | — | 0.47 | 7.8 | 2.6 | 2.6 | 4 | 10.4 ± 1.9 | |||||||||||
| j | 10–13 | 0.12 (0.16)* | 1.9 | — | — | 0.60 | 5.5 | 1.8 | 1.9 | 3 | 12.0 ± 3.6 | |||||||||||
| Mean ± SD | 1.9 ± 0.5 | 0.48 ± 0.27 | 6.4 ± 1.2 | 2.0 ± 0.4 | 2.2 ± 0.5 | 10.4 ± 3.0 | ||||||||||||||||
Column 1 identifies the rod; the same letter is used throughout the paper in the figures and text to identify data of the rod. Column 2 lists figures in which data from the rod appears. Columns 3–7 give specific parameters of activation and inactivation of responses in choline, obtained as follows: column 3 is the “amplification constant” determined by the rising phase of the response family (Lamb and Pugh, 1992; Pugh and Lamb, 1993); column 4 is the dominant time constant of inactivation, obtained from a linear regression applied to the recovery half-time data of saturating (or near-saturating responses), as in Fig. 5 A (typical 95% confidence interval for τc is ±0.2); column 5 is the time constant of the tail phase of inactivation, estimated as in Fig. 6; column 6 gives the number of responses that were averaged for the tail phase analysis; and column 7 gives the estimate of the nondominant time constant obtained from fitting the model to the choline response family as illustrated in Fig. 4 for rods a–b. Column 8 gives ΔT 0.5, the shift in time to 50% recovery for responses in choline and Ringer's, as in Fig. 5 A. Columns 9–11 give estimates of parameters derived from responses in Ringer's. Column 9 gives the dominant time constant of inactivation, obtained from a linear regression applied to the recovery half-time data of saturating (or near-saturating responses, as in Fig. 5 A; column 10 gives the time constant of the tail phase of the template saturating response in Ringer's (Fig. 9); column 11 gives the number of responses averaged to get the recovery template response in Ringer's. Column 12 is the estimate of α′max obtained at the point of 10% recovery, as in Fig. 8, computed with Eq. 10. In general, the estimates of A were the same for response families in choline and Ringer's; however, for the three entries marked by an asterisk the two estimates differed; the bracketed value is that obtained for responses in Ringer's. The data of rods i and j were collected in Lyubarsky et al. 1996; the calcium-clamping solution for those particular experiments was 0-Ca choline, and a saturating flash was given a fixed time after the jump into choline, precluding the tail-phase analysis.
Figure 9.
(top) Recovery templates (unbroken traces) for responses in Ringer's. Here the template represents the averaged response to a flash producing either Φ = 4,700 or 9,400 (the number of responses averaged varied between 9 and 28 for different rods, depending on how many times it was possible to repeat the entire response family series). The tail phase of the template was fitted with an exponential, as in Fig. 6, from the point marked with the filled symbol. a–h correspond to labels used in Fig. 6 and in Table II. (bottom) The data and fitted exponentials of the top panel are shown in semilog format.
Theoretical Analysis
We can formulate the observations illustrated in Fig. 3 in terms of the following functional equation:
 |
1a |
where F[Φ,t] is the circulating current present at time t after a flash producing Φ photoisomerizations at t = 0. The interval (Φ0, Φmax) is the intensity range over which Eq. 1a holds, t 0 is time at which F begins to show recovery from saturation by the flash Φ0, s is a positive number and h(s) is an unknown function. F is assumed to obey two boundary conditions:
 |
1b |
 |
1c |
In words, Eq. 1a states that when the intensity of a saturating flash producing Φ ≥ Φ0 photoisomerizations is scaled by a factor s ≥ 1, the response recovery at times greater than the fixed time t 0 is translated on the time axis without change of shape to the right by the amount h(s). Eq. 1b states that for any flash whose intensity lies within the specified range of Φ, at sufficiently long times recovery is complete; Eq. 1c states that even the most intense flash can only drive F to zero. A family {F [Φ,t]} of photoresponse recoveries satisfying Eq. 1 is said to obey Recovery Translation Invariance (RTI).1
In i(Lemma 1), we show that Recovery Translation Invariance is sufficient to completely determine the nature of the translation function h(s); specifically, if a family of recovery traces obeys RTI, then the only possible form that h(s) can take is
 |
2 |
where τc is a constant having the units of time. Once it has been established that RTI implies Eq. 2, then it is straightforward to prove the following result:
Theorem 1: Recovery Translation Invariance
A family of circulating current recovery traces {F [Φ,t]} obeys RTI if and only if
 |
3 |
where H(x) is a saturation function obeying H(x → Θ) = 0, H(0) = 1, and τc is a constant having the units of time.
Put into words, theorem 1 states that obedience of a family of saturating responses to Recovery Translation Invariance is equivalent to the requirement that there exists a transduction intermediate that is produced in an amount proportional to the flash intensity Φ (over the restricted intensity range), and which at appropriately long times decays with the time constant τc. Theorem 1 by no means states that the circulating current itself recovers with the time constant τc; quite the contrary, a saturating nonlinearity H can (and does) exist between the decaying transduction intermediate and the measured circulating current recovery. (Later, however, we establish conditions under which τc can be expected to be directly recoverable as the time constant of the “tail phase” of the recovering circulating current.)
We now note several consequences of theorem 1. First, theorem 1 reveals RTI to be both necessary and sufficient for Eq. 3 to hold. In other words, under the boundary restrictions placed on F, Eq. 3 and RTI are equivalent properties: one cannot exist without the other. This equivalence helps to resolve some confusion in the literature on the conditions under which one can infer the existence of a unique dominant time constant, a point to which we return in the discussion. Second, while theorem 1 appears to place only minimal constraints on the saturation function H, it nonetheless leads to the question of which late steps in the transduction cascade can be demonstrated analytically to preserve a dominant time constant established at an earlier step (Fig. 1) and thus serve jointly as an “H function.” We will address this question directly, and answer it in the section below entitled “The cGMP synthesis and hydrolysis reactions.” Third, the time scale τc of the logarithmic function h(Φ/Φ0) = τc ln (Φ/Φ0) is uniquely determined from the translation of the recovery curves per e-fold change in intensity, as noted by Pepperberg et al. (1992); see also Baylor et al. (1974, Eq. 51 and Fig. 19). In keeping with the terminology used by Pepperberg et al. (1992), we call this scale constant the “dominant time constant of recovery,” and have adopted for it the symbol τc, where “c” stands for “critical.” We next examine more fully the conditions under which one might expect the rod phototransduction cascade recovery to be governed by a dominant mechanism. In so doing, we find another characterization of a dominant time constant.
Phosphodiesterase activity modeled as a linear system.
The fact that rod photoresponse recoveries to saturating flashes obey RTI (Fig. 3) lends support to the hypothesis that during such recoveries the underlying process is being “dominated” by the first-order inactivation of a single molecular species. Based on general considerations about the established reactions of the transduction cascade (and specific considerations taken up below in presentation of the cGMP synthesis/hydrolysis reactions), it is reasonable to look to the reactions that occur at the disc surface for the identity of this molecular species. For mathematical purposes, we thus represent the disc-associated reactions of the transduction cascade as a linear system. Further support for this representation will be mentioned in the discussion.
We assume then that E*(t), the number of phosphodiesterase catalytic subunits active in the outer segment at time t in response to a flash given at t = 0 is a linear function of Φ: the scaled variable e*(t) = E*(t)/Φ is the impulse-response function of the system of disc-associated reactions. We emphasize that E*(t) does not represent the time course of activity of an impulse of instantaneously activated phosphodiesterase (PDE) molecules; rather, E*(t) represents the time course of activation and inactivation of E*s after an impulsive flash, a time course that necessarily includes the convolved kinetic effects of the lifetimes of R*, G*, and E* (see Fig. 1). Supposing that e*(t) can be represented as a cascade of n reactions, each of which exhibits first order decay, one can then prove that at sufficiently long times the reaction with the longest time constant always dominates, in the following specific sense.
Theorem 2: Dominant Time Constant of a Linear Cascade
Suppose that the impulse-activated activity of an enzymatic effector E*(t) can be represented as a cascade of n reactions, each exhibiting first-order decay, having time constants τ1 < τ2 < . . . < τn. Then, at sufficiently long times, the reaction with the longest time constant, τn, always dominates: that is, given any small number δ, it is always possible to find a time T δ such that to within error of a term of order δ
 |
4 |
where e* = E*/Φ, Φ is input strength (flash intensity) and C′ is a constant.
Theorem 2 follows straightforwardly from linear systems theory. Our goal in stating it is to show how to compute T δ, the time at which “dominance” is established. Based on current knowledge of the reactions of the rod phototransduction cascade, n is not expected to be large; recent models of E*(t) have used n = 3 (Tamura et al., 1991) and n = 2 (Lyubarsky et al., 1996). The model of e*(t) implemented here is that generated by the cascading of two first-order exponentials, one representing R* decay (time constant, τR) and one for concurrent G*–E* decay (time constant, τE) (Fig. 1):
 |
5 |
where νRP is the rate of generation of E* per fully active R*, and C RE = [τE τR/(τE − τR)] is a constant that renders E*(t) at early times consistent with the activation scheme of Lamb and Pugh (1992). Thus, in this particular case in Eq. 4, C′ = νRP C RE. Use of Eq. 5 as a description of the disc-associated reactions is not without problems, particularly inasmuch as it assumes R* activity to decay with first-order kinetics. In discussion, we address some issues concerning this obvious oversimplification of the biochemical reality of R* inactivation. Nonetheless, in the context of Eq. 5, the value Tδ can be thought of as setting the value of t 0 in theorem 1. Thus, for the two-stage model of E*(t) kinetics embodied in Eq. 5 and the specific values of the time constants τR and τE estimated below, we find T δ = 0.01 = 2.2 s; that is, 2.2 s after a flash is given, the intermediate R* or E* with the longer lifetime is expected to be strongly dominant, for flashes up to the intensity at which RTI fails.
In the context of theorem 1, and the empirical obedience of rod recoveries to RTI (Fig. 3), the overall significance of Eq. 4 is this: we can tentatively identify the scale constant τc of Eq. 3, estimated from recovery half-time data, with the component of the impulse response e*(t) having the longest time constant, τn. This identification will provide a satisfactory completion of the meaning of the term “dominant time constant.” However, such identification is premature unless it can be shown that the reactions of the phototransduction cascade subsequent to E* cannot contribute a dominant time constant, and yet are such as to preserve a dominant time constant established at an earlier stage in the cascade.
The cGMP synthesis and hydrolysis reactions.
Our primary goal in this section is to inquire whether the reactions governing cGMP hydrolysis and synthesis are such as to allow a dominant time constant present in e*(t) to be conserved. Our analysis answers this inquiry affirmatively, and also shows that while the hydrolysis/synthesis step of the cascade cannot be the source of the dominant time constant manifest in recoveries from saturating flashes, it nonetheless makes an important contribution to the time to peak of subsaturating responses.
The reactions governing the hydrolysis and synthesis of cGMP in a rod outer segment after an isotropic flash can be written
 |
6 |
where cG is the concentration of free cGMP, α the rate of cGMP synthesis by guanylyl cyclase, and β the rate constant of hydrolysis. Many investigations have established the applicability and generality of Eq. 6 (reviewed in Pugh and Lamb, 1993).
For a rod in normal Ringer's solution, α is time dependent, due to the decline in Ca2+ i that occurs during the light response and the dependence of guanylyl cyclase activity on Ca2+ i. For the specific condition in which Ca2+ i is held at its resting level (as in Fig. 3, A and C), α ≡ αdark and we can simplify Eq. 6 to the following:
 |
7 |
By further restricting attention to the recovery phase of the response when e*(t) is governed by its dominant mechanism, and by application of theorem 2, we can rewrite Eq. 7 as
 |
8 |
By analysis of Eq. 8, we can establish the following result.
Theorem 3: Conservation of the Dominant Time Constant of Recovery
When α = αdark, a constant, the family of recovery curves {cG(Φ,t)} generated by solving Eq. 8 for different saturating values of Φ obeys RTI. Thus, there exists a time t 0 such that for t > t 0 solutions to Eq. 6 for α = αdark are isomorphic, and translate on the time axis τc units for each e-fold increase in Φ, where τc is the largest time constant of the reactions governing the rod transduction cascade up to and including E *.
Before closing this section on the cGMP hydrolysis and synthesis reactions, we emphasize a feature of Eq. 7 important for full appreciation of RTI. While neither Eq. 6 nor 7 is the equation of a linear filter, at sufficiently low response amplitudes, Eq. 7 is in fact linear in Φ. Thus, the behavior of solutions of Eq. 7 is important for understanding the kinetics of photoresponses at low intensities and for understanding the tail phase of recovery from saturating flashes. The behavior is also important for excluding a role of cGMP hydrolysis and synthesis reaction in determining the dominant time constant. Thus, we formalize this behavior as follows.
Theorem 4: Dim-Flash Responses and Tail Phase of Responses in Calcium Clamp: The Filtering Effect of βdark
At appropriately low response amplitudes (such as those of responses to low intensity flashes), under calcium clamp the cGMP hydrolysis and synthesis reac-tion (Eq. 7) acts as a low pass filter with time constant τdark ≈ 1/βdark; at high intensities the reaction does not contribute a significant time constant to the cascade.
The effect of the Hill equation governing the cGMP-activated current.
The Hill equation governing the relationship between free cGMP, cG(t), and F, the fraction of circulating current present in normal Ringer's at time t, is given by
 |
9 |
where n H is the Hill coefficient. Eq. 9 is valid for time scales exceeding a few milliseconds because of the rapid equilibration of cGMP-gated channel currents with the ligand concentration. Inspection of Eq. 9 reveals that its application to a family of theoretical curves {cG(Φ,t)} generated as the solution to Eq. 8 will not alter the relative lateral positions of the members of the family on the time axis; rather, application of Eq. 9 with n H > 1 serves only to steepen each of the recovery curves in a manner that preserves their relative positions. The same conclusion applies to the modified version of Eq. 9 that governs responses in choline (Lyubarsky et al., 1996; see Eq. 10).
The overall consequence of theorems 2 and 3 is this: the dominant time constant of the reactions governing the time course of activation and inactivation of E* will be conserved through the subsequent reactions of the cascade, and be manifest in the spacing on the time axis of circulating current recovery traces. Illustrating this conclusion, Fig. 4 shows theoretical curves generated with the model, fitted to the photoresponses of the two rods of Fig. 3, and to those of an additional rod whose distinctive pattern of responses provides a basis for useful discussion later. In Fig. 4, we have fitted the response families of rods a–c twice: once (left) with n H = 2, and again (right) with n H = 3. As can be seen, other factors constant, the recoveries are somewhat better characterized by theory traces employing the higher value of the Hill coefficient. It is noteworthy that the values of the other parameters (A, τc, τnd), estimated by fitting the model to response families, were practically independent of whether the Hill coefficient is set to 2 or to 3; thus, for the families shown in Fig. 4, the estimates of the dominant and nondominant time constants giving the best-fitting curves differed in each case by <10%. (The notation adopted in Fig. 4 and Table I for the two time constants τR and τE of Eq. 5 is noncommittal as to their molecular identity since the constants are formally interchangeable. Thus, τc refers to the longer or dominant time constant and τnd to the shorter, nondominant time constant. The molecular identity of the mechanisms underlying the time constants will be taken up in discussion.)
The application of the model to the data of Figs. 3 and 4 underscores an important feature: for flashes exceeding ∼20,000 photoisomerizations, the linear E*(t) model (Eq. 5) fails systematically, predicting recoveries that are more rapid than those observed. This failure of RTI is illustrated further in Fig. 5, where we plot recovery half-time data for rods a and b, and the deviations of the recovery half-times from the constancy predicted by RTI for eight rods.
Figure 5.
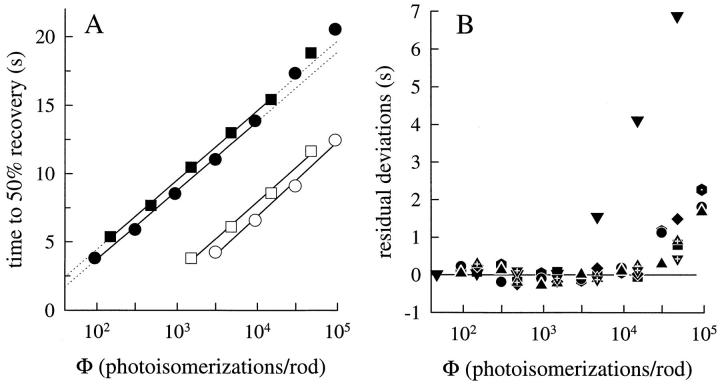
(A) Half-times of recovery for responses of rod a (circles) and rod b (squares) collected in choline (filled symbols) and in Ringer's (open symbols). Regression lines have been fitted to the choline data for flashes up to and including Φ = 10,000, and extrapolated (dotted lines); regression lines were fitted to the entire set of response half-times obtained in Ringer's. For rod a, the regression slopes (in unit of s per e-fold increase in intensity) are 2.2 and 2.3 for the Ringer's and choline data (○ and •, respectively); for rod b, the slopes are 2.1 and 2.3 (□ and ▪, respectively). The shift ΔT 0.5 between the choline and Ringer's recovery data is 7.7 s for the circles, and 7.0 s for the squares. (B) Choline recovery half-time data from eight rods for flashes up to Φ = 100,000. Linear regression lines as in the left panel were fitted to responses up to and including Φ = 10,000, and then extrapolated; the plotted points represent the residual deviations from the regression lines. All eight rods exhibit reliable deviations in the intensity range above Φ = 30,000. The downward triangles represent data of rod c.
Fig. 6 (top) serves to illustrate the degree to which the two-stage inactivation model accounts for the template recovery shape of each of the rods. The model was first fitted to the response family of each rod (as illustrated in Fig. 4); this generated the theory templates. The fitting also yielded estimates of the nondominant time constant (τnd) of each rod; these values are reported in Table II. Fig. 6 also provides evidence for testing a prediction resulting from theorems 2 and 4: providing the dominant time constant τc exceeds 1/βdark, the tail phase of the response recovery from any flash is predicted to decay exponentially with time constant τc; this prediction is not dependent on the value of the Hill coefficient, providing that the fitting is begun at a sufficiently low response amplitude.
Responses in Ringer's: Ca2+ i free to vary
An important goal of characterizing response recoveries in normal Ringer's solution is the determination of the way in which the decline in Ca2+ i that accompanies the light response affects the various cascade steps. At least two distinct sites of action of the decline of Ca2+ i have been described in previous physiological experiments (see Fig. 1): an increase of α, the rate of cGMP synthesis (Hodgkin and Nunn, 1988; Kawamura and Murakami, 1989; Koutalos et al., 1995a ); an apparent change in gain or amplification of an early transduction stage (Lagnado and Baylor, 1994; Pepperberg et al., 1994; Jones, 1995; Koutalos et al., 1995b ; Matthews, 1996; Murnick and Lamb, 1996; Gray-Keller and Detwiler, 1996). Our goal in this section is to provide evidence and analysis that will help dissect the relative contributions of these two actions of Ca2+ i to the speeding up of the recoveries to saturating flashes in Ringer's, relative to the same flashes in calcium clamp.
Theorem 3 applies for the situation in which α, the rate of cGMP synthesis, is a constant. Nonetheless, as seen in Fig. 2 and shown previously by other investigators, even in normal Ringer's solution in which Ca2+ i declines during a saturating response (thereby increasing α), response recoveries obey RTI to a first approximation. Moreover, as is shown in Figs. 3 and 5 A and documented previously (Lyubarsky et al., 1996), τc, the dominant time constant, is not significantly affected by the decline in Ca2+ i. What constraints do these empirical results impose on the theory of recovery?
For responses measured in Ringer's that obey RTI, theorem 1 is in force and we can conclude that the recoveries obey Eq. 3. Moreover, since the value of τc estimated in Ringer's and in Ca2+ i -clamping solution is statistically the same, on grounds of parsimony it can be concluded that one and the same biochemical mechanism, a mechanism whose time constant is not sensitive to the changes in Ca2+ i that normally occur, is responsible for τc. These considerations combine to yield the following.
Theorem 5: Recovery Translation Invariance in Ringer's
If a family {F[Φ,t]} of photoresponse recoveries obtained under conditions that allow α to vary freely obeys RTI, then α(t) itself must obey RTI and recover after a saturating flash in such a manner as to track the recovery of the incremental cGMP hydrolysis rate constant, at long times given by Δβ(t) ≈ ΦνRP C RE e −t/τc βsub.
Figs. 7 and 8 illustrate an application of theorem 5 to our results. Fig. 7 (top) reproduces from the investigation of Hodgkin and Nunn (1988) the response of a rod to a flash they estimated to yield Φ = 40,800, along with the response in Ringer's of the rod of Fig. 2 to the flash producing Φ = 30,000; Fig. 7 (bottom) shows Hodgkin and Nunn's estimates of α′ = α/cG dark and β, along with estimates of the same two variables obtained in a complementary manner from our data, as we now explain. We first introduce an expression for α′ = α/cG dark that can be derived by combining Eqs. 6 and 9:
 |
10 |
Figure 7.
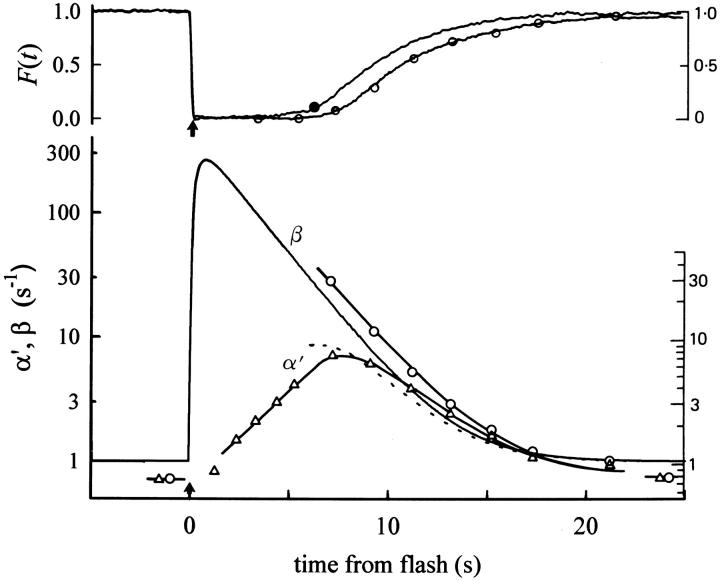
(top) This shows two photoresponses: the trace with open symbols attached is copied without alteration from Fig. 15 of Hodgkin and Nunn (1988); they obtained it as the response of a salamander rod to a flash estimated to yield Φ = 40,800. The second trace, with the filled symbol attached is from rod a (Table II) of this paper to a flash estimated to yield Φ = 30,000. The filled symbol indicates the point of 10% circulating current recovery. (bottom) Estimates of β and α′ = α/cG dark. The unbroken curves through the open symbols reproduce the estimates of the time course of these variables obtained by Hodgkin and Nunn (1988), based on the application of the IBMX jump method during the response of the rod of the top panel to the Φ = 40,800 flash at the points marked with the open circles. The unbroken trace labeled “β” gives an estimate of β(t) for the response of rod a to the Φ = 30,000 flash in the top panel; this estimate was obtained from the curve fitting analysis of Fig. 4. The dotted trace is the time course of α′(t) predicted from the relation α′(t) = β(t)F(t)(1/n H ), as described in the text. The purpose of reproducing the Hodgkin and Nunn (1988) data is to show how similar the estimates of β and α′ obtained here are to theirs. Note that we have reproduced the original figure scales of the Hodgkin and Nunn (1988) figure to the right of both panels.
Figure 8.
(top) Family of saturating responses obtained in Ringer's for rod a (see Table II); the point of 10% circulating current recovery on each trace is marked with a filled symbol. (bottom) Application of the analysis of Fig. 7 to the responses in the top panel: the unbroken traces give the estimates of β(t) obtained from the model analysis applied to the responses of the rod to the same flash series in choline (Fig. 3). The dotted curves are the predicted time courses of α′(t). The curves are only calculated for t such that F(t) ≥ 0.1, with the filled symbol marking the value of α′ associated with 10% circulating current recovery. The dotted line labeled βmax is an estimate of the highest possible rate constant of cGMP hydrolysis, computed as βmax = PDE tot βsub, where PDE tot is the total number of catalytic subunits in the outer segment (Dumke et al., 1994) and βsub is the hydrolytic rate constant of a single fully activated catalytic subunit in a well-stirred volume equal to that of the outer segment (Lamb and Pugh, 1992).
In their experiments, Hodgkin and Nunn estimated α′ by measuring the rate of change of the circulating current after rapid exposure of the outer segment to the phosphodiesterase inhibitor IBMX (3-isobutyl-1-methylxanthine); they then estimated β with the steady state approximation of Eq. 10, which neglects the second term; i.e., they used the relation β(t) = α′(t)/F(t)(1/n H ). In contrast to Hodgkin and Nunn's approach, we first estimated β by fitting the model to the responses of the rod obtained under Ca2+ i clamp (Fig. 4 A), and then derived α′(t). Thus, from the fitting we obtained β(t) = Φe*(t)βsub + βdark (see Eq. 7), and we then computed α′(t) = β(t)F(t)(1/n H ), which is plotted along with β(t) in Fig. 7 (bottom).
In Fig. 8, we apply the analysis of Fig. 7 to the complete set of saturating responses obtained in Ringer's of the same rod: unbroken lines are the estimates of β(t) obtained from the fitting of the cascade model to the responses obtained in calcium clamp (Fig. 4 A); gray thickened lines are the estimates of α′(t) obtained with the steady state approximation of Eq. 10, while the dotted trace gives the result of applying the complete equation, including the derivative term. As is seen in Fig. 8, we found generally that the derivative term of Eq. 10 contributed <5% to the estimate of α′(t) at any time after the point of 10% circulating current recovery.
The value of α′(t) at the time of 10% recovery is informative, since the concentration of Ca2+ i should have changed relatively little from the minimal value achieved during the saturated phase of the response; thus α′F = 0.1 provides an estimate of α′max. For the rod of Fig. 8, the average value of α′F = 0.1 estimated from the responses to the four highest intensities was 10.2 s−1. In Table II (rightmost column), we report the values of α′F = 0.1 obtained in this way for each rod. The average value α′F = 0.1 for these rods was 10.4 s−1; this value was the same if the two outlier values (Table II, rods f and g) were eliminated before averaging.
The focal issue of this section is the analysis of the mechanisms that underlie the accelerated recovery kinetics of saturated responses in Ringer's, relative to those measured in calcium clamp. The analysis of Figs. 7 and 8 provides an explanation of this acceleration, inasmuch as it shows that an ∼10-fold increase in cyclase activity during the saturated phase of the responses, along with Eq. 10, suffices to explain the acceleration. However, this analysis provides relatively little insight into the mechanistic details underlying the accelerated recoveries and, moreover, by assuming that none of the early steps in the cascade is affected by the decline in Ca2+ i, begs the question of whether another calcium-dependent process might be involved in the faster recoveries.
To gain deeper insight into the effect of cyclase activation on response recoveries in Ringer's, we adopted and applied three equations that have been used by several investigators to characterize fluxes of Ca2+ across the salamander rod outer segment membrane, free Ca2+ in the outer segment, and the Ca2+-dependent activity of guanylyl cyclase (Lagnado et al., 1992; Miller and Korenbrot, 1994; Koutalos et al., 1995a , 1995b ; see also Tamura et al., 1991; reviewed in Pugh et al., 1997):
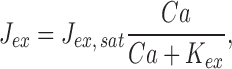 |
11 |
 |
12 |
 |
13 |
In these three equations, Ca represents the concentration of outer segment free calcium (i.e., Ca2+ i); the parameters of the equations are listed in Table III (𝔉 is the Faraday). Eq. 11 describes the dependence of the Na/Ca-K exchange current on Ca2+ i, while Eq. 12 describes the rate of change of Ca2+ i in terms of the balance between inward current through the cGMP-gated channels (−fCa F J dark) and outward pumping by the exchanger (J ex). (Note that J dark is an inward current, and therefore a negative quantity, and that while J ex is also a net-inward charge flow, it corresponds to a decrease in Ca2+ i.) Eq. 13 describes the dependence of the cyclase rate α on Ca2+ i. If these equations provide an adequate characterization of the mechanisms governing Ca2+ i, then, when combined with Eqs. 5, 6, and 9, they should in general yield a quantitative account of the responses in Ringer's and, more specifically, provide an account of the shift in recovery times between responses in calcium clamp and in Ringer's.
Table III.
Parameters Involving Calcium and Affecting Recovery
| Symbol | Value/Unit | Interpretation/comment | ||
|---|---|---|---|---|
| V cyto | 1.0 pl | Volume of the outer segment cytoplasm | ||
| J dark/f se | 70 pA | Dark/circulating current measured by suction electrode (s.e.) divided by s.e. collecting efficiency * ‡ § | ||
| f Ca | 0.1 | Fraction of inward circulating current carried by Ca2+‡ | ||
| Ca dark | 385 nM | Dark/resting concentration of Ca2+ i in outer segment; see ii ‡ | ||
| J ex,sat | 12.5 pA | Saturated magnitude of Na+/Ca2+-K+ exchange current‡ | ||
| K ex | 1600 nM | Ca2+ i giving rise to half-maximal exchange current‡ | ||
| K Ca | 100 nM | Ca2+ i at which cyclase activity is half-maximal§ | ||
| n Ca | 2.0 | Cooperativity coefficient for Ca2+ dependence of cyclase activity§ ‖ | ||
| βdark | 0.8–1.2 s−1 | Rate constant of cGMP hydrolysis in dark‖ ¶ | ||
| α′max | 10–15 s−1 | Maximum rate of cGMP synthesis divided by cG dark ¶ | ||
| γ | 5.6 s−1 | Factor for converting Ca2+ currents into concentration changes; Eq. 15 | ||
| η | 0.8 | Fraction of unused exchange current capacity at rest; Eq. 15 | ||
| μ | 2.7 s−1 | Real component of the oscillatory term governing cyclase feedback near Ca dark; Eqs. 15, 20, and A6.8 | ||
| ν | 4.5 s−1 | Imaginary component of the oscillatory feedback term; Eqs. 20 and A6.8 | ||
| θ | 3.8 radians | Phase term of the calcium feedback; Eqs. 20 and A6.8 |
Parameters in rows 1–8 were fixed at the values listed, based on the references. βdark was varied within the range given to optimize fitting; the most commonly used value was 1.0 s−1; in the perturbation analysis α′max is not free, but takes a value consequent to initial conditions based on equations 6, 11, and 13 (see Appendix II). The last five parameters in the table arise in the perturbation analysis of the dim-flash response in Ringer's (Theorem 6); the values listed are typical ones.
Koutalos et al., 1995;
We took two approaches to the application of Eqs. 11–13. First, we combined them with Eqs. 5, 6, and 9 and solved the ensemble of six equations numerically; further details, including a description of the initial conditions, are provided in ii. We will return to the numerical analysis below. Second, we expanded each of the six equations into perturbation approximations about the initial (i.e., dark/resting) values of the variables cG and Ca, thereby obtaining an analytic formula for the small signal response, and for the tail-phase response in Ringer's. This analysis yielded the following result.
Theorem 6: Tail Phase of Saturating Responses in Ringer's: Apparent Gain-control Effect of Cyclase Activation
The tail phase of the photoresponse in Ringer's will decay as a first-order exponential with the time constant τc of the dominant mechanism of the disc membrane– associated reactions, providing the inequality
 |
14 |
is satisfied, where
 |
15 |
and γ > 0 and 1 > η > 0. Moreover, if Eq. 14 is satisfied, the effect of cyclase activation alone on the position on the time axis of the late phase of recovery from a saturating photoresponse in Ringer's relative to that in calcium clamp can be expressed as
 |
16 |
where ΔT cyclase is the predicted shift, μ is given in Eq. 15, and
 |
17 |
Eqs. 14–17 in theorem 6 yield quantitative constraints for the theory of recovery, which we now explore. The constraint embodied in Eq. 14 appears generally satisfied, since the terms γ and η, and, therefore, μ are positive, and the values of the parameters involved yield an estimate for μ of 2.7 s−1 (Table III); thus, μ is more than fourfold larger than (1/τc), which is ∼0.5 s−1 (Table I). But does the prediction of theorem 6 hold that the tail phase of the responses in Ringer's should decay as a first-order exponential with time constant τc? And how does the prediction of Eq. 16 compare with the observed shift in recoveries between saturating responses in calcium clamp and Ringer's?
Figs. 9 and 10 address the first question. In Fig. 9, we show an averaged response of each rod in Ringer's, along with a decaying exponential fitted to the tail phase to estimate τtail. This analysis was similar to that used to analyze the calcium-clamp response tail phases (Fig. 6), except that we did not average responses obtained at different flash intensities. For most cells, we analyzed only the response to the conditioning flash, which was repeated many times over the course of an experiment (Table II, column 11). We adopted this procedure because of concern that systematic variation in τtail over intensity might be obscured by averaging, as we now explain.
Figure 10.
(A) Estimates of τtail obtained from responses in Ringer's are plotted as a function of flash intensity, Φ; the responses fitted were the averages of three to five responses obtained over the time course of an experiment. Data of different rods are represented by different symbols. The symbols with embedded crosses replot estimates of the first-order time constant of decay of Δβ obtained by Hodgkin and Nunn (1988). (B) Data in A are shown again, but with straight lines fitted to points lying between Φ ≈ 100 and 10,000, and to the points above Φ ≈ 10,000, as described in the text. (C) Local slopes of the empirical functions in A, computed by fitting a parabola by least-squares successively to each triplet of data points, and taking the derivative of the parabola at the center point of the triplet as the estimate of the slope. The slopes above Φ ≈ 10,000 lie reliably above those below this intensity. (D) τtail for each rod plotted against τc (obtained as in Fig. 5 A). Open symbols refer to estimates obtained for responses in Ringer's, filled symbols for responses obtained in choline; different symbols refer to different rods. Ringer's data (gray symbols) from a number of additional rods are included.
Since for some rods of this and of our previous investigation we had five or more responses to flashes of different intensities in Ringer's (obtained over the time course of a 2–3-h experiment), we were able to estimate τtail reliably from responses to these different flash intensities; these estimates are illustrated in Fig. 10 A (open symbols). Fig. 10 A (shaded circles) represents data from a rod of our previous investigation. Also plotted along with our data in Fig. 10 A as symbols with embedded crosses are estimates of the time constant of decline of Δβ(t) = β(t) − βdark obtained by Hodgkin and Nunn (1988; see Fig. 16) with their IBMX- and lithium-jump methods (see Fig. 8, above). Our estimates of τtail and theirs of the time constant of decline of Δβ(t) are in good agreement, as theorems 5 and 6 leads us to expect. Visual inspection of Fig. 10 A reveals that, in the middle range of intensities (Φ ≅ 100–10,000, depending on the cell), τtail is approximately constant, as expected from analysis of the recovery half-times (Fig. 5, open symbols; Lyubarsky et al., 1996). However, three systematic deviations from the simple ideal of an intensity-independent value of τtail deserve attention.
The first and most salient deviation from the simple ideal occurs at Φ ≅ 10,000, where for most rods τtail becomes systematically much longer, increasing by as much as twofold over the next 1-log unit range of intensities. This systematic lengthening of τtail occurs at approximately the same intensities at which RTI fails for calcium-clamp responses (Fig. 5). The second deviation from the simple ideal occurs at intensities Φ < 100, where for a number of rods τtail becomes systematically shorter. We will consider these latter deviations in more detail below. The third deviation from ideality occurs exactly in the middle range of intensities, and is characterized by a gradual increase of τtail. To put the deviations of the first and third kind into relative perspective, in Fig. 5 B we have fitted straight lines to points in the middle and upper range, picking (somewhat arbitrarily) a “break point” near Φ = 10,000. The average slopes of the lines fitted were 0.15 ± 0.12 s/log10(Φ) in the middle intensity range and 1.2 ± 0.2 s/log10(Φ) in the upper intensity range. In an effort to obviate the arbitrariness of first choosing a breakpoint to determine the slopes, we also derived local slopes from the data in Fig. 5 A, numerically estimating the derivative at each point; these running slopes are plotted in Fig. 5 C. The analyses in Fig. 5, B and C support the conclusion that a highly reliable increase in slope in the τtail vs. logΦ curves occurs at ∼Φ ≅ 10,000 for all rods, and that in the middle range the slope is relatively shallow or negligible. Also interesting is that the rods having the larger absolute values of τtail also have greater slopes.
Theorems 5 and 6 together lead to the conclusion that τc estimated from recovery half-time data and τtail should be the same for each rod. Fig. 10 D compares the τ's estimated from the tail phase analyses with the estimates of the dominant time constant τc for all the rods of this study, as determined in Ringer's (open symbols) and in calcium clamp (closed symbols). The values of τtail in this figure were obtained from the responses to the conditioning flashes (Φ = 4,700 or 9,400), which were repeated many times (Table II, column 4). Based on the relatively shallow slopes in Fig. 10 B, these estimates should be appropriate for examining the prediction that τc and τtail should be the same for each rod. To the data from the eight principal rods of this study, we have added to the figure points (gray symbols) obtained from responses in Ringer's of 15 additional rods involved in related experiments. The symbols in Fig. 10 D fall near the line of slope 1 through the origin, suggesting that the mechanism(s) underlying variation across rods (and, implicitly, over animals) affects τc and the response tail phases in the same manner. Interestingly, the rods exhibiting the smallest values of τc were obtained from animals obtained in the early Spring.
We return now to the second question posed above: can cyclase activation alone account for the shift between the response recoveries in calcium clamp and those in Ringer's? One issue that needs to be addressed first concerns the amplitude of the response recovery at which the shift should be measured: in Table II, we reported the shift at the point of 50% recovery (ΔT 0.5), but the theoretical prediction of Eq. 16 is valid only for response tail phases. To address this issue, we remeasured the shifts between the responses to saturating flashes in choline and in Ringer's at the points of 80% recovery; these values are reported as ΔT 0.8 in Table IV. The averaged absolute fractional difference, |ΔT 0.5 − T 0.8 |/ΔT 0.5 was 4%, with the maximum fractional difference being 10%. A second issue that must be addressed in order to apply Eq. 16 is the specific values of the various parameters in Eqs. 14–17. For the most part, the needed parameters have already been estimated for each rod or were estimated in previous investigations by others; these are given in Table III. Two particular parameters, however, stand out as requiring special attention: n H, the Hill coefficient of the cGMP-activated current, and BCa,rest, the calcium-buffering capacity of the rod near rest. Based on the quality of the fittings of the theoretical curves in Fig. 4, and on estimates of the Hill coefficient of cGMP-activated currents of excised patches of outer segment membrane, we might prefer the value n H = 3. Nonetheless, recent experiments on truncated salamander rods have yielded the estimate n H = 2 (Koutalos et al., 1995a ), and the value n H = 3 must be called into question. According to Lagnado et al. (1992, see Eq. 8), BCa in the salamander rod can be generally expressed as
 |
18 |
Table IV.
Parameters of Dim Flash Responses in Ringer's and Prediction of Recovery Shift Due to Cyclase Activation
| Rod | τc′ | τ′nd | B Ca,rest | ΔT 0.8 | ΔT cyclase | ΔT residual | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| s | s | s | s | s | ||||||||
| a | 1.4 | 0.43 | 15 | 6.6 | 5.5 | 1.1 | ||||||
| b | 1.8 | 0.37 | 18 | 6.0 | 5.5 | 1.5 | ||||||
| c | 1.3 | 0.73 | 28 | 7.7 | 5.7 | 2.0 | ||||||
| d | 1.7 | 0.31 | 10 | 7.6 | 4.8 | 2.8 | ||||||
| e | 1.4 | 0.33 | 13 | 6.5 | 4.4 | 2.1 | ||||||
| f | 1.4 | 0.32 | 14 | 5.7 | 4.3 | 1.4 | ||||||
| g | 1.2 | 0.27 | 7 | 4.0 | 4.5 | −0.5 | ||||||
| h | 1.2 | 0.35 | 18 | 5.7 | 4.5 | 1.2 | ||||||
| i | 1.7 | 0.41 | 25 | 7.8* | 5.7 | 2.1 | ||||||
| j | 1.7 | 0.35 | 27 | 5.5* | 4.6 | 0.9 | ||||||
| 1.5 ± 0.2 | 0.39 ± 0.12 | 17.5 ± 7.2 | 6.2 ± 1.2 | 5.0 ± 0.6 | 1.5 ± 0.9 |
Column 1 identifies the rod. Columns 2–4 give the parameters of the model used to fit the low intensity responses in Ringer's, as illustrated in Figs. 11–13; the value of the amplification constant used is given in Table II, and in all cases the Hill coefficient was set to n H = 2. τc′ is the value of the larger time constant of the disc-associated reactions, and τ′nd the shorter time constant (Eq. 5). Column 4 gives the value of α′max = αmax/cG dark, the maximal rate of guanylyl cyclase activity divided by the concentration of cGMP in the dark (see ii). Column 5 gives the observed shift at the point of 80% recovery (20% response amplitude) between saturating responses obtained in choline and in Ringer's. Column 6 gives the shift predicted on the assumption that cyclase activation alone is responsible, calculated with Eq. 16. Column 7 gives the residual shift; i.e., the observed minus the predicted shift.
Rods i and j were recorded from in 0-Ca2+ choline, and for the reasons given in the notes to Table II, we were unable to measure ΔT 0.8 and have instead substituted ΔT 0.5.
where C buff is the concentration of high affinity buffer, K buff is the dissociation constant of the high affinity buffer, Ca the calcium concentration, and B the buffer capacity of the rod “at high Ca2+ i.” Lagnado et al. (1992) provide the estimates C buff = 240 μM, K buff = 0.7 μM, Ca = Ca dark = 0.4 μM, B = 16; these values predict that in the salamander rod BCa,rest should be 156. Calculations with the analytical model of the dim flash response resulting from theorem 6 (see discussion, Eq. 20) led us to suspect that the value BCa,rest = 156 was problematically high.
Fig. 11 serves to illustrate for rods a and b the problem with BCa,rest arising from the application of Eq. 18, and shows how we obtained estimates of n H and BCa,rest. In brief, we numerically solved Eqs. 5, 6, 9, and 11–13 describing the transduction cascade in Ringer's, fitting the solution curve to the response of each rod to the least intense flash used to stimulate the rod, and using the optimized fittings to estimate the parameters. The theory predictions (Fig. 11, dashed lines) are seen to fail seriously if Eq. 18 is applied with C buff = 100 μM, a value <1/2 the estimate C buff = 240 μM reported by Lagnado et al. (1992). In contrast, the theoretical calculations with all other parameters unchanged appear to give an excellent account of the responses on the assumption that BCa,rest = 15 and 18, with n H = 2. Also shown in Fig. 11 are the best fitting theoretical curves that could be obtained with n H = 3; clearly these curves fit the data less well than those computed with n H = 2.
Figure 11.
Responses in Ringer's (noisy gray traces) of rods a (Φ = 94) and b (Φ = 47), along with theoretical curves. The thicker black theoretical traces were generated by numerically solving the ensemble of Eqs. 5, 6, 9, and 11–13, with the parameter values reported in Tables III and IV; the estimates of the resting calcium buffering capacity were fixed at B Ca = B Ca,rest = 15 and 18, for rods a and b, respectively. The dashed theoretical traces were generated by solving the same set of equations, but Eq. 18 was also added, with C buff = 100 μM and K buff = 0.7 μM; this corresponds to B Ca,rest ≈ 75. The dotted theoretical traces were computed with the analytical model of the change in cGMP (Eq. A6.10), produced by linearizing Eqs. 9, and 11–13, as explained in iin association with the proof of theorem 6. The cGMP-channel activation reaction, Eq. 5 was not linearized. For all theory traces in the left-hand panels, n H, the Hill coefficient of the cGMP channels was 2, for the right-hand panels, 3.
Fig. 12 shows the application of the theoretical analysis to the lowest intensity flash responses obtained in Ringer's from all the remaining rods of this investigation (Fig. 12, c–h), and from two rods from the previous investigation (Fig. 12, i and j). In Table IV, the resulting parameter estimates are given. The average estimated value of BCa,rest is 17.5 ± 7.2. To fit the responses well, the value of the “dominant” or larger time constant of Eq. 5 for every rod had to be set to a value systematically lower than the estimate τc obtained from the translation and tail-phase analysis of saturating responses. A similar observation was reported by Hodgkin and Nunn (1988) as lower estimates of the time constant of decay of Δβ(t) at low flash intensities (see Fig. 10 A). In Table IV, we identify this value as τ′c.
Figure 12.
Theoretical traces generated by fitting numerical solutions of Eqs. 5, 6, 9, and 11–13, to the responses in Ringer's of rods c–h to the dimmest flash used to stimulate each rod, and to four responses of each of two other rods (i and j) stimulated with a series of low intensity flashes. The ordinate is the normalized response amplitude, as in Fig. 11. The traces were filtered at 25 Hz. The noisiness of the traces corresponds roughly with the numbers of individual responses averaged, which were as follows: c (n = 1); d (n = 2); e (n = 3); f (n = 2); g (n = 2); h (n = 5); i (n = 5, 4, 4, 4, respectively, from least to most intense); j (n = 2, 2, 3, 2, respectively). The plots give the flash intensities used in the model calculations; for rod i, the intensity values 8 and 100 were substituted for the nominal values 11 and 94, respectively, in the calculations. The parameters of the fitted traces are given in Tables III and IV; for all theoretical traces in this figure n H = 2.
Finally, with BCa,rest (and all other relevant parameters) now estimated, we can examine the prediction of theorem 6, Eq. 16. Thus, in Table IV we report the predicted shift between the recoveries of saturating responses in calcium clamp and in Ringer's, predicted on the hypothesis that cyclase activation alone underlies the shifts. The average residual difference between the observed shift (ΔT 0.8) and that predicted by cyclase activation alone (ΔT cyclase) is 1.5 ± 0.9 s; the residuals range from −0.5 to 2.8 s.
As noted at the beginning of this section, recent evidence has supported the existence of a calcium-sensitive mechanism that affects the gain of an early activation step. Because it appears that such an effect can provide a reasonable account of the residual shift not accounted for by cyclase activation, it is useful to conclude by formalizing the manner in which calcium, acting on a nondominant mechanism, will affect the recoveries to saturating responses in Ringer's.
Theorem 7: Gain Control Via a Nondominant Mechanism
If calcium feedback acts to diminish the gain or shorten the lifetime of a nondominant component of the cascade up to and including E*, then such an effect will be manifested in the recoveries of saturating photoresponses in Ringer's only as a shifting of the family of recoveries to shorter times, with no change in the spacing on the time axis of the members of the family.
discussion
Linearity of the Phosphodiesterase Response Revealed by Recovery Translation Invariance
An earlier investigation concluded that during the rising phase of the salamander rod photoresponse the number of active phosphodiesterase catalytic subunits, E*(t), is linear in intensity up to Φ ≅ 10,000–20,000 photoisomerizations per rod, equivalent to 1 photoisomerization for each 7–16 μm2 of disc membrane (Lamb and Pugh, 1992). The phenomenon of Recovery Translation Invariance (Figs. 3 and 4) now leads via theorem 1 to the conclusion that for responses obtained in clamped Ca2+ i, linearity holds for the entire time course of E*(t), both activation and inactivation, for flashes up to approximately the same intensity. The likely explanation of this linearity is that the reactions governing the activation and inactivation of R*, G*, and E* (Fig. 1) for such intensities occur in completely nonoverlapping domains on the disc membranes, and involve no significant competition for cascade reactants.
Two essential nonlinearities intervene between E*(t) and the suppression of circulating current in clamped Ca2+ i, the reactions governing cGMP hydrolysis/synthesis (Eq. 6) and the Hill relation (Eq. 9). Theorem 3 establishes that these nonlinearities are such as to conserve a dominant time constant in the disc-associated inactivation reactions; i.e., that these nonlinearities can serve as an appropriate “H” saturation function in theorem 3. It bears emphasis in this context that the nonlinearity represented by Eqs. 6 and 7 cannot be considered an “instantaneous saturating nonlinearity” of the sort often used in modeling photoresponses; quite the contrary, these latter equations act as filters in which 1/β(t) is a time- and intensity-dependent “time constant” (theorem 4).
Saturating responses in Ringer's over the intensity range from Φ ≅ 1,000–10,000 also obey Recovery Translation Invariance approximately, and thus we conclude that for such saturating responses the entire time course of E*(t) of rods in Ringer's is also to a good approximation a linear function of flash intensity, despite the changes in Ca2+ i that necessarily occur. Theorems 5 and 7 show that it is reasonable to expect such linear behavior, provided declining Ca2+ i acts on the lifetime or gain of a nondominant disc-associated intermediate, as previously proposed by Murnick and Lamb (1996) and Matthews (1996, 1997).
Generality of τc and Its Independence of Ca2+ i
We have shown that a single time constant, τc, governs two major features of the photoresponse recovery to saturating flashes, the spacing of traces obeying Recovery Translation Invariance (Figs. 3–5) and the tail phase kinetics (Figs. 6 and 9). Moreover, to a very good approximation, τc is the same whether the responses are measured under calcium clamp or in Ringer's, in which Ca2+ i is free to vary (Figs. 5 A and 10 D). These observations further strengthen the conclusion that the biochemical mechanism underlying τc is not sensitive to calcium (Lyubarsky et al., 1996). Because the recovery half-time to a saturating flash given in Ringer's is typically 5–7 s shorter than the recovery half-time to the same flash given in calcium clamping choline, it may seem surprising that the time constants of the tail phases of the recoveries in both solutions are equal. Theorem 6 defines a quantitative condition (Eq. 14) under which such equality will occur, and this condition is met by the parameters of the salamander rod (Table III).
Partitioning the Overall Recovery Speed-Up Produced by Changing Ca2+ i
As just noted, recoveries to saturating flashes in Ringer's are typically sped up 5–7 s relative to those to the same flash obtained with Ca2+ i maintained near its resting value (Fig. 5 A). Our results and analysis lead to the likely conclusion that ∼4–6 s of the total shift is due solely to the activation of cyclase by the decline in Ca2+ i (Table IV). The residual shift not accounted for by cyclase activation is 1.5 s ± 0.9 s. This latter value is greater, though not significantly different from that (0.8 ± 0.2 s) obtained by Matthews (1997). Matthews (1997) rapidly jumped salamander rod outer segments into calcium-clamping solution before a saturating flash (Φ ≈ 11,000), and then restored them to Ringer's 1.7 s after the flash, while the photoresponse was still in saturation. Matthews (1997) measured the shift of the recovery of rods exposed to calcium-clamping (choline) solution, relative to the recovery of the control response the same flash delivered in Ringer's alone. Since the saturated phase of the response in choline continued after the return jump into Ringer's for an additional 5–6 s before circulating current recovery commenced, cyclase activity should have been equalized and maximal for the rod at the time recovery from saturation commenced, in both the control (Ringer's) and experimental (choline) conditions (see Figs. 7 and 8). Thus, the shift in recovery time courses was unlikely due to differential cyclase activation, and a calcium-sensitive step of transduction was uncovered. Matthews (1997) then went on to show that this calcium sensitivity decayed with a time constant of 0.5 s. The closeness of the time constant obtained, 0.5 s, to the value of the nondominant time constant, 0.48 ± 0.27 s, estimated from the analysis of responses in calcium clamp (Fig. 4; Table II) and in Ringer's (Fig. 12; Table IV), supports the hypothesis that the calcium sensitivity of one and the same nondominant mechanism underlies the residual shift between responses in Ringer's and choline not accounted for by cyclase activation.
It seems highly likely that the calcium-sensitive mechanism described by Matthews (1997) is the same as that characterized by Murnick and Lamb (1996). Calculations based on a simple model of the Murnick/Lamb effect (along the lines they discuss) show that if the gain of R* (with τR = τnd ≅ 0.5 s) is regulated by the decline in calcium, and if the lifetime of E* is τE = τc = 2 s, then one would expect this gain effect alone to produce a shift of 0.8 s in our experiments. In contrast, if E* were nondominant and its gain/lifetime were the target of the Murnick/Lamb effect, then the shift predicted is 2.7 s, nearly twice as large as the mean shift in our experiments not accounted for by cyclase activation. In other words, based on the time course and magnitude of the effect of Murnick and Lamb (1996), the decline in Ca2+ i that accompanies a single saturating response of a dark-adapted salamander rod in Ringer's can be predicted to feed back on the activity of R* in such a way as to produce a leftward shift of ∼1 s of the recovery, relative to what the recovery would be were this effect not present. It seems then, that the combination of the 4–6-s shift effect due to cyclase activation (Table IV) and an ∼1-s shift due to the gain–control effect characterized by Murnick and Lamb (1996) and Matthews (1997) can provide a full account of the total 6.4 ± 1.2-s shift between recoveries of saturating responses in calcium-clamp and Ringer's.
Breakdown in E* Linearity and Its Significance for Identifying the Mechanism of the Dominant Time Constant
Pepperberg et al. (1992) argued that the mechanism responsible for the dominant time constant was R* inactivation; i.e., that τc = τR. The principal evidence they cited in favor of this identification was that the 10% point of the recovery phase of the salamander rod response in Ringer's translated on the time axis by approximately the same magnitude per geometric increment in flash intensities up to Φ = 106 or more; in contrast to R*, the disc-associated cascade intermediates G* and E* would be expected to saturate at lower intensities. Their argument needs to be reevaluated in the light of our results and analysis, and other recent results. In Figs. 3–6, we have presented evidence that Recovery Translation Invariance fails for responses in calcium clamp for Φ ≥ 20,000. Our theoretical analysis shows that in the absence of RTI no unequivocal conclusion can be drawn about the existence of a unique dominant time constant. Thus, the principal argument in favor of the identification of τc with τR does not apply to photoresponses measured with Ca2+ i clamped near its resting level.
If we reject the argument for the identification of τc as the lifetime of R* as being valid for responses obtained in choline, there remains little reason to accept the argument as valid for responses in Ringer's, particularly since, in the intensity regime Φ = 1,000–10,000 where RTI holds reasonably well in both Ringer's and choline (Fig. 3), τc has the same value (Fig. 10, A and B; Lyubarsky et al., 1996; see Fig. 9). Further reason to reject the argument of Pepperberg et al. (1992) is also provided in Fig. 10, where it is shown that the time constant of the tail phases of responses in Ringer's, as well as the time constant of decay of Δβ as measured by Hodgkin and Nunn (1988), also gets systematically longer for Φ > 10,000. Mindful that the principal argument in favor of identification of τc with the lifetime of R* activity is now in doubt, we now evaluate other evidence pertinent to the identification of the mechanisms underlying the dominant and nondominant time constants.
Biochemical Identities of the Intermediates Underlying the Dominant and Nondominant Constants
Support for identifying the simultaneous decay of the G*/E* complex (Fig. 1) as the mechanism underlying τc includes (a) that the decay of G*/E* activity measured under appropriate in vitro conditions has a lifetime approximately equal to the value of τc (Arshavsky and Bownds, 1992; Arshavksy et al., 1994; He et al., 1997), and (b) that the decay of G*/E* activity has been shown not to be calcium sensitive (Arshavsky et al., 1991). Another argument in favor of this identification can be made based on our data, and the finding that GTPase-activating factors or proteins, available in the rod outer segment in limited supply, are required for rapid hydrolysis of the terminal phosphate of G* = Gt -GTP. One such factor implicated in GTPase acceleration is the γ-subunit of the PDE (Arshavsky and Bownds, 1992; Arshavsky et al., 1994). Evidence for a second factor was presented by Angleson and Wensel (1994). He et al. (1997) have now identified this latter factor as a novel protein, RGS9, a member of the RGS family of GTPase-activating proteins (GAPs), have established its localization in rod outer segments, and have demonstrated that it can accelerate the G* GTPase rate constant to 1 s−1 at room temperature. Calculations based on the estimated rate of activation of G* per R* in situ (Lamb and Pugh, 1992) suggest that exhaustion of either or both of these GAP factors should occur by Φ = 20,000 photoisomerizations/rod; a relative slow down of recovery kinetics should occur at greater intensities (Figs. 5 and 10). The identification of G*/E* decay as the mechanism of τc also finds support in the recent work of Sagoo and Lagnado (1997) on truncated, dialyzed salamander rod outer segments, who make the case that the slowest step in circulating current recovery in their preparation is Gtα-GTP terminal phosphate hydrolysis.
Several additional lines of argumentation suggest that the mechanism underlying the nondominant time constant is the decay of R* enzymatic activity. First, in vitro experiments have shown that R* activity is sensitive to calcium via an effect of the calcium-binding protein recoverin on rhodopsin kinase (Kawamura, 1993; Klenchin et al., 1995; Chen et al., 1995), though it remains moot whether the relatively high calcium sensitivity of this mechanism, K 1/2 = 1.5–3 μM, would produce much effect when Ca2+ i declines from its resting level near 400 nM (Erickson et al., 1996). Second, independently of whether or not the calcium sensitivity of activation gain involves recoverin, there is substantial physiological evidence of an early activation intermediate that is calcium sensitive (Lagnado and Baylor, 1994; Pepperberg et al., 1994; Jones, 1995; Koutalos et al., 1995a ; Matthews, 1996; Murnick and Lamb, 1996; Gray-Keller and Detwiler, 1996; Matthews, 1997; Sagoo and Lagnado, 1997). The simplest reconciliation of this body of evidence with the insensitivity of τc to calcium is, as argued by Murnick and Lamb (1996) and Matthews (1997), that the lifetime and/or gain of the mechanism underlying the nondominant time constant is calcium sensitive. Theorem 7 embodies this conclusion.
In sum, it is natural to identify the primary decay of R* activity as the mechanism underlying the nondominant time constant, and the R* lifetime and/or catalytic gain as calcium sensitive, and G*/E* decay as the mechanism of τc. Nonetheless, we caution that these identifications remain tentative until a definitive experiment is performed in which the dominant time constant is shortened in situ by a biochemical manipulation highly specific for R* or G*/E* decay.
In the context of discussion of the biochemical identities of the mechanisms underlying the dominant and nondominant time constants, the question naturally arises, Why should the decay of R* activity be describable in terms of a single time constant, as assumed in Eq. 5? The simplest answer is this: while a first-order R* decay model certainly oversimplifies the well established biochemistry of R* inactivation by phosphorylation and arrestin binding, the conditions of the present investigation are not such as would be expected to reveal evidence for such “biochemical fine structure.” Specifically, the responses reported here were to flashes that produced at least 10 photoisomerizations, and typically a number of such responses were averaged. Only at the single-photon response level might the detailed (and possibly stochastic) character of R* decay manifest its structure, as it clearly has in the responses of rods of mice with mutations affecting R* inactivation biochemistry (Chen et al., 1995; Xu et al., 1997). On the other hand, a “slowdown” in R* decay kinetics could be responsible for the systematic failure of the two-time constant linear model of E*(t) above Φ = 20,000 (Figs. 4 and 5). For example, there could be an accumulation at such intensities of a relatively long lived but intrinsically low activity decay product of R*.
Parameters Governing Photoresponse Recoveries in Calcium Clamp and Ringer's
To gain perspective on the factors that govern the time course of recovery of the photoresponse, it is useful to compare analytical expressions for the dim-flash responses in calcium clamp and Ringer's. For calcium-clamp responses, theorem 4 (see Eq. A4.3) yields
 |
19 |
while for dim-flash responses in Ringer's, theorem 6 gives
 |
20 |
The parameters of Eqs. 19 and 20 have been identified in Tables I and III, respectively; g(s) is a second- order polynomial that arises in obtaining the perturbation solution of theorem 6 (see Eq. A6.8). Fig. 13 shows application of expressions closely relating Eqs. 19 and 20 to dim-flash responses of rods i and j.
Figure 13.
Responses of rods i and j to the lowest intensity flashes used to stimulate each rod in Ringer's and in choline, compared with theoretical traces. The noisy darker gray traces are the responses in Ringer's; the lighter gray traces are the responses in choline. The choline traces were scaled to correspond to the Ringer's traces during the activation phase; the responses so plotted are governed by the same amplification constant, A. (The choline traces are noisier in part because of the scaling, in part because the unscaled amplitudes were smaller, and in part because they represent averages of fewer traces.) The “calcium-clamp” responses of both rods were obtained in 0-Ca2+ choline (see Table II), and had slowly increasing baselines, as illustrated in Fig. 4, rod c. Correction for the baseline was made by computing F(t) = J(t)/J dark(t), where J dark(t) is the baseline current in the dark recorded after a jump into choline over a period equal to that of the response, and J(t) is the current trace recorded when the flash is delivered. For the two panels at left, the theory traces were computed as in Fig. 12 for fittings to the Ringer's responses, and by numerically solving Eqs. 5, 6, and 9 for fitting the responses in choline; the solutions to the latter equations were generated with the same method used to fit calcium-clamp responses by Lyubarsky et al. (1996). For the two panels at right, the analytical solutions for ΔcG(t) = cG(t) − cG dark were used (i, theorems 4 and 6). At the peak of the ΔcG(t) response, the values were not sufficiently small for the perturbation expansion of the Hill relation (Eq. A4.3) to be accurate. Thus, rather than use Eqs. 19 and 20 to generate the curves in this figure, the appropriate Hill relation was applied to cG(t)/cG dark. The Hill coefficient was n H = 2 for all theory traces; other parameter values are given in Table IV.
Each of the expressions (Eqs. 19 and 20) has three terms; a fourth first-order term due to the filtering of the membrane time constant (τmem ≈ 20 ms) has been left out for simplicity. For the dim-flash responses to which Eqs. 19 and 20 apply, the effect of the membrane time constant can be incorporated along with an absolute transduction delay (teff ≈ 15 ms) by using the reduced time t′ = t − t′eff, where t′eff = teff + τmem ≅ 35 ms (Lamb and Pugh, 1992; Pugh and Lamb, 1993). While the terms corresponding to R* and E* decay are similar in Eqs. 19 and 20, the first-order decay term due to βdark, the dark rate of cyclic GMP hydrolysis in calcium clamp in Eq. 19 is supplanted for responses in Ringer's by a second-order oscillating term, as previously noted by Hodgkin (1988). This oscillating term arises because of the negative feedback coupling between cGMP and Ca2+ i through guanylyl cyclase. This latter term embodies the calcium-dependent cyclase activation and appears solely responsible for the threefold change in sensitivity and time-to-peak of the dim-flash response in calcium clamp and Ringer's, and likewise responsible for most of the 5–7-s shift in the recoveries of saturated responses (theorem 6).
In closing, we now consider briefly specific parameters governing the time course of inactivation whose values deserve note. In what follows, it should be kept in mind that τc and τnd are aliases for τR and τE, though the identifications remain uncertain, as discussed above.
τc and τ′c.
To fit the response of each of the rods to the dimmest flash used to stimulate it, the longer of the two time constants τR or τE had to be on average 25% shorter than τc; that is, the average ratio τ′c /τc was 0.75 ± 0.06 (n = 10). The tail phase analysis and the data of Hodgkin and Nunn (1988) presented in Fig. 10 A are also consistent with the notion that the longer of the two time constants of the disc-associated reactions is smaller at subsaturating intensities than in the middle range of intensities, where RTI is obeyed. Speculation about the apparent shortening of the longer time constant at low intensities seems premature before the definitive identification of the biochemical mechanism underlying τc. Nonetheless, a hypothesis that bears consideration is that longitudinal inhomogeneities in cG, outer segment cGMP, and Ca2+ i might play some role. Longitudinal variation in cG is likely present during the responses to subsaturating flashes such as reported in Figs. 12 and 13, and such variation should produce systematic longitudinal variation in Ca2+ i and guanylate cyclase activity. At present, however, we are uncertain that such variations would act to produce an apparent shortening of the longer time constant.
τnd.
The values of the shorter time constant attributed to the inactivation of the disc-associated reactions were generally consistent across conditions. Thus, comparing the estimates obtained from the analysis of responses measured in Ringer's and in calcium clamp (Tables II and IV), we find τ′nd /τnd = 0.9 ± 0.2 (mean ± SD, n = 9), very close to unity. This ratio omits the data of rod c, whose nondominant time constant was unusually long. The very large nondominant time of rod c (see Fig. 4 C) may have been caused by elevated Ca dark. Such an effect would be consistent with many observations in the literature (e.g., Torre et al., 1986; Baylor and Lagnado, 1994; Sagoo and Lagnado, 1997), suggesting that the effective lifetime of R* may increase with elevated Ca2+ i, as mentioned above in the discussion of the biochemical identity of the mechanisms underlying τnd and τc.
nH.
During the activation phase, the Hill coefficient is absorbed into the amplification constant, A (Lamb and Pugh, 1992; Pugh and Lamb, 1993). Since A must be fixed to fit the rising phase data of any response family, the value of n H used in the model has no effect on the quality of the fitting of theory traces to the activation data. The value of n H, however, does affect the fitting of the recovery phases, both in Ringer's and in choline. We have generally found that the responses in choline are well fitted with a value of n H of 2.5–3 (Fig. 4; see also Lyubarsky et al., 1996). However, the responses to low intensity flashes in Ringer's are clearly better fitted with n H = 2 than 3 (Fig. 11). Given the estimate n H = 2 obtained by Koutalos et al. (1995a) in experiments on truncated salamander rods, the best estimate for n H in Ringer's responses now has to be taken as 2.
αmax, maximum guanylyl cyclase rate.
Estimates of α′max (Table II, α′F = 0.1) derived from the combined analysis of responses in choline and Ringer's (Figs. 8 and 9; Table II) were almost independent of whether n H was chosen as 2 or 3. This follows from Eq. 10 because, while β(t) is diminished by the ratio 2/3 (for any value of Φ) to fit a particular response when n H is changed from 3 to 2, the value of (0.1)(1/n H ) almost perfectly compensates. If the dark level of cGMP, cG dark, is taken to be 2–3 μM, then αmax = α′max cG dark is predicted to be 20–30 μM s−1, which corresponds to the range of values obtained by Koutalos et al. (1995a) in their study of truncated salamander rods. Another way to look at αmax is to consider the ratio αmax/αdark = α′max/βdark. Previously published biochemical results reviewed by Pugh et al. (1997) and new biochemical data recently presented by Calvert et al. (1997) show that αmax/αdark in amphibian rods is ∼10, when αdark is taken to be the cyclase activity at ∼400 nM Ca2+. Since βdark is ∼1 s−1, we again arrive at the expectation α′max ≈ 10 s−1. Three potential caveats need to be mentioned about our estimates of α′max, however. The first, which also applies to the method of Hodgkin and Nunn (1988), arises because it is likely that at the point of 10% recovery in Ringer's, Ca2+ i may reach 20–30 nM, which should partially inhibit cyclase; correcting for this effect would lead to a higher estimate of α′max. The second arises because of the gain effect characterized by Murnick and Lamb (1996), and by Matthews (1997), which will act to diminish the magnitude of β in Ringer's relative to that estimated in choline by the fitting analysis. Correcting for this effect would lead to a diminution of our estimate of α′max (Table IV); we estimate that this correction would not exceed 30%. A third caveat arises because of a possible decrease in the K 1/2 of the cGMP channels for cGMP during the saturated phase of the light response when Ca2+ i is very low. This shift in the K 1/2 of the channels, effected by calmodulin binding (Hsu and Molday, 1993; Koutalos and Yau, 1996), if present at the point of 10% circulating current recovery, would also cause α′max to be overestimated.
BCa,rest.
Perhaps the greatest surprise of the modeling of the responses to low intensity flashes in Ringer's is the estimate of the calcium buffering capacity at or near rest, B Ca,rest = 17.5 ± 7.2 (Table IV). The analysis of Fig. 11 shows that B Ca,rest must be far lower than that predicted by the investigation of Lagnado et al. (1992), though in fact our estimate corresponds to that, 17, which they obtained as the low affinity buffer capacity “at high calcium.” Theoretical curves such as those in Figs. 11–13 are very sensitive to B Ca,rest, which by retarding the change in Ca2+ i increases the peak amplitude of subsaturating responses, and also causes the “noselike” behavior of the response immediately after the peak. While B Ca,rest is thus likely to be <20, both modeling efforts and previous work with calcium dyes indicates that B Ca is surely much higher when Ca2+ i declines below its resting level. Estimates of B Ca at all levels of Ca2+ i will be crucial for the development of a complete account of response families in Ringer's.
In conclusion, the activation of guanylyl cyclase by the decline in Ca2+ i that accompanies the response in Ringer's is apparently the principal factor responsible for the shift in recoveries of saturating responses of dark-adapted rods in Ringer's and calcium clamp, and is likewise responsible for the difference in kinetics and peak sensitivity of the dim-flash responses of dark-adapted rods in Ringer's and calcium clamp. Indeed, the activation of cyclase clearly exerts a powerful effect on the response recovery kinetics even at the very dimmest light response levels (Fig. 13).
Acknowledgments
We are grateful to A. Lyubarsky and L. Zhang for helpful criticisms.
Supported by National Institutes of Health grant EY-02660.
appendix i
Proofs of Theorems
We begin with a result that makes it straightforward to prove theorem 1.
Lemma.
If a family of recovery functions {F[Φ, t]} obeys RTI (i.e., Eq. 1), then h(s) = τ ln(s), where ln() is the natural logarithm and τ is a time unit.
Proof.
Suppose that RTI (Eq. 1) holds. Then, for any Φ ≥ Φ0, Φ = sΦ0 for some s ≥ 1, and so we can write
 |
A1.1 |
Thus, writing any Φ ≥ Φ0 as Φ = s 1 , s 2 Φ0, with s 1, s 2 > 0, we have
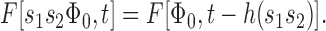 |
A1.2 |
But we also have from Eq. A1.1
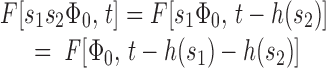 |
A1.3 |
It thus follows that h obeys one of Cauchy's functional equations (Aczel, 1966, p. 37ff):
 |
A1.4 |
The only solution to the functional Eq. A1.4 for s in the domain of positive real numbers is
 |
A1.5 |
(Aczel, 1966); dimensional analysis of Eq. A1.1 shows that τ has the units of time. This establishes that obedience of a family of recovery traces to RTI is sufficient to completely determine the form of h. We can now readily prove theorem 1.
Theorem 1: Recovery Translation Invariance.
A family of photoresponse recovery traces {F [Φ, t]} obeys RTI if and only if F [Φ,t] = H[Φe−t/τ], Φ0 ≤ Φ ≤ Φmax, t ≥ t 0 where H(x) is a saturation function obeying H(x→ ∞•) = 0, H(0) = 1, and τ a constant having the units of time.
Proof.
Sufficiency of RTI. Suppose RTI (Eq. 1) holds. Then, we have
 |
A1.6 |
where g 1(x) = F[Φ0, x + τln(Φ0)], g 2(x) = g1(−τx), g 3(x) = g 2(ln(x)).
Necessity of RTI. Suppose that F[Φ,t] = H[Φe−t/τ] for Φ0 ≤ Φ ≤ Φmax, where H() is an appropriate saturation function. Then writing sΦ0 = Φ, we can reexpress F as follows:
 |
A1.7 |
Thus, RTI is obeyed, with h(s) = τln(s). This completes the proof.
E*(t) Modeled as a Cascade of First-Order Exponentials
E*(t), the number of active catalytic subunits of phosphodiesterase in the outer segment at time t generated by a brief flash at t = 0 has been modeled as a cascade of reactions having first-order exponential inactivations. To present theorem 2 in a generalized form, we now consider a system formed of a cascade of n reactions having first-order exponential decays; in linear systems terminology (Jaeger, 1966), we consider a system that cascades n low pass filters. Each stage of such a system has impulse response
 |
A2.1 |
where subscript i refers to the ith filter (or ith stage), τi is the time constant of the ith filter, and Ci is the peak value of response of this stage to a Dirac delta function impulse input. We now assume that the n time constants are all different (i.e., nonrepeating), and without loss of generality that they satisfy the following inequalities:
 |
A2.2 |
Taking ai ≡ τi −1, the impulse response can be expressed (Jaeger, 1966) as
 |
 |
A2.3 |
where, C ≡C1C2C3 . . . Cn, and * indicates the convolution operator. For this system, which we may call an n-d-LP system (where “d” stands for “different”), the following theorem holds:
Theorem 2: dominant time constant of a linear cascade.
Suppose that the impulse response e *(t) = E *(t)/Φ of an enzymatic effector E* can be represented as an n-d-LP linear cascade. Then at sufficiently long times the stage with the longest time constant, τn always dominates. Specifically, given any small number δ where 0 < δ << 1, it is always possible to find time Tδ such that for t > Tδ, the impulse response of the system is given approximately as
 |
A2.4 |
for t > T δ, where
 |
 |
Proof.
Since τ1 < τ2 < τ3 < . . .< τn, it is clear that a 1 > a 2 > a 3 >. . . > an. In Eq. A2.3, there are n exponential functions with different time constants. If we consider any two consecutive terms having time constants τi and τi + 1, we can find the time beyond which the magnitude of the term with exp(−ait) is always less than any given fraction δi + 1 of the magnitude of the term with exp(–ai + 1 t). If this time is denoted by Ti + 1, then for t > Ti + 1, we have
 |
A2.5 |
The time Ti + 1 is given explicitly as
 |
A2.6 |
Let us denote the largest value among Ti + 1 as, T δ max; i.e.,
 |
A2.7 |
where δ is a small positive number chosen to be the same for all δi + 1. Considering the inequality a 1 > a 2 > a 3 >. . . > an, and denoting T δ max as T δ, we note that “to order δ,” the impulse response of the n-d-LP system is dominated by the term involving exp(−ant); i.e., it can be approximately written as
 |
A2.8 |
where
 |
A2.9 |
For the situation in which the time constants of the cascade are not all different, a generalized version of theorem 1 can be proved. However, care must be taken in expressing e *(t) for such a system.
Our calcium-clamp data are consistent with a two-stage model of E * given by Eq. 5 (Fig. 4; see also Lyubarsky et al., 1996). For the two-stage E* model with time constants τ1 = 0.4 s and τ2 = 2.0 s, Eq. A2.7 yields T δ = 1.4 s for δ = 0.05 and T δ = 2.2 s for δ = 0.01; for calcium-clamp responses, recoveries from saturation by flashes of Φ ≥ 1,500 commence near T δ = 0.01 (Fig. 4). Results in Figs. 7 and 8 also serve to illustrate theorem 2: not long after reaching its maximum, the plot of log[β(t)] = log[Φe*(t)βsub + βdark] becomes a straight line with slope −2.2 s; this is the time period when the inactivation phase of e*(t) is governed by the dominant time constant; later the straight line bends toward the asymptotic value βdark as e*(t) declines toward zero.
Theorem 3: conservation of the dominant time constant of recovery
When α = αdark, a constant, the family of recovery curves {cG(Φ,t)} generated by solving Eq. 8 for different saturating values of Φ obeys RTI. That is, there exists a time t 0 such that for t > t 0 solutions of Eq. 7 conserve the dominant time constant τc of a set of linear reactions governing the rod transduction cascade up to and including E *.
Proof.
An intuitive proof comes from consideration of the differential Eq. 8: the time-dependent coefficient of cG in the right-hand side includes the term Φe −t/τc, which obeys RTI; i.e., solving Eq. 8 for a flash of intensity sΦ (s > 1) and initial time t 0 is equivalent to solving Eq. 8 for a flash of intensity Φ, after shifting the initial condition to the right by the amount τc ln(s). Unfortunately, with this approach no single initial condition applies to the whole family of response recoveries. A more satisfactory proof requires care in dealing with the initial condition.
The general solution of Eq. 6 subject to the initial condition cG(Φ, 0) = cG dark = αdark /βdark can be written as
 |
A3.1 |
Eq. A3.1 can be normalized with respect to cG dark; thus, we get
 |
A3.2 |
For large Φ, the value of cĜ is saturated (i.e., vanishingly small); given any small number ε, 0 < ε << 1, there is an intensity εΦ0 such that cĜ will be less than ε in a time interval ε t 0l < t < ε t 0u. Put formally,
 |
A3.3 |
In Eq. A3.3, ε t 0l and ε t 0u are the first (lower) and the second (upper) times at which cĜ (Φ,t) = ε, respectively. The first time occurs during the “activation phase,” and the latter at the beginning of the “recovery phase ” from a saturating flash, when the circulating current is just coming out of saturation. We note that the greater εΦ0 is, the wider the time interval Δε t = ε t 0u− ε t 0l.
In theorem 2, it was shown that for t > T δ, the function e*(t) can be approximated by a single decaying exponential function with time constant equal to that of the dominant time constant τc; i.e., e*(t) ≈ C′e −t/τc. If the small number ε and εΦ0 are chosen such that ε t 0u> T δ, then one can effectively write the solution to Eq. 6 for t > ε t 0u with a new initial condition of cĜ (Φ,t) = ε at t = ε t 0u, because our interest is in the recovery phase of cG to flashes of intensity Φ ≥ εΦ0. Denoting εΦ0 as Φ0, ε t 0u as t 0 and Φ as sΦ0, then we have
 |
A3.4 |
for Φ > Φ0 and t > t 0. After t = t 0, the contribution of the term involving ε declines very rapidly with time, since the integrand [sΦ0 C′e −t′/τcβsub + βdark] of the exponential term outside the curly brackets is always positive, and its magnitude at the time when the response is emerging from saturation is expected to be 3- to 10-fold greater than βdark. Thus, the term in Eq. A3.4 involving ε can be neglected in the solution. By expanding Eq. A3.4 after dropping the term involving ε and integrating, we arrive at this expression:
 |
A3.5 |
The lower limit of the integration in Eq. A3.5 was extended to −∞• for convenience in what follows; integration of the integrand of Eq. A3.5 between −∞• and t 0 introduces an error whose magnitude can be shown not to exceed e [−sΦ0C ′τcβsub(e−t 0/τc−e−t/τc) − βdark(t − t 0)]. The maximum value of this latter term is unity, and occurs at t = t 0; the term decays initially as e −[sΦ0C ′βsub + βdark](t − t 0) and even more rapidly thereafter. The term is thus negligibly small because the hydrolytic rate constant sΦ0 C′βsub is by itself sufficient to drive cĜ to a very low value in a fraction of a second.
To complete the proof, we expand Eq. A3.5 to
 |
A3.6 |
and by introducing the change of variable, u = t′ − τc ln(s) obtain
 |
A3.7 |
where the second line of Eq. A3.7 comes from comparing the first with Eq. A3.5. This completes the proof.
Theorem 4: Dim-flash responses and tail phase of responses in calcium clamp: the filtering effect of βdark.
At appropriately low response amplitudes (such as those of responses to dim flashes), under calcium clamp the cGMP hydrolysis and synthesis reaction, Eq. 7, acts as a low pass filter with time constant τdark ≈ 1/βdark; at high intensities, the reaction does not contribute a significant time constant to the cascade.
Proof.
Into Eq. 7,
 |
7 |
make the substitution cG = cG dark + ΔcG, so that the perturbation variable ΔcG obeys
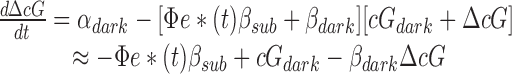 |
A4.1 |
since αdark = βdark cG dark, and since, by the perturbation assumption, Φe*(t)βsub << βdark. The solution to Eq. A4.1 is
 |
A4.2 |
which represents the convolution of e*(t) with a first- order filter having time constant 1/βdark. Assuming the two-stage model of E*(t) given by Eq. 5 is correct, Eq. A4.2 can be rewritten in the general form for a linear cascade given by Eq. A2.3. An alternative useful expression is given as Eq. 19 of the main text.
For responses to intense flashes, such as those that saturate the response (driving cG to a level much less than cG dark), the effective time constant of the filter represented by Eq. 6 is much shorter than 1/βdark and the filtering effect of 1/β is minimal; nonetheless, as the circulating current recovers toward cG dark, the “β filter” gradually kicks in. In closing, we note that Eq. A4.2 makes no specific assumption about the number of steps of the linear cascade governing e*(t). At sufficiently long times when e*(t) can be assumed to obey theorem 2, however, Eq. A4.2 dictates that ΔcG(t) will decay as a first-order exponential. Thus, during the tail phase of the response ΔcG(t) should decay exponentially, with a time constant equal to the longest time constant of the E* cascade, or equal to 1/βdark, whichever is longer. This concludes theorem 4.
It is useful to add here an expression for the normalized perturbation photocurrent response. Thus,
 |
A4.3 |
which is normally positive, since ΔcG is normally negative. This expression illustrates the point made previously by Lamb and Pugh (1992) that the Hill coefficient n H serves purely as an amplification factor between the change in cGMP concentration and the response for perturbations. It follows from Eq. A4.3 then that the tail phase of the calcium-clamp response is predicted to decay exponentially with time constant equal to the longest time constant of the E* cascade or equal to 1/βdark, whichever is longer.
Theorem 5: Recovery Translation Invariance in Ringer's.
If a family {F[Φ, t]} of photoresponse recovery curves obtained under conditions that allow α to vary freely obeys RTI, then α(t) itself must obey RTI and recover from a flash in such a manner as to track the recovery of the cGMP hydrolysis rate constant β(t).
Proof.
If the response family {F[Φ, t]} obeys RTI, then because Eq. 9 is such as to preserve RTI, the corresponding family of recovery curves {cG(Φ, t)} of cGMP also obeys RTI. Thus, we focus attention on the general solution to Eq. 9 over the intensity range and time period t > t 0 when RTI is obeyed. Letting Φ = sΦ0, we begin with the analogue of Eq. A3.4:
 |
A5.1 |
where α′ = α/cG dark. Eq. A5.1 expresses α as a function of the flash intensity. It is clear within the present framework of knowledge about the phototransduction cascade that this dependence is indirect, operating mechanistically through the changes in Ca2+ i that accompany the light response, and not through any direct signaling mechanism involving R*, G*, or E*. It is this indirect dependence that we wish to characterize.
Based on the lack of dependence of the empirically measured dominant time constant of recovery on Ca2+ i, we have also assumed in Eq. A5.1 that we can write e*(t) = C′e −t/τc; the constant C′ need not be the same as that in Eq. A3.4, reflecting a different effective gain and/or lifetime of the nondominant mechanism (see theorem 7). By the same argument that led to Eq. A3.5, we drop the term involving ε, and extend the lower limits of the integrals formally to −∞•. Integration over the range −∞• to t0 can be shown to introduce an error at time t whose magnitude does not exceed α′max e [−sΦ0C′τcβsub(e−t0/τc−e−t/τc) − βdark(t − t0)]; assuming α′max ≈ 10 (Table II), this means for example that by t − t 0 = 1 s, the error in Δc Ĝ cannot exceed 0.15. And so we arrive at the following sequence of identities:
 |
A5.2 |
where, in going from the third to fourth lines of Eq. A5.2, we have made the substitutions u = t′ + τc ln(s), w = t ′′ + τc ln(s). Thus, from comparison of the first and final lines of Eq. A5.2, α(t) itself must obey RTI, as claimed. Because α(t) obeys RTI during recovery from saturating responses, it also satisfies the conditions of theorem 1, and must therefore satisfy Eq. 3. In other words, during recovery in Ringer's for saturating responses that obey RTI, α(t) = H[Φe −t/τc] = H[Φ0 e −(t−τc ln(s))/τc], where H is an appropriate saturation function, Φ0 is the lowest saturating intensity that gives rise to an invariant recovery, and s = Φ/Φ0 ≥ 1. Boundary conditions dictate that H(x → ∞•) = αmax and H(x → 0) = αdark; τc ln(s) gives the displacement time, relative to some minimum time, at which α reaches a constant value during the recovery to flashes of intensity greater than Φ0.
Theorem 5 confirms the intuition that after different saturating flashes that all drive Ca2+ i sufficiently low, the return of cyclase activity to its dark level should follow a common time course, and that this time course is set by the recovery time course of the dominant mechanism of the disc-associated reactions, as hypothesized by Pepperberg et al. (1992).
Theorem 6: dim-flash responses and tail phase of saturating responses in Ringer's: apparent gain control effect of cyclase activation.
The tail phase of the photoresponse in Ringer's will decay as a first-order exponential with the time constant τc of the dominant mechanism of the disc membrane–associated reactions, providing the inequality μ > 1/τc is satisfied, where μ is given by Eq. 15. Moreover, the effect of cyclase activation per se on the recovery in Ringer's from a saturating flash at long times, relative to its position in calcium clamp, is to shift the curve to shorter time, by a time factor given by Eq. 16.
Proof.
The framework of the theorem is provided by Eqs. 11–13, along with Eqs. 6 and 9; moreover, E*(t) is assumed to be a linear cascade, so that theorem 2 is in force. The first step in proving the theorem is the expansion of Eqs. 11–13 into perturbation approximations. To do this, we introduce the four perturbation variables
 |
Using these variables, we next reexpress Eqs. 9, 11, and 13 as first-order expansions:
 |
A6.1 |
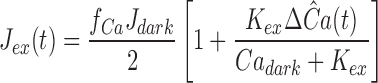 |
A6.2 |
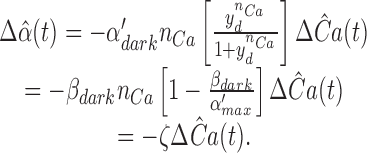 |
A6.3 |
In Eq. A6.3, we substituted α′dark = αdark/cG dark, α′max = αmax/cG dark, and y d = Ca dark/K Ca. The second line of Eq. A6.3 is an alternative expression, which comes from applying the initial condition α′dark = βdark, and a straightforward substitution into Eq. 13; it is useful because it obviates the need to use the ratio Ca dark/K Ca. The third line of Eq. A6.3 serves to define the parameter, ζ > 0, while underscoring the fact that increases in Ca2+ i relative to its dark level cause cyclase activity to decrease, and vice-versa.
By using the Eqs. A6.1–A6.3 and dropping second-order terms, we obtain a pair of coupled first-order differential equations, which are perturbation expansions of Eqs. 6 and 12, respectively:
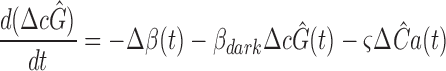 |
A6.4 |
 |
A6.5 |
in which we have introduced the positive parameters (compare Eq. 15)
 |
We next take the Laplace transforms of Eqs. A6.4 and A6.5, and arrive at the systems-response equations for the perturbation response in Ringer's, which we express in a matrix format:
 |
A6.6 |
Here we have used the “~” over the symbols to indicate the transformed variables. It is straightforward to invert the matrix in Eq. A6.6 and thus solve for ΔcG̃ (s) and ΔC̃a (s). We need to consider explicitly only the expression for the former, which is given by
 |
A6.7 |
The denominator of Eq. A6.7 is the second-order “calcium-cGMP feedback” system function, which we will call g(s). For realistic values of the parameters involved (see Table III), g(s) has complex conjugate roots. Thus, we can write
 |
A6.8 |
where μ = (βdark + γη)/2 (Eq. 15) and ν2 = n Hγζ − μ2.
To complete the theorem, we need to consider now two special cases of Eq. A6.7. The first case is that which governs the responses at long times after saturating flashes. In this case, Eq. A6.7 should be well approximated by
 |
A6.9 |
This follows, because even if the differential equation system is “reinitialized” at some time long after the flash (say, well into the recovery from a saturating flash), the contributions of the new initial conditions, embodied in Δc Ĝ (0) and Δ Ĉa (0), will become negligible within a few time units of length either 1/μ or τc, whichever is longer. Moreover, during the tail phase of recovery from a saturating flash the conditions of theorem 2 clearly apply, so that Δβ(t) = Φe*(t)βsub ≈ ΦC′βsub e −t/τc. In this case, then, by Laplace inversion of Eq. A6.9 we obtain
 |
A6.10 |
where k c = 1/τc, and
 |
Thus, providing k c < μ (i.e., Eq. 14 of the theorem's premise is met) at sufficiently long times only the first term in Eq. A6.10 survives, as was claimed.
Next we consider the case of the dim-flash response, a perturbation from the dark steady state. We assume the two-stage cascade for E* (Eq. 5). In this case, Δc Ĝ (0) and Δ Ĉa (0)are both zero, and the Laplace inversion of Eq. A6.7 yields Δc Ĝ (t), which by application of Eq. A4.3 gives Eq. 20 of the text, with
 |
Finally, to complete the theorem, we need to establish Eq. 16. We can readily do this by taking the ratio of the terms in Eqs. 19 and 20 of the text that represent the dominant mechanism. Thus, for example, if, as we suspect, E* decay is dominant, the predicted shift ΔT cyclase will satisfy
 |
A6.11 |
Solving for ΔT cyclase, we find
 |
A6.12 |
which is equivalent to Eq. 16 of the text, with τc = τE = 1/k E. This completes the proof.
Theorem 7: gain control via a nondominant mechanism.
If calcium feedback acts to diminish the gain or shorten the lifetime of a nondominant component of the cascade up to and including E*, then such an effect will be manifest in the recoveries of saturating photoresponses in Ringer's only as a shifting of the family of recoveries, with no change in the spacing on the time axis of the members of the family.
Proof.
Theorem 2 shows that in the absence of calcium feedback at adequately long times and for sufficiently intense flashes, e*(t) satisfies Eq. A2.4. The factors C i represent the “gains” of each of the steps involved, while τi = 1/ai are the time constants of the stages. Even with calcium feedback operative in Ringer's, the dominant time constant remains unchanged, so that during the time period and for the intensities for which RTI is obeyed, e*(t) = C′e −t/τc. Here the exact expression Eq. A2.4 becomes important, because the constant
 |
expresses both the amplification contributed by each stage, and the “gain” or integrating effect of the nondominant time constants, τj = 1/aj, j ≠ n.
Suppose then that the effect of the feedback is to diminish dynamically the lifetime τj of a nondominant intermediate; this will be equivalent to an increase in aj, so that the denominator term (a j − an) is now larger than it would be without feedback, reducing the magnitude of the constant C′. Likewise, if feedback operates to diminish one of the gain factors Cj, the result, in effect, is to reduce the constant C′. But changes in C′ are equivalent to changes in flash intensity Φ, since during this period of recovery β(t) = ΦC′e −t/τcβsub + βdark. A hidden assumption involved here is that the calcium feedback mechanism operates identically upon the nondominant intermediates independent of the flash intensities involved. This assumption seems reasonable for saturating flashes in the intensity range of interest (Figs. 3, B and DA), but surely breaks down for subsaturating flashes (as does RTI itself), because Ca2+ i declines to different levels, depending on flash strength. The assumption may also break down seriously at higher intensities if the calcium-binding proteins that carry the feedback signal to a nondominant intermediate can be exhausted.
In the two-stage model of E* (Eq. 5), the constant C′ takes the specific form
 |
A6.13 |
assuming E* is dominant over R*. From Eq. A6.13, it is clear that diminution of the gain νRP of a nondominant R* or decrease of the time constant τR both serve to diminish C′. Indeed, if τE >> τR, then changes in gain and time scale are equivalent, since then C′ ≈ νRPτR. Murnick and Lamb's (1996) analysis takes specific advantage of this relation.
appendix ii
Considerations for Numerical Solutions
To solve the differential equations governing the cascade under calcium clamp and in Ringer's, in addition to selection of the parameters, assumptions must be made about initial conditions. In calcium clamp, the only initial condition (from Eq. 6) is that αdark = βdark cG dark; this condition must also be met for the solutions governing the responses in Ringer's.
For responses in Ringer's, initial conditions dictated by Eqs. 11–13 must also be met and these conditions must be mutually consistent. We took the following approach. (a) We fixed cG dark = 2 μM; (b) Since βdark was varied (between 0.8 and 1.2 s−1) to optimize the fittings, we set αdark = βdark cG dark = 2 βdark (μM s−1); (c) The dark exchange current was calculated from J ex,dark = f Ca J dark (Eq. 12, dCa/dt = 0), and then the initial calcium concentration was computed from Eq. 11 as Ca dark = υK ex/(1 − υ), where υ = J ex,dark/J ex,sat. With the parameters listed in Table III, this yielded Ca dark = 385 nM, very near the estimates in the literature (reviewed in Pugh et al., 1997). (d) Finally, the maximum cyclase activity was calculated from Eq. 13 as
 |
While the value of αmax is not required as an initial condition, it implicitly enters into the perturbation analysis of the dim-flash response in Ringer's (Eq. A6.3).
The same initialization procedure was used for computing both numerical and analytical solutions (Eqs. 19 and 20). Numerical solutions to the coupled differential Eqs. 6 and 12, combined with Eqs. 11 and 13 were computed with the fourth- and fifth-order Runge-Kutta routine ode45 of the MatLab™ software package. Once the solution cG(t) was obtained, Eq. 9 was used to compute the fraction of cGMP current present for responses in Ringer's, while Eq. 10 of Lyubarsky et al. (1996) was used for responses in choline. The normalized current response was convolved with a first-order filter representing the membrane time constant, 20–30 ms. For adequately low intensity flashes (Φ < 5) and typical parameters, the numerical solutions agreed exactly with the analytical solutions, Eqs. 19 and 20; (compare Fig. 13, left and right).
Footnotes
Abbreviations used in this paper: PDE, phosphodiesterase; RTI, Recovery Translation Invariance.
references
- Aczel, J. 1966. Lectures on functional equations and their applications. Academic Press, New York.
- Adelson EH. The delayed rod afterimage. Vision Res. 1982a;22:1313–1328. doi: 10.1016/0042-6989(82)90144-4. [DOI] [PubMed] [Google Scholar]
- Adelson EH. Saturation and adaptation in the rod system. Vision Res. 1982b;22:1299–1312. doi: 10.1016/0042-6989(82)90143-2. [DOI] [PubMed] [Google Scholar]
- Angleson JK, Wensel TG. Enhancement of rod outer segment GTPase accelerating protein activity by the inhibitory subunit of GMP phosphodiesterase. J Biol Chem. 1994;269:16290–16296. [PubMed] [Google Scholar]
- Arshavsky VY, Gray-Keller MP, Bownds MD. cGMP suppresses GTPase activity of portion of transducin equimolar to phosphodiesterase in frog rod outer segments. Light-induced cGMP decreases as a putative feedback mechanism of the photoresponse. J Biol Chem. 1991;266:18530–18537. [PubMed] [Google Scholar]
- Arshavsky VY, Bownds MD. Regulation of deactivation of photoreceptor G protein by its target enzyme and cGMP. Nature. 1992;357:416–417. doi: 10.1038/357416a0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arshavsky VY, Dumke CL, Zhu Y, Artemyev NO, Skiba NP, Hamm HE, Bownds MD. Regulation of transducin GTPase activity in bovine rod outer segments. J Biol Chem. 1994;269:19882–19887. [PubMed] [Google Scholar]
- Baylor DA, Hodgkin AL, Lamb TD. Reconstruction of the electrical responses of turtle cones to flashes and steps of light. J Physiol (Camb) 1974;242:759–791. doi: 10.1113/jphysiol.1974.sp010733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breton ME, Schueller AW, Lamb TD, Pugh EN., Jr Analysis of ERG a-wave amplification and kinetics in terms of the G-protein cascade of phototransduction. Invest Ophthalmol Vis Sci. 1994;35:295–309. [PubMed] [Google Scholar]
- Calvert PD, Ho TW, LeFebvre YM, Arshavsky VY. Onset of feedback reactions underlying vertebrate rod photoreceptor light adaptation. J Gen Physiol. 1998;111:39–51. doi: 10.1085/jgp.111.1.39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen CK, Inglese J, Lefkowitz RJ, Hurley JB. Ca2+-dependent interaction of recoverin with rhodopsin kinase. J Biol Chem. 1995;270:18060–18066. doi: 10.1074/jbc.270.30.18060. [DOI] [PubMed] [Google Scholar]
- Cideciyan AV, Jacobson SG. Alternative phototransduction model for human rod and cone ERG a-waves: normal parameters and variation with age. Vision Res. 1996;36:2609–2621. doi: 10.1016/0042-6989(95)00327-4. [DOI] [PubMed] [Google Scholar]
- Cobbs WH, Pugh EN., Jr Kinetics and components of the flash photocurrent of isolated retinal rods of the larval salamander, Ambystoma tigrinum. J Physiol (Camb) 1987;394:529–572. doi: 10.1113/jphysiol.1987.sp016884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dumke CL, Arshavsky VY, Calvert PD, Bownds MD, Pugh EN., Jr Rod outer segment structure influences the apparent kinetic parameters of cyclic GMP phosphodiesterase. J Gen Physiol. 1994;103:1071–1098. doi: 10.1085/jgp.103.6.1071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erickson MA, Lagnado L, Zozulya S, Neubert T, Stryer L, Baylor DA. The effect of recoverin upon the recovery of the light response occurs at high levels of calcium. Invest Ophthalmol Vis Sci. 1996;37:S215. [Google Scholar]
- Fain GL, Lamb TD, Matthews HR, Murphy RLW. Cytoplasmic calcium as the messenger for light adaptation in salamander rods. J Physiol (Camb) 1989;416:215–243. doi: 10.1113/jphysiol.1989.sp017757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gray-Keller MP, Detwiler PB. Ca2+dependence of dark- and light-adapted flash responses in rod photoreceptors. Neuron. 1996;17:323–331. doi: 10.1016/s0896-6273(00)80163-4. [DOI] [PubMed] [Google Scholar]
- He, W., C.W. Cowan, and T.G. Wensel. 1998. RGS9, a GTPase accelerator for phototransduction. Neuron. In press. [DOI] [PubMed]
- Hodgkin AL, Nunn BJ. Control of light-sensitive current in salamander rods. J Physiol (Camb) 1988;403:439–471. doi: 10.1113/jphysiol.1988.sp017258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin AL. Modulation of ionic currents in vertebrate photoreceptors. Proceedings of the Retina Research Foundation Symposium. 1988;1:6–30. [Google Scholar]
- Hood DC, Birch DG. Rod phototransduction in retinitis pigmentosa: estimation and interpretation of parameters derived from the rod a-wave. Invest Ophthalmol Vis Sci. 1994;35:2948–2961. [PubMed] [Google Scholar]
- Jaeger, J.C. 1966. Introduction to the Laplace Transformation. Methuen & Co., London.
- Jones GJ. Light adaptation and the rising phase of the flash photocurrent of salamander retinal rods. J Physiol (Camb) 1995;487:441–451. doi: 10.1113/jphysiol.1995.sp020891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsu Y-T, Molday RS. Modulation of the cGMP-gated channel of rod photoreceptor cells by calmodulin. Nature. 1993;361:76–79. doi: 10.1038/361076a0. [DOI] [PubMed] [Google Scholar]
- Kawamura S. Rhodopsin phosphorylation as a mechanism of cyclic GMP phosphodiesterase regulation by S-modulin. Nature. 1993;362:855–857. doi: 10.1038/362855a0. [DOI] [PubMed] [Google Scholar]
- Kawamura S, Murakami M. Regulation of cGMP levels by guanylate cyclase in truncated frog rod outer segments. J Gen Physiol. 1989;94:649–668. doi: 10.1085/jgp.94.4.649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klenchin VA, Calvert PD, Bownds MD. Inhibition of rhodopsin kinase by recoverin. J Biol Chem. 1995;270:16147–16152. doi: 10.1074/jbc.270.27.16147. [DOI] [PubMed] [Google Scholar]
- Koutalos Y, Nakatani K, Tamura T, Yau K-W. Characterization of guanylate cyclase activity in single retinal rod outer segments. J Gen Physiol. 1995a;106:863–890. doi: 10.1085/jgp.106.5.863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koutalos Y, Nakatani K, Yau K-W. The cGMP-phosphodiesterase and its contribution to sensitivity regulation in retinal rods. J Gen Physiol. 1995b;106:891–921. doi: 10.1085/jgp.106.5.891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koutalos Y, Yau K-W. Regulation of sensitivity in vertebrate rod photoreceptors by calcium. Trends Neurosci. 1996;19:73–81. doi: 10.1016/0166-2236(96)89624-x. [DOI] [PubMed] [Google Scholar]
- Kraft TW, Schneeweis DM, Schnapf JL. Visual transduction in human rod photoreceptors. J Physiol (Camb) 1993;464:747–765. doi: 10.1113/jphysiol.1993.sp019661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lagnado L, Cervetto L, McNaughton PA. Calcium homeostasis in the outer segments of retinal rods from the tiger salamander. J Physiol (Camb) 1992;455:111–142. doi: 10.1113/jphysiol.1992.sp019293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lagnado, L., and D.A. Baylor. 1994. Calcium controls light-triggered formation of catalytically active rhodopsin. Nature 367: 273–277. [DOI] [PubMed]
- Lamb TD, Pugh EN., Jr A quantitative account of the activation steps involved in phototransduction in amphibian photoreceptors. J Physiol (Camb) 1992;449:719–758. doi: 10.1113/jphysiol.1992.sp019111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyubarsky AL, Nikonov SS, Pugh EN., Jr The kinetics of inactivation of the rod phototransduction cascade with constant Ca2+ i . J Gen Physiol. 1996;107:19–34. doi: 10.1085/jgp.107.1.19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthews HR. Effects of lowered cytoplasmic calcium concentration and light on the responses of salamander rod photoreceptors. J Physiol (Camb) 1995;484:267–286. doi: 10.1113/jphysiol.1995.sp020664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthews HR. Static and dynamic actions of cytoplasmic Ca2+in the adaptation of responses to saturating flashes in salamander rods. J Physiol (Camb) 1996;490:1–15. doi: 10.1113/jphysiol.1996.sp021123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthews HR. Actions of Ca2+ on an early stage in phototransduction revealed by the dynamic fall in Ca2+concentration during the bright flash response. J Gen Physiol. 1997;109:141–146. doi: 10.1085/jgp.109.2.141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller JL, Korenbrot JI. Differences in calcium homeostasis between retinal rod and cone photoreceptors revealed by the effects of voltage on the cGMP-gated conductance in intact cells. J Gen Physiol. 1994;104:909–940. doi: 10.1085/jgp.104.5.909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murnick JG, Lamb TD. Kinetics of desensitization induced by saturating flashes in toad and salamander rods. J Physiol. 1996;495:1–13. doi: 10.1113/jphysiol.1996.sp021569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pepperberg DR, Cornwall MC, Kahlert M, Hofmann KP, Jin J, Jones GJ, Ripps H. Light-dependent delay in the falling phase of the retinal rod photoresponse. Visual Neurosci. 1992;8:9–18. doi: 10.1017/s0952523800006441. [DOI] [PubMed] [Google Scholar]
- Pepperberg DR, Jin J, Jones GJ. Modulation of transduction gain in light adaptation of retinal rods. Visual Neurosci. 1994;11:53–62. doi: 10.1017/s095252380001110x. [DOI] [PubMed] [Google Scholar]
- Pugh EN, Jr, Lamb TD. Amplification and kinetics of the activation steps in phototransduction. Biochim Biophys Acta. 1993;1141:111–149. doi: 10.1016/0005-2728(93)90038-h. [DOI] [PubMed] [Google Scholar]
- Pugh EN, Jr, Sitaramayya A, Duda T, Sharma R. Photoreceptor guanylate cyclases: a review. Biosci Rep. 1997;17:429–474. doi: 10.1023/a:1027365520442. [DOI] [PubMed] [Google Scholar]
- Sagoo MS, Lagnado L. G-protein deactivation is rate-limiting for shut-off of the phototransduction cascade. Nature. 1997;389:392–394. doi: 10.1038/38750. [DOI] [PubMed] [Google Scholar]
- Smith NP, Lamb TD. The a-wave of the human electroretinogram recorded with a minimally invasive technique. Vision Res. 1997;37:2943–2952. doi: 10.1016/s0042-6989(97)00094-1. [DOI] [PubMed] [Google Scholar]
- Tamura T, Nakatani K, Yau K-W. Calcium feedback and sensitivity regulation in primate rods. J Gen Physiol. 1991;98:95–130. doi: 10.1085/jgp.98.1.95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torre V, Matthews HR, Lamb TD. Role of calcium in regulating the cGMP cascade of phototransduction in retinal rods. Proc Natl Acad Scie USA. 1986;83:7109–7113. doi: 10.1073/pnas.83.18.7109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu J, Dodd RL, Makino CL, Simon MI, Baylor DA, Chen J. Prolonged photoresponses in transgenic mice rods lacking arrestin. Nature. 1997;389:505–509. doi: 10.1038/39068. [DOI] [PubMed] [Google Scholar]