Abstract
Genetically encoded Ca2+ sensors promise sustained in vivo detection of Ca2+ signals. However, these sensors are sometimes challenged by inconsistent performance and slow/uncertain kinetic responsiveness. The former challenge may arise because most sensors employ calmodulin (CaM) as the Ca2+-sensing module, such that interference via endogenous CaM may result. One class of sensors that could minimize this concern utilizes troponin C as the Ca2+ sensor. Here, we therefore probed the reliability and kinetics of one representative of this class (cyan fluorescence protein/yellow fluorescent protein-fluorescence resonance energy transfer (FRET) sensor TN-L15) within cardiac ventricular myocytes. These cells furnished a pertinent live-cell test environment, given substantial endogenous CaM levels and fast reproducible Ca2+ transients for testing sensor kinetics. TN-L15 was virally expressed within myocytes, and Indo-1 acutely loaded to monitor “true” Ca2+ transients. This configuration permitted independent and simultaneous detection of TN-L15 and Indo-1 signals within individual cells. The relation between TN-L15 FRET responses and Indo-1 Ca2+ transients appeared reproducible, though FRET signals were delayed compared to Ca2+ transients. Nonetheless, a three-state mechanism sufficed to map between measured Ca2+ transients and actual TN-L15 outputs. Overall, reproducibility of TN-L15 dynamics, coupled with algorithmic transforms between FRET and Ca2+ signals, renders these sensors promising for quantitative estimation of Ca2+ dynamics in vivo.
INTRODUCTION
Calcium is a ubiquitous second messenger that is fundamental to many cellular processes including gene transcription, neuronal signaling, and muscle contraction (1,2). Furthermore, it is widely known that Ca2+ is inhomogenously distributed within cells, and it is the nature of this subcellular Ca2+ distribution that underlies intriguing local versus global Ca2+ regulation of cellular processes (3,4). As such, it has been a long interest to measure intracellular Ca2+ concentration with fidelity and subcellular resolution.
Revolutionizing such measurements has been the advent of chemical fluorescent Ca2+ indicators (e.g., Fura 2, Fluo 4), which feature outstanding kinetic responsiveness and dynamic range (5). However, these sensors require custom chemical strategies for targeting to particular cellular locations or cell types (6), and are not convenient for long-term monitoring, particularly in the in vivo setting. More recently, genetically encoded Ca2+ indicators (GECIs) promise to overcome these challenges (7–9). Because GECIs comprise proteins, these sensors readily permit site-specific targeting to particular cell types and subcellular regions, via cell-specific promoters and cell localization signals (7). Nonetheless, their success has been limited by slow kinetic responsiveness to dynamic Ca2+ fluctuations (10), limited dynamic range (7), and potentially inconsistent performance in different biological settings (8,11). Some of the latter challenges may relate specifically to the use of calmodulin (CaM) as the Ca2+ sensing moiety within many GECIs, such that variable degrees of interference from endogenous CaM may produce capricious performance (12,13). Moreover, the CaM within such GECIs could potentially perturb numerous CaM-based signaling processes, such as those disposing to cardiac hypertrophy (9,14). These limitations notwithstanding, the impact of GECIs as valuable tools in cell biology has already been demonstrated, and the performance of future GECIs will in due course rival that of chemical fluorescent dyes.
Nonetheless, it would be advantageous if at least some of the above-mentioned limitations could be overcome at the current time. GECIs based on the Ca2+-sensing element troponin C (TnC) may facilitate steps toward this immediate goal (12,15). TnC is the Ca2+ sensor triggering striated muscle contraction (2). As Ca2+ signaling through TnC is naturally resistant to interference from high levels of endogenous CaM within striated muscle (2), it seems likely that TnC-based sensors would share the same resistivity (12,15). A promising and key representative of this class of sensors is TN-L15, a cyan fluorescence protein (CFP)/Citrine fluorescence resonance energy transfer (FRET)-based GECI derived from chicken skeletal muscle troponin C (12). TnC resists CaM interference and has qualitatively demonstrated consistent performance across different biological settings, good dynamic range, photostability, and ratiometric property (11). These TnC-based GECIs can be seen as a complement to newer generations of CaM-based sensors, wherein computational redesign of sensor CaM/peptide interfaces attenuates interference from endogenous CaM and perturbation of native biology (13). A remaining and salient challenge is the slow kinetic responsiveness of all current generation GECIs. Moreover, whereas TnC-based GECIs have appeared insensitive to interference by endogenous moieties in neurons (11,12,15), there remains the legitimate concern that significant degradation of sensor performance might arise from the native contractile machinery in striated muscle (13).
Here, therefore, we explored whether the kinetic slowing of GECIs could be partially overcome via the existence of a quantitatively consistent transform between true Ca2+ fluctuations and GECI outputs. We choose TN-L15 as a candidate because of qualitative indications of consistency. To accomplish this task, we utilized tests in rat cardiac ventricular myocytes, which feature rapid (τ ∼ 200 ms) and reproducible Ca2+ transients, ideal for sensor testing. Additionally, these muscle cells feature high levels of both endogenous CaM and contractile proteins (2), so as to severely test for sensor interference by endogenous elements. We find that a quantitative interrelation between Ca2+ fluctuations and sensor FRET outputs is indeed upheld over multiple cells, such that algorithmic transforms permit mapping between slowed sensor responses and dynamically rapid Ca2+ transients. Overall, some of the strategies devised here may prove convenient and generalizable for minimizing the kinetic limitations of existing and future-generation GECIs.
MATERIALS AND METHODS
Construction of adenoviral vectors bearing TN-L15
The vector TN-L15/pAdLox was constructed by transferring the coding region for TN-L15 from TN-L15/pcDNA3 (12) into the multiple cloning site of the adenoviral shuttle-vector pAdLox (16–18), via BamHI and EcoRI restriction sites. Recombinant adenovirus, bearing TN-L15, was then generated by Cre-lox recombination, according to previously described methods (18). Briefly, 60-mm diameter dishes containing CRE 8 cells at ∼20% confluence were cotransfected with 3 μg TN-L15/pAdLox and 3 μg ψ5 viral DNA using FuGENE 6 (Roche Diagnostics, Basel, Switzerland). Following observation of cytopathic effects, usually after 7–10 days, cells were harvested, subjected to three freeze-thaw cycles, and centrifuged to remove cellular debris. The resulting supernatant (1 ml) was used to infect a 10-cm dish of 90% confluent CRE 8 cells. Following observation of cytopathic effects after 2–3 days, cell supernatants were used to reinfect a new plate of CRE 8 cells. This procedure was repeated two to three more times, followed by viral expansion and purification as previously described (18). Viral particle numbers, determined by absorbance at 260 nm, were present at ∼1012 particles ml−1.
Isolation, culture, and infection of rat cardiac myocytes
Adult Sprague-Dawley rats were killed with an overdose of sodium pentobarbital or halothane. Hearts were excised and ventricular myocytes isolated by enzymatic digestion using a Langendorf perfusion apparatus, as previously described (18). Healthy, rod-shaped cardiac myocytes were cultured on 35-mm culture dishes, with laminin-coated No. 0 glass bottoms (MatTek, Ashland, MA). After initial plating, cells were maintained in Medium 199 supplemented with 5 mM carnitine, 5 mM creatine, 5 mM taurine, 1% antibiotic antimycotic, and 5% fetal bovine serum to promote attachment to the coverslips (all from Sigma-Aldrich, St. Louis, MO). After 1 h, the culture medium was switched to serum-free Medium 199, otherwise supplemented as described above. Cultures were equilibrated with 6% CO2 and 94% air at 37°C in a water-jacketed CO2 incubator. As needed, cells were infected by adding 2–3 μl of the TN-L15 virus stock directly onto the cells, in a final volume of 200 μl. After 1–2 h, fresh serum-free media was added to a final volume of 2 ml for overnight incubation. For details, see Alseikhan et al. (18).
Indo-1 loading of cardiac myocytes
When required, cells were loaded with Indo-1 by incubating with Indo-1 AM (Teflabs, Suffolk, England) at a bath concentration of 0.5 μM for 10 min at 37°C. Then, the cells were washed thoroughly with HEPES-buffered 2 mM Ca2+ Tyrode's solution (pH 7.4) to remove residue Indo-1 AM. Tyrode's solution was comprised of 138 mM NaCl, 4 mM KCl, 1 mM MgCl2, 10 mM HEPES (pH 7.35 with NaOH), 5 mM glucose (all from Sigma-Aldrich).
Field stimulation of myocytes
Field stimulation (square pulse, 20 V × 4 ms) was produced by a Grass SD9 pulse generator through a pair of platinum electrodes. The electrodes were closely spaced and positioned in the Tyrode's solution directly above the center of the objective lens, so as to achieve local stimulation. To facilitate Ca2+ transients in field-stimulated rat cardiac myocytes, cells were initially bathed in a 2 mM Ca2+ Tyrode's solution (with 1 μM Forskolin, Sigma-Aldrich) for 15 min, before switching to a 10 mM Ca2+ Tyrode's solution (without Forskolin) for fluorescence imaging.
Fluorescence measurements
Cells were imaged with a Nikon TE300 Eclipse microscope (40×, 1.3 n.a. objective) and custom fluorometer system (University of Pennsylvania Biomedical Instrumentation Group, Philadelphia, PA). Excitation light was delivered by a 150-W short-gap Xenon arc-lamp (Optiquip, Highland Mills, NY) with servo control, and gated by a computer-controlled shutter (Vincent Associates, Rochester, NY). Filter cubes (Chroma, Rockingham, VT) employed were (excitation, dichroic, emission): Indo405 (D340×, 380DCLP, D405/30m), Indo485 (D340×, 380DCLP, D485/25m), CFP (D440/20×, 455DCLP, D480/30m) and FRET (D436/20×, 455DCLP, D535/30m). During one cycle of acquisition, the filter cubes were sequentially rotated by a motorized Hex-Filter (Conix Research, Springfield, OR), with a 20-s interval between 2.4-s imaging periods by individual filter cubes. The shutter limited excitation to these imaging periods. Ten cycles of measurements were taken for each myocyte, and the results averaged. Normally, neutral density filters were engaged such that only 1/32 of the light source was transmitted. However, due to the weaker power output of the arc-lamp at ultraviolet wavelengths, it was necessary to boost the excitation signals for Indo-1 by allowing 1/4 of the light source to be transmitted during imaging with Indo-1 cubes. Epifluorescence emission from entire individual cells was selected by an image-plane pinhole, and measured with an ambient temperature photomultiplier tube (PMT) (30 mm EMI 9124B, Electron Tubes, Rockaway, NJ). PMT signals were low-pass filtered at 10 kHz, and then digitized (ITC 18, Instrutech, Port Washington, NY). Shutter control, electrical stimulation, automated switching of filter cubes, dark-current subtraction, and data acquisition were all controlled by custom MATLAB (MathWorks, Natick, MA) software. To correct for autofluorescence and background light scatter, averages from individual uninfected myocytes were subtracted from same-day experimental values for each filter cube.
Numerical processing for forward-backward transforms
Custom scripts in EXCEL 2003 (Microsoft, Seattle, WA) were used to elaborate the Euler integration steps for transforms as described in the Results section.
Statistical analysis
Data were expressed as mean ± SD. Nonlinear curve fitting and least-squares linear regression (Solver add-in tool, EXCEL 2003) were used when appropriate.
RESULTS
To explore the relationship between “output” TN-L15 FRET responses and “input” Ca2+ concentration dynamics, we sought means to monitor both signals simultaneously during field-stimulated Ca2+ transients within individual rat ventricular myocytes. In this manner, the reproducibility and nature of input-output relations could be assessed quantitatively within the context of live cells.
Independent detection of Indo-1 and TN-L15 signals within individual cells
To monitor the “genuine” Ca2+ signal, we required a customary chemical fluorescent Ca2+ dye whose spectral properties would permit optical interrogation, independently from that for the CFP/yellow fluorescent protein (YFP) FRET signals of TN-L15. Given the spectra of CFP and YFP, candidate dyes included those with ultraviolet excitation (e.g., Indo-1 and Fura-2), and others with far red-shifted emission (e.g., Rhod-2). Of these, the ultraviolet candidates were favored because they readily permitted ratiometric determination of Ca2+ concentration. One ultraviolet dye, Fura-2, did exhibit detectable (albeit small) cross talk with CFP/YFP FRET (not shown).
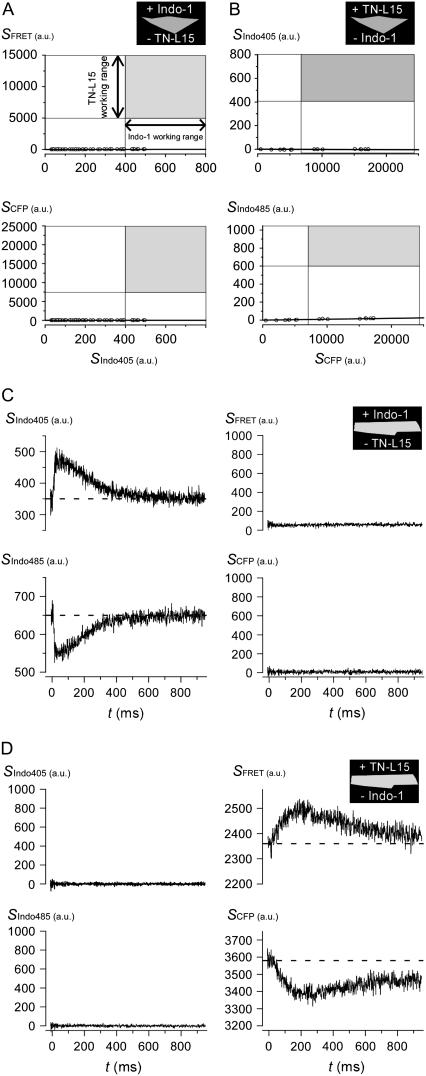
We therefore favored the use of the ultraviolet dye Indo-1, which featured no detectable cross talk with CFP/YFP FRET under explicit quantitative testing, as follows. An initial set of experiments was performed in HEK293 cells. When Indo-1 was loaded into HEK293 cells lacking TN-L15 expression, fluorescence output from CFP and FRET cubes (SCFP and SFRET) was negligible, despite working levels of Indo-1 as detected by Indo-1 fluorescence (SIndo405) through the Indo405 cube (Fig. 1 A). In particular, each symbol plots SCFP vs. SIndo405 (bottom), or SFRET vs. SIndo405 (top), wherein each symbol corresponds to a separate cell. The gray boxes represent the working ranges of TN-L15 (ordinate) and Indo-1 (abscissa) signals in single cardiac myocytes, as spanned by resting and contracting conditions. The negligible ordinate values of symbols, relative to the green regions, explicitly document the absence of Indo-1 to CFP/YFP cross talk. Conversely, for HEK293 cells expressing TN-L15 but lacking Indo-1 loading, fluorescence output from Indo405 and Indo485 cubes (SIndo405 and SIndo485) was negligible, despite working levels of TN-L15 (SCFP). The near-zero ordinate values for plots of SIndo405 vs. SCFP (Fig. 1 B, top), or SIndo485 vs. SCFP (bottom), demonstrates the absence of appreciable CFP/YFP to Indo-1 cross talk.
FIGURE 1.
Distinctive sensor spectra permitted independent detection of Indo-1 and TN-L15 in the same cells. (A) Data points represent HEK293 cells, loaded with Indo-1 and lacking TN-L15, that were imaged under CFP (bottom panel) and FRET (top panel) cubes. The gray box represents the working range of TN-L15 (y axis) and Indo-1 (x axis) signals in cardiac myocytes between resting and contracting conditions. Line of data regression falls near zero. (B) Data points represent HEK293 cells, expressing TN-L15 and lacking Indo-1, that were imaged under Indo405 (top panel) and Indo485 (bottom panel) cubes. Format similar to panel A. (C) Myocytes loaded with Indo-1 and lacking TN-L15, were stimulated to contract and imaged under Indo405, Indo485, CFP, and FRET cubes. Average of 10 traces for each cube were shown. (D) Myocytes expressing TN-L15 and lacking Indo-1 were imaged. Procedure same as panel C.
Additional experiments within myocytes further substantiated the lack of cross talk between Indo-1 and TN-L15. Myocytes loaded with Indo-1, but lacking TN-L15, were field-stimulated to contract once under each filter cube (at time 0) and imaged. One “cycle” of measurements therefore incorporated data obtained under Indo405, Indo485, CFP, and FRET cubes. As data were highly reproducible over subsequent contractions, we frequently signal averaged data over 10 such cycles. Exemplar traces of this kind are displayed in Fig. 1 C, which illustrates the characteristic rise and fall of respective Indo405 and Indo485 signals (left) during a triggered cytoplasmic Ca2+ transient. Importantly, neither SCFP nor SFRET signals were detected under these same conditions, demonstrating the absence of cross talk from Indo-1 into TN-L15 optical channels in myocytes. By contrast, for myocytes expressing TN-L15, but lacking Indo-1, the Indo405 and Indo485 channels are devoid of appreciable signal (Fig. 1 D, left), whereas SCFP and SFRET channels clearly exhibit TN-L15 responsiveness to a triggered Ca2+ transient (right). This outcome directly confirms the absence of cross talk from TN-L15 to Indo-1 optical channels within the myocardial context.
Simultaneous detection of Indo-1 and TN-L15 signals in cardiac myocytes
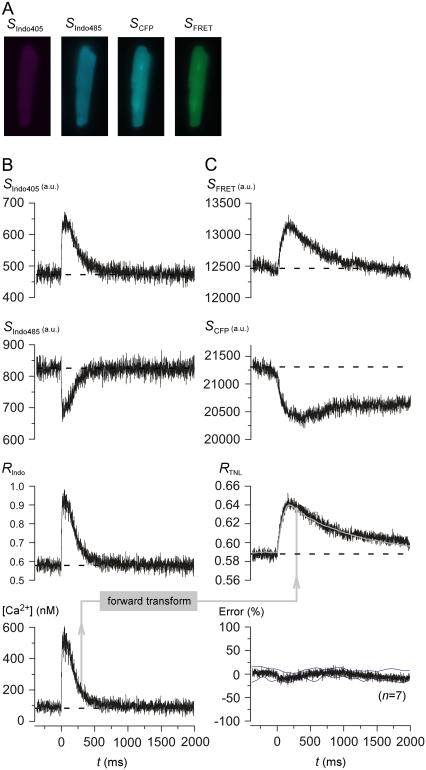
Having established that Indo-1 and TN-L15 permit independent readouts, we proceeded to simultaneously detect both sensor signals from single myocytes. In these experiments, cardiocytes expressing TN-L15 were also loaded with Indo-1, and imaging was then performed under Indo405, Indo485, CFP, and FRET cubes (Fig. 2 A). For Indo-1 outputs, exemplar traces show the respective rise and fall of Indo405 and Indo485 signals (Fig. 2 B, SIndo405 and SIndo485) during a field-stimulated Ca2+ transient. Note that the time course of these Indo-1 transients was closely similar to that obtained in the absence of TN-L15 expression (Fig. 1 C), suggesting that our expression of TN-L15 does not appreciably alter native Ca2+ transients. The ratio of SIndo405 and SIndo485 signals (Fig. 2 B, RIndo) was then used to calculate the phasic time course of free intracellular Ca2+ concentration (Fig. 2 B, [Ca2+]), according to the classic equation (5)
 |
(1) |
where the apparent dissociation constant Kd,Indo was 800 nM as previously established for myocytes (19); the respective maximal and minimal ratio values, under Ca2+-bound and free conditions (Rmax,Indo, Rmin,Indo), were 2.715 and ∼0.47; the β-parameter (= ratio of SIndo485 signals for Indo-1 under Ca2+-free and bound conditions) was 2.632 (Table 1).
FIGURE 2.
Simultaneous detection of TN-L15 and Indo-1 signals from single contractions in cardiac myocytes. (A) Cardiac myocytes expressing TN-L15 were simultaneously loaded with Indo-1 and imaged under Indo405, Indo485, CFP, and FRET cubes. (B) Exemplar traces showing the simultaneous rise of Indo405 signal (SIndo405) (top panel) and the fall of Indo485 signal (SIndo485) (second panel) when myocytes were field-stimulated at time 0. The Indo-1 ratio, RIndo (third panel) (RIndo = SIndo405/SIndo485) was converted into free intracellular Ca2+ concentration, [Ca2+] (bottom panel), according to Eq. 1. Average of 10 traces for each cube were shown. (C) Exemplar traces showing the simultaneous rise of FRET signal (SFRET) (top panel) and fall of CFP signal (SCFP) (second panel) at time 0. The TN-L15 ratio, RTNL,expt = SFRET/SCFP (third panel, black). RTNL,sim (third panel, gray) was obtained using our “forward transform”. The average percentage error between the RTNL,expt and RTNL,sim (error normalized to the peak of RTNL,sim) (n = 7) was plotted with the standard deviations shown as thin black lines (bottom panel).
TABLE 1.
Refined Ca2+ sensor parameters for live cardiocytes
| Parameter | Final sensor parameters for myocyte experiments |
|---|---|
| Indo-1 Kd,Indo | 800 nM |
| Indo-1 Rmin,Indo | ∼0.47* |
| Indo-1 Rmax,Indo | 2.71 |
| Indo-1 β | 2.63 |
| TN-L15 Kd,TNL | 815 nM† |
| TN-L15 Rmin,TNL | 0.538 |
| TN-L15 Rmax,TNL | 1.27 |
| TN-L15 α | 1.47 |
Subject to minor cell-to-cell optimization (Supplementary Material, section 2).
Calculated with the α-value listed in bottom row.
Concerning TN-L15 signals, exemplar traces from the same cell illustrate the respective rise and fall of SFRET and SCFP signals (Fig. 2 C), confirming robust sensor function during single Ca2+ transients. In principle, the ratio of these two signals (Fig. 2 C, RTNL = SFRET / SCFP, black trace) should then be quantitatively related to the actual [Ca2+] waveform (Fig. 2 B, bottom). Indeed, this general interrelation between RTNL and [Ca2+] was qualitatively reproduced across many myocytes. However, RTNL seemed kinetically slow compared to [Ca2+]: RTNL remained elevated above baseline levels at the 2000 ms, whereas [Ca2+] had long reached resting levels by this time point. Such kinetic slowing is common among genetically encoded Ca2+ sensors (9,11).
Determination of TN-L15 sensor parameters within live myocytes
Given the apparent reproducibility of the relation between [Ca2+] and RTNL, we wondered whether a quantitatively accurate “transform” between these two entities could be deduced. Such transforms would find broad utility among genetically encoded Ca2+ sensors, but the existence of these mapping functions has thus far been little explored (9). Toward this end, a prerequisite was to determine key sensor parameters appropriate for the intracellular milieu of myocytes. The crucial Indo-1 parameters were Rmax,Indo, Rmin,Indo and β, as defined above. The analogous TN-L15 parameters were Rmax,TNL, Rmin,TNL, and α (= ratio of SCFP for TN-L15, under Ca2+-free and bound conditions). To determine these parameters, we studied either myocytes that lacked TN-L15 expression while loaded with Indo-1 (for specification of Indo-1 parameters), or myocytes expressing TN-L15 without Indo-1 loading (for TN-L15 parameters). To ensure strong elevation of intracellular Ca2+ during determination of Rmax, cardiocytes were preexposed for 15 min to a bath solution containing 5 μM 2,3-butanedione monoxime (BDM) to counter hypercontraction during subsequent Ca2+ elevation, and 5 μM cyclopiazonic acid (CPA) with 10 μM ryanodine to limit buffering of intracellular Ca2+ during ensuing maneuvers that elevate Ca2+. The pretreatment was followed by a 15-min exposure to 5 μM ionomycin within a Tyrode's solution containing elevated 10 mM Ca2+, before imaging for Rmax values. To obtain Rmin parameters, myocytes were exposed for 15 min to 5 μM ionomycin in a Ca2+-free Tyrode's solution (4 mM EGTA), and then subject to imaging. For the β-parameter, a myocyte was initially pretreated with BDM, CPA, and ryanodine (as above), then exposed for 15 min to 5 μM ionomycin in Ca2+-free Tyrode's solution, before measuring the Ca2+-free SIndo485 signal. Subsequently, the same myocyte was exposed to 5 μM ionomycin in a 10 mM Ca2+ Tyrode's solution for 15 min, before imaging SIndo485 in saturating Ca2+; β was thus determined as the ratio of these SIndo485 measurements. An analogous procedure was used to determine the TN-L15 parameter-α. After refinement by a sequential procedure (Supplementary Material, section 1), the average values for sensor parameters are summarized in Table 1.
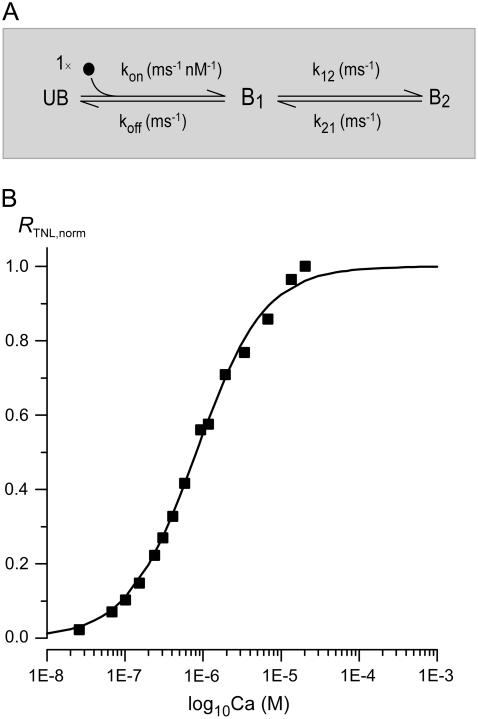
Mapping from [Ca2+] into RTNL via a three-state mechanism
With sensor parameters in hand, we tested for the existence of a quantitative relationship between dynamic [Ca2+] inputs and TN-L15 outputs (RTNL). Because the steady-state relationship between RTNL and [Ca2+] conforms well to a Hill function with a coefficient of unity (12), we considered approximate mechanistic schemes in which a single Ca2+ binding site dominates control of FRET conformational changes. Configurations encompassing only Ca2+-unbound (UB) and bound (B) states invariably failed to cohere to the experimental data in Fig. 2, with inability to explain the degree of kinetic slowing in the falling phase of RTNL (not shown). By contrast, the next simplest model, in which there are two Ca2+-bound conformations (Fig. 3 A, B1 and B2), proved remarkably successful in mapping Indo-1-derived [Ca2+] into experimentally measured RTNL. This mapping is explicitly illustrated (Fig. 2, B and C) by the conversion of the experimentally determined [Ca2+] transient (Fig. 2 B, bottom) into the predicted RTNL,sim (Fig. 2 C, gray curve in third row), via a “forward transform” algorithm. The specifics of the transformation, with its in-depth validation, are as follows.
FIGURE 3.
TN-L15 mechanism for mapping between [Ca2+] and RTNL, and the steady-state profile of this mapping function. (A) Three-state mechanism mapping [Ca2+] into RTNL, with parameters shown in Table 2. (B) Model prediction of steady-state TN-L15 response. The black curve is the TN-L15 steady-state response predicted using our model parameters according to Eq. 5. The black data points were obtained from Heim et al. (12) but with the [Ca2+] divided by TN-L15 α (estimated to be 1.47). The scaling was necessary because the data points were plotted using the apparent TN-L15 Kd, which is the product of TN-L15 α and the true TN-L15 Kd, whereas the black curve was plotted using our true TN-L15 Kd. The results of scaling were the black data points plotted in Fig. 3 B.
To compute RTNL,sim, we presumed the Ca2+-unbound state (UB) to be associated with a FRET ratio of Rmin,TNL, whereas both Ca2+-bound states (B1, B2) would be affiliated with the same maximal FRET ratio of Rmax,TNL. Accordingly, RTNL at any instant of time would be given by
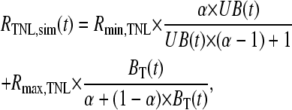 |
(2) |
where UB(t) is the probability of occupying state UB at time t, and BT(t) is the sum of the probabilities of occupying B1 and B2 at time t. All that remained, then, was to evaluate UB(t) and BT(t) via numerical integration of the equations corresponding to Fig. 3A, utilizing the experimentally determined [Ca2+] transient (Fig. 2 B, bottom) as a multiplicative factor specifying the overall rate constant from UB to B1. For initial conditions at a time point before the onset of contraction (typically t ∼ −400 ms), we set UB(t), B1(t), and B2(t) to their predicted steady-state values with respect to the average resting [Ca2+] ([Ca2+]rest) determined from TN-L15 measurements, according to the analytical solutions
 |
(3A) |
 |
(3B) |
 |
(3C) |
From this initial time point onward, UB(t), B1(t) and B2(t) were calculated by Euler's integration using the iterative equations
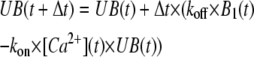 |
(4A) |
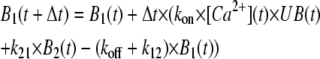 |
(4B) |
 |
(4C) |
Given the strategy embodied in Eqs. 2–4, we asked whether a single set of rate constants (Fig. 3 A, kon, koff, k12, and k21) could produce close conformation of simulated RTNL,sim to experimentally determined RTNL dynamic waveforms, while simultaneously predicting the steady-state relation between RTNL and [Ca2+]. Accordingly, for the exemplar myocyte in Fig. 2, we numerically minimized the sum of squared errors between RTNL,sim (Fig. 2 C, gray trace) and the experimental RTNL waveform (Fig. 2 C, gray trace), yielding the set of rate constant parameters in Table 2. Reassuringly, the steady-state TN-L15 response entailed by these parameters (Fig. 3 B, smooth black curve) closely matched the experimental relation (symbols). The predicted response is computed from the following relation
 |
(5) |
TABLE 2.
TN-L15 three-state mechanism parameters
| Parameter | Value |
|---|---|
| kon | 3.64 × 10−6 nM−1 ms−1 |
| koff | 0.0123 ms−1 |
| k12 | 0.00498 ms−1 |
| k21 | 0.00159 ms−1 |
To assess the generality of this forward transform, we mapped [Ca2+] to RTNL,sim in other myocytes, using the same set of parameters (Table 2). In fact, the average percentage error between RTNL,sim and the experimentally observed RTNL was nearly zero with small standard deviations (Fig. 2 C, bottom), confirming generalization across cells.
As a more stringent test, we considered whether the forward transform would suffice even during closely spaced Ca2+ transients, in which TN-L15 responses would become fused. Appropriate prediction of nonlinear summation during these fusion events represents a challenging regime for predictive algorithms (20). Fig. 4 shows the results of experiments in which myocytes were stimulated twice with a coupling interval of 600 ms. The format is closely similar to that for the single-twitch experiment in Fig. 2, and double- and single-twitch data were often obtained in the same myocytes. In fact, the same exemplar myocyte is used for Figs. 2 and 4. The forward transform output (Fig. 4 B, third row, gray curve) indicates excellent prediction of fused events. Moreover, the near-zero average percentage error (Fig. 4 B, bottom) confirms the quality of the predictions for overlapping responses over multiple cells. These results (Figs. 2 and 4) support the broad applicability of the forward transform.
FIGURE 4.
Simultaneous detection of TN-L15 and Indo-1 signals from fused double contractions in cardiac myocytes. Format as in Fig. 2. Average of six traces for each cube were shown.
Back calculation of rapid Ca2+ transients from TN-L15 FRET responses
Given the existence of a quantitative relation between dynamic Ca2+ concentration waveforms and TN-L15 FRET responses, we wondered whether the time course of rapid Ca2+ transients could be deduced from TN-L15 signals, based on an inversion of the aforementioned forward transform. Such a capability would enhance the potential of TnC-based Ca2+ sensors for quantitative dynamic in vivo measurements. Toward this end, we devised and tested the following “backward transform”.
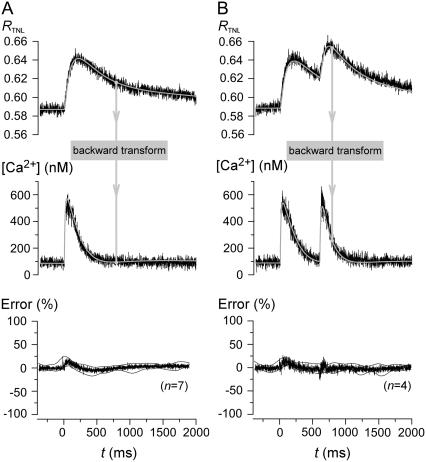
Because the forward transform resembles low-pass filtering, the reverse operation would approximate a high-pass filtering operation, which would greatly amplify noise. To avoid confounding noise amplification, an initial step is to fit smooth functions to experimentally measured TN-L15 RTNL outputs, yielding RTNL,fit waveforms (Fig. 5 A, top row, gray trace). BT(t) could then be computed as
 |
(6) |
FIGURE 5.
TN-L15 model back-calculates rapid Ca2+ transients based only on the slow TN-L15 response. (A) The TN-L15 ratio, RTNL,expt (top panel, black) for single-pulse contraction was fitted with a smooth function to give RTNL,fit (top panel, gray). [Ca2+] was calculated from RTNL,fit using our “backward transform” to give [Ca2+]back (t) (middle panel, gray). Indo-predicted [Ca2+] (middle panel, noisy) is shown for comparison. The average percentage error between [Ca2+]back (t) and Indo-predicted [Ca2+] (error normalized to the peak of [Ca2+]back) (n = 7) was plotted with the standard deviations shown as thin black lines (bottom panel). (B) Back-calculation for double-pulse contractions (format same as panel A).
With knowledge of BT(t), B1(t) and B2(t) are then deduced in a straightforward manner. Their initial values, at a time point before contraction (e.g., at −400 ms), are specified by considering their steady-state distribution according to  Since
Since 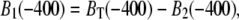 it follows that
it follows that
 |
(7) |
From this instant of time onwards, we could use numerical integration to calculate B1 and B2 using the iterative relations
 |
 |
(8) |
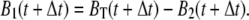 |
(9) |
To deduce the back-calculated [Ca2+]back, we recalled that UB(t) = 1 − BT(t), so that
 . .
|
Rearranging yields
 |
We therefore solved for [Ca2+]back as
 |
(10) |
Equations 6–10 thereby enabled mapping from RTNL,fit to [Ca2+]back. Fig. 5 A illustrates this backward transform for an exemplar myocyte (gray waveforms, top and middle row). Visual inspection confirms a close similarity between predicted and measured [Ca2+] (middle row, gray and black waveforms). The near-zero average percentage errors for population data establishes the adequacy of the backward transform over multiple cells (Fig. 5 A, bottom row). Fig. 5 B reveals equally impressive performance of the backward transform for the dual-stimulus paradigm. Overall, the existence of a quantitative relation between [Ca2+] and TN-L15 FRET responses, together with effective forward and backward transforms, heightens the potential utility of TnC-based GECIs for in vivo imaging.
DISCUSSION
This study establishes the quantitative reproducibility of interrelations between rapid Ca2+ concentration transients and FRET signals from genetically encoded Ca2+ sensors with TnC as the Ca2+-sensing element (12,15). This reproducibility permits deduction of computational algorithms that map between Ca2+ “inputs” and FRET “outputs”, thereby furnishing means to compensate for the kinetic slowing inherent to current GECIs (9,11). These findings enhance the prospects for deployment of GECIs within the in vivo context (7), as developed below.
TnC-based GECIs resist interference by endogenous CaM and contractile elements
Unlike many GECIs that incorporate CaM as the Ca2+-motile module (13,21), TnC-based sensors promise less sensitivity to interference by endogenous CaM (11,12,15). However, one remaining concern for these sensors has been the potential for interference by endogenous contractile proteins within striated muscle (13). Thus, whereas these GECIs may perform consistently within neurons (11), they may prove inadequate in contractile tissues. Accordingly, the findings in this study are particularly significant because experimental tests were performed in cardiac myocytes, where both endogenous CaM and contractile proteins are found in abundance (2). The well-behaved profile of TnC-based GECIs within this environment furnishes strong empirical evidence for insensitivity to these forms of interference.
To further exclude the possibility that TnC-based GECIs might be compromised by incorporation into the matrix of muscle contractile proteins, we performed fluorescence recovery after photobleaching (FRAP) experiments on TN-L15 expressed in myocytes. Rapidly motile recovery of photobleached segments (over ∼10 s) directly excludes appreciable incorporation (not shown). Otherwise, darkened regions should persist from appreciably longer durations. This stands in contrast to older generation GECIs based on CaM, wherein a large fraction of such sensors was not freely diffusible as gauged by FRAP (8).
Such resistance to interference from endogenous factors may also be shared by newer generations of CaM-based sensors GCaMP2 reportedly functions well within intact heart of transgenic mice (9). More intriguingly, computationally redesigned CaM/peptide elements within GECIs also hold enormous promise for enhanced resistivity to endogenous interference (13).
Algorithmic correction for slow kinetics of current-generation GECIs
Beyond reproducibility of GECI sensor responses to Ca2+ transients, a remaining limitation is the relatively slow kinetic responsiveness of current sensors, compared with the characteristic time constants of native Ca2+ transients (10). Here we demonstrate that first-order quantitative maps between Ca2+ and sensor outputs may be deduced from simultaneous recordings of a “gold-standard” Ca2+ input signal and simultaneous GECI sensor outputs. These maps may then be used to infer rapid Ca2+ transient behavior from slowed GECI sensor responses, thereby expanding the capabilities of current-generation sensors.
The approach we have taken for deducing these maps appears convenient and generalizable to other GECIs. The paradigm of obtaining simultaneous recordings of Ca2+ concentration “inputs” and FRET sensor “outputs” greatly facilitates deduction of approximate transform mechanisms, with appropriate emphasis on those features with greatest relevance for native Ca2+ transient behavior. The adequacy and simplicity of the sensor scheme in Fig. 3 A suggest that a full-bore mechanism may not be required to afford reasonably accurate dynamic maps between Ca2+ waveforms and FRET responses. It will be interesting to explore whether a like approach may prove successful for other GECIs like GCaMP2 (9) and novel computationally redesigned CaMs (13).
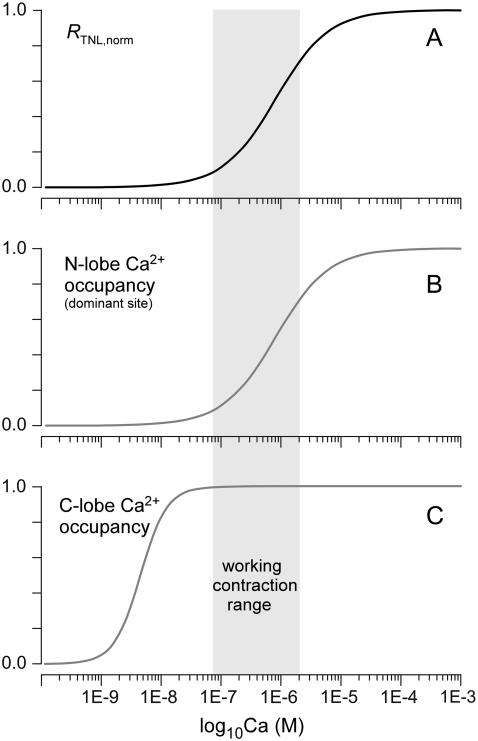
It is nonetheless worth emphasizing the likely profile of more in-depth formulations of TnC-based sensors. In particular, how can an approximate scheme (Fig. 3 A) emphasize the dominance of a single Ca2+ binding event, whereas TnC clearly possesses four Ca2+ binding sites? Insight into this question arises from the fact that the two Ca2+ binding sites in the C-terminal lobe of TnC may exhibit very high affinity and slow kinetics, such that these sites may already be constitutively occupied if resting Ca2+ levels exceed a certain minimum level (22–24). This would leave Ca2+ binding to the two sites in the N-terminal lobe as potentially important in gating the FRET response of GECIs. Even here, there is precedent from cardiac TnC that one of these sites may predominate in controlling physiological phasic Ca2+ responses (2). Given this context, we hypothesize that the in-depth mechanism for TN-L15 may include ancillary Ca2+ binding sites that are constitutively occupied in resting Ca2+, leaving a single key Ca2+ site to control FRET responses during cardiac twitch Ca2+ events (Fig. 6). Ca2+ binding to the C-terminal lobe sites of TnC may be necessary, but insufficient to trigger a TnC sensor conformational change that is detectable by an alteration in FRET. Thus, there is no change in the baseline of RTNL within the Ca2+ concentration range from 0 to 100 nM. As Ca2+ sweeps higher above the ∼100 nM resting level, the relevant N-terminal lobe site becomes progressively occupied, and this is reflected rather directly by variations in FRET (RTNL). The Ca2+ occupancy of the C-terminal sites may well impact the nature of how Ca2+ binding to the critical N-terminal site is transduced to changes in FRET. However, since both C-terminal sites may be saturated at Ca2+ concentrations greater than ∼100 nM, RTNL increases according to Ca2+ occupancy of the key N-terminal site over this range of Ca2+. Hence, RTNL would rise with a Hill coefficient of unity, just as observed experimentally for TN-L15 (12).
FIGURE 6.
Hypothesized full-bore Ca2+ response of TN-L15 Ca2+ sensor. (A) FRET ratio (RTNL) change as a function of steady-state Ca2+ concentration, reproduced from fit in Fig. 3 B. (B) Schematic of Ca2+ occupancy of key N-terminal lobe Ca2+ site as a function of Ca2+ concentration. This occupancy is the “rate-limiting step” that specifies FRET changes; hence, the shape of this curve corresponds closely to that in panel A. (C) Hypothetical Ca2+ occupancy of C-terminal lobe Ca2+ sites as a function of Ca2+ concentration. This occupancy might be obligatory for subsequent FRET changes controlled by N-terminal lobe sites, but C-terminal lobe occupancy may by itself be insufficient to drive FRET changes.
Limitations to kinetic compensation of GECIs
There are limitations to the back-calculation algorithm, which merit emphasis. First, before back calculation, we found it necessary to smooth the raw TN-L15 outputs (RTNL waveforms). Specifically, we fit idealized mathematical functions to the actual RTNL waveforms. This procedure was necessary because back-calculation is rather like taking derivatives of the RTNL waveforms; unfettered noise would become intolerably amplified in the procedure. Although the smoothing procedure is of little consequence if actual Ca2+ transients lack high-frequency components, this procedure would inevitably preclude back calculation of high-frequency components in the Ca2+ transients. As a rough estimate, empirical tests indicate that Ca2+ transient components exceeding ∼20 Hz cannot be accommodated by the current back-calculation algorithm. Thus, it is unlikely that sub-10-ms Ca2+ sparks in heart muscle could be inferred from RTNL outputs (25). Nonetheless, much useful Ca2+ transient information (with components <∼50 Hz) can be recaptured via the back-calculation algorithm.
Overall, as future generations of GECIs are developed, their intrinsic kinetic responsiveness promises to improve. In this evolution, forward-backward “transforms” as devised here will continue to expand the kinetic boundary for inferences regarding the actual underlying Ca2+ signaling events.
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Supplementary Material
Acknowledgments
We thank Peter Bedner for tireless aid with myocyte isolation and FRAP analysis.
This work was supported by grants from the National Institute of Mental Health (R01 MH65531 to D.T.Y.), National Heart, Lung, and Blood Institute (R37 HL076795 to D.T.Y.), and Kleberg Foundation. An abstract version of some of this work was awarded a Biophysical Society SRAA Poster Competition Award in 2006 (to L.H.T.).
Editor: Eduardo Perozo.
References
- 1.Berridge, M. J., M. D. Bootman, and H. L. Roderick. 2003. Calcium signalling: dynamics, homeostasis and remodelling. Nat. Rev. Mol. Cell Biol. 4:517–529. [DOI] [PubMed] [Google Scholar]
- 2.Bers, D. M. 2001. Excitation-Contraction Coupling and Cardiac Contractile Force. Kluwer, Boston.
- 3.Deisseroth, K., H. Bito, and R. W. Tsien. 1996. Signaling from synapse to nucleus: postsynaptic CREB phosphorylation during multiple forms of hippocampal synaptic plasticity. Neuron. 16:89–101. [DOI] [PubMed] [Google Scholar]
- 4.Liang, H., C. D. DeMaria, M. G. Erickson, M. X. Mori, B. A. Alseikhan, and D. T. Yue. 2003. Unified mechanisms of Ca2+ regulation across the Ca2+ channel family. Neuron. 39:951–960. [DOI] [PubMed] [Google Scholar]
- 5.Grynkiewicz, G., M. Poenie, and R. Y. Tsien. 1985. A new generation of Ca2+ indicators with greatly improved fluorescence properties. J. Biol. Chem. 260:3440–3450. [PubMed] [Google Scholar]
- 6.Martin, B. R., B. N. Giepmans, S. R. Adams, and R. Y. Tsien. 2005. Mammalian cell-based optimization of the biarsenical-binding tetracysteine motif for improved fluorescence and affinity. Nat. Biotechnol. 23:1308–1314. [DOI] [PubMed] [Google Scholar]
- 7.Griesbeck, O. 2004. Fluorescent proteins as sensors for cellular functions. Curr. Opin. Neurobiol. 14:636–641. [DOI] [PubMed] [Google Scholar]
- 8.Hasan, M. T., R. W. Friedrich, T. Euler, M. E. Larkum, G. Giese, M. Both, J. Duebel, J. Waters, H. Bujard, O. Griesbeck, R. Y. Tsien, T. Nagai, et al. 2004. Functional fluorescent Ca2+ indicator proteins in transgenic mice under TET control. PLoS Biol. 2:e163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tallini, Y. N., M. Ohkura, B. R. Choi, G. Ji, K. Imoto, R. Doran, J. Lee, P. Plan, J. Wilson, H. B. Xin, A. Sanbe, J. Gulick, et al. 2006. Imaging cellular signals in the heart in vivo: cardiac expression of the high-signal Ca2+ indicator GCaMP2. Proc. Natl. Acad. Sci. USA. 103:4753–4758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Pologruto, T. A., R. Yasuda, and K. Svoboda. 2004. Monitoring neural activity and [Ca2+] with genetically encoded Ca2+ indicators. J. Neurosci. 24:9572–9579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Reiff, D. F., A. Ihring, G. Guerrero, E. Y. Isacoff, M. Joesch, J. Nakai, and A. Borst. 2005. In vivo performance of genetically encoded indicators of neural activity in flies. J. Neurosci. 25:4766–4778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Heim, N., and O. Griesbeck. 2004. Genetically encoded indicators of cellular calcium dynamics based on troponin C and green fluorescent protein. J. Biol. Chem. 279:14280–14286. [DOI] [PubMed] [Google Scholar]
- 13.Palmer, A. E., M. Giacomello, T. Kortemme, S. A. Hires, V. Lev-Ram, D. Baker, and R. Y. Tsien. 2006. Ca2+ indicators based on computationally redesigned calmodulin-peptide pairs. Chem. Biol. 13:521–530. [DOI] [PubMed] [Google Scholar]
- 14.Colomer, J. M., M. Terasawa, and A. R. Means. 2004. Targeted expression of calmodulin increases ventricular cardiomyocyte proliferation and deoxyribonucleic acid synthesis during mouse development. Endocrinology. 145:1356–1366. [DOI] [PubMed] [Google Scholar]
- 15.Mank, M., D. F. Reiff, N. Heim, M. W. Friedrich, A. Borst, and O. Griesbeck. 2006. A FRET-based calcium biosensor with fast signal kinetics and high fluorescence change. Biophys. J. 90:1790–1796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hardy, S., M. Kitamura, T. Harris-Stansil, Y. Dai, and M. L. Phipps. 1997. Construction of adenovirus vectors through Cre-lox recombination. J. Virol. 71:1842–1849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Johns, D. C., R. Marx, R. E. Mains, B. O'Rourke, and E. Marban. 1999. Inducible genetic suppression of neuronal excitability. J. Neurosci. 19:1691–1697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Alseikhan, B. A., C. D. DeMaria, H. M. Colecraft, and D. T. Yue. 2002. Engineered calmodulins revealed the unexpected eminence of Ca2+ channel inactivation in controlling heart excitation. Proc. Natl. Acad. Sci. USA. 99:17185–17190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bassani, J. W., R. A. Bassani, and D. M. Bers. 1995. Calibration of indo-1 and resting intracellular [Ca]i in intact rabbit cardiac myocytes. Biophys. J. 68:1453–1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kuo, B. C. 1975. Automatic Control Systems. Prentice-Hall, Englewood Cliffs, NJ.
- 21.Miyawaki, A., J. Llopis, R. Heim, J. M. McCaffery, J. A. Adams, M. Ikura, and R. Y. Tsien. 1997. Fluorescent indicators for Ca2+ based on green fluorescent proteins and calmodulin. Nature. 388:882–887. [DOI] [PubMed] [Google Scholar]
- 22.Gordon, A. M., E. Homsher, and M. Regnier. 2000. Regulation of contraction in striated muscle. Physiol. Rev. 80:853–924. [DOI] [PubMed] [Google Scholar]
- 23.Potter, J. D., and J. Gergely. 1975. The calcium and magnesium binding sites on troponin and their role in the regulation of myofibrillar adenosine triphosphatase. J. Biol. Chem. 250:4628–4633. [PubMed] [Google Scholar]
- 24.Robertson, S. P., J. D. Johnson, and J. D. Potter. 1981. The time-course of Ca2+ exchange with calmodulin, troponin, parvalbumin, and myosin in response to transient increases in Ca2+. Biophys. J. 34:559–569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Cheng, H., W. J. Lederer, and M. B. Cannell. 1993. Calcium sparks: elementary events underlying excitation-contraction coupling in heart muscle. Science. 262:740–744. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.