Abstract
Charged residues in the S4 transmembrane segment of voltage-gated cation channels play a key role in opening channels in response to changes in voltage across the cell membrane. However, the molecular mechanism of channel activation is not well understood. To learn more about the role of the S4 in channel gating, we constructed chimeras in which S4 segments from several divergent potassium channels, Shab, Shal, Shaw, and Kv3.2, were inserted into a Shaker potassium channel background. These S4 donor channels have distinctly different voltage-dependent gating properties and S4 amino acid sequences. None of the S4 chimeras have the gating behavior of their respective S4 donor channels. The conductance–voltage relations of all S4 chimeras are shifted to more positive voltages and the slopes are decreased. There is no consistent correlation between the nominal charge content of the S4 and the slope of the conductance–voltage relation, suggesting that the mutations introduced by the S4 chimeras may alter cooperative interactions in the gating process. We compared the gating behavior of the Shaw S4 chimera with its parent channels, Shaker and Shaw, in detail. The Shaw S4 substitution alters activation gating profoundly without introducing obvious changes in other channel functions. Analysis of the voltage-dependent gating kinetics suggests that the dominant effect of the Shaw S4 substitution is to alter a single cooperative transition late in the activation pathway, making it rate limiting. This interpretation is supported further by studies of channels assembled from tandem heterodimer constructs with both Shaker and Shaw S4 subunits. Activation gating in the heterodimer channels can be predicted from the properties of the homotetrameric channels only if it is assumed that the mutations alter a cooperative transition in the activation pathway rather than independent transitions.
Keywords: Shaker, voltage-dependent gating, patch clamp
introduction
Voltage-dependent cation channels respond to changes in the electric field across the cell membrane by undergoing conformational changes that open and close an ion-permeable pore. These conformational changes involve the rearrangement of charges within the channel protein, making the rates of the conformational changes voltage dependent. The movement of the charge within the channel protein can be measured as gating current (Schneider and Chandler, 1973; Armstrong and Bezanilla, 1974; Keynes and Rojas, 1974; Stühmer et al., 1991; Bezanilla et al., 1991, 1994; Schoppa et al., 1992; Stefani et al., 1994; Zagotta et al., 1994 a, 1994b). The elucidation of the molecular mechanism of the voltage- dependent conformational change has been a major goal of ion channel biophysics. This effort has been facilitated by the combination of powerful electrophysiological techniques and the ability to determine and alter the primary structure of channel proteins by recombinant DNA technology. For voltage-gated potassium channels, the minimum requirement to make a functional channel is the association of four alpha subunits, each with a core region containing six putative transmembrane segments and a pore loop (MacKinnon, 1991; Heginbotham and MacKinnon, 1992; Kavanaugh et al., 1992; Liman et al., 1992). A distinctive feature of voltage-dependent cation channels is the fourth transmembrane segment (S4). The S4 is ∼21 amino acids long with positively charged basic amino acids, either arginine or lysine, at every third position, separated by hydrophobic and neutral residues (Noda et al., 1984, 1986; Salkoff et al., 1987; Tanabe et al., 1987, 1988; Papazian et al., 1987; Tempel et al., 1988; Baumann et al., 1988; Ellis et al., 1988; Kayano et al., 1988). Because of the high nominal charge density in this membrane spanning segment and the fact that the motif is highly conserved among voltage-gated cation channels, the S4 was initially proposed to be part of the voltage sensor (Noda et al., 1986; Catterall, 1988; Durrell and Guy, 1992).
If the S4 is part of the voltage sensor, the S4 and its charges should move through the electric field in response to membrane depolarization. Evidence from both skeletal muscle sodium channels and Shaker potassium channels indicates that a conformational change in the S4 or in adjacent channel regions occurs in the channel protein upon activation (Yang and Horn, 1995; Yang et al., 1996; Larsson et al., 1996; Mannuzzu et al., 1996; Aggarwal and MacKinnon, 1996; Seoh et al., 1996; Yusaf et al., 1996). Another prediction, that neutralization of S4 charges should decrease the amount of charge moved during channel activation, has also been confirmed in Shaker (Aggarwal and MacKinnon, 1996; Seoh et al., 1996). These experiments provide strong evidence for a role for the S4 in sensing voltage. However, the individual S4 charges do not seem to contribute equally to the gating charge, and properties of the charged residues other than the charge are also important determinants of gating behavior (see also Perozo et al., 1994). There is also evidence that a negatively charged residue in the S2 of Shaker potassium channels may serve as a counter ion for S4 charges and participate in the voltage-sensing process (Papazian et al., 1995; Seoh et al., 1996; Tiwari-Woodruff et al., 1997).
Mutation of nonbasic residues in the S4 through the S5 segments can also cause significant changes in voltage-dependent gating in Shaker potassium channels (Zagotta and Aldrich, 1990; Gautam and Tanouye, 1990; Lichtinghagen et al., 1990; McCormack et al., 1991, 1993; Lopez et al., 1991; Schoppa et al., 1992; Logothetis et al., 1993; Aggarwal and MacKinnon, 1996) and in sodium channels (Auld et al., 1988). In experiments by Aggarwal and MacKinnon (1996), simultaneous substitution of several nonbasic S4 residues, with no change in the charged residues, alters the voltage range over which gating charge moves but not the total amount of gating charge moved. Mutation of noncharged residues in this region could alter the coupling between voltage sensing and opening of the channel, or could alter movement of the charge through the membrane electric field.
Evidence for cooperative transitions leading to potassium channel activation has come from studies of activation kinetics in Shaker (Sigworth, 1993; Zagotta et al., 1994 b; Bezanilla et al., 1994) and from studies of steady state channel kinetics in heteromultimeric mammalian potassium channels (Tytgat and Hess, 1992; Hurst et al., 1992). All of the several kinetic models that have been proposed to describe Shaker channel activation have in common multiple voltage-dependent transitions, with at least one transition involving the cooperative movement of subunits (Sigworth, 1993; Bezanilla et al., 1994; Zagotta et al., 1994 a; McCormack et al., 1994). Because cooperativity can be a major determinant of the voltage dependence of channel opening, assessment of the contribution of cooperative interactions to the activation process is essential to a mechanistic understanding of potassium channel gating. Mutations that change cooperativity can lead to large changes in the slope of the conductance–voltage curve, giving the erroneous appearance of a change in the total gating charge (Schoppa et al., 1992; Sigworth, 1993; Sigg et al., 1994; Zagotta et al., 1994 a).
In this study, we investigated further the role of the S4 in channel activation by generating several Shaker channel variants with chimeric S4 insertions. Much of the previous work targeted specific amino acids for replacement based on presumed functions of the residues or their conservation among related channels. Our goal was to reveal properties of the S4 not evident from this previous work. The strength of the chimeric approach is that it does not make assumptions a priori about the functional and structural importance of specific amino acids in the S4 sequence (see also Logothetis et al., 1993; Tang and Papazian, 1997; Koopmann et al., 1997).
While we generated several S4 chimeras, we focused our study on the Shaw S4 chimera because its gating behavior differs most significantly from that of the Shaker channel. Our analysis is based on a simplified model for Shaker gating, which we use to differentiate changes in the amount of charge moved during channel gating from changes in cooperativity in the activation pathway. We also examine activation in channels assembled from tandem heterodimer constructs with Shaker and Shaw S4 subunits to investigate further whether the mutations alter cooperative or independent transitions in the activation pathway. In the following paper, we determine which of the amino acid substitutions in the Shaw S4 chimera are responsible for differences in gating between Shaw S4 and Shaker and we present a more detailed model that can account for changes in both the kinetic and steady state properties of the mutant macroscopic ionic currents. The importance of these residues in determining the properties of voltage-dependent activation was not previously recognized. Preliminary results have been reported previously in abstract form (Smith-Maxwell et al., 1993, 1994; Ledwell et al., 1995).
materials and methods
Chimera Construction
All S4 chimeras were generated in a mutant form of ShB (Papazian et al., 1987; Kamb et al., 1987; Pongs et al., 1988), designated ShBΔ6-46, in which fast N-type inactivation was removed by deletion of amino acids 6–46 (Hoshi et al., 1990; Zagotta et al., 1990). This allowed us to study activation in isolation from the fast (N-type) inactivation process. This Shaker construct still undergoes a relatively slow inactivation process (C-type inactivation). The time constant for C-type inactivation of ∼1.5 s is sufficiently slow that it does not interfere with measurement of activation parameters (Hoshi et al., 1991). ShBΔ6-46 cDNA was further modified by introduction of a unique “silent” StuI restriction enzyme site 3′ to the S4 coding region, at amino acid positions 380–382 (see Fig. 1). This modification, which does not alter the amino acid sequence, was made using the polymerase chain reaction method to generate a cassette that was inserted between two naturally occurring unique restriction enzyme sites within the Shaker cDNA, StyI and NsiI. To generate the S4 chimeras, sense and antisense oligonucleotides were made based on the S4 sequences of the cloned channels Shab, Shal, Shaw, and Kv3.2 (RKShIIIA) (Butler et al., 1989; McCormack et al., 1990). Sense and antisense oligonucleotides were annealed and inserted into the S4 of ShBΔ6-46 between the unique StyI site 5′ to the S4 coding region, at amino acids 357–359, and the silent StuI site 3′ to the S4 (see Fig. 1). An S4 chimera with the S4 of Shaker inserted into Shaw was also constructed but did not express functional channels in oocytes. Verification of the inserted sequences was carried out in all instances using the dideoxy termination sequencing method (Sanger et al., 1977).
Figure 1.
Amino acid sequences for the S4 chimeras and Shaker. S4 sequences from several Drosophila potassium channels including Shab, Shal, and Shaw, and one rat potassium channel, Kv3.2 (RKShIIIA), were substituted into the Shaker background channel as indicated. The standard single letter abbreviations are used to designate amino acids in the sequences. Dashes in the substituted segment indicate amino acids identical to Shaker. Numbers above the sequences designate the position of each of the seven basic residues in Shaker. Symbols at the positions where Shaker has basic residues are in bold. Numbers beneath the sequences indicate the number of each amino acid in the Shaker sequence, taken from Tempel et al. (1987). Unique restriction enzyme sites used for construction of the chimeras are indicated. The number of amino acids in each mutant sequence that differ from Shaker is given in the column designated aa diff. The net charge of the S4 assuming one positive charge for each arginine and lysine, one negative charge for each glutamate, and no charge for histidine is given in the column designated net chg.
Terminology
Chimeric channels are designated as the species of S4 substituted for the Shaker S4 sequence in ShBΔ6-46. For instance, the Shal S4 chimera was made by substituting the S4 sequence of Shal into the Shaker channel in place of the Shaker S4 sequence. The specific amino acid replacements are shown in Fig. 1.
Dimer Construction
Tandem dimers were constructed by splicing together DNA coding for A and B protomers (Heginbotham and MacKinnon, 1992; Ogielska et al., 1995). The original protomers contain the sequence for Shaker potassium channels with the NH2-terminal deletion to remove N-type inactivation, ShH4Δ6-46. The amino acid sequences of ShB and ShH4 are nearly identical, differing by only two amino acids, both near the COOH-terminal end of the protein (Schwarz et al., 1988; Kamb et al., 1988). The A protomer contains DNA coding for a hydrophilic linker (NNNNNNAMV) inserted in frame between the coding regions of each protomer. Protomers were spliced together at the NcoI and KpnI restriction enzyme sites. Shaw S4 was spliced into the A protomer or B protomer using RsrII and NsiI restriction enzyme sites. For the protomers Ak, Bk, Aw, and Bw, the A and B designate the NH2- and COOH-terminal protomer, respectively, with each protomer containing either the Shaker (k) or Shaw S4 (w) construct. All combinations of dimers were constructed: AkBk, AwBk, AkBw, and AwBw.
Expression System
Channels were expressed in Xenopus oocytes by injection of G(5′)ppp(5′)G capped cRNA from the different channel constructs. cRNA was transcribed in vitro from linearized plasmid containing channel DNA constructs as described previously (Zagotta et al., 1989; Hoshi et al., 1990). For Shaker and the S4 chimeras, cRNA was made from KpnI-linearized DNA with T7 RNA polymerase. For Shaw and the S4 chimera in Shaw, cRNA was made from SacI- or SalI-linearized DNA with T3 RNA polymerase. For the tandem dimers, cRNA was made from EcoRI-linearized DNA with T7 RNA polymerase. Recordings were typically carried out 1–21 d after injection.
Electrophysiology and Data Analysis
Electrophysiological recordings of macroscopic ionic currents were carried out from excised membrane patches in the inside-out configuration (Hamill et al., 1981). Currents were recorded with either a List EPC-7 (Medical Systems Corp., Greenvale, NY) or an Axopatch 1B (Axon Instruments Inc., Foster City, CA) patch clamp amplifier and low pass filtered using an eight-pole Bessel filter (Frequency Devices, Inc., Haverhill, MA). Macroscopic currents from Shaw and Shal S4 were filtered at 9 kHz. All other data were filtered at 2 kHz unless otherwise noted. Two different systems were used to generate pulses and to digitize and store data for later analysis. The first was a Digital Equipment Corp. LSI 11/73-based minicomputer system (Indec Systems, Sunnyvale, CA). The second was a Macintosh-based system with hardware interface from Instrutech Corp. (Great Neck, NY) and software from HEKA (Lambrecht, Germany). Patch pipettes were constructed from VWR borosilicate glass and had initial resistances of 0.4–0.8 MΩ. No series resistance compensation was used. The maximum error due to uncompensated series resistance for this series of experiments was ∼4 mV; however, the error was typically <2 mV. Linear leak and capacitive currents were subtracted with either a P/4 protocol or appropriately scaled averaged responses to repeated 20-mV depolarizing steps, both typically from a holding potential of −110 mV. The temperature was held at 20 ± 0.2°C.
For Shaker, Shab S4, and Kv3.2 S4, conductance–voltage curves were constructed by calculation of the chord conductance (Gchord) from maximum currents (Imax) during the test pulse at several voltages, assuming a reversal potential (Vrev) of −80 mV: Gchord = Imax/(V − Vrev). Conductance–voltage curves generated in this way are minimally affected by the nonlinearity of the single channel conductance if, as with these channel species, activation occurs over a more negative voltage range. For all other channel species, conductance–voltage curves were constructed from isochronal measurements of tail currents recorded at a fixed voltage following steps to voltages that activate the channels. Typically, isochronal measurements were made between 0.2 and 1 ms after the end of the test pulse. Conductance–voltage curves were normalized to the maximum value for comparison between patches and between channel species. Conductance– voltage curves were fit by a first or fourth power Boltzmann function of the form
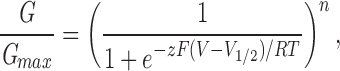 |
with n equal to 1 or 4, to determine the voltage-dependent parameters of activation. G/Gmax is the conductance normalized to the maximum value for each channel. For a first power Boltzmann function, V1/2 is the voltage at which the channels are open half maximally. For a fourth power Boltzmann function, V1/2 is the voltage at which each subunit is activated half of the time. V is the voltage of the test pulse, z is the equivalent charge, F is the Faraday constant, R is the gas constant, and T is the absolute temperature. The slope factor is equal to RT/zF.
Typically, a holding potential of −80 mV followed by a 1-s prepulse to −100 mV was used before the test pulses. For Shaw, 10-ms prepulses to −100 mV were often used. In some experiments with Shaw, a holding potential of 0 mV was used to minimize the capacitive transient during large positive voltage steps. This can be done because Shaw does not inactivate even during long depolarizations to 0 mV and its activation kinetics are not sensitive to holding potential (data not shown; see also Wei et al., 1990; Tsunoda and Salkoff, 1995).
The activation time course of the macroscopic ionic currents was fit using a single exponential function for times greater than the delay: I(t) = A{1 − exp[(−t + d)/τ]}. I(t) is the fit to the current at time t, A is the scale factor, τ is the time constant, and d is the delay required to obtain an adequate fit of a single exponential function, which was required for some channel species. Tail currents were fit with a single exponential function.
Xenopus oocytes have endogenous potassium and chloride channels, which are known to activate at more positive membrane potentials (Dascal, 1987). The currents measured in this study from channel species requiring large positive voltage steps to activate, such as from Shaw or the Shaw S4 chimera, were clearly identified as currents through the exogenously expressed potassium channels for the following reasons. Our intracellular solutions typically contained 11 mM EGTA with little or no added Ca++, which is expected to prevent activation of the calcium-activated chloride channels in Xenopus oocytes (Dascal, 1987). We never saw Shaw or Shaw S4-like currents in membrane patches from uninjected oocytes when using the standard recording solutions. Shaw S4 properties were similar whether expression levels gave currents of several nA or only 50–100 pA. This was true for Shaw as well. Also, Shaw S4 and Shaw currents clearly reverse near the calculated reversal potential for K+, between −80 and −100 mV, and not near the 0-mV reversal potential for Cl− ions. Finally, expression levels for Shaw S4 and Shaw channels could give rise to several nanoamperes of current in a single patch, which is orders of magnitude larger than endogenous currents from similar membrane patches in uninjected oocytes.
Single channel currents for Shaker, Shaw, and Shaw S4 were recorded from inside-out membrane patches using the standard solutions (see below), unless otherwise stated. Currents were digitized at 20 kHz and filtered at 2 kHz, unless otherwise stated. Single channel conductance was calculated from single channel currents recorded during steps to voltages between −50 and +80 mV by fitting a linear function to the single channel current–voltage relation. Single channel current–voltage relations for all three channels are linear in this voltage range. Results from single channel analysis of ShBΔ6-46 are taken from Hoshi et al. (1994).
Kinetic simulations were carried out as outlined in Zagotta et al. (1994 b). Transitions between conformational states are assumed to obey time-homogeneous Markov processes. Voltage- dependent rate constants are assumed to be exponentially dependent on voltage.
Solutions
The standard extracellular (pipette) solution used for these experiments contained (mM): 140 NaCl, 2 KCl, 6 MgCl2, 5 HEPES (NaOH), pH 7.1. The standard intracellular solution (bath) contained (mM): 140 KCl, 2 MgCl2, 11 EGTA, 1 CaCl2, 10 HEPES (N-methylglucamine), pH 7.2. For Shal S4, Shaw S4, and Shaw, the intracellular solution was modified by removing MgCl2 and CaCl2, unless otherwise noted. This was done because intracellular Mg++ blocks these channels in a time- and voltage-dependent manner. Block of macroscopic currents becomes evident at voltages above +80 mV for these channels (data not shown), voltages at which the probability of opening for Shal S4, Shaw S4, and Shaw has not reached a maximum value. Even though intracellular Mg++ blocks Shaker channels also, it was not necessary to record Shaker ionic currents in Mg++-free solution since Shaker is fully activated at voltages well below those at which Mg++ blocks the channel. Similar block by intracellular Mg++ has been shown for the closely related Kv1.1 potassium channel (Ludewig et al., 1993). For Shaker and Shaw S4 channels, both the time course of activation and the position of the conductance–voltage curve along the voltage axis is unchanged by Mg++ at voltages where there is little or no block (data not shown).
results
Alterations of Potassium Channel Gating by S4 Chimeric Substitutions
Chimeras were generated by substituting 21 amino acids from the S4 of several divergent potassium channels for the S4 of Shaker potassium channels (Fig. 1). The substituted potassium channel sequences were derived from Drosophila channel genes Shab, Shal, and Shaw, and from a rat Shaw homolog, Kv3.2 (RKShIIIA). Comparison of S4 amino acid sequences between these channels and Shaker reveals significant differences in amino acid composition. The sequence identity with Shaker S4 ranges from as little as 43% for Shab to as much as 62% for Kv3.2. The nominal net charge in the S4 regions ranges from +3 in Shaw to +7 in Shaker, assuming that arginine and lysine have a net charge of +1, glutamate has a charge of −1, and histidine is uncharged.
Macroscopic ionic currents and normalized conductance–voltage curves from the S4 chimeras and the Shaker parent channel are shown in Figs. 2 and 3 (see also Table I). All S4 chimeras activate at more positive voltages and with a shallower conductance–voltage relation than Shaker. However, Shaw S4 requires much larger positive steps to activate than the other chimeras. This shift in the voltage range of activation indicates that the S4 substitutions tend to bias gating toward the closed states more than the wild-type S4 sequence of Shaker. Activation kinetics of Shab S4, Shal S4, and Kv3.2 S4 are relatively fast, similar to Shaker. In contrast, activation kinetics of the Shaw S4 chimera are much slower.
Figure 2.

Macroscopic ionic currents from S4 chimeras and Shaker. Currents were measured in response to 50-ms positive voltage steps, after 1-s prepulses to −100 mV from a holding potential of −80 mV. Currents were recorded in the voltage ranges indicated in 10-mV increments. The last 6 ms of the prepulse preceding the test pulse is shown for each trace. The beginning of each test pulse is indicated by the left edge of the calibration bars.
Figure 3.
Normalized conductance–voltage curves for S4 chimeras. Means and SEM are shown for Shab S4 (▾), Shal S4 (▪), Shaw S4 (♦), Kv3.2 S4 (▴), and Shaker (•). For Shaker, Shab S4, and Kv3.2 S4, G/G max was constructed from the chord conductance as outlined in materials and methods. For Shaw S4, the normalized conductance was constructed from isochronal currents measured at 0 mV at a fixed time after reaching the maximal current, ranging between 0.4 and 1.0 ms after the positive voltage step to activate the channel. Similar measurements of isochronal tail currents were carried out for Shal S4 at −50 mV. Smooth curves through the data represent fits to the mean values for each channel species with a fourth power Boltzmann function, as outlined in materials and methods. The values from these fits are given below, with n representing the number of patches included to calculate each mean. Shaker, V1/2 = −57.4 mV, slope factor = 10.0 mV, n = 8. Shab S4, V1/2 = −58.1 mV, slope factor = 14.9 mV, n = 3. Shal S4, V1/2 = −1.1 mV, slope factor = 19.8 mV, n = 5. Shaw S4, V1/2 = 31.2 mV, slope factor = 28.4 mV, n = 7. Kv3.2 S4, V1/2 = −49.3 mV, slope factor = 25.0 mV, n = 5.
Table I.
Boltzmann Relation Fits For S4 Chimeras and Shaker
| Fourth power Boltzmann | First power Boltzmann | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Channel | V1/2 | SEM | Slope | SEM | V1/2 | SEM | Slope | SEM | n | |||||||||
| S4 chimeras | mV | mV | mV | mV | ||||||||||||||
| Kv3.2 S4 | −48.7 | ±4.2 | 25.0 | ±1.0 | −6.9 | ±3.6 | 17.8 | ±0.8 | 5 | |||||||||
| Shab S4 | −56.7 | ±4.1 | 14.1 | ±0.2 | −32.6 | ±3.9 | 10.5 | ±0.2 | 3 | |||||||||
| Shal S4 | −1.2 | ±3.1 | 19.4 | ±1.5 | +32.0 | ±2.1 | 13.7 | ±1.1 | 5 | |||||||||
| Shaw S4 | +37.3 | ±4.9 | 26.3 | ±1.9 | +81.3 | ±5.4 | 18.3 | ±1.5 | 5 | |||||||||
| ShBΔ6-46 | −56.9 | ±0.7 | 9.2 | ±1.0 | −40.0 | ±1.2 | 6.8 | ±0.8 | 8 | |||||||||
Normalized conductance was calculated for each channel construct and plotted as a function of voltage as outlined in materials and methods. The conductance–voltage relation from each patch was fit with either a first or fourth power Boltzmann function as outlined in materials and methods. For first power Boltzmann fits, V1/2 is the voltage at which the channels are open half maximally. For fourth power Boltzmann fits, V1/2 is the voltage at which half the subunits are activated. The values for V1/2 and slope are means from the fits, and n represents the number of patches used to calculate the means. The slope is the mean slope factor, RT/zF, and is a measure of the steepness of the voltage dependence of channel opening.
Contribution of S4 Charges to Voltage Dependence of Activation
One of the questions addressed in this study is whether or not a correlation exists between the charges in the S4 of the chimeras and the slope of the conductance– voltage relation. S4-charged residues have been shown to contribute to the gating charge associated with channel activation (Aggarwal and MacKinnon, 1996; Seoh et al., 1996). Although total gating charge per channel determines the slope of the conductance–voltage relation at very low open probabilities (Almers, 1978; Schoppa et al., 1992; Zagotta et al., 1994 a, 1994b; Sigg and Bezanilla, 1997), the shape and slope of the relationship at higher open probabilities is additionally influenced by interactions between subunits (Zagotta et al., 1994 a; Sigworth, 1993). Therefore, we were interested in studying the role of the S4 charges in determining the slope of the conductance–voltage relation in the voltage range of moderate probability of channel opening (Wei et al., 1990; Schoppa et al., 1992; Logothetis et al., 1993; Zagotta et al., 1994 a).
For all S4 chimeras, the conductance–voltage relation is significantly more shallow than for Shaker, as might be predicted by the smaller number of basic residues present in the mutants (Fig. 3, Table I). The most shallow slope of the conductance–voltage relation appears in Shaw S4, consistent with the S4 of Shaw having the least amount of charge (+3) of the chimeras as well as the fewest of those charges thought to contribute most to channel activation (Aggarwal and MacKinnon, 1996; Seoh et al., 1996; Larsson et al., 1996). However, an almost equivalent slope occurs with Kv3.2 S4, which has the highest nominal charge density (+6) in the S4 of all the chimeras. Kv3.2 S4 includes the same five basic residues present in Shab S4 and Shal S4, which have fewer charges. Kv3.2 S4 contains all five of the S4 basic residues thought to contribute most to the gating charge. The only charge substitution in Kv3.2 S4 is a neutralization at the seventh charged residue in Shaker, a position that seems to contribute little to the overall charge movement associated with gating (Aggarwal and MacKinnon, 1996; Larsson et al., 1996). Clearly, the similar steepness of the conductance–voltage curves for Shaw S4 and Kv3.2 S4, despite the large difference in charge content of the S4 segments, indicates that properties of the S4 other than the amount of charge are important determinants of the voltage dependence of channel opening. Furthermore, these results suggest that molecular mechanisms other than charge movement, such as subunit cooperativity, greatly influence the shape of the conductance–voltage curve.
Distinguishing between Changes in Independent and Cooperative Transitions
To investigate further the role of S4 residues and cooperative interactions between subunits in gating, we wanted to use a prototypical model for channel gating that would incorporate several key features of voltage-dependent Shaker channel activation and thus would yield insights that are readily generalizable to models with more complexity. All of the several kinetic models that have been proposed to describe Shaker channel activation have in common multiple voltage-dependent transitions with at least one transition involving the cooperative movement of subunits (Bezanilla et al., 1994; Zagotta et al., 1994 a; McCormack et al., 1994; Sigworth, 1993). The six-state model in Fig. 4 is the simplest kinetic model for a homotetrameric channel with both independent and concerted conformational changes. It incorporates a single independent conformational change in each of four identical subunits followed by a single concerted conformational change, and it can reproduce many of the key features of Shaker activation. Parameters for the six-state model were found that predict ionic currents similar to Shaker (control) and to those predicted by a more complete model for Shaker activation that quantitatively fits data from macroscopic ionic currents, single channel recordings, and gating currents (Zagotta et al., 1994 a). The six-state model fits the steady state and kinetic properties of the macroscopic ionic currents of Shaker reasonably well using very few free parameters and predicts a considerable amount of delay in the activation time course. While the cooperative transition in this six-state model in Fig. 4 is voltage independent, the steady state and kinetic properties of Shaker activation can just as easily be fit by a cooperative transition that is voltage dependent (see Fig. 8; see also Zagotta et al., 1994 a; Smith-Maxwell et al., 1998). The six-state model does not fit as well as the more complete model because it does not have enough transitions to fully account for the large delay in Shaker activation or enough gating charge. More complex models for Shaker increase the amount of charge moved during channel activation and the amount of delay in the activation time course by adding more independent transitions in each of the four channel subunits and by adding one or more concerted transitions. General conclusions from this six-state model are directly and easily transferable to other models in the literature that have been proposed for Shaker, despite differences in the details of the kinetic schemes (see Smith-Maxwell et al., 1998).
Figure 4.
Model predictions for voltage-dependent channel opening. (top left) The six-state model used for these simulations is a simplified model for Shaker channel activation gating with properties similar to the larger 15-state model previously developed for Shaker channel gating (Zagotta et al., 1994 a). Despite the decrease in complexity, the six-state model fits the conductance–voltage relation of Shaker and has kinetic properties similar to Shaker. In the model, a single independent transition in each identical channel subunit is followed by a final concerted transition leading to channel opening. Values for the rate constants α and β are taken from the first set of identical and independent transitions in each subunit of the 15-state model, since they are largely responsible for the voltage-dependent properties of opening in Shaker. Expressions for the voltage-dependent rate constants assume an exponential dependence on voltage where α = α0 ez αFV/RT and β = β0 e −z βFV/RT, α0 and β0 are values for the rate constants at 0 mV, and z α and z β are the equivalent charge moved between each state and the transition state. The rate constants for the final concerted transition, γ and δ, are voltage independent. Model parameters for the control simulations with Shaker-like properties are: α0 = 1,120 s−1, β0 = 373 s−1, z α = 0.25, z β = 1.0, γ = 8,000 s−1, and δ = 100 s−1. (left) Normalized conductance–voltage curves for the control simulations and for the indicated modifications. Conductance–voltage curves predicted for three types of changes in the model are shown. Charge associated with the forward (z α) and backward (z β) transitions is decreased (top); the 0-mV rate constant (α0) for all forward independent transitions is decreased (middle); and the forward rate constant for the final concerted transition (γ) is decreased (bottom). Normalized conductance–voltage curves were constructed from simulated currents by normalizing isochronal tail currents as outlined in materials and methods. *Values used for the control simulations. (middle) Simulated ionic currents for the control parameters and for the indicated modifications to the control parameters. The simulation with z β = 0.25 decreases the total charge moved for the channel from 5.0 electronic charges to 2.0 by decreasing z β from 1.00 to 0.25 electronic charges in each of four subunits. The simulation with α0 = 10 s−1 decreases all 0-mV forward rate constants by two orders of magnitude. The simulation with γ = 10 s−1 decreases the forward rate constant for the concerted final transition by almost three orders of magnitude. (right) Simulated currents from the middle panel scaled for analysis of sigmoidicity. Simulated currents at all voltages were normalized to the same maximum value. Then the slopes at the half maximum current level were made equal by changing scaling along the time axis. This manipulation of the current traces facilitates comparison of the relative delay in the currents at different voltages and from different channel species. For scaled currents that follow a single exponential time course, the time it takes to reach the half maximum current is defined as 1.0. Values >1.0 are indicative of a delay in the activation time course. Arrowheads point to scaled current traces with the smallest and largest relative delays and indicate the voltage range over which currents were scaled.
Figure 8.
Voltage-dependent opening of Shaw S4 and Shaker dimer constructs. (left) Macroscopic ionic current traces recorded from dimer constructs. 1-s prepulses to −100 mV, from a holding potential of −80 mV, preceded each test pulse to the voltages indicated. (right) G/G max was determined as outlined in materials and methods from dimer constructs AkBk (○, n = 5), AkBw (♦, n = 8), AwBk (•, n = 6), AwBw (▴, n = 1), and the Shaker (▾, n = 8) and Shaw S4 (⋄, n = 6) monomers. Mean values are plotted as a function of voltage with error bars indicating SEM. Note that data from AwBw superimpose on data from the Shaw S4 monomer and data from AkBk superimpose on data from the Shaker monomer. (top right) Predictions for steady state activation from an independent model. The independent model, based on the model of Hodgkin and Huxley (1952), assumes four identical and independent transitions lead to channel opening. The normalized conductance– voltage curves from AkBk and Shaw S4 were each fit with a fourth power Boltzmann function, as described in results, to determine the voltage-dependent properties of activating a single subunit in the tetrameric channel protein. The following values were obtained from fits to data from the homotetramers: for AkBk, Vk = −52.83 mV and z k = 2.62; for Shaw S4, Vw = 32.29 mV and z w = 0.88. The independent model predicts that the voltage dependence of the conductance–voltage curve will be equal to the product of first power Boltzmann functions for each of the individual subunits making up the channel tetramer. The solid line between the fits is the prediction of the independent model for a channel with two Shaker subunits and two Shaw S4 subunits. (bottom right) Predictions for steady state activation from two cooperative models. Model 1: the first model assumes that Shaker and Shaw S4 channels open from a single closed state to a single open state, and that the forward and backward transitions between the two states involve the concerted movement of all four subunits. Data for AkBk and Shaw S4 were each fit with a single Boltzmann function, as described in results (fits not shown). Values from fits of the homotetramers are: for AkBk, V1/2 = −35.55 mV and z = 3.53; for Shaw S4, V1/2 = +80 mV and z = 1.24. The predicted conductance–voltage curve for channels with two Shaw S4 and two Shaker subunits is represented by the dotted line in the bottom right panel. Model 2: the second model, which includes several independent transitions as well as a cooperative transition, is identical to the six-state kinetic scheme outlined in Fig. 4. Values for transitions in Shaker and Shaw S4 channels were obtained from fits to data from the AkBk dimer and the Shaw S4 monomer constructs, respectively. The probability of opening and the normalized conductance were calculated as outlined in Fig. 4. For Shaker, two variations of the model were used with the same values for the independent transitions, but differing by whether or not the final concerted transition is voltage dependent. The 0-mV rate constants and associated charge used for the independent transitions for both variations are: α0 = 1,120 s−1, z α = 0.25, β0 = 373 s−1, z β = 1.0. For the voltage-independent concerted transition, γ = 8,000 s−1 and δ = 100 s−1. These values are identical to those used for the control simulations in Fig. 4 and predict the conductance–voltage relation described by the dashed line through the data for AkBk. For the Shaker variation with a voltage- dependent concerted transition, the rate constants γ and δ, like α and β, were assumed to be exponentially related to voltage with γ = γ0 e z γF V/RT, δ = δ0 e −z δF V/RT, γ0 = 10,000 s−1, δ0 = 100 s−1, and z γ = z δ = 0.1. These parameters predict a conductance–voltage relation described by the solid line through the data for AkBk. The Shaw S4 conductance–voltage relation was simulated by slowing the final concerted transition in the activation pathway of the Shaker models and increasing the voltage dependence of the transition. For the Shaw S4 kinetic scheme, the independent transitions have the same values as in the Shaker models and the concerted transition has the following values: γ0 = 1 s−1, z γ = 0.8, δ0 = 50 s−1 and z δ = 0.4. The conductance–voltage curve calculated for the Shaw S4 model is shown by the solid line through the data for Shaw S4. Since the models simulating Shaker and Shaw S4 differ only in the final transition, energy additive predictions for heterodimer opening were calculated, as described in results, by summing the energy contributions of each subunit to this final transition, assuming all other transitions have the same properties as Shaker. The solid line near the heterodimer data shows the prediction for steady state activation of a channel with two Shaw S4 and two Shaker subunits when the concerted transition in Shaker has a small voltage dependence, while the dashed line shows the prediction when the concerted transition in Shaker is voltage independent.
Steady state and kinetic behavior for the Shaker (control) model and for several variations are presented in Fig. 4. Control simulations have steady state activation properties and gating kinetics similar to Shaker (see Fig. 2 and Fig. 8, bottom right). The opening kinetics are sigmoid and have a voltage-dependent pattern of delay similar to the pattern observed for Shaker currents and for the complete model for Shaker activation described by Zagotta et al. (1994 a, 1994b). Shaker channel opening is delayed because it undergoes multiple voltage-dependent transitions between closed states before it opens. The relative delay compared with the overall rate of activation can be determined by scaling the currents at all voltages to the maximum current level and then changing the scaling of the currents along the time axis so that the slope at the half maximal current is the same for all traces. This manipulation of the current traces facilitates comparison of the relative delay, or sigmoidicity, at all voltages and between different channel species, despite differences in current magnitude and absolute rates of activation (Zagotta et al., 1994 a, 1994b). For the control simulations, as with Shaker, there is little delay in channel opening during small depolarizing voltage steps due to the relatively slow rate of return from the open state. With larger depolarizations, the relative delay increases because the relative contribution of the slow first closing rate to the overall rate of activation decreases. With even larger positive voltage steps, the relative delay tends to saturate because the dominant transitions in channel activation have similar rates over this voltage range (Zagotta et al., 1994 a, 1994b). In contrast, with an independent model such as the Hodgkin-Huxley model (Hodgkin and Huxley, 1952), the sigmoidicity of the activation time course is a constant function of voltage.
Since the channels under study are homotetramers, identical substitutions within each subunit could alter four independent transitions in the kinetic scheme. Alternatively, if the mutations change a cooperative transition, a single transition in the kinetic scheme can be affected. To illustrate the predicted effects of such mutations, three distinct types of modifications to the control parameters are considered. In the first, the total charge associated with channel gating is decreased by decreasing the gating charge associated with either the forward (zα) or the backward (zβ) rate constants in each of the four subunits. In the second, the forward rate constant of the independent transitions in all four subunits (α0) is decreased without changing its voltage dependence. In the third, cooperativity is altered by decreasing the forward rate constant only in the concerted transition leading to channel opening (γ) (see Zagotta et al., 1994 a).
These different types of modifications of the gating transitions predict distinct changes in channel activation. Decreasing the amount of charge associated with each of the four voltage sensors decreases the slope of the conductance–voltage curve and predicts a shift to more negative voltages, regardless of whether charge associated with the forward or backward rate constants is decreased. This result was not observed with any of the chimeras, despite the fact that all chimeras decreased the number of basic residues in the S4 region. The predicted channel kinetics and sigmoidicity are similar to the properties of the control channel, though the voltage range is negatively shifted.
Decreasing the rate at which each individual subunit changes conformation, α0, without changing its voltage dependence, causes a positive shift in the conductance–voltage curve along the voltage axis but does not change the slope of the curve. The slowing of the independent transitions slows activation kinetics but has little effect on the sigmoidicity of the kinetics when compared with the control. This voltage-dependent pattern of sigmoidicity occurs, as with the control, because of the cooperativity of the final transition (see also Zagotta et al., 1994 a).
Altering subunit cooperativity by decreasing the forward rate constant for the final opening transition, γ, causes the time course of activation to become less sigmoid. As γ is decreased more and more, activation is slowed and the cooperative transition becomes rate limiting. When the transition is slowed sufficiently, the activation time course becomes single exponential, as shown in Fig. 4. Decreasing γ also gives rise to a positive shift in the conductance–voltage curve and a decrease in the apparent voltage dependence. While the cooperative transition in our six-state model is voltage independent, making the transition voltage dependent does not change the predictions (see Smith-Maxwell et al., 1998). Thus, we can decrease the slope of the conductance–voltage relation either by changing the cooperative interactions in a channel or by decreasing the amount of charge moved per channel (see also Zagotta et al., 1994 a). The amount of charge per channel can be determined independently from gating current measurements in combination with fluctuation analysis or toxin binding to determine the number of channels present (Schoppa et al., 1992; Aggarwal and MacKinnon, 1996). However, in terms of the model, we can distinguish between changes in cooperativity and changes in the amount of charge moved independently in each subunit, without charge per channel measurements, because they differ in their predictions for the position of the conductance–voltage curve along the voltage axis and in the effect on sigmoidal delay.
Interpretation of mutant data is not completely straightforward, however, since there is no reason to expect that a mutation, even a single amino acid substitution, will change only a single parameter of activation or a single transition. Even if a mutation were to change the energy of a single state, more than one transition will likely be affected, depending on how the states are connected together. The positive shift in the voltage range of activation for the S4 chimeras and the decrease in slope suggest that the substituted S4 segments may alter cooperativity in the Shaker channel in addition to any changes due to charge content of the S4. We tested this idea further in the Shaw S4 chimeric channel.
Comparison of the Shaw S4 Chimera to Shaw and Shaker
The most dramatic changes in channel function were introduced into Shaker by substitution with the S4 of Shaw. Before proceeding with the determination of the types of conformational changes that are altered, we compared Shaw S4 to both of its parent channels, Shaker and Shaw, to determine which gating properties resemble those of the parent channels. Current traces and conductance–voltage relations are shown in Fig. 5 and analysis of the gating kinetics is shown in Fig. 6.
Figure 5.
Macroscopic ionic currents and conductance–voltage curves for Shaker, Shaw S4, and Shaw. (left) Macroscopic ionic currents measured during positive steps to the voltages indicated. For Shaw S4 and Shaker, test pulses to activate the channels followed prepulses to −100 mV from a holding potential of −80 mV. For Shaw, a holding potential of 0 mV was used. (right) Normalized conductance plotted as a function of voltage. Normalized conductance–voltage curves were constructed for Shaker and Shaw S4 as outlined in Fig. 3. For Shaw, isochronal measurements of tail currents were made at −40 mV, between 0.2 and 0.3 ms after the end of the test pulse. Since the maximum probability of opening for Shaw currents was not reached in the voltage range studied, Shaw isochronal currents were normalized to the maximum current obtained at +180 mV. Data shown represent six patches for Shaw, six patches for Shaw S4, and eight patches for Shaker.
Figure 6.
Gating kinetics for Shaker, Shaw S4, and Shaw. (left) Single exponential fits to activation time course. Macroscopic ionic currents typical of each channel type are shown in response to positive voltage steps to the voltages indicated to the right of each trace (millivolts). For Shaker and Shaw S4, the voltage steps followed prepulses to −100 mV from a holding potential of −80 mV. For Shaw, a holding potential of 0 mV was used and positive test pulses were preceded by 10-ms prepulses to −100 mV. Superimposed on the current traces during activation are fits with a single exponential function, as outlined in materials and methods. For Shaw and Shaw S4, each trace was fit over most of the time course of activation, from between 1 and 5% of the maximum current to the maximum current obtained during the test pulse. For Shaker, traces were fit starting at 10–20% of the maximum current and up to the maximum current obtained during the test pulse because of large delays in Shaker opening that are not well fit by a single exponential function. (middle) Relative delay of the activation time course. Current traces measured at the voltages indicated were scaled to compare the relative delay between voltages and channel species as outlined for Fig. 4. The scale bar indicates the time it takes for a channel to activate half maximally when it activates with a single exponential time course and no delay. Arrowheads point to scaled current traces from Shaker with the smallest and largest relative delays and indicate the voltage range over which currents were scaled. (right) Time constants plotted as a function of voltage. Time constants were obtained from fits of single exponential functions to currents during channel opening and closing, as outlined in materials and methods. The time course of channel closing was reasonably well fit by a single exponential function for all three channel types. The time constants for Shaker and Shaw S4 were derived from 7 patches each, while the time constants for Shaw came from 13.
The steady state voltage dependence of Shaw S4 activation is much more shallow than that of Shaker and is shifted to more positive voltages, in the direction of the conductance–voltage curve of the S4 donor Shaw, but not to such extreme voltages. Fits of a first power Boltzmann function to conductance–voltage curves from Shaw S4 and Shaker channels show that activation of Shaw S4 is shifted ∼+120 mV, and the slope is decreased 2.7-fold. The S4 donor channel, Shaw, requires even more positive voltages to fully activate than Shaw S4 and has an even shallower voltage dependence (see also Wei et al., 1990; Tsunoda and Salkoff, 1995). We cannot quantify the voltage dependence of Shaw activation by fitting with a Boltzmann function because the probability of opening does not saturate within the limits of our measurements (<+200 mV). The conductance– voltage relation for Shaw is normalized to the value of the conductance at +180 mV in Fig. 5 to facilitate comparison with Shaw S4 and Shaker. The probability of opening for Shaw increases with a very shallow voltage dependence over a wide voltage range. Shaw begins to open at voltages more negative than Shaw S4, around −60 mV, and does not reach a maximum open probability until voltages well above the voltage where Shaw S4 open probability saturates. In contrast, the probability of opening for the Shaw S4 chimera, which begins to increase at voltages greater than 0 mV and saturates around +180 mV, has a steeper voltage dependence than Shaw.
In Fig. 6 (left), currents recorded in response to positive voltage steps are shown for each channel species. Superimposed on the current traces are fits by a single exponential function as outlined in materials and methods. Note the different time scales, which were selected to enable comparison of the relative amounts of delay at the beginning of the activation time course for each of the three channel species. It is clear from these fits that Shaw S4 and Shaw currents follow a single exponential time course to activate with little or no delay. This can be seen more clearly for a wide range of voltages by scaling the currents to compare the delay in activation relative to the overall time course of activation (Fig. 6, middle). The lack of delay in the activation time course of Shaw and Shaw S4 suggests that the activation kinetics are dominated by a single rate-limiting transition over a wide range of voltages. In contrast, Shaker requires the addition of 1–4-ms delays for adequate fit to the activation time course. Previous work on Shaker has indicated that this large sigmoidal delay is the result of multiple voltage-dependent transitions, each moving relatively small amounts of charge of similar magnitude (Sigworth, 1993; Hoshi et al., 1994; Zagotta et al., 1994 a; Bezanilla et al., 1994). A kinetic model for Shaw has not yet been developed.
Time constants obtained from fits to the activation time course similar to those shown in the Fig. 6 (left), from several patches with the Shaw S4 chimera and its parent channels, are plotted in Fig. 6 (right). Also plotted are time constants from single exponential fits to tail currents at negative membrane potentials. Tail currents measured during closing of all three channels are reasonably well fit by a single exponential function. Shaw S4 opens and closes much more slowly than either Shaw or Shaker. The kinetics of Shaw S4 are strongly voltage dependent, as are those of Shaker. The voltage range over which the kinetics of Shaw S4 change most dramatically is shifted to more positive voltages compared with Shaker and is shifted to the same extent as the probability of channel opening. In contrast to both Shaker and Shaw S4, the opening and closing kinetics of Shaw exhibit a very shallow voltage dependence over a wide range of voltages, encompassing 360 mV. Thus, while the activation time course for both Shaw and Shaw S4 is dominated by a single, rate-limiting transition, for Shaw S4 this transition is strongly voltage dependent while for Shaw it is nearly voltage independent. This difference in voltage dependence suggests that the rate-limiting conformational changes in the activation of Shaw and Shaw S4 may be different.
Differences between Shaw S4 and the parent channels can also be seen at the single channel level (Fig. 7). The first latencies of Shaw S4 are substantially longer than the first latencies of Shaker and Shaw, consistent with altering transitions in the activation pathway (data not shown). However, once the channel opens, the Shaw S4 single channel events much more closely resemble the behavior of Shaker than Shaw in their kinetics and single channel conductance (Fig. 7). The single channel conductance for Shaw S4 of 9.5 pS (n = 18) is the same as the 9–10 pS conductance of Shaker (Hoshi et al., 1994), and much smaller than the 23.3 pS (n = 3) single channel conductance of Shaw (see also Tsunoda and Salkoff, 1995).
Figure 7.
Single channel openings recorded from Shaker, Shaw, and Shaw S4 during voltage steps to the indicated voltages. Shaw and Shaw S4 records were filtered at 2 kHz. Shaker recordings were taken from Hoshi et al. (1994; see Fig. 1) with filtering ranging from 0.5 kHz at −50 mV to 1.2 kHz at 0 mV. Shaker and Shaw S4 currents were recorded from excised inside-out patches while Shaw currents were recorded from a cell-attached patch. The oocyte used for the cell-attached patch was bathed in the standard intracellular solution with a high concentration of potassium, depolarizing the resting potential to near 0 mV. A holding potential of −80 mV was used in all cases. The patch with Shaw contained at least two channels, the patch with Shaker contained one channel, and the patch with Shaw S4 contained two channels. The intracellular solutions for Shaker and Shaw S4 contained 2 mM MgCl2.
The rate of inactivation of Shaw S4 ionic currents (1.57 ± 0.28 s [SEM] at +50 mV, n = 5) closely resembles the 1.5-s C-type inactivation rate of Shaker (Hoshi et al., 1991). In contrast, there is no detectable inactivation in the macroscopic ionic currents of Shaw during positive voltage steps lasting 20–30 s (data not shown; see also Wei et al., 1990; Tsunoda and Salkoff, 1995). These results are consistent with the Shaw S4 substitution primarily altering conformational changes in the activation pathway and not introducing global changes that perturb other channel functions.
Alteration of Cooperative Gating by Shaw S4 Substitution
The slower gating kinetics and decreased sigmoidicity suggest that the Shaw S4 mutations alter activation gating fairly specifically, slowing a highly cooperative transition in the activation pathway sufficiently to make it rate limiting. Since introducing the S4 of Shaw into all four subunits of Shaker changes the activation time course from sigmoid to single exponential, the rate-limiting transition in Shaw S4 cannot be due to the slowing of independent transitions in each subunit. This suggests that the single rate-limiting transition in Shaw S4 is a highly cooperative transition in the activation pathway. The simplified model for Shaker gating is illustrative (Fig. 4). While slowing the independent transitions slows channel gating, the time course of channel opening maintains considerable sigmoidicity, a characteristic clearly different from the single exponential time course of Shaw S4 activation. However, we can simulate currents with properties similar to Shaw S4 simply by slowing the forward rate of the final cooperative transition in the activation pathway (Fig. 4, bottom). Decreasing only the rate constant, γ, with no other changes, leads to slowing of activation kinetics, a positive shift in the voltage range of activation, a decrease in the slope of the conductance–voltage curve, and activation kinetics with a single exponential time course over the entire voltage range of activation. These are all characteristic of Shaw S4 macroscopic currents.
Although we used the six-state model for our predictions, as discussed previously, it does not fully account for the large delay in the activation time course of Shaker or the large amount of charge associated with activation gating. We used the six-state model to interpret the results of the S4 substitutions because it is the simplest model possible that will describe several key features of activation gating in Shaker. Therefore, conclusions from this model are fairly general and are not obscured by complexities introduced by models with many more transitions. However, more complex models are necessary to fit quantitatively the wild-type and mutant kinetics. For example, simply decreasing the forward rate constant of the cooperative transition in the six-state model predicts many of the functional changes observed with Shaw S4, but it does not predict the maximum probability of opening observed in the single channel records. However, as seen in the next paper (Smith-Maxwell et al., 1998), modifications to the final closing step in the more complete model for Shaker (Zagotta et al., 1994 a) can quantitatively account for Shaw S4 kinetics. Therefore, our conclusion that a late cooperative step is altered in Shaw S4 is valid both for a simple model that incorporates the key features of Shaker gating and a more complex model that quantitatively fits Shaker activation.
Shaw S4 and Shaker Tandem Dimers
The change to slow, single exponential kinetics upon substituting the S4 of Shaw for the S4 of Shaker indicates that a single transition in the activation pathway has become rate limiting. Since we can assume from studies with the Shaker channel (MacKinnon, 1991; Heginbotham and MacKinnon, 1992; Kavanaugh et al., 1992; Liman et al., 1992) that the Shaw S4 chimera assembles into a tetramer with four identical subunits, the rate-limiting transition in Shaw S4 activation most likely arises from highly cooperative interactions between subunits. To test further the hypothesis that the Shaw S4 mutation slows a cooperative transition, we constructed tandem heterodimers containing the slowly activating Shaw S4 subunit and the rapidly activating Shaker subunit in either position of the dimer (AkBw and AwBk) along with homodimers containing either two Shaker subunits (AkBk) or two Shaw S4 subunits (AwBw) (see Tytgat and Hess, 1992; McCormack et al., 1992; Heginbotham and MacKinnon, 1992; Ogielska et al., 1995). Macroscopic currents and normalized conductance–voltage curves from the dimer constructs are shown in Fig. 8, along with predictions for the independent or cooperative movement of subunits. Values from fits of Boltzmann functions to data from the dimer constructs are given in Table II. Macroscopic currents recorded from channels assembled from the homodimer constructs, AwBw and AkBk, activate with properties that are indistinguishable from the properties of channels assembled from Shaw S4 and Shaker monomers, respectively (Figs. 2 and 8, Tables I and II), demonstrating that the nine amino acid linker between subunits in the tandem dimer constructs does not perturb channel activation.
Table II.
Boltzmann Relation Fits of Dimers
| Fourth power Boltzmann | First power Boltzmann | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Channel | V1/2 | SEM | Slope | SEM | V1/2 | SEM | Slope | SEM | n | |||||||||
| mV | mV | mV | mV | |||||||||||||||
| AkBk | −52.8 | ±2.2 | 9.6 | ±1.0 | −35.5 | ±1.2 | 7.2 | ±0.8 | 5 | |||||||||
| AkBw | −37.9 | ±1.8 | 26.8 | ±0.8 | +7.0 | ±1.8 | 19.4 | ±0.6 | 8 | |||||||||
| AwBk | −29.1 | ±3.0 | 24.0 | ±0.9 | +10.8 | ±2.9 | 16.9 | ±0.6 | 6 | |||||||||
| AwBw | +29.5 | — | 28.2 | — | +75.2 | — | 19.4 | — | 1 | |||||||||
Normalized conductance–voltage curves were calculated and fit with a first or fourth power Boltzmann function as outlined in materials and methods. V1/2, slope, and n are as described in Table I.
Macroscopic currents from heterodimer constructs AkBw and AwBk activate in a voltage range roughly midway between Shaker and Shaw S4, with a shallow voltage dependence much more like that of Shaw S4 than Shaker (Fig. 8). Heterodimer activation kinetics are slower than Shaker, though not nearly as slow as Shaw S4 (Fig. 8), and yet the time course of activation approximates a single exponential like Shaw S4 (Fig. 9). Currents from heterodimer channels scaled for analysis of sigmoidicity show little relative delay or voltage- dependent change in the delay. The voltage independence of the scaled activation time course in the heterodimers is similar to that of Shaw S4 and unlike the large voltage-dependent changes in relative delay found in Shaker. These results suggest that only two subunits in the channel tetramer need the Shaw S4 substitution to alter cooperativity in the activation process in such a way as to make a single transition rate limiting.
Figure 9.
Sigmoidicity of Shaw S4 and Shaker dimer constructs. Macroscopic ionic current traces from dimer constructs AkBk, AkBw, AwBk, and AwBw were scaled to compare the relative delay between voltages and channel species as outlined in Fig. 4. Currents were measured at the voltages indicated. Currents for the heterodimer prediction were simulated using the six-state model in Fig. 8. Rate constants for the independent transitions were the same as those used for the Shaker and Shaw S4 models, while rate constants for the final cooperative transition were predicted from the rate constants for Shaker and Shaw S4, assuming energy-additive contributions from each of four channel subunits. Rate constants for the final transition in opening of Shaker and Shaw S4 channels are given in Fig. 8. Calculation of rate constants predicted for heterodimer channels was carried out as outlined in results. The Shaker variation without charge movement in the final transition was used for the simulations shown; however, similar results were obtained from the Shaker variation with a small amount of charge movement in the final transition. The simulated currents were scaled for analysis of sigmoidicity in the same way that currents measured from the dimer constructs were scaled. The scale bars indicate the time it takes for a channel with a single exponential time course to activate half maximally.
Conductance–voltage curves from channels formed from heterodimers of both orientations were compared as a test for misassembly of subunits in the channel tetramer (Fig. 8). The curves from AkBw and AwBk are very similar. However, small differences in the voltage range of activation occur in the direction expected for a slight preferential insertion of the NH2-terminal subunit. Similar observations have been reported previously for concatenated channel subunits (McCormack et al., 1992; Ogielska et al., 1995). The close agreement between results from the two heterodimer constructs indicates that only a small proportion of the functional channels include improperly assembled subunits. We tested further for misassembly of heterodimers by looking for kinetically distinct populations of channels that might be proportionately more active at different voltages. We found no change in deactivation rates after activation of channels at different voltages, supporting the idea that the heterodimer constructs tend to assemble into a homogeneous population of channels. Therefore, the relatively small percentage of channels we encountered with incorrect subunit assembly should not affect our conclusions.
Independent and Cooperative Models: Predictions for Heterodimers
We constructed several models to determine whether activation of the dimers is more consistent with the independent movement of Shaker and Shaw S4 channel subunits or with cooperative interactions between them. Predictions of a simple independent model, based on the model of Hodgkin and Huxley (1952), are illustrated in Fig. 8 (top right). This model assumes that each of the four channel subunits undergoes a single independent voltage-dependent conformational change leading to channel opening. The normalized conductance–voltage curves of AkBk and Shaw S4 were each fit with a fourth power Boltzmann function to determine the voltage-dependent properties of activating a single subunit in the tetrameric channel protein. The Boltzmann function used for these fits is given by:
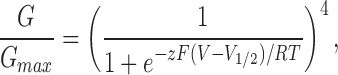 |
where V1/2 is the half activation voltage and z is the equivalent charge associated with activation of each subunit. For a channel with two Shaw S4 and two Shaker subunits, the prediction for steady state channel activation is given by:
 |
where Vw and Vk are the half activation voltages for each Shaw S4 and Shaker subunit, respectively, and z w and z k are the equivalent charge for each Shaw S4 and Shaker subunit. The model predicts that the conductance–voltage curve for channels with two Shaw S4 and two Shaker subunits will be much closer to the curve for Shaw S4 than the curve for Shaker because the channel will not open until all subunits are activated, including the less likely to activate Shaw S4 subunits. The dimers AkBw and AwBk activate at much more negative voltages than predicted by the independent model.
The large disparity between the heterodimer data and the prediction of the independent model argues strongly that the independent movement of the subunits cannot account for the dominant transition in Shaw S4. This evidence for a cooperative transition in gating agrees with earlier findings from studies of gating using concatenated dimers and tetramers (Tytgat and Hess, 1992; Hurst et al., 1992) and from detailed analysis of Shaker gating kinetics (Sigworth, 1993; Zagotta et al., 1994 a, 1994b; Bezanilla et al., 1994).
To test this idea further, we used two different cooperative models to compare with the data from AkBw and AwBk and to investigate the predictions of cooperative subunit interactions. The first cooperative model makes the simplest assumption, that channel opening involves a single fully cooperative or concerted transition, wherein all four channel subunits activate simultaneously by undergoing a single voltage-dependent conformational change from the closed state into the open state. Therefore, the energetic contribution to channel opening by each of the four subunits will be additive. The free energy change for activation of each subunit, ΔG, was calculated from fits of a first power Boltzmann function to the normalized conductance–voltage relation for homotetrameric channels with all Shaker subunits or all Shaw S4 subunits from the following:
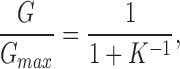 |
where K is the voltage-dependent equilibrium constant for channel opening given by K = ezF (V − V1/2 )/RT. The free energy change for activation of each of the four subunits in each homotetramer was calculated from
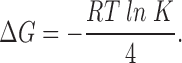 |
The total free energy change, ΔGtot, for opening a channel with two Shaw S4 and two Shaker subunits was calculated from ΔG tot = 2(ΔG w + ΔG k), where ΔG w and ΔG k represent the free energy change for activation of single Shaw S4 and Shaker subunits, respectively. The predicted conductance–voltage curve for a channel with two Shaw S4 and two Shaker subunits was then reconstructed from
 |
and is represented by the dotted line in Fig. 8 (bottom right). Even with this overly simple model, the predicted conductance–voltage relation for channels with half Shaw S4 subunits and half Shaker subunits approximates the heterodimer data much more closely than the independent model. This model assumes the maximum possible cooperativity between subunits. The prediction of heteromultimeric conductance–voltage curves at voltages more negative than the heteromultimer data is consistent with the well known departure from first order gating in Shaker channels (Sigworth, 1993; Bezanilla et al., 1994; Zagotta et al., 1994 a) and suggests that the relative contribution of cooperative transitions to channel opening differs in Shaker and Shaw S4.
In a second model, we investigated the prediction of activation schemes with both independent and cooperative transitions by using the simple six-state gating model in Fig. 4. We assumed for Shaker that a single independent voltage-dependent transition in each of the four subunits is followed by a concerted transition that opens the channel. For Shaker, we used two variations of the model, one in which the final concerted transition is voltage independent, as in Fig. 4, and one in which a small amount of charge movement is incorporated into the final concerted transition. We considered a voltage-dependent variation because there is evidence in Shaker for a transition near the open state that moves a small amount of charge (Koren et al., 1990; Bezanilla et al., 1994; Hoshi et al., 1994; Zagotta et al., 1994 a). The independent transitions have identical properties in both variations of the Shaker model. As with the six-state model in Fig. 4, we assumed that the rate constants of all voltage-dependent transitions have an exponential dependence on voltage (see legend to Fig. 4). We calculated the probability of channel opening, P open, from the equilibrium constants for each transition:
 |
1 |
 |
P open was normalized to the maximum P open and plotted as a function of voltage.
The solid and dashed lines through the data for Shaker dimer AkBk in Fig. 8 (bottom right) show the fit of both variations to the AkBk data, demonstrating that both variations can reasonably approximate steady state Shaker activation. Simulated currents from the Shaker variation without charge movement in the final transition are shown as the control in Fig. 4. To simulate Shaw S4, the final conformational transition leading to channel opening in the Shaker model was slowed and the voltage dependence was increased. The solid line through the Shaw S4 data shows that this simple modification of the six-state Shaker model gives a good approximation for the effect of the introduced mutations on the conductance–voltage curve. Simulated currents from this model have single exponential activation kinetics like Shaw S4 (data not shown; but see simulation in Fig. 4, γ = 10).
Since modification of a single transition can account for the steady state behavior of Shaw S4, we can assess the role of energy additivity in the heterotetramers for this single transition in a multi-state scheme that approximates the gating of the channels. Rate constants taken from the final transition before opening in the models for Shaw S4 and AkBk were used to calculate the energetic contribution of each Shaw S4 and Shaker subunit to the transition. The free energy change, ΔG, contributed by each subunit to the concerted transition was calculated from the rate constants in the models for the homotetramers where
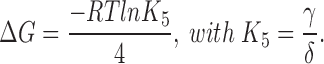 |
The total free energy change, ΔG tot, for the concerted transition with two Shaw S4 and two Shaker subunits was calculated from the free energy change per subunit, as for the two-state concerted model above, from ΔG tot = 2(ΔG w + ΔG k). The resultant equilibrium constant for the final step in the heterodimer model, K 5, was computed from K 5 = e −ΔGtot/RT.
The predicted probability of opening, P open, was calculated from the equation for the steady state probability of opening (Eq. 1), changing only the equilibrium constant for the concerted transition, K 5. P open was normalized to the maximum open probability. The curves for the predictions are shown in Fig. 8 (bottom right). The solid line through the heterodimer data is from the Shaker model with a voltage-dependent concerted transition and the dashed line is from the variation with the voltage-independent concerted transition. This multi-state model with both independent and cooperative transitions, in which only the cooperative transition is changed, improves on the fit of the two-state cooperative model to the heterodimer channel data, presumably because the multi-state model more accurately describes gating in these channels and takes into account the different contributions of cooperativity to gating in Shaker and Shaw S4.
To test further the validity of the predictions from the six-state model, we simulated ionic currents for the heterodimer channels. Rate constants taken from the final transition before opening in the models for Shaw S4 and AkBk were used to calculate the energetic contribution of each Shaw S4 and Shaker subunit to the rate constants in the final transition in the heterodimer model. Forward and backward rate constants were calculated separately. The activation energy contributed by each Shaker and Shaw S4 subunit, respectively, is given by:
 |
where k k and k w are the rate constants for Shaker and Shaw S4, respectively, A is the attempt frequency, and k B is the Boltzmann constant. The predicted rate constant for the final transition for channels with two Shaker and two Shaw S4 subunits was calculated from
 |
The calculated rate constants for the forward and backward transitions were then incorporated into the final transition of the six-state model, assuming all other transitions were unchanged, and the predicted currents for the heterodimer channels were simulated. Activation kinetics of simulated currents predicted by this analysis are similar to the kinetics of the heterodimer channels (data not shown) and the activation time course has a greatly reduced sigmoidicity, similar to that found with the heterodimer mutant channels (Fig. 9). Our results indicate that activation involves multiple voltage-dependent transitions with at least one cooperative transition, that the Shaw S4 substitution alters a cooperative transition, and that the contribution of the cooperative transition to channel opening differs in the Shaker and Shaw S4 channels.
Since macroscopic ionic currents from channels with two or four Shaw S4 subunits can be simulated simply by altering the final transition in the activation pathway, making it rate limiting, it is likely that the same transition is affected in both the heterodimer and homomeric Shaw S4 channels. While the two cooperative models provide good estimates of steady state activation and sigmoidicity for the heterodimer constructs, they do not fit the heterodimer results perfectly. The small discrepancy between the cooperative predictions and the data may be the result of not using the full model for Shaker activation (Zagotta et al., 1994 a) or it may be due to the slight differences in gating we observe when only two Shaw S4 subunits are present, as opposed to when all four channel subunits have the Shaw S4 substitution. Activation kinetics of Shaw S4 have a much steeper voltage dependence than activation kinetics of Shaker. Exponential fits to the activation time constants estimate the equivalent charge associated with the final opening transition to be 0.42 electronic charge for Shaker (Zagotta et al., 1994 b) and 0.78 electronic charge for Shaw S4 (Smith-Maxwell et al., 1998). However, for channels with two Shaw S4 and two Shaker subunits, similar fits of activation time constants estimate the equivalent charge to be 0.45 electronic charge, suggesting that while two Shaw S4 subunits are sufficient to make the transition rate limiting, they are not sufficient to change the voltage dependence of the rate-limiting transition.
The fact that the cooperative models fit the heterodimer data much better than the independent model and that the cooperative models give qualitatively similar results despite differences in the specific details of the kinetic schemes, indicates that some form of cooperativity provides the best explanation for the steady state activation properties of heteromultimeric channels with both Shaker and Shaw S4 subunits. Cooperativity can be introduced into kinetic schemes in a number of different ways and there is as yet no consensus on the mechanism by which cooperativity participates in Shaker channel activation. Our intention was not to explore extensively all possible classes of models that could lead to this behavior, but rather to determine whether an independent scheme or some form of cooperative scheme provides a more likely explanation for our results. Along with the analysis of Shaw S4 kinetics presented earlier, the heterodimer results strongly suggest that a cooperative transition in the activation pathway is slowed by the Shaw S4 substitution.
discussion
We used chimeric substitutions to explore further the role of the S4 in voltage-dependent gating. Chimeric substitutions have been used in the past to pinpoint regions of importance for gating in several voltage- dependent cation channels (Tanabe et al., 1990, 1991; Stocker et al., 1991; Chen et al., 1992; Logothetis et al., 1993; Zhang et al., 1994; Nakai et al., 1994; Mathur et al., 1997; Tang and Papazian, 1997; Shieh et al., 1997; Koopmann et al., 1997). We substituted into a Shaker channel background S4 segments from several divergent potassium channels with different kinetic and steady state gating properties (Butler et al., 1989; Wei et al., 1990; Tsunoda and Salkoff, 1995; McCormack et al., 1990). Activation of all S4 chimeras in our study differed from Shaker, however, the S4 substitutions did not confer on Shaker the gating properties of the S4 donor channels.
Relationship Between Net S4 Charge and Conductance–Voltage Relations
The total charge associated with channel opening has been estimated for Shaker, using several different methods, to be between 12 and 14 electronic charges (Schoppa et al., 1992; Zagotta et al., 1994 b; Aggarwal and MacKinnon, 1996; Seoh et al., 1996; Noceti et al., 1996; Sigg and Bezanilla, 1997). Total charge moved for channel opening can be calculated by measuring gating currents and the total number of channels contributing to the gating currents. Charge per channel measurements, wherein each charged residue is neutralized in turn, suggest that the first five positive charges from the NH2-terminal side of the S4 and possibly a negative charge in the S2 provide most of the gating charge (Aggarwal and MacKinnon, 1996; Seoh et al., 1996). In the S4 chimeras we studied, at most one or two of these charged residues were substituted at a time. The decrease expected from these neutralizations, assuming equal contribution from each of the six implicated charged residues, ranges from ∼15 to 35% of the total gating charge. For Shaw S4, this decrease in gating charge is potentially even greater due to a charge reversal at the position of the first basic residue.
We found that neither the net charge content nor the presence of specific charges in the S4 are predictive for changes in the slope of the conductance–voltage relation. All S4 chimeras, except Shaw S4, activate with some delay, providing evidence that these channels activate with multiple voltage-dependent transitions, like Shaker. Changes in steepness of the conductance–voltage relation can come about either from changing the total gating charge or from changing cooperativity. Taken together, our results are most consistent with subunit cooperativity being the major determinant of the voltage dependence of the conductance–voltage relation at moderate probability of being open. Because both charge movement and cooperativity are important in determining the shape and position of the conductance–voltage curve, mutations that change cooperativity could obscure changes in the amount of gating charge, which could be determined by charge per channel measurements. However, the shift of the conductance–voltage curves to more positive voltages that accompanies the decrease in slope cannot be explained by a decrease in gating charge alone (see also Sigworth, 1993).
Our conclusion that the charge content of the S4 does not necessarily correlate with the voltage dependence of channel opening differs from that reached by two previous studies of the effects of S4 chimeric substitutions. Logothetis et al. (1993) studied a Shab S4 chimera made in the RCK1 (Kv1.1) background in which the conductance–voltage curve is negatively shifted and the slope is decreased. These changes follow the predictions for a decrease in gating charge (see Fig. 4). However, the activation kinetics of the chimera are significantly slower than the kinetics of either parent channel, which is not consistent with a decrease in gating charge alone. The slow activation kinetics suggest that channel cooperativity may be altered and that a more comprehensive analysis is necessary to determine the relative contributions of cooperativity and charge movement to activation gating in the RCK1/Shab S4 chimera. Tang and Papazian (1997) studied two S4 chimeras made by transferring portions of the S4 from the rat olfactory cyclic nucleotide-gated channel into the S4 of the eag potassium channel. They suggest that the decrease in charge content of the S4 may be responsible for the decrease in slope of the conductance–voltage curves. However, a positive shift in the position of the conductance–voltage curve cannot be explained by simply decreasing the charge content of the voltage sensor, as predicted from the model in Fig. 4 or the more complete model shown in the next paper (Smith-Maxwell et al., 1998; see also Sigworth, 1993; Zagotta et al., 1994 a). The position of the conductance–voltage curve suggests that the decrease in slope of the conductance–voltage relation may be due primarily to a change in subunit cooperativity rather than due to a change in the charge content of the S4. While some of the results from these previous studies are very similar to results obtained with our S4 chimeras, our interpretation of the kinetic and steady state properties of the mutant channels has led to different conclusions about the effects of S4 mutations on channel gating.
S4 and Cooperative Steps in Gating
The single exponential time course of Shaw S4 activation is significant in light of the very pronounced and voltage-dependent sigmoidicity of the Shaker parent channel. In contrast to Shaker, where channel opening arises from multiple voltage-dependent transitions within each of the four subunits (Schoppa et al., 1992; Zagotta et al., 1994 a; Bezanilla et al., 1994), Shaw S4 activates with a rate-limiting transition in the activation pathway that is slow compared with other transitions. We have presented evidence that the rate-limiting transition in Shaw S4 activation is a cooperative step, implying a role for the S4 in cooperative interactions between subunits. The rate of Shaw S4 opening is sufficiently slow that the rate-limiting cooperative transition could easily mask the faster transitions that give rise to the sigmoidal time course of Shaker activation (Smith-Maxwell et al., 1998). If the rate-limiting transition in Shaw S4 represents a transition normally present in Shaker that has been slowed, further study of Shaw S4 may be useful for understanding the final transition in Shaker opening.
It is also possible that the Shaw S4 mutation alters channel gating more profoundly by decreasing the number of closed states in the activation pathway, possibly to a single closed state. In this case, Shaw S4 would not activate like the Shaker channel by undergoing multiple transitions between closed states, but instead would undergo a single transition between the closed state and the open state. Both kinetic schemes can produce opening kinetics that follow a single exponential time course with no delay. Further experiments will be needed to determine which kinetic scheme more accurately describes Shaw S4 activation gating. However, both kinetic schemes require inclusion of a cooperative step in the activation pathway.
Transfer of Gating Characteristics by S4 Substitutions
The Shaw S4 chimera shares some functional properties with each of its parent channels, Shaw and Shaker. The Shaw S4 substitution makes a single transition in the activation pathway rate limiting, giving rise to single exponential activation kinetics. This shifts the voltage range of channel activation to more positive voltages, compared with the Shaker parent channel, and decreases the steepness of the conductance–voltage curve. These characteristics of Shaw S4 activation are changed in the direction of the S4 donor, Shaw. Conversely, functional characteristics of the Shaw S4 chimera not directly involved in activation gating, such as single channel conductance and the rate of C-type inactivation, closely resemble properties of the Shaker parent channel.
Our results from Shaw S4 are consistent with our results from all S4 substitutions in that changing the S4 sequence alters activation, but the S4 alone is not sufficient to transfer all the functional properties of activation between channels (see also Logothetis et al., 1993; Tang and Papazian, 1997; Koopmann et al., 1997). Regions of the channel required to transfer the full activation phenotype may be quite extensive. For Shaker potassium channels, evidence exists for interactions between the S4 and residues in S2 and S3 (Papazian et al., 1995; Seoh et al., 1996; Tiwari-Woodruff et al., 1997; see also Planells-Cases et al., 1995), effects on activation kinetics from mutations in the S3–S4 linker (Mathur et al., 1997; Tang and Papazian, 1997), and changes in voltage dependence of channel activation from mutations in the S4 through the S5 (Gautam and Tanouye, 1990; Zagotta and Aldrich, 1990; Lichtinghagen et al., 1990; Isacoff et al., 1991; Papazian et al., 1991; McCormack et al., 1991, 1993; Lopez et al., 1991; Perozo et al., 1994; Shieh et al., 1997).
It is clear from this and previous work that substitutions of all types of amino acids in the S4, including polar, nonpolar, and hydrophobic amino acids, can lead to dramatic changes in the slope of the conductance– voltage relation and the voltage range of channel activation (McCormack et al., 1991, 1993; Lopez et al., 1991; Liman et al., 1991; Schoppa et al., 1992; Logothetis et al., 1992; Tytgat and Hess, 1992). Additionally, substitutions of S4 basic residues can cause changes in the voltage dependence that cannot be explained by changes in charge alone (Liman et al., 1991; Logothetis et al., 1992; Aggarwal and MacKinnon, 1996). We suggest that it is likely that these observed changes in activation gating, from substitution of charged and uncharged residues alike, include changes in subunit cooperativity. In the next paper, we examine the relative contributions of the charged and uncharged S4 residues to the cooperative interactions in activation gating.
Acknowledgments
The authors thank L. Salkoff for kindly sending cDNA for Shaw in the bacterial vector pBSK (Butler et al., 1989) and R. MacKinnon for the kind gift of the A and B protomers for constructing dimers. We also thank Melinda Przetak, Joan Haab, Peter Drain, and Adrienne Dubin for help with making the mutant channel constructs. We thank Tom Middendorf, Max Kanevsky, and Gargi Talukder for helpful comments on the manuscript.
This work was supported by a grant from the National Institutes of Health (NS-23294). R.W. Aldrich is an investigator with the Howard Hughes Medical Institute. J.L. Ledwell was supported by an NSERC 1967 Science and Engineering Scholarship from the Natural Sciences and Engineering Research Council of Canada.
references
- Aggarwal S, MacKinnon R. Contribution of the S4 segment to gating charge in the Shaker K+channel. Neuron. 1996;16:1169–1177. doi: 10.1016/s0896-6273(00)80143-9. [DOI] [PubMed] [Google Scholar]
- Almers W. Gating currents and charge movements in excitable membranes. Rev Physiol Biochem Pharmacol. 1978;82:96–190. doi: 10.1007/BFb0030498. [DOI] [PubMed] [Google Scholar]
- Armstrong CM, Bezanilla F. Charge movement associated with the opening and closing of the activation gates of Na channels. J Gen Physiol. 1974;63:533–552. doi: 10.1085/jgp.63.5.533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Auld VJ, Goldin AL, Krafte DS, Marshall J, Dunn JM, Catterall WA, Lester HA, Davidson N, Dunn RJ. A rat brain Na+ channel α subunit with novel gating properties. Neuron. 1988;1:449–461. doi: 10.1016/0896-6273(88)90176-6. [DOI] [PubMed] [Google Scholar]
- Baumann A, Grupe A, Ackermann A, Pongs O. Structure of the voltage-dependent potassium channel is highly conserved from Drosophilato vertebrate central nervous systems. EMBO (Eur Mol Biol Organ) J. 1988;7:2457–2463. doi: 10.1002/j.1460-2075.1988.tb03092.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bezanilla F, Perozo E, Papazian DM, Stefani E. Molecular basis of gating charge immobilization in Shakerpotassium channels. Science. 1991;254:679–683. doi: 10.1126/science.1948047. [DOI] [PubMed] [Google Scholar]
- Bezanilla F, Perozo E, Stefani E. Gating of Shaker K+channels: II. The components of gating currents and a model of channel activation. Biophys J. 1994;66:1011–1021. doi: 10.1016/S0006-3495(94)80882-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butler A, Wei A, Baker K, Salkoff L. A family of putative potassium channel genes in Drosophila. . Science. 1989;243:943–947. doi: 10.1126/science.2493160. [DOI] [PubMed] [Google Scholar]
- Catterall WA. Structure and function of voltage-sensitive ion channels. Science. 1988;242:50–61. doi: 10.1126/science.2459775. [DOI] [PubMed] [Google Scholar]
- Chen L-Q, Chahine M, Kallen RG, Barchi RL, Horn R. Chimeric study of sodium channels from rat skeletal and cardiac muscle. FEBS Lett. 1992;309:253–257. doi: 10.1016/0014-5793(92)80783-d. [DOI] [PubMed] [Google Scholar]
- Dascal N. The use of Xenopusoocytes for the study of ion channels. CRC Crit Revs Biochem. 1987;22:317–387. doi: 10.3109/10409238709086960. [DOI] [PubMed] [Google Scholar]
- Durrell SR, Guy HR. Atomic scale structure and functional models of voltage-gated potassium channels. Biophys J. 1992;62:238–247. doi: 10.1016/S0006-3495(92)81809-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellis SB, Williams ME, Ways NR, Brenner R, Sharp AH, Leung AT, Campbell KP, McKenna E, Koch WJ, Hui A, et al. Sequence and expression of mRNAs encoding the α1 and α2subunits of the DHP-sensitive calcium channel. Science. 1988;241:1661–1664. doi: 10.1126/science.2458626. [DOI] [PubMed] [Google Scholar]
- Gautam M, Tanouye MA. Alteration of potassium channel gating: molecular analysis of the Drosophila Sh5mutation. Neuron. 1990;5:67–73. doi: 10.1016/0896-6273(90)90034-d. [DOI] [PubMed] [Google Scholar]
- Hamill OP, Marty A, Neher B, Sakmann B, Sigworth FJ. Improved patch clamp techniques for high-resolution current recording from cells and cell-free membrane patches. Pflügers Archiv. 1981;391:85–100. doi: 10.1007/BF00656997. [DOI] [PubMed] [Google Scholar]
- Heginbotham L, MacKinnon R. The aromatic binding site for tetraethylammonium ion on potassium channels. Neuron. 1992;8:483–491. doi: 10.1016/0896-6273(92)90276-j. [DOI] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol (Camb) 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoshi T, Zagotta WN, Aldrich RW. Biophysical and molecular mechanisms of Shakerpotassium channel inactivation. Science. 1990;250:533–538. doi: 10.1126/science.2122519. [DOI] [PubMed] [Google Scholar]
- Hoshi T, Zagotta WN, Aldrich RW. Two types of inactivation in Shaker K+channels: effects of alterations in the carboxy-terminal region. Neuron. 1991;7:547–556. doi: 10.1016/0896-6273(91)90367-9. [DOI] [PubMed] [Google Scholar]
- Hoshi T, Zagotta WN, Aldrich RW. Shakerpotassium channel gating I: transitions near the open state. J Gen Physiol. 1994;103:249–278. doi: 10.1085/jgp.103.2.249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hurst RS, Kavanaugh MP, Yakel J, Adelman JP, North RA. Cooperative interactions among subunits of a voltage-dependent potassium channel. J Biol Chem. 1992;267:23742–23745. [PubMed] [Google Scholar]
- Isacoff EY, Jan YN, Jan LY. Putative receptor for the cytoplasmic inactivation gate in the Shaker K+channel. Nature. 1991;353:86–90. doi: 10.1038/353086a0. [DOI] [PubMed] [Google Scholar]
- Kamb A, Iverson LE, Tanouye MA. Molecular characterization of Shaker, a Drosophilagene that encodes a potassium channel. Cell. 1987;50:405–413. doi: 10.1016/0092-8674(87)90494-6. [DOI] [PubMed] [Google Scholar]
- Kamb A, Tseng-Crank J, Tanouye MA. Multiple products of the Drosophila Shakergene may contribute to potassium channel diversity. Neuron. 1988;1:421–430. doi: 10.1016/0896-6273(88)90192-4. [DOI] [PubMed] [Google Scholar]
- Kavanaugh MP, Hurst RS, Yakel J, Varnum MD, Adelman JP, North RA. Multiple subunits of a voltage-dependent potassium channel contribute to the binding site for tetraethylammonium. Neuron. 1992;8:493–497. doi: 10.1016/0896-6273(92)90277-k. [DOI] [PubMed] [Google Scholar]
- Kayano T, Noda M, Flockerzi V, Takahashi H, Numa S. Primary structure of rat brain sodium channel III deduced from the cDNA sequence. FEBS Lett. 1988;228:187–194. doi: 10.1016/0014-5793(88)80614-8. [DOI] [PubMed] [Google Scholar]
- Keynes RD, Rojas E. Kinetics and steady-state properties of the charged system controlling sodium conductance in the squid giant axon. J Physiol (Camb) 1974;239:393–434. doi: 10.1113/jphysiol.1974.sp010575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koopmann R, Benndorf K, Lorra C, Pongs O. Functional differences of a Kv2.1 channel and a Kv2.1/Kv1.2 S4-chimera are confined to a concerted voltage shift of various gating parameters. Receptors Channels. 1997;5:15–28. [PubMed] [Google Scholar]
- Koren G, Liman ER, Logothetis DE, Nadal-Ginard B, Hess P. Gating mechanism of a cloned potassium channel expressed in frog oocytes and mammalian cells. Neuron. 1990;2:39–51. doi: 10.1016/0896-6273(90)90442-i. [DOI] [PubMed] [Google Scholar]
- Larsson HP, Baker OS, Dhillon DS, Isacoff EY. Transmembrane movement of the Shaker K+channel S4. Neuron. 1996;16:387–397. doi: 10.1016/s0896-6273(00)80056-2. [DOI] [PubMed] [Google Scholar]
- Ledwell, J.L., C.J. Smith-Maxwell, and R.W. Aldrich. 1995. Substitution of the S4 region is not sufficient to confer the voltage-dependent properties of Shaw on Shaker. >Biophys. J 68:A32. (Abstr.)
- Lichtinghagen R, Stocker M, Wittka R, Boheim G, Stühmer W, Ferrus A, Pongs O. Molecular basis of altered excitability in Shaker mutants of Drosophila melanogaster. . EMBO (Eur Mol Biol Organ) J. 1990;9:4399–4407. doi: 10.1002/j.1460-2075.1990.tb07890.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liman ER, Hess P, Weaver F, Koren G. Voltage-sensing residues in the S4 region of a mammalian K+channel. Nature. 1991;353:752–756. doi: 10.1038/353752a0. [DOI] [PubMed] [Google Scholar]
- Liman ER, Tytgat J, Hess P. Subunit stoichiometry of a mammalian K+channel determined by construction of multimeric cDNAs. Neuron. 1992;9:861–871. doi: 10.1016/0896-6273(92)90239-a. [DOI] [PubMed] [Google Scholar]
- Logothetis DE, Kammen BF, Lindpaintner K, Bisbas D, Nadal-Ginard B. Gating charge differences between two voltage-gated K+channels are due to the specific charge content of their respective S4 regions. Neuron. 1993;10:1121–1129. doi: 10.1016/0896-6273(93)90060-5. [DOI] [PubMed] [Google Scholar]
- Logothetis DE, Movahedi S, Satler C, Lindpaintner K, Nadal-Ginard B. Incremental reductions of a positive charge within the S4 region of a voltage-gated K+channel result in corresponding decreases in gating charge. Neuron. 1992;8:531–540. doi: 10.1016/0896-6273(92)90281-h. [DOI] [PubMed] [Google Scholar]
- Lopez GA, Jan YN, Jan LY. Hydrophobic substitution mutations in the S4 sequence alter voltage-dependent gating in Shaker K+channels. Neuron. 1991;7:327–336. doi: 10.1016/0896-6273(91)90271-z. [DOI] [PubMed] [Google Scholar]
- Ludewig U, Lorra C, Pongs O, Heinemann SH. A site accessible to extracellular TEA+ and K+influences intracellular Mg2+ block of cloned potassium channels. Eur Biophys J. 1993;22:237–247. doi: 10.1007/BF00180258. [DOI] [PubMed] [Google Scholar]
- MacKinnon R. Determination of the subunit stoichiometry of a voltage-activated potassium channel. Nature. 1991;350:232–235. doi: 10.1038/350232a0. [DOI] [PubMed] [Google Scholar]
- Mannuzzu LM, Moronne MM, Isacoff EY. Direct physical measure of conformational rearrangement underlying potassium channel gating. Science. 1996;271:213–216. doi: 10.1126/science.271.5246.213. [DOI] [PubMed] [Google Scholar]
- Mathur R, Zheng J, Yan Y, Sigworth FJ. Role of the S3-S4 linker in Shakerpotassium channel activation. J Gen Physiol. 1997;109:191–199. doi: 10.1085/jgp.109.2.191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCormack K, Joiner WJ, Heinemann SH. A characterization of the activating structural rearrangements in voltage-dependent Shaker K+channels. Neuron. 1994;12:301–315. doi: 10.1016/0896-6273(94)90273-9. [DOI] [PubMed] [Google Scholar]
- McCormack K, Lin L, Iverson LE, Tanouye MA, Sigworth FJ. Tandem linkage of Shaker K+channel subunits does not ensure the stoichiometry of expressed channels. Biophys J. 1992;63:1406–1411. doi: 10.1016/S0006-3495(92)81703-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCormack K, Lin L, Sigworth FJ. Substitution of a hydrophobic residue alters the conformational stability of Shaker K+channels during gating and assembly. Biophys J. 1993;65:1740–1748. doi: 10.1016/S0006-3495(93)81202-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCormack K, Tanouye MA, Iverson LE, Lin J-W, Ramaswami M, McCormack T, Campanelli JT, Mathew MK, Rudy B. A role for hydrophobic residues in the voltage- dependent gating of Shaker K+channels. Proc Natl Acad Sci USA. 1991;88:2931–2935. doi: 10.1073/pnas.88.7.2931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCormack T, Vega-Saenz de Miera C, Rudy B. Molecular cloning of a member of a third class of Shaker-family K+channel genes in mammals. Proc Natl Acad Sci USA. 1990;87:5227–5231. doi: 10.1073/pnas.87.13.5227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakai J, Adams BA, Imoto K, Beam KG. Critical roles of the S3 segment and S3-S4 linker of repeat I in activation of L-type calcium channels. Proc Natl Acad Sci USA. 1994;91:1014–1018. doi: 10.1073/pnas.91.3.1014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noceti F, Baldelli P, Wei X, Qin N, Toro L, Birnbaumer L, Stefani E. Effective gating charges per channel in voltage-dependent K+ and Ca2+channels. J Gen Physiol. 1996;108:143–155. doi: 10.1085/jgp.108.3.143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noda M, Ikeda T, Kayano T, Suzuki H, Takeshima H, Kurasaki M, Takahashi H, Numa S. Existence of distinct sodium channel messenger RNAs in rat brain. Nature. 1986;320:188–192. doi: 10.1038/320188a0. [DOI] [PubMed] [Google Scholar]
- Noda M, Shimizu S, Tanabe T, Takai T, Kayano T, Ikeda T, Takahashi H, Nakayama H, Kanaoka Y, Minamino N, et al. Primary structure of Electrophorus electricussodium channel deduced from cDNA sequence. Nature. 1984;312:121–127. doi: 10.1038/312121a0. [DOI] [PubMed] [Google Scholar]
- Ogielska EM, Zagotta WN, Hoshi T, Heinemann SH, Haab J, Aldrich RW. Cooperative subunit interactions in C-type inactivation of K channels. Biophys J. 1995;69:2449–2457. doi: 10.1016/S0006-3495(95)80114-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papazian DM, Schwarz TL, Tempel BL, Jan YN, Jan LY. Cloning of genomic and complementary DNA from Shaker, a putative potassium channel gene from Drosophila. . Science. 1987;237:749–753. doi: 10.1126/science.2441470. [DOI] [PubMed] [Google Scholar]
- Papazian DM, Shao XM, Seoh S-A, Mock AF, Huang Y, Wainstock DH. Electrostatic interactions of S4 voltage sensor in Shaker K+channel. Neuron. 1995;14:1293–1301. doi: 10.1016/0896-6273(95)90276-7. [DOI] [PubMed] [Google Scholar]
- Papazian DM, Timpe LC, Jan YN, Jan LY. Alteration of voltage-dependence of Shakerpotassium channel by mutations in the S4 sequence. Nature. 1991;349:305–310. doi: 10.1038/349305a0. [DOI] [PubMed] [Google Scholar]
- Planells-Cases R, Ferrer-Montiel AV, Patten CD, Montal M. Mutation of conserved negatively charged residues in the S2 and S3 transmembrane segments of a mammalian K+channel selectively modulates channel gating. Proc Natl Acad Sci USA. 1995;92:9422–9426. doi: 10.1073/pnas.92.20.9422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perozo E, Santacruz-Toloza L, Stefani E, Bezanilla F, Papazian DM. S4 mutations alter gating currents of ShakerK channels. Biophys J. 1994;66:345–354. doi: 10.1016/s0006-3495(94)80783-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pongs O, Kecskemethy N, Muller R, Krah-Jentgens I, Baumann A, Klitz HH, Canal I, Llamazares S, Ferrus A. Shaker encodes a family of putative potassium channel proteins in the nervous system of Drosophila. . EMBO (Eur Mol Biol Organ) J. 1988;7:1087–1096. doi: 10.1002/j.1460-2075.1988.tb02917.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salkoff L, Butler A, Wei A, Scavarda N, Giffen K, Ifune C, Goodman R, Mandel G. Genomic organization and deduced amino acid sequence of a putative sodium channel gene in Drosophila. . Science. 1987;237:744–749. doi: 10.1126/science.2441469. [DOI] [PubMed] [Google Scholar]
- Sanger F, Nicklen S, Coulson AR. DNA sequencing with chain-terminating inhibitors. Proc Natl Acad Sci USA. 1977;74:5463–5467. doi: 10.1073/pnas.74.12.5463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider MF, Chandler WK. Voltage-dependent charge movement in skeletal muscle: a possible step in excitation-contraction coupling. Nature. 1973;242:244–246. doi: 10.1038/242244a0. [DOI] [PubMed] [Google Scholar]
- Schoppa NE, McCormack K, Tanouye MA, Sigworth FJ. The size of gating charge in wild-type and mutant Shakerpotassium channels. Science. 1992;255:1712–1715. doi: 10.1126/science.1553560. [DOI] [PubMed] [Google Scholar]
- Schwarz TL, Tempel BL, Papazian DM, Jan YN, Jan LY. Multiple potassium-channel components are produced by alternative splicing at the Shaker locus in Drosophila. . Nature. 1988;331:137–142. doi: 10.1038/331137a0. [DOI] [PubMed] [Google Scholar]
- Seoh S-A, Sigg D, Papazian DM, Bezanilla F. Voltage-sensing residues in the S2 and S4 segments of the Shaker K+channel. Neuron. 1996;16:1159–1167. doi: 10.1016/s0896-6273(00)80142-7. [DOI] [PubMed] [Google Scholar]
- Shieh C-C, Klemic KG, Kirsch GE. Role of transmembrane segment S5 on gating of voltage-dependent K+channels. J Gen Physiol. 1997;109:1–12. doi: 10.1085/jgp.109.6.767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigg D, Bezanilla F. Total charge movement per channel. The relation between gating charge displacement and the voltage sensitivity of activation. J Gen Physiol. 1997;109:27–39. doi: 10.1085/jgp.109.1.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigg D, Stefani E, Bezanilla F. Gating current noise produced by elementary transitions in Shakerpotassium channels. Science. 1994;264:578–582. doi: 10.1126/science.8160016. [DOI] [PubMed] [Google Scholar]
- Sigworth FJ. Voltage gating of ion channels. Q Rev Biophys. 1993;27:1–40. doi: 10.1017/s0033583500002894. [DOI] [PubMed] [Google Scholar]
- Smith-Maxwell CJ, Ledwell JL, Aldrich RW. Uncharged S4 residues and cooperativity in voltage-dependent potassium channel activation. J Gen Physiol. 1998;111:421–439. doi: 10.1085/jgp.111.3.421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith-Maxwell CJ, Kanevsky M, Aldrich RW. Potassium channel activation can be slowed by mutations in the S4 and S4-S5 linker regions. Biophys J. 1993;64:A200. . (Abstr.) [Google Scholar]
- Smith-Maxwell CJ, Taylor RA, Aldrich RW. Amino acids responsible for slowing activation kinetics in Shakerpotassium channel mutants. Soc Neurosci Abstr. 1994;20:863. . (Abstr.) [Google Scholar]
- Stefani E, Toro L, Perozo E, Bezanilla F. Gating of Shaker K+channels: I. ionic and gating currents. Biophys J. 1994;66:996–1010. doi: 10.1016/S0006-3495(94)80881-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stocker M, Pongs O, Hoth M, Heinemann S, Stühmer W, Schroter K-H, Ruppersberg JP. Swapping of functional domains in voltage-gated K+channels. Proc R Soc Lond Ser B. 1991;245:101–107. doi: 10.1098/rspb.1991.0094. [DOI] [PubMed] [Google Scholar]
- Stühmer W, Conti F, Stocker M, Pongs O, Heinemann SH. Gating currents of inactivating and non-inactivating potassium channels expressed in Xenopusoocytes. Pflügers Archiv. 1991;418:423–429. doi: 10.1007/BF00550881. [DOI] [PubMed] [Google Scholar]
- Tanabe T, Adams BA, Numa S, Beam KG. Repeat I of the dihydropyridine receptor is critical in determining calcium channel activation kinetics. Nature. 1991;352:800–803. doi: 10.1038/352800a0. [DOI] [PubMed] [Google Scholar]
- Tanabe T, Beam KG, Adams BA, Niidome T, Numa S. Regions of the skeletal muscle dihydropyridine receptor critical for excitation-contraction coupling. Nature. 1990;346:567–569. doi: 10.1038/346567a0. [DOI] [PubMed] [Google Scholar]
- Tanabe T, Beam KG, Powell JA, Numa S. Restoration of excitation-contraction coupling and slow calcium current in dysgenic muscle by dihydropyridine receptor complementary DNA. Nature. 1988;336:134–139. doi: 10.1038/336134a0. [DOI] [PubMed] [Google Scholar]
- Tanabe T, Takeshima H, Mikami A, Flockerzi V, Takahashi H, Kangawa K, Kojima M, Matsuo H, Hirose T, Numa S. Primary structure of the receptor for calcium channel blockers from skeletal muscle. Nature. 1987;328:313–318. doi: 10.1038/328313a0. [DOI] [PubMed] [Google Scholar]
- Tang C-Y, Papazian DM. Transfer of voltage independence from a rat olfactory channel to the Drosophila ether-à-go-go K+channel. J Gen Physiol. 1997;109:301–311. doi: 10.1085/jgp.109.3.301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tempel BL, Jan YN, Jan LY. Cloning of a probable potassium channel gene from mouse brain. Nature. 1988;332:837–839. doi: 10.1038/332837a0. [DOI] [PubMed] [Google Scholar]
- Tempel BL, Papazian DM, Schwarz TL, Jan YN, Jan LY. Sequence of a probable potassium channel component encoded at Shaker locus of Drosophila. . Science. 1987;237:770–775. doi: 10.1126/science.2441471. [DOI] [PubMed] [Google Scholar]
- Tiwari-Woodruff SK, Schulteis CT, Mock AF, Papazian DM. Electrostatic interactions between transmembrane segments mediate folding of Shaker K+channel subunits. Biophys J. 1997;72:1489–1500. doi: 10.1016/S0006-3495(97)78797-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsunoda S, Salkoff L. Genetic analysis of Drosophila neurons: Shal, Shaw, and Shabencode most embryonic potassium currents. J Neurosci. 1995;15:1741–1754. doi: 10.1523/JNEUROSCI.15-03-01741.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tytgat J, Hess P. Evidence for cooperative interactions in potassium channel gating. Nature. 1992;359:420–423. doi: 10.1038/359420a0. [DOI] [PubMed] [Google Scholar]
- Wei A, Covarrubias M, Butler A, Baker K, Pak M, Salkoff L. K+ current diversity is produced by an extended gene family conserved in Drosophilaand mouse. Science. 1990;248:599–603. doi: 10.1126/science.2333511. [DOI] [PubMed] [Google Scholar]
- Yang N, George AL, Jr, Horn R. Molecular basis of charge movement in voltage-gated sodium channels. Neuron. 1996;16:113–122. doi: 10.1016/s0896-6273(00)80028-8. [DOI] [PubMed] [Google Scholar]
- Yang N, Horn R. Evidence for voltage-dependent S4 movement in sodium channels. Neuron. 1995;15:213–218. doi: 10.1016/0896-6273(95)90078-0. [DOI] [PubMed] [Google Scholar]
- Yusaf SP, Wray D, Sivaprasadarao A. Measurement of the movement of the S4 segment during the activation of a voltage-gated potassium channel. Pflügers Archiv. 1996;433:91–97. doi: 10.1007/s004240050253. [DOI] [PubMed] [Google Scholar]
- Zagotta WN, Hoshi T, Aldrich RW. Gating of single Shaker potassium channels in Drosophila muscle and in Xenopus oocytes injected with ShakermRNA. Proc Natl Acad Sci USA. 1989;86:7243–7247. doi: 10.1073/pnas.86.18.7243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zagotta WN, Aldrich RW. Alterations in activation gating of single Shaker A-type potassium channels by the Sh5mutation. J Neurosci. 1990;10:1799–1810. doi: 10.1523/JNEUROSCI.10-06-01799.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zagotta WN, Hoshi T, Aldrich RW. Restoration of inactivation in mutants of Shaker potassium channels by a peptide derived from ShB. . Science. 1990;250:568–571. doi: 10.1126/science.2122520. [DOI] [PubMed] [Google Scholar]
- Zagotta WN, Hoshi T, Aldrich RW. a. Shakerpotassium channel gating III: evaluation of kinetic models for activation. J Gen Physiol. 1994;103:321–362. doi: 10.1085/jgp.103.2.321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zagotta WN, Hoshi T, Dittman J, Aldrich RW. b. Shakerpotassium channel gating II: transitions in the activation pathway. J Gen Physiol. 1994;103:279–319. doi: 10.1085/jgp.103.2.279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J-F, Ellinor PT, Aldrich RW, Tsien RW. Molecular determinants of voltage-dependent inactivation in calcium channels. Nature. 1994;372:97–100. doi: 10.1038/372097a0. [DOI] [PubMed] [Google Scholar]










