Abstract
Another research group has proposed an interesting model for calcium channel selectivity. However, on the basis of their reported results we find it impossible to assess the merits of their model because their results and claims concerning selectivity are based on an extrapolation over four orders of magnitude to low Ca2+ concentration. Their results and claims have been presented in several articles and reviews in several journals and, thus, need attention. In this article, we first establish that we obtain results on electrostatics and channel occupancies similar to the high-concentration simulations they present. We then perform grand canonical ensemble simulations that enable us to study micromolar Ca2+ concentrations. We find that their model channel is only weakly Ca2+ selective. A crucial problem with their model appears to be the placement of the negatively charged glutamate structural elements in fixed positions inside the protein rather than as flexible units inside the filter.
INTRODUCTION
Ion channels are essential for the proper function of cells and organisms (1). The task of ion channels is to pass ions through their pore selectively. In particular, calcium (Ca) channels play an important role in vital physiological functions such as neurotransmitter release, muscle contraction, cell signaling, and many others. Ca channels selectively conduct Ca2+ ions when these are present in millimolar or larger concentration even if other ions (Na+ or K+) are present in a much larger quantity. On the other hand, Ca2+ ions block the current of monovalent ions when Ca2+ is present at a lower concentration. This Ca2+-block occurs in the L-type Ca channel at micromolar Ca2+ concentrations (2–6). Several attempts to explain the mechanisms of these important selectivity phenomena have been made in the literature. A study of one model is given in this article with the goal of obtaining a better understanding of the behavior of Ca2+-selective channels.
In the past few years, our understanding of Ca channels has dramatically improved. Nonner et al. (7,8) have proposed a simple intuitive model, based on a theory of homogeneous fluids, in which the selectivity of a particular cation-selective channel (the Ca channel in this study) is produced by the competition between the attractive Coulombic interactions of the cations with the net negatively charged structural elements of the channel filter and the repulsive excluded volume of the ions and structural elements in a small volume. In this competition cations are attracted into the filter but, because of the restricted geometry of the channel and the excluded volume of the ions and channel structural elements, divalent (Ca2+) ions are more effective at balancing the −4e negative charge of the selectivity filter of the Ca channel than are monovalent (Na+) ions since they deliver twice the charge while occupying almost the same volume. Thus, the Ca2+ ions preferentially occupy the filter even when the concentration of the Ca2+ ions in the surrounding reservoir is several orders-of-magnitude smaller than the concentration of Na+ ions in this reservoir. This model can be extended to sodium (Na) channels (9,10).
This appealing mechanism for selectivity can be called charge/space competition (CSC) and is not only intuitively attractive but is in accord with thermodynamics. In contrast to a mechanical system, where the stable state is the state with the lowest energy, a stable thermodynamic system is the state with the lowest free energy, A = U – TS, where U is the thermodynamic energy, T is the temperature, and S is the entropy. The minimum in A is the result of the competition between U and S. In general, attractive forces contribute to U and volume exclusion forces, due to particle size, contribute to S. This division is absolute in the well-known van der Waals theory that is a useful starting point for a theory of a liquid and is quite accurate in more refined theories of liquids (11). In the context of a channel, Coulombic forces contribute primarily to U while the volume exclusion forces due to the size of the particles contribute primarily to S.
The CSC mechanism accounts not only for the selectivity of Ca2+ versus Na+ ions in Ca and Na channels but accounts for the selectivity of cations on the basis of ion diameter. The CSC mechanism has been applied to the ryanodine receptor Ca channel, where it reproduces or predicts >50 data curves (12,13). The intuitive ideas of Nonner et al. (7,8) have been made rigorous by means of the continuously refined studies of Boda et al. (14–16). In these studies, we have made Monte Carlo (MC) simulations that most recently have included the effects of charge polarization due to dielectric boundaries (17,18) and, by means of grand canonical (GC) ensemble MC simulations, have been able to obtain results for exceedingly low concentrations (10−6 M) of Ca2+ ions. The statistical sampling in the filter is enhanced by means of preferential sampling (14).
A second approach, due to Corry et al. (19), Krishnamurthy and Chung (20), Corry and Chung (21), and Corry et al. (22) (this body of work hereinafter called Chung and co-workers), also describes the channel using an idealized geometry (the structure of the Ca channel is not known). The ions move in a dielectric continuum solvent and the wall of the channel protein forms a dielectric boundary. Chung and co-workers used Brownian dynamics (BD) simulations at high (typically ±200 mV) applied voltages to calculate the current flowing through the channel and extrapolated their results to the low Ca concentrations that are of physiological interest. Chung and co-workers state that their model reproduces the micromolar Ca2+ versus Na+ selectivity of the L-type Ca channel. These claims have been stated several times in different places and deserve examination. Their bold extrapolation needs particular attention.
This article analyzes consequences of two crucial differences between the approaches of Chung and co-workers and Boda et al. (14–18).
Chung and co-workers performed BD simulations at rather high Ca2+ ion concentrations (>18 mM). Their claim that their model reproduces micromolar Ca2+-selectivity is based on a large extrapolation (four orders of magnitude) to the low Ca2+ concentrations of interest. In contrast, we simulate micromolar concentrations directly using the GC ensemble. In this work, simulating the micromolar regime directly, we show that the model of Chung and co-workers does not have the strong Ca2+-selectivity properties that they had extrapolated.
Another significant difference between approaches of Boda et al. (14–18) and Chung and co-workers is that the latter group places the negative structural charges of the selectivity filter behind the wall in fixed positions. This rigid model is in sharp contrast with the flexible environment in the selectivity filter of our model. In the studies using the CSC mechanism (7–10, 12–18), the oxygens of the glutamate side chains are treated as mobile structural ions that are restricted to the selectivity filter but otherwise free to move inside the filter. Thus, these ions form a liquidlike self-adjusting environment for the passing Na+ and Ca2+ ions. Chung and co-workers claim that, in their model, selectivity is due only to Coulomb forces. Quoting from Corry and Chung's review (21), “Indeed, the electrostatic attraction of the protein is all that is required to account for ion permeation and selectivity in this model.” We argue that electrostatics alone is not sufficient to produce micromolar selectivity in their model and that excluded volume effects cannot be ignored. By placing the structural ions inside the selectivity filter, the Ca2+ selectivity of the model can be improved.
The simulation results of Chung and co-workers have been presented without critique in many reviews (6,20–22). The objective of this article is to report direct simulation results in the Ca2+ concentration range where Chung and co-workers have extrapolated and where, in experiments, Ca2+ block is observed. Presenting simulation results with a CSC model of the filter embedded in the channel geometry of Chung and co-workers permits us to draw conclusions for the possible mechanism of selectivity as viewed by their group and us.
THE MODELS
We adopt the standard usage in statistical mechanics and distinguish between a model (which is defined by a Hamiltonian that gives the energy of the system in terms of the particle positions and momenta and their interaction with any fixed boundaries in the system) and a method (a theory or in our case a simulation, that permits the study of the consequences of a model).
The model of Chung and co-workers
Geometry
The model of Chung and co-workers is shown in our Fig. 1 A and consists of a rotationally symmetric channel that is a cylinder of length 50 Å with a variable radius that defines the boundary of the channel (see Corry et al. (19), their Fig. 1). The z axis of the coordinate system is along the central axis of the channel cylinder. The cylinder is centered at z = 0 and extends from −25 Å to 25 Å. The region in the interval −25 Å < z < 25 Å that is beyond the channel wall is the channel protein. At its most narrow part (10 Å < z < 15 Å), the radius of the channel is 2.8 Å. This region represents the selectivity filter. The region |z| > 25 Å consists of the two reservoirs of the system. Each reservoir is a cylinder of radius 30 Å with a height of ∼33 Å. The walls of the confining simulation cell are hard.
FIGURE 1.
Geometries of the Chung and co-workers' model (A) and the CSC model (B). Red spheres represent negative structural charges in the filter. In the Chung and co-workers' model (A) these four charges are in fixed positions and embedded in the protein body, whereas in the CSC model (B) these charges are eight mobile half-charged oxygen ions confined to the filter lumen but free to move inside. Blue and yellow spheres represent charges forming dipoles at the intracellular entrance. Gray and green spheres represent Ca2+ and Na+ ions, respectively. The surface grid is that used in solving the integral equations of the electrostatics.
Chung and co-workers use what they call a stochastic boundary at the far ends of the reservoirs, whose purpose is to maintain the two reservoirs at constant concentration. It means that once an ion crosses the channel, say, from right to left, another ion is transplanted from the left-hand side of the simulation cell to the right-hand side in a position where it does not overlap with other ions. The applicability of this step without a grand-canonical acceptance test of the new position of the ion, which ensures that the chemical potential of the system has not been changed, is questionable. Chung and co-workers performed a check (23) following Im et al. (24) and demonstrated that they obtain the same results with the two methods. Nevertheless, they used a simpler channel and high concentrations in their test.
The structural elements of the channel (glutamates in the case of a calcium channel) are modeled as fixed point (fractional) charges of magnitude −0.811e that are 1 Å inside the protein arranged in a spiral at the channel filter (the red spheres in Fig. 1 A). Additional positive and negative fractional charges (±0.374e) form dipoles (yellow and blue spheres in Fig. 1 A) at the intracellular entrance of the channel to decrease the large dielectric barrier for the passing ions.
The region outside the protein and within the channel contains the electrolyte. Only the ions in the electrolyte are modeled explicitly. Water is represented by a dielectric continuum. The dielectric coefficients of the electrolyte and protein are taken to be 60 and 2, respectively.
In our implementation of the model of Chung and co-workers, we have a different cell and procedure; we use a much larger cell (a radius of 64 Å and length of 300 Å). Our simulations are performed by MC using the GC ensemble rather than BD. Thus, we do not need the questionable stochastic boundary to maintain the reservoir concentrations. Instead, the GC ensemble allows us to simulate micromolar bath concentrations without introducing statistical bias. These points are discussed in more detail below. For the sake of comparison with Chung and co-workers, in implementing their model, we used their values for the energetic parameters (the values for the parameters in Eqs. 1–4) and did not concern ourselves with the question of whether these are the optimal values.
Ion-wall potential
We describe the short-range interaction of an ion and the channel wall by
 |
(1) |
where F0 = 2 × 10−10 Newtons, Ri is the radius of the ion (the value of Ri for Ca2+, Na+, and Cl− are 0.99 Å, 0.9 Å, and 1.81 Å, respectively), RW = 1.4 Å is the radius of the atoms making up the wall, and r is the perpendicular distance of an ion from the nearest portion of the protein wall. (Please note that Eq. 1 is referred to as “the usual inverse 9 repulsive potential”. Some comment is required. The usual inverse 9 potential is applicable to a flat surface of infinite extent. It is obtained by integration over half-space of a repulsive-inverse 12 potential between the volume elements of the flat surface and a given particle located a perpendicular distance outside this surface. Its application to a cylinder with a small radius and a finite length is questionable.)
Our Eq. 1 differs from Eq. 4 in Corry et al. (19), where (Rc(z) + RW – a)9 appears in the denominator (note that Rc(z) is the channel's radius as a function of z and a is the ion's distance from the z axis). Their Eq. 4 does not give an inverse 9 relation to normal distance between ion and wall when the angle of the tangent of the surface and the z axis is larger than zero. Furthermore, using this radial distance, the ion-wall potential is not defined for the region where the surface is perpendicular to the z axis. This is the region near the protein wall in the reservoir (|z| > 25 Å), where Chung and co-workers applied a hard wall to prevent the ions from crossing the surface of the protein. We used our Eq. 1 because it gives the same potential everywhere near the protein surface; therefore, it is more consistent than the one used by Chung and co-workers. In the selectivity filter (our main region of interest), the two equations are equivalent.
Ion-ion potential
The ion-ion interaction of Chung and co-workers is taken to be the pairwise sum of Coulomb interactions plus a short-range interaction,
 |
(2) |
where the contact distance is  for cation-anion pairs, while it is
for cation-anion pairs, while it is  for like ions, the origin of the hydration force is
for like ions, the origin of the hydration force is  (positive for like ions and negative otherwise), cW = 2.76 Å, and ce = 1 Å. The values of
(positive for like ions and negative otherwise), cW = 2.76 Å, and ce = 1 Å. The values of  are 16.8, 8.5, 1.7, 2.5, 0.8, and 1.4 kT for Ca2+-Cl−, Na+-Cl−, Ca2+-Na+, Na+-Na+, Ca2+-Ca2+, and Cl−-Cl− pairs, respectively. The potential parameters were fitted to the potentials of mean force given by Guàrdia et al. (25–27).
are 16.8, 8.5, 1.7, 2.5, 0.8, and 1.4 kT for Ca2+-Cl−, Na+-Cl−, Ca2+-Na+, Na+-Na+, Ca2+-Ca2+, and Cl−-Cl− pairs, respectively. The potential parameters were fitted to the potentials of mean force given by Guàrdia et al. (25–27).
The presence of the repulsive-inverse 9 term in Eq. 2 seems to disagree with the assertion of Chung and co-workers that volume exclusion forces do not play a role in their model. If this assertion were valid, the first term would be unnecessary.
The purpose of the sum of the repulsive 1/r9 potential and the exponentially decaying oscillating hydration force is to mimic the results of molecular dynamics (MD) simulations. Chung and co-workers assert that the radial distribution functions (RDFs) for NaCl that result from the use of Eq. 2 are similar to those obtained by Lyubartsev and Laaksonen (28) by a self-consistent iteration involving an MD simulation.
Chung and co-workers find that the locations of the maxima in their RDFs roughly match those of the MD RDFs. Matching the location of the maxima only requires that the effective ion diameters be reasonable. The height of the maximum is a much more important issue that is not mentioned in the articles by these authors. The maximum of the Na+-Cl− RDF obtained from the model of Chung and co-workers significantly underestimates the maximum obtained from the MD simulation. As a matter of fact, it can be seen in Fig. 2 of Corry et al. (19) that this maximum is lower than the first maximum of the Na+-Na+ pair. It is a strange electrolyte, indeed, where like ions attract each other more strongly than cation-anion pairs. Lyubartsev and Laaksonen (28) (their Fig. 3) shows the opposite behavior.
FIGURE 2.
Convergence of the MC simulation of the Chung and co-workers' model toward equilibrium. The average number of Na+ (upper panel) and Ca2+ (lower panel) ions is plotted versus the index of the attempt. The baths contained 10−5 M CaCl2 plus 150 mM NaCl.
FIGURE 3.
Comparison of axial profiles of potential energy in the Chung and co-workers' model. A single probe ion is moved through the pore and allowed to find its minimal-energy position in the cross-section at each axial location. The upper and lower sets of profiles are obtained with the structural charges of the model set to zero or their normal values, respectively. (Curves, Chung and co-workers; symbols, our results.)
Corry et al. (19) claim that “simpler ion-ion interactions … are not suitable for use in calcium channels” because “they allow cations to pass each other in the selectivity filter, thus making it impossible to explain the observed blocking of sodium ions by calcium, and vice versa.” It is our belief that explanation of Ca2+-block of Na+-current in Ca channels does not require single filing (more about this later) (7,12). Thus, the above reasoning for using Eq. 2 cannot be accepted. Ions do not enter the narrow channel with their whole hydration shell, therefore the potential fitted to bulk simulation results cannot be applied.
Born energy
The ions in the model of Chung and co-workers experience a change in Born energy at the axial locations where the pore joins the baths (zc = −22.5 Å and zc = 22.5 Å). The Born energy change upon entering the pore is
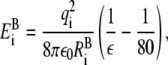 |
(3) |
where ε = 60 is the dielectric constant in the channel and  is the Born radius of the ion species i of charge qi. In the model of Chung and co-workers, the transition of Born energy is smoothed over a 3 Å interval centered on zc using the interpolation
is the Born radius of the ion species i of charge qi. In the model of Chung and co-workers, the transition of Born energy is smoothed over a 3 Å interval centered on zc using the interpolation
 |
(4) |
where s = (z – zc)/(1.5 Å) for the left boundary, and s = – (z – zc)/(1.5 Å) for the right boundary.
Chung and co-workers refer to their earlier article (29) for further description on this method, but we found the value of  only for K+ ion. Therefore, we used Born radii fitted to experimental hydration energies reported in the literature (30) (−1608.3, −423.7, and −304.0 kJ/mol for Ca2+, Na+, and Cl−, respectively). The corresponding
only for K+ ion. Therefore, we used Born radii fitted to experimental hydration energies reported in the literature (30) (−1608.3, −423.7, and −304.0 kJ/mol for Ca2+, Na+, and Cl−, respectively). The corresponding  values in kT (at 298 K) are 2.737, 0.721, and 0.517 for Ca2+, Na+, and Cl−, respectively.
values in kT (at 298 K) are 2.737, 0.721, and 0.517 for Ca2+, Na+, and Cl−, respectively.
Chung et al. (29) qualify this procedure of accounting for the difference in the polarization properties of pore and bath as a “compromise.” In reality, the ions induce charge on the dielectric boundary between pore and baths. The interaction of every ion with that charge should be calculated in a self-consistent treatment. Simulation of ions crossing dielectric boundaries is difficult, which is the reason of the “compromise” used by their group. With the dielectric boundary effects described by the Born energy, Chung and co-workers solve the electrostatics using a dielectric coefficient of 60 for the baths, which might produce unrealistically large ion-ion interactions in the bath solutions.
The CSC model
We also study a realization of the CSC model. Here the structural charges of the EEEE locus are placed inside the lumen of the channel rather than into a rigid channel wall (Fig. 1 B). The channel is otherwise kept identical to that of Chung and co-workers to focus the comparison on the difference in the placement of charged groups. The terminal carboxylate groups of the glutamate residues are represented in the CSC model as eight half-charged oxygen ions. Each oxygen ion is a hard sphere with radius 1.4 Å. The oxygen ions are allowed to overlap with the wall of the filter, but their center cannot approach the wall closer than 0.5 Å. These oxygen ions, that now are part of the electrolyte filling the filter, are confined by a cylinder with radius 3.7 Å and length 9.352 Å. They are confined to be within this volume but are otherwise free to move in this space. The oxygen ions interact with other charges in the simulation cell through the Coulomb potential. They interact with other ions (including other oxygen ions and counterions) through the hard sphere potential instead of the soft-core potential in Eq. 2. The hard-core radii used for Na+, Ca2+, and Cl− were 1, 0.99, and 1.81 Å (31). (The soft-core potential is still used for pairs of Na+, Ca2+, and Cl− ions because we wish to convert the model of Chung and co-workers to the CSC type of model without making other changes.) The oxygen ions are not subject to the soft interaction potential with the channel wall in Eq. 1.
In the CSC model the glutamate groups occupy filter space and they accommodate to the movement of passing cations so the grand potential of the system is minimized. Note that these structural charges now are in the dielectric domain of the solution space, whereas in the model of Chung and co-workers they are in the dielectric of the pore wall. This has consequences for the polarization charge produced by these structural ions on the protein/pore interface.
SIMULATION METHOD
MC simulations were performed in the grand canonical ensemble (32,33) using the Metropolis sampling. Details of our sampling are described in Boda et al. (18). In brief, our attempts for moving a particle included:
Step 1. Small changes in position (we use only this movement to displace oxygen ions in the CSC model).
Step 2. Large changes in position.
Step 3. A preferential change between positions in the channel and bath subvolumes.
Step 4. Insertion/removal of a neutral group of ions (Na+ and Cl−, or Ca2+ and 2Cl−) into/from the simulation cell (32).
Step 5. A GC attempt similar to Step 4, but involving preferred subvolumes of the simulation cell (Na+ and Ca2+, the pore region; Cl−, the whole simulation cell).
The acceptance criterion for preferential MC Step 3 considered the volume ratio of the respective regions. It was shown that this MC step accelerates sampling considerably (14).
The preferential GC Step 5 is an additional variety of MC attempt not used in our previous works (9,17,18). It was included to accelerate convergence toward equilibrium in these simulations. Without this step, we equilibrated the bulk region of the simulation cell with an external bath of fixed chemical potentials (and thus with fixed salt concentrations) and then we equilibrated the channel region with this bulk region using the preference sampling of Step 3. The basic idea of the new method is that we can equilibrate the channel region with the external bath directly without applying the intermediate step of equilibration with the bulk region of the cell. If a system is in equilibrium with an external bath, any subsystem of it is also in equilibrium with the external bath. Therefore, we can insert cations directly into the pore and thus increase the percentage of MC steps occurring between the pore and the external bath.
An example of convergence is shown in Fig. 2, where the number of Ca2+ and Na+ ions in the selectivity filter (10 < z < 15 Å) is plotted versus the index of the attempt. The bath concentration of Ca2+ in this test was 10−5 M, a value important for the purpose of this article. The convergence of the simulation is much faster when the preferential GC Step 5 is used (note the logarithmic scale of the abscissa). A production run comprised 6 × 108 to 1.2 × 109 attempts.
In GC simulations, bath concentrations are a computed consequence of the chemical potentials assigned to the ions in the system. We determined chemical potentials needed to establish targeted bath concentrations using an iteration (34). The reported bath concentrations are the average ion concentrations in the bulklike regions of our large baths.
In the BD simulations of Chung and co-workers, the charges induced by ions on the dielectric boundaries were computed using a boundary element method (35). The contributions of these charges to the field were computed by an iterative method and tabulated for a set of ion positions; during the BD simulation, the field contributions were estimated from the tabulated values using interpolation considering the actual ion positions. This method was chosen for computational efficiency.
In our MC simulation, we solve the electrostatics by a boundary element method (18,36) that we called the induced charge-computation method. Rather than using an iterative method we generate the LU-decomposition of the matrix that results from the boundary integral equations. Since boundaries are fixed in space during our simulation, this computation can be done as part of the overhead at the beginning of the simulation. Specific solutions are obtained for each particle distribution during the MC simulation using back-substitution. Thus our computation of potential does not involve interpolations like those used by Chung and co-workers. We divide the boundary surface into 1811 (generally curved) tiles (outlined by the grid shown in Fig. 1) and use an accurate method to include surface curvature into the computation of the electrostatics (18). Our simulation cell is considerably larger (radius 64 Å, length 300 Å) than that used by Chung and co-workers. This cell typically contains ∼300 Na+. Thus, the baths in our simulations approximate bulk conditions.
RESULTS AND DISCUSSION
Profiles of potential energy and ion concentrations
Chung and co-workers have computed potential energies in a test in which a single Na+ or Ca2+ was used to probe the pore along the z axis; the ion was allowed to find lowest energy positions in the cross-section of the pore (see Fig. 5 of Corry et al. (19)). These results allow us to compare our different methods used to compute the electrostatics. The lines of our Fig. 3 represent the results of Corry et al. (19); the symbols are computed with our method. The agreement is very good. We had expected to find differences because we estimated some details of the surface geometry that were not numerically specified in Corry et al. (19). The agreement confirms the validity of both numerical approaches for the model of Chung and co-workers.
FIGURE 5.
The AMFE experiment of Almers et al. (2) compared to simulation results. (Top panel, circles) Experimental currents normalized with respect to the current at [Ca2+] = 10−7.2 (Ca2+ was added externally); (squares) BD simulated currents of Chung and co-workers (normalized to their maximal value); and (dashed and dotted lines) Na+ and Ca2+ currents, respectively, estimated by Chung and co-workers using an extrapolation based on BD simulation results obtained with bath Ca2+ concentrations ≥18 mM. The Chung and co-workers Ca2+ and Na+ results are separately normalized (see text). (Bottom panel) Summary of our MC simulation results for the Chung and co-workers' model with varied bath concentration of Ca2+ and a fixed concentration of 150 mM NaCl. The symbols give the simulated occupancies of the filter region (10 ≤ z ≤ 15 Å). The curves are first-order isotherms; their limiting value at low Ca2+ concentration is constrained by a simulation done with Ca2+-free baths (point not shown). The arrow marks the concentration where Na+ occupancy is reduced to one half that found in the absence of Ca2+.
It is unfortunate for a comparison with equilibrium simulations that Chung and co-workers presented axial concentration profiles only for conditions that produced ion flow (an applied voltage of −200 or +200 mV; see Figs. 9 and 10 of Corry et al. (19)). Our Fig. 4 shows superpositions of the nonequilibrium profiles of Chung and co-workers and equilibrium profiles (corresponding to zero applied voltage) that we computed with the MC method. Chung and co-workers find rather small differences between the Na+ profiles for −200 and +200 mV, so that we might expect to find a profile that is well bracketed by theirs. This is the case (our Fig. 4 A).
FIGURE 4.
Histograms of axial distribution of ions in the Chung and co-workers' model. The pore is axially divided into 30 bins normal to the axis; the ordinate gives the average number of ions per bin. The solid lines and shaded areas represent the MC results.
The difference between the profiles for Ca2+ for Chung and co-workers between the two voltages is much larger than for Na+ (Fig. 4 B). Our equilibrium profile differs from both profiles computed by Chung and co-workers. The difference is smaller for the Ca2+ distribution on the sink side than on the source side of their nonequilibrium distributions, which is consistent with their conclusion that Ca2+ conduction in their model is limited by a substantial dielectric barrier that arises in the cavity region of the model pore. When ions flow this barrier causes an accumulation of Ca2+ on the source side of the barrier, above any accumulation that occurs in equilibrium. With these considerations, we feel that the ion distributions obtained by Chung and co-workers under conditions of flow and our equilibrium results are mutually consistent.
The anomalous mole fraction effect
A signature of Ca channel conduction is the anomalous mole fraction effect (AMFE) first observed in whole-cell currents (2,37) and subsequently in currents recorded from individual Ca channels (38). When the extracellular Ca2+ concentration is <10−7 M but the Na+ concentration is 30–150 mM, the Ca channel conducts a Na+ current. Increasing the Ca2+ concentration into the micromolar range reduces the current carried by Na+ by an order of magnitude. Only if the Ca2+ concentration is raised to the millimolar level, does the channel preferentially conduct Ca2+ (reviewed in (6)). The AMFE appears to be less strong (that is, the current is less reduced in the presence of micromolar Ca2+) when the membrane voltage is ≤−50 mV (39).
Chung and co-workers have used BD simulation results obtained with rather large concentrations of Ca2+ (≥18 mM) at the applied voltage of −200 mV to extrapolate to the Ca2+ concentration and voltage ranges where the AMFE has been experimentally observed. They find nearly perfect agreement with the experimental observation of Almers et al. (2), that 0.9 μM Ca2+ reduces Na+ current to half that observed when Ca2+ concentration is 10−8 M or less. These experimental currents were measured between −20 and +7 mV applied voltage; in experiments at low Ca2+ concentrations (<10−4M), symmetrical Na+ concentrations of 32 mM were present. The extrapolation to low Ca2+ concentrations used by Chung and co-workers was described as based on entry and exit rates of Ca2+ simulated at high [Ca2+] but no mathematical description of the procedure was provided in their article. The extrapolation to experimental voltages is questionable, because it is unknown whether the physical conditions underlying the AMFE arise in a biological channel tested at −200 mV. Experiments are done at voltages much smaller in magnitude than −200 mV. Indeed, Fukushima and Hagiwara (39) found that the AMFE is substantially weakened when the test voltage is ≤−50 mV.
Our Fig. 5 shows the computed AMFE curves of Corry et al. (19) (our Fig. 5 A, lines) superimposed on the published experimental points of Almers and McCleskey (3) (our Fig. 5 A, circles) (please note that Fig. 16B in Corry et al. (19) shows a representation of these data in which the reduction of the Na+ current by Ca2+ is complete, whereas the data of Almers and McCleskey (3) show incomplete reduction). The reduction of Na+ current found by Chung and co-workers in the extrapolated AMFE is complete. Their extrapolated simulation results have been presented in several reviews (6,20–22) but have not been corroborated by a direct calculation. Our MC method using the grand canonical ensemble permits us to directly simulate Ca2+ concentrations in the range where the experimental AMFE is observed. We have reexamined Ca2+ binding as the basis for an AMFE in the model of Chung and co-workers using this independent and direct simulation method.
Our results obtained for a range of Ca2+ concentration added to a 0.15 M NaCl bath are summarized in Fig. 5 B. These results, obtained for the GC ensemble, indicate that the model accumulates Ca2+ far less avidly than the extrapolated computations of Chung and co-workers suggested. Approximately 0.2 mM Ca2+ is required in the bath to displace one-half of the Na+ ions from the pore (see the arrow in Fig. 5 B). Chung and co-workers extrapolated a half-point near 10−6 M Ca2+. At 10−6 M Ca2+, we detect a very small concentration of Ca2+ in the selectivity filter of the model of Chung and co-workers; the total occupancy by Ca2+ in the filter region is ∼0.007. The blockade that Chung and co-workers have predicted by extrapolation would require that one Ca2+ be present in the filter region at least one half of the time.
Our Fig. 6 shows axial concentration profiles for several of the Ca2+ concentrations that were included in the summary presented in Fig. 5 B. We detect no significant accumulation anywhere in the model pore when bath Ca2+ concentration is 1 μM. On the other hand, Na+ profiles are hardly influenced by the presence of 1 μM Ca2+ in the bath. Thus, the results of our MC simulations do not support the conclusion of Chung and co-workers that their model accounts for the experimental AMFE.
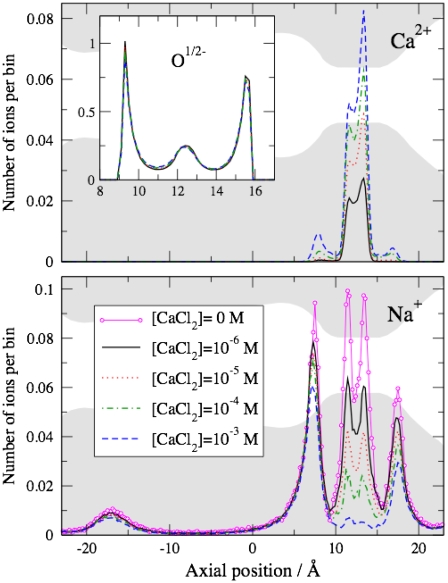
FIGURE 6.
Axial distributions of ions. MC results; spatial bins are 0.2 Å wide and normal to the axis. The baths contained 150 mM NaCl plus the indicated concentration of CaCl2. (Inset) Ca2+ distributions in the filter at an enlarged scale. Shaded areas are shown to help relate the ion distributions to pore geometry.
Our MC simulations are restricted to equilibrium (zero applied voltage). This condition is included in the range of experimental voltages where the AMFE is observed, whereas the voltage simulated by Chung and co-workers is far outside the experimental range. (Neither simulation includes the Ca2+ gradient present in the experiments.) It seems possible that the AMFE extrapolated by Chung and co-workers does occur in their model, as a consequence of the strong applied voltage: Ca2+ might be accumulated up to a large local concentration near the intracellular end of the filter (compare Fig. 4 B), because inward flow of Ca2+ is restricted by a high electrostatic barrier in the central cavity of the Chung and co-workers' model channel. To the extent that this voltage-driven accumulation of Ca2+ is required for AMFE behavior, the model of Chung and co-workers is not adequate. The fact that the AMFE occurs at negative and positive voltages of small magnitude is experimentally established (2,37,38). (Note, however, that all these experiments involve strong asymmetry in Ca2+ concentrations and some involve asymmetries in monovalent cation concentrations and/or species.)
Chung and co-workers state that the AMFE requires that the ions be described by hydrated-ion force fields, which increase ion diameters to the extent that a Na+ ion is unlikely to pass a Ca2+ ion in the filter. An alternate mechanism for the AMFE, not depending on the single-file restriction or excessive voltage but involving depletion of an ion species from a region of the channel, has been described generically (40) and in L-type and RyR Ca channels (7,12). In three cases, a hitherto unknown AMFE has been predicted by theory as an effect of ion depletion and subsequently been found by experiment (12,13).
The electrostatic barrier in the cavity region apparently limits Ca2+ current to unrealistically small values. The simulated Ca2+ currents (Fig. 5 A, open squares) are much smaller than the experimental currents (solid circles). Moreover, the Na+ and Ca2+ branches of the simulation results in Fig. 16 A of Corry et al. (19) (reproduced in our Fig. 5 A) have been separately normalized and the authors state that “the magnitude of the calcium current is significantly lower than that for sodium”. Thus, the pore model of Chung and co-workers also gives unrealistic results for the Ca branch of the AMFE curve.
The weak Ca2+ affinity that we find for the model of Chung and co-workers under equilibrium conditions might underlie an excessive block of Ca2+ inflow in the presence of extracellular Na+ that they have observed in their BD simulations. Fig. 17 of Corry et al. (19) shows that extracellular Na+ blocks simulated Ca2+ currents supported by a bath concentration of 150 mM Ca2+. In the experiments of Polo-Parada and Korn (41) (which are quoted by Corry et al. (19)), extracellular Na+ partially blocks inward current when the extracellular Ba2+ concentration is 1 mM but Na+ has little blocking effect when the extracellular Ba2+ concentration is 10 mM (Polo-Parada and Korn (41), their Fig. 6). Ca2+ is thought to bind more strongly than Ba2+ in Ca channels (38).
The CSC model of the EEEE locus produces stronger Ca2+ affinity than the model of Chung and co-workers
The Chung and co-workers' model involves a rigid structure for the functional groups that chelate Ca2+: these groups are embedded in a hard pore wall. We have tested the possibility that this restriction is excessive and actually limits Ca2+ affinity to the low level that our simulations have revealed. We test a CSC model in which the carboxylate groups of the EEEE side chains are modeled by tethered half-charged oxygen anions that are allowed to associate freely with counterions within the volume of the selectivity filter (Fig. 1 B). The only restriction to their motion is that they cannot leave the pore section that we call “filter”. Thus the structural anions of the model channel behave like the particles of a confined fluid. This model of the selectivity filter has been proposed by some of us and has been studied using a variety of methods (7–10,12–18). To make comparisons of the CSC and Chung and co-workers' models clearer, we change only the description of the charged groups but otherwise maintain the Chung and co-workers description of the system (see The CSC model in The Models).
Simulation results concerning competitive Ca2+ and Na+ accumulation in the CSC selectivity filter are shown in our Fig. 7 (solid symbols). The simulation results obtained with the Chung and co-workers' model are also shown for comparison (open symbols). Allowing the structural anions to interact with ions in a liquidlike setting greatly increases the Ca2+ affinity of the model. Regarding the AMFE, we note that a Ca2+ bath concentration of only 5 μM suffices to displace one half of the Na+ that is accumulated in the absence of Ca2+, compared to 0.2 mM Ca2+ needed in the model of Chung and co-workers (see arrows in our Fig. 7).
FIGURE 7.
Ion accumulation in the CSC and Chung and co-workers' models. Results of MC simulations; ions are counted in the axial range 10 ≤ z ≤ 15 Å. (Solid symbols) CSC model; (open symbols) Chung and co-workers' model. The baths contained a fixed concentration of 150 mM NaCl and the indicated concentration of Ca2+. The lines represent first-order isotherms; their limiting value at low Ca2+ concentration is constrained by simulations done with Ca2+-free baths; these Na+ occupancies were 1.562 (Chung and co-workers) and 1.572 (CSC). Arrows mark concentrations where Na+ occupancy is reduced to one-half that found in the absence of Ca2+.
In the CSC filter, the structural oxygen ions form a spontaneous flexible coordinating structure with the counterions (our Fig. 8). The filter accumulates a significant amount of Ca2+ when the bath contains 10−6 M Ca2+. Also, Na+ distribution is substantially modified when 1 μM Ca2+ is added to the baths.
FIGURE 8.
Axial ion distributions in the CSC model. MC results; spatial bins are 0.2 Å wide and normal to the axis. (Inset) Distribution of the oxygen ions inside the filter region. The baths contained 150 mM NaCl plus the indicated concentration of CaCl2. Shaded areas are shown to help relate the ion distributions to pore geometry.
The Chung and co-workers' and CSC models differ in their treatment of both their excluded volume and electrostatics. In the CSC model all the charge of the oxygen ions (−4e) contributes to the electrical flux ( ) in the pore, but in the model of Chung and co-workers, only part of the electrical flux produced by the structural charge of the filter (−3.244e) enters the pore because of the peripheral position of these charges (Fig. 1). Neutralization of the larger electrical flux of the CSC model requires a larger ionic countercharge in the pore than in the Chung and co-workers' model. Our Fig. 7, however, shows that the number of cations attracted into the filter regions of both models asymptotes toward similar values in the zero calcium and millimolar calcium regimes. On the other hand, the CSC filter attracts a substantial countercharge to the regions just outside the filter in both the zero calcium and millimolar calcium regimes (Fig. 8). In the CSC model, neither Ca2+ nor Na+ are able to neutralize the filter charge locally because a strong excluded-volume repulsion counteracts electrostatic attraction. In the model of Chung and co-workers, signs of exclusion from the filter are virtually absent (Fig. 6). Thus we observe, in the CSC model, both stronger electrostatic attraction and stronger excluded-volume repulsion than in the model of Chung and co-workers. The net result (Fig. 7) is an increased selectivity of the CSC model for Ca2+ which carries twice the charge of Na+ in approximately the same particle volume. This interpretation of our simulation results of the CSC model is supported by theoretical analysis: the excluded volume of ions and oxygen ions (7,8,12) is an important determinant of selectivity. (Please note that Yang et al. (42) have made an applied-field molecular dynamics (MD) study of a model calcium channel using a molecular model of water and crude atomistic channel protein. This work is occasionally cited as indicating that, with molecular water, the CSC mechanism does not lead to calcium selectivity. However, this work was directed to the study of permeation and not selectivity. MD studies inevitably involve shorter chains of events because velocities as well as positions must be updated. Including water molecules only adds to this problem and restricts the study to relatively high ion concentrations. In principle, MD can be performed in the GC ensemble by means of a constraint but this was not done in the study of Yang et al., nor did their MD simulation include methods equivalent to the preference sampling that has been essential in our work. Lastly, we note that the effect of the dielectric coefficient of the protein and membrane was not considered. As a result of these considerations, the valuable Yang et al. study is not relevant to selectivity and was not claimed to be by the authors.)
) in the pore, but in the model of Chung and co-workers, only part of the electrical flux produced by the structural charge of the filter (−3.244e) enters the pore because of the peripheral position of these charges (Fig. 1). Neutralization of the larger electrical flux of the CSC model requires a larger ionic countercharge in the pore than in the Chung and co-workers' model. Our Fig. 7, however, shows that the number of cations attracted into the filter regions of both models asymptotes toward similar values in the zero calcium and millimolar calcium regimes. On the other hand, the CSC filter attracts a substantial countercharge to the regions just outside the filter in both the zero calcium and millimolar calcium regimes (Fig. 8). In the CSC model, neither Ca2+ nor Na+ are able to neutralize the filter charge locally because a strong excluded-volume repulsion counteracts electrostatic attraction. In the model of Chung and co-workers, signs of exclusion from the filter are virtually absent (Fig. 6). Thus we observe, in the CSC model, both stronger electrostatic attraction and stronger excluded-volume repulsion than in the model of Chung and co-workers. The net result (Fig. 7) is an increased selectivity of the CSC model for Ca2+ which carries twice the charge of Na+ in approximately the same particle volume. This interpretation of our simulation results of the CSC model is supported by theoretical analysis: the excluded volume of ions and oxygen ions (7,8,12) is an important determinant of selectivity. (Please note that Yang et al. (42) have made an applied-field molecular dynamics (MD) study of a model calcium channel using a molecular model of water and crude atomistic channel protein. This work is occasionally cited as indicating that, with molecular water, the CSC mechanism does not lead to calcium selectivity. However, this work was directed to the study of permeation and not selectivity. MD studies inevitably involve shorter chains of events because velocities as well as positions must be updated. Including water molecules only adds to this problem and restricts the study to relatively high ion concentrations. In principle, MD can be performed in the GC ensemble by means of a constraint but this was not done in the study of Yang et al., nor did their MD simulation include methods equivalent to the preference sampling that has been essential in our work. Lastly, we note that the effect of the dielectric coefficient of the protein and membrane was not considered. As a result of these considerations, the valuable Yang et al. study is not relevant to selectivity and was not claimed to be by the authors.)
SUMMARY
The studies of Chung and co-workers have been presented widely in several journals and at different meetings. Because of the bold claims of Chung and co-workers and the unsubstantiated nature of their extrapolation, an independent investigation is essential. We have performed MC simulations for the Chung and co-workers' model channel. We have constructed an accurate representation of their model and obtained good agreement in computations of energy and of channel occupancy with pure bath solutions for which they report BD results. In addition, we have made GC ensemble simulations for Ca2+ concentrations as low as 10−6 M in the presence of 150 mM Na+. These simulations reveal a Ca2+ affinity that is much weaker than the extrapolation of Chung and co-workers would suggest, and is much less than the affinity commonly ascribed to the L-type Ca channel. Placement of the structural elements of the channel within the filter (the CSC model of the EEEE locus) improves the calcium selectivity by 40-fold. Reconsideration of other features of the model of Chung and co-workers including a dielectric barrier of excessive magnitude may also be warranted. Regarding the mechanism for high Ca2+ selectivity, volume exclusion among the ions and the glutamate oxygens is an integral part of the function of Ca channels that should not be ignored.
Acknowledgments
A generous allotment of computer time by the Ira and Marylou Fulton Supercomputing Center at Brigham Young University is acknowledged with thanks.
The support of the National Institutes of Health (grant No. GM076013 to B.E. and grant No. GM067241 to B.E. and D.G.) and the Hungarian National Research Fund (OTKA No. K63322, to D.B.) are gratefully acknowledged.
Editor: Klaus Schulten.
References
- 1.Hille, B. 2001. Ionic Channels of Excitable Membranes. Sinauer Associates, Sunderland, MA.
- 2.Almers, W., E. McCleskey, and P. Palade. 1984. Non-selective cation conductance in frog muscle membrane blocked by micromolar external calcium ions. J. Physiol. 353:565–583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Almers, W., and E. McCleskey. 1984. Non-selective conductance in calcium channels of frog muscle: calcium selectivity in a single-file pore. J. Physiol. 353:585–608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ellinor, P., J. Yang, W. Sather, J. Zhang, and R. Tsien. 1995. Ca2+ channel selectivity at a single locus for high-affinity Ca2+ interactions. Neuron. 15:1121–1132. [DOI] [PubMed] [Google Scholar]
- 5.Yang, J., P. Ellinor, W. Sather, J. Zhang, and R. Tsien. 1993. Molecular determinants of Ca2+ selectivity and ion permeation in L-type Ca2+ channels. Nature. 366:158–161. [DOI] [PubMed] [Google Scholar]
- 6.Sather, W., and E. McCleskey. 2003. Permeation and selectivity in calcium channels. Annu. Rev. Physiol. 65:133–159. [DOI] [PubMed] [Google Scholar]
- 7.Nonner, W., L. Catacuzzeno, and B. Eisenberg. 2000. Binding and selectivity in L-type Ca channels: a mean spherical approximation. Biophys. J. 79:1976–1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Nonner, W., D. Gillespie, D. Henderson, and B. Eisenberg. 2001. Ion accumulation in a biological calcium channel: effects of solvent and confining pressure. J. Phys. Chem. B. 105:6427–6436. [Google Scholar]
- 9.Boda, D., W. Nonner, M. Valiskó, D. Henderson, B. Eisenberg, and D. Gillespie. 2007. Steric selectivity in Na channels arising from protein polarization and mobile side chains. Biophys. J. 93:1960–1980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Boda, D., D. Busath, B. Eisenberg, D. Henderson, and W. Nonner. 2002. Monte Carlo simulations of ion selectivity in a biological Na+ channel: charge-space competition. Phys. Chem. Chem. Phys. 4:5154–5160. [Google Scholar]
- 11.Barker, J., and D. Henderson. 1976. What is “liquid”? Understanding the states of matter. Rev. Mod. Phys. 48:587–671. [Google Scholar]
- 12.Gillespie, D. 2008. Energetics of divalent selectivity in a calcium channel: the ryanodine receptor case study. Biophys. J. 94:1169–1184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Gillespie, D., L. Xu, Y. Wang, and G. Meissner. 2005. (De)constructing the ryanodine receptor: modeling ion permeation and selectivity of the calcium release channel. J. Phys. Chem. B. 109:15598–15610. [DOI] [PubMed] [Google Scholar]
- 14.Boda, D., D. Henderson, and D. Busath. 2002. Monte Carlo study of the selectivity of calcium channels: improved geometrical mode. Mol. Phys. 100:2361–2368. [Google Scholar]
- 15.Boda, D., D. Henderson, and D. Busath. 2001. Monte Carlo study of the effect of ion and channel size on the selectivity of a model calcium channel. J. Phys. Chem. B. 105:11574–11577. [Google Scholar]
- 16.Boda, D., D. Busath, D. Henderson, and S. Sokolowski. 2000. Monte Carlo simulations of the mechanism of channel selectivity: the competition between volume exclusion and charge neutrality. J. Phys. Chem. B. 104:8903–8910. [Google Scholar]
- 17.Boda, D., M. Valiskó, B. Eisenberg, W. Nonner, D. Henderson, and D. Gillespie. 2007. The combined effect of pore radius and protein dielectric coefficient on the selectivity of a calcium channel. Phys. Rev. Lett. 98:168102. [DOI] [PubMed] [Google Scholar]
- 18.Boda, D., M. Valiskó, B. Eisenberg, W. Nonner, D. Henderson, and D. Gillespie. 2006. The effect of protein dielectric coefficient on the ionic selectivity of a calcium channel. J. Chem. Phys. 125:034901. [DOI] [PubMed] [Google Scholar]
- 19.Corry, B., T. Allen, S. Kuyucak, and S. Chung. 2001. Mechanisms of permeation and selectivity in calcium channels. Biophys. J. 80:195–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Krishnamurthy, V., and S. Chung. 2007. Large-scale dynamical models and estimation for permeation in biological membrane ion channels. Proc. IEEE. 95:853–880. [Google Scholar]
- 21.Corry, B., and S. Chung. 2006. Mechanisms of valence selectivity in biological ion channels. Cell. Mol. Life Sci. 63:301–315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Corry, B., T. Vora, and S. Chung. 2006. Electrostatic basis of valence selectivity in cationic channels. Biochim. Biophys. Acta. 1711:72–86. [DOI] [PubMed] [Google Scholar]
- 23.Corry, B., M. Hoyles, T. Allen, M. Walker, S. Kuyucak, and S. Chung. 2002. Reservoir boundaries in Brownian dynamics simulations of ion channels. Biophys. J. 82:1975–1984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Im, W., S. Seefeld, and B. Roux. 2000. A grand canonical Monte Carlo-Brownian dynamics algorithm for simulating ion channels. Biophys. J. 79:788–801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Guàrdia, E., and J. Padró. 1996. On the influence of ionic charge on the mean force potential of ion pairs in water. J. Chem. Phys. 104:7219–7222. [Google Scholar]
- 26.Guàrdia, E., R. Rey, and J. Padró. 1991. Na+-Na+ and Cl−-Cl− ion pairs in water: mean force potentials by constrained molecular dynamics. J. Chem. Phys. 95:2823–2831. [Google Scholar]
- 27.Guàrdia, E., R. Rey, and J. Padró. 1991. Potential of mean force by constrained molecular dynamics: a sodium chloride ion-pair in water. Chem. Phys. 155:187–195. [Google Scholar]
- 28.Lyubartsev, A., and A. Laaksonen. 1995. Calculation of the effective interaction potentials from radial distribution functions: a reverse Monte Carlo approach. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 52:3730–3737. [DOI] [PubMed] [Google Scholar]
- 29.Chung, S., T. Allen, M. Hoyles, and S. Kuyucak. 1999. Permeation of ions across the potassium channel: Brownian dynamics studies. Biophys. J. 77:2517–2533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Fawcett, W. 1999. Thermodynamic parameters for the solvation of monatomic ions in water. J. Phys. Chem. B. 103:11181–11185. [Google Scholar]
- 31.Shannon, R., and C. Previtt. 1969. Effective ionic radii in oxides and fluorides. Acta Crystallogr. B. 25:925–946. [Google Scholar]
- 32.Valleau, J., and L. Cohen. 1980. Primitive model electrolytes. I. Grand canonical Monte Carlo computations. J. Chem. Phys. 72:5935–5941. [Google Scholar]
- 33.Gibbs, J. 1948. Elementary Principles of Statistical Mechanics. Yale University Press, New Haven, CT.
- 34.Malasics, A. D., D. Gillespie, and D. Boda. 2008. Simulating prescribed particle densities in the grand canonical ensemble using iterative algorithms. J. Chem. Phys. In press. [DOI] [PubMed]
- 35.Hoyles, M., S. Kuyucak, and S. Chung. 1998. Solutions of Poisson's equation in channel-like geometries. Comput. Phys. Commun. 115:45–68. [Google Scholar]
- 36.Boda, D., D. Gillespie, W. Nonner, D. Henderson, and B. Eisenberg. 2004. Computing induced charges in inhomogeneous dielectric media: application in a Monte Carlo simulation of complex ionic systems. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 69:046702. [DOI] [PubMed] [Google Scholar]
- 37.Kostyuk, P., S. Mironov, and Y. Shuba. 1983. Two ion-selective filters in the calcium channel of the somatic membrane of mollusk neurons. J. Membr. Biol. 76:83–93. [Google Scholar]
- 38.Lansman, J., P. Hess, and R. Tsien. 1986. Blockade of current through single calcium channels by Cd2+, Mg2+, and Ca2+. Voltage and concentration dependence of calcium entry into the pore. J. Gen. Physiol. 88:321–347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Fukushima, A., and S. Hagiwara. 1985. Currents carried by monovalent cations through calcium channels in mouse neoplastic B lymphocytes. J. Physiol. 358:255–284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Nonner, W., D. Chen, and B. Eisenberg. 1998. Anomalous mole fraction effect, electrostatics, and binding in ionic channels. Biophys. J. 74:2327–2334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Polo-Parada, L., and S. Korn. 1997. Block of N-type calcium channels in chick sensory neurons by external sodium. J. Gen. Physiol. 109:693–702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Yang, Y., D. Henderson, and D. Busath. 2003. Applied-field molecular dynamics study of a model calcium channel selectivity filter. J. Chem. Phys. 118:4213–4220. [Google Scholar]