Abstract
We have developed an evolutionary approach to predicting protein side-chain conformations. This approach, referred to as the Gaussian Evolutionary Method (GEM), combines both discrete and continuous global search mechanisms. The former helps speed up convergence by reducing the size of rotamer space, whereas the latter, integrating decreasing-based Gaussian mutations and self-adaptive Gaussian mutations, continuously adapts dihedrals to optimal conformations. We tested our approach on 38 proteins ranging in size from 46 to 325 residues and showed that the results were comparable to those using other methods. The average accuracies of our predictions were 80% for χ1, 66% for χ1 + 2, and 1.36 Å for the root mean square deviation of side-chain positions. We found that if our scoring function was perfect, the prediction accuracy was also essentially perfect. However, perfect prediction could not be achieved if only a discrete search mechanism was applied. These results suggest that GEM is robust and can be used to examine the factors limiting the accuracy of protein side-chain prediction methods. Furthermore, it can be used to systematically evaluate and thus improve scoring functions.
Keywords: Evolutionary algorithm, Gaussian mutation, protein-structure prediction, side-chain conformation, rotamer library
Side-chain conformation prediction is important in modeling protein tertiary structures. Two factors are essential for a good prediction method, these being a good scoring function and an efficient algorithm for searching conformational spaces (Levitt et al. 1997).
A good scoring function should be able to distinguish between correct and incorrect conformations. Various scoring functions have been developed to predict side-chain conformations, including simple molecular force fields which, for the sake of fast computation, usually employ a Lennard-Jones 12-6 form (Lee and Subbiah 1991; Koehl and Delarue 1994; Hwang and Liao 1995) or 6-9 form (Holm and Sander 1992; Väsquez 1995) to remove close-range interactions. More sophisticated and longer range functions (Tuffery et al. 1991), as well as statistically derived contact potentials (Samudrala and Moult 1998), have also been studied.
Until recently (Xiang and Honig 2001), the combinatorial nature of side-chain placement was generally considered the major obstacle in protein side-chain prediction. Various approaches have been developed to circumvent the combinatorial problem and can be roughly divided into three categories: knowledge-based statistical methods, tree-based elimination methods, and stochastic search methods.
Knowledge-based statistical methods include the homology modeling methods (Holm and Sander 1992; Laughton 1994; Bower et al. 1997), in which side-chain conformations are predicted on the basis of localized similarity between target structures and database templates. Other examples are approaches that use a rotamer library, in which the statistical distributions of side-chain orientations derived from known structures are tabulated. In general, there are two kinds of rotamer library, one in which the rotamers are dependent on the local main-chain environment (Dunbrack and Karplus 1993) and one in which they are not (Ponder and Richards 1987; Tuffery et al. 1991; De Maeyer et al. 1997; Xiang and Honig 2001). The information in these two different kinds of rotamer libraries can also be implicitly captured in neural networks (Hwang and Liao 1995). The dead-end elimination algorithm (Desmet et al. 1992; Looger and Hellinga 2001) and A* algorithm (Leach 1994; Leach and Lemon 1998) are tree-based elimination approaches to reduce search spaces. Whereas homology rotamer library and tree-based approaches are deterministic stochastic methods, such as simulated annealing (Lee and Subbiah 1991; Laughton 1994; Hwang and Liao 1995), genetic algorithms (Tuffery et al. 1991), and mean field theory (Koehl and Delarue 1994; Mendes et al. 1999), use biased sampling to reach approximated solutions.
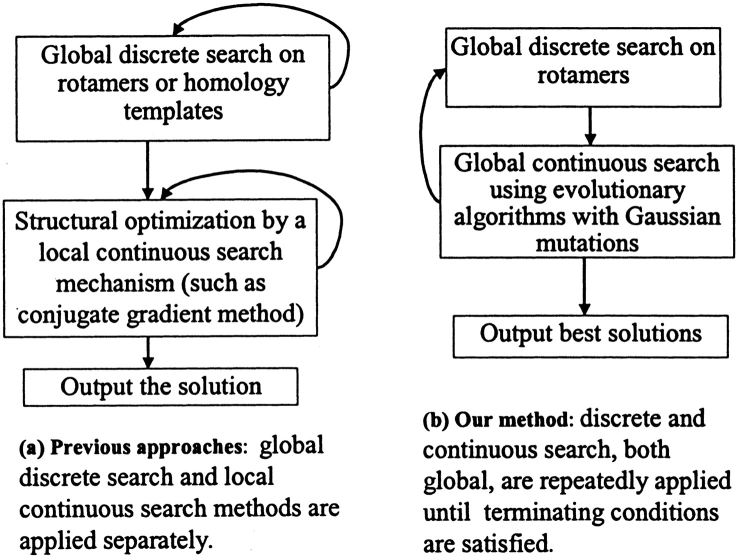
Despite the diversity of the strategies, algorithms, and energy functions used in these methods, they all seem to produce comparable results, with, for example, an accuracy of ∼70–80% in the χ1 angles of all residues (Levitt et al. 1997). However, it is not yet fully understood which factors (e.g., search algorithms, energy functions, or experimental errors) are mainly responsible for the 20%–30% of errors (Levitt et al. 1997). In addition, many methods use a discrete search to identify an optimal combination of side-chain rotamer states before finding the optimal side-chain conformations by energy minimization (Fig. 1 ▶), and it is not clear to what extent the nature of discrete search has limited the theoretical accuracy of a search method in protein side-chain prediction.
Fig. 1.
Main differences in search mechanisms for side-chain conformation prediction between previous approaches and our Gaussian Evolutionary Method (GEM).
Here we addressed these questions using an evolutionary approach, referred to as the Gaussian Evolutionary Method (GEM). Evolution-based algorithms (Goldberg 1989; Fogel 1995; Bäck 1996) can generally be adapted to solve difficult optimization problems and have been successfully applied to problems of structural biology (Morris et al. 1998; Tuffery et al. 1991, 1993; Yang and Kao 2000a). The present work is an extended application of our recently developed evolutionary algorithm that combines adaptive mutations and family competition to solve optimization problems in widely differing fields (Yang et al. 2000; Yang and Kao 2000a,b, 2001).
The main difference in methodology between the present work and our previous studies is the addition of a global discrete-search to a continuous-search mechanism. To the best of our knowledge, the present work on protein side-chain prediction is also the first to integrate global discrete- and global continuous-search mechanisms (Fig. 1 ▶). This is distinct from previous studies in which, although both discrete- and continuous-search mechanisms have been used (e.g., Dunbrack and Karplus 1993; Väsquez 1995; Bower et al. 1997; Xiang and Honig 2001), they were used separately, with the result that the continuous search was only a local search.
Results and Discussion
Overall accuracy of prediction and comparison with other methods
The overall accuracy of GEM in predicting the side-chain conformation of 38 test proteins (4313 residues) is shown in Table 1. The geometric parameters evaluated were those used commonly by others, namely the χ1 and χ1 + 2 angles for all residues and the root mean square deviation (RMSD) error in side-chain heavy atoms. The 38 structures selected constitute a minimal set encompassing most of the common structures tested in different prediction methods, allowing comparison with these other methods (Holm and Sander 1992; Dunbrack and Karplus 1993; Laughton 1994; Hwang and Liao 1995; Samudrala and Moult 1998; Looger and Hellinga 2001). The results of the comparison are shown in Tables 2 and 3.
Table 1.
Gaussian Evolutionary Method (GEM) results for side-chain conformation prediction for 38 high-resolution structures
| A (all) | A (corea) | B (all) | ||||||||
| PDB code | Number residues | RMSD (Å) | χ1 | χ1+2 | RMSD (Å) | χ1 | χ1+2 | RMSD (Å) | χ1 | χ1+2 |
| 1aac | 105 | 1.05 | 0.92 | 0.69 | 0.83 | 0.97 | 0.82 | 0.17 | 1 | 1 |
| 1amm | 174 | 1.66 | 0.73 | 0.61 | 1.18 | 0.954 | 0.77 | 0.22 | 0.99 | 0.99 |
| 1arb | 263 | 1.37 | 0.75 | 0.67 | 1.54 | 0.817 | 0.68 | 0.17 | 1 | 0.99 |
| 1bab | 146 | 1.63 | 0.85 | 0.58 | 1.13 | 0.933 | 0.68 | 0.19 | 1 | 1 |
| 1bpi | 58 | 1.26 | 0.8 | 0.65 | 0.97 | 1 | 0.75 | 0.14 | 1 | 1 |
| 1cbn | 46 | 0.87 | 0.95 | 0.78 | 0.54 | 1 | 1 | 0.18 | 1 | 1 |
| 1ccr | 111 | 1.21 | 0.84 | 0.6 | 1.01 | 0.911 | 0.73 | 0.22 | 1 | 0.99 |
| 1cex | 197 | 1.09 | 0.8 | 0.71 | 1.04 | 0.854 | 0.74 | 0.19 | 1 | 1 |
| 1crn | 46 | 0.84 | 0.95 | 0.84 | 1.11 | 0.888 | 0.88 | 0.14 | 1 | 1 |
| 1ctf | 68 | 0.88 | 0.87 | 0.7 | 0.32 | 1 | 0.91 | 0.18 | 1 | 1 |
| 1ctj | 89 | 1.23 | 0.85 | 0.62 | 0.73 | 1 | 0.85 | 0.15 | 1 | 1 |
| 1cus | 197 | 1.27 | 0.82 | 0.66 | 0.94 | 0.92 | 0.79 | 0.18 | 1 | 1 |
| 1igd | 61 | 1.28 | 0.76 | 0.74 | 0.24 | 1 | 1 | 0.15 | 1 | 1 |
| 1isu | 62 | 1.12 | 0.84 | 0.74 | 0.47 | 1 | 0.9 | 0.15 | 1 | 1 |
| 1lzl | 130 | 1.16 | 0.82 | 0.66 | 0.86 | 0.913 | 0.84 | 0.26 | 0.99 | 0.97 |
| 1plc | 99 | 1.24 | 0.82 | 0.7 | 0.76 | 1 | 0.82 | 0.2 | 1 | 1 |
| 1pmy | 123 | 1.23 | 0.83 | 0.63 | 0.94 | 0.976 | 0.86 | 0.19 | 1 | 0.99 |
| 1ptx | 64 | 1.73 | 0.74 | 0.61 | 0.94 | 0.882 | 0.82 | 0.2 | 1 | 1 |
| 1whi | 122 | 1.52 | 0.73 | 0.65 | 0.55 | 0.972 | 0.91 | 0.16 | 0.99 | 0.99 |
| 1xnb | 185 | 1.89 | 0.78 | 0.66 | 1.25 | 0.878 | 0.75 | 0.19 | 1 | 0.99 |
| 1xso | 150 | 1.43 | 0.75 | 0.6 | 1.28 | 0.867 | 0.73 | 0.23 | 0.99 | 0.97 |
| 256b | 106 | 1.53 | 0.73 | 0.53 | 0.58 | 1 | 0.95 | 0.16 | 1 | 0.98 |
| 2cro | 65 | 1.58 | 0.75 | 0.57 | 0.81 | 0.882 | 0.76 | 0.18 | 1 | 1 |
| 2end | 137 | 1.37 | 0.79 | 0.64 | 1.14 | 0.883 | 0.65 | 0.2 | 1 | 1 |
| 2erl | 40 | 1.28 | 0.79 | 0.74 | 0.1 | 1 | 1 | 0.2 | 1 | 1 |
| 2hbg | 147 | 1.34 | 0.76 | 0.61 | 1.01 | 0.891 | 0.78 | 0.19 | 1 | 0.99 |
| 2ihl | 129 | 1.43 | 0.81 | 0.65 | 0.54 | 0.973 | 0.94 | 0.15 | 1 | 1 |
| 2sga | 169 | 1.27 | 0.73 | 0.73 | 0.99 | 0.821 | 0.78 | 0.19 | 1 | 0.99 |
| 2tmn | 316 | 1.52 | 0.77 | 0.64 | 1.05 | 0.888 | 0.72 | 0.21 | 1 | 0.99 |
| 3app | 323 | 1.4 | 0.77 | 0.68 | 1.3 | 0.903 | 0.71 | 0.21 | 1 | 0.99 |
| 3apr | 325 | 1.32 | 0.78 | 0.67 | 1.06 | 0.875 | 0.7 | 0.21 | 1 | 0.99 |
| 3fxn | 138 | 1.72 | 0.75 | 0.56 | 1.22 | 0.847 | 0.69 | 0.18 | 0.99 | 1 |
| 3sdh | 145 | 1.47 | 0.85 | 0.59 | 0.84 | 0.954 | 0.84 | 0.18 | 1 | 0.99 |
| 3tln | 316 | 1.53 | 0.75 | 0.62 | 1.24 | 0.881 | 0.67 | 0.25 | 1 | 0.98 |
| 4fxn | 138 | 1.35 | 0.74 | 0.56 | 1.16 | 0.911 | 0.77 | 0.16 | 1 | 0.98 |
| 5pti | 58 | 1.15 | 0.83 | 0.67 | 0.97 | 1 | 0.76 | 0.15 | 1 | 1 |
| 7rsa | 124 | 1.44 | 0.79 | 0.71 | 1.01 | 0.952 | 0.8 | 0.17 | 1 | 1 |
| 9rnt | 104 | 1.84 | 0.75 | 0.65 | 1.15 | 0.962 | 0.7 | 0.19 | 1 | 0.99 |
| Average | 1.36 | 0.80 | 0.66 | 0.92 | 0.93 | 0.8 | 0.19 | 1 | 0.99 | |
χ1+2 is defined as those side-chains for which χ1 and χ2 are correct (within 30°) at the same time; side-chains with only a χ1 angle are included in χ1+2.
A, using equation 2 as the fitness function.
B, using equation 1 as the fitness function.
a refers to residues for which solvent exposure is ∼20% as calculated using the Naccess program (Hubbard and Thornton, 1993).
Table 2.
Comparison with other methods
| Gaussian Evolutionary Methodb | Laughton (1994)b | Samudrala and Moult (1998)a | Holm and Sander (1992)b | Hwang and Liao (1995)c | Dunbrack and Karplus (1993)c | ||||||
| PDB code | RMSDd | χ1 | RMSD | χ1 | RMSD | χ1 | RMSD | χ1 | RMSD | χ1 | χ1 |
| 1cm | 0.84 | 0.95 | 1.43 | 0.68 | 1.4 | 0.87 | — | — | 1.34 | 0.95 | 0.92 |
| 1ctf | 0.88 | 0.87 | 1.59 | 0.53 | 1.69 | 0.72 | 1.7 | 0.81 | 1.4 | 0.94 | — |
| 1lzl | 1.16 | 0.82 | 2.22 | 0.56 | 1.97 | 0.76 | 1.6 | 0.88 | 1.61 | 0.89 | 0.77 |
| 2cro | 1.58 | 0.75 | — | — | 2.29 | 0.66 | 2.3 | 0.57 | — | — | — |
| 2tmn | 1.52 | 0.77 | 1.72 | 0.62 | — | — | — | — | — | — | — |
| 3app | 1.4 | 0.77 | 1.22 | 0.7 | 1.2 | 0.81 | — | — | 1.24 | 0.83 | — |
| 3apr | 1.32 | 0.78 | — | — | 1.44 | 0.85 | 1.4 | 0.84 | — | — | 0.82 |
| 3fxn | 1.72 | 0.75 | — | — | 1.76 | 0.63 | 1.9 | 0.61 | — | — | — |
| 3tln | 1.53 | 0.75 | — | — | 1.62 | 0.77 | 1.7 | 0.77 | — | 0.79 | 0.74 |
| 4fxn | 1.35 | 0.74 | 1.96 | 0.46 | — | — | — | — | 1.8 | 0.68 | — |
| 5pti | 1.15 | 0.83 | 1.49 | 0.69 | 1.73 | 0.79 | 1.9 | 0.78 | 1.8 | 0.91 | 0.85 |
| 7rsa | 1.44 | 0.79 | 2.02 | 0.54 | 2.02 | 0.67 | 1.8 | 0.79 | 1.73 | 0.78 | 0.79 |
a Excludes proline and uses a 30° cutoff for χ1 angles.
b Includes proline and uses a 30° cutoff for χ1 angles.
c Includes proline and uses a 40° cutoff for χ1 angles.
dRMSD, root mean square deviation.
Table 3.
Comparison with other methods of the prediction accuracy of χ1 for specific side-chain types
| Residue | Gaussian Evolutionary Method | Dunbrack and Karplus (1993) | Laughton (1994) | Koehl and Delarue (1994) | Hwang and Liao (1995) | Bower et al. (1997) |
| Val | 0.88 | 0.91 | 0.81 | 0.84 | 0.85 | 0.83 |
| Leu | 0.89 | 0.68 | 0.73 | 0.85 | 0.82 | 0.83 |
| Ile | 0.88 | 0.86 | 0.86 | 0.82 | 0.79 | 0.87 |
| Ser | 0.58 | 0.65 | 0.51 | 0.42 | 0.61 | 0.62 |
| Cys | 0.83 | 0.93 | 0.79 | 0.81 | 0.81 | 0.74 |
| Thr | 0.73 | 0.84 | 0.68 | 0.8 | 0.79 | 0.83 |
| Met | 0.77 | 1 | 0.5 | 0.84 | 0.82 | 0.72 |
| Pro | 0.94 | 0.79 | 0.79 | 0.55 | 0.93 | 0.87 |
| Phe | 0.92 | 0.83 | 0.96 | 0.88 | 0.89 | 0.9 |
| Tyr | 0.93 | 0.86 | 0.87 | 0.93 | 0.88 | 0.9 |
| Trp | 0.86 | 0.82 | 0.71 | 0.87 | 0.74 | 0.87 |
| His | 0.92 | 0.92 | 0.81 | 0.81 | 0.85 | 0.85 |
| Lys | 0.77 | 0.66 | 0.56 | 0.68 | 0.6 | 0.68 |
| Arg | 0.62 | 0.74 | 0.41 | 0.66 | 0.64 | 0.65 |
| Asp | 0.66 | 0.74 | 0.64 | 0.64 | 0.73 | 0.76 |
| Glu | 0.73 | 0.61 | 0.53 | 0.66 | 0.71 | 0.63 |
| Asn | 0.76 | 0.76 | 0.64 | 0.73 | 0.77 | 0.73 |
| Gln | 0.59 | 0.72 | 0.59 | 0.73 | 0.75 | 0.68 |
| No. of proteins | 38 | 6 | 8 | 30 | 12 | 299 |
The results for other methods are taken from the literature.
As shown in Table 1, GEM yielded values for the χ1 angles that were within 30° of those determined from the crystal structure in 80% of cases and side-chain atomic positions with a mean RMSD of 1.36 Å. For core residues with <20% solvent exposure, the prediction accuracy increased to 93% for χ1 and the mean RMSD was reduced to 0.92 Å. Thus, even though no energy minimization was applied to the final structure and the bond lengths and bond angles used were those of standard templates and not of the individual residues in the individual X-ray structures (see Materials and Methods), our results for core residues, on a limited test set, were approaching those from a recent study in which a very detailed rotamer library (7560 rotamers) and experimental bonds and angles for every residue were used (Xiang and Honig 2001).
In terms of residue types, it appears easier to predict the orientation of small nonpolar or aromatic side chains, as evidenced by a significantly better accuracy in χ1 angles (90%) being achieved for these residues (Fig. 2a,b ▶). This means that prediction errors are contributed mainly by polar and charged amino acids, for which interaction with the solvent plays a significant role in determining their side-chain orientation. The largest error was the 58% χ1 accuracy for serine, which was probably attributable to its small size and its conformation therefore being dictated by hydrogen bonding (Koehl and Delarue 1994). These results indicate that, in general, it is harder to predict the conformation of those amino acids in which the side-chain conformation is more susceptible not only to steric hindrance, but also to environmental factors, such as hydrogen bonds, salt bridges, and solvent interactions. This observation is consistent with the findings of previous studies (Table 3; Dunbrack and Karplus 1993; Koehl and Delarue 1994), as well as with the fact that the conformation of residues in the protein core can be more accurately predicted (Levitt et al. 1997).
Fig. 2.
Gaussian evolutionary method (GEM) results using different search mechanisms (discrete search only in white; discrete and continuous search in black) and different fitness functions. (a, b) The energy-based function (equation 2); (c, d) the exact root mean square deviation (RMSD) function (equation 1).
In general, it is neither straightforward nor completely fair to compare the results of different protein side-chain prediction methods, as different accuracy measures, energy functions, and proteins have been used, and, with the exception of the studies of Bower et al. (1997) and Xiang and Honig (2001), tests have been performed on a rather small set of proteins (Tables 2, 3). Despite this, a number of common characteristics emerge. For example, whereas no obvious structures or classes of proteins emerge as particularly easy or difficult to predict by any of the different prediction methods, on the whole, the prediction accuracy does not differ significantly from one method to another. Furthermore, as mentioned above, the prediction accuracy for χ1 angles in terms of amino acid type is quite consistent between these methods (Table 3). The availability of SCWRL (Side-chain placement With a Rotamer Library) (Bower et al. 1997) through the Internet (http://www.fccc.edu/research/labs/dunbrack/scwrl/), one of the more recent and widely used side-chain modeling programs allowed a more straightforward comparison, and the results of SCWRL we obtained on the 38 test proteins using the same accuracy criteria of GEM (Table 1) were also similar, with the overall average RMSD being 1.46 Å, χ1 accuracy being 81%, and χ1+2 accuracy being 64%. These results suggest that the accuracy of GEM is comparable with those of previous prediction methods. However, the GEM approach, as discussed below, can be used to analyze elements of methodology, such as search scheme and energy function, and should therefore help in moving toward error-free prediction of protein side-chain conformations.
Evaluation of the energy function used
The main objective of this study was to evaluate whether the evolutionary algorithm that we recently developed and applied to flexible ligand docking (Yang and Kao 2000a) was also applicable to the prediction of side-chain conformations of proteins. To simplify the task, we adopted a typical van der Waals–type energy function used in previous studies (see Materials and Methods). However, to enable the global continuous search mechanism of GEM to energetically discriminate between different torsions, we found it necessary to add a torsion term. In two previous studies in which a very large set of rotamer states were sampled, a torsion function was also used (Lee and Subbiah 1991; Xiang and Honig 2001). The torsion term used in the present work was that employed in the HIV protease-inhibitor docking study of Gehlhaar et al. (1995).
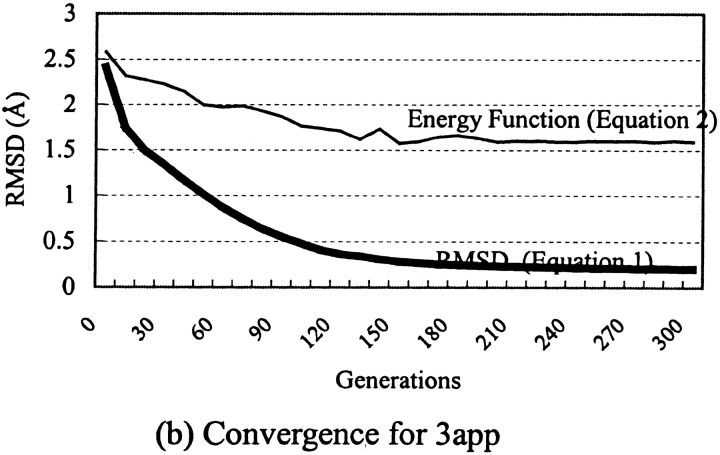
The fact that although we did not attempt to refine any parameters of the energy function used, we still achieved a comparable prediction accuracy attested to the viability of the use of GEM for protein side-chain prediction. However, with uncertainty in the scoring (fitness) function, the robustness of GEM was difficult to assess. To address this question, we made use of the high adaptability of GEM and simply replaced the force-field energy function with a perfect-scoring function (i.e., one that would produce zero RMSD in atom positions). As shown in Table 1 and Figure 2, c and d ▶, using the RMSD scoring function (equation 1; Materials and Methods), GEM could indeed approach perfect prediction. Not only were almost all χ1 angles predicted to within 30° (Fig. 2c ▶; Table 1), but the absolute values of the angles were very accurately reproduced, with >90% having an error of <5° compared to a value of only 30% when the force-field energy function (equation 2) was used (Fig. 3a ▶). The residual errors can be attributed to the use of not completely flexible side-chain templates (Materials and Methods), which have rigid bond lengths and bond angles. This attribution is supported by the work of Xiang and Honig (2001), which showed that the use of a standardized geometry could lead to considerable errors. This was most evident in the RMSD results for lysine and arginine, and, to a lesser extent, those for glutamate and glutamine (Fig. 2d ▶), that is, those amino acids with side chains that are charged or polar and are relatively long and flexible. Interestingly, in the case of lysine and arginine, although almost all the χ1 angles were predicted without error, the RMSD value was as large as that obtained using the force-field energy function (Fig. 2 ▶), reinforcing the fact that either RMSD or χ1 alone cannot provide a complete assessment of side-chain prediction accuracy. It is also worthy of note that GEM converges much faster with the perfect-fitness function (Fig. 3b ▶).
Fig. 3.
Gaussian evolutionary method (GEM) results for different scoring functions. (a) Distribution in χ1 errors. Errors for the energy-based function (equation 2) are shown in white and for the exact function (equation 1) in black. (b) GEM convergence for a typical structure.
Limitation of discrete search
The purpose of discrete search, such as the use of a rotamer library or uniformly divided torsion angles, is to reduce the side-chain conformational space to render computational search tractable. However, it frequently happens that many side-chain conformations cannot be covered if only discrete angle values are used. Indeed, the average prediction accuracy of GEM with discrete search alone was 70.9% for χ1 and 1.72 Å for RMSD for the 38 test proteins (Table 4). GEM with both discrete and continuous search consequently enjoyed an improvement of 9.1% in average χ1 prediction and 0.36 Å in average RMSD of side-chain positions (Fig.2a,b ▶). Furthermore, even using the perfect-fitness function, GEM with discrete search alone resulted in substantial errors, especially for flexible residues, such as serine, lysine, and arginine (Fig. 2c,d ▶).
Table 4.
Gaussian Evolutionary Method (GEM) results on the 38 test proteins (Table 1) with two different rotamer libraries
| 103 states | 330 states | |||
| RMSD (Å) | χ1 | RMSD (Å) | χ1 | |
| GEM (Con + Dis + E2) | 1.36 | 79.8% | 1.37 | 79.9% |
| GEM (Dis + E2) | 1.72 | 70.9% | 1.65 | 71.1% |
| GEM (Dis + E1) | 1.26 | 78.8% | 0.87 | 85.6% |
RMSD, root mean square deviation; Con, continuous search; Dis, discrete search; E1, equation 1; E2, equation 2.
The shortcoming of discrete search over a limited number of rotamer states (103 in this study) is even more evident in the case of strained conformations (Schrauber et al. 1993), which may be defined as those with a χ1 angle deviating by >30° from the three energetically favored values (+/−60° and 180°). As shown in Figure 4 ▶, the discrete search with GEM yielded a difference as large as 30% in the χ1 accuracy between nonstrained and strained side-chain conformations. Such a large difference could often be easily overlooked using statistical averages because strained residues represent a small minority of all amino acid side-chain conformations (e.g., of the 4313 residues examined here, only 177 [5%] were strained).
Fig. 4.
Gaussian evolutionary method (GEM) results using different search mechanisms on strained and nonstrained residues (see text). Dis, discrete search; Con, continuous search; E1: equation 1 (the perfect scoring function).
A more detailed rotamer library may improve side-chain prediction accuracy (De Maeyer et al. 1997; Liang and Grishin 2002). Using a very large library with 7560 rotamer states, Xiang and Honig (2001) indeed obtained very good performance, especially for core residues. However, larger rotamer states have not generally proven more accurate for side-chain prediction than smaller states (Holm and Sander 1992; Laughton 1994; Väsquez 1995). Using a library of 330 states (De Maeyer et al. 1997), GEM with the energy-based scoring function (equation 2) yielded very marginal improvements over the results with 103 states when only the discrete-search mechanism was used, and essentially no improvements when discrete search was combined with continuous search (Table 4). However, it should be noted that because the statistics of this larger library were not available, the statistics of the 103 states were transferred and equal probability was assigned to each of the additional states in the larger library, and, as such, the calculation could not take full advantage of the evolutionary parameters optimized in GEM. Interestingly, using the exact RMSD scoring function (equation 1), the discrete-only prediction of GEM improved significantly with the larger library (χ1 from 78.8% to 85.6% and RMSD from 1.26 Å to 0.87 Å; Table 4). These results may suggest that the scoring function is a key accuracy-determining factor in side-chain prediction, and that the efficiency of utilizing a larger library depends on search mechanisms. The suggestion is consistent with a very recent finding of Liang and Grishin (2002), who specifically optimized a scoring function to achieve very accurate side-chain predictions.
In summary, we have demonstrated the robustness and adaptability of GEM for exploring the conformational space of protein side chains and efficiently finding the combinatorial solution under the constraint of the fitness function used. The key novelty of the present work is the seamless ability of GEM to blend global discrete search and global continuous search, the former being required for efficiency and the latter for accuracy, and to allow them to work cooperatively. This was achieved through the incorporation of a number of genetic operators, each having unique search mechanisms (Table 5). For example, whereas the rotamer mutation operator performs a discrete search on the global rotamer space of the rotamer library, the self-adaptive Gaussian mutation performs a local, but continuous, search on torsional conformations, etc. Importantly, the flexibility of GEM should allow us to begin to systematically improve the forms and parameters of energy function for protein side-chain and other protein-structure prediction problems.
Table 5.
Gaussian Evolutionary Method (GEM) search mechanisms and genetic operators
| Genetic operator (see Materials and Methods) | Local | Global | Discrete | Continuous |
| Rotamer mutation operator | no | yes | yes | no |
| Decreasing-based Gaussian mutation | no | yes | no | yes |
| Self-adaptive Gaussian mutation | yes | noa | no | yes |
| Family competition | yes | no | yes | yes |
a Self-adaptive Gaussian mutation may be viewed as both a local and a global search operator.
Materials and methods
GEM parameters and computational details
The GEM parameters used in this paper are listed in Table 6. These parameters were selected after many attempts to predict conformations for test proteins with various initial values. GEM optimization stops when either the convergence is below a certain threshold value or when the iterations exceed a preset maximum value. In this paper, the maximal number of generations was set to be 100 + K/2 or 250 if 100 + K/2 > 250, where K is the residue number of a protein. A set of 38 high-resolution crystal structures of proteins (resolution better than 2 Å) ranging in size from 46 to 325 amino acid residues was used to test the performance of GEM. This set was selected from those used in many previous studies (Holm and Sander 1992; Dunbrack and Karplus 1993; Laughton 1994; Hwang and Liao 1995; Samudrala and Moult 1998; Looger and Hellinga 2001) to compare our results with those obtained using other methods. All calculations were performed on a 500-mHz Pentium III processor. A typical run time for a protein of 300 amino acids was ∼25 min.
Table 6.
Gaussian Evolutionary Method parameters
Root mean square deviation (RMSD) of atomic positions and the percentage of side-chain dihedral angles that were correctly predicted within 30° were used to assess the accuracy of the prediction. The RMSD was calculated using the formula
 |
(1) |
where M is the number of atoms in a protein and (Xi, Yi, Zi) and (xi, yi, zi) the coordinates of the ith atom of the X-ray crystal and the predicted structure, respectively. The calculation of RMSD included the heavy atoms of side chains. The accuracies for χ1 and χ1+2 were calculated excluding glycine and alanine residues. The accuracy for χ1+2 refers to those cases in which both χ1 and χ2 were correctly predicted.
Rotamer library and side-chain construction
A main-chain independent rotamer library was built using a modification of the method of Tuffery et al (1991). For each amino acid, only up to ten of the highest populated rotamers were considered. The number of rotamers was 1 for Pro; 3 for Cys, Ser, Thr, Val, Asp, and Phe; 4 for Asn; 5 for Ile; 6 for His, Leu, and Tyr; 7 for Trp; and 10 for the remaining amino acids (excluding Ala and Gly, which have no rotamers). The total number of rotamers was 103.
The side-chain atoms were geometrically constructed by placing side-chain templates onto the main chain of the X-ray structures, using the side-chain dihedral angles generated by GEM. These templates have standard bond lengths and bond angles according to the AMBER force field (Weiner et al. 1984). The initial dihedral angles of the side chains came either from the rotamer library or from an assigned value within the feasible region (−π to π). GEM then adapted these dihedral angles to search for optimal side-chain conformations by minimizing the scoring function.
Scoring energy function
Our scoring energy function was modified from Levitt (1983) and Hwang and Liao (1995):
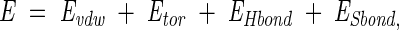 |
(2) |
where Evdw is the van der Waals interaction potential, Etor the torsional potential, and EHbond and ESbond are the potentials of hydrogen bonds and disulfide bonds, respectively. Evdw was computed using a Lennard-Jones 6–12 potential:
 |
(3) |
where ɛij and rij are constants which depend on the chemical characteristics of atoms i and j; Rij is the distance between the atoms i and j; M is the number of atoms in a protein; NB is the number of atoms within a preset distance (8 Å) of atom i; ɛij is the depth of the energy well, and rij is the equilibrium interatomic distance for the van der Waals interaction between atoms i and j. The same function form was used to compute the potential of the hydrogen bonds (EHbond) and disulfide bonds (ESbond). Table 7 shows the values used for these parameters. We restricted the Evdw energy to a maximal value of 20 kcal/mole for each atom pair, as described by Levitt (1983), to avoid infinite energies.
Table 7.
Energetic parameters used for side-chain conformation prediction
| Atom | ra | ɛa |
| O | 3.1 | 0.185 |
| N | 3.817 | 0.413 |
| C | 4.315 | 0.0738 |
| S | 4.315 | 0.0738 |
| H-bondb | 2.9 | 3.0 |
| S-bondc | 2.9 | 6 |
a For atom pairs i and j the parameter values are rij = (ri + rj)/2 and ɛij = (ɛiɛj)1/2.
b The parameter values are used for either oxygen or nitrogen to simulate the energy of hydrogen bonds.
c The parameter values are used for disulfide bonds.
For the torsional energy, the equation of Gehlhaar (1995) was used:
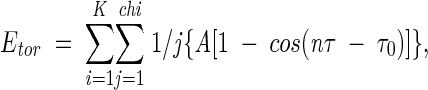 |
(4) |
where K is the residue number of a protein and chi is the number of dihedral angles of a residue. The values for A, n, and τ0 were 3, 3, and π, respectively, for the sp3-sp3 type and 1.5, 6, and 0, respectively, for the sp3-sp2 type (Gehlhaar et al. 1995).
GEM algorithm details
Here, we provide an outline of our evolutionary approach for predicting protein side-chain conformations, which can be represented by adjustable variables of dihedral angles as
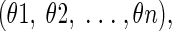 |
(5) |
where n is the number of dihedral angles of a side-chain conformation. Generally, the steps involved are as follows:
Initialize the side-chain conformation of each residue on a given backbone. The initial values for the dihedral angles are selected either from the rotamer library or from the feasible region (−π, π). Repeat this N times to generate the initial population of N side-chain conformations for a protein structure. Evaluate the objective value of each conformation based on the scoring function.
Change the dihedral angles of side-chain conformations by genetic operators to generate offspring. Evaluate the objective values of the offspring.
Use selection operators to select N solutions from the side-chain conformations of both parent and offspring solutions.
Repeat steps 2 and 3 until one of the terminating conditions is satisfied.
Main procedure
In the following subsections, we present the details of our approach for side-chain prediction. The method integrates a global discrete-search mechanism based on a rotamer library and continuous-search mechanisms based on Gaussian mutations. The basic structure of the method is as follows (Fig. 5 ▶): N solutions are generated as the initial population. Each solution (side-chain conformation) is represented as a set of three n-dimensional vectors (θi, σi, υi), where n is the number of adjustable variables (dihedral angles) of a side-chain conformation and i = 1,. . .,N. The vector θ in equation 5 represents the adjustable variable to be optimized, and σ and υ are the step-size vectors of decreasing-based mutation and self-adaptive Gaussian mutation, respectively (Yang and Kao 2000a,b). In other words, each solution, θ, is associated with some parameters for step-size control. In this paper, the initial value of θjwas randomly selected either from the rotamer library or from −π to π in radians. The initial step sizes, σ and υ, were 0.8 and 0.2 radians, respectively.
Fig. 5.
Overview of Gaussian Evolution Method (GEM). (a) Main procedure; (b) FC_adaptive procedure.
The main optimization procedure consists of three stages in one generation: a rotamer-search stage, a decreasing-based Gaussian mutation stage, and a self-adaptive Gaussian mutation stage. The rotamer-search stage is a discrete-search mechanism that uses the rotamer mutation operator to find an optimal combination of rotamer conformations. The decreasing-based Gaussian mutation and self-adaptive Gaussian mutation are continuous-search mechanisms that mutate dihedral angles to find an optimal side-chain conformation in continuous-search spaces. As shown in Figure 5 ▶, each stage uses a general procedure, FC_adaptive, with two parameters to generate a new quasi-population (with N solutions) as the parent of the next stage. These stages differ only in the mutations used. The recombination and mutation operators will be described below.
The FC_adaptive procedure employs two parameters, the population operator (P, with N solutions) and the mutation operator (M), to generate a new quasi-population. The main purpose of the FC_adaptive procedure is to produce offspring and then perform the family competition. Each individual in the population sequentially becomes the "family father." This family father and another solution randomly chosen from the rest of the parent population are used as parents for a recombination operation, with a probability of recombination of pc; then a mutation operates on the new offspring or the family father (if recombination does not occur). For each family father, this procedure is repeated L times (family competition length). Finally, L children are produced, but only the one with the lowest objective value survives. Because we create L children from one family father and perform a selection, this is a family-competition strategy.
For easy description of operators, we use a = ( θa, σa, υa) to represent the family father and b = ( θb, σb, υb) as another parent (only for the recombination operator). The offspring of each operation is represented as c = ( θc, σc, υc). We also use the symbol θjd to denote the jth dihedral angle of a side-chain conformation d.
Recombination operators
Modified discrete recombination
Because experience indicated that our method was more robust if the child inherited genes from the family father with a higher probability, we therefore modified the original discrete recombination (Bäck 1996) as follows:
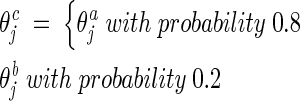 |
(6) |
Intermediate recombination
This operator is applied in the continuous-search stages as follows:
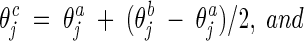 |
(7) |
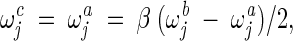 |
(8) |
where ω is σ or υ, depending on the mutation operator applied. For example, if the self-adaptive Gaussian mutation was used in this FC_adaptive procedure, ω is υ. β is a constant set as 0.5 in this work.
Mutation operators
Mutations are the main operators of our method. After recombination, a mutation operator is applied to the family father or to the new offspring generated by a recombination operator.
Rotamer mutation operator
This operator is used at the rotamer-search stage to find a combination of rotamer conformations. For each residue, this operator is biased to select rotamers of higher probabilities and mutates all of the dihedral angles of a residue according to the rotamer library. For example, this operator changes 3 dihedral angles (θj, θj + 1, and θj + 2) if the residue is Gln, Glu, or, Met. For each of these dihedral angles, this operator is applied with probability 0.2 as follows:
 |
(9) |
where γki and pki are the angle value and probability, respectively, of the ith rotamer of the kth residue type. The values of γki and pki are defined in the rotamer library.
Self-adaptive Gaussian mutation
The mutation is accomplished by first mutating the step size υj and then mutating the dihedral angle θj as follows:
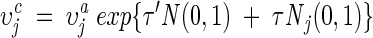 |
(10) |
 |
(11) |
where N(0, 1) is the standard normal distribution and Nj(0, 1) is a new value with distribution N(0, 1) that must be regenerated for each index j. We followed Bäck (1996) in setting τ and τ as (√2n)−1 and (√2√n)−1, respectively.
Decreasing-based Gaussian mutations
The decreasing-based Gaussian mutation is accomplished by mutating the step-size vector σ with a fixed decreasing rate γ = 0.95 as follows:
 |
(12) |
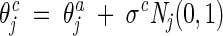 |
(13) |
Previous results (Yang and Kao 2000b) showed that self-adaptive mutations converge faster than decreasing-based mutations, whereas, for rugged functions, self-adaptive mutations tend to yield optimization results that are confined to local minima more easily than decreasing-based mutations.
Acknowledgments
The work was supported in part by grant NSC-90-2316-B-009-001 from the National Science Council of Taiwan.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked "advertisement" in accordance with 18 USC section 1734 solely to indicate this fact.
Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.4940102.
References
- Bäck, T. 1996. Evolutionary algorithms in theory and practice. Oxford University Press, New York.
- Bower, M.J., Cohen, F.E., and Dunbrack, R.L.J. 1997. Prediction of protein side-chain rotamers from a backbone-dependent rotamer library: A new homology modeling tool. J. Mol. Biol. 267 1268–1282. [DOI] [PubMed] [Google Scholar]
- De Maeyer, M., Desmet, J., and Lasters, I. 1997. All in one: A highly detailed rotamer library improves both accuracy and speed in the modeling of sidechains by dead-end elimination. Fold. Des. 2 53–66 [DOI] [PubMed] [Google Scholar]
- Desmet, J., De Maeyer, M., Hazes, B, and Lasters, I. 1992. The dead-end elimination theorem and its use in protein side-chain positioning. Nature 356 539–542. [DOI] [PubMed] [Google Scholar]
- Dunbrack, R.L.J. and Karplus, M. 1993. Backbone-dependent rotamer library for proteins: Application to side-chain prediction. J. Mol. Biol. 230 543–574. [DOI] [PubMed] [Google Scholar]
- Fogel, DB. 1995. Evolutionary computation: Toward a new philosophy of machine intelligence. IEEE Press, Piscataway, NJ.
- Gehlhaar, D.K., Verkhivker, G.M., Rejto, P., Sherman, C.J., Fogel, D.B., Fogel, L.J., and Freer, S.T. 1995. Molecular recognition of the inhibitor AG-1343 by HIV-1 protease: Conformationally flexible docking by evolutionary programming. Chem. Biol. 2 317–324. [DOI] [PubMed] [Google Scholar]
- Goldberg, D.E. 1989. Genetic algorithms in search, optimization and machine learning. Addison-Wesley Publishing Company, Reading, MA.
- Holm, L. and Sander, C. 1992. Fast and simple Monte Carlo algorithm for side-chain optimization in proteins: Application to model building by homology. Proteins 14 213–223. [DOI] [PubMed] [Google Scholar]
- Hubbard, S.J. and Thornton, J.M. 1993. NACCESS, computer program. Department of Biochemistry and Molecular Biology, University College London.
- Hwang, H.K. and Liao W.F. 1995. Side-chain prediction by neural networks and simulated annealing optimization. Protein Eng. 18 363–370. [DOI] [PubMed] [Google Scholar]
- Koehl, P. and Delarue, M. 1994. Application of a self-consistent mean field theory to predict protein side-chains conformation and estimate their conformational entropy. J. Mol. Biol. 239 249–275. [DOI] [PubMed] [Google Scholar]
- Laughton, C. 1994. Prediction of protein side-chain conformations from local three-dimensional homology relationships. J. Mol. Biol. 235 1088–1097. [DOI] [PubMed] [Google Scholar]
- Leach, A.R. 1994. Ligand docking to proteins with discrete side-chain flexibility. J. Mol. Biol. 235 345–356. [DOI] [PubMed] [Google Scholar]
- Leach, A.R. and Lemon, A.P. 1998. Exploring the conformational space of protein side chains using dead-end elimination and the A* algorithm. Proteins 33 227–239. [DOI] [PubMed] [Google Scholar]
- Lee, C. and Subbiah, S. 1991. Prediction of protein side chain conformation by packing optimization. J. Mol. Biol. 217 373–388. [DOI] [PubMed] [Google Scholar]
- Levitt, M. 1983. Protein folding by constrained energy minimization and molecular dynamics. J. Mol. Biol. 170 723–764. [DOI] [PubMed] [Google Scholar]
- Levitt, M., Gerstein, M., Huang, E., Subbiah, S., and Tsai, J. 1997. Protein folding: The endgame. Annu. Rev Biochem. 66 549–579. [DOI] [PubMed] [Google Scholar]
- Liang, S. and Grishin, N.V. 2002. Side-chain modeling with an optimized scoring function. Protein Sci. 11 322–331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Looger, L.L. and Hellinga, H.W. 2001. Generalized dead-end elimination algorithms make large-scale protein side-chain structure prediction tractable: Implications for protein design and structural genomics. J. Mol. Biol. 307 429–445. [DOI] [PubMed] [Google Scholar]
- Mendes, J., Soares, C.M., and Carrondo, M.A. 1999. Improvement of side-chain modeling in proteins with the self-consistent mean field theory method based on an analysis of the factors influencing prediction. Biopolymers 50 111–131. [DOI] [PubMed] [Google Scholar]
- Morris, G.M., Goodsell, D.S., Halliday, R.S., Huey, R., Hart, W.E., Belew, R.K., and Olson, A.J. 1998. Automated docking using a Lamarckian genetic algorithm and empirical binding free energy function. J. Comp. Chem. 19 1639–1662. [Google Scholar]
- Ponder, J.W. and Richards, F.M. 1987. Tertiary templates for proteins. Use of packing criteria in the enumeration of allowed sequences for different structural classes. J. Mol. Biol. 193 775–791. [DOI] [PubMed] [Google Scholar]
- Samudrala, R. and Moult, J. 1998. Determinants of side chain conformational preferences in protein structures. Protein Eng. 11 991–997. [DOI] [PubMed] [Google Scholar]
- Schrauber, H., Eisenhaber, F., and Argos, P. 1993. Rotamers: To be or not to be? An analysis of amino acid side-chain conformations in globular proteins. J. Mol. Biol. 230 592–612. [DOI] [PubMed] [Google Scholar]
- Tuffery, P., Etchebest, C., Hazout, S., and Lavery, R. 1991. A new approach to the rapid determination of protein side-chain conformations. J. Biomol. Struct. Dyn. 8 1267–1289. [DOI] [PubMed] [Google Scholar]
- ———. 1993. A critical comparison of search algorithms applied to the optimization of protein side-chain conformations. J. Comp. Chem. 14 790–798. [Google Scholar]
- Väsquez, M. 1995. An evaluation of discrete and continuum search techniques for conformational analysis of side-chains in proteins. Biopolymers 36 53–70. [Google Scholar]
- Weiner, S.J., Kollman, P.A., Case, D.A., Singh, U.C., Ghio, C., Alagona, G., Profeta Jr., S., and Weiner, P. 1984. A new force field for molecular mechanical simulation of nucleic acids and proteins. J. Am. Chem. Soc. 106 765–784. [Google Scholar]
- Xiang, Z. and Honig, B. 2001. Extending the accuracy limits of prediction for side-chain conformations. J. Mol. Biol. 311 421–430. [DOI] [PubMed] [Google Scholar]
- Yang, J.M. and Kao, C.Y. 2000a. Flexible ligand docking using a robust evolutionary algorithm. J. Comp. Chem. 21 988–998. [Google Scholar]
- ———. 2000b. Integrating adaptive mutations and family competition into genetic algorithms as function optimizer. Soft Computing 4 89–102. [Google Scholar]
- ———. 2001. An evolutionary algorithm for the synthesis of multiplayer coatings at oblique light incidence. IEEE/OSA J. Lightwave Technol. 19 559–570. [Google Scholar]
- Yang, J.M., Horng, J.T., and Kao, C.Y. 2000. A genetic algorithm with adaptive mutations and family competition for training neural networks. Int. J. Neural Syst. 10 333–352. [DOI] [PubMed] [Google Scholar]