Abstract
Previously, investigations using single-fluorescent-molecule tracking at frame rates of up to 65 Hz, showed that the transmembrane MHC class II protein and its GPI-anchored modified form expressed in CHO cells undergo simple Brownian diffusion, without any influence of actin depolymerization with cytochalasin D. These results are at apparent variance with the view that GPI-anchored proteins stay with cholesterol-enriched raft domains, as well as with the observation that both lipids and transmembrane proteins undergo short-term confined diffusion within a compartment and long-term hop diffusion between compartments. Here, this apparent discrepancy has been resolved by reexamining the same paradigm, by using both high-speed single-particle tracking (50 kHz) and single fluorescent-molecule tracking (30 Hz). Both molecules exhibited rapid hop diffusion between 40-nm compartments, with an average dwell time of 1–3 ms in each compartment. Cytochalasin D hardly affected the hop diffusion, consistent with previous observations, whereas latrunculin A increased the compartment sizes with concomitant decreases of the hop rates, which led to an ∼50% increase in the median macroscopic diffusion coefficient. These results indicate that the actin-based membrane skeleton influences the diffusion of both transmembrane and GPI-anchored proteins.
INTRODUCTION
Recently, Vrljic et al. (1,2) and Nishimura et al. (3), using single-fluorescent-molecule tracking (SFMT) at frame rates smaller than 65 Hz, found that the GPI-anchored modified form of MHC class II protein (GPI-I-Ek) expressed in CHO cells undergoes simple Brownian diffusion, with an average effective diffusion coefficient slightly greater than that of the native transmembrane form of the MHC class II molecule (TM-I-Ek, by a factor of 1.3–1.9). Furthermore, the diffusion was not affected by partial actin depolymerization using cytochalasin D. These results appear to be at variance with the “membrane-skeleton fence model” and the “anchored-protein picket model” proposed previously (Fig. 1; (4–21)).
FIGURE 1.
Proposed mechanisms for the compartmentalization of the plasma membrane for the translational diffusion of transmembrane proteins and GPI-anchored proteins in the membrane: corralling by the membrane-skeleton “fences” and the anchored-protein “pickets.” The plasma membrane may be parceled up into closely apposed domains (compartments) for the translational diffusion of transmembrane proteins and lipids (or GPI-anchored proteins). All of the membrane constituent molecules undergo short-term confined diffusion within a compartment and long-term hop diffusion between these compartments. This may be due to corralling by two mechanisms: the membrane-skeleton “fences” and the anchored-protein “pickets.” In this study, we examined two varieties of MHC class II molecules, I-Ek (I-Ek indicates the k allele in the I-E region): the native single-pass transmembrane type (TM-I-Ek) and a modified protein with a GPI-anchor (GPI-I-Ek). Both the GPI-linked and TM-I-Ek molecules share the same extracellular domain. In GPI-I-Ek, the cytoplasmic and transmembrane moieties of the TM-I-Ek are replaced by two GPI-linkers that tether it to the outer leaflet of the plasma membrane (72). These molecules were expressed in CHO cells, and those located in the upper plasma membrane were observed. (a) The side-view schematic representation of TM-I-Ek, GPI-I-Ek, and an MSK-anchored protein (membrane skeleton-anchored proteins, gray cylinder). The former two molecules are mobile, whereas MSK-anchored proteins are immobile. (b) The membrane-skeleton “fence” or “corral” model, showing that transmembrane proteins are confined within the mesh of the actin-based membrane skeleton, as viewed from inside the cell. Meanwhile lipids and GPI-anchored proteins, located in the outer leaflet of the membrane, do not directly interact with the membrane skeleton. (c) The anchored-protein “picket” model, showing MSK-anchored proteins, effectively represent the immobile obstacles to the diffusion of transmembrane proteins, lipids, and GPI-anchored proteins, as viewed from outside the cell.
In these models, the plasma membrane is parceled up into apposed domains of 30–200 nm in diameter, due to the presence of the actin-based membrane skeleton, which is closely associated with the cytoplasmic surface of the plasma membrane. In the membrane-skeleton fence model, transmembrane proteins protrude into the cytoplasm, and the cytoplasmic domains of the transmembrane proteins collide with the membrane skeleton, which induces temporary confinement of the transmembrane proteins in the membrane-skeleton mesh (compartments) (Fig. 1, a and b). In the anchored-protein picket model, various transmembrane proteins, which are anchored to and aligned along the membrane skeleton, effectively form rows of pickets, thus creating a barrier against the free diffusion of both lipids (even those in the outer leaflet of the membrane) and transmembrane proteins (Fig. 1, a and c). This barrier effect may be due to steric hindrance and circumferential slowing (5). Circumferential slowing is the collective term for hydrodynamic friction (in terms of hydrodynamic theory (22,23)) and increased packing (in terms of free-volume theory (24,25)), and is highly enhanced near transmembrane proteins. In terms of the hydrodynamic theory, the viscosity within the membrane is ∼100 times greater than that in water. Therefore, in the vicinity of immobilized molecules in the membrane, the movement of other molecules is greatly suppressed, due to the hydrodynamic dragging effects of the pickets. This hydrodynamic dragging effect of immobile proteins propagates over several nanometers from the protein surface. Therefore, the compartment boundaries do not have to be totally closed off by picket proteins to induce temporary confinement of phospholipids within the compartment. The “fences” would act on transmembrane proteins, whereas the “pickets” would act on both lipids (including lipid-anchored proteins) and transmembrane proteins. Therefore, transmembrane proteins are corralled by both fences and pickets. In both models, membrane proteins and lipids can hop from a compartment to an adjacent one (hop diffusion), probably when thermal fluctuations of the membrane and the membrane skeleton create a sufficiently large space between them to allow the passage of integral membrane proteins, and/or when an actin filament is temporarily severed. The compartmentalization of the cell membrane and the hop diffusion of the phospholipid molecules among the compartments were found in all of the eight cultured mammalian cell lines examined thus far (6), and the very dense rows of anchored-protein pickets in the initial segment region of the neuronal plasma membrane were found to form the macroscopic diffusion barrier in this region (26).
Furthermore, Morone et al. (27) have determined the distribution of the membrane skeleton mesh size right on the cytoplasmic surface of the membrane by the three-dimensional reconstruction of the inner surface of the plasma membrane, using electron tomography. The distributions of the surface mesh sizes agree well with the compartment sizes determined from the hop diffusion of a nonraft unsaturated phospholipid, 1,2-dioleoyl-sn-glycero-3-phosphorylethanolamine (DOPE) in high-speed single-particle tracking (SPT). These results strongly support the membrane-skeleton-based “fence” and “picket” models.
On the other hand, it is still unknown how GPI-anchored molecules diffuse in the compartmentalized plasma membrane. Since GPI-anchored molecules may be trapped in cholesterol-enriched raft domains (28,29), the diffusion rates of GPI-anchored proteins might be much smaller than those for nonraft molecules, but this has not been found (Table 1; (1–3,30–34)). More recently, Wieser et al. (35) reported that CD59, a GPI-anchored protein, basically underwent unconfined simple Brownian diffusion in T24 cells. In contrast, Schütz et al. (36) found that a putative raft-associating molecule was trapped within a 700-nm domain (0.2–2 μm) for long periods (300 ms) in human coronary artery smooth muscle cells. Furthermore, Shvartsman et al. (37) found that the mobility of a GPI-linked form of influenza hemagglutinin was slower than that in a transmembrane nonraft form. In addition, Lenne et al. (38) and Wenger et al. (39) reported that GFP-GPI was compartmented within tens of milliseconds into φ < 120 nm domains (the best estimate being ∼80 nm) in COS-7 cells.
TABLE 1.
Effective macroscopic diffusion coefficients for MHC class II proteins and GPI-anchored proteins
| Molecule* | Cell† | Probe‡/Method | Deff mean (± SD) (μm2/s) | Mobile fraction (%) | Frame time (ms) | Temp. (°C) | Ref. |
|---|---|---|---|---|---|---|---|
| TM-I-Ek | CHO | Alexa594-Fab/SFMT | 0.15 (± 0.12) | 91 | 33 | 37 | ¶ |
| Cy3-peptide/SFMT | 0.15 (± 0.078) | 95 | 33 | 37 | ¶ | ||
| TM-I-Ek | CHO | Cy5-peptide/SFMT | 0.59 (± 0.04) | ? | 15.4 | 37 | (3) |
| 0.15 (± 0.0033) | ? | 15.4 | 22 | (3) | |||
| TM-I-Ek | CHO | Cy5-peptide/SFMT | 0.18 (± 0.013) | 100 | 100 | 22 | (1) |
| HLA-DR | M1DR1 | PE-IgG/SPT | 0.13–1.9 × 10−4 | ? | ‖ | RT§ | (61) |
| HLA-DR | HT29 | FITC-IgG/FRAP | ∼0.2 | 60–70 | NA§ | ? | (62) |
| I-Ad | A20 | TRITC-Fab/FRAP | 0.017 | ∼60 | NA | 37 | (63) |
| I-Ak | M12.C3 | TAMRA-Fab/FRAP | 0.011–0.023 | 75 | NA | RT | (64) |
| I-Ak | M12.C3 | FITC-Fab/FRAP | 0.010–0.030 | 36–73 | NA | 20/30 | (65) |
| I-Ak | TA3 | FITC-IgG/FRAP | 0.42 (± 0.24) | 65 | NA | 23 | (66) |
| I-A | Normal B cell | FITC-Fab/FRAP | 0.05–0.09 | 24–61 | NA | 22 | (67) |
| GPI-I-Ek | CHO | Alexa594-Fab | 0.33 (± 0.30) | 93 | 33 | 37 | ¶ |
| Cy3-peptide/SFMT | 0.32 (± 0.23) | 97 | 33 | 37 | ¶ | ||
| GPI-I-Ek | CHO | Cy5-peptide/SFMT | 1.1 (± 0.06) | ? | 15.4 | 37 | (3) |
| 0.19 (± 0.0059) | ? | 15.4 | 22 | (3) | |||
| GPI-I-Ek | CHO | Cy5-peptide/SFMT | 0.22 (± 0.031) | 94–100 | 100 | 22 | (1) |
| Thy-1 | 3T3 fibroblast | Gold-IgG/SPT | 0.19 | ? | ** | 37 | (68) |
| Thy-1 | C3H 10T1/2 fibroblast | Gold-IgG/SPT | 0.0035–0.081 | 90 | 33 | 37 | (69) |
| GFP-GPI | Rat hippocampal neuron | Q-dot-(Fab′)2/SPT | ∼0.4 | ? | 70 | 37 | (70) |
| GFP-GPI, GFP-CD59, YFP-GL-GPI | COS-7, NRK, BHK-21 | GFP, YFP/confocal FRAP | 0.4–0.7 | ∼90 | NA | 37 | (34) |
| HA-GPI (trimer) | CHO | TRITC-Fab′/FRAP | 0.099 | 67 | NA | 37 | (71) |
| GFP-GPI, GFP-Thy-1 | COS-7 | GFP/FCS, confocal FRAP | ∼1.1 | ∼90 | NA | 37 | (38) |
GPI, glycosylphosphatidylinositol; YFP-GL-GPI, yellow fluorescent protein-N-glycosylated-GPI; and HA-GPI, GPI-anchored modified form of influenza hemagglutinin (HA).
CHO, Chinese hamster ovary; COS-7, transformed African green monkey kidney fibroblast; NRK, normal rat kidney; and BHK-21, baby hamster kidney.
SFMT, single fluorescent molecule tracking; PE, R-phycoerythrin; SPT, single particle tracking; TRITC, tetramethylrhodamine isothiocyanate; FRAP, fluorescence recovery after photobleaching; TAMRA, 6-(tetramethylrhodamine-5-(and-6)-carboxamindo) hexanoic acid succinimidyl ester; FITC, fluorescein isothiocyanate; Q-dot, quantum dot; and FCS, fluorescence correlation spectroscopy.
This work.
NA, not applicable; RT, room temperature.
Images were typically recorded every 1 or 2 min with an exposure time of 5 s.
Two frames every 10 s.
In this investigation, we used exactly the same molecules expressed in the same cell type as those previously used by Vrljic et al. (1,2) and Nishimura et al. (3), i.e., TM-I-Ek and GPI-I-Ek expressed in CHO cells, and carried out high-speed SPT with 40-nm-φ colloidal gold probes at a frame rate of 50 kHz (20-μs resolution, enhanced from video rate by a factor of 1667) as well as single fluorescent-molecule tracking (SFMT) with the use of fluorescent probes at 30 Hz (video rate). The diffusion coefficients for the MHC class II proteins and the GPI-anchored proteins reported thus far are summarized in Table 1, but it is difficult to deduce the mechanisms that regulate the diffusion of these molecules in the plasma membrane. By observing both TM-I-Ek and GPI-I-Ek, and by using single-molecule high-speed tracking, we hope to gain more insights in this mechanism.
We examined the following three key problems with regard to the diffusion of GPI-anchored proteins using GPI-I-Ek, and compared the results with those for TM-I-Ek:
Do GPI-anchored proteins actually undergo hop diffusion if they are observed at higher frame rates?
Does GPI-I-Ek, but not TM-I-Ek, exhibit confinement within 80-nm or 700-nm domains for several 10s of milliseconds or longer, as previously suggested for putative raft-associating molecules (36,38,39)?
Does the treatment of cells with drugs that affect actin polymerization, such as cytochalasin D and latrunculin A, induce changes in the diffusion of GPI-anchored proteins? (Note that Vrljic et al. (1,2) and Nishimura et al. (3) previously failed to detect any changes in the diffusion characteristics, after the cells were treated with cytochalasin D.)
MATERIALS AND METHODS
Cell culture
For the details of culturing CHO cells expressing TM-I-Ek or GPI-I-Ek, see Vrljic et al. (1). Cells expressing these proteins were plated on 18 × 18-mm coverslips (IWAKI, Chiba, Japan) for SPT observations or on 12 mm-φ glass-bottom dishes (IWAKI) for SFMT observations, and were grown for a day before the microscope experiment. The glass surface was coated with 50 μg/ml fibronectin from human plasma (CalBiochem, San Diego, CA), as described previously (1).
Preparation of colloidal gold probes
The TM-I-Ek and GPI-I-Ek expressed on the CHO cell surface were first labeled with anti-I-Ek-Fab, and then the cells were further incubated with anti-mouse IgG-Fab-coated 40 nm colloidal gold particles. The anti-I-Ek-Fab was prepared from anti-I-Ek-IgG (14-4-4s) purified from the hybridoma (HB32, ATCC, Manassas, VA) supernatant. The minimal protecting amount (MPA, defined as the minimum concentration of the protein needed to stabilize colloidal gold particles in suspension) of anti-mouse IgG-antibody Fab (Cappel, Organon Teknica, Durham, NC) was determined to be 3.3 μg/ml (40,41). Colloidal-gold probes coated with the MPA of Fab were prepared by mixing 50 μl of 36 μg/ml anti-mouse IgG Fab in 2 mM borate buffer (pH 9.2) and a 500 μl suspension of colloidal gold (BBInternational, Cardiff, UK) on a slowly tumbling shaker for 15 min at room temperature. The gold probe was stabilized by the further addition of bovine serum albumin (BSA) at a final concentration of 1% (w/v). After sedimentation, the gold probe was resuspended in RPMI medium supplemented with 10% fetal bovine serum and 1% BSA, sterilized by filtration through a 0.22-μm filter (Millipore, Bedford, MA), and then used within 5 h.
SFMT of fluorophore-labeled TM-I-Ek, GPI-I-Ek, and DOPE
See Fig. 2 (left). TM-I-Ek and GPI-I-Ek were labeled by using either anti-I-Ek Fab conjugated with Alexa594 (Molecular Probes, Eugene, OR); the final molar ratio of fluorochrome to protein was 0.2–0.3:1) or Moth Cytochrome c peptide, MCC 95–103 (IAYLKQATK, custom-ordered from the Peptide Institute, Osaka, Japan) labeled at the N-terminus with Cy3 mono functional dye (Amersham-Pharmacia, Uppsala, Sweden; precisely one dye molecule per peptide chain). Cells were incubated with 4–40 nM Alexa594-anti-I-Ek Fab or with 30–300 nM (0.05–0.5 μg/ml) Cy3-MCC 95–103 peptide for 15–30 min at 37°C, in RPMI 1640 medium supplemented with 10% FBS and 1% BSA without phenol red (the same medium was used for microscope observations). For SFMT of DOPE, first Alexa594-DOPE (custom-ordered from Molecular Probes) in methanol (14 μM) was mixed with RPMI 1640 medium without 10% FBS and phenol red by vigorous vortexing (70 nM final concentration), and then this solution was added to the cells cultured on a glass-bottom dish at 37°C (final concentration 7 nM).
FIGURE 2.
Experimental design for single fluorescent-molecule tracking (SFMT, left) and single-particle tracking (SPT, right). (Left) Single fluorescent-molecule tracking (SFMT), carried out at video rate (30 Hz; 33-ms resolution), providing the effective diffusion coefficient on the timescale of 100 ms, Deff(33ms)100ms. TM-I-Ek and GPI-I-Ek were labeled with either Alexa594-conjugated anti-I-Ek Fab fragments or the Cy3-tagged peptide (Moth Cytochrome c peptide, MCC 95–103 (IAYLKQATK)) at its N-terminus. Alexa594-conjugated DOPE was incorporated in the cell membrane. (right) Single-particle tracking (SPT), carried out at a 50,000 Hz frame rate (20-μs resolution), providing the compartment size sensed by the diffusant. TM-I-Ek and GPI-I-Ek were labeled with anti-I-Ek Fab fragments and then labeled with gold probes coated with anti-mouse IgG antibodies' Fab fragments. For SPT of DOPE, gold probes coated with anti-fluorescein antibody Fab fragments were bound to fluorescein-DOPE, which was preincorporated in the cell membrane (5,6).
All observations of the cells were carried out at 37°C for up to 20 min. No efforts for deoxygenation, such as the procedures employed by Vrljic et al. (1,2) and Nishimura et al. (3), were made. Individual Alexa594 molecules were monitored on the upper cell membrane at video rate (30 Hz), using the oblique illumination mode of a homebuilt objective lens-type total internal reflection fluorescence microscope (42–44). Briefly, a 594.1-nm laser beam (He-Ne laser; Melles Griot, Carlsbad, CA) and a 532-nm laser beam (the second harmonic of the Nd:YAG laser beam, Model 4501-050; Uniphase, San Jose, CA) were attenuated with neutral density filters, circularly polarized, and then steered into the edge of a high numerical aperture (NA) objective lens (PlanApo 100×, NA = 1.4; Olympus, Tokyo, Japan) with a focus at the back-focal plane of the objective lens on an Olympus inverted microscope (IX-70).
The precision of the position determination was estimated from the standard deviation of the coordinates of Alexa594-Fab and Cy3-peptide adsorbed to a poly-L-lysine-coated coverslip, overlaid by a 15% polyacrylamide gel (5% cross-linker) (16,45), and was ≈20 nm at a time resolution of 33 ms.
SPT of TM-I-Ek, GPI-I-Ek, and DOPE, tagged by 40-nm-φ colloidal gold particles
See Fig. 2 (right). For the TM-I-Ek and GPI-I-Ek observations, these membrane molecules were labeled with anti-I-Ek Fab fragments and then labeled with gold probes coated with anti-mouse IgG antibody Fab fragments (gold particles could not be directly coated with anti-I-Ek Fab fragments, due to the inability of these Fab fragments to protect the gold surface). First, the anti-I-Ek Fab (8 μg/ml final concentration) was incubated with CHO cells expressing TM-I-Ek or GPI-I-Ek, which were cultured on coverslips, and then after washing the cells, gold probes conjugated with anti-mouse IgG Fab were applied to the cells. All observations of the gold probes were carried out at 37°C within 20 min after the application of the gold probes to the cells, which was very effective for reducing the number of gold particles exhibiting slow diffusion or immobilization.
For SPT of DOPE, gold probes coated with anti-fluorescein antibody Fab fragments were bound to fluorescein-DOPE (fluorescein was simply used as a tag, rather than a fluorescent probe), which was preincorporated in the cell membrane, as described in Fujiwara et al. (5) and Murase et al. (6). Briefly, after fluorescein-DOPE was incorporated in the cell membrane by the addition of 2 μg/ml (final concentration) of fluorescein-DOPE, gold probes conjugated with the anti-fluorescein antibodies' Fab fragments were applied to cells cultured on 18 × 18-mm coverslips. For the observations with enhanced frame rates, a digital high-speed camera with a C-MOS sensor was used (Fastcam-APX RS; Photron, Tokyo, Japan (5,6,14,19)). For high-speed video microscopy, bright-field optical microscopy, rather than Nomarski microscopy, was employed. We used an Alpha-Plan-Fluar 100× oil immersion objective lens with a numerical aperture of 1.45 (Carl Zeiss, Oberköchen, Germany). The sequence of images was replayed at the video rate (30 Hz) with analog and digital enhancements by an image processor (DVS-3000, Hamamatsu Photonics, Hamamatsu, Japan), and was recorded on a digital video tape recorder (DSR-20, Sony, Tokyo, Japan).
The precision of the position determination was estimated by the same method employed in SFMT using 40-nm-φ gold particles, and was 16 nm at a time resolution of 20 μs.
Obtaining the trajectories of membrane molecules and the plots of mean-square displacement (MSD) versus time
The positions (x and y coordinates) of the selected gold particles or fluorescent molecules were determined by a computer that employs the method developed by Gelles et al. (46). For each trajectory, the mean-square displacement (MSD), 〈Δr(Δt)2〉, for every time interval (Eq. 1) was calculated according to the formula (16,47,48)
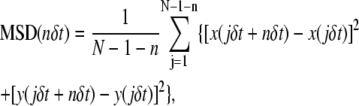 |
(1) |
where δt is the video frame time and x(jδt + nδt), y(jδt + nδt) describes the particle position after a time interval Δtn = nδt after starting at position (x(jδt), y(jδt)), N is the total number of frames in the video recording sequence, n and j are positive integers, and n determines the time increment.
To keep the statistical spread in the MSD within reasonable levels for the duration of 0–1 s, TM-I-Ek, GPI-I-Ek, and DOPE trajectories of 3 s (90 video frames) were used for the quantitative analysis ((49–51); see Figs. 3–5).
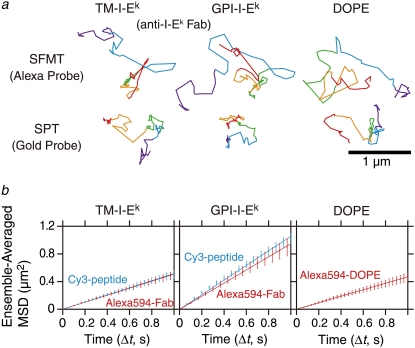
FIGURE 3.
Representative trajectories and ensemble-averaged MSD-Δt plots for TM-I-Ek, GPI-I-Ek, and DOPE observed at a 33-ms resolution. (a) Representative trajectories in the CHO cell plasma membrane for 3 s (total number of frames, N, is 90). The colors (purple, cyan, green, orange, and red) represent the passage of time (every 600 ms or 18 video frames). (b) Ensemble-averaged mean-square displacement (MSD) as a function of time (t) for TM-I-Ek, GPI-I-Ek, and DOPE averaged over all molecules examined in this study. (Cyan line) Cy3-peptide probe. (Red line) Alexa594-Fab probe for TM-I-Ek and GPI-I-Ek or Alexa594-DOPE. Ensemble-averaged MSD-Δt plots for these molecules were fitted by straight lines in the range between 0 and 1 s. Deff(33ms)500ms values of TM-I-Ek, GPI-I-Ek, and DOPE with Alexa594-Fab probes were 0.13, 0.25, and 0.12 μm2/s, respectively. Deff(33ms)500ms values of TM-I-Ek and GPI-I-Ek with Cy3-peptide probes were 0.13 and 0.24 μm2/s, respectively. The averaged MSD values for TM-I-Ek, GPI-I-Ek, and DOPE were obtained by averaging the corrected MSD of each molecule over all molecules. The corrected MSD for each molecule was obtained by subtracting the y intercept of the straight line fitted for MSD(2δt), MSD(3δt), and MSD(4δt) (as noise) from the uncorrected MSD for each molecule (16). Error bars for each ensemble-averaged MSD represent standard errors. For the viewability of the plots, the experimentally obtained points of TM-I-Ek and those of GPI-I-Ek are alternatingly shown.
FIGURE 4.
Theoretical curves for MSD-Δt plots of simple Brownian diffusion, directed diffusion, and confined diffusion, and the distributions of RD(N, n) for TM-I-Ek, GPI-I-Ek, and DOPE, observed at video rate (30 Hz), employing fluorescent and colloidal-gold probes (N = 90; n = 30). (a) Theoretical curves for simple Brownian diffusion (I), directed diffusion (II), and confined-hop diffusion (III) are shown for two-dimensional diffusion. The curves were plotted according to the equations in Classification of the Mode of Diffusion, Calculation of the Diffusion Coefficient, and Analysis of the High-Speed SPT Trajectories. The graphs were drawn assuming that the short-term diffusion coefficients (1/4 of the initial slope at Δt = 0) are the same for all of the cases. RD(N, n) where N = total number of frames and n = time windows for the analysis, is defined as the ratio of an experimental MSD(nδt) to the fictitious MSD at time nδt (4D2–4nδt), assuming that the molecule undergoes simple Brownian diffusion without confinement or directed diffusion with a diffusion coefficient determined from the initial slope (4D2–4 is the slope determined from a linear fit to the MSD values at the second, third, and fourth steps of elapsed time, shown as red line). The larger the RD is from 1, the higher the probability of directed diffusion. Meanwhile, the smaller the RD is from 1, the higher the probability of confined-diffusion. (b) The distribution of RD(N, n) = MSD(N, n)/[4 × Deff(33ms)100ms × 0.033n] for N = 90 and n = 30, i.e., the ratio of the observed MSD(N, n) averaged over an N-step trajectory versus the MSD(N, n) expected from the initial slope of the MSD-Δt curve (averaged over the N-step trajectory). Here, N (the total trajectory length) = 90 frames, and the analysis time window n = 30 steps (1 s). For the classification of the trajectories into different diffusion modes, first, many simple Brownian trajectories were generated by Monte Carlo simulation to determine the distribution of RD(90, 30) for simple Brownian particles, and then RD(90, 30) values of 2.5% of population at each edge of the distribution were taken as limits to simple Brownian behavior and are referred to as RD(90, 30)min (red line) and RD(90, 30)max (cyan line) (16). If a molecule (a particle) exhibits an RD(90, 30) <RDmin(90, 30), between RDmin(90, 30) and RDmax(90, 30), or >RDmax(90, 30), then it is classified as having a confined-hop, simple Brownian, or directed diffusion mode, respectively. The sum of the percent values may not be 100 due to the presence of immobile fluorescent spots (all of the gold particles attached to the plasma membrane were mobile). The majority of the TM-I-Ek, GPI-I-Ek, and DOPE (mobile) trajectories were classified into the simple Brownian mode, irrespective of the probes employed here.
FIGURE 5.
Distributions of the effective diffusion coefficients for a 100-ms window, Deff(33ms)100ms, using different probes. (a) (Top) Determination of the lowest Deff(33ms)100ms distinguishable from the immobile spot (this is determined by the noise level). Alexa594-Fab (gray bars) or Cy3-peptide (orange bars) attached to the cover glass exhibited the nominal Deff(33ms)100ms in the range below 0.009 μm2/s (median values shown by arrowheads). Due to statistical dispersion of MSD values, many trajectories gave negative values for Deff(33ms)100ms, which are represented by a bar for spots exhibiting 0.0001 μm2/s or smaller. A spot exhibiting the top 2.5 percentile value in this distribution was selected as the lowest detectable limit for Deff(33ms)100ms, i.e., 0.007 μm2/s (shown by the cyan line). Any spot exhibiting a Deff(33ms)100ms value < 0.007 μm2/s was classified into the immobile mode in this experiment (in the sense that it cannot be distinguished from the immobilized probe on the coverslip). (Middle and bottom boxes) TM-I-Ek and GPI-I-Ek labeled with Alexa594-Fab (gray bars) or Cy3-peptide (orange bars), showing no statistically significant difference between the Fab and peptide probes. Arrowheads indicate the median values. There were no significant differences in these diffusion coefficients between the labels. GPI-I-Ek diffused 1.6-fold faster than TM-I-Ek and DOPE (the Wilcoxon statistical test result; p < 0.05, also see b). (b) TM-I-Ek and GPI-I-Ek were labeled with colloidal-gold probes coated with the MPA of anti-mouse IgG-antibody Fab, whereas DOPE was labeled with gold probes coated with the threefold MPA of the anti-fluorescein antibodies' Fab fragments in the presence of the free anti-fluorescein antibodies' Fab fragments. Gold probes (open bars with black outlines) exhibited diffusion coefficients 3–7-fold smaller than fluorescent Alexa probes (gray bars), probably due to steric hindrance and/or crosslinking. The lower-limit of the diffusion coefficients that can be evaluated by SPT of gold-Fab was 0.0003 μm2/s, which is indicated by a black vertical line (at video rate; 16). No gold-tagged molecule was classified into the immobile mode.
Classification of the mode of diffusion, calculation of the diffusion coefficient, and analysis of the high-speed SPT trajectories
For a detailed description of the data analysis methods, see Fujiwara et al. (5) and Suzuki et al. (19).
We designate the effective diffusion coefficients (with an indication of the midpoint of the linear fitting) as Deff(time resolution)midpoint. For example, Deff(33ms)100ms (in this case, 33 ms is the time resolution employed for the observation) and Deff(20μs)60μs (observation rate of 20 μs/frame) correspond to D2–4, defined in Kusumi et al. (16) and described in Suzuki et al. (19).
A statistical method for classifying each trajectory into confined-hop diffusion, simple Brownian diffusion, simple-Brownian diffusion with a drift, or immobile modes, based on the MSD-Δt plot, was described by Kusumi et al. (16). Briefly, all of the trajectories were first classified into mobile and immobile ones (see Fig. 5 and its related text in Results), and the mode-of-motion classification was carried out only for the trajectories that were classified as mobile (see Fig. 4 a and its related text in Results). The ensemble-averaged RD is ≪, ≈, or ≫ 1, when the molecules are undergoing confined-hop diffusion, simple Brownian diffusion, or simple-Brownian diffusion with a drift (directed diffusion mode), respectively. Fig. 4 a shows the theoretical curves for
Simple Brownian diffusion, in which MSD(Δt) = 4DΔt.
Directed diffusion mode, in which a molecule moves in a direction at a constant drift velocity (vx, vy), with superimposed random diffusion, MSD(Δt) = 4DΔt + v2 (Δt)2, where
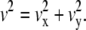
Confined diffusion, in which a molecule undergoes Brownian diffusion while totally confined within a limited area (compartment; 0 ≤ x ≤ Lx, 0 ≤ y ≤ Ly) during the observation period.
The MSD-Δt plot levels off and asymptotically approaches a constant value, as expressed by
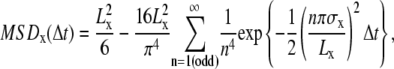 |
 |
 |
For the analysis of the trajectories obtained by using high-speed SPT with 20-μs resolutions and classified into the confined diffusion mode (under the analysis conditions employed therein), the MSD-Δt plots in the x or y directions were fitted with a homemade program based on the hop diffusion theory of Powles et al. (52), in which a particle undergoes diffusion in the presence of semipermeable barriers placed at an equal distance (termed “hop fit” in this article; see also (5,6,19)). In the analysis, the time evolution of the probability distribution depends on three parameters: the distance between barriers, L, the true diffusion coefficient in the absence of barriers, Dmicro, and the permeability of the barriers, P. Powles et al. (52) also derived a relationship between the permeability and the long-term diffusion coefficient, DMACRO, DMACRO/Dmicro = [1 + (PL)−1]−1.
The correct hop rate (or the residency time within a compartment) was evaluated from the macroscopic diffusion coefficient, determined by SFMT with a fluorescent probe, and the compartment size, determined by SPT with a gold probe. Individual compartments for each trajectory were automatically identified by the computer program (5,6,19).
Drug treatments
Latrunculin A (Molecular Probes) and cytochalasin D (Sigma, St. Louis, MO) were dissolved in methanol. The treatment of cells with latrunculin A was done by incubating the cells in the RPMI medium supplemented with 1% BSA (Sigma), containing 1 μM latrunculin A (0.01% methanol) under the microscope observation at 37°C, and the observation was carried out between 5 and 20 min after the drug addition. Likewise, with 1 μM and 10 μM cytochalasin D (0.006% and 0.06% methanol), the cells were treated for 1 min at 37°C, and then the observation was continued for up to 5 or 12 min. Control cells were treated with an equivalent amount of methanol alone.
RESULTS
Typical SFMT trajectories for TM-I-Ek, GPI-I-Ek, and Alexa594-DOPE obtained at video rate
All experiments were carried out at 37°C. Vrljic et al. (1,2) and Nishimura et al. (3) observed the diffusion of individual TM-I-Ek and GPI-I-Ek using a Cy5-peptide (MCC 95–103 peptide, with one Cy5 dye attached per peptide at its N-terminus) that binds to a specific site on MHC class II molecules with high specificity. In this study, we used Alexa594-conjugated anti-I-Ek Fab (the final molar ratio of fluorochrome to protein was 0.2–0.3:1) in addition to the peptide (conjugated with Cy3) (Fig. 2). They were observed at a 33-ms resolution for a period of 3 s in the upper cell membrane of CHO cells by SFMT, using the oblique illumination mode of a homebuilt objective lens-type total internal reflection fluorescence microscope. Each fluorescent spot of the Alexa594-conjugated anti-I-Ek Fab and Cy3-peptide in the microscope image was found to represent a single molecule, based on the single-step photobleaching (1,5,42).
Fig. 3 a shows typical trajectories of Alexa594-conjugated anti-I-Ek-Fab bound to TM-I-Ek and to GPI-I-Ek, and Alexa594-DOPE, a DOPE molecule tagged with Alexa594 in the headgroup region and incorporated in the cell membrane of CHO cells. Fig. 3 b shows ensemble-averaged MSD-Δt plots for TM-I-Ek and GPI-I-Ek observed with Alexa594-Fab (red) and Cy3-peptide (cyan), as well as Alexa594-DOPE (right) on the timescale of 1 s. These plots were fitted by straight lines in the range between 0 and 1 s, suggesting that TM-I-Ek, GPI-I-Ek, and DOPE on average underwent apparent simple Brownian diffusion on the 1-s scale. The averaged Deff(33ms)500ms values of TM-I-Ek and GPI-I-Ek labeled with Alexa594-Fab and of Alexa-DOPE were 0.13, 0.25, and 0.12 μm2/s, respectively (designated as Deff(time resolution)midpoint; see Materials and Methods). The diffusion coefficients of TM-I-Ek and GPI-I-Ek with the Cy3-peptide probes were virtually the same as those with the Alexa594-Fab probes.
Classification of single-molecule trajectories into different diffusion modes
We next performed a statistical analysis of each single-molecule trajectory to classify each trajectory into simple Brownian, directed, confined-hop, or immobile modes, based on the MSD-Δt plot (16), rather than characterizing the collective diffusion properties. Fig. 4 a shows representative theoretical curves of MSD-Δt plots for simple Brownian diffusion, directed diffusion, and confined-hop diffusion, with the same microscopic diffusion coefficient.
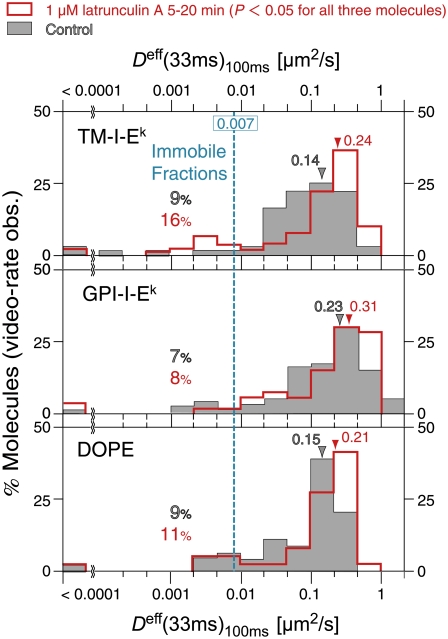
Firstly, any fluorescent spot exhibiting a diffusion coefficient in a 100-ms time-window (Deff(33ms)100ms) <0.007 μm2/s was classified into the immobile mode in this experiment, in the sense that it cannot be distinguished from the immobilized probe on the coverslip. The value of 0.007 μm2/s was selected as the lowest detectable limit for Deff(33ms)100ms, because it was a spot exhibiting the top 2.5 percentile value in the distribution of the nominal Deff(33ms)100ms in the range below 0.009 μm2/s, which the Alexa594-Fab or Cy3-peptide attached to the cover glass exhibited (Fig. 5 a, top). The fraction classified as the immobile mode was in the range of 3–9% for all of the molecules studied here. These immobile probes might be the probes that are bound to the cell surface nonspecifically.
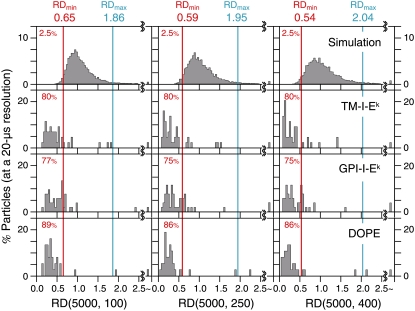
Next, the mode-of-motion classification was carried out, but only for trajectories that were classified into the mobile mode. This method employs the parameter RD(N, n), which describes the long-term deviation of the actual MSD(N, n) at the time nδt (N = the full length in the number of image frames in a trajectory; n = the number of frames used for the analysis in the MSD-Δt plot, δt = duration of each frame) from the expected MSD based on the initial slope of the MSD-Δt plot, 4D2-4nδt, i.e., RD(N, n) = MSD(N, n)/[4D2-4nδt] (Fig. 4 a and see Materials and Methods). In the case of molecules undergoing simple Brownian diffusion, the average value of RD(N, n) is 1, although the value for each individual trajectory of Brownian molecules would show a statistical spread at ∼1. Using Monte Carlo simulation, we generated 5000 90-step trajectories (here N is 90), and the ideal statistical spread of the RD(90, 30) was obtained, as shown in Fig. 4 b (top). For the classification of the trajectories into different diffusion modes, RD(90, 30) values that gave the 2.5 percentile of particles from both ends of the distribution, referred to as RDmin(90, 30) and RDmax(90, 30), were determined, as described by Kusumi et al. (16) (shown in Fig. 4 b by vertical red and cyan lines, respectively). When the trajectory of an experimental molecule shows an RD value between RDmin and RDmax, it is classified into the simple Brownian diffusion mode, and when RD > RDmax or RD < RDmin, it is classified into the directed or confined-hop diffusion mode, respectively. Greater than 74% of the TM-I-Ek, GPI-I-Ek, and DOPE trajectories were classified into the simple Brownian diffusion mode, irrespective of the probes employed here (Fig. 4 b). These results were consistent with the results reported by Vrljic et al. (1,2) and Nishimura et al. (3), but not with those reported by Schütz et al. (36). None of the trajectories exhibited confinement within φ ∼ 80 nm domains, as reported by Lenne et al. (38) and Wenger et al. (39), but the video-rate (a frame rate at once every 33 ms) might be too slow to detect transient confinement for several 10s of milliseconds.
The Alexa594-Fab and Cy3-peptide probes display similar diffusion behaviors
Since the majority of the mobile molecules exhibited apparent simple Brownian diffusion at video rate (Fig. 4 b), the motion of each molecule observed at this frame rate can be characterized by a single effective diffusion coefficient. The distributions of the effective diffusion coefficients, Deff(33ms)100ms, for the median values TM-I-Ek and GPI-I-Ek labeled with Alexa594-Fab or Cy3-peptide, as well as the distributions for these probes bound to the glass surface (control for immobile molecules), are shown in Fig. 5 a. The median values for TM-I-Ek and GPI-I-Ek with Alexa-Fab were 0.14 and 0.23 μm2/s, respectively, and those with the Cy3-peptide were 0.15 and 0.23 μm2/s, respectively (excluding the immobile fraction, defined as the spots with Deff(33ms)100ms <0.007 μm2/s; see the cyan line in Fig. 5 a). There were no significant differences in these diffusion coefficients of TM-I-Ek and GPI-I-Ek between the two different labels (Alexa594-Fab and Cy3-peptide). These results, along with the results of the ensemble-averaged MSD-Δt plots for the Alexa594-Fab and Cy3-peptide probes (Fig. 3 b), indicate that both of these probes can be employed to study the dynamics of TM-I-Ek and GPI-I-Ek. Since the labeling efficiency of Alexa594-Fab is much better than that of Cy3-peptide, we performed all of the following experiments using Alexa594-Fab probes.
Video-rate SPT observations of gold-tagged TM-I-Ek, GPI-I-Ek, and DOPE
Next, we intended to observe the diffusion of these molecules at a much higher frame rate to examine the possibility of anomalous diffusion, such as hop diffusion or confinement within ∼80-nm domains for tens of milliseconds (5,6,14,19). Since achieving higher time resolutions with fluorescent probes is difficult due to the problem of low signal/noise ratios, we carried out single-particle tracking (SPT) with 40-nm-φ colloidal gold probes (see Fig. 2 and Materials and Methods).
We first observed gold-labeled molecules at video rate, to compare their diffusions with those of fluorescently-labeled molecules. Fig. 3 a (bottom) shows typical trajectories of gold-labeled TM-I-Ek, GPI-I-Ek, and DOPE, observed at a 33-ms resolution using SPT. No gold-tagged molecule was classified into the immobile mode. A statistical analysis classified almost all of the trajectories of the gold-tagged molecules, as well as those of the fluorescently-labeled molecules, into the simple Brownian diffusion mode (Fig. 4 b, bottom). The distributions of Deff(33ms)100ms for these molecules are shown in Fig. 5 b (black open bars; compare those with gray bars, representing data with the Alexa-Fab probe). The median values of the diffusion coefficients of gold-labeled TM-I-Ek, GPI-I-Ek, and DOPE in a 100-ms time-window (Deff(33ms)100ms) were 0.044, 0.032, and 0.061 μm2/s, respectively, which are 3–7-fold smaller than those of the Alexa594-labeled molecules. These results suggest that the diffusion of gold-labeled molecules may be slowed, due to steric hindrance and/or the crosslinking effect of gold probes attached to these molecules.
Previously, in the NRK cell membrane using the same Cy3-DOPE and gold-tagged DOPE, Fujiwara et al. (5) found that these probes gave the same diffusion coefficients, as long as the time-window for evaluating the diffusion coefficient was <100 ms. This difference is probably due to the very small compartment size in the CHO cell membrane (40 vs. 230 nm in NRK cells), as described below. Gold-labeled molecules collide with the compartment boundaries ∼30-fold ([230/40]2) more often in CHO cells than in NRK cells, which is likely to make the Deff(33ms)100ms of these gold-labeled molecules very sensitive to low levels of gold-induced crosslinking.
High-speed SPT with gold-tags revealed the hop diffusion of TM-I-Ek, GPI-I-Ek, and DOPE
The movements of gold-tagged TM-I-Ek, GPI-I-Ek, and DOPE were examined at a time resolution of 20 μs (at 50,000 frames/s), an enhancement by a factor of 1667 from the normal video rate (once every 33 ms). Their typical trajectories, shown in Fig. 6 a, suggest that all of these molecules undergo hop diffusion in the plasma membrane. In Fig. 6 a, each color indicates plausible confinement within a compartment. Individual plausible compartments were identified by software developed in our laboratory as well as by visual examination (5,6,19). The residency time for each compartment is indicated in the same color.
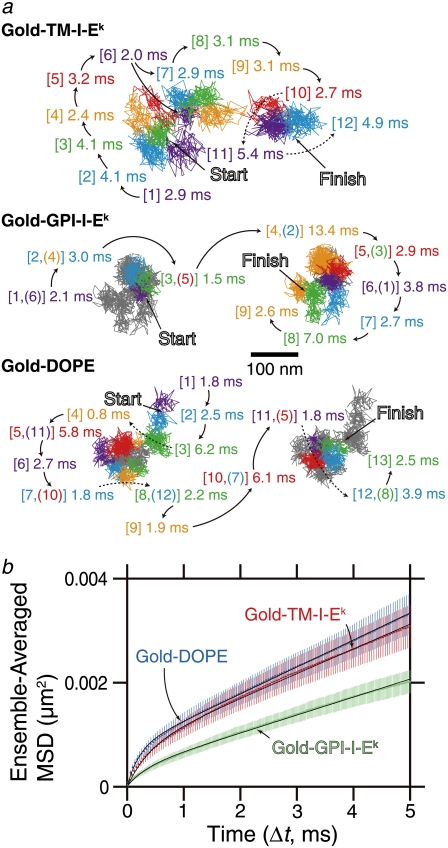
FIGURE 6.
TM-I-Ek, GPI-I-Ek, and DOPE, tagged with gold particles and observed at a 20-μs resolution, exhibited hop diffusion. (a) Representative 40-ms trajectories (containing 2000 determined coordinates) of TM-I-Ek, GPI-I-Ek, and DOPE. Each color (purple, cyan, green, orange, red, and then back to purple and so on; this sequence was always used in this article) represents a plausible compartment detected by computer software (5). The residency time within each compartment is shown and is color-coordinated with respective compartment. The numbers in the square brackets indicate the order of the compartments the molecules entered. In the Gold-GPI-I-Ek and Gold-DOPE trajectories, due to repeated entrance into the same compartments, the continuous trajectories of GPI-I-Ek and DOPE were shown in two separate trajectories placed side-by-side for the viewability, whereas the overall trajectories except for the portions shown in colored trajectories are displayed in gray lines. When repeated passages across the same compartment took place in these trajectories, the compartment is numbered by two numbers. These results suggest that the compartments move slightly even during 2–20 ms. (b) Ensemble-averaged MSD-Δt plots. Mean-square displacement (MSD) of TM-I-Ek, GPI-I-Ek, and DOPE tagged with gold particles observed at a 20-μs resolution, averaged over all copies of molecules examined here. (Red) TM-I-Ek. (Green) GPI-I-Ek. (Blue) DOPE. The MSD corrected for the single-step noise was obtained as described in the caption to Fig. 3 b. The error bar for each ensemble-averaged MSD(Δt) represents the standard error. These plots were fitted with theoretical curves representing hop diffusion over equally spaced, semipermeable barriers (52). For further details of the analysis, see Suzuki et al. (19). For the plots for TM-I-Ek and DOPE, due to the overlap of the points, only half of the experimentally obtained points for these molecules are alternatingly plotted. The smaller long-term slope for GPI-I-Ek is likely due to the greater tendency of GPI-I-Ek clustering beneath the gold-particle probes (see the text).
Fig. 6 b shows the ensemble-averaged MSD-Δt plots of the gold-tagged molecules, on a timescale of 5 ms (out of 100-ms trajectory or 250 frames out of 5000 frames). In this display, it is clear that the MSD-Δt curve is not linear, particularly in the range of 0–0.5 ms, indicating that these molecules undergo anomalous diffusion. These plots should be compared with those in Fig. 3 b, where the first point is at 66 ms (the first point in the MSD-Δt curve is removed, because all of the high-frequency noise components are accumulated in the first point in the MSD-Δt plot). Note that in the MSD-Δt plots shown in Fig. 6 b, the main curvature is seen between 0 and 0.5 ms, and the MSD value at 0.5 ms is only 0.0004–0.001 μm2.
These ensemble-averaged MSD-Δt plots were fitted with a theoretical equation representing hop diffusion over equally spaced, semipermeable barriers (52). The fit parameters included L, Dmicro, and DMACRO (due to the lack of time resolution or insufficient frame rate, even at 50,000 frames per second for the compartment size of ∼40 nm, the correct Dmicro cannot be obtained). For further details of the analysis, see Classification of the Mode of Diffusion, Calculation of the Diffusion Coefficient, and Analysis of High-Speed SPT Trajectories. The following hop parameters were obtained from this fitting. For TM-I-Ek: L = 52 nm and DMACRO = 0.12 μm2/s. For GPI-I-Ek: L = 36 nm and DMACRO = 0.086 μm2/s. For DOPE, L = 50 nm and DMACRO = 0.13 μm2/s. These should be compared with the data shown later in Fig. 8 and Table 2. It is interesting to find that DMACRO for GPI-I-Ek are smaller than that for TM-I-Ek or DOPE. Since SFMT with fluorescent probes, which do not induce aggregation of the target molecules, exhibited more or less similar DMACRO for all of the three molecules (Figs. 3 and 5; also see Table 2), this suggests the readiness of GPI-I-Ek for being crosslinked with gold particles. Therefore, although DMACRO for GPI-I-Ek is slightly greater than that for TM-I-Ek or DOPE, GPI-I-Ek molecules might have greater tendency to associate with each other.
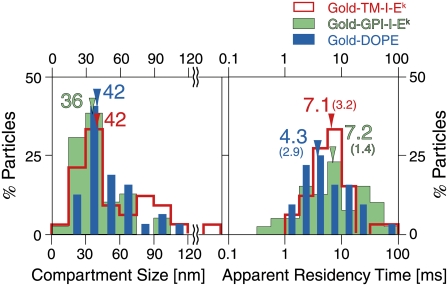
FIGURE 8.
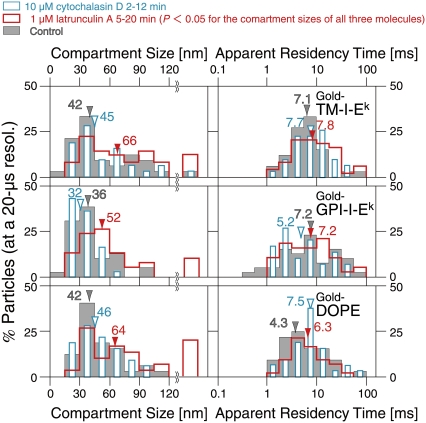
At a 20-μs resolution (with gold probes), TM-I-Ek, GPI-I-Ek, and DOPE exhibited rapid hop diffusion between ∼40-nm compartments with a median dwell time of 4–7 ms in each compartment. The distributions of compartment sizes and the apparent residency times for TM-I-Ek (red), GPI-I-Ek (green), and DOPE (blue). The compartment size L was obtained by fitting the MSD-Δt plot for each trajectory with a theoretical curve for hop diffusion (52), and the residency time was calculated from L and DMACRO, also obtained from the curve fitting (L2/4DMACRO). Color-coordinated arrows and numbers show medians of respective distributions. All three gold-particle-tagged molecules exhibited similar compartment sizes and residency times within a compartment. These residency times are prolonged due to cross-linking by gold probes. The “corrected” residency time can be evaluated by using the macroscopic diffusion rate of a fluorescently-tagged molecule (median value) and the compartment size obtained by a gold-tagged molecule (median value), and is listed in Table 2. The numbers in the parentheses indicate the “corrected” residency times.
TABLE 2.
Compartment size, residency time, effective macroscopic diffusion coefficient (Deff(33ms)100ms) (median (mean ± SE)), and probability of passing a barrier (PP)
| SPT
|
SFMT
|
||||||
|---|---|---|---|---|---|---|---|
| Drug | Confined-hop (%) | Compartment size (nm) | Deff(20μs)20ms (μm2/s) | Deff(33μs)100ms (μm2/s) | Deff(33ms)100ms (μm2/s) | Corrected residency time (τ, ms)§ | PP‖ |
| TM-I-Ek | |||||||
| — | 80 | 42 | 0.045 | 0.044 | 0.14 | 3.2 | 0.0087 |
| (53 ± 5) | (0.090 ± 0.017) | (0.081 ± 0.012) | (0.15 ± 0.015) | ||||
| Lat-A† | 95 | 66 | 0.076 | 0.066 | 0.24 | 4.5 | 0.0096 |
| (76 ± 6) | (0.11 ± 0.019) | (0.095 ± 0.011) | (0.25 ± 0.015) | ||||
| Cyt-D‡ | 97 | 45 | 0.039 | 0.036 | — | — | — |
| (61 ± 7) | (0.11 ± 0.026) | (0.085 ± 0.019) | |||||
| GPI-I-Ek | |||||||
| — | 75 | 36 | 0.046 | 0.032 | 0.23 | 1.4 | 0.014 |
| (41 ± 3) | (0.057 ± 0.0064) | (0.040 ± 0.0053) | (0.33 ± 0.030) | ||||
| Lat-A† | 82 | 52 | 0.066 | 0.044 | 0.31 | 2.2 | 0.014 |
| (64 ± 7) | (0.13 ± 0.020) | (0.058 ± 0.0063) | (0.34 ± 0.033) | ||||
| Cyt-D‡ | 79 | 32 | 0.031 | 0.035 | — | — | — |
| (34 ± 2) | (0.047 ± 0.0086) | (0.047 ± 0.0065) | |||||
| DOPE | |||||||
| — | 86 | 42 | 0.045 | 0.061 | 0.15 | 2.9 | 0.0080 |
| (50 ± 4) | (0.095 ± 0.018) | (0.088 ± 0.019) | (0.15 ± 0.015) | ||||
| Lat-A† | 97 | 64 | 0.10 | 0.12 | 0.21 | 4.9 | 0.0074 |
| (83 ± 10) | (0.14 ± 0.028) | (0.15 ± 0.022) | (0.22 ± 0.018) | ||||
| Cyt-D‡ | 97 | 46 | 0.037 | 0.040 | — | — | — |
| (50 ± 4) | (0.073 ± 0.016) | (0.066 ± 0.015) | |||||
| Cyt-D¶ | 100 | 44 | 0.034 | 0.028 | — | — | — |
| (50 ± 4) | (0.049 ± 0.0086) | (0.042 ± 0.0085) | |||||
For SPT observations, 39–61 particles were measured, whereas for SFMT, 62–112 molecules were observed, for specimens under different conditions.
1 μM latrunculin A, 5–20 min treatment.
10 μM cytochalasin D, 2–12 min treatment.
10 μM cytochalasin D, 1–5 min treatment.
The residency time was calculated using Deff(33ms)100ms (median), obtained from SFMT observations, and the compartment size (L, median), obtained from SPT using the equation τ = L2/4Deff(33ms)100ms.
PP = RDRL/(RD(2RL−1)+1) is the probability of passing a barrier when the membrane molecules are already at the boundary (a parameter for the diffusion in one dimension), where RD = Dmicro/DMACRO and RL = I/L. I is the average distance traveled per frame, which is = (2Dmicro × 20 μs)1/2 (52). As Dmicro, we used 8 μm2/s for DOPE (5,6) and GPI-I-Ek, and 6 μm2/s for TM-I-Ek ((19); see text). Fujiwara et al. (5) and Murase et al. (6) showed that Dmicro for DOPE inside a compartment is the same for NRK and FRSK cells, which have very different compartment sizes, suggesting that the Dmicro values in any cell membrane are probably similar to each other. As DMACRO, we employed Deff(33ms)100ms.
A statistical classification of each individual trajectory into the categories of simple Brownian, confined-hop, and directed diffusion was carried out, as described in Fig. 4 and the related text, and shown in Fig. 7. Here all of the analyzed trajectories are 5000 frames' long (100 ms), and for each trajectory, MSD-Δt was calculated from all of the possible combinations of any two points in the trajectories, to produce MSD-Δt for the full timescales of 2, 5, and 8 ms (100, 250, and 400 points). These results indicated that 75–89% of the TM-I-Ek, GPI-I-Ek, and DOPE molecules undergo confined-hop diffusion, which was totally missed in the observations made at video rate.
FIGURE 7.
The distributions of RD(N, n) for TM-I-Ek, GPI-I-Ek, and DOPE tagged with gold particles observed at a 20-μs resolution. The distributions of RD(N, n) for TM-I-Ek, GPI-I-Ek, and DOPE (second to bottom rows) are quite different from those expected from simple Brownian particles (generated by Monte Carlo stimulations, top row). Here, N was fixed at 5000, and n was varied (100, 250, and 400 steps, corresponding to analysis time windows of 2, 5, and 8 ms, respectively). For the classification of the trajectories into different diffusion modes, RD(5000, n) values that gave the 2.5 percentile of the particles from both ends of the distribution for simulated simple Brownian trajectories, referred to as RDmin(5000, n) and RDmax(5000, n), shown by red and cyan vertical lines in all panels, respectively, were used (16). When a particle exhibited an RD(5000, n) smaller than RDmin(5000, n), its trajectory was classified into the confined-hop diffusion mode. The percent number (red) to the left of the red line indicated the fraction of trajectories classified into the confined-hop diffusion mode, showing that the majority of the TM-I-Ek, GPI-I-Ek, and DOPE trajectories are classified into the confined-hop diffusion mode.
The MSD-Δt plot for each trajectory (between 0 and 5 ms) was fitted with a theoretical equation representing hop diffusion over equally spaced, semipermeable barriers (52), as described above. The compartment size L and the macroscopic diffusion coefficient were the fit parameters, and the average residency time over a single trajectory was calculated from L and DMACRO (L2/4DMACRO).
Fig. 8 shows the distributions of the compartment sizes and the residency times within each compartment, determined for each trajectory. There were no significant differences in the compartment sizes sensed by the three molecules (medians, ∼40 nm). The median residency times were 4–7 ms, but note that these values are for gold-tagged molecules, which might be crosslinked by the gold probes. The correct values for the ensemble-averaged residency times of these three molecules were estimated in the following manner (the correct values for each individual molecule could not be determined).
Recently, Morone et al. (27) succeeded in directly determining the mesh size of the membrane skeleton on the cytoplasmic surface of the plasma membrane, by determining the three-dimensional structure of the membrane skeleton using electron tomography. They found that the compartment sizes determined by the high-speed diffusion measurements of gold-tagged molecules (crosslinked at various degrees, depending on the molecule under investigation) agreed well with the mesh size of the membrane skeleton on the cytoplasmic surface of the plasma membrane. From this agreement, it can be deduced that high-speed SPT of gold probes provides the correct compartment size. However, SPT may not give the correct hop rate, due to the crosslinking by gold particles. In contrast, Alexa594-labeled molecules would give more correct macroscopic diffusion rates over many compartments, whereas the low time resolution of SFMT does not allow direct observations of the hop events and the compartment size. Therefore, the correct hop rate (averaged value) can be estimated using the median Deff(33ms)100ms of Alexa594-labeled molecules and the median compartment sizes obtained by using gold-labeled molecules. The median residency times are 3.2 ms for TM-I-Ek ([0.042 μm]2/4 × 0.14 μm2/s), 1.4 ms for GPI-I-Ek, and 2.9 ms for DOPE (indicated in parentheses in Fig. 8 and listed in Table 2). In summary, all of the molecules we examined here exhibited rapid hop diffusion between ∼40-nm compartments, with a dwell time of 1–3 ms in each compartment on average. Confinement within φ ∼ 80 nm domains for several 10s of milliseconds was never observed for any single molecule inspected in this study.
A useful parameter, which can be calculated from DMACRO, Dmicro, and the compartment size, as described by Powles et al. (52) and Murase et al. (6), is the probability of passing a barrier when the membrane molecules are already at the boundary (PP). This shows how easily a molecule in the plasma membrane at a compartment boundary can pass the barrier. As Dmicro, we used 8 μm2/s for DOPE (5,6) and GPI-I-Ek (assuming that its microscopic diffusion coefficient is the same as that for the phospholipid DOPE), and 6 μm2/s for TM-I-Ek (based on 4.5–6 μm2/s by (19) for G-protein-coupled receptor, which contains seven transmembrane domains, and employing the upper-limit value for TM-I-Ek, because it has only two transmembrane domains in the dimeric structure). The PP value of GPI-I-Ek was approximately twofold larger than those for DOPE and TM-I-Ek (Table 2). In other words, GPI-I-Ek tends to pass through the barrier two-times more readily than TM-I-Ek and DOPE. The mechanism underlying this greater hop probability for the GPI-anchored protein is unknown.
The actin-based membrane skeleton is responsible for cell membrane compartmentalization
We have examined the effects of drugs that affect actin organization on the diffusion of TM-I-Ek, GPI-I-Ek, and DOPE in the plasma membrane. CHO cells were incubated in the observation medium containing latrunculin A (final 1 μM) on the microscope stage at 37°C for 5 min. To avoid the secondary and/or large-scale drug effects, microscope observations were completed within 20 min after the drug addition. The latrunculin A treatment induced slight decreases in the rhodamine-stainable actin filaments visible by fluorescence microscopy (see our Supplementary Material, Data S1, Fig. S1, row b). Fig. 9 (red open bars) shows the distributions of the compartment sizes and the apparent residency times within each compartment, determined for each high-speed SPT trajectory of TM-I-Ek, GPI-I-Ek, and DOPE after latrunculin A treatment. Under these conditions, larger compartments appeared, with the median diameter increased by a factor of ∼1.5, or the area by a factor of ∼2.3. Meanwhile, the apparent residency times (called “apparent” due to the use of gold particle probes for high-speed SPT, which would crosslink the target molecules, prolonging the residency time) were not affected at a statistically meaningful level.
FIGURE 9.
The distributions of the compartment sizes (left) and the residency times (right) after latrunculin A or cytochalasin D treatment. Latrunculin A (final 1 μM, observed between 5 and 20 min, red open bars) or cytochalasin D (final 10 μM, observed between 2 and 12 min, cyan open bars) was added to the cultured cells on the microscope stage (control: gray bars). Arrowheads indicate median values. Upon the latrunculin A treatment, larger compartments appeared, with the median diameter increased by a factor of ∼1.5, or the area by a factor of ∼2.3 (the Wilcoxon statistical test result, comparing treated and untreated cells; p < 0.05). Meanwhile, the apparent residency times were not affected at a statistically meaningful level. However, the treatment with cytochalasin D had no effect (all p > 0.05), as reported previously using slower observation rates (1). These results indicate the necessity for caution in interpreting the pharmacological data.
Under the same conditions, the macroscopic diffusion coefficients for fluorescently-tagged molecules were determined by SFMT at video rate (Fig. 10). Deff(33ms)100ms (macroscopic diffusion coefficient) was increased by 30–70% (p < 0.05; Fig. 10, red open bars). From these observations, the averages of the corrected residency times and PP (probability of passing the barrier) were calculated, as summarized in Table 2. The residency times increased, but the PP remained about the same, suggesting that the latrunculin-induced increases of the macroscopic diffusion are due to the expansion of the compartments, rather than the increased probability of passing the compartment boundaries (the increases of the residency times would also probably be due to the expanded compartments, which would decrease the frequency of the molecule reaching the compartment boundaries, rather than the increase in the probability of passing the fence).
FIGURE 10.
Latrunculin A treatment increased the effective macroscopic diffusion coefficients, Deff(33ms)100ms, of TM-I-Ek, GPI-I-Ek, and DOPE, tagged with Alexa594-Fab (red open bars, after the treatment; gray bars, before the treatment). All of the observations were carried out between 5 and 20 min after the addition of 1 μM latrunculin A. Color-coordinated arrows and numbers show medians of the respective Deff(33ms)100ms distributions. The cyan line represents the lowest detectable mobile Deff(33ms)100ms of 0.007 μm2/s (defined in Fig. 5 a). Color-coordinated percent values shown to the left of the cyan line in all panels represent the immobile fraction. Latrunculin A treatment increased the effective macroscopic diffusion coefficients of all three molecules (the Wilcoxon statistical test result between treated and untreated cells; p < 0.05).
The effect of cytochalasin D on the diffusion of TM-I-Ek, GPI-I-Ek, and DOPE in CHO cells
We next examined the effects of another drug, cytochalasin D. Its mode of action on actin organization is different from that of latrunculin A. While latrunculin A binds to actin monomers and blocks their polymerization, resulting in the amount of actin filaments (53,54), cytochalasin D at micromolar concentrations binds to both the barbed and pointed ends of actin filaments and prevents their further polymerization, as well as their interactions with other barbed-end binding proteins (55).
While the treatment with 1 μM latrunculin A for 5–20 min (all of the observations were conducted within 20 min after latrunculin addition) strongly affected the molecular motion, the treatment with 1 and 10 μM cytochalasin D for 2–12 min influenced neither the compartment size nor the apparent residency time, under the conditions where the cells did not round up, but the number of stress fibers was decreased and actin clusters were formed (Fig. 9, cyan open bars, Data S1, Fig. S1 rows c and d, and Table 2). These results, obtained at a 20-μs resolution, are consistent with the report by Vrljic et al. (1), showing no influence of cytochalasin D (for 30 min or 60 min at 37°C with 1, 10, and 40 μM) on the movement of TM-I-Ek and GPI-I-Ek at a 100-ms resolution.
DISCUSSION
We have observed the diffusion of single molecules of the transmembrane TM-I-Ek and its GPI-anchored modified form GPI-I-Ek, using high-speed SPT with gold probes and SFMT with fluorescent probes. The results obtained in this study are compared with the diffusion data of the same molecules in the same cell type (CHO cells), previously reported by Vrljic et al. (1,2) and Nishimura et al. (3).
SFMT observations at low frame rates
We found that the average Deff(33ms)100ms values for fluorescently-labeled TM-I-Ek, GPI-I-Ek, and DOPE at 37°C are 0.15, 0.33, and 0.15 μm2/s, respectively (the medians are 0.14, 0.23, and 0.15 μm2/s, respectively). Vrljic et al. (1) reported that the mean diffusion coefficients of TM-I-Ek and GPI-I-Ek were 0.18 and 0.22 μm2/s, respectively, at a 100-ms resolution at 22°C. Nishimura et al. (3) reported them to be 0.59 and 1.1 μm2/s, respectively, at a 15.4-ms resolution at 37°C. The diffusion coefficients of MHC class II proteins and GPI-anchored proteins reported previously are summarized in Table 1. The diffusion coefficients of transmembrane MHC class II proteins exhibited broad distributions of 0.13 × 10−4–0.59 μm2/s. In addition, the reported diffusion coefficients of GPI-linked proteins are also broadly distributed (0.0035–1.1 μm2/s). The recent results reported by Lenne et al. ((38); ∼1.1 μm2/s) and Nishimura et al. ((3); 1.1 μm2/s) are the largest in Table 1, whereas the values found in this study lie in the middle of these distributions. The FCS used by Lenne et al. (38) might be quite insensitive to slowly-diffusing or immobile molecules, and thus the reported data might be skewed toward fast-diffusing species (D > 0.1 μm2/s; for a review, see (56)). Meanwhile, Vrljic et al. (1) and Nishimura et al. (3) measured Deff(100ms)50–250ms and Deff(15.4ms)15.4ms, respectively, which might be sensitive to high-frequency noise components (see the Supplementary Material text 1 of (19)). In addition, Vrljic et al. (2) noted that the diffusion coefficients slightly depended on the fetal bovine serum used to culture the CHO cells (see the Supplementary Material Fig. S1 of (2)), which might partially explain these differences. Accordingly, it is concluded that the effective diffusion coefficients of TM-I-Ek and GPI-I-Ek found here are in general agreement with the data presented by Vrljic et al. (1) and Nishimura et al. (3).
We found that GPI-I-Ek diffused 1.6-fold faster than TM-I-Ek (p < 0.05, in the Wilcoxon test; Fig. 5 a), in agreement with the previous observations (1,3,30–34). Meanwhile, Shvartsman et al. (37) found the diffusion coefficient measured by FRAP for the GPI-linked modified form of influenza hemagglutinin was slightly smaller than that for the native transmembrane form. However, a simple comparison of our results with the data reported by Shvartsman et al. (37) cannot be done, because the native transmembrane hemagglutinin is in a trimeric form, with raft-associating properties.
In the following, we address the three key questions we posed in the introduction of this report.
Do GPI-anchored proteins actually undergo hop diffusion if they are observed at higher frame rates?
High-speed SPT at a 20-μs resolution, with the aid of SFMT at video rate, revealed that all three of the molecules examined here, TM-I-Ek, GPI-I-Ek, and DOPE, undergo rapid hop diffusion between 40-nm compartments, with an average dwell time of 1–3 ms in each compartment in CHO cells. However, these results are at variance with the data published by Wieser et al. (35). They observed a GPI-anchored protein, CD59, labeled with Alexa647-Fab in T24 cells using SFMT. Their MSD-Δt plots contained only six points on the timescale of 0–6 ms, whereas we have 250 points on the timescale of 0–5 ms (Fig. 6 b). They stated that the MSD-Δt plot for CD59, extrapolated to time 0 from the linear region, gave the y intercept of ∼0, and concluded that CD59 intrinsically undergoes slow simple Brownian diffusion. The data in Fig. 6 b suggest that it would be very difficult to find the correct y intercept with only six points, given the large single-molecule tracking errors (see the error bars in Fig. 6 b).
Does GPI-I-Ek and not TM-I-Ek exhibit confinement within 80-nm or 700-nm domains for several 10s of milliseconds or longer?
Previously, Schütz et al. (36), as well as Lenne et al. (38) and Wenger et al. (39), suggested that raft-associating molecules exhibit confinement within 700-nm (36) and 80-nm domains (38,39) for several 10s of milliseconds or longer. Therefore, in this study, we paid special attention to whether we could find confinement with GPI-I-Ek, but not with TM-I-Ek. If such confinement occurs, then it should be easily detectable with our time resolution of 20 μs, because the trajectory should contain stationary periods over 1000 image frames, and the precision of our determination of the particle's coordinates is sufficiently high (16 nm). However, we have never seen such a trajectory in our SPT observations. Furthermore, we failed to see any immobilized particles (throughout the observation period of 100 ms).
Instead, we found that virtually all of the molecules we observed undergo hop diffusion, indicating that the entire plasma membrane of the CHO cell is parceled up into apposed domains of ∼40 nm, with regard to the translational diffusion of GPI-I-Ek, TM-I-Ek, and DOPE. These molecules undergo short-term confined diffusion within these 40-nm compartments for 1–3 ms on average, and long-term hop diffusion between these compartments, and thus undergo macroscopic diffusion. Therefore, such macroscopic diffusion was detected in observations with slow frame rates as slow simple Brownian diffusion, characterized by an effective macroscopic diffusion coefficient of 0.14–0.23 μm2/s.
The residency times, compartment sizes, and probabilities of passing barrier (PP) of GPI-anchored proteins are similar to those found for transmembrane proteins and DOPE (summarized in Table 2). Given that ∼35–50% of GPI-I-Ek, ∼5–25% of TM-I-Ek, and nearly 0% of DOPE were found in the Triton X-100-resistant fractions (1,57,58), these results suggest that either the raft association affects the diffusion of membrane molecules only slightly or the raft domain might be very small and/or short-lived.
Does the treatment of cells with drugs that affect actin polymerization, such as cytochalasin D and latrunculin A, induce changes in the diffusion of GPI-anchored proteins?
Vrljic et al. (1,2) and Nishimura et al. (3) previously failed to detect any changes in the diffusion characteristics, after the cells were treated with cytochalasin D. Furthermore, Frick et al. (59) and Schmidt and Nichols (60) found that the disruption of the actin cytoskeleton by treating the cells with latrunculin A, gelsolin, or siRNA of spectrin had no detectable effect on the diffusion of membrane molecules by FRAP.
Therefore, in this investigation, the effects of both latrunculin A and cytochalasin D on the translational diffusion of GPI-I-Ek, TM-I-Ek, and DOPE were examined. Consistent with the results by Vrljic et al. (1) and Nishimura et al. (3), cytochalasin D treatments, under the conditions where the global cell morphology is not seriously affected, did not induce any changes in the diffusion of the three molecules examined here. In contrast, in the high-speed SPT experiments by Murase et al. (6), cytochalasin D greatly affected the compartment size in the fetal rat skin keratinocyte cells in culture.
The effect of cytochalasin D on the diffusion of membrane molecules is complex, probably because it depends on the level of actin expression as well as the feedback reactions of the cell (summarized in the On-line Supporting Information of (20,44), and Supplementary Materials of (19)). The cell could react to the loss of the links between the plasma membrane and the actin filaments, due to the barbed-end capping by cytochalasin D, by generating more actin filaments. This might compensate for the initial effect of cytochalasin D. Such compensation effects should always be considered in any study modulating actin filaments (59,60). Therefore, these results indicate that due caution is required for interpreting the pharmacological data.
The cell treatment with another actin-depolymerizing drug, latrunculin A, increased the compartment size for all three molecules examined in this study, without affecting the probability of passing the barrier when the membrane molecule was already in the boundary area between the compartments. This suggested that the actin-based membrane skeleton is responsible for the partitioning of the plasma membrane for the translational diffusion of both transmembrane and GPI-anchored proteins. This explains the ∼50% increase in the median macroscopic diffusion coefficient after the latrunculin treatment for all three molecules. Furthermore, it should be emphasized that such changes are observable only under well-controlled conditions: 1 μM latrunculin A and only during 5–20 min after the drug addition. Milder treatments had much milder effects, whereas harsher treatments would elicit compensating reactions of the cell or harm the cells.
Small changes in the macroscopic diffusion coefficient, such as a ∼50% increase in its median value, would be difficult to detect with normal SFMT at low frame rates, with a few observed points in the MSD-Δt plot, or with techniques observing ensemble-averaged values. In this study, SFMT at video rate for 1 s (30 observed points in the MSD-Δt plot, see Fig. 3 b) was combined with high-speed SPT. This combination allows sensitive detection of the changes in the diffusion of membrane molecules, upon drug addition.
In conclusion, all three of the molecules, GPI-I-Ek, TM-I-Ek, and DOPE, undergo hop diffusion in the plasma membrane, which is sensitive to changes in the actin-based membrane skeleton. The compartment size for these molecules is the same (∼40 nm). This result supports the fence and picket models. Meanwhile, the residency time for GPI-I-Ek is 1.4 ms (median), which is approximately twofold shorter than those for TM-I-Ek (3.2 ms) and DOPE (2.9 ms). Namely, GPI-I-Ek hops faster than TM-I-Ek or DOPE. The reason for the faster hop rate for GPI-I-Ek is still unknown.
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Acknowledgments
We thank Profs. Harden M. McConnell, W. E. Moerner, and Mark M. Davis for providing the CHO cells expressing TM-I-Ek and GPI-I-Ek and for helpful discussions, and Ms. J. Kondo for preparing the figures.
Editor: Gerard Marriott.
References
- 1.Vrljic, M., S. Y. Nishimura, S. Brasselet, W. E. Moerner, and H. M. McConnell. 2002. Translational diffusion of individual class II MHC membrane proteins in cells. Biophys. J. 83:2681–2692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Vrljic, M., S. Y. Nishimura, W. E. Moerner, and H. M. McConnell. 2005. Cholesterol depletion suppresses the translational diffusion of class II major histocompatibility complex proteins in the plasma membrane. Biophys. J. 88:334–347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Nishimura, S. Y., M. Vrljic, L. O. Klein, H. M. McConnell, and W. E. Moerner. 2006. Cholesterol depletion induces solid-like regions in the plasma membrane. Biophys. J. 90:927–938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kusumi, A., and Y. Sako. 1996. Cell surface organization by the membrane skeleton. Curr. Opin. Cell Biol. 8:566–574. [DOI] [PubMed] [Google Scholar]
- 5.Fujiwara, T., K. Ritchie, H. Murakoshi, K. Jacobson, and A. Kusumi. 2002. Phospholipids undergo hop diffusion in compartmentalized cell membrane. J. Cell Biol. 157:1071–1081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Murase, K., T. Fujiwara, Y. Umemura, K. Suzuki, R. Iino, H. Yamashita, M. Saito, H. Murakoshi, K. Ritchie, and A. Kusumi. 2004. Ultrafine membrane compartments for molecular diffusion as revealed by single molecule techniques. Biophys. J. 86:4075–4093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sheetz, M. P. 1983. Membrane skeletal dynamics: role in modulation of red cell deformability, mobility of transmembrane proteins, and shape. Semin. Hematol. 20:175–188. [PubMed] [Google Scholar]
- 8.Tsuji, A., K. Kawasaki, S. Ohnishi, H. Merkle, and A. Kusumi. 1988. Regulation of band 3 mobilities in erythrocyte ghost membranes by protein association and cytoskeletal meshwork. Biochemistry. 27:7447–7452. [DOI] [PubMed] [Google Scholar]
- 9.Tsuji, A., and S. Ohnishi. 1986. Restriction of the lateral motion of band 3 in the erythrocyte membrane by the cytoskeletal network: dependence on spectrin association state. Biochemistry. 25:6133–6139. [DOI] [PubMed] [Google Scholar]
- 10.Saxton, M. J. 1989. The spectrin network as a barrier to lateral diffusion in erythrocytes. A percolation analysis. Biophys. J. 55:21–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Saxton, M. J. 1990. The membrane skeleton of erythrocytes. A percolation model. Biophys. J. 57:1167–1177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sako, Y., and A. Kusumi. 1995. Barriers for lateral diffusion of transferrin receptor in the plasma membrane as characterized by receptor dragging by laser tweezers: fence versus tether. J. Cell Biol. 129:1559–1574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sako, Y., and A. Kusumi. 1994. Compartmentalized structure of the plasma membrane for receptor movements as revealed by a nanometer-level motion analysis. J. Cell Biol. 125:1251–1264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Tomishige, M., Y. Sako, and A. Kusumi. 1998. Regulation mechanism of the lateral diffusion of band 3 in erythrocyte membranes by the membrane skeleton. J. Cell Biol. 142:989–1000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Jacobson, K., E. D. Sheets, and R. Simson. 1995. Revisiting the fluid mosaic model of membranes. Science. 268:1441–1442. [DOI] [PubMed] [Google Scholar]
- 16.Kusumi, A., Y. Sako, and M. Yamamoto. 1993. Confined lateral diffusion of membrane receptors as studied by single particle tracking (nanovid microscopy). Effects of calcium-induced differentiation in cultured epithelial cells. Biophys. J. 65:2021–2040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Saxton, M. J., and K. Jacobson. 1997. Single-particle tracking: applications to membrane dynamics. Annu. Rev. Biophys. Biomol. Struct. 26:373–399. [DOI] [PubMed] [Google Scholar]
- 18.Sako, Y., A. Nagafuchi, S. Tsukita, M. Takeichi, and A. Kusumi. 1998. Cytoplasmic regulation of the movement of E-cadherin on the free cell surface as studied by optical tweezers and single particle tracking: corralling and tethering by the membrane skeleton. J. Cell Biol. 140:1227–1240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Suzuki, K., K. Ritchie, E. Kajikawa, T. Fujiwara, and A. Kusumi. 2005. Rapid hop diffusion of a G-protein-coupled receptor in the plasma membrane as revealed by single-molecule techniques. Biophys. J. 88:3659–3680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kusumi, A., I. Koyama-Honda, and K. Suzuki. 2004. Molecular dynamics and interactions for creation of stimulation-induced stabilized rafts from small unstable steady-state rafts. Traffic. 5:213–230. [DOI] [PubMed] [Google Scholar]
- 21.Kusumi, A., C. Nakada, K. Ritchie, K. Murase, K. Suzuki, H. Murakoshi, R. S. Kasai, J. Kondo, and T. Fujiwara. 2005. Paradigm shift of the plasma membrane concept from the two-dimensional continuum fluid to the partitioned fluid: high-speed single-molecule tracking of membrane molecules. Annu. Rev. Biophys. Biomol. Struct. 34:351–378. [DOI] [PubMed] [Google Scholar]
- 22.Dodd, T. L., D. A. Hammer, A. S. Sangani, and D. L. Koch. 1995. Numerical simulations of the effect of hydrodynamic interactions on the diffusivities of integral membrane proteins. J. Fluid Mech. 293:147–180. [Google Scholar]
- 23.Bussell, S. J., D. L. Koch, and D. A. Hammer. 1995. Effect of hydrodynamic interactions on the diffusion of integral membrane proteins: diffusion in plasma membranes. Biophys. J. 68:1836–1849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Almeida, P. F., W. L. Vaz, and T. E. Thompson. 1992. Lateral diffusion and percolation in two-phase, two-component lipid bilayers. Topology of the solid-phase domains in-plane and across the lipid bilayer. Biochemistry. 31:7198–7210. [DOI] [PubMed] [Google Scholar]
- 25.Sperotto, M. M., and O. G. Mouritsen. 1991. Monte Carlo simulation studies of lipid order parameter profiles near integral membrane proteins. Biophys. J. 59:261–270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Nakada, C., K. Ritchie, Y. Oba, M. Nakamura, Y. Hotta, R. Iino, R. S. Kasai, K. Yamaguchi, T. Fujiwara, and A. Kusumi. 2003. Accumulation of anchored proteins forms membrane diffusion barriers during neuronal polarization. Nat. Cell Biol. 5:626–632. [DOI] [PubMed] [Google Scholar]
- 27.Morone, N., T. Fujiwara, K. Murase, R. S. Kasai, H. Ike, S. Yuasa, J. Usukura, and A. Kusumi. 2006. Three-dimensional reconstruction of the membrane skeleton at the plasma membrane interface by electron tomography. J. Cell Biol. 174:851–862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Gaus, K., E. Gratton, E. P. Kable, A. S. Jones, I. Gelissen, L. Kritharides, and W. Jessup. 2003. Visualizing lipid structure and raft domains in living cells with two-photon microscopy. Proc. Natl. Acad. Sci. USA. 100:15554–15559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gaus, K., M. Rodriguez, K. R. Ruberu, I. Gelissen, T. M. Sloane, L. Kritharides, and W. Jessup. 2005. Domain-specific lipid distribution in macrophage plasma membranes. J. Lipid Res. 46:1526–1538. [DOI] [PubMed] [Google Scholar]
- 30.Ishihara, A., Y. Hou, and K. Jacobson. 1987. The Thy-1 antigen exhibits rapid lateral diffusion in the plasma membrane of rodent lymphoid cells and fibroblasts. Proc. Natl. Acad. Sci. USA. 84:1290–1293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Edidin, M., and I. Stroynowski. 1991. Differences between the lateral organization of conventional and inositol phospholipid-anchored membrane proteins. A further definition of micrometer scale membrane domains. J. Cell Biol. 112:1143–1150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zhang, F., B. Crise, B. Su, Y. Hou, J. K. Rose, A. Bothwell, and K. Jacobson. 1991. Lateral diffusion of membrane-spanning and glycosylphosphatidylinositol-linked proteins: toward establishing rules governing the lateral mobility of membrane proteins. J. Cell Biol. 115:75–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Subczynski, W. K., and A. Kusumi. 2003. Dynamics of raft molecules in the cell and artificial membranes: approaches by pulse EPR spin labeling and single molecule optical microscopy. Biochim. Biophys. Acta. 1610:231–243. [DOI] [PubMed] [Google Scholar]
- 34.Kenworthy, A. K., B. J. Nichols, C. L. Remmert, G. M. Hendrix, M. Kumar, J. Zimmerberg, and J. Lippincott-Schwartz. 2004. Dynamics of putative raft-associated proteins at the cell surface. J. Cell Biol. 165:735–746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wieser, S., M. Moertelmaier, E. Furtbauer, H. Stockinger, and G. J. Schutz. 2007. (Un)confined diffusion of CD59 in the plasma membrane determined by high-resolution single molecule microscopy. Biophys. J. 92:3719–3728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Schütz, G. J., G. Kada, V. P. Pastushenko, and H. Schindler. 2000. Properties of lipid microdomains in a muscle cell membrane visualized by single molecule microscopy. EMBO J. 19:892–901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Shvartsman, D. E., M. Kotler, R. D. Tall, M. G. Roth, and Y. I. Henis. 2003. Differently anchored influenza hemagglutinin mutants display distinct interaction dynamics with mutual rafts. J. Cell Biol. 163:879–888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lenne, P. F., L. Wawrezinieck, F. Conchonaud, O. Wurtz, A. Boned, X. J. Guo, H. Rigneault, H. T. He, and D. Marguet. 2006. Dynamic molecular confinement in the plasma membrane by microdomains and the cytoskeleton meshwork. EMBO J. 25:3245–3256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Wenger, J., F. Conchonaud, J. Dintinger, L. Wawrezinieck, T. W. Ebbesen, H. Rigneault, D. Marguet, and P. F. Lenne. 2007. Diffusion analysis within single nanometric apertures reveals the ultrafine cell membrane organization. Biophys. J. 92:913–919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.De Mey, J. 1983. Colloidal-gold probes in immunocytochemistry. In Immunocytochemistry (Practical Applications in Pathology and Biology). J. M. Polak and S. van Noorden, editors. WRIGHT PSG, Bristol, UK.
- 41.Leunissen, J. L. M., and J. R. De Mey. 1989. Preparation of gold probes. In Immuno-Gold Labeling in Cell Biology. A. J. Verkleij and J. L. M. Leunissen, editors. CRC Press, Boca Raton, FL.
- 42.Iino, R., I. Koyama, and A. Kusumi. 2001. Single molecule imaging of green fluorescent proteins in living cells: E-cadherin forms oligomers on the free cell surface. Biophys. J. 80:2667–2677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Koyama-Honda, I., K. Ritchie, T. Fujiwara, R. Iino, H. Murakoshi, R. S. Kasai, and A. Kusumi. 2005. Fluorescence imaging for monitoring the colocalization of two single molecules in living cells. Biophys. J. 88:2126–2136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Murakoshi, H., R. Iino, T. Kobayashi, T. Fujiwara, C. Ohshima, A. Yoshimura, and A. Kusumi. 2004. Single-molecule imaging analysis of Ras activation in living cells. Proc. Natl. Acad. Sci. USA. 101:7317–7322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Dickson, R. M., A. B. Cubitt, R. Y. Tsien, and W. E. Moerner. 1997. On/off blinking and switching behavior of single molecules of green fluorescent protein. Nature. 388:355–358. [DOI] [PubMed] [Google Scholar]
- 46.Gelles, J., B. J. Schnapp, and M. P. Sheetz. 1988. Tracking kinesin-driven movements with nanometer-scale precision. Nature. 331:450–453. [DOI] [PubMed] [Google Scholar]
- 47.Sheetz, M. P., S. Turney, H. Qian, and E. L. Elson. 1989. Nanometer-level analysis demonstrates that lipid flow does not drive membrane glycoprotein movements. Nature. 340:284–288. [DOI] [PubMed] [Google Scholar]
- 48.Qian, H., M. P. Sheetz, and E. L. Elson. 1991. Single particle tracking. Analysis of diffusion and flow in two-dimensional systems. Biophys. J. 60:910–921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Saxton, M. J. 1994. Anomalous diffusion due to obstacles: a Monte Carlo study. Biophys. J. 66:394–401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Saxton, M. J. 1996. Anomalous diffusion due to binding: a Monte Carlo study. Biophys. J. 70:1250–1262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Saxton, M. J. 1997. Single-particle tracking: the distribution of diffusion coefficients. Biophys. J. 72:1744–1753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Powles, J. G., M. J. D. Mallett, G. Rickayzen, and W. A. B. Evans. 1992. Exact analytic solutions for diffusion impeded by an infinite array of partially permeable barriers. Proc. R. Soc. Lond. A. 436:391–403. [Google Scholar]
- 53.Ayscough, K. 1998. Use of latrunculin-A, an actin monomer-binding drug. Methods Enzymol. 298:18–25. [DOI] [PubMed] [Google Scholar]
- 54.Spector, I., N. R. Shochet, Y. Kashman, and A. Groweiss. 1983. Latrunculins: novel marine toxins that disrupt microfilament organization in cultured cells. Science. 219:493–495. [DOI] [PubMed] [Google Scholar]
- 55.Sampath, P., and T. D. Pollard. 1991. Effects of cytochalasin, phalloidin, and pH on the elongation of actin filaments. Biochemistry. 30:1973–1980. [DOI] [PubMed] [Google Scholar]
- 56.Marguet, D., P. F. Lenne, H. Rigneault, and H. T. He. 2006. Dynamics in the plasma membrane: how to combine fluidity and order. EMBO J. 25:3446–3457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Suzuki, K. G., T. K. Fujiwara, M. Edidin, and A. Kusumi. 2007. Dynamic recruitment of phospholipase C gamma at transiently immobilized GPI-anchored receptor clusters induces IP3-Ca2+ signaling: single-molecule tracking study 2. J. Cell Biol. 177:731–742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Suzuki, K. G., T. K. Fujiwara, F. Sanematsu, R. Iino, M. Edidin, and A. Kusumi. 2007. GPI-anchored receptor clusters transiently recruit Lyn and Gα for temporary cluster immobilization and Lyn activation: single-molecule tracking study 1. J. Cell Biol. 177:717–730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Frick, M., K. Schmidt, and B. J. Nichols. 2007. Modulation of lateral diffusion in the plasma membrane by protein density. Curr. Biol. 17:462–467. [DOI] [PubMed] [Google Scholar]
- 60.Schmidt, K., and B. J. Nichols. 2004. A barrier to lateral diffusion in the cleavage furrow of dividing mammalian cells. Curr. Biol. 14:1002–1006. [DOI] [PubMed] [Google Scholar]
- 61.Wilson, K. M., I. E. Morrison, P. R. Smith, N. Fernandez, and R. J. Cherry. 1996. Single particle tracking of cell-surface HLA-DR molecules using R-phycoerythrin labeled monoclonal antibodies and fluorescence digital imaging. J. Cell Sci. 109:2101–2109. [DOI] [PubMed] [Google Scholar]
- 62.Magnusson, K. E., M. Gustafsson, K. Holmgren, and B. Johansson. 1990. Small intestinal differentiation in human colon carcinoma HT29 cells has distinct effects on the lateral diffusion of lipids (ganglioside GM1) and proteins (HLA class 1, HLA class 2, and neoplastic epithelial antigens) in the apical cell membrane. J. Cell. Physiol. 143:381–390. [DOI] [PubMed] [Google Scholar]
- 63.Barisas, B. G., W. F. Wade, T. M. Jovin, D. Arndt-Jovin, and D. A. Roess. 1999. Dynamics of molecules involved in antigen presentation: effects of fixation. Mol. Immunol. 36:701–708. [DOI] [PubMed] [Google Scholar]
- 64.Munnelly, H. M., C. J. Brady, G. M. Hagen, R. D. Horvat, W. F. Wade, D. A. Roess, and B. G. Barisas. 2001. Molecular dynamics of point mutated I-A(k) molecules expressed on lymphocytes. Immunol. Lett. 77:187–196. [DOI] [PubMed] [Google Scholar]
- 65.Wade, W. F., Z. Z. Chen, R. Maki, S. McKercher, E. Palmer, J. C. Cambier, and J. H. Freed. 1989. Altered I-A protein-mediated transmembrane signaling in B cells that express truncated I-Ak protein. Proc. Natl. Acad. Sci. USA. 86:6297–6301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Griffith, I. J., N. Nabavi, Z. Ghogawala, C. G. Chase, M. Rodriguez, D. J. McKean, and L. H. Glimcher. 1988. Structural mutation affecting intracellular transport and cell surface expression of murine class II molecules. J. Exp. Med. 167:541–555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Mecheri, S., M. Edidin, G. Dannecker, R. S. Mittler, and M. K. Hoffmann. 1990. Immunogenic Ia-binding peptides immobilize the Ia molecule and facilitate its aggregation on the B cell membrane. Control by the M1s-1 gene. J. Immunol. 144:1361–1368. [PubMed] [Google Scholar]
- 68.de Brabander, M., R. Nuydens, A. Ishihara, B. Holifield, K. Jacobson, and H. Geerts. 1991. Lateral diffusion and retrograde movements of individual cell surface components on single motile cells observed with Nanovid microscopy. J. Cell Biol. 112:111–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Sheets, E. D., G. M. Lee, R. Simson, and K. Jacobson. 1997. Transient confinement of a glycosylphosphatidylinositol-anchored protein in the plasma membrane. Biochemistry. 36:12449–12458. [DOI] [PubMed] [Google Scholar]
- 70.Thoumine, O., E. Saint-Michel, C. Dequidt, J. Falk, R. Rudge, T. Galli, C. Faivre-Sarrailh, and D. Choquet. 2005. Weak effect of membrane diffusion on the rate of receptor accumulation at adhesive contacts. Biophys. J. 89:L40–L42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Kemble, G. W., Y. I. Henis, and J. M. White. 1993. GPI- and transmembrane-anchored influenza hemagglutinin differ in structure and receptor binding activity. J. Cell Biol. 122:1253–1265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Wettstein, D. A., J. J. Boniface, P. A. Reay, H. Schild, and M. M. Davis. 1991. Expression of a class II major histocompatibility complex (MHC) heterodimer in a lipid-linked form with enhanced peptide/soluble MHC complex formation at low pH. J. Exp. Med. 174:219–228. [DOI] [PMC free article] [PubMed] [Google Scholar]