Abstract
Puffs and sparks are localized intracellular Ca2+ elevations that arise from the cooperative activity of Ca2+-regulated inositol 1,4,5-trisphosphate receptors and ryanodine receptors clustered at Ca2+ release sites on the surface of the endoplasmic reticulum or the sarcoplasmic reticulum. While the synchronous gating of Ca2+-regulated Ca2+ channels can be mediated entirely though the buffered diffusion of intracellular Ca2+, interprotein allosteric interactions also contribute to the dynamics of ryanodine receptor (RyR) gating and Ca2+ sparks. In this article, Markov chain models of Ca2+ release sites are used to investigate how the statistics of Ca2+ spark generation and termination are related to the coupling of RyRs via local [Ca2+] changes and allosteric interactions. Allosteric interactions are included in a manner that promotes the synchronous gating of channels by stabilizing neighboring closed-closed and/or open-open channel pairs. When the strength of Ca2+-mediated channel coupling is systematically varied (e.g., by changing the Ca2+ buffer concentration), simulations that include synchronizing allosteric interactions often exhibit more robust Ca2+ sparks; however, for some Ca2+ coupling strengths the sparks are less robust. We find no evidence that the distribution of spark durations can be used to distinguish between allosteric interactions that stabilize closed channel pairs, open channel pairs, or both in a balanced fashion. On the other hand, the changes in spark duration, interspark interval, and frequency observed when allosteric interactions that stabilize closed channel pairs are gradually removed from simulations are qualitatively different than the changes observed when open or both closed and open channel pairs are stabilized. Thus, our simulations clarify how changes in spark statistics due to pharmacological washout of the accessory proteins mediating allosteric coupling may indicate the type of synchronizing allosteric interactions exhibited by physically coupled RyRs. We also investigate the validity of a mean-field reduction applicable to the dynamics of a ryanodine receptor cluster coupled via local [Ca2+] and allosteric interactions. In addition to facilitating parameter studies of the effect of allosteric coupling on spark statistics, the derivation of the mean-field model establishes the correct functional form for cooperativity factors representing the coupled gating of RyRs. This mean-field formulation is well suited for use in computationally efficient whole cell simulations of excitation-contraction coupling.
INTRODUCTION
Localized intracellular Ca2+ elevations, known as puffs and sparks, are cellular signals of great interest that arise from the cooperative activity of clusters of Ca2+-regulated inositol 1,4,5-trisphosphate receptors and ryanodine receptors (RyRs). Not only are puffs, sparks, and other localized Ca2+ elevations highly specific regulators of cellular function, they also contribute to global Ca2+ release events in eukaryotic cells (1–6). For example, the process of excitation-contraction (EC) coupling in cardiac myocytes is initiated when electrical depolarization of the sarcolemma allows a small amount of Ca2+ to enter the cell via voltage-gated L-type Ca2+ channels (dihydropyridine receptors). This trigger Ca2+ activates a much larger release of Ca2+ from the sarcoplasmic reticulum (SR) via Ca2+-activated RyRs clustered at a Ca2+ release site, a process known as Ca2+-induced Ca2+-release, resulting in a Ca2+ spark. Although the increase in [Ca2+] due to individual sparks is localized to Ca2+ release sites, the cell-wide summation of many sparks provides the increase in the cytosolic [Ca2+] that initiates the mechanical contraction of the myocyte.
Experimental evidence suggests that the dynamics of RyR gating, Ca2+ sparks, and EC coupling are affected by interprotein allosteric interactions between neighboring RyRs at Ca2+ release sites. Each RyR channel is an oligomer composed of four identical 565 kDa RyR proteins surrounding a central pore, and groups of 10–100 RyR homotetramers form regular two-dimensional checkerboard-like lattices on the surface of the SR membrane (4,7–12) (see Fig. 1 A). When channels are reconstituted to mimic this in situ crystalline lattice, RyRs maintain physical contact with neighboring channels (9). Moreover, Marx and co-workers observed that physically coupled RyRs incorporated into planar lipid bilayers exhibit coupled gating even when Ca2+ is not the charge carrier (13,14). While such Ca2+-independent coupling has not been uniformly observed in other labs (15,16), functional coupling may require the association of FK-binding proteins (FKBPs) that conjugate with the RyR homotetramer in approximately stoichiometric proportions (16–18).
FIGURE 1.
(A) Schematic representation of a Ca2+ release site following Yin et al. (9). Each ryanodine receptor Ca2+ release channel (RyR) is composed of four identical subunits (shaded squares) surrounding a central pore (solid circle). Subunits physically contact neighboring subunits and homotetrameric channels form a right-handed checkerboard-like lattice. (B) In the Ca2+ release site model, two-state Ca2+-activated RyRs (solid circles) are globally coupled via the buffered diffusion of intracellular Ca2+ (not shown) and locally coupled to 2–4 nearest neighbors via allosteric interactions (dotted lines). Consistent with experimentally measured RyR lattice dimensions, the pore-to-pore interchannel distance is 30 nm.
The biophysical theory connecting single-channel kinetics of inositol 1,4,5-trisphosphate receptors and RyRs to the collective phenomena of Ca2+ puffs and sparks and global phenomena such as EC coupling is not as well developed as our understanding of the association of Ca2+ with endogenous and exogenous buffers (e.g., Ca2+-binding proteins, chelators, and indicators) (19–27). However, several theoretical studies have demonstrated that dynamics reminiscent of Ca2+ puffs and sparks may arise due to the cooperative activity of a cluster of Ca2+-regulated Ca2+-release channels modeled as a continuous-time discrete-state Markov chain (28–38). In such simulations, individual Ca2+-release channels are coupled via a time-dependent or time-independent representation of the local [Ca2+], the so-called Ca2+ microdomain, and exhibit stochastic Ca2+ excitability where channels open and close in a concerted fashion. The phenomena of Ca2+ activation and inactivation, the dynamics of the buffered diffusion of intracellular Ca2+, and the release site density and geometry, all significantly contribute to the statistics of simulated puffs and sparks (31,38,39).
Several theoretical studies to date have investigated the effects of interprotein allosteric coupling on the dynamics of Ca2+ sparks. Stern et al. demonstrated that models of single channel gating derived from planar lipid bilayer experiments fail to produce stable EC coupling in release site models (36). However, when release site models include nearest-neighbor allosteric interactions in addition to Ca2+ coupling, Ca2+ sparks can be recovered (36). Allosteric couplings in Stern et al. (36) are defined as free energies of interactions between neighboring channels and have the effect of modifying the affinity of release site transitions.
Using a formulation for allosteric coupling that is minimal compared to Stern's, Sobie et al. (40) studied the effects of allosteric interactions on spark statistics such as duration and frequency. This sticky-cluster model of Ca2+-induced Ca2+ release includes so-called coupling factors that scale the transition rates of the single channel model allowing the gating of each channel to be influenced by the number of open and closed RyRs at the release site. Although these coupling factors are post hoc additions to the single-channel RyR model, and there is no account of release site geometry or nearest-neighbor interactions, the sticky-cluster model demonstrated that allosteric coupling may contribute to spark termination.
To clarify how the microscopic parameters of allosteric interactions and Ca2+ coupling simultaneously contribute to the generation and termination of spontaneous Ca2+ sparks, we construct and analyze release site models composed of 16–49 two-state Ca2+-activated RyRs organized on a Cartesian lattice and instantaneously coupled using linearized equations for the buffered diffusion of microdomain Ca2+ (25). Using the methodology introduced by Stern et al. (36), RyRs also experience nearest-neighbor allosteric interactions that promote synchronous gating of channels (see Fig. 1 B). Importantly, these synchronizing allosteric interactions may be incorporated to stabilize closed channel pairs, open channel pairs, or both in a balanced fashion. We probe how these different types of synchronizing allosteric interactions affect the presence or absence of Ca2+ excitability and the statistics of spontaneous Ca2+ sparks. In addition, we derive and validate a mean-field modeling approach that is applicable to the dynamics of RyR clusters coupled via microdomain Ca2+ and nearest-neighbor allosteric interactions. Similar to the sticky-cluster model presented by Sobie et al. (40), the mean-field approach aggregates states based on the number of open RyRs at a Ca2+ release site; however, the coupling factors representing allosteric interactions are not post hoc additions to the model, but rather derived from the microscopic parameters of the Ca2+ release site.
Some of these results have previously appeared in abstract form (41).
MODEL FORMULATION
A two-state Ca2+-activated RyR model
Stochastic models of single channel gating often take the form of continuous-time discrete-state Markov chains (for review, see (42,43)). For example, the state-transition diagram for a two-state Ca2+-activated RyR model is defined as
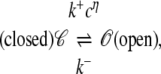 |
(1) |
where k+cη and k− are transition rates with units of time−1, k+ is an association rate constant with units conc−η time−1, η is the cooperativity of Ca2+ binding (usually chosen to be η = 2), and c is the local [Ca2+]. If c(t) is specified, then Eq. 1 defines a discrete-state continuous-time stochastic process, S(t), with the state space S ∈ {𝒞, 𝒪}. When the local [Ca2+] is not time-varying—for example, a fixed background [Ca2+] that we denote as c∞—then Eq. 1 corresponds to the well-known telegraph process with infinitesimal generator or Q-matrix (42,44) given by
 |
(2) |
Each off-diagonal element of Eq. 2 is the probability per unit time of a transition from state i to state j,
 |
and the diagonal elements are selected to ensure that the row sums of Q are zero  This condition ensures conservation of probability
This condition ensures conservation of probability  where
where
 |
is the element in the ith row and jth column of the matrix exponential. For example, during a small time step Δt, the probability that a channel initially in state i makes a transition into state j is approximated by pij ≈ [I + QΔt]ij, and in this case it is clear that 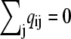 is required for
is required for  Note that all of the statistical properties of the two-state channel model diagrammed in Eq. 1 can be calculated from the Q-matrix (Eq. 2), and that this matrix can be decomposed as
Note that all of the statistical properties of the two-state channel model diagrammed in Eq. 1 can be calculated from the Q-matrix (Eq. 2), and that this matrix can be decomposed as
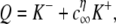 |
(3) |
where the matrices
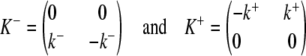 |
collect the dissociation and association rate constants, respectively.
Collective gating of RyR clusters
In a natural extension of the single channel modeling approach, a model Ca2+ release site composed of N channels is the vector-valued Markov chain,  where Sn(t) is the state of channel n at time t (45). We will denote release site configurations as a vector
where Sn(t) is the state of channel n at time t (45). We will denote release site configurations as a vector 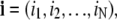 where in is the state of channel n. The transition rate from release site configuration
where in is the state of channel n. The transition rate from release site configuration  to
to  denoted by qij,
denoted by qij,
 |
(4) |
is nonzero if the origin (i) and destination (j) release site configurations are identical with the exception of one channel—that is, in = jn for all n ≠ n′ where 1 ≤ n′(i, j) ≤ N is the index of the channel changing state—and the in′ → jn′ transition is included in the single-channel model.
More formally, the transition rates qij for a release site composed of N identical Ca2+-regulated channels (Eq. 2) are given by
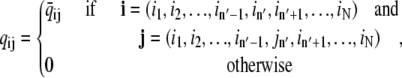 |
(5a) |
 |
(5b) |
where either K −[in′, jn′] or K+[in′, jn′] is the rate constant for the transition being made (only one of which is nonzero) and c(i, j) is the relevant [Ca2+], that is, the concentration experienced by channel n′(i, j) in the origin configuration i. In the following section, we show how c(i, j) depends on the mathematical representation of the release site ultrastructure and buffered Ca2+ diffusion.
Although it may not be practical to do so for large release sites, the infinitesimal generator matrix, Q = (qij), for a model Ca2+ release site can be constructed by enumerating transition rates according to Eq. 5 and selecting the diagonal elements qii to ensure the rows sum to zero.
Release site ultrastructure and the Ca2+ microdomain
Because Ca2+-activated RyRs experience coupling mediated by the buffered diffusion of intracellular Ca2+, the model includes a mathematical representation for the landscape of local [Ca2+] near the Ca2+ release site (the so-called Ca2+ microdomain) required to specify c(i, j) in Eq. 5b. For simplicity, we assume channels are instantaneously coupled via the Ca2+ microdomain (30,31)—that is, the formation and collapse of the local peaks in the Ca2+ profile are fast compared to the closed and open dwell times of the channels—and we assume the validity of linearly superposing local [Ca2+] increases due to individual channels at the release site (25,27). We also assume that all channels are localized on a planar section of SR membrane (z = 0) so that the position of the pore of channel n can be written as 
Assuming a single high concentration Ca2+ buffer and using the steady-state solution of the linearized equations for the buffered diffusion of intracellular Ca2+ (25,26), the increase in [Ca2+] above background at position  is given by
is given by
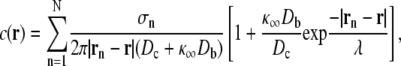 |
(6a) |
where
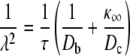 |
(6b) |
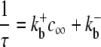 |
(6c) |
and
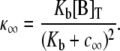 |
(6d) |
In these equations, the sum is over all channels at the release site, σn is the source amplitude of channel n (number of Ca2+ ions per unit time); Dc and Db are the diffusion coefficients for free Ca2+ and the Ca2+ buffer, respectively;  is the buffer association rate constant;
is the buffer association rate constant;  is the buffer dissociation rate constant,
is the buffer dissociation rate constant,  and [B]T is the total concentration of the Ca2+ buffer. Assuming all RyRs have identical source amplitudes,
and [B]T is the total concentration of the Ca2+ buffer. Assuming all RyRs have identical source amplitudes,
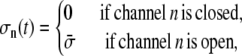 |
(7a) |
and
 |
(7b) |
where iCa is the unitary current of each channel, 2 is the valence of Ca2+, and F is Faraday's constant.
While Eqs. 6 and 7 define the [Ca2+] at any position r for a given release site ultrastructure, {rn}, it is helpful to summarize channel-to-channel Ca2+ interactions using an N × N coupling matrix C = (cnm) that provides the increase in [Ca2+] over the background (c∞) experienced by channel m when channel n is open. If  specifies the position of the Ca2+ regulatory site for channel m located a small distance rd above the channel pore, then
specifies the position of the Ca2+ regulatory site for channel m located a small distance rd above the channel pore, then
 |
(8) |
Using this expression we can determine the Ca2+ concentrations needed to specify the rates of Ca2+-mediated transitions in Eqs. 5a and 5b, that is,
 |
(9a) |
where
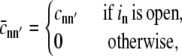 |
(9b) |
n′(i, j) is the index of the channel changing state, and in is the state of channel n.
Fig. 2 A uses Eqs. 6 and 7 and calmodulin-like buffer parameters (see Table 1) to calculate the Ca2+ microdomain near a cluster of N = 25 open RyRs organized on a Cartesian lattice (Fig. 1 B). The strength of Ca2+ interactions at the release site can be modified by changing any of the parameters in Eqs. 6 and 7, including the channel source amplitude, buffer parameters, or the diffusion constant for free Ca2+. For example, Fig. 2 B shows that increasing the total buffer concentration ([B]T) decreases the local [Ca2+] experienced by the RyRs. Similarly, Fig. 2 C shows that the Ca2+ coupling strength defined as the average of the off-diagonal elements of the coupling matrix,
 |
(10) |
is a decreasing function of the total buffer concentration [B]T for any fixed unitary current iCa and an increasing function of iCa for any fixed [B]T. Note that the unitary current of RyRs in vivo has been estimated to be <0.6 pA and as low as 0.07 pA in the presence of physiological concentrations of Mg2+ (46–48). Because the model does not explicitly include localized depletion of luminal Ca2+, a phenomenon that is expected to reduce the effective unitary current of RyRs in vivo, our standard parameter set includes a unitary current of 0.04 pA (see Table 1).
FIGURE 2.
(A and B) The linearized equations for the buffered diffusion of Ca2+ (Eqs. 6a–7b) give the steady-state [Ca2+] near (z = rd = 30 nm) a 360 × 360 nm section of planar SR membrane for a cluster of 25 open RyRs (solid dots) organized on a Cartesian lattice with interchannel spacing of 30 nm (see Fig. 1 B). Individual channels have an effective unitary current of iCa = 0.04 pA and the background [Ca2+] is c∞ = 0.1 μM, while the total Ca2+ buffer concentration is (A) [B]T = 300 μM or (B) [B]T = 2000 μM and buffer parameters are as in Table 1. (C) Isoclines showing the average Ca2+ coupling strength (c*) are plotted against [B]T and the effective unitary current of channels (iCa) for the 25 channel Ca2+ release site shown in A and B.
TABLE 1.
Default parameters used in Ca2+ release site simulations for both the full model and the mean-field reduction (when applicable)
| Parameter | Value | Unit | Description |
|---|---|---|---|
| Single channel parameters | |||
| k+ | 0.04 | μM−ηms−1 | Association rate constant |
| k− | 1 | ms−1 | Dissociation rate constant |
| c∞ | 0.1 | μM | Background [Ca2+] |
| η | 2 | Cooperativity of Ca2+ binding | |
| iCa | 0.04 | pA | Effective unitary current |
| rd | 30 | nm | Pore to regulatory site distance |
| Buffer parameters | |||
 |
100 | μM−1 s−1 | Association rate constant |
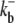 |
38 | s−1 | Dissociation rate constant |
| Dc | 250 | μm2 s−1 | Ca2+ diffusion coefficient |
| Db | 32 | μm2 s−1 | Buffer diffusion coefficient |
Single-channel kinetic parameters are selected for a dissociation constant or Kd = 5 μM (70). Buffer parameters correspond to calmodulin (27,82). Although the exact location of the Ca2+-regulatory site is unknown, the pore-to-regulatory site distance is consistent with cryo-electron microscopy data that suggests the RyR oligomer has a large 29 × 29 × 12 nm cytoplasmic assembly and a transmembrane assembly that protrudes 7 nm from the center of the cytoplasmic assembly (16,83).
Allosteric interactions between physically coupled channels
Following the methodology presented in Stern et al. (36), the RyR cluster model with Ca2+-mediated coupling is extended to include allosteric interactions between neighboring channels. We begin by defining dimensionless free energies of interaction ɛij (units of kBT) that specify the change in free energy experienced by a channel in state j when allosterically coupled to a channel in state i. For convenience we collect these interaction energies in an M × M matrix ℰ where M is the number of states in the single-channel model and ɛij = ɛji (i ≠ j) to satisfy the requirement of thermodynamic reversibility. For the two-state single-channel model considered in this article,
 |
(11) |
where 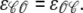 Because allosteric interactions require physical contact between neighboring RyRs, the model formulation includes a symmetric N × N adjacency matrix defined as
Because allosteric interactions require physical contact between neighboring RyRs, the model formulation includes a symmetric N × N adjacency matrix defined as
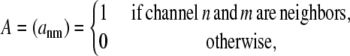 |
(12) |
where ann = 0 because channels do not experience allosteric interactions with themselves. The nonzero elements of A are chosen consistent with release site ultrastructure (e.g., dotted lines in Fig. 1 B).
To include the effect of allosteric coupling in the Ca2+ release site model, the total allosteric energy experienced by channel n′(i, j) in the origin and destination configurations of an i → j transition are calculated as
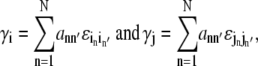 |
(13) |
where the sum is over all N channels, ann′ are elements of A, and  and
and  are entries of ℰ. The difference between these total allosteric energies (γj − γi) is used to modify the equilibrium constant of the i → j transition, that is,
are entries of ℰ. The difference between these total allosteric energies (γj − γi) is used to modify the equilibrium constant of the i → j transition, that is,
 |
(14a) |
 |
(14b) |
and
 |
(14c) |
where  and
and  denote unmodified rates calculated using Eq. 5 and the parameters 0 ≤ νij ≤ 1 and νji = 1 −νij (36) partition contributions due to allosteric coupling between the forward (qij) and reverse (qji) rates. While νij and νji can potentially have different values for every transition i → j, we assume transition rates involving the association of Ca2+ are diffusion-limited. Thus, transition rates for release site configuration changes where channels make 𝒞 → 𝒪 transitions are assigned ν = 0. Conversely, ν = 1 for all other configuration changes where channels make 𝒪 → 𝒞 transitions.
denote unmodified rates calculated using Eq. 5 and the parameters 0 ≤ νij ≤ 1 and νji = 1 −νij (36) partition contributions due to allosteric coupling between the forward (qij) and reverse (qji) rates. While νij and νji can potentially have different values for every transition i → j, we assume transition rates involving the association of Ca2+ are diffusion-limited. Thus, transition rates for release site configuration changes where channels make 𝒞 → 𝒪 transitions are assigned ν = 0. Conversely, ν = 1 for all other configuration changes where channels make 𝒪 → 𝒞 transitions.
RESULTS
Ca2+ and allosteric coupling at a three RyR cluster
To clarify the model formulation, transition rate expressions corresponding to the example configuration changes shown in Fig. 3 A are written below. These configuration changes involve a triangular cluster of three two-state RyRs experiencing Ca2+ coupling and nearest-neighbor allosteric interactions. The corresponding Ca2+ coupling matrix and allosteric adjacency matrix are
 |
(15) |
respectively, where the cnm are determined using Eq. 8. In each panel of Fig. 3 A, the total allosteric energy experienced by the RyR changing state (labeled with asterisks) is calculated for both the origin (i) and destination (j) configurations using Eq. 13.
FIGURE 3.
(A) Example configuration changes involving three two-state RyRs with pore-to-pore interchannel spacing of 30 nm. Allosteric interactions are indicated by solid and dashed lines. Transition rates depend on the allosteric interactions of the channel changing state (solid lines) shown above each configuration. (B) RyR collective gating when channels experience coupling via the Ca2+ microdomain ([B]T = 3566 μM, c* = 0.75 μM) but no allosteric interactions ɛ𝒞𝒞 = ɛ𝒪𝒪 = 0. Shaded bars show the steady-state probability distribution for the number of open channels N𝒪 at the release site. Open bars give the binomial distribution with the same mean as shaded bars; the difference shows that channels do not gate independently. (C–E) RyR collective gating. In addition to Ca2+ coupling (c* = 0.75 μM), channels experience allosteric interactions that stabilize closed channel pairs (C, ɛ𝒞𝒞 = −0.8, ɛ𝒪𝒪 = 0) open channel pairs (D, ɛ𝒞𝒞 = 0, ɛ𝒪𝒪 = −0.8) or both in a balanced fashion (E, ɛ𝒞𝒞 = ɛ𝒪𝒪 = −0.8) Parameters: k+ = 1.5 μM−η ms−1, k− = 0.5 ms−1, and as in Table 1.
The i → j configuration changes shown in Fig. 3 A each involve an RyR making a Ca2+-mediated 𝒞 → 𝒪 transition (see Eq. 1) at rate qij that is a function of c(i,j), that is, the [Ca2+] experienced by the channels changing state (Eq. 9). Let us number the RyRs in a counterclockwise fashion beginning with the channel changing state. For the 𝒞𝒞𝒞 → 𝒪𝒞𝒞 configuration change shown in Fig. 3 Aa, c(i,j) = c∞ because all channels are closed in the origin configuration 𝒞𝒞𝒞. For the 𝒞𝒞𝒪 → 𝒪𝒞𝒪 configuration change, c(i,j) = c∞ + c31 because channel 3 is open in configuration 𝒞𝒞𝒪 (Fig. 3 Ab). Similarly, for the 𝒞𝒪𝒪 → 𝒪𝒪𝒪 configuration change,  (Fig. 3 Ac). Having determined the appropriate [Ca2+] concentrations, Eq. 5b is needed to calculate the transition rates:
(Fig. 3 Ac). Having determined the appropriate [Ca2+] concentrations, Eq. 5b is needed to calculate the transition rates:
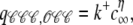 |
(16a) |
 |
(16b) |
and
 |
(16c) |
Because it is assumed that configuration changes involving the binding of Ca2+ are diffusion limited, these rates are not modified due to allosteric interactions (i.e., νij = 0).
Conversely, j → i configuration changes shown in Fig. 3 A involve channels making unimolecular 𝒪 → 𝒞 transitions at the base rate qji = k− that is modified by the change in allosteric interaction energy experienced by the channel changing state. Using νji = 1, the rates for j → i configuration changes are given by (Eq. 14c)
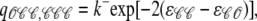 |
(17a) |
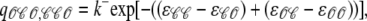 |
(17b) |
and
 |
(17c) |
Note that in these transition rate expressions, the elements of the allosteric interaction energy matrix occur as the differences ɛ𝒞𝒞 − ɛ𝒞𝒪 and ɛ𝒪𝒞 − ɛ𝒪𝒪. This is true regardless of the number of channels, and we may without loss of generality fix ɛ𝒞𝒪 = ɛ𝒪𝒞 = 0. That is, we will probe the effects of allosteric interactions on Ca2+ release site dynamics by varying only the change in free energy due to allosterically interacting closed-closed (ɛ𝒞𝒞) and open-open (ɛ𝒪𝒪) channel pairs. Because we are primarily concerned with the effects of allosteric interactions that promote synchronous gating, we assume allosteric interactions stabilize closed-closed and/or open-open channel pairs (i.e., ɛ𝒞𝒞 ≤ 0 and ɛ𝒪𝒪 ≤ 0). For simplicity, we focus on three allosteric coupling paradigms in which allosteric interactions stabilize
Closed-closed channel pairs (ɛ𝒞𝒞 = < 0, ɛ𝒪𝒪 = 0).
Open-open channel pairs (ɛ𝒪𝒪 = 0, ɛ𝒪𝒪 < 0).
Both closed-closed and open-open channel pairs in a balanced fashion (ɛ𝒪𝒪 = ɛ𝒪𝒪 < 0).
The simulations shown in Fig. 3, B–E, demonstrate how synchronizing allosteric interactions included in these three ways affect the dynamics of the synchronous gating of the three RyRs. Simulations are carried out using the exact numerical method presented in Appendix A and, for simplicity, the configuration of the RyRs is summarized by plotting only the number of open channels (N𝒪) as a function of time. Interestingly, Fig. 3 B demonstrates that synchronizing allosteric interactions are not required (ɛ𝒞𝒞 = ɛ𝒪𝒪 = 0) for channels to exhibit synchronous gating. Rather, channels may exhibit coupled gating that is mediated entirely via the buffered diffusion of local Ca2+ as long as the average Ca2+ coupling strength is sufficient (c* = 0.75 μM) (31). Shaded bars in the left panel of Fig. 3 B show the steady-state probability distribution for the number of open RyRs (N𝒪) directly calculated from the relevant Q-matrix as described in Appendix B. The disagreement between these results and the open bars, showing a binomial distribution with the same mean, is a signature of the cooperative gating of these RyRs.
While Fig. 3 B demonstrates that the synchronous gating of channels can be mediated entirely via Ca2+, Fig. 3, C–E, show how synchronizing allosteric interactions affect the dynamics of coupled gating. For example, Fig. 3 C demonstrates that when closed channel pairs are stabilized (ɛ𝒞𝒞 = −0.8, ɛ𝒪𝒪 = 0), the steady-state probability of having zero open channels (N𝒪 = 0) increases while the probability of N𝒪 = 3 decreases relative to Fig. 3 B. Conversely, Fig. 3 D illustrates that when allosteric interactions stabilize open channel pairs (ɛ𝒞𝒞 = 0, ɛ𝒪𝒪 = −0.8), the probability of having a maximally activated release site (N𝒪 = 3) increases. In Fig. 3 E allosteric interactions stabilize closed-closed and open-open channel pairs in a balanced fashion (ɛ𝒞𝒞 = ɛ𝒪𝒪 = −0.8) and the probability of both N𝒪 = 0 and N𝒪 = 3 increases while the probability of N𝒪 = 1 and N𝒪 = 2 decreases compared to Fig. 3 B.
Effects of Ca2+ and allosteric coupling strength on spontaneous sparks
The previous section demonstrated how the dynamics of coupled RyR gating may depend on synchronizing allosteric interactions that stabilize closed channel pairs, open channel pairs, or both in a balanced fashion. In this section, release sites composed of 25 nearest-neighbor coupled RyRs organized on a Cartesian lattice (see Fig. 1 B) are used to investigate how Ca2+ spark generation and termination depend on both the strength of coupling mediated by the Ca2+ microdomain and the strength of synchronizing allosteric interactions introduced in one of these three ways. Note that nearest-neighbor coupling implies that each channel experiences allosteric interactions with 2–4 other channels, while increases in the Ca2+ microdomain due to open RyRs are experienced by all channels.
Fig. 4 A shows a simulation in which the strength of allosteric interactions (ɛ𝒞𝒞 = −0.2, ɛ𝒪𝒪 = 0) and Ca2+ coupling (c* = 0.55 μM) are selected to illustrate the phenomenon of stochastic Ca2+ excitability reminiscent of spontaneous Ca2+ sparks. While the channels at the release site are closed most of the time (N𝒪 < 5), on occasion the RyRs simultaneously open (N𝒪 ≈ 25). Fig. 5 shows that the sparks observed in Fig. 4 A are sensitive to changes in the strength of allosteric interactions that stabilize closed channel pairs. For example, the release site is tonically active when allosteric interactions are not included in simulations (ɛ𝒞𝒞 = ɛ𝒪𝒪 = 0, Fig. 5 A). On the other hand, sparks fail to initiate when the strength of allosteric interactions that stabilize closed channel pairs is greater than in Fig. 4 A (ɛ𝒞𝒞 = −0.4, ɛ𝒪𝒪 = 0, Fig. 5 B).
FIGURE 4.
(A) Ca2+ release site simulation involving 25 RyRs organized on a Cartesian lattice exhibits stochastic Ca2+ excitability reminiscent of spontaneous sparks when channels experience coupling via increases in the local [Ca2+] ([B]T = 937.5 μM, c* = 0.55 μM) and nearest-neighbor allosteric interactions that stabilize closed channel pairs (ɛ𝒞𝒞 = −0.2, ɛ𝒪𝒪 = 0). Insets expand 50 ms of the simulation beginning at the times indicated by arrows and show snapshots giving the states of all 25 RyRs at the release site. (B) The Ca2+ spark Score corresponding to the simulation is calculated using Eq. 18 and the steady-state probability distribution for the number of open channels (N𝒪) at the release site (right panel) estimated from a long (>20 s) Monte Carlo simulation as described in Appendix B. Parameters as in Table 1.
FIGURE 5.
Ca2+ sparks exhibited in Fig. 4 are sensitive to changes in the strength of allosteric interactions that stabilize closed channel pairs only when the strength of Ca2+ interactions is fixed (c* = 0.55 μM). (A) Sparks fail to terminate when allosteric interactions are not included (ɛ𝒞𝒞 = 0, ɛ𝒪𝒪 = 0). (B) Sparks fail to initiate when the strength of allosteric interactions that stabilize closed channel pairs is increased (ɛ𝒞𝒞 = −0.4, ɛ𝒪𝒪 = 0). Histograms for the number of open channels shown in right panels (see Fig. 4) are used to calculate the Score of each simulation. Parameters as in Table 1.
A response measure that is strongly correlated with the presence of sparks in Monte Carlo simulations is the so-called Ca2+ spark Score introduced in (31). The Score is defined as the index of dispersion of the fraction of open channels (fO = N𝒪/N) and is given by
 |
(18) |
Score values >0.3 are indicative of spark-like excitability in stochastic Ca2+ release site simulations (30,31). For example, using the observed probability distribution for the number of open channels at the release site estimated from a long Monte Carlo simulation as described in Appendix B (Fig. 4 B), the Score corresponding to the simulation shown in Fig. 4 is a high value of 0.71. Conversely, the tonically active release site shown in Fig. 5 A has a low Score of 0.013 because E[N𝒪] is large. The quiescent release site shown in Fig. 5 B also has a low Score of 0.082.
While Figs. 4 and 5 demonstrated that Ca2+ sparks are sensitive to changes in the strength of allosteric interactions that stabilize closed channel pairs, Fig. 6 A shows that sparks observed in simulations of a 25 RyR release site are also sensitive to the Ca2+ coupling strength. For example, triangles show the Score (reported as the mean ± SD of 10 Monte Carlo simulations) as a function of c* when the strength of allosteric interactions that stabilize closed channel pairs is ɛ𝒞𝒞 = −0.2 as in Fig. 4. The Ca2+ coupling strength (c*) is systematically varied by increasing or decreasing the total buffer concentration ([B]T). Note that sparks are observed in simulations (Score > 0.3) over a range of Ca2+ coupling strengths but are not observed (Score < 0.3) in simulations that use c* < 0.4 μM because the Ca2+ coupling strength is insufficient to initiate sparks. Similarly, Score < 0.3 when c* > 0.7 μM because the Ca2+ coupling strength is too large to allow spark termination. Fig. 6 A also shows that the optimal Ca2+ coupling strength—that is, the c* resulting in the highest Score—is sensitive to the strength of allosteric interactions that stabilize closed channels. Indeed, comparing circles (ɛ𝒞𝒞 = 0) and squares (ɛ𝒞𝒞 = −0.4) to triangles (ɛ𝒞𝒞 = −0.2), we notice that the optimal c* is an increasing function of the magnitude of ɛ𝒞𝒞. In comparison, Fig. 6 B demonstrates that as the strength of allosteric interactions that stabilize open channel pairs increases, the optimal c* decreases. On the other hand, Fig. 6 C shows that increasing the strength of allosteric interactions that stabilize both closed-closed and open-open channel pairs in a balanced fashion has little effect on the optimal value of c*.
FIGURE 6.
(A–C) The Ca2+ spark Score (mean ± SD of 10 long (>20 s) Monte Carlo simulations involving 25 RyRs organized on a Cartesian lattice with random initial conditions) as a function of the Ca2+ coupling strength (c*) and the strength of nearest-neighbor allosteric interactions that stabilize closed channel pairs (A) ɛ𝒪𝒪 = 0 and ɛ𝒞𝒞 = 0 (circles), ɛ𝒞𝒞 = −0.2 (triangles), or ɛ𝒞𝒞 = −0.4 (squares); open channel pairs (B) ɛ𝒞𝒞 = 0 and ɛ𝒪𝒪 = 0 (circles), ɛ𝒪𝒪 = −0.2 (triangles), or ɛ𝒪𝒪 = −0.4 (squares); or both in a balanced fashion (C) ɛ𝒞𝒞 = ɛ𝒪𝒪 = 0 (circles), ɛ𝒞𝒞 = ɛ𝒪𝒪 = −0.2 (triangles), or ɛ𝒞𝒞 = ɛ𝒪𝒪 = −0.4 (squares). Data are interpolated with cubic splines (dashed lines) for clarity. Parameters as in Table 1.
Fig. 6 demonstrates that sparks depend on c*, ɛ𝒪𝒪, and ɛ𝒞𝒞 in a complicated manner. For example, sparks that are eliminated as c* increases may be recovered by increasing the strength of allosteric interactions that stabilize closed channel pairs (ɛ𝒞𝒞) or by decreasing the strength of allosteric interactions that stabilize open channel pairs (ɛ𝒪𝒪). On the other hand, sparks that are eliminated as c* decreases may be recovered by decreasing the magnitude of ɛ𝒞𝒞 or increasing the magnitude of ɛ𝒪𝒪. Note that for all three types of allosteric interactions there are Ca2+ coupling strengths (c*) for which stronger interactions lead to more robust sparks. Indeed, summary plots in Fig. 7 A show that the Score at these optimal c* values is a monotonically increasing function of the strength of allosteric interactions. Interestingly, the Score is enhanced the most when both closed-closed and open-open channel pairs are increasingly stabilized in a balanced fashion (circles).
FIGURE 7.
(A) The Score at the optimal c* (maximum Score) and (B) the full width at half-maximum (FWHM) of the cubic spline fits of data in Fig. 6 are plotted as a function of the strength of stabilizing allosteric interactions (ɛ) when allosteric interactions stabilize closed channel pairs (triangles, ɛ𝒞𝒞 = ɛ, ɛ𝒪𝒪 = 0), open channel pairs (squares, ɛ𝒞𝒞 = 0, ɛ𝒪𝒪 = ɛ), or both in a balanced fashion (circles, ɛ𝒞𝒞 = ɛ𝒪𝒪 = ɛ).
In Fig. 7 B the sensitivity of sparks to the Ca2+ coupling strength is quantified using the full width at half-maximum (FWHM) of cubic spline fits to the results of Fig. 6 (dashed lines); a larger FWHM implies less sensitivity to changes in c*. The triangles of Fig. 7 B show that sparks are less sensitive to variations in c* as the strength of allosteric interactions that stabilize closed channel pairs increases. Conversely, the squares show that sparks are more sensitive to c* as the strength of allosteric interactions that stabilize open channel pairs increases. The circles show that increasing the strength of allosteric interactions that stabilize both closed-closed and open-open channel pairs in a balanced fashion has little effect on the FWHM.
The effect of washing out allosteric interactions on spark statistics
In the previous section we showed how the presence or absence of Ca2+ sparks depends on both the strength of Ca2+ coupling (c*) and the strength of stabilizing allosteric interactions (ɛ𝒞𝒞 and ɛ𝒪𝒪). Next, we investigate how spark statistics (duration, interspark interval, and frequency) are affected by washing-out stabilizing allosteric interactions, that is, we study how these spark statistics change as an increasing fraction of nearest-neighbor allosteric couplings are removed. Many experimental studies show that genetic deficiencies in, and the pharmacological washout of, the FK-binding proteins that mediate allosteric interactions lead to cardiac arrhythmias and changes in spark dynamics (49–51). The following simulations aim to clarify how these experimental results may be interpreted as evidence for allosteric interactions that stabilize closed channel pairs, open channel pairs, or both (see Discussion).
The shaded bars in Fig. 8 A are probability distributions of spark duration and interspark interval estimated from multiple spark simulations (the mean is indicated by shaded triangles). As in Fig. 4, twenty-five RyRs experience nearest-neighbor allosteric interactions that stabilize closed channel pairs (ɛ𝒞𝒞 = −0.2, ɛ𝒪𝒪 = 0), and the Ca2+ coupling strength is selected to ensure a high Score (c* = 0.58 μM). Spark duration is defined as the period beginning when one-fifth of the channels at the release site open (N𝒪 = 4 → 5) and ending when all channels close (N𝒪 = 0), thus excluding small sparks from the calculation. Interspark interval is the time between the end of a spark and the beginning of the subsequent spark.
FIGURE 8.
Shaded bars are probability distributions of Ca2+ spark duration and interspark interval estimated from simulations involving 25 RyRs organized on a Cartesian lattice (means indicated by shaded triangles). RyRs experience coupling via the Ca2+ microdomain (A) c* = 0.58, (B) c* = 0.40, and (C) c* = 0.48 μM; and nearest-neighbor allosteric interactions that stabilize closed channel pairs (A) ɛ𝒞𝒞 = −0.2, ɛ𝒪𝒪 = 0; open channel pairs (B) ɛ𝒞𝒞 = 0, ɛ𝒪𝒪 = −0.2; or both in a balanced fashion (C) ɛ𝒞𝒞 = ɛ𝒪𝒪 = −0.2. Open bars (and triangles) are spark statistic distributions (and means) calculated when one-fifth of the nearest-neighbor allosteric couplings are selected at random and removed from simulations. Each histogram is calculated using 1200–6333 simulated sparks. Parameters as in Table 1.
For comparison, open bars in Fig. 8 A are the spark duration and interspark interval distributions after one-fifth of the nearest-neighbor allosteric couplings are selected at random and eliminated from the simulations. Notice that this washout of allosteric interactions that stabilize closed channel pairs has the effect of increasing the expected spark duration and decreasing the expected interspark interval (compare open and shaded triangles). On the other hand, Fig. 8 B shows that when allosteric interactions stabilize open channel pairs (ɛ𝒞𝒞 = 0, ɛ𝒞𝒞 = −0.2, and c* = 0.40 μM), removing one-fifth of these couplings decreases the expected spark duration with little change to the interspark interval. When both closed-closed and open-open channel pairs are stabilized in a balanced fashion (ɛ𝒞𝒞 = ɛ𝒪𝒪 = −0.2, c* = 0.48 μM), washout of allosteric couplings decreases interspark interval but has little effect on spark duration (Fig. 8 C).
To further probe the effects of washing out allosteric interactions, Fig. 9, A and B, show the mean and standard deviation of spark duration and interspark interval plotted against the fraction of allosteric couplings removed from simulations (denoted as φ). Similar to Fig. 8, allosteric interactions are included to stabilize closed channel pairs (triangles), open channel pairs (squares), or both in a balanced fashion (circles). In each case, the Ca2+ coupling strength of c* = 0.58, 0.40, and 0.48 μM, respectively, is selected to maximize the Ca2+ spark Score before the washout of synchronizing allosteric interactions (φ = 0); thus, the Score is always a decreasing function of φ (not shown). When the squares and circles of Fig. 9, A and B, are recalculated using c* = 0.58 μM, qualitatively similar results are obtained.
FIGURE 9.
(A and B) The (A) Ca2+ spark duration and (B) interspark interval (mean + SD of distributions such as those in Fig. 8 calculated using 334–14,290 simulated sparks) are plotted against the fraction of allosteric couplings randomly removed from simulations (φ). Using parameters identical to Fig. 8 the 25 RyRs experience Ca2+ coupling and allosteric interactions that stabilize closed channel pairs (triangles), open channel pairs (squares), or both in a balanced fashion (circles). Multiple symbols at each φ show results from simulations that use different realizations of the allosteric adjacency matrix A (see text). (C) The spark frequency plotted against φ is calculated using the data from A and B that include error bars. Spark statistics are reported at a given value of φ only if the Ca2+ spark Score > 0.3.
The results shown in Fig. 9, A and B, are consistent with those shown in Fig. 8. When allosteric interactions that stabilize closed channel pairs are washed out (increasing φ), spark duration increases and interspark interval decreases (triangles). When allosteric interactions that stabilize open channel pairs are washed out, spark duration decreases but interspark interval is largely unchanged (squares). When both closed-closed and open-open channel pairs are stabilized in a balanced fashion, washout causes interspark interval to decrease but spark duration is unchanged (circles). Notice that the standard deviations (bars) of spark statistics are approximately proportional to the means regardless of the degree of washout.
Because the allosteric couplings washed out in the simulations of Fig. 9, A and B, are randomly selected, there are many realizations of the allosteric adjacency matrix A consistent with any nonzero φ. To show the effects of variations in allosteric connectivity on spark dynamics, multiple symbols plotted at each value of φ show the mean spark duration and interspark interval using different realizations of A. The proximity of these symbols to each other at any given value of φ indicates that the dynamics of Ca2+ sparks—as measured by duration and interspark interval—are largely insensitive to these variations in allosteric connectivity.
Fig. 9 C shows the spark frequency—defined as the reciprocal of the sum of the mean spark duration and interspark interval—plotted against φ for the three allosteric coupling paradigms. When allosteric interactions that stabilize closed channel pairs are washed out, spark frequency increases but ultimately decreases (triangles). When allosteric interactions stabilize open channel pairs (squares), spark frequency is a nearly constant function of φ. When both closed-closed and open-open channel pairs are stabilized in a balanced fashion, spark frequency increases during washout (circles).
A mean-field RyR cluster model
In previous sections, we used Monte Carlo simulations to study how both the strength of Ca2+ coupling and stabilizing allosteric interactions contribute to the dynamics of sparks. Much of the complexity of these simulations is due to the spatially explicit account of channel-to-channel coupling represented by the Ca2+ coupling matrix C and the allosteric adjacency matrix A. To facilitate parameter studies of the effects of allosteric coupling on spark statistics, this section presents a mean-field approximation applicable to a cluster of two-state RyRs coupled via the buffered diffusion of Ca2+ and nearest-neighbor allosteric interactions.
The mean-field approximation is perhaps best introduced by considering a simplified Ca2+ coupling matrix that takes the form (31)
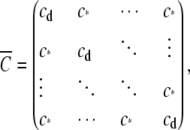 |
(19) |
where the identical off-diagonal elements (c*) are the average of the N(N – 1) off-diagonal elements of the original Ca2+ coupling matrix C (Eq. 10). (The diagonal elements cd that represent domain Ca2+ are inconsequential to simulations involving clusters of RyRs with no Ca2+-mediated transition out of an open state.) Consider also an allosteric adjacency matrix that takes a similar simplified form,
 |
(20) |
where 0 ≤ a* ≤ 1 is the average allosteric connectivity calculated from the off-diagonal elements of the original allosteric adjacency matrix A = (anm),
 |
(21) |
Note that it is not possible to choose a release site ultrastructure so that  is equal to C with N > 3 channels on a planar membrane. Likewise,
is equal to C with N > 3 channels on a planar membrane. Likewise,  will not be equal to A unless allosteric coupling is all-to-all, a situation not consistent with RyR clusters in which the extent of interchannel physical coupling is limited to nearest neighbors. Nevertheless, in simulations performed using
will not be equal to A unless allosteric coupling is all-to-all, a situation not consistent with RyR clusters in which the extent of interchannel physical coupling is limited to nearest neighbors. Nevertheless, in simulations performed using  and
and  the RyRs are indistinguishable and the [Ca2+] and allosteric interaction energy experienced by channels depends only on the number of open and closed RyRs at the release site. Importantly, simulations using
the RyRs are indistinguishable and the [Ca2+] and allosteric interaction energy experienced by channels depends only on the number of open and closed RyRs at the release site. Importantly, simulations using  and
and  satisfy a lumpability condition that allows all release site configurations with the same number of channels in each state to be agglomerated without further approximation (31,52). This yields a contracted Markov chain with state-transition diagram
satisfy a lumpability condition that allows all release site configurations with the same number of channels in each state to be agglomerated without further approximation (31,52). This yields a contracted Markov chain with state-transition diagram
 |
(22) |
where the state of the system S(t) ∈ {0, 1, …, N} is the number of open channels N𝒪 at the release site and qij is the rate of the N𝒪 = i → j transition (see below). The number of closed channels is given by N𝒞 = N − N𝒪.
Equation 22 describes a birth-death process with boundaries with skip-free transitions that increase (N𝒪 = n → n + 1) or decrease (N𝒪 = n → n − 1) the number of open channels at the release site. The N + 1 by N + 1 generator matrix corresponding to Eq. 22 is tridiagonal,
 |
(23) |
with diagonal elements (⋄) selected to ensure row sums of zero. The birth rate (qn, n+1) for the n → n + 1 transition is given by
 |
(24) |
where (N – n) is the number of closed channels at the release site that may potentially open and c∞ + N𝒪c* is the [Ca2+] experienced by all RyRs. While our assumption that the binding of Ca2+ is diffusion-limited leads to birth rates that are not dependent on allosteric energies, the death rates are modified due to allosteric interactions and are given by
 |
(25) |
where n is the number of open channels at the release site that may potentially close, the coefficients (n – 1) and (N – n) are the number of open and closed neighbors, and ɛ𝒪𝒞 − ɛ𝒪𝒪 and ɛ𝒞𝒞 − ɛ𝒞𝒪 are the differences in free energies experienced by a transitioning channel due to allosteric couplings with neighboring open and closed channels. Because we have without loss of generality set ɛ𝒞𝒪 = ɛ𝒪𝒞 = 0, Eq. 25 simplifies to
 |
(26) |
Note that the mean-field RyR cluster model has only nine parameters: N, k+, k−, η, c∞, c*, ɛ𝒞𝒞, ɛ𝒪𝒪, and a*.
Representative mean-field simulations
Fig. 10 A shows representative simulations of 25 mean-field coupled RyRs arranged according to the strength of Ca2+ coupling (c*) and allosteric interactions (ɛ𝒞𝒞) used. These allosteric interactions stabilize closed channel pairs (ɛ𝒪𝒪 = 0) and the average allosteric connectivity is a* = 0.13, as calculated using the adjacency matrix for 25 nearest-neighbor coupled RyRs organized on a Cartesian lattice (see Fig. 1). Notice that sparks are only observed on the diagonal panels of Fig. 10 A, indicating that increased c* can be compensated for by more negative ɛ𝒞𝒞. Release sites are tonically active when c* is large and  represents weak allosteric interactions (upper right panels), while release sites are quiescent when c* is small and
represents weak allosteric interactions (upper right panels), while release sites are quiescent when c* is small and  represents strong allosteric interactions (lower left panels). These mean-field results are consistent with simulations that use the full model when allosteric interactions stabilize closed channel pairs (Figs. 4 and 5, and Fig. 6 A). Mean-field simulations that include allosteric interactions that stabilize open channel pairs or both closed-closed and open-open channel pairs in a balanced fashion (not shown) are also consistent with the full model (Fig. 6, B and C).
represents strong allosteric interactions (lower left panels). These mean-field results are consistent with simulations that use the full model when allosteric interactions stabilize closed channel pairs (Figs. 4 and 5, and Fig. 6 A). Mean-field simulations that include allosteric interactions that stabilize open channel pairs or both closed-closed and open-open channel pairs in a balanced fashion (not shown) are also consistent with the full model (Fig. 6, B and C).
FIGURE 10.
The mean-field approximation for a cluster of two-state RyRs is a birth-death process where transitions increase (N𝒪 = n → n+1) or decrease (N𝒪 = n → n−1) the number of open channels (N𝒪) at the release site. (A) 3 × 3 grid showing example simulations involving 25 mean-field coupled RyRs as a function of c* and ɛ𝒞𝒞 (ɛ𝒪𝒪 = 0). The average allosteric connectivity is a* = 0.13. The Score and steady-state probability distribution of NO are also shown as calculated from Q (Appendix B). (B) Birth rates (qn, n+1) used in columns of A as a function of the number of open channels (n = N𝒪). (C) Death rates (qn, n–1) used in rows of A. Dashed lines show the qn, n–1 when allosteric interactions are not included (ɛ𝒞𝒞 = ɛ𝒪𝒪 = 0). Parameters as in Table 1.
The panels of Fig. 10 B show the birth rates (qn, n+1) used in each column of Fig. 10 A plotted as a function of the number of open channels at the release site (n = N𝒪). Note that while the qn, n+1 are small when n is either small or large, the birth rates are accelerated for intermediate n, and this acceleration is enhanced as c* increases. The panels of Fig. 10 C show the death rates (qn, n–1) used in the simulations of each row of Fig. 10 A plotted as a function of n. Notice that when allosteric interactions are not included in simulations (top panel, ɛ𝒞𝒞 = ɛ𝒪𝒪 = 0), the death rates qn, n–1 are a linear increasing function of n. However, as the magnitude of ɛ𝒞𝒞 increases, qn, n–1 is accelerated for all values of n < N with the most significant acceleration at intermediate n. While Fig. 10 C shows how the death rates change with the strength of allosteric interactions that stabilize closed channel pairs, qualitatively different changes in the death rates are observed when allosteric interactions stabilize open channel pairs, or both closed-closed and open-open channel pairs in a balanced fashion. For example, when ɛ𝒞𝒞 = 0, the death rates qn, n–1 decrease for all n > 1 as ɛ𝒪𝒪 becomes more negative. On the other hand, the birth rates qn, n–1 increase for small n but decreases for large n when both ɛ𝒞𝒞 and ɛ𝒪𝒪 become more negative (results not shown).
Comparison of mean-field approximation and full model
In the previous section, we demonstrated mean-field simulations may exhibit stochastic Ca2+ excitability reminiscent of Ca2+ sparks. Similar to full model simulations, these sparks are sensitive to variations of the Ca2+ coupling strength (c*) and the allosteric coupling strengths (ɛ𝒞𝒞,ɛ𝒪𝒪) used. In this section we validate the mean-field approximation by comparing the Ca2+ spark Score estimated from Monte Carlo simulations of the full model to the Score calculated directly from the Q-matrix of the corresponding mean-field model. In this comparison, the c* and a* of the mean-field model are calculated from the C and A of the full model, and the parameters of the single-channel models used are identical.
The symbols in Fig. 11 A plot the Score (mean ± SD of 10 trials) of Monte Carlo simulations using the full model as a function of the Ca2+ coupling strength (c*) for release sites of different sizes (N) when allosteric interactions stabilize closed channel pairs (ɛ𝒞𝒞 = −0.2, ɛ𝒪𝒪 = 0). The dashed lines show the Score calculated using Q of the corresponding mean-field approximations. Both full and reduced models demonstrate that the optimal Ca2+ coupling strength, that is, the c* that yields the highest Score, decreases as a function of N. Moreover, the range of c* values that result in sparks (Score > 0.3) decreases as N increases. This inverse relationship between the optimal c* and the release site size N, and the increase in the sensitivity of sparks to variations in c* as N increases, are also observed when allosteric interactions stabilize open channel pairs (ɛ𝒞𝒞 = 0, ɛ𝒪𝒪 = −0.2) or both closed and open channel pairs in a balanced fashion (ɛ𝒞𝒞 = ɛ𝒪𝒪 = −0.2) (not shown).
FIGURE 11.
(A) The Ca2+ spark Score (mean ± SD of 10 trials) plotted as a function of the average Ca2+ coupling strength (c*) and release site size for N = 16 (diamonds), N = 25 (triangles), N = 36 (squares), and N = 49 (circles) when allosteric coupling stabilizes closed channel pairs (ɛ𝒞𝒞 = −0.2, ɛ𝒪𝒪 = 0). Dashed lines show the Score calculated using the mean-field approximation. The average allosteric connectivity (Eq. 21) is a* = 0.20 (diamonds), 0.13 (triangles), 0.095 (squares), and 0.071 (circles). Other parameters as in Table 1. (B) Data from simulations with N = 25 in A are expanded (open triangles and dashed line). Open circles show results from Monte Carlo simulations of the full model with nearest-neighbor allosteric coupling (A) but mean-field Ca2+ coupling ( ). Solid circles show results from simulations with mean-field allosteric coupling (
). Solid circles show results from simulations with mean-field allosteric coupling ( ) but using the full Ca2+ coupling matrix (C).
) but using the full Ca2+ coupling matrix (C).
Although the Score obtained using the full model and the mean-field approximation agree qualitatively (Fig. 11 A), the optimal c* and the maximum Score for any given value of N show quantitative differences that becomes more evident with large N. Fig. 11 B shows that the Score (open circles) of simulations that use mean-field Ca2+ coupling ( ) and nearest-neighbor allosteric coupling (A) are similar to mean-field model results (dashed line). Similarly, the Score (solid circles) of simulations that use the full Ca2+ coupling matrix (C) and mean-field allosteric interactions (
) and nearest-neighbor allosteric coupling (A) are similar to mean-field model results (dashed line). Similarly, the Score (solid circles) of simulations that use the full Ca2+ coupling matrix (C) and mean-field allosteric interactions ( ) show improved agreement with full model results (open triangles). These results suggest that the differences between the full model and the mean-field approximation are a consequence of the assumption of mean-field Ca2+ coupling and not the assumption of mean-field allosteric coupling.
) show improved agreement with full model results (open triangles). These results suggest that the differences between the full model and the mean-field approximation are a consequence of the assumption of mean-field Ca2+ coupling and not the assumption of mean-field allosteric coupling.
Effect of allosteric coupling on Ca2+ spark statistics
The reduced state space of the mean-field approximation (N + 1) as opposed to the full model (2N) greatly facilitates the calculation of spark statistics. For release site size of N = 25, the 2N × 2N Q-matrices of the full model exceed the memory limitations of modern workstations; consequently, the probability distribution for N𝒪 and the Score must be estimated from Monte Carlo simulation. Because the N + 1 × N + 1 Q-matrices of the mean-field approximation are comparatively small, direct matrix analytic methods can be used to calculate these response measures (Appendix B) as well as spark statistics such as duration, interspark interval, and frequency (Appendix C).
In this matrix analytic approach it is convenient to reduce the number of parameters of the mean-field model via nondimensionalization. Accordingly, we express Ca2+ concentrations in units of the dissociation constant of Ca2+ binding (K where Kη = k−/k+) and denote the nondimensional Ca2+ coupling strength and background [Ca2+] as  and
and  respectively. Substituting
respectively. Substituting  and
and  into Eq. 23 and expressing time in units of the reciprocal of the dissociation rate constant (1/k−), we arrive at the dimensionless generator matrix
into Eq. 23 and expressing time in units of the reciprocal of the dissociation rate constant (1/k−), we arrive at the dimensionless generator matrix  After nondimensionalizing, the nine parameters of the mean-field model (N, η, ɛ𝒞𝒞, ɛ𝒪𝒪, k+, k−, c∞, c*, and a*) are reduced to seven dimensionless parameters (N, η, ɛ𝒞𝒞, ɛ𝒪𝒪,
After nondimensionalizing, the nine parameters of the mean-field model (N, η, ɛ𝒞𝒞, ɛ𝒪𝒪, k+, k−, c∞, c*, and a*) are reduced to seven dimensionless parameters (N, η, ɛ𝒞𝒞, ɛ𝒪𝒪,  and a*).
and a*).
Using the  for 25 mean-field coupled RyRs, Fig. 12 shows spark duration, interspark interval, and spark frequency (grayscale) as a function of the strength of dimensionless Ca2+ coupling (
for 25 mean-field coupled RyRs, Fig. 12 shows spark duration, interspark interval, and spark frequency (grayscale) as a function of the strength of dimensionless Ca2+ coupling ( ) and allosteric interactions that stabilize closed (ɛ𝒞𝒞) and open (ɛ𝒪𝒪) channel pairs. Each panel explores a slice of this three-dimensional parameter space indicated by the shaded region of the cubes shown at the left. These correspond to allosteric interactions that stabilize closed channel pairs (Fig. 12 A, ɛ𝒞𝒞 < 0, ɛ𝒪𝒪 = 0), open channel pairs (Fig. 12 B, ɛ𝒞𝒞 = 0, ɛ𝒪𝒪 < 0), and both in a balance fashion (Fig. 12 C, ɛ𝒞𝒞 = ɛ𝒪𝒪 < 0). Spark statistics are only shown when sparks are present (Score > 0.3).
) and allosteric interactions that stabilize closed (ɛ𝒞𝒞) and open (ɛ𝒪𝒪) channel pairs. Each panel explores a slice of this three-dimensional parameter space indicated by the shaded region of the cubes shown at the left. These correspond to allosteric interactions that stabilize closed channel pairs (Fig. 12 A, ɛ𝒞𝒞 < 0, ɛ𝒪𝒪 = 0), open channel pairs (Fig. 12 B, ɛ𝒞𝒞 = 0, ɛ𝒪𝒪 < 0), and both in a balance fashion (Fig. 12 C, ɛ𝒞𝒞 = ɛ𝒪𝒪 < 0). Spark statistics are only shown when sparks are present (Score > 0.3).
FIGURE 12.
Spark duration, interspark interval, and spark frequency (in dimensionless units) of simulations involving 25 RyRs plotted as a function of the dimensionless strength of Ca2+ coupling ( ) and allosteric interactions when they stabilize closed channel pairs (A, ɛ𝒪𝒪 = 0); open channel pairs (B, ɛ𝒞𝒞 = 0); or both in a balanced fashion (C, ɛ𝒞𝒞 = ɛ𝒪𝒪). Results are only shown when parameters result in robust sparks (Score > 0.3). The average allosteric connectivity is a* = 0.13 and the dimensionless Ca2+ coupling strength is
) and allosteric interactions when they stabilize closed channel pairs (A, ɛ𝒪𝒪 = 0); open channel pairs (B, ɛ𝒞𝒞 = 0); or both in a balanced fashion (C, ɛ𝒞𝒞 = ɛ𝒪𝒪). Results are only shown when parameters result in robust sparks (Score > 0.3). The average allosteric connectivity is a* = 0.13 and the dimensionless Ca2+ coupling strength is  Other parameters as in Table 1.
Other parameters as in Table 1.
Note that similar to simulations using the full model (Figs. 6 and 7), the magnitude and range of  values that result in sparks increase as the strength of allosteric interactions that stabilize closed channel pairs increases (Fig. 12 A) and decreases as the strength of allosteric interactions that stabilize open channel pairs increases (Fig. 12 B). The magnitude and range of
values that result in sparks increase as the strength of allosteric interactions that stabilize closed channel pairs increases (Fig. 12 A) and decreases as the strength of allosteric interactions that stabilize open channel pairs increases (Fig. 12 B). The magnitude and range of  values that result in sparks does not vary significantly as the magnitude of ɛ𝒞𝒞 and ɛ𝒪𝒪 increases in a balanced fashion (Fig. 12 C). Regardless of how stabilizing allosteric interactions are introduced, spark duration and interspark interval are increasing and decreasing functions of
values that result in sparks does not vary significantly as the magnitude of ɛ𝒞𝒞 and ɛ𝒪𝒪 increases in a balanced fashion (Fig. 12 C). Regardless of how stabilizing allosteric interactions are introduced, spark duration and interspark interval are increasing and decreasing functions of  respectively. In Fig. 12, A–C, spark duration increases and interspark interval decreases in such a manner that spark frequency at first increases but ultimately decreases as a function of
respectively. In Fig. 12, A–C, spark duration increases and interspark interval decreases in such a manner that spark frequency at first increases but ultimately decreases as a function of 
While similar changes of spark statistics are seen as  increases regardless of how stabilizing allosteric interactions are included, qualitatively different changes are observed in Fig. 12, A–C, as the strength of allosteric interactions increases. Fig. 12 A shows that increasing the strength of allosteric interactions that stabilize closed channel pairs decreases spark duration and increases interspark interval. Fig. 12 B shows that increasing the strength of allosteric interactions that stabilize open channel pairs increases spark duration but has little effect on interspark interval. Fig. 12 C shows that increasing the strength of allosteric interactions that stabilize both closed-closed and open-open channel pairs in a balanced fashion decreases interspark interval, while spark duration is largely unaffected. While in Fig. 12 C spark frequency is a decreasing function of the strength of allosteric interactions, in Fig. 12, A and B, spark frequency may increase, decrease, or both, depending on the coupling strength
increases regardless of how stabilizing allosteric interactions are included, qualitatively different changes are observed in Fig. 12, A–C, as the strength of allosteric interactions increases. Fig. 12 A shows that increasing the strength of allosteric interactions that stabilize closed channel pairs decreases spark duration and increases interspark interval. Fig. 12 B shows that increasing the strength of allosteric interactions that stabilize open channel pairs increases spark duration but has little effect on interspark interval. Fig. 12 C shows that increasing the strength of allosteric interactions that stabilize both closed-closed and open-open channel pairs in a balanced fashion decreases interspark interval, while spark duration is largely unaffected. While in Fig. 12 C spark frequency is a decreasing function of the strength of allosteric interactions, in Fig. 12, A and B, spark frequency may increase, decrease, or both, depending on the coupling strength  Fig. 12, A–C, is qualitatively unchanged when the dimensionless background [Ca2+] (
Fig. 12, A–C, is qualitatively unchanged when the dimensionless background [Ca2+] ( ) is doubled or halved (not shown).
) is doubled or halved (not shown).
DISCUSSION
Although the biophysical mechanism of FK-binding protein-mediated coupling between RyRs is not well understood (13,14), several studies have presented Ca2+ release site models that represent physical coupling using single channel transition rates that are functions of the state of other channels at the release site (28,36,40). In this study, physical coupling between channels is implemented using a previously introduced methodology (36,53,54) where transition rates are modified by state-dependent allosteric interaction energies. In this formalism the physical coupling of N M-state channels is specified by an M × M matrix of interaction energies, a N × N adjacency matrix specifying the geometry of allosteric couplings, and a partitioning coefficient for each transition that determines how the allosteric interaction energies are divided between forward and reverse rate constants. Although this formalism does not explicitly model the binding and unbinding of RyRs or FK-binding proteins to allosteric sites on neighboring channels, Fig. 3, B–E, show trajectories reminiscent of experimentally observed coupled channel gating (13,14) when this methodology is used to represent stabilizing allosteric interactions. This study aims to advance our understanding of the connection between the microscopic parameters of RyR gating and the collective phenomena of Ca2+ sparks. The minimal formulation has facilitated extensive parameter studies investigating how the statistics of coupled gating (e.g., the Ca2+ spark Score and mean spark duration) depend on the strength of stabilizing allosteric interactions and Ca2+ coupling.
Allosteric coupling and Ca2+ spark generation and termination
A significant result of this study is the observation that synchronizing allosteric interactions always promote Ca2+ sparks (i.e., result in a higher Score) for some value of the strength of Ca2+ coupling (c*), regardless of whether synchronizing allosteric interactions stabilize closed channel pairs, open channel pairs, or both (see Figs. 6 and 7). When the strength of Ca2+ coupling is sufficiently large to preclude termination of simulated sparks, allosteric interactions that stabilize closed channel pairs can promote spark termination. Similarly, allosteric interactions that stabilize open channel pairs facilitate spark initiation when Ca2+ coupling is too weak to mediate stochastic Ca2+ excitability. Sparks are less sensitive to variations in c* when the strength of allosteric interactions that stabilize closed channel pairs is increased, and more sensitive to c* when the strength of allosteric interactions that stabilize open channel pairs is increased.
Allosteric coupling washout, cardiac dysfunction, and Ca2+ spark statistics
A substantial body of experimental evidence demonstrates that normal cardiac function requires the association of the 12.6 kDa FK506 binding protein FKBP12.6 to the RyR channel complex (55–58). For example, pharmacological or exercise-induced PKA hyperphosphorylation of RyRs has been shown to substantially dissociate FKBP12.6 from RyRs and has been linked to increased frequency of ventricular arrhythmias and sudden cardiac death (58,59). In addition, the absence of FKBP12.6 in knockout mice has been associated with increased systolic [Ca2+] and cardiac hypertrophy (60).
While the connection between FKBP12.6 depletion and cardiac dysfunction is not clearly established, evidence that FK-binding proteins are responsible for coupled gating of RyRs suggests that organ-level failure may be inherited from defects in the collective gating of channels leading to irregularities in the dynamics of Ca2+ sparks. In striated (skeletal and cardiac) and smooth muscle, both the frequency and duration of spontaneous sparks increase upon knockout of genes encoding relevant FK-binding proteins or treatment with FK506 or rapamycin, two drugs that physically and/or functionally dissociate FK-binding proteins from RyRs (17,49,50,60–64). Conversely, overexpression of FKBP12.6 has been shown to decrease spark frequency (51). Interestingly, these experimentally observed changes in spark duration and frequency are consistent with simulated washout of allosteric interactions that stabilize closed-closed channel pairs or both closed-closed and open-open channel pairs, but inconsistent with simulations involving the washout of allosteric interactions that stabilize only open-open channel pairs (Figs. 8 and 9). While in principle these different types of allosteric coupling could leave a signature in the distribution of spark durations, this does not appear to be the case for the minimal two-state RyR model used here (Fig. 8). While these simulations aim to clarify how changes in spark statistics due to pharmacological washout of the accessory proteins mediating allosteric coupling may indicate the type of synchronizing allosteric interactions exhibited by physically coupled RyRs, it is unclear the degree to which the results will generalize to more complicated and realistic RyR models (see below).
The mean-field approximation for allosteric interactions
The mean-field approximation formulated in this study is applicable to a cluster of RyRs coupled via both Ca2+ and allosteric interactions. Although this reduced model has a drastically contracted state space compared to full model simulations, the mean-field coupled RyRs exhibit Ca2+ sparks that are qualitatively similar to sparks of the full model (Fig. 11). However, for mean-field simulations involving a fixed number of channels and fixed allosteric coupling parameters, the Ca2+ coupling strength (c*) that results in the highest Score is slightly elevated compared to the optimal c* of corresponding full model simulations. This difference becomes more evident as the number of channels at release sites increases (Fig. 11), and may be a consequence of the spatial spread of activation or the clustering of open channels in full model simulations.
The mean-field reduction formulated here is analogous to the sticky cluster model of Sobie et al. (40) where the coupled gating of RyRs is represented by multiplying the 𝒞 → 𝒪 and 𝒪 → 𝒞 transition rates by cooperativity factors (χ𝒪 and χ𝒞) that depend on the number of open and closed channels in the cluster. For example, in Sobie et al. (40) the death rates are given by  where
where
 |
(27) |
and the scaling factor kcoop sets the strength of RyR coupling. By inspecting the death rates presented in this article (Eq. 26), one finds that the cooperativity factor in the mean-field model is
 |
(28) |
which when expressed in terms of  is
is
 |
(29) |
Note that Eq. 27 is an increasing function of N𝒞, consistent with Eq. 29, when ɛ𝒪𝒪 + ɛ𝒞𝒞 < 0, as in most of the simulations presented here. However, Eq. 29 is a nonlinear function of N𝒞 (Eq. 27 is linear), and the scaling factor for the strength of allosteric coupling (a*) enters Eq. 29 differently than kcoop in Eq. 27. Furthermore, χ′c = 1 when N𝒞 = 0 and ɛ𝒪𝒪 = 0 (and when  and ɛ𝒞𝒞 = 0) regardless of the strength of allosteric coupling (not so for χc in Eq. 27). While Eq. 27 has only one free parameter (kcoop), we would recommend using Eq. 29 because the three parameters (a*, ɛ𝒪𝒪, ɛ𝒞𝒞) are not post hoc additions to an N + 1 state model, but rather derived from the microscopic parameters of the 2N state Ca2+ release site that is reduced to N + 1 states using the mean-field approximation. Equation 29 has the additional advantage of being able to incorporate synchronizing (or desynchronizing) allosteric interactions that stabilize (or destabilize) closed channel pairs, open channel pairs, or both. Perhaps most importantly, the comparatively small state space of mean-field coupled RyR clusters could be used to mitigate against the difficulties inherent in realistic multiscale modeling of cardiac myocyte excitation-contraction coupling (65–68).
and ɛ𝒞𝒞 = 0) regardless of the strength of allosteric coupling (not so for χc in Eq. 27). While Eq. 27 has only one free parameter (kcoop), we would recommend using Eq. 29 because the three parameters (a*, ɛ𝒪𝒪, ɛ𝒞𝒞) are not post hoc additions to an N + 1 state model, but rather derived from the microscopic parameters of the 2N state Ca2+ release site that is reduced to N + 1 states using the mean-field approximation. Equation 29 has the additional advantage of being able to incorporate synchronizing (or desynchronizing) allosteric interactions that stabilize (or destabilize) closed channel pairs, open channel pairs, or both. Perhaps most importantly, the comparatively small state space of mean-field coupled RyR clusters could be used to mitigate against the difficulties inherent in realistic multiscale modeling of cardiac myocyte excitation-contraction coupling (65–68).
Generalizing the mean-field approximation
Although the single-channel model used in this article includes only two states (closed and open), the mean-field approximation can be applied to clusters of channels with more complicated single-channel dynamics that include mechanisms suspected to contribute to Ca2+ spark dynamics in situ such as luminal regulation, Ca2+-dependent inactivation, or adaptation (15,69,70). For N M-state channels there are n-choose-k{N + M – 1, N} states in the mean-field approximation, each of which can be expressed as a vector of the form (N1, N2, ···, NM) where Nm is the number of channels in state m, 1 ≤ m ≤ M, and  If the current state of the release site is (N1, N2, ···, NM) and a channel makes an i → j transition, the transition rate is Nikijχij and the appropriate cooperativity factor is
If the current state of the release site is (N1, N2, ···, NM) and a channel makes an i → j transition, the transition rate is Nikijχij and the appropriate cooperativity factor is
 |
(30) |
where νij is the previously encountered coefficient that partitions allosteric coupling between the forward and reverse transitions (0 ≤ νj ≤ 1 and νji = 1 – νij), and δki is the Krönecker delta function defined by
 |
(31) |
Limitations of the model
A potential limitation of this study is the assumption of instantaneous coupling via the local [Ca2+]. Theoretical studies of two-state Ca2+-activated channels coupled via a time-dependent Ca2+ microdomain demonstrate that the time constant of Ca2+ domain formation and collapse can affect the dynamics of puffs and sparks (29,32). For example, slow domain formation can make the triggering of sparks less likely while slow domain collapse can prohibit the termination of Ca2+ release events. On the other hand, Ca2+ release via clusters of RyRs in ventricular myocytes occurs within dyadic clefts, spatially restricted regions of the cytosol located between the sarcolemma of T-tubules and the sarcoplasmic reticulum membrane (4,71,72). Theoretical studies indicate that the time constant of Ca2+ domain formation decreases as the volume of a dyad decreases and may be <1 ms (73,74), while the decay of elevated [Ca2+] to background levels after termination of release may require 10s of milliseconds due to low affinity binding sites on the cytosolic face of the sarcolemma (74). Thus, in the context of Ca2+ release via RyR clusters in ventricular myocytes, the assumption of instantaneous coupling is more justified during the rising phase of Ca2+ release events than during the falling phase. Our prior work (29,30,32) suggests that this feature of the modeling formalism will increase the likelihood that all the open RyRs will close simultaneously, a mechanism referred to as stochastic attrition (15,71).
While the analysis of this article is simplified by assuming instantaneous Ca2+ coupling and a minimal two-state RyR, the lack of an explicit mechanism for spark termination—e.g., depletion of luminal Ca2+, Ca2+-dependent inactivation, or adaptation—results in sparks that terminate exclusively via stochastic attrition. Consequently, sparks of physiologically realistic durations are only observed over a finite range of Ca2+ coupling strengths, even when allosteric interactions are included. While allosteric interactions that stabilize closed channel pairs may potentiate spark termination via stochastic attrition when the Ca2+ coupling strength (c*) is elevated (resulting in sparks that are less sensitive to c*; see Figs. 6 A and 7 A), stabilizing allosteric interactions between closed channels do not result in robust termination of sparks at all Ca2+ coupling strengths. Taken as a whole, our simulations demonstrate that allosteric interactions may facilitate spark generation, and are often sufficient for spark termination in the absence of another mechanism such as depletion of luminal Ca2+ or Ca2+-dependent inactivation. When the strength of Ca2+ coupling is not optimal, the strength of allosteric coupling can usually be adjusted to yield robust Ca2+ sparks (Fig. 12). On the other hand, for fixed allosteric coupling parameters, the range of Ca2+ coupling strengths leading to robust sparks was never observed to be greater than 25% of the optimal Ca2+ coupling strength.
While many buffers with various binding kinetics, affinities, and diffusion constants contribute to the landscape of [Ca2+] in vivo, the mathematical representation of the Ca2+ microdomain used in this article assumes a single Ca2+ buffer. Because the single-channel model does not include mechanisms that would promote spark termination, high buffer concentrations are required to achieve Ca2+ coupling strengths that allow sparks to spontaneously terminate via stochastic attrition. For example, when the RyR is modeled with dissociation constant Kd = 5 μM and unitary current of iCa = 0.04 pA, simulations that do not include allosteric interactions require [B]T ≈ 1.2 mM to achieve the optimal Ca2+ coupling strength of c* ≈ 0.48 μM. As shown in Fig. 2 C, this coupling strength can be obtained using a variety of different values for [B]T or iCa; as expected, simulations using lower buffer concentrations with lower unitary current yield results that are similar to Fig. 6. When allosteric interactions stabilizing closed channel pair are included (ɛ𝒞𝒞 = −0.4, squares of Fig. 6 A), the optimal coupling strength of c* ≈ 0.71 μM corresponds to a total buffer concentration of [B]T ≈ 570 μM. Utilization of complex RyR gating schemes and explicit modeling of the depletion of luminal Ca2+ would likely decrease the total buffer concentration required for spark termination.
Perhaps the most significant limitation of this study is that the degree to which the results will generalize to more complicated and realistic RyR models is unknown. This concern is ever present when minimal single-channel models that reproduce select features of Ca2+-regulation are used to study the collective gating that gives rise to Ca2+ sparks (28–38). Although beyond the scope of this article, it might be possible to extend inference methods commonly used in conjunction with single-channel recording (75–77) to the collective gating of mean-field coupled intracellular channels. In this way, experimentally observed statistics of sparks (e.g., the shape of the distribution of spark durations and interspark intervals) might be used to distinguish between channels that are coupled via local [Ca2+], allosteric interactions, or both.
For now, the generalization of our results to other single-channel models can only be addressed on a case-by-case basis. For example, in the absence of allosteric interactions, instantaneously coupled two-state RyRs do not exhibit Ca2+ sparks unless the cooperativity of Ca2+ binding is two or more (η ≥ 2) (30,31). Similarly, a preliminary survey of all possible three-state single-channel models that include unimolecular Ca2+ binding suggests that multiple Ca2+-binding transitions are required for sparks (not shown). However, when stabilizing allosteric interactions are included, cooperative Ca2+ binding is no longer required, that is, η = 1 can yield robust sparks (not shown).
Our validation of the mean-field approach to modeling allosteric interactions suggests that studies utilizing more realistic RyR models could be performed using the coupling factors (Eq. 30) that are derived here for the first time. Our attempts at this further analysis include simulations of mean-field coupled three-state RyRs that include a long-lived closed state (R),
 |
(32) |
These simulations demonstrate that both Ca2+-dependent and Ca2+-independent inactivation often reduce the sensitivity of sparks to variations in the coupling strength (78). In preliminary studies we have found that stabilizing allosteric interactions can further extend the range of c* values that result in robust sparks (not shown). However, it remains to be determined whether the statistics of Ca2+ sparks can ever be used to rule out allosteric coupling as a synchronization mechanism.
Acknowledgments
This material is based upon work supported by the National Science Foundation under grants No. 0133132 and 0443843. G.D.S. gratefully acknowledges a research leave during academic year 2007–2008 supported by the College of William and Mary and a long-term visitor position at the Mathematical Biosciences Institute at Ohio State University.
APPENDIX A: EXACT NUMERICAL SIMULATION
The Ca2+ release site models presented in this article are continuous-time Markov chains simulated using Gillespie's method, a numerical method with no intrinsic time step (31,43,79). After choosing an initial release site configuration, i = (i1, i2,…,iN), this method requires the nonzero rates qij for the allowed transitions i → j to determine the subsequent release site configuration. An exponentially distributed random variable τ with mean 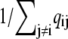 is then generated giving the dwell time in the current release site configuration i. The destination configuration j is selected by choosing a random variable Y uniformly distributed on a partitioned interval of length
is then generated giving the dwell time in the current release site configuration i. The destination configuration j is selected by choosing a random variable Y uniformly distributed on a partitioned interval of length 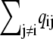 where the i → j transition occurs if Y falls on the partition associated with qij (i ≠ j). The release site configuration as a function of time is produced by repeating these steps.
where the i → j transition occurs if Y falls on the partition associated with qij (i ≠ j). The release site configuration as a function of time is produced by repeating these steps.
It remains to show how the qij rates are determined. When Q is sufficiently small to be held in memory, the required transition rates are the nonzero off-diagonal elements of the row corresponding to configuration i. When forming Q is impractical due to memory constraints, an efficient approach is to represent the release site configuration as the N × M matrix Σ where
 |
(33) |
and in is the state of channel n in release site configuration i. By arranging the required transition rates in an N × M matrix R = (rnm) where rnm gives the rate at which channel n makes an in → m transition, these rates can be found by evaluating the matrix analytic expression,
 |
(34) |
where the ° operator denotes an element × element Hadamard product. In this expression, the M × M matrices  and
and 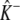 are identical to K+ and K− (Eq. 3) but with zeros on the principal diagonals, C is the N × N Ca2+ coupling matrix (Eq. 8), e is a N × 1 column vector of ones, and u is a M × 1 column vector where entries of 0 and 1 denote closed and open states in the single-channel model. Note that the column vector Σu indicates channels that are open in release site configuration i,
are identical to K+ and K− (Eq. 3) but with zeros on the principal diagonals, C is the N × N Ca2+ coupling matrix (Eq. 8), e is a N × 1 column vector of ones, and u is a M × 1 column vector where entries of 0 and 1 denote closed and open states in the single-channel model. Note that the column vector Σu indicates channels that are open in release site configuration i,  is the [Ca2+] experienced by each channel, and left multiplication by the diagonal matrix
is the [Ca2+] experienced by each channel, and left multiplication by the diagonal matrix 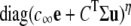 scales the association rate constants (
scales the association rate constants ( ) by the appropriate [Ca2+].The matrices
) by the appropriate [Ca2+].The matrices  and
and  that account for allosteric coupling are formed from the N × M matrix
that account for allosteric coupling are formed from the N × M matrix
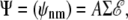 |
(35) |
where A is the N × N adjacency matrix (Eq. 12), ℰ is the M × M allosteric energy matrix (Eq. 11), and ψnm is the allosteric interaction energy that channel n would experience in release site configuration Σ provided it was in state m. The elements of the N × M matrix Ω = (ωnm) where ωnm = ψnm − ψnin give the change in allosteric energy that channel n would experience if it were to make an in → m transition. Finally, the elements of the matrices 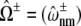 used in Eq. 34 are given by
used in Eq. 34 are given by  where ν± partition allosteric contributions between forward and reverse rates (ν− = 1 – ν+). In this article, ν+ = 0,
where ν± partition allosteric contributions between forward and reverse rates (ν− = 1 – ν+). In this article, ν+ = 0,  is an N × M matrix of ones, and
is an N × M matrix of ones, and  where
where 
APPENDIX B: CALCULATING THE STATIONARY PROBABILITY DISTRIBUTION
A continuous-time Markov chain model of a Ca2+ release site such as that considered in this article has a finite number of states and is irreducible. Consequently, the limiting probability distribution (as would be observed over an infinitely long simulation) does not depend on the initial condition. This limiting probability distribution is equal to the unique stationary distribution π satisfying global balance and conservation of probability (80), that is,
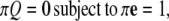 |
(36) |
where Q is the infinitesimal generator matrix, π is a row vector, and e is a commensurate column vector of ones.When Q is sufficiently small to be held in memory, Eq. 36 was solved by defining the stochastic matrix W = I + QΔt, where I is a commensurate identity matrix and Δt < 1/maxi|qii| so that wij ≥ 0. It follows from Eq. 36 and We = e that πW = π. Thus, π was found by calculating the eigenvector of W having a corresponding eigenvalue of 1.
When storage requirements for Q become excessive, π cannot be calculated directly. Instead, we estimate π from Monte Carlo simulations using
 |
(37) |
where  is the indictor set function and T is a sufficiently long observation period. While the T necessary for convergence of π may be excessive, we only require the probability distribution of the number of open channels to calculate spark statistics such as the Score. Because this distribution is a contraction of π, good estimates require a substantially shorter observation window (T).
is the indictor set function and T is a sufficiently long observation period. While the T necessary for convergence of π may be excessive, we only require the probability distribution of the number of open channels to calculate spark statistics such as the Score. Because this distribution is a contraction of π, good estimates require a substantially shorter observation window (T).
APPENDIX C: CALCULATING SPARK STATISTICS
Because the infinitesimal generator (Q) for a cluster of mean-field coupled RyRs is sufficiently small to be held in memory, the following matrix analytic method can be used to directly calculate the probability distribution of spark duration and interspark interval, as opposed to estimating these statistics from Monte Carlo simulations. Using the notation of the literature (45,81), the state space is partitioned and reorganized into aggregate classes 𝒜 and ℬ such that A is the release site configuration with no open channels (N𝒪 = 0) and ℬ represents all configurations with N𝒪 > 0. As defined above, spark duration is the sojourn time in ℬ assuming the sojourn begins with N𝒪 = κ (selected to be one-fifth the release site size, i.e., κ = 5 when N = 25). Writing Q as
 |
(38) |
where each partition contains rates for transitions between aggregate classes, the probability density function for the spark duration (X) is given by
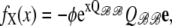 |
(39) |
where e is a N – 1 × 1 column vector of ones and φ is a 1 × N – 1 row vector containing the probability of a sojourn starting in the various states of ℬ. Because we define spark initiation as a N𝒪 = κ − 1 → κ transition,
 |
(40) |
The expectation of X is found by integrating Eq. 39,
 |
(41) |
The probability density function for interspark interval can be calculated in a similar fashion and requires only that the aggregate classes 𝒜 and ℬ be redefined and Q repartitioned such that ℬ represents all states with N𝒪 ≠ κ and 𝒜 is the state with N𝒪 = κ. In this case φ is all zeros except for the entry corresponding to N𝒪 = 0, which is set to unity.
Editor: Ian Parker.
References
- 1.Berridge, M. J. 1993. Inositol trisphosphate and calcium signaling. Nature. 361:315–325. [DOI] [PubMed] [Google Scholar]
- 2.Berridge, M. J. 1997. Elementary and global aspects of calcium signaling. J. Physiol. 499:291–306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Berridge, M. J. 2006. Calcium microdomains: organization and function. Cell Calcium. 40:405–412. [DOI] [PubMed] [Google Scholar]
- 4.Bers, D. M. 2002. Cardiac excitation-contraction coupling. Nature. 415:198–205. [DOI] [PubMed] [Google Scholar]
- 5.Cheng, H., M. R. Lederer, W. J. Lederer, and M. B. Cannell. 1996. Calcium sparks and [Ca2+]i waves in cardiac myocytes. Am. J. Physiol. 270:C148–C159. [DOI] [PubMed] [Google Scholar]
- 6.Cheng, H., W. J. Lederer, and M. B. Cannell. 1993. Calcium sparks: elementary events underlying excitation-contraction coupling in heart muscle. Science. 262:740–744. [DOI] [PubMed] [Google Scholar]
- 7.Franzini-Armstrong, C., F. Protasi, and V. Ramesh. 1999. Shape, size, and distribution of Ca2+ release units and couplons in skeletal and cardiac muscles. Biophys. J. 77:1528–1539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Franzini-Armstrong, C., F. Protasi, and V. Ramesh. 1999. Comparative ultrastructure of Ca2+ release units in skeletal and cardiac muscle. Ann. N. Y. Acad. Sci. 853:20–30. [DOI] [PubMed] [Google Scholar]
- 9.Yin, C.-C., L. M. Blayney, and F. A. Lai. 2005. Physical coupling between ryanodine receptor-calcium release channels. J. Mol. Biol. 349:538–546. [DOI] [PubMed] [Google Scholar]
- 10.Yin, C.-C., H. Han, R. Wei, and F. A. Lai. 2005. Two-dimensional crystallization of the ryanodine receptor Ca2+ release channel on lipid membranes. J. Struct. Biol. 149:219–224. [DOI] [PubMed] [Google Scholar]
- 11.Serysheva, I. I. 2005. Structural insights into excitation-contraction coupling by electron cryomicroscopy. Biochemistry (Mosc.). 69:1226–1232. [DOI] [PubMed] [Google Scholar]
- 12.Lai, F. A., M. Misra, L. Xu, H. A. Smith, and G. Meissner. 1989. The ryanodine receptor-Ca2+ release channel complex of skeletal muscle sarcoplasmic reticulum. Evidence for a cooperatively coupled, negatively charged homotetramer. J. Biol. Chem. 264:16776–16785. [PubMed] [Google Scholar]
- 13.Marx, S. O., K. Ondrias, and A. R. Marks. 1998. Coupled gating between individual skeletal muscle Ca2+ release channels (ryanodine receptors). Science. 281:818–821. [DOI] [PubMed] [Google Scholar]
- 14.Marx, S. O., J. Gaburjakova, M. Gaburjakova, C. Henrikson, K. Ondrias, and A. R. Marks. 2001. Coupled gating between cardiac calcium release channels (ryanodine receptors). Circ. Res. 88:1151–1158. [DOI] [PubMed] [Google Scholar]
- 15.Stern, M. D., and H. Cheng. 2004. Putting out the fire: what terminates calcium-induced calcium release in cardiac muscle? Cell Calcium. 35:591–601. [DOI] [PubMed] [Google Scholar]
- 16.Fill, M., and J. A. Copello. 2002. Ryanodine receptor calcium release channels. Physiol. Rev. 82:893–922. [DOI] [PubMed] [Google Scholar]
- 17.Wang, Y.-X., Y.-M. Zheng, Q.-B. Mei, Q.-S. Wang, M. L. Collier, S. Fleischer, H.-B. Xin, and M. I. Kotlikoff. 2003. FKBP12.6 and cADPR regulation of Ca2+ release in smooth muscle cells. Am. J. Physiol. Cell Physiol. 286:C538–C546. [DOI] [PubMed] [Google Scholar]
- 18.Timerman, A. P., E. Ogunbumni, E. Freund, G. Wiederrecht, A. R. Marks, and S. Fleischer. 1993. The calcium release channel of sarcoplasmic reticulum is modulated by FK-506-binding protein. Dissociation and reconstitution of FKBP-12 to the calcium release channel of skeletal muscle sarcoplasmic reticulum. J. Biol. Chem. 268:22992–22999. [PubMed] [Google Scholar]
- 19.Neher, E., and W. Almers. 1986. Patch pipettes used for loading small cells with fluorescent indicator dyes. Adv. Exp. Med. Biol. 211:1–5. [DOI] [PubMed] [Google Scholar]
- 20.Sala, F., and A. Hernández-Cruz. 1990. Calcium diffusion modeling in a spherical neuron. Relevance of buffering properties. Biophys. J. 57:313–324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Allbritton, N. L., T. Meyer, and L. Stryer. 1992. Range of messenger action of calcium ion and inositol 1,4,5-trisphosphate. Science. 258:1812–1815. [DOI] [PubMed] [Google Scholar]
- 22.Wagner, J., and J. Keizer. 1994. Effects of rapid buffers on Ca2+ diffusion and Ca2+ oscillations. Biophys. J. 67:447–456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Smith, G. D. 1996. Analytical steady-state solution to the rapid buffering approximation near an open Ca2+ channel. Biophys. J. 71:3064–3072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gabso, M., E. Neher, and M. E. Spira. 1997. Low mobility of the Ca2+ buffers in axons of cultured Aplysia neurons. Neuron. 18:473–481. [DOI] [PubMed] [Google Scholar]
- 25.Naraghi, M., and E. Neher. 1997. Linearized buffered Ca2+ diffusion in microdomains and its implications for calculation of [Ca2+] at the mouth of a calcium channel. J. Neurosci. 17:6961–6973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Neher, E. 1998. Usefulness and limitations of linear approximations to the understanding of Ca++ signals. Cell Calcium. 24:345–357. [DOI] [PubMed] [Google Scholar]
- 27.Smith, G. D., L. Dai, R. Miura, and A. Sherman. 2001. Asymptotic analysis of buffered calcium diffusion near a point source. SIAM J. Appl. Math. 61:1816–1838. [Google Scholar]
- 28.Hinch, R. 2004. A mathematical analysis of the generation and termination of calcium sparks. Biophys. J. 86:1293–1307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Mazzag, B., C. J. Tignanelli, and G. D. Smith. 2005. The effect of residual Ca2+ on the stochastic gating of Ca2+-regulated Ca2+ channel models. J. Theor. Biol. 235:121–150. [DOI] [PubMed] [Google Scholar]
- 30.DeRemigio, H., and G. D. Smith. 2005. The dynamics of stochastic attrition viewed as an absorption time on a terminating Markov chain. Cell Calcium. 38:73–86. [DOI] [PubMed] [Google Scholar]
- 31.Nguyen, V., R. Mathias, and G. D. Smith. 2005. A stochastic automata network descriptor for Markov chain models of instantaneously coupled intracellular Ca2+ channels. Bull. Math. Biol. 67:393–432. [DOI] [PubMed] [Google Scholar]
- 32.Huertas, M. A., and G. D. Smith. 2007. The dynamics of luminal depletion and the stochastic gating of Ca2+-activated Ca2+ channels and release sites. J. Theor. Biol. 246:332–354. [DOI] [PubMed] [Google Scholar]
- 33.Rengifo, J., R. Rosales, A. González, H. Cheng, M. D. Stern, and E. Ríos. 2002. Intracellular Ca2+ release as irreversible Markov process. Biophys. J. 83:2511–2521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ríos, E., and M. D. Stern. 1997. Calcium in close quarters: microdomain feedback in excitation-contraction coupling and other cell biological phenomena. Annu. Rev. Biophys. Biomol. Struct. 26:47–82. [DOI] [PubMed] [Google Scholar]
- 35.Shuai, J. W., and P. Jung. 2002. Optimal intracellular calcium signaling. Phys. Rev. Lett. 88:068102. [DOI] [PubMed] [Google Scholar]
- 36.Stern, M. D., L. S. Song, H. Cheng, J. S. Sham, H. T. Yang, K. R. Boheler, and E. Ríos. 1999. Local control models of cardiac excitation-contraction coupling. A possible role for allosteric interactions between ryanodine receptors. J. Gen. Physiol. 113:469–489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Swillens, S., P. Champeil, L. Combettes, and G. Dupont. 1998. Stochastic simulation of a single inositol 1,4,5-trisphosphate-sensitive Ca2+ channel reveals repetitive openings during “blip-like” Ca2+ transients. Cell Calcium. 23:291–302. [DOI] [PubMed] [Google Scholar]
- 38.Swillens, S., G. Dupont, L. Combettes, and P. Champeil. 1999. From calcium blips to calcium puffs: theoretical analysis of the requirements for interchannel communication. Proc. Natl. Acad. Sci. USA. 96:13750–13755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.DeRemigio, H., J. Groff, and G. Smith. 2007. The spatial organization of calcium release sites and the dynamics of puffs and sparks. Biophysical Society Annual Meeting Abstracts, Program No. 1211, Baltimore, MD.
- 40.Sobie, E. A., K. W. Dilly, J. dos Santos Cruz, W. J. Lederer, and M. S. Jafri. 2002. Termination of cardiac Ca2+ sparks: an investigative mathematical model of calcium-induced calcium release. Biophys. J. 83:59–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Groff, J., and G. Smith. 2007. A computational investigation of the effects of allosteric coupling between ryanodine receptors on the dynamics of calcium sparks. Biophysical Society Annual Meeting Abstracts, Program No. 1209, Baltimore, MD.
- 42.Colquhoun, D., and A. Hawkes. 1995. A Q-matrix cookbook: how to write only one program to calculate the single-channel and macroscopic predictions for any kinetic mechanism. In Single-Channel Recording. B. Sakmann and E. Neher, editors. Plenum Press, New York.
- 43.Smith, G. 2002. Modeling the stochastic gating of ion channels. In Computational Cell Biology. C. Fall, E. Marland, J. Wagner, and J. Tyson, editors. Springer-Verlag, London, Heidelberg.
- 44.Norris, J. 1997. Markov Chains. Cambridge University Press, Cambridge, UK.
- 45.Ball, F. G., R. K. Milne, and G. F. Yeo. 2000. Stochastic models for systems of interacting ion channels. IMA J. Math. Appl. Med. Biol. 17:263–293. [PubMed] [Google Scholar]
- 46.Mejía-Alvarez, R., C. Kettlun, E. Ríos, M. Stern, and M. Fill. 1999. Unitary Ca2+ current through cardiac ryanodine receptor channels under quasi-physiological ionic conditions. J. Gen. Physiol. 113:177–186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kettlun, C., A. González, E. Ríos, and M. Fill. 2003. Unitary Ca2+ current through mammalian cardiac and amphibian skeletal muscle ryanodine receptor channels under near-physiological ionic conditions. J. Gen. Physiol. 122:407–417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Guatimosim, S., K. Dilly, L. F. Santana, M. S. Jafri, E. A. Sobie, and W. J. Lederer. 2002. Local Ca2+ signaling and EC coupling in heart: Ca2+ sparks and the regulation of the [Ca2+]i transient. J. Mol. Cell. Cardiol. 34:941–950. [DOI] [PubMed] [Google Scholar]
- 49.Ji, G., M. E. Feldman, K. S. Greene, V. Sorrentino, H.-B. Xin, and M. I. Kotlikoff. 2004. RyR2 proteins contribute to the formation of Ca2+ sparks in smooth muscle. J. Gen. Physiol. 123:377–386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Yoshihara, S., H. Satoh, M. Saotome, H. Katoh, H. Terada, H. Watanabe, and H. Hayashi. 2005. Modification of sarcoplasmic reticulum (SR) Ca2+ release by FK506 induces defective excitation-contraction coupling only when SR Ca2+ recycling is disturbed. Can. J. Physiol. Pharmacol. 83:357–366. [DOI] [PubMed] [Google Scholar]
- 51.Gómez, A. M., I. Schuster, J. Fauconnier, J. Prestle, G. Hasenfuss, and S. Richard. 2004. FKBP12.6 overexpression decreases Ca2+ spark amplitude but enhances [Ca2+]i transient in rat cardiac myocytes. Am. J. Physiol. Heart Circ. Physiol. 287:H1987–H1993. [DOI] [PubMed] [Google Scholar]
- 52.Nicola, V. 1998. Lumping in Markov Reward Processes. Technical report, RC14719. IBM Thomas Watson Research Centre, Yorktown Heights, NY.
- 53.Duke, T. A., and D. Bray. 1999. Heightened sensitivity of a lattice of membrane receptors. Proc. Natl. Acad. Sci. USA. 96:10104–10108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Duke, T. A., N. L. Novère, and D. Bray. 2001. Conformational spread in a ring of proteins: a stochastic approach to allostery. J. Mol. Biol. 308:541–553. [DOI] [PubMed] [Google Scholar]
- 55.Lehnart, S. E., X. H. T. Wehrens, A. Kushnir, and A. R. Marks. 2004. Cardiac ryanodine receptor function and regulation in heart disease. Ann. N. Y. Acad. Sci. 1015:144–159. [DOI] [PubMed] [Google Scholar]
- 56.Lehnart, S. E., X. H. T. Wehrens, and A. R. Marks. 2004. Calstabin deficiency, ryanodine receptors, and sudden cardiac death. Biochem. Biophys. Res. Commun. 322:1267–1279. [DOI] [PubMed] [Google Scholar]
- 57.Wehrens, X. H. T., S. E. Lehnart, F. Huang, J. A. Vest, S. R. Reiken, P. J. Mohler, J. Sun, S. Guatimosim, L. S. Song, N. Rosemblit, J. M. D'Armiento, C. Napolitano, M. Memmi, S. G. Priori, W. J. Lederer, and A. R. Marks. 2003. FKBP12.6 deficiency and defective calcium release channel (ryanodine receptor) function linked to exercise-induced sudden cardiac death. Cell. 113:829–840. [DOI] [PubMed] [Google Scholar]
- 58.Wehrens, X. H. T., S. E. Lehnart, S. R. Reiken, S.-X. Deng, J. A. Vest, D. Cervantes, J. Coromilas, D. W. Landry, and A. R. Marks. 2004. Protection from cardiac arrhythmia through ryanodine receptor-stabilizing protein calstabin2. Science. 304:292–296. [DOI] [PubMed] [Google Scholar]
- 59.Marx, S. O., S. Reiken, Y. Hisamatsu, T. Jayaraman, D. Burkhoff, N. Rosemblit, and A. R. Marks. 2000. PKA phosphorylation dissociates FKBP12.6 from the calcium release channel (ryanodine receptor): defective regulation in failing hearts. Cell. 101:365–376. [DOI] [PubMed] [Google Scholar]
- 60.Xin, H.-B., T. Senbonmatsu, D.-S. Cheng, Y.-X. Wang, J. A. Copello, G.-J. Ji, M. L. Collier, K.-Y. Deng, L. H. Jeyakumar, M. A. Magnuson, T. Inagami, M. I. Kotlikoff, and S. Fleischer. 2002. Estrogen protects FKBP12.6 null mice from cardiac hypertrophy. Nature. 416:334–338. [DOI] [PubMed] [Google Scholar]
- 61.Xiao, R. P., H. H. Valdivia, K. Bogdanov, C. Valdivia, E. G. Lakatta, and H. Cheng. 1997. The immunophilin FK506-binding protein modulates Ca2+ release channel closure in rat heart. J. Physiol. 500:343–354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.McCall, E., L. Li, H. Satoh, T. R. Shannon, L. A. Blatter, and D. M. Bers. 1996. Effects of FK-506 on contraction and Ca2+ transients in rat cardiac myocytes. Circ. Res. 79:1110–1121. [DOI] [PubMed] [Google Scholar]
- 63.Lukyanenko, V., T. F. Wiesner, and S. Gyorke. 1998. Termination of Ca2+ release during Ca2+ sparks in rat ventricular myocytes. J. Physiol. 507:667–677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Acker, K. V., G. Bultynck, D. Rossi, V. Sorrentino, N. Boens, L. Missiaen, H. D. Smedt, J. B. Parys, and G. Callewaert. 2004. The 12 kDa FK506-binding protein, FKBP12, modulates the Ca2+-flux properties of the type-3 ryanodine receptor. J. Cell Sci. 117:1129–1137. [DOI] [PubMed] [Google Scholar]
- 65.Greenstein, J. L., and R. L. Winslow. 2002. An integrative model of the cardiac ventricular myocyte incorporating local control of Ca2+ release. Biophys. J. 83:2918–2945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Greenstein, J. L., R. Hinch, and R. L. Winslow. 2006. Mechanisms of excitation-contraction coupling in an integrative model of the cardiac ventricular myocyte. Biophys. J. 90:77–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Hinch, R., J. L. Greenstein, and R. L. Winslow. 2006. Multi-scale models of local control of calcium induced calcium release. Prog. Biophys. Mol. Biol. 90:136–150. [DOI] [PubMed] [Google Scholar]
- 68.Williams, G. S. B., M. A. Huertas, E. A. Sobie, M. S. Jafri, and G. D. Smith. 2007. A probability density approach to modeling local control of calcium-induced calcium release in cardiac myocytes. Biophys. J. 92:2311–2328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Györke, I., and S. Györke. 1998. Regulation of the cardiac ryanodine receptor channel by luminal Ca2+involves luminal Ca2+ sensing sites. Biophys. J. 75:2801–2810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Györke, S. 1999. Ca2+ spark termination: inactivation and adaptation may be manifestations of the same mechanism. J. Gen. Physiol. 114:163–166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Stern, M. D. 1992. Theory of excitation-contraction coupling in cardiac muscle. Biophys. J. 63:497–517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Franzini-Armstrong, C., F. Protasi, and P. Tijskens. 2005. The assembly of calcium release units in cardiac muscle. Ann. N. Y. Acad. Sci. 1047:76–85. [DOI] [PubMed] [Google Scholar]
- 73.Koh, X., B. Srinivasan, H. S. Ching, and A. Levchenko. 2006. A 3D Monte Carlo analysis of the role of dyadic space geometry in spark generation. Biophys. J. 90:1999–2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Langer, G. A., and A. Peskoff. 1996. Calcium concentration and movement in the diadic cleft space of the cardiac ventricular cell. Biophys. J. 70:1169–1182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Ball, F. G., and M. S. Sansom. 1989. Ion-channel gating mechanisms: model identification and parameter estimation from single channel recordings. Proc. R. Soc. Lond. B. Biol. Sci. 236:385–416. [DOI] [PubMed] [Google Scholar]
- 76.Yeo, G. F., R. K. Milne, R. O. Edeson, and B. W. Madsen. 1988. Statistical inference from single channel records: two-state Markov model with limited time resolution. Proc. R. Soc. Lond. B. Biol. Sci. 235:63–94. [DOI] [PubMed] [Google Scholar]
- 77.Hodgson, M., and P. J. Green. 1999. Bayesian choice among Markov models of ion channels using Markov chain Monte Carlo. Proc. Math. Phys. Eng. Sci. 455:3425–3448. [Google Scholar]
- 78.Groff, J., and G. Smith. 2007. Calcium-dependent inactivation and the dynamics of calcium puffs and sparks. J. Theor. Biol. In press. [DOI] [PubMed]
- 79.Gillespie, D. T. 1976. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 22:403–434. [Google Scholar]
- 80.Stewart, W. 1994. Introduction to the Numerical Solution of Markov Chains. Princeton University Press, Princeton, NJ.
- 81.Ball, F., and Y. Geoffrey. 2000. Superposition of spatially interacting aggregated continuous time Markov chains. Methodol. Comput. Appl. Probab. 2:93–116. [Google Scholar]
- 82.Falke, J. J., S. K. Drake, A. L. Hazard, and O. B. Peersen. 1994. Molecular tuning of ion binding to calcium signaling proteins. Q. Rev. Biophys. 27:219–290. [DOI] [PubMed] [Google Scholar]
- 83.Radermacher, M., V. Rao, R. Grassucci, J. Frank, A. P. Timerman, S. Fleischer, and T. Wagenknecht. 1994. Cryo-electron microscopy and three-dimensional reconstruction of the calcium release channel/ryanodine receptor from skeletal muscle. J. Cell Biol. 127:411–423. [DOI] [PMC free article] [PubMed] [Google Scholar]














