Abstract
The sarcoplasmic reticulum (SR) in ventricular myocytes contains releasable Ca2+ for activating cellular contraction. Recent measurements of intra-SR (luminal) Ca2+ suggest a high diffusive Ca2+-mobility constant (DCaSR). This could help spatially to unify SR Ca2+-content ([Ca2+]SRT) and standardize Ca2+-release throughout the cell. But measurements of localized depletions of luminal Ca2+ (Ca2+-blinks), associated with local Ca2+-release (Ca2+-sparks), suggest DCaSR may actually be low. Here we describe a novel method for measuring DCaSR. Using a cytoplasmic Ca2+-fluorophore, we estimate regional [Ca2+]SRT from localized, caffeine-induced SR Ca2+-release. Caffeine microperfusion of one end of a guinea pig or rat myocyte diffusively empties the whole SR at a rate indicating DCaSR is 8–9 μm2/s, up to tenfold lower than previous estimates. Ignoring background SR Ca2+-leakage in our measurement protocol produces an artifactually high DCaSR (>40 μm2/s), which may also explain the previous high values. Diffusion-reaction modeling suggests that a low DCaSR would be sufficient to support local SR Ca2+-signaling within sarcomeres during excitation-contraction coupling. Low DCaSR also implies that [Ca2+]SRT may readily become spatially nonuniform, particularly under pathological conditions of spatially nonuniform Ca2+-release. Local control of luminal Ca2+, imposed by low DCaSR, may complement the well-established local control of SR Ca2+-release by Ca2+-channel/ryanodine receptor couplons.
INTRODUCTION
The sarcoplasmic reticulum (SR) is the primary store of releasable Ca2+ within a mammalian myocyte. In ventricular cells, the SR is a reticular, luminally continuous compartment, occupying 3%–4% of cell volume (1,2). Free Ca2+-ion concentration in the loaded SR ([Ca2+]SR) is probably 0.5–1.0 mM, 5000–10,000-fold higher (3) than diastolic Ca2+-ion concentration in the cytoplasm ([Ca2+]i). Ca2+-release from the SR is central to excitation-contraction coupling in the heart. It accounts for most of the cytosolic Ca2+-transient required to activate the myofilaments (4). Release is controlled locally through couplons, small units composed of a sarcolemmal L-type Ca2+-channel (LCC), closely apposed to several ryanodine receptor (RyR) channels in the SR membrane (5). Influx of extracellular Ca2+ through the LCC opens the attendant RyRs via a process of Ca2+-induced Ca2+-release, allowing a local release of Ca2+, from SR to cytosol (4,5). Using fluorescent techniques, this release can be measured as a Ca2+-spark (6). The synchronized operation of many thousands of couplons within a cardiac cell underpins the global Ca2+-transient that is triggered by an action potential (4).
The local nature of SR Ca2+-release via couplons is reinforced by a low cytoplasmic Ca2+-mobility (∼14 μm2/s) (7), which limits the spatial spread of Ca2+ from its source. This ensures that rogue Ca2+-sparks, when they occur randomly, do not readily induce a global Ca2+-release from the SR. Although Ca2+ released at couplons is localized by low Ca2+-mobility in cytoplasm, it is far from clear whether Ca2+-movements are equally localized in the lumen of the SR. The use of a low-affinity Ca2+-fluorophore, Fluo-5N, to measure ionized Ca2+-concentration ([Ca2+]SR) within isolated cardiomyocytes, was pioneered by Bers and colleagues (8,9). Using this technique in rabbit ventricular myocytes, they and others have observed a transient fall of global [Ca2+]SR (termed a Ca2+-scrap (8)), which coincides with the electrically evoked cytosolic Ca2+-transient.
Within a sarcomere, the time course of the scrap appears uniform throughout the SR, suggesting that high luminal Ca2+-mobility may be minimizing local [Ca2+]SR gradients. The result is of great interest, given that Ca2+ released from terminal cisternae of the junctional SR (jSR) is resequestered remotely by SR Ca2+-ATPase (SERCA) pumps located on network SR (nSR) (2,10), which then diffusively feeds the Ca2+ back into the jSR, a recycling distance of 1–2 μm. The proposal for high SR Ca2+-mobility (DCaSR) has gained further support from Fluo-5N measurements of global Ca2+-diffusion within the SR, suggesting DCaSR is four- to fivefold higher (60 μm2/s) (9) than Ca2+-mobility in cytoplasm. Such high mobility would be occurring in the face of high SR tortuosity and high-capacity luminal buffers like calsequestrin, which are expressed in the jSR (2,11). A high DCaSR has also been proposed recently to be necessary for the propagation of cytosolic Ca2+-waves in cardiac cells subjected to intracellular Ca2+-overload (12).
The concept of high DCaSR appears to be challenged by the observation of local jSR Ca2+-depletions (termed Ca2+-blinks (2,13,14)), which coincide with the generation of cytosolic Ca2+-sparks. A Ca2+-blink is the luminal consequence of local jSR Ca2+-release. The Ca2+-blink occurs with no apparent change in adjacent nSR [Ca2+]i (2) and recovers to control levels in 100–200 ms. If, as proposed (2,14), recovery is due to Ca2+-diffusion from nSR to jSR, this implies significant resistance to luminal Ca2+-movement, at least at the nSR-jSR junction. Such an arrangement would predict that global movement of Ca2+ throughout the SR, such as measured previously using Fluo-5N, would be rate limited by low mobility and high Ca2+-buffering in the jSR. If this were so, the global DCaSR would appear low, not high. A low global DCaSR may also be compounded by the tenuous nSR that links successive sarcomeres within a myocyte (2) and that may functionally isolate adjacent SR pools of Ca2+. In an attempt to resolve the apparently discrepant predictions for DCaSR, we reexamined the question of global SR Ca2+-mobility in a ventricular myocyte.
We have designed a, to our knowledge, novel method for measuring DCaSR, without using Fluo-5N loaded into the SR. This avoids the possibility of the fluorophore (KCa ≈ 0.4 mM) (9) artifactually enhancing luminal Ca2+-mobility through its action as a mobile Ca2+-buffer. Our method involves draining Ca2+ slowly from the SR by opening RyRs at one end, using a local exposure to caffeine. The drainage rate is estimated by then applying caffeine to the rest of the SR, after a given time interval, and measuring the residual Ca2+ released, using a cytoplasmic Ca2+-fluorophore (Fluo-3). The technique has allowed us to estimate DCaSR in both rat and guinea pig ventricular myocytes. Interestingly, these particular cells cannot be loaded reliably with the SR dye, Fluo-5N (15); so this method is the only one available for measuring their DCaSR. It appears to be low, equal to or even lower than estimates of cytoplasmic Ca2+-mobility. Possible reasons for the discrepancy between our measurement of DCaSR and the high values suggested previously are considered. We use mathematical modeling to investigate the potential consequences of low DCaSR for the cycling of SR Ca2+ within a sarcomere and for the localization of luminal Ca2+-events such as Ca2+-blinks and other nanoscopic or microscopic SR phenomena.
METHODS
Solutions
Normal Tyrode (NT) contained 130 mM NaCl, 4.5 mM KCl, 20 mM Hepes, 2 mM CaCl2, 1 mM MgCl2, 11 mM glucose. 0Na0Ca Tyrode contained 120 mM N-methyl-D-glucamine (NMDG), 4.5 mM KCl, 20 mM Hepes, 1 mM MgCl2, 0.5 mM EGTA, 11 mM glucose. 0Na10Ca Tyrode was as for 0Na0Ca, but with 10 mM CaCl2 and 110 mM NMDG and no EGTA. Solution pH was adjusted to 7.4 with 5 M HCl (0Na0Ca/0Na10Ca) or 4 M NaOH (NT). Cyclopiazonic acid (CPA), caffeine, and tetracaine (Tet) were obtained from Sigma (Dorset, UK).
Cell preparation
Rat and guinea pig ventricular myocytes were isolated by a combination of enzymatic (Roche Blendzyme III for rat (Roche, Basle, Switzerland); Sigma collagenase for guinea pig) and mechanical dispersion (16,17). Cells in Dulbecco's modified Eagle's medium were loaded (10 min) with the AM-ester of Fluo-3 (stock in DMSO; final concentration 10 μM) or, in one experimental series, carboxy-SNARF-1 (10 μM). Cells were superfused at 37°C in a chamber mounted on a DM-IRBE microscope (Leica, Wetzlar, Germany). Cell adhesion was improved by pretreating the chamber with poly-L-lysine (0.01%). Pacing (to load SR) was achieved by field stimulation through two platinum wires in the chamber.
Confocal imaging and analysis
Cells were imaged confocally (Leica TCS-NT). Fluo-3 was excited (488 nm argon laser), and fluorescence emission (>515 nm) was collected by a photomultiplier tube (for dye calibration, see Fig. S1 in Supplementary Material, Data S1). Images in xyt-mode were acquired at 256 × 256 pixels every 1.1 s. Line scans along the long axis of a myocyte were acquired at 256 pixels every 2.5 ms. In-house ImageJ (National Institutes of Health, Bethesda, MD) macros were used for background-subtraction and myocyte-edge detection. Fluorescence was averaged in regions of interest (ROIs) and then normalized to diastolic fluorescence (F0). Data are presented as mean ± SE.
Protocol for Ca2+-loading and stabilizing SR
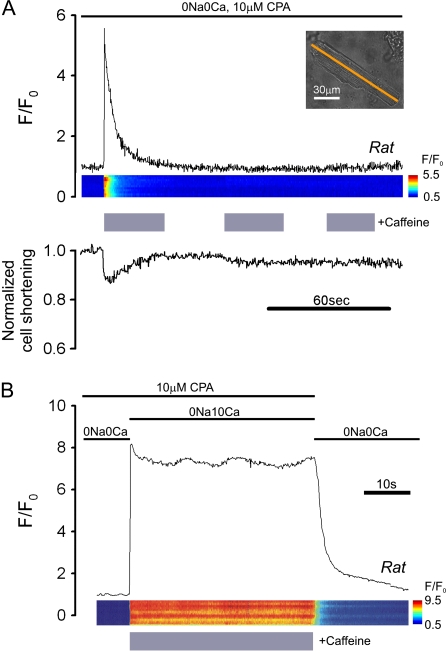
Before experiments, myocytes were initially paced electrically (2 Hz) for up to 2 min to load the SR with Ca2+. Sarcolemmal Ca2+-flux (through L-type channels and Na+/Ca2+ exchange) was then eliminated by halting stimulation and superfusing myocytes with Na+-free Ca2+-free solution (0Na0Ca) (9,18,19). This did not alter resting [Ca2+]i, but it initially triggered Ca2+-waves (Fig. 1 A). These suggested fluctuations in [Ca2+]SR, which would complicate our analysis. We therefore blocked SERCA by including 10 μM CPA in 0Na0Ca (“stabilizing solution”, SS), and we attenuated SR Ca2+-leak (which blocked the occurrence of Ca2+-waves) with 0.3 mM or 2 mM Tet. In the presence of SS + Tet, steady-state F/F0 decreased by 25%, within 2 min, following a similar time course in both doses of Tet (Fig. 1 B). This fall in fluorescence was not due to quenching of Fluo-3 fluorescence by Tet or CPA, as it was absent in cells AM-loaded with 100 μM BAPTA, an intracellular Ca2+-buffer that clamps [Ca2+]i (Fig. 1 C). Cells stabilized in SS + Tet were used for the main experimental work. Once experiments performed in SS were completed, cells were superfused in NT again. This was used to correct for dye leakage by fixing F/F0 at 1.0 in NT at steady state ([Ca2+]i = 100 nM).
FIGURE 1.
Protocol for stabilizing SR Ca2+ load. Rat myocytes. (A) Fluo-3 fluorescence (F/F0) was measured in cells paced at 2 Hz in NT, and then superfused with 0Na0Ca medium (fluorescence normalized to diastolic levels in NT). Ca2+-waves were observed in the first 2 min in 0Na0Ca. After waves ceased, diastolic F/F0 was ∼1. (B) In 0Na0Ca solution with SERCA inhibited by 10 μM CPA (stabilizing solution, SS), RyRs were dose-dependently inhibited by 0.3 or 2 mM Tet. Inclusion of Tet in SS-superfusate blocked Ca2+-waves. At both doses of Tet, resting F/F0 stabilized (at a 25% lower level) with a half-time of ∼36 s. Cells stabilized in SS + Tet were then used for the main experiments. (C) The reduction of resting F/F0 observed in the presence of SS + Tet was absent in rat cells preloaded with 100 μM BAPTA-AM. (A–C) Mean of 7–10 cells.
Measuring total SR Ca2+-content
Total SR Ca2+ ([Ca2+]SRT; free + buffered) was estimated by superfusing Tet-free SS containing 10 mM caffeine (to activate maximally RyR channel opening) (20) and then measuring the peak rise of [Ca2+]i (with Fluo-3; Fig. 2 A). Superfusion details are given in the next section. Although the fluorescence rise was transient, further caffeine challenges induced no additional Ca2+-release (even after six consecutive caffeine episodes), confirming that the caffeine-sensitive store had been discharged completely and that SERCAs were fully inhibited by CPA. The recovery of [Ca2+]i observed in caffeine (Fig. 2 A) is most likely caused by Ca2+-extrusion from the cell on PMCA (plasmalemmal Ca2+-ATPase) (19), as recovery was reversibly inhibited by raising superfusate [Ca2+] to 10 mM (Fig. 2 B), a maneuver known to inhibit the pump (19,21).
FIGURE 2.
Mobilizing SR Ca2+ with caffeine. (A) Rat myocyte, AM-loaded with Fluo-3 and initially paced at 2 Hz in NT was then superfused with 0Na0Ca medium containing 10 μM CPA (stabilizing solution, SS), interspersed with three 30-s episodes of SS + 10 mM caffeine. (Upper panel) time course for F/F0 averaged along a longitudinal line scan (inset indicates position of line scan axis); (middle panel) F/F0 line scan; (lower panel) cell shortening. The first caffeine exposure mobilizes all SR Ca2+. (B) Different rat myocyte exposed to SS containing 10 mM caffeine and 10 mM [Ca2+]o; note lack of  -recovery, suggesting block of sarcolemmal PMCA. Final recovery in 0Na0Ca (with zero CPA) is attributable to SERCA and PMCA activity.
-recovery, suggesting block of sarcolemmal PMCA. Final recovery in 0Na0Ca (with zero CPA) is attributable to SERCA and PMCA activity.
Some experiments required estimating [Ca2+]SRT with a caffeine challenge immediately after a period of Tet superfusion. This was possible, as the inhibitory effects of Tet on RyR channels and the SR Ca2+ leak are fast (<3 s) and reversible (22,23). This was confirmed in this work from measurements of  in the absence of CPA, showing that resting F/F0 reversibly decreased by 19.5% ± 1.7% with a half-time of 2.7 ± 0.3 s on 0.3 mM Tet application and removal (n = 5; data not illustrated), consistent with rapid and reversible attenuation of SR Ca2+ leak. A slow Tet washout might be expected to reduce subsequent RyR activation by caffeine, and thus the mobilization of SR Ca2+. It is notable, therefore, that pretreating cells with 0.3 mM or 2 mM Tet for 2 min did not attenuate the caffeine-induced rise of
in the absence of CPA, showing that resting F/F0 reversibly decreased by 19.5% ± 1.7% with a half-time of 2.7 ± 0.3 s on 0.3 mM Tet application and removal (n = 5; data not illustrated), consistent with rapid and reversible attenuation of SR Ca2+ leak. A slow Tet washout might be expected to reduce subsequent RyR activation by caffeine, and thus the mobilization of SR Ca2+. It is notable, therefore, that pretreating cells with 0.3 mM or 2 mM Tet for 2 min did not attenuate the caffeine-induced rise of  (measured in Tet-free SS), again consistent with rapid Tet washout. After 2 min pretreatment with SS + 0.3 mM Tet, the caffeine-evoked peak F/F0 was 5.0 ± 0.4 (fluorescence-rise normalized to resting fluorescence in NT solution; n = 8); after 2 min pretreatment with SS + 2 mM Tet, F/F0 = 5.6 ± 0.2 (n = 7); after 2 min pretreatment with SS + zero Tet, F/F0 = 4.9 ± 0.7 (n = 6).
(measured in Tet-free SS), again consistent with rapid Tet washout. After 2 min pretreatment with SS + 0.3 mM Tet, the caffeine-evoked peak F/F0 was 5.0 ± 0.4 (fluorescence-rise normalized to resting fluorescence in NT solution; n = 8); after 2 min pretreatment with SS + 2 mM Tet, F/F0 = 5.6 ± 0.2 (n = 7); after 2 min pretreatment with SS + zero Tet, F/F0 = 4.9 ± 0.7 (n = 6).
Localizing the caffeine exposure
Rapid caffeine exposure was performed using a dual-microperfusion apparatus (16,17,24,25), which can switch between solutions in <1 s. The device releases two microstreams from a double-barreled square-bore pipette, maintaining a sharp interstream boundary (<10 μm) due to high flow (1–2 mL/min) (16,25). The width of a single microstream (∼300 μm) is sufficient to ensure that a whole myocyte, oriented at right angles to the flow, can be exposed uniformly to a solution held in one of the barrels. In this way, a myocyte could be uniformly exposed to a caffeine-containing solution. When required, a myocyte was regionally exposed to the drug by positioning the interstream boundary such that ∼25% of the cell length was enveloped by the caffeine microstream, whereas the rest of the cell was exposed to a caffeine-free microstream. To visualize the boundary optically, one microstream also contained 10 mM sucrose, which itself had no effect on Ca2+-signaling (16).
During partial exposure of a myocyte to caffeine, the drug's high membrane permeability (20 μm/s (26)) will ensure that its intracellular compartmentalization is similar to that imposed extracellularly. Caffeine, as a solute of molecular mass 200 Da, is expected to diffuse at ∼50 μm2/s (estimated from Swietach and Vaughan-Jones (17)). For a 120-μm-long myocyte exposed proximally along 25% of its length to 10 mM caffeine, steady-state [caffeine]i at the distal end of the cell is expected to be <20 nM. [caffeine]i will fall to 1% (0.1 mM) within 6 μm of the midpoint of the microstream boundary (see Fig. S2 in Data S1 for the solution to a mathematical model of intracellular caffeine diffusion during partial extracellular exposure). Since the half-maximal caffeine dose for RyR channel opening in intact cells is 2–3 mM (27), the sharp compartmentalization of [caffeine]i will translate into a sharp compartmentalization of caffeine-induced RyR channel opening. Due to low cytosolic Ca2+-mobility, the spread of  will exceed the [caffeine]i profile by only 7% of cell length (see Appendix 1).
will exceed the [caffeine]i profile by only 7% of cell length (see Appendix 1).
RESULTS
Estimating SR Ca2+-leak
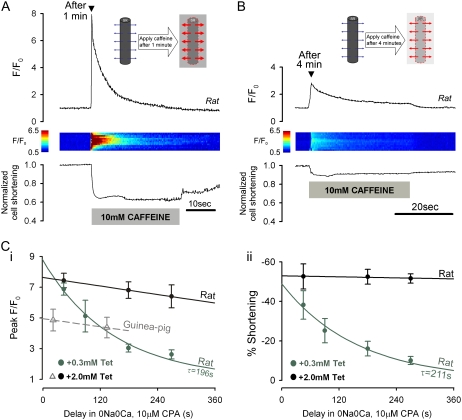
When SERCA is inhibited (for example, with CPA), SR-membrane leakage slowly depletes the SR (18). As described later, the leakage must be known when estimating DCaSR. Leakage was assessed by assaying [Ca2+]SRT with caffeine at various times after switching a cell into SS. Fig. 3, A and B, shows specimen confocal longitudinal line scan recordings of [Ca2+]i (rat myocytes), indicating that caffeine-induced Ca2+-release was smaller after 4 min than after 1 min, consistent with SR leakage depleting [Ca2+]SRT. Data pooled in Fig. 3 C indicate a time constant of ∼200 s for the decline with 0.3 mM Tet but a much slower decline with 2 mM Tet. Fig. 3 Cii shows that the decline was paralleled by a similar fall in the peak contracture (Fig. 3, A and B) that coincided with SR Ca2+-release. A comparable rate of rundown of [Ca2+]SRT in 2 mM Tet was also observed in guinea pig myocytes (Fig. 3 Ci). We conclude that Tet dose-dependently reduces SR-membrane leakage.
FIGURE 3.
Assessing SR Ca2+-leak. Myocytes paced at 2 Hz in NT were then superfused with SS containing 0.3 or 2.0 mM Tet. (A) After 1 min in SS + 0.3 mM Tet, rat myocyte was exposed to Tet-free SS + 10 mM caffeine for 30 s. (Upper panel) longitudinal line scan average for F/F0; (middle panel) F/F0 line scan (y axis normalized to cell length); (lower panel) cell shortening. (B) Different rat myocyte, exposed to caffeine after 4 min in SS + 0.3 mM Tet. Smaller Ca2+-release is due to longer preceding period of SR-membrane Ca2+-leakage. (C) (i) Peak F/F0 during caffeine-exposure, measured after 1–6 min delay (normalized to F/F0 at switch into SS) in rat myocytes in 0.3 mM (green) or 2 mM (black) Tet, and in guinea pig myocytes in 2 mM Tet (gray) (n = 5–10 cells/data-point). (ii) Cell shortening responses to caffeine in rat myocytes. Rundown of both F/F0 and cell shortening gives time course of SR depletion caused by Ca2+-leak.
Experimental protocol for measuring DCaSR
A rat myocyte was positioned within a stream of SS plus 0.3 mM Tet, emerging from one barrel of a dual-microstream apparatus (Fig. 4 A; configuration 0). The other stream contained 10 mM caffeine in Tet-free SS. The interstream boundary was quickly (<1 s) moved (Fig. 4 A; configuration 1), exposing one end of the cell (proximal end) to caffeine (24.0% ± 1.3% and 23.0% ± 3.0% of the length in rat and guinea pig, respectively; n = 87 and 24). This resulted in proximal SR Ca2+-release which was measured (as F/F0) over the proximal 20% of the line scan (ROI-P, Fig. 4 A). After 30 s (Fig. 4 Bi), the solution boundary was readjusted, exposing the whole cell to caffeine (Fig. 4 A; configuration 2). There was now a local SR Ca2+-release from the remainder of the cell (Fig. 4 Bi), which was measured (as F/F0) over the distal 20% of the line scan (distal ROIs; ROI-D; Fig. 4 A). This distal Ca2+ rise was frequently accompanied by a smaller, slower  rise in the proximal region, caused by back diffusion of cytoplasmic Ca2+. Ca2+-release events from the SR were associated with cell contractures.
rise in the proximal region, caused by back diffusion of cytoplasmic Ca2+. Ca2+-release events from the SR were associated with cell contractures.
FIGURE 4.
Measuring SR Ca2+-mobility. Caffeine is used to estimate the decline of distal [Ca2+]SRT, while Ca2+ is being drained from the proximal end of SR. (A) Dual-microperfusion apparatus is used to deliver two solutions: SS (without Tet or with 0.3 or 2 mM Tet) and SS + caffeine (10 mM with no Tet). Myocyte is first bathed in SS + Tet (configuration 0). Throughout the experiment, intracellular Fluo-3 fluorescence (F/F0) is averaged in two ROIs, each 20% of cell length, one positioned proximally (ROI-P) and one distally (ROI-D), at the ends of a line scan (see schematic diagram shown to the right of configuration 0). SS + caffeine is then applied to proximal end of myocyte to start SR-drainage (configuration 1); after a 30–240 s delay, SS + caffeine is applied to whole cell (configuration 2) to assess remaining SR Ca2+-content. At the end of the experiment, cells are returned to 0Na0Ca, free of CPA, Tet, and caffeine (not illustrated, denoted by arrow 3 in B and C). (B) SS microstream (but not SS + caffeine microstream) contained 0.3 mM Tet. (i) Rat myocyte; delay of 30 s between configurations 1 and 2. (Upper panel) F/F0-time course for [Ca2+]i averaged in ROI-P (black trace) and ROI-D (gray trace). Dashed line shows predicted decline of caffeine-mobilizable Ca2+-release because of SR Ca2+-leak (from Fig. 3). (Middle panel) Longitudinal F/F0 line scan (y axis normalized to cell length). (Lower panel) cell shortening. (ii) Rat myocyte; delay of 240 s between configurations 1 and 2. (C) SS microstream (but not SS + caffeine microstream) contained 2.0 mM Tet. (i) Rat myocyte; delay of 120 s between configurations 1 and 2. (ii) Guinea pig myocyte; delay of 180 s between configurations 1 and 2. (D) Ratio of distal fluorescence rise (configuration 2) to initial proximal rise (configuration 1), ΔF2/ΔF1, for different delay times. Rat myocytes with 2 mM Tet (black), 0.3 mM Tet (green), and zero Tet (blue). Guinea pig myocytes with 2 mM Tet (gray) (4–12 cells/data point). Time constants (τ) obtained from monoexponential fits.
Thus localizing a cell's exposure to caffeine allows one to assess local [Ca2+]SRT. Fig. 4 Bii shows that, in a different cell, increasing the time period (to 4 min) before readjusting the interstream boundary resulted in a considerably smaller caffeine-induced Ca2+-release from the distal end of the cell. Thus prolonged exposure of a proximal SR region to caffeine also empties the unexposed distal region. Although some of this emptying may be caused by Ca2+-leakage across the distal SR-membrane (the dashed line indicates the predicted leakage), there may also be emptying via luminal Ca2+-diffusion from distal to proximal SR regions, where Ca2+ escapes through caffeine-opened RyRs. This luminal diffusion was examined further by repeating the experimental protocol, but with 2.0 mM rather than 0.3 mM Tet, to inhibit most of the SR-membrane leak (Fig. 4 C). After a 2 min exposure of proximal SR to caffeine, the Ca2+-content of the distal SR region again became depleted, but this was now clearly more than expected from SR-membrane leakage alone (dashed line). Reducing the SR leak with 2 mM Tet, therefore, reveals that exposure of proximal SR to caffeine can drain distal areas via luminal Ca2+-diffusion.
Fig. 4 D plots the time course of decline of the distal SR Ca2+-content during proximal caffeine exposure in the presence of 0, 0.3, and 2 mM Tet (from a total of 87 rat myocytes and 24 guinea pig myocytes). In all cases, the Ca2+-content decreased, but more slowly at higher Tet concentrations, reflecting the reduced SR-membrane leak. In 2 mM Tet, SR-membrane leak is minimal, and the decline will be caused largely by spatial SR Ca2+-diffusion from distal to proximal areas. Note that this rate of decline (in 2 mM Tet) was similar in both guinea pig and rat myocytes.
As shown in Fig. 5, local [Ca2+]SRT can be assessed from the contracture during a local caffeine challenge. To check that Ca2+-binding by Fluo-3, used in this work, did not affect the rate of local SR depletion, we monitored the decline of the distal contracture with caffeine after increasing periods of proximal caffeine exposure. It declined at the same rate irrespective of whether a cell was AM-loaded with Fluo-3 or with carboxy-SNARF-1, a fluorescent dye that does not bind Ca2+ (Fig. 5 B). Thus the presence of the Ca2+-fluorophore does not affect the rate at which luminal Ca2+-diffusion and Ca2+-leak drains the SR.
FIGURE 5.
Distal SR depletion with proximal caffeine is unaffected by Fluo-3. (A) Myocyte AM-loaded with carboxy-SNARF-1, a non-Ca2+ binding fluorophore. Upper panel: fluorescence line scan (y axis shows cell length) used to monitor cell shortening (carboxy-SNARF-1 excitation at 514 nm, emission at 580 nm). (Lower panel) time course of cell shortening (derived from upper panel) in response to caffeine. Protocol of Fig. 4 was applied. Cell initially exposed to SS + 0.3 mM Tet. At circle 1, the proximal end of the cell exposed to SS + 10 mM caffeine; at circle 2 the whole cell exposed to SS + 10 mM caffeine. (B) Ratio of second/first shortening-event is plotted versus time delay between circles 1 and 2 in the presence of intracellular carboxy-SNARF-1 (black; n = 8, 7) or Fluo-3 (gray; n = 6–13). Time constants (τ) obtained from monoexponential fits. The presence of the Ca2+-binding fluorophore, Fluo-3, does not affect the rate of decline of distal contraction (and hence distal SR-depletion) during proximal caffeine exposure.
Calculating DCaSR: simple diffusion model
Rates of local SR-depletion were used to quantify DCaSR by applying a simple one-dimensional (1-D) diffusion model of the SR, featuring both longitudinal Ca2+-diffusion and lateral membrane Ca2+-leak (Fig. 6 Ai):
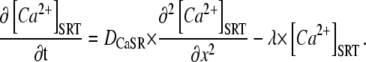 |
The model makes no assumptions about the cause of any deviation of Ca2+-mobility from its high value in water (DCa ≈ 1000 μm2/s) (28). SR-membrane leak is defined as the product of rate constant λ (estimated from Fig. 3 Ci for different Tet doses) and total SR Ca2+ content.
FIGURE 6.
Quantifying DCaSR. (A) (i) Schematic diagram of the simple Ca2+-diffusion model, incorporating SR-membrane leak and proximal SR-exposure to caffeine (see Appendix 1). (ii) Best-fitting of diffusion model (SERCA activity = 0, simulating CPA-addition) to data in Fig. 4 D gives displayed values for DCaSR (0.3 mM Tet, green; 2 mM Tet, black: rat myocytes; 2 mM Tet, gray: guinea pig myocytes). Note unique value for DCaSR (8–9 μm2/s). (iii) Best-fitting when SR Ca2+-leak is ignored; note lack of unique value for DCaSR (42, 23, and 10 μm2/s for rat myocyte data (Fig. 4 D) with 0, 0.3, and 2 mM Tet, respectively). (B) (i) Schematic diagram of diffusion-reaction model showing principal reaction elements (see Appendix 1). (ii) Displayed DCaSR: best-fit values averaged between 0 and 240 s. (Green) rat, 0.3 mM Tet; (black) rat, 2 mM Tet; (gray) guinea pig, 2 mM Tet. Note similarity with DCaSR values from Aii. (C) Output of cellular diffusion-reaction model simulating experimental protocol (Fig. 4). (i) Time course of F/F0 from simulated line scan in proximal (black) and distal (gray) ROIs. (ii) Simulated line scans for F/F0, [Ca2+]i and [Ca2+]SR.
This definition of SR-membrane leak is in agreement with the monoexponential decline in SR content (Fig. 3 Ci and Bassani and Bers (18)) and allows for local variation in SR leak that can arise from SR depletion, driven by intra-SR Ca2+-diffusion. The caffeine-induced rise in Fluo-3 fluorescence was converted to [Ca2+]i and, after accounting for cytoplasmic (intrinsic + Fluo-3) buffering (29), to [Ca2+]SRT (for full details, see Appendix 1). The time course of depletion of distal [Ca2+]SRT by proximal caffeine (Fig. 4 D) was solved by best-fitting a single DCaSR value in the diffusion model. Depletion can be fitted in this way because [Ca2+]SR equilibrates relatively rapidly (∼10 ms) with [Ca2+]SRT (30), and the two parameters will be linearly related, given that the binding constant (3,30,31) of the principal luminal buffer, calsequestrin, is greater than or similar to [Ca2+]SR. Fitting results are shown in Fig. 6 Aii. The least-squares best-fit value for DCaSR is low, 8–9 μm2/s and is similar in both rat and guinea pig myocytes. The same best-fit value is obtained for conditions of high or low SR leak (0.3 and 2.0 mM Tet, respectively), suggesting that the model makes adequate correction for this. Interestingly, when the influence of the leak is ignored (λ forced to equal 0), the predicted DCaSR value is not unique. It increases with leak size and appears to be 42 μm2/s in the absence of Tet. Thus accurate measurement of global DCaSR requires a full correction for the effects of SR-membrane leak.
Calculating DCaSR: mechanistic diffusion-reaction model
DCaSR was quantified a second way, this time using a mechanistic, 1-D diffusion-reaction model (Fig. 6 Bi). This approach attempts to account for elements affecting both luminal and cytoplasmic Ca2+, such as RyR-permeability, luminal and myoplasmic Ca2+-buffers (including Fluo-3), and, where appropriate, the membrane transporters SERCA and PMCA. Parameters for these elements were derived either from the literature or from this work (see Appendix 1 and Table 1). The model best fits experimental data with a single Ca2+-diffusion coefficient  This value is lower than its free aqueous value DCa because of SR tortuosity. The effective Ca2+-diffusion coefficient (DCaSR) in the SR is, however, reduced further because of luminal buffering by calsequestrin (3,31):
This value is lower than its free aqueous value DCa because of SR tortuosity. The effective Ca2+-diffusion coefficient (DCaSR) in the SR is, however, reduced further because of luminal buffering by calsequestrin (3,31):
 |
(1) |
Ccsq and Kcsq are the total concentration and Ca2+-binding constant for calsequestrin, respectively. The least-squares best-fits of the model to the experimental data are shown in Fig. 6 Bii. These fits are very similar to those achieved using the simple diffusion model (Fig. 6 Aii). In both cases, the goodness of fit was high (sum of squares < 0.01). Because of luminal buffering, the effective DCaSR in the model will vary with [Ca2+]SR, and so the value quoted for each curve in Fig. 6 Bii has been time-averaged over the whole period of local SR depletion to produce a mean for the experiment. This value is again low (7.9–9.1 μm2/s) and is independent of the size of prevailing SR-membrane leak. The value is also similar in both rat and guinea pig cells. The confidence interval for our DCaSR estimate can be approximated by best fitting data within their mean ± SE. This interval was ±4.4 and ±3.6 μm2/s for rat and guinea pig myocytes, respectively.
TABLE 1.
Model parameters
| Symbol | Definition | Value | Reference |
|---|---|---|---|
| [Ca2+]i,0 | Diastolic myoplasmic Ca2+ in NT | 100 nM (75 nM in Tet) | (39,40,43,46) |
| [Ca2+]SR,0 | Diastolic fully loaded SR Ca2+ in NT | 520 μM (700 μM in Tet) | (3,31,46) |
| vcell | Total cell volume | 33 pL | (43,47) |
| vSR | Total SR volume | 3.5% of Vcell | (1,48) |
| vmyo | Total nonmitochondrial volume | 65% of Vcell | (1,43,48) |
| ρSL | SL surface area/volume ratio | 0.89 μm−1 | (47,49) |
| ρSR | SR surface area/volume ratio | 1.19 μm−1 | (1,48) |
| L | Cell length | 120 μm (rat); 113 μm (g-p) | Measured |
| E | % SR mobilized during partial caffeine exposure | 24% (rat); 23% (g-p) | Measured |
| kleak | SR leak rate constant | See text | Fig. 2 |
| krel | Caffeine-evoked Ca2+-release rate constant | 9 s−1 | (50) |
 |
Maximum rate of SERCA | 100 μM s−1 | Estimated* |
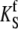 |
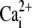 affinity of SERCA (forward) affinity of SERCA (forward) |
0.246 μM | (43) |
 |
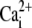 affinity of SERCA (reverse) affinity of SERCA (reverse) |
1.7 μM | (43) |
| nS | Hill cooperativity of SERCA | 1.787 | (43) |
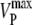 |
Maximum rate of PMCA in 0Na0Ca media (estimated from relaxation time constant) | 30.0 μM s−1 (rat); 25.4 μM s−1 (g-p) | e.g., Fig. 1 A |
| KP |
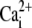 affinity of PMCA affinity of PMCA |
0.5 μM | (43) |
| Jbal | SL Backflux to balance PMCA and stabilize [Ca2+]i | Adjustable | |
| Cbuf | Cytoplasmic (fast) buffer concentration | 175 μM | (29) |
| Kbuf | Cytoplasmic (fast) buffer equilibrium constant | 0.59 μM | (29) |
| CCSQ | Calsequestrin buffer concentration (estimated from rise in total cytosolic Ca2+ during caffeine exposure) | 4.4 mM (rat); 2.3 mM (g-p) | Estimated* |
 |
Calsequestrin Ca2+ off-rate | 109 s−1 | (30) |
| KCSQ | Calsequestrin Ca2+ binding constant | 0.63 mM | (3,31) |
| CFluo | Fluo-3 buffer concentration | 25 μM | Data S1 |
| KFluo | Fluo-3 buffer Ca2+ affinity | 832 nM | Data S1 |
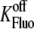 |
Fluo-3 buffer Ca2+ off-rate | 100 s−1 | Assumed |
| DCai | Cytosolic effective Ca2+ mobility (absence of Fluo-3) | 15 μm2/s | (7,39–41) |
| DFluo | Fluo-3 diffusion coefficient | 25 μm2/s | (39,40) |
| DCaff | Caffeine diffusion coefficient | 50 μm2/s | Data S1 |
| PCaff | Caffeine permeability constant | 9 μm/s | (26) |
SL, sarcolemma; SR, sarcoplasmic reticulum; r, rat; g-p, guinea pig.
P. Swietach, K. W. Spitzer, and R. D. Vaughan-Jones, unpublished.
A final cross-check was made for the experimental estimates of DCaSR. If the Ca2+-diffusion models used in the analysis are reliable, DCaSR estimated during longitudinal SR-depletion with proximal caffeine should be the same, irrespective of where the depletion in the distal SR is estimated. We therefore positioned two ROI-Ds at different known distances downstream from the initial proximal area of caffeine exposure (where ROI-P was positioned). When the whole SR was eventually exposed to caffeine (configuration 2 of Fig. 4 A), the rise of  in each ROI-D could be used to estimate DCaSR, as described previously. ROI-D1 was positioned near the middle of the cell, such that its near border was at the cell's center, whereas ROI-D2 was positioned at the extreme distal end of the cell (this was the default position for ROI-D used in all other experiments). When best-fitted by our diffusion-reaction model, mean DCaSR estimated using ROI-P in combination with ROI-D1 was 7.2 μm2/s (n = 87), which is similar to the estimate obtained using ROI-P in combination with ROI-D2 (8.6 μm2/s; n = 87), confirming the validity of the analytical technique. We preferred to use the more extreme ROI-D measurements for general analysis, as these exhibited the better signal/noise ratio for SR Ca2+-release (a larger Fluo-3 fluorescence increase), thus providing a more accurate estimate of SR Ca2+-mobility.
in each ROI-D could be used to estimate DCaSR, as described previously. ROI-D1 was positioned near the middle of the cell, such that its near border was at the cell's center, whereas ROI-D2 was positioned at the extreme distal end of the cell (this was the default position for ROI-D used in all other experiments). When best-fitted by our diffusion-reaction model, mean DCaSR estimated using ROI-P in combination with ROI-D1 was 7.2 μm2/s (n = 87), which is similar to the estimate obtained using ROI-P in combination with ROI-D2 (8.6 μm2/s; n = 87), confirming the validity of the analytical technique. We preferred to use the more extreme ROI-D measurements for general analysis, as these exhibited the better signal/noise ratio for SR Ca2+-release (a larger Fluo-3 fluorescence increase), thus providing a more accurate estimate of SR Ca2+-mobility.
Fig. 6 C shows a model simulation of an experiment on a rat ventricular myocyte, demonstrating that proximal caffeine application is predicted to deplete distal SR regions by an amount very similar to that assessed experimentally (Fig. 4 D). We conclude that the low DCaSR detected in our experiments here is consistent with the expected effects on Ca2+-diffusion of SR tortuosity and luminal Ca2+-buffering.
DISCUSSION
SR is continuous, and global DCaSR is low
We find that, in both rat and guinea pig ventricular myocytes, locally opening RyRs at one end of the SR can drain it slowly of Ca2+, indicating a low SR Ca2+-mobility of 8–9 μm2/s. This remains true, even after natural Ca2+-leakage across the SR membrane has been minimized with 2 mM Tet. Diffusion of Ca2+ down the SR, a distance of ∼60 sarcomeres, is consistent with previous observations that, when Fluo-5N is loaded into the SR, both Ca2+-ions and the fluorophore can, over minutes, access all luminal regions, including the nuclear envelope (9). SR lumen therefore appears to be continuous and to extend beyond individual sarcomeres, as also suggested from anatomical observations of nSR breaching the Z-line region (2).
Our low value for DCaSR is a global average, which includes both jSR and nSR Ca2+-mobility. It also refers to a partially mobilized SR ([Ca2+]SR ≈ 0.25 mM). By extrapolation, DCaSR in loaded SR ([Ca2+]SR ≈ 0.5 mM) of guinea pig and rat would be 11–13 μm2/s (up to [Ca2+]SR ≈ 1 mM, the [Ca2+]SR-dependence of DCaSR is near linear; Eq. 1). It is of interest to compare it with global cytoplasmic Ca2+-mobility, DCai. This latter parameter is difficult to quantify using Ca2+-fluorophores because they act as mobile buffers, enhancing Ca2+-mobility. However, a value for skeletal myoplasm (7), measured using radiotracers rather than Ca2+-fluorophores, is 14 μm2/s at 21°C. At 37°C this will be higher, ∼20 μm2/s (28). The value is similar to estimates of DCai in neurons (16 μm2/s; fluorophore corrected) (32) and similar to the value predicted in the absence of fluorophore by our cardiomyocyte diffusion-reaction model (16 μm2/s at 37°C). Global DCaSR is therefore likely to be even lower than DCai.
Ca2+-mobility in water, DCa, is 1000 μm2/s at 37°C (7,28). Mobility in luminal SR is therefore reduced by about two orders of magnitude. Diffusion-reaction modeling of our experimental data (Fig. 6 D) suggests that one order of magnitude reduction is likely to be due to SR tortuosity (see Appendix 1), whereas the other can be attributed to luminal Ca2+-buffering. Assuming a similar total nSR and jSR volume (2), the jSR concentration of calsequestrin, the principal luminal buffer, is between 6 mM (3) and 28 mM (31), and Kcsq for Ca2+ is ∼0.6 mM (3,31), a value close to [Ca2+]SR in loaded SR, thus ensuring a maximal Ca2+-buffering capacity. As calsequestrin is poorly mobile (molecular mass of 45 kDa), it will significantly attenuate luminal Ca2+-mobility.
Our estimate of DCaSR (8–9 μm2/s) is nearly 10-fold lower than a previous measurement (9) (60 μm2/s at 20°C approximates to 84 μm2/s at 37°C (28)), obtained using luminal Fluo-5 N to measure SR Ca2+-movement directly. It is not immediately apparent why the two estimates would differ so dramatically. Species differences (rabbit versus the guinea pig and rat here) are an unlikely explanation as, among the three cells, SR volume, and Ca2+-content are believed to be similar (18). Furthermore, revising the earlier mobility measurement to the higher temperature of 37°C only accentuates the discrepancy (28). As mentioned already, the previous use of Fluo-5N for direct measurement of [Ca2+]SR may have enhanced DCaSR, but running our diffusion-reaction model suggests the effect would be by <2%, given the dye's low luminal concentration (50–100 μM (9)) compared with calsequestrin and [Ca2+]SR. Thus although Ca2+-fluorophores like Fluo-3 and Fura-2 significantly affect cytoplasmic Ca2+-mobility, the same is unlikely to be true for the effect of Fluo-5N on luminal Ca2+-mobility (providing [Ca2+]SR ≫ [Fluo-5N]).
Unlike the previous work, we did not measure [Ca2+]SR directly, but inferred it from local Ca2+-release with caffeine. Indeed, direct [Ca2+]SR measurements in rat and guinea pig ventricular myocytes were not an option, as reliable SR-loading of Fluo-5N in these cells has not so far been achieved (15). There is, therefore, the possibility of errors in our own work. The use of rapid caffeine application to assess [Ca2+]SRT has, however, been well validated (18,29,31), as has the use of dual microperfusion to localize extracellular solutes with high precision (16,24,25). Due to caffeine's high membrane permeability (26), intracellular caffeine compartmentalization will also be similar to the extracellular compartmentalization imposed by dual microperfusion (see Methods and Data S1). Although caffeine-application gauges [Ca2+]SRT rather than [Ca2+]SR, the two levels equilibrate in ∼0.01 s (calsequestrin unloading rate constant = 109 s−1 (30)) and will thus decline in synchrony during local drainage, as jSR and nSR are interconnected throughout the cell.
One possible source for the discrepancy is the correction for SR membrane leakage. Our estimates of the time constant of Ca2+-leakage (in low or zero Tet) are in agreement with previous estimates (18) and would produce 45% SR depletion during the time required to measure luminal Ca2+-diffusion (∼2 min). Although SR leakage was accounted for in this work, no leakage was apparent in the earlier determination of DCaSR (see Fig. 7 of Wu and Bers (9)). Given that SR leakage is known to occur, this may indicate some residual SERCA activity in the earlier work (9), despite a 90 s exposure to 5 μM thapsigargin. It is notable that failure to account for leakage in this work results in artifactually high values for DCaSR (up to ∼42 μm2/s; Fig. 6 Aiii). We show, in Fig. S3 in Data S1, that it may also lead to an overestimate of DCaSR using the experimental protocol adopted in the earlier work. If so, DCaSR may be low in all three species. Alternatively, rabbit ventricular myocytes may be unusual in exhibiting a high luminal Ca2+-mobility.
FIGURE 7.
Effect of DCaSR on longitudinal [Ca2+]SR profile during simulated local Ca2+-release. Diffusion-reaction model was run to simulate local SR Ca2+-release (see Appendix 1). [Ca2+]SR was calculated 250 ms after increasing SR-membrane permeability to 1.35 μM/s in a central 2 μm length of SR. This estimate of DCaSR (9 μm2/s) supports large and localized SR-depletion, with only small effects on adjacent luminal regions. Higher DCaSR significantly depletes SR Ca2+ from regions beyond the release site. (Dashed line) 5% depletion threshold.
Functional consequences of low DCaSR: microscopic localization of SR Ca2+-signaling
Although the SR lumen appears continuous throughout the ventricular myocyte, this need not imply functional continuity. A low global value for DCaSR means that local displacements of [Ca2+]SR will not necessarily be transmitted to other regions, particularly if they are rapid and transient. This can be illustrated in our diffusion-reaction model (Fig. 7) by locally increasing RyR permeability to release Ca2+ along a 2 μm stretch of SR (roughly equivalent to Ca2+-release from a single sarcomere) and computing [Ca2+]SR after 250 ms. If global DCaSR in the model is set to a high value (>60 μm2/s), Ca2+-release (in the presence of local reuptake by SERCA) is associated with only a modest local fall of [Ca2+]SR, as Ca2+ drawn diffusively from adjacent SR regions (and hence from adjacent sarcomeres) limits the local depletion. As a result, an extended length of lumen becomes significantly depleted (9 μm of lumen, at 5% depletion threshold, with DCaSR = 300 μm2/s and 7 μm with DCaSR = 60 μm2/s; Fig. 7). Thus a localized Ca2+-release is predicted to produce a more generalized SR depletion.
In contrast, when global DCaSR is set to the value measured experimentally (9 μm2/s), Ca2+-release is associated with a considerably larger fall of [Ca2+]SR but one that is more localized spatially (5% depletion in <4 μm of lumen; Fig. 7). Ca2+ is no longer drawn so extensively from adjacent regions (i.e., from adjacent sarcomeres), thereby preserving their integrity. Under these circumstances, local control of SR Ca2+-release is complemented by a local control of [Ca2+]SR. Although the above modeling is simplistic (it does not, for example, reproduce the real geometry within an SR release site), it nevertheless implies that a low global value for both luminal and cytoplasmic Ca2+-mobility may result in local cytoplasmic Ca2+-microdomains being mirrored spatially by inverse luminal Ca2+-microdomains—as indeed appears to happen for a Ca2+-spark and its corresponding Ca2+-blink (2,13), and for a cytoplasmic Ca2+-wave and its corresponding wave of SR Ca2+-depletion (13,33). Indeed, given that [Ca2+]SR is suggested to be an important regulator of RyR channel gating (34), a low DCaSR, by optimizing the amplitude and minimizing the spatial extent of local [Ca2+]SR depletion, may play an important role in the luminal regulation of the Ca2+-release process itself.
Changes in luminal Ca2+-mobility may be relevant to recent reports of abnormal Ca2+-signaling in ventricular myocytes. In one (34), increasing intra-SR Ca2+ buffering capacity with citrate or maleate was found to increase Ca2+ spark amplitude and duration. One possible explanation is an increase of DCaSR, as these low molecular weight molecules will function as mobile Ca2+-buffers within the SR lumen. An increased DCaSR will finance a greater and more spatially diffuse Ca2+-release, as illustrated in Fig. 7, and this may account for enhancement of the local Ca2+ spark. In a second report, the absence of calsequestrin from jSR in Casq2-null mice was found to be accompanied by an increased incidence of electrical arrhythmia (35). Results of this work predict that calsequestrin deletion, by reducing fixed luminal Ca2+-buffers, would increase the effective DCaSR (Eq. 1), again enhancing local Ca2+-release. Such abnormal release may then contribute to the arrhythmic phenotype of Casq2-null mice (35). Conversely, calsequestrin overexpression would be expected to decrease DCaSR (Eq. 1), which may play a role in the reduced spark frequency and Ca2+-release observed recently in transgenic mice (36).
The low DCaSR measured in this work has implications for models of Ca2+-wave propagation during pathological conditions of  -overload. Current hypotheses conflict, in that some assume a wave of [Ca2+]SR depletion is coincident with the cytosolic Ca2+-wave (13,33), whereas a recent hypothesis suggests an SR wave of luminal Ca2+-loading that travels ahead of the cytosolic Ca2+-wave (12). As discussed earlier, Eq. 1 predicts that, even when [Ca2+]SR is as high as 1 mM, as may occur during the incidence of Ca2+-waves, DCaSR would still not be significantly greater than DCai, which tends to argue against the latter proposal. Finally, a low DCaSR implies that conditions associated with spatially nonuniform Ca2+-release within the cell, such as regional
-overload. Current hypotheses conflict, in that some assume a wave of [Ca2+]SR depletion is coincident with the cytosolic Ca2+-wave (13,33), whereas a recent hypothesis suggests an SR wave of luminal Ca2+-loading that travels ahead of the cytosolic Ca2+-wave (12). As discussed earlier, Eq. 1 predicts that, even when [Ca2+]SR is as high as 1 mM, as may occur during the incidence of Ca2+-waves, DCaSR would still not be significantly greater than DCai, which tends to argue against the latter proposal. Finally, a low DCaSR implies that conditions associated with spatially nonuniform Ca2+-release within the cell, such as regional  alternans, will, at times, be associated with significant spatial nonuniformity of [Ca2+]SR (15,37).
alternans, will, at times, be associated with significant spatial nonuniformity of [Ca2+]SR (15,37).
Possible causes of low DCaSR: local heterogeneity of SR Ca2+-mobility
Although global DCaSR is low, it is unlikely that Ca2+-mobility is uniform throughout the SR, given its complex geometry and the heterogeneous distribution of luminal Ca2+-buffers. It is therefore appropriate to ask which regional elements within the SR may limit the global movement of Ca2+. One such element is likely to be jSR, which will have implications for SR Ca2+-cycling within the sarcomere. The other may be the intersarcomeric portion of the nSR.
We deal first with jSR. During excitation-contraction coupling, after Ca2+-release from jSR cisternae, Ca2+-ion movement from nSR (the main site of Ca2+-reuptake by SERCA) refills jSR within each cardiac cycle. In rabbit and canine myocytes, this refilling appears to occur with a time constant (τ) of 29 ms (2) and 98 ms (13), respectively, as derived from the recovery time course of a Ca2+-blink (Fig. 8 Aii, inset for τ = 29 ms). Such recovery will be a more direct measure of local jSR refilling than, for example, Ca2+ spark restitution, as the latter appears to depend on factors other than SR load, such as RyR refractoriness (38). If local cisternal refilling is by passive Ca2+-diffusion, local [Ca2+]SR recovery during a blink suggests that Ca2+-mobility into or within jSR is low. Within each rabbit sarcomere, one jSR cisterna (diameter ≈ 0.6 μm) is supplied, on average, by four nSR elements (2) (Fig. 8 Ai; see Appendix 2 for derivation of geometry), with volume being distributed equally between jSR and nSR (2).
FIGURE 8.
Modeling Ca2+-diffusion in SR nanoarchitecture. (A) (i) 2-D geometry for a unit of sarcomeric SR (jSR-cisterna connected to four nSR-tubes) triangulated for diffusion modeling. (ii) To simulate jSR Ca2+-recovery after local Ca2+-release, [Ca2+]jSR was set instantaneously to 0.25 (50% depletion), whereas [Ca2+]nSR was set initially to 0.5 mM and the distal ends of the nSR elements were coupled to an infinite 0.5 mM Ca2+ source. The time constant (τ) of recovery of [Ca2+]jSR was then derived for a range of jSR Ca2+-mobility values (DCajSR), with Ca2+-mobility in nSR assumed to be 1000 μm2/s. The predicted time courses of change for [Ca2+]jSR and [Ca2+]nSR are shown in the inset. Filled circle denotes τ = 29 ms, which has been determined experimentally for rabbit SR Ca2+-blinks. (iii) Spatial [Ca2+]SR map after 29 ms of jSR-refilling for a DCajSR of 1.8 μm2/s. (B) (i) 63 × 10 SR units based on Ai, coupled into a 2-D network for simulating whole-SR during proximal caffeine exposure (see Appendix 2). (ii) Predicted relationship between global DCaSR and DCajSR. DCajSR of 1.8 μm2/s (derived from normal Ca2+-blink recovery rate) predicts a global DCaSR of 8 μm2/s, similar to the value measured experimentally. In contrast, a high global DCaSR (60 μm2/s) predicts a relatively high DCajSR (41 μm2/s), which would then predict an ultrafast Ca2+-blink recovery τ of <1 ms (see Aii). (Inset) Close-up of DCaSR range between 0 and 10 μm2/s. (iii) Model of nSR/jSR unit featuring a minimal length nSR (0.65 μm), divided into snSR and inSR. Diffusion in the inSR is slower than in the snSR (see Appendix 2 for details).
If one makes the simplifying assumption that, during an isolated Ca2+-blink, the distal ends of the nSR elements are coupled to an infinite source of Ca2+ (because of diffusive coupling to quiescent elements of the SR and because of Ca2+-uptake on SERCA), then local jSR refilling can be simulated by setting effective jSR Ca2+-mobility to 1.8 μm2/s (for recovery τ = 29 ms; Fig. 8 Aii and iii; see Appendix 2 for details). This is a very low value, consistent with restricted access to jSR from nSR and also consistent with the known high expression in jSR of calsequestrin (2,11). Thus, a very low, local DCaSR may underpin the local luminal Ca2+-flux required to refill jSR cisternae. But a predicted jSR Ca2+-mobility of 1.8 μm2/s is significantly lower than the global value of DCaSR measured in guinea pig and rat myocytes (8–9 μm2/s) here. This may reflect a relatively high Ca2+-mobility in non-jSR elements (i.e., in nSR), as implied in the SR-unit model (Fig. 8 Ai and Appendix 2). Indeed such an arrangement has already been proposed (2), as nSR is believed to be devoid of known Ca2+-buffers, which would permit faster Ca2+-diffusion (2,11).
A two-dimensional (2-D) model network of jSR-nSR elements (Fig. 8 Bi) with unbuffered Ca2+-mobility in nSR and low, buffered Ca2+-mobility in jSR (1.8 μm2/s) can be used to predict the global value for DCaSR (see Appendix 2 for details). Imposing zero-[Ca2+] at one end of the 2-D network (equivalent to tonically exposing one end of the SR to caffeine) predicts universal depletion, with an average DCaSR of 8 μm2/s (Fig. 8 Bii), which is in agreement with the global value measured experimentally. Thus, if we assume heterogeneity of Ca2+-mobility between jSR and nSR, as proposed previously, our experimentally determined value for DCaSR would be sufficient to support local SR Ca2+-signaling, as well as global luminal Ca2+ movement within the cardiac cell. The modeling implies that, at the nanoscopic level, luminal Ca2+-diffusion will vary, being very slow in jSR but faster in nSR. The global Ca2+ diffusion rate through the combined SR elements will tend toward the lower of the two individual limits, as shown in Fig. 8 Bii.
What about intersarcomeric SR? The above modeling of luminal Ca2+-diffusion takes no account of possible heterogeneity of Ca2+-mobility within nSR itself. For example, it is possible that SR Ca2+-diffusion is severely limited between adjacent sarcomeres (2), i.e., via intersarcomeric network SR (we call this inSR). Local Ca2+-mobility for inSR may be significantly lower than for intrasarcomeric nSR, i.e., the part of the nSR that ramifies within each sarcomere and makes connection with jSR cisternae (we call this intrasarcomeric network snSR). Low Ca2+-mobility for inSR would be consistent with the apparently sparse nature of inSR elements compared with the more densely arranged snSR elements (2). Subdividing nSR into inSR and snSR in our 2-D model network (Fig. 8 Biii) would have no effect on the predicted value for global DCaSR, as the influence of the combined inSR-snSR would need to be identical to the original lumped nSR. In the simplest case, the subelements may be arranged in series, as shown in Fig. 8 Biii.
Analysis of the 2-D network indicates that the effective Ca2+-mobility for a lumped nSR would be 110 μm2/s for a DjSR of 1.8 μm2/s and a global DCaSR of 8 μm2/s (see Appendix 2). Ascribing specific values to Ca2+-mobility in the inSR or snSR subelements must await an anatomical description of their volume and tortuosity. But if Ca2+-mobility for inSR were as low as for jSR (i.e., 1.8 μm2/s), then the total nSR could be represented by a short inSR element with low Ca2+-mobility coupled to a longer snSR element with high Ca2+-mobility, where inSR is ∼1.5% of total nSR length (see Appendix 2). Thus, in effect, the inSR would occupy only a tiny fraction of total nSR volume, and so its limiting influence on global Ca2+-mobility would not be large. In this way, effective Ca2+-mobility in the whole nSR would still be 110 μm2/s. At this time, subdividing local Ca2+-mobility within the nSR is purely speculative. Furthermore, it takes no account of other regions of the SR/ER system, such as the nuclear envelope. As all these regions are interconnected (9), a comprehensive model of local Ca2+-mobility will require detailed characterization of all these noncisternal elements.
We can now attempt to answer the question of which regional elements within the SR may limit the global diffusion of luminal Ca2+. Assuming that the published recovery time for a Ca2+-blink represents diffusive refilling of jSR, it seems likely that the effective Ca2+-mobility in jSR is much lower than that averaged throughout the rest of the SR/ER. Because jSR occupies around half of total SR volume (2), its limiting effect on global Ca2+-mobility will be large. Effects of intersarcomeric nSR are more difficult to quantify, but, when lumped with the rest of the nSR, they probably limit global Ca2+-mobility far less than does jSR.
Low DCaSR and SR Ca2+-scraps
The spatial uniformity of [Ca2+]SR during Ca2+-scraps, where global SR Ca2+-release during an action potential appears to deplete both jSR and nSR elements, has led to suggestions for a high global value for DCaSR (8). In contrast, the recovery time course of a Ca2+-blink, with little or no Ca2+ depletion in adjacent nSR, suggests DCaSR is low (2). Observations on Ca2+-scraps and Ca2+-blinks are not necessarily contradictory. The Ca2+-blink is measured as an isolated, low-probability event (2,14). Thus fast Ca2+ movement from neighboring, quiescent SR elements may minimize local nSR depletion, as observed experimentally ((2) and Fig. 8 Aii, inset). But during an action potential, the high spatial density of Ca2+-blinks may prevent this from happening, leading to global nSR depletion accompanying the global Ca2+-discharge from jSR. As suggested previously (2,13), the recoveries of [Ca]jSR during an isolated Ca2+-blink and a global Ca2+-scrap (8) are likely to occur via different mechanisms, the former being via simple Ca2+-diffusion and the latter via active Ca2+-reuptake on SERCA pumps. A low global DCaSR need not, therefore, be inconsistent with spatially uniform Ca2+-scraps. In contrast, a high rather than low global DCaSR of, say, 60 μm2/s would, from Fig. 8, Aii and 8 Bii, predict ultrafast diffusive jSR refilling after an isolated Ca2+-blink, with a time constant of <1 ms, which could not be resolved experimentally. The fact that localized Ca2+-blinks recover with a much longer time constant of 29–98 ms (2,13) thus reinforces our own proposal for a low DCaSR.
CONCLUSIONS
We conclude that global DCaSR in guinea pig and rat ventricular myocytes is 8–9 μm2/s, a low value that is, nevertheless, consistent with the demands of SR Ca2+-cycling during excitation-contraction coupling. Low global Ca2+-mobility in the SR raises the possibility of local luminal control. This may, for example, help to preserve global Ca2+-stores during aberrant local SR-release and may represent an additional layer in the local control of  -signaling, complementing that exerted through the couplon.
-signaling, complementing that exerted through the couplon.
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Supplementary Material
Acknowledgments
We thank Philip Cobden for excellent technical assistance.
We thank the British Heart Foundation (Programme Grant to R.D.V.-J.), National Institutes of Health (MERIT award 5R37HL042873 to K.W.S.), and the Nora Eccles Treadwell Foundation (K.W.S.).
APPENDIX 1: ESTIMATING DCaSR
Simple Ca2+ diffusion model
A 1-D diffusion model (Fig. 6 Ai) was solved for total SR [Ca2+] ([Ca2+]SRT) over a compartment (length = myocyte length) featuring a passive leak (rate constant λ) to obtain an estimate of DCaSR:
 |
(A1) |
In experiments, local [Ca2+]SRT was probed using caffeine application and was deduced from the resulting rise in total cytosolic [Ca2+] (free + buffered, [Ca2+]iT), which, in turn, was derived from Fluo-3 fluorescence (F/F0). To convert F/F0 to [Ca2+]iT, it must first be converted to free cytosolic [Ca2+] ([Ca2+]i):
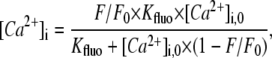 |
where [Ca2+]i,0 is diastolic [Ca2+]i (75 nM in Tet and 100 nM in the absence of Tet; Fig. 1). [Ca2+]iT is then estimated from [Ca2+]i knowing the characteristics of intrinsic (29) and Fluo-3 buffering (details of Fluo-3 calibration and buffering are given in Fig. S1 in Data S1):
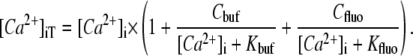 |
To estimate initial [Ca2+]SRT and the SR leak constant λ, Eq. A1 (without the diffusive term) was fitted to the time courses of SR-depletion shown in Fig. 3 (no net spatial SR-diffusion in these experiments). This gave initial [Ca2+]SRT values in rat and guinea pig myocytes of 135 and 88 μM in units of cytosolic volume (equivalent to 2.5 and 1.6 mM expressed in units of SR volume). The leak constant λ was rat: 4.5 × 10−3 and 4.4 × 10−4 s−1 at 0.3 and 2 mM Tet, respectively; guinea pig: 8.3 × 10−4 s−1 at 2 mM Tet.
The experimental protocol for measuring DCaSR consisted of measuring the rate of depletion of distal [Ca2+]SRT during proximal caffeine exposure (Fig. 4). As pointed out in the Results section, this is a valid approach, as i), [Ca2+]SRT will equilibrate rapidly with [Ca2+]SR (nonbuffered SR Ca2+) because the principal SR buffer, calsequestrin, has rapid binding/unbinding kinetics (30); and ii), [Ca2+]SR and [Ca2+]SRT are linearly related (hence Eq. A1 is linear) because the Ca2+-binding constant of calsequestrin (Kcsq) is ≥ [Ca2+]SR. On the timescale of the our experiments here (30–240 s), [Ca2+]SRT and [Ca2+]SR can be amalgamated into one diffusion equation.
The protocol of proximal caffeine exposure (Fig. 4) was simulated by assuming a nonuniform initial concentration profile (Fig. 6 Ai): [Ca2+]SRT in the proximal region was set to equal diastolic [Ca2+]i (75 nM in Tet). In the experiments, the boundary of the locally mobilized SR was determined optically from the position of the interstream boundary (Fig. 4 A, configuration 1) where it intersected the myocyte (highlighted by including 10 mM sucrose in one of the microstreams (16)). The boundary position could be confirmed by measuring the half-maximal width of F/F0-rise on proximal caffeine exposure. This half-maximal width spans beyond the caffeine-exposed region by 7% due to cytosolic Ca2+-diffusion (estimated using a diffusion-reaction model, see below). Experimentally, the boundary position was at 24% ± 1.3% and 23% ± 3.0% of cell length in rat and guinea pig myocyte experiments, respectively. To derive DCaSR, the time-dependent depletion of distal [Ca2+]SRT (Fig. 4 D) was best-fitted with the model. Results of fitting are shown in Fig. 6 Aii.
Mechanistic Ca2+ diffusion-reaction model
Estimating DCaSR
The compartments (myoplasm and SR) and fluxes featured in the 1-D diffusion-reaction model are shown in Fig. 6 Bi. The system consists of six equations describing diffusion (vector D) and reaction (vector R) of participating solutes [Ca2+]i, [Ca-Fluo]i, [Fluo]i, [Ca]SR, [Ca-CSQ]SR, and [Caff]i (vector u = [u1,…u6], respectively):
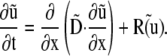 |
(A2) |
The model output for Ca2+-bound Fluo-3 was used to best-fit experimental data (F/F0). Ca2+ buffering in the myoplasm consisted of a lumped fast Ca2+ buffer, characterized empirically (29), and Fluo-3 (for details of Fluo-3 buffering see Fig. S1 in Data S1). Ca2+-buffering in SR was attributed to calsequestrin (3). All participating solutes diffuse with their respective coefficients except calsequestrin, which is treated as immobile. In agreement with previous work (7,39–41), effective cytosolic Ca2+-mobility in the presence of Fluo-3 was 16 μm2/s at resting [Ca2+]i. The unknown parameter elucidated in this study is DCaSR. In the SR, free Ca2+ mobility is reduced by i) tortuosity (mobility reduced to  and ii) buffering (mobility further reduced to DCaSR) (32,42):
and ii) buffering (mobility further reduced to DCaSR) (32,42):
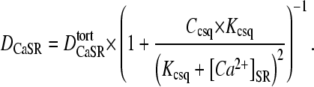 |
Best-fitting experimental data yielded estimates for  and hence DCaSR (Fig. 6 B). The latter was time-averaged over the period between partial and whole-cell caffeine exposure (Fig. 4).
and hence DCaSR (Fig. 6 B). The latter was time-averaged over the period between partial and whole-cell caffeine exposure (Fig. 4).
Ca2+ can exit the SR passively through a leak pathway or a caffeine-activated RyR pathway (treated separately in the model). The position of the caffeine microstream is modeled using a discrete (0 or 1) function S(x,t). SR leak was modeled as a first-order equation to account for local variations in SR leak during local SR depletion. The rate-constant of SR leak (kleak) was derived empirically from experiments (Fig. 3 Ci). The model did not incorporate Ca2+-flux through LCC or NCX as these were blocked in 0Na0Ca solutions. Ca2+ in the myoplasm can be sequestered into the SR by CPA-sensitive SERCA (3):
 |
In the presence of CPA, JSERCA is set to zero. The model included a sarcolemmal PMCA pump and a net flux pathway (Jbal) to keep diastolic [Ca2+] at the desired level. To simulate Fig. 1 B, Jbal was set to 3.9 μM/s. The kinetics of the PMCA pump (based on previous work (43)) were scaled to fit the time course of [Ca2+] recovery in 0 Na0Ca solution with caffeine + CPA,
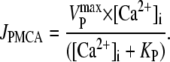 |
The reaction term in Eq. A2 is therefore (see Table 1 for parameter values),
 |
Modeling a local SR Ca2+-release event
The model includes SERCA and SR leak (but no PMCA activity), which are balanced to maintain [Ca2+]i = 100 nM. To simulate a localized microscopic SR release event lasting 250 ms, RyR permeability at a central 2 μm region of the SR was set to 1.35 μM/s (at this permeability, the SR depletes locally by 50% after 250 ms when DCaSR = 0). The simulations were run for a range of DCaSR (Fig. 7).
APPENDIX 2: LOCAL HETEROGENEITY OF DCaSR: MODELING LUMINAL Ca2+ DIFFUSION IN SR NANOARCHITECTURE
Constructing nSR/jSR geometry
To approximate solute diffusion within the SR nanostructure of a sarcomere, we used the finite element method (Fig. 8 Ai) to solve Eq. A1 (for simplicity, SR leak was ignored). The geometry for a jSR cisterna and its connecting nSR tubes was derived from recent electron micrograph data (2). The jSR cisterna is modeled as a cylinder (2) of height 30 nm and diameter 592 nm and is connected, on average, to 4.3 nSR tubes. For the modeling here, we simplified this to a coupling ratio of 4 and represented the combination of jSR and nSR interaction as a sarcomeric “unit” (Fig. 8 Ai). Multiple units can be combined in 2-D to form a cellular SR network, as shown in Fig. 8 Bi. The SR geometry is thin along the z axis, so variation in the third dimension can be assumed to be negligible; therefore this 2-D model can approximate the three-dimensional solution. The jSR cisternae of individual units coincide with the Z-lines (2), whereas the nSR spans the distance in between. Although resting sarcomeres are 1.9 μm long (8), the nSR tubes may meander across the sarcomere and consequently be much longer and, thus, contribute to SR tortuosity.
The geometry of nSR tubes is not known in detail, but it must be compatible with the tortuosity imposed by the whole SR on unbuffered solute diffusion. Recent work has suggested that the environment of the ER in Chinese hamster ovary cells reduce mobility of green fluorescent protein, an unbuffered solute, by 2.6- to 6.2-fold, relative to cytosol (44). In cardiac myocytes, mobility of Fluo-5N in the SR (9) is 8 μm2/s. The mobility of a related fluorophore, Fluo-3, in the cytoplasm has been estimated to be between 25 μm2/s (allowing binding to muscle proteins) and 90 μm2/s (without binding to muscle proteins) (40,45). SR Fluo-5N mobility is therefore between 3.1- and 11.3-fold lower than Fluo-3 mobility in cytoplasm. Based on green fluorescent protein and Fluo-5N mobility data, SR tortuosity is predicted to reduce mobility, on average, by a factor of 5.8 relative to cytoplasm, i.e., 11.6 relative to water (7).
Assuming that the nSR/jSR volume ratio is 1.1 (2), mean nSR half-length (ℓ, Fig. 8 Ai) and mean nSR tube radius (r) obey ℓ × r2 ≈ 6.72 × 10−4 nm3. A 120-μm-long myocyte will contain 63 sarcomeres along its length and 10 sarcomeres across its width. A fully stretched nSR would be 126 × ℓ long in total. To determine nSR geometry, the geometrical model was run for a range of values of ℓ (hence r) until the geometry conformed to an 11.6-fold reduction in “effective” diffusion coefficient. Effective diffusion mobility was estimated by a simpler diffusive model, solved over a 1-D compartment as long as a myocyte, starting from a nonuniform initial concentration condition. Concentration was fixed at zero at one end of the SR along 25% of its length, whereas the remainder of the SR featured a reflection boundary condition and initial solute concentration of unity. Best-fit values for ℓ and r were 1.6 μm and 20 nm, respectively (Fig. 8 Ai). This would predict a 3.8 μm distance between cisternae centers, i.e., twice the intersarcomeric spacing. Thus, on the above model, nSR tubes would be predicted to meander and coil between adjacent cisternae, causing the measured level of SR tortuosity.
Modeling the kinetics of cisternal Ca2+ refilling
In rabbit myocytes, jSR refilling is proposed to occur with an average time constant of 29 ms, as derived from the time course of a Ca2+-blink recovery (2). Recovery is too slow to be explained by rapid Ca2+ unbinding from calsequestrin (30) (i.e., buffer reequilibration); thus it is plausible to suggest that the time course of jSR Ca2+-recovery is due to a diffusive process (2,14). The geometry of a unit of SR (Fig. 8 Ai) can be used to approximate the kinetics of cisternal Ca2+ refilling. The half-length (ℓ) for nSR was set to 1.6 μm to simulate tortuosity (as described above). The SR unit was coupled to an infinite source of Ca2+, implemented by introducing a constant concentration boundary condition at the distal ends of the nSR tubes (it is assumed that, for an isolated cisternal refilling event, the kinetics of SERCA are not rate limiting). To simulate jSR refilling, cisternal [Ca2+] is rapidly halved and the recovery of jSR [Ca2+] is modeled for a range of Ca2+-diffusion coefficients at the jSR (DCajSR) and nSR (DCanSR). During Ca2+-blinks, no change in nSR [Ca2+] has been detected (2), implying a high local DCanSR in the nSR. Our model can simulate the measured jSR refilling rate when DCajSR is 1.8 μm2/s (see Fig. 8 Aii) and DCanSR is equal to free Ca2+ mobility (1000 μm2/s). Note that, during jSR refilling, the simulation predicts only a small (<3%) transient decrease of [Ca2+]SR in the nSR elements. Further modeling (not shown) has revealed that similar refilling kinetics can be achieved for DCanSR > 300 μm2/s without significant (<10%) nSR depletion.
Relationship between global Ca2+ mobility (DCaSR) and jSR Ca2+ mobility (DCajSR)
To investigate the relationship between DCajSR and global DCaSR, we adopted the geometry (Fig. 8 Bi) based on a 63 × 10 array of nSR/jSR units (Fig. 8 Ai), i.e., proposing that the nSR meanders between Z-lines such that 3.2 μm of nSR spans a distance of 1.3 μm (sarcomere length, less jSR diameter). For this model, the nSR is assumed to be homogeneous, within which Ca2+ diffuses freely (DCa = 1000 μm2/s (7,28)). To drive diffusion, [Ca2+]SR in one end of the SR (along 25% of the SR length) was set to 0.25 mM, simulating a localized exposure to caffeine (as illustrated in Fig. 8 Bi), and a zero-concentration boundary condition was imposed therein. The remainder of the SR featured a reflection boundary condition and initial concentration of 0.5 mM. The output of the model was then fitted with a simple diffusion equation, solved in a 120-μm-long homogeneous 1-D compartment with no geometrical restrictions, to derive “effective” mobility, i.e., the value for global DCaSR. The predicted relationship between global DCaSR and DCajSR is plotted in Fig. 8 Bii.
In an extension to our SR model, we incorporated heterogeneity of Ca2+-mobility in nSR (Fig. 8 Biii) with fast (1000 μm2/s) diffusion in snSR and restricted diffusion (<1000 μm2/s) in the intersarcomeric nSR (inSR). The value of the latter cannot be determined without a detailed geometrical description. However, overall nSR Ca2+-mobility, averaged over its length, must be 110 μm2/s to be consistent with the estimated DCajSR and measured global DCaSR. The effect of restricted inSR Ca2+-diffusion on overall Ca2+-mobility is maximized when nSR half-length ℓ is minimal, i.e., 0.65 μm (as short as the Z-line to Z-line spacing permits minus cisterna diameter). By modeling this scenario, we found that the percentage of total nSR length occupied by inSR would equal inSR Ca2+-mobility (expressed in μm2/s) multiplied by 0.85%. If, for example, Ca2+-mobility in inSR was comparable to DCajSR, the inSR would occupy 1.5% of the nSR length.
Editor: David A. Eisner.
References
- 1.Page, E. 1978. Quantitative ultrastructural analysis in cardiac membrane physiology. Am. J. Physiol. 235:C147–C158. [DOI] [PubMed] [Google Scholar]
- 2.Brochet, D. X., D. Yang, A. Di Maio, W. J. Lederer, C. Franzini-Armstrong, and H. Cheng. 2005. Ca2+ blinks: rapid nanoscopic store calcium signaling. Proc. Natl. Acad. Sci. USA. 102:3099–3104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Shannon, T. R., K. S. Ginsburg, and D. M. Bers. 2000. Reverse mode of the sarcoplasmic reticulum calcium pump and load-dependent cytosolic calcium decline in voltage-clamped cardiac ventricular myocytes. Biophys. J. 78:322–333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bers, D. M. 2002. Sarcoplasmic reticulum Ca2+ release in intact ventricular myocytes. Front. Biosci. 7:1697–1711. [DOI] [PubMed] [Google Scholar]
- 5.Stern, M. D. 1992. Theory of excitation-contraction coupling in cardiac muscle. Biophys. J. 63:497–517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cheng, H., W. J. Lederer, and M. B. Cannell. 1993. Calcium sparks: elementary events underlying excitation-contraction coupling in heart muscle. Science. 262:740–744. [DOI] [PubMed] [Google Scholar]
- 7.Kushmerick, M. J., and R. J. Podolsky. 1969. Ionic mobility in muscle cells. Science. 166:1297–1298. [DOI] [PubMed] [Google Scholar]
- 8.Shannon, T. R., T. Guo, and D. M. Bers. 2003. Ca2+ scraps: local depletions of free [Ca2+] in cardiac sarcoplasmic reticulum during contractions leave substantial Ca2+ reserve. Circ. Res. 93:40–45. [DOI] [PubMed] [Google Scholar]
- 9.Wu, X., and D. M. Bers. 2006. Sarcoplasmic reticulum and nuclear envelope are one highly interconnected Ca2+ store throughout cardiac myocyte. Circ. Res. 99:283–291. [DOI] [PubMed] [Google Scholar]
- 10.Meissner, G. 1975. Isolation and characterization of two types of sarcoplasmic reticulum vesicles. Biochim. Biophys. Acta. 389:51–68. [DOI] [PubMed] [Google Scholar]
- 11.Scriven, D. R., P. Dan, and E. D. Moore. 2000. Distribution of proteins implicated in excitation-contraction coupling in rat ventricular myocytes. Biophys. J. 79:2682–2691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Keller, M., J. P. Kao, M. Egger, and E. Niggli. 2007. Calcium waves driven by “sensitization” wave-fronts. Cardiovasc. Res. 74:39–45. [DOI] [PubMed] [Google Scholar]
- 13.Kubalova, Z., D. Terentyev, S. Viatchenko-Karpinski, Y. Nishijima, I. Gyorke, R. Terentyeva, D. N. da Cunha, A. Sridhar, D. S. Feldman, R. L. Hamlin, C. A. Carnes, and S. Gyorke. 2005. Abnormal intrastore calcium signaling in chronic heart failure. Proc. Natl. Acad. Sci. USA. 102:14104–14109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Niggli, E., and N. Shirokova. 2007. A guide to sparkology: the taxonomy of elementary cellular Ca2+ signaling events. Cell Calcium. 42:379–387. [DOI] [PubMed] [Google Scholar]
- 15.Venetucci, L., A. W. Trafford, and D. A. Eisner. 2003. Illuminating sarcoplasmic reticulum calcium. Circ. Res. 93:4–5. [DOI] [PubMed] [Google Scholar]
- 16.Spitzer, K. W., P. R. Ershler, R. L. Skolnick, and R. D. Vaughan-Jones. 2000. Generation of intracellular pH gradients in single cardiac myocytes with a microperfusion system. Am. J. Physiol. Heart Circ. Physiol. 278:H1371–H1382. [DOI] [PubMed] [Google Scholar]
- 17.Swietach, P., and R. D. Vaughan-Jones. 2005. Relationship between intracellular pH and proton mobility in rat and guinea-pig ventricular myocytes. J. Physiol. 566:793–806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bassani, R. A., and D. M. Bers. 1995. Rate of diastolic Ca release from the sarcoplasmic reticulum of intact rabbit and rat ventricular myocytes. Biophys. J. 68:2015–2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bassani, R. A., J. W. Bassani, and D. M. Bers. 1992. Mitochondrial and sarcolemmal Ca2+ transport reduce [Ca2+]i during caffeine contractures in rabbit cardiac myocytes. J. Physiol. 453:591–608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Rousseau, E., and G. Meissner. 1989. Single cardiac sarcoplasmic reticulum Ca2+-release channel: activation by caffeine. Am. J. Physiol. 256:H328–H333. [DOI] [PubMed] [Google Scholar]
- 21.Berlin, J. R., J. W. Bassani, and D. M. Bers. 1994. Intrinsic cytosolic calcium buffering properties of single rat cardiac myocytes. Biophys. J. 67:1775–1787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Shannon, T. R., K. S. Ginsburg, and D. M. Bers. 2002. Quantitative assessment of the SR Ca2+ leak-load relationship. Circ. Res. 91:594–600. [DOI] [PubMed] [Google Scholar]
- 23.Nieman, C. J., and D. A. Eisner. 1985. Effects of caffeine, tetracaine, and ryanodine on calcium-dependent oscillations in sheep cardiac Purkinje fibers. J. Gen. Physiol. 86:877–889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Spitzer, K. W., and J. H. Bridge. 1989. A simple device for rapidly exchanging solution surrounding a single cardiac cell. Am. J. Physiol. 256:C441–C447. [DOI] [PubMed] [Google Scholar]
- 25.Swietach, P., C. H. Leem, K. W. Spitzer, and R. D. Vaughan-Jones. 2005. Experimental generation and computational modeling of intracellular pH gradients in cardiac myocytes. Biophys. J. 88:3018–3037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.O'Neill, S. C., P. Donoso, and D. A. Eisner. 1990. The role of [Ca2+]i and [Ca2+] sensitization in the caffeine contracture of rat myocytes: measurement of [Ca2+]i and [caffeine]i. J. Physiol. 425:55–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.O'Neill, S. C., and D. A. Eisner. 1990. A mechanism for the effects of caffeine on Ca2+ release during diastole and systole in isolated rat ventricular myocytes. J. Physiol. 430:519–536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Vanysek, P. 1999. Ionic conductivity and diffusion at infinite dilution. In CRC Handbook of Chemistry and Physics, Thermochemistry, Electrochemistry and Kinetics. D. R. Lide, editor. CRC, London. 93–95.
- 29.Trafford, A. W., M. E. Diaz, and D. A. Eisner. 1999. A novel, rapid and reversible method to measure Ca2+ buffering and time-course of total sarcoplasmic reticulum Ca2+ content in cardiac ventricular myocytes. Pflugers Arch. 437:501–503. [DOI] [PubMed] [Google Scholar]
- 30.Beltran, M., G. Barrientos, and C. Hidalgo. 2006. Fast kinetics of calcium dissociation from calsequestrin. Biol. Res. 39:493–503. [DOI] [PubMed] [Google Scholar]
- 31.Shannon, T. R., and D. M. Bers. 1997. Assessment of intra-SR free [Ca2+] and buffering in rat heart. Biophys. J. 73:1524–1531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Gabso, M., E. Neher, and M. E. Spira. 1997. Low mobility of the Ca2+ buffers in axons of cultured Aplysia neurons. Neuron. 18:473–481. [DOI] [PubMed] [Google Scholar]
- 33.Stern, M. D., and H. Cheng. 2004. Putting out the fire: what terminates calcium-induced calcium release in cardiac muscle? Cell Calcium. 35:591–601. [DOI] [PubMed] [Google Scholar]
- 34.Terentyev, D., S. Viatchenko-Karpinski, H. H. Valdivia, A. L. Escobar, and S. Gyorke. 2002. Luminal Ca2+ controls termination and refractory behavior of Ca2+-induced Ca2+ release in cardiac myocytes. Circ. Res. 91:414–420. [DOI] [PubMed] [Google Scholar]
- 35.Knollmann, B. C., N. Chopra, T. Hlaing, B. Akin, T. Yang, K. Ettensohn, B. E. Knollmann, K. D. Horton, N. J. Weissman, I. Holinstat, W. Zhang, D. M. Roden, L. R. Jones, C. Franzini-Armstrong, and K. Pfeifer. 2006. Casq2 deletion causes sarcoplasmic reticulum volume increase, premature Ca2+ release, and catecholaminergic polymorphic ventricular tachycardia. J. Clin. Invest. 116:2510–2520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wang, W., L. Cleemann, L. R. Jones, and M. Morad. 2000. Modulation of focal and global Ca2+ release in calsequestrin-overexpressing mouse cardiomyocytes. J. Physiol. 524:399–414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Diaz, M. E., D. A. Eisner, and S. C. O'Neill. 2002. Depressed ryanodine receptor activity increases variability and duration of the systolic Ca2+ transient in rat ventricular myocytes. Circ. Res. 91:585–593. [DOI] [PubMed] [Google Scholar]
- 38.Sobie, E. A., L. S. Song, and W. J. Lederer. 2006. Restitution of Ca2+ release and vulnerability to arrhythmias. J. Cardiovasc. Electrophysiol. 17(Suppl 1):S64–S70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Baylor, S. M., and S. Hollingworth. 1998. Model of sarcomeric Ca2+ movements, including ATP Ca2+ binding and diffusion, during activation of frog skeletal muscle. J. Gen. Physiol. 112:297–316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Cordeiro, J. M., K. W. Spitzer, W. R. Giles, P. E. Ershler, M. B. Cannell, and J. H. Bridge. 2001. Location of the initiation site of calcium transients and sparks in rabbit heart Purkinje cells. J. Physiol. 531:301–314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Allbritton, N. L., T. Meyer, and L. Stryer. 1992. Range of messenger action of calcium ion and inositol 1,4,5-trisphosphate. Science. 258:1812–1815. [DOI] [PubMed] [Google Scholar]
- 42.Wagner, J., and J. Keizer. 1994. Effects of rapid buffers on Ca2+ diffusion and Ca2+ oscillations. Biophys. J. 67:447–456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Shannon, T. R., F. Wang, J. Puglisi, C. Weber, and D. M. Bers. 2004. A mathematical treatment of integrated Ca dynamics within the ventricular myocyte. Biophys. J. 87:3351–3371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Dayel, M. J., E. F. Hom, and A. S. Verkman. 1999. Diffusion of green fluorescent protein in the aqueous-phase lumen of endoplasmic reticulum. Biophys. J. 76:2843–2851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Harkins, A. B., N. Kurebayashi, and S. M. Baylor. 1993. Resting myoplasmic free calcium in frog skeletal muscle fibers estimated with fluo-3. Biophys. J. 65:865–881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Hinch, R., J. L. Greenstein, A. J. Tanskanen, L. Xu, and R. L. Winslow. 2004. A simplified local control model of calcium-induced calcium release in cardiac ventricular myocytes. Biophys. J. 87:3723–3736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Satoh, H., L. M. Delbridge, L. A. Blatter, and D. M. Bers. 1996. Surface:volume relationship in cardiac myocytes studied with confocal microscopy and membrane capacitance measurements: species-dependence and developmental effects. Biophys. J. 70:1494–1504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Page, E., L. P. McCallister, and B. Power. 1971. Sterological measurements of cardiac ultrastructures implicated in excitation-contraction coupling. Proc. Natl. Acad. Sci. USA. 68:1465–1466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Soeller, C., and M. B. Cannell. 1999. Examination of the transverse tubular system in living cardiac rat myocytes by 2-photon microscopy and digital image-processing techniques. Circ. Res. 84:266–275. [DOI] [PubMed] [Google Scholar]
- 50.Snyder, S. M., B. M. Palmer, and R. L. Moore. 2000. A mathematical model of cardiocyte Ca2+ dynamics with a novel representation of sarcoplasmic reticular Ca2+ control. Biophys. J. 79:94–115. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.