Abstract
The heterotrimeric G protein transducin is a key component of the vertebrate phototransduction cascade. Transducin is peripherally attached to membranes of the rod outer segment, where it interacts with other proteins at the membrane-cytosol interface. However, upon sustained activation by light, the dissociated Gtα and Gβ1γ1 subunits of transducin translocate from the outer segment to other parts of the rod cell. Here we used a computational approach to analyze the interaction strength of transducin and its subunits with acidic lipid bilayers, as well as the range of orientations that they are allowed to occupy on the membrane surface. Our results suggest that the combined constraints of electrostatics and lipid anchors substantially limit the rotational degrees of freedom of the membrane-bound transducin heterotrimer. This may contribute to a faster transducin activation rate by accelerating transducin-rhodopsin complex formation. Notably, the membrane interactions of the dissociated transducin subunits are very different from those of the heterotrimer. As shown previously, Gβ1γ1 experiences significant attractive interactions with negatively charged membranes, whereas our new results suggest that Gtα is electrostatically repelled by such membranes. We suggest that this repulsion could facilitate the membrane dissociation and intracellular translocation of Gtα. Moreover, based on similarities in sequence and electrostatic properties, we propose that the properties described for transducin are common to its homologs within the Gi subfamily. In a broader view, this work exemplifies how the activity-dependent association and dissociation of a G protein can change both the affinity for membranes and the range of allowed orientations, thereby modulating G protein function.
The G protein transducin is a key molecular switch in vertebrate rod cells (1-3). Like other heterotrimeric G proteins, transducin is peripherally attached to the lipid bilayer by covalent lipid modifications of the N terminus of the α subunit and the C terminus of the γ subunit (4, 5). During the rapid course of a photoresponse, each photoexcited rhodopsin activates tens of transducin heterotrimers (Gt) at a rate of hundreds of Gt molecules per second (6, 7). This activation catalyzes GDP/GTP exchange on Gtα, which then dissociates from Gβ1γ1 and proceeds to activate the effector, cGMP phosphodiesterase. The fact that these protein-protein interactions take place at the membrane-cytosol interface is a key reason why the phototransduction cascade operates so rapidly and efficiently (8, 9), thus motivating a more detailed investigation of Gt-membrane interactions.
The attachment of transducin to the disk membranes of rod outer segments is reversible, allowing transducin to undergo activation-dependent translocation from the light-sensitive outer segment compartment to the rest of the photoreceptor cell (10). A similar phenomenon was also shown for the invertebrate visual G protein, Gq (11). The efficiency of transducin translocation can be modulated by the interaction strength of the subunits with membranes (12, 13). However, the mechanisms underlying Gt translocation are still under intensive investigation (reviewed in Refs. 14, 15), thus providing a rationale for quantitative characterization of the membrane interactions of transducin and its individual subunits.
Several investigators examined the crystal structures of Gt and proposed a number of distinct Gt orientations relative to the membrane surface, based on constraints imposed by Gt lipid anchorage and evidence from Gt-rhodopsin interaction experiments. In some orientations the N-terminal helix of Gtα was placed parallel to the membrane (“parallel orientations”) (16-23), whereas in others this helix was placed at a large angle with respect to the membrane plane (“tilted orientations”) (24, 25). In addition to their lipid anchors, Gt and its individual subunits can interact electrostatically with the negatively charged membrane surface (16, 18), and these interactions can affect both the affinity of transducin for the membrane and its orientation on the membrane surface. For instance, both Gt and its subunits can be detached from membranes by hypotonic but not isotonic buffers (26-29), presumably because electrostatic repulsion becomes dominant in low ionic strengths. In a previous computational study, Murray et al. (30) showed that Gβ1γ1 is attracted to the membrane electrostatically, accounting for experimental observations that Gβ1γ1 binds more strongly to negatively charged membranes than to neutral membranes (5, 31). Murray et al. (30) also suggested that electrostatics play a role in optimally positioning Gβ1γ1 at the membrane surface to facilitate its interactions with other proteins. On the other hand, the electrostatic contribution to the interactions of Gtα with membranes is less clear. The membrane affinity of Gtα was shown to be smaller than the affinity of Gβ1γ1 in vitro, and several observations hint that Gtα could be repelled by the membrane (4, 5, 31). Electrostatic repulsion is consistent with a qualitative examination of Gα subunits from the Gi subfamily, including Gtα, showing that their surfaces are dominated by negatively charged patches (32).
Here we used a quantitative computational approach to characterize the membrane affinity of transducin and the range of its allowed orientations next to the membrane as determined by lipid anchors and electrostatic interactions. We calculated electrostatic free energies using the Finite-Difference Poisson-Boltzmann (FDPB)4 method, which has been successfully applied to numerous protein-membrane systems, yielding results that reproduce experimental measurements with high accuracy (30, 33-37). We found that, in addition to the lipid anchorage of Gt, electrostatic repulsion further constrains the orientations of membrane-associated Gt, regardless of its orientation in the complex with rhodopsin, making some of the previously suggested Gt orientations more favorable than others. In contrast, Gβ1γ1 is attracted to the membrane in many lipid-allowed orientations. Finally, we showed that monomeric Gtα experiences a comparable degree of electrostatic repulsion.
EXPERIMENTAL PROCEDURES
Using the FDPB Method to Calculate Electrostatic Potential and Free Energy—Electrostatic potentials and free energies were calculated with a modified version of the DelPhi program, adapted to solve the nonlinear Poisson-Boltzmann equation for protein-membrane systems. DelPhi yields finite-difference solutions to the Poisson-Boltzmann equation (the FDPB method) for a system where the solvent is described in terms of a bulk dielectric constant and concentrations of mobile ions, whereas the solutes (here, the proteins and membrane) are described in atomic detail by the coordinates of the individual atoms, their atomic radii, and their partial charges. The FDPB methodology has been applied to numerous peptide-membrane and protein-membrane systems, producing results that predict successfully and with high accuracy the following: 1) macroscopic properties, such as quantitative differences between the membrane interactions of homologous proteins and effects of lipid composition or ionic strength; and 2) microscopic properties, such as the effect of point mutations or binding of metal ions on membrane interactions (for examples see Refs. 30, 33, 35-40).
Atomic Structural Models of Proteins and Membranes—The atomic model we used for the Gt heterotrimer was based on the Gαt/i1β1γ1 crystal structure (PDB code 1GOT) solved by Lambright et al. (16). Because the Gα subunit in this structure is a chimera of Gtα and Gi1α (residues 216-294 of bovine Gtα were replaced with residues 220-298 of rat Gi1α to improve protein expression), a composite model was built for heterotrimeric Gtα by manually copying the backbone and side chains of these residues from the corresponding region of native Gtα, taken from the Gtα-GDP structure (1TAG) (41). The structure of these two corresponding regions is highly similar (16), and their backbone root mean square deviation is 0.5 Å. The structure of bovine Gβ1γ1 (PDB code 2TRC) (42) was used in calculations for dissociated Gβ1γ1, as in a previous study (30). Both Gγ1 termini in the heterotrimeric model, which are slightly shorter than in the structure of dissociated Gβ1γ1, were extended by manually copying the extra residues from the structure of dissociated Gβ1γ1. The resulting structures contain all the charged residues of native transducin. The N terminus of Gtα, in its heterotrimeric form, is in an extended helical conformation and is stabilized by interactions with Gβ1γ1 (see supplemental Fig. S1 and Ref. 16). After dissociation from Gβ1γ1, this subdomain does not have any significant stabilizing interactions with the membrane (supplemental Fig. S2). Available structures of monomeric Gtα are not applicable to our calculations because they lack the entire N terminus, which was cleaved prior to crystallization. This raises the possibility that the N terminus of Gtα is intrinsically unstructured. However, we note that the N terminus in the crystal structure of the homologous Gi1α-GDP (68% sequence identity to Gtα) refolds onto the bulk of the protein to form a compact subdomain that is stabilized by a network of interacting residues that are conserved between Gi1α and its homologs Goα and Gtα (43). A folded and highly ordered Gi1α N terminus was also shown for the myristoylated form of Gi1α in solution, and it was suggested that this feature is conserved in homologous Gα subunits (44). We therefore assumed that soluble GDP-bound Gtα adopts a similar conformation, and we modeled it on the structure of monomeric Gi1α-GDP (PDB code 1GDD) using the program Nest (45) and remodeled unconserved side chains using Scap (46).
Hydrogen atoms were added to the protein structures with the program CHARMM, and the structures were subjected to conjugate gradient minimization with a harmonic restraint force of 50 kcal/mol/Å applied to the heavy atoms located at the original crystallographic coordinates. Hydrogens were added to the guanine nucleotides bound to the Gα subunits using the builder module in Insight II (Accelrys).
Phospholipid bilayers of lateral dimensions ∼165 × 172 Å and ratios of 0:1, 1:8, 1:5, 1:3, 1:2, and 1:1 acidic lipid (phosphatidylserine) to neutral lipids (phosphatidylcholine) were built as described in previous work (30, 33-37, 39, 47). In vivo, the distribution of acidic lipids is known to be asymmetric across the bilayer, and following previous studies (30, 33, 35-40, 48, 49), we assume that all of the phosphatidylserine is located on the cytosolic leaflet of the rod outer segment membranes. Except where specified otherwise, in our calculations we used bilayers with a ratio of 1:2 phosphatidylserine/phosphatidylcholine; this ratio has been assumed to be a reasonable approximation for the lipid composition facing the transducin under physiological conditions (30), and indeed, as shown in Fig. 4 and discussed below, this membrane composition is representative of the wider range of possible compositions. As in previous work, we assume that the bilayer does not change structure or position when it interacts with the protein (see Ref. 30).
FIGURE 4.
Dependence of transducin-membrane electrostatic interactions on membrane composition. Calculation of the electrostatic free energy of interaction of different Gt states with bilayers of different acidic lipid composition. The vertical dashed line marks the lipid composition used in most calculations here (33% acidic lipids), whereas the two vertical dotted lines mark the range of possible lipid compositions facing transducin in rod outer segment disks (see text for details).
Calculating Electrostatic Free Energies for Protein-Membrane Interactions—The protein/membrane model was mapped onto a fine three-dimensional grid, where each small cube represents a small region of the peptide, membrane, or solvent. As in previous studies of comparable protein-membrane systems (30, 33-37, 39), we took the charges and radii used for the amino acids from the CHARMM22 parameter set and for the lipids from Ref. 47. Regions inside the molecular surfaces of the protein and membrane were assigned a dielectric constant of 2, and those outside were assigned a dielectric constant of 80, combined with an ion exclusion layer of 2 Å around the solute. Unless stated otherwise, the salt concentration was set to 100 mm, as in previous studies (30, 33, 35-40). The numerical calculation of the potential was iterated to convergence, defined as the point at which the potential changes less than 10-5 kT/e between successive iterations. A sequence of focusing runs of increasing resolution was employed to calculate the electrostatic potentials (e.g. 0.3, 0.6, 1.2, and 2.4 grid/Å). Electrostatic energies were obtained using the calculated potentials, and the electrostatic energy of a protein-membrane interaction was determined as the difference between the following: 1) the electrostatic free energy of the protein in a specific orientation and distance relative to the membrane surface; and 2) the electrostatic free energies of the protein and membrane infinitely far apart (i.e. calculated separately). The numerical error of the free energy calculations, estimated by the difference between the calculations of the two highest resolution scales, was <0.1 kcal/mol in all calculations. More details on the methodology can be found in Refs. 30, 33-37, 39, 40.
The nonspecific electrostatic interactions calculated here are relatively insensitive to local changes in conformation. Different combinations of composite models from two separate PDB structures or different minimization protocols, which produced global root mean square deviations of up to 2 Å between models, changed the calculated electrostatic energies of interactions by less than the numerical error for a given protein-membrane complex.
Global Sampling of Transducin Orientations to Calculate Transducin-Membrane Interactions—Previous studies used visual inspection to find an approximate minimum free energy orientation of a protein relative to the membrane and then sampled extensively close to this orientation to find the minimum free energy orientation (30, 33-37). Here, however, visual inspection could not reliably determine the approximate minimum-energy orientation of the Gt heterotrimer and Gtα with respect to the membrane, because these proteins do not have prominent positively charged patches that clearly determine the orientation of minimum energy. We therefore implemented a global sampling of all nonredundant Euler rotations, rotating the protein around the point in the structure closest to the lipid attachment point. This point corresponds to the N terminus in Gtα calculations, the C terminus of Gγ1 in Gβ1γ1 calculations, and the midpoint between them for the heterotrimer structure (where the two termini are ∼15 Å apart). For each orientation, the membrane was moved so as to place the molecular surfaces of the protein and membrane 3 Å apart (R = 3 Å), and the electrostatic energy was calculated as above. R = 3 Å was chosen because at orientations where the electrostatic interaction is attractive, the energy value at this distance is minimal (see supplemental material and Refs. 30, 33, 35, 40).
Combining Lipid Anchor Constraints with Global Orientation Sampling—The transducin structures used here do not have coordinates for the lipid anchors nor for the termini to which the anchors are covalently attached as follows: the myristoyl-GAGA- at the N terminus of Gtα and the -GGC-farnesyl at the C terminus of Gγ1. For each orientation we assumed that a lipid anchor can reach the membrane if the measured distance between each relevant terminus and the membrane was equal to or less than 13 Å for Gtα and 10 Å for Gγ1, thresholds corresponding to the length of the fully extended linkers. This assumption considers these linkers as flexible (as suggested in Ref. 16, based on their amino acid sequence) and able to adopt fully extended conformations. When we determined that a lipid anchor can reach the membrane in a specific orientation, we assigned to this orientation an energetic contribution of -6 kcal/mol, which corresponds to the estimated energetic contribution of an individual lipid modification (see under “Discussion” for more details on these estimates). When both lipid anchors could reach the membrane, we assigned to such an orientation an energetic contribution of -12 kcal/mol.
Calculation of Average Energy and Entropy—Previous work
established that when the peripheral association between a protein and a
membrane is of substantial attractive nature, the relative binding energies
and the electrostatic contribution to binding are well approximated by the
energy value at the minimum free energy orientation
(30,
33-37,
39). In addition to finding
the minimal free energy value, we also calculated the Boltzmann-weighted
average energy, as in Ref. 37,
and see Equation 1,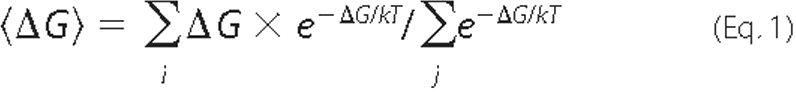
where k is the Boltzmann constant, and T is the absolute temperature. The calculations were repeated twice, with and without the constraints of the lipid anchor. The latter can show whether specific orientations provide sufficient attraction to the membrane to compensate for the energetic penalty associated with removing the lipid anchor out of the bilayer (see above), and represent the effect of electrostatics on the soluble forms of the proteins (i.e. before the lipid anchors attach to the membrane). We used the “bootstrapping” re-sampling method to check the statistical significance of our results (as in Ref. 50), which were precise to within 0.05 kcal/mol.
The free energy cost because of the entropic penalty associated with
limiting Gt rotations was approximated by Equation
2,
where S2 is the entropy of Gt with the additional constraints (lipid anchor and/or electrostatics), and S1 is the reference state (having the same number of microstates but with an equal probability of being in each state and with all of these probabilities summing to unity). We estimated the error in the entropy calculation by adding a random value (in the range of the numerical error, 0.1 kcal/mol) to the calculated free energies and repeated the entropy calculations 100 times, reaching an estimated error of 0.02 kcal/mol.
We translated differences in the free energy of interaction to changes in association/dissociation rates (Δk) using Equation 3,
 |
(Eq.3) |
Visualizing Three-dimensional Potential Maps—Three-dimensional potential maps were visualized by mapping the values onto the molecular surface of the protein and by drawing equi-potential contour meshes that connect all the points in space having a specific potential value (here ±1 kT/e, which are equal to ± 25 mV).
RESULTS
Characterizing the Interaction of the Gt Heterotrimer with the Lipid Bilayer—We analyzed the interaction of Gt with the membrane using global orientation sampling, using the FDPB method to calculate the electrostatic free energy of interaction at each orientation (Fig. 1A). At each orientation, we also measured whether each of the two lipid anchors can reach the lipid bilayer (marked as “lipid-allowed” orientations in Fig. 1A with magenta and cyan lines). These measurements show that ∼11% of all possible Gt orientations enable both lipid anchors to reach the membrane. By calculating the effects of electrostatics and the lipid anchors separately, we can examine their individual contributions and analyze cases in which only one of these factors is significant for membrane interactions (e.g. when soluble transducin targets back to the membrane from the cytosol, or when transducin interacts in vitro with neutral membranes). When we determined that a lipid anchor can reach the membrane in a specific orientation, we assigned to this orientation an energetic contribution of -6or -12 kcal/mol, corresponding to the estimated energetic contribution of one or two lipid modifications, respectively (see “Discussion” for more details on these estimates). We assumed that a lipid anchor can reach the membrane when the distance between the bilayer and the relevant terminus in the structure was equal to or less than predetermined distance thresholds (see “Experimental Procedures”). This assumption considers the terminal 3-4 amino acids that connect to the lipid anchors and are not present in the crystal structure as conformationally flexible linkers that are able to fully extend, as was suggested previously based on their amino acid sequence (16). Nevertheless, our results are not dependent on the exact values of these distance thresholds; because of the large size of Gt, its geometry, and the close proximity of the two relevant termini, increasing or decreasing these distance thresholds by up to 50% resulted in essentially the same ensemble of lipid-allowed orientations.
FIGURE 1.
Interactions of the Gt heterotrimer with the membrane. A, global orientation sampling of the Gt heterotrimer. The x (θ) and y axes (μ) mark Euler angles of rotation from the initial orientation (supplemental Fig. S1). The z axis and the color code both mark the calculated electrostatic free energy of interaction with the membrane; positive (red) energies will result in repulsion, whereas negative (blue) energies will result in attraction. The magenta and cyan lines enclose lipid-allowed orientations, which enable the Gγ1 (magenta) and the Gtα (cyan) lipid anchors to reach the membrane. Representative Gt orientations are marked on the plot of global orientation sampling for Gt, with letters corresponding to subsequent panel captions. B, Gt orientation of minimum free energy, which is representative of tilted orientations; ΔGel = -0.8 kcal/mol. C, electrostatic potential map of the Gt heterotrimer in the orientation of minimum free energy (the same orientation as in B). Electrostatic potential maps were visualized by drawing equi-potential contour meshes for the values +1 kT/e (25mV, blue mesh) and -1 kT/e (-25 mV, red mesh). Gt subunits are shown in Connolly surface representation and colored pink (α), light green (β), and light blue (γ), and the functionally relevant termini are annotated. Two large negatively charged patches on Gtα and Gβ1γ1 are marked with orange and red arrows, respectively; these patches cause the repulsion observed in the lipid-allowed orientations at μ ∼ 0° and μ > 60°. D, representative parallel orientation; ΔGel = 1.1 kcal/mol. E, lipid-allowed orientation with moderate repulsive electrostatics; ΔGel = 1.8 kcal/mol. F, lipid-disallowed orientation, where the Gγ1 lipid anchor cannot reach the membrane; ΔGel = 4 kcal/mol. G, lipid-disallowed orientation, where both lipid anchors cannot reach the membrane; ΔGel = 3.5 kcal/mol. B and D-G, Gt subunits are shown in worm representation and are colored red (α), green (β), and blue (γ). The N-terminal helix of Gtα is colored magenta, and the C terminus of Gtα is colored orange. The lipid bilayer is depicted in gray CPK representation.
Most Gt orientations are strongly repelled by the bilayer (Fig. 1A). Only a minor ensemble of orientations (∼6%) exhibits either a small attraction (∼3% of all orientations) or a weak repulsion. We label orientations with an interaction energy (ΔGel) within 2 kcal/mol of the minimum electrostatic free energy (-0.8 kcal/mol, see Table 1), as “electrostatically favorable orientations.” We chose this threshold because it corresponds to a substantial (∼30-fold) decrease in the occupation probability with respect to the energy minimum. (Note that the results are relatively insensitive to the precise value of the threshold because the selected value is far enough from the minimum so that changing it by ±0.5 kcal/mol has a small effect on which orientations are labeled as favorable.) The electrostatically favorable orientations of Gt are clustered around the orientation of minimum electrostatic free energy (Fig. 1A). In these orientations, a small positively charged patch around the attachment points of the two lipid anchors is proximal to the membrane, whereas the negative potential around most of Gt is positioned further away from the membrane (e.g. Fig. 1C). This results in a weak attraction at the orientation of minimum electrostatic free energy (-0.8 kcal/mol) and an even smaller average energy of interaction (-0.3 kcal/mol, see Table 1).
TABLE 1.
Minimum and average electrostatic free energies of interaction of heterotrimeric/dissociated transducin with the lipid bilayer
The electrostatic free energy values are in kcal/mol, and the numerical error is <0.1 kcal/mol.
| Transducin state | ΔGel, min (lipid anchor's in membrane) | ΔGel, min (all possible orientations)a | <ΔGel>b(lipid anchor/s in membrane) | <ΔGel>b(all possible orientations)a |
|---|---|---|---|---|
| αβγ | −0.8 | −0.8 | −0.3 | ~0 |
| βγ | −3.2 | −3.2 | −2.8 | −2.7 |
| α | +1.8 | −1.2 | +2.2 | −0.4 |
Calculated by sampling of all possible orientations (i.e. without the constraints of the lipid anchor/s).
Boltzmann-weighted averaged energies (see “Experimental Procedures” for details).
Fig. 1 also shows specific examples of Gt orientations. The orientation of minimum free energy (Fig. 1, B and C) places the N-terminal helix of Gtα at an angle of ∼30° to the membrane surface and is similar to the tilted orientations suggested previously (see above). On the other hand, parallel orientations (as in Fig. 1D) position negatively charged patches near the C terminus of Gtα (marked with an orange arrow in Fig. 1C) close to the membrane and therefore result in electrostatic repulsion. Because of this repulsion, parallel orientations are less favorable than the orientation of minimum free energy (a tilted orientation) by ∼2 kcal/mol, which corresponds to ∼30-fold difference in occupancy probability. Furthermore, large negatively charged patches on Gβ1γ1 (marked with a red arrow in Fig. 1C) oppose rotations of Gt to orientations that position the N-terminal α-helix of Gtα at angles >60° to the membrane surface (Fig. 1, A and E). These electrostatic repulsions limit Gt rotation and constrain the Gtα C terminus, which is essential for binding activated rhodopsin, to face the membrane surface in all of the allowed orientations of Gt.
To estimate at the ensemble level how rotational electrostatic and/or lipid anchor constraints affect membrane-associated Gt, we calculated the difference in the entropic component of the rotational free energy that results from these constraints. The reference state was a membrane-attached Gt that can occupy all possible orientations with an equal probability (i.e. without any rotational constraints). Note that the effect on the degrees of freedom of Gt does not depend on the strength of the Gt-membrane interactions in specific orientations, but rather is a result of the global shape and characteristics of the energy-orientation landscape on Gt (as shown in Fig. 1A). When we applied the rotational constraints of both lipid anchors, the entropic “cost” was 1.1 kcal/mol. Applying only the constraint of the electrostatic interactions with the membrane results in an entropic cost of 1.3 kcal/mol (with an estimated error of 0.02 kcal/mol, see “Experimental Procedures” for details). When these constraints were applied together, the entropic energy cost was 1.8 kcal/mol, i.e. electrostatics further enhance the effect of the lipid anchors by a factor of ∼3.5.
Membrane Interactions of Dissociated Gβ1γ1—Electrostatic interactions of the dissociated Gtα and Gβ1γ1 with the lipid bilayer are very different from one another and from those of the transducin heterotrimer (Figs. 2 and 3 versus Fig. 1). Using global orientation sampling of Gβ1γ1 (Fig. 2A), we found a similar orientation of minimum electrostatic free energy (with a similar ΔGel = -3.2 kcal/mol; Table 1) as reported in a previous study (30), which sampled around an initial orientation chosen by visual inspection. We also observed that, unlike the Gt heterotrimer, Gβ1γ1 is attracted to the membrane in many orientations (∼18% of all possible orientations), allowing membrane-attached Gβ1γ1 to sample a wide range of dissimilar orientations that are both lipid-allowed and electrostatically favorable (Fig. 2).
FIGURE 2.
Interactions of Gβ1γ1 with the membrane. A, global orientation sampling of Gβ1γ1. The magenta line encloses lipid-allowed orientations, which enable the Gγ1 C-terminal farnesyl to reach the membrane. Representative lipid-allowed and electrostatically favorable Gβ1γ1 orientations are marked with letters corresponding to subsequent panel captions. B, Gβ1γ1 orientation of minimum free energy; ΔGel = -3.2 kcal/mol. C, electrostatic potential map of Gβ1γ1 in the orientation of minimum free energy (the same orientation as in B), but rotated 90° around the z axis to better visualize the segregation of charges. D, orientation with ΔGel = -2.3 kcal/mol. E, orientation with ΔGel = -1.2 kcal/mol. F, orientation with ΔGel = -1.8 kcal/mol. Gβ1γ1 subunits and the lipid bilayer are depicted as in Fig. 1. B and D-F, the C terminus of Gβ1 is marked with a black arrow, and the C terminus of Gγ1 is marked with a magenta arrow.
FIGURE 3.
Interactions of Gtα with the membrane. A, global orientation sampling of Gtα. The cyan line encloses lipid-allowed orientations, which enable the Gtα N-terminal lipid anchor to reach the membrane. The lipid-allowed orientation with minimal free energy of interaction (ΔGel = 1.8 kcal/mol) is marked with a black arrow. The lipid-disallowed orientation with minimal global electrostatic free energy (-1.2 kcal/mol) is marked with a yellow arrow. B, electrostatic potential map of Gtα in the lipid-allowed orientation with the minimal free energy of interaction, depicted as in Fig. 1.
Furthermore, most of the electrostatically favorable orientations of Gβ1γ1 and particularly all orientations with ΔGel less than -2 kcal/mol enable the lipid anchor to reach the membrane (Fig. 2A). The larger range of lipid-allowed orientations with significant electrostatic attraction to the membrane is also reflected in a stronger Boltzmann-weighted average interactions energy (-2.8 kcal/mol; see Table 1 for a detailed comparison). Increasing or decreasing the distance threshold for determining whether the lipid anchor can reach the membrane by 50% had no effect on these results. Additionally, when we removed the constraints of the lipid anchor and sampled all possible orientations of Gβ1γ1, the electrostatic free energies of interaction did not change (Table 1). Taken together, these results suggest that the contributions of the lipid anchor and electrostatics to the free energy of Gβ1γ1 interaction with the membrane are independent of one another and therefore additive.
Membrane Interactions of Dissociated Gtα—Within the Gt heterotrimer, the lipidated N terminus of Gtα assumes an extended helical conformation stabilized by interactions with Gβ1γ1 (e.g. Fig. 1B) (16). However, this N-terminal helix is likely to refold into a compact conformation upon the dissociation of Gtα from Gβ1γ1. Although no available crystal structure of monomeric Gtα contains this part of the molecule, because of its proteolytic removal prior to crystallization, the crystal structure of the homologous Gi1α-GDP (43) does contain the N terminus, which is folded onto the bulk of Gtα and is stabilized by a network of interacting residues conserved between Gi1α and Gtα (and also Goα) (43). Furthermore, a folded and highly ordered Gi1α N terminus was shown for the myristoylated form of Gi1α-GDP in solution, and it was suggested that this structural feature is conserved in homologous Gα subunits (44). We therefore proceeded with calculations for dissociated Gtα-GDP modeled on the structure of Gi1α-GDP (43) as a template (Fig. 3).
Global orientation sampling of this Gtα conformation showed repulsion by the negatively charged membrane in most orientations (Fig. 3A), because the entire surface of Gtα is dominated by negative charges (Fig. 3B). In particular, all the lipid-allowed orientations of Gtα (∼11% of all possible orientations) were repulsive. A few orientations that exhibited a small attraction to the membrane (up to -1.2 kcal/mol; see Fig. 3A and Table 1) placed the lipid attachment point on the distal face of Gtα relative to the membrane, and because of the energetic cost of removing the lipid anchor from the bilayer (approximately -6 kcal/mol, see “Discussion”), these orientations are disallowed.
We quantified how the repulsive interactions, which characterize the lipid-allowed orientations of Gtα, affect its membrane affinity (Table 1). For significant membrane attraction, the minimal free energy of interaction provides a good estimate and an upper bound to the membrane affinity of the protein (30, 33, 35, 39). However, for repulsive interactions, as in the case of monomeric Gtα, the magnitude of the minimal electrostatic repulsion in the lipid-allowed ensemble (1.8 kcal/mol) provides a lower bound to the overall repulsion. Because all the other lipid-allowed orientations are more repulsive, the Boltzmann-weighted average of all Gtα lipid-allowed orientations is higher (2.2 kcal/mol), reducing the membrane affinity of Gtα in this conformation by ∼40-fold. A 50% increase in the distance threshold for determining whether the lipid anchor can reach the membrane had a small effect on these results (<0.2 kcal/mol). Conversely, decreasing the distance threshold (i.e. assuming the linker is not fully flexible) resulted in significantly increased repulsion.
Dependence of the Electrostatic Interactions on Distance and Membrane Composition—We investigated whether the choice of protein-bilayer distance (3 Å) influenced our major conclusions. Calculation of the free energy of interaction as a function of distance showed a weak dependence (supplemental Fig. S3), as long as the surfaces of the Gt subunits and the membrane are ≥3 Å apart, a likely assumption given their highly charged nature and the strong repulsion at distances <3 Å (see Refs. 30, 33, 35-40).
As in previous work (30), we used a bilayer model containing 33% acidic lipids to reproduce the bulk electrostatic properties of the cytosolic leaflet of disk membranes that faces transducin. Previous investigations reported various proportions of acidic to neutral lipids in rod outer segment membranes (51-54) with the percentage of acidic lipids ranging from 13 to 20%. The distribution of acidic lipids is known to be asymmetric across the bilayer, and previous studies assumed that all of the phosphatidylserine is located on the cytosolic leaflet of the membrane (30, 33, 35-40, 48, 49). Accordingly, the percentage of acidic lipids facing Gt can range from 25 to 40%. Fig. 4 shows that within this range, the membrane composition has almost no effect on the electrostatic interaction of the charged bilayer with Gt/Gβ1γ1/Gtα in their minimal free-energy orientation; these different membrane compositions change the calculated electrostatic interaction by less than 0.1 kcal/mol for Gt and less than 0.3 kcal/mol for Gtα and Gβ1γ1.
Dependence of the Electrostatic Interactions on Ionic Strength and Implications for Transducin Purification Protocols—The membrane interactions of the transducin heterotrimer and its dissociated subunits depend on the ionic strength, with each of the three molecules exhibiting a unique salt dependence (Fig. 5). Increasing the salt concentration from 100 mm, at which our calculations were performed, to the physiological conditions of ∼150 mm, changes the membrane interaction energies of transducin and its subunits by <10% (<0.03 kcal/mol for the heterotrimer, <0.2 kcal/mol for Gtα, and <0.3 kcal/mol for Gβ1γ1) and therefore does not significantly affect our major conclusions. In contrast, hypotonic conditions change the interaction energies for all three species dramatically. The small attraction of the Gt heterotrimer to the membrane at physiological ionic strength changes to a strong repulsion under hypotonic conditions. As shown previously (30), the electrostatic interaction of dissociated Gβ1γ1 exhibits a parabolic dependence on the ionic strength, with a maximal attraction at ∼50 mm salt and a reduction in affinity under more extreme hypotonic conditions. Unlike Gβ1γ1, Gtα is electrostatically repelled by the membrane at physiological ionic strength, and this repulsion increases considerably when the ionic strength is reduced; a 10-fold reduction increases the repulsion to ∼8 kcal/mol, more than the membrane affinity conferred by the lipid anchor (-6 kcal/mol, see below).
FIGURE 5.
Dependence of transducin-membrane electrostatic interactions on ionic strength.
DISCUSSION
In this study, we quantified how the interplay between lipid anchorage and electrostatics determines both membrane affinity and the range of allowed transducin orientations on the membrane surface. These properties change dramatically upon the activation-dependent dissociation of transducin into Gtα and Gβ1γ1 and are likely to significantly affect the protein-protein interactions and the subcellular localization of the transducin heterotrimer and its individual subunits.
Interactions of Gt with the Membrane and Their Implication for Transducin Activation—It is well established that the membrane affinity of Gt is determined predominantly by its lipid anchors (4): the heterogeneous N-terminal acylation of Gtα (13, 55-58) and the C-terminal farnesylation of Gγ1 (59, 60). The majority of Gtα subunits are acylated by C12 or C14:2 lipids, which contribute approximately -6 kcal/mol to membrane binding (61). Farnesylation was shown to confer a membrane affinity comparable with that of a lauryl (C12) anchor (62) and therefore can also add approximately -6 kcal/mol to membrane binding. In a maximal estimate, the contributions of both anchors are additive and sum to approximately -12 kcal/mol. Our results show that under physiological conditions the electrostatic contribution to the membrane affinity of the heterotrimer is insignificant (-0.3 kcal/mol), and therefore its membrane attachment is likely to be set exclusively by the lipid anchors. Under hypotonic conditions, however, strong electrostatic repulsion counteracts the lipid anchors of Gt (Fig. 5) and facilitates its release from membranes, as has been successfully utilized in several transducin purification protocols (26-29).
Global orientation sampling enabled us to compare the probabilities of all previously proposed Gt orientations on the membrane surface. The tilted orientations suggested by Hessel et al. and Chabre and le Maire (24, 25) are similar to the Gt orientation identified by our analysis as the most favorable. On the other hand, parallel orientations (16-23) place the negatively charged patches around the C terminus of Gtα close to the negatively charged bilayer, making these orientations less favorable by ∼2 kcal/mol (∼30-fold difference in occupancy probability). Although the magnitude of these energetic differences is relatively small, they are consistent with the dramatic charge distribution on Gt, where most of the surface of the heterotrimer is negatively charged except for the small area around the lipid anchor attachment points (Fig. 1C). Furthermore, we observe that in the electrostatically favorable orientations of Gt, the Gt-bilayer interface is relatively small (e.g. Fig. 1C). This small, positively charged Gt“footprint” on the membrane is consistent with the results of Hessel et al. (24), who showed that only a small number of negatively charged lipids directly interact with membrane-bound Gt. They speculated that such a small interface might contribute to the fast diffusion of Gt along the crowded membrane surface of rod outer segment disks, which is necessary for the rapid activation of many Gt molecules by each rhodopsin (see discussion in Ref. 2 and see below). Notably, these results may appear to contradict the cryo-EM structure of membrane-bound Gt (63), which suggested a parallel Gt orientation with a larger membrane interface and a close contact between the C terminus of Gtα and the membrane surface. However, the membranes used in that study contained 20% cationic lipids, which presumably attracted the negatively charged patches around the C terminus of Gtα. Our calculations predict that these very patches are repelled by negatively charged biological membranes.
Our analysis also shows that electrostatic repulsion by the membrane is one of the factors limiting the rotational degrees of freedom of the heterotrimer. Interestingly, all Gt orientations that are lipid-allowed and electrostatically favorable are sterically predisposed to interact with rhodopsin (supplemental Fig. S4). This suggests that the orientational confinement of transducin by lipid anchorage and electrostatics may contribute to its extremely rapid activation rate. Indeed, the rate of transducin activation on the surface of photoreceptor membranes can reach several hundred Gt molecules per photoexcited rhodopsin/s (2, 6, 7), whereas in detergent solution the maximal speed of Gt activation is only 30-50 Gt molecules per second (9, 64). The faster Gt activation rate in native membranes was attributed by Ernst et al. (9) to the orientation of Gt at the membrane surface before it encounters rhodopsin. In agreement with this hypothesis and, assuming that our calculated reduction in rotational entropy (1.8 kcal/mol) lowers the activation energy for Gt-rhodopsin complex formation by a similar value, this orientation confinement would accelerate Gt activation by ∼20-fold.
It should be noted that although our calculations were performed with a membrane bilayer, a significant portion of the photoreceptor membrane surface is occupied by rhodopsin. Therefore, any direct projection of our analysis to transducin activation in vivo should be treated cautiously. Quantification of the effect of Gt orientation by the membrane on activation kinetics in vivo would require a more detailed understanding of the surface characteristics of native photoreceptor membranes and remains beyond the scope of this study. Nevertheless, the ability of a single photoexcited rhodopsin to activate hundreds of Gt molecules/s requires rapid diffusion of Gt along the membrane bilayer (2, 6, 7, 65). Therefore, any interactions between Gt and nonactivated rhodopsin are expected to be weak enough not to impede this fast lateral diffusion.
The orientation of transducin in relation to the membrane was also debated in the context of whether transducin binds to a monomeric or dimeric rhodopsin form (Ref. 25 and see Ref. 66 for the most recent review on G protein-coupled receptor oligomerization). It has been suggested that monomeric rhodopsin can bind transducin in a tilted orientation (25), whereas dimeric rhodopsin was modeled in a complex with transducin in a parallel orientation (67). The tilted orientation we find would appear to be more consistent with monomeric rhodopsin. However, the energy differences we calculate are not large enough to preclude a reorientation of transducin so as to optimize its interaction with a rhodopsin dimer.
Membrane Interactions of Dissociated Gβ1γ1 and Gtα—Our analysis indicates that the electrostatic properties of Gtα and Gβ1γ1 are different from one another and from those of Gt. In the case of Gβ1γ1, our calculations reproduce the previous findings of Murray et al. (30), who described a significant electrostatic attraction of Gβ1γ1 to the membrane, despite its negative net charge of -12. Because the averaged electrostatic affinity of Gb1γ1 to the membrane is the same with or without the constraints imposed by the farnesyl anchor, we consider these two energetic contributions as independent and additive. We estimate that electrostatics increase the membrane affinity of Gβ1γ1 from approximately -6 kcal/mol (because of the farnesyl anchor alone) to approximately -9 kcal/mol. In comparison with Gt, Gβ1γ1 can occupy a wider range of orientations that are both lipid-allowed and electrostatically favorable (Fig. 2). Interestingly, the sites on Gβγ subunits that interact with different effectors are distributed over much of the Gβγ surface (68), and therefore this wide range of allowed Gβγ orientations relative to the membrane can facilitate productive interaction with various effectors.
Calculations of Gtα interactions with the membrane are not as straightforward as those of Gβ1γ1 because the lipidated N terminus was proteolytically removed in all available Gtα structures. Although we cannot rule out the possibility that the N terminus of monomeric Gtα is intrinsically unstructured, previous studies of its close homolog Gi1α showed that although its N terminus is present as an extended helix in the heterotrimer, in the monomer it packs against the rest of the subunit in a compact conformation (43). A highly ordered and compact conformation of the myristoylated N terminus of Gi1α was also shown in solution, and it was suggested that this property is conserved in homologous Gα subunits (44). On the basis of this evidence, we assumed in our calculations that, following dissociation from Gβ1γ1, the extended N-terminal helix of Gtα undergoes a similar conformational rearrangement.
Although Gtα and Gβ1γ1 have nearly identical net charges (-13 and -12, respectively), the distributions of negative charges on their surfaces are different. The entire surface of Gtα is predominantly negative (Fig. 3B), and our calculations predict that, unlike Gβ1γ1, Gtα is repelled by the membrane in all lipid-allowed orientations. This reduces the membrane affinity of the compact Gtα conformation from the -6 kcal/mol provided by C12 or C14:2 lipid anchors to less than -4 kcal/mol. Similarly, the membrane affinity of the minority of Gtα subunits that are modified by C14:1 or C14 lipids (providing -7or -8 kcal/mol membrane affinity, respectively) is reduced to less than -5or -6 kcal/mol. The membrane repulsion of Gtα could be lower if its N terminus is unstructured, or higher if the N-terminal linker of Gtα to its lipid anchor is not fully extended and flexible as we assumed. Unlike Gt and Gβ1γ1, the linker length does matter for Gtα. A shorter or less flexible linker will increase Gtα repulsion by the membrane because the least repulsive orientation of Gtα falls right at the edge of the lipid-allowed region, where the electrostatic repulsion increases steeply (Fig. 3A). The repulsive Gtα-membrane interactions that we predict are consistent with the following experimental evidence. 1) Gtα binding to negatively charged membranes is significantly weaker than the binding of Gβ1γ1 (4, 5, 31), despite the similar hydrophobicity of their lipid anchors. 2) Gβ1γ1 binding to nonmyristoylated Gtα lowers Gβ1γ1 affinity to negatively charged membranes (4). 3) Acidic pH facilitates the binding of Gtα to negatively charged membranes, which is non-detectable at neutral pH (5).
Mechanistic Implications for Transducin Translocation—One of the properties of transducin that has attracted much attention in the past 5 years is its ability to undergo reversible, light-induced translocation from the rod outer segment to other subcellular compartments (10, 69-72). This massive translocation is thought to contribute to photoreceptor light adaptation and survival (reviewed in Refs. 14, 15, 73, 74). Gtα and Gβ1γ1 translocate apart from one another, and up to 90% of Gtα and 80% Gβ1γ1 move out of the rod outer segment within minutes (10). The consensus is that transducin translocation in the light-induced direction requires subunit dissociation and is accomplished by diffusion (14, 15, 72, 75). Surprisingly, the rate of this diffusion is comparable with that of soluble green fluorescent protein through the same compartment (75), despite the fact that lipidated Gtα and Gβ1γ1 have to pass through narrow cytosolic spaces between hundreds of tightly packed membranous disks.
Our results suggest that the efficient translocation of monomeric Gtα may be facilitated by electrostatic repulsion, which is expected to reduce the affinity of Gtα to membranes. This may both accelerate the detachment of Gtα from the membrane and enable faster Gtα diffusion through the rod outer segment with minimal retardation by the disks. As would be expected, the translocation of the majority of Gtα subunits, which are modified by C12 or C14:2 lipids, is more pronounced than the translocation of the minority of Gtα subunits modified by slightly more hydrophobic lipids C14:1 and C14 (13). In the case of Gβ1γ1, its electrostatic properties enhance membrane binding, which is expected to impede translocation. Accordingly, it has been shown that the efficient translocation of Gβ1γ1 requires phosducin (76), a protein that stabilizes the binding of the farnesyl moiety inside a cleft within Gβ1 (77) and neutralizes the electrostatic attraction of Gβ1γ1 to the membrane (30).
Our results also reflect on how soluble transducin could reattach to the membrane from the cytosol, as occurs in rods recovering from illumination. Although it remains to be determined experimentally whether transducin reattaches to the membrane in a heterotrimeric or in a dissociated state (14), our results suggest the following. 1) The electrostatically favorable orientations of Gt enable it to approach the membrane without experiencing an electrostatic energy barrier (Fig. 1), despite the -25 net charge of the heterotrimer. 2) Soluble Gβ1γ1 is actively attracted to the membrane in many orientations (Fig. 2). 3) Electrostatic interactions orient the lipid anchors of soluble Gt or Gβ1γ1 toward the membrane, thereby favoring lipid anchor insertion into the membrane for both Gt and Gβ1γ1.4)Incontrast, electrostatic interactions oppose the approach of soluble Gtα to the membrane in orientations that enable membrane insertion of its lipid anchor (Fig. 3), supporting the suggestion in Ref. 78 that association with Gβ1γ1 is required to efficiently reattach Gtα to membranes.
Implications for Membrane Interactions of Other G Proteins—Our calculations were performed on bovine Gt, but they are also applicable to all mammalian Gtα orthologs because they are >98% identical in sequence. Gtα orthologs in more distantly related vertebrates also show >90% sequence identity, both globally and when considering only their charged residues. Similarly, Murray et al. (30) showed that the electrostatic properties of not just Gβ1γ1 from different species, but all mammalian Gβ subunits (which share >80% sequence identity), are generally conserved and resemble those of Gβ1γ1.
Other members of the Giα subunit subfamily (Go1, Go2, Gi1, Gi2, and Gi3) share a lower sequence identity with Gtα, ranging between 60 and 70%. Nevertheless, the electrostatic potential maps of these related Gα subunits are similar, and in particular the dominant negative patches that produce Gtα-membrane repulsion are also observed in these proteins (32). These similarities suggest that the electrostatic repulsion of dissociated Gα subunits by the membrane is common among all members of the Gi subfamily. Additionally, when we compared the electrostatic potential map of the Gi1β1γ2 heterotrimer (79) (Fig. 6) with that of the Gt heterotrimer (Fig. 1C), we observed similar electrostatic characteristics. In particular, the negatively charged patches that limit the rotation of Gt are also present in the Gi1β1γ2 heterotrimer (marked with arrows in Fig. 6). Therefore, the characteristics of the dynamic interactions of the Gt heterotrimer with the membrane are expected to apply to the entire Gi subfamily.
FIGURE 6.
Conserved electrostatic potential maps of the Gi1 heterotrimer. Visualization of the Gi1αβ1γ2 heterotrimer (PDB code 1GP2) in a similar orientation to that of Gt in Fig. 1C. The subunits are shown in Connolly surface representation and colored pink (α), light green (β), and light blue (γ). The functionally relevant termini are marked with arrows. The conserved negatively charged patches discussed in the text are marked with red (Gβ1γ2) and orange (Gi1α) arrows.
Unlike Gi subfamily members, Gα subunits that are palmitoylated only (e.g. Gq, Gs, and G12) contain prominent basic patches at their N termini (32). A number of these proteins have been shown to undergo cycles of reversible membrane association and dissociation, mediated by the cleavage and re-attachment of their labile palmitate anchors (11, 80, 81). The basic electrostatic motif in these Gα subunits may initiate membrane binding (32), whereas their subsequent palmitoylation would strengthen this attachment (80, 81). This interdependence, which could be viewed as an example of the “two-signal model of membrane binding” (80, 81), was recently observed in experiments analyzing the roles of the basic N-terminal motif and palmitoylation in membrane attachment of Gq, Gs, G14, and G16 (82, 83). These results support the hypothesis that, unlike Gtα and its homologs, the α subunits of the Gq, Gs, and G12 subfamilies are attracted to the membrane.
In a broader context, it is well established that both membrane binding and subcellular localization of numerous peripheral membrane proteins are determined by various combinations of lipid anchorage and electrostatic interactions (30, 33-40). Although G proteins follow this general theme, they also represent an example of how the activity-dependent dissociation of a multisubunit protein complex changes the interplay between lipid anchors and electrostatics. The unique electrostatic properties of the heterotrimer and its subunits thereby provide different membrane binding affinities and contribute to the specificity of their protein-protein interactions. Therefore, extending the computational approaches used here to analyzing differences among a broad range of G proteins is a promising direction of future work.
Supplementary Material
Acknowledgments
We thank Diana Murray for important contributions and advice; Avinoam Ben-Shaul, Nir Ben-Tal, and the members of the Honig group, in particular Marc Fasnacht, Lucy Forrest, Rachel Kolodny, Remo Rohs, and Chris Tang, for fruitful discussions; and Sid Gospe and Zvi Selinger for careful reading of the manuscript.
This work was supported, in whole or in part, by National Institutes of Health Grant EY10336 (to V. Y. A.). This work was also supported by National Science Foundation Grant MCB-0416708 (to B. H.) and a long term postdoctoral fellowship from the Human Frontier Science Program (to M. K.). The costs of publication of this article were defrayed in part by the payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 U.S.C. Section 1734 solely to indicate this fact.
The on-line version of this article (available at http://www.jbc.org) contains supplemental Figs. S1-S4 and additional references.

Author's Choice—Final version full access.
Footnotes
The abbreviations used are: FDPB, Finite-Difference Poisson-Boltzmann; PDB, Protein Data Bank.
References
- 1.Burns, M. E., and Baylor, D. A. (2001) Annu. Rev. Neurosci. 24 779-805 [DOI] [PubMed] [Google Scholar]
- 2.Arshavsky, V. Y., Lamb, T. D., and Pugh, E. N., Jr. (2002) Annu. Rev. Physiol. 64 153-187 [DOI] [PubMed] [Google Scholar]
- 3.Ridge, K. D., Abdulaev, N. G., Sousa, M., and Palczewski, K. (2003) Trends Biochem. Sci. 28 479-487 [DOI] [PubMed] [Google Scholar]
- 4.Bigay, J., Faurobert, E., Franco, M., and Chabre, M. (1994) Biochemistry 33 14081-14090 [DOI] [PubMed] [Google Scholar]
- 5.Seitz, H. R., Heck, M., Hofmann, K. P., Alt, T., Pellaud, J., and Seelig, A. (1999) Biochemistry 38 7950-7960 [DOI] [PubMed] [Google Scholar]
- 6.Leskov, I. B., Klenchin, V. A., Handy, J. W., Whitlock, G. G., Govardovskii, V. I., Bownds, M. D., Lamb, T. D., Pugh, E. N., Jr., and Arshavsky, V. Y. (2000) Neuron 27 525-537 [DOI] [PubMed] [Google Scholar]
- 7.Heck, M., and Hofmann, K. P. (2001) J. Biol. Chem. 276 10000-10009 [DOI] [PubMed] [Google Scholar]
- 8.Calvert, P. D., Govardovskii, V. I., Krasnoperova, N., Anderson, R. E., Lem, J., and Makino, C. L. (2001) Nature 411 90-94 [DOI] [PubMed] [Google Scholar]
- 9.Ernst, O. P., Gramse, V., Kolbe, M., Hofmann, K. P., and Heck, M. (2007) Proc. Natl. Acad. Sci. U. S. A. 104 10859-10864 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sokolov, M., Lyubarsky, A. L., Strissel, K. J., Savchenko, A. B., Govardovskii, V. I., Pugh, E. N., and Arshavsky, V. Y. (2002) Neuron 34 95-106 [DOI] [PubMed] [Google Scholar]
- 11.Kosloff, M., Elia, N., Joel-Almagor, T., Timberg, R., Zars, T. D., Hyde, D. R., Minke, B., and Selinger, Z. (2003) EMBO J. 22 459-468 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kassai, H., Aiba, A., Nakao, K., Nakamura, K., Katsuki, M., Xiong, W. H., Yau, K. W., Imai, H., Shichida, Y., Satomi, Y., Takao, T., Okano, T., and Fukada, Y. (2005) Neuron 47 529-539 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lobanova, E. S., Finkelstein, S., Song, H., Tsang, S. H., Chen, C. K., Sokolov, M., Skiba, N. P., and Arshavsky, V. Y. (2007) J. Neurosci. 27 1151-1160 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Calvert, P. D., Strissel, K. J., Schiesser, W. E., Pugh, E. N., Jr., and Arshavsky, V. Y. (2006) Trends Cell Biol. 16 560-568 [DOI] [PubMed] [Google Scholar]
- 15.Artemyev, N. O. (2008) Mol. Neurobiol. 37 44-51 [DOI] [PubMed] [Google Scholar]
- 16.Lambright, D. G., Sondek, J., Bohm, A., Skiba, N. P., Hamm, H. E., and Sigler, P. B. (1996) Nature 379 311-319 [DOI] [PubMed] [Google Scholar]
- 17.Bourne, H. R. (1997) Curr. Opin. Cell Biol. 9 134-142 [DOI] [PubMed] [Google Scholar]
- 18.Bohm, A., Gaudet, R., and Sigler, P. B. (1997) Curr. Opin. Biotechnol. 8 480-487 [DOI] [PubMed] [Google Scholar]
- 19.Onrust, R., Herzmark, P., Chi, P., Garcia, P. D., Lichtarge, O., Kingsley, C., and Bourne, H. R. (1997) Science 275 381-384 [DOI] [PubMed] [Google Scholar]
- 20.Wall, M. A., Posner, B. A., and Sprang, S. R. (1998) Structure (Lond.) 6 1169-1183 [DOI] [PubMed] [Google Scholar]
- 21.Hamm, H. E. (1998) J. Biol. Chem. 273 669-672 [DOI] [PubMed] [Google Scholar]
- 22.Cherfils, J., and Chabre, M. (2003) Trends Biochem. Sci. 28 13-17 [DOI] [PubMed] [Google Scholar]
- 23.Cabrera-Vera, T. M., Vanhauwe, J., Thomas, T. O., Medkova, M., Preininger, A., Mazzoni, M. R., and Hamm, H. E. (2003) Endocr. Rev. 24 765-781 [DOI] [PubMed] [Google Scholar]
- 24.Hessel, E., Heck, M., Muller, P., Herrmann, A., and Hofmann, K. P. (2003) J. Biol. Chem. 278 22853-22860 [DOI] [PubMed] [Google Scholar]
- 25.Chabre, M., and le Maire, M. (2005) Biochemistry 44 9395-9403 [DOI] [PubMed] [Google Scholar]
- 26.Kuhn, H. (1980) Nature 283 587-589 [DOI] [PubMed] [Google Scholar]
- 27.Fung, B. K., Hurley, J. B., and Stryer, L. (1981) Proc. Natl. Acad. Sci. U. S. A. 78 152-156 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Baehr, W., Morita, E. A., Swanson, R. J., and Applebury, M. L. (1982) J. Biol. Chem. 257 6452-6460 [PubMed] [Google Scholar]
- 29.Bigay, J., and Chabre, M. (1994) Methods Enzymol. 237 139-146 [DOI] [PubMed] [Google Scholar]
- 30.Murray, D., McLaughlin, S., and Honig, B. (2001) J. Biol. Chem. 276 45153-45159 [DOI] [PubMed] [Google Scholar]
- 31.Matsuda, T., Takao, T., Shimonishi, Y., Murata, M., Asano, T., Yoshizawa, T., and Fukada, Y. (1994) J. Biol. Chem. 269 30358-30363 [PubMed] [Google Scholar]
- 32.Kosloff, M., Elia, N., and Selinger, Z. (2002) Biochemistry 41 14518-14523 [DOI] [PubMed] [Google Scholar]
- 33.Ben-Tal, N., Honig, B., Peitzsch, R. M., Denisov, G., and McLaughlin, S. (1996) Biophys. J. 71 561-575 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Murray, D., Arbuzova, A., Hangyas-Mihalyne, G., Gambhir, A., Ben-Tal, N., Honig, B., and McLaughlin, S. (1999) Biophys. J. 77 3176-3188 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Murray, D., Hermida-Matsumoto, L., Buser, C. A., Tsang, J., Sigal, C. T., Ben-Tal, N., Honig, B., Resh, M. D., and McLaughlin, S. (1998) Biochemistry 37 2145-2159 [DOI] [PubMed] [Google Scholar]
- 36.Murray, D., and Honig, B. (2002) Mol. Cell 9 145-154 [DOI] [PubMed] [Google Scholar]
- 37.Murray, P. S., Li, Z., Wang, J., Tang, C. L., Honig, B., and Murray, D. (2005) Structure (Lond.) 13 1521-1531 [DOI] [PubMed] [Google Scholar]
- 38.Honig, B., and Nicholls, A. (1995) Science 268 1144-1149 [DOI] [PubMed] [Google Scholar]
- 39.Murray, D., Ben-Tal, N., Honig, B., and McLaughlin, S. (1997) Structure (Lond.) 5 985-989 [DOI] [PubMed] [Google Scholar]
- 40.Ben-Tal, N., Honig, B., Miller, C., and McLaughlin, S. (1997) Biophys. J. 73 1717-1727 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lambright, D. G., Noel, J. P., Hamm, H. E., and Sigler, P. B. (1994) Nature 369 621-628 [DOI] [PubMed] [Google Scholar]
- 42.Gaudet, R., Bohm, A., and Sigler, P. B. (1996) Cell 87 577-588 [DOI] [PubMed] [Google Scholar]
- 43.Mixon, M. B., Lee, E., Coleman, D. E., Berghuis, A. M., Gilman, A. G., and Sprang, S. R. (1995) Science 270 954-960 [DOI] [PubMed] [Google Scholar]
- 44.Preininger, A. M., Van Eps, N., Yu, N. J., Medkova, M., Hubbell, W. L., and Hamm, H. E. (2003) Biochemistry 42 7931-7941 [DOI] [PubMed] [Google Scholar]
- 45.Petrey, D., Xiang, Z., Tang, C. L., Xie, L., Gimpelev, M., Mitros, T., Soto, C. S., Goldsmith-Fischman, S., Kernytsky, A., Schlessinger, A., Koh, I. Y., Alexov, E., and Honig, B. (2003) Proteins 53 Suppl. 6, 430-435 [DOI] [PubMed] [Google Scholar]
- 46.Xiang, Z., and Honig, B. (2001) J. Mol. Biol. 311 421-430 [DOI] [PubMed] [Google Scholar]
- 47.Peitzsch, R. M., Eisenberg, M., Sharp, K. A., and McLaughlin, S. (1995) Biophys. J. 68 729-738 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Hubbell, W. L. (1990) Biophys. J. 57 99-108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Tsui, F. C., Sundberg, S. A., and Hubbell, W. L. (1990) Biophys. J. 57 85-97 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Wang, J., Gambhir, A., McLaughlin, S., and Murray, D. (2004) Biophys. J. 86 1969-1986 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Borggreven, J. M., Daemen, F. J., and Bonting, S. L. (1970) Biochim. Biophys. Acta 202 374-381 [PubMed] [Google Scholar]
- 52.Anderson, R. E., and Maude, M. B. (1970) Biochemistry 9 3624-3628 [DOI] [PubMed] [Google Scholar]
- 53.Fliesler, S. J., and Anderson, R. E. (1983) Prog. Lipid. Res. 22 79-131 [DOI] [PubMed] [Google Scholar]
- 54.Boesze-Battaglia, K., Organisciak, D. T., and Albert, A. D. (1994) Exp. Eye Res. 58 293-300 [DOI] [PubMed] [Google Scholar]
- 55.Kokame, K., Fukada, Y., Yoshizawa, T., Takao, T., and Shimonishi, Y. (1992) Nature 359 749-752 [DOI] [PubMed] [Google Scholar]
- 56.Neubert, T. A., Johnson, R. S., Hurley, J. B., and Walsh, K. A. (1992) J. Biol. Chem. 267 18274-18277 [PubMed] [Google Scholar]
- 57.Johnson, R. S., Ohguro, H., Palczewski, K., Hurley, J. B., Walsh, K. A., and Neubert, T. A. (1994) J. Biol. Chem. 269 21067-21071 [PubMed] [Google Scholar]
- 58.Neubert, T. A., and Hurley, J. B. (1998) FEBS Lett. 422 343-345 [DOI] [PubMed] [Google Scholar]
- 59.Lai, R. K., Perez-Sala, D., Canada, F. J., and Rando, R. R. (1990) Proc. Natl. Acad. Sci. U. S. A. 87 7673-7677 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Fukada, Y., Takao, T., Ohguro, H., Yoshizawa, T., Akino, T., and Shimonishi, Y. (1990) Nature 346 658-660 [DOI] [PubMed] [Google Scholar]
- 61.Peitzsch, R. M., and McLaughlin, S. (1993) Biochemistry 32 10436-10443 [DOI] [PubMed] [Google Scholar]
- 62.Silvius, J. R., and l'Heureux, F. (1994) Biochemistry 33 3014-3022 [DOI] [PubMed] [Google Scholar]
- 63.Zhang, Z., Melia, T. J., He, F., Yuan, C., McGough, A., Schmid, M. F., and Wensel, T. G. (2004) J. Biol. Chem. 279 33937-33945 [DOI] [PubMed] [Google Scholar]
- 64.Arshavksy, V. Y., Antoch, M. P., Dizhoor, S. V., Rakhilin, S. V., and Philippov, P. P. (1987) in Retinal Proteins (Ovchinnikov, Y. A., ed) pp. 497-503, VNU Science Press, Utrecht, The Netherlands
- 65.Pugh, E. N., Jr., and Lamb, T. D. (2000) in Molecular Mechanisms in Visual Transduction (Stavenga, D. G., DeGrip, W. J., and Pugh, E. N., Jr., eds) pp. 183-255, Elsevier Science Publishers B.V., Amsterdam
- 66.Gurevich, V. V., and Gurevich, E. V. (2008) Trends Neurosci. 31 74-81 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Filipek, S., Krzysko, K. A., Fotiadis, D., Liang, Y., Saperstein, D. A., Engel, A., and Palczewski, K. (2004) Photochem. Photobiol. Sci. 3 628-638 [DOI] [PubMed] [Google Scholar]
- 68.Ford, C. E., Skiba, N. P., Bae, H., Daaka, Y., Reuveny, E., Shekter, L. R., Rosal, R., Weng, G., Yang, C. S., Iyengar, R., Miller, R. J., Jan, L. Y., Lefkowitz, R. J., and Hamm, H. E. (1998) Science 280 1271-1274 [DOI] [PubMed] [Google Scholar]
- 69.Brann, M. R., and Cohen, L. V. (1987) Science 235 585-587 [DOI] [PubMed] [Google Scholar]
- 70.Philp, N. J., Chang, W., and Long, K. (1987) FEBS Lett. 225 127-132 [DOI] [PubMed] [Google Scholar]
- 71.Whelan, J. P., and McGinnis, J. F. (1988) J. Neurosci. Res. 20 263-270 [DOI] [PubMed] [Google Scholar]
- 72.Rosenzweig, D. H., Nair, K. S., Wei, J., Wang, Q., Garwin, G., Saari, J. C., Chen, C. K., Smrcka, A. V., Swaroop, A., Lem, J., Hurley, J. B., and Slepak, V. Z. (2007) J. Neurosci. 27 5484-5494 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Burns, M. E., and Arshavsky, V. Y. (2005) Neuron 48 387-401 [DOI] [PubMed] [Google Scholar]
- 74.Fain, G. L. (2006) BioEssays 28 344-354 [DOI] [PubMed] [Google Scholar]
- 75.Nair, K. S., Hanson, S. M., Mendez, A., Gurevich, E. V., Kennedy, M. J., Shestopalov, V. I., Vishnivetskiy, S. A., Chen, J., Hurley, J. B., Gurevich, V. V., and Slepak, V. Z. (2005) Neuron 46 555-567 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Sokolov, M., Strissel, K. J., Leskov, I. B., Michaud, N. A., Govardovskii, V. I., and Arshavsky, V. Y. (2004) J. Biol. Chem. 279 19149-19156 [DOI] [PubMed] [Google Scholar]
- 77.Loew, A., Ho, Y. K., Blundell, T., and Bax, B. (1998) Structure (Lond.) 6 1007-1019 [DOI] [PubMed] [Google Scholar]
- 78.Kerov, V., Rubin, W. W., Natochin, M., Melling, N. A., Burns, M. E., and Artemyev, N. O. (2007) J. Neurosci. 27 10270-10277 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Wall, M. A., Coleman, D. E., Lee, E., Iniguez-Lluhi, J. A., Posner, B. A., Gilman, A. G., and Sprang, S. R. (1995) Cell 83 1047-1058 [DOI] [PubMed] [Google Scholar]
- 80.Resh, M. D. (1999) Biochim. Biophys. Acta 1451 1-16 [DOI] [PubMed] [Google Scholar]
- 81.Marrari, Y., Crouthamel, M., Irannejad, R., and Wedegaertner, P. B. (2007) Biochemistry 46 7665-7677 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Crouthamel, M., Thiyagarajan, M. M., Evanko, D. S., and Wedegaertner, P. B. (2008) Cell. Signal. 20 1900-1910 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Pedone, K. H., and Hepler, J. R. (2007) J. Biol. Chem. 282 25199-25212 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.








