Abstract
Misfolding and oligomerization of unstructured proteins is involved in the pathogenesis of Parkinson’s (PD), Alzheimer’s (AD), Huntington’s, and other neurodegenerative disorders. Elucidation of possible conformations of these proteins and their interactions with the membrane is necessary to understand the molecular mechanisms of neurodegeneration.
We developed a strategy that makes it possible to elucidate the molecular mechanisms of of alpha-synuclein aggregation- a key molecular event in the pathogenesis of PD. This strategy can be also useful for the study of other unstructured proteins involved in neurodegeneration. The results of these theoretical studies have been confirmed with biochemical and electrophysiological studies.
Our studies provide insights into the molecular mechanism for PD initiation and progression, and provide a useful paradigm for identifying possible therapeutic interventions through computational modeling.
Keywords: Unstructured proteins, Parkinson’s disease, alpha-synuclein, molecular dynamics
1. Introduction
The study of unstructured proteins, their aggregation and/or membrane penetration is an important aspect of Nanomedicine [1]. Examples of unstructured proteins include the synucleins associated with Parkinson’s Disease (PD) [2], amyloid beta protein associated with Alzheimer’s Disease (AD) [2], and prion proteins [3]. Because these proteins exist in partially or completely unstructured states in solution, one must use molecular dynamics simulations to explore the possible conformations that are energetically accessible to these proteins, even when crystal or NMR structures of such proteins are available. The increasing power of high performance computers [4], together with programs that scale well with the increased number of processors available, makes it possible to conduct molecular dynamics simulations over ever-increasing time scales (for example NAMD program for Blue Gene computer [5]). Despite advances in hardware and software, simulations of protein aggregates with membranes are still large enough (> 500,000 atoms) to be computationally challenging, and even under the best performance conditions, the structural dynamics of such systems cannot easily be simulated beyond the nanosecond time regime. Unfortunately, the processes of interest occur on micro-, and millisecond time regimes in large biological system that involve many proteins and/or many other types of molecules (for example, ion transport, and multimeric protein assembly. More development will be required to achieve and validate simulations of biomolecular processes from picosecond through millisecond time scales.
As an alternative to micro- or millisecond simulations constructed by a linear succession of nanosecond time increments, one can approach the simulation of long events by breaking them up into a series of sub-processes with overlapping times lines and/or event horizons. In other words, a micro- to millisecond event by a large biological system can be decomposed into a series of conformational “milestones” that overlap in time, in space, or both. In such an approach, a biomolecular system is simulated as a ‘sequence of events’ instead of using a single continuous simulation of an entire micro- or milli-second event. For example, one can imagine a simulation of membrane channel proteins that treats ion movement as a connected series of events where the ion is embedded at various depths within the channel. By varying the ion starting point across a number of simulations, one can produce a trajectory for the ion that is far more reliable than one inferred in a single, continuous simulation over several milliseconds. Here we describe the application of such a strategy to simulations of the tendency of alpha-synuclein (aS) to form higher level aggregates in solution and at the surface of phospholipid bilayers.
aS is an unstructured protein of 140 amino acids that is present in presynaptic terminals. The synuclein family of proteins plays an important role in synaptic plasticity and neurotransmitter release. Misfolding and aggregation of aS has been implicated in the pathogenesis of PD. It is inferred that the root cause of non-familial PD is the direct or indirect interaction of environmental factors with aS in a way that promotes aggregation of this protein [6–10]. Clearly, understanding how structural factors and environmental conditions predispose aS to aggregate into multimeric structures and how these multimeric structures cause neuronal death is of critical importance in understanding disease progression.
The simulations of the solution behavior of aS reported here are based on 1) the NMR solution structure of aS, which provides a starting point for evaluating the tendency of the aS protein to form aggregates [11] and 2) a number of studies showing that aS conformation and aggregation state are highly sensitive to interactions with lipids [12] and local environmental conditions [14–15]. Interaction of aS monomers with detergent micelles or unilamellar vesicles converts the molecule from a disordered conformation to a helical structure [12]. Overexpression and mutation in aS have been associated with autosomal dominant early onset PD, along, with the development of aggregated protein inclusions (Lewy bodies) in the cytosol of surviving neurons [2]. Three mutations in aS (A53T, A30P, and E46K) have been identified with inherited forms of PD, as well as triploidy of the aS encoding gene [7–10]. Since idiopathic forms of PD are far more common than inherited forms, it is reasonable to infer that a number of other environmental factors can influence aS aggregation. Accordingly, oxidative stress, phosphorylation and cleavage of aS have been shown to play an important role in disease progression. Better understanding of the steps involved in cytotoxic aS aggregation will be necessary to complete our understanding of the pathogenesis of PD and to develop new therapies.
The aS molecule exists in 3 distinct sets of conformations: unstructured monomeric forms that predominate in solution; soluble multimers referred to as a protofibrils [12]; and insoluble amyloid fibrils, which coalesce to form the Lewy bodies. The latter are the key neuropathological feature in brains of PD patients. Studies have shown that toxicity of aggregated aS proteins correlates most closely with kinetics of protofibril formation [13], and it is widely believed that the toxicity of the protofibril may arise through insertion of the protofibrils into cell membranes. Ultrastructural and biochemical studies suggest that aS oligomers and protofibrils can form channel like structures, and abnormal ion conductance that can lead to cell death.
Uversky et al. [14, 15] showed that the predominant aS form in solution is the set of disordered monomers, which exist in equilibrium with a set of semi-structured forms. The semi-structured forms are present at low concentration, and seem to be in rapid equilibrium with the unstructured forms. Unlike the disordered forms of aS, the semi-structured forms have a strong tendency to self-aggregate into a higher order structures, typically a mixture of dimers and smaller oligomers. Moreover, solution conditions that stabilize the semi-structured forms cause significant increases in aggregation of aS into multimeric forms. Uversky et al. further showed [15] that the secondary structure of aS is stabilized in self-assembled dimers, suggesting that dimerization may lead to further oligomerization. aS aggregates can assume several different forms, including sphere-like, donut-like, fibrils, etc [15]. The formation of higher level aggregates of aS is a subject of ongoing study, as are the pathway(s) for the assembly of aS into soluble protofibrils and insoluble fibrils.
In contrast to the rapid equilibrium between disordered and semi-structured aS monomers, the equilibrium between monomeric and multimeric states is quite slow, owing to the slow rate of dissociation of monomers from the oligomeric state. Thus, multimeric aS aggregates are present at low concentrations, but have a comparatively long half life, and can explore a variety of conformations during their lifetime. Previous studies show that multimeric forms can be stabilized on a phospholipid bilayer, and that association with the membrane can lead to membrane penetration and pore creation [13]. Since translocation of individual cell-penetrating peptides can occur without formation of pores [16], aS monomers may associate with and penetrate the membrane without forming a pore. However, formation of a specific pore-forming oligomer would provide a molecular basis for the observed collapse of cellular membrane potentials attributed to toxic aS protofibrils. Glabe [17] showed that oligomerization is an important stage in permeabilization of cellular membranes and lipid bilayers leading to neurodegenerative diseases. Here we study a formation of oligomers by aS on the membrane and their possible penetration to the membrane.
In the present study, we describe a strategy to simulate the sequence of events that occurs in the formation of aS protofibrils in the presence of a phospholipid bilayer. Rather than attempt to simulate the entire process with a single algorithm that considers all of the relevant forces over a millisecond time regime, the process was separated to sample individual stages of the process. The process involves first examining the conformational space accessible to the monomeric protein, then exploring the interaction of monomers with a phospholipid bilayer, assembly of monomers into multimers on the lipid surface, and finally penetration of the assemblies into the bilayer. At each stage, the results of the MD analysis were synthesized into a tractable number of archetypal structures that could be examined to infer likely behavior within the entire simulated system for the next step in the process. This computational strategy was used to predict the following individual interaction types: (1) individual protein conformational changes; (2) protein:lipid interactions; (3) protein interactions and/or aggregation/disaggregation at the bilayer interface; and (4) behavior of a homo-oligomeric (in this case pentameric) aS protein assembly complex at the surface of a phospholipid bilayer.
2. Methods
We began with the working hypothesis that the aS molecule samples many different conformations, and that these undergo rapid interconversion in aqueous solution at room temperature. By simulating the various conformations sampled by aS in solution, we can further investigate the likelihood of its forming multimeric complexes both in solution and at the surface of a phospholipid bilayer. Experimental results suggest the possibility that aS undergoes aggregation toward pore-like structure that may penetrate a phospholipid bilayer. This behavior would create a pore that permits unregulated ion flow, thus causing the lethal collapse of any existing membrane potential by permitting (e.g. by a calcium-mediated caspase cascade followed by cellular apoptosis). Simulations of this complex event can be made more computationally tractable by breaking it into separate interaction types, and analyzing each interaction type using several different algorithmic approaches.
Molecular dynamics
Two types of MD simulations were used in this work. The first – MD of aS in water box, the second –MD of the aS oligomer constructed with the MD conformers showing maximum of membrane-contacting score (in this study – 4 ns pentamer, that had shown the best membrane-contacting score on the POPC membrane) on the surface of the membrane. It is known that aS can exist in membrane-bound form and in the unbound form in the cell [14]. The justification of using MD of aS in water as a first step comes from the fact that it was shown in experiments that initial binding of aS to the membrane in many cases is not stable and aS molecules return to the solution. Our simulations of aS in water box model this situation –when aS that initially is in contact with the membrane is disengages from it and exists for some time in solution, undergo conformational changes and then binds back to the membrane surface.
We used periodic boundary conditions at constant pressure (1 atm) and temperature (300 K). The NAMD molecular dynamics program [18] version 2.5 was used with the CHARMM27 force-field parameters [19], cutoff 12 Å, to simulate behavior of aS molecule in water in normal conditions, time step 1 fs. The temperature was maintained at 300 K by means of Langevin dynamics using a damping coefficient of 1/ps (this type of temperature control is used quite often with the NAMD program [20]. A constant pressure (1 atm) was employed as implemented in the NAMD software package. For modeling and simulations we used an NMR structure of aS (PDB id=1xq8). Initial coordinates were taken from a previously equilibrated 500 ps system. Data for analysis were taken between 50 ps and 5 ns of the simulation.
Molecular dynamics (MD) simulations of single aS molecule (first type MD) were conducted in water box; the shortest distance between the protein molecule and the box walls was held at 30Å. The system had 2016 atoms of protein and 237826 atoms of water.
The second type of simulation modeled the dynamics of the membrane bound form. We used the POPC membrane model, with dimensions 180 × 180 Å. The pentamer was constructed with aS molecules (4 ns conformers from single molecule MD simulations that had shown the best membrane-contacting scores) using minimum energy docking with the predicted membrane-contacting surfaces facing plane surface. Then the pentamer was located on the surface of the membrane. The shortest distances between the atoms of the aS molecules and the membrane atoms were in the range of vdW contact. The system was inserted into the water box with the following geometrical parameters: the shortest distance between the protein molecule and the box walls 25Å, the shortest distance between the membrane molecules (on the surfaces not contacting proteins) and the box walls 10Å. The system contained 10080 protein atoms, 95542 lipid atoms, 228450 water atoms.
Both simulations were conducted in four steps. Initially the system of protein and water molecules (or the system of protein, membrane and water) was minimized for 10,000 iterations. Then the system was heated in 0.1° increments and equilibrated for 10ps; then the molecular dynamics simulation was conducted. Data for analysis were taken between 50 ps and 5.0 ns of the simulation.
Clustering of MD conformers
Four separate MD runs were conducted. The resulting snapshots of each 100 ps of each run were compared using the CE algorithm [21]. For each cluster, conformers that have a Z-score less than 5.5 were selected. The clusters were filtered such that differences between each cluster and the structural alignment made by CE included no less than 80% of the protein sequence. The cluster ‘core’ conformer was selected as the structure model having the lowest summary Z-score vs. each of conformers in its cluster.
Membrane-contacting surface of proteins prediction
Membrane-contacting surfaces of proteins were predicted using the program MAPAS developed [22]. MAPAS allows one to predict whether a given protein has a “likely” membrane-contacting region. The MAPAS algorithm deconvolutes the protein surface into a set of planes, and then identifies the planes that are likely to form strong membrane contacts by several different scoring concepts. Using all the scoring concepts concordantly reduces the number of false positives [22].
The MAPAS program was applied to the intermediate conformations of aS clusters identified in step 2 above. Conformers with top membrane–contacting scores were used for further docking/aggregation simulation studies. MAPAS program uses three scoring parameters: membranephilic residues score (MRS), membranephilic area score (MAS), and coefficient of “membranephilic asymmetry” (Kmph). MRS is calculated the following way: MRS = (Σw(Nui * Sui/Suimax) + Σ((W*Nci)/(Nui+ Nci). Where W = the membrane disengagement score [18] for each amino acid (we call it “membranephilicity” of the residue); Nui = the number of uncharged residues in the putative membrane-contacting plane; Nci = number of charged residues in the plane; Sui– solvent accessible surface of the uncharged residue that is included to the plane; Suimax– maximum solvent accessible surface of the uncharged residue that is included to the plane; Nci– number of charged residues in the plane. MAS is calculated the following way: MAS = (Stop(plane)/Sall(plane)); where Stop(plane) is the solvent-accessible surface of a selected number of the residues having top membranephilicity in the best putative membranephilic plane; and Sall(plane) is the solvent-accessible surface of all residues in this plane. Kmph is calculated the following way: Kmph = (MAS)/(Stop(protein)/Sall(protein)), where Stop(protein) is the solvent-accessible surface of a selected number of the top membranephilic residues of the entire protein, Sall(protein) is the solvent-accessible surface of all residues of the protein (see more description of these parameters and prediction strategy in [22] and its web supplements).
Molecular docking
To examine the possible self-assembly among individual aS molecules, the programs DOT [23] and Hex [24] were used to predict docking of between aS conformers that had the best membrane-contacting scores in MAPAS. The final docking refinement was done with the Docking module of InsightII program (Accelrys, 2007), using the 1 Å grid with the cutoff 14 Å. Only docking complexes with vdW energy of interaction less than −10 kcal/mole were selected for further consideration. The lowest energy two-molecular complexes where both molecules contact the same membrane surface by the predicted membrane-contacting amino acids were selected for further docking of the next aS molecules.
3. Results
Initial simulations were conducted to explore the range of possible aS structures in solution. Four separate simulation runs (three 5 ns runs and one 3.7 ns MD run of aS) with different starting random generator seed numbers produced a wide variety of conformations. Structures observed in simulations ranged from globular forms with helical N-termini to more extended conformations. We presume that protein (aS) expression in the cell is reasonably constant, and that the whole assortment of proteins we examined will be sampled on a biologically relevant time scale, so all conformers must be sampled for possible further membrane docking and oligomerization. To narrow this starting population into a manageable number of archetypal structures, we binned the structures according to 10 ps intervals in which each structure was observed, and clustered the structures based on RMSD of alpha carbon positions between the neighboring conformers of aS along the trace of MD within the 10 ps interval as a criterion for selection (Fig 1a). This approach avoids giving a preference to conformations that arise earlier or later on the simulation.
Figure 1.
a) RMSD between aS conformers within runs; b) Evolution of α-helix content in aS during MD; c) Evolution of π-helix content in aS during MD; d) Typical representatives of 5 most populated clusters of MD conformers from four MD runs
Results of RMSD calculations show that rapid changes of conformations occur within each run. There was a general tendency toward more stability as the simulation time approached 5ns MD, but there was no specific correlation of RMSD with time across all runs (Figure 1a). There is, however, a significant concordance in evolution of secondary structures of aS conformers across all runs. During MD the percentage of α-helices gradually diminished, with a corresponding increase in π-helix content (Figures 1b, 1c). The α-helical content decreased from an initial value around 60% to less than 30% for runs 1, 2, and 4, and to less than 40% for run 3 (run 4 has been stopped at 3.7 ns for the technical reasons unrelated to the current studies). In the same time regime the π-helix content of the aS conformers increased from 0 (in the initial conformation) to more than 20%. π-helix is known to be involved in protein-protein and protein-membrane contacts [25]. The observed α to π-helix ‘evolution’ (which also happen in the case of amyloid β [26]) may be an important factor for increasing aS membrane interactions and eventual pore formation/organization.
To examine the potential for interaction with a phospholipid bilayer, we selected the top 5 representatives from among the most populated clusters containing more than 5 members, (Figure 1d), and evaluated their membrane-contacting potential using the program MAPAS [19]. By selecting structures from this population, we insure that the conformations under study are likely to remain bound to the membrane surface for a time period long enough to form multimeric aggregates with other aS molecules. Representative results (for run 1) are shown on Figure 2a. The figure shows all three individual membrane contacting parameter scores calculated by MAPAS for each of the different MD time conformers. For purposes of display, the plotted parameters were normalized to percentage of the threshold value that is considered a ‘strong’ membrane contacting score for each parameter [22]. One can see that each score increases during MD (Figure 2b), finally crossing the 100% threshold at 4 ns. This shows that the conformations of aS examined here have a strong potential for becoming tightly associated with the membrane.
Figure 2.
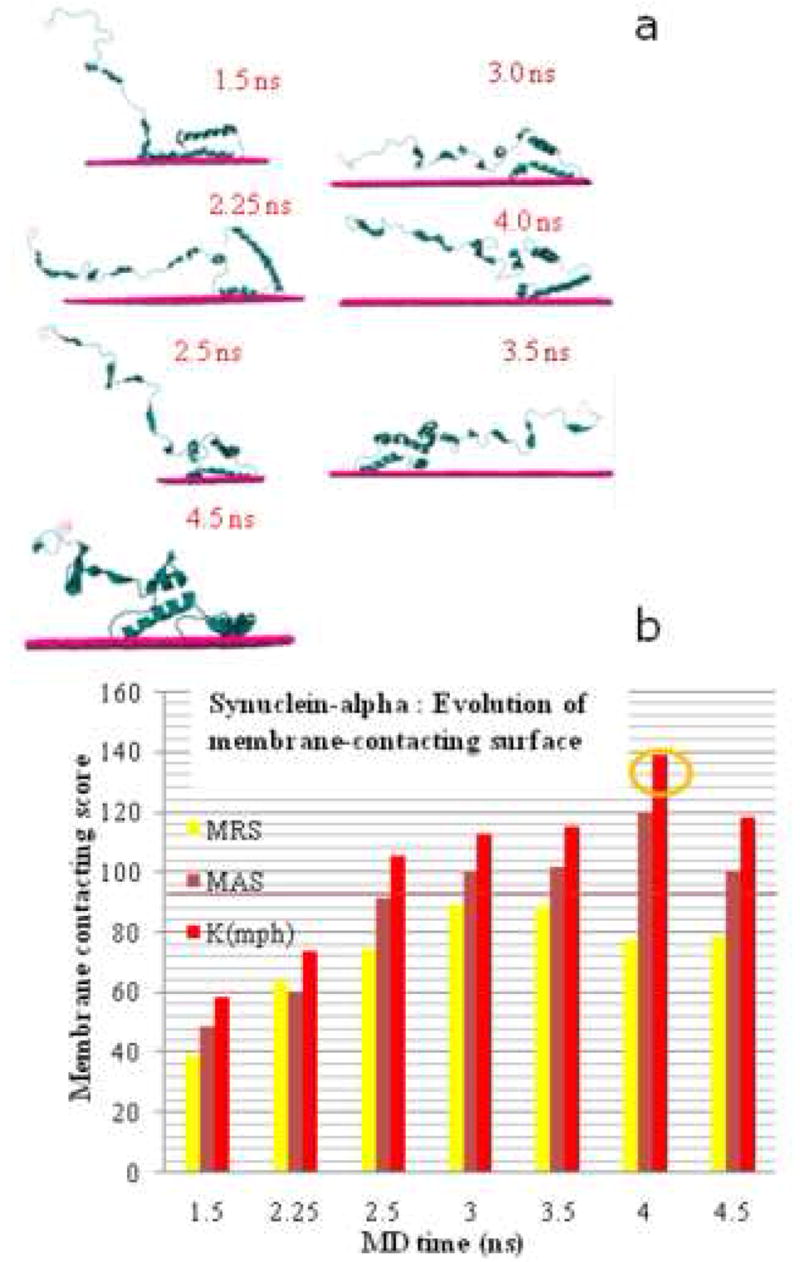
a)Membrane-contacting positions of different MD conformers calculated by the program MAPAC. b) Evolution of the membrane-contacting surface of aS during MD. MRS - membranephilic residues score, MAS - membranephilic area score, Kmph - coefficient of membranephilic asymmetry. All parameters are normalized to 100% (a value that correspond to the reliable membrane contact prediction).
The next step is to examine the tendency of the highest scoring membranephilic conformations of aS to propagate into multimeric aggregates at the surface of the POPC bilayer. These experiments were conducted by sequentially adding another monomeric unit to docking calculations, as long as the electrostatic energy (with vdW interaction energy in all cases less than –10kcal/mol) of aggregate formation continued to decrease. One of the resulting structures is shown in Figure 3a. In these experiments, the energy of formation reached a minimum at the homo-pentameric stage (Figure 3b).
Figure 3.

a). Consecutive docking of the 4.0 ns conformers (red, blue, green, violet, yellow ribbons0 on the membrane (cyan) leads to creation of the pentameric ring-like structure. b). Electrostatic energy diminishes during organization of this structure (each next aggregation step creates more stable complex).
It worth noting that our docking calculations predict aggregation of aS by two different mechanisms that are structurally distinct. The first mechanism is based on interaction of the N-terminus of one aS to the C-terminus of another aS molecule. The resulting homo-dimers are typically produced in docking of aS without taking in consideration the bilayer contact (solution forms of aS). These structures in our docking experiments (results not shown) do not propagate into larger complexes. The second mechanism (shown in Figure 3a) is propagation into ring-like structures. These “propagating” structures begin as homo-dimers and but add to higher order oligomers. The formation of the “propagating” aggregates requires a membrane surface. Thesimulations showed that these structures experience a decreasing electrostatic energy of formation up to the pentameric stage, as shown in Figure 3b. The mechanism of the differences is detailed in [27].
The final MD simulations examined the behavior of the assembled aS multimers on the surface of a POPC bilayer. These simulations show clear penetration of the aS pentamer to the bilayer within 0.5 ns of the simulation (Figure 4). Further experiments show that the aS homo-pentamer eventually can penetrate toward the other side of the membrane, showing some of its parts on the other side of the membrane (data not shown).
Figure 4.

a). Portions of the synuclein-alpha (aS) pentamer that are seen behind the surface of the membrane at the beginning of MD (1) and after 0.5 ns MD (2) on the POPC membrane that are below the level of membrane surface. Pentamer is a result of docking of 4.0 ns MD aS conformers. b). Synuclein-alpha pentamer (white) embedded to the membrane (green) during 0.5 ns unrestrained MD. Pentamer is cut on the level of the top membrane atom.
4. Discussion
aS is a natively unstructured “chameleon protein” [14]. Its conformation and the composition of secondary structure elements change depending on the local environment. Our studies show that even with such variations one can predict behavior of this protein in a specified environment. Such a prediction has to take in consideration the following factors: the full spectrum of aS conformations in solution, then selecting the aS conformers that can bind the membrane and spend sufficient time in the bound state until other aS molecules can bind and organize into multimers on the membrane surface. We have shown that aS during MD simulations in water undergoes significant changes in its secondary structure: from having almost 60% to around 30% of α-helix and π-helix content increase from 0 to more than 20%. Such π-helix appearance was also noted in amyloid-beta studies. It is quite possible that such changes accompany an increase in the membrane-binding affinity of aS. This would be a very important factor in promoting formation of higher order oligomers.
The first ‘core’ step of the ‘propagating’ oligomerization is formation of the stable aS homo-dimers on the surface of the membrane. These dimers with high membrane contacting potential will remain bound to the membrane for sufficient amounts of time to become a core that propagates toward higher order oligomerization. Such oligomerization can happen in different ways. Organization of the “ring-like” pentameric oligomers is just one of the possible outcomes of this process. Our modeling shows that it is also possible for oligomerization of aS to proceed in a way that create conglomerates that cannot lead to ring-like structures (data not shown). Thus, the development of oligomers on the membrane can proceed along different pathways, and produce different outcomes, depending on the exact local conditions, and presumably stochastic considerations. We can assume that these factors influence whether development produces the ring-like oligomers that can lead to the pores in the membrane or ‘conglomerate’ oligomers that may lead ultimately to organization of aS into large fibrils.
In this work, we used a multi-step calculation strategy to elucidate the individual processes where an aS molecule first contacts membrane and undergoes conformational changes leading to the high α-helix content, then is temporarily disengaged from the membrane and stays for some time in the cytoplasm, and after that returns to the membrane in a different conformation (with different secondary structures) and creates possible dimers and higher oligomers. We show that the process of such oligomerization depends highly on the appearance of aS conformers with proper membrane-contacting surfaces. We also show that oligomerization leading to specific “ring-like” structures is driven by electrostatic energy interactions between the neighboring aS molecules during the ring growth. Our studies of the aS pentamer initial stages of the membrane penetration show that such a structure is very stable when interacting with the membrane and remains the ring-like structure while penetrating the first 15A of the bilayer. Further penetration of the aS pentamer (or other ring-like structures) can lead to creation of active pores in the membrane. We previously showed [27] that cells transduced with aS displayed significant increases in Zn2+-sensitive ion channel activity that might correspond to Zn2+-sensitive non-selective cation channels. This is in agreement with a recent study showing that human neuronal cells expressing mutant aS have high plasma membrane ion permeability that was sensitive to calcium chelators [28].
The strategy reported here can be applied to simulations of a wide variety of complex molecular systems, including, but not limited to, those involving associations between membranes and large proteins or protein aggregates. Simulation of these systems is extremely costly from a computational standpoint if one wishes to consider many simulations over the entire msec time regime required. Our strategy eliminates much of this overhead by sampling within the conformational spaces accessible to the individual protein components, then sampling the interaction of archetypal representatives of these states in the aggregation of the protein, or its interaction with a lipid bilayer. The strategy saves time by using a sparse sampling of each individual process, while still representing the essential accessible states for each of the components. We plan to further test this strategy by applying it to other, similar systems.
Acknowledgments
This work was supported by NIH grants AG18440, AG02074, and DOE INCITE grant. The authors are also grateful to IBM for funding under its Institutes of Innovation program, and for computational support on its BlueGene computers at the San Diego Supercomputer Center and at the Argonne National Laboratory. Material written in this article does not have any commercial associations, current and within the past five years, that might pose a potential, perceived or real conflict of interest.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Kransnoslobodtsev AV, Shlyakhtenko LS, Ukraintsev E, Zaikova TO, Keana JF, Lyubchenko YL. Nanomedicine and protein misfolding diseases. Nanomedicine. 2005;1:300–5. doi: 10.1016/j.nano.2005.10.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Jellinger KA. Neuropathological aspects of Alzheimer disease, Parkinson disease and frontotemporal dementia. Neurodegener Dis. 2008;5:118–21. doi: 10.1159/000113679. [DOI] [PubMed] [Google Scholar]
- 3.Shewmaker F, Ross ED, Tycko R, Wickner RB. Amyloids of shuffled prion domains that form prions have a parallel in-register beta-sheet structure. Biochemistry. 2008;47:4000–4007. doi: 10.1021/bi7024589. [DOI] [PubMed] [Google Scholar]
- 4.Top 500 supercomputer sites, Top500org. 2007 http://www.top500.org/
- 5.Phillips JC, Zheng G, Kumar S, Kale LV. NAMD: Biomolecular simulation on thousands of processors. Proc. Supercomputing 2002; Baltimore, MD. September 2002. [Google Scholar]
- 6.Bertoncini C, Jung Y, Fernandez C, Hoyer W, Griesinge C, Jovin T, Zweckstetter M. Release of long-range tertiary interactions potentiates aggregation of natively unstructured {alpha}-synuclein. Proc Natl Acad Sci USA. 2005;102:1430–5. doi: 10.1073/pnas.0407146102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Polymeropoulos M, Higgins J, Golbe LS. Mapping of a gene for Parkinson’s disease to chromosome 4q21–q23. Science. 1996;274:1197–9. doi: 10.1126/science.274.5290.1197. [DOI] [PubMed] [Google Scholar]
- 8.Glasera CB, Yamin G, Vladimirm N, Uversky VN, Fink AL. Methionine oxidation, alpha -synuclein and Parkinson’s disease. Biochimica et Biophysica Acta. 2005;1703:157–69. doi: 10.1016/j.bbapap.2004.10.008. [DOI] [PubMed] [Google Scholar]
- 9.Ibáñez P, Bonnet A-M, Débarges B, et al. Causal relation between alpha-synuclein gene duplication and familial Parkinson’s disease. Lancet. 2004;364:1169–71. doi: 10.1016/S0140-6736(04)17104-3. [DOI] [PubMed] [Google Scholar]
- 10.Moore D, West A, Dawson W, Dawson TM. Molecular pathophysiology of Parkinson’s disease. Annu Rev Neurosci. 2005;28:57–87. doi: 10.1146/annurev.neuro.28.061604.135718. [DOI] [PubMed] [Google Scholar]
- 11.Ulmer T, Bax A, Cole N, Nussbaum R. Structure and dynamics of micelle-bound human alpha-synuclein. J Biol Chem. 2005;280:9595–603. doi: 10.1074/jbc.M411805200. [DOI] [PubMed] [Google Scholar]
- 12.Davidson W, Jonas A, Clayton D, George J. Stabilization of alpha-synuclein secondary structure upon binding to synthetic membranes. J Biol Chem. 1998;273:9443–9. doi: 10.1074/jbc.273.16.9443. [DOI] [PubMed] [Google Scholar]
- 13.Volles M, Lansbury PJ. Zeroing in on the pathogenic form of alpha-synuclein and its mechanism of neurotoxicity in Parkinson’s disease. Biochemistry. 2003;42:7871–8. doi: 10.1021/bi030086j. [DOI] [PubMed] [Google Scholar]
- 14.Uversky V, Lee H, Li J, Fink A, Lee S. Stabilization of partially folded conformation during alpha-synuclein oligomerization in both purified and cytosolic preparations. J Biol Chem. 2001;276:43495–8. doi: 10.1074/jbc.C100551200. [DOI] [PubMed] [Google Scholar]
- 15.Uversky V. A protein-chameleon: conformational plasticity of alpha-synuclein, a disordered protein involved in neurodegenerative disorders. J Biomol Struct Dyn. 2003;21:211–34. doi: 10.1080/07391102.2003.10506918. [DOI] [PubMed] [Google Scholar]
- 16.Henriques ST, Quintas A, Bagatolli LA, Homblé F, Castanho MA. Energy-independent translocation of cell-penetrating peptides occurs without formation of pores. A biophysical study with pep-1. Mol Membr Biol. 2007;24:282–93. doi: 10.1080/09687860601142936. [DOI] [PubMed] [Google Scholar]
- 17.Glabe CG. Common mechanisms of amyloid oligomer pathogenesis in degenerative disease. Neurobiol Aging. 2006;27:570–5. doi: 10.1016/j.neurobiolaging.2005.04.017. [DOI] [PubMed] [Google Scholar]
- 18.Kalé L, Skeel R, Bhandarkar M, Brunner R, Gursoy A, Krawetz N, Phillips J, Shinozaki A, Varadarajan K, Schulten K. NAMD2: Greater scalability for parallel molecular dynamics. J Comp Physics. 1999;151:282–312. [Google Scholar]
- 19.Feller S, MacKerell A. An improved empirical potential energy function for molecular simulations of phospholipids. J Phys Chem B. 2000;104:7510–5. [Google Scholar]
- 20.Gao M, Schulten K. Onset of Anthrax Toxin Pore Formation. Biophys J. 2006;90:3267–3279. doi: 10.1529/biophysj.105.079376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Shindyalov IN, Bourne PE. A database and tools for 3-D protein structure comparison and alignment using the Combinatorial Extension (CE) algorithm. Nucleic Acids Res. 2001;29:228–9. doi: 10.1093/nar/29.1.228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sharikov Y, Walker RC, Greenberg J, Kouznetsova V, Nigam S, Miller MA, Masliah E, Tsigelny I. MAPAS: a tool for predicting membrane-contacting protein surfaces. Nature|Methods. 2008;5:119. doi: 10.1038/nmeth0208-119. [DOI] [PubMed] [Google Scholar]
- 23.Law DS, Ten Eyck LF, Katzenelson O, Tsigelny I, et al. Finding needles in haystacks: Reranking DOT results by using shape complementarity, cluster analysis, and biological information. Proteins. 2003;52:33–40. doi: 10.1002/prot.10395. [DOI] [PubMed] [Google Scholar]
- 24.Ritchie DW, Kemp GJL. Protein docking using spherical polar Fourier correlations. Proteins. 2000;39:178–94. [PubMed] [Google Scholar]
- 25.Weaver TM. The pi-helix translates structure into function. Protein Sci. 2000;9:201–206. doi: 10.1110/ps.9.1.201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Flock D, Colacino S, Giorgio C, Di Nola A. Misfolding of the amyloid beta protein: A molecular dynamics study. Proteins. 2006;62:183–192. doi: 10.1002/prot.20683. [DOI] [PubMed] [Google Scholar]
- 27.Tsigelny IF, Bar-On P, Sharikov Y, et al. Dynamics of alpha-synuclein aggregation and inhibition of pore-like oligomer development by beta-synuclein. FEBS J. 2007;274:1862–1877. doi: 10.1111/j.1742-4658.2007.05733.x. [DOI] [PubMed] [Google Scholar]
- 28.Furukawa K, Matsuzaki-Kobayashi M, et al. Plasma membrane ion permeability induced by mutant alpha-synuclein contributes to the degeneration of neural cells. J Neurochem. 2006;97:1071–7. doi: 10.1111/j.1471-4159.2006.03803.x. [DOI] [PubMed] [Google Scholar]



