Abstract
The NEURON simulation environment has been extended to support parallel network simulations. Each processor integrates the equations for its subnet over an interval equal to the minimum (interprocessor) presynaptic spike generation to postsynaptic spike delivery connection delay. The performance of three published network models with very different spike patterns exhibits superlinear speedup on Beowulf clusters and demonstrates that spike communication overhead is often less than the benefit of an increased fraction of the entire problem fitting into high speed cache. On the EPFL IBM Blue Gene, almost linear speedup was obtained up to 100 processors. Increasing one model from 500 to 40,000 realistic cells exhibited almost linear speedup on 2000 processors, with an integration time of 9.8 seconds and communication time of 1.3 seconds. The potential for speed-ups of several orders of magnitude makes practical the running of large network simulations that could otherwise not be explored.
Keywords: computer simulation, realistic modeling, parallel computation, spiking networks
Introduction
The growing availability of multi-processor systems has led to increasing interest in enhancing neuronal network simulation performance by utilizing these machines. With a few exceptions such as pGENESIS (Goddard and Hood, 1998), which has been used for several large biologically realistic network models, including a large scale model of the cerebellar cortex running on a 128-processor Cray T3E (Howell, et. al, 2000), simulators that have been adapted to these supercomputers generally utilize simplified integrate-and-fire neuron models in order to permit maximal network size, e.g. NEST, NCS, NEOSIM and SpikeNET (Wilson et. al. 2001, Morrison et al 2005, Delorme and Thorpe 2003, Goddard et.al. 2001, Hammarlund et al. 1996). Although complex single neuron models can be inserted into these discrete-event algorithms, optimal simulation of networks of realistic multi-compartment neurons presents additional difficulties and opportunities that cannot be directly addressed in this type of hybrid model (Lytton and Hines 2005).
As of 1994, the NEURON simulation environment has provided a simple LINDA-like persistent message bulletin board (Carriero and Gelernter, 1989) to help with the management of "embarassingly parallel" simulations, e.g. parameter sensitivity or similar simulations which can be split into several independent runs. However, there has been increasing demand for parallelization of networks of realistic neurons. In preliminary simulations, we found that even the apparently very inefficient bulletin board system could be used to implement a spike-exchange mechanism that resulted in superlinear speed-up. These preliminary positive results with such wildly out-of-design usage strongly suggested extending native NEURON to support distributed simulations of networks.
In approaching the problem of extending NEURON to the parallel environment, we kept several factors in mind. We were interested in providing a useable environment both for the average NEURON user who has access to relatively small clusters of 10–50 processors as well as for users of the state-of-the-art Blue Gene supercomputer, whose 8000 processors are proposed for simulations of the order of 10,000 morphologically complex neurons in a cortical microcircuit (Markram, 2006). As part of this, we wanted to provide an easy transition from the single-CPU to multi-CPU environment so that previously developed simulations could be scaled and ported with a minimum of error-prone code-rewriting. Moreover, we wanted to allow parallel simulations to run without change on a single CPU in cases where the size did not preclude this. Because of this emphasis on practical mid-scale problems, we tested the system on existing network simulations derived from experimental findings (all available from ModelDB, http://senselab.med.yale.edu/senselab/ModelDB). We optimized for ease of use and applicability to simulations from the literature rather than for the massive simulations that will be the subject of future reports.
In this paper, we describe an extension to NEURON's ParallelContext class, built on the standard and widely available Message Passing Interface (MPI), and now included in the standard NEURON distribution. The simple spike distribution mechanism (MPI_Allgather) distributes all spike times to all processors. This provides a baseline for future comparison with more sophisticated point-to-point routing methods (MPI_Send/MPI_Receive). However, some architectures provide an optimized vendor implementation of MPI_Allgather that may give it advantages that would be hard to match without extensive programming and testing (Almási et al., 2005).
We have applied this method to three published network models involving neurons composed of several compartments that include realistic active properties and connectivity. This porting process suggested additional functions that were then added to further simplify network specification in the parallel environment. Superlinear speedup was achieved with increasing CPU number in all three models.
Methods
All the simulations were carried out with the NEURON v5.8 simulation program (Hines and Carnevale, 1997). Parallel network management services are available when NEURON is configured with the --with-mpi option, which requires preinstallation of an implementation of the Message Passing Interface (MPI). On those machines that did not already have an MPI installation, we used MPICH (http://www-unix.mcs.anl.gov/mpi/mpich). Performance tests were carried out on one or more of the following multiprocessor systems:
- 2 processor 2 GHz Power Mac G5, with 512KB L2 cache for each processor
- 12 64-bit processor Beowulf cluster, 3.2 GHz Intel Xeon with 1024KB cache
- 25 32-bit processor Beowulf cluster, 2.4GHz Intel Xeon with 512KB cache
- 1024 processor CINECA IBM Linux cluster, 2.8GHz Xeon with 512KB cache
- 8196 processor EPFL IBM Blue Gene
Neuron morphology, electrophysiology, and network connectivity
To illustrate the general behavior and efficiency of the implementation scheme used in this paper, we used a simple test network composed of identical conductance based neurons (see below). In addition, we assessed parallel performance using three published neuronal network models (Bush, et. al. 1999; Davison, et. al. 2003; Santhakumar, et. al. 2005), exhibiting very different spiking patterns. These were downloaded from the ModelDB model repository (http://senselab.med.yale.edu) and transformed into parallel models using the methods described below. All the parallel simulation files, which also work on serial machines without MPI installed, are available for public download under the ModelDB section of the Senselab database (http://senselab.med.yale.edu).
The test network consists of a variable number of neurons. Each neuron is implemented with a variable number of compartments (10–200), modeling a stretch of membrane 1000µm long with a 2µm diam, and uniform passive and active (Na and KDR) properties that results in regular firing behavior. Kinetics for the Na, and KDR conductances were from CA1 hippocampal neurons (Migliore et al, 1999), with a peak density of 80 and 70pS/µm2, respectively. Unless otherwise noted, neurons in this model were connected in a ring. Excitatory synaptic conductances were modeled with a double exponential time course (2 and 5ms for rise and decay time, respectively) and a reversal potential of 0 mV. Network activity was initiated by activating the synaptic input of one neuron, and simulations were carried out for 200 or 1000ms. Suprathreshold excitatory synaptic conductance (3 nS) was activated after a 3 ms delay whenever the corresponding presynaptic compartment crossed a threshold of −10mV. To test the communication-limited-domain we used a scalable version of the Bush et al. (1999) model with sizes ranging from 10,000 to 160,000 cells, and networks of 65,536 and 262,144 integrate-and-fire cells where each cell was randomly connected to 1000 and 10000 other cells respectively with 1 ms connection delay and each cell intrinsically fired with a uniform random interval between 10 and 20 ms. In the artificial networks, to eliminate connection dependent response behavior, all connection weights were set to 0, but this does not affect, or at least does not increase, cell computation time with respect to interprocessor spike exchange or intraprocessor spike distribution time.
Parallel Model Specification
On a single processor, source cell to target synapse connections are instantiated in NEURON through the creation of a NetCon object
in which the first argument identifies a discrete event source and the second argument identifies the synapse object it connects to (Hines and Carnevale, 2004). Setup of a parallel network model uses NetCon as much as possible. Only a few additional parallel specific functions are required — globally identify a cell even though the cell actually exists only on one processor; create a NetCon that connects the globally identified cell to a specific synapse — and those are provided by NEURON's extended ParallelContext class. In what follows, we use the object reference pc to refer to an instance of this class.
The critical notion which distinguishes a parallel network implementation from the serial implementation is the introduction of an integer global identifier (gid) to identify a spiking cell. It is unnecessary to introduce the corresponding notion of target gid because NEURON takes a synapse-centric view of the network, in which the network connection with synaptic weight and axonal delay is made to exist on the processor where the synapse exists. That is,
returns a NetCon object and can only be executed on the processor where the target cell exists. At the source end of the connection, on a different processor than the target, it is necessary to unambiguously identify some location on the cell at which action potentials are detected and this is done by creating a temporary NetCon with the idiom
that in the past was only used as the first step in recording spikes from output cells. That NetCon is then used to associate the gid with spike source via
In normal simulations, a gid can be considered to represent an entire cell, and for simplicity we will restrict ourselves to that situation. However, it is certainly possible for a cell simulation to have multiple threshold detection sites as, for example, is required for olfactory bulb Mitral to Granule cell dendrodendritic reciprocal synapses.
The above, though incomplete, provides a sufficient conceptual framework. For further programming details the reader is referred to the documentation for the ParallelNetManager and ParallelContext class at http://www.neuron.yale.edu.
Parallel Model Execution
A schematic representation of the flow of information in a parallel system is shown in Fig.1. As can be seen, there is no master, and all the processors execute exactly the same program (on different subsets of neurons). Every processor integrates the equations for its subnet over an interval equal to the minimum (interprocessor) presynaptic spike generation to postsynaptic spike delivery connection delay. One MPI_Allgather collective operation is used to exchange, with all other processors, all the (gid, spiketime) pairs for spikes generated in that interval; occasional spike buffer overflow is handled by a second MPI_Allgatherv. After a processor has received all the (gid, spiketime) pairs from all other processors, it uses a very fast, O(1), hash table with binary tree buckets (Myers, 2000) to find the NetCon list associated with each gid and sends it the spiketime. Note that this spiketime is less than the current integration time, but the delivery time is guaranteed to be in the future since the NetCon delay is greater than the just completed integration interval.
Figure 1.
Schematic representation of the algorithm used to implement a network of realistic neurons on a parallel system using NEURON.
Results
Figure 2 shows runtime results for a simple ring network in which we could control cell number, and cell complexity. In Figure 2A, the fixed size 128-neuron network with 50 compartments per neuron exhibits a dramatic, more than linear, reduction in runtime with increasing numbers of processors. On the other hand, in the same panel, a network with size proportional to the number of processors is slightly less than perfect with respect to the constant runtime ideal. Morrison, et. al. (2005) observe similar performance improvements and attribute it to the reduction in the overall memory requirements for each processor when a fixed size network runs on a greater number of processors, with a consequent better use of the faster cache memory. There is no such effect for networks of increasing size (Fig.2A, triangles), since memory used per processor is constant. In this case, one notices that using many processors results in a slight loss of performance due to extra work required for an MPI_Allgather.
Figure 2.
Performance of the parallel implementation. A) Simulation time for different networks as a function of the number of processors. Dashed lines represent ideal scaling for each case. Circles: simulation time for a network of 128-neuron, 50 compartments/neuron (comp/neuron), running on different numbers of processors; Triangles: simulation time for networks with an increasing number of neurons running on an increasing number of processors (1 neuron/processor). B) Simulation time on a single processor as a function of the number of neurons in a network (circles) using different numbers of comp/neuron. The dashed lines represent the case of ideal scaling and the filled triangles indicate the simulation times for a 4-neuron network with the neurons having a correspondingly larger number of comp/neuron.
We studied the cache effect in more detail by running different size networks with varying compartments/neuron on a single processor (Fig.2B). The runtime for a 2-neuron network of 50 compartments/neuron (a total number of 100 compartments) was chosen as reference value to compare the scalability as a function of neuron and network size. The reference lines in Fig.2B represent the ideal runtime (twice as long for twice the size) for single processor simulations. On the upper line, measured run times begin to depart from linearity at a total size of between 400 and 800 compartments and eventually return to linearity at a vertically translated (approximately a factor of 2) line after 6400 total compartments (not shown). This is consistent with the notion that main memory transfer has become the rate-limiting step. Departure from the ideal in the upper part of the curves showing measured runtime for 5 and 1 compartment/neuron networks is roughly a constant factor and can be attributed to constant per cell overhead that is independent of neuron size. Further, nonlinear departure from the ideal on the lower part of the measured runtimes (relatively small for 5 compartments/neuron but quite dramatic for lightweight 1 compartment cells) is attributed to constant interpreter and integrator overhead which is independent of the number of equations being solved. Runtime measurements with 4 neuron networks but a larger number of compartments/neuron so that total size is equivalent to the 64 and 128 neuron networks are shown as filled triangles in figure 2B. Clearly, the constant per cell overhead is negligible in the two lower curves but the main memory transfer limitation remains. These results suggest that relatively large networks could benefit the most from a parallel implementation if they could be distributed among several processors in such a way that each processor operates on a portion of the network that is small enough to be entirely contained in the (faster) cache memory. Superlinear efficiency could be obtained in this case.
The efficiency for networks of realistic neurons of different complexity is plotted in Fig.3, as a function of the number of processors used. As can be seen, superlinear (>1) efficiency can be reached with relatively high values (up to ~2) that could be rather easily obtained in most cases with an appropriate choice of neuronal network and computer system size. These results suggest that, with the active properties of our model neurons, networks of ~100 neurons composed of 10–50 comp/neuron could be run with superlinear efficiency using a cluster of 4 to 64 processors (Fig.3, left), whereas more complex morphologies require larger clusters to reach the same efficiency. To further show that there is an optimal range of neuron complexity and computer system size that maximizes the efficiency for a given neuronal network, in Fig.3B we plot the efficiency as a function of the runtime. Very low or relatively large runtime (corresponding to biophysically simple or complex neurons, respectively) results in low efficiency because of the minimum overhead or cache memory effects, respectively, as discussed above (Fig.2). Smaller networks (Fig.3, right) require more complex morphologies (more than ~200comp/neuron) to run with a superlinear efficiency of 1.5–2.
Figure 3.
A) Efficiency of the parallel implementation for 128-neuron networks having different numbers of compartments/neuron (comp/neuron), as a function of the number of processors (left), or fraction of simulated time, Tstop (right). B) Efficiency of networks of increasing size and different number of comp/neuron; the number of processors used in each simulation (np) was the same as the number of neurons in the network. Ts, simulation time on a single processor; np, number of processors; Tp, simulation time on np processors. In all cases the simulated time was 0.5s.
In order to test for the effects of network connectivity or spiking activity, the ring connectivity was replaced by all-to-all connectivity and the simulations were repeated. No qualitative differences were found in the simulation times in all cases (data not shown).
To test the implementation on a broader set of realistic examples, three (serial) published network models were downloaded from the ModelDB database, and adapted to run on parallel systems using the schema described in this work. For each model, a representative raster plot and the simulation times as a function of the number of processors used are presented in Fig.4. Table 1 shows some of the model properties and size statistics. Runtime exhibits a substantial superlinear cache effect on the Beowulf and IBM Linux clusters, although the overall speed-up depended on the particular model. For the Davison et al (2003) model the last two points at 500 and 505 processors show an abrupt runtime difference due to the fact that the 25 mitral cells and 2500 granule cells give better, though not perfect, balance in the 505 processor case. In all cases, setup time scaled with number of CPUs except for a small fixed overhead per CPU (data not shown).
Figure 4.
Parallel implementation of published network models from the ModelDB database. (left) Spike raster plot for each model; (right) Runtime for each model using different parallel systems. In all cases, the dashed lines represent the case of ideal scaling.
Table 1.
Properties and statistics for the parallel implementation of models downloaded from ModelDB
| Santhakumar et al., (2005) | Davison et al., (2003) | Bush et al., (1999) |
|---|---|---|
| 527 cells | 2525 cells | 500 cells |
| 500 Granule, 9 comp., 7 mech. | 25 Mitral, 7 comp., 7 mech. | 100 Pyramidal, 9 comp., 5 mech. |
| 6 Basket, 17 comp., 7 mech. | 2500 Granule, 5 comp., 4 mech. | 300 Pyramidal2, 8 comp., 6 mech. |
| 15 Mossy, 17 comp., 8 mech. | 48,476 States | 100 Basket, 7 comp., 3 mech. |
| 6 HIPP, 13 comp., 8 mech. | 21,874 States | |
| 15,000 connections | ||
| 11,293 connections, 4875 syn. | 2550 AMPA, 2500 NMDA syn. | 41,380 connections |
| 1500 stim., 1700 AMPA, 1200 NMDA | ||
| 2,861 spikes generated | 6,267 spikes generated | 1500 GABA-A, 1200 GABA-B |
| 50,136 spikes delivered | 47,838 spikes delivered | |
| 3,493 spikes generated | ||
| 275,385 spikes delivered | ||
In general, using a larger number of processors, the size of subnet on each processor becomes small and the communication overhead for MPI_Allgather calls larger. Communication time thus begins to dominate the runtime. This effect could be seen in most of our models when using more than 64 processors. Models with larger or more complex individual cells would reduce this effect (see Fig. 2) and in the extreme case of networks of 3-d reconstructed neurons, one can expect almost linear speedup with substantially larger numbers of processors. Of more interest, though, is the behavior of larger networks on large resource machines such as the EPFL IBM Blue Gene where a network simulation can be distributed on up to 8196 CPUs.
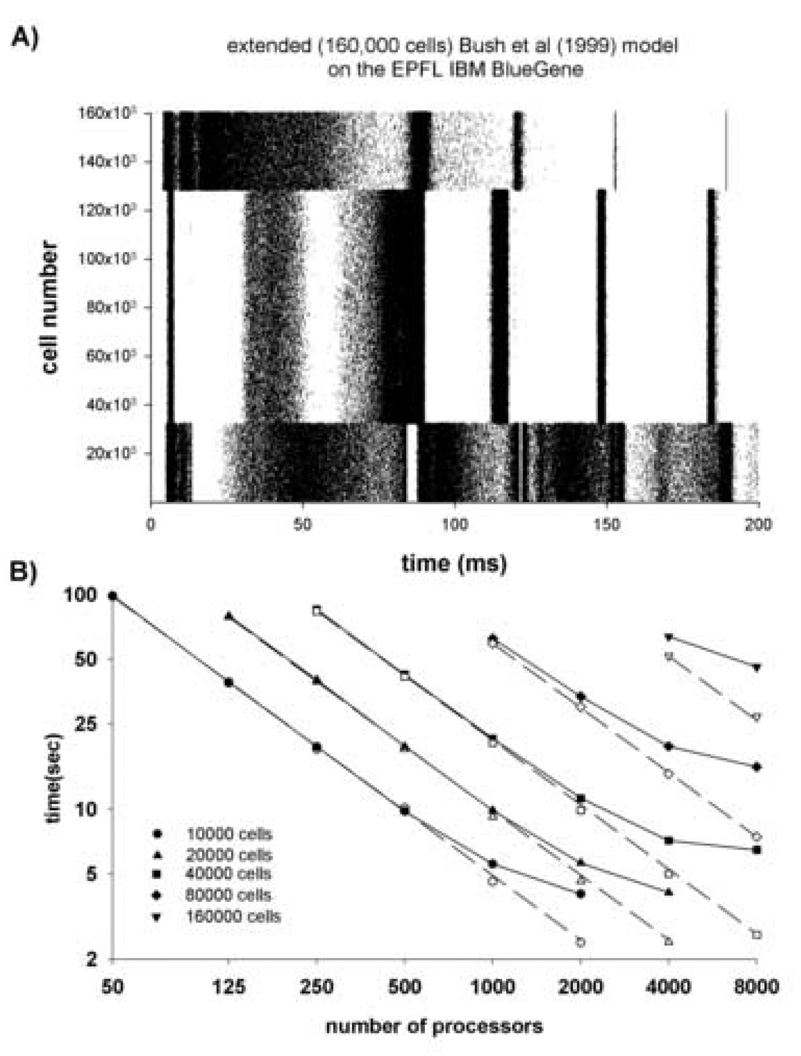
Fig 5 shows the performance results for the Bush et. al. (1999) model scaled from 500 cells to various sizes between 10,000 and 160,000 cells. Scaling was carried out by keeping population projection probabilities constant but reducing the (random) weights by the fractional increase in number of cells. Network size statistics are shown in Table 2. Note that number of connections is proportional to the square of the number of cells. Also, networks of different size differ considerably in the details of their overall spike patterns. The 160k cell network spike pattern is shown in Fig 5A. Simulations with model sizes 10k, 20k, and 40k cells exhibit the expected overall doubling of runtime as size was doubled (Fig.5B). Notice also that the (10k, 500 cpu) runtime is similar to the (20k, 1000 cpu) and (40k, 2000 cpu) cases. However, for model sizes above 20k cells, the increase in computation time for each cpu number is accompanied by almost the same factor increase in interprocessor spike exchange time. The spike exchange time has become proportional to the number of spikes generated. Thus, this model cannot efficiently use more than 2000 to 4000 CPUs regardless of how large it is.
Figure 5.
Simulations of large networks on the EPFL IBM Blue Gene. A) Spike raster plot of the parallel implementation of an extended version (160,000 cells) of the Bush et al. (1999) model; B) Runtime (filled symbols) and processor computation time (open symbols) as a function of the number of processors used for the model scaled up to various sizes; In all cases, the simulated time was 200ms. Dashed lines represent the ideal scaling for each model size. (Note: the 160k cell simulation was too large to run with 2000 CPUs since only 512 MB are available for each CPU).
Table 2.
Statistics for the parallel implementation of the Bush et al. (1999) model, and two examples of a large network of integrate and fire (I&F) cells.
| # cells | # states | # connections | # spikes generated | # spikes delivered |
|---|---|---|---|---|
| 500 | 21,874 | 41,380 | 3,493 | 275,385 |
| 10,000 | 444,664 | 17,167,785 | 31,118 | 52,040,794 |
| 20,000 | 888,664 | 68,655,566 | 33,960 | 110,634,002 |
| 40,000 | 1,777,664 | 274,591,128 | 69,529 | 452,987,907 |
| 80,000 | 3,553,664 | 1,098,302,267 | 294,974 | 2,147,483,647 |
| 160,000 | 7,107,664 | 4,393,084,577 | 844,175 | 22,847,784,937 |
| 65,536 I&F | 0 | 65,536,000 | 842,423 | 838,080,022 |
| 262,144 I&F | 0 | 2,621,440,000 | 3,369,556 | 33,522,955,857 |
The 80k and 160k models exhibit computation time increases of factors of 3 and 3.25 instead of the expected factor of 2. A substantial portion of the computation time, therefore, must be attributed to the handling of the respective 4.7 and 10.6 fold increase in number of delivered spikes. Nevertheless, the computation time vs number of CPUs in Fig 5 scales ideally for all sizes of the Bush model. It is not possible at present to to do execution profiling on the BlueGene and so we are unable to precisely measure the interleaved cell integration time, event queue processing, and synaptic event computation time. However, since all delays are random, the queue size is related to the number of delivered events instead of generated events and so it is not surprising that queue time would scale with cell number.
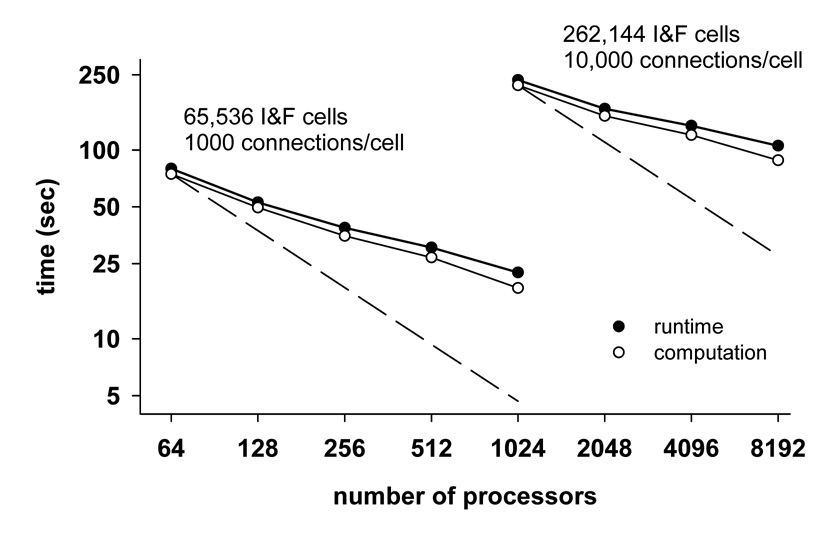
Fig 6 shows that the same cannot be said of NEURON's present method of simulating artificial cell models. Networks of artificial spiking cells have no integration overhead and a delivered spike results in very little non-queue related computation. Because all delays were defined to be the same for this model, only the generated spikes are managed on the event queue. At delivery time the spike is removed from the queue and then distributed to the appropriate target cells. Note that the number of delivered spikes scales with number of CPUs. However, up to a number of CPUs that approaches the number of connections per cell, almost every spike that is generated must be delivered to at least one cell on every CPU and consequently, every spike must be placed on every queue. NEURON's use of one queue for events on each CPU implemented as a splay tree (Lytton and Hines, 2005) is thus inefficient in this domain.
Figure 6.
Runtime (filled circles) as a function of the number of processors used for 65,536 or 262,144 integrate and fire cells (I&F) using 1000 or 10,000 connections/cell, respectively. The dashed lines represent ideal scaling.
Discussion
The NEURON simulation environment has been extended to support distributed simulations of networks. In this paper, we focused on the performance of the parallel implementation in a test case and for three realistic network models from ModelDB originally published as serial simulations. There is a great variety of cell complexity, network size, and connectivity but these published models are typical of a common problem in computational neuroscience: a relatively small network of about 100–1000 neurons with more than nearest neighbour but less than all to all connectivity, composed of from 10 to 100 compartments, with realistic channel properties and distributions, to be run on departmental machines with a few tens of processors. From this point of view, a major result of this work is that superlinear efficiency, up to ≈2, can be reached with an appropriate choice of network size, neuron biophysical properties, and computer system size.
For machines with fewer than 200 CPUs, the performance results over a range of network size, neuron complexity, and number of processors, are explained by the dominance of cache memory effects over the small extra time needed for interprocessor spike exchange. Clearly, efficient use of a parallel system is obtainable by distributing the neurons among the available processors in such a way that the subnet assigned to each processor: i) is biophysically complex enough so that integration times are both very similar on all processors and are much larger than an MPI_Allgather call, and ii) it can be run entirely in its cache or with little use of main memory. The superlinear speedup is due to more effective use of a processor's high-speed cache memory. Each processor's subnet problem size reduces with the number of available processors, and so a greater proportion of that problem fits into the processor's cache memory where memory access is more evenly matched to the cpu speed. Eventually, the problem size becomes small enough on each processor so that it fits entirely into the cache and increasing spike communication overhead then results in decreasing speed-up. This cache effect is not seen on the EPFL IBM Blue Gene since its low power consumption cpu speed, cache, and 512 MByte main memory are balanced so that every memory location has approximately the same access time by the cpu.
It is reasonable to take the view that superlinear speedup reflects an inefficient use of memory resources because of the excessive pointer distance between successively accessed memory. We intend to look at this issue in more detail in order to permit an increase in problem size before encountering this cache effect. Previously, in the early 90's, NEURON underwent a memory pointer vectorization code transformation in order to efficiently use the Cray YMP SIMD pipeline and those idioms remain available. However, with the use of object-oriented programming to support conceptual clarity and incremental evolution of NEURON, dynamic object creation has caused a loss of efficiency in memory access patterns. A promising performance transformation might be to reorganize the memory allocation process for a size N vector of membrane mechanism objects each having M data fields, into M data vectors of size N.
The most important performance determinant is the decision of how to distribute gids (cells) on the processors. It is extremely important that each processor is given approximately the same amount of work to do. Each processor has to wait for all the others when spikes are exchanged so if one processor takes twice as long as the others to do a maximum integration interval, that slows the other processors down by a factor of two (idle half the time). For this reason we generally chose the number of processors to be an integer fraction of the number of cells in our tests. For examples with multiple types of cells we chose, if possible, the number of processors to be an integer fraction of each type. Our tests always obtained good balancing by using the round robin or “card dealing” algorithm:
and we did not attempt any improvement in those cases where the count of a particular cell type was not an integer multiple of the number of available processors. A distant second in terms of likely benefit for performance optimization is the arrangement of gids that minimizes the number of spikes that have to be communicated (i.e. cell groups that are densely interconnected should as much as possible be on the same machine). The METIS (Karypis and Kumar, 1998) graph partitioning program can be used to define a ngid on nhost partition that optimizes balance and minimizes communication. In the performance tests of the three published models, communication overhead is such a small portion of the total simulation time that we have not tried to optimize the buffer size of the initial MPI_Allgather where there is a balance between almost always sending a too large buffer and occasionally having to do an MPI_Allgatherv to send the overflow. Presently, the default configuration value for the number of (gid, spiketime) pairs that can be sent along with the number of pairs is nrn_spikebuf_size = 0. i.e. only the number of spikes is sent. At CPU numbers where interprocessor spike exchange begins to affect the runtime, the subnets are so small that the most common maximum number of spikes generated in an integration interval is 1.
Interprocessor spike exchange time using MPI_Allgather for a constant number of CPUs can be approximated, at least for our family of scaled Bush models, as the sum of a fixed overhead and a term proportional to the number of spikes exchanged. On the EPFL IBM BlueGene, the fixed overhead seems to be effectively constant between 50 and 500 CPUs and then begins to double as the number of CPUs doubles from 1000 to 8000 CPUs. In this latter CPU range the proportionality factor increases less than linearly with number of CPUs. The lesson to be drawn from the Bush model scaling results is straightforward. Since it is generally the case that number of spikes generated is proportional to number of cells, there is a certain number of CPUs at which the spike exchange time is of the same order as the computation time and this number is independent of further increases in network size. In this regime, further improvement in communication time, if possible, will necessitate MPI_Send/MPI_Receive methods that take advantage of network connection topology.
A simulation domain where processor computation time no longer scales ideally with increasing number of CPUs is one involving a very large number of spikes with constant synaptic delay. Large nets with fast spiking artificial cells (Fig.6) make this point dramatically. The problem is that every spike generated must be delivered to at least one cell on every CPU. Thus queue handling is essentially the same on every CPU regardless of the number of CPUs. Ironically, this effect would not have been seen in a model with random delays since NEURON would not have been able to use the optimization of only putting generated spikes on the queue and instead would have filled the queue with the 1000/ncpu or 10000/ncpu fold greater number of "to be delivered" spikes, and so queue time would have scaled ideally just as it did with the random delay Bush et. al. (1999) model. However, the computation time would have been much larger. So this optimization gives greatest benefit on a serial machine. There are a number of further queue optimizations one can imagine which use special model properties (e.g. A small set of FIFO queues handling a small set of delays, (Mattia and Del Giudice, 2000)) or are limited to fixed step integration methods (e.g. a ring buffer equal in size to the maxdelay/dt). However, it should be noted that eliminating queue handling as a runtime factor still leaves a 17 second spike exchange time above the ideal runtime at 8196 CPUs with the large artificial net in Fig.6. To reduce that in an MPI_Allgather context would require spike compression techniques such as implemented in the NEST simulator (Morrison, et. al. 2005).
We do not anticipate spike exchange limited performance for the Blue Brain neocortical simulations. Those will use multi-hundred compartment 3D reconstructed morphologies for each cell. Thus communication overhead is potentially only a few percent or less on full 8196 processor simulations. On the other hand, cell heterogeneity will reduce performance by making it impossible for each CPU to have identical problem size. It is presently unclear whether the benefits of finer grained load balance by means of parallel distributed simulations of individual cells will justify the much greater communication costs of exchanging tightly coupled membrane potentials at each integration time step. Note that NEURON’s variable step integrators (Hindmarsh and Serban 2002) already support parallel equation solving. We are continuing research in this direction and it will be necessary to design convenient-to-use ParallelContext methods to separate user-level cell specification from the details of cell compartment distribution.
Although standard NEURON methods can be used to save any specific state trajectories to files and normal ParallelContext methods can be used to transfer data between any group of CPUs for further processing, it is most useful, and fastest, to save the entire network (gid, spiketime) pattern into a file, as was done for the raster plots in Fig. 4 and Fig. 5. This allows the subsequent playback of the spiketime pattern using the PatternStim class, into any subnet or single cell simulation run on a serial machine. The serial simulation is then a quantitatively exact replica of that portion of the full parallel simulation. This gives full GUI exploration capabilities and retroactive plotting capabilities for any state variable trajectory.
It should be noted that NEURON can be also configured at build time with the options -- with-neosim or --with-ncs in which spike distribution is managed respectively by the NEOSIM program (Goddard et.al. 2001 ; http://neosim.org org) or the NeoCortical Simulator (NCS) (Wilson et. al. 2003). In both cases NEURON is linked as a library and the overall network construction (i.e the distribution of cells and connectivity), simulation management, and spike distribution, is controlled by the NEOSIM or NCS core. The interface to NEURON's simulation engine is conceptually the same in both cases, involving just three operations. 1) The controlling program can tell NEURON on a specific processor to integrate to a specific time. 2) The controlling program can send NEURON spike information consisting of pairs of NetCon index or pointer and delivery time, with the only constraint being that the delivery time cannot be earlier than the current integration time. 3) When a NEURON cell fires (within the current integration request interval), NEURON sends the cell pointer or index along with the precise firing time to the controlling program. The spike distribution algorithms for NEOSIM and NCS are more carefully tailored to the actual processor to processor connectivity patterns and make use of individualized MPI_Send/MPI_Receive pairs. The increased (or decreased) performance compared to the naive MPI_Allgather approach is an experimental question that is machine and problem dependent.
Acknowledgements
We thank the Yale University Computer Science Department (New Haven, CT, USA) and the CINECA consortium (Bologna, Italy) for granting access to their parallel systems. We also thank Christian Clemencon of EPFL for providing essential technical assistance, and Felix Schuermann of EPFL for his feedback regarding the parallel interface. This work was supported by NIH grants NS11613, NS045612, and the Blue Brain Project.
References
- Almási G, Heidelberger P, Archer CJ, Martorell X, Erway CC, Moreira JE, Steinmacher-Burow B, Zheng Y. Optimization of MPI collective communication on BlueGene/L systems. Proc. 19th annual international conference on Supercomputing; Cambridge MA. 2005. pp. 253–262. [Google Scholar]
- Bush PC, Prince DA, Miller KD. Increased pyramidal excitability and NMDA conductance can explain posttraumatic epileptogenesis without disinhibition a model. J Neurophysiol. 1999;82:1748–1758. doi: 10.1152/jn.1999.82.4.1748. [DOI] [PubMed] [Google Scholar]
- Carriero N, Gelernter D. Linda in context. Communications of the ACM. 1989 Apr; 1989. [Google Scholar]
- Delorme A, Thorpe SJ. SpikeNET: an event-driven simulation package for modelling large networks of spiking neurons Network. 2003;14:613–627. [PubMed] [Google Scholar]
- Davison AP, Feng J, Brown D. Dendrodendritic inhibition and simulated odor responses in a detailed olfactory bulb network model. J. Neurophysiol. 2003;90:1921–1935. doi: 10.1152/jn.00623.2002. [DOI] [PubMed] [Google Scholar]
- Goddard NH, Hood G. Large-Scale Simulation using Parallel GENESIS. In: Bower JM, Beeman D, editors. The Book of GENESIS. 2nd ed. Springer-Verlag; 1998. [Google Scholar]
- Goddard N, Hood G, Howell F, Hines M, De Schutter E. NEOSIM: Portable large-scale plug and play modelling. Neurocomputing. 2001;38–40:1657–1661. [Google Scholar]
- Hammarlund P, Ekeberg Ö, Wilhelmsson T, Lansner A. Large neural network simulations on multiple hardware platforms. In: Bower JM, editor. The Neurobiology of Computation. Boston: 1996. [DOI] [PubMed] [Google Scholar]
- Hines ML, Carnevale T. The NEURON simulation environment. Neural Comp. 1997;9:178–1209. doi: 10.1162/neco.1997.9.6.1179. [DOI] [PubMed] [Google Scholar]
- Hines ML, Carnevale NT. Discrete event simulation in the NEURON environment. Neurocomputing. 2004;58–60:1117–1122. [Google Scholar]
- Hindmarsh A, Serban R. User documentation for cvodes, an ode solver with sensitivity analysis capabilities. Tech. rep., Lawrence Livermore National Laboratory. 2002 http://www.llnl.gov/CASC/sundials/
- Howell FW, Dyrhfjeld-Johnsen J, Maex R, Goddard N, De Schutter E. A large scale model of the cerebellar cortex using PGENESIS. Neurocomuting. 2000;32:1041–1046. [Google Scholar]
- Karypis G, Kumar V. Multilevel k-way partitioning scheme for irregular graphs. Journal of Parallel and Distributed Computing. 1998;48(1):96–129. [Google Scholar]
- Lytton WW, Hines ML. Independent variable time-step integration of individual neurons for network simulations. Neural Comput. 2005;17:903–921. doi: 10.1162/0899766053429453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markram H. The Blue Brain project. Nature Rev. Neurosci. 2006;7:153–160. doi: 10.1038/nrn1848. [DOI] [PubMed] [Google Scholar]
- Mattia M, Del Giudice P. Efficient event-driven simulation of large networks of spiking neurons and dynamical synapses. Neural Computation. 2000;12:2305–2329. doi: 10.1162/089976600300014953. [DOI] [PubMed] [Google Scholar]
- Migliore M, Hoffman DA, Magee JC, Johnston D. Role of an A-type K+ conductance in the back-propagation of action potentials in the dendrites of hippocampal pyramidal neurons. J. Comput. Neurosci. 1999;7:5–16. doi: 10.1023/a:1008906225285. [DOI] [PubMed] [Google Scholar]
- Morrison A, Mehring C, Geisel T, Aertsen A, Diesmann A. Advancing the Boundaries of High-Connectivity Network Simulation with Distributed Computing. Neural Comp. 2005;17:1776–1801. doi: 10.1162/0899766054026648. [DOI] [PubMed] [Google Scholar]
- Myers R. 2000. http://www.mtsu.edu/~csjudy/STL/HashMap.h.
- Santhakumar V, Aradi I, Soltesz I. Role of mossy fiber sprouting and mossy cell loss in hyperexcitability: a network model of the dentate gyrus incorporating cell types and axonal topography. J. Neurophysiol. 2005;93:437–453. doi: 10.1152/jn.00777.2004. [DOI] [PubMed] [Google Scholar]
- Wilson EC, Goodman PH, Harris FC. Implementation of a Biologically Realistic Parallel Neocortical-Neural Network Simulator. Proceedings of the Tenth SIAM Conf. on Parallel Process. for Sci. Comp.; March 12–14, 2001; Portsmouth, Virginia. 2001. [Google Scholar]