Abstract
Behavioral performance in detection and discrimination tasks is likely to be limited by the quality and nature of the signals carried by populations of neurons in early sensory cortical areas. Here we used voltage-sensitive dye imaging (VSDI) to directly measure neural population responses in the primary visual cortex (V1) of monkeys performing a reaction-time detection task. Focusing on the temporal properties of the population responses, we found that V1 responses are consistent with a stimulus-evoked response with amplitude and latency that depend on target contrast and a stimulus-independent additive noise with long-lasting temporal correlations. The noise had much lower amplitude than the ongoing activity reported previously in anesthetized animals. To understand the implications of these properties for subsequent processing stages that mediate behavior, we derived the Bayesian ideal observer that specifies how to optimally use neural responses in reaction time tasks. Using the ideal observer analysis, we show that 1) the observed temporal correlations limit the performance benefit that can be attained by accumulating V1 responses over time, 2) a simple temporal decorrelation operation with time-lagged excitation and inhibition minimizes the detrimental effect of these correlations, 3) the neural information relevant for target detection is concentrated in the initial response following stimulus onset, and 4) a decoder that optimally uses V1 responses far outperforms the monkey in both speed and accuracy. Finally, we demonstrate that for our particular detection task, temporal decorrelation followed by an appropriate running integrator can approach the speed and accuracy of the optimal decoder.
INTRODUCTION
A central goal of systems neuroscience is to understand how stimuli in the environment are encoded by neural responses in early sensory cortical areas and how these responses are, in turn, converted by downstream circuits into perceptual decisions and behavior. Information regarding even the simplest sensory stimulus is distributed over space and time in early sensory cortical areas. The decoding strategies implemented in the downstream circuits that make perceptual decisions and form motor plans are likely to be matched to the quality and nature of these distributed sensory neural responses.
Here we used voltage-sensitive dye imaging (Grinvald and Hildesheim 2004) to measure these distributed neural responses in V1 of monkeys while they attempted to detect a small, low-contrast, visual target. Our primary goal was to determine the nature and quality of the target-related V1 population responses. Our secondary goal was to determine the potential consequences of these properties to processing stages subsequent to V1 that must detect the target and decide if and when to report that the target is present based on the signals provided by V1 neurons.
The focus in the current study is on the temporal properties of the signal and the noise in V1 population responses (an earlier study focused on the spatial properties of V1 population responses; Chen et al. 2006). Specifically we determined the effect of target contrast on the dynamics of the target-evoked responses, and we examined the dynamics of the neural variability and compared it with previous reports of ongoing activity in the visual cortex of anesthetized cats (Arieli et al. 1996).
To understand the implications of the measured temporal dynamics of V1 population responses, we derived the optimal Bayesian temporal decoder for detecting the target from V1 population responses in a reaction time task. This optimal decoder evaluates V1 responses and decides, on a moment-by-moment basis, if and when sufficient evidence that the target is present has accumulated. This ideal observer allowed us to characterize how the target-related information in V1 evolves over time and to compare neuronal sensitivity with the monkey’s behavioral sensitivity in terms of accuracy and speed. An additional benefit of deriving the ideal observer is that it serves as a benchmark against which the performance of other candidate temporal decoding strategies can be compared.
Importantly, the goal of this ideal observer analysis is not to find the decoding model that best accounts for the monkey’s behavior in our task because behavior is likely to be mediated by complicated interactions between multiple cortical areas subsequent to V1. Complete understanding of these decoding and decision mechanisms will undoubtedly require measuring neural responses in these subsequent cortical areas. Therefore our goals in the current study are to characterize the information that is potentially available in V1 and to determine how V1 responses should be read out given the properties of V1 population responses.
METHODS
The results reported here are based on methods that have been described in detail previously (Chen et al. 2006; Seidemann et al. 2002). Here we focus on details that are of specific relevance to the current study. All procedures have been approved by the University of Texas at Austin Institutional Animal Care and Use Committee and conform to National Institutes of Health standards.
Behavioral task and visual stimulus
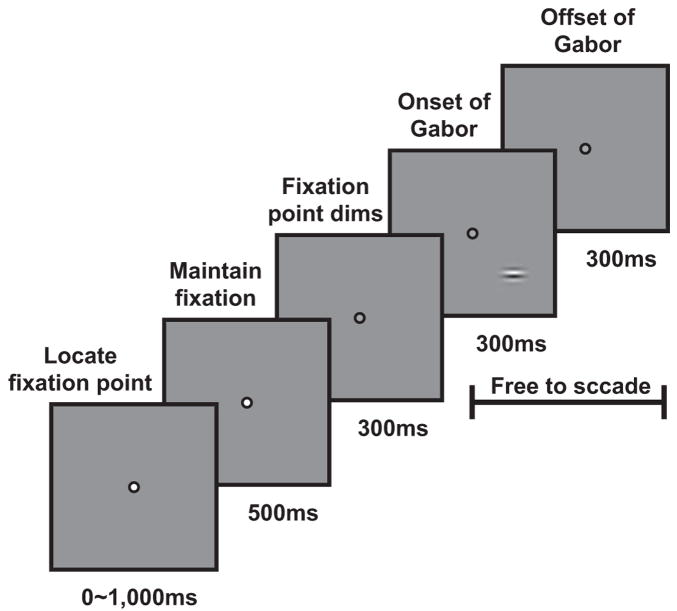
Two monkeys were trained to perform a reaction-time visual detection task (Fig. 1). After the monkey established fixation, fixation point dimming indicated to the monkey that 300 ms later the target may appear. The target was a small Gabor patch (σ = 0.25– 0.33°, spatial frequency = 1.4 –1.7 cycle/°, eccentricity = 2.7– 4.0°) that appeared at a fixed location. Target contrast was selected pseudorandomly from four to six contrast levels spanning the monkey’s detection threshold. In target-present trials (half of the trials), the monkey was required to shift gaze to the location of the target within 600 ms from target onset (but not sooner than 75 ms after target onset) and maintain gaze at that location for an additional 300 ms to receive the reward. The target remained on for 300 ms or until the monkey initiated the saccade to the target location. In the remaining target-absent (blank) trials, the monkey was required to maintain fixation within a small window (<2° full width) around the dimmed fixation point for an additional 1,500 ms to obtain a liquid reward.
FIG. 1.
Behavioral task and stimulus. Monkeys performed a reaction-time visual detection task with Gabor patches as targets. The monkey indicated detection of the target by making a saccadic eye movement to the target location. See METHODS for additional details.
Behavioral performance was fitted by a modified Weibull function (Quick 1974): P(C)=1 −(1−FA)· e−(C/α)β where FA is the false alarm rate, C is the target contrast, and α and β are the offset and slope parameters, respectively. The threshold was computed as the contrast at which overall accuracy is 75% (combined across target-present and target-absent trials).
Analysis of imaging data
The results reported here are based on eight VSDI experiments from the dorsal portion of V1 in two hemispheres of two macaque monkeys. Our basic analysis is divided into four steps. 1) We normalize the responses at each site (a binned group of pixels) by the average fluorescence at that site across all trials and frames. 2) We remove from each site on each trial a linear trend that is estimated based on the response in two short intervals (300 and 200 ms long, respectively), one immediately before and one immediately after the response period (a period from 0 to 600 after stimulus onset). 3) We average responses over a limited spatial region to obtain a single number on each frame. 4) We remove trials with aberrant VSD responses (generally <1% of the trials). The normalization in step 1 serves to minimize the effects of uneven illumination and staining. Step 2 serves to eliminate slow fluctuations in the VSD signals that are unrelated to neural responses. Such slow fluctuations over the course of many seconds can result from several sources of noise, including dye bleaching, slow fluctuations in the light source, respiration artifacts, and fluctuations in the absorption properties of the tissue due to slow hemodynamic changes (Grinvald et al. 1999). Because of their slow time course, these fluctuations are well captured by a linear trend in our 1.1-s-long trials (see Supplementary Fig. S11 for additional details regarding the removal of nonneural sources of noise). Note that the effect of a heart-beat artifact was reduced by synchronizing the data acquisition to the monkey’s electrocardiogram (Grinvald et al. 1999). Unless noted otherwise, the spatial averaging in step 3 is over a rectangular area of 1.0 mm2 centered around the location with the most reliable response (maximal d′) at high target contrast.
To remove trials with aberrant VSD responses, the average time course across all repetitions (within a given condition) was subtracted from the response in each trial, and the SD of the accumulated residuals was computed. Trials with accumulated residual responses that were >3 SD values were excluded from further analysis. This simple procedure eliminates trials where the animal made excessive movements.
Temporal pooling models
To optimally decode neural population responses over time, temporal correlations in the neural population responses must first be removed. Temporal correlations can be removed by a decorrelation (whitening) filter that, when convolved with the responses in single trials, produces responses that are independent across frames. To be biologically plausible, however, this filter has to be causal, that is, the output of the filter at time t must depend only on the response up to time t. For convenience, we chose to use a filter that is a difference of two Gamma functions. The four parameters of these two Gamma functions, and a parameter determining their relative weight, were selected to make the power spectrum of the filtered noise as flat as possible.
To ensure that we did not overestimate the speed and accuracy of the temporal pooling models, the analysis of the models was performed separately for each trial using a jackknife procedure (Efron and Tibshirani 1993). Unless noted otherwise, statistical tests were performed using a bootstrap method (Efron and Tibshirani 1993).
When comparing the performance of the temporal pooling models with the monkey, the maximal allowable evaluation time for the model was set to 1) the monkey’s response time minus a short interval to account for motor preparation and execution time (default value 18 ms or 2 camera frames) or if the monkey did not respond to 2) the maximal amount of time available for the monkey (600 ms). Therefore the optimal decoder is the one that maximizes the accuracy within these temporal limits imposed by monkeys’ reaction times. We also considered how different values of the maximal evaluation time and the motor preparation time affect the performance of the temporal pooling models.
RESULTS
Visual task and behavioral performance
The temporal interval over which sensory information is evaluated to form a perceptual decision is generally unknown. The duration of this interval is likely to depend on the nature of the task and its difficulty and to vary from trial to trial. Reaction-time tasks are useful because they give an upper bound on the duration of the evaluation interval, while providing useful information regarding the dynamics of the decision process.
In the current study, two monkeys were trained to perform a reaction-time visual detection task (Fig. 1). The monkey reported the appearance of a small oriented target by making a saccadic eye movement to the target location as soon as it was detected.
The proportion of trials in which the monkey reported that the target is present depended on target contrast (Fig. 2A). In this representative example, the probability of reporting that the target was present increased monotonically with target contrast and was fitted with a modified Weibull function (Quick 1974) (solid curve, see METHODS). Detection threshold (dashed line) was determined as the contrast at which overall accuracy across target-present and target-absent trials was 75% correct.
FIG. 2.
Behavioral performance in an example experiment and summary of reaction times across 8 experiments. A: proportion of trials in which the monkey reported that the target was present as a function of target contrast. Zero contrast represents target-absent trials (the probability at this point is the false alarm rate, which is 0 in this example). —, the best fitting Weibull function (Quick 1974); - - - and the corresponding number, the contrast threshold (see METHODS). Horizontal error bar: 95% confidence interval. B: mean ± SD of reaction times as a function of target contrast. C: cumulative probability of reaction times as a function of target contrast combined across 8 experiments. Median reaction times are short and variability is low at 25% target contrast (magenta). Median and variability of reaction times increase at lower target contrasts. Note that despite the fact that the monkeys were allowed to saccade to the target for up to 600 ms after target onset, almost all reaction times were shorter than 400 ms.
The monkey’s reaction times also depended on target contrast (Fig. 2B). Reaction times were shortest, on average, at high target contrast and increased monotonically as target contrast was lowered. In addition, the range and variability of reaction times tended to increase as target contrast was lowered. These two trends can be seen in the summary data of the cumulative reaction times from the eight experiments (Fig. 2C). The increase in the mean and the variance of reaction times with decreasing target contrast is consistent with the hypothesis that perceptual decisions in detection and discrimination tasks are formed by evaluating noisy neural representations until sufficient evidence regarding the stimulus has accumulated (e.g., Carpenter 2004; Cook and Maunsell 2002; Gold and Shadlen 2001, 2007; Huk and Shadlen 2005; Mazurek et al. 2003; Ratcliff 2001; Roitman and Shadlen 2002; Schall and Thompson 1999; Smith and Ratcliff 2004).
Dynamic properties of stimulus-evoked population responses in V1
Neural responses were measured in eight experiments from V1 in two hemispheres of two monkeys using the oxonol dyes RH-1691 or RH-1838 (Grinvald and Hildesheim 2004; Shoham et al. 1999). We use the results from one VSDI experiment as an illustrative example (Fig. 3). In a previous study, we focused on characterizing the spatial aspects of V1 responses and demonstrated that neural responses to a small visual target spread over a large area in V1 and are well fitted by a 2D Gaussian (Chen et al. 2006). Such large spread is expected even for extremely small visual stimuli because the receptive fields of V1 neurons that are located >1 mm apart can overlap substantially (e.g., Hubel and Wiesel 1974; McIlwain 1986). Here we focus on the temporal aspects of V1 population responses.
FIG. 3.

Dynamic properties of the target-evoked neural population responses in an example experiment. A: image of the cortical vasculature in a 8×8 mm2 area in V1. B: spatial pattern of changes in fluorescence in response to a 25% contrast Gabor patch in the same area as in A. Gabor patch parameters: σ = 0.33°, spatial frequency = 1.4 cycle/°, eccentricity = 2.7°. Values at each location represent the averaged difference in response between target and blank conditions during the 1st 200 ms after target onset. The blue square indicates a 1.0 mm2 region of interest centered around the location with the most reliable response (highest d′). The spatial pattern of the response was fitted with a 2-dimensional (2D) Gaussian. Thin ellipsoids represent iso-elevation contours at 50 and 60% of the amplitude of the fitted 2D Gaussian. C: time course of the optical responses at different target contrasts in the area indicated by the blue square in B. Time 0 indicates target onset. The optical response in blank trials was subtracted from each condition. Responses are averaged across repetitions (n = 10 at each target contrast in target-present trials; n = 50 in blank trials). Solid curves indicate average time courses and are terminated at the median reaction time of the monkey for each contrast with at least 4 reaction times (medians are indicated by arrows). Dashed curves, fits to the data in which the shape of the response was assumed to be fixed for all contrasts and only the amplitude and the latency were allowed to vary between contrasts. The rising and falling edges of the fitted curves were sigmoidal functions with one slope for all rising edges and one for all falling edges. D: response latency (time to half-maximum) as a function of response amplitude (ΔF/F) for 2 target contrasts (25 and 7%) and at different positions in the activated region. Response latency was measured in 10 annular elliptical regions that contained similar response amplitudes (as in B). For a given contrast, there were only small differences in response latency between locations near the peak and locations near the edge of the activated region. The rapid spread is not significantly different at the 2 contrasts. Response latency, however, strongly depended on target contrast. The difference in latency between the responses to these two target contrasts was 21.0 ms. As a result, response latency at locations near the peak of the activated region at low target contrast can be much longer than response latency at locations near the edge of the activated region at high target contrast despite the fact that the 2 responses have similar amplitudes.
Considering first the time course of the responses at locations near the peak of the activated region, two important characteristics of V1 responses are apparent. First, the amplitude of the response decreased monotonically as the contrast of the target was lowered (Fig. 3C). Second, the latency of the response significantly increased with decreasing target contrast. The spatial profile of the response, however, was largely independent of target contrast (i.e., responses to targets at different contrasts were scaled versions of each other over space) (Chen et al. 2006).
To examine how the latency of target-evoked responses depends on the target contrast and on the position in the activated region, we measured response latency for targets at different contrasts in 10 annular elliptical regions that contained similar response amplitudes (one of the regions is indicated by the pair of elliptical contours in Fig. 3B). These annular regions were obtained from a two-dimensional (2D) Gaussian fitted to the evoked response. To measure latency, the rising edge of the response was fitted with a sigmoidal function, and the latency was taken as the time to half-maximum. Figure 3D shows the latency as a function of the amplitude of the response for the inner eight elliptical regions for the 25% contrast target (magenta symbols) and for the inner five elliptical regions for the 7% target contrast (blue symbols). Responses in the remaining elliptical regions were too weak to be reliable. For a given contrast, response latency was almost constant across space (Fig. 3D). The latency of the response to the 25% contrast target in the peak region was only 5.7 ms faster than the latency several mm away at a region with response amplitudes that are only 20–30% of the peak. The rapid spread of activity from the location of the peak toward locations at the edge of the activated region was not significantly different at 25 and 7% target contrasts (F-test for the 2 linear regressions in Fig. 3D, P = 0.608). These results show that although response amplitude and latency strongly depend on target contrast, the spatial profile of the response and the speed of the response spread are largely independent of target contrast. In addition, these results demonstrate that population responses with the same amplitude can have very different latencies depending on the contrast of the target and the distance from the peak of the response. For example, response to 25% contrast target at the sixth inner elliptical region and response to 7% contrast target at the innermost elliptical region have similar amplitude of ~0.1% but differ in latency by ~20 ms.
Because the main focus of the current study is on the temporal properties of V1 population responses, we combined the VSDI signals over space by computing the average response over an area of 1.0 mm2 that was centered on the site that gave the most reliable (maximal d′) response (blue square in Fig. 3B). As shown later, the temporal properties of V1 responses are largely independent of the exact form of combining the responses over space.
Dynamic properties of response variability in V1
The quality of V1 population responses depends not only on the stimulus-evoked responses but also on the magnitude and properties of the neural variability, or noise (Fig, 4A). We found that the SD of the response was relatively constant in time and largely stimulus independent (Fig. 4B). This implies that the observed population responses are consistent with the sum of a reproducible stimulus-evoked response and a variable stimulus-independent spontaneous or ongoing activity, consistent with previous studies in the anesthetized cat (Arieli et al. 1996). The finding that response variability is stimulus independent may seem surprising given that in single neurons the variance of the spike count during a short interval is proportional to the mean (Geisler and Albrecht 1997; Tolhurst et al. 1983). However, variability that is largely stimulus independent is what one would expect in population responses.
FIG. 4.
Dynamic properties of the trial-to-trial variability (or noise) of the neural population responses in an example experiment. A: time course of the response in individual blank and 25% target contrast trials. B: time course of the SD of the response across trials. The SD was relatively constant over time and did not depend on target contrast. The SD was ~3.5 times smaller than the mean response to the 25% target contrast (i.e., d′ = 3.5). C: scatter plot of response amplitude before response onset and 45 ms later (see vertical lines in A). D: temporal correlations of the optical signals. Temporal correlations were computed separately in target-present and -absent trials. At each target contrast, the average time course was first subtracted from the response in each trial and the temporal correlation was computed for the residual responses in the 600 ms following the time of target onset. Temporal correlations are approximately the same in target-present and in target-absent trials, suggesting that the temporal correlations are largely stimulus independent. The thick solid curves represent an exponential fit to the temporal correlation functions (the time constant of the exponent is indicated in the panel). The temporal correlations in this experiment exhibit some periodicity. These periodic fluctuations, however, were not consistent across experiments (see Supplementary Fig. 3). E: average temporal correlation across all 8 experiments. Mean time constants are indicated in the panel.
To see this, consider a population of neurons within a small patch of cortex, each having a response variance that is proportional to the mean (e.g., the neurons generate spikes according to a Poisson-like process). Also like typical cortical neurons, suppose that these neurons have a baseline response that is low and that the response to an optimal stimulus is relatively high. Cortical neurons are tuned along a large number of stimulus dimensions and thus any given stimulus will be optimal for only a small fraction of the neurons within the pool. This implies that for a given stimulus, the average stimulus-evoked response will be much lower than the response of those few neurons tuned optimally to the stimulus. A simple analysis shows that under realistic assumptions regarding the tuning properties of V1 neurons in a small cortical patch, the average stimulus-evoked response across the population is in fact much smaller than the baseline response (see following text). In other words, at the level of the pool, the stimulus-dependent response is much smaller than the stimulus-independent baseline response. This implies that the stimulus-independent variability that is contributed by the baseline activity of the nonresponsive or weakly responsive neurons dominates the variability at the level of the pool. Therefore one would expect the SD of the pooled response to be nearly independent of the stimulus-evoked population response.
As an example, consider Fig. 5. Figure 5A shows the mean and the variance of the response of a typical V1 neuron to its optimal stimulus as a function of contrast (baseline response of 1 spike/s, max response of 50 spikes/s). As contrast increases, the variance grows proportional to the mean with a slope (Fano factor) of 1.3. Figure 5B shows the expected mean and variance of the pooled response of a population of 15,000 statistically independent neurons (the approximate number of neurons in a 250 × 250 μm2 imaging region) when the stimulus-evoked response is small relative to the baseline. As in the single unit, the variance grows proportional to the mean. However, the relevant measurements for characterizing the quality of the information transmitted by a neuron or a pool of neurons are the mean evoked response and its SD. Figure 5C plots these measurements for the single neuron. The SD changes substantially with contrast and hence the changes in the signal-to-noise ratio of the responses are due to the changes in both the mean and the SD. Figure 5D plots these measurements for the pool of neurons. As can be seen, in this case, the increase in SD with contrast is negligible, and hence the changes in the signal-to-noise ratio are due almost entirely to the changes in the mean. This striking difference between the single neuron and the pool is due to the fact that in the single neuron, the baseline response is small relative to the evoked response, whereas in the population the average evoked response is small relative to the baseline.
FIG. 5.
A largely stimulus-independent response variability is expected in large pools of neurons. A: mean (●) and variance (▲) of the response of a model V1 neuron as a function of stimulus contrast. The stimulus is assumed to be optimal for this neuron. The variance is assumed to be proportional to the mean with a slope (Fano factor) of 1.3. B: expected mean and variance of responses in a pool of 15,000 statistically independent neurons with average stimulus-evoked response that is much lower than the baseline response (see text for details). C: mean (●) and SD (▲) of stimulus-evoked response for the single neuron in A. D: mean and SD of stimulus-evoked response for the population of neurons in B.
To generate this figure, we obtained a rough estimate of the mean stimulus-evoked response of the neurons in the population by considering the known tuning properties of V1 neurons. From single-unit studies, V1 neurons are known to be tuned along at least the dimensions of position, orientation, spatial frequency, phase, direction of motion, depth, and wavelength. Using rough estimates of the range of tuning parameters of V1 neurons along these dimensions (DeAngelis et al. 1999; Geisler and Albrecht 1997), we obtained a value for the mean stimulus-evoked response that is more than an order of magnitude smaller than the average baseline response in the population. This value was used to generate the population responses in Fig. 5. These theoretical results are consistent with findings from a recent study in which we compared the response of single and multiple units in V1 (Palmer et al., 2007) and found that the ratio of the stimulus-evoked response to the baseline response decreases dramatically as the baseline of the multi-unit response increases. Importantly, we also found (in the process of doing these calculations) that largely stimulus-independent variability at the level of the pooled responses is expected under a wide range of assumptions regarding the pool size, the tuning properties of the neurons, and the average correlations between pairs of neurons in the pool. For example, we find largely stimulus-independent variability even if we assume that all neurons within the population simulated in Fig. 5 have identical orientation tuning. This occurs because of the scatter along the other stimulus dimensions.
In addition, as described in our previous study (Chen et al. 2006), as the size of the population increases, the weak correlated noise between pairs of neurons in the population will become the dominant source of noise in the pooled activity. This correlated noise may be stimulus independent and hence further contribute to the constancy of the response variance.
Temporal correlations of response variability in V1
Temporal correlations are an important property of the neural noise with significant implications for how the neural signals should be accumulated over time. Figure 4C shows the relationship between the amplitude of the VSDI signals in two frames separated by 45 ms (2 vertical lines in Fig. 4A) in all the individual target-absent trials (red symbols) and 25% target contrast trials (magenta symbols). There is a strong correlation between the amplitude of the VSDI signal in these two frames, and this correlation appears to be similar in target-present and -absent trials. To examine the temporal correlations in more detail, we computed the Pearson correlation between VSDI signals in two frames as a function of their separation in time. We found large and long-lasting temporal correlations in the VSDI responses (Fig. 4D). These temporal correlations were similar in target-present trials and target-absent trials and in the periods prior to and following target onset. These temporal correlations were well fitted by exponential functions with similar time constants and asymptotic values for target-present and target-absent trials. Similar results were obtained in all eight experiments (Fig. 4E). These findings are consistent with previous results from VSDI experiments in the visual cortex of the anesthetized cat (Arieli et al. 1996). While the exact parameters of the temporal correlation function depended somewhat on the specific procedure for removing the nonneural sources of noise from the imaging data, large and long-lasting temporal correlations, which are well fitted by an exponential decay, were observed under all preprocessing methods tested (see Supplementary Fig. S1). In contrast, no long-lasting temporal correlations could be observed in control experiments in which an inert surface was illuminated and imaged using the same system (Supplementary Fig. 2), indicating that these correlations are not due to the illumination or the imaging system.
In summary, we find that V1 population responses, as measured by VSDI, can be described as the sum of a stimulus-evoked response that varies in amplitude and latency as a function of stimulus contrast and a stationary stimulus-independent noise that is approximately Gaussian (Chen et al. 2006) with long-lasting, exponentially decaying, temporal correlations.
Effect of temporal correlations on temporal pooling
Given the properties of V1 population responses described in the preceding text, how should V1 responses be pooled over time to perform well in detection tasks? We begin to address this question by examining the effects of the observed temporal correlations on performance in a simplified detection task with only one possible target contrast. In the next section, we derive the ideal observer for detecting the target from the measured neural responses in our task.
For the purpose of this section, we focus on neural responses to a single low-contrast target (5% contrast) in the example experiment. Consider first the reliability of the neural response in a short temporal interval (i.e., the duration of a single imaging frame). A standard measure of reliability which is based on signal detection theory (Green and Swets 1966) is the signal-to-noise ratio d′
where ES represents the mean amplitude of the response in target-present trials (signal trials), EN represents the mean amplitude of the response in target-absent trials (noise trials), and σS and σN represent the corresponding SDs. In simple detection and discrimination tasks, d′ is monotonically related to the error rate. The solid red curve in Fig. 6A shows the normalized fitted time course of the mean response to the 5% contrast target (from Fig. 3C), and the dashed red curve shows the estimated SD of the response (from Fig. 4B) on the same scale. The red curve in Fig. 6B shows the time course of d′. Because the SD is constant in time (Fig. 4B), the d′ curve is a scaled version of the mean response curve.
FIG. 6.
Time courses of population responses, reliability, and expected behavioral performance in a simple detection task with 1 target contrast. A: red solid curve, normalized fitted response to 5% target contrast in the example experiment taken from Fig. 3C. Red dashed curve, estimated response SD on the same normalized scale. B: red solid curve, time course of instantaneous (single-frame) d′ based on the normalized mean and SDs from A. C: red solid curve, time course of the summed normalized responses from A. Red thick dashed curve, time course of the SD of the summed responses. Red thin dashed curve, expected SD of the summed responses if responses were temporally independent. D: red solid curve, time course of d′ of the summed response based on the mean and SDs in C. Thin red solid curve, expected time course of d′ of the summed responses if responses were independent over time. E: red solid curve, time course of expected error rate in the detection of the target based on the summed responses. Thin red solid curve, time course of the expected error rate based on the summed responses if responses were independent over time. F: causal decorrelation or whitening filter that when convolved with the responses in single trials, produces responses that are independent over time (see METHODS). Blue curves in A–E, same as red curves except that they are for signals after applying the whitening filter. Green curves in D and E, time course of d′ and error rate based on whitened responses that are summed with optimal weights (weights that are proportional to the time course of d′ of the whitened signals in B). Dotted horizontal line indicates maximal instantaneous d′ value in B and D and the corresponding error rate in E.
When detecting a weak signal that is embedded in noise, performance could potentially be improved by summing the neural responses over time. Figure 6C shows the time course of the mean (solid red curve) and SD (thick dashed red curve) of the summed responses from Fig. 6A. The thick red curve in Fig. 6D shows the time course of d′ for the summed responses. Surprisingly, the maximum value of d′ for the summed responses does not reach the maximum value of d′ for the single frames (the dotted horizontal lines in Fig. 6, B and D). Therefore the error rate based on the summed responses (thick red curve in Fig. 6E) never reaches the error rate that can be attained by considering a single frame during the sustained response in Fig. 6B (indicated by the dotted horizontal line in Fig. 6E).
Why does performance not improve with summation of the neural responses? The answer is the temporal correlations (Fig. 4, D and E). To see this, consider what would be the effect of summation if the responses were statistically independent across frames. In this case, the SD of the summed response would increase at a much slower rate than observed, in proportion to the square root of the number of frames (thin dashed red curve in Fig. 6C). The more rapid increase in the SD for the actual data dramatically reduces the reliability of the summed responses relative to what it would have been had the response been statistically independent in time (compare thick and thin red curves in Fig. 6, D and E). Thus the temporal correlations severely limit the benefit that can be attained by summing V1 signals over time.
The results of the preceding analysis demonstrate that the temporal correlations in V1 are potentially detrimental to performance in detection tasks. Could processing stages subsequent to V1 reduce (or eliminate) the detrimental effects of these temporal correlations, and, if so, how? The temporal correlations could be removed by applying a decorrelation (whitening) filter, which produces responses that are independent across frames. By analyzing the measured temporal correlation function (Fig. 4D), we derived a causal filter that removes the correlations in the V1 responses (see METHODS). This whitening filter is shown in Fig. 6F; it has a sharp positive peak immediately followed by a slightly smaller and slightly longer lasting negative peak. Such a filter could be implemented biologically with rapid excitation followed by time-lagged inhibition.
The consequences of the whitening filter are shown by the solid and dashed blue curves in Fig. 6A. As can be seen, the whitening operation emphasizes the transients at response onset relative to the sustained responses and it increases the relative magnitude of the SD of the response. As a result, the d′ values for the single fames following whitening fall below those without whitening (blue curve in Fig. 6B). However, the whitening filter does improve the reliability of the summed response (blue curves in Fig. 6, D and E), thus demonstrating that a simple biologically plausible whitening operation could reduce the detrimental effects of the temporal correlations in V1.
Although whitening prior to summation can improve performance, simple summation is not the optimal way to pool the whitened signals over time because it assigns equal weights to intervals in which there is strong and reliable signal (such as during response onset) and intervals in which there is weak or less reliable response (such as during the sustained response). The optimal way to pool whitened signals is linear summation with weights that are proportional to the mean (whitened) response (see Chen et al. 2006) (see also supplementary materials). Using these optimal weights, d′ will increase according to the well-known formula (Green and Swets 1966)
| (1) |
The values of d′ based on the optimally pooled responses are shown as the green curve in Fig. 6D. These values increase more rapidly than the values of the simple summed whitened signals. When the whitened signals are summed optimally, the error rate drops to <8% in the first 150 ms and then continues to drop at a slower rate, reaching an error rate of <4% at the end of the accumulation period (green curve in Fig. 6E). Notice, however, that even with optimal pooling, performance falls far short of what would be possible if the responses were statistically independent over time. In other words, the temporal correlations have a detrimental effect that cannot be entirely overcome.
Importantly, the performance obtained with both simple and optimal summation of the whitened responses shows that due to the nature of the temporal correlations there is more information per unit time in the first 150 ms of the response than later in the response (see DISCUSSION). Note, however, that there is information to be gained even after the first 150 ms. Whether it is advantageous to continue integrating information beyond the initial period depends on the specific speed-accuracy tradeoff selected by the animal.
Optimal temporal pooling in reaction time detection tasks
In the previous section, we considered the implications of our physiological measurements for a simplified detection task. The actual task that the monkey performed was more complicated in two ways. First, there was uncertainty about the contrast of the target, which could take on several values (4 – 6 contrast levels, depending on the experiment). Second, the monkey was free to respond at any point in time ≤600 ms following target onset. The fact that the monkeys’ reaction times varied from trial to trial and depended on target contrast suggests that the monkeys were dynamically evaluating the sensory signals and deciding, on a moment-by-moment basis, if and when to respond. The primary goal of this section is to derive the optimal dynamic pooling model for this more complicated reaction time detection task and to use it to evaluate how the information relevant for the task evolves over time. The secondary goal is to compare the performance of the optimal decoder with the performance of the monkey, both in terms of accuracy and in terms of speed (reaction times).
Plausible models for decoding sensory responses in reaction time tasks require dynamic decision variables. The standard framework for such models (e.g., Edwards 1965; Gold and Shadlen 2007; Luce 1986; Ratcliff and Rouder 1998; Ratcliff and Smith 2004; Smith 2000; Stone 1960; Swets and Green 1961; Usher and McClelland 2001) is shown in Fig. 7. At each time step T (an imaging frame in our case), the decision variable is compared with a criterion. If the decision variable exceeds the criterion, the model reports “target present.” If the decision variable does not exceed the criterion, time is incremented (T = T + 1), the decision variable is updated and reevaluated against the criterion, and so on, until a response is initiated or the maximal allowable evaluation time is reached. If the criterion is not reached before the maximal evaluation time, then the model reports “target absent.”
FIG. 7.
Schematic diagram of a general framework for dynamic decoding models that could explain behavioral performance in reaction-time detection tasks. See text for additional details.
The critical component of the optimal dynamic pooling model is the decision variable. Under some circumstances, the optimal decision variable is a simple sum or a difference of sums (Gold and Shadlen 2002; also see DISCUSSION and supplementary materials). However, given the nature of our task and the observed properties of the neural population responses, simple summation is highly inefficient (Fig. 6). To be optimal in our task, the decision variable must reflect several factors including: the shape of the temporal response profile, the effect of contrast on response latency, the nature of the variance and the temporal correlations in the neural responses, and the trial-to-trial uncertainty about the target contrast.
The optimal temporal decoder takes all these factors into account by computing the dynamic posterior probability of each possible stimulus given the observed neural responses. In detection tasks, the optimal decoder would report that the target is present if its posterior probability exceeds a criterion. In our task, in each target-present trial the target was randomly selected from one of four to six contrast levels, and the monkey was trained to report target present for any of those contrasts. Accordingly, the optimal model should trigger a target-present response when the posterior probability that a target is present, or equivalently, that the stimulus is not a blank, exceeds the criterion. The proper value for the criterion depends on the costs and benefits assigned to the accuracy and speed of the responses.
Using Bayes’ rule, the posterior probably that the stimulus is from category i after T frames is given by
| (2) |
where pi(0) is the prior probability of category i and p[X(1), …, X(T)|i] is the likelihood of the neural response from stimulus onset up to frame T given that the category is i. For our task, the prior probability of a blank p0(0) is 0.5, and the prior probability of the ith target contrast pi(0) is 0.5/n, where n is the number of possible target contrasts. The optimal strategy is therefore to trigger a ‘target-present response’ at frame T if 1 − p0(T) > criterion.
To evaluate Eq. 2, we need to calculate the likelihoods p[X(1), …, X(T)|i]. If the neural responses were statistically independent in time, then this is simply the product of the likelihoods at each frame. However, we observed strong temporal correlations in V1 population responses (Fig. 4, D and E). We therefore removed the effect of these temporal correlations by using the decorrelation operation as the first step in evaluating the likelihoods. Once the neural responses have been whitened, Eq. 2 reduces to the following, given that the distribution of the neural responses is approximately Gaussian (Chen et al. 2006)
| (3) |
where Y(t) is the whitened response at time t, μ0(t) is the average whitened response to a blank stimulus, μi(t) is the average whitened response to the ith contrast.
Using Eq. 3, we found that the average posterior probability of target present increased rapidly following target onset at all target contrasts other than the lowest, and decreased rapidly in blank trials (Fig. 8A). We selected an upper criterion on the posterior probability that maximized accuracy (horizontal black line, Fig. 8, A and B). The posterior probability in six example individual trials exceeded the criterion in all target-present trials, but not in the blank trial (Fig. 8B). The dynamic posterior probabilities for each possible target contrast were highly sensitive to small changes in the neural response, particularly around the time of response onset (Supplementary Fig. 4).
FIG. 8.
Performance of the optimal Bayesian temporal decoder in the example experiment. A: the posterior probability that the target is present as a function of time averaged across all trials of a given contrast. The average posterior probability is terminated at the median reaction time in conditions with ≥4 hits. Horizontal black line indicates the criterion that maximizes accuracy. The overall accuracies of the monkey and the optimal decoder are indicated in the panel. B: posterior probability as a function of time for 6 individual trials. All trials are classified correctly by the model. The optimal decoder “detected” the target in all target-present trials and made no “false alarm” in the target-absent trial (red curve). C: proportion of trials in which the subject (monkey or optimal decoder) reported that the target was present as a function of target contrast. Same conventions as in Fig. 2A. D: mean ± SD of reaction times of the subject (monkey or optimal decoder) as a function of target contrast. Same conventions as in Fig. 2B.
The optimal temporal pooling model performed significantly better than the monkey in the example experiment (96% correct vs. 77% correct for the monkey; P < 0.001). In addition, the neurometric function of the optimal temporal pooling model (Fig. 8C, blue curve) had a significantly lower threshold than the monkey (threshold = 2.6% for the model, threshold = 4.8% for the monkey; P < 0.001). Finally, the reaction times of the optimal temporal pooling model were much faster, on average, than the monkey’s reaction times (Fig. 8D).
The average accuracy of the optimal temporal pooling model across all eight experiments was significantly higher (Fig. 9A) and the average threshold significantly lower (Fig. 9B) than those of the monkeys. The accuracy of the optimal temporal pooling model can be improved further (by 1.2% on average) by combining signals over space using the optimal spatial pooling rule (Chen et al. 2006) rather than averaging the signals in a 1.0 mm2 region (Supplementary Fig. S5).
FIG. 9.
Comparison of the performance of the optimal decoder and the running integrator model with the performance of the monkey across all 8 experiments. A: average ± SE of the difference in accuracy between the monkey and the 2 models. Asterisks indicate significance. B: scatter plot of the monkeys’ thresholds vs. the optimal decoder’s thresholds. Filled symbols represent experiments in which the threshold of the monkey and the model were significantly different. P value indicates significance of difference in mean threshold between the monkeys and the optimal decoder (paired t-test, n = 8). C: average ± SE of reaction times of the monkey and the models combined across all 8 experiments. D: temporal weighting function for the running integrator model (see text for details).
In addition, the average reaction time of the optimal temporal pooling model was much shorter than the average reaction time of the monkey at all target contrasts (Fig. 9C), indicating that neural population responses provide reliable information that could guide behavior even in brief temporal intervals (the average reaction time of the optimal model across all target contrasts was 104 ms). Similar to the monkeys reaction times, the mean of the model’s reaction time increases with decreasing target contrast (Fig. 9C). However, the reaction time increases at a faster rate for the monkey than for the model.
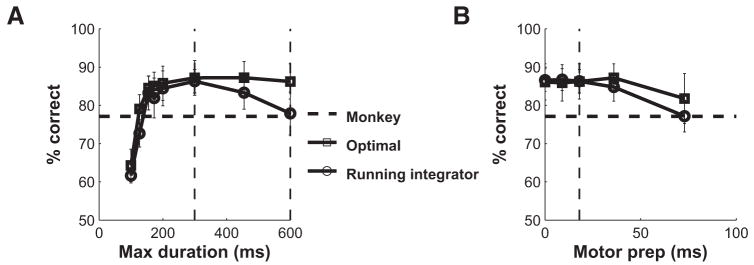
An important issue is the extent to which our assumptions about the temporal evaluation interval influence the performance of the optimal decoder (see METHODS). Shortening the maximal evaluation interval down to 200 ms and increasing the motor preparation time up to 36 ms had little effect on the accuracy of the optimal decoder (Fig. 10). Motor preparation times longer than 36 ms led to a drop in the performance of the optimal decoder mainly due to a drop in performance at the high contrast conditions, where reaction times were extremely short.
FIG. 10.
Effect of the evaluation interval on the mean and SE of the accuracy of the temporal pooling models across the 8 experiments. A: effect of maximal evaluation duration. B: effect of motor preparation time. Dashed vertical lines in A and B represent default values.
DISCUSSION
The goals of the current study were threefold: to characterize the temporal properties of V1 population responses, to derive the optimal Bayesian temporal decoder for detecting the target from the measured neural responses in our reaction-time task, and to compare the speed and accuracy of the optimal decoder with those of the monkey. We find that the variability in V1 population responses is highly correlated over time. The detrimental effect of these correlations on temporal pooling can be minimized by a simple temporal decorrelation operation (whitening) with time-lagged excitation and inhibition. We find that simple decoding models that accumulate the sensory information over time are highly inefficient (Fig. 6, D and E). Optimal decoding is achieved by combining a whitening operation with a posterior probability calculation in which the probability that the target is present is dynamically computed based on the incoming sensory information. The optimal decoder performed much better than the monkey, which implies that there are substantial losses of target-related information downstream to the neural signals we measured in V1.
Ongoing activity and temporal correlations in V1
Our finding of significant temporal correlations in the population responses is consistent with previous VSDI studies that showed large and slow varying ongoing activity in the visual cortex of anesthetized cats (Arieli et al. 1996). The temporal correlations in our measurements appear to decay more rapidly than in these previous studies and they asymptote at a positive level (Fig. 4, D and E), but these differences could be related to the specific methods used for removing the nonneural sources of noise (see Supplementary Fig. S1). The main difference between the previous and current findings is the relative magnitudes of the ongoing activity and the stimulus-evoked response. In the anesthetized cat, the SD of the ongoing activity was comparable to the amplitude of the response evoked by a high contrast stimulus (amplitude/SD ratio ≅ 1.0). However, in our experiments, the SD of the ongoing activity was typically much smaller than the amplitude of the response evoked by a medium or low contrast stimulus (e.g., mean amplitude/SD ratio = 3.8 ± 1.0 at 25% contrast, n = 8). These differences cannot be attributed to the different procedures for removal of nonneural sources of noise used in the two studies (see Supplementary Fig. S1). Our results, therefore suggest that the impact of variable ongoing activity on sensory perception may be significantly weaker than expected based on studies in anesthetized cats.
Time course of neural detection sensitivity
Application of the optimal decoder to the measured V1 responses shows that the neural information relevant for target detection is concentrated in the initial response following stimulus onset; optimal integration of responses beyond the first 150 ms results in a much slower improvement in performance (green curves in Fig. 6, D and E). This result is consistent with previous studies (e.g., Frazor et al. 2004; Muller et al. 2001; Osborne et al. 2004; Thorpe et al. 1996; Uka and DeAngelis 2003). There are at least two reasons why the rate of improvement in performance can be most rapid shortly after response onset. First, the rate of information accumulation will obviously be more rapid in the first 150 ms if the responses are transient (assuming constant noise or variance proportional to the mean). Second, as demonstrated here (Fig. 6, D and E), the rate of information accumulation could be more rapid at response onset, even if the responses are not transient, because of the temporal correlations (Fig. 4, D and E). If the responses were statistically independent over time, performance would increase at the same rate throughout the period of sustained activity (thin red curves in Fig. 6, D and E). It may seem puzzling that information is concentrated in the onset of the response given that the response is sustained and that the temporal correlation is constant over time. This occurs because response onset contains high temporal frequencies and most of the power in the correlated noise is in the low temporal frequencies.
Why are the monkeys performing suboptimally?
Surprisingly, we find that it is possible to substantially outperform monkeys in detection tasks (in both speed and accuracy) using neural population responses recorded from the monkeys’ primary visual cortex. This implies that there are inefficiencies either at or subsequent to V1 that limit the monkeys’ behavioral performance. There are many possible sources for such inefficiencies: 1) variability in the monkey’s level of motivation, 2) subsequent processing stages at or downstream to V1 may add neural noise or lose signal, 3) subsequent processing stages may be optimized for many different tasks and hence are suboptimal for our specific task, 4) subsequent motor stages may require significantly more preparation time than we assumed, 5) and the optimal Bayesian decoder may be too complicated to implement biologically.
Careful analysis of behavioral performance in this task suggests that the monkeys were highly motivated and performed at their perceptual limit (for details, see Chen et al. 2006). Therefore variability in the monkey’s motivation is unlikely to be an important factor.
VSDI signals contain a significant contribution from sub-threshold neural responses; therefore, it is likely that some of the measured responses were not transmitted from V1 because of thresholding in the process of spike generation. However, it is important to keep in mind that the subthreshold signals we measured are dominated by activity in the superficial layers. Thus these signals are likely to be a product of spiking activity in the deeper layers of V1.
In addition, there are many stages of processing downstream from V1, and each may contribute in a complicated way to behavioral performance in our detection task. Thus to fully evaluate the sources (2) and (3) would require measuring and analyzing task-related information in the population responses of the key subsequent processing stages.
With respect to source (4), motor preparation times of up to 36 ms have no impact on the performance of the optimal decoder (Fig. 10B). It is unlikely that the motor preparation time is significantly longer than 40 ms because the monkeys’ reaction times at the 25% contrast targets were often extremely short (Fig. 2C). The reason that reaction times were so short is that the target location and onset time were fixed, thus allowing the monkey to prepare motor responses in advance (Fischer and Boch 1983; Rohrer and Sparks 1993).
With respect to source (5), recall that the optimal Bayesian decoder in our detection task keeps track of the posterior probability of each possible target contrast over time. Although not explicit in Eq. 3, this can be accomplished by keeping a separate temporally weighted sum of the response for each possible target contrast, applying an accelerating nonlinearity to each sum, and then applying a divisive normalization. Although each one these steps could be implemented with known neural mechanisms, it is an open question as to whether the brain could combine them all in this task. However, as we show in the following text, in our task a significantly simpler decoding strategy can approach the performance of the optimal decoder, indicating that the complexity of the decoding strategy is unlikely to be the source of the monkeys’ behavioral inefficiency.
Nonoptimal decoding strategies
The Bayesian ideal observer approach has three key benefits: 1) it tells us what factors need to be considered and how best to take them into account, 2) it allows us to determine what aspects of the computation are most important for efficient performance, and 3) it provides a benchmark against which to evaluate other decoding strategies. There are two aspects of the neural responses in our task that may allow a much simpler temporal pooling mechanism to reach near-optimal performance. First, as shown in Fig. 6, D and E, target-related information is concentrated in the initial transient response. Second, the shape of the response profile remains invariant with contrast, with only a 20 –30-ms variation in latency (e.g., Fig. 3, C and D). Given these two constraints, one should, in principle, be able to approach ideal performance by following a whitening operation with a single running integrator that matches the shape of the transient response. The output of this single running integrator would be the decision variable; in other words, in this case, there would be no need to keep track of multiple separate templates and to compute a separate weighted sum for each possible target contrast. Figure 9D shows the shape of the temporal weighting function for a running integrator that integrates over a period of 100 ms. This weighting function is simply the initial 100 ms of the d′ function of the whitened response (see blue curve in Fig. 6B). Figure 9, A and C, shows the performance of this running integrator model with a maximum evaluation time of 300 ms. This running integrator is performing almost as well as the optimal in both accuracy and speed. Extending the evaluation period beyond 300 ms leads to a drop in performance (Fig. 10A) because the running integrator has a limited memory (100 ms) and because most of the stimulus-related information is contained in the initial period after stimulus onset (Fig. 6D). The near-optimal performance of the running integrator shows that the inefficiency of the monkey in the detection task is not due to the computational complexity of approximating the optimal Bayesian decoder.
Although this simple running integrator performs near optimal in our task, this will not generally be the case. For example, if the shapes of the temporal response profiles and/or the response latencies were more dependent on the stimulus, then a single running integrator would fall short of optimal by a greater amount. Similarly, if the speed-accuracy tradeoff of the subject places more weight on accuracy than on speed, then the running integrator will perform relatively poorly. Specifically, as the desired level of accuracy increases, the difference in the speed of the ideal and the running integrator will increase.
Importantly, we note again that the goal of deriving and evaluating the optimal Bayesian decoder and the simple running integrator is to characterize the nature and quality of signals in V1 and to determine what computations would be most appropriate for reading out these signals in detection tasks. While it would certainly be possible to approximate the monkeys’ accuracy and reaction times by adding hypothetical post-V1 processing stages to our analysis of V1 responses, we do not believe that this would be a useful exercise without additional constraints. Such constraints could be provided by measurements from subsequent processing stages while monkeys perform detection tasks.
Other applications of optimal neural decoding
The previous section described how, in our experiment, the optimal decoder could be approximated by a simpler decoding strategy. Here we discuss other situations under which the dynamic posterior probability reduces to, or can be approximated by, a simpler decision variable. For example, in our previous study of optimal spatial pooling (Chen et al. 2006), we used a linear spatial summation rule to detect the target. In the supplementary materials, we show that under the specific circumstances that apply in our spatial pooling analysis, a linear summation rule can provide a good approximation to the posterior probability calculation.
Another example is a recent study by Gold and Shadlen (2002) in which they considered possible neural mechanisms for discriminating between two opposite directions of motion in dynamic random dot displays. Gold and Shadlen demonstrated that under certain conditions, the dynamic posterior probability calculation reduces to accumulating the difference between the responses of two neurons (or pools of neurons) with opposite preferred directions. The conditions under which this simplification applies, however, are quite limited: the task must include only two alternatives and there must be no other uncertainty regarding the stimulus, the neural response must have constant mean amplitude over time and be statistically independent over time, and there must exist neurons with exactly opposite tuning properties with respect to the relevant stimulus dimension.
In general, neural responses to sensory stimuli are time varying and show significant correlations over time as demonstrated by our results and by previous findings (Arieli et al. 1996; Bair et al. 2001; Osborne et al. 2004; Uka and DeAngelis 2003). Furthermore, in many tasks including all detection tasks, populations of neurons with opposite tuning properties are not likely to exist. For example, neurons throughout the visual system exhibit responses that are monotonically increasing with stimulus contrast and no “opposite” neurons (responses monotonically decreasing with stimulus contrast) have been found. Finally, most natural tasks involve significant uncertainty regarding some aspects of the stimulus. These considerations suggest that in most realistic natural tasks, the posterior probability calculation cannot be reduced to a simple accumulation of differences in neural responses.
Conclusions
In conclusion, we have analyzed the dynamic properties of neural population responses in V1 during a reaction-time detection task. We find that the noise in the neural population response is additive and highly correlated over time. As a result, target-related information is concentrated in the onset of the response, and simple accumulator models are highly inefficient. The detrimental effects of the temporal correlation can be minimized by a whitening operation that could be implemented with simple time-lagged excitation and inhibition. We derived the optimal Bayesian decoder, which combines the whitening operation with a dynamic posterior probability calculation, and found that it performs much better than the monkey in both speed and accuracy. Finally, we find that a running integrator, preceded by the whitening operation, can approach the performance of the optimal decoder, implying that the inefficiency of the monkey cannot be explained by the computational complexity of approximating the optimal temporal decoder. A simple running integrator will not be optimal for all tasks. On the other hand, the optimal Bayesian temporal decoder presented here is generally optimal, and hence, can be used to motivate the formulation of candidate decoding strategies and to evaluate their efficiency for arbitrary reaction-time detection and discrimination tasks.
Supplementary Material
Acknowledgments
We thank M. Shadlen and J. Schall for comments on earlier version of this manuscript, W. Bosking, T. Matsui, C. Michelson, C. Palmer, Y. Sit, and Z. Yang for assistance with experiments and for discussions, and T. Cakic, C. Creeger, and M. Wu for technical support.
GRANTS
This work was supported by National Eye Institute Grants EY-016454 and EY-016752 to E. Seidemann and EY-02688 to W. S. Geisler and by a Sloan Foundation Fellowship to E. Seidemann.
Footnotes
The online version of this article contains supplemental data.
References
- Arieli A, Sterkin A, Grinvald A, Aertsen A. Dynamics of ongoing activity: Explanation of the large variability in evoked cortical responses. Science. 1996;273:1868–1871. doi: 10.1126/science.273.5283.1868. [DOI] [PubMed] [Google Scholar]
- Bair W, Zohary E, Newsome WT. Correlated firing in macaque visual area MT: time scales and relationship to behavior. J Neurosci. 2001;21:1676–1697. doi: 10.1523/JNEUROSCI.21-05-01676.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carpenter RHS. Contrast, probability, and saccadic latency: Evidence for independence of detection and decision. Curr Biol. 2004;14:1576–1580. doi: 10.1016/j.cub.2004.08.058. [DOI] [PubMed] [Google Scholar]
- Chen Y, Geisler WS, Seidemann E. Optimal decoding of correlated neural population responses in the primate visual cortex. Nat Neurosci. 2006;9:1412–1420. doi: 10.1038/nn1792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cook EP, Maunsell JHR. Dynamics of neuronal responses in macaque MT and VIP during motion detection. Nat Neurosci. 2002;5:985–994. doi: 10.1038/nn924. [DOI] [PubMed] [Google Scholar]
- DeAngelis GC, Ghose GM, Ohzawa I, Freeman RD. Functional micro-organization of primary visual cortex: receptive field analysis of nearby neurons. J Neurosci. 1999;19:4046–4064. doi: 10.1523/JNEUROSCI.19-10-04046.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards W. Optimal strategies for seeking information: models for statistcs, choice reaction times and human information processing. J Math Psychol. 1965;2:312–329. [Google Scholar]
- Efron B, Tibshirani RJ. An Introduction to the Bootstrap. London: Chapman and Hall; 1993. [Google Scholar]
- Fischer B, Boch R. Saccadic eye movements after extremely short reaction times in the monkey. Brain Res. 1983;260:21–26. doi: 10.1016/0006-8993(83)90760-6. [DOI] [PubMed] [Google Scholar]
- Frazor RA, Albrecht DG, Geisler WS, Crane AM. Visual cortex neurons of monkeys and cats: temporal dynamics of the spatial frequency response function. J Neurophysiol. 2004;91:2607–2627. doi: 10.1152/jn.00858.2003. [DOI] [PubMed] [Google Scholar]
- Geisler WS, Albrecht DG. Visual cortex neurons in monkeys and cats: detection, discrimination, and identification. Visual Neurosci. 1997;14:897–919. doi: 10.1017/s0952523800011627. [DOI] [PubMed] [Google Scholar]
- Gold JI, Shadlen MN. Neural computations that underlie decisions about sensory stimuli. Trends Cognit Sci. 2001;5:10–16. doi: 10.1016/s1364-6613(00)01567-9. [DOI] [PubMed] [Google Scholar]
- Gold JI, Shadlen MN. Banburismus and the brain: decoding the relationship between sensory stimuli, decisions, and reward. Neuron. 2002;36:299–308. doi: 10.1016/s0896-6273(02)00971-6. [DOI] [PubMed] [Google Scholar]
- Gold JI, Shadlen MN. The neural basis of decision making. Annu Rev Neurosci. 2007;30:535–574. doi: 10.1146/annurev.neuro.29.051605.113038. [DOI] [PubMed] [Google Scholar]
- Green DM, Swets JA. Signal Detection Theory and Psychophysics. New York: Wiley; 1966. [Google Scholar]
- Grinvald A, Hildesheim R. VSDI: a new era in functional imaging of cortical dynamics. Nat Rev Neurosci. 2004;5:874–885. doi: 10.1038/nrn1536. [DOI] [PubMed] [Google Scholar]
- Grinvald A, Shoham D, Shmuel A, Glaser DE, Vanzetta I, Shtoyerman E, Slovin H, Wijnbergen C, Hildesheim R, Sterkin A, Arieli A. In-vivo optical imaging of cortical architecture and dynamics. In: Windhorst U, Johansson H, editors. Modern Techniques in Neuroscience Research. New York; Springer: 1999. pp. 893–969. [Google Scholar]
- Hubel DH, Wiesel TN. Uniformity of monkey striate cortex: a parallel relationship between field size, scatter and magnification factor. J Comp Neurol. 1974;158:295–306. doi: 10.1002/cne.901580305. [DOI] [PubMed] [Google Scholar]
- Huk AC, Shadlen MN. Neural activity in macaque parietal cortex reflects temporal integration of visual motion signals during perceptual decision making. J Neurosci. 2005;25:10420–10436. doi: 10.1523/JNEUROSCI.4684-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luce RD. Response Times: Their Role in Inferring Elementary Mental Organization. London: Oxford; 1986. [Google Scholar]
- Mazurek ME, Roitman JD, Ditterich J, Shadlen MN. A role for neural integrators in perceptual decision making. Cereb Cortex. 2003;13:1257–1269. doi: 10.1093/cercor/bhg097. [DOI] [PubMed] [Google Scholar]
- McIlwain JT. Point images in the visual system: new interest in an old idea. Trends Neurosci. 1986;9:354–358. [Google Scholar]
- Muller JR, Metha AB, Krauskopf J, Lennie P. Information conveyed by onset transients in responses of striate cortical neurons. J Neurosci. 2001;21:6978–6990. doi: 10.1523/JNEUROSCI.21-17-06978.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osborne LC, Bialek W, Lisberger SG. Time course of information about motion direction in visual area MT of macaque monkeys. J Neurosci. 2004;24:3210–3222. doi: 10.1523/JNEUROSCI.5305-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quick RF., Jr A vector-magnitude model of contrast detection. Kybernetik. 1974;16:65–67. doi: 10.1007/BF00271628. [DOI] [PubMed] [Google Scholar]
- Ratcliff R. Putting noise into neurophysiological models of simple decision making. Nat Neurosci. 2001;4:336–336. doi: 10.1038/85956. [DOI] [PubMed] [Google Scholar]
- Ratcliff R, Rouder JN. Modeling response times for two-choice decisions. Psychol Sci. 1998;9:347–356. [Google Scholar]
- Ratcliff R, Smith PL. A comparison of sequential sampling models for two-choice reaction time. Psychol Rev. 2004;111:333–367. doi: 10.1037/0033-295X.111.2.333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rohrer WH, Sparks DL. Express saccades: the effects of spatial and temporal uncertainty. Vision Res. 1993;33:2447–2460. doi: 10.1016/0042-6989(93)90125-g. [DOI] [PubMed] [Google Scholar]
- Roitman JD, Shadlen MN. Response of neurons in the lateral intraparietal area during a combined visual discrimination reaction time task. J Neurosci. 2002;22:9475–9489. doi: 10.1523/JNEUROSCI.22-21-09475.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schall JD, Thompson KG. Neural selection and control of visually guided eye movements. Annu Rev Neurosci. 1999;22:241–259. doi: 10.1146/annurev.neuro.22.1.241. [DOI] [PubMed] [Google Scholar]
- Seidemann E, Arieli A, Grinvald A, Slovin H. Dynamics of depolarization and hyperpolarization in the frontal cortex and saccade goal. Science. 2002;295:862–865. doi: 10.1126/science.1066641. [DOI] [PubMed] [Google Scholar]
- Shoham D, Glaser DE, Arieli A, Kenet T, Wijnbergen C, Toledo Y, Hildesheim R, Grinvald A. Imaging cortical dynamics at high spatial and temporal resolution with novel blue voltage-sensitive dyes. Neuron. 1999;24:791–802. doi: 10.1016/s0896-6273(00)81027-2. [DOI] [PubMed] [Google Scholar]
- Smith PL. Stochastic dynamic models of response time and accuracy: a foundational primer. J Math Psychol. 2000;44:408–463. doi: 10.1006/jmps.1999.1260. [DOI] [PubMed] [Google Scholar]
- Smith PL, Ratcliff R. Psychology and neurobiology of simple decisions. Trends Neurosci. 2004;27:161–168. doi: 10.1016/j.tins.2004.01.006. [DOI] [PubMed] [Google Scholar]
- Stone M. Models for choice reaction time. Psychometrika. 1960;25:251–260. [Google Scholar]
- Swets JA, Green DM. Sequential observations by human observers of signals in noise. In: Swets JA, editor. Signal Detection and Recognition by Human Observers: Contemporary Readings. New York: Wiley; 1961. pp. 221–242. [Google Scholar]
- Thorpe S, Fize D, Marlot C. Speed of processing in the human visual system. Nature. 1996;381:520–522. doi: 10.1038/381520a0. [DOI] [PubMed] [Google Scholar]
- Tolhurst DJ, Movshon JA, Dean AF. The statistical reliability of Signals in single neurons in cat and monkey visual cortex. Vision Res. 1983;23:775–785. doi: 10.1016/0042-6989(83)90200-6. [DOI] [PubMed] [Google Scholar]
- Uka T, DeAngelis GC. Contribution of middle temporal area to coarse depth discrimination: comparison of neuronal and psychophysical sensitivity. J Neurosci. 2003;23:3515–3530. doi: 10.1523/JNEUROSCI.23-08-03515.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Usher M, McClelland JL. The time course of perceptual choice: the leaky, competing accumulator model. Psychol Rev. 2001;108:550–592. doi: 10.1037/0033-295x.108.3.550. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.