A CARTILAGE GROWTH MIXTURE MODEL WITH COLLAGEN REMODELING: VALIDATION PROTOCOLS

Stephen M Klisch; Anna Asanbaeva; Sevan R Oungoulian; Koichi Masuda; Eugene J-MA Thonar; Andrew Davol; Robert L Sah

doi:10.1115/1.2907754

. Author manuscript; available in PMC: 2009 Jun 8.

Published in final edited form as: J Biomech Eng. 2008 Jun;130(3):031006. doi: 10.1115/1.2907754

A CARTILAGE GROWTH MIXTURE MODEL WITH COLLAGEN REMODELING: VALIDATION PROTOCOLS

Stephen M Klisch ^*, Anna Asanbaeva ^†, Sevan R Oungoulian ^*, Koichi Masuda ^#, Eugene J-MA Thonar ^#,⁺, Andrew Davol ^*, Robert L Sah ^†

PMCID: PMC2692927 NIHMSID: NIHMS115320 PMID: 18532855

Abstract

A cartilage growth mixture (CGM) model is proposed to address limitations of a model used in a previous study. New stress constitutive equations for the solid matrix are derived and collagen (COL) remodeling is incorporated into the CGM model by allowing the intrinsic COL material constants to evolve during growth. An analytical validation protocol based on experimental data from a recent in vitro growth study is developed. Available data included measurements of tissue volume, biochemical composition, and tensile modulus for bovine calf articular cartilage (AC) explants harvested at three depths and incubated for 13 days in 20% FBS and 20% FBS+β-aminopropionitrile. The proposed CGM model can match tissue biochemical content and volume exactly while predicting theoretical values of tensile moduli that do not significantly differ from experimental values. Also, theoretical values of a scalar COL remodeling factor are positively correlated with COL crosslink content, and mass growth functions are positively correlated with cell density. The results suggest that the CGM model may help to guide in vitro growth protocols for AC tissue via the a priori prediction of geometric and biomechanical properties.

Introduction

Articular cartilage (AC) has a poor intrinsic healing capacity likely related to its relatively low cellularity, metabolic activity, and avascularity [1]. Clinical repair strategies include the use of chondral or osteochondral autografts or allografts and tissue-engineered constructs, among others [2, 3]. The attainment of a number of specific design goals related to tissue composition, structure, and function may be critical to the development of a consistently successful strategy for the repair of AC defects. The long-term goal of the research proposed here is to develop continuum mechanics models of cartilage growth that may be used with experimental approaches to improve repair strategies.

Growth and remodeling are biological processes that, together, transform AC tissue in vivo or in vitro from one biomechanical state to another. Growth (or resorption) may be defined as a change in tissue size or geometry due to deposition (or removal) of material similar to that already present, while remodeling may be defined as a change in tissue composition and/or structure and, concomitantly, a change in mechanical properties [4, 5]. AC can be viewed as a composite material for which interstitial tissue growth must involve both growth and remodeling, since accretion of a single tissue component will change the overall tissue structure and mechanical properties. The term “growth” is used here to refer, collectively, to both growth and remodeling of individual constituents and the composite tissue either in vivo or in vitro.

The extracellular solid matrix (SM) of AC contains proteoglycans (PGs) and a crosslinked collagen (COL) network (Figure 1) that appear to be predominantly responsible for the functional mechanical properties of the SM [6-8] and have distinct mechanical roles. The PGs are aggregate molecules containing glycosaminoglycans (GAGs) that provide the tissue with a fixed charge density (FCD) that causes a swelling pressure that resists compressive loading [9, 10]. The crosslinked COL network resists the PG swelling pressure and provides the tissue with both tensile and shear stiffnesses and strengths [7, 11, 12].

The major components of the articular cartilage solid matrix: proteoglycans (PG), collagen (COL), and pyridinoline (PYR) crosslinks.

The general continuum mixture theory of growth used here has been previously developed [13-15] and used to propose specific cartilage growth mixture (CGM) models [5, 13, 16-18]. In an earlier study using AC explants [5], the theoretically predicted COL shear modulus was positively correlated with experimental measures of pyridinoline (PYR) crosslink content, in agreement with other studies that found mechanical properties to be correlated with crosslink content [19-21]. However, that earlier study [5] had three major limitations. First, the stress constitutive equations used for the PGCOL SM were not capable of accurately modeling the mechanical response of AC. In particular, a parameter study found that the CGM predictions are significantly different for different forms of the COL stress constitutive equation. The AC mechanical response is complex; both the Young's moduli and Poisson's ratios are strain-dependent, anisotropic, and bimodular (e.g., tensile values can be ∼ two orders of magnitude greater than compressive values) [22-30]. Second, the experimental data used to quantify growth parameters in the CGM model were limited. Since the data corresponded to explants harvested at distinct developmental stages (i.e., fetal, newborn, and adult), it was not possible to quantify the overall growth in tissue size since material regions were not tracked. Third, tensile properties were not considered, thereby preventing definitive conclusions regarding the role of COL remodeling during growth.

In recent years, there has been much interest in the development of continuum growth models for single constituents [31-38], mixtures [39, 40], and mixtures that employ a stress balance hypothesis [41-44]. However, little attention has been focused on protocols for measuring a comprehensive set of growth model parameters and developing validation analyses. The present study is aimed at developing a CGM model with COL remodeling and related analytical protocols that address model validation.

A key assumption that greatly simplifies the mechanical description of the tissue's biochemistry is the “stress balance hypothesis” between two growing elastic materials: the SM stress is equal to the sum of a COL network stress and a PG swelling stress generated by FCD. Of course, there are numerous COL types, PG types, and other microstructural features that affect the tissue's mechanical properties. However, there are no definitive results pertaining to the desired complexity of a tissue growth model: retaining too complex a model inhibits parameter estimation and model development whereas using an overly simplified model inhibits the ability to predict general trends.

In this study, it is hypothesized that: 1) a CGM model employing a PG-COL stress balance and COL remodeling can match tissue composition and volume while predicting tensile modulus for selected in vitro growth protocols; 2) a single scalar measure of COL remodeling can be correlated to experimental measures of crosslink content; and 3) the growth laws can be correlated to cell content. To address these hypotheses, new PG and COL stress constitutive equations are used that more accurately describe the mechanical behavior of the AC SM than the equations used in an earlier study [5]. An analytical protocol for model validation is developed that is based on a recent in vitro growth study [45] in which newborn bovine AC explants at three depths were incubated in 20% FBS and 20% FBS+β-aminopropionitrile (BAPN). Since BAPN inhibits PYR crosslink formation and has little to no effect on chondrocyte metabolism [46, 47], these experimental protocols produced a wide range in crosslink content without substantially altering metabolism that may be useful in obtaining statistical measures of the importance of COL remodeling in the CGM model.

The specific aims are to: 1) refine the CGM model to include COL remodeling and more accurate stress constitutive equations; 2) develop analytical protocols for model validation using experimental data; 3) test the hypotheses related to model validation; and 4) determine baseline (i.e. free-swelling) growth laws for the PGs and COLs.

Methods

Cartilage Growth Mixture (CGM) Model

Here, the CGM of [5] is extended to include COL remodeling and new stress constitutive equations. The CGM model employs a mixture of a water constituent and a growing SM with the following features. First, the SM is modeled as a mixture of two growing elastic materials, PG and COL, with distinct mechanical roles that are crucial to tissue function.¹ The PG and COL constituents are defined to include the constituents responsible for a FCD-induced swelling pressure and the network restraining this swelling pressure, respectively. Second, growth laws describe the amount and orientation of mass deposition for the PG and COL constituents. Third, these growth laws allow the PG and COL constituents to grow in a differential manner (i.e., at different rates of mass deposition/removal). Fourth, the intrinsic COL material properties may remodel during growth.

The analysis is limited to pre- and post-growth equilibrium states of unloaded AC SM elements because the experimental quantification of these states can be used to estimate the growth laws.² Furthermore, the analysis corresponds to the homogeneous growth of a SM element with homogeneous biomechanical properties in its reference configuration. Due to these assumptions and the equilibrium equations (discussed below), the SM element is stress-free in all unloaded configurations. In the experimental study, thin (∼ 0.25 – 0.4 mm) AC explants were harvested in an attempt to obtain nearly homogeneous growth and biomechanical properties; consequently, the AC explants are assumed to correspond to the homogeneous SM element.³

Kinematics

The superscripts p and c will be used to designate the PG and COL constituents, respectively. The configurations κ_R, κ_M, and κ_G specify unloaded stress-free configurations of the SM element before growth (κ_R), after mass deposition (κ_M), and after mass deposition and remodeling (κ_G). The model assumes an immobility constraint that holds during both mass deposition and remodeling: all of the PG and COL molecules are bound to the SM, so that their total deformation gradient tensors F^p and F^c are equal to the SM deformation gradient tensor F. Although not needed in this study, the CGM model also uses the constraint of solid-fluid intrinsic incompressibility [48-50].

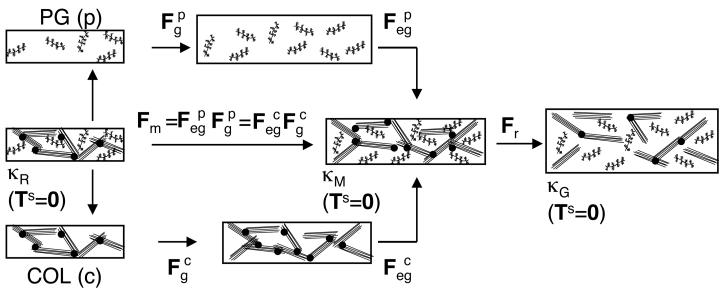
During growth and remodeling of an unloaded element, F is decomposed into a tensor F_m due to mass deposition and a tensor F_r due to COL remodeling (Figure 2):

F = F_{r} F_{m} .

(1)

The tensor F_m describes the evolution of the SM stress-free configuration, relative to κ_R, due to mass deposition. It is decomposed into constituent elastic and growth tensors; using the immobility constraint one obtains

F_{m} = F_{eg}^{p} F_{g}^{p} = F_{eg}^{c} F_{g}^{c} .

(2)

The growth tensors $F_{g}^{p}$ and $F_{g}^{c}$ describe the amount and orientation of PG and COL mass deposition; as seen below, their determinants can be determined from experimental mass measures. The elastic growth tensors $F_{eg}^{p}$ and $F_{eg}^{c}$ ensure continuity of the SM; as seen below, they can be determined from the equilibrium equations and the immobility constraint. The tensor F_r describes the change in the SM stress-free configuration, relative to κ_M, due to COL remodeling.⁴ Here, COL remodeling will be defined by7 allowing the intrinsic COL material properties to evolve during growth in a homogeneous manner. Since the SM element also is homogeneous, this results in a homogeneous F_r. Finally, a superposed elastic deformation F_l represents applied loading to κ_G (e.g., loading applied during mechanical testing). Consequently, the total elastic tensors of the PG and COL constituents ( $F_{e}^{p}, F_{e}^{c}$ ) are decomposed as

F_{e}^{p} = F_{l} F_{r} F_{eg}^{p}, F_{e}^{c} = F_{l} F_{r} F_{eg}^{c},

(3)

and the total deformation gradient tensor of the solid matrix can be represented as

F = F_{e}^{p} F_{g}^{p} = F_{e}^{c} F_{g}^{c} .

(4)

Kinematics of growth and remodeling for a homogeneous stress-free solid matrix (SM) element. F_m is the SM deformation gradient tensor due to mass deposition. The growth tensors $F_{g}^{p}$ and $F_{g}^{c}$ describe differential mass deposition of the PG (p) and COL (c) constituents. The elastic growth tensors $F_{eg}^{p}$ and $F_{eg}^{p}$ ensure continuity of the SM during mass deposition. F_r is the SM deformation gradient tensor due to COL remodeling.

A crucial assumption in the CGM model used here, which has been elaborated upon in [14, 17, 31], is needed to provide experimental prescriptions for the elastic and growth tensors: the mass density and stress functions are independent of the growth tensors $F_{g}^{p}$ and $F_{g}^{c}$ . Without remodeling, this assumption leads to experimental prescriptions for both the elastic and growth tensors via destructive experiments designed to relieve residual stresses [17], resulting in a “testable” theory. However, 1 with the remodeling feature presented here, those destructive experiments cannot distinguish between the elastic growth and remodeling tensors (i.e., $F_{eg}^{p}$ or $F_{eg}^{c}$ and F_r). An aim of this study is to show how experimental measurements of mass deposition and volume change, combined with accurate stress constitutive equations, can be used to theoretically distinguish among these various elastic tensors.

Balance Laws

Mass growth functions c^p and c^c that quantify the rate of mass deposition per unit current mass, having units of s⁻¹⁸, are introduced into the balance of mass; the resulting continuity equations are [14, 15]:

ρ^{p} J_{e}^{p} J_{g}^{p} = ρ_{R}^{p} \exp (\int_{τ = t_{0}}^{t} c^{p} d τ), ρ^{c} J_{e}^{c} J_{g}^{c} = ρ_{R}^{c} \exp (\int_{τ = t_{0}}^{t} c^{c} d τ),

(5)

where $ρ_{R}^{p}$ and $ρ_{R}^{c}$ are the apparent densities in κ_R, $J_{e}^{p} = \det F_{e}^{p}$ , $J_{e}^{c} = \det F_{e}^{c}$ , $J_{g}^{p} = \det F_{g}^{p}$ , $J_{g}^{c} = \det F_{g}^{c}$ , and det is the determinant operator. Upon assuming that the apparent densities are independent of the growth tensors and, consequently, $J_{g}^{p}$ and $J_{g}^{c}$ (as stated above), elastic continuity equations are obtained: $ρ^{p} J_{e}^{p} = ρ_{R}^{p}$ and $ρ^{c} J_{e}^{c} = ρ_{R}^{c}$ . Then, growth continuity equations are obtained from (5):

J_{g}^{p} = \exp (\int_{τ = t_{0}}^{t} c^{p} d τ), J_{g}^{c} = \exp (\int_{τ = t_{0}}^{t} c^{c} d τ) .

(6)

In this study, c^p and c^c are assumed to be constant with respect to time; consequently, (6) lead to

J_{g}^{p} = \exp (c^{p} Δ t), J_{g}^{c} = \exp (c^{c} Δ t),

(7)

where Δt is the time increment of growth. Since mass deposition takes place at constant apparent density and is assumed to be homogeneous, $J_{g}^{p}$ and $J_{g}^{c}$ can be calculated from experimental mass measurements as:

J_{g}^{p} = 1 + Δ m^{p} ∕ m_{o}^{p}, J_{g}^{c} = 1 + Δ m^{c} ∕ m_{o}^{c},

(8)

where $m_{o}^{p}$ , $m_{o}^{c}$ represent the initial masses and Δm^p, Δm^c represent the added (or resorbed) masses. It is emphasized that equations (7-8), which define the growth tensor determinants in terms of experimental mass measurements, are obtained only after assuming that the apparent densities are independent of the growth tensors.

Since the SM element is homogeneous and unloaded in κ_R, κ_M, and κ_G, the traction-free boundary condition on all surfaces and the equations of motion at equilibrium (i.e. divT^s = 0 are satisfied if the SM element is stress-free:

T^{s} = 0,

(9)

where div is the divergence operator, T^s is the solid matrix stress, T^s = T^p + T^c due to the stress balance hypothesis, and T^p and T^c are the PG and COL stresses.

Growth laws

To obtain a complete theory, growth response functions, i.e. the time-rate of changes $F_{g}^{p}$ and $F_{g}^{c}$ , are required. The results presented here are based on the assumption of isotropic growth⁵; isotropic growth tensors can be represented as

F_{g}^{p} = {[J_{g}^{p}]}^{1 ∕ 3} I, F_{g}^{c} = {[J_{g}^{c}]}^{1 ∕ 3} I,

(10)

where I is the identity tensor. The growth laws may depend on any of the primitive variables of the model; for example, they may depend on stress, strain, strain energy, the rate of strain, and interstitial fluid velocity. However, an aim of 1 this paper is to use experimental data to quantify (10) and, consequently, to estimate AC growth laws for specific in vitro protocols.

Following [14], growth laws Ġ^p and Ġ^c are used to describe growth relative to the current configuration, as opposed to the fixed reference configuration κ_R.⁶ In Eqn. 5.6 of [14], it was shown that c = Ġ·I for a growing elastic body; consequently, for isotropic growth one obtains:

{\dot{G}}^{p} = (1 ∕ 3) c^{p} I, {\dot{G}}^{c} = (1 ∕ 3) c^{c} I .

(11)

In [17], it was shown that for a growing elastic body ${\dot{F}}_{g} = F_{e}^{- 1} \dot{G} F_{e} F_{g}$ ; thus, the growth laws (11) can be expressed relative to κ_R as

{\dot{F}}_{g}^{p} = (1 ∕ 3) c^{p} F_{g}^{p}, {\dot{F}}_{g}^{c} = (1 ∕ 3) c^{c} F_{g}^{c} .

(12)

Stress constitutive equations

The stress constitutive equations used for the PG and COL constituents are discussed in detail in the Appendix; here, an overview is provided. Due to the assumption that the PG and COL stresses only depend on their respective elastic tensors, in addition to a COL stress dependence on a scalar remodeling factor χ, general stress constitutive equations are defined relative to κ_R:

T^{p} = {\hat{T}}^{p} κ_{R} (F_{e}^{p}), T^{c} = {\hat{T}}^{c} κ_{R} (χ, F_{e}^{c}) .

(13)

For the PG constituent, an isotropic polyconvex strain energy function is chosen with two material constants (α₁, α₂) that are specified relative to a PG reference configuration $κ_{o}^{p}$ that coincides with κ_R. Consequently, a PG stress equation (see A3) is obtained that represents the required function ${\hat{T}}^{p} κ_{R} (F_{e}^{p})$ of (13). Swelling pressure data for isolated PG solutions [52, 53] are used to determine (α₁, α₂) using a microstructural model that calculates an effective fixed charge density based on the two-compartment water (i.e., extra- and intra-fibrillar) model proposed in [10].

The COL stress equation is defined relative to a COL stress-free reference configuration $κ_{0}^{c}$ so that the COL network has a tensile pre-stress in κ_R that restrains the PG swelling pressure. The COL elastic swelling strain is represented by the deformation gradient tensor $F_{0}^{c}$ and maps $κ_{0}^{c}$ to κ_R. Thus, the COL stress function defined relative to κ_R is related to a COL stress function defined relative to $κ_{0}^{c}$ via the relation

{\hat{T}}^{c} κ_{R} (χ, F_{e}^{c}) = {\hat{T}}^{c} κ_{0} (χ, F_{e}^{c} F_{0}^{c}) \equiv {\hat{T}}^{c} κ_{0} (χ, F_{e 0}^{c})

(14)

where the definition $F_{e 0}^{c} = F_{e}^{c} F_{0}^{c}$ is used to simplify the presentation of the constitutive function T̂^c_κ0. The COL strain energy function W^c is based on a formulation recently used for the SM [54] and has the following features: 1) it is bimodular, i.e. individual strain energy terms are only mechanically active when corresponding fiber directions are in tension; 2) it is a polyconvex function of $F_{e 0}^{c}$ and satisfies material stability criteria; and 3) it includes “strong interaction terms” that facilitate modeling asymmetric strain dependent Poisson's ratios. Primary fiber families are aligned with the orthonormal basis vectors E₁ (parallel to the local split-line direction), E₂ (perpendicular to the split-line direction and parallel to the surface), and E₃ (perpendicular to the articular surface) (Figure 3). Strong interaction terms are generated by secondary fiber families in each of the three planes formed by the basis vectors. Three material constants (γ₁, γ₂, γ₃) represent strengths of corresponding primary fiber families and one material constant (δ) represents the strength of the secondary fiber families.

The coordinate system and experimental specimen orientations in relation to anatomical directions. The unit vector E₁ is parallel to the local split-line direction, the unit vector E₃ is perpendicular to the articular surface, and the unit vector E₂ is perpendicular to the split-line direction and parallel to the surface. The rectangular slices labeled S, M1, and M2 represent ∼0.4, 0.25, and 0.25 mm thick specimens used in the control and experimental groups.

COL remodeling is implemented by allowing the intrinsic COL material constants (γ₁, γ₂, γ₃, δ) to evolve during growth. Due to a lack of comprehensive mechanical property data, two simplifying assumptions are made. First, each of the COL material constants is multiplied by the same scalar remodeling factor χ. From a physiological perspective, χ should be related to one or more measures of the COL network microstructure (as discovered in the Results section). The remodeling factor χ=1 before growth and remodeling occur; thus, initial parameters (γ₁, γ₂, γ₃, δ) correspond to κ_R. Second, since only the tensile modulus in the 2-direction is available for this study, it is assumed that γ₂ = γ₁, γ₃, = 0.5γ₁, and δ = γ₁, while the orientations of the secondary fiber families are based a previous study [54]. These assumptions result in SM mechanical properties relative to κ_R that generally agree with other studies as discussed in the Appendix.

Experimental data

The experimental data was available from a previous study [45]. AC was harvested from the patellofemoral groove of five newborn bovine knees. Specimens from three successive layers (Figure 3) were prepared: (S) superficial layer ∼0.4 mm thick, including the intact articular surface; (M1) first middle zone layer ∼0.25 mm thick; and (M2) second middle zone layer ∼0.25 mm thick. The long axes of the blocks were in the anterior-posterior direction and, thus, approximately perpendicular to the split line direction. Blocks were initially weighed wet (WWI). Some blocks were analyzed immediately (day 0 control groups S-D0, M1-D0, M2-D0). Other blocks were incubated for 13 days in medium (DMEM supplemented with 20% fetal bovine serum (FBS) and 100 μg/mL of ascorbate; experimental groups S-FBS, 1 M1-FBS, M2-FBS) or medium with 0.1mM BAPN (experimental groups S-BAPN, M1-BAPN, M2-BAPN). At termination, blocks were weighed wet (WWF) and punched to form a tapered tensile test specimen oriented in the 2-direction. Tapered tensile specimens were tested (rate = 5 mm/min) and dynamic ramp modulus was calculated as the linear regression slope of the stress-strain curve from 25-75% of the maximum load. Since these destructive tests were performed in a previous study that did not measure equilibrium values, the dynamic moduli were scaled by factors based on more recent measurements of equilibrium and dynamic moduli [55]. Specifically, equilibrium secant tension moduli at 20% strain (i.e., equilibrium stress divided by 0.20) were estimated by multiplying the dynamic ramp moduli by 0.14, 0.14, and 0.19 for the S, M1, and M2 layers, respectively. Failed portions of the tensile specimen and residual cartilage were analyzed together to quantify DNA, GAG, COL, and PYR contents [45].

Parameter estimation

The five analysis steps used to quantify growth for each experimental group are illustrated in Figure 4. Since biomechanical and biochemical properties of an individual specimen in the experimental groups are only measured using destructive experiments in the grown configuration κ_G, it is not possible to define that specimen's reference configuration. Consequently, growth is analyzed in an averaged sense. The averaged values of the control (S-D0, M1-D0, M2-D0) and experimental (S-FBS, M1-FBS, M2-FBS, S-BAPN, M1-BAPN, M2-BAPN) groups (Table 1) are used to quantify growth. Reference configuration values of GAG and COL masses for the experimental groups are estimated by scaling the related masses of the control groups using the ratio of experimental to control group WWIs. These reference configuration values are estimated in a layer- and treatment-specific manner, resulting in a specific κ_R for each of the six experimental groups.

Steps in the analysis procedure to model the *in vitro* growth protocols. Step 1 defines the reference configuration by determining the SM material constants and the COL swelling strain $F_{o}^{c}$ . Step 2 determines the SM deformation gradient tensor due to mass deposition F_m. Steps 3 and 4 determine the SM deformation gradient tensor due to COL remodeling F_r needed to match final tissue volume. Step 5 determines the mechanical properties relative to the grown configuration by solving boundary-value problems defined by the applied SM deformation gradient tensor F₁.

Table 1.

Experimental values of initial tissue wet weight (WWI), % wet weight change during growth (% WW CHANGE), composition (GAG, COL, PYR/WWF; WWF is final tissue wet weight), and calculated equilibrium secant tensile modulus at 20% strain in the 2-direction. % WW CHANGE is the average of experimental values of WW change, and not the percent change in the average initial and final WWs. GAG, COL, and PYR measurements correspond to the WWF configuration. Values presented are mean ±1 standard deviation; n = 9-21 blocks from 5 animals.

GROUP (layer-treatment)	WWI (mg)	%WW CHANGE	GAG (mg)	COL (mg)	CELLS (million)	PYR/WWF (nmol/g)	MODULUS (MPa)
S-D0	8.6±0.2	N/A	0.25±0.06	0.71±0.33	1.22±0.43	91.5±30.5	1.01±0.3
S-FBS	7.0±0.1	73.1±20.9	0.35±0.12	0.67±0.37	0.96±0.34	71.2±47.5	0.46±0.2
S-BAPN	7.6±0.2	98.2±21.0	0.36±0.09	0.61±0.27	0.95±0.38	49.0±31.6	0.23±0.1
M1-D0	9.5±0.2	N/A	0.34±0.08	1.03±0.35	0.83±0.25	122.0±88.4	1.31±0.7
M1-FBS	6.8±0.2	45.4±13.5	0.35±0.12	0.85±0.24	0.64±0.30	113.3±133.7	0.69±0.3
M1-BAPN	7.1±0.2	54.0±18.8	0.34±0.16	0.72±0.29	0.58±0.35	61.9±13.9	0.31±0.1
M2-D0	8.3±0.1	N/A	0.31±0.04	1.11±0.33	0.75±0.25	137.1±125.4	2.54±0.8
M2-FBS	7.1±0.1	38.2±15.8	0.37±0.15	0.92±0.37	0.54±0.30	137.4±43.5	1.09±0.4
M2-BAPN	7.4±0.1	44.0±5.3	0.38±0.15	0.91±0.30	0.53±0.15	88.6±8.7	0.64±0.4

Open in a new tab

Step 1

The material constants for the PG and COL constituents are specified for each of the control groups (S-D0, M1-D0, M2-D0; Table 2). For the PG constituent, the experimental measures of wet weight (WW), dry weight, GAG mass, and COL mass are used to calculate the material constants (α₁, α₂) as discussed in the Appendix. With the assumptions stated above, the COL stress equation has only one adjustable parameter, γ₁, that is determined from the experimental data in an iterative fashion. For each control group, an initial guess for α₁ is made and the COL swelling strain, $F_{0}^{c}$ , is calculated using the equilibrium equations (9),

T^{s} = 0 = {\hat{T}}^{p} κ_{R} (I) + {\hat{T}}^{c} κ_{0} (F_{0}^{c}),

(15)

since $F_{e}^{p} = F_{e}^{c} = I$ in κ_R. Then, the uniaxial tension (UT) boundary-value problem for loading in the 2-direction is solved using the stress equation

T^{s} = {\hat{T}}^{p} κ_{R} (F_{1}) + {\hat{T}}^{c} κ_{0} (F_{1} F_{0}^{c}),

(16)

where $F_{1} = F_{e}^{p} = F_{e}^{c}$ corresponds to the applied UT displacement field. From this solution, the secant tensile modulus at 20% strain is calculated, compared to the experimental value (Table 1), and γ₁ is changed until the theoretical and experimental secant tensile moduli agree.

Table 2.

Parameters used to identify the stress-strain equations for the control groups. All parameters are defined in MPa except for the angles (ϕ₁₂,ϕ₁₃,ϕ₂₃), which are defined in degrees.

	CONTROL GROUP
PARAMETER	S-D0	M1-D0	M2-D0
$T_{R}^{p}$	−0.020	−0.033	−0.046
α₁	0.020	0.033	0.046
α₂	1.13	2.08	2.02
γ₁	0.20	0.23	0.53
γ₂	0.20	0.23	0.53
γ₃	0.10	0.12	0.27
δ	0.20	0.23	0.53
ϕ₁₂	45	45	45
ϕ₁₃	35	35	35
ϕ₂₃	35	35	35

Open in a new tab

Step 2

The growth and elastic growth tensors for the PG and COL constituents are determined. Experimental measures of PG and COL masses for the control and experimental groups are used to calculate the growth tensor determinants ( $J_{g}^{p}, J_{g}^{c}$ ) using (8), the mass growth functions (c^p, c^c) using (7), and the growth tensors ( $F_{g}^{p}, F_{g}^{c}$ ) using (10). Due to the immobility constraint, (2) is used to obtain $F_{eg}^{p} = F_{eg}^{c} F_{g}^{c} {(F_{g}^{p})}^{- 1}$ and the equilibrium equations (9) become

T^{s} = 0 = {\hat{T}}^{p} κ_{R} (F_{eg}^{c} F_{g}^{c} {(F_{g}^{p})}^{- 1}) + {\hat{T}}^{c} κ_{R} (F_{eg}^{c}),

(17)

which are solved for $F_{eg}^{c}$ and, consequently, $F_{eg}^{p}$ , F_m using (2), and J_m = detF_m. Note that J_m and the initial tissue volume can be used to calculate the tissue volume in κ_M, a discussed below.

Step 3

Since the calculated theoretical tissue volume for κ_M is always less than the experimental value, it is hypothesized that the COL network remodels during these growth protocols to produce a weaker material that enhances volumetric expansion during growth. Since the dependence of the COL remodeling factor χ on tissue microstructure is unknown, a value for χ first is assumed, and the remodeling deformation tensor of the solid matrix, F_r, is calculated from the equilibrium equations (9):

T^{s} = 0 = {\hat{T}}^{p} κ_{R} (F_{r} F_{eg}^{p}) + {\hat{T}}^{c} κ_{R} (F_{r} F_{eg}^{c}) .

(18)

Consequently, J_r = detF_r and the total determinant of the solid matrix deformation gradient tensor due to growth and remodeling can be calculated using (1): J = J_rJ_m. Based on the homogeneity assumptions, J can be used to calculate the tissue volume in κ_G using:

J = 1 + \frac{Δ V}{V_{0}}

(19)

where V₀ is the initial volume of the explant in κ_R and ΔV represents the change in tissue volume due to growth and remodeling.

Step 4

This is an iterative step that determines the value of χ needed to theoretically match the experimental tissue volume. Since complete geometry measurements were not made on these specimens, experimental measurements of tissue WW are used to calculate the volume change and, consequently, J between the control and experimental groups. Upon assuming constant total tissue density,⁷ one obtains:

\frac{Δ V}{V_{0}} = % WW CHANGE \Rightarrow J = 1 + % WW CHANGE,

(20)

where % WW CHANGE was experimentally measured (Table1). Consequently, the theoretical prediction of J from Step 3 is compared to the value calculated from experimental data using (20) and χ is changed until theoretical and experimental values for J agree.

Step 5

Validation is assessed by statistical tests of the first two hypotheses. First, the analytical protocol allows for the theoretical prediction of mechanical properties relative to the grown configuration κ_G by solving specific boundary-value problems using the stress equation:

T^{s} = {\hat{T}}^{s} κ_{G} (F_{1}) = {\hat{T}}^{p} κ_{G} (F_{1}) + {\hat{T}}^{c} κ_{G} (F_{1}) = {\hat{T}}^{p} κ_{R} (F_{1} F_{r} F_{eg}^{p}) + {\hat{T}}^{c} κ_{R} (F_{1} F_{r} F_{eg}^{c})

(21)

where T̂^s_κG (F_l) is the solid matrix stress function relative to κ_G and F_l represents the deformation due to boundary conditions. It is emphasized that (21) quantifies how the solid matrix stress-strain equation evolves during growth and remodeling using the CGM theory. Since only the experimental tensile modulus in the 2-direction was measured, the UT boundary-value problem for loading in the 2-direction is solved and the secant tensile modulus at 20% strain is calculated for the six experimental groups. A paired t-test is performed between the sets of theoretical predictions and experimental values of secant tensile moduli for the six experimental groups.

Second, since the only adjustable parameter used to match the grown tissue configuration κ_G was the remodeling factor χ, validation is further enhanced if χ is statistically related to some measure of COL microstructure. Thus, the correlative relationship between χ and PYR concentration (Table 1) is analyzed using linear regression and a t-test is performed to determine the existence of significant trends.

To test the third hypothesis, correlative relationships are investigated between the mass growth functions c^p and c^c and cell content (Table 1) and t-tests are performed to determine the existence of significant trends.

Results

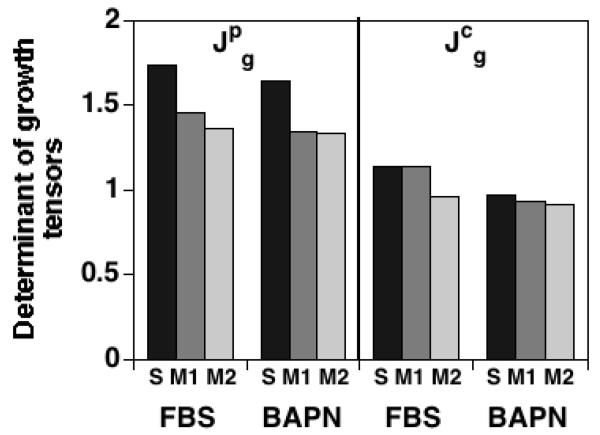
The parameters used to describe the SM stress response function relative to each control group's reference configurations (S-D0, M1-D0, M2-D0) are shown in Table 2; the predicted control group mechanical properties are further discussed in the Appendix. The determinant of the growth tensor for the PG constituent is greater than that for the COL constituent for each of the experimental groups, with values ranging from 1.34-1.74 for $J_{g}^{p}$ and 0.92-1.14 for $J_{g}^{c}$ (Figure 5); this difference is significant when pooling all experimental groups (p<0.001, n=6). The volumetric increase due to COL remodeling is predicted to be higher than that due to mass deposition (i.e., J_r > J_m) for all protocols except for FBSM1, with values ranging from 1.19-1.90 for J_r and 1.00-1.22 for J_m (Figure 6); this difference is significant when pooling all experimental groups (p<0.05, n=6).

Determinants of the constituent growth tensors $J_{g}^{p}$ and $J_{g}^{c}$ calculated from experimental measurements of PG (p) and COL (c) masses: $J_{g}^{p} > J_{g}^{c} (p < 0.001, n = 6)$ .

Determinants of the overall SM deformation gradient tensor (J) calculated from ex tensors perimental measurements of tissue WW, and determinants of SM deformation gradient tensors due to mass deposition (J_m) and COL remodeling (J_r) predicted from the CGM model. J_r > J_m (p>0.05, n=6).

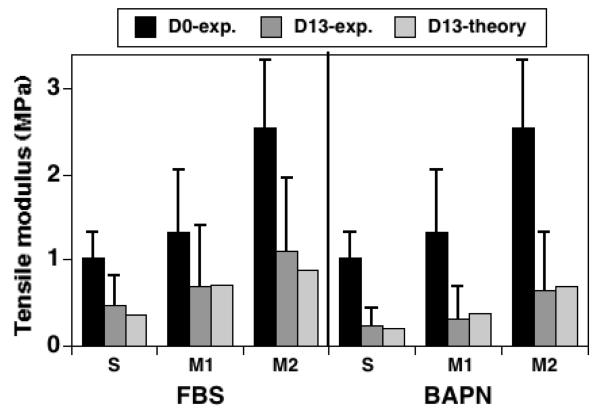
The theoretical values of secant tensile modulus at 20% strain predicted by the CGM model for all experimental groups are within ± 1 standard deviations of experimental means; there is not a significant difference between theoretical and experimental values (p=0.40, n=6) (Figure 7). The theoretical remodeling factor (χ) required to match the final tissue volume exhibits a positive trend with PYR crosslink content that is not significant when pooling all experimental groups (R²=0.37, p=0.20, n=6, Figure 8-left). However, the trend exhibits a strong positive correlation when only the S and M1 experimental groups are pooled (R²=1.00, p<0.0001, n=4, Figure 8-right).

Experimental and theoretical values of secant tensile modulus at 20% strain in the 2-direction. Experimental values measured before (D0-exp.) and after (D13-exp.) growth for three layers (S, M1, M2) and two growth medium types (FBS, BAPN); error bars represent ± 1 standard deviations. Theoretical values represent predictions of D13 values using the CGM model. No significant difference is detected between the theoretical and experimental D13 values using a paired t-test (p=0.40, n=6).

Linear regression analysis of the theoretical remodeling factor (χ) vs. crosslink content (PYR/WWF). Left: trend is not significant when all groups are considered (p=0.20, n=6). Right: trend is significant when only S and M1 layers are considered (p<0.0001, n=4).

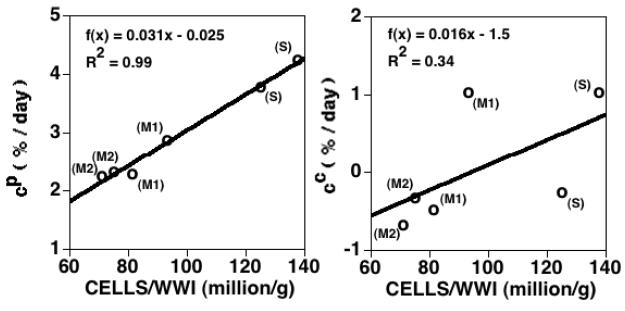
The calculated mass growth function for the PG constituent, c^p, exhibits a strong positive correlation with cell density (R²=0.98, p<0.0001, n=6, Figure 9-left), while the mass growth function for the COL constituent, c^c, exhibits a positive trend that is not significant (R²=0.34, p=0.22, n=6, Figure 9-right). Although both c^p and c^c are lower in the BAPN protocols, as compared to the FBS protocols, for each of the S, M1, and M2 layers, this trend is not significant (p=0.11 for both c^p and c^c, n=6).

Linear regression analysis of the calculated mass growth functions c^p and c^c (% mass increase per day) vs. cell density (number of cells normalized by initial tissue WW). Left: trend for c^p is significant (p<0.001, n=6). Right: trend for c^c is not significant (p=0.22, n=6).

Discussion

The major aim of this study was to develop and conduct validation protocols for a continuum mechanics model of cartilage growth. In order to do that, this study addressed limitations of a previous cartilage growth study [5]. Here, more accurate stress constitutive equations were developed based on a PG-COL stress balance hypothesis. This model can describe strain-dependent, asymmetric, and anisotropic Young's moduli and Poisson's ratios in UT and UCC as well as stress softening in UCC, in general agreement with previous results (see the Appendix). Also, this study includes experimental measurements of the evolution of tissue volume and tensile properties during growth.

An in vitro growth protocol designed to test the PG-COL stress balance hypothesis provides experimental evidence that confirms the model's prediction that volumetric growth (i.e., J) will be enhanced when the COL network is weakened via inhibition of crosslink formation with BAPN (Figure 6). The CGM model predictions provide further evidence for the model assumptions and, specifically, the critical role that the PG-COL stress balance has for these in vitro growth protocols. In particular, validation is obtained in three manners: (1) the CGM model is capable of matching final tissue composition and tissue volume exactly, via the specification of the PG and COL growth tensors and χ; (2) the CGM model provides theoretical predictions of secant tensile moduli for three layers (S, M1, M2) and two free-swelling in vitro growth protocols (FBS, BAPN) that do not significantly differ from experimental values; and (3) χ is positively correlated with experimental measures of PYR crosslink content.

A secondary aim was to obtain mass growth function that estimate baseline growth laws for free-swelling protocols for the chosen tissue source. The results suggest that: (1) the daily % increase in PG mass (i.e., c^p), ranging from 2.3-4.3 %/day, is greater than the daily % increase in COL mass (i.e., c^c), ranging from −0.7-1.0 %/day (Figure 9); and (2) both c^p and c^c can be defined as increasing functions of cell density (although only c^p exhibited a significant trend; Figure 9). These results may be used to define the growth laws relative to the current configuration (i.e., Ġ^p and Ġ^c) using (11) or relative to the reference configuration (i.e., ${\dot{F}}_{g}^{p}$ and ${\dot{F}}_{g}^{c}$ ) using (12). Since these results are for free-swelling protocols, future studies are planned to quantify the effect of applied external loading on the growth laws.

Limitations of the experimental data include the lack of comprehensive geometric measurements (e.g., length, width, thickness) and mechanical properties that may be used to completely characterize anisotropic geometry and mechanical changes, respectively. A preliminary study considered anisotropic growth. When the growing tissue explant is assumed homogeneous, anisotropic growth does not affect the predicted tensile modulus (or any of the evolving mechanical properties) because the PG stress is assumed to be spherical. However, anisotropic growth does affect the predicted explant dimensions (e.g. length, width, thickness) even when the final tissue volume is matched. Since these dimensions were not available in this study, only isotropic growth is detailed.

Also, a preliminary study considered anisotropic remodeling by changing the intrinsic COL material constants by different scalar remodeling factors. Those results show that anisotropic remodeling affects the predicted tensile modulus and explant dimensions. However, there is insufficient data to determine how to implement anisotropic remodeling in this study; future studies should include direction-dependent mechanical property tests before and after growth to better characterize anisotropic growth and remodeling. Despite these limitations in the experimental data, the results of this study do provide justification for conducting experiments that are designed to more rigorously validate the CGM model.

A limitation of the analysis is the assumption of homogeneous properties in all configurations. Our protocol attempts to mitigate these error sources by using 0.25 – 0.4 mm thick specimens and provides growth laws that may be used to study nonhomogeneous growth using computational solutions, such as the recently developed cartilage growth finite element model [18]. It may be suggested that there are other limitations related to the limited complexity of the model used here. A common theme in our work has been to provide experimental prescriptions for all model parameters so that the theory can be rigorously tested, as discussed in [17]. Due to a lack of comprehensive experimental data the CGM model proposed here is kept as simple as possible to facilitate the calculation of growth model parameters while still providing the capability to predict specific biomechanical changes during in vitro growth. Here, no attempt is made to distinguish between different types of PGs (such as the primary PG molecule aggrecan and the smaller PGs decorin, biglycan, and fibromodulin), different types of COLs (such as the primary type II molecule and several other types), mobile vs. immobile PGs and COLs, and non-equilibrium properties related to diffusion, transport, viscoelasticity, etc. However, the CGM model is derived from a general continuum theory of growth that models the tissue as a fluid and an arbitrary number of growing elastic materials, where all growing tissue constituents can experience distinct, yet interdependent, stresses, strains, diffusive velocities, mechanical properties, and mass deposition/removal rates [13, 15]. Thus, as more experimental data become available, the CGM model may be generalized to accommodate these features.

The long-term goal of this work is to develop analytical models that may aid in experimental approaches related to the growth of tissue for the repair of native AC defects. Clinical repair strategies include the use of chondral or osteochondral autografts or allografts and tissue-engineered constructs, among others [2, 3]. Goals of cartilage repair strategies may include the identification of a “target” implant with the desired geometry to fill a defect and biomechanical properties to successfully integrate with surrounding native tissue. Difficulties associated with osteochondral grafts include a limited tissue area recommended for treatment, development of a smooth convex joint surface, lateral integration with surrounding tissue, concern about transplantation from low to high weight-bearing sites, and mismatch between donor and repair site thickness [2, 56, 57]. In the future, it is possible that an implant's requirements for a specific anatomic site may be identified by non-invasive methods such as MRI or ultrasound [58, 59]. If the CGM model can be calibrated for an in vitro growth protocol within a range of biochemical and biomechanical stimuli, then it may be used to predict the protocol needed to produce an implant with the targeted properties. The results of this study suggest that a CGM model may help to guide in vitro growth protocols for AC tissue via the a priori prediction of construct geometric and biomechanical properties.

Ackowledgements

This material is based upon work supported by the National Science Foundation (SK, AD, RS), the Office of Naval Research (SK, AD), the Donald E. Bently Center for Engineering Innovation (SK), the National Institutes of Health (SK, KM, ET, RS), and the Howard Hughes Medical Institute Professor's Program (RLS).

Appendix

This appendix provides details of the stress constitutive equations used in this study.

Methods

For a growing elastic material with an elastic tensor F^e, the stress T is derived from an elastic strain energy function W as established in [14, 15]:

T = \frac{2}{J_{e}} F_{e} (\frac{\partial W}{\partial C_{e}}) F_{e}^{T}

(A1)

For the PG constituent, an isotropic polyconvex strain energy function is chosen:

W^{p} = \frac{α_{1}}{α_{2} - 1} {(J_{e}^{p})}^{- (α_{2} - 1)}

(A2)

which is polyconvex if the material constants α₁ > 0 and α₂ > 0. Using (A1) this produces a Cauchy stress function:

T^{p} = - \frac{α_{1}}{{(J_{e}^{p})}^{α_{2}}} I .

(A3)

The material constants (α₁, α2) are specified relative to a PG reference configuration $κ_{o}^{p}$ that coincides with κ_R. Consequently, (A3) represents the required function ${\hat{T}}^{p} κ_{R} (F_{e}^{p})$ of (13). The two-compartment water (i.e., extra- and intra-fibrillar) model [10] is used to calculate the PG stress component in κ_R ( $T_{R}^{p}$ ) and its extension presented in [60] is used to calculate (α₁, α2). The following equations are used:

{FC}_{tot} = 3.76 (458 ∕ 502) \times m^{p} ∕ 1000,

(A4)

{FCD}_{eff} = 1000 \times {FCD}_{tot} ∕ m_{ef}^{w},

(A5)

m_{ef}^{w} = m^{ww} - m^{dw} - m_{if}^{w},

(A6)

m_{if}^{w} = (0.726 + 0.538 \times \exp [- 0.258 \times p^{p}]) \times m^{c},

(A7)

p^{p} = {\begin{matrix} 0.0375 \times (1 - \exp [15.14 \times {FCD}_{eff}]) if {FCD}_{eff} \leq 0.23 \\ 155.1 \times \exp [0.12 \times {FCD}_{eff}] - 158.3 if {FCD}_{eff} \geq 0.23 \end{matrix}},

(A8)

where ( ${FC}_{tot}, {FCD}_{eff}, m_{ef}^{w}, m^{ww}, m^{dw}, m_{if}^{w}, p^{p}$ ) represent total fixed charge (mEq), effective fixed charge density (mEq/g; normalized to extrafibrillar water content), extrafibrillar water mass (mg), WW mass (mg), dry weight mass (mg), interfibrillar water mass (mg), and PG swelling pressure (atm). Eqn. (A4) is from [53] where it was assumed that chondroitin sulfate (CS) contains two ionized charge groups, the molecular weight of dissociated CS disaccharide is 458 g/mol, and 86% of cartilage PG are CS GAGs. GAG content was measured from DMB assay using C6S (502 g/mol) as a standard; hence, the conversion factor (458/502) is used. Eqns. (A5-A7) are from [10] while Eqn. (A8) is not, because the PG densities for newborn bovine cartilage are typically less than those of the aged human samples in [10]. Eqn. (A8) was obtained in [60] by curve-fitting swelling pressure data for low PG content [52, 53] in addition to using the relation from [10] for specimens with high PG content.

Given experimental mass measurements, (A4-A8) represents 5 coupled algebraic equations for 5 unknowns ( ${FC}_{tot}, {FCD}_{eff}, m_{ef}^{w}, m_{if}^{w}, p^{p}$ ). Since p^p is in units of atm (1 atm=−0.101MPa) and represents a true stress (i.e., normalized by constituent area), while the mixture theory uses apparent stress (i.e., normalized by total tissue area), the following conversion is needed to obtain the apparent PG stress component T^p (MPa):

T^{p} = - 0.101 \times \frac{m_{ef}^{w}}{V} p^{p}

(A9)

where V is the volume of the tissue (mm³). Thus, (A4-A9) are solved using experimental data for each layer's reference configuration to obtain $T_{R}^{p}$ for each layer [60]. PG stress values are also calculated for specimens with ±1 standard deviations in PG density for each layer, and nonlinear regression is performed to determine unique PG material constants for each layer. This approach yielded the PG material constants (α₁, α₂) for each control group (Table 2) with R²=0.96, 0.95, 0.91 for the S-DO, M1-D0, and M2-D0 control groups, respectively.

The COL stress equation is based on a formulation recently used for the SM [54] that was based on Spencer's theory of fiber-reinforced anisotropy [61]. The COL right Cauchy-Green elastic deformation tensor $C_{e 0}^{c}$ corresponds to the deformation gradient tensor $F_{e 0}^{c} = F_{e}^{c} F_{0}^{c}$ defined relative to the COL stress-free reference configuration $κ_{0}^{c}$ . Following [54], nine fiber families are defined. Three primary fiber families are aligned with the orthonormal basis vectors E₁, E₂, and E₃ (Figure 3). Strong interaction terms are generated by considering secondary fiber families in each of the three planes formed by the basis vectors.⁸ Then, W^c is assumed to depend on the nine strain invariants that are equivalent to the squares of the stretches along each fiber direction:

\begin{matrix} {I_{11}^{c}, I_{22}^{c}, I_{33}^{c}, I_{\pm 12}^{c}, I_{\pm 13}^{c}, I_{\pm 23}^{c}} = {C_{e 0, 11}^{c}, C_{e 0, 22}^{c}, C_{e 0, 33}^{c}, \\ C_{e 0, 11}^{c} \cos^{2} ϕ_{12} + C_{e 0, 22}^{c} \sin^{2} ϕ_{12} \pm 2 C_{e 0, 12}^{c} \cos ϕ_{12} \sin ϕ_{12}, \\ C_{e 0, 11}^{c} \cos^{2} ϕ_{13} + C_{e 0, 33}^{c} \sin^{2} ϕ_{13} \pm 2 C_{e 0, 13}^{c} \cos ϕ_{13} \sin ϕ_{13}, \\ C_{e 0, 22}^{c} \cos^{2} ϕ_{23} + C_{e 0, 33}^{c} \sin^{2} ϕ_{23} \pm 2 C_{e 0, 23}^{c} \cos ϕ_{23} \sin_{23}} \end{matrix}

(A10)

where (ϕ₁₂, ϕ₁₃, ϕ₂₃) are angles that define the orientation of the secondary fibers in the E₁–E₂, E₁–E₃, and E₂–E₃ planes, respectively. Here, the anisotropic strain energy function of [54] is generalized to include χ:

\begin{matrix} W^{c} = \frac{χ}{6} {γ_{1} [I_{11}^{c}] {(I_{11}^{c} - 1)}^{3} + γ_{2} [I_{22}^{c}] {(I_{22}^{c} - 1)}^{3} + γ_{3} [I_{33}^{c}] {(I_{33}^{c} - 1)}^{3} \\ + δ [I_{\pm 12}^{c}] {(I_{\pm 12}^{c} - 1)}^{3} + δ [I_{\pm 13}^{c}] {[I_{\pm 13}^{c} - 1)}^{3} + δ [I_{\pm 23}^{c}] {[I_{\pm 23}^{c} - 1)}^{3}} \end{matrix}

(A11)

where the material constants (α₁, α₂, α₃, δ) are only active when their corresponding fibers are in tension:

γ_{1} [I_{11}^{c}] = {\begin{matrix} γ_{1} > 0 & if I_{11}^{c} > 1 \\ 0 & if I_{11}^{c} < 1 \end{matrix}, δ [I_{\pm 12}^{c}] = {\begin{matrix} δ > 0 & if I_{\pm 12}^{c} > 1 \\ 0 & if I_{\pm 12}^{c} < 1 \end{matrix}, etc .

(A12)

The COL material constants are determined as outlined in Step 1 of the Methods section.

Results

The predicted mechanical response is qualitatively similar for all three control groups; uniaxial tension (UT) and unconfined compression (UCC) results are detailed only for the M2 layer. The nonlinear stress response is anisotropic and asymmetric, with strain-dependent Young's moduli and Poisson's ratios higher in UT than in UCC (Figure 10) and nearly equal tensile properties in the 1- and 2-directions as demonstrated for this tissue site [21]. The predicted secant UCC moduli at 15% strain were (E₁, E₃)=(0.39, 0.34 MPa) (Figure 11) as compared to values of (0.55, 0.61 MPa) for a deeper layer (∼ 2 mm) at this tissue site [30]. The predicted UCC Poisson's ratios at 15% strain were (ν₁₂, ν₁₃, ν₃₁, ν32)=(0.09, 0.17, 0.16, 0.16) (Figure 10) as compared to experimental values of (0.14, 0.22, 0.14, 0.13) for a deeper layer (∼ 2 mm) at this tissue site [30]. The predicted strain-dependent confined compression modulus (H_A) increases with depth from the articular surface in agreement with experimental observations [62, 63], from values at 15% strain of 0.15, 0.28, and 0.40 MPa in the S, M1, and M2 layers at depths of ∼ 0-0.4, 0.4-0.65, and 0.65-0.90 mm, respectively (data not shown), as compared to an experimental value of 0.56 MPa for a deeper layer (∼ 2 mm) at this tissue site [30]. Also, the UCC response exhibited experimentally observed stress softening behavior [28, 30, 62, 63], with secant moduli decreasing between 0 and 20% strain (Figure 11).

Description of the mechanical response of the M2 control group predicted by the PG-COL stress equations. Left: Cauchy stress vs. Biot strain for uniaxial tension (UT) and unconfined compression (UCC). Right: Poisson's ratios (ν_ij) at 15% strain for UT and UCC; i=loading direction, j=direction of transverse strain component.

Description of stress softening behavior in UCC for the M2 control group predicted by the PG-COL stress equations. Left: Cauchy stress vs. Biot strain for UT and UCC. Right: secant UCC modulus vs. UCC Biot strain.

Footnotes

In [16], an additional constituent representing the other non-collagenous proteins is included that is assumed to not directly affect the mechanical properties of the SM.

The fluid stress at equilibrium is assumed to be zero everywhere due to homogeneity assumptions.

For exact and computational solutions of nonhomogeneous problems, the SM element would correspond to a virtual configuration and a finite element, respectively, and additional elastic compatibility deformations would be required. See [18] for details.

⁴

The introduction of F_r is similar to previous tensorial descriptions of tissue remodeling [38, 51]. In nonhomogeneous problems, F_r may differ between adjacent elements and a compatibility deformation may be introduced to ensure continuity of the SM.

⁵

The effect of anisotropic growth is presented in the discussion and has been studied in [14, 16].

⁶

In [14], it is shown how these growth laws can be used to determine the “incremental growth tensor” using a first order Taylor series approximation.

⁷

Calculations show that tissue density changes by less than 2% during these growth protocols.

⁸

The reader is referred to [54] for full details.

References

1.Buckwalter JA, Mankin HJ. Articular cartilage repair and transplantation. Arthritis Rheum. 1998;41:1331–1342. doi: 10.1002/1529-0131(199808)41:8<1331::AID-ART2>3.0.CO;2-J. [DOI] [PubMed] [Google Scholar]
2.Smith GD, Knutsen G, Richardson JB. A clincial review of cartilage repair techniques. Journal of Bone and Joint Surgery. 2005;87B(4):445–449. doi: 10.1302/0301-620X.87B4.15971. [DOI] [PubMed] [Google Scholar]
3.Hunziker EB. Articular cartilage repair: basic science and clinical progress. A review of the current status and prospects. Osteoarthritis and Cartilage. 2001;10:432–463. doi: 10.1053/joca.2002.0801. [DOI] [PubMed] [Google Scholar]
4.Taber LA. Biomechanics of cardiovascular development. Annu Rev Biomed Eng. 2001;3:1–25. doi: 10.1146/annurev.bioeng.3.1.1. [DOI] [PubMed] [Google Scholar]
5.Klisch SM, Chen SS, Sah RL, Hoger A. A growth mixture theory for cartilage with applications to growth-related experiments on cartilage explants. J Biomech Eng. 2003;125:169–179. doi: 10.1115/1.1560144. [DOI] [PubMed] [Google Scholar]
6.Maroudas A, Venn M. Chemical composition and swelling of normal and osteoarthrotic femoral head cartilage. II. Swelling. Ann Rheum Dis. 1977;36(5):399–406. doi: 10.1136/ard.36.5.399. [DOI] [PMC free article] [PubMed] [Google Scholar]
7.Mow VC, Ratcliffe A. Structure and function of articular cartilage and meniscus. In: Mow VC, Hayes WC, editors. Basic Orthopaedic Biomechanics. Raven Press; New York: 1997. pp. 113–178. [Google Scholar]
8.Grodzinsky AJ. Electromechanical and physicochemical properties of connective tissue. CRC Crit Rev Bioeng. 1983;9:133–199. [PubMed] [Google Scholar]
9.Lai WM, Hou JS, Mow VC. A triphasic theory for the swelling and deformation behaviors of articular cartilage. J Biomech Eng. 1991;113:245–258. doi: 10.1115/1.2894880. [DOI] [PubMed] [Google Scholar]
10.Basser PJ, Schneiderman R, Bank RA, Wachtel E, Maroudas A. Mechanical properties of the collagen network in human articular cartilage as measured by osmotic stress technique. Arch Biochem Biophys. 1998;351:207–219. doi: 10.1006/abbi.1997.0507. [DOI] [PubMed] [Google Scholar]
11.Woo SL-Y, Akeson WH, Jemmott GF. Measurements of nonhomogeneous directional mechanical properties of articular cartilage in tension. J Biomech. 1976;9:785–791. doi: 10.1016/0021-9290(76)90186-x. [DOI] [PubMed] [Google Scholar]
12.Venn MF, Maroudas A. Chemical composition and swelling of normal and osteoarthritic femoral head cartilage. I. Chemical composition. Ann Rheum Dis. 1977;36:121–129. doi: 10.1136/ard.36.2.121. [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Klisch SM, Sah RL, Hoger A. A growth mixture theory for cartilage. In: Casey J, Bao G, editors. Mechanics in Biology AMD 242 & BED 46. ASME; New York: 2000. pp. 229–242. [Google Scholar]
14.Klisch SM, Van Dyke T, Hoger A. A theory of volumetric growth for compressible elastic materials. Math Mech Solids. 2001;6:551–575. [Google Scholar]
15.Klisch SM, Hoger A. Volumetric growth of thermoelastic materials and mixtures. Math Mech Solids. 2003;8:377–402. [Google Scholar]
16.Klisch SM, Sah RL, Hoger A. A cartilage growth mixture model for infinitesimal strains: solutions of boundary-value problems related to in vitro growth experiments. Biomech Model Mechanobiol. 2005;3(4):209–223. doi: 10.1007/s10237-004-0060-9. [DOI] [PubMed] [Google Scholar]
17.Klisch SM. Continuum models of growth with special emphasis on articular cartilage. In: Holzapfel GA, Ogden RW, editors. Mechanics of Biological Tissue. Springer-Verlag; Berlin Heidelberg: 2006. pp. 119–133. [Google Scholar]
18.Davol A, Bingham MS, Sah RL, Klisch SM. A nonlinear finite element model of cartilage growth. Biomech Model Mechanobiol. 2007 doi: 10.1007/s10237-007-0098-6. In Press. [DOI] [PubMed] [Google Scholar]
19.Wong M, Ponticiello M, Kovanen V, Jurvelin JS. Volumetric changes of articular cartilage during stress relaxation in unconfined compression. J Biomech. 2000;33(9):1049–1054. doi: 10.1016/s0021-9290(00)00084-1. [DOI] [PubMed] [Google Scholar]
20.Williamson AK, Chen AC, Sah RL. Compressive properties and function-composition relationships of developing bovine articular cartilage. J Orthop Res. 2001;19:1113–1121. doi: 10.1016/S0736-0266(01)00052-3. [DOI] [PubMed] [Google Scholar]
21.Williamson AK, Chen AC, Masuda K, Thonar EJ-MA, Sah RL. Tensile mechanical properties of bovine articular cartilage: variations with growth and relationships to collagen network components. J Orthop Res. 2003;21:872–880. doi: 10.1016/S0736-0266(03)00030-5. [DOI] [PubMed] [Google Scholar]
22.Chang DG, Lottman LM, Chen AC, Schinagl RM, Albrecht DR, Pedowitz RA, Brossman J, Frank LR, Sah RL. The depth-dependent, multi-axial properties of aged human patellar cartilage in tension. Trans Orthop Res Soc. 1999;24:644. [Google Scholar]
23.Korhonen RK, Toyras J, Nieminen MT, Rieppo J, Hirvonen J, Helminen HJ, Jurvelin JS. Effect of ionic environment on the compression-tension nonlinearity of articular cartilage in the direction perpendicular to articular surface. Trans Orthop Res Soc. 2001:439. [Google Scholar]
24.Elliot DM, Narmoneva DA, Setton LA. Direct measurement of the Poisson's ratio of human patella cartilage in tension. J Biomech Eng. 2002;124:223–228. doi: 10.1115/1.1449905. [DOI] [PubMed] [Google Scholar]
25.Laasanen M, Toyras J, Korhonen R, Rieppo J, Saarakkala S, Nieminen M, Hirvonen J, Jurvelin JS. Biomechanical properties of knee articular cartilage. Biorheology. 2003;40:133–140. [PubMed] [Google Scholar]
26.Charlebois M, McKee MD, Buschmann MD. Nonlinear tensile properties of bovine articular cartilage and their variation with age and depth. J Biomech Eng. 2004;126:129–137. doi: 10.1115/1.1688771. [DOI] [PubMed] [Google Scholar]
27.Wang CC, Chahine NO, Hung CT, Ateshian GA. Optical determination of anisotropic material properties of bovine articular cartilage in compression. J Biomech. 2003;36(3):339–353. doi: 10.1016/s0021-9290(02)00417-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
28.Chahine NO, Wang CC, Hung CT, Ateshian GA. Anisotropic strain-dependent material properties of bovine articular cartilage in the transitional range from tension to compression. J Biomech. 2004;37:1251–1261. doi: 10.1016/j.jbiomech.2003.12.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
29.Huang CY, Stankiewicz A, Ateshian GA, Mow VC. Anisotropy, inhomogeneity, and tension-compression nonlinearity of human glenohumeral cartilage in finite deformation. J Biomech. 2005;38(4):799–809. doi: 10.1016/j.jbiomech.2004.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
30.Ficklin TP, Thomas GC, Barthel JC, Asanbaeva A, Thonar EJ, Masuda K, Chen AC, Sah RL, Davol A, Klisch SM. Articular cartilage mechanical and biochemical property relations before and after in vitro growth. J Biomech. 2007;40:3607–3614. doi: 10.1016/j.jbiomech.2007.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
31.Chen YC, Hoger A. Constitutive functions for elastic materials in finite growth and deformation. J Elast. 2000;59:175–193. [Google Scholar]
32.Epstein M, Maugin GA. Thermomechanics of volumetric growth in uniform bodies. Int J Plast. 2000;16:951–978. [Google Scholar]
33.DiCarlo A, Quiligotti S. Growth and balance. Mech Res Commun. 2002;29:449–456. [Google Scholar]
34.Lubarda VA, Hoger A. On the mechanics of solids with a growing mass. Int J Solids Struct. 2002;39:4627–4664. [Google Scholar]
35.Kuhl E, Steinmann P. Mass- and volume-specific views on thermodynamics for open systems. Proceeding of the Royal Society of London. 2003;459A:2547–2568. [Google Scholar]
36.Huang Z. The equilibrium equations and constitutive equations of the growing deformable body in the framework of continuum theory. Int J Non-Linear Mech. 2004;39(6):951–962. [Google Scholar]
37.Lappa M. A CFD level-set method for soft tissue growth: theory and fundamental equations. J Biomech. 2005;38(1):185–190. doi: 10.1016/j.jbiomech.2004.02.037. [DOI] [PubMed] [Google Scholar]
38.Menzel A. Modelling of anisotropic growth in biological tissues: a new approach and computational aspects. Biomech Model Mechanobiol. 2005;3(3):147–171. doi: 10.1007/s10237-004-0047-6. [DOI] [PubMed] [Google Scholar]
39.Quiligotti S. On bulk growth mechanics of solid-fluid mixtures: kinematics and invariance requirements. Theor Appl Mech. 2002;28-29:277–288. [Google Scholar]
40.Ganghoffer J-F, Haussy B. Mechanical modeling of growth considering domain variation. Part 1: constitutive framework. Int J Solids Structures. 2005;42(15):4311–4337. [Google Scholar]
41.Humphrey JD, Rajagopal KR. A constrained mixture model for growth and remodeling in soft tissues. Math Model Meth Appl Sci. 2002;12(3):407–430. [Google Scholar]
42.Preziosi L, Farina A. On darcy's law for growing porous media. Int J Non-Linear Mech. 2002;37:485–491. [Google Scholar]
43.Breward CJ, Byrne HM, Lewis CE. A multiphase model describing vascular tumour growth. Bull Math Biol. 2003;65(4):609–640. doi: 10.1016/S0092-8240(03)00027-2. [DOI] [PubMed] [Google Scholar]
44.Garikipati K, Arruda EM, Grosh K, Narayanan H, Calve S. A continuum treatment of growth in biological tissue: the coupling of mass transport and growth. J Mech Phys Sol. 2004;52(7):1595–1625. [Google Scholar]
45.Asanbaeva A, Masuda K, Thonar EJ-MA, Klisch SM, Sah RL. Cartilage growth and remodeling: modulation of balance between proteoglycan and collagen in vitro with beta-aminopropionitrile. Osteoarthritis Cartilage. 2007 doi: 10.1016/j.joca.2007.05.019. In Press. [DOI] [PubMed] [Google Scholar]
46.Ahsan T, Lottman LM, Harwood FL, Amiel D, Sah RL. Integrative cartilage repair: inhibition by beta-aminoproprionitrile. J Orthop Res. 1999;17:850–857. doi: 10.1002/jor.1100170610. [DOI] [PubMed] [Google Scholar]
47.DiMicco MA, Waters SN, Akeson WH, Sah RL. Integrative articular cartilage repair: dependence on developmental stage and collagen metabolism. Osteoarthritis Cartilage. 2002;10:218–225. doi: 10.1053/joca.2001.0502. [DOI] [PubMed] [Google Scholar]
48.Mills N. Incompressible mixtures of Newtonian fluids. Int J Eng Sci. 1966;4:97–112. [Google Scholar]
49.Mow VC, Kuei SC, Lai WM, Armstrong CG. Biphasic creep and stress relaxation of articular cartilage in compression: theory and experiment. J Biomech Eng. 1980;102:73–84. doi: 10.1115/1.3138202. [DOI] [PubMed] [Google Scholar]
50.Frank EH, Grodzinsky AJ. Cartilage electromechanics-II. A continuum model of cartilage electrokinetics and correlation with experiments. J Biomech. 1987;20:629–639. doi: 10.1016/0021-9290(87)90283-1. [DOI] [PubMed] [Google Scholar]
51.Garikipati K, narayanan H, Arruda EM, Grosh K, Calve S. Material forces in the context of biotissue remodelling. In: Steinmann P, Maugin GA, editors. Mechanics of Material Forces. Springer; New York: 2005. pp. 77–84. [Google Scholar]
52.Williams RP, Comper WD. Osmotic flow caused by polyelectrolytes. Biophys Chem. 1990;36:223–234. doi: 10.1016/0301-4622(90)80028-6. [DOI] [PubMed] [Google Scholar]
53.Buschmann MD, Grodzinsky AJ. A molecular model of proteoglycan-associated electrostatic forces in cartilage mechanics. J Biomech Eng. 1995;117:179–192. doi: 10.1115/1.2796000. [DOI] [PubMed] [Google Scholar]
54.Klisch SM. A bimodular polyconvex anisotropic strain energy function for articular cartilage. J Biomech Eng. 2007;129:250–258. doi: 10.1115/1.2486225. [DOI] [PubMed] [Google Scholar]
55.Asanbaeva A. Cartilage growth and remodeling: modulation of growth phenotype and tensile integrity. University of California; San Diego, La Jolla, CA: 2006. Ph.D. dissertation. [Google Scholar]
56.Hangody L, Fules P. Autologous osteochondral mosaicplasty for the treatment of full-thickness defects of weight-bearing joints. Ten years of experimental and clinical experience. J Bone Joint Surg. 2003;85-A(Supplement 2):25–32. doi: 10.2106/00004623-200300002-00004. [DOI] [PubMed] [Google Scholar]
57.Horas U, Pelinkovic D, Herr G, Aigner T, Schnettler R. Autologous chondrocyte implantation and osteochondral cylinder transplantation in cartilage repair of the knee joint. A prospective, comparative trial. J Bone Joint Surg Am. 2003;85-A(2):185–192. doi: 10.2106/00004623-200302000-00001. [DOI] [PubMed] [Google Scholar]
58.Nieminen MT, Toyras J, Rieppo J, Hakumaki JM, Silvennoinen J, Helminen HJ, Jurvelin JS. Quantitative MR microscopy of enzymatically degraded articular cartilage. Magn Reson Med. 2004;43:676–681. doi: 10.1002/(sici)1522-2594(200005)43:5<676::aid-mrm9>3.0.co;2-x. [DOI] [PubMed] [Google Scholar]
59.Nissi MJ, Toyras J, Laasanen MS, Rieppo J, Saarakkala S, Lappalainen R, Jurvelin JS, Nieminen HJ. Proteoglycan and collagen sensitive MRI evaluation of normal and degenerated articular cartilage. J Orthop Res. 2004;22(3):557–564. doi: 10.1016/j.orthres.2003.09.008. [DOI] [PubMed] [Google Scholar]
60.Oungoulian SR, Chen SS, Davol A, Sah RL, Klisch SM. Extended two-compartmental swelling stress model and isotropic cauchy stress equation for articular cartilge proteoglycans; ASME Summer Bioengineering Conference; Keystone, CO. 2007. [Google Scholar]
61.Spencer AJM. Continuum theory of the mechanics of fibre-reinforced composites. Springer; New York: 1984. [Google Scholar]
62.Schinagl RM, Gurskis D, Chen AC, Sah RL. Depth-dependent confined compression modulus of full-thickness bovine articular cartilage. J Orthop Res. 1997;15:499–506. doi: 10.1002/jor.1100150404. [DOI] [PubMed] [Google Scholar]
63.Chen SS, Falcovitz YH, Schneiderman R, Maroudas A, Sah RL. Depth-dependent compressive properties of normal aged human femoral head articular cartilage: relationship to fixed charge density. Osteoarthritis Cartilage. 2001;9:561–569. doi: 10.1053/joca.2001.0424. [DOI] [PubMed] [Google Scholar]

[R1] 1.Buckwalter JA, Mankin HJ. Articular cartilage repair and transplantation. Arthritis Rheum. 1998;41:1331–1342. doi: 10.1002/1529-0131(199808)41:8<1331::AID-ART2>3.0.CO;2-J. [DOI] [PubMed] [Google Scholar]

[R2] 2.Smith GD, Knutsen G, Richardson JB. A clincial review of cartilage repair techniques. Journal of Bone and Joint Surgery. 2005;87B(4):445–449. doi: 10.1302/0301-620X.87B4.15971. [DOI] [PubMed] [Google Scholar]

[R3] 3.Hunziker EB. Articular cartilage repair: basic science and clinical progress. A review of the current status and prospects. Osteoarthritis and Cartilage. 2001;10:432–463. doi: 10.1053/joca.2002.0801. [DOI] [PubMed] [Google Scholar]

[R4] 4.Taber LA. Biomechanics of cardiovascular development. Annu Rev Biomed Eng. 2001;3:1–25. doi: 10.1146/annurev.bioeng.3.1.1. [DOI] [PubMed] [Google Scholar]

[R5] 5.Klisch SM, Chen SS, Sah RL, Hoger A. A growth mixture theory for cartilage with applications to growth-related experiments on cartilage explants. J Biomech Eng. 2003;125:169–179. doi: 10.1115/1.1560144. [DOI] [PubMed] [Google Scholar]

[R6] 6.Maroudas A, Venn M. Chemical composition and swelling of normal and osteoarthrotic femoral head cartilage. II. Swelling. Ann Rheum Dis. 1977;36(5):399–406. doi: 10.1136/ard.36.5.399. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R7] 7.Mow VC, Ratcliffe A. Structure and function of articular cartilage and meniscus. In: Mow VC, Hayes WC, editors. Basic Orthopaedic Biomechanics. Raven Press; New York: 1997. pp. 113–178. [Google Scholar]

[R8] 8.Grodzinsky AJ. Electromechanical and physicochemical properties of connective tissue. CRC Crit Rev Bioeng. 1983;9:133–199. [PubMed] [Google Scholar]

[R9] 9.Lai WM, Hou JS, Mow VC. A triphasic theory for the swelling and deformation behaviors of articular cartilage. J Biomech Eng. 1991;113:245–258. doi: 10.1115/1.2894880. [DOI] [PubMed] [Google Scholar]

[R10] 10.Basser PJ, Schneiderman R, Bank RA, Wachtel E, Maroudas A. Mechanical properties of the collagen network in human articular cartilage as measured by osmotic stress technique. Arch Biochem Biophys. 1998;351:207–219. doi: 10.1006/abbi.1997.0507. [DOI] [PubMed] [Google Scholar]

[R11] 11.Woo SL-Y, Akeson WH, Jemmott GF. Measurements of nonhomogeneous directional mechanical properties of articular cartilage in tension. J Biomech. 1976;9:785–791. doi: 10.1016/0021-9290(76)90186-x. [DOI] [PubMed] [Google Scholar]

[R12] 12.Venn MF, Maroudas A. Chemical composition and swelling of normal and osteoarthritic femoral head cartilage. I. Chemical composition. Ann Rheum Dis. 1977;36:121–129. doi: 10.1136/ard.36.2.121. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R13] 13.Klisch SM, Sah RL, Hoger A. A growth mixture theory for cartilage. In: Casey J, Bao G, editors. Mechanics in Biology AMD 242 & BED 46. ASME; New York: 2000. pp. 229–242. [Google Scholar]

[R14] 14.Klisch SM, Van Dyke T, Hoger A. A theory of volumetric growth for compressible elastic materials. Math Mech Solids. 2001;6:551–575. [Google Scholar]

[R15] 15.Klisch SM, Hoger A. Volumetric growth of thermoelastic materials and mixtures. Math Mech Solids. 2003;8:377–402. [Google Scholar]

[R16] 16.Klisch SM, Sah RL, Hoger A. A cartilage growth mixture model for infinitesimal strains: solutions of boundary-value problems related to in vitro growth experiments. Biomech Model Mechanobiol. 2005;3(4):209–223. doi: 10.1007/s10237-004-0060-9. [DOI] [PubMed] [Google Scholar]

[R17] 17.Klisch SM. Continuum models of growth with special emphasis on articular cartilage. In: Holzapfel GA, Ogden RW, editors. Mechanics of Biological Tissue. Springer-Verlag; Berlin Heidelberg: 2006. pp. 119–133. [Google Scholar]

[R18] 18.Davol A, Bingham MS, Sah RL, Klisch SM. A nonlinear finite element model of cartilage growth. Biomech Model Mechanobiol. 2007 doi: 10.1007/s10237-007-0098-6. In Press. [DOI] [PubMed] [Google Scholar]

[R19] 19.Wong M, Ponticiello M, Kovanen V, Jurvelin JS. Volumetric changes of articular cartilage during stress relaxation in unconfined compression. J Biomech. 2000;33(9):1049–1054. doi: 10.1016/s0021-9290(00)00084-1. [DOI] [PubMed] [Google Scholar]

[R20] 20.Williamson AK, Chen AC, Sah RL. Compressive properties and function-composition relationships of developing bovine articular cartilage. J Orthop Res. 2001;19:1113–1121. doi: 10.1016/S0736-0266(01)00052-3. [DOI] [PubMed] [Google Scholar]

[R21] 21.Williamson AK, Chen AC, Masuda K, Thonar EJ-MA, Sah RL. Tensile mechanical properties of bovine articular cartilage: variations with growth and relationships to collagen network components. J Orthop Res. 2003;21:872–880. doi: 10.1016/S0736-0266(03)00030-5. [DOI] [PubMed] [Google Scholar]

[R22] 22.Chang DG, Lottman LM, Chen AC, Schinagl RM, Albrecht DR, Pedowitz RA, Brossman J, Frank LR, Sah RL. The depth-dependent, multi-axial properties of aged human patellar cartilage in tension. Trans Orthop Res Soc. 1999;24:644. [Google Scholar]

[R23] 23.Korhonen RK, Toyras J, Nieminen MT, Rieppo J, Hirvonen J, Helminen HJ, Jurvelin JS. Effect of ionic environment on the compression-tension nonlinearity of articular cartilage in the direction perpendicular to articular surface. Trans Orthop Res Soc. 2001:439. [Google Scholar]

[R24] 24.Elliot DM, Narmoneva DA, Setton LA. Direct measurement of the Poisson's ratio of human patella cartilage in tension. J Biomech Eng. 2002;124:223–228. doi: 10.1115/1.1449905. [DOI] [PubMed] [Google Scholar]

[R25] 25.Laasanen M, Toyras J, Korhonen R, Rieppo J, Saarakkala S, Nieminen M, Hirvonen J, Jurvelin JS. Biomechanical properties of knee articular cartilage. Biorheology. 2003;40:133–140. [PubMed] [Google Scholar]

[R26] 26.Charlebois M, McKee MD, Buschmann MD. Nonlinear tensile properties of bovine articular cartilage and their variation with age and depth. J Biomech Eng. 2004;126:129–137. doi: 10.1115/1.1688771. [DOI] [PubMed] [Google Scholar]

[R27] 27.Wang CC, Chahine NO, Hung CT, Ateshian GA. Optical determination of anisotropic material properties of bovine articular cartilage in compression. J Biomech. 2003;36(3):339–353. doi: 10.1016/s0021-9290(02)00417-7. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R28] 28.Chahine NO, Wang CC, Hung CT, Ateshian GA. Anisotropic strain-dependent material properties of bovine articular cartilage in the transitional range from tension to compression. J Biomech. 2004;37:1251–1261. doi: 10.1016/j.jbiomech.2003.12.008. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R29] 29.Huang CY, Stankiewicz A, Ateshian GA, Mow VC. Anisotropy, inhomogeneity, and tension-compression nonlinearity of human glenohumeral cartilage in finite deformation. J Biomech. 2005;38(4):799–809. doi: 10.1016/j.jbiomech.2004.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R30] 30.Ficklin TP, Thomas GC, Barthel JC, Asanbaeva A, Thonar EJ, Masuda K, Chen AC, Sah RL, Davol A, Klisch SM. Articular cartilage mechanical and biochemical property relations before and after in vitro growth. J Biomech. 2007;40:3607–3614. doi: 10.1016/j.jbiomech.2007.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R31] 31.Chen YC, Hoger A. Constitutive functions for elastic materials in finite growth and deformation. J Elast. 2000;59:175–193. [Google Scholar]

[R32] 32.Epstein M, Maugin GA. Thermomechanics of volumetric growth in uniform bodies. Int J Plast. 2000;16:951–978. [Google Scholar]

[R33] 33.DiCarlo A, Quiligotti S. Growth and balance. Mech Res Commun. 2002;29:449–456. [Google Scholar]

[R34] 34.Lubarda VA, Hoger A. On the mechanics of solids with a growing mass. Int J Solids Struct. 2002;39:4627–4664. [Google Scholar]

[R35] 35.Kuhl E, Steinmann P. Mass- and volume-specific views on thermodynamics for open systems. Proceeding of the Royal Society of London. 2003;459A:2547–2568. [Google Scholar]

[R36] 36.Huang Z. The equilibrium equations and constitutive equations of the growing deformable body in the framework of continuum theory. Int J Non-Linear Mech. 2004;39(6):951–962. [Google Scholar]

[R37] 37.Lappa M. A CFD level-set method for soft tissue growth: theory and fundamental equations. J Biomech. 2005;38(1):185–190. doi: 10.1016/j.jbiomech.2004.02.037. [DOI] [PubMed] [Google Scholar]

[R38] 38.Menzel A. Modelling of anisotropic growth in biological tissues: a new approach and computational aspects. Biomech Model Mechanobiol. 2005;3(3):147–171. doi: 10.1007/s10237-004-0047-6. [DOI] [PubMed] [Google Scholar]

[R39] 39.Quiligotti S. On bulk growth mechanics of solid-fluid mixtures: kinematics and invariance requirements. Theor Appl Mech. 2002;28-29:277–288. [Google Scholar]

[R40] 40.Ganghoffer J-F, Haussy B. Mechanical modeling of growth considering domain variation. Part 1: constitutive framework. Int J Solids Structures. 2005;42(15):4311–4337. [Google Scholar]

[R41] 41.Humphrey JD, Rajagopal KR. A constrained mixture model for growth and remodeling in soft tissues. Math Model Meth Appl Sci. 2002;12(3):407–430. [Google Scholar]

[R42] 42.Preziosi L, Farina A. On darcy's law for growing porous media. Int J Non-Linear Mech. 2002;37:485–491. [Google Scholar]

[R43] 43.Breward CJ, Byrne HM, Lewis CE. A multiphase model describing vascular tumour growth. Bull Math Biol. 2003;65(4):609–640. doi: 10.1016/S0092-8240(03)00027-2. [DOI] [PubMed] [Google Scholar]

[R44] 44.Garikipati K, Arruda EM, Grosh K, Narayanan H, Calve S. A continuum treatment of growth in biological tissue: the coupling of mass transport and growth. J Mech Phys Sol. 2004;52(7):1595–1625. [Google Scholar]

[R45] 45.Asanbaeva A, Masuda K, Thonar EJ-MA, Klisch SM, Sah RL. Cartilage growth and remodeling: modulation of balance between proteoglycan and collagen in vitro with beta-aminopropionitrile. Osteoarthritis Cartilage. 2007 doi: 10.1016/j.joca.2007.05.019. In Press. [DOI] [PubMed] [Google Scholar]

[R46] 46.Ahsan T, Lottman LM, Harwood FL, Amiel D, Sah RL. Integrative cartilage repair: inhibition by beta-aminoproprionitrile. J Orthop Res. 1999;17:850–857. doi: 10.1002/jor.1100170610. [DOI] [PubMed] [Google Scholar]

[R47] 47.DiMicco MA, Waters SN, Akeson WH, Sah RL. Integrative articular cartilage repair: dependence on developmental stage and collagen metabolism. Osteoarthritis Cartilage. 2002;10:218–225. doi: 10.1053/joca.2001.0502. [DOI] [PubMed] [Google Scholar]

[R48] 48.Mills N. Incompressible mixtures of Newtonian fluids. Int J Eng Sci. 1966;4:97–112. [Google Scholar]

[R49] 49.Mow VC, Kuei SC, Lai WM, Armstrong CG. Biphasic creep and stress relaxation of articular cartilage in compression: theory and experiment. J Biomech Eng. 1980;102:73–84. doi: 10.1115/1.3138202. [DOI] [PubMed] [Google Scholar]

[R50] 50.Frank EH, Grodzinsky AJ. Cartilage electromechanics-II. A continuum model of cartilage electrokinetics and correlation with experiments. J Biomech. 1987;20:629–639. doi: 10.1016/0021-9290(87)90283-1. [DOI] [PubMed] [Google Scholar]

[R51] 51.Garikipati K, narayanan H, Arruda EM, Grosh K, Calve S. Material forces in the context of biotissue remodelling. In: Steinmann P, Maugin GA, editors. Mechanics of Material Forces. Springer; New York: 2005. pp. 77–84. [Google Scholar]

[R52] 52.Williams RP, Comper WD. Osmotic flow caused by polyelectrolytes. Biophys Chem. 1990;36:223–234. doi: 10.1016/0301-4622(90)80028-6. [DOI] [PubMed] [Google Scholar]

[R53] 53.Buschmann MD, Grodzinsky AJ. A molecular model of proteoglycan-associated electrostatic forces in cartilage mechanics. J Biomech Eng. 1995;117:179–192. doi: 10.1115/1.2796000. [DOI] [PubMed] [Google Scholar]

[R54] 54.Klisch SM. A bimodular polyconvex anisotropic strain energy function for articular cartilage. J Biomech Eng. 2007;129:250–258. doi: 10.1115/1.2486225. [DOI] [PubMed] [Google Scholar]

[R55] 55.Asanbaeva A. Cartilage growth and remodeling: modulation of growth phenotype and tensile integrity. University of California; San Diego, La Jolla, CA: 2006. Ph.D. dissertation. [Google Scholar]

[R56] 56.Hangody L, Fules P. Autologous osteochondral mosaicplasty for the treatment of full-thickness defects of weight-bearing joints. Ten years of experimental and clinical experience. J Bone Joint Surg. 2003;85-A(Supplement 2):25–32. doi: 10.2106/00004623-200300002-00004. [DOI] [PubMed] [Google Scholar]

[R57] 57.Horas U, Pelinkovic D, Herr G, Aigner T, Schnettler R. Autologous chondrocyte implantation and osteochondral cylinder transplantation in cartilage repair of the knee joint. A prospective, comparative trial. J Bone Joint Surg Am. 2003;85-A(2):185–192. doi: 10.2106/00004623-200302000-00001. [DOI] [PubMed] [Google Scholar]

[R58] 58.Nieminen MT, Toyras J, Rieppo J, Hakumaki JM, Silvennoinen J, Helminen HJ, Jurvelin JS. Quantitative MR microscopy of enzymatically degraded articular cartilage. Magn Reson Med. 2004;43:676–681. doi: 10.1002/(sici)1522-2594(200005)43:5<676::aid-mrm9>3.0.co;2-x. [DOI] [PubMed] [Google Scholar]

[R59] 59.Nissi MJ, Toyras J, Laasanen MS, Rieppo J, Saarakkala S, Lappalainen R, Jurvelin JS, Nieminen HJ. Proteoglycan and collagen sensitive MRI evaluation of normal and degenerated articular cartilage. J Orthop Res. 2004;22(3):557–564. doi: 10.1016/j.orthres.2003.09.008. [DOI] [PubMed] [Google Scholar]

[R60] 60.Oungoulian SR, Chen SS, Davol A, Sah RL, Klisch SM. Extended two-compartmental swelling stress model and isotropic cauchy stress equation for articular cartilge proteoglycans; ASME Summer Bioengineering Conference; Keystone, CO. 2007. [Google Scholar]

[R61] 61.Spencer AJM. Continuum theory of the mechanics of fibre-reinforced composites. Springer; New York: 1984. [Google Scholar]

[R62] 62.Schinagl RM, Gurskis D, Chen AC, Sah RL. Depth-dependent confined compression modulus of full-thickness bovine articular cartilage. J Orthop Res. 1997;15:499–506. doi: 10.1002/jor.1100150404. [DOI] [PubMed] [Google Scholar]

[R63] 63.Chen SS, Falcovitz YH, Schneiderman R, Maroudas A, Sah RL. Depth-dependent compressive properties of normal aged human femoral head articular cartilage: relationship to fixed charge density. Osteoarthritis Cartilage. 2001;9:561–569. doi: 10.1053/joca.2001.0424. [DOI] [PubMed] [Google Scholar]

PERMALINK

A CARTILAGE GROWTH MIXTURE MODEL WITH COLLAGEN REMODELING: VALIDATION PROTOCOLS

Stephen M Klisch

Anna Asanbaeva

Sevan R Oungoulian

Koichi Masuda

Eugene J-MA Thonar

Andrew Davol

Robert L Sah

Abstract

Introduction

Figure 1.

Methods

Cartilage Growth Mixture (CGM) Model

Kinematics

Figure 2.

Balance Laws

Growth laws

Stress constitutive equations

Figure 3.

Experimental data

Parameter estimation

Figure 4.

Table 1.

Step 1

Table 2.

Step 2

Step 3

Step 4

Step 5

Results

Figure 5.

Figure 6.

Figure 7.

Figure 8.

Figure 9.

Discussion

Ackowledgements

Appendix

Methods

Results

Figure 10.

Figure 11.

Footnotes

References

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases