Skip to main content
NCBI home page
Bioinformatics logoLink to Bioinformatics
. 2008 Jun 27;24(17):1850–1857. doi: 10.1093/bioinformatics/btn331

Context-dependent DNA recognition code for C2H2 zinc-finger transcription factors

Jiajian Liu 1, Gary D Stormo 1,*
PMCID: PMC2732218  PMID: 18586699

Abstract

Motivation: Modeling and identifying the DNA-protein recognition code is one of the most challenging problems in computational biology. Several quantitative methods have been developed to model DNA-protein interactions with specific focus on the C2H2 zinc-finger proteins, the largest transcription factor family in eukaryotic genomes. In many cases, they performed well. But the overall the predictive accuracy of these methods is still limited. One of the major reasons is all these methods used weight matrix models to represent DNA-protein interactions, assuming all base-amino acid contacts contribute independently to the total free energy of binding.

Results: We present a context-dependent model for DNA–zinc-finger protein interactions that allows us to identify inter-positional dependencies in the DNA recognition code for C2H2 zinc-finger proteins. The degree of non-independence was detected by comparing the linear perceptron model with the non-linear neural net (NN) model for their predictions of DNA–zinc-finger protein interactions. This dependency is supported by the complex base-amino acid contacts observed in DNA–zinc-finger interactions from structural analyses. Using extensive published qualitative and quantitative experimental data, we demonstrated that the context-dependent model developed in this study can significantly improves predictions of DNA binding profiles and free energies of binding for both individual zinc fingers and proteins with multiple zinc fingers when comparing to previous positional-independent models. This approach can be extended to other protein families with complex base-amino acid residue interactions that would help to further understand the transcriptional regulation in eukaryotic genomes.

Availability:The software implemented as c programs and are available by request. http://ural.wustl.edu/softwares.html

Contact: stormo@ural.wustl.edu

1 INTRODUCTION

The specific interaction between transcription factors and their cognate DNA sites is critical for regulation of gene expression in cells. Identifying the rules that govern the relationship between the amino acid sequence of a transcription factor (TF) and its binding site specificity would be of great utility in molecular biology and has been sought after for many years (Pabo and Sauer, 1984; Seeman et al., 1976). However, unraveling the recognition code that specifies the amino acid-base interactions remains a very challenging problem.

Early studies primarily tried to deduce a qualitative binding code from the solved crystal structures of DNA-protein complexes, but it soon became clear that there is no simple, universal recognition code (Matthews, 1988). More recently several groups have developed methods to infer quantitative codes, where the goal is to model the binding energies to many different DNA sequences based on the protein sequence (Benos et al., 2002; Kaplan et al., 2005; Kono and Sarai, 1999; Mandel-Gutfreund and Margalit, 1998; Suzuki and Yagi, 1994). Gutfreund and Margalit used the data from 53 co-crystals and a simple log-odds scoring system to generate the base-amino acid interaction weight matrix model (Mandel-Gutfreund and Margalit, 1998), while Keno and Sarai derived pairwise potentials between base and amino acid by a statistical analysis of 52 protein-DNA complex structures (Kono and Sarai, 1999). Both studies assumed similar base-amino acid preferences for all proteins and at all binding positions. However, structural analysis of protein-DNA complexes clearly showed that these two assumptions are oversimplified (Choo and Klug, 1997; Luscombe et al., 2000). Suzuki and Yagi developed a model that took both position-specific interactions and DNA binding geometries for proteins that belong to different protein families into account (Suzuki and Yagi, 1994), but with limited structural data and a simple, empirical scoring system this approach still has limited accuracy.

An alternative approach is to learn the recognition code from extensive in vitro selection data. Two groups have developed sophisticated statistical methods (Benos et al., 2002; Kaplan et al., 2005) to model DNA-protein interactions with specific focus on the single protein family, C2H2 zinc-finger proteins. Based on statistical mechanics theory, Benos et al. developed an algorithm to estimate the probabilistic code for zinc-finger proteins (Benos et al., 2002). Kaplan et al. employed the expectation maximization (EM) algorithm to optimize the model for DNA–zinc-finger interactions (Kaplan et al., 2005). Both methods significantly improved the predictions of DNA-protein interactionscompared to previous methods. In many cases, they can accurately predict DNA binding sites for given proteins. However, the overall accuracy of their predictions is still limited for at least two reasons. One is that there are limited data upon which to infer the model parameters. And the other is that both methods assumed the positional independence for DNA–zinc-finger protein interactions. Methods based on the independence assumption are simple, with a small numbers of parameters, making them easy to implement, but their predictions are limited by the degree of validity this assumption. Benos et al. have shown that the positional independence can be a reasonably good approximation for the DNA sites based on their analysis of a large set of affinity data for five zinc-finger proteins (Benos et al., 2002), but several studies have indicated that positional correlations do exist among the zinc-finger protein residue positions (Elrod-Erickson and Pabo, 1999; Michael Gromiha et al., 2004; Miller and Pabo, 2001), or over the base-amino acid contact positions (Liu and Stormo, 2005). Because the assumption of positional independence is likely to be oversimplified, we developed the context dependent models for DNA–zinc-finger protein interactions described in this work.

One approach that takes the positional dependency into account is to extend the position-independent weight matrix model by adding extra parameters to capture interactions between positions (Barash et al., 2003; Zhou and Liu, 2004). However, only considering dependencies between adjacent amino acid residues requires nearly 8000 additional parameters for just a single zinc-finger. Such an approach is not currently possible because of the limited experimental data. We proposed to overcome this difficulty by using the non-linear neural net (NN) model to represent DNA–zinc-finger interactions. NNs are structured computational models with a long history in pattern recognition that have been extensively used in biology for such tasks as identifying signal peptides (Bendtsen et al., 2004), predicting protein secondary structure (Qian and Sejnowski, 1988), characterizing the yeast transcriptional network (Hart et al., 2006) and analyzing the DNA-binding proteins and their binding residues (Ahmad et al., 2004). When comparing models for binary predictions, we found that the non-linear NN models significantly outperformed the linear perceptron model (equivalent to a weight matrix), suggesting that the positional dependency is involved in DNA–zinc-finger interactions. The structures of DNA–zinc-finger protein complexes include a set of non-canonical zinc fingers that differ from the simple set of interactions used for the positional independent model and probably contribute to the limited accuracy of its predictions. Using the NN model, we can predict DNA binding profiles for any given a C2H2 zinc-finger protein. By comparing our predictions with a large collection of published experimental data and those predicted by previous methods (Benos et al., 2002; Kaplan et al., 2005), we demonstrate that the integration of the positional dependency for modeling DNA–zinc-finger interactions can significantly improve predictive performance.

The C2H2 zinc-finger protein is the largest TF family in all completely sequenced eukaryotic model genomes. For instance, about 30% of all TFs in the human genome are C2H2 zinc-finger proteins (Messina et al., 2004). Various zinc-finger proteins have been demonstrated to play essential roles in regulating different biological processes, including cell growth, differentiation, development and tumorigenesis through their selectively binding to particular DNA sites in the genome (Wolfe et al., 2000, 2001). An improvement in the recognition code for zinc-finger proteins will enhance our ability to identify target genes for specific zinc-finger TFs and our modeling of the regulation of gene expression in eukaryotes.

2 METHODS

2.1 Datasets

The datasets used in this study include positive interaction data and negative non-interaction data. The interaction data were initially collected by Benos et al. (2002) from the published in vitro selection experiments for variants of the EGR proteins. There are a total of 1033 instances where each interaction pair contains a 10 bp long DNA site and the amino acid residues for three recognition helixes in EGR proteins. With these raw data and the DNA binding model as shown in Figure 1, we converted them into two sets of non-redundant data for DNA-single finger interactions: One is 647 sets of tetra-nucleotides–zinc-finger interaction pairs, and the other is 447 sets of DNA tri-nucleotide–zinc-finger interaction pairs, in which the residues at position +2 along with their recognized bases are ignored. For each set of positive interaction data, we created negative non-interaction data of either 1000 or 1500 examples, for the tri- and tetra-nucleotide models, respectively, using three different methods. First, random permutations of DNA bases and shuffling of protein sequences for an interaction pair that was randomly chosen from the interaction dataset. Second, generation of random protein and DNA sequences by assignment of a DNA base and an amino acid residue according to a uniform distribution. Third, while DNA sites were created based on the uniform distribution, the random protein sequences were created based on the distributions of key residues of zinc fingers in pfam database (Finn et al., 2006).

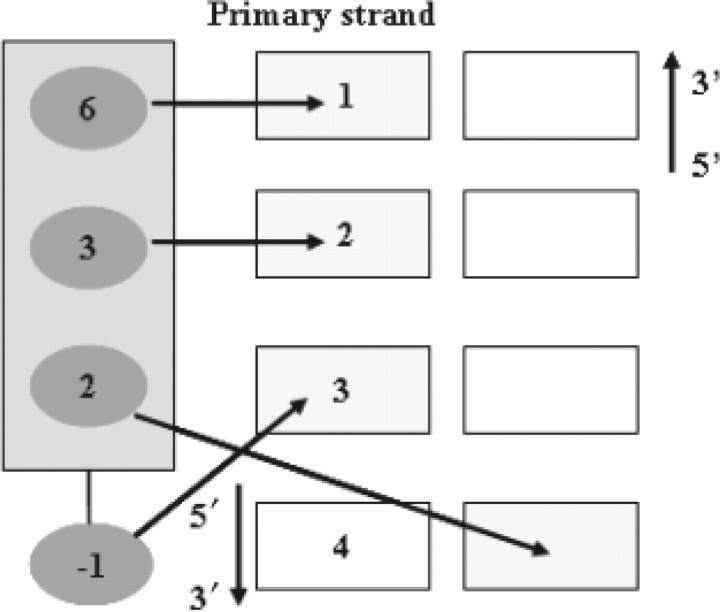
Fig. 1.

Fig. 1.

Open in a new tab

The canonical DNA–zinc-finger binding model. The amino acid residues at −1, +2, +3, and +6 of the helix for zinc-finger domain contact the DNA bases at 3, 4, 2, and 1.

2.2 Sequence representation and transformation

For a binding site of length L, each DNA base N in the target site N1..NL is encoded with 4 binary digits, a = (0001), c = (0010), g = (0100), and t = (1000), while each amino acid residue A in the interacting amino acid residues, A1..AL, is represented in the similar way using the corresponding 20 binary digits. Each pair of amino acid-base, AN1..ANL, is represented in a similar way with 80 binary digits with a single 1 and the rest 0.

2.3 Modeling base-amino acid residue preferences for DNA–zinc-finger interactions

With the canonical binding model for zinc fingers as shown in Figure 1, we first employed a single-layer perceptron model to model DNA–zinc-finger interaction (Mitchell, 1997). We are given a set of training example pairs (SAN, t), in which SAN is a pair of target DNA site N1…NL and the amino acid residues of a zinc-finger, A1…AL which is responsible for specific recognition of the DNA site, L indicates the number of interacting positions under consideration, which is 3 or 4, depending on whether a tri- or tetra-nucleotide DNA site is used for modeling. t denotes if the pair of a DNA site and zinc-finger for a given SAN interact or not. Instead of using 1 and 0 values, we used of 0.9 and 0.1 to represent the target value for interacting pairs and non-interacting pairs, respectively. Based on the physical contact model for DNA–zinc-finger interactions (Fig. 1), we transform SAN into L pairs of Inline graphic, for 1≤i≤L, which forms the input vector for the network model Λ. There is a weight vector, Inline graphic, that assigns a weight to each element of the input vector. The output of the single output unit of the network, o(SAN∣W,Λ), for the given weights W of the network model Λ, is computed through a feed forward step with the sigmoid function:

graphic file with name btn331um1.jpg

The training procedure seeks to minimize the sum of errors, E2. For each of the k training sequences, the error is the difference between the network output for that sequence, ok, and the target output for that sequence, tk:

graphic file with name btn331um2.jpg

This is done by taking the derivative of the error function with respect to network weights, W, and then changing those parameters in a gradient descent (Mitchell, 1997).

To consider the context dependence between DNA–zinc-finger protein interactions, we employed a two-layer neural network to model DNA–zinc-finger interaction. While keeping the same structure for both input layer and output layer as those in the perceptron model, we added a hidden layer with a varied number of hidden units between them in the neural network model to capture the positional dependent interactions that were not counted by the perceptron model. We now have weights between the input vectors, Inline graphic, and each of the j hidden nodes, Inline graphic, and from each hidden node to the output node, Inline graphic The outputs for each hidden node, and for the final output node, are computed using the same scoring procedure. The model for DNA–zinc-finger protein interactions are optimized by minimizing the sum of errors (E2) between the target value and the computed network output for all training examples using bckpropagation algorithm (Mitchell, 1997; Rumelhart, 1994). The program package ZifNet used to build perceptron and neural network models were written in the C program language and are available upon request.

2.4 Cross validation to estimate model parameters

We used the cross validation procedure to optimize our models while the predictive performances were examined simultaneously. Each dataset consisting of both positive and negative data was randomly partitioned into three parts. 80% of the dataset was used to train the network model, 80% of the remaining dataset was used as the validation set to monitor an appropriate stopping point for gradient descent, and the remaining data was used to measure the prediction performances. The randomized partitions were repeated six times. The average of their predictive performances was used to assess the model performance. The predictive performance was measured with accuracy, sensitivity and specificity with the formulae shown below. We used the network output value 0.81 and 0.11 as stringent cut offs for positive and negative pairs, respectively. Network outputs between those values are always considered false predictions.

graphic file with name btn331um3.jpg
graphic file with name btn331um4.jpg
graphic file with name btn331um5.jpg

where TP: true positive, TN: true negative, FP: false positive, FN: false negative.

2.5 Prediction of DNA binding models for C2H2 zinc-finger proteins

To estimate DNA binding profiles for a given zinc-finger, we first used the NN model to compute the network output scores for all possible 64 triplet sites. The value of the output unit of the network model, o(A1..AL,N1,..NL;W,Λ), for the given the binary classification model Λ and its weight W, is bounded between 0 and 1 and is interpreted as the probability of binding, P(bound∣AN1..ANL) (28). We chose the top 12 sites (20%) to calculate its weight matrix model using the formula below where a pseudo-count was introduced, as the additivity model was demonstrated to hold well for the side of DNA site for DNA–zinc-finger interactions (Benos et al., 2002).

graphic file with name btn331um6.jpg

where W(b, i) is the weight for base b at position i, nb,i is the number of instances of base b at position i, Ni is the total number of bases at position i, Pb is the frequency of base b in the background sequence, 0.25 is used here, and a pseudo-count of +1.

2.6 Assessment of the predictions

2.6.1 Compare predicted DNA binding profiles with experimentally determined profiles.

The DNA binding constants (Ka) for five zinc-finger proteins were downloaded from the website http://arep.med.harvard.edu/Bulyk/NAR2002supplementary/ (Bulyk et al., 2002). While the predictive DNA binding profiles for the 5 proteins were performed as described above, the experimentally determined profile represented as the probability of binding for base b at position i, P(b,i), for each protein was calculated by the following formulae

graphic file with name btn331um7.jpg

2.6.2 Assessment of different models with quantitative binding affinity data.

We collected 9 sets of binding constants (Ka) for 31 different zinc fingers (Bulyk et al., 2001; Elrod-Erickson and Pabo, 1999; Hamilton et al., 1998; Liu and Stormo, 2005; Segal et al., 1999). For the datasets from Bulyk et al. (2001), only binding constants of the preferred DNA binding sites for each of 5 proteins were used for assessment. We used the correlation coefficient between the experimentally determined energy differences and those predicted by different models for DNA–zinc-finger interactions to compare our model with the existing models. For any given protein sequence, each model predicts the binding energy (proportional to the output score) for all possible binding site sequences, which are used in the comparisons to the experimental energies.

2.6.3 Comparison of predicted DNA binding profiles for zinc-finger proteins with multiple fingers with those in TRANSFAC database.

To predict DNA bin-ding profiles for zinc-finger proteins with multiple fingers, we first determined the number of zinc-finger domains, and the key residues at positions of -1, +3 and +6 in each domain with the zinc-finger HMM model (Finn et al., 2006). After prediction of DNA binding profile for each individual finger with the method as described above, we assemble them together from C-terminal to N-terminal, as binding of zinc fingers to DNA sites follows the anti-parallel fashion (Elrod-Erickson et al., 1996, 1998). The assembled DNA binding profiles were then used to compare with those in TRANSFAC database.

3 RESULTS

3.1 Context dependencies in DNA–zinc-finger interactions

C2H2 zinc-finger proteins typically contain multiple fingers that make tandem contacts along the DNA. Since most zinc-finger proteins are believed to bind DNA in a modular fashion (Choo and Klug, 1997; Elrod-Erickson et al., 1996), we model DNA binding specificities for individual zinc fingers. In previous studies, Benos et al. and Kaplan et al. have developed context-independent models to estimate DNA recognition preferences of C2H2 zinc-finger proteins (Benos et al., 2002; Kaplan et al., 2005) based on the canonical binding model of the DNA-protein complex of EGR1 (Elrod-Erickson et al., 1996; Pavletich and Pabo, 1991). According to this model (Fig. 1), each zinc-finger employs three residues at positions −1, +3 and +6 (numbering with respect to the start of the α helix) to contact a triplet DNA site, while the residue at position +2 of the helix contacts a base that is complementary to the one recognized by the amino acid at the position +6 of its preceding finger. By comparing the performance of the linear perceptron (weight matrix) and the non-linear NN to model DNA–zinc-finger interactions, we can determine whether context dependence is critical for accurate modeling of the DNA–zinc-finger interactions.

Using a cross validation procedure (described in materials and methods) we optimized models for DNA–zinc-finger interactions while the model errors and performances were simultaneously assessed. Figure 2 shows the predictive accuracy, sensitivity and specificity for the optimized perceptron and NN models. We chose the NN models with two hidden units because in most cases additional hidden units did not significantly affect predictive performances and require many more parameters. If there were no context dependence across base-amino acid interacting positions, the predictive performances for the perceptron models would be expected to be similar to those achieved by the non-linear NN models. However, statistical t-tests indicated that non-linear network models performed significantly better than their corresponding perceptron models with regard to predictive accuracy (P-value = 0.01), sensitivity (P-value = 0.04) and specificity (P-value = 0.01). This indicates that interactions between base-amino acid contacting positions contribute to the affinity between the DNA sites and the zinc fingers.

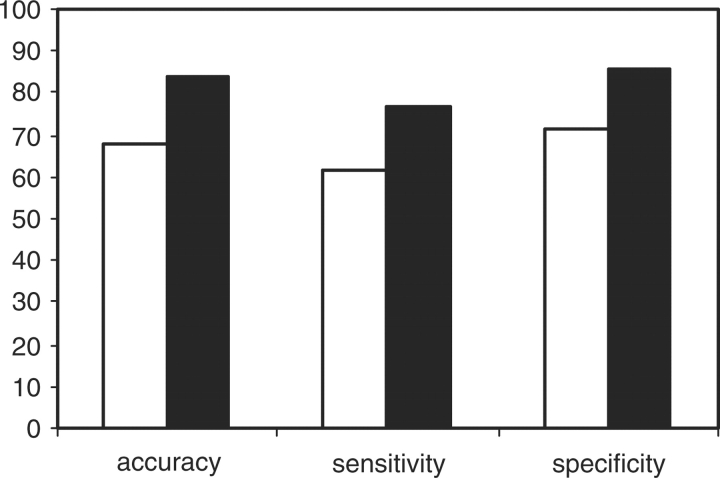
Fig. 2.

Fig. 2.

Open in a new tab

Predictive performance of DNA–zinc-finger interactions for both the perceptron model and the two-layer NN model with two hidden units. Black and white bars present the NN model and perceptron models, respectively. The performances were assessed as predictive accuracy, sensitivity and specificity. The data presented in this figure was derived from the dataset II as described in Section 2.

3.2 Physical basis of context dependencies for DNA–zinc-finger protein interactions

The inter-positional dependencies for DNA–zinc-finger interactions are consistent with the observed structures in many complexes.

The program HBPLUS (Nucplot package) (Luscombe et al., 2000, 1998) was used to extract amino acid-DNA base contacts from each of more than 20 co-crystals of DNA-C2H2 zinc-finger protein complexes collected from the PDB database. Analysis of these structures indicated there are many variations from the canonical zinc fingers (Elrod-Erickson et al., 1998; Elrod-Erickson and Pabo, 1999; Wolfe et al., 2000) as shown in Figure 1. Figure 3 shows three examples of non-canonical zinc-finger interactions with DNA. There are examples of a single amino acid contacting more than one base, and also of one base being contacted by multiple amino acids (Figure 3A–C). Figure 3C shows a finger with atypical base-amino acid contacts, in which the residue at position +2, rather than −1, contacts the base at position 3 in the site. While these non-canonical interactions had been reported previously (Elrod-Erickson and Pabo, 1999; Fairall et al., 1993; Wolfe et al., 2000, 2001) they had not been incorporated into the quantitative methods for modeling DNA–zinc-finger protein interactions. Additionally, the side chain-side chain interactions between protein residues of zinc fingers (e.g. the interaction between residues at position −1 and +2 for EGR1) can also contribute to the positional dependencies, although they are not detected by the Nuplot package. In a recent study on quantification of the specificity of intermolecular and intramolecular readout for a set of DNA-protein complexes (including 5 C2H2 zinc fingers), Gromiha et al. (Michael Gromiha et al., 2004) further showed that the intermolecular readout plays a major role in DNA binding for two canonical zinc-finger proteins, Iiia and 1MEY, but the intramolecular readouts were found to significantly contribute to recognition of DNA sites for three non-canonical zinc-finger proteins, YY1, TTK and GATA-1. These structural studies emphasize the need to consider the context dependencies in order to improve our modeling of DNA–zinc-finger protein interactions.

Fig. 3.

Fig. 3.

Open in a new tab

Examples of the non-canonical zinc fingers observed from structural analysis of DNA–zinc-finger protein complexes.

3.3 Estimation of DNA triplet binding profiles for individual C2H2 zinc fingers

While structural studies indicate that four amino acids from each finger may interact with four positions in the binding site, most phage display experiments were screened against various DNA triplets in the context of the zif268 binding site (Choo and Klug, 1994; Segal et al., 1999). This leads to a distinct lack of variability in the datasets for the bases in the fourth position of the canonical model (5′−>3′) (Fig. 1) and residues at position +2 of the helix in zinc fingers, which results in a strongly biased training set. To circumvent this problem, we simplified our model by focusing on the core triplet DNA–zinc-finger interactions. While this model will be incomplete, we can still compare its performance to context independent models over the same positions to determine how much improvement is obtained when allowing for context dependencies. We chose the NN model with two hidden units to represent triplet–zinc-finger interactions based on its near optimal accuracy in the previous tests and the decreased number of parameters compared to models with additional hidden units. In this case we have used all of the data from Benos et al., (2002) for training the model, and we have evaluated its accuracy, and compared it to previous models, on independent sets of quantitative binding affinity data. Once the complete NN model is obtained, it provides quantitative predictions for the binding affinity to all 64 possible triplets, given any specific amino sequence at positions −1, +3 and +6. The goal is to obtain a model capable of making accurate quantitative binding affinity predictions even though the training data is entirely qualitative.

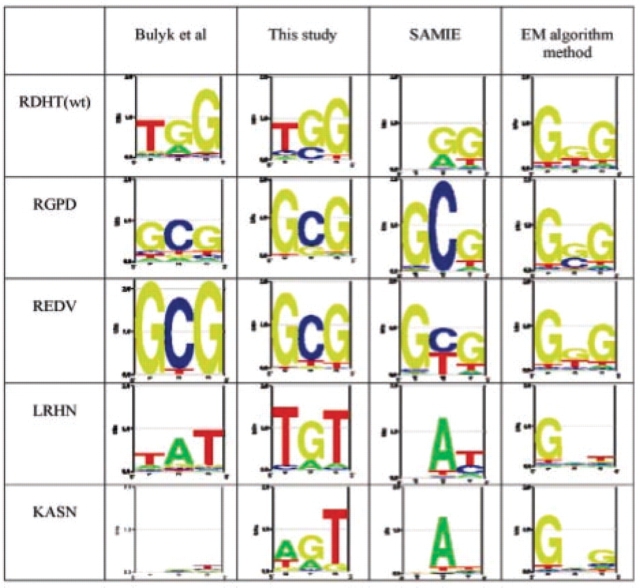
Figure 4 shows graphically, with use of Logos (Workman et al., 2005), the results on the data from Bulyk et al. (2001). They used the protein-binding micrarray technology to measure binding affinities for the wild-type zif268, and four variants with residue substitutions at the middle finger of the protein, to all possible central triplet binding sites. The experimentally determined sequence logos, based on the relative affinity of all 64 sites, is shown in the left column. The other columns show the predicted affinities for our NN model and the SAMIE method of Benos et al., (2002) and the EM method of Kaplan et al., (2005). As shown in this figure, the predictions of the NN model for three proteins, wild-type zif268, RGPD, REDV, are in excellent agreement with the experimental results. Our model over-predicts the specificity of the KASN protein, which is very non-specific, and the prediction for LRHN, T(G/a)T deviates from its real specificity, T(A/g)T. Overall there is a general consistency between our predictions and the experimental results, which is better than the predictions of the other two models.

Fig. 4.

Fig. 4.

Open in a new tab

The experimentally determined sequence logos for five zinc fingers and those predicted by our model and two previous quantitative models. The five zinc fingers are the middle finger of wild-type zif268 and its four derivatives.

Figure 5 summarizes the results of prediction accuracies to several different datasets. For each protein in each study, the predicted binding energies were compared, using the Pearson correlation coefficient, to the measured binding energies for each DNA binding site that was included in the study. The top rows are for the data from Bulyk et al., (2002), which is shown graphically in Figure 4. The other results in Figure 5 include 9 sets of binding constants (Ka) for 31 different zinc fingers (Bulyk et al., 2001; Elrod-Erickson and Pabo, 1999; Hamilton et al., 1998; Liu and Stormo, 2005; Segal et al., 1999). These include examples where the affinity of the same protein was measured to different binding sites, and also examples where the affinity of the same binding site was measured for different proteins. In each case the models allow one to predict the differences in binding energy, and we calculate the Pearson correlation coefficient between those predictions and the measured differences. While the accuracy of each method varies considerably in different datasets, the NN model typically has the highest correlation or close to it. If the average correlation is computed over each set of experiments, or over the set of fingers that were tested, the NN method is substantially better. These results are consistent with our first analysis showing that allowing for context dependence, via the hidden layers of the NN, can lead to more accurate predictions of the binding affinities of zinc-finger proteins.

Fig. 5.

Fig. 5.

Open in a new tab

Correlation analysis between experimentally measured free energies of binding and those predicted with different models.

3.4 Prediction of DNA-binding profiles for multiple zinc-finger transcription factors

Using the NN model for individual zinc fingers, we can predict the binding specificities of TFs with multiple fingers by simply concatenating the individual predictions together following the direction from C-terminal to N-terminal (Elrod-Erickson et al., 1998, 1996, Elrod-Erickson et al., 1998). For any given a zinc-finger protein, we first used the pFAM zinc-finger HMM model (Finn et al., 2006) to determine the number of zinc-finger domains, and the key residues at positions −1, +3 and +6 responsible for recognition of DNA bases. To examine the reliability of this approach, we compared the predicted specificities to the DNA-binding profiles from the TRANSFAC database, which is a repository for transcription factors and their sites from many eukaryotes (Matys et al., 2006). It includes 48 non-redundant weight matrices for C2H2 zinc-finger TFs with numbers of zinc-finger domains ranging from 2 to 20. We chose all matrices based on at least 6 binding sites and with 2, 3 or 4 zinc fingers. The predicted sequence logos and those directly from the TRANSFAC database are shown in Figure 6. In most cases there is good agreement between the predicted specificity and that in the TRANSFAC matrices, although the TRANSFAC motif may be longer. For example, NGFIC, Krox20, Krox24 and EGR3 all have the same key amino acids in three zinc fingers, and so the predicted binding sites are all the same. The predicted motif does match closely to the common 9-base core in the TRANSFAC matrices for those four TFs, but their TRANSFAC motifs are each extended with weakly conserved bases to a 12-long motif. While the preferred, or consensus, sequence often matches between the predicted motifs and those in TRANSFAC, the quantitative predictions are more variable. This could be due to a limited accuracy of the quantitative model, but is probably also due to the small sample size for some of the TRANSFAC datasets. And while the majority of predictions are at least very similar to the TRANSFAC motifs, there are a few that bear little resemblance.

Fig. 6.

Fig. 6.

Open in a new tab

Sequence logos for zinc-finger proteins in TRANFAC database and those predicted by our model. Ap-2*: Ap-2Arep; CCF*: CACCC-binding factor.

4 DISCUSSION

We have presented a general model for DNA–zinc-finger protein interactions that is capable of estimating DNA binding specificities for C2H2 zinc-finger TFs. In comparison to previous quantitative models (Benos et al., 2002; Kaplan et al., 2005), this model takes the context dependency into account. Evaluation with a large set of qualitative and quantitative experimental data demonstrates that the integration of context dependency for modeling DNA-protein interactions can improve predictive accuracy.

Independence between positions is an assumption that is widely used in computational approaches that model binding sites and DNA-protein interactions, but the accuracy of this approximation remains controversial (Benos et al., 2002; Michael Gromiha et al., 2004; O'Flanagan et al., 2005; Tomovic and Oakeley, 2007). A typical method to assess positional independence is to statistically compare a set of experimentally measured free energies of binding (or binding affinities) with those estimated by either context independent or dependent models (Benos et al., 2002; Liu and Stormo, 2005; O'Flanagan et al., 2005; Tomovic and Oakeley, 2007). In this study we compare the perceptron model, which assumes additivity between the binding site positions, with the two-layer NN model which can incorporate non-independence between the positions. We found that the NN model significantly outperformed the perceptron model in a cross-validation study, suggesting that dependence between positions contributes significantly in the DNA recognition by zinc-finger proteins. This finding agrees with many previous mutagenesis studies, quantitative binding affinity assays and structural analyses (Elrod-Erickson and Pabo, 1999; Liu and Stormo, 2005; Michael Gromiha et al., 2004; Miller and Pabo, 2001; Wolfe et al., 2000).

As shown in Figures 1 and 3, zinc fingers may form either canonical or non-canonical complexes. However, for any given C2H2 zinc-finger, we have no means to know the class of its interaction before its co-crystal structure is solved. While it is possible to include non-independent interactions by explicitly including all possible pairs within the binding site and the protein, this leads to an enormous increase in the number of parameters, far beyond the limited training data available. Instead we applied the non-linear NN approach to model the general DNA–zinc-finger protein interactions and found that only 2 nodes in the hidden layer are sufficient for a significant increase in prediction accuracy in both cross-validation tests and also on extensive published experimental data sets. We obtained a 66% correlation between our predictions and experimental data compared to only 48% correlations using our previously published SAMIE method (Fig. 5). Since both our model and SAMIE were trained from the same set of data, this shows that the integration of positional dependency can significantly improve predictive performances. The approach developed in this study is not limited to model DNA–zinc-finger protein interactions. It can be extended to other protein families such as helix-turn-helix, Homeodomain and basic helix-loop-helix (bHLH) TFs, (Albright and Matthews, 1998; Damante et al., 1996; Mahony et al., 2007) in which the complicated base-amino acid contacts have been observed.

While our model attained reasonably good predictions, there is still ample room for improvement. Just like previous methods, we know that our current model is also limited by lack of sufficient training data, and in particular would benefit from quantitative binding data. Additionally, due to the biased training data collected from phage display experiments, we could not consider the contribution of residues at position +2 to DNA binding for both individual fingers and proteins with multiple fingers. Although the specific role of position +2 in sequence specificity has not been well understood (Wolfe et al., 2000), ignoring the contribution of residues at position +2 in the modeling of DNA–zinc-finger protein interaction is obviously over-simplified. With the development of high-throughput dsDNA microarray technology, bacterial one-hybrid systems, and improved SELEX methods (Bulyk et al., 2001; Liu and Stormo, 2005; Meng et al., 2005; Roulet et al., 2002), binding site data is becoming increasingly easy and inexpensive to obtain, which will lead to more accurate modeling that will facilitate the understanding the regulation of gene expression.

ACKNOWLEDGEMENTS

We thank David Granas for his examination on the distribution of key amino acid residues of zinc-finger proteins in Pfam dataset. We also thank Ryan Christensen for his independent tests of our prediction performance and comparisons with other methods.

Funding: This work was supported by NIH grant HG00249 to G.D.S.

Conflict of Interest: none declared.

REFERENCES

  1. Ahmad S, et al. Analysis and prediction of DNA-binding proteins and their binding residues based on composition, sequence and structural information. Bioinformatics. 2004;20:477–486. doi: 10.1093/bioinformatics/btg432. [DOI] [PubMed] [Google Scholar]
  2. Albright RA, Matthews BW. How Cro and lambda-repressor distinguish between operators: the structural basis underlying a genetic switch. Proc. Natl Acad. Sci. USA. 1998;95:3431–3436. doi: 10.1073/pnas.95.7.3431. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Barash Y, et al. Proceedings of the Seventh Annual International Conference on Computational Molecular Biology (RECOMB)NY, ACM. 2003. Modeling dependencies in protein–DNA binding sites. [Google Scholar]
  4. Bendtsen JD, et al. Improved prediction of signal peptides: SignalP 3.0. J. Mol. Biol. 2004;340:783–795. doi: 10.1016/j.jmb.2004.05.028. [DOI] [PubMed] [Google Scholar]
  5. Benos PV, et al. Additivity in protein-DNA interactions: how good an approximation is it? Nucleic Acids Res. 2002;30:4442–4451. doi: 10.1093/nar/gkf578. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Benos PV, et al. Probabilistic code for DNA recognition by proteins of the EGR family. J. Mol. Biol. 2002;323:701–727. doi: 10.1016/s0022-2836(02)00917-8. [DOI] [PubMed] [Google Scholar]
  7. Bulyk ML, et al. Exploring the DNA-binding specificities of zinc fingers with DNA microarrays. Proc. Natl Acad. Sci. USA. 2001;98:7158–7163. doi: 10.1073/pnas.111163698. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Bulyk ML, et al. Nucleotides of transcription factor binding sites exert interdependent effects on the binding affinities of transcription factors. Nucleic Acids Res. 2002;30:1255–1261. doi: 10.1093/nar/30.5.1255. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Choo Y, Klug A. Selection of DNA binding sites for zinc fingers using rationally randomized DNA reveals coded interactions. Proc. Natl Acad. Sci. USA. 1994;91:11168–11172. doi: 10.1073/pnas.91.23.11168. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Choo Y, Klug A. Toward a code for the interactions of zinc fingers with DNA: selection of randomized fingers displayed on phage. Proc. Natl Acad. Sci. USA. 1994;91:11163–11167. doi: 10.1073/pnas.91.23.11163. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Choo Y, Klug A. Physical basis of a protein-DNA recognition code. Curr. Opin. Struct. Biol. 1997;7:117–125. doi: 10.1016/s0959-440x(97)80015-2. [DOI] [PubMed] [Google Scholar]
  12. Damante G, et al. A molecular code dictates sequence-specific DNA recognition by homeodomains. EMBO J. 1996;15:4992–5000. [PMC free article] [PubMed] [Google Scholar]
  13. Elrod-Erickson M, et al. High-resolution structures of variant Zif268-DNA complexes: implications for understanding zinc-finger-DNA recognition. Structure. 1998;6:451–464. doi: 10.1016/s0969-2126(98)00047-1. [DOI] [PubMed] [Google Scholar]
  14. Elrod-Erickson M, Pabo CO. Binding studies with mutants of Zif268. Contribution of individual side chains to binding affinity and specificity in the Zif268 zinc-finger-DNA complex. J. Biol. Chem. 1999;274:19281–19285. doi: 10.1074/jbc.274.27.19281. [DOI] [PubMed] [Google Scholar]
  15. Elrod-Erickson M, et al. Zif268 protein-DNA complex refined at 1.6 A: a model system for understanding zinc-finger-DNA interactions. Structure. 1996;4:1171–1180. doi: 10.1016/s0969-2126(96)00125-6. [DOI] [PubMed] [Google Scholar]
  16. Fairall L, et al. The crystal structure of a two zinc-finger peptide reveals an extension to the rules for zinc-finger/DNA recognition. Nature. 1993;366:483–487. doi: 10.1038/366483a0. [DOI] [PubMed] [Google Scholar]
  17. Finn RD, et al. Pfam: clans, web tools and services. Nucleic Acids Res. 2006;34:D247–251. doi: 10.1093/nar/gkj149. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Hamilton TB, et al. Comparison of the DNA binding characteristics of the related zinc-finger proteins WT1 and EGR1. Biochemistry. 1998;37:2051–2058. doi: 10.1021/bi9717993. [DOI] [PubMed] [Google Scholar]
  19. Hart CE, et al. Connectivity in the yeast cell cycle transcription network: inferences from neural networks. PLoS Comput. Biol. 2006;2:e169. doi: 10.1371/journal.pcbi.0020169. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Kaplan T, et al. Ab initio prediction of transcription factor targets using structural knowledge. PLoS Comput. Biol. 2005;1:e1. doi: 10.1371/journal.pcbi.0010001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Kono H, Sarai A. Structure-based prediction of DNA target sites by regulatory proteins. Proteins. 1999;35:114–131. [PubMed] [Google Scholar]
  22. Liu J, Stormo GD. Combining SELEX with quantitative assays to rapidly obtain accurate models of protein-DNA interactions. Nucleic Acids Res. 2005;33:e141. doi: 10.1093/nar/gni139. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Liu J, Stormo GD. Quantitative analysis of EGR proteins binding to DNA: assessing additivity in both the binding site and the protein. BMC Bioinform. 2005;6:176. doi: 10.1186/1471-2105-6-176. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Luscombe NM, et al. An overview of the structures of protein-DNA complexes. Genome Biol. 2000;1 doi: 10.1186/gb-2000-1-1-reviews001. REVIEWS001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Luscombe NM, et al. NUCPLOT: a program to generate schematic diagrams of protein-nucleic acid interactions. Nucleic Acids Res. 1997;25:4940–4945. doi: 10.1093/nar/25.24.4940. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Luscombe NM, et al. New tools and resources for analysing protein structures and their interactions. Acta Crystallogr. D Biol. Crystallogr. 1998;54:1132–1138. doi: 10.1107/s0907444998007318. [DOI] [PubMed] [Google Scholar]
  27. Mahony S, et al. Regulatory conservation of protein coding and microRNA genes in vertebrates: lessons from the opossum genome. Genome Biol. 2007;8:R84. doi: 10.1186/gb-2007-8-5-r84. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Mandel-Gutfreund Y, Margalit H. Quantitative parameters for amino acid-base interaction: implications for prediction of protein-DNA binding sites. Nucleic Acids Res. 1998;26:2306–2312. doi: 10.1093/nar/26.10.2306. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Matthews BW. Protein-DNA interaction. No code for recognition. Nature. 1988;335:294–295. doi: 10.1038/335294a0. [DOI] [PubMed] [Google Scholar]
  30. Matys V, et al. TRANSFAC and its module TRANSCompel: transcriptional gene regulation in eukaryotes. Nucleic Acids Res. 2006;34:D108–D110. doi: 10.1093/nar/gkj143. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Meng X, et al. A bacterial one-hybrid system for determining the DNA-binding specificity of transcription factors. Nat. Biotechnol. 2005;23:988–994. doi: 10.1038/nbt1120. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Messina DN, et al. An ORFeome-based analysis of human transcription factor genes and the construction of a microarray to interrogate their expression. Genome Res. 2004;14:2041–2047. doi: 10.1101/gr.2584104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Michael Gromiha M, et al. Intermolecular and intramolecular readout mechanisms in protein-DNA recognition. J. Mol. Biol. 2004;337:285–294. doi: 10.1016/j.jmb.2004.01.033. [DOI] [PubMed] [Google Scholar]
  34. Miller JC, Pabo CO. Rearrangement of side-chains in a Zif268 mutant highlights the complexities of zinc-finger-DNA recognition. J. Mol. Biol. 2001;313:309–315. doi: 10.1006/jmbi.2001.4975. [DOI] [PubMed] [Google Scholar]
  35. Machine Learning. The McGraw-Hill Companies, Inc.; 1997. [Google Scholar]
  36. O'Flanagan RA, et al. Non-additivity in protein-DNA binding. Bioinformatics. 2005;21:2254–2263. doi: 10.1093/bioinformatics/bti361. [DOI] [PubMed] [Google Scholar]
  37. Pabo CO, Sauer RT. Protein-DNA recognition. Annu. Rev. Biochem. 1984;53:293–321. doi: 10.1146/annurev.bi.53.070184.001453. [DOI] [PubMed] [Google Scholar]
  38. Pavletich NP, Pabo CO. zinc-finger-DNA recognition: crystal structure of a Zif268-DNA complex at 2.1 A. Science. 1991;252:809–817. doi: 10.1126/science.2028256. [DOI] [PubMed] [Google Scholar]
  39. Qian N, Sejnowski TJ. Predicting the secondary structure of globular proteins using neural network models. J. Mol. Biol. 1988;202:865–884. doi: 10.1016/0022-2836(88)90564-5. [DOI] [PubMed] [Google Scholar]
  40. Roulet E, et al. High-throughput SELEX SAGE method for quantitative modeling of transcription-factor binding sites. Nat. Biotechnol. 2002;20:831–835. doi: 10.1038/nbt718. [DOI] [PubMed] [Google Scholar]
  41. Rumelhart D, et al. The basic ideas in neural networks. Comminications pf the ACM. 1994;37:87–92. [Google Scholar]
  42. Seeman NC, et al. Sequence-specific recognition of double helical nucleic acids by proteins. Proc. Natl Acad. Sci. USA. 1976;73:804–808. doi: 10.1073/pnas.73.3.804. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Segal DJ, et al. Toward controlling gene expression at will: selection and design of zinc-finger domains recognizing each of the 5′-GNN-3′ DNA target sequences. Proc. Natl Acad. Sci. USA. 1999;96:2758–2763. doi: 10.1073/pnas.96.6.2758. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Suzuki M, Yagi N. DNA recognition code of transcription factors in the helix-turn-helix, probe helix, hormone receptor, and zinc-finger families. Proc. Natl Acad. Sci. USA. 1994;91:12357–12361. doi: 10.1073/pnas.91.26.12357. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Tomovic A, Oakeley EJ. Position dependencies in transcription factor binding sites. Bioinformatics. 2007;23:933–941. doi: 10.1093/bioinformatics/btm055. [DOI] [PubMed] [Google Scholar]
  46. Wolfe SA, et al. Beyond the “recognition code”: structures of two Cys2His2 zinc-finger/TATA box complexes. Structure. 2001;9:717–723. doi: 10.1016/s0969-2126(01)00632-3. [DOI] [PubMed] [Google Scholar]
  47. Wolfe SA, et al. DNA recognition by Cys2His2 zinc-finger proteins. Annu. Rev. Biophys. Biomol. Struct. 2000;29:183–212. doi: 10.1146/annurev.biophys.29.1.183. [DOI] [PubMed] [Google Scholar]
  48. Workman CT, et al. enoLOGOS: a versatile web tool for energy normalized sequence logos. Nucleic Acids Res. 2005;33:W389–W392. doi: 10.1093/nar/gki439. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Zhou Q, Liu JS. Modeling within-motif dependence for transcription factor binding site predictions. Bioinformatics. 2004;20:909–916. doi: 10.1093/bioinformatics/bth006. [DOI] [PubMed] [Google Scholar]

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES