Findings in Schizophrenia by Tract-Oriented DT-MRI Analysis

1 Introduction

Schizophrenia is one of the major disabling brain disorders. It has been hypothesized that oligodendroglial dysfunction and subsequent myelin abnormalities contribute to the schizophrenic syndrome [1]. Diffusion tensor MRI has been employed by several groups in the past to investigate myelin integrity in patients with schizophrenia. Reduced diffusion anisotropy has been reported in prefrontal cortex [2], cingulum [3], uncinate fasciculus [4, 5], corpus callosum [6, 7], and arcuate facsiculus [4]. However, other studies find no significant difference in some of the above structures [3, 8, 9]. We believe that the inconsistency in experimental results is in part due to the difference in specifying the regions over which the anisotropy is measured. Clinical studies in the past are mostly either based on averaging the quantitative parameters over expert-specified regions of interest (ROIs) or used a voxel-by-voxel comparison. The former is sensitive to the accuracy of specifying the ROI, while the latter are susceptible to registration errors. Most recently, a tract-specific analysis has been proposed to more accurately define the measurement regions [10]. Jones et. al perform tractography to obtain the pathways of each fiber tract and then report a single number by averaging the parameter of interest along all pathways that belong to a given tract. However, local variation of the quantitative parameters is not captured in their analysis.

In this work, we propose a tract-oriented analysis in which parameters of interest are studied along the arc length of the tract. This allows us to study local variations that are missed in an ROI-based analysis or in the study performed in [10]. We apply the proposed procedure on a population of 18 patients with chronic schizophrenia and 19 normal subjects, analyze several fiber bundles that have been indicated in schizophrenia research, and demonstrate the sensitivity of our approach to identifying the group differences in diffusivity measures such as fractional anisotropy (FA) and mean diffusivity (MD).

2 Method

In this study, the probabilistic tract-oriented quantitative analysis described in [11] is extended to incorporate an anatomical atlas of fiber tracts. We use an atlas of fiber tracts [12], which is composed of a set of labeled ROIs, each corresponding to an anatomically-known bundle of fiber tracts in human brain. These ROIs are used to seed the tractography and to guide the clustering algorithm as detailed in this section. We add prototype curves to the atlas to represent the shape of the trajectories in each tract. This is a one-time process done by an expert by manual selection of trajectories that are representative of the shape of the tracts. These prototype curves are also used as the initial cluster centers in the clustering algorithm.

Fractional anisotropy maps calculated from DT-MRI data are first mapped into a common coordinate system using a congealing registration [13] and then into the atlas (MNI) space using an affine registration [14]. As opposed to a series of pair-wise subject-template registrations, this approach prevents the introduction of bias in the population study.

Atlas-specified regions corresponding to each fiber tract are mapped to the coordinate system of each case using the affine transformation obtained from registration. We then apply a dilation operation on those regions to ensure that they contain the fiber tract of interest. These regions are used to seed a streamline tractography [15] that produces fiber trajectories by following the principal eigenvector of the tensor at each voxel. We terminate the trajectory propagation when an FA value less than 0.15 is reached. The quantitative parameters of interest, such as fractional anisotropy and the diffusivity eigenvalues, are collected at each point on the trajectories and stored for further quantitative analysis.

Trajectories obtained from the tractography algorithm on each case are all mapped into the common MNI space and then clustered using our expectation-maximization (EM) algorithm first proposed in [11]. We employ the atlas-specified ROIs as the spatial prior information while the prototype trajectories of the atlas are used as the initial cluster centers for initializing the EM iteration. A gamma mixture model is used to describe the distribution of the distance between the trajectories and 3D cluster centers as detailed in [11]. This distance includes both the Euclidean distance and the shape difference between the trajectories and cluster centers and is obtained by establishing the point-by-point correspondences between them. Atlas-specified membership prior for each trajectory is determined by mapping the trajectory to the atlas ROI and counting the number of overlapping points. The membership likelihood from the mixture model is then combined with the atlas prior in a Bayesian framework to determine the membership probability. The output of the clustering algorithm is the probabilistic assignment of the trajectories to each cluster, a set of cluster centers, and the point correspondence between the trajectories and the cluster centers. Outliers are identified as those trajectories that receive small membership likelihood from all clusters, and they are removed from further processing.

Tract-oriented quantitative analysis is performed by calculating the weighted averages of the parameters of interest along the arc length of the cluster centers. By doing so, trajectories with low membership probability contribute less to the quantitative analysis. Such analysis can be performed on a case-by-case basis or on all cases that belong to a group. Analysis of variance (ANOVA) and permutation test with 1000 iterations are used for statistical group analysis. The correction for multiple comparison is not made.

3 Experiments and Results

For this experiment, we used DTI images acquired on a 3 Tesla GE system using an echo planar imaging (EPI) DTI sequence. We used a double echo option to reduce eddy-current related distortions, and an 8-Channel coil that allows us to perform parallel imaging using ASSET (Array Spatial Sensitivity Encoding Techniques, GE) with a SENSE-factor (speed-up) of 2 to reduce the impact of EPI spatial distortions. Eighty-five axial slices parallel to the AC-PC line covering the whole brain were acquired, with the following parameters: 51 directions with b = 900, 8 baseline scans with b = 0, TR = 17000 ms, TE = 78 ms, FOV = 24 cm, 144×144 encoding steps, and 1.7 mm slice thickness.

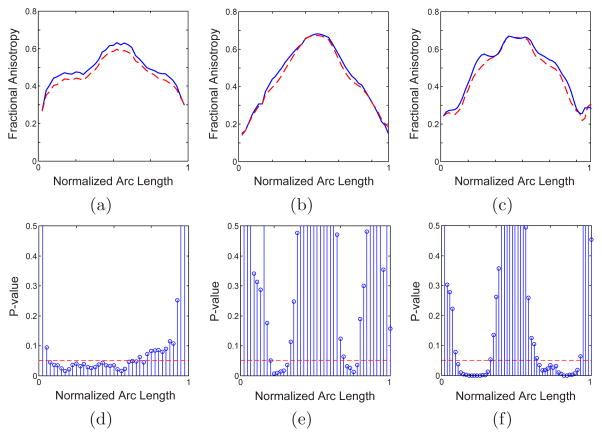
As mentioned above, at least some of the schizophrenia symptoms are hypothesized to be related to the disruptions of the interhemisphere connectivity, which makes study of corpus collasum of great interest. To analyze corpus callosum in schizophrenia, we analyzed DTI data from 19 control subjects, and 18 chronic schizophrenics, matched on age, gender and parental socioeconomic status. Figure 1 shows the clustered trajectories from genu and splenium of the corpus collasum, colored based on the local fractional anisotropy. Our method allows us to divide the splenium into its upper and lower parts (tracts interconnecting parietal and occipital lobes respectively), as they pose different shapes. Figure 2 compares the fractional anisotropy in genu and upper and lower splenium for healthy and schizophrenic subjects. Significant FA reduction is observed in genu, which confirms earlier reports of similar observations [16]. Moreover, our analysis clearly indicates that FA reduction is primarily in left part of the genu which is consistent with a few detailed voxel-based studies [16].

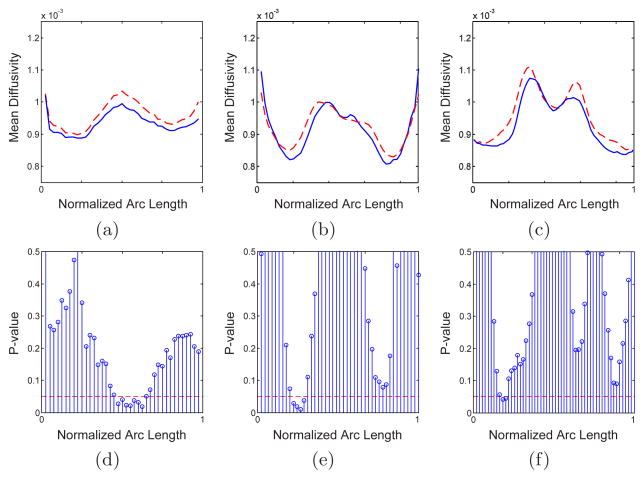
We also observed significant reduction of the fractional anisotropy in splenium, especially in its lower part. As can be seen in Fig. 2, the FA reduction is seen bilaterally, in the middle of each side. To our knowledge, only one voxelwise analysis [7] was sensitive enough to observe such a bilateral FA reduction in splenium. Similar analysis is performed for mean diffusivity and the results are given in Fig. 3. Increased mean diffusivity is only significant in small portions of the genu (in the middle) and the splenium (in the left).

Besides corpus callosum, fronto-temporal connections are the second most frequently indicated fiber tracts in pathophysiology of schizophrenia. In this work, we thus examined the uncinate fasciculus, which is the most prominent of all white matter fiber tracts connecting the frontal and temporal lobes, and which has been implicated in schizophrenia in several publications [4]. Figure 4(a) depicts the trajectories from left uncinate fasciculus from all subjects mapped into the atlas space and colored with the local fractional anisotropy. As shown in Fig. 4, increase in FA and MD is significant only for a small part at the middle of this structure. However, significant increase in the major diffusivity eigenvalue, i.e. parallel to the tract, is observed. This observation, which has not been reported in the past, indicates that FA alone is not enough for DTI analysis. Although the origins of increased parallel diffusivity are unknown and it opposes general views of axonal damage, it should be noted that such an increase is not impossible. In fact, increased parallel diffusivity has been reported previously for displaced fiber tracts [17].

4 Discussion

As shown in the previous section, our tract-oriented method is able to reveal the local variations of the diffusion parameters. This approach is thus very sensitive compared to ROI-based methods, as the differences might be lost when parameters (such as FA) over the entire tract are being averaged and compared between groups. Although voxel-based methods are potentially able to show the local variations, the results are very sensitive to registration errors. Abnormalities within the genu of the corpus callosum are localized in the midsagittal region, thus appear in the portion of the tract where the fibers of the tract run all alone, which suggests disruptions in tracts interconnecting frontal lobes. On the other hand, changes observed in schizophrenia group in the parasagittal, but not midsagittal portion of the splenium of the corpus callosum are suggestive of factors other than disruption of corpus collasum integrity, such as interfering and crossing fibers.

We would like to stress that a comprehensive DTI analysis requires examination of both anisotropy measures, such as FA, and the diffusivity magnitude, e.g. MD, or equivalently the parallel and radial diffusivity eigenvalues [18]. The diffusivity perpendicular to the fiber tract reflects changes in axonal membrane, myelin, or extracellular space [19], whereas membrane disintegration and gliosis may create diffusion barriers in the direction of the fiber tract and reduce the parallel diffusivity [19]. Axonal damage may also result in reduced diffusivity perpendicular to the fiber tract [19]. The analysis performed on the uncinate fasciculus clearly demonstrates the fact that fractional anisotropy alone is not sufficient to study white matter integrity.

Another important issue, which is essential in group analysis and was discussed in previous schizophrenia studies [10], is the age and/or disease-dependence of the diffusion parameters. To illustrate this point, in Fig. 5 we have plotted the age-dependence of the fractional anisotropy in the mid-saggital point of the lower splenium. While healthy subjects exhibit small age-dependence in our age range, considerable reduction of FA is observed in schizophrenic cases upon aging.

5 Conclusion

A tract-oriented quantitative analysis of genu, splenium, and left uncinate fasiculus in schizophrenia was presented. The method is able to reveal the local variations of the fiber integrity, which are lost when the quantitative parameters are averaged over the entire fiber tract in ROI-based methods. Significant reduction in fractional anisotropy in the left part of the genu and bilaterially in the middle of each side of the splenium was observed. While FA analysis shows no significant change in uncinate fasciculus, significant increase in the parallel diffusivity was observed in this structure. Although the origins of this increase are unknown, this finding emphasizes the fact that FA alone is not enough for quantitative analysis. Finally, it was shown that age-dependence of the diffusivity parameters is an important factor when performing group analysis.