Abstract
Sensory integration is a characteristic feature of superior colliculus (SC) neurons. A recent neural network model of single-neuron integration derived a set of basic biological constraints sufficient to replicate a number of physiological findings pertaining to multisensory responses. The present study examined the accuracy of this model in predicting the responses of SC neurons to pairs of visual stimuli placed within their receptive fields. The accuracy of this model was compared to that of three other computational models (additive, averaging and maximum operator) previously used to fit these data. Each neuron’s behavior was assessed by examining its mean responses to the component stimuli individually and together, and each model’s performance was assessed to determine how close its prediction came to the actual mean response of each neuron and the magnitude of its predicted residual error. Predictions from the additive model significantly overshot the actual responses of SC neurons and predictions from the averaging model significantly undershot them. Only the predictions of the maximum operator and neural network model were not significantly different from the actual responses. However, the neural network model outperformed even the maximum operator model in predicting the responses of these neurons. The neural network model is derived from a larger model that also has substantial predictive power in multisensory integration, and provides a single computational vehicle for assessing the responses of SC neurons to different combinations of cross-modal and within-modal stimuli of different efficacies.
Keywords: Within-modal, multisensory, computation, maximum, averaging
1. Introduction
Stimulus detection and localization are primary functions of the superior colliculus (SC). These behavioral functions are facilitated by its multiple sensory representations (i.e. visual, auditory, and somatosensory), and the ability of its neurons to integrate the information derived from cross-modal events. Consequently, concordant cross-modal stimuli evoke SC responses that can be well above those elicited by their individual component stimuli (e.g., Meredith and Stein 1983; Wallace et al., 1998; Jiang et al., 2001; Calvert et al., 2004; Perrault et al., 2005; Stanford et al., 2005). Multisensory response enhancement in single neurons in the cat SC depends mostly on the synergistic interaction of unisensory descending influences from the anterior ectosylvian cortex (AES) (Wallace and Stein 1994; Wilkinson et al., 1996; Jiang, et al., 2001, 2002; Stein 2005; Stein and Stanford 2008). Previous studies have shown that inactivation of the AES compromises this multisensory enhancement, but somehow does so without eliminating its modality-specific drive; thus, SC neurons still respond to multiple modality-specific stimuli, but fail to integrate their inputs to produce enhancement.
Rowland et al., (2007) recently proposed a biologically-inspired neural network model that incorporates the specific role played by cortico-collicular input s i n multisensory integration. It successfully replicates a number of physiological observations pertaining to multisensory integration. This model contains two essential features. First, that all excitatory inputs (cortically-derived or otherwise) are balanced by inhibitory inputs through contacts onto interneurons and second, that cortico-collicular afferent terminals conveying information from different senses cluster preferentially to end on the same electrotonic compartments of target neurons. Each compartment is modeled as implementing a synergistic computation (see Experimental Procedures) predicated on the expected interaction between real synapses utilizing AMPA and NMDA receptors. Physiologically, the voltage-dependency of NMDA receptors introduces a nonlinear transformation such that greater levels of input yield disproportionately greater output currents. This biological feature is represented in the model as a squaring operation on the summed inputs received by each compartment. The summed output of each compartment, interpreted as the net excitatory input to the neuron, is divided by the net inhibitory input, which is proportional to the sum of all inputs (see Experimental Procedures; Eqs. 1, 2).
Given the specificity of the constraints dictating the form of the Rowland et al., (2007) neural network model, we sought to determine if its predictions would generalize and account for other physiological characteristics of SC neurons. One prediction of interest is how responses evoked by multiple within-modal stimuli would differ from those evoked by cross-modal stimuli. Unlike cortico-collicular cross-modal afferents, afferents stimulated by different within-modal stimuli are specified not to cluster together within electrotonic compartments (Figure 1). Thus, according to the model, these excitatory inputs should be squared then summed rather than summed then squared. Consequently, the model predicts that the response to multiple within-modal stimuli should be similar to either the average or maximum of the single-stimulus responses. A series of recent physiological studies by Alvarado et al., (2007a, 2007b) explored the unisensory integrative capabilities of multisensory SC neurons using multiple visual stimuli. Here we evaluate the accuracy of the neural network model in predicting those data. Its accuracy in predicting the data in objectively quantified by comparing it to the accuracy of three other (not biologically based) mathematical models used previously: 1) a maximum operator model (which predicts that the response to two stimuli will be identical to the best response to either stimulus individually), 2) an averaging model (which predicts that the response to two stimuli will be identical to the average of the two single stimulus responses), and 3) an additive model (which predicts that the response to two stimuli will be identical to the summed responses to the two single stimuli). The predictions of the neural network not only closely matched the data, but proved to be the most accurate overall. Furthermore, the prediction errors of the non-biologically based models are consistent with expectations based on the neural network model: the additive and maximum operator models overestimate response magnitudes while the averaging model underestimates them.
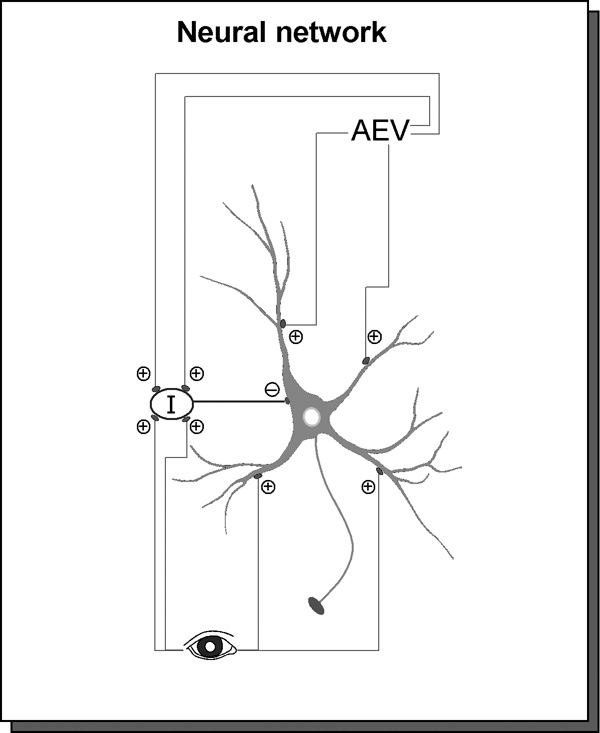
Figure 1. An illustration of the essential architecture of the neural network model.
Stimulus information is conveyed to the SC through ascending and cortically-derived descending afferents. The inputs independently stimulated by two visual stimuli are depicted as separate channels. These inputs contact principal SC neurons (as illustrated in the schematic) and an interneuron population (I) which projects inhibitory (GABAergic) connections to the principal neuron. Inputs belonging to the same sensory channel do not preferentially cluster together on the principal neuron, thus establishing a balance of excitation and inhibition that predicts responses to two stimuli that are no greater than the response to a single stimulus.
2. Results
A total of 158 visually-responsive neurons were studied in the multisensory (deep) layers of the SC. Because unisensory visual integration takes place in both multisensory and unisensory neurons (Alvarado et al., 2007a; 2007b), both were included in this sample population (multisensory: n = 87 [55%]; unisensory: n = 71 [45%]).
2.1. Responses to within-modal tests
2.1.1. Multisensory neurons
Figure 2 shows the results of within-modal tests in a typical multisensory neuron. These tests consisted of interleaved trials in which the two visual stimuli (V1 and V2) were presented within the neuron’s receptive field individually and in combination, and at 3 levels of effectiveness. As shown previously, responses to within-modal stimuli did not significantly exceed those to the most effective of the component stimuli at any effectiveness level (Alvarado et al., 2007a; 2007b). This result is in marked contrast to the response enhancement typically observed when visual and non-visual stimuli (cross-modal) are combined (e.g., see Meredith and Stein, 1986; Kadunce et al., 1997; Stein 1998; Wallace et al., 1998; Jiang et al., 2001; Perrault et al., 2003; Stanford et al., 2005) and speaks to differences in the mechanisms underlying multisensory and unisensory integration.
Figure 2. Within-modal test: multisensory neuron.
The visual (dark ovoid) receptive fields and the positions of the visual stimuli within the receptive fields are shown in the schematics of visual space (each circle = 10E) at the top of the figure. The visual stimuli were moving bars of light (arrow) as indicated by the electronic traces shown as ramps. Below the receptive fields and electronic stimulus traces, are shown the neuronal responses to these stimuli. These are displayed in rasters, histograms and summary bar graphs at three ascending levels of visual stimulus effectiveness. The within-modal tests in a multisensory neuron produced responses that were no different from that to the best unisensory component stimulus and the computational operation utilized was subadditive at all levels of stimulus effectiveness.
The absence of enhancement from the combination of the two visual stimuli was reflected in enhancement index values, which were generally near zero or below (see summary bar graphs in Figure 2). Accordingly, unisensory integration proved to be subadditive in all cases.
2.1.2. Unisensory neurons
The results from unisensory neurons paralleled those described above for multisensory neurons. Once again, presenting two effective visual stimuli simultaneously within a neuron’s visual receptive field rarely produced an enhanced response regardless of their individual effectiveness. A representative example is shown in Figure 3. The responses of this neuron to the stimulus combination were either statistically indistinguishable from, or less than those evoked by the most effective stimulus component alone (see summary bar graphs in Figure 2) and were subadditive at all levels of stimulus effectiveness.
Figure 3. Within-modal test: unisensory neuron.
Here are shown the results of within-modal tests in a unisensory visual neuron. The results are similar to those obtained in multisensory neurons. Essentially no response enhancement resulted from the addition of the second visual stimulus and responses to the stimulus combination were subadditive at all levels of stimulus effectiveness. Conventions are the same as in Figure 2.
2.2. Population responses
At the population level, the responses to within-modal combinations yielded a mean enhancement index of −7.0 ± 3.0 %. Consistent with the individual examples shown above, the mean enhancement indices were not significantly different for multisensory (−9.7 ± 4.4 %) and unisensory neurons (−3.6 ± 3.9 %). Statistically significant enhancement was observed for only 5.7 % (9/158) of the sample, with similar incidence in multisensory (5.8 %, 5/87) and unisensory (5.6 %, 4/71) neurons. In fact, it was far more common to observe response depression (25.3 %, 40/158) in these neurons. Response depression was most often manifest as an approximate averaging of the responses to the component stimuli, and was observed with similar frequency in multisensory (27.6 %, 24/87) unisensory (22.5 %, 16/71) neurons.
2.3. Evaluating models for unisensory integration
In order to evaluate the accuracy of the neural network model in describing the products of unisensory integration, its predictions were compared to those of three other computational models (maximum operator, averaging, and additive) used previously to analyze these data (Alvarado et al., 2007a, 2007b).
The neural network model predicts that the response to two modality-specific stimuli will be determined by Eq. 2; that is, it will reflect a nonlinear combination of the responses evoked by either stimulus individually. The additive model predicts that the response to two stimuli will be equivalent to the sum of the responses evoked by the stimuli individually (Stanford et al., 2005; Alvarado et al., 2007a, 2007b). The averaging model predicts that the response to two stimuli will be equivalent to the mean of the responses evoked by the stimuli individually (Heeger, 1992; Rolls and Tovee, 1995; Carandini et al., 1997; Recanzone et al., 1997; Britten and Heuer, 1999; Reynolds et al., 1999; Treue et al., 2000; Heuer and Britten, 2002; Zoccolan et al., 2005). The maximum operator model predicts that the response to two stimuli will be equivalent to the strongest response evoked by either stimulus individually (Riesenhuber and Poggio 1999; Gawne and Matin 2003; Lampl et al., 2004). An illustration of the predictions of each model is shown in Figure 4.
Figure 4. Predicted responses according to the different models.
The histograms show the predicted responses for each one of the model evaluated. In the neural network model (A) the predicted combined response will fall along a continuum determined by Equation 2. This equation predicts that the responses approximate those predicted by a maximum operator (described in D, below) when the effectiveness of the two visual stimuli is very far apart as illustrated in the plot on the left. However, it also predicts a mix of averaging (as shown in the plot on the right, and described in C, below) and maximum operator responses when the effectiveness of the two visual stimuli is closer together. In the additive model (B) the predicted combined response is similar to the sum of the responses evoked by the stimuli individually. In the averaging model (C) the predicted combined response is similar to the mean of the responses evoked by the stimuli individually. In the maximum operator model (D) the predicted combined response is similar to the strongest response evoked by either stimulus individually
The predictions of the neural network model for the mean within-modal response and those for the additive, averaging, and maximum operator computations were compared to the actual mean response obtained. Figure 5 displays the observed within-modal mean response (gray) and those predicted by each of the four models. The predictions of the neural network (blue) and maximum operator (red) models were statistically indistinguishable from the actual mean response (neural network (t = −0.60, df = 314, p > 0.05), maximum operator (t = 0.84, df = 314, p > 0.05)). In contrast, the additive model prediction (green) significantly exceeded the actual mean response (t = 5 . 3 8 , d f = 3 1 4 , p < 0 . 0 0 0 1 ) and the averaging model (yellow) significantly underestimated the responses that were actually observed (t = −2.20, df = 314, p < 0.05).
Figure 5. Mean impulses of the actual and predicted responses.
Shown here are population data consisting of the mean impulses number of the actual unisensory responses and those predicted by the 4 models evaluated. There were significant differences between the actual responses and those predicted by the additive and averaging models. The additive model overestimated the responses, the averaging model underestimated the responses, but no significant differences were found between the actual and predicted responses of the maximum operator and the neural network models. ** p < 0.01; * p < 0.05.
The relationships between the predicted and the observed within-modal responses are shown in greater detail in Figure 6 which plots predicted values against observed values for each model. As expected, the predictions of the additive (Figure 6A) and averaging (Figure 6B) models deviated consistently from the observed values, with points scattered above (overestimate) and below (underestimate) the line of equality, respectively. Note also that the predictions became less accurate as a function of response strength. In contrast, the predictions of both the maximum operator (Figure 6C) and neural network (Figure 6D) models were in good agreement with the observed values with each showing a relatively tight clustering around the line of equality at all levels of response vigor. However, a close inspection of the lower end of the plots showed a slightly better fit in the neural network model compared to the maximum operator model (compare inset in Figure 6C with inset in Figure 6D).
Figure 6. Unisensory responses are predicted better by the maximum operator and neural network models.
The graphs show each neuron’s mean response to the stimulus combination plotted against the mean of its predicted responses by the additive (A), averaging (B), maximum operator (C) and neural network (D) models. In the additive model (A), the majority of the responses to the within-modal tests fell below the line of unity, reveal response overestimation. Conversely, in the averaging model (B), most of the combined unisensory responses fell above the line of unity, revealing response underestimation. In the maximum operator (C) and neural network (D) models, the predicted unisensory responses were clustered around the line of unity, revealing better prediction by these two models than the additive and averaging models. Insets: a blow-up of the first ten values of each plot.
A more direct and quantitative comparison of each model’s performance is shown in Fig. 7 which used a simple contrast index to examine the magnitude of the differences between the predicted and actual responses (see Experimental Procedures). Values can be distributed between −1 and 1, with positive values indicative of predictive overestimates and negative values predictive underestimates. Note that the majority of responses predicted by the additive model yielded positive contrast values (Figure 7A) with a mean of 0.26 ± 0.02. On the contrary, values for averaging (Figure 7B), maximum operator (Figure 7C) and neural network (Figure 7D) models were closer to zero, with a slight shift to left (−0.05 ± 0.02) for the averaging model (Figure 7B) and to the right (0.07 ± 0.02) for the maximum operator model (Figure 7C). Values for the neural network model (Figure 7D) were more evenly distributed about zero (0.01 ± 0.02), indicating that the predicted responses did not differ significantly from that in the actual combined responses. The differences among models are readily apparent in the comparison of cumulative density functions shown in Figure 7E.
Figure 7. Contrast index reveals the predictive accuracy of the neural network model.
The graphs illustrate the distributions contrast index values for additive (A), averaging (B), maximum operator (C) and neural network (D) models. A: In the additive model the majority of the predicted responses yielded positive contrast values, indicating response overestimation. Although, values for average (B), maximum operator (C) and neural network (D) models yielded predications much closer to the actual combined responses, the neural network (D) model was the most accurate having a mean nearest to zero. The relative performance of the 4 models is compared directly in (E) by plotting the cumulative density functions for each model’s distribution on the same axes.
3. Discussion
The principal result of this analysis is that the neural network model of the SC proposed by Rowland et al. (2007) not only predicted the products of unisensory integration with accuracy, but also generated more accurate predictions than other models previously used to characterize these products (additive, averaging, and maximum operator models). This result is somewhat surprising because the constraints of the neural network model were derived from observations of multisensory responses and their neural circuit dependencies without a deliberate attempt to model unisensory integration. The additive model was the worst in characterizing the dataset, the averaging model was slightly better, and the maximum operator model generated performance only slightly inferior to that of the neural network model. The maximum operator model typically overestimated the actual within-modal responses and the averaging model typically underestimated them, while the mean error of the neural network model prediction was very close to zero.
The fact that the additive model used in the evaluation of multisensory integration in SC neurons was the worst of all the models examined, with a systematic overestimation of the unisensory responses, is in agreement with previous observations indicating that unisensory integration consisted mainly of subadditive interactions (Alvarado et al., 2007a, 2007b). Similarly, it has been reported that the product of within-modal visual interactions in cortical visual neurons is in most cases subadditive (Movshon et al., 1978; Henry et al., 1978, Britten and Heuer, 1999; Carandini et al., 1997; Reynolds et al., 1999; Gawne and Martin, 2002; Lampl et al., 2004; Li and Basso, 2005). These observations prompt the search for more appropriate models to describe the products of unisensory integration. Some researchers have found evidence of products approximating an averaging model in diverse areas such as V1 (Heeger, 1992; Carandini et al., 1997), V2 and V4 (Reynolds et al., 1999), MT (Recanzone et al., 1997; Britten and Heuer, 1999; Treue et al., 2000; Heuer and Britten, 2002), and IT (Rolls and Tovee, 1995; Zoccolan et al., 2005). Other researchers have found evidence for the implementation of a maximum operation during unisensory integration for complex cells in V1 (Lampl et al., 2004) and V4 (Gawne and Martin, 2002).
In previous observations both averaging and maximum operator models could partially explain the data from SC neurons, but uniform implementations of these two models were not frequently observed (Alvarado et al., 2007a). For instance, while the implementation of maximum operator was noted in about 10% of the sample, the implementation of averaging was found in about 20%. More common, however, was that in about 60% of neurons there was not a consistent pattern of the maximum or averaging operations across stimulus level or stimulus efficacy (Alvarado et al., 2007a). Similar results have been reported in V4 visual cortical neurons (Gawne and Martin, 2002). In this latter study, the authors using within-modal tests suggested that the maximum operator as well as the averaging models did a relatively good job predicting the unisensory combined response, with a slightly better performance of the maximum operator model over the averaging model (Gawne and Martin, 2002). The absence of a consistent pattern of unisensory integration in the majority of the neurons (Alvarado et al., 2007a) as well as the relatively good performance of both maximum operator and averaging models to predict the unisensory combined responses, raised the question of whether unisensory integration could not be explained by maximum operator or averaging alone.
As noted earlier, Rowland and colleagues (2007) have developed a neural network model to help explain the physiological components underlying multisensory integration in the SC. The model specifies that all excitatory inputs are paralleled by inhibitory inputs (through contacts onto interneurons), and a synergistic interaction between cortico-collicular inputs derived from different sensory modality. This synergistic interaction is interpreted as resulting from the interactions between synapses clustered onto the same dendritic compartment. If the cortex is deactivated (V=A=0 in Eq. 2), the predicted response does not vary substantially from the response to a single stimulus in isolation, which reproduces the empirical finding (Jiang et al., 2001; Alvarado et al., 2007b). Interestingly, because the model specifies that descending and ascending inputs from the same modality will not cluster together, it also predicts that the response to multiple stimuli from the same modality will not evidence the synergistic computation observed for stimuli from different modalities. Thus, as is the case with the multisensory response when the cortex is deactivated, the responses to multiple unisensory stimuli are predicted to resemble the response to a single stimulus in isolation. A quantitative prediction for the unisensory product was obtained by simplifying Eq. 2 by removing the logarithm and scalar terms, allowing direct access to the underlying computation for multiple non-synergistic inputs: [(X2+Y2)/(X+Y)]. This equation behaves like a maximum operator when X and Y are very far apart, but a mix of averaging and maximum operator when they are closer together. Consequently it does a better job at predicting the data that either of the other models, but more importantly, is rooted in a computational framework that explains how the biological implementation of unisensory integration in the SC might be related to other aspects of SC physiology. Thus, present observations are consistent with the idea that the processes underlying multisensory and unisensory integration in SC neurons are substantially different (Alvarado et al., 2007a, 2007b), and both can be explained by the neural network model (Rowland et al., 2007).
It may be surprising that responses to two stimuli from the same sensory modality are not significantly enhanced over the response to a single stimulus, as two stimuli have double the energy and consequently might be expected to increase signal to noise ratios. One possible explanation is that multiple modality-specific stimuli cannot be precisely co-localized, and thus their simultaneous presentation increases the ambiguity in the optimal target location (although cross-modal stimuli in similar configurations do produce strongly enhanced multisensory responses). Another possibility is that the differing products of multisensory and unisensory integration properly reflect the pooling of information from two independent sources in the former, and the covariance between information sources in the latter. In either case, these data speak to an important caveat in the interpretation of multisensory enhancements as being produced by a “redundant targets effect” (e.g., Miller, 1982; Gondan et al., 2005; Leo et al., 2007; Lippert et al., 2007; Sinnett et al., 2008), as redundant targets from the same sensory modality do not yield equivalent enhancements either physiologically or behaviorally.
4. Experimental procedures
The protocols used were in accordance with the Guide for the Care and Use of Laboratory Animals (National Institutes of Health Publication 86-23) and were approved by the Animal Care and Use Committee of Wake Forest University School of Medicine, an AAALAC accredited institution.
4.1. Surgical procedures
Surgical procedures were performed as described previously (Jiang et al., 2001; Alvarado et al., 2007a, 2007b). Briefly, each cat (n=6) was anesthetized with ketamine hydrochloride (30 mg/kg i.m.) and acepromazine maleate (3–5 mg/kg im), intubated through the mouth, and maintained during the surgery with isoflurane (0.5–3%). After placing the animal into a stereotaxic head-holder, a craniotomy exposed the cortex overlying the SC. A hollow stainless steel cylinder, which provided access to the SC and that served to hold the cat’s head during recording experiments (McHaffie and Stein 1983), was attached stereotaxically to the skull over the craniotomy. During the surgery and recovery from anesthesia, a heating pad was used to maintain body temperature (37–38°C). Following surgery the animal received analgesics (butorphanol tartrate, 0.1– 0.4 mg/kg /6 h) as needed and antibiotics for 7–10 days (ceftriaxone 20 mg/kg/bid). The first recording session was performed 1–5 days after completing the antibiotic regimen.
4.2. Recording
For recording, the cat was anesthetized with ketamine hydrochloride (30 mg/kg im) and acepromazine maleate (3–5 mg/kg im), and maintained with continuous i.v. infusion of ketamine hydrochloride (4–6 mg/kg) and pancuronium bromide (0.1– 0.2 mg/kg/h; initial dose was 0.3 mg/kg) in 5% dextrose Ringer solution (3–6 ml/h). During the experiment, the cat was artificially respired, and respiratory rate and volume were adjusted to maintain end tidal CO2 at approximately 4.0%. The pupil of the eye contralateral to the SC to be studied was dilated with an ophthalmic solution of atropine sulfate (1%). A contact lens corrected the contralateral eye’s refractive error, and an opaque lens occluded the other eye. The recording chamber was cleaned and disinfected prior to recording. A glass-insulated tungsten electrode (tip diameter: 1–3 µm, impedance: 1–3 MΩ at 1 kHz) was advanced into the SC using a hydraulic microdrive. Sensory neurons were identified by their responses to visual, auditory and somatosensory “search” stimuli (see below). Neuronal responses were amplified, displayed on an oscilloscope, and played through an audio monitor. The X-Y coordinates and the recording depth of each neuron encountered were systematically recorded. At the end of the recording session the anesthetic and paralytic were discontinued and when stable respiration and locomotion were reinstated, the cat was returned to its home cage.
4.3. Neuronal search paradigm, receptive field mapping
Visual search stimuli included either moving or stationary flashed light bars projected onto a tangent screen 45 cm in front of the animal. Auditory search stimuli consisted of broadband (20–20,000 Hz) noise bursts, clicks and taps. A neuron was classified as multisensory when it was possible to evoke responses with more than one modality of search stimulus. In the present study only visually-responsive unisensory and visual-auditory multisensory neurons were included. After a neuron was isolated its visual receptive field was mapped, using the moving light bars, and plotted on standardized representations of visual and auditory space (Stein and Meredith 1993).
4.4. Visual tests
Visual test stimuli consisted of either one or two moving or stationary light bars placed within the neuron’s receptive field, close to its center. The light bars (0.11–13.0 cd/m2 against a 0.10 cd/m2 background) were generated by a Silicon Graphics workstation and projected by a Barcodata projector onto a tangent screen that subtended approximately 60° of visual angle in each hemifield. The stimuli could be moved in all directions across the receptive field at amplitudes of 1–110° and speeds of 1–400°/s.
4.5. General testing paradigm
To evaluate unisensory integration in SC neurons, neuronal responses were tested with two modality-specific (V1 alone and V2) stimuli alone and in combination (V1-V2). A rough determination of threshold and saturation was first made, and one additional, stimulus intensity was chosen to span these extremes (see also Perrault et al., 2005 and Stanford et al., 2005; Alvarado et al., 2007a; 2007b). Once determined, these same stimulus parameters (effectiveness and duration) were used for individual modality-specific and combined stimuli. During the tests, the light bars were located to have non-overlapping trajectories within the receptive field. Eight repetitions of each stimulus were presented and the stimulus conditions were interleaved in pseudo-random fashion with 8–20 seconds between trials. The resulting number of trials for each neuron was 24 (8 repetitions × 3 stimuli).
4.6. Data analysis and models for unisensory integration
All the data were analyzed using Statistica for Windows, release 7.0 (StatSoft, Inc), and expressed as mean ± standard error with the statistical significance set at the p<0.05 level. The differences among neuronal responses were assessed with statistical treatments that depended on whether the sample distributions met the assumptions of normality based on the Kolmogorov-Smirnov goodness of fit test. The following measures were used to evaluate neuronal activity:
Mean impulse count
The mean number of impulses evoked during a common time window his was calculated for each visual stimulus and visual stimulus combination. Spontaneous rates were measured for 1-s prior to the onset of the first stimulus during each set of trials and then normalized for the time window in which responses were counted (Jiang et al., 2001; Jiang and Stein, 2003; Alvarado et al., 2007a; 2007b). Although generally low, these rates were subtracted from the stimulus-evoked responses for subsequent analyses.
Enhancement index
This index quantifies the degree to which the response to a combined visual-visual stimulus exceeds the most effective modality-specific component stimulus according to the formula (Meredith and Stein 1983):
Where CR is the response (mean number of impulses/trial) evoked by the combined visual-visual stimuli and MSRmax is the response (mean number of impulses/trial) evoked by the most effective of the two modality-specific (visual) stimuli.
Additive model
To obtain the predicted distribution, for any given neuron all possible sums of V1 and V2 responses were computed as described elsewhere (Stanford et al., 2005; Alvarado et al., 2007a, 2007b). Thus, a sample distribution of 64 (8 × 8) possible sums was created from which 8 trials were randomly selected to create a mean of the combined response. This operation was repeated 10,000 times to obtain the predicted mean of the combined response.
Averaging model
Following a similar procedure to that described for the additive model, all possible averages of V1 and V2 responses were computed (Alvarado et al., 2007a). A sample distribution of 64 (8 × 8) possible averages was created and from that 8 trials were randomly selected to create a mean of the combined response. Again, the operation was repeated 10,000 times to obtain the final predicted mean of the combined response.
Maximum operator model
The maximum operator model predicts that the combined response to a within-modal test will be similar to that evoked by the most effective unisensory stimulus component (see Riesenhuber and Poggio 1999; Gawne and Matin 2003; Lampl et al., 2004). For each neuron studied, mean number of impulses was calculated for each of the two visual stimuli (V1 and V2) and the larger of the two means corresponded to the maximum prediction.
Neural network model
The Rowland et al., (2007) models specifies the following equation for predicting the influences of clustered (cortical) and non-clustered (ascending; other sources) inputs on the response of an SC multisensory neuron;
| Eq. 1 |
Where (Vu, Au) are ascending (non-clustered) inputs, (Vd,Ad) are cortico-collicular (clustered) inputs, and (T,Q) are scalars. The descending excitatory inputs are summed before squaring in the numerator, implementing a synergistic computation interpreted as resulting from the interaction expected between real synapses utilizing AMPA and NMDA receptors made on the same electrotonic compartments of target neurons. This equation can be simplified by assuming that ascending and descending influences from the same modality have the same strength, producing Eq. 2:
| Eq. 2 |
Based on these formulae, the predicted within modal response is given by equation
| Eq. 3 |
Where V1 and V2 are the two visual responses. This is a simplification that ignores the logarithmic transfer function and parameters otherwise used to scale the responses to physiologically realistic values (Rowland et al., 2007).
Contrast index
To compare model performance, the differences between actual combined responses and the predicted responses for each model were quantified using a standard contrast index according to the following formula (see Motter et al., 1994; Alvarado et al., 2007b):
Where PR is the predicted response (for each model evaluated) and CR is the actual response evoked by the combined visual-visual stimulus. Values obtained with this index will be distributed in the range of −1 to 1, with zero corresponding to a predicted response that is identical to the combined unisensory response. Positive values correspond to prediction overestimates and negative values underestimates.
Acknowledgment
We thank N. London for editorial assistance.
Grants: This work was supported by NIH Grants NS36916 and EY016716.
REFERENCES
- Alvarado JC, Vaughan JW, Stanford TR, Stein BE. Multisensory versus unisensory integration: contrasting modes in the superior colliculus. J. Neurophysiol. 2007a;97(5):3193–3205. doi: 10.1152/jn.00018.2007. [DOI] [PubMed] [Google Scholar]
- Alvarado JC, Stanford TR, Vaughan JW, Stein BE. Cortex mediates multisensory but not unisensory integration in superior colliculus. J. Neurosci. 2007b;27(47):12775–12786. doi: 10.1523/JNEUROSCI.3524-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Britten KH, Heuer HW. Spatial summation in the receptive fields of MT neurons. J Neurosci. 1999;19:5074–5084. doi: 10.1523/JNEUROSCI.19-12-05074.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calvert GA, Spence C, Stein BE. The Handbook of the Multisensory Processes. Cambridge, MA: MIT Press; 2004. [Google Scholar]
- Carandini M, Heeger DJ, Movshon JA. Linearity and normalization in simple cells of the macaque primary visual cortex. J Neurosci. 1997;17:8621–8644. doi: 10.1523/JNEUROSCI.17-21-08621.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gawne TJ, Martin JM. Responses of primate visual cortical V4 neurons to simultaneously presented stimuli. J. Neurophysiol. 2002;88:1128–1135. doi: 10.1152/jn.2002.88.3.1128. [DOI] [PubMed] [Google Scholar]
- Gondan M, Niederhaus B, Rösler F, Röder B. Multisensory processing in the redundant-target effect: a behavioral and event-related potential study. Percept. Psychophys. 2005;67(4):713–726. doi: 10.3758/bf03193527. [DOI] [PubMed] [Google Scholar]
- Heeger DJ. Normalization of cell responses in cat striate cortex. Vis. Neurosci. 1992;9(2):181–197. doi: 10.1017/s0952523800009640. [DOI] [PubMed] [Google Scholar]
- Henry GH, Goodwin AW, Bishop PO. Spatial summation of responses in receptive fields of single cells in cat striate cortex. Exp. Brain. Res. 1978;32:245–266. doi: 10.1007/BF00239730. [DOI] [PubMed] [Google Scholar]
- Heuer HW, Britten KH. Contrast dependence of response normalization in area MT of the rhesus macaque. J. Neurophysiol. 2002;88(6):3398–3408. doi: 10.1152/jn.00255.2002. [DOI] [PubMed] [Google Scholar]
- Jiang W, Wallace MT, Jiang H, Vaughan JW, Stein BE. Two cortical areas mediate multisensory integration in superior colliculus neurons. J. Neurophysiol. 2001;85(2):506–522. doi: 10.1152/jn.2001.85.2.506. [DOI] [PubMed] [Google Scholar]
- Jiang W, Jiang H, Stein BE. Two corticotectal areas facilitate multisensory orientation behavior. J. Cogn. Neurosci. 2002;14(8):1240–1255. doi: 10.1162/089892902760807230. [DOI] [PubMed] [Google Scholar]
- Jiang W, Stein BE. Cortex controls multisensory depression in superior colliculus. J. Neurophysiol. 2003;90(4):2123–2135. doi: 10.1152/jn.00369.2003. [DOI] [PubMed] [Google Scholar]
- Kadunce DC, Vaughan JW, Wallace MT, Benedek G, Stein BE. Mechanisms of within- and cross-modality suppression in the superior colliculus. J. Neurophysiol. 1997;78(6):2834–2847. doi: 10.1152/jn.1997.78.6.2834. [DOI] [PubMed] [Google Scholar]
- Lampl I, Ferster D, Poggio T, Riesenhuber M. Intracellular measurements of spatial integration and the MAX operation in complex cells of the cat primary visual cortex. J. Neurophysiol. 2004;92:2704–2713. doi: 10.1152/jn.00060.2004. [DOI] [PubMed] [Google Scholar]
- Leo F, Bertini C, di Pellegrino G, Làdavas E. Multisensory integration for orienting responses in humans requires the activation of the superior colliculus. Exp. Brain Res. 2007 doi: 10.1007/s00221-007-1204-9. In press. [DOI] [PubMed] [Google Scholar]
- Li X, Basso MA. Competitive stimulus interactions within single response fields of superior colliculus neurons. J. Neurosci. 2005;25:11357–11373. doi: 10.1523/JNEUROSCI.3825-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lippert M, Logothetis NK, Kayser C. Improvement of visual contrast detection by a simultaneous sound. Brain Res. 2007;1173:102–109. doi: 10.1016/j.brainres.2007.07.050. [DOI] [PubMed] [Google Scholar]
- McHaffie JG, Stein BE. A chronic headholder minimizing facial obstructions. Brain Res. Bull. 1983;10:859–860. doi: 10.1016/0361-9230(83)90220-4. [DOI] [PubMed] [Google Scholar]
- Meredith MA, Stein BE. Interactions among converging sensory inputs in the superior colliculus. Science. 1983;221(4608):389–391. doi: 10.1126/science.6867718. [DOI] [PubMed] [Google Scholar]
- Meredith MA, Stein BE. Visual, auditory, and somatosensory convergence on cells in superior colliculus results in multisensory integration. J. Neurophysiol. 1986;56(3):640–662. doi: 10.1152/jn.1986.56.3.640. [DOI] [PubMed] [Google Scholar]
- Miller J. Divided attention evidence for coactivation with redundant signals. Cog. Psych. 1982;14:247–279. doi: 10.1016/0010-0285(82)90010-x. [DOI] [PubMed] [Google Scholar]
- Motter BC. Neural correlates of attentive selection for color or luminance in extrastriate area V4. J. Neurosci. 1994;14(4):2178–2189. doi: 10.1523/JNEUROSCI.14-04-02178.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Movshon JA, Thompson ID, Tolhurst DJ. Spatial summation in the receptive fields of simple cells in the cat's striate cortex. J. Physiol. 1978;283:53–77. doi: 10.1113/jphysiol.1978.sp012488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perrault TJ, Jr, Vaughan JW, Stein BE, Wallace MT. Neuron-specific response characteristics predict the magnitude of multisensory integration. J, Neurophysiol. 2003;90(6):4022–4026. doi: 10.1152/jn.00494.2003. [DOI] [PubMed] [Google Scholar]
- Perrault TJ, Jr, Vaughan JW, Stein BE, Wallace MT. Superior colliculus neurons use distinct operational modes in the integration of multisensory stimuli. J. Neurophysiol. 2005;93(5):2575–2586. doi: 10.1152/jn.00926.2004. [DOI] [PubMed] [Google Scholar]
- Recanzone GH, Wurtz RH, Schwarz U. Responses of MT and MST neurons on one and two moving objects in the receptive field. J. Neurophysiol. 1997;78:2904–2915. doi: 10.1152/jn.1997.78.6.2904. [DOI] [PubMed] [Google Scholar]
- Reynolds JH, Chelazzi L, Desimone R. Competitive mechanisms subserve attention in macaque areas V2 and V4. J. Neurosci. 1999;19:1736–1753. doi: 10.1523/JNEUROSCI.19-05-01736.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riesenhuber M, Poggio T. Hierarchical models of object recognition in cortex. Nat. Neurosci. 1999;2(11):1019–1025. doi: 10.1038/14819. [DOI] [PubMed] [Google Scholar]
- Rolls ET, Tovee MJ. The responses of single neurons in the temporal visual cortical areas of the macaque when more than one stimulus is present in the receptive field. Exp. Brain Res. 1995;103:409–420. doi: 10.1007/BF00241500. [DOI] [PubMed] [Google Scholar]
- Rowland BA, Stanford TR, Stein BE. A model of the neural mechanisms underlying multisensory integration in the superior colliculus. Perception. 2007;36:1431–1443. doi: 10.1068/p5842. [DOI] [PubMed] [Google Scholar]
- Sinnett S, Soto-Faraco S, Spence C. The co-occurrence of multisensory competition and facilitation. Acta Psychol. (Amst) 2008 doi: 10.1016/j.actpsy.2007.12.002. In press. [DOI] [PubMed] [Google Scholar]
- Stanford TR, Quessy S, Stein BE. Evaluating the operations underlying multisensory integration in the cat superior colliculus. J. Neurosci. 2005;25(28):6499–6508. doi: 10.1523/JNEUROSCI.5095-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stein BE, Meredith MA. The Merging of the Senses. Cambridge, MA: MIT Press; 1993. [Google Scholar]
- Stein BE. Neural mechanisms for synthesizing sensory information and producing adaptive behaviors. Exp. Brain Res. 1998;123(1–2):124–135. doi: 10.1007/s002210050553. [DOI] [PubMed] [Google Scholar]
- Stein BE, Jiang W, Stanford TR. The Handbook of Multisensory Processes. Cambridge, MA: MIT Press; 2004. Multisensory integration in single neurons of the midbrain; pp. 243–264. [Google Scholar]
- Stein BE. The development of a dialogue between cortex and midbrain to integrate multisensory information. Exp. Brain Res. 2005;166(3–4):305–315. doi: 10.1007/s00221-005-2372-0. [DOI] [PubMed] [Google Scholar]
- Stein BE, Stanford TR. Multisensory Integration: Current issues from the perspective of the single neuron. Nature Neuroscience Reviews. 2008 doi: 10.1038/nrn2331. In Press. [DOI] [PubMed] [Google Scholar]
- Treue S, Hol K, Rauber HJ. Seeing multiple directions of motion-physiology and psychophysics. Nat. Neurosci. 2000;3:270–276. doi: 10.1038/72985. [DOI] [PubMed] [Google Scholar]
- Wallace MT, Stein BE. Cross-modal synthesis in the midbrain depends on input from cortex. J. Neurophysiol. 1994;71(1):429–432. doi: 10.1152/jn.1994.71.1.429. [DOI] [PubMed] [Google Scholar]
- Wallace MT, Meredith MA, Stein BE. Multisensory integration in the superior colliculus of the alert cat. J. Neurophysiol. 1998;80(2):1006–1010. doi: 10.1152/jn.1998.80.2.1006. [DOI] [PubMed] [Google Scholar]
- Wilkinson LK, Meredith MA, Stein BE. The role of anterior ectosylvian cortex in cross-modality orientation and approach behavior. Exp. Brain Res. 1996;112:1–10. doi: 10.1007/BF00227172. [DOI] [PubMed] [Google Scholar]
- Zoccolan D, Cox DD, DiCarlo JJ. Multiple object response normalization in monkey inferotemporal cortex. J. Neurosci. 2005;25:8150–8164. doi: 10.1523/JNEUROSCI.2058-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]