Abstract
Behavioral and economic theories have long maintained that actions are chosen so as to minimize demands for exertion or work, a principle sometimes referred to as the “law of less work.” The data supporting this idea pertain almost entirely to demands for physical effort. However, the same minimization principle has often been assumed also to apply to cognitive demand. We set out to evaluate the validity of this assumption. In six behavioral experiments, participants chose freely between courses of action associated with different levels of demand for controlled information processing. Together, the results of these experiments revealed a bias in favor of the less demanding course of action. The bias was obtained across a range of choice settings and demand manipulations, and was not wholly attributable to strategic avoidance of errors, minimization of time on task, or maximization of the rate of goal achievement. Remarkably, the effect also did not depend on awareness of the demand manipulation. Consistent with a motivational account, avoidance of demand displayed sensitivity to task incentives and co-varied with individual differences in the efficacy of executive control. The findings reported, together with convergent neuroscientific evidence, lend support to the idea that anticipated cognitive demand plays a significant role in behavioral decision-making.
Decision Making and the Avoidance of Cognitive Demand
Choosing adaptively among competing lines of action requires a cost-benefit analysis. The potential rewards of each option must be considered, but must also be weighed against anticipated costs (Kahneman & Tversky, 1979; Stephens & Krebs, 1986). The costs of action can take many forms, ranging from physical pain (Gabriel, 1993), to monetary loss (Bechara, Tranel, Damasio, & Damasio, 1996), to social exclusion (Cialdini & Goldstein, 2004).
While most such outcomes involve effects of action on the environment, one form of cost is intrinsic to action itself, namely the cost associated with effort. It is a time-honored principle in both psychology and economics that, ceteris paribus, actions will be selected so as to minimize effort or work. This idea was famously codified in Hull's (1943) law of less work:
If two or more behavioral sequences, each involving a different amount of energy consumption or work, have been equally well reinforced an equal number of times, the organism will gradually learn to choose the less laborious behavior sequence leading to the attainment of the reinforcing state of affairs. (p. 294)
The basic idea behind this proposition has held currency in psychology since at least the 1920s (see Solomon, 1948) and remains widely accepted today (e.g. Salamone, Correa, Farrar, & Mingote, 2007; Walton, Kennerley, Bannerman, Phillips, & Rushworth, 2006). Frequently encountered variants include the idea that effort is aversive (e.g., Blough, 1966; Cuvo, Lerch, Leurquin, Gaffaney, & Poppen, 1998; Eisenberger, 1992; Friedrich & Zentall, 2004), and in economics the idea that effort is associated with intrinsic disutility. The law of less work is supported by extensive empirical evidence. The most frequent and direct approach to testing the principle has been to place subjects (animals or humans) in situations where they must choose between two courses of action associated with different exertional demands. When rewards are equated, a bias is typically observed toward the less demanding course of action (see, e.g., Solomon, 1948; Thompson, 1944).
From Physical to Cognitive Work
Hull's (1943) principle addressed physical effort, and subsequent experiments have focused almost exclusively on physical forms of demand. However, it has been routinely assumed that the law of less work extends to situations involving differential cognitive demands. In a frequently quoted passage, Allport (1954) wrote,
We like to solve problems easily. We can do so best if we can fit them rapidly into a satisfactory category and use this category as a means of prejudging the solution.... So long as we can get away with coarse overgeneralizations we tend to so. Why? Well, it takes less effort, and effort, except in the area of our most intense interests, is disagreeable. (pp. 20-21)
Similar assertions can be found in many places. For example, Baroody and Ginsburg (1986) accounted for strategy selection in arithmetic by invoking a “drive for cognitive economy.” In discussing the processing of political messages, McGuire (1969) characterized human beings as “lazy organisms,” seeking to spend as little mental energy as possible. Taylor (1981) characterized humans as “cognitive misers.” And according to Camerer and Hogarth (1999), “Economists instinctively assume thinking is a costly activity...mental effort is like physical effort—people dislike both.” Smith and Walker (1993) formalized this idea, proposing a theory of economic choice centering on the role of decision costs, costs linked to the cognitive or computational effort required by decision-making strategies.
The concept of an internal cost of effort has been particularly influential in the field of judgment and decision-making. It has long been observed that human decision-makers tend to fall short of optimal outcomes, in part through a reliance on simplifying strategies for gathering and integrating information (e.g., Gigerenzer & Goldstein, 1996; Simon, 1955; Tversky & Kahneman, 1974). Simplifying strategies might be favored for non-effort-related reasons; they might speed decisions or lend tractability to complex situations. However, an influential idea has been that decision-makers evaluate tradeoffs between the effort-related costs and the accuracy-related benefits of computationally intensive strategies (e.g., Payne, Bettman, & Johnson, 1993; Shah & Oppenheimer, 2008; Shugan, 1980; Smith & Walker, 1993). Adopting a simpler but less accurate decision strategy could be subjectively optimal when internal costs of effort are taken into account (for relevant discussion see Anderson, 1990; Simon, 1956).
Underscoring the ubiquity of the idea that mental effort is aversive, the notion has even been invoked to describe individuals who appear to seek out cognitively demanding tasks. For example, Eisenberger (1992) proposed that ‘learned industriousness’ arises from external reinforcement of effortful behavior, which “reduces effort's aversiveness” (p. 248). Here as elsewhere, the costs of cognitive demand are not considered to operate in isolation, but rather to weigh against countervailing incentives. Some such incentives may arise internally (e.g., a sense of efficacy or ‘flow’; see Moneta & Csikszentmihalyi, 1996, for relevant results and discussion).
Among the many researchers who have invoked the idea of demand avoidance, a few have made explicit the link to the Hullian tradition, propounding a “law of least mental effort” (e.g., Ballé, 2002; see also Rosch, 1999; Zipf, 1949). Integrating this idea with related proposals, ‘effort’ is most compellingly understood as relating to demands for controlled information processing or executive function (Posner & DiGirolamo, 1998; Shiffrin & Schneider, 1977). Indeed, there is direct precedent for the idea that decision making involves a tendency to minimize control or executive demands: a number of cognitive modeling enterprises have explicitly incorporated a principle of “minimal control” (Taatgen, 2007; Yeung & Monsell, 2003) or “least-effort,” again referring to executive control (Gray, 2000; see also Anderson, 1990). There is also direct evidence that human agents ‘offload’ control demands when possible, relying on information in the perceptual environment rather than internal working memory or cognitive control representations (Ballard, Hayhoe, Pook, & Rao, 1997; Droll & Hayhoe, 2007).
Available Evidence
The ‘law of least mental effort’ clearly has intuitive appeal, in part from the strong analogical relationship between mental and physical effort (for discussion, see Eisenberger, 1992). It also makes sense from a normative perspective, since a bias against mental effort would steer cognition toward more efficient tasks (see Botvinick, 2007), and might preserve limited cognitive resources (see Muraven & Baumeister, 2000). Remarkably however, despite its widespread application, the ‘law of least mental effort’ appears never to have been subjected to a direct experimental test.
To be sure, a wide range of observations have been discussed in terms of effort avoidance, such as preferences for particular strategies in mathematics (Baroody & Ginsburg, 1986), route selection (Christenfeld, 1995), attitude formation (Allport, 1954), decision-making (Payne et al., 1988) and task switching (Todd, Cohen, Botvinick, & Dayan, submitted; Yeung & Monsell, 2003). However, in the vast majority of such cases, effort minimization has been proposed as an explanatory principle rather than a hypothesis to be tested in its own right.
In one test of effort-guided strategy selection (MacLeod, Hunt, & Mathews, 1978; Mathews, Hunt, & MacLeod, 1980), participants performed a sentence-picture verification task that afforded either a visual-spatial or a verbal strategy. Strategy selection correlated with abilities, such that subjects with relatively high verbal working memory capacity tended to employ the verbal strategy, and subjects with relatively high visual working memory capacity tended to employ the visual-spatial strategy. Reichle, Carpenter, and Just (2000) characterized this pattern as evidence for “one basis for strategy selection: minimization of cognitive workload” (p. 261). Nevertheless, even here, the evidence is correlational rather than experimental, and pertains to the selection of covert strategies rather than overt actions. More importantly, these and related results leave open the possibility that people choose less effortful strategies not in order to avoid effort per se, but instead in order to minimize response times or error rates.
In sum, despite continual invocation over the years, and notwithstanding some indirect empirical evidence, the ‘law of least mental effort’ — the idea that anticipated cognitive demand weighs as a cost in behavioral decision-making — remains in need of a straightforward experimental test.
The Present Experiments
Our experiments were built around a novel behavioral paradigm, involving what we call demand selection tasks (DSTs). Here the participant faces a recurring choice between two alternative lines of action, associated with different levels of cognitive demand. In our first experiments, the choice situation itself was modeled loosely on earlier studies of reward-based decision-making by Bechara and colleagues (Bechara, Damasio, Damasio, & Lee, 1999; Bechara, Damasio, Tranel, & Damasio, 1997; Bechara et al., 1996), in which participants chose between decks of cards with different payoffs. Here and in subsequent elaborations of the DST paradigm, our general prediction was that participants would develop a tendency to select the course of action associated with the least cognitive demand.
Following the work reviewed above, we associate mental effort with demands for controlled information processing or executive function. In keeping with this, we began with an experiment that manipulated cognitive demand by varying the frequency of shifts between tasks. Task switching is generally understood to demand executive control (see Monsell, 2003) and evidence suggests that when two task-sets are available, people tend to follow the same task repeatedly (Arrington & Logan, 2004). Participants in Experiment 1 chose freely between two response options that carried different subsequent task-switching requirements. Our entry-level prediction was that participants would favor courses of action that committed them to less-frequent task switching.
Experiment 1
Methods
Participants
Forty-three subjects from the University of Pennsylvania community (18-26 years of age, 25 females) participated. In this and all subsequent experiments, participants were compensated with course credit or nominal payment for participation, and provided informed consent following procedures approved by the applicable Institutional Review Board.
Materials and procedure
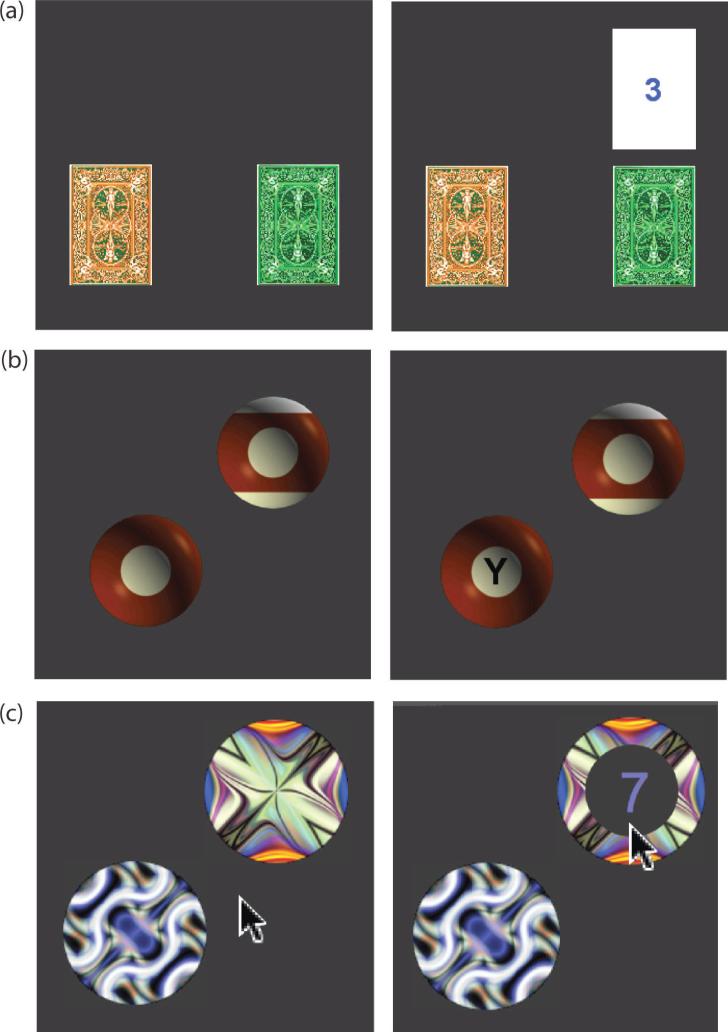
The DST was computer based, and programmed using E-Prime (Psychology Software Tools, Inc.). On each of 500 trials, the monitor displayed two cards (digitized images of face-down playing cards), symmetrically positioned to the left and right of center, one tinted orange the other green (see Figure 1a). Subjects used the keyboard to select one card, pressing F to select the left card and J to select the right. The ‘face’ of the selected card then appeared above the card's original position, displaying a single Arabic numeral (between 1 and 9, inclusive, but excluding 5) on a white field. The numeral was displayed in either purple or blue. If blue, subjects were to make a magnitude judgment, saying “yes” if the number was less than five and otherwise responding “no”. For purple, subjects were to make a parity judgment, responding “yes” if the number was even and otherwise responding “no”. Verbal responses were registered by a voice key, which immediately restored the original face-down display, beginning the next trial.
Figure 1.
(a): Example of cues in the DST of Experiment 1. Cues appeared as decks of cards. Subjects used the keyboard to select one deck, causing it to reveal a blue or purple number. They then made a vocal response to the number. (b): Examples of cues in Experiment 2, which were depicted as striped or solid-colored balls. (c): Examples of cues in Experiments 3-5. Subjects were presented with 8 separate pairs of choice cues over the course of one session.
Subjects initially practiced the classification tasks with numerals presented in isolation (rather than on cards). Ten-trial blocks were performed until a within-block accuracy of 90% was attained. Subjects were introduced to the decks task with the explanation that all cards would show a colored number, with both colors occurring in each deck, and that they should respond to each number just as in the practice task. Subjects were told that they were free to choose from either deck on any trial, and that they should “feel free to move from one deck to the other whenever you choose,” but also that “if one deck begins to seem preferable, feel free choose that deck more often”.
Unannounced to subjects, there was one important difference between the two decks. In one deck (referred to as the low-demand deck) the color of each numeral matched the color occurring on the previous trial on 90% of occasions. In the other (high-demand) deck, a match occurred on only 10% of occasions. The latter deck thus required more frequent switching from one task to the other. The relative positions of the high-and low-demand decks were counterbalanced across subjects. On each trial, the subject's deck choice was recorded, as were choice reaction time (RT) and verbal response RT.
We took measures to guard against three potential alternative sources of a low-demand choice bias. First, we were concerned that participants might select the low-demand deck in order to minimize the length of the session. To prevent this, participants were told they would perform the task for a fixed one-hour period, and that they could go at their own chosen pace (although in fact the task was terminated after 500 trials, always well ahead of the hour mark). Second, we were concerned that if errors were more frequent on the high-demand deck, participants might favor the low-demand deck as a strategy to optimize their accuracy. To address this possibility we recorded response accuracy and conducted followup analyses on the subgroup of participants who ultimately committed errors at a lower rate on the high-demand deck than the low-demand deck. Third, we were concerned that participants might draw inferences about the goals of the experiment and adjust their choice behavior to comply with perceived expectations. To assess this, participants completed a follow-up questionnaire evaluating their awareness of the difference between the decks (the questionnaire is shown in Table 1).
Table 1.
Debriefing questionnaire used in Experiment 1. This questionnaire was administered following the DST in order to assess each participant's overt awareness of the demand manipulation.
| Debriefing questionnaire |
|---|
| 1 What was it like performing the task? |
| 2 How did you choose between decks? |
| 3 Did you develop a preference for one of the decks? |
| 4 Was there any difference between the decks? |
| 5 For some participants, one of the two decks had a tendency to switch between colors more often while the other deck tended to repeat the same color. Did it seem like this was the case for you? If so, which deck tended to switch more often (left or right)? |
| If you answered yes to the previous question (indicating that one of the decks seemed to switch between colors more often, was this something you became EXPLICITLY aware of DURING THE EXPERIMENT, or something that you realized only in retrospect. |
Analysis
To validate the task-switching manipulation, verbal RTs were compared via a two-way repeated measures ANOVA with factors for trial-type (repetition vs. switch) and deck. Error rates for the high- and low-demand decks were compared in a Wilcoxon signed-rank test. To test for deck preference, the low-demand selection rates for individual subjects were tested against the chance rate of 0.50 in a Wilcoxon signed-rank test. As a result of equipment loss, deck-wise error rates were ultimately available for 39 subjects. Additional analyses, described below, were conducted for participants who happened to commit a higher proportion of errors on the low-demand deck than the high-demand deck, and for participants who denied awareness of any difference between the decks.
Results
Verbal RT
Verbal RT for the two decks and two trial types (task repetition, switch) are listed in Table 2. The means shown are based on subjects who contributed to all four cells of the analysis (four subjects did not). A two-way repeated measures ANOVA, based on the same data set, indicated a significant effect of deck (F(1, 38) = 6.55, p = 0.02); a significant effect of trial type, (F(1, 38) = 35.28, p < 0.01); and a significant interaction, (F(1, 38) = 16.78, p < 0.01).
Table 2.
Response times (means of medians) with standard deviations in parentheses, for each trial type (task switch vs. task repetition) and response alternative (low-demand vs. high-demand) in experiments involving task-switching.
| Low-Demand Option | High-Demand Option | |||
|---|---|---|---|---|
| Task Repeat | Task Switch | Task Repeat | Task Switch | |
| Experiment 1 | 946 (230) | 1260 (292) | 1248 (528) | 1318 (382) |
| Experiment 2 | 506 (122) | 571 (117) | -- | 702 (228) |
| Experiment 3 | 739 (125) | 1,057 (250) | 896 (201) | 1,043 (253) |
| Experiment 5 | 645 (93) | 950 (124) | 804 (164) | 1009 (227) |
Error rates
Mean error rates were 1.73% for the low-demand deck and 2.58% for the high-demand deck, a marginally significant difference on Wilxocon signed-rank test, p = 0.054.
Deck choice
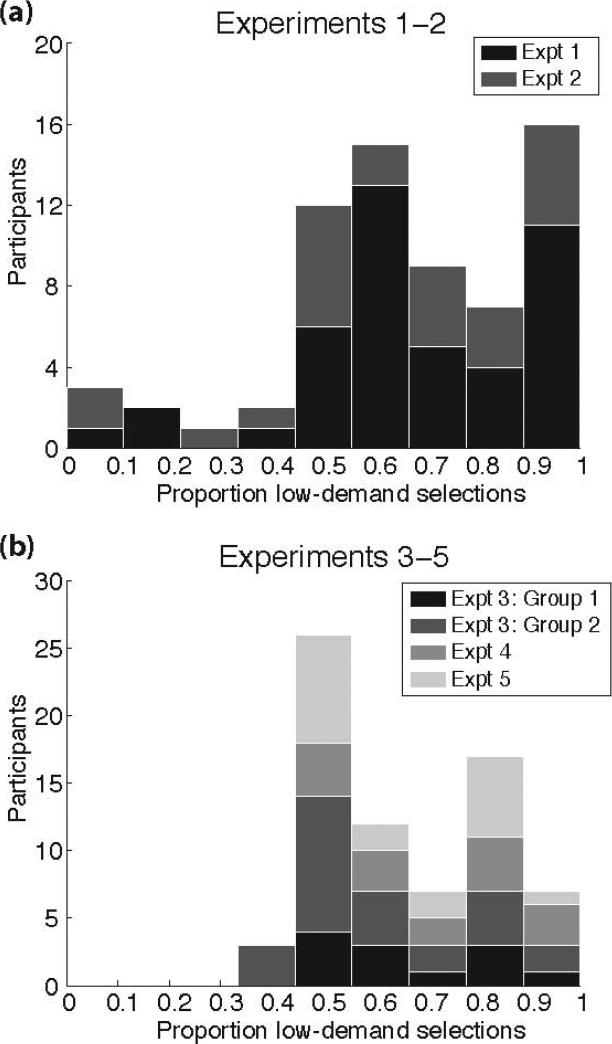
Figure 2a shows the progression of choice rates over the course of 500 trials. Across subjects, the mean proportion of trials on which the low-demand deck was selected was 0.68 (standard deviation: 0.24). Thirty-six subjects (84%) selected the low-demand deck more often than the high-demand deck, and choice rates differed significantly from chance (Wilcoxon signed-rank test, p < 0.0001). A histogram showing the distribution of single-subject choice rates appears in Figure 3a.
Figure 2.
Ten-trial running average showing the proportion of choices from the low-demand alternative, across the span of the session, in Experiments 1 (panel a) and 2 (panel b). Timecourses begin at trial 10, the first point for which the running average exists.
Figure 3.
(a): Distribution of individual subjects’ low-demand selection rates across Experiments 1 and 2 (n = 67). (b): Distribution of low-demand selection rates across Experiments 3, 4, and 5 (n = 72), in which each subject faced multiple pairs of choice cues. Experiment 3 includes two groups of subjects (see text). When testing involved multiple runs, no subject showed an extreme choice bias in favor of a higher-demand alternative.
Impact of error commission on deck choice
Fourteen subjects committed errors at a greater rate on the low-demand deck than the high-demand deck. The mean proportion of trials on which these subjects selected the low-demand deck was 0.80, and all but one (93%) chose most often from the low-demand deck (Wilcoxon signed-rank test, p < 0.01).
Impact of awareness on deck choice
Twelve subjects denied having had any awareness during the task that the probability of task switches differed between the two decks, even in retrospect, after being informed of the difference. Specifically, these subjects answered ‘no’ to questions four and five in the questionnaire (Table 1). Among these subjects, the mean proportion of trials on which the low-demand deck was chosen was 0.71. Eight chose most often from the low-demand deck (Wilcoxon signed-rank test, p = 0.02).
Discussion
The present experiment tested whether subjects would show a tendency to choose courses of action that involved fewer task switches. Reaction times and error rates verified that task-switching requirements imposed cognitive demands, and choice data revealed a clear tendency to choose the low-demand alternative.
Results appear consistent with a ‘law of least mental effort,’ the idea that, all else being equal, actions tend to be selected so as to minimize cognitive demand. We can rule out three alternative explanations. First, participants favored the low-demand deck despite believing they would perform the task for a fixed time period; this suggests the bias does not reflect a strategic attempt to reduce the length of the testing session. Second, the bias was evident among participants who committed a higher proportion of errors on the low-demand deck, countering the possibility that the observed bias reflects error avoidance. Third, the choice asymmetry was present among participants who denied any awareness of a difference between the decks. This makes it unlikely that choice behavior depended on participants’ inferences about the experimenters’ expectations or other demand characteristics.
The results from Experiment 1 leave open at least one further alternative explanation for the observed choice bias. In the experiment, the color of the numeral appearing on each trial depended on the previous trial's color, regardless of which deck was selected. If a participant happened to prefer either the magnitude task or the parity task, this property of the paradigm allowed them to maximize the number of trials involving that task. Specifically, participants could have selected the low-demand deck to obtain their preferred task repeatedly, and whenever the task switched they could have moved briefly to the high-demand deck to recover their preferred task. This ‘task seeking’ strategy would result in a higher proportion of selections from the low-demand deck. We ran a small followup experiment with eight new participants to rule out this possibility. The procedure was the same except that when a deck was chosen, the task (numeral color) depended on the last card chosen from that deck, not necessarily the immediately previous trial. With the task-seeking strategy unavailable, participants still selected the low-demand deck at a rate greater than chance (mean = 0.78, signed-rank p < 0.01), replicating the main finding of Experiment 1.
Experiment 2
The results of Experiment 1 comport well with a tendency to avoid lines of action associated with high levels of cognitive demand. Experiment 2 was conducted to evaluate the generality of the effect. If demand avoidance is a ubiquitous characteristic of behavior, then it should occur under demand manipulations different from those used in our first experiments. Nor should it be dependent on the mechanics of the choice situation involved in those experiments. In order to test this, Experiment 2 used a DST involving a new type of demanding task embedded in a new type of choice environment. This experiment used a modified version of the A-X continuous performance task (Servan-Schreiber, Cohen, & Steingard, 1996). In this task, responses to target stimuli are dependent on the context established by a preceding cue. Frequent changes of context were assumed to introduce demands on executive functions including working memory updating and controlled response selection (Barch et al., 1997). We thus expected subjects to avoid choices associated with frequent contextual shifts.
Multiple features distinguished the two choice cues in Experiment 1: location (left vs. right), appearance (green vs. orange), and associated response (left vs. right keypress). Here the two alternatives were distinguished only by appearance, varying from trial to trial both in location and in the physical responses they required. Replication of the demand avoidance bias in such a context would provide evidence that people avoid high-demand courses of action systematically rather than, for instance, merely growing less likely to repeat their last motor response when the task is more demanding.
Methods
Participants
Twenty-four members of the Princeton University community participated (14 female, age 18–40).
Materials and procedure
The experiment was programmed using E-Prime (Psychology Software Tools, Inc.). Each task trial consisted of two successively shown letters (see Figure 1b). The first was a cue, A or B. The second was a probe, X or Y. Subjects make a left or right key-press to each probe in the following manner: the cue A established the mapping X-left, Y-right; the cue B established the opposite mapping. Subjects made task responses with their left hand. The cue was shown for 250ms and followed by a 750ms blank interval, after which the probe appeared and remained until a response was made. Trials were separated by a 500ms response-cue interval.
The task was divided into six-trial blocks. At the beginning of each block participants used a mouse to select one of two choice alternatives. The two alternatives were pictured as two differently patterned pool balls (one striped, one solid-colored). Stimuli for six task trials were then displayed in a circular window on the chosen ball.
The critical manipulation of cognitive demand involved the sequence of cue letters within each 6-trial block. Selecting the high-demand alternative resulted in a cue sequence of the form ABABAB or BABABA, requiring five shifts of context (with an X or Y probe following each cue). The low-demand alternative always showed a cue sequence of the form AAABBB or BBBAAA, requiring only a single contextual shift. The assignment of demand levels to the pictured choice stimuli remained fixed throughout the session for individual subjects, and was counterbalanced across subjects.
The two choice alternatives always appeared along the perimeter of an imaginary circle separated by an angular distance of 45 degrees. Their positions were randomly reset for every block. The mouse cursor always began in the center of the screen, equidistant from the two alternatives.
The session began with a preliminary task intended to familiarize subjects with the choice setup. For 100 trials, the response options appeared in randomized locations while an explicit cue at the center instructed subjects to click on either the “striped” or “solid” ball (with trials evenly divided between the two).
Subjects were then introduced to the A-X task and performed 20 trials of practice (which were repeated if necessary). Here and throughout, errors in the task produced a brief warning message (“Incorrect response”). Subjects then performed 65 trials of the A-X task in isolation to gain additional familiarity with it. Finally, subjects performed seven runs of the choice task. Each run lasted a timed duration of five minutes. Subjects were instructed that they should do their best to respond accurately and work steadily for the entire time period. Instructions also stated that subjects could feel free to choose one ball more often than the other if they wished.
Subjects worked at their own pace, as there was no response deadline either for choice responses or probe responses. Fixed-duration runs removed any incentive to choose the low-demand alternative as a means of shortening the experiment.
Analysis
The proportion of blocks in which the low-demand alternative was selected was computed for each subject and tested against 0.50 in a Wilcoxon signed-rank test. The trajectory of demand selection over time was evaluated by computing the mean proportion of choices from the low-demand deck in each of the seven experimental runs and testing the effect of run number on choice rate in a one-way repeated-measures ANOVA. A further analysis, focusing on the effect of errors on choice behavior, is described in conjunction with results.
Results
Target response accuracy and latency
The mean accuracy rate at the A-X task was 0.93 (standard deviation: 0.06). Accuracy during high-demand blocks was 0.90 (0.08), while accuracy during low-demand blocks was 0.95 (0.05), and these rates were significantly different (t(23) = 5.49, p < 0.01).
The average median RT (and standard deviation) for task repetition trials in low-demand blocks (i.e., trials 2, 3, 5, and 6 of low-demand blocks) was 506 ms (122 ms), which was significantly faster than task switch trials on the low-demand option (i.e., trial 4; 571 ms [117 ms]; t(23) = 4.10, p < 0.01). Task switch trials in high-demand blocks (i.e., trials 2–6) were slower still (702 ms [228 ms]; t(23) = 3.26, p < 0.01).
Choice performance
Subjects completed a mean of 125.5 task blocks over the course of the experiment (standard deviation: 10.0; range: 106 to 142). Each block began with a choice between the high- and low-demand alternatives. The low-demand option was selected at a mean rate of 0.64 (standard deviation: 0.27). A Wilcoxon signed-rank test found this proportion to differ significantly from chance (p = 0.03). A histogram showing the distribution of single-subject choice rates appears in Figure 3a.
Examination of choice rate across runs revealed a monotonic trend. No bias was evident in the first run, but a strong bias developed by run three and persisted until the end of the session. A repeated measures ANOVA confirmed a significant effect of experimental run on choice rate (F [6, 138] = 3.26, p < 0.01). The choice rate as a function of trial number for the first 106 trials (the minimum completed by any subject) is shown in Figure 2b.
Impact of errors
A substantial proportion of subjects (12 of 24) made an error during the first task block. Only 2 of 24 subjects made more errors on the low-demand deck than on the high-demand deck overall, making it infeasible to test for a bias in just this subset as in Experiment 1. However, data from the A-X task did support an analysis probing for local effects of errors on subsequent choices. We examined whether the occurrence of an error while responding to one choice cue, either high-demand or low-demand, affected the likelihood that the same cue would be selected again in the subsequent block. A straightforward error avoidance account would predict that committing an error on one option should reduce its attractiveness.
On any given block, participants were more likely to repeat their immediately preceding choice than to change it, repeating at a mean rate of 0.73 (standard deviation: 0.24). To assess the influence of errors, individual blocks were coded as correct if all six trials were performed accurately, or as error-containing if one or more errors occurred. The mean proportion of error-containing blocks was 0.30 (standard deviation: 0.20). The probabilities of choice repetition after error-free and error-containing blocks respectively were 0.73 and 0.72; these two values did not differ (signed-rank test, p = 0.61), and were strongly correlated across subjects (r = 0.93, p < 0.01). This correlation suggests that subjects varied in the rates with which they repeated vs. alternated the two choice alternatives, but there is no evidence that recent error commission affected choices.
Discussion
The present experiment replicated the basic findings of Experiment 1, extending them to a new demand manipulation and choice paradigm. The results support the generality of the demand-avoidance principle. A further test of generality is reported in Experiment 4 below. Presently, we turn to a not-yet-discussed aspect of the results of Experiments 1 and 2, namely the variability in observed demand-avoidance tendencies across participants.
Experiment 3
Individual subject data from Experiments 1 and 2, shown in Figure 3a, made it appear that some participants, albeit a small minority, were biased toward high cognitive demand, rather than away from it, as a law of least mental effort would require. One possible explanation is that these individuals made their choices by focusing on dimensions other than demand, such as the location and appearance of the choice cues. Indeed, in early tests of the law of less (physical) work, arbitrary position-based preferences were found to compete with rats’ avoidance of physical effort (McCulloch, 1934). In our experiments, this gives rise to the prediction that reducing the influence of arbitrary cue-related preferences should reduce the frequency of pronounced biases toward high demand.
Experiment 3 set out to test this prediction. It employed the same logic as the previous studies, presenting participants with two choice cues that were associated with different levels of demand. Additionally, however, testing was divided into multiple runs, with the appearance and location of the choice cues changing from run to run. Individuals minimizing cognitive demand would be expected to show a consistent bias toward the low-demand alternative across runs. Cue- or position-related preferences, in contrast, would not be expected to favor either the high-demand or low-demand alternative consistently.
Methods
Participants
Twelve members of the Princeton University community participated in a half-hour session (age 18–22, 7 females). Analyses also include a second group of participants (referred to as Group 2) who completed a similar testing session in connection with a neuroimaging experiment. Group 2 consisted of 25 individuals (age 18–30, 14 females). While neuroimaging results will be described in full elsewhere, data from the behavioral segments of these studies are reported here in order to underscore the reproducibility of the present findings. Total n for the expanded sample equaled 37.
Materials and procedure
Experiment 3 used the same magnitude/parity judgment task as Experiment 1. Each subject was presented with 8 separate pairs of choice cues over the course of one session. Cues appeared as abstract color patches (Figure 1c). Subjects used the mouse to click on a cue, causing it to reveal a colored number. They then responded to the number by pressing one of two keys with their left hand.
The experiment was divided into eight runs, each featuring a visually different pair of choice cues. There were 75 trials in each run (600 in the entire experiment). Each run featured one high-demand cue, on which numerals switched colors relative to the previous trial with a probability of 0.9, and one low-demand cue, which switched colors with a probability of 0.1.
The position of the choice cues remained fixed within each run but changed from run to run, always appearing along the perimeter of an imaginary circle separated by an angular distance of 45 degrees. The mouse cursor was positioned midway between the two patches at the beginning of each choice.
For participants in Groups 2 the task was programmed using the Psychophysics Toolbox extensions for Matlab (Brainard, 1997; Pelli, 1997). These participants completed the task in a behavioral testing room following approximately 90 minutes of other testing. The earlier testing included performance of magnitude/parity task switching, but had not allowed participants to express demand-based preferences, nor had it involved the choice cues used in the DST. The demand selection session itself was equivalent to that described above except that each of the 8 runs consisted of 60 trials (there were thus 480 trials in total).
Analysis
To test for a behavioral bias against cognitive demand, each subject's proportion of low-demand selections was computed across all trials. Internal consistency was assessed by calculating Cronbach's α, treating the 8 runs of the DST as subtests. Additional tests, described below, were conducted to compare the distribution of choice rates across Experiment 1–2 with that in Experiment 3.
Results
Task performance
Mean accuracy of number judgments was 0.95 (0.06) for the low-demand alternative and 0.94 (0.07) for the high-demand alternative, and the difference between these rates was significant (signed-rank, p = 0.01). Target keypress RTs for task switch and task repetition trials within each demand condition are shown in Table 1. Among the 36 of 37 subjects contributing data to all 4 cells, a two-way repeated measures ANOVA revealed a significant main effect of the alternative chosen (high-demand vs. low-demand; F(1,35) = 21.59, p < 0.01), a main effect of task switch vs. repetition (F(1,35) = 74.44, p < 0.01), and a significant interaction between the two (F(1,35) = 19.73, p < 0.01).
Demand selection
The mean rate of low-demand selections was 0.67 (0.16) in Group 1 and 0.61 (0.17) in Group 2; rates in both groups differed significantly from 0.50 (Wilcoxon signed-rank p < 0.01 in each case). Figure 3b shows the distribution of total choice rates for each group. It reveals that individual subjects’ responses ranged mainly from indifference to aversion toward high demand; no participants showed an extreme rate of bias in the high-demand direction.
The DST showed internal consistency in assessing the bias of individual subjects to avoid cognitive demand: across both groups, Cronbach's α = 0.85.
The multiple-run design was intended to attenuate the impact of arbitrary cue-related preferences on total choice rates. Such preferences still may, of course, occasionally work in favor of one demand level or the other. The distribution of low-demand selection rates extended to a minimum score of 0.373. In order to test the visual impression that the distribution in Figure 3b lacks the lower tail seen in Figure 3a, we computed the probability that in 37 samples drawn from the distribution shown in Figure 3a, zero samples would occur in the range (0, 0.373). In the empirical data from Experiments 1 and 2, this range held 6 of 67 cases (0.09). The estimated probability that zero of 37 subjects drawn from the same distribution would fall into this range is therefore (1-6/67)37 = 0.03. This indicates that the data observed in Experiment 3 would be unlikely if the underlying distribution included a lower tail equivalent to that observed in Experiments 1–2.
Discussion
Experiment 3 introduced a manipulation to minimize the influence of demand-independent cue or response preferences in the DST. With this modification in place, no evidence was found that any subset of individuals exhibited a strong and systematic preference for the high-demand alternative (see Figure 3b).
Naturally, it cannot be guaranteed that no individual in a larger sample would ever exhibit a strong preference for high cognitive demand. However, the results of Experiment 3 show it to be improbable that such preferences exist in the population at the frequency suggested by Experiments 1 and 2. These results make it appear more likely that individuals who appeared to seek high cognitive demand may have been guided mainly by demand-irrelevant factors.
Experiment 4
Together, the experiments described so far provide convergent evidence for a tendency to avoid or minimize cognitive demand. In Experiment 4, we revisited the question of whether this tendency applies across different varieties of cognitive demand. Participants were asked to perform two-digit mental subtraction problems; we manipulated whether the problem required carrying a digit. It is well established that carry operations increase the computational complexity of a mental arithmetic problem (Hitch, 1978), and there is evidence that carries place demand specifically on executive processes involved in working memory (Fürst & Hitch, 2000). We thus hypothesized that participants would avoid solving problems requiring carrying, choosing instead to solve less demanding problems.
Method
Participants
Sixteen members of the Princeton University community completed the experiment (age 18-22, 10 females).
Materials and procedure
Participants performed a DST using the same choice interface as in Experiment 3. Instead of switching between magnitude and parity judgments, participants verified the accuracy of subtraction problems. As before, two choice cues were shown (see Figure 1c). Either cue, when selected, revealed a completed subtraction problem including the minuend (30 or greater), subtrahend (10 or greater), and difference (greater than 10). Participants were asked to press the “1” key if the solution shown was correct, or the “2” key if it was wrong. Half of the problems displayed the correct answer; for the other half, the answer shown was off by a value of 1 or 2. Response accuracy feedback was provided through the appearance of a check mark (correct) or an X (incorrect) on the screen.
The two choice cues differed in the complexity of the problems they presented. The low-demand alternative showed problems in which the ones digit of the minuend was greater than the ones digit of the subtrahend, so no carry was required. For the high-demand alternative, the opposite relationship held, so the solution involved carrying a single digit.
Participants completed 8 runs of the task, with each run lasting for a fixed duration of 5 minutes.
Results
Task performance
Participants completed an average of 828.62 trials over the course of the experiment (range: 472-1,103). Error rates were 0.05 for low-demand trials and 0.07 for high-demand trials, and these rates differed significantly (Wilcoxon signed-rank, p = 0.02). Mean RTs were 1,207ms for low-demand trials and 2,026ms for high-demand trials, and these also were significantly different (Wilcoxon signed-rank. p < 0.01).
Demand selection performance
The mean low-demand selection rate was 0.73 (range: 0.50 - 0.99), and these rates differed significantly from 0.50 (Wilcoxon signed-rank. p < 0.01).
Figure 3b shows the distribution of overall choice rates for the participants in Experiment 4. Again, a clear skew toward the low-demand option is evident. Examined at the individual level, 7 participants (44%) showed a low-demand bias that was statistically significant in a signed-rank test across the 8 DST runs. Choice rates for the remaining 9 participants did not differ significantly from 0.50. Crucially, no participant showed a significant bias in the opposite of the expected direction. The DST showed high internal consistency (Cronbach's α = 0.93), suggesting that individual participants tended to show consistent degrees of bias across the 8 runs.
We wished to show here, as we have previously done for the task-switching protocol, that behavioral preferences for low cognitive demand did not merely reflect avoidant reactions to error commission. To do this, we recalculated each run's low-demand selection rate using only choices that preceded the first error in the run. That is, we used trials during which a given pair of choice cues could not be differentiated based on which had been the location of a larger number of errors. The resulting single-run proportions (8 per subject) were then averaged to produce each subject's mean pre-error rate of low-demand selections. The number of trials contributing to this analysis ranged from 1 to 105 for individual runs, and an average of 7.13 to 74.25 trials per run for individual subjects (mean 24.02). Thus, this analysis is based on a relatively small subset of the data. Nevertheless, the low-demand selection rate for trials preceding each run's first error commission was 0.62, which differed significantly from 0.50 (Wilcoxon signed-rank p = 0.04).
Correlations were examined between demand selection rates and parameters of behavioral performance. Low-demand selection rates were not related to low-demand error rates (r = -0.06, p = 0.82) or high-demand error rates (r = -0.09, p = 0.73). Low-demand selection rates were also unrelated to low-demand RT (r = -0.17, p = 0.52), but showed a strong relationship to high-demand RT (r = 0.70, p < 0.01).
Discussion
The present results add to those of Experiment 2 in extending the ‘law of least mental effort’ beyond the setting of task switching. As in earlier experiments, results indicated that demand avoidance could not be attributed entirely to a motivation to avoid errors or minimize session length.
An interesting ancillary finding was the significant correlation between high-demand RT and preference for the low-demand alternative. This must be interpreted with caution, as the direction of causality cannot be established. It might be that individuals who drew more trials from the high-demand option gained more practice at mentally carrying digits, allowing them to speed up their performance. Taken at face value, however, the correlation would suggest that those individuals who found the high-demand task to be more cognitively demanding also showed stronger avoidance, just as one would anticipate based on a ‘law of least mental effort.’ In Experiment 5, we tested this possibility more directly.
Experiment 5
Experiments 3 and 4 reduced the incidence of apparent demand-seeking behavior by varying the appearance and location of choice cues across runs of testing. Remaining variability appeared largely confined to a range between neutrality and strong demand avoidance. Furthermore, the DST showed a reasonable degree of internal consistency in measuring the demand avoidance tendencies of individuals. Individual differences provide us with an opportunity to test further predictions of the law of least mental effort.
It has been suggested that skills (or “capital,” in the economic metaphor of Camerer and Hogarth, 1999) help determine the relationship between effort (“labor”) and level of performance (“production”). In a similar spirit, Just and Carpenter (1992) proposed that individuals might differ not only in the capacity of working memory, but also in the efficiency with which that capacity is used (more generally, the efficiency of cognitive resource utilization has been a topic of longstanding interest; Navon & Gopher, 1979). Varying levels of ability might influence the amount of cognitive demand experienced by individual participants in the same task. The experience of cognitive demand, in turn, could influence avoidance behavior.
To evaluate this idea, we focused on the task-switching version of the DST used in Experiment 3. The processing costs involved with task switching can be estimated based on the difference in reaction time between task-switch and task-repetition trials. Previous work has provided evidence that individual variability in switch cost can be attributed to a single factor even across multiple specific task contexts (Salthouse, Fristoe, McGuthry & Hambrick, 1998). Thus, it is reasonable to hypothesize that meaningful individual differences in task switching abilities may be present within our samples of participants.
Experiment 5 tested for correlations between individual participants’ DST performance and a separately obtained estimate of RT switch cost. As noted above, it is not feasible to assess task switching ability based on performance during the DST itself, because individuals who develop a greater low-demand bias will thereby (1) obtain less practice at task switching, and (2) tend to perform a single task for a longer period of time before each switch occurs. Indeed, switch costs in previous experiments tended to be larger on the low-demand deck (where switches are less frequent) than on the high-demand deck, even within participants (see Table 2). RT switch costs were therefore measured in a preliminary period of task switching, involving isolated stimuli, before the choice paradigm was introduced. If variation in demand avoidance were related to ability, then individuals showing a larger switch cost in the preliminary period would be expected to go on to show higher levels of avoidance.
Methods
Participants
Nineteen members of the Princeton University community completed the experiment (age 18-27, 11 females).
Materials and procedure
This experiment employed a DST very similar to that used in Experiment 3. Participants selected one of two patterned patches on the screen (see Figure 1c), which revealed an imperative stimulus within a magnitude/parity task switching protocol. Numbers were colored blue (indicating magnitude) or yellow (indicating parity). Participants completed 8 runs of 75 trials each, with each run featuring choice cues that differed in appearance and screen position. In every run, stimuli from one choice cue switched tasks relative to the previous trial with a probability of 0.90, while stimuli from the other cue switched tasks with a probability of 0.10.
Small ergonomic improvements were made to the choice interface from Experiment 3. Participants selected a choice cue by simply rolling the mouse cursor over the desired cue, and registered their magnitude or parity judgments by pressing one of the two mouse buttons. After each trial the choice cues appeared dimmed, and a small cue marked a home position halfway between the two choice cues. When participants rolled the mouse cursor to the home position, choice cues appeared normally and could be selected. This change ensured that participants began each trial with the mouse cursor equidistant from the two alternatives, while remaining in full control of the cursor position.
Participants completed a preliminary block of task switching trials before being introduced to the DST, but after having received instructions and practice in the task switching protocol. The preliminary block contained 126 trials. On each trial a colored number was presented in the center of the monitor against a gray background. The sequence of colors (i.e., tasks) followed an m-sequence-based order, in which half the trials repeated the previous color. Participants made a response to each number using the mouse buttons. Trials were separated by a 500ms response-stimulus interval.
Analysis
To test for the expected bias against cognitive demand, participants’ total low-demand choice rates in the DST were tested against 0.50 using a Wilcoxon signed-rank test. To evaluate the effect of ability on preferences, we tested the correlation of total low-demand preference rates with RT switch costs from the preliminary, choice-free block.
Results
Preliminary block performance
Within the preliminary block, mean accuracy for task switch trials was 0.95 (standard deviation: 0.04), while accuracy for task repeat trials was 0.97 (standard deviation: 0.03). Mean switch trial RT, using only correct trials, was 1,080ms (standard deviation: 173ms), while repeat trial RT was 725ms (standard deviation: 103ms). The switch cost was computed by subtracting mean repeat trial RT from mean switch trial RT. The resulting switch costs were positive in all cases, and ranged from 49ms to 717ms (mean 355 ms, standard deviation: 173 ms).
DST performance
The response accuracy rate was 0.93 for the high-demand alternative and 0.95 for the low-demand alternative, and these rates differed significantly (Wilcoxon signed-rank p < 0.01). Mean RTs are shown in Table 1. RT showed a main effect of demand level (F(1,18) = 11.94, p < 0.01), a main effect of task switch vs. repetition (F(1,18) = 47.00, p < 0.01), and a significant interaction between these factors (F(1,18) = 5.75, p = 0.03).
DST choices
The average low-demand selection rate was 0.67, (range, 0.45 to 0.95), which differed significantly from 0.50 (Wilcoxon signed-rank p < 0.01). The DST again showed high internal consistency (Cronbach's α = 0.91).
Figure 3b shows the distribution of total choice rates of the participants in Experiment 5. As in Experiment 3, we found that individual subjects’ responses ranged mainly from indifference to aversion toward high demand. Seven individuals showed a low-demand selection rate that reliably exceeded 0.50 in a single-subject signed-rank test across the 8 DST runs. The bias did not reach significance for 12 subjects, and no subject showed a significant bias in the reverse direction.
Across-subject correlations
Choice rates during the DST showed a significant positive correlation with the switch cost estimated during the preliminary block (r = 0.54, p = 0.02). That is, as predicted, individuals who initially showed greater switch costs went on to show more extreme demand avoidance (see Figure 4). This correlation was not driven solely by a correlation between choice rate and either switch-trial RT or repeat-trial RT (r = 0.34 and -0.34, p = 0.15 and 0.16, respectively). Choices also were not predicted by error rates in the preliminary block for switch trials (r = -0.19, p = 0.44), repeat trials (r = 0.03, p = 0.91), or the difference between the two (r = -0.20, p = 0.42).
Figure 4.
Scatterplot of individual low-demand selection rates against switch cost (task switch RT – task repetition RT) in Experiment 5. Demand selection rates showed a significant positive correlation with switch costs (r = 0.54, p = 0.02).
Discussion
The principle of demand avoidance implies that individual differences in cognitive ability should correlate with differences in avoidance behavior. Individuals whose resources for controlled information processing are more heavily taxed by a given task should avoid that task relatively strongly. The results of Experiment 5 match this expectation. The results also provide further support for the generality of demand avoidance. Across Experiments 3–5, no evidence was found that any subset of individuals exhibited a systematic preference for the high-demand alternative (see Figure 3b).
Of course, differences in ability or cognitive resource availability are not the only potential source of variation in demand-avoidance behavior. In particular, such differences might stem additionally from differences in the appraisal of mental-effort-related costs. That is, individuals might place different amounts of value on effort, perhaps in line with personality variables such as “need for cognition” (Cacioppo & Petty, 1982), “learned industriousness” (Eisenberger, 1992), or tolerance for mental effort (Dornic, Ekehammar & Laaksonen, 1991). We return to this important consideration in the General Discussion.
Experiment 6A
The results reported so far square well with a tendency toward demand avoidance. An important aspect of these results is that they provide evidence against error avoidance or minimization of time-on-task as full explanations for avoidance behavior; instead, results are consistent with the idea that cognitive demand itself carries intrinsic costs. However, Experiments 1-5 leave open a subtler alternative hypothesis. Bogacz and colleagues (2006) proposed that decision strategies are chosen so as to minimize the time required to achieve task objectives. In simple forced-choice decision tasks, like those employed in our Experiments 1-5 (and those addressed by Bogacz and colleagues), this amounts to minimizing RT. Since the high-demand option in all of our experiments so far was associated with a larger mean RT, it is possible that participants’ avoidance behavior reflected a motivation to minimize RTs on individual trials, thus minimizing the time required to achieve task goals. Experiment 6A aimed to address this alternative explanation by decoupling simple RTs from the time required to accomplish central task objectives.
The experiment employed a new DST, which we refer to as the fill/clear task. The task involved a series of ‘games.’ At the outset of each game, an 8 by 11 grid (the ‘board’) appeared, with a random subset of cells filled, all in either green or blue (Figure 5). From here, the participant used two response keys to fill or clear cells (‘add or remove pieces’), a few at a time, with the ultimate objective of either completely clearing or completely filling the board. Participants were free to choose, on every step in the game, between adding and subtracting pieces, and between the goals of filling and clearing the board.
Figure 5.
Sequence of events in the fill/clear task. At the outset of each game, an 8 by 11 board appeared, with a random subset of pieces filled in either green or blue. Participants filled or cleared pieces, with the ultimate objective of either completely clearing or completely filling the board. In the current example, the participant presses the right key to fill four pieces at the outset of the game. As the color changes after this response, the participant presses the left key to fill four subsequent pieces. Next, a jump occurs and only four pieces remain on the board. The participant decides to switch strategies and clears all remaining pieces in the grid, thereby winning the game.
Importantly, the effects of the two response keys depended on the color of the pieces in the current display, which varied randomly across steps of the task. One of the keys (say, the left) added four pieces if the color was blue, but removed four pieces if the color was green. The other key (right) had the opposite pattern effects. Thus, if a participant were operating under a ‘fill’ strategy, it would be appropriate to respond left to blue and right to green. The ‘clear’ strategy would call for the opposite stimulus-response mapping. Note that this made it cognitively costly to switch between strategies.
This brings us to one final, crucial detail of the task. At some point during many (but not all) games, the participant's key-press yielded a sudden, unpredictable change in the number of pieces on the board. Following such ‘jumps,’ the game continued as before, with participants free as always to choose between fill and clear strategies. Our primary interest was in cases where the jump invited a change in strategy: cases where (1) the participant was filling the board and a jump yielded a relatively empty board, or (2) the participant was clearing the board and a jump yielded a relatively full board. In each of these scenarios, a motive to minimize the time to goal attainment would call for a task switch following the jump. In contrast, a motive to avoid cognitive demand would call for the less time-efficient strategy of sticking with the strategy in force before the jump.
Methods
Participants
Sixty-two members of the Princeton University and 22 members of the Leiden University communities (17-33 years of age; 50 females) participated in the study. Participation in the study was compensated for with course credit or a nominal payment. All participants provided informed consent, following procedures approved by the Princeton University Institutional Review Board and the Leiden University ethics committee.
Stimuli, design, and procedures
The experiment was computer-based and programmed using the Psychophysics Toolbox extensions for Matlab (Brainard, 1997; Pelli, 1997). The protocol alternated between two tasks: the fill/clear task and a filler task involving trustworthiness judgments on face stimuli.
In the fill/clear task, the number of pieces at the outset of each ‘game’ was always a multiple of four, but was otherwise selected randomly without replacement. Participants responded using the F and J keys, with key-effect mappings (as characterized above) counterbalanced across subjects. Except for when ‘jumps’ occurred, each response either added or subtracted four pieces, at randomly selected locations. The color of the pieces in the display (blue or green) was selected randomly following each response. The task was self-paced. When a board was successfully filled or cleared, the words “You win!” were briefly displayed.
Jumps in the state of the board, accompanied by a brief tone, occurred (only once) in a randomly selected 76% of games. On these trials, the timing of the jump was established probabilistically: The chance of a jump after a key press, given that no jump had yet occurred, was established as:
where n is the number of pieces before the jump, and strategy was inferred from the participant's last response prior to the jump. This means that at each step of a game involving a jump, the jump was equally likely to occur on every subsequent step, given a fixed strategy, and also that the jump was guaranteed to occur before the end of the game. The number of pieces following the jump was selected randomly, with the constraint that it could not equal the number prior to the jump or the number that would have normally resulted from the participant's last response.
Upon completion of each fill/clear game, participants were prompted to press the two response keys simultaneously. As a result, a face from the Productive Aging Lab Face Database (Minear & Park, 2004) was presented for 3-5 seconds. Participants were instructed to verbally judge the trustworthiness of the face on a scale from 1 to 5, with 1 being lowest and 5 being highest. This filler task served to isolate rounds of the fill/clear task, minimizing carryover of strategy from one round to the next.
Midway through the study a minor modification to the paradigm was introduced. Initially, 57 participants each played a fixed total of 110 games; the remaining participants played a variable number of games for a fixed session duration of 30 minutes.
Analysis
Transitions from one strategy to another in the fill/clear task were predicted to carry switch costs. In order to confirm this, a paired Student's t-test was used to compare mean RTs immediately following jumps between cases where responses did or did not maintain the previously established strategy.
The strategy chosen at the outset of each game was predicted to vary depending on the number of pieces present. To confirm this, the 21 possible initial piece-counts were organized into seven bins (first bin: 4, 8 and 12 pieces, second: 16, 20, and 24 pieces, etc.). For each bin and each subject, we calculated the proportion of cases in which the fill strategy was adopted at game outset, labeling this OFPi (Outset Fill Proportion in bin i). For illustration, see the blue trace in Figure 6.
Figure 6.
The fill proportions OPFi, JPFi,stay and JPFi,switch are plotted for all bin numbers i (one through seven). The overall pattern reveals that participants reasonably chose the fill strategy more often when the initial board state was nearer to full than nearer to empty. Post-jump strategy choice revealed that participants tended to maintain their established strategy, instead of switching to the other strategy. The shaded areas delineate the contrast JIP - OIP, as described in the text.
A similar approach was adopted in analyzing strategy choice following jumps. Post-jump board states were binned as above, and in each bin we calculated the proportion of cases in which the fill strategy was adopted immediately following the jump (Jump Fill Proportion; JFP). This calculation was made separately for cases where the participant had been following the fill strategy immediately before the jump (JFPi,stay), and cases where the participant had been following the clear strategy (JFPi,switch). For illustration, see the green and red traces in Figure 6.
To evaluate whether participants were biased against switching strategies following jumps, we compared post-jump strategy selection to game-outset behavior. For each participant we averaged OFPi, JFPi,stay and JFPi,switch across bins, labeling the resulting means OFP, JFPstay and JFPswitch. We then used Wilcoxon signed-ranks tests to perform pair-wise comparisons, predicting first that JFPstay would be significantly larger than JFPswitch, and at a more detailed level that JFPstay would be significantly larger than OFP, while JFPswitch would be smaller than OFP.
A second analysis focused in on strategy choice in situations where switch avoidance was likely to delay game completion. This involved focusing on the slice of the data marked out by the gray areas in Figure 6. The highlighted points in the green data series derive from situations in which the fill strategy was being pursued just before a jump to a relatively empty board state. The highlighted points in the red data series derive from situations in which the clear strategy was being pursued just before a jump to a relatively full board state. In both of these situations, minimizing the average time to game completion required a switch to the opposite strategy. (Note that, given the presence of switch costs, it might sometimes have been more time-efficient to stay with the pre-jump strategy, even when the opposite strategy would allow game completion in fewer steps. That is, in such cases, the time-cost of the additional steps required would be outweighed by the time saved by avoiding switch costs. Preliminary analyses indicated that, across participants, this situation would only hold in board-state bin four. This bin was therefore excluded from the relevant analyses.)
To quantify choice behavior in the relevant game situations, we calculated for each participant the proportion of trials on which the pre-jump strategy was maintained post-jump, despite it being time-inefficient, labeling it JIP (Jump Inefficiency Proportion):
We predicted that this value would be greater than OIP (Outset Inefficiency Proportion):
the proportion of cases in which the participant selected the time-inefficient strategy at game outset. This prediction was tested using a Wilcoxon signed-ranks test. The grey areas in Figure 6 mark out the portions of the choice data involved in the contrast.
Post-jump strategy maintenance might plausibly reflect participants’ indifference or inattention when performing the task. To evaluate this possibility, we repeated our analyses, focusing on a subset of games involving what we termed strategy coherence. A game was judged to show strategy coherence if (1) the strategy selected at game outset was identical to the strategy selected in the pre-jump state, and (2) the strategy selected immediately post-jump matched the strategy on the final step of the game. We assumed that such consistency in strategy selection reflected a reasonable level of attention to the content of the task.
Results
Preliminary analyses confirmed that there were no statistically significant differences between the Leiden and Princeton groups, or between the group run with a fixed number of games and the group run for a fixed time, in the number of responses per game, number of responses per game in which a jump occurred, switch costs, the difference between OIP and JIP, or mean RT. Subsequent analyses therefore collapsed across these divisions.
RTs
The results showed that post-jump transitions from one strategy to another were associated with higher mean RTs (1421 ms, standard deviation: 366 ms) than when maintaining the established strategy (1014 ms, standard deviation: 269 ms), and this difference was statistically significant (t(56) = 13.08, p < 0.0001).
Strategy selection
The green trace in Figure 6 shows the mean values for OFPi (as defined under Methods). The green and red traces in the figure show, respectively, mean values for JFPi,stay and JFPi,switch,. Mean values over bins were 0.53 for OFP, 0.38 for JFPswitch, and 0.66 for JFPstay. In line with predictions, JFPstay was significantly larger than JFPswitch (p < 0.0001); JFPstay was significantly larger than than OFP (p < 0.0001); and JFPswitch was significantly smaller than OFP (p < 0.0001). Also in line with predictions, we found that JIP (mean: 0.43) was significantly greater than OIP (mean: 0.34, p < 0.001).
In this experiment, 72% of all games displayed strategy coherence, as defined under Methods. In this subset of games, an analogous pattern of results emerged. JFPstay was significantly larger than JFPswitch (p < 0.0001); JFPstay was significantly larger than than OFP (p < 0.0001); and JFPswitch was significantly smaller than OFP (p < 0.0001); JIP (mean: 0.27) was significantly greater than OIP (mean: 0.20, p < 0.05).
Discussion
The present experiment replicated in a new setting the finding that, absent compensating incentives, people tend to avoid cognitive demand. During performance of a multi-step task, participants tended to avoid switching task strategies, even when circumstances made this the fastest way to achieve task objectives. Participants were willing to delay goals in order to avoid a cognitively demanding task switch. This result goes some distance toward assuaging the concern that the bias observed in earlier experiments reflected simply a motivation to meet task goals as quickly as possible.
One potential concern attaching to the results of the present experiment is that the task-switch avoidance observed might simply reflect priming. That is, the adoption of a particular strategy might prime associations between stimulus color and manual responses, so that after a jump these associations would bias responding toward the existing strategy (see Hommel, 2004). Note that this would constitute a non-motivational explanation of the avoidance effect. Thus, if priming entirely explained the results of Experiment 6A, the inclusion of incentives should not affect the magnitude of the switch-avoidance effect. On the other hand, if switch-avoidance in the fill/clear task is reflective at least in part of a motivation to avoid cognitive demand, then introducing incentives for early task completion should reduce the effect. Experiment 6B tested this prediction.
Experiment 6B
Methods
Participants
Fifty-one subjects from the Princeton University community (17-21 years of age, 39 females) participated.
Materials and procedure
The task and procedure were the same as those in Experiment 6A, with the important exception that participants were rewarded for each game they completed. Thirty-seven people received 10¢ for each completed game, and fourteen participants were rewarded with 1¢ per game.
Analysis
Choice behavior was characterized using the measures introduced in Experiment 6A. The central predictions, using the terminology established in Experiment 6A, were that the new set of rewarded participants group, when compared to the unrewarded group of Experiment 6A, would show (1) a smaller difference between JFPswitch and JFPstay, and (2) more informatively, a smaller difference between JIP and OIP. These differences of differences were tested using Wilcoxon two sample tests.
Results
Initial analyses revealed that there were no significant differences between the 1¢ and 10¢ groups in the number of steps per game, number of steps per game in which a jump occurred, switch costs or the difference between JIP and OIP (p > 0.31 in all cases). In the remaining analyses, we collapsed across the two groups.
RTs
As in Experiment 6A, rewarded participants responded more slowly when switching strategies (1446 ms, standard deviation: 375 ms) than when maintaining the established strategy (1101 ms, standard deviation: 311 ms) post-jump, and this difference was statistically significant (t(50) = 11.80, p < 0.0001).
Strategy selection
When the initial board was nearer to full than nearer to empty, participants chose the fill strategy more often. Mean values over bins were 0.60 for OFP, 0.45 for JFPswitch, and 0.55 for JFPstay. Consistent with our earlier findings, JFPstay was significantly larger than JFPswitch (p < 0.0001); JFPstay was significantly larger than OFP (p < 0.05); and JFPswitch was significantly smaller than OFP (p < 0.0001). In contrast with Experiment 6A, JIP (mean: 0.32) was numerically but not statistically greater than OIP (mean: 0. 30, p = 0.65).
In this study, 74% of all games were classified as involving strategy coherence, as defined earlier. In this subset of games, JFPstay was significantly larger than JFPswitch (p < 0.05); JFPstay was numerically but not statistically larger than OFP (p = 0.80); and JFPswitch was significantly smaller than OFP (p < 0.05); JIP (mean: 0.15) was not statistically different from OIP (mean: 0.16, p = 0.15).
Paid vs. unpaid
Our central prediction was that the inclusion of incentives for early task completion would reduce the bias against strategy switching. This was tested by comparing (JFPswitch – JFPstay) and (JIP – OIP) between paid participants and the unpaid participants from Experiment 6A. As seen in figure 7, the difference between JFPswitch and JFPstay was smaller in the paid group when compared to the unpaid group (p < 0.01). More informatively, the paid group also displayed a smaller difference between JIP and OIP when compared to the unpaid group (Wilcoxon test, p < 0.05).
Figure 7.
The differences between JPFstay and JPFswitch and the difference between JIP and OIP and their standard errors are given for the paid and unpaid groups of Experiments 6A and 6B. Both differences were significantly smaller for the paid group than for the unpaid group. * p < 0.05, ** p < 0.01
Overall, 73% of all games displayed strategy coherence. In this subset of games, the difference between JFPswitch and JFPstay was also smaller in the paid group when compared to the unpaid group (p < 0.001). And the paid group again displayed a smaller difference between JIP and OIP when compared to the unpaid group (Wilcoxon test, p < 0.01).
Discussion
Throughout the present paper, we have been considering the idea that cognitive demand weighs as a cost in the cost-benefit analyses underlying decision-making. All of the experiments we have presented, including Experiment 6A, indicated that, ceteris paribus, people tend to avoid demand. The idea that demand registers as a cost predicts, additionally, that avoidance should be reduced when incentives are introduced that offset the cost of cognitive effort. The present experiment confirmed this prediction in the task setting introduced in Experiment 6A. When rewards were introduced for effortful lines of action, the avoidance tendency observed in 6A was reduced.
The results of the present experiment additionally rule out an alternative explanation for our findings in 6A, which was that switch avoidance might have simply reflected S-R priming. If this were the entire explanation, it is unclear why the effect would be altered by an incentive manipulation.
Even though the reward of our two incentive groups differed by a factor 10 (1¢ and 10¢), they did not display differential behavior on the fill/clear task. Although this result was not predicted, it may reflect a ceiling effect, since in both groups the difference between JIP and OIP was not significantly different from zero. Of course, however, despite the rather large sample sizes our experiments involved, it is not possible to rule out insufficient power. In any event, though provocative, the absence of a difference between the two reward groups does not undermine the interpretability of our more central findings.
General Discussion
The law of less work, a time-honored principle in research on decision making, has been widely assumed to apply to mental effort. It has frequently been asserted that, all things being equal, people tend to avoid situations carrying a high demand for effortful cognitive processing. To our knowledge, no attempt has previously been made to test this assumption in a controlled and systematic fashion. We have presented results from six experiments, which collectively appear to support a ‘law of least mental effort.’ Participants in each experiment chose between two actions associated with different subsequent cognitive demands. In each case, participants as a group displayed a clear bias toward the less demanding option. Our first experiment provided evidence that the bias did not simply arise from a strategy of minimizing errors or session length, nor did it depend upon an ability to describe how the two options differed, minimizing the likelihood that demand characteristics lay behind it. Experiment 2 and 4 supported the generality of the effect by detecting it in different task paradigms, tapping executive functions in other ways. Experiments 3 and 5 addressed the meaningfulness of variability in individual subjects’ demand selection performance. Experiment 3 also found that the frequency of apparent preferences for high demand was reduced by a method designed to mitigate the contribution of arbitrary cue- or position-based preferences, a finding replicated by Experiments 4 and 5. In addition, Experiment 5 found that cognitive demand avoidance varies inversely with task-relevant ability. Experiment 6A ruled out that behavior observed in our experiments reflected a drive to reach task objectives as quickly as possible. Experiment 6B showed that the cost of mental effort could be compensated for by monetary reward.
All in all, the present findings seem to provide convergent evidence for a bias against responses tied to requirements for cognitively demanding executive processing.
Relation to previous behavioral research
As reviewed in the introduction, a wide variety of studies, on topics ranging from arithmetic to judgment and decision making, have recognized the potential explanatory relevance of a tendency to avoid high cognitive demand. The present results provide independent support for the existence of such a tendency, lending force to its explanatory role in such earlier work. Previous discussions (e.g., MacLeod et al., 1978; Nieuwenhuis & Monsell, 2002; Payne et al., 1993; Wilcox, 1993; Yeung & Monsell, 2003) have considered ways in which demand avoidance might impact decisions when only a single task is available to be performed. Decision-making in such situations concerns which strategy to apply, and which resources to devote to the task at hand (Navon & Gopher, 1979).
The concept of effort minimization has been particularly influential in the field of judgment and decision-making. Several investigators have noted that if mental effort carries internal costs, decision-makers might find it subjectively optimal to use simplifying heuristics rather than more accurate procedures (Hauser & Wernerfelt, 1990; Payne, Bettman, & Johnson, 1988; 1993; Shah & Oppenheimer, 2008; Shugan, 1980; Smith & Wicox, 1993). In this way, externally suboptimal behaviors could arise from a rational evaluation of costs and benefits. For example, effort-minimization might be among the reasons why decision-makers to adopt non-compensatory strategies for aggregating evidence (Bröder & Schiffer, 2003; Payne et al., 1988) or rule out alternatives without fully evaluating them (Hauser & Wernerfelt, 1990).
The present work provides the most direct support to date for a key premise of the above work, namely the idea that mental effort carries subjective costs. We have shown that effort minimization influences behavioral choices; this bolsters the likelihood that effort avoidance guides covert strategy-selection decisions as well. The behavioral DST we have introduced might also be a useful tool in testing questions of specific relevance to decision-making. For example, a DST could be used to test the proposal that an activity's internal cost corresponds to the number of “elementary information processes” it comprises (Payne et al., 1988), or the idea that it is more internally costly to retrieve information from memory than from the environment (Bröder & Schiffer, 2003). In light of our findings, it may also be worth investigating the specific relevance of an effort minimization motive to cases where decisions are deferred or avoided altogether (e.g., Tversky & Shafir, 1992).
Another category of past work has focused on instances where individuals gravitate toward cognitively demanding mental activity; this category includes research on ‘learned industriousness’ (Eisenberger, 1992) or ‘need-for-cognition’ (Cacioppo, Petty, Feinstein, Blair, & Jarvis, 1996). Such work may appear to pose a basic challenge to the notion of demand avoidance. Indeed, if demand avoidance is a general principle then one may reasonably wonder why so many people spontaneously engage in effortful recreational tasks such as crossword puzzles or Sudoku. As it turns out, previous work on effort-seeking itself provides a potential answer. As noted earlier, the standard assumption in work on ‘learned industriousness’ has been that effort is aversive, but its aversiveness can be outweighed by other factors, including a rewarding sense of efficacy. The same basic perspective also appears in work on ‘need-for-cognition’ (Cacioppo et al., 1996), and in work on social judgment, where information-processing effort has been understood as driven by a desire to arrive at correct attitudes (Petty & Wegener, 1999). Selection of high-effort courses of action need not contradict the proposition that effort weighs negatively in the underlying tradeoff. The crossword-puzzle player is like a weight lifter: both are subject to the law of least (physical or mental) effort, but effort-related costs may be countered by other incentives.
Admitting the existence of multiple costs and benefits may appear to render the principle of demand avoidance impossible to disconfirm. However, this is not the case. The hypothesis clearly predicts that when the secondary rewards of cognitive effort are minimized (or equalized), effort avoidance should be observed in choice behavior. This is precisely the prediction tested and confirmed in the present work. Clearly, the results of cognitive effort can carry rewards. The question is whether one can explain the patterns of behavior observed in our studies, and in particular the patterns shown in Figures 2 and 3b, without appealing to the notion that cognitive demand itself is intrinsically costly or aversive. To us, the answer to this question appears to be no.
Relevant findings from neuroscientific research
We have suggested that cognitive demand factors into cost-benefit analyses that guide behavior. A prediction from this idea is that demand levels should exert influence on neural mechanisms involved in registering the incentive value of ongoing events, such as the dopaminergic projection to the nucleus accumbens (NAcc). We have recently reported evidence that a manipulation of task-switching demand, similar to the manipulations used in the present work, indeed influences NAcc response to associated rewards (Botvinick, Huffstetler, & McGuire, 2009). Specifically, rewards appeared to be discounted by an associated demand for effort. Both high and low reward outcomes were paired with high and low levels of cognitive demand, and outcome-related NAcc activity showed a main effect of both factors. NAcc response was greater for high-reward than low-reward outcomes, consistent with past research (Delgado, Nystrom, Fissell, Noll, & Fiez, 2000). In addition, NAcc response was reduced for higher levels of cognitive demand, suggesting that demand exerts a negative influence on neurally represented reward values. Insofar as the NAcc participates in value-based learning, demand-based modulations of reward appraisal might support learned avoidance of cognitive demand such as we have documented in the present behavioral experiments. Anticipatory activation of avoidance mechanisms is one possible explanation for elevated skin-conductance responses observed just before the selection of a high-demand alternative (Botvinick & Rosen, 2009).
Given that both behavior and NAcc response appear to be influenced by a signal of demand-related cost, it would be useful to understand the neural dynamics from which this cost first originates. One possibility, in principle, is that demand-related costs could arise from the consumption of resources throughout the brain (e.g., from the use of any resource pool in a multiple-capacity system of working memory; Reichle et al., 2000). In the present work, however, we have focused on the possibility that intrinsic costs may be specifically related to the functioning of cognitive control (Miller & Cohen, 2001). This perspective would suggest that costs originate in brain regions showing consistent involvement in situations where control is required. Two such regions are the lateral prefrontal cortex (LPFC) and anterior cingulate cortex (ACC; Duncan & Owen, 2000).
In the report of effort discounting in NAcc, Botvinick and colleagues (2009) noted that reward-related activity in NAcc was negatively correlated with task-evoked activity in ACC. This correlation held across task events for individual participants, even within each externally manipulated demand level. This observation suggests that the ACC might participate in effort-related discounting of rewards, an idea that is consistent with other evidence for ACC involvement in encoding adverse outcomes (see Botvinick, 2007).
Other work has linked LPFC activity as well to the registration of intrinsic costs (McGuire & Botvinick, in press). LPFC activity has also been seen in association with a potentially costly strategy of ‘proactive’ cognitive control (Braver, Gray, & Burgess, 2007; Paxton, Barch, Racine, & Braver, 2008). The interplay between ACC and LPFC in driving costs remains a promising topic for future work. Already, however, evidence provides support for the general point that intrinsic costs are linked to the activity of control-relevant regions of the frontal lobes.
Questions for further investigation
Strength of the bias
One issue for further investigation pertains to the strength of the observed bias. Even while tending to prefer the low-demand alternative, subjects typically sampled both alternatives throughout the experiment. Even in Experiments 3–5, in which the bias was more uniform, its average strength did not approach 100%. Furthermore, data suggested that individual subjects maintained relatively consistent degrees of bias across the session. Various explanations might be considered, ranging from the relatively uninteresting possibility that subjects interpreted the instructions to mean that they should continue to choose from both decks, to the more interesting possibilities that subjects’ sampling behavior reflected information-seeking (Tversky & Edwards, 1966), a desire for variety or change (McAlister & Pessemier, 1982), or a version of probability matching (Vulkan, 2000).
While the origins of the observed choice variability are an important target for further investigation, it is important to note that the presence of that variability does not undermine the interpretability of our results. Obviously, the ‘law of least mental effort,’ in line with the law of less work before it, does not imply that human decision makers should categorically and uniformly avoid cognitive demand under any and all circumstances (indeed, studies of physical effort avoidance have almost universally reported graded rather than categorical effects; see, e.g., Solomon, 1948). Rather, the ‘law of least mental effort’ stipulates that anticipated cognitive demand weighs as a cost in the cost-benefit analyses that underlie decision-making. To the extent that decision-making also involves other factors orthogonal to demand (e.g., a desire for novelty or change), and to the extent that decisions are stochastically related to the outcome of cost-benefit analyses (as is the case in many models of human and animal decision making), effort avoidance can be expected to assume a graded rather than categorical form. Once again, the key question concerning the present work is whether the pattern of results obtained (e.g., the data shown in Figures 2 and 3b) can be explained without appealing to the notion that cognitive demand weighs as a cost in decision-making.
Evaluation of demand
A second goal for further work is to examine which specific aspects of the situations imposed in the present experiments are most directly responsible for the observed pattern of avoidance. We have provided evidence that demand avoidance cannot be accounted for entirely in terms of error avoidance or maximization of reward rates. The same basic pattern of avoidance was also obtained across a variety of task settings, suggesting that the critical aspect of information processing is relatively generic, rather than something tied specifically to, say, demands for task switching. We have suggested that the critical factor in demand evaluation may be the degree of executive control required for task performance. However, executive functions are notoriously complex and multifaceted, and a finer-grained account, specifying which aspects of control function are most relevant for demand evaluation and avoidance would be desirable. One possibility is that avoidance is driven by the need to encode and maintain a new task set (Rogers & Monsell, 1995) or other context information (see, e.g., O'Reilly, Braver & Cohen, 1999) into working memory. Another possibility is that costs arise directly from the exertion of top-down control (e.g., Yeung & Monsell, 2003), which may involve processes that serve to overcome interference from recently active tasks (Wylie & Allport, 2000) and prepotent response tendencies (Miller & Cohen, 2001). A third possibility is that costs are associated with even more general aspects of demanding task performance, such as internal signals representing cognitive conflict (Botvinick, 2007). As noted above, we have begun to pursue neuroimaging work aimed at disentangling some of these possibilities (Botvinick et al., 2009; McGuire & Botvinick, in press).
Another inviting challenge for further research would be to understand the relationship between situations that impose demand-related costs and those that bring about self-regulatory depletion (Muraven & Baumeister, 2000). Demanding mental activities such as emotion regulation have been shown to reduce people's later cognitive performance. Even the basic mental act of making a decision among alternatives has been argued to deplete cognitive resources (Vohs et al., 2008). If the demanding tasks that people tend to avoid are the same tasks that also deplete their cognitive resources, then resource-preservation might provide a normative account for the demand avoidance bias we have observed.
The above questions and others might be productively addressed through examination of individual differences in the strength of the demand avoidance bias. If a procedure such as that implemented in Experiment 3 were found to be reliable across time (and/or across multiple types of demanding tasks), then perhaps it could provide a stable estimate of an individual's position on a continuum from indifference to strong aversion toward effort. As such, it might be administered in conjunction with other measures to test both the mechanisms and the practical implications of strong vs. weaker biases against cognitive demand. Combining this paradigm with functional neuroimaging might permit assessment of the physiological correlates of bias magnitude (see McGuire & Botvinick, in press). It would also be of interest to test the paradigm in conjunction with motivation-related individual difference scales (e.g. the BIS/BAS; Carver & White, 1994), personality indices, clinical phenomenology, (Cohen, Weingartner, Smallberg, Pickar, & Murphy, 1982), or applied behavioral correlates.
Acknowledgments
The present research was conducted with assistance from Stacy Huffstetler, Steven Ibara, Joseph Luka, Idu Azogu, Francisco Pereira, Janani Prabhakar, and Sydney Schiff. This research was supported by National Institute of Mental Health Grant MH062196.
Footnotes
Publisher's Disclaimer: The following manuscript is the final accepted manuscript. It has not been subjected to the final copyediting, fact-checking, and proofreading required for formal publication. It is not the definitive, publisher-authenticated version. The American Psychological Association and its Council of Editors disclaim any responsibility or liabilities for errors or omissions of this manuscript version, any version derived from this manuscript by NIH, or other third parties. The published version is available at www.apa.org/pubs/journals/xge
References
- Allport GW. The nature of prejudice. Addison Wesley; New York: 1954. [Google Scholar]
- Anderson JR. The adaptive character of thought. Lawrence Erlbaum; Hillsdale, NJ: 1990. [Google Scholar]
- Arrington CM, Logan GD. The cost of a voluntary task switch. Psychological Science. 2004;15:610–615. doi: 10.1111/j.0956-7976.2004.00728.x. [DOI] [PubMed] [Google Scholar]
- Ballard DH, Hayhoe MM, Pook PK, Rao RPN. Deictic codes for the embodiment of cognition. Behavioral and Brain Sciences. 1997;20:723–742. doi: 10.1017/s0140525x97001611. [DOI] [PubMed] [Google Scholar]
- Ballé M. La loi du moindre effort mental. Sciences Humaines. 2002;128:36–39. [Google Scholar]
- Barch DM, Braver TS, Nystrom LE, Forman SD, Noll DC, Cohen JD. Dissociating working memory from task difficulty in human prefrontal cortex. Neuropsychologia. 1997;35:1373–1380. doi: 10.1016/s0028-3932(97)00072-9. [DOI] [PubMed] [Google Scholar]
- Baroody AJ, Ginsburg HP. The relationship between initial meaningful and mechanical knowledge of arithmetic. In: Hiebert J, editor. Conceptual and procedural knowledge: The case of mathematics. Erlbaum; Hillsdale, NJ: 1986. pp. 75–112. [Google Scholar]
- Bechara A, Damasio H, Damasio AR, Lee GP. Different contributions of the human amygdala and ventromedial prefrontal cortex to decision-making. Journal of Neuroscience. 1999;19:5473–5481. doi: 10.1523/JNEUROSCI.19-13-05473.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bechara A, Damasio H, Tranel D, Damasio AR. Deciding advantageously before knowing the advantageous strategy. Science. 1997;275:1293–1295. doi: 10.1126/science.275.5304.1293. [DOI] [PubMed] [Google Scholar]
- Bechara A, Tranel D, Damasio H, Damasio AR. Failure to respond autonomically to anticipated future outcomes following damage to prefrontal cortex. Cerebral Cortex. 1996;6:215–225. doi: 10.1093/cercor/6.2.215. [DOI] [PubMed] [Google Scholar]
- Blough DS. The study of animal processes by operant methods. In: Honig WK, editor. Operant behavior: Areas of research and application. Appleton-Century-Crofts; New York: 1966. [Google Scholar]
- Bogacz R, Brown E, Moehlis J, Holmes P, Cohen JD. The physics of optimal decision making: a formal analysis of models of performance in two-alternative forced-choice tasks. Psychological Review. 2006;113:700–765. doi: 10.1037/0033-295X.113.4.700. [DOI] [PubMed] [Google Scholar]
- Botvinick MM. Conflict monitoring and decision making: Reconciling two perspectives on anterior cingulate function. Cognitive, Affective, & Behavioral Neuroscience. 2007;7:356–366. doi: 10.3758/cabn.7.4.356. [DOI] [PubMed] [Google Scholar]
- Botvinick MM, Rosen Z. Anticipation of cognitive demand during decision-making. Psychological Research. 2009 doi: 10.1007/s00426-008-0197-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Botvinick MM, Huffstetler S, McGuire JT. Effort discounting in human nucleus accumbens. Cognitive, Affective, & Behavioral Neuroscience. 2009;9:16–27. doi: 10.3758/CABN.9.1.16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brainard D. The psychophysics toolbox. Spatial Vision. 1997;10:433–436. [PubMed] [Google Scholar]
- Braver TS, Gray JR, Burgess GC. Explaining the many varieties of working memory variation: Dual mechanisms of cognitive control. In: Conway ARA, Jarrold C, Kane MJ, Miyake A, Towse JN, editors. Variation in working memory. Oxford University Press; New York: 2007. pp. 76–106. [Google Scholar]
- Bröder A, Schiffer S. Take the best versus simultaneous feature matching: Probabilistic inferences from memory and effects of representation format. Journal of Experimental Psychology: General. 2003;132:277–293. doi: 10.1037/0096-3445.132.2.277. [DOI] [PubMed] [Google Scholar]
- Cacioppo JT, Petty RE. The need for cognition. Journal of Personality and Social Psychology. 1982;42:116–131. doi: 10.1037//0022-3514.43.3.623. [DOI] [PubMed] [Google Scholar]
- Cacioppo JT, Petty RE, Feinstein JA, Blair W, Jarvis G. Dispositional differences in cognitive motivation: The life and times of individuals varying in need for cognition. Psychological Bulletin. 1996;119:197–253. [Google Scholar]
- Camerer C, Hogarth R. The effects of financial incentives in experiments: A review and capital-labor-production framework. Journal of Risk and Uncertainty. 1999;19:7–42. [Google Scholar]
- Carver CS, White TL. Behavioral inhibition, behavioral activation, and affective responses to impending reward and punishment: The BIS/BAS scales. Journal of Personality and Social Psychology. 1994;67:319–319. [Google Scholar]
- Christenfeld N. Choices from identical options. Psychological Science. 1995;6:50–55. [Google Scholar]
- Cialdini RB, Goldstein NJ. Social influence: Compliance and conformity. Annual Review of Psychology. 2004;55:591–621. doi: 10.1146/annurev.psych.55.090902.142015. [DOI] [PubMed] [Google Scholar]
- Cohen RM, Weingartner H, Smallberg SA, Pickar D, Murphy DL. Effort and cognition in depression. Archives of General Psychiatry. 1982;39:593–597. doi: 10.1001/archpsyc.1982.04290050061012. [DOI] [PubMed] [Google Scholar]
- Cuvo AJ, Lerch LJ, Leurquin DA, Gaffaney TJ, Poppen RL. Response allocation to concurrent fixed-ratio reinforcement schedules with work requirements by adults with mental retardation and typical preschool children. Journal Of Applied Behavior Analysis. 1998;31:43–64. doi: 10.1901/jaba.1998.31-43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delgado MR, Nystrom LE, Fissell C, Noll DC, Fiez JA. Tracking the hemodynamic responses to reward and punishment in the striatum. Journal of Neurophysiology. 2000;84:3072–3077. doi: 10.1152/jn.2000.84.6.3072. [DOI] [PubMed] [Google Scholar]
- Dornic S, Ekehammar B, Laaksonen T. Tolerance for mental effort: Self-ratings related to perception, performance, and personality. Personality and Individual Differences. 1991;12:313–319. [Google Scholar]
- Droll JA, Hayhoe MM. Trade-offs between gaze and working memory use. Journal of Experimental Psychology: Human Perception and Performance. 2007;33:1352–1365. doi: 10.1037/0096-1523.33.6.1352. [DOI] [PubMed] [Google Scholar]
- Duncan J, Owen AM. Common regions of the human frontal lobe recruited by diverse cognitive demands. Trends in Neurosciences. 2000;23:475–483. doi: 10.1016/s0166-2236(00)01633-7. [DOI] [PubMed] [Google Scholar]
- Eisenberger R. Learned industriousness. Psychological Review. 1992;99:248–267. doi: 10.1037/0033-295x.99.2.248. [DOI] [PubMed] [Google Scholar]
- Friedrich AM, Zentall TR. Pigeons shift their preference toward locations of food that take more effort to obtain. Behavioural Processes. 2004;67:405–415. doi: 10.1016/j.beproc.2004.07.001. [DOI] [PubMed] [Google Scholar]
- Fürst AJ, Hitch GJ. Separate roles for executive and phonological components of working memory in mental arithmetic. Memory & cognition. 2000;28:774–782. doi: 10.3758/bf03198412. [DOI] [PubMed] [Google Scholar]
- Gabriel M. Discriminative avoidance learning: A model system. In: Vogt BA, Gabriel M, editors. Neurobiology of cingulate cortex and limbic thalamus: A comprehensive handbook. Birkhauser; Boston: 1993. pp. 478–523. [Google Scholar]
- Gigerenzer G, Goldstein DG. Reasoning the fast and frugal way: Models of bounded rationality. Psychological Review. 1996;103:650–669. doi: 10.1037/0033-295x.103.4.650. [DOI] [PubMed] [Google Scholar]
- Gray WD. The nature and processing of errors in interactive behavior. Cognitive Science. 2000;24:205–248. [Google Scholar]
- Hauser JR, Wernerfelt B. An evaluation cost model of consideration sets. Journal of Consumer Research. 1990;16:393–408. [Google Scholar]
- Hitch GJ. The role of short-term working memory in mental arithmetic. Cognitive Psychology. 1978;10:302–323. [Google Scholar]
- Hommel B. Event files: feature binding in and across perception and action. Trends in Cognitive Sciences. 2004;8:496–500. doi: 10.1016/j.tics.2004.08.007. [DOI] [PubMed] [Google Scholar]
- Hull CL. Principles of behavior. Appleton-Century; New York: 1943. [Google Scholar]
- Just MA, Carpenter PA. A capacity theory of comprehension: Individual differences in working memory. Psychological Review. 1992;99:122–149. doi: 10.1037/0033-295x.99.1.122. [DOI] [PubMed] [Google Scholar]
- Kahneman D, Tversky A. Prospect theory: An analysis of decision under risk. Econometrica. 1979;47:263–291. [Google Scholar]
- MacLeod CM, Hunt EB, Mathews NN. Individual differences in the verification of sentence-picture relationships. Journal of Verbal Learning & Verbal Behavior. 1978;17:493–507. [Google Scholar]
- Mathews N, Hunt E, MacLeod CM. Strategy choice and strategy training in sentence-picture verification. Journal of Verbal Learning & Verbal Behavior. 1980;19:531–548. [Google Scholar]
- McAlister L, Pessemier E. Variety seeking behavior: An interdisciplinary review. Journal of Consumer Research. 1982;9:311–322. [Google Scholar]
- McCulloch TL. Performance preferentials of the white rat in force-resisting and spatial dimensions. Comparative Psychology. 1934;18:85–111. [Google Scholar]
- McGuire JT, Botvinick MM. Prefrontal cortex, cognitive control, and the registration of decision costs. Proceedings of the National Academy of Sciences. doi: 10.1073/pnas.0910662107. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGuire WJ. The nature of attitudes and attitude change. In: Lindzey G, Aronson E, editors. Handbook of social psychology. 2 ed. Vol. 3. Addison-Wesley; Reading, MA: 1969. pp. 136–314. [Google Scholar]
- Miller EK, Cohen JD. An integrative theory of prefrontal cortex function. Annual Reviews in Neuroscience. 2001;24:167–202. doi: 10.1146/annurev.neuro.24.1.167. [DOI] [PubMed] [Google Scholar]
- Minear M, Park DC. A lifespan database of adult facial stimuli. Behavior Research Methods, Instruments, & Computers. 2004;36:630–633. doi: 10.3758/bf03206543. [DOI] [PubMed] [Google Scholar]
- Moneta GB, Csikszentmihalyi M. The effect of perceived challenges and skills on the quality of subjective experience. Journal of Personality. 1996;64:275–310. doi: 10.1111/j.1467-6494.1996.tb00512.x. [DOI] [PubMed] [Google Scholar]
- Monsell S. Task switching. Trends in Cognitive Sciences. 2003;7:134–140. doi: 10.1016/s1364-6613(03)00028-7. [DOI] [PubMed] [Google Scholar]
- Muraven M, Baumeister RF. Self-regulation and depletion of limited resources: Does self-control resemble a muscle? Psychological Bulletin. 2000;126:247–259. doi: 10.1037/0033-2909.126.2.247. [DOI] [PubMed] [Google Scholar]
- Navon D, Gopher D. On the economy of the human-processing system. Psychological Review. 1979;86:214–255. [Google Scholar]
- Nieuwenhuis S, Monsell S. Residual costs in task switching: Testing the failure-to-engage hypothesis. Psychonomic Bulletin & Review. 2002;9:86–92. doi: 10.3758/bf03196259. [DOI] [PubMed] [Google Scholar]
- O'Reilly RC, Braver TS, Cohen JD. A biologically-based computational model of working memory. In: Miyake A, Shah P, editors. Models of working memory: Mechanisms of Active Maintenance and Executive Control. Cambridge University Press; New York: 1999. pp. 375–411. [Google Scholar]
- Paxton JL, Barch DM, Racine CA, Braver TS. Cognitive control, goal maintenance, and prefrontal function in healthy aging. Cerebral Cortex. 2008;18:1010–1028. doi: 10.1093/cercor/bhm135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Payne JW, Bettman JR, Johnson EJ. Adaptive strategy selection in decision making. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1988;14:534–552. [Google Scholar]
- Payne JW, Bettman JR, Johnson EJ. The adaptive decision maker. Cambridge University Press; Cambridge, UK: 1993. [Google Scholar]
- Pelli D. The videotoolbox software for visual psychophysics: Transforming numbers into movies. Spatial Vision. 1997;10:437–442. [PubMed] [Google Scholar]
- Petty RE, Wegener DT. The Elaboration Likelihood Model: Current status and controversies. In: Chaiken S, Trope Y, editors. Dual-process models in social psychology. Guilford; New York: 1999. pp. 41–72. [Google Scholar]
- Posner MI, DiGirolamo GJ. Executive attention: Conflict, target detection, and cognitive control. In: Parasuraman R, editor. The attentive brain. MIT Press; Cambridge, MA: 1998. pp. 401–423. [Google Scholar]
- Reichle ED, Carpenter PA, Just MA. The neural bases of strategy and skill in sentence-picture verification. Cognitive Psychology. 2000;40:261–295. doi: 10.1006/cogp.2000.0733. [DOI] [PubMed] [Google Scholar]
- Rogers RD, Monsell S. Costs of a predictable switch between simple cognitive tasks. Journal of Experimental Psychology: General. 1995;124:207–231. [Google Scholar]
- Rosch E. Principles of categorization. In: Margolis E, Laurence S, editors. Concepts: Core readings. MIT Press; Cambridge, MA: 1999. [Google Scholar]
- Salamone JD, Correa M, Farrar A, Mingote SM. Effort-related functions of nucleus accumbens dopamine and associated forebrain circuits. Psychopharmacology. 2007;191:461–482. doi: 10.1007/s00213-006-0668-9. [DOI] [PubMed] [Google Scholar]
- Salthouse TA, Fristoe N, McGuthry KE, Hambrick DZ. Relation of task switching to speed, age, and fluid intelligence. Psychology and Aging. 1998;13:445–461. doi: 10.1037/0882-7974.13.3.445. [DOI] [PubMed] [Google Scholar]
- Servan-Schreiber D, Cohen JD, Steingard S. Schizophrenic deficits in the processing of context: A test of a theoretical model. Archives of General Psychiatry. 1996;53:1105. doi: 10.1001/archpsyc.1996.01830120037008. [DOI] [PubMed] [Google Scholar]
- Shah AK, Oppenheimer DM. Heuristics made easy: An effort-reduction framework. Psychological Bulletin. 2008;134:207–222. doi: 10.1037/0033-2909.134.2.207. [DOI] [PubMed] [Google Scholar]
- Shiffrin RM, Schneider W. Controlled and automatic human information processing: II. Perceptual learning, automatic attending, and a general theory. Psychological Review. 1977;84:127–190. [Google Scholar]
- Shugan SM. The cost of thinking. Journal of Consumer Research. 1980;7:99–111. [Google Scholar]
- Simon HA. A behavioral model of rational choice. The Quarterly Journal of Economics. 1955;69:99–118. [Google Scholar]
- Simon HA. A comparison of game theory and learning theory. Psychometrika. 1956;21:267–272. [Google Scholar]
- Smith V, Walker JM. Monetary Rewards and Decision Cost in Experimental Economics. Economic Inquiry. 1993;31:245–261. [Google Scholar]
- Solomon RL. The influence of work on behavior. Psychological Bulletin. 1948;45:1–40. doi: 10.1037/h0055527. [DOI] [PubMed] [Google Scholar]
- Stephens DW, Krebs JR. Foraging theory. Princeton University Press; Princeton, NJ: 1986. [Google Scholar]
- Taatgen NA. The minimal control principle. In: Gray W, editor. Integrated models of cognitive systems. Oxford University Press; Oxford: 2007. pp. 368–379. [Google Scholar]
- Taylor SE. The interface of cognitive and social psychology. In: Harvey JH, editor. Cognition, social behavior, and the environment. Erlbaum; Hillsdale, NJ: 1981. pp. 189–211. [Google Scholar]
- Thompson ME. Learning as a function of the absolute and relative amounts of work. Journal of Experimental Psychology. 1944;34:506–515. [Google Scholar]
- Todd M, Cohen JD, Botvinick MM, Dayan P. Task switching and cost minimization. Submitted. Manuscript submitted for publication.
- Tversky A, Edwards W. Information versus reward in binary choices. Journal of Experimental Psychology. 1966;71:680–683. doi: 10.1037/h0023123. [DOI] [PubMed] [Google Scholar]
- Tversky A, Kahneman D. Judgment under uncertainty: Heuristics and biases. Science. 1974;185:1124–1131. doi: 10.1126/science.185.4157.1124. [DOI] [PubMed] [Google Scholar]
- Tversky A, Shafir E. Choice under conflict: The dynamics of deferred decision. Psychological Science. 1992;3:358–361. [Google Scholar]
- Vohs KD, Baumeister RF, Schmeichel BJ, Twenge JM, Nelson NM, Tice DM. Making choices impairs subsequent self-control: A limited-resource account of decision making, self-regulation, and active initiative. Journal of Personality and Social Psychology. 2008;94:883–898. doi: 10.1037/0022-3514.94.5.883. [DOI] [PubMed] [Google Scholar]
- Vulkan N. An economist's perspective on probability matching. Journal of Economic Surveys. 2000;14:101–118. [Google Scholar]
- Walton ME, Kennerly SW, Bannerman DM, Phillips PEM, Rushworth MFS. Weighing up the benefits of work: Behavioral and neural analyses of effort-related decision making. Neural Networks. 2006;19:1302–1314. doi: 10.1016/j.neunet.2006.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilcox NT. Lottery choice: Incentives, complexity and decision time. Economic Journal. 1993;103:1397–1417. [Google Scholar]
- Wylie G, Allport A. Task switching and the measurement of “switch costs”. Psychological Research. 2000;63:212–233. doi: 10.1007/s004269900003. [DOI] [PubMed] [Google Scholar]
- Yeung N, Monsell S. Switching between tasks of unequal familiarity: The role of stimulus-attribute and response-set selection. Journal of Experimental Psychology: Human Perception and Performance. 2003;29:455–469. doi: 10.1037/0096-1523.29.2.455. [DOI] [PubMed] [Google Scholar]
- Zipf GK. Human behavior and the principle of least effort. Addison-Wesley; Cambridge, MA: 1949. [Google Scholar]