Abstract
While chemically synthesized superparamagnetic microparticles have enabled much new research based on MRI-tracking of magnetically labeled cells, signal-to-noise levels still limit the potential range of applications. Here it is shown how, through top-down microfabrication, contrast agent relaxivity can be increased several-fold, which should extend the sensitivity of such cell tracking studies. Microfabricated agents can benefit from both higher magnetic moments and higher uniformity than their chemically synthesized counterparts, implying increased label visibility and more quantitative image analyses. To assess the performance of microfabricated micrometer-sized contrast agent particles, analytic models and numerical simulations are developed and tested against new microfabricated agents described in this paper, as well as against results of previous imaging studies of traditional chemically synthesized microparticle agents. Experimental data showing signal effects of 500-nanometer thick, 2-micrometer diameter, gold-coated iron and gold-coated nickel disks verify the simulations. Additionally, it is suggested that measures of location better than the pixel resolution can be obtained and that these are aided using well-defined contrast agent particles achievable through microfabrication techniques.
Keywords: contrast agent, microfabrication, microparticle, nanoparticle, MPIO
The strong T2*-contrast surrounding magnetizable particles has made them promising candidates for MRI labeling, especially at the cellular level (1–4). Prominent among these particulate agents are chemically synthesized nanoscale and ultrasmall superparamagnetic particles of iron oxide (SPIOs, USPIOs) and their micrometer-sized equivalents (MPIOs). The larger amount of superparamagnetic material delivered with MPIOs has enabled MRI tracking down to the single cell level and it has been suggested that even single MPIO agents can be detected and used to label cells in vivo (5–11). Nevertheless, the limited magnetic moment that can be achieved with traditional MPIOs, and the limited total agent volume that can be introduced into a cell without compromising viability, has thus far prevented single particle detection and in vivo tracking of individually labeled cells from becoming routine. A further imaging challenge relating to chemically synthesized particles is the relatively large variability in size and amount of iron oxide from particle to particle. Being able to increase particle magnetic moments, or equivalently, being able to package similar moments into smaller particles, as well as being able to increase particle uniformity, would therefore help advance MRI cellular labeling and tracking.
Here the use of top-down microfabrication is considered for the production of high-moment, high-uniformity T2*-agents based on micrometer-sized particles. Recently, it has been shown that microfabrication techniques can be used to fashion MRI contrast agents with novel properties (12–14). This earlier work concentrated on precisely shaping the agents to produce desired properties. Here the advantages of using microfabrication to make simpler shaped, but higher moment, particles are considered. The expected effects of increasing the magnetic moments of micrometer scale particles through microfabrication techniques are demonstrated in simulations and experimentally. As specific examples, microfabricated gold-coated magnetic disk-shaped particles are described and their imaging performance compared to that of a traditional chemically synthesized MPIO equivalent. Besides their higher achievable moments, microfabricated particles are also more monodisperse, simplifying image analyses and suggesting possible sub-voxel-level particle tracking.
THEORY
To quantify the value of high-moment, micrometer-sized T2*-agents, signal intensities are first modeled theoretically. Transverse dephasing around objects or regions of varied magnetic susceptibility has been considered many times before and numerous studies of resulting free induction decays and frequency densities of states can be found covering various effective particle moments, concentrations, and diffusion regimes (15–22). However, previous work focused either on ensembles of particles or, in the case of individual particles or regions, on those of relatively low magnetic susceptibility difference with their surroundings. Here we concentrate instead on individual, high-moment micrometer-sized particles and high-resolution imaging. With individual particles, rather than ensembles, signal decay is well-known to no longer be exponential in time (16). However, for high-moment individual particles it will be seen that signal behavior deviates further from that traditionally stated in that: (i) the oft-quoted quadratic short-time dependence (16) vanishes, (ii) depending on image resolution, k-space shifting introduces signal losses that do not vanish as echo time (TE) tends to zero, and (iii) sub-voxel-level location becomes significant, leading to analytic calculations often substantially over-estimating particle visibility. To clarify these effects, limiting analytical approximations are first derived, and then numerical simulations used to extend analysis to more experimentally realistic situations.
Transverse dephasing
For the particle types considered in this paper, calculations are simplified by working in the static dephasing regime. In the vicinity of high-moment, micrometer-sized particles the static dephasing assumption, Δω·τc >> 1, is easily satisfied. Here, as usual, the diffusion correlation time τc represents the time for water to diffuse a distance of order the particle size, while Δω characterizes the local precession frequency due to the particle’s field (taken, for concreteness, in the particle equatorial plane). Temporarily ignoring k-space shifting effects, the time-dependent modification to the signal S caused by the magnetic particle is therefore simply proportional to an integral over the precessing proton spins within the volume of interest:
| [1] |
Here t measures time following an initial π/2 excitation, r⃗ is the spin location relative to the magnetic particle, ρ is the spin density, and φ, working in the rotating frame, is the additional accrued transverse phase due to the particle field. Since the microparticle size is always far less than the voxel size, signal is dominated by spins from the particle’s far-field region. Regardless of particle shape, therefore, the field may be modeled as that of a dipole, and the particle assumed, for concreteness, to be a sphere of radius determined by its net dipole moment pm and the magnetic saturation of its constituent material. For a B0-field aligned in the z-direction, the z-component of the field produced by such a particle when magnetized by B0 is: Bz = pm·(μ0/4π)(3cos2θ−1)/|r⃗|3 for magnetic permeability of vacuum μ0 = 4π·10−7 H/m and polar angle θ. For a ferro- or superparamagnetic particle of radius a and saturation magnetic polarization Js, the dipole moment is pm = (Js/μ0)·4πa3/3, yielding an equatorial precession frequency of Δω = γJs/3 for gyromagnetic ratio γ. Here, neither B0 nor the magnetic susceptibility difference Δχ, in terms of which dipole moments are usually expressed, appears, since ferro- or superparamagnetic substances are magnetized to saturation by typical B0 fields. The normalized signal decay from such a particle centered in a (spherical) voxel of radius R and of homogeneous spin density therefore becomes:
| [2] |
Similar integral forms have been described previously (16); focus shifts, however, when considering single-voxel-level imaging of high-moment particles. For a start, if the argument of the exponential were always small, that is, Δω· t << 1, then Taylor expansion would lead to the well-known quadratic time dependence for the initial signal decay. Although this characterizes dephasing across regions with low susceptibility differences, it is physically irrelevant for strongly magnetized particles: since Js is of order one tesla for ferromagnetic materials, for such an expansion to be valid everywhere about the particle it could describe just the first few nanoseconds of signal evolution.
While high moments preclude immediate expansion of the above integrand, simplification is still possible if the ratio of voxel to particle radius is such that Δω·t·(a/R)3 is of order unity or less. For millisecond timescales and micrometer-sized ferromagnetic particles, this becomes true at resolutions of the order of a hundred micrometers or larger. Integrating first, and then simplifying resultant functions of Δω·t and of Δω·t·(a/R)3 through asymptotic and power series expansions, respectively, approximates the signal magnitude to second order in Δω·t·(a/R)3 as:
| [3] |
The leading order time coefficient c1 is equivalent to one originally derived by Yablonskiy and Haacke (16); the c2 coefficient, however, is not present in that work since, focusing on NMR, their spatial integration was unbounded. Here the quadratic term indicates the onset of saturation due to finite voxel size. Despite the limited expansion, Eq. [3] accurately approximates Eq. [2] for initial signal decay and saturation (see Fig. 1a). Comparing linear and quadratic terms in Eq. [3] estimates the dephasing period required to appreciably saturate out the voxel signal, which we label tsat. The asymptotic nature makes definition somewhat arbitrary, but as a first measure we consider the point where S(t) becomes stationary, at least as approximated by Eq. [3], giving:
| [4] |
Defining the fractional hypointensity, i ≡ 1−|S(t)/S(0)|, at t = tsat, the saturation hypointensity isat therefore amounts to c12/4c2 ≈ 90 %, coincidentally matching conventional rise- or decay-time definitions for exponential-like processes. Alternatively, inverting Eq. [3] yields the period needed to reach any particular fractional hypointensity level, i < isat, as tsat·[1−(1−i/isat)1/2], which simplifies to (tsat/2)·i/isat in the linear regime where i << isat.
Figure 1.
Theoretical single-voxel signal intensity due to transverse dephasing. (a),(b) show calculations for spherical and cubic voxels, respectively. Solid lines are numerical integrations of text Eq. [2]; dashed lines are based on analytical text Eq. [3] (and are therefore not plotted beyond t = tsat). Curve labels indicate image voxel diameter (a) or width (b) in micrometers. All curves are for a single 1-µm diameter, Js = 1 T, particle centered within the imaging voxel.
The above assumes spherical voxels but can be adapted to approximate more realistic cubic voxels. Estimates are imperfect since different voxel shapes capture different precession frequency distributions, but a simple adaptation yielding fair approximation, as seen in Fig. 1b, is to replace R with an effective cubic “radius” Rc that incorporates at least the different voxel volumes. For a cubic voxel of half-width R, (4/3)π Rc3=8R3, implying signal decays about twice as slow for cubic voxels as they would be for spherical voxels of similar diameter. As a quantitative example then, according to Eq. [4] a hypothetical 1-µm diameter, spherical ferromagnetic particle with Js = 1 T would substantially saturate out a surrounding 100-µm diameter spherical volume in about 15 ms, and a surrounding cubic 100-µm voxel in a little over twice that. Note, however, that Eqs. [2–4] represent a “best-case” scenario that assumes particles centered within the surrounding voxel. As such, they determine only upper- and lower-limits for signal decay and tsat, respectively. Depending on actual particle location with respect to the imaging voxel grid, however, voxel dephasing rates may often be substantially slower (explained below).
With the above caveat in mind, tsat gives a quick order-of-magnitude starting point for estimating whether an intended label is likely to be large enough to give decent detectability. For example, consider 100-µm resolution imaging limited by endogenous T2 dephasing to a 10 ms echo time. Assuming cubic voxels, a 1-µm pure magnetite particle (Js ≈ 0.5 T) would have a (best-case) tsat of over 60 ms rendering it barely visible, if at all. Switching to a higher-moment material such as iron (Js ≈ 2 T) would cut tsat four-fold; staying with magnetite, on the other hand, would require a substantially larger particle. Being able to fabricate particles from pure, solid, high-moment materials is clearly advantageous, however, with chemically synthesized MPIOs generally only a fraction (often 10 % – 50 %) of the particle is comprised of relatively low-moment magnetite. Thus, microfabrication can increase sensitivity by increasing both the magnetic volume fraction of the particle as well as the moment of the material used.
Image distortion
A limitation of Eqs [2–4] is that they address signal loss due to transverse dephasing only. While such dephasing often dominates, for high-resolution imaging and short echo times, geometrical image distortion can also appreciably modify signal intensity. Effective k-space shifting due to superposition of the particle field onto the read gradient (and in the case of 2D imaging also onto the slice select gradient) translates into image distortions that yield local hypo- and hyperintense signal regions near the particle. As with transverse dephasing, numerous studies exist on such image distortion (23–27), but that work is not focused at the individual voxel level where the concern is no longer the exact distortion geometry, but simply its overall size. In particular, if the resulting hypo- and hyperintense regions fall within the same imaging voxel, then conservation of spin number ensures that spatial variations in apparent spin density cancel and image distortion is negligible. For high resolution imaging and high-moment particles, however, the apparent spatial translation of spins may yield hypo- and hyperintense signal regions separated over a distance greater than the voxel size, thereby appreciably changing voxel signal intensities.
In approximating distortion length scales, we ignore higher-order slice selection effects and assume 3D imaging with a read gradient of strength G in the x-direction. Ignoring the B0 offset, the field during read-out is therefore Gx + Bz. Accordingly, spins located at position x, map to an apparent position x + Bz/G, and hyper- and hypointense signal maxima result when |∂Bz/∂x| takes on a minimum or maximum value, respectively. Simplifying to y = z = 0, setting ∂Bz/∂x = 0 gives x = −(Jsa3/G)1/4 and an associated hypointense signal maximum mapped a distance d away from the particle given by:
| [5] |
With compensating hyperintense signal maxima similarly displaced, the ratio of d to the voxel size therefore predicts whether image distortion significantly modifies initial signal magnitude. Although distortion differs depending on whether B0 is parallel or perpendicular to the image plane, the distance d (determined as it was for the case y = z = 0) is unchanged, and overall distortion sizes do not depend strongly on B0 direction. Because d scales as the fourth root of dipole moment, even with high-moment particles image distortion is significant only for high-resolution imaging. However, for detecting single particles, such high-resolution imaging is common. For example, substituting again for a hypothetical 1-µm diameter, Js = 1 T, ferromagnetic particle and typical high-resolution imaging gradients of a few tens of mT / m, Eq. [5] shows that image distortion starts contributing non-negligibly around voxel sizes of order one hundred micrometers.
For high particle moments and high-resolution imaging, therefore, distortion will often dominate in the first few milliseconds following the initial excitation before the signal transitions over to the dephasing-dominated regime described by Eq. [3], which remains valid until the voxel signal starts to appreciably saturate around the time tsat defined by Eq. [4]. To capture, simultaneously, dephasing, distortion, and saturation effects, we numerically simulate gradient-echo imaging of individual magnetic particles of various moments and at various image resolutions and echo times. The model tracks the phases of a volume of spins precessing in the field surrounding a magnetic dipole, with intravoxel dephasing captured through a grid spacing many times smaller than any voxel size. Apparent image location of each spin is determined by the field at that spin’s real location, given by the sum of the perturbing dipole field and a simulated readout gradient. Figure 2 compares simulated results, which include image distortion and dephasing, to those derived from numerical solution of Eq. [2], which include dephasing only. As expected, deviations from Eq. [2] are largest for high resolution imaging, showing increased hypointensity, but slower signal decay, at short timescales.
Figure 2.
Comparison of theoretical single-voxel signals with and without image distortion correction. Solid curves are numerical simulations including distortion and transverse dephasing; dashed curves include only dephasing and are numerical integrations of Eq. [2]. Curve labels show image resolution in micrometers. All curves are for a single 1-µm diameter particle with Js = 1 T centered in the imaging voxel.
Image simulation
To compare directly with imaging experiments described below, we model specific chemically synthesized MPIOs as well as the sample microfabricated disks described above. As a reference MPIO we take a commonly used commercial 1.63-µm mean diameter bead (Bangs Laboratories Inc., Fishers, IN (28)), which is composed of 42.5 % magnetite by weight and has a total magnetite content of 1.5 pg (6). These chemically synthesized beads are contrasted against the microfabricated disk particles that comprise 2-µm diameter, 300-nm thick disks of magnetic material surrounded by 50 to 100-nm thick gold shells. With these dimensions all particles have roughly comparable total volumes; however, since microfabrication allows for pure, solid cores of magnetic material, and since iron oxide, pure nickel, and pure iron have different Js values of approximately 0.5 T, 0.6 T, and 2.2 T (29), respectively, the respective magnetic dipole moments of these particles are approximately 0.1·10−12 A·m2, 0.45·10−12 A·m2, and 1.65·10−12 A·m2 (that is, scaling roughly as 1:4:42). Connection between the simulation and imaging experiments is also facilitated by the intermediate moment (that of the nickel disk) corresponding closely to that of the hypothetical Js = 1 T, 1-µm sphere used in the above theory and in the example graphs of Figs. 1 and 2.
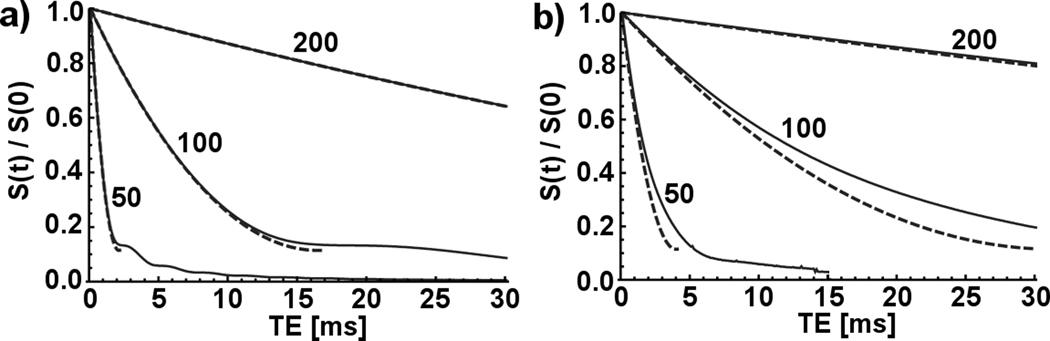
Figure 3 shows imaging simulations for the MPIO, nickel, and iron particles (based on the same simulation code described above for calculations in Fig. 2) that capture image darkening over several voxels rather than in only the central voxel as quantified by Eqs. [2–4] and Figs. 1 and 2. The images show theoretical (noise-free) pixelized gradient-echo signals for various echo times from individual particles at 50 and at 100 micrometer (cubic) isotropic resolution and for B0 oriented in-plane and perpendicular to the imaging plane. As expected, image distortion modifies high-moment particle signals initially, before dephasing begins to dominate.
Figure 3.
Simulated gradient-echo MRI. Graphs show theoretical (noise-free) images expected for single MPIO, single microfabricated nickel, and single microfabricated iron particles, for various TE and image resolutions, for B0 oriented parallel (in-plane) and perpendicular (out-of-plane) to the image slices, and for a read-gradient running from left to right in all images.
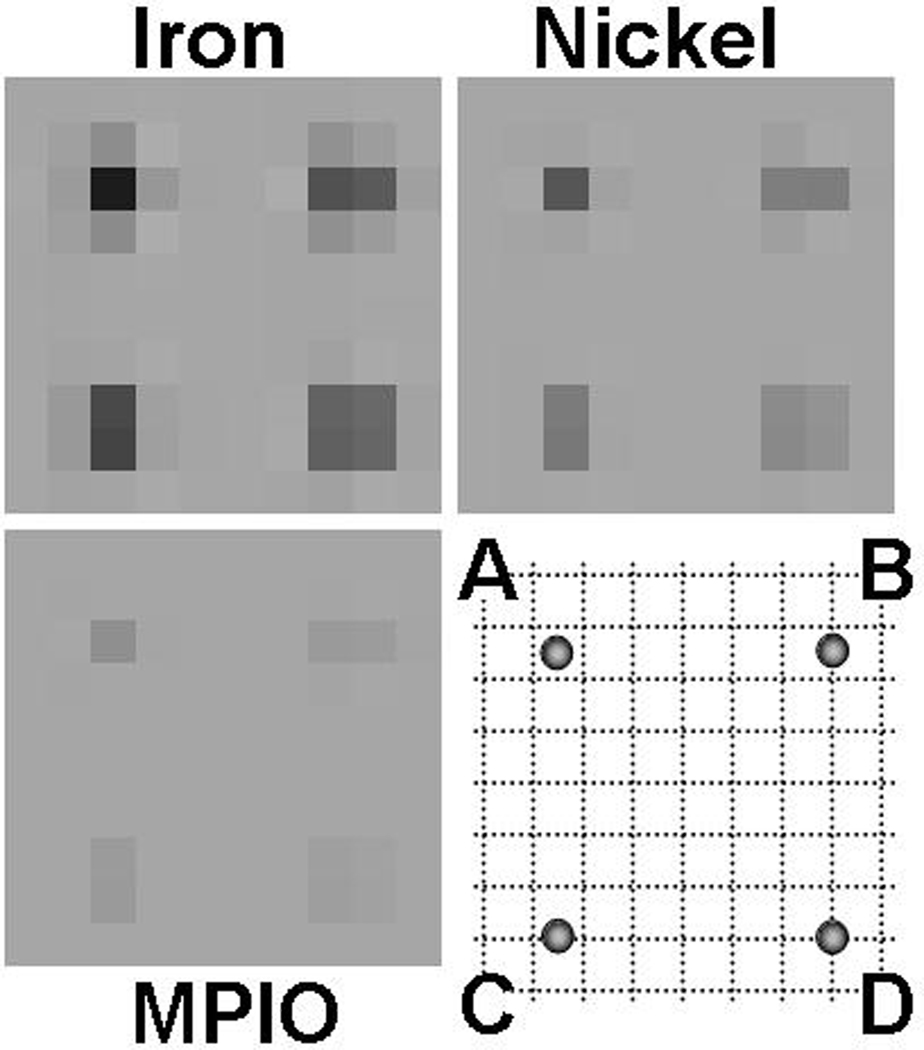
The above simulations assume particles centered within a voxel; signals differ for particles offset from the voxel center. Fractional voxel offsets have little impact at those resolutions where image darkening extends over many voxels, but for lower resolution imaging (larger voxel sizes), signal hypointensities drop substantially due to increased signal dilution arising from partial volume effects. Even for particles aligned in the middle of an imaging slice, therefore, identical particles can appear different depending on their lateral registration with regard to the imaging voxel. Figure 4 models such position-dependent dilution for the same particles modeled in Fig. 3, at 100-µm resolution and for a typical 10 ms echo time. Signal hypointensity decreases as dephasing effects are averaged over an increasing number of voxels, disadvantaging lower moment particles, which can be rendered invisible against background noise if unfortunately located. Although non-centered particles complicate analytic calculation, overall signal hypointensity ranges can still be approximated, at least in those cases where image distortion is negligible and where there is not yet much saturation of the surrounding voxel. For example, in moving from a central point, labeled “A”, to a corner point, labeled “D”, (see Fig. 4), signal hypointensity drops nearly four-fold, as can be understood by noting that the offset particle at “D” could be regarded as centered in a surrounding voxel whose linear dimensions were double that of the original voxel. Similarly, in three dimensions an offset from voxel center to corner reduces signal as much as eight-fold.
Figure 4.
Off-center contrast dilution. Graphs show theoretical (noise-free) images expected for single MPIO, single microfabricated nickel, and single microfabricated iron particles, at 100-µm isotropic resolution and 10 ms TE. For each particle type, expected signal intensity is shown for particles situated at various 2D offsets from the voxel center, shown in the bottom right corner schematic. (A) represents a centered particle; (B) represents a particle offset to the side, midway between two voxels; (C) is as for (B) but offset vertically; D represents a particle offset to the voxel corner.
Sub-voxel localization
The several-fold variation in signal intensity over a displacement range of just one half of a voxel, has several consequences. On the one hand, it complicates quantification of signal hypointensities, demanding a more statistical description, and it can pull weaker MPIO signals below the noise level. On the other hand, it suggests the possibility of a form of sub-voxel level tracking where the large changes in neighboring voxel intensities may allow for more accurate determination of particle position than that normally afforded by the voxel size.
Such sub-voxel tracking or locating of magnetic particles is not the main focus of this paper but we outline the possibility here because it reflects on two differences between microfabricated and chemically synthesized particles, namely, magnetic moment and variability in that moment. An obvious requirement for sub-voxel tracking is that position-dependent variations in voxel hypointensities exceed random signal variations from one voxel to the next due to background noise. Since signal intensities scale with particle moment, so too do the position-dependent variations in those signals (provided that one is not too far into the saturation limit). The higher the particle moment, therefore, the easier it is for position-dependent variation to dominate over experimental noise. Another advantage to microfabricated particles stems from the low variability in magnetic moment from one particle to the next, allowing absolute intensities to be used in addition to ratios of neighboring voxel intensities when back-calculating particle location. Taken together, high moment, high monodispersity, microfabricated particles appear well suited for potential sub-voxel tracking.
Although not shown here, note that contrast variation due to a shift in particle location must be equivalent to that due to an opposite shift in the spatial image field of view (FOV). Since shifting the FOV is, by the Fourier Shift Theorem, equivalent to multiplying the underlying k-space data by a linear phase in the shift direction, sub-voxel level particle position could also be determined by observing voxel hypointensities as a function of the magnitude of an applied linear phase modulation. Either way, well-defined, high moments are advantageous.
METHODS
Microfabrication
Apart from recently described examples of microengineered multi-spectral agents (12–14) and in-situ B1-field modifiers (30), MRI contrast agents are typically chemically synthesized. Chemical synthesis has much to recommend it, being often simpler and more efficient than top-down microfabrication. Nevertheless, the enhanced geometrical and compositional control possible through common microfabrication techniques (31) can increase agent functionality, compensating for increased processing complexity. The previously described multi-spectral agents are one example of this trade-off between complexity and functionality. Here, as a second example, the goal was to demonstrate microfabrication’s ability to produce agents that generate greater, and more consistent, T2*-contrast than chemically synthesized counterparts.
While chemically synthesized MPIOs are often spherical, the microfabricated agents described here are disk-shaped objects, better suited to microfabrication technology. However, since particle sizes fall well below resolution limits, in terms of average T2*-contrast across a voxel, particle shapes play little role and only overall magnetic moments matter.
Disk-shaped particles can be easily fabricated using standard micropatterning techniques. For example, to create the particles described in this paper, a 10-nm thick titanium adhesion layer was first evaporated onto a supporting substrate followed by a 100-nm thick sacrificial copper layer and a 100-nm thick gold layer. A double-layer of resist was then spin-coated over this titanium-copper-gold trilayer with the top layer being photosensitive while the bottom layer was an isotropically developing, lift-off resist (LOR). Following exposure through a mask containing an array of 2 µm-diameter circular holes, patterned development and dissolution of the top resist layer then led to isotropic development and dissolution of those physically exposed portions of the underlying LOR. Appropriately timed, undercut profiles, such as those sketched in Fig. 5a, result. An approximately 300-nm thick layer of iron or of nickel, followed by a 200-nm thick layer of gold, were then evaporated (Fig. 5b). Because of local shadowing by the undercut resist profile, metal deposited on top of the photoresist is physically disconnected from metal deposited on the substrate. Subsequent removal of the resist bi-layer therefore removes the top metal layers while leaving the metal on the substrate untouched. A 100-nm deep argon ion-milling can then remove the exposed gold on the substrate and half of the top 200-nm gold layer. During this process some of the back-sputtered gold ion-milled from the substrate redeposits on the iron / nickel sidewalls (Fig. 5c) leaving magnetic disks completely encased in gold, with 100-nm thick top and bottom gold coatings, and approximately 50-nm thick gold coatings around their circumferential sidewalls (Fig. 5d). Finally, a selective wet-etch of the underlying copper releases the particles from the substrate and, using simple bulk magnetic separation, they can then be repeatedly washed to remove any remaining etchant solution. Note that the above sequence of steps and chosen particle dimensions demonstrate only one possible fabrication protocol; many other particle sizes and microprocessing strategies would be equally plausible.
Figure 5.
Process flow schematic for microfabricated contrast agents: (a) patterned bi-layer lift-off resist (undercut profile) atop a titanium-copper-gold base layer; (b) magnetic material and gold top evaporation; (c) ion-milling through base gold layer and half-way through top gold layer; (d) resputtered gold from ion-milling process yields magnetic particles completely encased in gold.
Figure 5 shows only two representative particles but the parallel nature of photolithographic patterning allows arrays of many millions of particles to be simultaneously fabricated. While the magnetic moments of these nominally identical particles are far more monodisperse than those of MPIOs, it should be noted that, even with top-down microfabrication, inter-particle variation is never completely non-existent. Small position-dependent process variations will typically introduce variations in particle moments on the order of several percent across the full area of typical 3- to 6-inch processing wafers. However, because millions of microparticles can easily fit within just a few millimeter square area of the processing wafer, realized experimental inter-particle variations may be as low as fractions of a percent, rendering them effectively negligible.
RESULTS
Figure 6a shows sample scanning electron micrographs (SEMs) of arrays of 500-nm thick, 2-µm diameter, gold-coated disks, microfabricated according to the above-described process protocol. Figure 6b shows the same microfabricated disks once they have been removed from their original processing substrate, washed multiple times in de-ionized water, re-pipetted out onto a new surface, and left to dry.
Figure 6.
Angled scanning electron micrographs (SEM) of microfabricated particles. (a) Arrays of gold-coated magnetic disk particles (low and high magnification) on their original processing substrate. (b) Particles removed from processing substrate, washed, and re-pipetted out onto fresh substrate.
Figure 7 shows slices from 12 ms TE, 3D gradient-echo images at 50- and at 100-µm isotropic resolution, comparing agarose suspensions of above-mentioned 1.63-µm MPIOs to equivalent suspensions of the above-described microfabricated nickel and iron disks. Images were acquired using an 11.7 T scanner, with read gradients of 5.4 G / cm, and at bandwidths of 44 and 22 kHz, for 50- and 100-µm resolutions, respectively. Localized hypointense regions in the images are primarily due to single particles. This assumption is based on the low particle concentrations used and further supported by good agreement, for the microfabricated particles, between theory and experiment discussed below.
Figure 7.
Gradient-echo MRI comparison of chemically synthesized and microfabricated contrast agents. Top row shows 50-µm isotropic resolution images; bottom row shows 100-µm isotropic resolution images. (a) and (d) show MPIOs; (b) and (e) show microfabricated nickel particles; (c) and (f) show microfabricated iron particles. All images taken at a TE of 12 ms.
As expected, higher-moment particles cause more pronounced signal loss due to dephasing during the TE. To quantify these visibility differences and compare with above theory, all 100-micrometer resolution image slices (slices shown in Fig. 7 represent just a few of many image slices taken through each agar sample) were run through an image analysis code that automatically selected out the localized dark regions in each image. The data are collected in histograms shown in Fig. 8, which show normalized signal intensities S(TE)/S(0) approximated from the images by taking the ratio of signal intensity of the darkest voxel in each darkened region to that averaged from a particle-free region of the sample. The experimental intensity distributions integrate over variation in particle moment, variation in particle registration with respect to lateral voxel position and slice height, and variation due to background noise. Also shown in Fig. 8 are simulated histograms of theoretical (noise-free) distributions for ensembles of identical, but randomly distributed, particles, calculated using the same modeling code used to generate the image simulations of Figs. 3 and 4. Both the simulated and the experimental histograms show hypointensity distributions that are non-Gaussian and too broad to be explained by background noise alone; instead they point to signals dominated by sub-voxel-level variation in particle location. By contrast, a reference intensity histogram integrated over the background, particle-free, regions of the samples is clearly Gaussian.
Figure 8.
Single-voxel signal intensities quantifying contrast generated by magnetic particles. All signals S are for 12 ms echo time, 100-µm isotropic resolution, and are normalized to the background signal S0. Simulations for microfabricated iron, microfabricated nickel, and chemically synthesized MPIO agents are shown in the histograms on the left; experimental data are on the right. The reference background experimental signal distribution, which closely matches an expected Gaussian curve, is centered below. The non-Gaussian nature of the iron and the nickel signal distributions shows the impact of sub-voxel level particle location, while the shift between theoretical and experimental MPIO signal distributions reveals observer bias effects resulting from relatively low-moment, high-variability, particles (see text).
DISCUSSION
Despite suggestive agreement between predicted and observed hypointensities, the distributions of Fig. 8 do differ somewhat. First, background noise in the experimental histograms, which only slightly distorts high-moment particle distributions, has a disproportionately large effect on recorded low-moment particle signals. In particular, background noise introduces an effective cut-off hypointensity below which particles cannot be unambiguously distinguished from background. Exact visibility cut-offs depend on the exact image analysis, but assuming simply that a particle is unambiguously present in a given voxel only if the hypointensity of that voxel exceeds that of its nearest neighbors, implies a cut-off level on the order of twice the standard deviation in the background noise signal. For example, in our case the standard deviation was around 7 to 8 % and experimental histogram counts dropped rapidly around 15 % hypointensity, rendering lower-moment particles undetectable. A second, smaller, difference between theory and experiment arises from the possibility that some particles may have clumped together, or be spaced so closely that their hypointense regions overlap, adding the small one-sided tails evident in the experimental nickel and MPIO histograms (for iron, the effect is less apparent because voxel saturation compresses this tail).
While noise and clumping probably account for residual differences between experiment and theory for the microfabricated particles, discrepancies remain in the MPIO data. For example, for the iron particles the predicted and experimental mean signal intensity reductions show reasonable agreement, with values of 65 % and 73 %, respectively. Likewise, for the nickel particles agreement remains good with corresponding values of 31 % and 32 %, respectively. However, for the MPIOs used, theory predicts 10 % mean intensity reduction while experiment gives 25 %, more than twice as large.
The disagreement exposes an observer bias effect resulting from a combination of the particular MPIOs’ relatively low moments and the large variation in those moments due to manufacturing. To be sure, the large moment distribution leads to a hypointensity distribution that differs from that of the more tightly defined microfabricated particles because it now reflects variation in both moment and position. But, to first order, one might expect moment variations to average out, leaving at least the mean hypointensity unaffected. This is not the case, however, because the particular MPIOs’ relatively low average moments lead to a sizable fraction of those MPIOs falling below the noise cut-off and thus going uncounted. The problem is exacerbated by the large variation in moments, leading to those MPIOs that do remain detectable being unrepresentative of the average population, skewed towards larger, higher moment, particles or possibly multi-particle clumps. From a cell counting or tracking viewpoint, therefore, low-moment MPIOs can mislead. For example, certain labeled cells may be undetectable, or some may intermittently move in and out of detectability depending on sub-voxel location. Those labeled cells that do remain consistently visible likely carry larger particles, multiple particles, or multi-particle clumps. Either way, higher-moment, lower-variability microfabricated agents should mitigate these problems, helping to simplify and better quantify image analyses.
As a generalization from the samples of Fig. 8, hypointensity distribution variation as a function of particle moment, image resolution, and echo times can be considered. This issue is not unlike that already considered analytically by Eqs. [2–4], except that now, including random particle location, the distributions provide a statistically more complete answer. Figure 9 summarizes such distributions by delineating expected hypointensity ranges together with median hypointensity levels for ensembles of randomly positioned, but identical, particles. Since the above analytics approximates only the upper limit of the range, Fig. 9 illustrates that detectability can be overestimated if particle registration with respect to the voxel grid is ignored.
Figure 9.
Log-linear plots showing range of signal loss, expressed as fractional hypointensity level, 1 – S / S0, as a function of dipole moment, pm. Left and right columns show ranges for 50- and 100-µm isotropic (cubic) resolutions, respectively, at 5-, 10-, and 20-ms echo times. Dashed curves outline the maximum and minimum fractional hypointensities; the solid curve shows the median fractional hypointensity. Solid circles on the 10-ms, 50- and 100-µm plots compare empirical values for various MPIOs from refs. (7) and (8), respectively.
Given knowledge of experimental background noise levels, Fig. 9 also answers the inverse question of what minimum particle moments are required to ensure detectability. For example, particles are always detectable if, for the selected particle moment, the minimum hypointensity lies above the background noise level. Similarly, half of the particles would be visible if their moments yielded a median hypointensity matching the noise level (although, which individual particles are visible at any time would change as locations shift within a voxel). Note that the graphed hypointensity ranges are due solely to particle location effects; they do not include additional variation incurred by possibly broad particle moment distributions, as may be the case with some chemically synthesized MPIOs, particular the lower-moment ones. In such cases, ensuring reliable detectability would require higher average moments than those needed for more monodisperse particles.
The sample distributions in Fig. 8, each of which may be recognized as single, albeit more detailed, vertical slices through the distributions of Fig. 9, already compare theory with data for the microfabricated and MPIO agents of this paper. As additional comparisons, superposed onto Fig. 9 are empirical data from a variety of different commercial MPIOs, taken from references (7,8). Agreement is good for particle moments large enough to afford hypointensities well above background noise levels. (Empirical values cluster near the upper-edge of the predicted range – coincidentally, therefore, closely matching theory Eq. [3] – because those particular analyses were based on the darkest spots visible in each image). For smaller, higher variability particles, however, apparent hypointensities fall above the predicted range, with fractional discrepancies increasing with larger voxel sizes or, equivalently, reduced hypointensities. Such apparently high experimental visibilities do not indicate any special property of smaller MPIOs; instead, just like the MPIO data described above and detailed in Fig. 8, they expose background noise rendering some particles invisible and biasing observation toward larger particles and/or clumps.
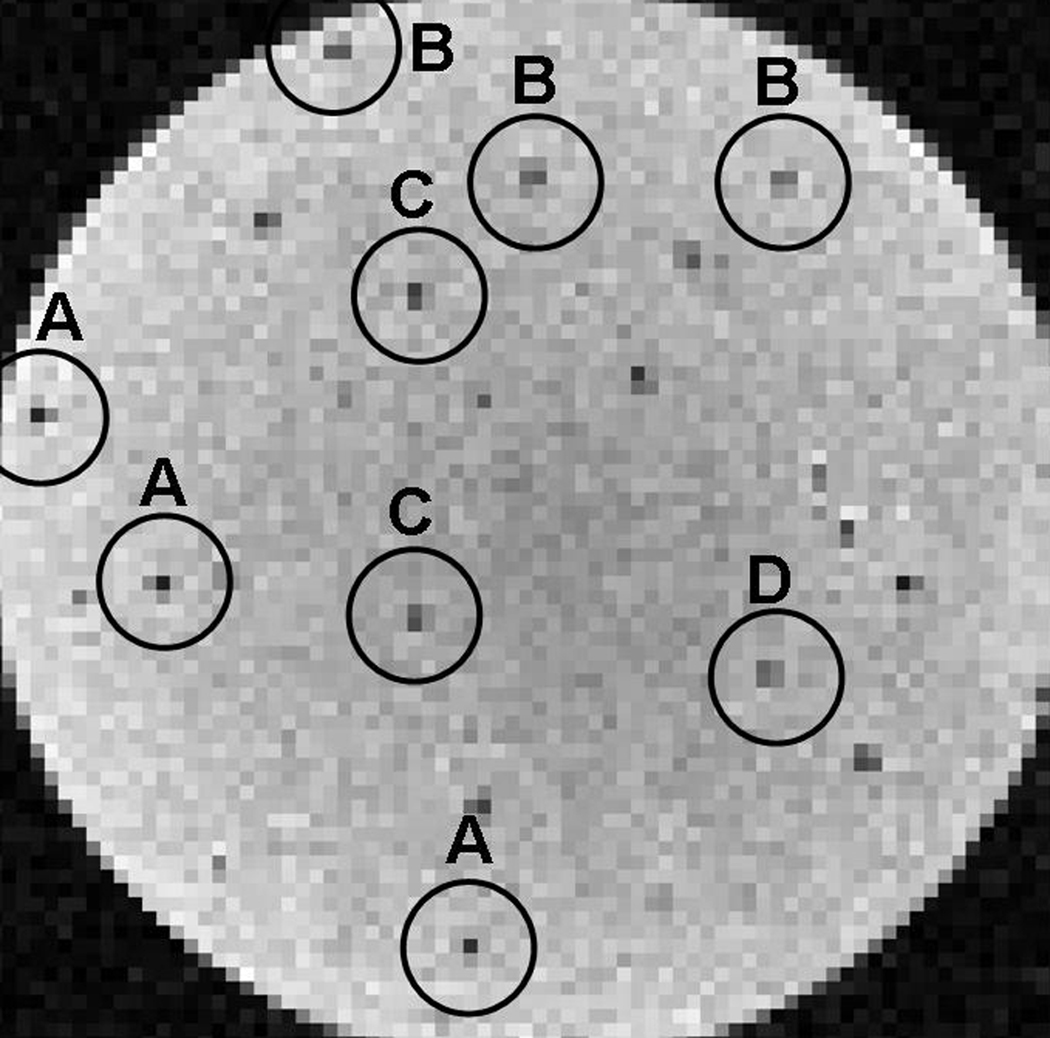
Returning to the more monodisperse microfabricated agents, the similarity between theoretical and experimental hypointensity distributions (Fig. 8) lends support to the above-mentioned potential for sub-voxel level tracking. Even at current background noise levels, Fig. 10 suggests that it may already be possible to discern such sub-voxel-level placement. The figure shows an image slice, equivalent to those in Fig. 7, through an agarose suspension of identical gold-coated iron particles, showing spatial intensity distributions that resemble those predicted in Fig. 4. Of course, not all hypointense features match those from Fig. 4, while those that do, do so only imperfectly because there is background noise present and because no particles are necessarily situated precisely at the voxel center, edge, or corner as assumed in Fig. 4. Nevertheless, the agreement that does exist, together with the matched, non-Gaussian, hypointensity distribution widths and profiles in Fig. 8, suggests that the spatial intensity patterns reveal more than just noise.
Figure 10.
Sub-voxel level registration. 100-µm isotropic resolution, 12 ms TE gradient-echo MRI of microfabricated iron disks suspended in agar. Variation in signal intensity is partially due to background noise, but primarily due to variation in sub-voxel particle position (see text). Circled regions show typical expected intensity distributions for various particle offsets from the voxel centers with letter labels indicating those offsets per the schematic in Fig. 4, where (A) represents a particle near the center of the voxel, (B) represents a particle shifted near the right or left edge of the voxel, (C) represents a particle shifted near the top or bottom edge of the voxel, and (D) represents a particle offset to a corner of the voxel.
CONCLUSION
This paper has considered some advantages of creating MRI contrast agents from simple microfabricated micrometer-scale magnetizable particles. Compared to chemically synthesized MPIOs, microfabricated agents can offer higher moments and, accordingly, increased detectabilities. Additionally, the greater particle uniformity resulting from the top-down approach leads to the potential for simplified image analyses, and the possibility of future sub-voxel level particle tracking.
The demonstrated microfabricated particles already have magnetic moments several times that of comparably sized, chemically synthesized iron-oxide particles. However, the disks microfabricated for the present work had almost half their volume consumed by their thick gold shells. Thus, a further doubling in moment, without appreciable size increase, should still be possible.
Unlike chemical synthesis, the more physical nature of the top-down, stepwise, metal deposition and removal processes means that the microfabrication approach readily extends to multilayered structures and allows for the substitution of a variety of alternative fabrication materials. Thus gold, a useful coating for bioconjugation protocols, may be replaced with, for example, titanium to increase biological inertness. Likewise, multiple different magnetic materials, as well as multilayered magnetic systems, can be substituted to control precisely the particles’ magnetic properties and behaviors, and various coating materials can be added to act as oxidation or diffusion barriers or even as magnetic buffer layers to reduce any possible magnetic particle clumping if needed. Material layer thicknesses can also all be easily selected by changing deposition rates and times. For this initial demonstration, however, materials and dimensions were chosen simply to provide particles of volume comparable to commonly used MPIOs, but with different, and higher, magnetic moments.
Approximate analytic expressions and numerical simulations were also developed, providing a means for estimating expected particle detectabilities for both MPIOs and microfabricated agents. While exact signal changes may differ slightly due to experimental differences in the exact imaging pulse sequences used and possible filtering schemes and analysis algorithms, the models outlined provide at least first-order guidance for selecting appropriate particle types for given imaging conditions. In particular, estimates of detectability for a given moment were generated, and the importance of exact particle position with respect to the voxel grid was discussed. It is clear that the higher moments available through microfabricated particles lead to greater detectability, especially useful for the short TEs required for high field imaging. The large signal changes detected for the iron based particles even at 100-micrometer resolution suggest the possibility that such microfabricated single particles may already border detection at resolutions that are being achieved in the human. For example, at resolutions of order 200 micrometers, which have now begun to be routinely approached in high-field (7T) clinical imaging, a microfabricated 1-µm thick, 2-µm diameter disk of iron would have a tsat of around 40 ms.
Finally, the greater uniformity of microfabricated particles should enable development of techniques that enable more quantitative analysis of cell tracking data including the possibility of determining relative positions at resolutions higher than the voxel dimensions for cases where particles are locally sparsely distributed.
ACKNOWLEDGMENT
This work was supported in part by the NINDS NIH Intramural Research Program.
REFERENCES
- 1.Dodd SJ, Williams M, Suhan JP, Williams DS, Koretsky AP, Ho C. Detection of single mammalian cells by high-resolution magnetic resonance imaging. Biophys. J. 1999;76:103–109. doi: 10.1016/S0006-3495(99)77182-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bulte JWM, Kraitchman DL. Iron oxide MR contrast agents for molecular and cellular imaging. NMR Biomed. 2004;17:484–499. doi: 10.1002/nbm.924. [DOI] [PubMed] [Google Scholar]
- 3.Foster-Gareau P, Heyn C, Alejski A, Rutt BK. Imaging single mammalian cells with a 1.5 T clinical MRI scanner. Magn. Reson. Med. 2003;49:968–971. doi: 10.1002/mrm.10417. [DOI] [PubMed] [Google Scholar]
- 4.Heyn C, Ronald JA, Mackenzie LT, MacDonald IC, Chambers AF, Rutt BK, Foster PJ. In vivo magnetic resonance imaging of single cells in mouse brain with optical validation. Magn. Reson. Med. 2006;55:23–29. doi: 10.1002/mrm.20747. [DOI] [PubMed] [Google Scholar]
- 5.Hinds KA, Hill JM, Shapiro EM, Laukkanen MO, Silva AC, Combs CA, Varney TR, Balaban RS, Koretsky AP, Dunbar CE. Highly efficient endosomal labeling of progenitor and stem cells with large magnetic particles allows magnetic resonance imaging of single cells. Blood. 2003;102:867–872. doi: 10.1182/blood-2002-12-3669. [DOI] [PubMed] [Google Scholar]
- 6.Wu YL, Ye Q, Foley LM, Hitchens TK, Sato K, Williams JB, Ho C. In situ labeling of immune cells with iron oxide particles: An approach to detect organ rejection by cellular MRI. Proc. Natl. Acad. Sci. 2006;103:1852–1857. doi: 10.1073/pnas.0507198103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Shapiro EM, Skrtic S, Sharer K, Hill JM, Dunbar CE, Koretsky AP. MRI detection of single particles for cellular imaging. Proc. Natl. Acad. Sci. 2004;101:10901–10906. doi: 10.1073/pnas.0403918101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Shapiro EM, Skrtic S, Koretsky AP. Sizing it up: cellular MRI using micron-sized iron oxide particles. Magn. Reson. Med. 2005;53:329–338. doi: 10.1002/mrm.20342. [DOI] [PubMed] [Google Scholar]
- 9.Shapiro EM, Sharer K, Skrtic S, Koretsky AP. In vivo detection of single cells by MRI. Magn. Reson. Med. 2006;55:242–249. doi: 10.1002/mrm.20718. [DOI] [PubMed] [Google Scholar]
- 10.Juan JY, Tracy K, Zhang LH, Munasinghe J, Shapiro E, Koretsky A, Kelly K. Noninvasive imaging of the functional effects of anti-VEGF therapy on tumor cell extravasation and regional blood volume in an experimental brain metastasis model. Clin. Exp. Metastasis. 2009;26:403–414. doi: 10.1007/s10585-009-9238-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sumner JP, Shapiro EM, Maric D, Conroy R, Koretsky AP. In vivo labeling of adult neural progenitors for MRI with micron sized particles of iron oxide: Quantification of labeled cell phenotype. Neuroimage. 2009;44:671–678. doi: 10.1016/j.neuroimage.2008.07.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zabow G, Dodd S, Moreland J, Koretsky A. Micro-engineered local field control for high-sensitivity multispectral MRI. Nature. 2008;453:1058–1063. doi: 10.1038/nature07048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zabow G, Koretsky AP, Moreland J. Design and fabrication of a micromachined multispectral magnetic resonance imaging agent. J. Micromech. Microeng. 2009;19:025020. [Google Scholar]
- 14.Zabow G, Dodd SJ, Moreland J, Koretsky AP. The fabrication of uniform cylindrical nanoshells and their use as spectrally tunable MRI contrast agents. Nanotechnology. 2009;20:385301. doi: 10.1088/0957-4484/20/38/385301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Brown RJS. Distribution of fields from randomly placed dipoles: free-precession signal decay as result of magnetic grains. Phys. Rev. 1961;121:1379–1382. [Google Scholar]
- 16.Yablonskiy DA, Haacke EM. Theory of NMR signal behavior in magnetically inhomogeneous tissues: the static dephasing regime. Magn. Reson. Med. 1994;32:749–763. doi: 10.1002/mrm.1910320610. [DOI] [PubMed] [Google Scholar]
- 17.Gillis P, Koenig SH. Transverse relaxation of solvent protons induced by magnetized spheres: application to ferritin, erythrocytes, and magnetite. Magn. Reson. Med. 1987;5:323–345. doi: 10.1002/mrm.1910050404. [DOI] [PubMed] [Google Scholar]
- 18.Cheng YN, Haacke EM, Yu YJ. An exact form for the magnetic field density of states for a dipole. Magn. Reson. Imag. 2001;19:1017–1023. doi: 10.1016/s0730-725x(01)00422-2. [DOI] [PubMed] [Google Scholar]
- 19.Seppenwoolde JH, van Zijtveld M, Bakker CJG. Spectral characterization of local magnetic field inhomogeneities. Phys. Med. Biol. 2005;50:361–372. doi: 10.1088/0031-9155/50/2/013. [DOI] [PubMed] [Google Scholar]
- 20.Ziener CH, Kampf T, Melkus G, Herold V, Weber T, Reents G, Jakob PM, Bauer WR. Local frequency density of states around field inhomogeneities in magnetic resonance imaging: effects of diffusion. Phys. Rev. E. 2007;76:031915. doi: 10.1103/PhysRevE.76.031915. [DOI] [PubMed] [Google Scholar]
- 21.Weisskoff RM, Zuo CS, Boxerman JL, Rosen BR. Microscopic susceptibility variation and transverse relaxation: theory and experiment. Magn. Reson. Med. 1994;31:601–610. doi: 10.1002/mrm.1910310605. [DOI] [PubMed] [Google Scholar]
- 22.Gillis P, Moiny F, Brooks RA. On T2-shortening by strongly magnetized spheres: a partial refocusing model. Magn. Reson. Med. 2002;47:257–263. doi: 10.1002/mrm.10059. [DOI] [PubMed] [Google Scholar]
- 23.Lüdeke KM, Röschmann P, Tischler R. Susceptibility artefacts in NMR imaging. Magn. Reson. Imag. 1985;3:329–343. doi: 10.1016/0730-725x(85)90397-2. [DOI] [PubMed] [Google Scholar]
- 24.Ericsson A, Hemmingsson A, Jung B, Sperber GO. Calculation of MRI artifacts caused by static field disturbances. Phys. Med. Biol. 1988;33:1103–1112. [Google Scholar]
- 25.Callaghan PT. Susceptibility-limited resolution in nuclear magnetic resonance microscopy. J. Magn. Reson. 1990;87:304–318. [Google Scholar]
- 26.Posse S, Aue WP. Susceptibility artifacts in spin-echo and gradient-echo imaging. J. Magn. Reson. 1990;88:473–492. [Google Scholar]
- 27.Bakker CJG, Bhagwandien R, Moerland MA, Ramos LMP. Simulation of susceptibility artifacts in 2D and 3D fourier transform spin-echo and gradient-echo magnetic resonance imaging. Magn. Reson. Imag. 1994;5:767–774. doi: 10.1016/0730-725x(94)92201-2. [DOI] [PubMed] [Google Scholar]
- 28.Identification of Bangs Laboratories MPIOs is only for the purpose of accurately specifying studies presented in this paper and does imply endorsement by NIH or NIST.
- 29.McCurrie RA. Ferromagnetic materials: structure and properties. London: Academic Press; 1994. [Google Scholar]
- 30.Ciocan R, Lenkinski RE, Bernstein J, Bancu M, Marquis R, Ivanishev A, Kourtelidis F, Matsui A, Borenstein J, Frangioni JV. MRI contrast using solid-state, B1-distorting, microelectromechanical systems (MEMS) microresonant devices (MRDs) Magn. Reson. Med. 2009;61:860–866. doi: 10.1002/mrm.21906. [DOI] [PubMed] [Google Scholar]
- 31.Madou MJ, editor. Fundamentals of microfabrication: the science of miniaturization. Florida: CRC Press; 2002. [Google Scholar]