Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2011 Apr 26.
Published in final edited form as: Genet Epidemiol. 2009 Dec;33(8):691–699. doi: 10.1002/gepi.20421

Gene-Environment Interaction Tests for Dichotomous Traits in Trios and Sibships

Thomas J Hoffmann a,*, Christoph Lange a,b, Stijn Vansteelandt c, Nan M Laird a
PMCID: PMC3082448  NIHMSID: NIHMS141754  PMID: 19365860

Abstract

When testing for genetic effects, failure to account for a gene-environment interaction can mask the true association effects of a genetic marker with disease. Family-based association tests are popular because they are completely robust to population substructure and model misspecification. However, when testing for an interaction, failure to model the main genetic effect correctly can lead to spurious results. Here we propose a family-based test for interaction that is robust to model misspecification, but still sensitive to an interaction effect, and can handle continuous covariates and missing parents. We extend the FBAT-I gene-environment interaction test for dichotomous traits to using both trios and sibships. We then compare this extension to joint tests of gene and gene-environment interaction, and compare the joint test additionally to the main effects test of the gene. Lastly we apply these three tests to a group of nuclear families ascertained according to affection with Bipolar Disorder.

Keywords: genetic association, genetic interaction, family-based test, FBAT-I

1 Introduction

Interactions between genetic and environmental factors are known to play an important role in Mendelian disorders [Ottman, 1990] and an increasing number of papers suggest evidence for interactions in complex disorders [Eley et al., 2004, Yaffe et al., 2000]. Here we define interaction in a statistical sense as a departure from additive main effects in a generalized linear model. Testing solely for an interaction in the presence of a potential main genetic and continuous environmental effect is dependent on the genetic model for disease being correct. Thus a test for the interaction is scale dependent, and cannot be completely model free [Greenland, 1993, Vansteelandt et al., 2008]. Case-control methods for a main genetic effect are used because they often have higher power than family-based designs, but family-based tests of the main genetic effect have the advantage of being completely model-free and robust to population substructure [Laird and Lange, 2006]. When testing for an interaction, robustness to model misspecification in family based designs hasn’t been thoroughly examined. The properties of being completely model-free and robust to population substructure are maintained in a joint test for a main genetic effect and a gene-environment interaction as shown in Lunetta et al. [2000]. This joint test is essentially testing if there is any departure from Mendel’s laws. An interaction test can also be robust to population substructure.

There are several different tests for gene-environment interaction for dichotomous traits. Each has different model assumptions, and is only applicable to certain family structures. Umbach and Weinberg [2000] introduce a test for trios for dichotomous exposures. In a series of papers, Cordell and Clayton [2002], Cordell [2004], Cordell et al. [2004], introduce a likelihood-based method for trios that extends to some cases of an offspring with only one parent. Dudbridge [2008] proposes an extension of this test to missing parents, but the approach is not completely robust to population substructure. Witte et al. [1999] introduce a different likelihood-based method for discordant sibpairs. Chatterjee et al. [2005] propose a more powerful version of this test under a rare disease assumption. Lastly, Lake and Laird [2004] introduce FBAT-I, a score-type test for trios. All of these methods, except for the Witte et al. [1999] approach, must also make an assumption concerning independence of the environment and genotype effects conditional on the parents.

Here we extend the FBAT-I gene-environment interaction test for dichotomous traits [Lake and Laird, 2004] to more general family structures. We propose a test that utilizes any combination of trios, sibpairs, and sibtrios. We prove that validity of the test holds when the main effect of the gene is misspecified, and when the marker is not the disease susceptibility locus (DSL). We also investigate the types of different sibship sampling strategies. We then compare the interaction test to a joint test of gene and gene-environment interaction, and also to a test of the main genetic effect, similar to Kraft et al. [2007]. We illustrate the extended FBAT-I test in a bipolar dataset with trios and sibships, comparing it to the main genetic effect and joint gene and gene-environment interaction tests.

2 Methods

Similar to the log-linear model given by Umbach and Weinberg [2000], the original FBAT-I test stratifies trios according to parental mating type Lake and Laird [2004]. This stratification makes the test robust to population substructure. It is motivated by an idea introduced in Umbach and Weinberg [2000]: if we have multiplicative penetrance of the disease, and the gene and the environment are independent, conditional on the parents, then the gene and the environment are still independent conditional on ascertainment of affected offspring. This conditional independence motivates the form of the test, shown below (equation 1).

We extend the FBAT-I test to more general family structures by stratifying by the sufficient statistic for parental mating type [Rabinowitz and Laird, 2000]. For example, when parents are observed, the sufficient statistic for parental mating type is the parents genotypes, and the test is identical to the original FBAT-I test. Table I shows the informative strata of sufficient statistics for parental mating type for sibpairs and sibtrios. Let s index the strata of sufficient statistics S, and let f index the offspring within the strata. Let Xsf = X(gsf) be a univariate coding of the genotype (e.g. additive) for the fth offspring in the sth strata, and let Zsf be the corresponding environmental exposure. We propose the following test statistic using only the affected probands

T=∑sTs=∑s,f{Xsf−E^(X∣S,Y=1)}{Zsf−E^(Z∣S,Y=1)}=∑s,f{Xsf−X‒s}{Zsf−Z‒s}, (1)

where X‒s and Z‒s are sample means of X and Z of the affected offspring in strata s. The test statistic can be viewed as a stratified sample covariance. We use a Monte-Carlo permutation test to break the correlation by permuting {Xsf−X‒s} within each strata of sufficient statistics, or equivalently permuting {Zsf−Z‒s}, as discussed in Lake and Laird [2004].

Table I.

Potential informative strata of sufficient statistics for parental mating type under an additive genetic model. For example, AA-AB indicates a parental mating type, and (AA,AB) indicates a configuration of sibpairs for each strata of suffcient statistic.

Trios (Parents Genotyped) AA-AB, AB-AB, AB-BB
Sibpairs (Parents Missing) (AA,AB), (AB,BB), (AA,BB)
Sibtrios (Parents Missing) (AA,AA,AB), (AA,AA,BB),
(AA,AB,AB), (AA,AB,BB),
(AA,BB,BB),
(AB,AB,BB), (AB,BB,BB)
Open in a new tab

The test requires similar assumptions to those assumed in Umbach and Weinberg [2000]. The first assumption is that the genotype and the environment are independent conditional on the parental mating type. The condition fails when the gene is causal to the environmental exposure, and will be reasonable in most situations. If this assumption does not hold, then the test will have an inflated type I error rate, as shown in Umbach and Weinberg [2000] along with an example. The second assumption is that the penetrance function is multiplicative under the null of no interaction, i.e.

P(Y=1∣g,Z,S)∝hg(g,S)he(Z,S), (2)

where hg(.) and he(.) are any function. With these two assumptions, the test has expectation zero by a proof similar to Lake and Laird [2004]. In the appendix we show that conditional independence of the genotype and exposure given the parental mating type implies conditional independence given the sufficient statistic for parental mating type. The proof is completed by replacing the parental mating type P in Lake and Laird [2004] with the sufficient statistic S for parental mating type. The result extends FBAT-I to sibships. In the rest of the paper, we use FBAT-I to refer to this extended test. The test remains valid under the null if either or both X(g) or Z is incorrectly coded, since there is no model for the conditional means E(X|Y = 1, S) and E(Z|Y = 1, S), they are estimated empirically in the test statistic (equation 1). However, the test will lose power if they are incorrectly coded.

We explore an additional validity issue not discussed in the original Lake and Laird [2004] paper. Suppose there is a disease susceptibility locus (DSL) that does not have an interaction effect, but has a main genetic effect. We show in the appendix that the test also remains valid when the marker tested is not the true DSL, but is instead in linkage disequilibrium and/or linked to the true DSL. Details are given in the appendix.

The last validity issue to be considered arises because we are extending the test to more general family configurations. The validity of the test requires that families be ascertained on the basis of having at least one affected offspring, and requires that only the proband contribute to the test statistic. For example, ascertaining families based on discordant sibpairs violates the conditional independence in the general case. However, in the appendix we show that ascertaining discordant sibpairs is valid in at least the following three circumstances: when there is no main genetic effect, no main environmental effect, or no phenotypic correlation between offspring. By simulation we find that ascertaining discordant sibpairs generally has negligible bias, unless the prevalence is high. Thus this is not a serious limitation of the test.

3 Simulations

We first assessed the validity of the test to model misspecification with and without population substructure. To simulate population substructure, let b index across subpopulations, and let πb indicate the allele frequency in each subpopulation. The probability of an individual being diseased was given by

P(Yi=1∣gi,Zi,b)=exp{βb+βgX(gi)+βeZi+βgeX(gi)Zi}. (3)

The data was drawn assuming conditional independence of genotype and environment given the parents according to the marginal distribution

P(Yi=1,gi,Zi,Si,b;πb)=P(Yi=1gi,Zi)P(gi∣Si)P(Zi∣Si,b)P(Si∣b;πb)P(b). (4)

Details of the joint distribution for discordant sibpairs to account for phenotypic correlation are provided in the appendix.

In all cases tested where sibpairs were drawn according to at least one affected, the FBAT-I test extended to sibpairs does not depart from a nominal α = 0.05 level, and so results are not shown. We tested the robustness of the test to misspecifying the functional form of the environmental main effect, for example exp(Z) for continuous exposures. We also investigated the robustness of the test to miscoding the main genetic effect - models were simulated under an additive, dominant, and recessive genetic coding, and tested under all other codings. Validity simulations were done under a variety of scenarios. The baseline disease prevalence, i.e. eβ0, does not matter for trios or sibpairs with at least one affected. We simulated allele frequencies between 0.05-0.5 when there was no population substructure. Dichotomous environmental exposures ranged from 0.1-0.5, and continuous exposures were also tested (normal, uniform, chi-squared). To simulate population substructure, we used two very different subpopulations. The first had allele frequency 0.9 and environmental exposure 0.1, and the second had allele frequency 0.1 and environmental exposure 0.9. Sample sizes were tested in ranges from 150-1000. In all cases the FBAT-I test maintained the nominal α level.

In the case of discordant sibpairs, the FBAT-I test generally showed negligible bias (results not shown). The scenarios described above were repeated here. Here the disease prevalence matters (since the sibs must be discordant), and so was set between 0.1-0.001. For population substructure, the second subpopulation had a baseline disease prevalence of 14 to 4 times that of the first subpopulation. When eβg , eβe ≤ 3, and the phenotypic odds ratio ≤ 3, all validity simulations showed for α = 0.05 an empirical type I error rate of < 0.054 (SE≈ 0.002), with the large majority at or below 0.05. For more extreme cases when both eβg = eβge = 5, the empirical type I error rate was slightly inflated up to approximately 0.065.

To assess the efficiency of the FBAT-I test, we compared the power of several different designs. For power, there was very little effect of phenotypic correlation, and so results are shown with no phenotypic correlation. All power simulations use 500 cases. For example trios consisted of 500 offspring and their parents, for a total of 1500 genotyped individuals. Sibpairs consisted of 500 sibpairs with at least one affected, for a total of 1000 genotyped individuals.

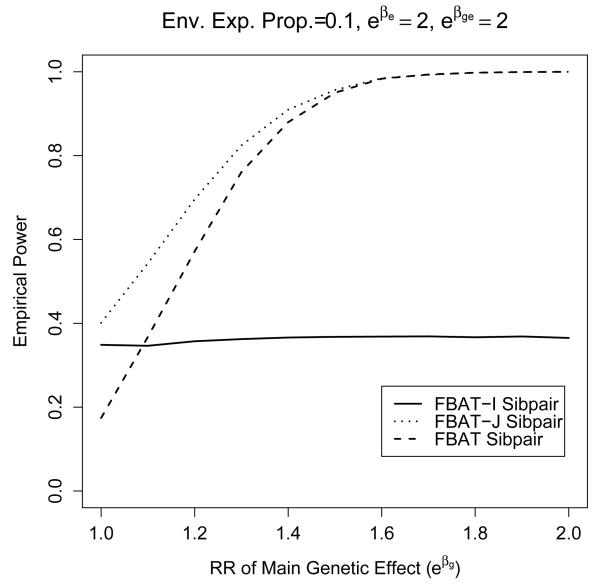
For the family-based designs, we see in figure 1 that trios are the most powerful, followed by sibtrios and sibpairs. This is always the case, even under other genetic models, such as recessive. A very rough rule of thumb given by Witte et al. [1999] is that sibpairs are generally about half as powerful as trios. Recall that interaction tests are scale dependent on the underlying disease model. The previous three ascertainments, all based on using the proband of at least one affected, do not depend on the baseline prevalence, and were designed for a relative-risk or log-linear disease model. Case-control designs are based on a logistic model for disease, so results are not comparable unless the disease prevalence is small. We show in figure 1 a case-control design with equal numbers of cases and controls where the disease prevalence is 0.01. Figure 1 shows the effect of exposure proportion when there is a modest environmental effect. Trios can be more powerful than case-control, but for the most part, they are comparable. Altering the allele frequency has minimal impact on the relative order. We examine the remaining parameters in the next figure. Figure 2 shows how power varies with the strength of the main genetic relative risk eβg and the interaction relative risk eβge, under a modest main environmental relative risk eβe. The main genetic effect has little effect on the power unless the main genetic effect is very strong. This phenomenon is probably due to reduced variance in the genotype. Results of varying the main environmental risk eβe are similar to varying the main genetic effect eβg , and so are not shown.

Figure 1.

Figure 1

Open in a new tab

Power results comparing FBAT-I under different family structures and a 1-1 case/control design, for a type I error rate of 0.05. The disease prevalence was 0.01. 500 cases were simulated with parameters as indicated in the plot. Simulations are based on a dichotomous covariate and additive genetic model. Approximate standard error is less than 0.005 (based on 10000 simulations).

Figure 2.

Figure 2

Open in a new tab

Power results of trios and sibpairs under various different parameters. Again, the type I error rate was set to 0.05, and 500 cases were drawn. Approximate standard error is less than 0.005 (based on 10000 simulations).

We then compared the interaction tests to joint tests for both the main genetic effect and interaction, denoted FBAT-J, as well as tests based purely on the main genetic effect under the standard FBAT test (with no interaction term) [Laird and Lange, 2006]. The results are shown in figure 3. The results comparing main genetic effect to the joint test are similar to the comparison of similar tests in case-control simulations in Kraft et al. [2007]. The joint test generally does better than the main genetic effect test when there is some gene-environment interaction contribution, but otherwise worse (results not shown). In our family-based design, we find that the FBAT-J joint test always performs better than the FBAT-I interaction test, as in all cases shown in figure 3. The difference is smaller when there is a low proportion exposed and no main genetic effect. However, the joint test is not testing solely for an interaction, so the results are less conclusive.

Figure 3.

Figure 3

Figure 3

Open in a new tab

Power results comparing testing the main genetic effect, the joint test of gene and gene-environment interaction, and the gene-environment interaction test when there is no environmental correlation between the sibs. 500 cases were again simulated with a dichotomous exposure with α = 0.05. Approximate standard error is less than 0.005 (based on 10000 simulations).

4 Application to Bipolar Disorder

For illustrative purposes only, we apply the FBAT-I test, the standard FBAT test for the main genetic effect, and the joint gene and gene-environment interaction test to a subset of the family data on Bipolar Disorder from the NIMH Genetics Initiative [Moldin, 2003] using sex as an “environmental” covariate. The phenotyping is described in McQueen et al. [2005]. A set of 3064 SNPs were selected on a linkage peak in chromosome 6q (spanning 105.34 to 125.73 Mb, NCBI build 34), genotyped using the Illumina BeadArray System at the Broad Institute. SNPs with a call rate of less than 90%, SNPs with Hardy-Weinberg equilibrium p-values less than 10−6, and individuals with call rates less than 90% were excluded. The results of association analysis will be presented elsewhere. Here we use a set of 2805 SNPs genotyped in a linkage region of chromosome 6. The subset consists of 318 nuclear families ascertained for Bipolar I Disorder affection, a disease that has an estimated 0.4-1.6% prevalence [American Psychiatric Association, 1994]. These data are ideal to illustrate the use of this test, as they are a mixture of family types. Of the families, 231 had parents, 27 were sibpairs, and 60 were sibtrios. In total, there were 370 male affected offspring and 244 female affected offspring, with an average of 1.7 affected offspring per family. The tests were run for each of the 2805 markers under an additive model, using one affected offspring per family. The top 20 results presented in table II are sorted by the joint test p-value, and are not corrected for multiple comparisons. After correction, the results are not significant. However, the results show how the joint test is concordant with either the interaction test or the main effects test. The top 20 results by the joint test include the top 3 interaction tests and the top 8 main effects tests.

Table II.

Application to bipolar dataset. Results are sorted by joint test p-value. P-values are shown for the joint main genetic effect and interaction test (FBAT-J), the FBAT main genetic effects test (FBAT), and the FBAT-I interaction test (FBAT-I). The last two columns indicate the p-value ranking when sorting by the respective tests (FBAT Rank and FBAT-I Rank).

Marker Allele Freq Inf FBAT-J FBAT-I FBAT FBAT-I Rank FBAT Rank
rs12213914 4 0.1073 91 0.0007179 0.7805 0.000154 2092 1
rs3756939 1 0.3813 208 0.001224 0.000716 0.1896 3 487
rs1190053 1 0.1052 86 0.001759 0.1544 0.000795 342 2
rs12661427 4 0.1564 135 0.00182 0.000378 0.7179 1 1950
rs17073644 4 0.1548 128 0.002014 0.07395 0.005281 160 21
rs6931341 1 0.3285 187 0.002216 0.1616 0.003302 367 16
rs472059 4 0.3830 186 0.002834 0.1301 0.002422 294 8
rs17084747 2 0.08468 89 0.00322 0.000658 0.915 2 2514
rs17071722 4 0.08037 53 0.003388 0.2279 0.001421 534 5
rs2358056 3 0.1294 104 0.00373 0.009735 0.3884 10 1012
rs484754 4 0.3229 194 0.004179 0.955 0.000933 2566 3
rs9487643 2 0.1106 81 0.004676 0.3488 0.00128 840 4
rs10484479 3 0.1090 87 0.005003 0.03871 0.003436 66 18
rs12198581 4 0.1402 131 0.005555 0.2591 0.002035 623 7
rs2817778 1 0.1019 79 0.005781 0.3247 0.002796 784 14
rs12216134 4 0.04746 50 0.005927 0.3158 0.002653 759 13
rs802718 2 0.07551 85 0.006719 0.2456 0.002439 587 10
rs6924401 2 0.2352 137 0.007323 0.3188 0.00182 772 6
rs2503770 1 0.2481 163 0.008068 0.1681 0.003576 385 19
rs6914322 4 0.1602 123 0.008096 0.05631 0.04459 110 103
Open in a new tab

5 Discussion

We have extended the FBAT-I test to more general family structures, and shown that the test remains valid under H0 even when the marker is linked and/or in linkage disequilibrium with a true disease susceptibility locus which does not interact with the environmental covariate. The test is robust to miscoding the main genetic effect, and is robust to misspecification of the functional form of the environmental effect, so long as it is multiplicative. An advantage of our work is that we can combine trios with sibpairs and sibtrios.

The test performs well when there are not too many strata of sufficient statistics. However, with arbitrary pedigrees, the number of strata can be too large for this test to be applicable for efficiency reasons. With missing parents, a typical strategy is to ascertain the proband and siblings. The strata is determined by what can be inferred by the missing parents [Rabinowitz and Laird, 2000]. With missing parents the number of offspring can affect which strata an individual falls into. Thus genotyping all siblings when parents are missing could potentially have too many strata to estimate the conditional means empirically.

In order to avoid specifying the form of the interaction entirely, one can instead do a joint test for the gene and gene-environment interaction. This test has the advantage that it doses not require a multiplicative model. Although one can no longer decouple whether a significant result is just a genetic effect or also a gene-environment interaction, the test is almost as powerful as the main genetic effects test when there is no interaction and is generally more powerful when there is an interaction present for identifying potential loci of interest. The joint test is also always more powerful than the interaction test. In screening for potential gene-environment interactions, a useful method may be using the joint test to find SNPs of interest and testing afterward if there is any interaction. With a specific hypothesis in mind, the interaction test is to be preferred.

The free ‘fbat-i’ R package [R Development Core Team, 2008] implements the FBAT-I and FBAT-J tests, and is licensed under the GPL. The package utilizes the data loading routines of the R package ‘pbatR’, using data in the same format as described in Hoffmann and Lange [2006].

A Proof that g ⊥ Z|P ⇒ g ⊥ Z|S

In this section, additionally let P be the parental mating type, and let S still be the sufficient statistic for the parental mating type P. First we claim that g ⊥ Z|P ⇒ g ⊥ Z|P, S. The proof of this claim proceeds by contradiction. Suppose that this did not hold. Then for some g, g* ∈ S

f(Z∣P,S,g)≠f(Z∣P,S,g⋆).

Consider first the case where both parents are missing. Then g completely determines S, so we have that f(Z|P, S, g) = f(Z|P, g), and furthermore this implies that

f(Z∣P,g)≠f(Z∣P,g⋆).

However, then g is no longer independent of Z given P, and we have a contradiction.

Next consider the case when just one parent is missing. In that case the nonmissing parent and g completely determine the distribution and we have the same contradiction as above. When both parents are available, S = P, and there is nothing to show.

With this, the rest of the proof is straight-forward. Let P ∈ S denote the compatible parental genotypes for a given sufficient statistic. Then

f(g,Z∣S)=∑P∈Sf(g,Z∣P,S)f(P∣S)=∑P∈Sf(g∣P,S)f(Z∣P,S)f(P∣S)=f(g∣S)∑P∈Sf(Z∣P,S)f(P∣S)=f(g∣S)f(Z∣S),

where f(g|S, P) = f(g|S) since S is the sufficient statistic.

B FBAT-I with Discordant Sibpairs

Using discordant sibpairs is generally not strictly valid for multiple affected individuals under discordant sibpair ascertainment. However there are several circumstances when the test is valid under this ascertainment. The first case is when there is no main genetic effect. It is also valid when there is no main environmental main effect. Lastly, the test is valid if we assume that there is no phenotypic correlation between the two offspring and P(Yi = yi|g1, g2, Z1, Z2, S) = P(Yi = yi|gi, Zi, S). The heart of the proof in Lake and Laird [2004] that the test statistic for trios has expectation 0 relies on the fact that E(Xsf Zsf|S, Ysf = 1) = E(Xsf|S, Ysf = 1)E(Zsf|S, Ysf = 1), where for trios S = P. This results from P(Xsf, Zsf|S, Ysf = 1) factoring into environmental and genotypic components. A similar idea can be considered for sibs, where S refers to the genotype configuration for the sibpair. If we ascertain based on Ysf1 = 1 and arbitrary Ysf2, then conditional independence still holds directly. However, in the case of discordant sibs, this result no longer holds in general. We now drop the first two indexes in our notation, and consider two sibs.

When there is either no genetic effect or no environmental effect, then the condition still holds. We first consider the case when there is no environmental effect. Then under the null hypothesis of no gene-environment interaction we have that P(Y1 = 1|g1, Z1, S) = P(Y1 = 1|g1, S). Thus we have that

P(g1,Z1∣S,Y1=1,Y2=0)=P(Y1=1,Y2=0,g1,Z1,S)P(Y1=1,Y2=0,S)=∫g2,Z2P(Y1=1,Y2=0∣g1,g2,S)P(Z1,Z2∣S)P(g1,g2∣S)∫g1,g2,Z1,Z2P(Y1=1,Y2=0∣g1,g2,S)P(Z1,Z2∣S)P(g1,g2∣S)=P(Z1∣S)⋅∫g2P(Y1=1,Y2=0∣g1,g2,S)P(g1,g2∣S)∫g1,g2P(Y1=1,Y2=0∣g1,g2,S)P(g1,g2∣S),

by conditional independence. One can easily see that these two terms are just

P(Z1∣S,Y1=1,Y2=0)⋅P(g1∣S,Y1=1,Y2=0),

and so it follows that the expectations factor. Similarly, when there is no gene effect, we instead have that P(Y1 = 1|g1, Z1, S) = P(Y1 = 1|Z1, S). It follows from similar calculations that

P(g1,Z1∣S,Y1=1,Y2=0)=P(g1∣S)⋅∫Z2P(Y1=1,Y2=0∣Z1,Z2,S)P(Z1,Z2∣S)∫Z1,Z2P(Y1=1,Y2=0∣g1,g2,S)P(Z1,Z2∣S)=P(g1∣S,Y1=1,Y2=0)⋅P(z1∣S,Y1=1,Y2=0).

Next consider the case when there is no phenotype correlation, i.e. Y1 ⊥ Y2|g, Z, S. We have here that

P(g1,Z1∣S,Y1=1,Y2=0)=∫g2,Z2P(Y1=1,Y2=0,g1,g2,Z1,Z2,S)∫g1,g2,Z1,Z2P(Y1=1,Y2=0,g1,g2,Z1,Z2,S)=∫g2,Z2P(Y1=1,Y2=0∣g1,g2,Z1,Z2,S)P(g1,g2∣S)P(Z1,Z2∣S)P(S)∫g1,g2,Z1,Z2P(Y1=1,Y2=0∣g1,g2,Z1,Z2,S)P(g1,g2∣S)P(Z1,Z2∣S)P(S)=∫g2,Z2P(Y1=1,Y2=0∣g1,g2,Z1,Z2,S)P(Z1,Z2∣S)∫g1,g2,Z1,Z2P(Y1=1,Y2=0∣g1,g2,Z1,Z2,S)P(Z1,Z2∣S),

by conditional independence and since P(g1, g2|S) is constant for all (g1, g2) ∈ S for sibpairs. Then, since there is no phenotype correlation this becomes

P(g1,Z1∣S,Y1=1,Y2=0)=P(Y1=1∣g1,z1,S)∫g2,Z2P(Y2=0∣g2,Z2,S)P(Z1,Z2∣S)∫g1,g2,z1,z2P(Y1=1∣g1,Z1,S)P(Y2=0∣g2,Z2,S)P(Z1,Z2∣S)={hg(g1,S)∫g1hg(g1,S)}{he(Z1,S)∫g2,Z2P(Y2=0∣g2,Z2,S)P(Z1,Z2∣S)∫g2,Z1,Z2he(Z1,S)P(Y2=0∣g2,Z2,S)P(Z1,Z2∣S)}

under the null hypothesis of no gene-environment interaction. It is easy to see that this is just P(g1|S, Y1 = 1, Y2 = 0)P(Z1|S, Y1 = 1, Y2 = 0). Thus the test is also valid when there is no phenotype correlation.

C When the Marker is Not the true Disease Susceptibility Locus

Recall from the previous section that the heart of the proof in Lake and Laird [2004] that the test statistic for trios has expectation 0 relies on P(Xsf, Zsf|S, Ysf = 1) factoring into environmental and genotypic components. Here we show that this is still the case when the marker is only in LD and/or linkage to the true DSL.

Let gM indicate the marker genotype and gD represent the DSL genotype. Validity requires assuming a more general multiplicative penetrance to account for both genotypes as follows

P(Y=1∣Z,gD,SD,gM,SM)=he(Z,SD,SM)hgD(gD,SD)hgM(gM,SM),

where he(.), hgD(.), and hgM(.) are any function. A key assumption here is that the disease prevalence does not depend on a haplotype, and there is no epistasis [Cordell, 2002]. Suppose that gM and SM are the genotype and sufficient statistic for parental mating type of the marker, and gD and SD are for the DSL. By definition, the joint distribution of the observed marker and covariate, gM and Z, given Y = 1 and SM is given by

P(gM,Z∣Y=1,SM)=P(Y=1,gM,Z,SM)∫Z⋆,gM⋆∈SMP(Y=1,gM⋆,Z⋆,SM). (5)

Now by assumption, the genotype and the environment are independent conditional on the parental mating type, so we have

P(gD,gM,Z∣SD,SM)=P(gD,gM∣SD,SM)P(Z∣SD,SM).

In this case, LD can be ignored because we assume no haplotype effect or epistasis. Thus we have that

P(gM,gD∣SM,SD)=P(gM∣gD,SM,SD)P(gD∣SM,SD)=P(gM∣SM)P(gD∣SD).

by Mendel’s laws and the concept of sufficient statistic for parental genotypes. Using these last two results, we have that the numerator of equation 5 can be given by

P(Y=1,gM,Z,SM)=∫SD,gD∈SDP(Y=1∣Z,gD,SD,gM,SM)P(gD,gM,Z∣SD,SM)P(SD,SM)=∫SD,gD∈SDhgD(gD,SD)hgM(gM,SM)he(Z,SD,SM)⋅P(gD∣gM∣SD∣SM)P(Z∣SD,SM)P(SD,SM)=hgM(gM,SM)P(gM∣SM)⋅∫SD,gD∈SDhgD(gD,SD)he(Z,SD,SM)P(gD∣SD)P(Z∣SD,SM)P(SD,SM)

Thus, in this case, equation 5 simplifies to

P(gM,Z∣Y=1,SM)={hgM(gM,SM)P(gM∣SM)∫gM⋆∈SMhgM(gM⋆,SM)P(gM⋆∣SM)}⋅{∫SD,gD∈SDhg(gD,SD)he(Z,SD,SM)P(gD∣SD)P(Z∣SD,SM)P(SD,SM)∫Z⋆,SD⋆,gD⋆∈SD⋆hg(gD⋆,SD⋆)he(Z⋆,SD⋆,SM)P(gD⋆∣SD⋆)P(Z⋆∣SD⋆,SM)P(SD⋆,SM)}=P(gM∣Y=1,SM)P(Z∣Y=1,SM).

Hence the test is also valid when the marker is linked to and/or in linkage disequilibrium to a true disease locus that does not interact with Z.

D Data Simulation

Suppose b indices across subpopulations, and π indicates the allele frequency. For trios drawn from a stratified population, we generate the data as follows from equation 4

  1. Draw b from f(b).

  2. Draw π from f(π|b).

  3. Draw the parents P from f(P|π), assuming Hardy-Weinberg equilibrium and random mating.

  4. Draw the children g from f(g|P).

  5. Draw Z from f(Z|b).

  6. Draw Y (as in equation 3), and discard if Y ≠ 1.

Under Mendelian assumptions f(g|S, b, Z) = f(g|S), so it is easy to see that conditional independence in a subpopulation implies conditional independence in the population. We use the following for generating sibpairs with at least one affected (SP1A) and discordant sibpairs (DSP), branching off from the above

  • Draw S from f(S|π).

  • Draw Z1, Z2 from f(Z|b) for each sib (Z2 only for DSP).

    1. For SP1A, draw Y=(Y1Y2)T, and discard if Y1 ≠ 1 (the proband).
    2. For DSP, draw Y, and discard if Y1 ≠ 1 or Y2 ≠ 0.

In order to both adjust for an arbitrary correlation in the phenotypes for other risk factors the sibs might share, we used odds ratios to model the joint distributions from the marginal distributions. We fixed the conditional pairwise odds ratios ψ12 = ψY1,Y2|g1,g2,Z1,Z2,S to construct the joint distribution from the distribution of the marginal probabilities P{Yi = 1|gi, Zi, S}. Note that we are assuming that the odds ratio of the joint distribution is constant, and not depending on any of the other parameters between these marginal distributions.

6 Acknowledgements

We would like to thank Matthew B. McQueen for his help in preparing the dataset. Genotyping was done by Jinbo Fan in the laboratory of Pamela Sklar. We would also like to thank Dawn Demeo and Edwin Silverman for useful discussions, and Peter Kraft for his useful comments. Funding was provided in part by grants MH17119, ES007142, RO1-MH059532, and R01-MH063445.

The principal investigators of the Genetic Determinants of Bipolar Disorder Project (B.D., S.V.F., N.M.L., V.L.N., P.S., and J.W.S) and M.B.M. were supported by NIMH grants R01-MH063445, MH63420, and MH0667288; M.B.M. was additionally supported by NIMH grant T32-MH017119. Collection of data and biomaterials from the Bonn study was supported by the Deutsche Forschungsgemeinschaft. Data and biomaterials from the four NIMH studies were collected in four projects that participated in the NIMH Bipolar Disorder Genetics Initiative. In 1991–1998, the principal investigators and coinvestigators were: J.I.N., Marvin J. Miller, H.J.E., T.F., and Elizabeth S. Bowman, grant U01 MH46282 to Indiana University, Indianapolis; Theodore Reich, Allison Goate, and J.P.R., grant U01 MH46280 to Washington University, St. Louis; J.R.D., Sylvia Simpson, and Colin Stine, grant U01 MH46274 to Johns Hopkins University, Baltimore; Elliot Gershon, Diane Kazuba, and Elizabeth Maxwell, NIMH Intramural Research Program, Clinical Neurogenetics Branch, Bethesda. Data and biomaterials were collected as part of 10 projects that participated in the NIMH Bipolar Disorder Genetics Initiative. In 1999–2003, the principal investigators and coinvestigators were: J.I.N., Marvin J. Miller, Elizabeth S. Bowman, N. Leela Rau, P. Ryan Moe, Nalini Samavedy, Rif El-Mallakh, (at University of Louisville, Louisville), Husseini Manji and Debra A. Glitz (at Wayne State University, Detroit), Eric T. Meyer, Carrie Smiley, T.F., Leah Flury, Danielle M. Dick, H.J.E., grant R01 MH59545 to Indiana University, Indianapolis; J.P.R., Theodore Reich, Allison Goate, Laura Bierut, grant R01 MH059534 to Washington University, St. Louis; M.G.M., J.R.D., Dean F. MacKinnon, Francis M. Mondimore, J.B.P., P.P.Z., Dimitrios Avramopoulos, and Jennifer Payne, grant R01 MH59533 to Johns Hopkins University, Baltimore; W. Berrettini, grant R01 MH59553 to University of Pennsylvania, Philadelphia; W. Byerley and Mark Vawter, grant R01 MH60068 to University of California at Irvine, Irvine; W.C. and Raymond Crowe, grant R01 MH059548 to University of Iowa, Iowa City; Elliot Gershon, Judith Badner, F.J.M., Chunyu Liu, Alan Sanders, Maria Caserta, Steven Dinwiddie, Tu Nguyen, and Donna Harakal, grant R01 MH59535 to University of Chicago, Chicago; J.R.K. and Rebecca McKinney, grant R01 MH59567 to UCSD, San Diego; W.S., Howard M. Kravitz, Diana Marta, Annette Vaughn-Brown, and Laurie Bederow, grant R01 MH059556 to Rush University, Chicago; F.J.M., Layla Kassem, Sevilla Detera-Wadleigh, Lisa Austin, D.L.M., grant 1Z01MH002810-01 to NIMH Intramural Research Program, Bethesda. Genotyping services were provided in part by the Center for Inherited Disease Research (CIDR). CIDR is fully funded through federal contract N01-HG-65403 from the National Institutes of Health to Johns Hopkins University. Data and biomaterials for the Columbia data set were collected and supported by NIMH grant R01 MH59602 (to M.B.) and by funds from the Columbia Genome Center and the New York State Office of Mental Health. The main contributors to the Columbia project were M.B. (principal investigator), Jean Endicott (coprincipal investigator), Jo Ellen Loth, John Nee, Richard Blumenthal, Lawrence Sharpe, Barbara Lilliston, Melissa Smith, and Kristine Trautman, all from Columbia University Department of Psychiatry, New York. A small subset of the sample was collected in Israel in collaboration with B.L. and Kyra Kanyas, from the Hadassah–Hebrew University Medical Center, Jerusalem. We are grateful to the patients and their family members, for their cooperation and support, and to the treatment facilities and other organizations that collaborated with us in identifying families. [McQueen et al., 2005]

References

  1. American Psychiatric Association Diagnostic and Statistic Manual of Mental Disorders. (4th edition) 1994 [Google Scholar]
  2. Chatterjee N, Kalaylioglu Z, Carroll RJ. Exploiting gene-environment independence in family-based case-control studies: Increased power for detecting associations, interactions and joint effects. Genetic Epidemiology. 2005;28(2):138–156. doi: 10.1002/gepi.20049. URL http://dx.doi.org/10.1002/gepi.20049. [DOI] [PubMed]
  3. Cordell HJ. Epistasis: what it means, what it doesn’t mean, and statistical methods to detect it in humans. Hum Mol Genet. 2002 Oct;11(20):2463–2468. doi: 10.1093/hmg/11.20.2463. [DOI] [PubMed] [Google Scholar]
  4. Cordell HJ. Properties of case/pseudocontrol analysis for genetic association studies: effects of recombination, ascertainment, and multiple affected offspring. Genet Epidemiol. 2004 Apr;26(3):186–205. doi: 10.1002/gepi.10306. doi: 10.1002/gepi.10306. URL http://dx.doi.org/10.1002/gepi.10306. [DOI] [PubMed]
  5. Cordell HJ, Clayton DG. A unified stepwise regression procedure for evaluating the relative effects of polymorphisms within a gene using case/control or family data: application to HLA in type 1 diabetes. Am J Hum Genet. 2002 Jan;70(1):124–141. doi: 10.1086/338007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Cordell HJ, Barratt BJ, Clayton DG. Case/pseudocontrol analysis in genetic association studies: A unified framework for detection of genotype and haplotype associations, gene-gene and gene-environment interactions, and parent-of-origin effects. Genet Epidemiol. 2004 Apr;26(3):167–185. doi: 10.1002/gepi.10307. doi: 10.1002/gepi.10307. URL http://dx.doi.org/10.1002/gepi.10307. [DOI] [PubMed]
  7. Dudbridge F. Likelihood-based association analysis for nuclear families and unrelated subjects with missing genotype data. Hum Hered. 2008;66(2):87–98. doi: 10.1159/000119108. doi: 10.1159/000119108. URL http://dx.doi.org/10.1159/000119108. [DOI] [PMC free article] [PubMed]
  8. Eley TC, Sugden K, Corsico A, Gregory AM, Sham P, McGuffin P, Plomin R, Craig IW. Gene-environment interaction analysis of serotonin system markers with adolescent depression. Mol Psychiatry. 2004 Oct;9(10):908–915. doi: 10.1038/sj.mp.4001546. doi: 10.1038/sj.mp.4001546. URL http://dx.doi.org/10.1038/sj.mp.4001546. [DOI] [PubMed]
  9. Greenland S. Basic Problems in Interaction Assessment. Environmental Health Perspectives. 1993;101:59–66. doi: 10.1289/ehp.93101s459. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Hoffmann T, Lange C. P2bat: a massive parallel implementation of pbat for genome-wide association studies in r. Bioinformatics. 2006 Dec;22(24):3103–3105. doi: 10.1093/bioinformatics/btl507. doi: 10.1093/bioinformatics/btl507. URL http://dx.doi.org/10.1093/bioinformatics/btl507. [DOI] [PubMed]
  11. Kraft P, Yen Y-C, Stram DO, Morrison J, Gauderman WJ. Exploiting gene-environment interaction to detect genetic associations. Hum Hered. 2007;63(2):111–119. doi: 10.1159/000099183. doi: 10.1159/000099183. URL http://dx.doi.org/10.1159/000099183. [DOI] [PubMed]
  12. Laird NM, Lange C. Family-based designs in the age of large-scale gene-association studies. Nat Rev Genet. 2006 May;7(5):385–394. doi: 10.1038/nrg1839. ISSN 1471-0056. URL http://dx.doi.org/10.1038/nrg1839. [DOI] [PubMed]
  13. Lake SL, Laird NM. Tests of gene-environment interaction for case-parent triads with general environmental exposures. Ann Hum Genet. 2004 Jan;68(Pt 1):55–64. doi: 10.1046/j.1529-8817.2003.00073.x. [DOI] [PubMed] [Google Scholar]
  14. Lunetta KL, Faraone SV, Biederman J, Laird NM. Family-based tests of association and linkage that use unaffected sibs, covariates, and interactions. Am J Hum Genet. 2000 Feb;66(2):605–614. doi: 10.1086/302782. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. McQueen MB, Devlin B, Faraone SV, Nimgaonkar VL, Sklar P, Smoller JW, Jamra RA, Albus M, Bacanu S-A, Baron M, Barrett TB, Berrettini W, Blacker D, Byerley W, Cichon S, Coryell W, Craddock N, Daly MJ, Depaulo JR, Edenberg HJ, Foroud T, Gill M, Gilliam TC, Hamshere M, Jones I, Jones L, Juo S-H, Kelsoe JR, Lambert D, Lange C, Lerer B, Liu J, Maier W, Mackinnon JD, McInnis MG, McMahon FJ, Murphy DL, Nothen MM, Nurnberger JI, Pato CN, Pato MT, Potash JB, Propping P, Pulver AE, Rice JP, Rietschel M, Scheftner W, Schumacher J, Segurado R, Steen KV, Xie W, Zandi PP, Laird NM. Combined analysis from eleven linkage studies of bipolar disorder provides strong evidence of susceptibility loci on chromosomes 6q and 8q. Am J Hum Genet. 2005 Oct;77(4):582–595. doi: 10.1086/491603. doi: 10.1086/491603. URL http://dx.doi.org/10.1086/491603. [DOI] [PMC free article] [PubMed]
  16. Moldin SO. Nimh human genetics initiative: 2003 update. Am J Psychiatry. 2003 Apr;160(4):621–622. doi: 10.1176/appi.ajp.160.4.621. [DOI] [PubMed] [Google Scholar]
  17. Ottman R. An epidemiologic approach to gene-environment interaction. Genet Epidemiol. 1990;7(3):177–185. doi: 10.1002/gepi.1370070302. doi: 10.1002/gepi.1370070302. URL http://dx.doi.org/10.1002/gepi.1370070302. [DOI] [PMC free article] [PubMed]
  18. R Development Core Team . R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna, Austria: 2008. URL http://www.R-project.org. ISBN 3-900051-07-0. [Google Scholar]
  19. Rabinowitz D, Laird N. A unified approach to adjusting association tests for population admixture with arbitrary pedigree structure and arbitrary missing marker information. Hum Hered. 2000;50(4):211–223. doi: 10.1159/000022918. [DOI] [PubMed] [Google Scholar]
  20. Umbach DM, Weinberg CR. The use of case-parent triads to study joint effects of genotype and exposure. Am J Hum Genet. 2000 Jan;66(1):251–261. doi: 10.1086/302707. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Vansteelandt S, Demeo DL, Lasky-Su J, Smoller JW, Murphy AJ, McQueen M, Schneiter K, Celedon JC, Weiss ST, Silverman EK, Lange C. Testing and estimating gene-environment interactions in family-based association studies. Biometrics. 2008 Jun;64(2):458–467. doi: 10.1111/j.1541-0420.2007.00925.x. doi: 10.1111/j.1541-0420.2007.00925.x. URL http://dx.doi.org/10.1111/j.1541-0420.2007.00925.x. [DOI] [PubMed]
  22. Witte JS, Gauderman WJ, Thomas DC. Asymptotic bias and efficiency in case-control studies of candidate genes and gene-environment interactions: basic family designs. Am J Epidemiol. 1999 Apr;149(8):693–705. doi: 10.1093/oxfordjournals.aje.a009877. [DOI] [PubMed] [Google Scholar]
  23. Yaffe K, Haan M, Byers A, Tangen C, Kuller L. Estrogen use, apoe, and cognitive decline: evidence of gene-environment interaction. Neurology. 2000 May;54(10):1949–1954. doi: 10.1212/wnl.54.10.1949. [DOI] [PubMed] [Google Scholar]

RESOURCES