Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2011 Dec 6.
Published in final edited form as: J Biomol NMR. 2011 May 25;50(3):237–245. doi: 10.1007/s10858-011-9515-3

31P NMR correlation maps of 18O/16O chemical shift isotopic effects for phosphometabolite labeling studies

Nenad Juranić 1,✉, Emirhan Nemutlu 2, Song Zhang 3, Petras Dzeja 4, Andre Terzic 5, Slobodan Macura 6
PMCID: PMC3230932  NIHMSID: NIHMS339551  PMID: 21611840

Abstract

Intramolecular correlations among the 18O-labels of metabolic oligophosphates, mapped by J-decoupled 31P NMR 2D chemical shift correlation spectroscopy, impart stringent constraints to the 18O-isotope distributions over the whole oligophosphate moiety. The multiple deduced correlations of isotopic labels enable determination of site-specific fractional isotope enrichments and unravel the isotopologue statistics. This approach ensures accurate determination of 18O-labeling rates of phosphometabolites, critical in biochemical energy conversion and metabolic flux transmission. The biological usefulness of the J-decoupled 31P NMR 2D chemical shift correlation maps was validated on adenosine tri-phosphate fractionally 18O labeled in perfused mammalian hearts.

Keywords: 31P NMR chemical shift correlation, 18O/16O isotopic effects, ATP turnover, Isotopologue distribution, Oxygen-18, High-energy phosphoryl dynamics, Phosphotransfer, Phosphometabolomics

Introduction

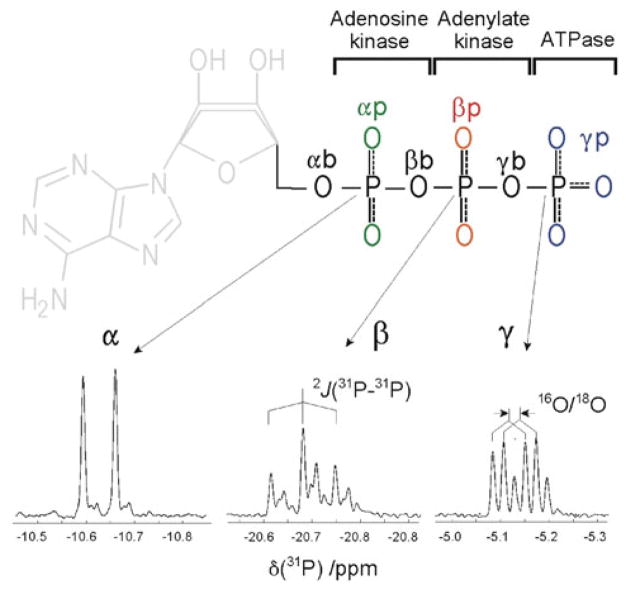
Effects of 18O/16O isotopic substitutions on 31P NMR chemical shifts of metabolic nucleotide oligo-phosphates, such as adenosine di- and tri-phosphate (ADP, ATP), have been used for elucidation of enzymatic reaction mechanisms, determination of metabolite turnover rates, and metabolic flux analysis (Cohn 1982; Cohn and Hu 1978; Cohn and Rao 1982; Hackney et al. 1979; Pucar et al. 2002; Pucar et al. 2004; Pucar et al. 2001; Pucar et al. 2000; Schneck et al. 2010). The 18O isotope effect is readily visible in the high-resolution 1D 31P NMR spectra of phosphometabolites. For instance, in ATP the 31P resonances (α, β and γ) are incrementally shifted upfield with each 18O/16O substitution within the respective phosphate group (Fig. 1, bottom). However, the isotopic effect induced by chemically equivalent oxygen atoms cannot be distinguished. Thus, in ATP only 6 groups of oxygen atoms can be identified by the isotopic effect (Fig. 1, top). Due to the nature of enzymatic reactions (by ATPase, adenylate kinase, and adenosine kinase) the extent of 18O/16O isotope exchange varies across nucleotide oligophosphate moieties. More 18O-shifted peaks of high intensity are seen in the γ spectral region than in the α or β regions, since the efficacy of isotopic substitutions generally decreases from γ to α position. A complicating feature of 1D spectra is the 31P–31P spin–spin coupling, the size of which (~ 20 Hz) is comparable to the spread of 18O/16O isotopic shifts.

Fig. 1.

Fig. 1

Open in a new tab

Metabolic enzymatic reactions in ATP differentiate 6 phosphate-oxygen positions according to degree of isotopic 18O/16O substitutions (top): peripheral oxygens at γ position (γp, blue), the bridging oxygen between the γ and β position (γb), peripheral oxygens at β position (βp, red), the bridging oxygen between β and α position (βb), peripheral oxygen at α position (αp, green), and the bridging oxygen between the ribose carbon and α position (αb). In the 1D 31P NMR spectrum (bottom) chemical shifts caused by isotopic substitution overlap with 31P–31P spin–spin couplings

The relative intensities of the isotope-shifted peaks contain information on the fractional 18O-isotopic enrichments at each of the oxygen positions. However, determination of fractional enrichments within a group of chemically equivalent atoms is not straightforward because it depends on the distribution of isotopologues within a group. Although the distribution is generally assumed to be statistical (Dawis et al. 1989), that assumption may not always hold in enzymatic reactions (Bock and Cohn 1978). Therefore, it is desirable to have techniques that can map not only the population of isotopic labels (as 1D NMR or mass spectroscopy do) but also their intramolecular correlations. This would, in principle, enable detection of preferential processes that may cause deviations from statistical distribution. Such information could be provided by 2D chemical shift correlation spectroscopy (Aue et al. 1976), in which the same 31P–31P spin–spin couplings that complicate 1D spectra help to establish correlations along chemical bonds. Recent improvements also eliminate J-coupling features from detected 2D spectra and provide clean chemical-shift correlations (Bermel et al. 2005). Here we report the use of J-decoupled 2D 31P–31P chemical shifts correlation spectroscopy in mapping correlations of 18O labels within oligophosphate moieties. We also present a method to analyze 31P chemical shift correlations of 18O/16O isotopic effects, which enables extraction of the fractional 18O enrichments in nucleotide phosphates.

Results and discussion

We adopted the technique of virtual decoupling (Bermel et al. 2005) to eliminate one homonuclear coupling in the acquisition domain, and to fully decouple a doublet 31P signal at the α or γ position of ATP. In this way, the α and γ 31P-chemical shifts were in the acquisition domain while the β chemical shifts were consistently in the evolution domain. The spin decoupling in the evolution domain was achieved by selective inversion of both the α and γ resonances. Consequently, in an unlabeled sample, a single 2D peak was obtained for the α/β or γ/β chemical shift correlations. In the 18O enriched sample the corresponding spectra show numerous 2D peaks, in which chemical shifts and intensities depend on the position and the number of introduced 18O labels (Fig. 2).

Fig. 2.

Fig. 2

Open in a new tab

The 283-MHz 31P chemical shift correlations of 18O/16O isotopic effects, for α/β (top) and γ/β (bottom). Assignments of 1D spectral projections (row-wise or column-wise sums of 2D peaks) are given by groups of 18O/16O substitutions that induce the corresponding shifts. Isotopic identity of several 2D peaks is represented by graphs displaying oxygen atoms (18O solid circle, 16O open circle) directly bound to the observed 31P. The starred peak (slightly less shifted along the γ-axis than the peripheral) exemplifies an unequal influence of the γ-bridge oxygen isotopic substitution on the γ versus β chemical shifts. Recorded from an extract of a single rat heart metabolically 18O labeled for 10 min

Assignment of 2D peaks can be made considering only direct, one-bond 18O/16O 31P isotopic effects, assuming that multiple effects are additive, and that the peripheral oxygen substitution shift is stronger than the bridge substitution (Cohn and Hu 1980). For example, in the α/β 31P correlations (Fig. 2 top) the main peak at −10.65/−20.68 ppm (lower left corner) corresponds to all-16O moiety, whereas a series of peaks detected at δ(α-31P) = −10.65 ppm belongs to the isotopologues with an increasing number of 18O atoms around β-31P nuclei (excluding the αβ-bridge position). A single 18O substitution of the αβ bridge generates crosspeaks with the increments along both (α and β) axes, similar to the substitution of 1 peripheral α and 1 peripheral β, but smaller in magnitude. The 18O substitution of the βγ bridge should be identifiable from the β/γ correlation spectrum (Fig. 2, bottom) by the analogous reasoning. However, the isotopic shift of 31P γ-signal induced by oxygen in the γ bridge (γb) has never been resolved from that of the peripheral (γp) oxygen isotopic shift by 1D spectroscopy. Yet, from the small chemical shift difference along the γ-axis in 2D correlation spectrum (Fig. 2 bottom, starred peak) it is clear that the isotopic effect of the γb oxygen is only slightly smaller than that of the γp oxygen. Therefore, the 1D spectrum of β signals nicely resolves the bridge oxygen isotopic shifts from the peripheral ones, whereas γ signals do not resolve them (Cohn and Hu 1980). Caution must be exercised in interpreting peak intensity of this “resolved” bridge signal in the 1D spectrum, because both the γb and αb peaks from 2D correlation projects into that same 1D peak (Fig. 2, top). Consequently, in the presence of the α-phosphate oxygen labeling, determination of the γb and αb labeling from 1D spectra remains ambiguous. This exemplifies novel insight into the site-specific labeling achieved by a better resolution in the 2D correlation spectra and elimination of the J-coupling features. However, even in 2D not all connectivities are resolved. For instance, in the γ/β correlation, the isotopic shifts of the single γb substitution is practically coincidental with the double γp + βb substitutions (Fig. 2, bottom, four boxed structures).

In addition to better determination of the one-bond isotopic shifts, the increased spectral resolution in 2D enabled us to observe a more remote, three-bond 18O/16O–P–O–31P isotopic effect. The most visible are the three-bond effects of γp oxygen isotopic substitutions on 31P β signals, as shown in Fig. 3.

Fig. 3.

Fig. 3

Open in a new tab

The 283-MHz γ/β 31P chemical shift correlations of 18O/16O isotopic effects. 2D peaks are shifted in the 31P β domain due to the three-bond 18O/16O–P–O–31P isotopic effects. Recorded from an extract of a single rat heart metabolically 18O labeled for 10 min

Due to the partial overlap, about 70% of observed 2D peaks could be uniquely assigned (in terms of 6 chemically different phosphate oxygens of ATP) to their respective isotopologues. In contrast to 2D, most of the peaks in 1D spectra (or 1D sum-projections of J-resolved 2D spectra) are superpositions of the spectral signals from several isotopologues with similar isotope shift. Consequently, in 1D most of the specific peak-intensity information is lost. Therefore, we chose to determine the 18O/16O isotopic enrichment at each phosphate oxygen by fitting all experimental 2D peaks with simulated 2D spectra.

For simulation of 2D spectra, the spectral intensities at each spectral position are needed. This requires knowledge of the statistical weight of each isotopic configuration of the tri-phosphate moiety and the 31P chemical shift of each. Because of the three-bond isotopic effects that we observed, the simulation of the α/β and γ/β chemical shift correlations has to consider the whole tri-phosphate moiety. Thus, all isotopologue combinations of 18O/16O occupancies for 10 oxygen atoms (210) must be taken into account. To calculate the statistical weights of 18O/16O isotopologues we assumed that a priori probabilities for 18O or 16O occupancies at each oxygen are the same and that only the rates of the labeling cause differences in isotopic enrichment of oxygen sites. Accordingly, an isotopologue with N oxygen sites is defined by isotope occupancies νj (vj = 1 for 18O and vj = 0 for 16O) at each of the N sites (j = 1, 2, …, N), and each oxygen site has its own 18O/16O fractional isotopic enrichment fj. Then, the probability of finding a specific isotope in a single site j is fj for 18O and (1 − fj) for 16O. Using the occupancy factor vj, the probability of finding either isotope in a single site can be expressed by the Bernstein binomial polynomials (Bernstein 1912):

wj(vj)=(1vj)fjvj(1−fj)1−vj,vj={0forO161forO18

where the occupancy factor selects corresponding isotope. Each isotopologue is defined by its own combination of occupancies (for N sites, total of 2 N); then, the statistical weight (w) of a single isotopologue is given by the product of probabilities for all sites with respective occupancies (v1, …, vN):

w(v1,…,vN)=∏j=1N(1vj)fjvj(1−fj)1−vj,vj∈0,1 (1)

In the case of ATP, the chemical equivalency sorts 10 oxygen atoms into 6 groups (Fig. 1). If oxygen atoms within the groups are truly equivalent (not only in chemical shifts but also throughout the process of isotopic biochemical labeling) the probability of labeling inside a group should also obey the binomial distribution. Therefore it is practical to recast (1) in terms of the six (k) chemically different groups of oxygen atoms:

w(vαb,vαp,vβb,vβp,vγb,vγp)=∏k(nkvk)fkvk(1−fk)nk−vkvk∈0…nkk=αb,αp,βb,βp,γb,γpnαb=nβb=nγb=1nαp=nβp=2vγp=3 (2)

where the product expands over k groups of phosphate oxygen types in ATP, nk is a number of oxygen atoms in each group (e.g, for the γp nk = 3) and νk is the 18O isotopic occupancy of the nk oxygen sites. Here, we should stress that recasting (1) into (2) decreases the number of unknown fractional isotopic enrichments but introduces bias toward the perceived chemical equivalency of some groups of oxygen atoms. If such equivalency is doubtful, then (1) can always be applied and groups of equivalent atoms can be defined later according to derived fractional isotopic enrichments. Obviously, if (2) works then (1) would work also.

Equation (2) has an advantage for the present study because the chemically equivalent oxygen atoms also exhibit the same isotopic effect; that is, they overlap in the 2D correlation spectrum. An isotopologue given by (2) has associated 31P isotopic chemical shifts given by:

δp=δ0p+∑kvkΔkp,p∈α,β,γ (3)

Here δ0P is the chemical shift of unlabeled ATP, and isotopic 18O/16O chemical shifts ( Δkp) have significant value if 31P(p) and 18O(k) are less than 4 bonds apart (by far the most significant are one-bond isotopic shifts, as discussed above).

Considering only the one-bond isotopic effect and neglecting possible spectral overlap, the three 31P nuclei have 32 distinct isotope-induced chemical shifts which can produce 240 crosspeaks in the two correlated spectra. The objective is to find fractional isotopic enrichments fk for each group, which in the case of ATP amounts to 6. Since we can unambiguously assign about 70% of all 2D peaks, the system is rather overdetermined. To find the degree of the enrichments, we chose to minimize the differences between the experimental and simulated α/β and β/γ 2D-correlation spectra by a grid search of 6 fractional isotopic enrichments. Additional spectral parameters, which are mainly predetermined (experimental spectral line-widths, one-bond and three-bond isotopic chemical shifts), were subjected to a more limited grid search. Spectral intensity at almost every point of the spectral regions included in the simulation is significant for determination of the fractional isotopic enrichments fk, as is indicated by simulated spectra corresponding to all fk = 0.5 (Fig. 4, bottom). The final values of fk, given in Table 1, yield a high linear regression coefficient (r2 = 0.98) between the fitted and experimental spectral intensities. The quality of the obtained simulation can also be seen from comparison of 2D contour plots and peak cross-sections between the fitted and the experimental spectra (Fig. 4).

Fig. 4.

Fig. 4

Open in a new tab

Comparison of experimental (red) and simulated (black) spectra of 31P chemical shift correlations α/β (left) and γ/β (right) of 18O/16O isotopic effects. Spectral regions within the dashed boxes were simulated (appearance of these regions for all fk = 0.5 is shown in the bottom inserts). Positions of all possible peaks in the chemical shift correlations are shown by crosses. Chemical shifts are given relative to the corresponding signal of the 18O unlabeled ATP

Table 1.

Positional (p) 31P chemical shift difference induced by 18O/16O isotopic substitutions at 6 (k) phosphate-oxygen groups of atoms in ATP (isotopic shift Δkp), and extracted fractional isotopic enrichment (fk, the α/β- and γ/β-correlation values given separately) for an isolated rat heart sample metabolically 18O-labeled for 10 min

31P signal 18O position One-bond 18O/16 O–31P shift Three-bond 18O/16 O–P–O–31P shift* Fractional 18O/16O isotopic enrichment**
p k Δkp ppm Δkp ppm fk
(α/β) (γ/β)
α Bridge (αb) −0.0160 ± 0.0005 0.03 ± 0.02
Peripheral (αp) −0.0289 ± 0.0002 0.04
Bridge (βb) −0.0173 ± 0.0003 0.05
Peripheral (βp) +0.0003
β Bridge (βb) −0.0164 ± 0.0002 0.05 0.05
Peripheral (βp) −0.0280 ± 0.0002 0.21 0.22
Bridge (γb) −0.0165 ± 0.0002 0.23 0.23
Peripheral (αp) −0.0003
Peripheral (γp) +0.0005
γ Bridge (γb) −0.0206 ± 0.0002 0.23
Peripheral (γp) −0.0225 ± 0.0002 0.25 ± 0.005
Open in a new tab
*

All zero within experimental error (0.0002) except those given

**

Error ± 0.01 if not stated otherwise

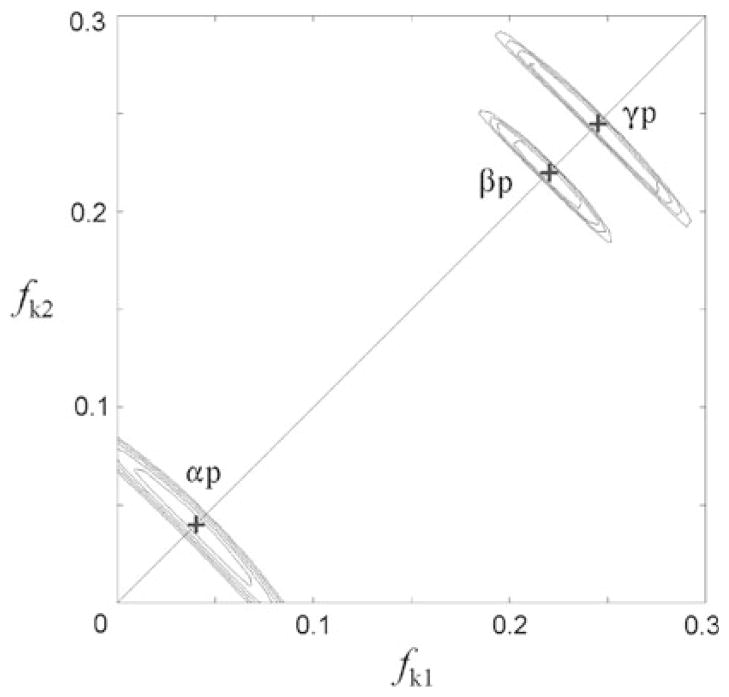
The excellent agreement between the simulated and experimental spectra indicates that the exchange reaction takes place in an unbiased statistical manner. The eventual stereospecific exchange (different enrichment within a chemically equivalent group of oxygen atoms, e.g. two atoms from a group having different fractional enrichments, fk1, fk2 instead of common, fk) that can be induced by some enzymatic reactions (Bock and Cohn 1978), appears to be absent. Observation of the stereospecific effect depends on the different dependence of isotopologues statistical weights (w ~ fk1fk2) and peak intensities (I ~ fk1 + fk2) on the fractional isotope enrichment. Thus, if fractional isotopic enrichments of the chemically equivalent atoms differ, then (1) and (2) give different intensities for these overlapping peaks. This difference originates in multiplicative terms which by (1) have form fk1fk2 and by (2) form (fk)2. To test for potential presence of stereospecificity we analyzed the error dependence of overall fit as a function of the fractional enrichment. For each 31P site we varied fk1, fk2 within the equivalent groups of atoms (αp, βp, γp) in a grid search manner and using (1) simulated 2D spectra for each combination (Fig. 5). In all cases minimal error was obtained for fk1, fk2 = fk, thus justifying use of (2) although for the small isotopic enrichments i.e. fαp = 0.04, the error of using fαp1 = 0, fαp2 = 0.08 instead of fαp1 = fαp2 = 0.04 is within the S/N threshold. In aggregate, there is no need to invoke the stereospecific enrichments in the present case, however, this analysis shows that method could detect stereospecificity, especially at larger isotopic enrichments. The derived fractional isotopic enrichments can therefore be interpreted as a consequence of labeling rates for the 6 chemically equivalent phosphate oxygen sites in the metabolic (rat heart) 18O labeling of ATP.

Fig. 5.

Fig. 5

Open in a new tab

Error of the spectral fit (r.m.s.d. between the experimental and simulated 2D spectra) as function of unequal fractional isotopic enrichments (fk1, fk2) of the chemically equivalent oxygen atoms (αp, βp, γp), represented by equidistant contours from the error minimum (+) to the spectral noise threshold level (set at 3 noise standard deviations). The simulated spectra were calculated applying (1), varying fk1 and fk2 independently for one group at a time, and keeping all other fractional isotopic enrichments at their optimal values given in Table 1. Although the errors are strongly correlated along the line fk1 + fk2 = const. the error minima (+) are observed at fk1 = fk2

An interesting aspect of the simultaneous fitting of the α/β and γ/β correlated 2D spectra is that fractional isotopic enrichments of β-phosphate oxygen sites derived from two correlations should be the same if the statistical distribution over the whole tri-phosphate moiety holds. To investigate this, we allowed the enrichments to adjust independently, and found agreement between the α/β and γ/β derived fractional values within the error limits. The final results for both the fractional isotopic enrichments and the isotopic chemical shifts are given in Table 1.

The one-bond 31P chemical shifts induced by 18O/16O isotopic substitutions, determined here for the first time for all three phosphate groups in ATP, exhibit substantial variations between the groups. The difference between the peripheral and the bridge isotopic shift can be as small as 0.0021 ppm (γ phosphate) and as large as 0.0129 ppm (α phosphate). Notably, the total isotopic shifts (in going from P16O4 to P18O4 moieties) for each of the 3 phosphates is almost the same, amounting to −0.0989 ± 0.0012 ppm. As expected, the fractional isotopic enrichment is highest at the γ phosphate, slightly lower at the β phosphate, and much lower at the α phosphate, due to the dominant γ- and β-phosphoryl group transfer in the cardiac-energetic metabolic reactions (Pucar et al. 2000). The rather low 18O/16O metabolic fractional isotopic enrichments of the ATP α-phosphate oxygen sites are determined for the first time with a good error threshold and indicate that the oxygen bridge to ribose is less labeled than the bridge to the β phosphate (with clear alliance of all four oxygen atoms to the AMP fragment of ATP). The fractional enrichments of oxygen sites in the α, β and γ bridges (0.03, 0.05, and 0.23, respectively) place their values consistently above the peripheral labels in the enclosing moieties (AMP, ADP), indicating the presence of the “X-group transfer” (Cohn 1982) and positional isotopic exchange (Lowe and Sproat 1978), the processes that randomize effects of the isotopic labeling introduced by the phosphoryl group transfers.

Conclusion

The superior resolution of the J-decoupled 31P 2D-NMR chemical shift correlation spectroscopy in this study enabled the determination of 18O/16O isotopic shifts for all ATP phosphate groups, thereby resolving the γ-phosphate peripheral versus bridge 18O/16O isotopic shifts, and the determination of several shifts over three chemical bonds. More important, the 2D method provided maps of numerous correlations among isotopic labeled sites. The abundance of correlations, in turn, allowed an efficient statistical deciphering of isotopologue distributions, enabling determination of fractional isotopic enrichments individually for each site, and identifying groups of oxygen sites that are indistinguishable during metabolic isotopic labeling. In the case of the rat heart metabolic labeling of ATP, the chemically equivalent phosphate oxygen sites were also found to be metabolically equivalent.

The result of this work are readily applicable to ADP, AMP and other phosphates. The use of 2D correlation maps will greatly improve 18O-assisted 31P NMR technology which is being increasingly used for comprehensive evaluation of muscle and cellular bioenergetics and phosphotransfer metabolomics and fluxomics.

This work also relates to a large field of research that is focused on direct NMR observation of isotopic labels such as 13C in metabolic processes (Sauer 2006) and especially to the graph theory approach (Weitzel et al. 2007) which in principle can provide connectivity needed for interpretation of correlated NMR spectroscolpy.

Materials and methods

Sample preparation

Methods used for heart perfusion (perfusion of excised rat hearts with oxygen saturated Krebs-Henseleit solution), 18O phosphoryl labeling (perfusion for 10 min with 30% H2[18O] in Krebs-Henseleit solution), and sample preparation for NMR spectroscopy (extraction and purification of labeled ATP from the perfused hearts) have been described in detail previously (Dzeja et al. 1999; Pucar et al. 2000). A single heart was used for the sample preparation.

NMR spectroscopy

The 283-MHz 31P NMR spectra were recorded on a 700-MHz Avance Bruker spectrometer (Bruker) equipped with an indirect detection broadband probe (applied for direct 31P observation). Temperature was controlled at 25.0 ± 0.1 C. Two-dimensional α/β and γ/β 31P chemical shift correlation spectra were acquired overnight (128 transients; 128 increments; repetition rate 1 s) with spectral resolution of ~0.5 Hz in both domains (spectral widths 1 ppm in direct and 0.3 ppm in indirect domain), and processed to ~0.2 Hz digital resolution in both domains (1024 × 256 points). The Bruker program splitcomb (IPAP 2) was used for the virtual-decoupling processing. The pulse sequence used for 31P chemical shift correlations of 18O/16O isotopic effects and corresponding experimental details, are given in Fig. 6.

Fig. 6.

Fig. 6

Open in a new tab

Implementation of IPAP filtered pulse program for fully decoupled 2D-HSQC chemical shift correlation of ATP γ (acquisition) and β (evolution) 31P resonances. The program is analogous to one given in (Bermel et al. 2005), except for semi-constant-time evolution (adopted from Bruker Avance pulse program “c_caco_ia”) and addition of three 180 decoupling pulses at α-resonances during evolution. Narrow and wide round shaped bars represent selective 90 and 180 pulses, respectively. For the 283 MHz 31P NMR spectra recorded at 700 MHz Avance Bruker spectrometer equipped with indirect detection broadband probe (applied for direct 31P observation), the Sinc1.1000 pulses of 2 ms duration were used. Delays were calculated for J = 20 Hz. The pulse field gradient was 1 ms long, sine shaped, with maximum intensity (z-axis) of ~10 G/cm. Composite 1H decoupling (Waltz 16) used 320 μs 90 degree pulse. The carrier frequency was centered at γ-resonance (−5.2 ppm) while shaped pulses for α- and β-resonances where shifted to −10.9 and −20.7 ppm, respectively. The pulses phase was to x-axis, unless stated differently. Phase cycling was φ1 = x, −x, φ2 = 4(x), 4(y), φ3 = x, x, −x, −x, φ4 = −y, −y, y, y, φrec = x, −x, −x, x, −x, x, x, −x. Phase-sensitive spectra in evolution domain were obtained by φ1 incrementing in a States-TPPI manner. IPAP filter was switched between in-phase and anti-phase by counter flag, for subsequent processing in “IPAP 2” mode. The pulse program for α/β 2D correlation is same except α and β pulses are interchanged

To maximize the S/N ratio the repetition rate was 1 s which created the steady state condition with ~10% difference between the slowest relaxing γ 31P signal and the fastest relaxing β 31P signal intensities, resulting in slightly unequal intensities between the α/β and γ/β 2D spectra. Because in these 2D spectra we observe only one cross-peak (α/β or γ/β) just shifted around by 18O-isotope effect, all intensity differences can be accounted for by bringing the β (evolution dimension) sum-projections on the same scale.

2D spectra simulation

Experimental 2D spectra (2rr serial files (of length = 1024×256)) were read into Matlab (MATLAB R2007a; The MathWorks, Inc) and reshaped from a 262,124 words vector into 1024×256 matrix. Out of it, a submatrix (128×128) containing only spectral region of interest (−0.031 to 0.109 ppm from the 31P signal of 18O unlabeled ATP) was selected for further analysis.

The stick spectrum of the same size, was generated by calculating intensities (2) at respective positions (3) applying trial values of the isotopic fractionation factors and chemical shift parameters. The synthetic spectrum is obtained by convoluting the stick spectrum with the parameters from experimental lineshapes. This “stick-spectrum” was first 2D Fourier transformed, multiplied by the same window function as original fid (skewed sine-square), and also multiplied with Gaussian line shape to account for experimental line broadening. Parameters of the skewed sine square were constant while the Gaussian width was varied within the fitting procedure. Thus obtained synthetic fid was 2D Fourier transformed creating the synthetic spectrum of the same size and shape as experimental one. The spectrum was subtracted from the experimental one and point-wise r.m.s.d. were calculated. The statistical analysis and underlying assumptions were analogous to the earlier described procedure for 2D spectra simulations (Schmidt 1997). Using this routine, the best-fit spectrum was obtained by a grid search of the isotopic enrichment factors.

In the first run, a separate grid-search for each fk in steps of 0.005 from 0 to 1 was performed, while keeping all other fk at zero. In all cases a smooth U-shaped first minimum of r.m.s.d. (in going from fk = 0up) was also the global minimum, and changed less than 0.1 in the subsequent refinement. An additional shallower minimum at higher fk was observed only in one case (γp). In the next runs all 6 fractional isotopic enrichments were grid searched jointly in the range of 0.2 around the current best values (with step 0.02). The same was then repeated in the range of 0.1 (step 0.01) and range 0.05 (step 0.005). After each refinement stage, the line widths and spectral positions were also adjusted in a grid search manner. The spectral positions were searched in rather small range (0.005 ppm) justified by the uncertainty of the directly measured experimental positions. On a Linux workstation (HP xw9400) the whole process takes several hours. Inclusion of the small three-bond isotopic shifts were allowed only if the linear regression between calculated and experimental spectral intensities passed the statistical test (only 3 such shifts were significant, Table 1).

Errors of the derived parameters were evaluated by inspection of their profiles along manifold dimensions of the error space. Figure 7 shows two-dimensional fβb error pro-files obtained by a pairwise grid calculation with each of the fk parameters (top and bottom inserts). The middle insert of Fig. 7 shows the one dimensional profile of fβb error in relation to the noise threshold level (set to 3 noise standard deviations), which is also the level of contours in the 2D error plots. The fβb error appears uncorrelated to the errors of the peripheral oxygen isotopic enrichment factors (fαp, fβp, fγp), and correlated with the errors of the bridging oxygen factors (fαb, fγb), as can be expected based on the proximity of the isotopic chemical shifts (Table 1) that cause spectral overlap. The size of error at the threshold contour is much influenced by the level of isotopic enrichment, i.e. for the high fk the error ellipsoids are thinner (Fig. 7, top insert vs. bottom insert). Notably, the width of the error ellipsoids along fβb axis is fairly constant in all cases and adequately represented by the 1D error profile. The half of that width is reported as fβb error in Table 1. The analogous analysis was applied for all parameters.

Fig. 7.

Fig. 7

Open in a new tab

Plot fβb errors obtained by a pair-wise grid calculation with each of the fk parameters (top and bottom inserts). The middle insert shows 1D profile of fβb error in relation to the noise threshold level (set to 3 noise standard deviations), which is also the level of contours in the 2D error plots

Acknowledgments

Supported by the National Institutes of Health, the Marriott Heart Disease Research Program, the Marriott Foundation and Mayo Clinic.

Contributor Information

Nenad Juranić, Email: juranic.nenad@mayo.edu, Department of Biochemistry and Molecular Biology, Mayo Clinic, 200 First Street SW, Rochester, MN 55905, USA.

Emirhan Nemutlu, Division of Cardiovascular Diseases, Department of Medicine, Mayo Clinic, Rochester, MN 55905, USA. Department of Analytical Chemistry, Faculty of Pharmacy, University of Hacettepe, 06100 Ankara, Turkey.

Song Zhang, Division of Cardiovascular Diseases, Department of Medicine, Mayo Clinic, Rochester, MN 55905, USA.

Petras Dzeja, Division of Cardiovascular Diseases, Department of Medicine, Mayo Clinic, Rochester, MN 55905, USA.

Andre Terzic, Division of Cardiovascular Diseases, Department of Medicine, Mayo Clinic, Rochester, MN 55905, USA.

Slobodan Macura, Department of Biochemistry and Molecular Biology, Mayo Clinic, 200 First Street SW, Rochester, MN 55905, USA.

References

  1. Aue WP, Bartholdi E, Ernst RR. 2-dimensional spectrosopy—application to nuclear magnetic resonance. J Chem Phys. 1976;64:2229–2246. [Google Scholar]
  2. Bermel W, Bertini I, Duma L, Felli IC, Emsley L, Pierattelli R, Vasos PR. Complete assignment of heteronuclear protein resonances by protonless NMR spectroscopy. Angewandte Chemie-Int Ed. 2005;44:3089–3092. doi: 10.1002/anie.200461794. [DOI] [PubMed] [Google Scholar]
  3. Bernstein S. Demonstration du theoreme de Weierstrass fondee sur le calcul des probabilities. Comm Soc Math Kharkov. 1912;13:1–2. [Google Scholar]
  4. Bock JL, Cohn M. Metal dependence of the phosphate (oxygen)-water exchange reaction of Escherichia coli alkaline phosohatase. J Biol Chem. 1978;253:4082–4085. [PubMed] [Google Scholar]
  5. Cohn M. 18O and 17O effects on 31P NMR as probe of enzymatic reactions of phosphate compounds. Ann Rev Biophys Bioeng. 1982;1:23–42. doi: 10.1146/annurev.bb.11.060182.000323. [DOI] [PubMed] [Google Scholar]
  6. Cohn M, Hu A. Isotopic (18O) shift in 31P nuclear magnetic resonance applied to a study of enzyme-catalyzed phosphate-phosphate exchange and phosphate (oxygen)-water exchange reactions. Proc Natl Acad Sci USA. 1978;75:200–2003. doi: 10.1073/pnas.75.1.200. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Cohn M, Hu A. Isotopic 18O shifts in 31P NMR of adenosine nucleotides synthesized with 18O in various positions. J Am Chem Soc. 1980;103:913–916. [Google Scholar]
  8. Cohn M, Rao NBD. 31P NMR Studies of Enzymatic Reactions. Bull Magn Reson. 1982;1:38. [Google Scholar]
  9. Dawis SM, Walseth TF, Deeg MA, Heyman RA, Graef RM, Goldberg ND. Adenosine triphosphate utilization rates and metabolic pool sizes in intact cells measured by transfer of 18O from water. Biophys J. 1989;55:79–99. doi: 10.1016/S0006-3495(89)82782-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Dzeja PP, Vitkevicius KT, Redfield MM, Burnett JC, Terzic A. Adenylate kinase-catalyzed phosphotransfer in the myocardium—increased contribution in heart failure. Circ Res. 1999;84:1137–1143. doi: 10.1161/01.res.84.10.1137. [DOI] [PubMed] [Google Scholar]
  11. Hackney DD, Rosen G, Boyer PD. Subunit interaction during catalysis: alternating site cooperativity on phosphorylation shown by substrate modulation of 18O ATP species formation. Proc Natl Acad Sci USA. 1979;76:3646–3650. doi: 10.1073/pnas.76.8.3646. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Lowe G, Sproat BS. Evidence of a dissociative SN1(P) mechanism of phosorhtyl transfer by rabbit muscle pyrvate kinase. J Chem Soc Perkin Trans. 1978;1:1622–1630. [Google Scholar]
  13. Pucar D, Janssen E, Dzeja PP, Juranic N, Macura S, Wieringa B, Terzic A. Compromised energetics in the adenylate kinase AK1 gene knockout heart under metabolic stress. J Biol Chem. 2000;275:41424–41429. doi: 10.1074/jbc.M007903200. [DOI] [PubMed] [Google Scholar]
  14. Pucar D, Dzeja PP, Bast P, Juranic N, Macura S, Terzic A. Cellular energetics in the preconditioned state—Protective role for phosphotransfer reactions captured by O-18-assisted P-31 NMR. Journal of Biological Chemistry. 2001;276:44812–44819. doi: 10.1074/jbc.M104425200. [DOI] [PubMed] [Google Scholar]
  15. Pucar D, Bast P, Gumina RJ, Lim L, Drahl C, Juranic N, Macura S, Janssen E, Wieringa B, Terzic A, Dzeja PP. Adenylate kinase AK1 knockout heart: energetics and functional performance under ischemia-reperfusion. Am J Physiol Heart Circ Physiol. 2002;283:H776–H782. doi: 10.1152/ajpheart.00116.2002. [DOI] [PubMed] [Google Scholar]
  16. Pucar D, Dzeja PP, Bast P, Gumina RJ, Drahl C, Lim L, Juranic N, Macura S, Terzic A. Mapping hypoxia-induced bioenergetic rearrangements and metabolic signaling by O-18-assisted P-31 NMR and H-1 NMR spectroscopy. Mol Cell Biochem. 2004;256:281–289. doi: 10.1023/b:mcbi.0000009875.30308.7a. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Sauer U. Metabolic networks in motion: 13C-based flux analysis. Mol Syst Biol. 2006;2(62):1–10. doi: 10.1038/msb4100109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Schmidt JM. Conformational equilibria in polypeptides.1. Determination of accurate (3)J(HC) coupling constants in antamanide by 2D NMR multiplet simulation. J Magn Reson. 1997;124:298–309. [Google Scholar]
  19. Schneck JL, Briand J, Chen S, Lehr R, McDevitt P, Zhao BG, Smallwood A, Concha N, Oza K, Kirkpatrick R, Yan K, Villa JP, Meek TD, Thrall SH. Kinetic mechanism and rate-limiting steps of focal adhesion kinase-1. Biochemistry. 2010;49:7151–7163. doi: 10.1021/bi100824v. [DOI] [PubMed] [Google Scholar]
  20. Weitzel M, Wiechert W, Noh K. The topology of metabolic isotope labeling networks. BMC Bioinformatics. 2007;8(315):1–27. doi: 10.1186/1471-2105-8-315. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES