SUMMARY
Actin filaments and myosin-II are evolutionarily conserved force generating components of the contractile ring during cytokinesis. Here we show that in budding yeast actin filament depolymerization plays a major role in actomyosin ring constriction. Cofilin mutation or chemically stabilizing actin filaments attenuates actomyosin ring constriction. Deletion of myosin-II motor domain or the myosin regulatory light chain reduced the contraction rate and also the rate of actin depolymerization in the ring. We constructed a quantitative microscopic model of actomyosin ring constriction via filament sliding driven by both actin depolymerization and myosin-II motor activity. Model simulations based on experimental measurements supports the notion that actin depolymerization is the predominant mechanism for ring constriction. The model predicts invariability of total contraction time irrespective of the initial ring size as originally reported for C elegans embryonic cells. This prediction was validated in yeast cells of different sizes due to having different ploidies.
INTRODUCTION
The actomyosin ring is a transient structure built with a network of actin filaments and myosin-II motor proteins required for the generation of force for cytokinesis in animal cells and yeast. The actomyosin ring is assembled during specific phases of mitosis and is precisely positioned to bisect the elongating anaphase spindle such that sister chromosomes are segregated to opposing sides of the cleavage plane (Balasubramanian et al., 2004; Barr and Gruneberg, 2007; Field et al., 1999; Pollard, 2010). Cell cycle kinases activated at mitotic exit signal the initiation of actomyosin ring constriction to drive furrow ingression (Glotzer, 2001; McCollum and Gould, 2001; Pollard, 2010; Wolfe and Gould, 2005; Wolfe et al., 2009; Yoshida et al., 2006). The actomyosin ring disassembles promptly on the completion of furrow closure. Cytokinesis is a key process in development and growth, and impairment of cytokinesis leads to genome instability (Li, 2007; Normand and King, 2010; Storchova and Pellman, 2004). Considerable progress has been made in recent years to understand the regulatory processes and cytoskeletal components required for actomyosin ring assembly and function (Pollard, 2010). However, the basic mechanism of force generation orchestrated by actin filaments and myosin-II has remained elusive.
Inferred from actomyosin force production in striated muscle, it was originally proposed that contractile stress in the actomyosin ring is generated via a “sliding filament” mechanism, in which bipolar myosin motor filaments walk along actin filaments within an organized sarcomere-like arrays (Schroeder, 1975). However, both classical and recent studies have noted important distinctions between cytokinetic structures and muscle sarcomeres. Electron microscopy studies in cultured mammalian cells and fission yeast showed that actin filaments are more isotropically oriented with respect to each other than forming strictly antiparallel arrays (Kamasaki et al., 2007; Mabuchi et al., 1988; Maupin and Pollard, 1986; Sanger and Sanger, 1980; Schroeder, 1973). Furthermore, unlike sarcomeric actomyosin structures, which conserve in mass during cycles of contraction and relaxation, it has been widely observed that actomyosin ring reduces in mass, often manifested as the roughly constant ring width and actin and myosin density as the ring shortens in circumference (Carvalho et al., 2009a; Schroeder, 1972; Wu and Pollard, 2005). Consistent with the constant width and density, previous studies reported a constant contraction speed during cleavage furrow ingression (Carvalho et al., 2009a; Zumdieck et al., 2007a).
Although myosin motor activity is required for cytokinesis in many experimental models, several examples are known where the myosin-II or myosin-II motor activity is not strictly required for cytokinesis (Fang et al., 2010; Gerisch and Weber, 2000; Lord et al., 2005). Particularly relevant to this study, cytokinesis in the budding yeast Sacharomyces cerevisiae involves a ring structure composed of actin filaments and myosin-II (Myo1), and indeed, in euploid strains of both the S288c and W303 backgrounds (two commonly studied genetic backgrounds), myosin-II is essential for cell division (Rancati et al., 2008; Tolliday et al., 2003). Although Myo1 is required for actin assembly in the ring (Bi et al., 1998), surprisingly the motor domain of Myo1 is not required for ring constriction or cytokinesis (Fang et al., 2010; Lord et al., 2005). Myosin-II independent cytokinesis has also been well documented in myosin-II deleted Dictyostelium discoideum cells (De Lozanne and Spudich, 1987; Knecht and Loomis, 1987; Neujahr et al., 1997; Zang et al., 1997). In this system actin filaments and cortexillin, an actin crosslinker, are thought to be important in addition to contributions from microtubules and relaxation of the polar cortex (Simson et al., 1998; Stock et al., 1999; Weber et al., 1999). Considering the differences between species in the extent by which myosin-II is required for cytokinesis, it is unclear whether a common framework can be found to explain the basic force generation mechanism in the actomyosin ring.
A possible conceptual breakthrough is the consideration that, in addition to motor action, filament dynamics in actin bundles may have the ability to generate contractile stress. A recent theoretical paper (Zumdieck et al., 2007a) proposed a macroscopic model combining material exchange with force balance. This model was able to recapitulate the observation of roughly constant contraction speed and constant filament density observed in dividing C. elegans embryos. The authors also proposed microscopic concepts where parallel or antiparallel actin filament configurations could generate force through either myosin-II motor or actin depolymerization in the presence of end-tracking crosslinkers. However, it remained to be tested if actin filament dynamics are indeed crucial for cytokinesis and how such mechanism may be integrated with myosin-II motor activity.
In this study, we build upon the work of Zumdieck et al to propose a quantitative microscopic model accounting for both motor action and filament dynamics to explain the observed properties of the actomyosin ring during budding yeast cytokinesis. We demonstrate, using a combination of model and experimental analyses, that the primary contractile force during budding yeast cytokinesis results from actin depolymerization mediated by cofilin and myosin-II motor activity. Our model also predicts the independence of the contraction time on the initial size of the contractile ring, a phenomenon recently reported in the developing C. elegans embryos (Carvalho et al., 2009a).
RESULTS
Protein dynamics and material balance during actomyosin ring constriction
We measured the rates describing actin dynamics and ring constriction during cytokinesis first in the wild-type S288c budding yeast cells. To visualize actin filaments in the contractile ring and due to the inability to directly tag filamentous actin (Nakano and Mabuchi, 2006), we utilized a probe (iqgCH-GFP), which contains a fragment of Iqg1/Cyk1 (aa 1–446), harboring the actin-binding calponin homology (CH) domain and tagged at the COOH terminus with green fluorescent protein (GFP). The homologous region of Rng2 in fission yeast specifically labels actin filaments in the actomyosin ring but not other actin structures (Takaine et al., 2009). We confirmed that the iqgCH-GFP also specifically labels contractile ring actin in an F-actin dependent manner (Fig.1A and Fig.S1C). To observe Myo1 dynamics, a GFP tag was introduced to the 3’ end of the MYO1 ORF at the genomic locus (Fang et al., 2010; Lister et al., 2006) (Fig.1B). Contraction speed observed with these probes were consistent with those previously observed in wild-type cells (Fang et al., 2010; Lippincott and Li, 1998; Lister et al., 2006; Lord et al., 2005).
Figure 1. Time-lapse imaging of actin and Myo1 ring dynamics in various yeast strains.
(A) Wild-type haploid (wt), cof1-22, Δmlc2 and myo1Δm cells expressing the actin probe iqgCH-GFP and Spc42-mCherry-spindle pole body probe (seen as the two dots near the cell poles).
(B) wt, cof1-22, Δmlc2 and myo1Δm cells expressing Myo1-GFP and Spc42-mCherry. Shown are representative time-lapse images of constricting rings for the actin probe and Myo1-GFP. The images of each montage are 23.6 s apart, and each image represents the temporal average of 6 consecutive frames (3.93 s apart) in the corresponding movie. The first panel in each row shows the the whole-cell image corresponding to the first image of the montage to the right that corresponds to a cropped area around the bud neck. Scale bars are 1µm. See also Movies S1,S2.
Actin and Myo1 ring constricted at a roughly constant speed (Fig.2A and Movie S1A and B). We measured the average fluorescence intensity of iqgCH-GFP or Myo1-GFP in the ring, which reports the relative density of actin filaments or myosin-II density, respectively, during ring constriction. The average intensity of the actin probe moderately decreased as the ring constricted whereas Myo1 density remained roughly constant as previously shown (Haviv et al., 2008) (Fig.1 and 2A). The apparent decline in actin density was not due to photobleaching, as it occurred only during contraction and our method of intensity measurement accounts for photobleaching (see Experimental Procedures).
Figure 2. Quantification of the parameters of actin dynamics in various yeast strains.
(A) Kinetic profile ring diameter (open circles) and protein density (closed circles) changes over time during contraction observed with the actin probe iqgCH-GFP and Myo1-GFP.
(B) Actin ring contraction rate (α) and density loss rates (β) for wt, cof1-22, Δmlc2, myo1Δm. Box range represents the standard error of the mean (SEM); whiskers are the standard deviation; the small square is the mean; and the line inside the box is the median. The p-values above each plot are for comparison with wt.
To compute in vivo parameters of actin dynamics from the above microscopy recording, we started with the material balance equation of Zumdieck et al:
| (1) |
where kp and kd are the rates of actin polymerization and depolymerization respectively and D denotes the ring diameter. The last term on the right describes the change in actin density c due to contraction in absence of filaments polymerization and depolymerization. Neglecting filament polymerization (kp=0) during contraction (see below for justification of this assumption), we arrive at the equation:
| (2) |
where all terms in the equation has a dimension of inverse time (s−1). Introducing the normalized rate of contraction α = −1/ D · (dD/dt) and the normalized rate of density loss β = −1/ c · (dc/dt) into Eq. (2), we obtained
| (3) |
We note that the relation Eq. (3) is valid only for normalized rates that have the same dimension of s−1. The simple relationship of Eq. (3) was used for obtaining actin depolymerization rate from the experimental estimates of α and β (see Experimental Procedures). Eq. (3) also implies that depolymerization contributes to both actin density loss and ring contraction in some proportion, as further explored below.
Effect of myosin-II motor inactivation on ring constriction and actin depolymerization
We next performed measurements to quantify the role of myosin-II motor in actomyosin dynamics during cytokinesis. We generated a yeast strain expressing GFP-tagged Myo1 lacking the motor domain (Myo1Δm-GFP) at the native MYO1 locus. Consistent with the previous finding, the motorless construct rescued the cytokinesis defect of Δmyo1 (Fang et al., 2010) while the strain remained euploid (data not shown). However, the contraction rate α was significantly reduced (by 40%) compared to the wild-type rate, and the actin density loss rate was also slightly reduced (Fig.2B, Movie S2E and F, Table 1). kd estimate based on Eq. (3) found myo1Δm to reduce the actin depolymerization rate by 42%. Mlc2 is the regulatory light chain for the yeast myosin-II expected to be important for Myo1 motor activity (Luo et al., 2004). We tested if Δmlc2 exhibited a similar effect. Indeed, Δmlc2 also significantly reduced the contraction rate and the rate of actin depolymerization (Fig.1, Movie S2C and D, Fig.2B, Table 1). However, unlike the case in fission yeast (see YFP-MYO2 experiments in Stark et al., 2010), an extra copy of MYO1-GFP in budding yeast merely broadened the ring along the bud-mother axis without any increase in Myo1 concentration or alteration of ring contraction dynamics (data not shown). The above results nonetheless suggest that yeast myosin-II motor activity is important for actomyosin ring constriction and actin depolymerization during the constriction process.
Table 1. Experimental and model predicted parameters of actin ring dynamics.
N: number of cells imaged for the experimental values. The model predicted values were averages from 100 simulations. Values are experimental and used in model simulations. The error estimates were S.E.M.
| N | α | β | |||
|---|---|---|---|---|---|
| Experimental | Predicted | Experimental | Predicted | ||
| wt | 38 | 3.3 ± 0.1 | 3.3 ± 0.04 | 1.2 ± 0.2 | 1.5 ± 0.06 |
| wt + DMSO | 14 | 3.5 ± 0.2 | 3.5 ± 0.05 | 1.3 ± 0.4 | 1.6 ± 0.09 |
| wt + Jaspl 100µM | 17 | 2.6 ± 0.1 | 2.8 ± 0.05 | 1.2 ± 0.2 | 1.3 ± 0.08 |
| cof1-22 | 26 | 2.6 ± 0.1 | 2.6 ± 0.04 | 0.8 ± 0.2 | 0.9 ± 0.07 |
| cof1-22 + DMSO | 45 | 3.1 ± 0.2 | 3.4 ± 0.04 | 1.3 ± 0.2 | 0.9 ± 0.01 |
| cof1-22 + Jaspl 100µM | 29 | 1.1 ± 0.1 | 1.2 ± 0.04 | 0.8 ± 0.1 | 0.8 ± 0.01 |
| cof1-22 + Jaspl 100µM | 6 | 0 | 0 | 0 | 0 |
| Δmlc2 | 30 | 2.4 ± 0.1 | 2.6 ± 0.04 | 1.1 ± 0.2 | 1.2 ± 0.06 |
| myo1Δm | 13 | 2.0 ± 0.1 | 1.9 ± 0.03 | 0.6 ± 0.2 | 0.8 ± 0.05 |
| myo1Δm + DMSO | 9 | 2.0 ± 0.1 | 1.9 ± 0.03 | 0.5 ± 0.1 | 1.0 ± 0.04 |
| myo1Δm+ Jaspl 100µM | 16 | 1.6 ± 0.1 | 1.4 ± 0.02 | 0.3 ± 0.2 | 0.6 ± 0.03 |
| myo1Δm+ Jaspl 100µM | 16 | 0 | 0 | 0 | 0 |
Evidence that actin depolymerization is important for actomyosin ring constriction
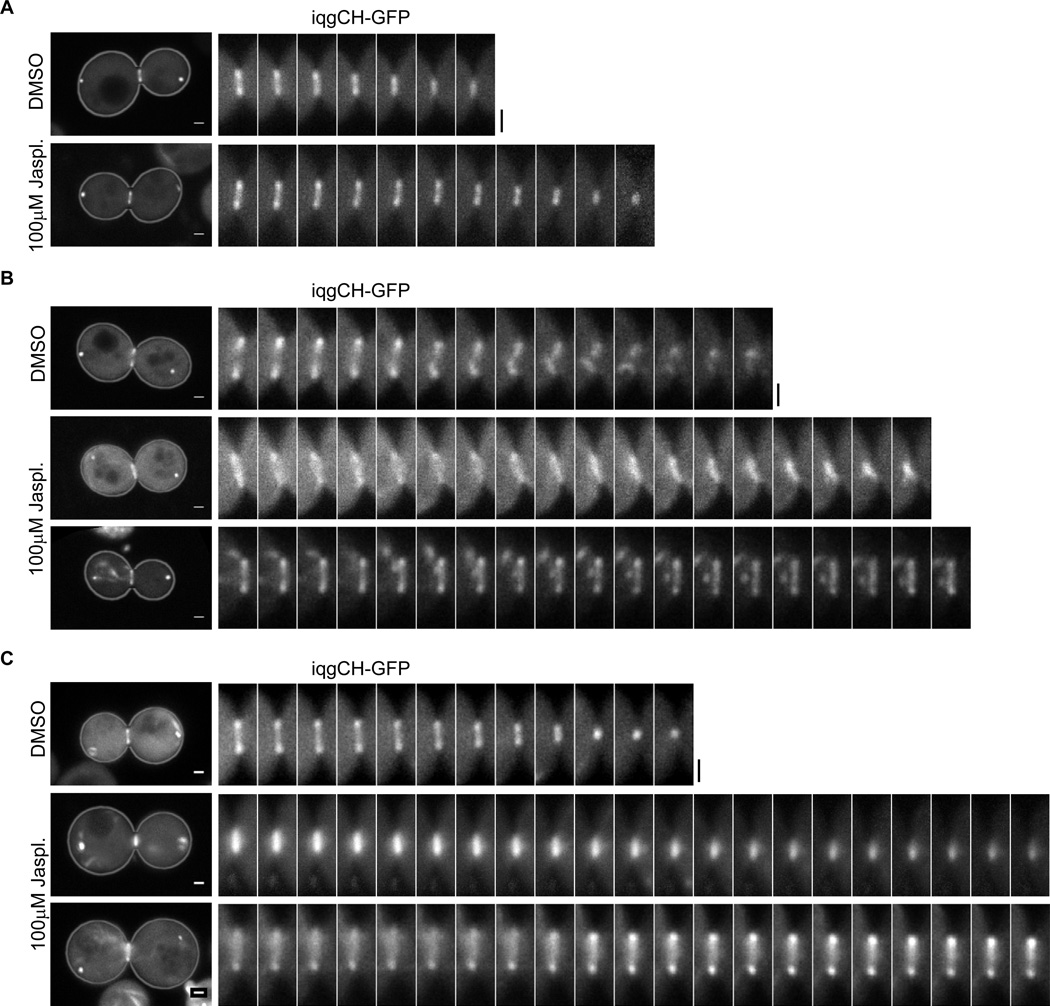
To evaluate the role for actin depolymerization in cytokinesis, we tested the effect of blocking actin depolymerization by the actin stabilizing drug, Jasplakinolide (Ayscough, 2000; Ayscough et al., 1997; Bubb et al., 1994; Bubb et al., 2000; Cramer, 1999; Lee et al., 1998) on actomyosin ring constriction. First, a titration experiment was performed to determine a concentration of Jasplakinolide sufficient to cause a considerable reduction in the rate of actin disassembly in yeast cells without inducing gross disorganization of actin structures (Fig.S1D and Movie S3B). We then imaged actomyosin ring constriction in the presence of this concentration (100µM) of Jasplakinolide. The Jasplakinolide treatment led to a significant decrease (26%) in the contraction rate compared to DMSO-treated cells (Fig.3A, Movie S3, Fig.4A and B, Table 1). Interestingly, the drug had a minimal and insignificant effect on actin density change in the contractile ring compared to the DMSO-treated control (Fig.4C), suggesting that the actin depolymerization blocked by Jasplakinolide (by 21% compared to DMSO control) was quantitatively correlated with the slowdown of ring constriction.
Figure 3. Inhibition of actin depolymerization with Jasplakinolide slows down contraction.
(A) Representative time-lapse sequences of constricting rings in wt cells expressing the actin probe iqgCH-GFP and Spc42-mCherry and treated with DMSO or 100µM of Jasplakinolide.
(B) Representative time-lapse sequences of constricting contractile rings in myo1Δm cell expressing the actin probe iqgCH-GFP and Spc42-mCherry and treated with DMSO or 100µM of Jasplakinolide (bottom two rows). The top montage for the Jasplakinolide-treated cells show a slow contracting ring, representing 16/32 cells observed in this experiment; the bottom montage show a non-contracting ring, representing also 16/32 cells observed (see Movie S4 to observe the movement of the SPBs indicating mitotic exit during the movie).
(C) Representative time-lapse sequences of constricting contractile rings in cof1-22 cell expressing the actin probe iqgCH-GFP and Spc42-mCherry and treated with DMSO or 100µM of Jasplakinolide (bottom two rows). The top montage for the Jasplakinolide-treated cells show a slow contracting ring, representing 29/35 cells observed in this experiment; the bottom montage show a non-contracting ring, representing also 6/35 cells observed (see Movie S5 to observe the movement of the SPBs indicating mitotic exit during the movie). The images of each montage are 39.3 s apart, and each image represents the temporal average of 10 consecutive frames (3.93 s apart) in the corresponding movie. The first panel in each row shows the whole-cell image corresponding to the first image of the montage to the right that corresponds to a cropped area around the bud neck. Scale bars are 1µm. See also Movies S3–S5.
Figure 4. Quantification of actin dynamics in the contractile ring in the presence of Jasplakinolide.
(A) Representative plots of normalized actin ring diameter versus time for wt, myo1Δm, and cof1-22 cells treated with DMSO or 100µM of Jasplakinolide.
(B) and (C) Contraction rate α (B) and protein density loss rate β (C) for wt, myo1Δm, cof1-22 cells treated with DMSO or 100µM of Jasplakinolide. Box plots are as described in Fig.2B legend.
To further investigate the role of actin depolymerization in ring constriction, we tested the effects of a mutation in COF1, encoding cofilin, the main actin depolymerizing factor in yeast (Lappalainen and Drubin, 1997; Moon et al., 1993). cof1-22 was previously shown to impair the actin depolymerization activity of Cof1 in vivo and in vitro (Lappalainen and Drubin, 1997). cof1-22 cells are able to assembly a morphologically normal actomyosin ring. Consistent with the effect of Jasplakinolide, the rate of ring constriction was significantly reduced, while the rate of actin density change in the ring was not significantly altered (Fig.1, Movie S1, Fig.2B, Table 1). Based on Eq. (3), cof1-22 reduced actin depolymerization rate by 25% compared to the wild-type rate, consistent with the moderate effect of the mutant protein on actin depolymerization observed in vitro (Lappalainen and Drubin, 1997). However, this reduction of actin depolymerization rate was accompanied with a similar level of reduction (by 22%) in ring constriction rate (Fig.2B, Table 1), suggesting that the cofilin-mediated actin depolymerization largely contributed to actomyosin ring constriction. We then treated cof1-22 mutant cells with 100 µM Jasplakinolide (to combine the effects of both methods for blocking actin depolymerization). Under this condition, in 6 of the 35 cells imaged actomyosin ring contraction was completely blocked, whereas in the remaining 29 the ring contracted with a drastically reduced rate (by 65% compared to wild type DMSO control) (Fig.3C, Fig.4, Table 1, and Movie S5). These results strongly suggest that actin depolymerization plays a critical role in actomyosin ring contraction.
The synergy between motor action and actin depolymerization in ring constriction
The results above revealed two molecular functions contributing to actomyosin ring contraction in budding yeast, one relying on actin depolymerization while the other requiring the myosin-II motor. These functions are not independent as the latter also affects actin depolymerization during constriction. To examine the synergy between depolymerization and motor action, we tested the effect of 100µM Jasplakinolide on the constriction of Myo1Δm ring. In 16 out of 32 cells examined, Jasplakinolide completely blocked Myo1Δm ring contraction (Fig.3B, Movie S4C), and in the reminder 16, the contraction rate as well as the actin depolymerization rate were severely reduced (Fig.3B, Movie S4A and B, Fig.4, and Table 1). Note that in all the cells imaged, in the absence or presence of the very slow contraction, no build-up of actin density was observed. Treatment of these cells with LatA did not lead to reduced actin density in the ring (Fig.S1E), suggesting that the stable actin density was not due to balanced polymerization and depolymerization. This observation supports the assumption that actin polymerization was negligible during the time of ring constriction. Consistent with this assumption for actin, FRAP experiment suggests that Myo1 does not undergo turnover during the constriction phase (Fig.S1F).
A quantitative model of actomyosin ring contraction
To build a mechanistic framework explaining the experimental observations described above and to allow quantitative predictions of actomyosin ring behavior in the cell, we constructed a bottom-up model for ring contraction starting from a set of microscopic elements and their interactions and computationally predict macroscopic variables such as the rates of contraction and actin density loss in the actomyosin ring. The microscopic elements and our basic assumptions of their interactions are:
The contractile ring is made up of actin filaments, bipolar myosin-II motors, actin depolymerizing protein cofilin, and an actin crosslinker with the possibility to maintain association with shortening filament ends (Fig.5A and Fig.S2A).
Based on the classical assumption of myosin II motor function, Myo1 can slide an actin filament relative to the other in a given filament pair at a single-motor rate of v (in unit of s−1).
A second type of actin sliding can be induced by actin depolymerization, preferentially at or near the pointed end, combined an actin crosslinker (Zumdieck et al., 2007a) (Fig.5A). We introduce the rate k (in unit of s−1) for filament sliding caused by actin depolymerization, and parameter γ, representing the average fraction of time by which a crosslinker is in position to re-attach to the new filament end after a depolymerization event, such as a cut by cofilin (Fig.5A, left column). Thus, γ is essentially the frequency of productive crosslinking to allow depolymerization to cause filament sliding (Fig.5A).
The rate of the motor v is expected to be lower than the rate of depolymerization k, because otherwise there would be a general buildup of density in the ring during contraction, which was not normally observed (Fig.1B). We further estimate v to be roughly k/4 (Supplementary Information, where we also discuss the estimates for v and γ).
For pairs of filaments we consider all possible configurations in regards to filament orientations and positions of the motor and crosslinker. The formula for the combined rate of sliding of one filament (the lower one in each entry of Fig.S2A) with respect to the other (upper) is provided for each case (Fig.S2A). Examples are also shown in Figure 5C.
Figure 5. A quantitative microscopic model for the contraction of the yeast actomyosin ring.
(A) Schematic diagram illustrating an example of productive or non-productive actin depolymerization event (e.g., a cut produced by cofilin) for generating sliding between two actin filaments (long blue arrows). In the former case (left column), thermal fluctuation of the crosslinker and/or actin filament allows the crosslinker to re-attach to the newly produced actin end, and the resulting elastic force could lead to sliding of the lower filament (in the direction marked by the small green arrow) relative to the upper one. In the latter case, actin depolymerization is non-productive in generating filament sliding possibly due to the cut being too far away from the crosslinker (center column) or being between the filament end and the crosslinker (right column). A larger value for the model parameter γ implies that the former scenario occurs at a higher frequency than the latter.
(B) An example of a contractile ring constructed based on the assumptions of the model showing myosin motors (black) and crosslinkers (green) with respect to Fig.S2A. Colored arrows show the clockwise (red) and anticlockwise (blue) filament orientations. See also Movie S6.
(C) Examples of basic filament structures showing myosin motors and crosslinkers in the productive positions and giving formula for displacement rate of the lower filament relative to the upper one. See also Fig.S2A.
(D) Parameter space for the clustering coefficient ζ and crosslinkers activity γ values for which the ratio of the contraction rate α to the actin loss rate β is in the experimentally observed interval 2<α/β<4 for the haploid wt (blue dots) and myo1Δm (red dots) cells. The intersection of the parameter space corresponding to these two genotypes is shown in black. Each dot represents 200 simulations for randomly generated initial filament structures. The inset zooms into the rectangular area bounded by the broken lines and shows similar results in higher resolution (with the step size of 0.02 in both parameters); each dot corresponds to 300 simulations.
(E) Representative simulated contraction curves normalized to the initial ring diameter show roughly linear diameter decrease over time, similar to experimentally observed kinetic profile of contractions (compare with Fig.2A).
(F) and (G) Simulation of ring contraction (E) and actin density loss (F) rates for ζ=0.37 and γ=0.27 for the wild-type, myo1Δm and cof1-22 mutant cells successfully reproduces the contraction rates as experimentally observed (compare to Fig.2B). All computed non-dimensional rates were scaled to the corresponding mean experimental contraction rate α for wt. Box plots are as described in Fig.2B legend.
Having specified the structural components, we consider a relatively simple contractile ring represented by a one-dimensional chain of N actin filaments arranged in a ring (Fig.5B, Movie S6). The initial mean size of each filament is L0 with the standard deviation δL, the mean size of the overlapping region of the adjacent filaments is S0 with the standard deviation δS. Addition of each filament in the computation construction of the ring in general leads to lengthening of the structure. The initial orientations of the filaments are generated by a random process controlled by a clustering coefficient ζ describing filament clustering (grouping of parallel filaments, Supplementary Information). The extreme values of ζ are +1 and −1 and correspond to ordered ring structures, namely, all parallel filaments and filaments with alternating orientations, respectively. The values of ζ far from these extremes correspond to random filament orientations. A key simplification making the computation feasible is that the i-th filament interacts only with two adjacent (i-1)-th and (i+1)-th filaments. After a given time step we compute filament positions as a result of sliding based on the formulas described in Fig.S2A for any given filament configuration. Thus, Fig.S2A was essentially used as a look-up table for each step of the computation (see Supplemental Information for additional details).
Consider several examples of the displacement rate computation using Fig.S2A. The simplest structure is shown as the first example in Fig.5C (top pair). The relative filament positions do not allow any activity of the crosslinkers at the pointed end (tail of the arrows in the illustration), so that only the myosin motor activity can cause the lower filament to move to the right (positive direction) with the speed equal to 2v. A more complex configuration is shown as the structure corresponding to the middle example in Figure 5C, where a myosin motor and a single crosslinker slide the lower filament in same direction relative to the top filament. During the time step Δt the crosslinker is active for γΔt with the rate k, while the myosin motor contributes to the displacement for (1- γ)Δt with the speed v that leads to a shift of the lower filament to the left with the rate γk+(1- γ)v. An even more complex case is the bottom example in Figure 5C showing two crosslinkers competing with a myosin motor. The probability of one crosslinker to be inactive is (1- γ); assuming that they are working independently, we find total probability of both crosslinkers to be inactive as (1- γ)2, and thus the motor-driven displacement rate equal to (1- γ)2v. The contribution of the crosslinkers can be found given that at least one of them is active 1-(1- γ)2 = (2 γ - γ2) fraction of time, leading to a rate of (2 γ - γ2)k. Thus, the total rate of displacement of the lower filament to the left is (1- γ)2v+ (2 γ - γ2)k.
At the end of each time step of a simulation, the length of each filament, the size of the entire filament structure, and the current value of the actin density in the contracting ring were computed. This procedure was repeated until a certain minimal size of the ring was reached. The resulting data allowed us to compute the normalized rate of contraction α by fitting the data to the linear function L(1-αt), where L denotes the initial size of the filament structure. Similarly, the normalized actin density loss rate β was found by fitting of the computed actin density changes to the function C(1- βt), where C is the initial actin density in the ring, which can be estimated as C~ L0/(L0-S0). A real contractile ring can be considered as being composed of many simple contractile rings as modeled above, linked laterally with one another. Thus, the real contraction and density loss rates would be equal to the average rate of contraction for a number of such structures, built and contracting with the same parameters.
To search for reasonable parameter values of γ and ζ, we used the experimental data (Table 1) for two characteristic cases, wild type and Myo1 motor deletion, to compute all possible values of γ and ζ that produce a α/β ratio in the range of 2.0–4.0 as observed. The overlap of the parameter spaces from these two cases gave possible values of γ and ζ (Fig.5D). γ is in the range of 0.25–0.35 that is similar to the estimate given in Supplementary Information, meaning that less than 40% of the depolymerization events need to produce filament sliding. ζ is in the range of 0.2–0.4, representing filament orientations where there are slightly more parallel filaments than random. A direct validation of the model is to use parameter values from different regions of the parameter space to predict the contraction rate α and actin density loss rate β for all cases where these parameters were measured experimentally, given the estimated kd values. Using γ and ζ values of 0.27 and 0.37, respectively, the computed dynamics of ring contraction in wild type showed roughly constant contraction speed, consistent with the experimental observation (compare Fig.5E). The predicted values of α and β, which were non-dimensional, when scaled with the contraction rate α observed for wild type cells, were remarkably consistent with the experimentally measured ones under all conditions (Fig.5F and G, Table 1). The consistency between measured versus predicted α and β values was also observed when γ and γ pairs near the edges of the allowable parameter space were used (Fig.S2B).
It is important to note that our model rules allow both local contraction and expansion on the level of individual filament pairs (Fig.6). The overall contraction (α>0) or expansion (α<0) rate for an arbitrary ring structure can be estimated from averaging all the local contraction/expansion events for individual filament pairs. To examine the effects of various parameters on overall ring contraction or expansion, we estimated α with a large number of random ring structures. The result of this analysis shows positive contraction rate α for a wide range of the filament orientation parameter ζ in the presence of actin depolymerization (k>0) (Fig.6A,C). When the rate of actin depolymerization is zero, the myosin motor activity alone can lead to either contraction or expansion depending on filament orientation and the frequency of crosslinking for the filament configurations shown in Figure S3 (Fig.6B).
Figure 6. Parameter analysis of contraction vs expansion.
Comparison of the contraction rate estimates for different values of the filament orientation factor ζ and crosslinking frequency γ in three cases: both contraction mechanisms are active (A), only myosin motor based contraction mechanism is active (B) and only depolymerization-driven mechanism is active (C). (A) The ring contracts (positive α) with a wide range of filament orientation when both myosin motor and depolymerization-based mechanisms are active (k>0,v>0). An example of the simulated ring dynamics is shown in (D). The red dot in (A) corresponds to the parameter values used in model ring simulation in (D).
(B) When filament sliding is driven solely by myosin motor, the ring can either contract (positive α) or expand (negative α) depending on relative filament orientation and crosslinking efficiency. The green dot in (B) corresponds to the parameter values used in model ring simulation in (E).
(C) When filament sliding is driven solely with depolymerization-based mechanism, the ring always contracts when γ is nonzero.
(D) An example of a simulated contracting ring corresponding to the red dot in (A).
(E) An example of a simulated expanding ring corresponding to the green dot in (B).
A theoretical prediction on the mechanism by which myosin-II drives ring constriction
The observation that deletion of the Myo1 motor domain or MLC2 reduced the rate of actin depolymerization suggested that myosin-II could contribute to ring constriction through two possible mechanisms: 1) the classical motor-driven filament sliding; and 2) actin depolymerization. We used our model to evaluate the relative extent by which Myo1 is likely to drive ring constriction by these two mechanisms. We consider the hypothetical case where Myo1 generates contractile force only through filament sliding without any impact on actin depolymerization. In this hypothetical cell the actin depolymerization-driven sliding (k) would be equal to that in myo1Δm, but the activity of the motor (v) would be preserved as that in the wt cells. Simulation of the model based on this assumption gave the normalized contraction rate in this hypothetical cell αh to be 0.0021 s−1. Considering that the contribution of the motor to actin depolymerization accounts for a contraction rate of αwt − αh, and the total contribution of the motor to the contraction rate is αwt − αΔm, we estimate that 93% of the motor activity contributes to actin depolymerization whereas only 7% contributes to direct filament sliding.
Contraction rate is independent of the initial ring size
Recent observations of actomyosin ring constriction in developing C. elegans early embryos revealed an intriguing invariant property, namely, the contraction time is independent of the cell size (Carvalho et al., 2009a). In other words, the contraction rate (inverse of time in unit of s−1) as we defined here is invariant with respect to different initial ring size. We note that in Carvalho et al. “rate” was used to denote contraction velocity measured in µm·s−1 which scaled with cell size. The authors proposed a mechanism of “structural memory”, referring to a certain precisely defined and spaced contractile units shortening at a constant rate, the number of which scales with cell size. It was speculated that the scaling of contraction velocity with cell size may be an important property of rapidly dividing early embryos where the egg cytoplasm is successively divided during cell cycles of similar time. To test if this phenomenon can be recapitulated by our model, we simulated rings of various initial sizes where larger rings on average contained proportionally large numbers of actin filaments with the same length and overlap distributions. This simulation found that, indeed, the contraction velocity scales with the initial ring size such that the duration of contraction is invariant (Fig.7A).
Figure 7. Actin density and contraction and density loss rates are independent of the initial ring size.
(A) Model simulation of the ring diameter dynamics for ζ=0.37 and γ=0.27 for the wild-type cells with different initial ring diameter showing the contraction time to be independent of the initial ring size.
(B) Representative experimentally observed plots of ring diameter change over time for haploid (red), diploid (green), triploid (purple) and tetraploid (blue) cells. The dashed line shows the minimal size of the diameter below which the measurements are unreliable (see Experimental procedures and Fig.S1).
(C) Kymographs showing Myo1 and actin ring contraction and protein density dynamics for small haploid cells (first row) and large tetraploid cells (second row). The scale bar is 1µm. The total time of the kymograph is 424 s.
(D), (E) and (F) Relative actin density (D, see Experimental procedures), contraction rate α (E), and actin density loss rate β(F) at the neck measured in cells with ploidy range from 1N to 4N (color coding as in B), showing independence of these parameters on the initial ring diameter. The p-value is for comparison of the slope of the linear regression to a zero slope.
To test the above prediction, we investigated the relationship between the contraction rate and initial ring size at the bud neck. Because the natural variation of bud neck size is limited in a wild-type haploid population, we introduced the fluorescent probes into totally congenic diploid (2N), triploid (3N) and tetraploid (4N) strains (Pavelka et al., 2010), as cells of higher ploidy are in general larger in size, including the size of the bud neck, than cells of lower ploidy (Fig.7B–F). Time-lapse measurements of cell ranging from 1N to 4N found that both the contraction rate α and the density loss rate β are invariant across cells with different bud neck diameters (Fig.7E and F). This finding confirmed our model prediction and suggests that the observed invariant contraction rate (or time) irrespective of cell size is an intrinsic property of the actomyosin ring even in a unicellular organism. Interestedly, the initial density of the actin ring was also invariant across the range of bud neck sizes (Fig.7C and D), which would be predicted by invariant L0 and S0.
DISCUSSION
The function of myosin-II during budding yeast cytokinesis
The role of the actomyosin ring and the mechanism by which force is generated to drive its constriction in dividing budding yeast cells have been a subject of considerable debate. The confusion largely stemmed from inconsistent phenotypes of MYO1 gene knockout reported by different labs (Gologorsky et al., 2009; Huh et al., 2003; Mseka and Cramer, 2011; Rancati et al., 2008; Tolliday et al., 2003), and the observation that Myo1 motor domain is not required for ring constriction. In the commonly used yeast strain backgrounds S288c and W303a, MYO1 deletion leads to a nearly complete cytokinesis failure and cell lethality in the euploid genomic background. In S288c, viable Δ myo1 spores with massive growth and cytokinesis defects do occur at low frequencies (Rancati et al., 2008; Tolliday et al., 2003), however, upon further passage, innovation of novel cytokinetic mechanisms, not associated with formation of an actin ring, can be accomplished through aneuploidy (Rancati et al., 2008). Thus, in the experimental model used in our studies (S288c), Myo1 is indeed required for cytokinesis. However, this seems paradoxical with the observation that motor domain deletion could largely rescue the cytokinesis defects of Δmyo1 and the motor-less ring can still constrict (Fang et al., 2010; Lord et al., 2005).
The results in this study helps to resolve the above paradox by demonstrating that actin depolymerization, which occurs in the absence of the Myo1 motor activity, albeit at a slower rate, is a main mechanism for actomyosin ring constriction. Our experimental data and model analysis further indicate that the myosin-II motor plays a role in actin depolymerization, although it is presently unclear whether this role could be direct, given that cofilin and myosin-II binding to actin filaments are mutually exclusive (Galkin et al., 2011). A previous study in mammalian cultured cells also reported that inhibition of myosin-II ATPase activity with blebbistatin prevented actin turnover (Guha et al., 2005). A role for myosin-II in actin network disssembly was demonstrated recently in migrating fish keratocytes (Wilson et al., 2010). Another recent study suggests that tail retraction of migrating fibroblasts is a result of actin depolymerization, and myosin-II facilitates this process by influencing filament alignment (Mseka and Cramer, 2011). Thus, promoting actin depolymerization may be a key function of the non-muscle myosin-II.
Force generation via actin depolymerization
Force generation by depolymerizing cytoskeletal polymers is well known for the microtubule system. For example, microtubule depolymerization at the kinetochore contributes the force for poleward chromosome movement during anaphase (Bouck et al., 2008; Carvalho et al., 2010; Grishchuk et al., 2005; Koshland et al., 1988). During this process the linkage between kinetochore and the shrinking microtubule ends must be dynamically maintained. Actin polymerization and depolymerization have mostly been considered for the generation of protrusive forces via elongation at the barbed ends of filaments, whereas pointed end dynamics have mainly been implicated in actin subunit recycling. The possibility of actin depolymerization to produce contractile stress was recently proposed in a theoretical paper (Zumdieck et al., 2007a) and discussed in (Sun et al., 2010). Our observed effect of inhibition of actin depolymerization on the contraction rate provides the functional support for the idea of contractile force generation through actin depolymerization in the actomyosin ring.
Cofilin (Cof1) is the only essential actin depolymering/severing protein in budding yeast and has been shown to promote rapid actin turnover in cortical actin patches and actin cables (De La Cruz, 2009; Fan et al., 2008; Lappalainen and Drubin, 1997; Moon et al., 1993). Our results show that Cof1 also regulates actin depolymerization in the contractile ring and plays an important role in ring constraction. Although several previous studies have clearly implicated ADF/cofilin in actomyosin ring assembly and/or contraction (Coniglio et al., 2009; Hotulainen et al., 2005; Maldonado et al., 2009; Nakano and Mabuchi, 2006), the precise functional consequence of cofilin-mediated actin depolymerization in cytokinesis has been unclear. Our analysis suggests that cofilin can be a key component of the force generating machinery during cytokinesis. The action of cofilin must be augmented by actin crosslinking in order to generate contractile stress (Zumdieck et al., 2007a). Our model suggests such crosslinker does not need to track depolymerizing actin ends, as long as there is some probability (γ) for re-establishing the crosslinking after filament shortening (Fig. 5A). Iqg1 is a potential candidate for the critical actin crosslinker in our model as it is an actin crosslinker essential for cytokinesis (Carvalho et al., 2009b; Margato et al., 2009). The constant value of γ asummed in the model implies that the crosslinker concentration in the ring should be constant during constriction, which was indeed observed for Iqg1 (data not shown).
A quantitative microscopic model for depolymerization-driven actomyosin ring contraction
The study of actomyosin-based contractile structures in different systems have led to models that consider different types of organization of actin filaments undergoing myosin motor-driven sliding (Carlsson, 2006; Carvalho et al., 2009a; Stachowiak and O'Shaughnessy, 2009; Zemel and Mogilner, 2009; Zumdieck et al., 2007b). The model proposed by Carlsson (Carlsson, 2006) relies on actin turnover to ensure that the action of the motor leads to contraction and predicts that the contraction rate is limited by the rate of actin treadmilling. Another model (Stachowiak and O'Shaughnessy, 2009) is characterized by a specific organization of stress fibers in which active myosin is placed with constant spacing and the polarity of actin filaments alternate periodically along the fiber axis. Both these models assume the myosin motor being the necessary contractile stress generator. The model of Zumdieck et al (2007a) illuminates the possibility of actin depolymerization coupled with filament crosslinking to constitute an alternative driving force for filament sliding. The actin filaments are assumed to undergo treadmilling, which may be consistent with the observation made in fission yeast (Pelham and Chang, 2002).
The bottom-up model, based on microscopic elements of dynamic actin filaments, actin crosslinker and myosin-II motor, allowed us to compute macroscopic parameters describing contraction dynamics to compare with the experimentally measured values. An attractive feature of our model is the lack of requirement for precise filament configuration. Three-dimensional electron microscopy reconstruction of the fission yeast contractile ring at the start or during contraction showed a mixed filament polarity with perhaps a slight bias in one orientation (Kamasaki et al., 2007). The model predicts that indeed no bias in filament orientation is required for the ring contraction (Fig.6), but a small non-zero ζ is needed to obtain the observed rate of the actin loss in the contracting ring.
Our model correctly predicts the independence of contraction rate (or time) on the initial size of the actomyosin ring. This phenomenon was recently reported for early C. elegans embryos undergoing rapid mitotic cleavages (Carvalho et al., 2009a). The observation in yeast suggests that this property is a predictable outcome of an evolutionarily conserved aspect of actomyosin ring mechanics rather than an evolutionary innovation to accomplish precisely timed, consecutive embryonic divisions. In contrast to the model proposed by Carvalho et al, our model does not require spatially separate structural units of a fixed size, but rather, actin filaments can vary randomly in orientation, length and the amount of overlap within the defined distributions. Having overlapping filaments throughout the ring is likely to be important for maintaining its structural integrity during contraction and is also consistent with the EM reconstruction of the fission yeast ring (Kamasaki et al., 2007). Finally, although our model simulation predicts that in budding yeast actin depolymerization is the main mechanism driving actomyosin ring constriction, the model itself does not exclude a direct role for the motor and may thus be generalizable toward systems where filament sliding is more predominantly driven by myosin-II.
EXPERIMENTAL PROCEDURES
Yeast strains and plasmids
Media and genetic techniques were as previously described (Sherman et al., 1974). Yeast strains and plasmid construction are in extended Supplementary Information).
Live imaging and image analysis
3D confocal imaging was accomplished using a Carl Zeiss 510 Meta laser scanning microscope equipped with a Confocor 3 detection unit. This detection unit employs single photon counting avalanche photodiodes which are crucial for highly sensitive and quantitative imaging of contractile ring dynamics in yeast cells with native expression levels. For this study, two general methods were employed. For time-lapse imaging to observe density changes, it was crucial to avoid photo-bleaching. Therefore, the pinhole was set completely open with relatively low laser power and a Carl Zeiss C-Apochromat 40 × 1.2NA water objective was used. Under this condition, no photobleaching was observed in our timelapse movies.
All image processing was done using ImageJ, a free open source Java program from the NIH combined with several custom plugins written in house. For diameter measurements a thick line was drawn through the bud neck parallel to the ring such that the thickness of the line encompassed the observed thickness of the ring (Fig.S1A). A summed and smoothed profile of this region as a function of time represents a kymograph from which the background intensity was subtracted. For each time point profile the maximum intesity value was measured. Then the diameter defined as the profile width at the half maximum level was computed by searching inward from each edge of the profile and then interpolating near the half maximum (Fig.S1B). Because our measurements were near the limit of optical resolution, we measured the distance between the positions of the profile peaks representing the initial ring diameter and compared it to the half maximum width measurement. We found that the difference was roughly 350nm. The end time point of the contraction process for each individual cell measurement was defined as the time when the measured diameter reaches this critical value (see Fig.S1B). The start point of the contraction phase was determined as the start point of the diameter curve’s linear segment (see Fig.2A), which often correlates in time to a sudden inward movement of the spindle pole bodies, labeled with Spc42-mCherry, an event caused by spindle breaking down at mitotic exit. To generate the contraction curves each diameter measurement was normalized to the initial diameter determined as the average of the 10 time points before the start of contraction. The normalized contraction rate was computed in Mathematica (Wolfram Research Inc., Champaign, IL) as the slope of a linear fitting of the diameter profile during the defined contraction window. All images for presentation were adjusted for contrast to clearly show the maximum and minimum intensities. See Supplementary Information for the methods for actin density measurements.
Estimate of α and β
To estimate α and β from experimental measurements of ring diameter and intensity changes over contraction time (e.g. plots in Fig.2A), we used the following approximation:
where the last expression is obtained as the leading one in expansion when α is small. If α is constant, this approximation leads to the constant speed of contraction (measured in µm/s), as observed (Fig.2A), which is equal to α D(0) and scales with the initial ring diameter. Similar reasoning leads to approximated protein density dynamics c(t) = c(0)exp(−β · t) ≈ c(0)(1−β · t). Again, it is important to remind that α and β have the dimension of s−1, not µm/s.
Statistical analysis
Statistical analysis of the data was performed in Mathematica and Excel. The p-values were determined by the Student’s t-test.
Model computation
Model simulations were made using custom code written in Mathematica. The initial orientation, size and position of actin filaments were generated randomly using built-in Mathematica random number generator. The search for model parameters, such as the clustering coefficient ζ and the frequency γ of productive actin depolymerization was made by running, for each parameter set in the range −1<ζ<1 with the step 0.1 and 0<γ<1 with the step 0.05, 200 simulations starting with random initial filament structures, computing the average values of contraction rate α and actin loss rate β. The values of other parameters were selected as follows: initial filament mean size and standard deviation were L0=1 and δL=0.15, respectively, the overlapping mean size and standard deviation were S0=0.75 and δS=0.25, respectively, and initial number of filaments was 20. The depolymerization rate was chosen to be equal to k=0.01 and the myosin motor speed v=0.0025 for the wild type simulation. For the motorless simulation the depolymerization rate was reduced to k=0.0061 and myosin motor speed v was set to zero. To obtain a finer resolution in the sub-region in the parameter space in the range 0.2<ζ, γ<0.4, similar computations were done 300 times for each parameter set with step size of 0.02 in both parameters. In the simulation for the case of cof1-22 mutant the values k=0.0076 and v=0.0025 were used. For the simulations for different initial neck size, N=10, 15, 20 and 25 were used as the initial number of filaments.
Supplementary Material
ACKNOWLEDGEMENT
The authors thank J. Zhu (Stowers Institute) for assistance in strain genotyping; A. Mushegian (Stowers Institute) for supervision of A.K.; E. de Melo (ITQB and University of New Lisbon, Portugal), M. de Sousa, F. Carneiro and J. C. Lopes (GABBA program, Faculty of Medicine, University of Porto, Portugal) for their mentoring to I.M.P. The authors thank the reviewers of this manuscript for the constructive and helpful comments. This work was supported by NIH grant NIH RO1GM059964 to R.L.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Ayscough KR. Endocytosis and the development of cell polarity in yeast require a dynamic F-actin cytoskeleton. Curr Biol. 2000;10:1587–1590. doi: 10.1016/s0960-9822(00)00859-9. [DOI] [PubMed] [Google Scholar]
- Ayscough KR, Stryker J, Pokala N, Sanders M, Crews P, Drubin DG. High rates of actin filament turnover in budding yeast and roles for actin in establishment and maintenance of cell polarity revealed using the actin inhibitor latrunculin-A. J Cell Biol. 1997;137:399–416. doi: 10.1083/jcb.137.2.399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balasubramanian MK, Bi E, Glotzer M. Comparative analysis of cytokinesis in budding yeast, fission yeast and animal cells. Curr Biol. 2004;14:R806–R818. doi: 10.1016/j.cub.2004.09.022. [DOI] [PubMed] [Google Scholar]
- Barr FA, Gruneberg U. Cytokinesis: placing and making the final cut. Cell. 2007;131:847–860. doi: 10.1016/j.cell.2007.11.011. [DOI] [PubMed] [Google Scholar]
- Bi E, Maddox P, Lew DJ, Salmon ED, McMillan JN, Yeh E, Pringle JR. Involvement of an actomyosin contractile ring in Saccharomyces cerevisiae cytokinesis. J Cell Biol. 1998;142:1301–1312. doi: 10.1083/jcb.142.5.1301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouck DC, Joglekar AP, Bloom KS. Design features of a mitotic spindle: balancing tension and compression at a single microtubule kinetochore interface in budding yeast. Annu Rev Genet. 2008;42:335–359. doi: 10.1146/annurev.genet.42.110807.091620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bubb MR, Senderowicz AM, Sausville EA, Duncan KL, Korn ED. Jasplakinolide, a cytotoxic natural product, induces actin polymerization and competitively inhibits the binding of phalloidin to F-actin. J Biol Chem. 1994;269:14869–14871. [PubMed] [Google Scholar]
- Bubb MR, Spector I, Beyer BB, Fosen KM. Effects of jasplakinolide on the kinetics of actin polymerization. An explanation for certain in vivo observations. J Biol Chem. 2000;275:5163–5170. doi: 10.1074/jbc.275.7.5163. [DOI] [PubMed] [Google Scholar]
- Carlsson AE. Contractile stress generation by actomyosin gels. Phys Rev E Stat Nonlin Soft Matter Phys. 2006;74 doi: 10.1103/PhysRevE.74.051912. 051912. [DOI] [PubMed] [Google Scholar]
- Carvalho A, Desai A, Oegema K. Structural memory in the contractile ring makes the duration of cytokinesis independent of cell size. Cell. 2009a;137:926–937. doi: 10.1016/j.cell.2009.03.021. [DOI] [PubMed] [Google Scholar]
- Carvalho FM, Carvalho JP, Maluf FC, Bacchi CE. A new morphological variant of uterine PEComas with sex-cord-like pattern and WT1 expression: more doubts about the existence of uterine PEComas. Ann Diagn Pathol. 2010;14:129–132. doi: 10.1016/j.anndiagpath.2009.06.004. [DOI] [PubMed] [Google Scholar]
- Carvalho PS, Tillitt DE, Zajicek JL, Claunch RA, Honeyfield DC, Fitzsimons JD, Brown SB. Thiamine deficiency effects on the vision and foraging ability of lake trout fry. J Aquat Anim Health. 2009b;21:315–325. doi: 10.1577/H08-025.1. [DOI] [PubMed] [Google Scholar]
- Coniglio I, Garcia-Godoy F, Magni E, Carvalho CA, Ferrari M. Resin cement thickness in oval-shaped canals: oval vs. circular fiber posts in combination with different tips/drills for post space preparation. Am J Dent. 2009;22:290–294. [PubMed] [Google Scholar]
- Cramer LP. Role of actin-filament disassembly in lamellipodium protrusion in motile cells revealed using the drug jasplakinolide. Curr Biol. 1999;9:1095–1105. doi: 10.1016/s0960-9822(99)80478-3. [DOI] [PubMed] [Google Scholar]
- De La Cruz EM. How cofilin severs an actin filament. Biophys Rev. 2009;1:51–59. doi: 10.1007/s12551-009-0008-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Lozanne A, Spudich JA. Disruption of the Dictyostelium myosin heavy chain gene by homologous recombination. Science. 1987;236:1086–1091. doi: 10.1126/science.3576222. [DOI] [PubMed] [Google Scholar]
- Fan X, Martin-Brown S, Florens L, Li R. Intrinsic capability of budding yeast cofilin to promote turnover of tropomyosin-bound actin filaments. PLoS One. 2008;3:e3641. doi: 10.1371/journal.pone.0003641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fang X, Luo J, Nishihama R, Wloka C, Dravis C, Travaglia M, Iwase M, Vallen EA, Bi E. Biphasic targeting and cleavage furrow ingression directed by the tail of a myosin II. J Cell Biol. 2010;191:1333–1350. doi: 10.1083/jcb.201005134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Field C, Li R, Oegema K. Cytokinesis in eukaryotes: a mechanistic comparison. Curr Opin Cell Biol. 1999;11:68–80. doi: 10.1016/s0955-0674(99)80009-x. [DOI] [PubMed] [Google Scholar]
- Galkin VE, Orlova A, Kudryashov DS, Solodukhin A, Reisler E, Schroder GF, Egelman EH. Remodeling of actin filaments by ADF/cofilin proteins. Proc Natl Acad Sci U S A. 2011;108:20568–20572. doi: 10.1073/pnas.1110109108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerisch G, Weber I. Cytokinesis without myosin II. Curr Opin Cell Biol. 2000;12:126–132. doi: 10.1016/s0955-0674(99)00066-6. [DOI] [PubMed] [Google Scholar]
- Glotzer M. Animal cell cytokinesis. Annu Rev Cell Dev Biol. 2001;17:351–386. doi: 10.1146/annurev.cellbio.17.1.351. [DOI] [PubMed] [Google Scholar]
- Gologorsky E, Carvalho EM, Macedo FI, Salerno T. An intraoperative transesophageal echocardiography-guided maneuver to assist the removal of an intraventricular thrombus. Rev Bras Cir Cardiovasc. 2009;24:578–580. doi: 10.1590/s0102-76382009000500022. [DOI] [PubMed] [Google Scholar]
- Grishchuk EL, Molodtsov MI, Ataullakhanov FI, McIntosh JR. Force production by disassembling microtubules. Nature. 2005;438:384–388. doi: 10.1038/nature04132. [DOI] [PubMed] [Google Scholar]
- Guha M, Zhou M, Wang YL. Cortical actin turnover during cytokinesis requires myosin II. Curr Biol. 2005;15:732–736. doi: 10.1016/j.cub.2005.03.042. [DOI] [PubMed] [Google Scholar]
- Haviv L, Gillo D, Backouche F, Bernheim-Groswasser A. A cytoskeletal demolition worker: myosin II acts as an actin depolymerization agent. J Mol Biol. 2008;375:325–330. doi: 10.1016/j.jmb.2007.09.066. [DOI] [PubMed] [Google Scholar]
- Hotulainen P, Paunola E, Vartiainen MK, Lappalainen P. Actin-depolymerizing factor and cofilin-1 play overlapping roles in promoting rapid F-actin depolymerization in mammalian nonmuscle cells. Mol Biol Cell. 2005;16:649–664. doi: 10.1091/mbc.E04-07-0555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huh WK, Falvo JV, Gerke LC, Carroll AS, Howson RW, Weissman JS, O'Shea EK. Global analysis of protein localization in budding yeast. Nature. 2003;425:686–691. doi: 10.1038/nature02026. [DOI] [PubMed] [Google Scholar]
- Kamasaki T, Osumi M, Mabuchi I. Three-dimensional arrangement of F-actin in the contractile ring of fission yeast. J Cell Biol. 2007;178:765–771. doi: 10.1083/jcb.200612018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knecht DA, Loomis WF. Antisense RNA inactivation of myosin heavy chain gene expression in Dictyostelium discoideum. Science. 1987;236:1081–1086. doi: 10.1126/science.3576221. [DOI] [PubMed] [Google Scholar]
- Koshland DE, Mitchison TJ, Kirschner MW. Polewards chromosome movement driven by microtubule depolymerization in vitro. Nature. 1988;331:499–504. doi: 10.1038/331499a0. [DOI] [PubMed] [Google Scholar]
- Lappalainen P, Drubin DG. Cofilin promotes rapid actin filament turnover in vivo. Nature. 1997;388:78–82. doi: 10.1038/40418. [DOI] [PubMed] [Google Scholar]
- Lee E, Shelden EA, Knecht DA. Formation of F-actin aggregates in cells treated with actin stabilizing drugs. Cell Motil Cytoskeleton. 1998;39:122–133. doi: 10.1002/(SICI)1097-0169(1998)39:2<122::AID-CM3>3.0.CO;2-8. [DOI] [PubMed] [Google Scholar]
- Li R. Cytokinesis in development and disease: variations on a common theme. Cell Mol Life Sci. 2007;64:3044–3058. doi: 10.1007/s00018-007-7285-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lippincott J, Li R. Dual function of Cyk2, a cdc15/PSTPIP family protein, in regulating actomyosin ring dynamics and septin distribution. J Cell Biol. 1998;143:1947–1960. doi: 10.1083/jcb.143.7.1947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lister IM, Tolliday NJ, Li R. Characterization of the minimum domain required for targeting budding yeast myosin II to the site of cell division. BMC Biol. 2006;4:19. doi: 10.1186/1741-7007-4-19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lord M, Laves E, Pollard TD. Cytokinesis depends on the motor domains of myosin-II in fission yeast but not in budding yeast. Molecular biology of the cell. 2005;16:5346–5355. doi: 10.1091/mbc.E05-07-0601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo J, Vallen EA, Dravis C, Tcheperegine SE, Drees B, Bi E. Identification and functional analysis of the essential and regulatory light chains of the only type II myosin Myo1p in Saccharomyces cerevisiae. J Cell Biol. 2004;165:843–855. doi: 10.1083/jcb.200401040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mabuchi I, Tsukita S, Sawai T. Cleavage furrow isolated from newt eggs: contraction, organization of the actin filaments, and protein components of the furrow. Proc Natl Acad Sci U S A. 1988;85:5966–5970. doi: 10.1073/pnas.85.16.5966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maldonado J, Pereira T, Fernandes R, Carvalho M. Blood pressure distribution of a sample of healthy Portuguese children and adolescents: the AVELEIRA registry. Rev Port Cardiol. 2009;28:1233–1244. [PubMed] [Google Scholar]
- Margato R, Carvalho S, Ribeiro H, Mateus P, Fontes P, Moreira JI. Cardiac troponin I levels in acute pulmonary embolism. Rev Port Cardiol. 2009;28:1213–1222. [PubMed] [Google Scholar]
- Maupin P, Pollard TD. Arrangement of actin filaments and myosin-like filaments in the contractile ring and of actin-like filaments in the mitotic spindle of dividing HeLa cells. J Ultrastruct Mol Struct Res. 1986;94:92–103. doi: 10.1016/0889-1605(86)90055-8. [DOI] [PubMed] [Google Scholar]
- McCollum D, Gould KL. Timing is everything: regulation of mitotic exit and cytokinesis by the MEN and SIN. Trends Cell Biol. 2001;11:89–95. doi: 10.1016/s0962-8924(00)01901-2. [DOI] [PubMed] [Google Scholar]
- Moon AL, Janmey PA, Louie KA, Drubin DG. Cofilin is an essential component of the yeast cortical cytoskeleton. J Cell Biol. 1993;120:421–435. doi: 10.1083/jcb.120.2.421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mseka T, Cramer LP. Actin depolymerization-based force retracts the cell rear in polarizing and migrating cells. Curr Biol. 2011;21:2085–2091. doi: 10.1016/j.cub.2011.11.006. [DOI] [PubMed] [Google Scholar]
- Nakano K, Mabuchi I. Actin-depolymerizing protein Adf1 is required for formation and maintenance of the contractile ring during cytokinesis in fission yeast. Mol Biol Cell. 2006;17:1933–1945. doi: 10.1091/mbc.E05-09-0900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neujahr R, Heizer C, Gerisch G. Myosin II-independent processes in mitotic cells of Dictyostelium discoideum: redistribution of the nuclei, re-arrangement of the actin system and formation of the cleavage furrow. J Cell Sci. 1997;110(Pt 2):123–137. doi: 10.1242/jcs.110.2.123. [DOI] [PubMed] [Google Scholar]
- Normand G, King RW. Understanding cytokinesis failure. Adv Exp Med Biol. 2010;676:27–55. doi: 10.1007/978-1-4419-6199-0_3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pavelka N, Rancati G, Zhu J, Bradford WD, Saraf A, Florens L, Sanderson BW, Hattem GL, Li R. Aneuploidy confers quantitative proteome changes and phenotypic variation in budding yeast. Nature. 2010;468:321–325. doi: 10.1038/nature09529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pelham RJ, Chang F. Actin dynamics in the contractile ring during cytokinesis in fission yeast. Nature. 2002;419:82–86. doi: 10.1038/nature00999. [DOI] [PubMed] [Google Scholar]
- Pollard TD. Mechanics of cytokinesis in eukaryotes. Curr Opin Cell Biol. 2010;22:50–56. doi: 10.1016/j.ceb.2009.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rancati G, Pavelka N, Fleharty B, Noll A, Trimble R, Walton K, Perera A, Staehling-Hampton K, Seidel CW, Li R. Aneuploidy underlies rapid adaptive evolution of yeast cells deprived of a conserved cytokinesis motor. Cell. 2008;135:879–893. doi: 10.1016/j.cell.2008.09.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanger JM, Sanger JW. Banding and polarity of actin filaments in interphase and cleaving cells. J Cell Biol. 1980;86:568–575. doi: 10.1083/jcb.86.2.568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schroeder TE. The contractile ring. II. Determining its brief existence, volumetric changes, and vital role in cleaving Arbacia eggs. J Cell Biol. 1972;53:419–434. doi: 10.1083/jcb.53.2.419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schroeder TE. Actin in dividing cells: contractile ring filaments bind heavy meromyosin. Proc Natl Acad Sci U S A. 1973;70:1688–1692. doi: 10.1073/pnas.70.6.1688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schroeder TE. Dynamics of the contractile ring. Soc Gen Physiol Ser. 1975;30:305–334. [PubMed] [Google Scholar]
- Simson R, Wallraff E, Faix J, Niewohner J, Gerisch G, Sackmann E. Membrane bending modulus and adhesion energy of wild-type and mutant cells of Dictyostelium lacking talin or cortexillins. Biophys J. 1998;74:514–522. doi: 10.1016/S0006-3495(98)77808-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stachowiak MR, O'Shaughnessy B. Recoil after severing reveals stress fiber contraction mechanisms. Biophys J. 2009;97:462–471. doi: 10.1016/j.bpj.2009.04.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stark BC, Sladewski TE, Pollard LW, Lord M. Tropomyosin and myosin-II cellular levels promote actomyosin ring assembly in fission yeast. Mol Biol Cell. 2010;21:989–1000. doi: 10.1091/mbc.E09-10-0852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stock A, Steinmetz MO, Janmey PA, Aebi U, Gerisch G, Kammerer RA, Weber I, Faix J. Domain analysis of cortexillin I: actin-bundling, PIP(2)-binding and the rescue of cytokinesis. EMBO J. 1999;18:5274–5284. doi: 10.1093/emboj/18.19.5274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storchova Z, Pellman D. From polyploidy to aneuploidy, genome instability and cancer. Nat Rev Mol Cell Biol. 2004;5:45–54. doi: 10.1038/nrm1276. [DOI] [PubMed] [Google Scholar]
- Sun SX, Walcott S, Wolgemuth CW. Cytoskeletal cross-linking and bundling in motor-independent contraction. Current biology : CB. 2010;20:R649–R654. doi: 10.1016/j.cub.2010.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takaine M, Numata O, Nakano K. Fission yeast IQGAP arranges actin filaments into the cytokinetic contractile ring. EMBO J. 2009;28:3117–3131. doi: 10.1038/emboj.2009.252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tolliday N, Pitcher M, Li R. Direct evidence for a critical role of myosin II in budding yeast cytokinesis and the evolvability of new cytokinetic mechanisms in the absence of myosin II. Molecular biology of the cell. 2003;14:798–809. doi: 10.1091/mbc.E02-09-0558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weber I, Gerisch G, Heizer C, Murphy J, Badelt K, Stock A, Schwartz JM, Faix J. Cytokinesis mediated through the recruitment of cortexillins into the cleavage furrow. EMBO J. 1999;18:586–594. doi: 10.1093/emboj/18.3.586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson CA, Tsuchida MA, Allen GM, Barnhart EL, Applegate KT, Yam PT, Ji L, Keren K, Danuser G, Theriot JA. Myosin II contributes to cell-scale actin network treadmilling through network disassembly. Nature. 2010;465:373–377. doi: 10.1038/nature08994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolfe BA, Gould KL. Split decisions: coordinating cytokinesis in yeast. Trends Cell Biol. 2005;15:10–18. doi: 10.1016/j.tcb.2004.11.006. [DOI] [PubMed] [Google Scholar]
- Wolfe BA, Takaki T, Petronczki M, Glotzer M. Polo-like kinase 1 directs assembly of the HsCyk-4 RhoGAP/Ect2 RhoGEF complex to initiate cleavage furrow formation. PLoS Biol. 2009;7 doi: 10.1371/journal.pbio.1000110. e1000110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu JQ, Pollard TD. Counting cytokinesis proteins globally and locally in fission yeast. Science. 2005;310:310–314. doi: 10.1126/science.1113230. [DOI] [PubMed] [Google Scholar]
- Yoshida S, Kono K, Lowery DM, Bartolini S, Yaffe MB, Ohya Y, Pellman D. Polo-like kinase Cdc5 controls the local activation of Rho1 to promote cytokinesis. Science. 2006;313:108–111. doi: 10.1126/science.1126747. [DOI] [PubMed] [Google Scholar]
- Zang JH, Cavet G, Sabry JH, Wagner P, Moores SL, Spudich JA. On the role of myosin-II in cytokinesis: division of Dictyostelium cells under adhesive and nonadhesive conditions. Mol Biol Cell. 1997;8:2617–2629. doi: 10.1091/mbc.8.12.2617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zemel A, Mogilner A. Motor-induced sliding of microtubule and actin bundles. Phys Chem Chem Phys. 2009;11:4821–4833. doi: 10.1039/b818482h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zumdieck A, Kruse K, Bringmann H, Hyman AA, Julicher F. Stress generation and filament turnover during actin ring constriction. PLoS One. 2007;2:e696. doi: 10.1371/journal.pone.0000696. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.