Abstract
Background
Selecting controls that match cases on risk factors for the outcome is a pervasive practice in biomarker research studies. Yet, such matching biases estimates of biomarker prediction performance. The magnitudes of bias are unknown.
Methods
We examined the prediction performance of biomarkers and improvements in prediction gained by adding biomarkers to risk factor information. Data simulated from bivariate normal statistical models and data from a study to identify critically ill patients were used. We compared true performance with that estimated from case-control studies that do or do not use matching. Receiver operating characteristic curves quantified performance. We propose a new statistical method to estimate prediction performance from matched studies when data on the matching factors are available for subjects in the population.
Results
Performance estimated with standard analyses can be grossly biased by matching especially when biomarkers are highly correlated with matching risk factors. In our studies, the performance of the biomarker alone was underestimated while the improvement in performance gained by adding the marker to risk factors was overestimated by 2 to 10 fold. We found examples where the relative ranking of two biomarkers for prediction was inappropriately reversed by use of a matched design. The new approach to estimation corrected for bias in matched studies.
Conclusions
To properly gauge prediction performance in the population or the improvement gained by adding a biomarker to known risk factors, matched case-control studies must be supplemented with risk factor information from the population and must be analyzed with nonstandard statistical methods.
Keywords: design, diagnosis, prediction, prognosis, receiver operating characteristic curve
Introduction
Studies to evaluate biomarkers for use in diagnostic and prognostic settings often choose controls that are matched to cases in regards to risk factors for the outcome. For example, since age is a strong risk factor for cancer, studies to evaluate biomarkers for early detection of cancer usually select controls that have the same ages as the cases [1-7]. The rationale is straightforward: if the biomarker distribution is different in cases versus controls, it cannot be attributed to age differences in an age-matched study. In contrast, in an unmatched study where cases are older than controls, one would expect biomarker values to differ between cases and controls if the biomarker simply varies with age. Prostate specific antigen (PSA) is an example of a biomarker that is typically higher in older subjects. Consequently many studies of biomarkers for prostate cancer have employed age-matched controls [8].
Although matching is commonly used in the design of biomarker studies, it is not widely appreciated that the practice of matching severely limits the questions that can be addressed [9]. One cannot assess the classification performance of the biomarker in the general population using only data from a matched study. Neither can one quantify the improvement in performance that can be gained by addition of the biomarker to data on risk factors if the study has matched on risk factors. For example, relative to use of age alone, the improvement in prediction of prostate cancer risk that is gained by knowledge of PSA concentrations cannot be assessed by a case-control study in which controls are age-matched to prostate cancer cases. We emphasize that the problem with matching has to do with quantifying performance. With matched designs one can determine if there is some association between the marker and the outcome but one cannot evaluate how well the marker performs as a classifier.
In this paper we investigate the degree to which a matched study can mislead about the performance of the biomarker when applied to the general population. We also describe a modified analysis approach that provides corrected estimates. The method requires data on the distributions of risk factors used for matching in the cohort from which the cases and matched controls were drawn. These data items should be readily available when a well-designed case-control study is performed [10].
Methods
We generated biomarker and clinical risk factor data using simulation models. In each simulation scenario the true performances of the biomarker alone, risk factors alone and of the combination of the biomarker and risk factors were quantified with receiver operating characteristic (ROC) curves. We then generated a matched case-control study drawn from the cohort and evaluated biomarker performance with those data. For most of our investigations we used very large sample sizes so that the distortions caused by matching could be calculated exactly without sampling variability that is inherent to studies with moderate sample sizes. We also conducted analyses with moderate sample sizes.
Data for bivariate binormal scenarios
Let X denote the baseline risk factor variables, Y the biomarker and D the binary outcome with D=1 for a case and D=0 for a control. For a population of N=1,000,000 subjects we generated D with probability D=1 being 10%. For controls, (X,Y) were generated as bivariate normal with means (0,0), standard deviations (1,1) and correlation ρ = 0.1, 0.5 or 0.9. For cases, (X,Y) were bivariate normal with the same standard deviations and correlation as for controls but with means (μX, μY), where μX>0 and μY>0. In this scenario, the magnitude of μX determines the performance of X alone and μY determines the performance of Y alone. For example, the area under the ROC curve for X is where Φ is the standard normal cumulative distribution function, and the true positive rate corresponding to the threshold that allows a false positive rate f, denoted by ROCX(f), is ROCX(f)= Φ(μX+ Φ−1(f)). We fixed ROCX(0.2) (and ROCY(0.2) ) and used the corresponding values of μX (and μY) to generate data. For example, in Figure 1 we wanted a setting where ROC(0.2)=0.64 for X alone and for Y alone so we used values μX = μY=1.19 because the associated value of ROC(0.2)= Φ(μ+ Φ−1(0.2)) is 0.64.We selected 20,000 cases at random. For the ‘unmatched controls’ analyses we selected 20,000 controls at random from the population. For the ‘matched controls’ analyses we generated a matched control for each of the 20,000 cases. Specifically, with Xi the clinical risk factor predictor for the ith case, we selected a random control with the same value of X= Xi as the case. Technically we implemented this by generating the matched control’s biomarker, Yi, from the conditional distribution of Y given X=Xi and D=0, i.e. as a normal variable with mean = ρ × Xi and standard deviation = √(1-ρ2) where ρ is the correlation between X and Y.
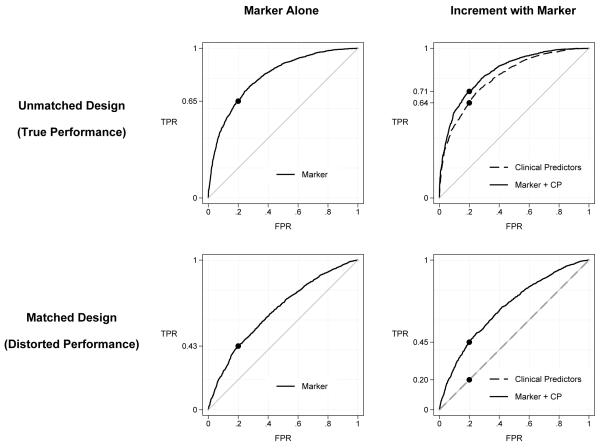
Figure 1.
ROC curves calculated with data from cases and unmatched controls and from a study where controls are selected to match cases in regards to clinical risk factor predictors (CP). Data for n=2000 cases and controls were simulated from bivariate binormal models corresponding to the scenario in Table 1 with ROCX(0.2)= ROCY(0.2)=0.64 and correlation=0.5.
To demonstrate that the magnitude of bias can affect conclusions drawn in studies with moderate sample sizes, we generated datasets with 100 cases and 100 controls rather than 20,000 cases and 20,000 controls.
We implemented two sets of simulations to investigate if matching can distort comparisons between markers. In the first scenario, where we compared markers YA and YB used on their own, (X,YA,YB) is multivariate normal in controls with means(0,0,0) and standard deviations (1,1,1) and correlation(X,YA)=0.7, correlation(X,YB)=0.1 and correlation (YA,YB)=0. In cases the means are (1.19, 1.19, 0.8) and the standard deviations and correlations are the same as in controls. In the second scenario, where we compared the incremental values of markers YA and YB over use of X alone, (X,YA,YB) is standard multivariate normal in controls. In cases (X,YA,YB) is multivariate normal with means(1,1,1), standard deviations (1,1,1) and correlation(X,YA)=0.1, correlation(X,YB)=0.7 and correlation(YA,YB)=0.
Data for predicting critical illness
We investigated the impact of matching controls to cases in the context of a study to identify patients in need of critical care services who undergo care in the prehospital setting (e.g. ambulance). We used a validation dataset of 57,647 patients from a population-based cohort study of an emergency medical services (EMS) system in King County, Washington. Methods and results of this study have been published [11]. In brief, the study developed a prediction model for critical illness in non-trauma non-cardiac-arrest adult patients transported to a hospital by EMS from 2002 through 2006. Critical illness was defined as severe sepsis, delivery of mechanical ventilation, or death during hospitalization. Predictors of risk in the model included older age, male gender, lower systolic blood pressure, abnormal respiratory rate, lower Glasgow Coma Scale, lower pulse oximetry and residence in a nursing home. Studies investigating biomarkers for use in this clinical context are ongoing but data are not yet available. We simulated a predictive biomarker informed by characteristics of whole blood lactate, which is a strong candidate biomarker [12-14]. Specifically we generated the marker as a log-normal variable with (mean, standard deviation) equal to (4.0, 2.6) and uncorrelated with risk factors in the 3121 patients with critical illness and equal to (2.5, 2.0) and uncorrelated with risk factors in the 54,526 controls without critical illness. Because of their common association with outcome, the biomarker and risk factors are correlated in the population that combines cases and controls. The log transformed marker was used in data analysis [15].
All 3121 cases that developed critical illness were included in data analyses. We generated a dataset of unmatched controls in which 3121 non-critical illness encounters were selected at random from the 54,526 available controls. For the ‘matched controls’ dataset, we selected controls who, on the basis of the clinical predictors alone, would be considered at similar risk of critical illness as the cases. Specifically, we adopted the risk score categories defined previously for these data [11], collapsing categories ≥5 into a single category. For each case, we selected a control at random from the same risk category as the case. Sampling was done without replacement in all categories but the highest where the number of controls available (n=247) was less than the number of cases (n=261). Sampling with replacement was used for this category.
Standard data analyses
We fit standard unconditional logistic regression models to derive linear combinations of risk factor predictors (denoted by X) and the biomarker (Y) [26]. Unconditional logistic regression is appropriate for the settings considered in this paper where data are frequency matched on explicit variables that can be included in the logistic model [27, chapter 6]. ROC curves were estimated empirically from the case-control data for X alone, for Y alone, and for the linear combination. These analyses were carried out separately for the cases and unmatched controls dataset and for the cases and matched controls dataset. We calculated the empirical AUC statistic for each ROC curve in addition to the ROC(0.2) statistic, which is the true positive rate corresponding to the threshold that allows a false positive rate of 0.2.
These analysis procedures were carried out for the bivariate binormal and critical illness datasets. In addition, confidence intervals were constructed and statistical tests were performed using bootstrap resampling methods for the smaller bivariate binormal dataset that included 100 cases and controls using the Stata software package [16].
Bootstrapping involved resampling separately from case and control subgroups and refitting the logistic regression models to derive the combination of X and Y in each resampled dataset. P-values were calculated with the Wald test using the bootstrap standard error estimate. We note recent concerns about the validity of P-values when testing for performance improvement [17,18] with changes in AUC or other metrics. By refitting the models we greatly improve performance of the P-values but further improvements are still warranted [19].
Analyzing cohort and matched case-control data together
In the Supplementary Data we describe in detail methods for combining cohort data on the matching factors with the matched case-control data to arrive at bias corrected estimates of ROC curves. Briefly, since ROC curves are derived from the case and control distributions of Y, the key task is to estimate the distribution of Y in the population of controls, which is distorted in the matched set by selecting controls matched to cases on X. This is accomplished by using the distribution of X for controls in the cohort to reweight the controls in the matched set. The ROC curve for the combination of (X,Y) requires the additional step of adjusting the combination derived from the matched set for associations between X and D in the population that are nullified by matching the controls to the cases on X.
Results
Bivariate binormal scenarios
For data simulated from a bivariate binormal model, performances of the marker and the clinical risk factor variables are displayed in Figure 1. The true performances of the marker in the population are shown in the upper panels. These are also the values that are estimated from an unmatched study. We see that use of the marker on its own provides good prediction performance (upper left panel). For example, the AUC is 0.80 and when the threshold is chosen so that 20% of controls are allowed to be biomarker positive, 64% of cases are detected (i.e. ROC(0.2)=0.64). In the matched study however, performance appears to be much less (lower left panel), with AUC=0.66 and only 40% of cases detected, ROC(0.2)=0.40. See the first column of Table 1 for a range of other scenarios. Biomarker performance is severely underestimated in the matched study when standard simple estimation methods are used. We see from the first two columns of Table 1 that the bias is most severe when the marker is highly correlated with the matching factor (ρ=0.9) and less so when the correlation is small (P=0.1). Note that, by definition, if the marker is uncorrelated with the matching factor, matching has no effect on the marker distribution of selected controls and no bias results from matching.
Table 1.
Performance calculated from simulated bivariate-binormal data with unmatched designs that choose controls randomly or with matched designs choosing controls to match cases on risk factors. Shown are proportions of cases detected when the biomarker threshold allows 20% of controls to be positive, i.e. ROC (0.20) are displayed. AUC values are shown in the lower panel.
| Controls | Marker | % Biasc | Risk Factors |
Combination | Combination vs. Risk Factors |
% Biasc,d | Corrb |
|---|---|---|---|---|---|---|---|
| ROC(0.2) | |||||||
| Unmatcheda | 0.64 | — | 0.64 | 0.78 | 0.14 | — | 0.1 |
| Matched | 0.59 | −7.8 | 0.20 | 0.59 | 0.39 | 179.6 | 0.1 |
| Unmatched | 0.64 | — | 0.64 | 0.70 | 0.06 | — | 0.5 |
| Matched | 0.40 | −37.5 | 0.20 | 0.44 | 0.24 | 300.0 | 0.5 |
| Unmatched | 0.63 | — | 0.63 | 0.64 | 0.007 | — | 0.9 |
| Matched | 0.24 | −61.9 | 0.20 | 0.29 | 0.090 | >1000.0 | 0.9 |
| Unmatched | 0.31 | — | 0.31 | 0.36 | 0.05 | — | 0.1 |
| Matched | 0.30 | −3.2 | 0.20 | 0.30 | 0.10 | 100.0 | 0.1 |
| Unmatched | 0.31 | — | 0.31 | 0.33 | 0.02 | — | 0.5 |
| Matched | 0.26 | −16.1 | 0.20 | 0.26 | 0.06 | 200.0 | 0.5 |
| Unmatched | 0.31 | — | 0.31 | 0.31 | 0.00 | — | 0.9 |
| Matched | 0.21 | −32.2 | 0.20 | 0.22 | 0.02 | >1000.0 | 0.9 |
| AUC | |||||||
| Unmatched | 0.801 | — | 0.800 | 0.873 | 0.073 | — | 0.1 |
| Matched | 0.775 | −3.2 | 0.500 | 0.776 | 0.276 | 278.1 | 0.1 |
| Unmatched | 0.800 | — | 0.802 | 0.836 | 0.033 | — | 0.5 |
| Matched | 0.660 | −17.5 | 0.500 | 0.683 | 0.183 | 454.5 | 0.5 |
| Unmatched | 0.799 | — | 0.799 | 0.805 | 0.006 | — | 0.9 |
| Matched | 0.535 | −33.0 | 0.500 | 0.578 | 0.078 | 1200.0 | 0.9 |
| Unmatched | 0.599 | — | 0.595 | 0.630 | 0.035 | — | 0.1 |
| Matched | 0.589 | −1.7 | 0.500 | 0.589 | 0.089 | 154.3 | 0.1 |
| Unmatched | 0.598 | — | 0.590 | 0.609 | 0.019 | — | 0.5 |
| Matched | 0.550 | −8.0 | 0.500 | 0.559 | 0.059 | 210.5 | 0.5 |
| Unmatched | 0.599 | — | 0.599 | 0.601 | 0.002 | — | 0.9 |
| Matched | 0.509 | −15.0 | 0.500 | 0.523 | 0.023 | 1050.0 | 0.9 |
unmatched random controls studies give true performance
correlation between X and Y in cases and in controls
100× (matched-unmatched)/unmatched
percent bias in the performance increment: (combination-risk factors)
The performance of the marker in the population may be partly attributed to its association with risk factors that are themselves associated with the outcome. How much does the marker add to the information already contained in the clinical data? This question concerning incremental value of the marker is best addressed by comparing the ROC curve for the combination of the marker and clinical risk factor variables with that for the clinical variables alone [20]. See the upper right panel of Figure 1 for an example where by adding the marker we only increase the proportion of cases detected by 6%, from 64% with the clinical predictors alone to 70% when the marker is added to them. The incremental value of the marker is small in the scenario of Figure 1. In the lower right panel of Figure 1 we see the ROC curves expected if controls are selected to exactly match the cases in regards to the clinical variables. The clinical variables on their own are completely uninformative in the matched study, a simple consequence of the design that chooses controls with the same clinical risk factor values as the cases. We see that the difference between the ROC curve for the marker combined with risk factors and the ROC curve for the clinical risk factors alone is much larger in the matched study than in the population. For example, again setting thresholds to allow 20% of controls positive, the case detection rate with the combination is 44% and when compared with that for the clinical predictors alone (20%), we see the improvement appears to be 24%. This is much larger than the actual increment in performance in the population, namely 6%. The apparent change in the AUC with addition of the marker is 0.183 in the matched study compared with the true value of 0.033. Therefore the apparent increment in performance due to the marker is severely biased by matching, this time towards over-estimation of performance. Table 1 shows numerical results for a variety of other scenarios in the column labeled ‘Combination versus Risk Factors’. In all the scenarios we studied, increments calculated from matched studies were many times larger than the true increments, ranging from 2 to more than 10 times larger than those observed in unmatched studies. The bias was more severe when the marker was highly correlated with risk factors (Table 1, column 6).
We used very large sample sizes in the simulated studies reported in Table 1 and Figure 1 in order to quantify the expected magnitudes of bias. Real studies with moderate samples have the additional issue of variability that may or may not overwhelm the biases. Figure 2 shows results for a simulated study from the same scenario as Figure 1 but with only 100 cases and 100 random or matched controls included.
Figure 2.
ROC curves calculated with data from cases and unmatched controls and from a study where controls are selected to match cases in regards to clinical risk factor predictors (CP). Data for n=100 cases and controls were simulated from bivariate binormal models corresponding to the scenario in Figure 1.
We found that for the biomarker alone (Figure 2 left panels) with random unmatched controls we estimated AUC = 0.76 (95%CI=(0.69,0.83)) and ROC(0.2)=0.53 (95%CI=(0.43,0.74)) while with matched controls AUC= 0.64 (95%CI=(0.56,0.71)) and ROC(0.2)=0.35 (95%CI=(0.23,0.49)). The downward bias in the matched data estimates resulted in confidence intervals that do not contain the true values (AUC=0.80, ROC(0.2)=0.64). This contrasts with the unmatched study estimates that do contain the true values. Moreover, the confidence intervals for the matched study barely overlap with those for the unmatched study.
Considering the increment in performance gained with the biomarker (Figure 2 right panels), with unmatched data we found that the change in the AUC is 0.019 and non-significant (P=0.12) while with matched data the estimated change in the AUC is much larger and statistically significant, AUC=0.17 (P =0.003). Similarly, we found that the change in the proportion of cases detected, ROC(0.2), is only 6% (P =0.36) with unmatched data but much inflated, 19% (P =0.08) with matched data. Substantially different conclusions are drawn about the magnitude and statistical significance of the marker in the matched and unmatched studies.
Predictors of critical illness
In the dataset concerning predictors of critical illness the performance of the biomarker alone is not biased by matching. The explanation is that the biomarker is uncorrelated with the matching factors among controls in this particular setting, so matching does not distort the distribution of the marker in study controls. However, the ROC curves for the risk factors and for the combination of marker with risk factors are biased by matching. In particular the true proportion of cases detected at threshold allowing 20% of controls positive is 67% without the marker and 75% with the marker, a gain of 8% in the detection rate. In the matched analysis, however, the apparent gain is much larger, 19% (Table 2, Figure 3). Similarly, the improvement in the AUC is 0.05 with use of the marker in the population, but the matched study indicates an improvement of 0.14, almost 3 times the true value. Note that the clinical predictors are somewhat predictive in this matched study, in contrast to results for the bivariate binormal setting. The reason is that we used a categorized score for selecting the matched controls here. Since we did not match controls exactly to cases on the values of the clinical risk factors, there is some residual predictive information in the risk factors even after matching.
Table 2.
Performance gained by the marker beyond baseline clinical variables in predicting critical illness. Shown are performance measures calculated with random unmatched controls and with controls that match to cases on quintile of baseline risk. Also shown are values calculated with use of data on matching variables in the cohort from which cases and controls were drawn in addition to the matched case-control dataset.
| TPR at FPR=0.2 | AUC | |||||
|---|---|---|---|---|---|---|
| Random Controls |
Matched Controls |
Cohort + Matched |
Random Controls |
Matched Controls |
Cohort + Matched |
|
| Clinical Predictors | 0.667 | 0.342 | 0.667 | 0.807 | 0.627 | 0.803 |
| Marker | 0.491 | 0.498 | 0.499 | 0.737 | 0.740 | 0.744 |
| CPa + Marker | 0.748 | 0.536 | 0.744 | 0.859 | 0.764 | 0.858 |
| Combination vs. CP | 0.081 | 0.194 | 0.077 | 0.052 | 0.137 | 0.055 |
CP: Clinical predictors
Figure 3.
ROC curves for critical illness calculated using the clinical predictors alone (CP), the marker alone or using the marker and clinical predictors combined (CP+marker).
We implemented our proposed methodology for calculating bias corrected ROC curves from matched studies when cohort data on the matching variable is available. Results are summarized in Table 2. We found that the curves were indistinguishable from those calculated with random unmatched controls (Supplemental Data Figure 1).
Comparisons between markers
Turning now to possible effects of matching on comparisons between markers we illustrate in the left panels of Figure 4 an example where in unmatched data (and in the population) the ROC curve for marker A is higher than for marker B but the reverse holds when controls are chosen to match cases on risk factors. In a second example (right panels of Figure 4) the combination of marker A and risk factor variables has a higher ROC curve than that of the combination of marker B and risk factor variables but again the reverse holds when controls are chosen to match cases.
Figure 4.
Comparison of markers in unmatched and matched studies. Left panels show performances of markers alone. Right panels show incremental value, i.e. performance of each marker combined with clinical predictors versus clinical predictors alone. The better marker is marker A in each scenario but it appears worse than marker B in a matched study.
Discussion
We have demonstrated here that simple analyses of matched data can give grossly biased impressions of a biomarker’s capacity for prediction or classification. When the biomarker was positively associated with risk factors and with outcome, the apparent performance of the biomarker on its own was generally deflated in a matched study compared with its true performance while the biomarker’s capacity to improve upon existing clinical predictors appeared to be inflated in matched studies. Biases were largest when the biomarker was most strongly correlated with the matching factors. Although the fact that matching leads to biased results has been mentioned previously [9], it is not widely appreciated amongst researchers and the magnitude of bias has not been investigated.
We focused on two commonly used measures of prediction performance: the case detection rate when the marker positivity threshold is fixed by setting a criterion on the false positive rate and the area under the ROC curve. Qualitatively similar results were found for other measures of prediction performance [21] including the Net Reclassification Index [22], the integrated discrimination improvement statistic [22] and the improvement in Net Benefit [23].
We observed (Figure 4) that these biases have consequences not only for evaluating a single biomarker, but also, potentially, for comparing biomarkers and for selecting biomarker combinations. The fact that matching can distort the rank order of markers for their prediction capacity raises concerns especially for discovery studies. In particular, discovery studies typically rank biomarkers according to their apparent performance with the goal of selecting the best performing markers to go forward for validation. It is possible that we are not selecting markers with the best prediction capacity or the best potential for improving upon existing risk factors when we use matched designs and standard analyses. This possibility should be investigated further in real datasets.
We proposed modified analysis methods that correct for biases caused by matching. Additional data on the distribution of the matching factors in the population is required for these analyses. Such data should be available when good principles of study design are employed in constructing the case-control study. For a good case-control design, a cohort representing the clinical setting of interest is identified and cases and controls are selected from that cohort [10, 24]. For matched case-control designs, one selects controls from that cohort who have the same matching variable values as the corresponding case. Therefore the supplementary data that is needed for the modified analysis, namely matching variable data on all subjects in the cohort, should be readily available if the matched study is conducted appropriately. However, many studies are done by selecting controls from a different population than the cases, and consequently the distribution of the risk factors in that population is not relevant or useful for correcting the bias. We and others have noted that studies that employ controls from a different population or clinical setting from which the cases are drawn are subject to many biases [10]. Our results here indicate that matching on known risk factors is not a means to eliminate bias in gauging the magnitude of a biomarker’s performance or the magnitude of its potential for improving performance over those risk factors.
Our results are directed at estimation of the magnitude of a biomarker’s prediction performance. We have shown that matching can lead to bias in the magnitude of estimated prediction performance when standard analysis methods are used. However, matching is not problematic when the focus is on the narrower question of assessing associations. In particular, matching is not a problem if one simply wants to determine if any association exists between the marker and outcome that is not due to risk factors. Neither is matching a problem if the intent is to examine performance within subpopulations defined by the risk factors. In fact, matching is known to be an efficient design strategy for evaluating subpopulation-specific ROC curves [9]. Furthermore, standard methods for estimating risk factor adjusted odds ratios for a biomarker apply to matched data and again, matching is an efficient design for this purpose [25]. However our concern is not with simply estimating associations. We are interested in estimating prediction performance metrics that depend on the distributions of the risk factors and biomarkers in the population in addition to their associations with outcome. We have shown here that matching invalidates the usual analysis methods for estimating prediction performance measures.
Although matching invalidates estimates derived using standard methods, we have developed bias correcting methods to estimate prediction performance measures if cohort data on matching factors are available. Therefore when cohort data on matching factors are available, we have the choice to do an unmatched design or to do a matched design. An advantage of the unmatched design is that standard analysis methods can be applied. However, this may not be as efficient in its use of data as a strategy that matches controls to cases and derives estimates with the nonstandard bias correcting methods. Preliminary results from simulation studies suggest in fact that the latter strategy may be optimal [20]. Further theoretical work and simulation modeling will be needed before recommending this approach.
Supplementary Material
Abbreviations
- PSA
prostate specific antigen
- ROC
receiver operating characteristic
- CI
confidence interval
References
- 1.Zhu CS, Pinsky PF, Cramer DW, Ransohoff DF, Hartge P, Pfeiffer RM, Urban N, et al. A framework for evaluating biomarkers for early detection: validation of biomarker panels for ovarian cancer. Cancer Prev Res. 2011;4:375–83. doi: 10.1158/1940-6207.CAPR-10-0193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Liu R, Chen X, Du Y, Yao W, Shen L, Wang C, et al. Serum MicroRNA Expression Profile as a Biomarker in the Diagnosis and Prognosis of Pancreatic Cancer. Clin Chem. 58:610–8. doi: 10.1373/clinchem.2011.172767. [DOI] [PubMed] [Google Scholar]
- 3.Moore LE, Pfeiffer RM, Zhang Z, Lu KH, Fung ET, Bast RC., Jr Proteomic biomarkers in combination with CA 125 for detection of epithelial ovarian cancer using prediagnostic serum samples from the Prostate, Lung, Colorectal, and Ovarian (PLCO) Cancer Screening Trial. Cancer. 2012;118:91–100. doi: 10.1002/cncr.26241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chapman CJ, Thorpe AJ, Murray A, Parsy-Kowalska CB, Allen J, Stafford KM. Immunobiomarkers in small cell lung cancer: potential early cancer signals. Clin Cancer Res. 2011;17:1474–80. doi: 10.1158/1078-0432.CCR-10-1363. [DOI] [PubMed] [Google Scholar]
- 5.Maeda J, Higashiyama M, Imaizumi A, Nakayama T, Yamamoto H, Daimon T. Possibility of multivariate function composed of plasma amino acid profiles as a novel screening index for non-small cell lung cancer: a case control study. BMC Cancer. 2010;10:690. doi: 10.1186/1471-2407-10-690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Mustafa A, Gupta S, Hudes GR, Egleston BL, Uzzo RG, Kruger WD. Serum amino acid levels as a biomarker for renal cell carcinoma. J Urol. 2011;186:1206–12. doi: 10.1016/j.juro.2011.05.085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Anderson GL, McIntosh M, Wu L, Barnett M, Goodman G, Thorpe JD, et al. Assessing lead time of selected ovarian cancer biomarkers: a nested case-control study. J Natl Cancer Inst. 2010;102:26–38. doi: 10.1093/jnci/djp438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Liang Y, Ankerst DP, Ketchum NS, Ercole B, Shah G, Shaughnessy JD, Jr, et al. Prospective evaluation of operating characteristics of prostate cancer detection biomarkers. J Urol. 2011;185:104–10. doi: 10.1016/j.juro.2010.08.088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Janes H, Pepe MS. Matching in studies of classification accuracy: Implications for analysis, efficiency, and assessment of incremental value. Biometrics. 2008;64:1–9. doi: 10.1111/j.1541-0420.2007.00823.x. [DOI] [PubMed] [Google Scholar]
- 10.Pepe MS, Feng Z, Janes H, Bossuyt P, Potter J. Pivotal evaluation of the accuracy of a biomarker used for classification or prediction: standards for study design. J Natl Cancer Inst. 2008;100:1432–8. doi: 10.1093/jnci/djn326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kahn JM, Cooke CR, Watkins TR, Heckbert SR, Rea TD, Seymour CW. Prediction of critical illness during out-of-hospital emergency care. JAMA. 2010;304:747–54. doi: 10.1001/jama.2010.1140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Guyette F, Suffoletto B, Castillo JL, Quintero J, Callaway C, Puyana JC. Prehospital serum lactate as a predictor of outcomes in trauma patients: a retrospective observational study. J Trauma. 2011;70:782–6. doi: 10.1097/TA.0b013e318210f5c9. [DOI] [PubMed] [Google Scholar]
- 13.Jones AE, Shapiro NI, Trzeciak S, Arnold RC, Claremont HA, Kline JA, et al. Lactate clearance vs central venous oxygen saturation as goals of early sepsis therapy: a randomized clinical trial. JAMA. 2010;303:739–46. doi: 10.1001/jama.2010.158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Mikkelsen ME, Miltiades AN, Gaieski DF, Goyal M, Fuchs BD, Shah CV, et al. Serum lactate is associated with mortality in severe sepsis independent of organ failure and shock. Crit Care Med. 2009;37:1670–7. doi: 10.1097/CCM.0b013e31819fcf68. [DOI] [PubMed] [Google Scholar]
- 15.Seymour CW, Cooke CR, Wang Z, Kerr K, Rea TD, Kahn JM, et al. Potential value of biomarkers for out-of-hospital risk stratification of critical illness. (submitted)
- 16.Pepe MS, Longton G, Janes H. Estimation and comparison of receiver operating characteristic curves. Stata J. 2009;9:1–16. [PMC free article] [PubMed] [Google Scholar]
- 17.Vickers AJ, Cronin AM, Begg CB. One statistical test is sufficient for assessing new predictive markers. BMC Med Res Meth. 2011;11:13. doi: 10.1186/1471-2288-11-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Demler OV, Pencina MJ, D’Agostino RB., Sr Misuse of DeLong test to compare AUCs for nested models. Stat Med. 2012 Mar 13; doi: 10.1002/sim.5328. [Epub ahead of print] as doi:10.1002/sim.5328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Pepe MS, Kerr KF, Longton GM, Wang Z. [Accessed May 2012];Testing for improvement in prediction model performance (March 2012) UW Biostat Working Paper Series Paper 379. http://biostats.bepress.com/uwbiostat/paper379.
- 20.Bansal A. Combining Biomarkers to Improve Performance in Diagnostic Medicine [PhD thesis] University of Washington; Seattle, WA: 2011. [Google Scholar]
- 21.Wacholder S, Hartge P, Prentice R, Garcia-Closas M, Feigelson HS, Diver WR, et al. Performance of common genetic variants in breast-cancer risk models. N Engl J Med. 2010;362:986–93. doi: 10.1056/NEJMoa0907727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Pencina MJ, D’Agostino RB, Sr, D’Agostino RB, Jr, Vasan RS. Evaluating the added predictive ability of a new marker: from area under the ROC curve to reclassification and beyond. Stat Med. 2008;27:157–72. doi: 10.1002/sim.2929. discussion 207-12. [DOI] [PubMed] [Google Scholar]
- 23.Vickers AJ, Elkin EB. Decision curve analysis: a novel method for evaluating prediction models. Med Decis Making. 2006;26:565–74. doi: 10.1177/0272989X06295361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Breslow NE. Case-control studies. In: Ahrens W, Pigeot I, editors. Handbook of Epidemiology. Springer; Berlin: 2005. pp. 287–319. [Google Scholar]
- 25.Thomas DC, Greenland S. The relative efficiencies of matched and independent sample designs for case-control studies. J Chronic Dis. 1983;36:685–97. doi: 10.1016/0021-9681(83)90162-5. [DOI] [PubMed] [Google Scholar]
- 26.McIntosh MW, Pepe MS. Combining several screening tests: Optimality of the risk score. Biometrics. 2002;58:657–64. doi: 10.1111/j.0006-341x.2002.00657.x. [DOI] [PubMed] [Google Scholar]
- 27.Breslow NE, Day NE. Statistical methods in cancer research. Volume 1 – The analysis of case-control studies. Lyon: 1980. IARC Scientific Publications No. 32. [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.