Abstract
Purpose
Quantify the impact of respiratory motion on the treatment of lung tumors with spot scanning proton therapy.
Methods and Materials
4D Monte Carlo simulations were used to assess the interplay effect, which results from relative motion of the tumor and the proton beam, on the dose distribution in the patient. Ten patients with varying tumor sizes (2.6-82.3cc) and motion amplitudes (3-30mm) were included in the study. We investigated the impact of the spot size, which varies between proton facilities, and studied single fractions and conventionally fractionated treatments. The following metrics were used in the analysis: minimum/maximum/mean dose, target dose homogeneity and 2-year local control rate (2y-LC).
Results
Respiratory motion reduces the target dose homogeneity, with the largest effects observed for the highest motion amplitudes. Smaller spot sizes (σ≈3mm) are inherently more sensitive to motion, decreasing target dose homogeneity on average by a factor ~2.8 compared to a larger spot size (σ≈13mm). Using a smaller spot size to treat a tumor with 30mm motion amplitude reduces the minimum dose to 44.7% of the prescribed dose, decreasing modeled 2y-LC from 87.0% to 2.7%, assuming a single fraction. Conventional fractionation partly mitigates this reduction, yielding a 2y-LC of 71.6%. For the large spot size, conventional fractionation increases target dose homogeneity and prevents a deterioration of 2y-LC for all patients. No correlation with tumor volume is observed. The effect on the normal lung dose distribution is minimal: observed changes in mean lung dose and lung V20 are <0.6Gy(RBE) and <1.7% respectively.
Conclusions
For the patients in this study, 2y-LC could be preserved in the presence of interplay using a large spot size and conventional fractionation. For treatments employing smaller spot sizes and/or in the delivery of single fractions, interplay effects can lead to significant deterioration of the dose distribution and lower 2y-LC.
Keywords: Lung cancer, Active scanning proton therapy, Interplay effect
Introduction
Charged particles offer the possibility to extend the survival benefit already demonstrated for small and peripheral lesions using photon techniques (1) to a larger group of patients. This is especially important because relatively few lung cancers are diagnosed at an early stage (2). Phase I/II trials have demonstrated the efficacy of passively scattered proton therapy in the lung (3, 4).
Spot scanning proton therapy has been shown to outperform passively scattered proton therapy (5). However, for targets that move during irradiation there is interference between dynamic pencil beam delivery and target motion, typically referred to as interplay effect (6-8). In passively scattered proton therapy, where all parts of the field are essentially delivered simultaneously, this effect is not significant (9).
Previous studies (6-8) were limited by the use of rigid image registration, small number of patients and analytical dose calculation methods, which are expected to have significant uncertainties in lung. In this study we use the current state-of-the-art Monte Carlo dose calculation and deformable image registration methods, applied to ten clinical lung cancer patients.
The aim of this study is to answer the following questions:
How does the interplay effect vary with tumor motion amplitude?
Is there an impact of the spot size on the interplay effect?
How much does conventional fractionation mitigate the interplay effect?
Materials & Methods
Ten patients treated for lung cancer at our institution were retrospectively included in this study. Cases were selected to give a representative range of tumor motion, volume and location. Table 1 gives an overview over peak-to-peak motion amplitude, gross tumor volume (GTV) in end-exhale and the average delivery time per field.
Table 1.
Patient characteristics
| Patient # |
motion amplitude [mm] |
GTV volume [cc] |
delivery time per field [s] |
|
|---|---|---|---|---|
| BigSpots | SmallSpots | |||
| 1 | 30.6 | 21.1 | 20.5 | 89.07 |
| 2 | 3.5 | 64.9 | 22.0 | 137.3 |
| 3 | 10.7 | 26.0 | 14.3 | 85.1 |
| 4 | 20.2 | 82.3 | 26.2 | 164.4 |
| 5 | 14.6 | 4.0 | 10.1 | 24.9 |
| 6 | 10.0 | 21.7 | 17.2 | 80.7 |
| 7 | 5.1 | 2.6 | 12.2 | 35.1 |
| 8 | 15.1 | 15.4 | 43.8 | 89.7 |
| 9 | 9.1 | 24.5 | 22.1 | 107.6 |
| 10 | 2.9 | 33.9 | 19.9 | 100.8 |
Treatment Planning
The treatment planning method was based on an ongoing clinical trial (ClinicalTrials.gov ID: NCT00495040) (3). The internal gross tumor volume (IGTV) was outlined on the maximum intensity projection CT (MIP-CT) and validated on the 4D-CT, to ensure it encompassed the gross tumor volume (GTV) in every phase. The clinical target volume (CTV) was defined as the GTV plus an 8-mm margin to account for microscopic disease, with the ICTV encompassing the CTV in all phases. A conventional PTV was defined as a 5-mm isotropic extension of the ICTV to account for uncertainties in patient setup and deformable image registration (DIR).
Treatment plans were designed on the average intensity projection CT (ave-IP CT) with the IGTV volume set to a generic tumor density (HU=50). This approach has been shown to provide tumor-coverage, while minimizing treatment uncertainties and dose to normal tissue (9).
We used the ASTROID (10) treatment planning system for proton beam scanning. The prescription dose was 87.5Gy(RBE), delivered to ≥;99% of the ICTV and ≥95% of the PTV. All plans employed 2 coplanar fields and satisfied our target coverage requirements and the clinical normal tissue constraints (11). Beam angles were chosen to minimize lung dose and to avoid placing a distal edge immediately proximal to a critical structure. The dominant motion direction was perpendicular to both beams for all patients. Normal lung was defined as the combined lungs, excluding the IGTV. The spot spacing is expressed relative to the spot size: we used a spacing of 1 sigma per default, reducing it to 0.7 sigma only if necessary to satisfy target coverage requirements.
Active Scanning Delivery System
The simulation of the delivery was based on the hardware available at Massachusetts General Hospital. We planned and simulated 2 different spot sizes, where the BigSpots (BS) sigma varies between 8-17mm (230-70MeV). The smallest spot size currently used for proton treatments has a sigma of 2-4mm (230-70MeV), which we define as SmallSpots (SS) (12). The treatment plans for the 10 patients were comprised of spot energies between 100-170MeV, reducing the used spot sizes to 11-15mm for BigSpots and 2-3mm for SmallSpots.
The dynamic delivery was simulated using 1s energy switching time, scanning speeds of 3/30m/s in x/y direction, 5ms spot settling time before beam delivery, and the delivery time based on a beam current of 2nA.
Monte Carlo Simulation and Post-Processing
Figure 1 shows an overview of the study design. After treatment planning (I. in the figure), Monte Carlo (MC) techniques were used to simulate the delivery to the patient. All calculations employed TOPAS, a toolkit using the well-established Geant4 Monte Carlo code (13).
Figure 1.
Study design in detail. Red roman numerals denote the processes: treatment planning (I), scripts for 3D simulation (II) and for 4D simulation (III).
In arm A, the fluence maps acquired from the treatment planning system were delivered to the static ave-IP CT, using an automated suite of scripts (MCAUTO-3D, II. in figure 1). The resulting dose distributions are denoted as static.
For arms B and C, MCAUTO-4D (III. in figure 1) retrieves the 4D-CT and combines it with the timing information of the proton gantry to deliver the pencil beams to the appropriate phase in the breathing cycle. The resulting dose distributions are then deformed back to the reference phase (T50=end exhale), via DIR using Plastimatch (plastimatch.org), a toolkit that has been extensively benchmarked (14).
For each patient, 4 different starting phases were simulated to determine any variation in the interplay effect based on the initial phase. Simulations were performed with the scanning treatment starting at T0 (peak inhale), T25 (mid exhale), T50 (end exhale) and T75 (mid inhale). This yielded 4 dose distributions with varying interplay effect as shown in Figure 2a-d for patient 1. The values reported for the 1-fraction case (arm B), are the average of the values of each metric obtained from these 4 dose distributions.
Figure 2.
Sagittal view of the dose distributions for patient 1 with CTV in end-exhale phase (red, small contour) and ICTV (pink, large contour). a-d denote the 1-fraction cases for the 4 initial phases, e the n-fraction and f the static case.
Simulation of fractionation: the n-fraction approximation
We define the n-fraction case (arm C, n=35, 2.5Gy/fx) as the average of the dose distributions from the 4 initial phases, as illustrated in figure 2: 2a-2d show the dose distributions for the 4 starting phases, revealing over- and under-dosage within the target. Averaging these 4 to arrive at the n-fraction case (2e), the hot- and cold-spots are reduced, yielding a dose distribution similar to the static case (2f). The quantities reported for n-fractions are the values obtained from this average dose distribution (2e).
Averaging the distributions of the 4 starting phases is a valid assumption, since it can be expected that at the delivery of each fraction, scanning would start at a random phase, leading to an even distribution after many fractions.
Our estimation of the n-fraction case rests on the following assumptions, which all cause a conservative assessment of the interplay effect:
We use 4 different starting phases to calculate the n-fraction case, notwithstanding it would be more accurate to use more starting points for the average. However, the interplay effect is thus overestimated: using more initial phases would lead to a more homogeneous dose distribution, since an even wider array of distributions to average would wash out the inhomogeneities caused in the delivery of single fractions to a greater extent.
We rely on a single 4D-CT scan, which assumes that the patient breathes the same way during a whole course of fractionated therapy lasting weeks. Varying the tumor trajectory for different fractions would decrease the interplay, since the same rationale holds true as for point 1.
We do not include a biological equivalent dose (BED) correction to account for the fact that different parts of the tumor receive on some days more, on some days less, dose. By not correcting for essentially non-uniform fraction sizes to different tumor sub-volumes, we underestimate the biological effect within the tumor. The concave dose response curve for doses relevant to this study means a non-uniform fractionation will always yield a biological effect greater or equal than uniform fractionation.
This n-fraction approximation estimates the interplay effect that can be expected over a conventionally fractionated treatment.
Finally, we note that this method, particularly point 2, assumes the tumor stays within the drawn IGTV over the course of the whole treatment. Geometrical misses due to increasing motion or a non-representative 4D-CT are not considered.
Metrics to assess the Interplay Effect
To quantify the impact of interplay on the target dose distribution, the minimum dose (Dmin), maximum dose (Dmax), mean dose (Dmean) and the dose homogeneity, quantified by D5-D95, were analyzed. To estimate the effect on treatment outcome, the tumor control probability (TCP), given by the 2-year local control rate (2y-LC) was calculated. The values used for the 2y-LC calculations were taken from Willner et al. (15) (γ50=3.52 and D50=74.5).
Additionally, changes in mean lung dose (MLD), lung V20 and lung V5 were calculated to determine any effect on normal lung resulting from interplay.
Results and Discussion
Interplay Effect in the Normal Lung
The V20 and V5 are often used during treatment planning to dictate the number of beams and their angles. The change in V20 and V5 for a single fraction compared to the static plan is on average −0.12 0.9%(range −1.4% to 1.5%) and 0.22% 1.1%(range −1.0% to 2.7%) for BigSpots, 0.12 0.7%(range −1.0% to 1.2%) and 0.52% 1.3%(range −1.1% to 3.2%) for SmallSpots. The average MLD occurring in all patients is 11.6Gy(RBE) (range 3.1-23.5) for BigSpots and 7.3Gy(RBE) (range 1.7-13.0) for SmallSpots. The changes caused by the interplay effect are <0.6Gy(RBE) for all patients. There is no significant correlation to tumor motion (Spearman’s p >0.21 for all parameters above) for these patients.
The difference in MLD between the spot sizes is primarily due to the larger penumbra of BigSpots, which leads to a higher volume of normal tissue being irradiated.
Interplay Effect in the Target: Dose Distribution
Figure 3 demonstrates the effect of motion on Dmin, Dmax and Dmean in the CTV. The 1-fraction values for Dmin and Dmax show a clear relationship with tumor motion. The effect is more pronounced for the SmallSpots, where the minimum dose in the CTV drops to 49% of the prescribed dose for the largest motion studied, compared to 78% for the same patient and motion amplitude using the larger spot size.
Figure 3.
Dmin (blue), Dmax (red) and Dmean (green) values for the CTV for the 1-fraction (open symbols) and n-fraction (closed symbols) case. The open and closed Dmean symbols coincide. The error bars for the 1-fraction values represent the standard deviation of the 4 initial phases. The shaded areas represent a linear fit through the maximum and minimum values of to guide the eye.
The 1-fraction mean dose stays within 1.2% of the static plan for all motion amplitudes, except for a small systematic loss (−3%) for the SmallSpots machine and the highest motion amplitude. The standard deviation increases with motion amplitude, implying that in the delivery of a single fraction, larger motion is more likely to cause a mean dose which differs from the static plan. The stability of the average mean dose confirms that the dosimetric impact on Dmin and Dmax is due to interplay.
There is a distinct difference in the Dmin and Dmax values for the 1-fraction and n-fraction cases. Fractionation partly mitigates the creation of hot- and cold-spots, as they occur at different locations for each starting phase.
Dmin and Dmax are widely used clinically, however they refer to a single voxel and thus may overestimate the dose degradation resulting from interplay. Previous work (6) has used D5-D95 as measure of the homogeneity of the dose distribution.
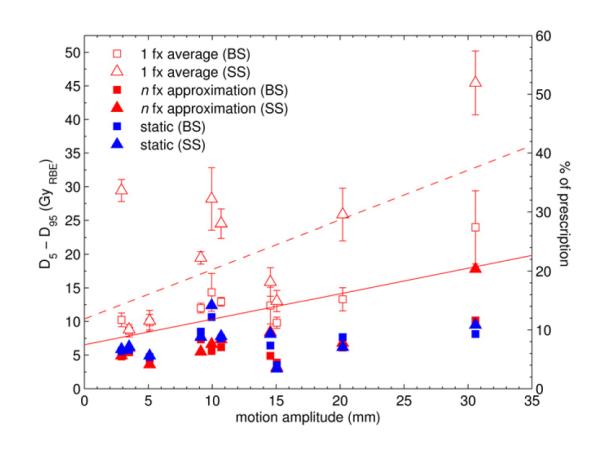
Figure 4 shows the change in D5-D95 for BigSpots and SmallSpots for the 1-fraction and n-fraction cases as a function of motion amplitude. For the static case, the DVH fall-off is comparable between the two spot sizes for all patients. If the plans are delivered on the 4D-CT, the 1-fraction values differ significantly between the two spot sizes. On average, the increase in D5-D95 is 5.6 4.2% of prescribed dose for BigSpots compared to 15.8 11.1% for SmallSpots.
Figure 4.
D5-D95 values for the CTV for the 1-fraction (open symbols) and n-fraction (closed symbols) case for BigSpots (squares) and SmallSpots (triangles). Blue symbols denote the static case. The error bars for the 1-fraction values represent the standard deviation of the 4 starting phases. The lines represent a linear fit through the 1-fraction values to guide the eye (full line: BigSpots, dotted line: SmallSpots).
The n-fraction values show little interplay effect for all motion amplitudes, except for the largest motion and small spot size. In that case D5-D95 increases by 9.48Gy(RBE), i.e. 10.8% of the prescribed dose.
For motion amplitudes <10mm, the n-fraction treatment yields dose distributions more homogeneous than the static plan. This is due to the intrinsically imperfect static plan, which always includes some hot- and cold-spots. Small motion smears the dose distribution such that the over- and under-dosage inherent in the static plan is lessened, thereby making it more homogeneous. A similar phenomenon has already been reported for multiple rescans of the target (6).
Interplay Effect in the Target: TCP
To quantify the change in tumor control, we calculate the 2y-LC for all simulated plans. The 1-fraction value here can be interpreted in 2 different ways: either as the worst-case scenario for a fractionated treatment in which scanning always starts at the same phase, or as the 1-fraction scenario where the prescribed dose is deposited at once. In the latter scenario the time to deposit the dose would be longer, possibly leading to additional smearing out of the interplay effect. However, it can serve as an estimation of the maximum TCP reduction in such a scenario.
Figure 5 shows the effect of motion on 2y-LC with varying tumor motion. For BigSpots, the TCP for the average 1-fraction case stays within 1.2% of the static case up to ~20mm tumor motion amplitude. Only for the patient with >30mm motion, 2y-LC decreases by an average of 7.7 6.2% (for the worst initial starting phase by 14.7%) for the 1-fraction case compared to the static plan. For the n-fraction case, however, TCP is retained for all patients (average change 0.4 0.8%, range −0.4% to 2.4%).
Figure 5.
2y-LC for the static (blue symbols), 1-fraction average (open symbols) and n-fraction (closed symbols) case. The error bars for the 1-fraction values represent the standard deviation of the 4 initial phases, and the cross denotes the worst 1-fraction result.
The same trend is visible for SmallSpots, but the magnitude of the changes is greater. The average loss in 2y-LC over all patients is −18.5 25.2%(range −84.3% to −0.3%) for the 1-fraction case. Even though the largest decrease is seen for the highest motion amplitudes, the changes are not significantly correlated with motion (Spearman’s p=0.26). For the patient with the lowest motion amplitude the 1-fraction value decreases on average by 24%, while there is little change (−2.5% and −1.8%) for the 2 patients with ~15mm motion. It appears motion amplitude alone is not a good predictor of the interplay effect and inter-patient variability is high.
In the n-fraction scenario for SmallSpots, the interplay effect seems to be mitigated for motion amplitudes up to ~20mm in this patient cohort, as modeled 2y-LC decreases <0.4%. Only for the patient with >30mm motion 2y-LC drops from 87% to 71.6%.
We did not observe a correlation between any of the chosen metrics and tumor volume (Spearman’s p>0.16 for all parameters).
Bert et al. (7) also ascertained the strong influence of starting phase on the interplay effect, yet in our patient cohort the motion amplitude seems to dominate the general appearance of possible interplay effects less: the changes in D5-D95 and TCP show little correlation to motion amplitude for the SmallSpots machine. Kraus et al. (8) observed a similar averaging out of the interplay effect for a fractionated treatment, which they also approximated by averaging over the initial phases. They also showed that irregular breathing motion, which was not included here, led to less distorted dose distributions.
Interplay effects can be reduced by a variety of techniques. Different re-scanning methods can provide additional averaging out of hot- and cold-spots. Gating reduces the effective motion of the tumor, thereby possibly reducing the interplay, but requires higher confidence in movement reproducibility. Tracking has been studied extensively for carbon-ion beams, but would not necessarily reduce the interplay effect.
To reduce the spot size at any established facility requires significant changes in hardware. However, several methods (e.g. decreasing quadrupole strength, inserting pre-absorbers) can be employed to increase the spot size, thereby making the system more robust against interplay.
Conclusion
For the 1-fraction scenario, Dmin and Dmax show a clear relationship with tumor motion, decreasing and increasing respectively, as the motion amplitude increases. This change is consistently higher for SmallSpots (σ≈3mm) than for BigSpots (σ≈13mm). The degradation of target homogeneity is on average a factor of 2.8 higher for SmallSpots than for BigSpots.
Even in the presence of the interplay effect from tumor motion up to ~30mm, local control is preserved using a large spot size and conventional fractionation for this patient cohort. Thus gating may not be required for treatments with these characteristics, except when its main purpose is to reduce the dose to normal lung. For motion amplitudes less than ~20mm, the large spot size mitigates deterioration in modeled 2y-LC for the delivery of a single fraction in our patient population.
For treatments with a small spot size, conventional fractionation retains dose homogeneity for motion less than ~20mm in our patient group. In the delivery of single fractions, however, modeled 2y-LC falls on average by 18.5%. The deterioration of the dose distribution is highly patient-specific, and is not predicted accurately by tumor motion amplitude alone.
While the smaller spot size is significantly less robust toward motion, we want to highlight that it also reduces dose to the normal lung considerably due to the sharper lateral penumbra, as can be seen in the different MLD values.
Hypofractionated regimens consisting of only a few fractions are not specifically simulated here, though it can be expected that the interplay effect in such a case will be bound by our estimates of the 1-fraction case and the n-fraction approximation.
Acknowledgements
The project was supported by the National Cancer Institute grant No. R01 CA111590. In addition, the authors gratefully acknowledge the assistance of Ben Clasie, Antje Knopf and Joost Verburg.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of Interest Notification: none
References
- 1.Timmerman R, Paulus R, Galvin J, et al. Stereotactic body radiation therapy for inoperable early stage lung cancer. JAMA. 2010;303:1070–1076. doi: 10.1001/jama.2010.261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Jemal A, Siegel R, Ward E, et al. Cancer Statistics, 2008. CA: A Cancer Journal for Clinicians. 2008;58:71–96. doi: 10.3322/CA.2007.0010. [DOI] [PubMed] [Google Scholar]
- 3.Chang JY, Komaki R, Wen HY, et al. Toxicity and patterns of failure of adaptive/ablative proton therapy for early-stage, medically inoperable non-small cell lung cancer. Int J Radiat Oncol Biol Phys. 2011;80:1350–1357. doi: 10.1016/j.ijrobp.2010.04.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chang JY, Komaki R, Lu C, et al. Phase 2 study of high-dose proton therapy with concurrent chemotherapy for unresectable stage III nonsmall cell lung cancer. Cancer. 2011;117:4707–4713. doi: 10.1002/cncr.26080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zhang X, Li Y, Pan X, et al. Intensity-modulated proton therapy reduces the dose to normal tissue compared with intensity-modulated radiation therapy or passive scattering proton therapy and enables individualized radical radiotherapy for extensive stage IIIB non-small-cell lung cancer: a virtual clinical study. Int J Radiat Oncol Biol Phys. 2010;77:357–366. doi: 10.1016/j.ijrobp.2009.04.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Knopf A-C, Hong TS, Lomax A. Scanned proton radiotherapy for mobile targets-the effectiveness of re-scanning in the context of different treatment planning approaches and for different motion characteristics. Phys Med Biol. 2011;56:7257–7271. doi: 10.1088/0031-9155/56/22/016. [DOI] [PubMed] [Google Scholar]
- 7.Bert C, Grozinger SO, Rietzel E. Quantification of interplay effects of scanned particle beams and moving targets. Phys Med Biol. 2008;53:2253–2265. doi: 10.1088/0031-9155/53/9/003. [DOI] [PubMed] [Google Scholar]
- 8.Kraus KM, Heath E, Oelfke U. Dosimetric consequences of tumour motion due to respiration for a scanned proton beam. Phys Med Biol. 2011;56:6563–6581. doi: 10.1088/0031-9155/56/20/003. [DOI] [PubMed] [Google Scholar]
- 9.Kang Y, Zhang X, Chang JY, et al. 4D Proton treatment planning strategy for mobile lung tumors. Int J Radiat Oncol Biol Phys. 2007;67:906–914. doi: 10.1016/j.ijrobp.2006.10.045. [DOI] [PubMed] [Google Scholar]
- 10.Kooy HM, Clasie BM, Lu H-M, et al. A case study in proton pencil-beam scanning delivery. Int J Radiat Oncol Biol Phys. 2010;76:624–630. doi: 10.1016/j.ijrobp.2009.06.065. [DOI] [PubMed] [Google Scholar]
- 11.Marks LB, Bentzen SM, Deasy JO, et al. Radiation dose-volume effects in the lung. Int J Radiat Oncol Biol Phys. 2010;76:S70–6. doi: 10.1016/j.ijrobp.2009.06.091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Pedroni E, Meer D, Bula C, et al. Pencil beam characteristics of the next-generation proton scanning gantry of PSI: design issues and initial commissioning results. Eur Phys J Plus. 2011;126:1–27. [Google Scholar]
- 13.Perl J, Schümann J, Shin J, et al. TOPAS: A Fast and Easy to Use Tool for Particle Simulation. Med Phys. 2011 (in press) [Google Scholar]
- 14.Murphy K, van Ginneken B, Reinhardt JM, et al. Evaluation of registration methods on thoracic CT: the EMPIRE10 challenge. IEEE Trans Med Imaging. 2011;30:1901–1920. doi: 10.1109/TMI.2011.2158349. [DOI] [PubMed] [Google Scholar]
- 15.Willner J, Baier K, Caragiani E, et al. Dose, volume, and tumor control prediction in primary radiotherapy of non-small-cell lung cancer. Int J Radiat Oncol Biol Phys. 2002;52:382–389. doi: 10.1016/s0360-3016(01)01823-5. [DOI] [PubMed] [Google Scholar]