Abstract
Dopamine modulates cortical circuit activity, in part, through its actions on GABAergic interneurons, including increasing the excitability of fast-spiking interneurons. Though such effects have been demonstrated in single cells, there are no studies that examine how such mechanisms may lead to the effects of dopamine at a neural network level. With this motivation, we investigated the effects of dopamine on synchronization in a simulated neural network, composed of excitatory and fast-spiking inhibitory Wang-Buzsaki neurons. The effects of dopamine were implemented through varying leak K+ conductance of the fast-spiking interneurons and the network synchronization within gamma band (~40 Hz) was analyzed. Parametrically varying the leak K+ conductance revealed an inverted-U shaped relationship, with low gamma band power at both low and high conductance levels, and optimal synchronization at intermediate conductance levels. We also examined the effects of modulating excitability of the inhibitory neurons more generically using an idealized model with theta neurons, with similar findings. Moreover, such relationship holds both when the external input is tonic vs. periodic. Our computational results mirror our empirical study of dopamine modulation in schizophrenia and healthy controls, which showed that amphetamine administration increased gamma power in patients but decreased it in controls. Together, our computational and empirical investigations indicate that dopamine can modulate cortical gamma band synchrony in an inverted-U fashion, and that the physiologic effects of dopamine on single fast-spiking interneurons can give rise to such non-monotonic effects at the network level.
Keywords: dopamine, schizophrenia, computational modeling, gamma band synchrony, auditory steady state response
Introduction
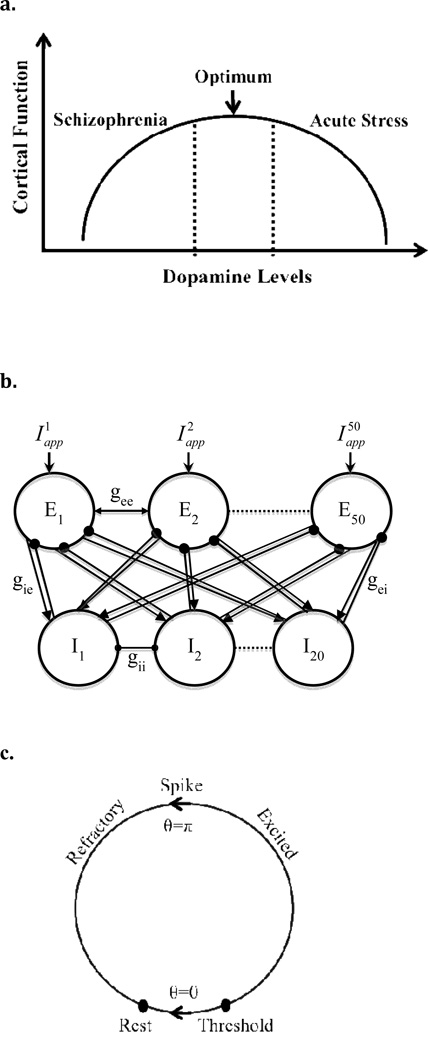
Cortical activity operates optimally within a limited range of dopamine (DA) transmission. Accumulating behavioral and physiological studies provide convergent evidence for this relationship, usually described as an inverted-U shape (Williams & Castner, 2006; see Fig. 1a) with poorer performance at the extremes in DA levels, e.g., arising from conditions such as aging and schizophrenia (low DA; left side of the curve) and acute stress (high DA; right side). However, despite good support for this inverted-U relationship, the exact mechanisms by which DA exerts such effects on cortical activity remain unclear.
FIG. 1.
(a) The inverted-U shaped relationship between dopamine levels and cortical function. This model assumes that under normal conditions, there is a reasonable range of dopamine concentration over which cortical neurons can operate efficiently. At the center of this range is an optimum level of dopamine leading to maximal performance. The model demonstrates lower cortical function for the extreme levels of DA; schizophrenia as an example of low DA on the left side of the curve and acute stress as an example of high DA shown on the right side of the curve. (b) Schematic diagram of the network architecture used for the Wang-Buzsaki neuron simulations. An arrow means that the connection is excitatory and a filled circle means that it is inhibitory. Connectivity between all the neurons in the network is all-to-all. (c) State diagram for the theta neuron. The filled circles represent critical points achieved by the model—rest and threshold.
One possible mechanism through which DA mediates its effects may be cortical oscillations, which are found in association with various perceptual and cognitive processes. Synchronization in the gamma-frequency range (30–80 Hz) has been associated with a wide range of processes including working memory (Tallon-Baudry et al., 1999), perceptual feature binding (Singer & Gray, 1995), attentional selection (Fries et al., 2001), associative learning (Miltner et al., 1999), simple sensory stimulation (Gray et al., 1989), as well as with higher order processes such as cognitive control, which is disturbed in individuals with schizophrenia in association with gamma oscillation disturbances (Cho et al., 2006). Initial studies in animals (Ma & Leung, 2000) and humans (Demiralp et al., 2007) have provided evidence that changes in DA levels can modulate gamma oscillatory activity, suggesting that gamma oscillations can be a useful index of DA’s modulatory effects on cortical activity.
Cortical DA has been shown to modulate the excitability of pyramidal cells via its actions on GABAergic fast-spiking interneurons (Zhou & Hablitz, 1999; Seamans et al., 2001; Kröner et al., 2007) through mechanisms that include suppression of a resting leak K+ current (Gorelova et al., 2002). However, it is unclear how DA’s physiologic effects at the single neuron level could give rise to non-monotonicity at the neural network level in the form of gamma band synchronization. In the current study, we hypothesized that altering the excitability of fast-spiking interneurons could be a mechanism by which DA induces its inverted-U shaped effects on gamma band synchrony in a simulated cortical network. Using a full biophysical model (Wang-Buzsaki model), we analyzed the effects of DA on network synchronization by varying the leak K+ conductance in inhibitory neurons, which revealed a non-monotonic relationship with gamma band synchrony. As this mechanism was just one way of changing interneuronal excitability, we extended this idea to a more general case using an idealized spiking neuron model (theta neuron) in which we more generically varied the excitability, replicating the finding of an inverted-U relationship. Further, in both models, the inverted-U shape held whether inputs to the network were tonic or periodic in nature, mirroring our findings in an empirical study of dopamine modulation in schizophrenia and healthy controls performing a periodic sensory stimulation task, which showed that amphetamine administration increased gamma power in schizophrenia but decreased it in healthy subjects, consistent with patients lying towards the left side of the inverted-U curve while healthy controls lie at the optimum levels of DA transmission.
Methods
Experimental Methods
To conduct an investigation of the effect of dopamine modulation on cortical gamma oscillations, 12 schizophrenia subjects and 12 healthy comparison subjects participated in a double-blind, cross-over, placebo-controlled study of single-dose amphetamine administration. Control subjects were aged 18–40 years, had no Axis I disorder diagnosis by SCID-NP (Spitzer et al., 1990b), no history of severe medical/neurological illnesses, and had no substance abuse (past 1 month) or dependence (past 6 months). For schizophrenia subjects, criteria were identical to controls except: fulfilling DSM-IV criteria for schizophrenia or schizoaffective disorder by patient SCID (Spitzer et al., 1990a) and medical records, being clinically stable (CGI less than or equal to 4 (moderately ill)), and not on benzodiazepines or mood stabilizers. All subjects provided informed consent in accordance with the Institutional Review Board at the University of Pittsburgh. To maintain clinical stability with amphetamine administration, patients were kept on their prescribed antipsychotics (aripiprazole, risperidone, clozapine, ziprasidone, olanzapine). Groups were matched for age (30.3±9.5 vs. 31.4±9.1 years, respectively), parental education (15.2±2.3 vs. 13.9±2.3 years, resp.) and gender (M:F, 7:5 vs. 7:5).
Testing on amphetamine vs. placebo occurred on separate days. Amphetamine was administered by body weight at 0.5 mg/kg, with a two-hour interval before the experimental task to allow adequate absorption (serum amphetamine levels 75±19 ng/ml at 2 hours and 76±7 ng/ml at 6 hours). Subjects performed the steady-state auditory evoked potential task, involving auditory click trains consisting of binaural presentations of 1 ms duration tones repetition frequencies of 40 Hz, 30 Hz, or 20 Hz. To ensure attention to stimuli, click trains were presented as an oddball paradigm. Subjects were asked to respond with a button press for Standard (click train consisting of 1000 Hz tones) vs. an Oddball stimulus (click train consisting of 2000 Hz tones; 10 trials/block). Each trial proceeded as follows: click train (500 ms); delay (200 ms); response interval (to indicate Standard vs. Oddball; 1000 ms); random ITI (0–800 ms). Each repetition frequency was presented in a separate block, with 120 trials/block. Electroencephalographic (EEG) data during task performance were collected on a 128 channel Geodesic Sensor Net (EGI, Eugene OR). Off-line de-noising and averaging will be performed with EEGLAB (Delorm & Makeig, 2004), and wavelet analyses with Brain Vision Analyzer (Brain Products, Munich, Germany). EEG data were acquired at 250 Hz, referenced to Cz and filtered on-line with a 0.1–100 Hz band pass hardware filter. Electrode impedances were kept below 50 kΩ. Epochs were defined as −500 to +1000 ms relative to the stimulus onset. Error trials and epochs containing artifacts were excluded (20 channels with amplitude range exceeding 200 µV within a segment and/or having 60 µV deviations between consecutive samples). Blink and ECG artifacts were removed with ICA based correction methods. Data were then filtered off-line using a 1–100 Hz IIR filter and submitted to final review using the above amplitude and gradient criteria and for 60 Hz line noise, with bad channel data being replaced by interpolation. Data were re-referenced to average reference. Time-frequency analyses were carried out using Brain Vision Analyzer (Brain Products GmbH, Munich, Germany). The data were transformed using complex Morlet wavelet transforms, defined by mo(x)=c·exp(−x2/2)·exp(iω0x), with c=7, using 40 frequency steps spanning 1–60 Hz and baseline corrected to a −350 to −150 ms pre-stimulus interval.
Computational Methods
Wang-Buzsaki model of an excitatory-inhibitory network
We simulated a network composed of 50 excitatory and 20 inhibitory Wang-Buzsaki (Wang & Buzsaki, 1996) cells, a ratio within the range used in the literature in line with physiological data (Fellous et al., 2001; Börgers & Kopell, 2003; Vierling-Claassen et al., 2008), coupled through synapses with an all-to-all connectivity (Fig. 1b). The membrane potentials of each excitatory and inhibitory neuron satisfy the following dynamics:
| (1) |
| (2) |
and are independent white noise processes with magnitudes ξe=1.2, and ξi=1.2.
The synaptic currents are governed by the following:
| (3) |
| (4) |
| (5) |
| (6) |
with gee=0.05, gei=0.7, gii=0.10, gie=0.6, , and , where the synaptic gating variables are given by:
| (7) |
| (8) |
with parameters αe = 1.1, αi = 5, βe = 0.19, βi = 0.1, where with parameters Vt = 2, Vs = and Tmax = 1 ms.
All the neurons in the system have the same initial conditions for the simulations as follows: V(0) = −64mV, h(0) = 0.78, and n(0) = 0.09.
There is heterogeneous external constant input current given to each excitatory neuron, denoted by , with a random distribution between 2.0 and 2.5 µA/cm2 in the tonic input model and 1.0 and 1.5 µA/cm2 in the periodic input model. Moreover, in the periodic forcing model both the excitatory and inhibitory cells receive additional periodic currents governed by Ie(t) = Aez(t) and Ii(t) = Aiz(t) with Ae=90 and Ai=50 representing the amplitude of the periodic drive given to the excitatory and inhibitory neurons, respectively. Also, z(t) is a filter function defined by dz/dt = (−z + P(t))/τ, where P(t) is a periodic square pulse of duration of 1 ms and period of 25 ms, with decay time constant τ=20. The fast sodium, INA and delayed rectifier IK currents are the same as in Wang and Buzsaki (1996). INaL = gNaL (V − ENa) with gNaL =0.017 mS/cm2 and IKL = gKL (V − EK) with gKL =0.083 mS/cm2, specifically for the excitatory neurons and was parametrically varied in the simulations.
In order to account for the observed slower firing rates of the excitatory cells (McCormick et al., 1985), there is spike frequency adaptation added to the excitatory neurons in the simulated network. This is produced mainly by a voltage-independent, Ca2+ -dependent K+ current and is associated with the slow after hyperpolarization after a burst of spikes (Hotson & Prince, 1980; Wang, 1998; Ermentrout & Terman, 2010), instead of using M-type currents mediated by voltage-dependent, high-threshold K+ channels (Brown & Adams, 1980), that could cause complications by converting type 1 cell to type 2. Currents associated with the spike frequency adaptation included in the membrane potentials of the excitatory neurons are ICa and IAHP. The high-threshold calcium current ICa = gCam∞ (V − ECa) with gCa=1 mS/cm2 and ECa=120 mV, where m is replaced by its steady-state m∞(V) = 1/(1+exp(−(V − Vlth) / Vshp)), with Vlth = −25 mV, and Vshp = 5 mV. The voltage-independent calcium-activated potassium current is IAHP = gAHP ([Ca+2]/([Ca+2]+ KD))(V − EK) with gAHP=5 mS/cm2 and KD=30 µM. The intracellular Ca+2 concentration is governed by , where α=0.002 [in µM (msµA)−1cm2] and ιCa=80 ms.
All simulations were performed using XPPAUT 6.10 using the Euler integration method with a time step of 0.01 ms. The network was simulated for 20 seconds and the mean voltage across the excitatory neurons in the network was calculated. These data were divided into 1 second time bins and Fast Fourier Transform (FFT) Analysis was run on the mean voltage in each time bin using MATLAB. In each time bin, FFT analysis was run to search for the frequency corresponding to the peak amplitude in the power spectrum in the tonic input case. Furthermore, in order to account for noise and to smooth the results, an average of the amplitude was calculated corresponding to ±1 Hz of the peak frequency. In the periodic forcing case, mean power corresponding to ±3 Hz of 40 Hz was calculated to specifically analyze the entrainment to the forcing frequency. The same process was repeated for each time bin and an average across the 20 different 1 second time bins was calculated.
Theta Neuron Model
For some of our analysis, we used an idealized spiking neuron model, theta neuron, to examine the dynamics and synchronization in a network of inhibitory and adapting excitatory neurons (Ermentrout & Kopell, 1986). The Wang-Buzsaki neuron model exhibits a saddle-node on an invariant circle (SNIC) bifurcation (Izhikevich, 2007). Therefore, if the system is close to the bifurcation, we can reduce this model to a theta neuron model with adaptation. The theta neuron is a simple, one-dimensional model for the spiking of a neuron that reduces the dimensionality from the Wang-Buzsaki biophysical model while still retaining type 1 dynamics and is able to reproduce behavior such as spiking and refractory period as depicted in Fig. 1c (Gutkin et al., 2003). Although fast-spiking neurons have been shown to be of type 2 excitability (Tateno et al., 2004), our simulations involved type 1 neurons since we used Wang-Buzsaki neurons for the full biophysical model which can be studied as a reduced model using theta neurons of type 1 excitability (c.f. Börgers et al., 2005). Using the reduced model, it is easier to understand the dynamics of the network and much more efficient in simulating larger networks.
We preserve the overall network architecture as in the Wang-Buzsaki model (50 excitatory and 20 inhibitory cells, full connectivity):
| (9) |
| (10) |
| (11) |
with parameters Ie=1, gz=0.2, gie=2, gee=0.1, ξe=0.5, τz=50, b=100, gii=0.15, gei=0.4, and ξi=0.02. The synaptic gating variables are given by:
| (12) |
| (13) |
with parameters τe=1 and τi=3.
Equation (9) describes the evolution of each excitatory neuron with external input Ie in the presence of spike frequency adaptation with strength gz. Each excitatory neuron receives the same external input, Ie, and a noisy component with strength ξe where is a white noise process and j=1,..,50. The adaptation current associated with each excitatory neuron j is discretely incremented with each spike and decays with a time constant τz with dynamics following equation (10). The evolution of each inhibitory neuron is shown in equation (11) with external drive Ii, and a white noise component, , with strength ξi. Equations (12) and (13) describe the excitatory and inhibitory synapses, respectively with parameter b defining how sharp the curve is when it crosses the synapse, equivalent to Vs in the Wang-Buzsaki model. For simulations with periodic input, we used the same stimuli as in the Wang-Buzsaki model, but altered the following parameters: Ie=0.4, gz=0.5, gie=3, gee=2, ξe=0.5, ξi=0.01 and Ae=70 and Ai=10. Simulation and analysis of the theta model was identical to that of the Wang-Buzsaki model; gamma power was measured by looking at the summed excitatory synaptic conductances.
Results
Experimental observations
The average evoked gamma power was derived for the 40 Hz stimuli over the interval 225–525 ms after stimulus onset. Repeated measures ANOVA with Diagnosis (schizophrenia vs. healthy control) as a between-subject factor and Drug Status (amphetamine vs. PBO) as a within-subject factor revealed a Drug Status X Diagnosis interaction (F=10.2, p<0.005). Post-hoc comparisons revealed that for the PBO condition, schizophrenia patients showed lower gamma power compared to controls (t=2.6, p<.05), consistent with many previous studies (Kwon et al., 1999; Spencer et al., 2008; Vierling-Claassen et al., 2008; Krishnan et al., 2009). However, schizophrenia patients showed increases in gamma power with amphetamine compared to PBO (t=2.3, p<.05), while controls showed decreases in gamma power with amphetamine (t=−2.3, p<.05). This pattern of findings (see Fig. 2) was specific to the 40 Hz stimuli as none of the main effects or interactions were significant for the 20 Hz and 30 Hz stimuli (data not shown) and all post-hoc comparisons were also not significant (all p’s > 0.25).
FIG. 2.
Time frequency plots of gamma power for healthy control and schizophrenia subjects for 40 Hz stimuli. Ordinate is frequency (0–60 Hz) and abscissa is time (−500 to 1000 ms with respect to stimulus onset. Controls have lower response with AMPH (amphetamine) vs. Placebo while patients show enhancement with AMPH vs. Placebo.
Tonic Input Models
Effects of leak K+ current in the biophysical model
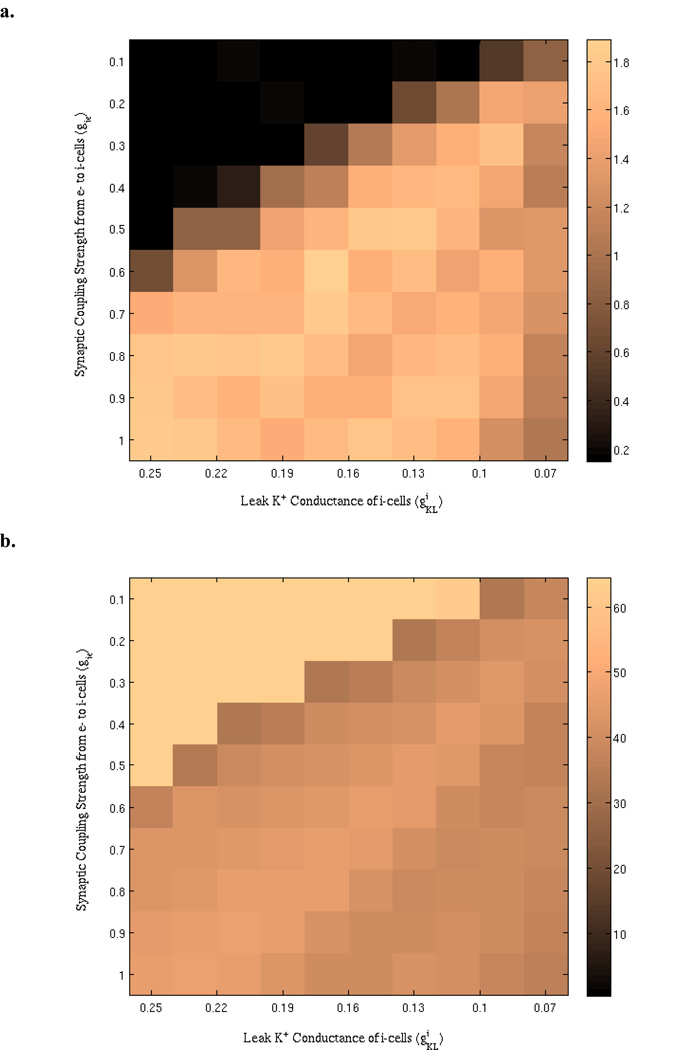
To examine the effects of leak K+ conductance of the inhibitory neurons on the network synchronization, we simulated a biophysical model composed of Wang-Buzsaki neurons and looked at how gamma power varied with respect to varying levels. Fig. 3 shows the results for the peak power and corresponding frequency obtained from simulations with two parameter variations, gie and . Although the effects of were the focus of this work, initially we parametrically varied gie also as another important determinant of inhibitory neuron activation to provide additional insights regarding the dynamic range for network activity. For instance, the network activity remained very low in terms of gamma power at low values of gie (e.g., gie = 0.1, 0.2, and 0.3). Conversely, very high gie values lead to consistently high network gamma power regardless of variations in values (gie =0.9, 1.0). Midrange values of gie better reveal the effects of on network synchronization, where it can be seen that there is a non-monotonic relationship between and network gamma power (Fig. 3a). Such a relationship, usually described as an inverted-U shape, is most clearly visible for gie values such as 0.6 and 0.7. Although gamma power increases with increasing levels initially, after a peak power value, it decreases with further increases in . As depicted in the Figure 3b, there is also good stability in the peak network frequency, which remains within the gamma band range with slight fluctuations.
FIG. 3.
Effects of varying the synaptic coupling strength from excitatory to inhibitory cells (gie) and the leak K+ conductance of inhibitory cells on the Wang-Buzsaki network synchronization. (a) The dependence of peak power on the parameters. (b) Peak frequency (in Hz) corresponding to the power values shown in (a).
Also of note is that network gamma power appears to also display a non-monotonic relationship with gie. For values of such as 0.13 or 0.17, there is an optimum gie that gives rise to a peak in gamma power, with changes in gie in either direction leading to decreases in power. This highlights the fact that modulating other determinants of interneuron excitability may also give rise to non-monotonic relationships in network level gamma synchrony.
Changes in gamma band synchrony in the idealized model
The key role leak K+ conductance plays in the detailed biophysical model is to modulate the excitability of the inhibitory neurons. High values of gKL increase the amount of K+ efflux, repolarizing the neuron, hence decreasing the excitability of the inhibitory neurons, whereas low values of gKL lead to increased excitability through the reverse mechanism. Therefore, the frequency output of a single Wang-Buzsaki neuron with respect to a fixed external drive increases as gKL decreases (Fig. 4). With this motivation in mind, an idealized model based on theta neuron was formulated to generalize the effects of varying gKL to a broader concept. With the network formulation, this model had varying levels of external drive to the inhibitory neurons in order to replicate the effects of varying in the full biophysical model by modulating the excitability of the inhibitory neurons in the network. However, the drive to the excitatory neurons was kept constant (Ie=1). The power spectrum obtained from FFT analysis for the peak power and corresponding frequency is shown in Fig. 5. Similar to the full biophysical model, here is also another non-monotonic relationship in the form of an inverted-U shape between the power and the drive to the inhibitory cells (Fig. 5a) corresponding to gamma band frequency range (Fig. 5b). Raster plots corresponding to three different Ii values on the curve depict how excitability and resulting firing patterns vary depending on the levels of external input (Fig. 5c–e). Low levels of drive (Ii=−0.13) fail to provide enough drive to excite the inhibitory cells and resulting low activity in the inhibitory cells cannot provide the necessary inhibition for the excitatory cells to synchronize, hence leading to low gamma power (Fig. 5c). However, increasing the external drive leads to optimum excitability of the inhibitory cells (Ii=0), thus providing the necessary inhibition for the excitatory cells to synchronize perfectly (Fig. 5d). Further increased drive (Ii=0.14) leads to inhibitory cells that are too excitable and fire spontaneously at high rates and, suppress the excitatory cells. The suppressed excitatory activity leads to low gamma power in the pool of excitatory neurons (Fig. 5e). These results suggest that any type 1 neuron model can be used to replicate the same findings as in the full biophysical model (Ermentrout, 1996). Such reduced neuron models provide computation efficiency and allow for further mathematical analysis that we plan on doing following this study.
FIG. 4.
Firing rate – current (f-I) dependence on the leak K+ conductance (gKL) of a single Wang-Buzsaki neuron. The effects of varying gKL of a single Wang-Buzsaki neuron were analyzed and depicted here with colored plots representing the f-I curves associated with various values of gKL.
FIG. 5.
The effects of varying drives to the inhibitory cells (Ii) in the theta neuron model with tonic input. (a) Peak power obtained for varying drives to the inhibitory cells and (b) the corresponding frequencies. The raster plots for points on the curve corresponding to (c) left side of the curve where Ii=−0.13, (d) optimum level with a peak in gamma power Ii=0, and (e) right side of the curve with Ii=0.14.
Effects of DA modulation of cortical entrainment to a periodic auditory stimulus
The entrainment of both networks to periodic stimuli and how such entrainment varied with respect to varying levels of excitability of the inhibitory cells was addressed by adding periodic forcing at 40 Hz to both networks. Results from Wang-Buzsaki model are represented in Fig. 6a and continue to preserve the non-monotonicity in the form of an inverted-U shape, with the associated raster plots corresponding to three different values on the curve. Network activity prior to the onset of the periodic stimuli are also demonstrated in the raster plots (t=0–150 ms), where it can be seen that the network maintains a low activity state at the baseline. High levels , corresponding to low DA levels, lead to poor excitability of the inhibitory cells and low 40-Hz power due to lack of sufficient temporal organization in the excitatory network (Fig. 6b). On the other hand, low levels—high DA— , lead to too much activity in the inhibitory pool, leading to too much suppression in the excitatory pool and low 40-Hz power due to low activity levels (Fig. 6d). In between those two extremes lies an optimum range for , where excitatory cells fire in perfect synchrony, leading to high 40-Hz power (Fig. 6c).
FIG. 6.
The network activity in the Wang-Buzsaki model with periodic forcing at gamma frequency (40 Hz). (a) Gamma power plotted as a function of the leak K+ conductance of the inhibitory cells in the Wang-Buzsaki network. The raster plots depict the network behavior at baseline (t=0–150 ms) and periodic stimulus comes on at t=150 ms The raster plots for points on the curve corresponding to (b) left side of the curve where , (c) optimum level with a peak in gamma power , and (d) right side of the curve with .
Results from the theta neuron network with periodic forcing and varying Ii levels are shown in Fig. 7, where the same non-monotonicity with 40-Hz power holds. Increases in the parameter Ii are associated with increases in DA levels and similar to the full biophysical model, low Ii (DA) levels (Ii=−1.32) lead to low 40-Hz power due to lack of enough inhibition necessary for synchrony in the excitatory pool (Fig. 7b) and high Ii (DA) levels (Ii=0) lead to low 40-Hz power due to too much suppression in the excitatory pool (Fig. 7d). Optimum levels (Ii=−0.45) lead to perfect synchrony in entrainment to the periodic stimuli (Fig. 7c).
FIG. 7.
The network activity in the theta neuron model with periodic forcing at gamma frequency (40 Hz). (a) Gamma power plotted as a function of the drive to the inhibitory cells (Ii). The raster plots depict the network behavior at baseline (t=0–150 ms) and periodic stimulus comes on at t=150 ms The raster plots for points on the curve corresponding to (b) left side of the curve where Ii=−1.32, (c) optimum level with a peak in gamma power Ii=−0.45, and (d) right side of the curve with Ii=0.
Discussion
In the current study, we found that increasing the excitability of fast-spiking interneurons could give rise to an inverted-U shaped relationship with synchrony, consistent with that between DA and cortical activity. Implementing DA’s effects on single neurons as a suppression of the leak K+ current, simulations using a full biophysical model composed of Wang-Buzsaki neurons with a tonic drive revealed an inverted-U shaped relationship with network gamma power as an index of cortical activity. Similarly, we replicated these findings in an idealized model composed of theta neurons with varying degrees of drive to the inhibitory neurons, showing the generalizability of the excitability of the inhibitory neurons as a potential mechanism for modulation of network synchrony. In a computational paper, van Vreeswisk et al. (1994) showed that inhibition often rather than excitation synchronizes firing, emphasizing the importance of interneurons in synchronization, and our results provide further evidence for the importance of interneuron activity for synchronization. Furthermore, simulations using identical network architectures but with periodic forcing showed a similar inverted-U shaped relationship of network gamma power as interneuron excitability was varied. These computational investigations provide a possible mechanistic account of the findings of our empirical study of dopamine modulation neural synchrony, which showed that amphetamine administration increased gamma synchrony in schizophrenia patients but decreased it in controls, consistent with patients residing on the left-hand side of the inverted-U curve with controls lying at more optimal, mid-range levels of DA transmission.
The direct link between DA and working memory was illustrated first by Brozoski and colleagues (1979), who showed that following lesions of the dorsolateral prefrontal cortex (DLPFC) of nonhuman primates via 6-hydroxdopamine administration, delay-dependent impairments in working memory were observed. Following this seminal work, other studies have shown that dopamine’s effects on working memory are mediated specifically by D1 receptors in the DLPFC (Sawaguchi & Goldman-Rakic, 1991, 1994). In schizophrenia, disturbances in dopamine projections (Akil et al., 1999) and D1 receptor physiology (Okubo et al., 1997; Abi-Dargham et al., 2002) and amelioration of cognitive deficits by amphetamine administration (Daniel et al., 1991; Goldberg et al., 1991; Goldman-Rakic et al., 2004; Barch & Carter, 2005) are consistent with reduced DA transmission contributing to working memory deficits in the illness. On the other hand, acute stress, which has been shown to increase prefrontal DA levels beyond the optimum range, in part through D1 receptor mechanisms (Arnsten & Goldman-Rakic, 1998; Hutson et al., 2004), also leads to poor cognitive performance as observed in working memory tests. Together, these findings imply an inverted-U shaped relationship between the strength of DA transmission and working memory function (Fig. 1; Williams & Castner, 2006).
Studies of the role of gamma band synchrony in working memory suggest a mechanism by which DA could affect cortical function. Gamma oscillations increase parametrically with working memory load (Howard et al., 2003) and impaired working memory in schizophrenia is associated with impaired gamma oscillatory activity (Haenschel et al., 2009). DA could have a direct role in such network oscillations through its effects on fast-spiking interneurons, cells which are critical to the dynamics of gamma oscillations in terms of generating them both in hippocampus and neocortex (Bartos et al., 2007). Gorelova and colleagues (2002) found that DA suppressed a voltage-independent leak K+ current via D1/D5 receptors in fast-spiking interneurons thus providing a potential mechanism by which network level synchrony could be modulated. In our simulations we manipulated the leak K+ conductance levels of the inhibitory neurons, with low leak K+ conductance representing high DA levels and vice versa, and both of those extremes lead to low gamma power. However, another important finding from Gorelova et al. (2002) was the suppression of a Cs+-sensitive inward rectifier K+ current by DA. While these two currents differ considerably in terms of their contributions to the membrane potential due to their different voltage-dependence properties (North, 2000), they both modulate the excitability of the fast-spiking interneurons. This motivated our extension to the broader framework of the theta neuron model, which more generically implemented interneuron excitability through varying external drive levels and reproduced qualitatively similar findings to the biophysical model. In both model simulations, increasing inhibitory neuron excitability improved network gamma synchrony, but only to a point, after which inhibition from interneurons played less of a role in regulating the timing of excitatory neuron firing, and increasingly suppressed excitatory cell firing altogether thereby decreasing network gamma oscillations. Thus, our computational simulation findings show that DA’s apparently simple modulation of interneuron excitability at the single cell level can have qualitatively different effects at the network level depending on the specific degree of induced excitability, helping to detail a plausible mechanism by which DA leads to the inverted-U shaped relationship with cortical activity.
As an empirical test of the putative role of DA in cortical gamma oscillations, we studied amphetamine’s effects on auditory cortical oscillations with findings that were broadly consistent with the inverted-U relationship. Perceptual deficits in the auditory domain have been shown in schizophrenia across various behavioral measures involving tone matching (Strous et al., 1995), temporal discrimination (Todd et al., 2003), and pitch discrimination (Leitman et al., 2010). One useful approach for characterizing the neurophysiological basis of auditory cortical deficits has been the utilization of steady state responses of the EEG in response to external stimuli, allowing testing of the functional state of the networks subserving neuronal synchrony (Lins & Picton, 1995). Individuals with schizophrenia show deficits in entraining to external auditory stimuli in the gamma frequency range, particularly at 40 Hz (Kwon et al., 1999; Brenner et al., 2003; Spencer et al., 2008; Krishnan et al., 2009;). Employing the auditory steady state paradigm in the current study, we hypothesized that administration of amphetamine, which increases DA levels by facilitating release and inhibiting reuptake, would improve gamma range auditory entrainment in schizophrenia patients and produce minimal change or decrease it for healthy controls. Our experimental findings were consistent with this hypothesis, with increases in gamma oscillations in patients interpretable as having a low baseline cortical dopamine state that was increased by amphetamine. In contrast, decreases in gamma oscillations for controls could be understood in terms of having already optimal dopamine levels at baseline, with amphetamine inducing an excess of dopamine that decreased gamma power.
Our empirical findings from a task paradigm that involved cortical steady state responses to periodic auditory stimuli motivated extensions of our simulation work with tonic inputs to the case of periodic forcing. We found that a similar inverted-U shaped relationship could be obtained by varying inhibitory neuron leak K+ conductance in the Wang-Buzsaki model and by varying the external drive applied to the inhibitory neurons in the theta model, indicating that DA’s modulation of interneuron excitability could give rise to the observed effects on network level synchrony for different types of cortical inputs that vary in their temporal structure.
Our mechanistic account of the non-monotonic relationship between DA and cortical function could have important implications for understanding the pathophysiology of various clinical disorders such as schizophrenia and inform novel therapeutic development. In our experimental study, we employed amphetamine in order to increase DA but as it does so in a nonspecific manner, it would be inappropriate for clinical use due to its propensity to induce psychosis through D2 receptor stimulation. However, since DA’s increasing of fast-spiking neuron excitability is D1 receptor mediated (Gorelova et al., 2002), a specific D1 agonist could help to ameliorate disturbances in cortical gamma oscillations without precipitating psychotic symptoms of the illness. Further, in addition to helping to correct any hypodopaminergic states, a D1 agonist could have beneficial effects on other types of neurotransmission disturbances thought to be important to the pathophysiology of schizophrenia such as in GABA (Gonzalez-Burgos & Lewis, 2008) and NMDA (Kantrowitz & Javitt, 2010) transmission. Since D1 agonists increase the excitability of fast-spiking interneurons, disturbances in GABA transmission could possibly be addressed through D1 stimulation even if the primary deficit was not in DA itself. Vierling-Claassen and colleagues (2008) conducted a computational study of gamma oscillatory disturbances in schizophrenia, modeling reductions in GAT-1 (GABA reuptake transporter) in schizophrenia as an increase in the time constant for the decay of inhibition. While it is not clear that acute DA increases could ameliorate such disturbances, increases in interneuron excitability could improve GABA neurotransmission, which, over time, may correct the reductions in GAT-1, which presumably first arose as a compensatory mechanism for reductions in GABA. Other computational studies have shown that NMDA glutamatergic transmission is important for sustaining gamma oscillations over a delay period (Compte et al., 2000) and can be positively modulated by D1 stimulation (Brunel & Wang, 2001), thus providing a potential alternate pathway by which DA agonists could help to correct impaired cortical oscillations in schizophrenia. Future computational studies will investigate more systematically the potential for dopamine-based mechanisms to correct disturbances in cortical oscillations due to other neurotransmitter systems in schizophrenia. We also plan to study the specificity of the computational mechanisms investigated here to oscillatory disturbances in the gamma band vs. those reported for other frequency bands in the illness. Finally, in a follow-up paper to their prior work, Vierling-Claassen and Kopell (2009) developed methods for analyzing locking patterns in a simple forced theta neuron network. Using our reduced theta model, future work will apply similar methods with a focus on the effects of varying the excitability of the inhibitory neurons.
Acknowledgements
We would like to thank Nicola Riccardo Polizzotto for insightful discussions regarding the manuscript. K.K. is supported by R.K. Mellon Foundation; G.B.E. is supported by NSF DMS 0817131; C.P.W. is supported by K08 MH080329 and P50 MH084053; R.Y.C. is supported by K08 MH080329, P50 MH084053 and NARSAD.
Abbreviations
- DA
dopamine
- EEG
electroencephalogram
- DLPFC
dorsolateral prefrontal cortex
- FFT
fast Fourier transform
- GABA
gamma amino acid butyric acid
- PFC
prefrontal cortex
References
- Abi-Dargham A, Mawlawi O, Lombardo I, Gil R, Martinez D, Huang Y, Hwang D, Keilp J, Kochan L, van Heertum R, Gorman JM, Laruelle M. Prefrontal dopamine D1 receptors and working memory in schizophrenia. J. Neurosci. 2002;22:3708–3719. doi: 10.1523/JNEUROSCI.22-09-03708.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akil M, Pierri JN, Whitehead RE, Edgar CL, Mohila C, Sampson AR, Lewis DA. Lamina-specific alterations in the dopamine innervation of the prefrontal cortex in schizophrenic subjects. Am. J. Psychiatry. 1999;156:1580–1589. doi: 10.1176/ajp.156.10.1580. [DOI] [PubMed] [Google Scholar]
- Arnsten AF, Goldman-Rakic PS. Noise stress impairs prefrontal cortical cognitive function in monkeys: evidence for a hyperdopaminergic mechanism. Arch. Gen. Psychiatry. 1998;55:362–368. doi: 10.1001/archpsyc.55.4.362. [DOI] [PubMed] [Google Scholar]
- Barch DM, Carter CS. Amphetamine improves cognitive function in medicated individuals with schizophrenia and in healthy volunteers. Schizophr. Res. 2005;77:43–58. doi: 10.1016/j.schres.2004.12.019. [DOI] [PubMed] [Google Scholar]
- Bartos M, Vida I, Jonas P. Synaptic mechanisms of synchronized gamma oscillations in inhibitory interneuron networks. Nat. Rev. Neurosci. 2007;8:45–56. doi: 10.1038/nrn2044. [DOI] [PubMed] [Google Scholar]
- Börgers C, Epstein S, Kopell NJ. Background gamma rhythmicity and attention in cortical local circuits: a computational study. Proc. Natl. Acad. Sci. USA. 2005;102:7002–7007. doi: 10.1073/pnas.0502366102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Börgers C, Kopell N. Synchronization in networks of excitatory and inhibitory neurons with sparse, random connectivity. Neural Comp. 2003;15:509–538. doi: 10.1162/089976603321192059. [DOI] [PubMed] [Google Scholar]
- Brown DA, Adams PR. Muscarinic suppression of a novel voltage-sensitive K+ current in a vertebrate neurone. Nature. 1980;283:673–676. doi: 10.1038/283673a0. [DOI] [PubMed] [Google Scholar]
- Brenner CA, Sporns O, Lysaker PH, O’Donnell BF. EEG synchronization to modulated auditory tones in schizophrenia, schizoaffective disorder, and schizotypal personality disorder. Am. J. Psychiatry. 2003;160:2238–2240. doi: 10.1176/appi.ajp.160.12.2238. [DOI] [PubMed] [Google Scholar]
- Brozoski TJ, Brown RM, Rosvold HE, Goldman PS. Cognitive deficit caused by regional depletion of dopamine in prefrontal cortex of rhesus monkey. Science. 1979;205:929–932. doi: 10.1126/science.112679. [DOI] [PubMed] [Google Scholar]
- Brunel N, Wang XJ. Effects of neuromodulation in a cortical network model of object working memory dominated by recurrent inhibition. J. Comput. Neurosci. 2001;11:63–85. doi: 10.1023/a:1011204814320. [DOI] [PubMed] [Google Scholar]
- Cho RY, Konecky RO, Carter CS. Impairments in frontal cortical γ synchrony and cognitive control in schizophrenia. Proc. Natl. Acad. Sci. 2006;103:19878–19883. doi: 10.1073/pnas.0609440103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Compte A, Brunel N, Goldman-Rakic PS, Wang XJ. Synaptic mechanisms and network dynamics underlying spatial working memory in a cortical network model. Cereb. Cortex (New York, N.Y.: 1991) 2000;10:910–923. doi: 10.1093/cercor/10.9.910. [DOI] [PubMed] [Google Scholar]
- Daniel DG, Weinberger DR, Jones DW, Zigun JR, Coppola R, Handel S, Bigelow LB, Goldberg TE, Berman KF, Kleinman JE. The effect of amphetamine on regional cerebral blood flow during cognitive activation in schizophrenia. J. Neurosci. 1991;11:1907–1917. doi: 10.1523/JNEUROSCI.11-07-01907.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delorme A, Makeig S. EEGLAB: an open source toolbox for analysis of single-trial EEG dynamics. J. Neurosci. Methods. 2004;134:9–21. doi: 10.1016/j.jneumeth.2003.10.009. [DOI] [PubMed] [Google Scholar]
- Demiralp T, Herrmann CS, Erdal ME, Ergenoglu T, Keskin YH, Ergen M, Beydagi H. DRD4 and DAT1 polymorphisms modulate human gamma band responses. Cereb. Cortex. 2007;17:1007–1019. doi: 10.1093/cercor/bhl011. [DOI] [PubMed] [Google Scholar]
- Ermentrout B. Type I membranes, phase resetting curves, and synchrony. Neural Comput. 1996;8:979–1001. doi: 10.1162/neco.1996.8.5.979. [DOI] [PubMed] [Google Scholar]
- Ermentrout GB, Kopell N. Parabolic bursting in an excitable system coupled with a slow oscillation. SIAM J. Appl. Math. 1986;46:233–253. [Google Scholar]
- Ermentrout GB, Terman D. Mathematical foundations of neuroscience. New York, NY: Springer; 2010. [Google Scholar]
- Fellous JM, Tiesinga PHE, José JV, Sejnowski TJ. Computational model of carbachol-induced delta, theta and gamma-like oscillations in hippocampus. Neurocomputing. 2001;38–40:587–593. doi: 10.1002/hipo.1041. [DOI] [PubMed] [Google Scholar]
- Fries R, Reynolds JH, Rorie AE, Desimone R. Modulation of oscillatory neuronal synchronization by selective visual attention. Science. 2001;291:1560–1563. doi: 10.1126/science.1055465. [DOI] [PubMed] [Google Scholar]
- Goldberg TE, Bigelow LB, Weinberger DR, Daniel DG, Kleinman JE. Cognitive and behavioral effects of the coadministration of dextroamphetamine and haloperidol in schizophrenia. Am. J. Psychiatry. 1991;148:78–84. doi: 10.1176/ajp.148.1.78. [DOI] [PubMed] [Google Scholar]
- Goldman-Rakic PS, Castner SA, Svensson TH, Siever LJ, Williams GV. Targeting the dopamine D1 receptor in schizophrenia: insights for cognitive dysfunction. Psychopharmacology (Berl) 2004;174:3–16. doi: 10.1007/s00213-004-1793-y. [DOI] [PubMed] [Google Scholar]
- Gonzalez-Burgos G, Lewis DA. GABA neurons and the mechanisms of network oscillations: implications for understanding cortical dysfunction in schizophrenia. Schizophr. Bull. 2008;34:944–961. doi: 10.1093/schbul/sbn070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorelova N, Seamans JK, Yang CR. Mechanisms of dopamine activation of fast-spiking interneurons that exert inhibition in rat prefrontal cortex. J. Neurophysiol. 2002;88:3150–3166. doi: 10.1152/jn.00335.2002. [DOI] [PubMed] [Google Scholar]
- Gray CM, König P, Engel AK, Singer W. Oscillatory responses in cat visual cortex exhibit inter-columnar synchronization which reflects global stimulus properties. Nature. 1989;338:334–337. doi: 10.1038/338334a0. [DOI] [PubMed] [Google Scholar]
- Gutkin B, Pinto D, Ermentrout B. Mathematical neuroscience: from neurons to circuits to systems. J. Physiol. Paris. 2003;97:209–219. doi: 10.1016/j.jphysparis.2003.09.005. [DOI] [PubMed] [Google Scholar]
- Haenschel C, Bittner RA, Waltz J, Haertling F, Wibral M, Singer W, Linden DEJ, Rodriguez E. Cortical oscillatory activity is critical for working memory as revealed by deficits in early-onset schizophrenia. J. Neurosci. 2009;29:9481–9489. doi: 10.1523/JNEUROSCI.1428-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howard MW, Rizzuto DS, Caplan JB, Madsen JR, Lisman J, Aschenbrenner-Scheibe R, Schulze-Bonhage A, Kahana MJ. Gamma oscillations correlate with working memory load in humans. Cereb. Cortex. 2003;13:1369–1374. doi: 10.1093/cercor/bhg084. [DOI] [PubMed] [Google Scholar]
- Hutson PH, Patel S, Jay MT, Barton CL. Stress-induced increase of cortical dopamine metabolism: attenuation by a tachykinin NK1 receptor antagonist. Eur. J. Pharmacol. 2004;484:57–64. doi: 10.1016/j.ejphar.2003.10.057. [DOI] [PubMed] [Google Scholar]
- Izhikevich EM. Dynamical systems in neuroscience: the geometry of excitability and bursting. Cambridge, Mass: MIT Press; 2007. [Google Scholar]
- Kantrowitz JT, Javitt DC. N-methyl-d-aspartate (NMDA) receptor dysfunction or dysregulation: the final common pathway on the road to schizophrenia? Brain Res. Bull. 2010;83:108–121. doi: 10.1016/j.brainresbull.2010.04.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krishnan GP, Hetrick WP, Brenner CA, Shekhar A, O’Donnell BF. Steady state and induced auditory gamma deficits in schizophrenia. Neuroimage. 2009;47:1711–1719. doi: 10.1016/j.neuroimage.2009.03.085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kröner S, Krimer LS, Lewis DA, Barrionuevo G. Dopamine increases inhibition in the monkey dorsolateral prefrontal cortex through cell type-specific modulation of interneurons. Cereb. Cortex. 2007;17:1020–1032. doi: 10.1093/cercor/bhl012. [DOI] [PubMed] [Google Scholar]
- Kwon JS, O’Donnell BF, Wallenstein GV, Greene RW, Hirayasu Y, Nestor PG, Hasselmo ME, Potts GF, Shenton ME, McCarley RW. Gamma frequency-range abnormalities to auditory stimulation in schizophrenia. Arch. Gen. Psychiatry. 1999;56:1001–1005. doi: 10.1001/archpsyc.56.11.1001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leitman IL, Laukka P, Juslin PN, Saccente E, Butler P, Javitt DC. Getting the cue: sensory contributions to auditory emotion recognition impairments in schizophrenia. Schizophr. Bull. 2010;36:545–556. doi: 10.1093/schbul/sbn115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis DA, Hashimoto T, Volk DW. Cortical inhibitory interneurons and schizophrenia. Nat. Rev. Neurosci. 2005;6:312–324. doi: 10.1038/nrn1648. [DOI] [PubMed] [Google Scholar]
- Lins OG, Picton TW. Auditory steady-state responses to multiple simultaneous stimuli. Electroencephalogr. Clin. Neurophysiol. 1995;96:420–432. doi: 10.1016/0168-5597(95)00048-w. [DOI] [PubMed] [Google Scholar]
- Ma J, Leung LS. Relation between hippocampal gamma waves and behavioral disturbances induced by phencyclidine and methamphetamine. Behav. Brain Res. 2000;111:1–11. doi: 10.1016/s0166-4328(00)00138-8. [DOI] [PubMed] [Google Scholar]
- McCormick DA, Connors BW, Lighthall JW, Prince DA. Comparative electrophysiology of pyramidal and sparsely spiny stellate neurons of the neocortex. J. Neurophysiol. 1985;54:782–806. doi: 10.1152/jn.1985.54.4.782. [DOI] [PubMed] [Google Scholar]
- Miltner WH, Braun C, Arnold M, Witte H, Taub E. Coherence of gamma-band EEG activity as a basis for associative learning. Nature. 1999;397:434–436. doi: 10.1038/17126. [DOI] [PubMed] [Google Scholar]
- North RA. Potassium-channel closure taken to TASK. Trends Neurosci. 2000;23:234–235. doi: 10.1016/s0166-2236(00)01592-7. [DOI] [PubMed] [Google Scholar]
- Okubo Y, Suhara T, Suzuki K, Kobayashi K, Inoue O, Terasaki O, Someya Y, Sassa T, Sudo Y, Matsushima E, Iyo M, Tateno Y, Toru M. Decreased prefrontal dopamine D1 receptors in schizophrenia revealed by PET. Nature. 1997;385:634–636. doi: 10.1038/385634a0. [DOI] [PubMed] [Google Scholar]
- Sawaguchi T, Goldman-Rakic PS. D1 dopamine receptors in prefrontal cortex: involvement in working memory. Science. 1991;251:947–949. doi: 10.1126/science.1825731. [DOI] [PubMed] [Google Scholar]
- Sawaguchi T, Goldman-Rakic PS. The role of D1-dopamine receptor in working memory: local injections of dopamine antagonists into the prefrontal cortex of rhesus monkeys performing an oculomotor delayed-response task. J. Neurophysiol. 1994;71:515–528. doi: 10.1152/jn.1994.71.2.515. [DOI] [PubMed] [Google Scholar]
- Seamans JK, Gorelova N, Durstewitz D, Yang CR. Bidirectional dopamine modulation of GABAergic inhibition in prefrontal cortical pyramidal neurons. J. Neurosci. 2001;21:3628–3638. doi: 10.1523/JNEUROSCI.21-10-03628.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singer W, Gray CM. Visual feature integration and the temporal correlation hypothesis. Annu. Rev. Neurosci. 1995;18:555–586. doi: 10.1146/annurev.ne.18.030195.003011. [DOI] [PubMed] [Google Scholar]
- Spencer KM, Salisbury DF, Shenton ME, McMarley RW. γ-band activity auditory steady-state responses are impaired in first episode psychosis. Biol. Psychiatry. 2008;64:369–375. doi: 10.1016/j.biopsych.2008.02.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spitzer RL, Williams JBW, Gibbon M, First MB. Structured Clinical Interview for DSM-III-R – Non-patient Edition (SCID-NP, Version 1.0) Washington, D.C.: American Psychiatric Press; 1990a. [Google Scholar]
- Spitzer RL, Williams JB, Gibbon M, First MB. User's guide for the structured clinical interview for DSM-III-R: SCID. Washington, D.C.: American Psychiatric Press, Inc.; 1990b. [Google Scholar]
- Strous RD, Cowan N, Ritter W, Javitt DC. Auditory sensory (“echoic”) memory dysfunction in schizophrenia. Am. J. Psychiatry. 1995;152:1517–1519. doi: 10.1176/ajp.152.10.1517. [DOI] [PubMed] [Google Scholar]
- Tateno T, Harsch A, Robinson HP. Threshold firing frequency-current relationships of neurons in rat somatosensory cortex: type 1 and type 2 dynamics. J. Neurophysiol. 2004;92:2283–2294. doi: 10.1152/jn.00109.2004. [DOI] [PubMed] [Google Scholar]
- Tallon-Baudry C, Kreiter A, Bertrand O. Sustained and transient oscillatory responses in the gamma and beta bands in a visual short-term memory task in humans. Vis. Neurosci. 1999;16:449–459. doi: 10.1017/s0952523899163065. [DOI] [PubMed] [Google Scholar]
- Todd J, Michie PT, Jablensky AV. Association between reduced duration mismatch negativity (MMN) and raised temporal discrimination thresholds in schizophrenia. Clin. Neurophysiol. 2003;114:2061–2070. doi: 10.1016/s1388-2457(03)00246-3. [DOI] [PubMed] [Google Scholar]
- Van Vreeswijk C, Abbott LF, Ermentrout GB. When inhibition not excitation synchronizes neural firing. J. Comput. Neurosci. 1994;1:313–321. doi: 10.1007/BF00961879. [DOI] [PubMed] [Google Scholar]
- Vierling-Claassen D, Kopell N. The dynamics of a periodically forced cortical microcircuit, with an application to schizophrenia. SIAM J. Appl. Dyn. Syst. 2009;8:710–733. [Google Scholar]
- Vierling-Claassen D, Siekmeier P, Stufflebeam S, Kopell N. Modeling GABA alterations in schizophrenia: a link between impaired inhibition and altered gamma and beta range auditory entrainment. J. Neurophysiol. 2008;99:2656–2671. doi: 10.1152/jn.00870.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang XJ, Buzsaki G. Gamma oscillation by synaptic inhibition in a hippocampal interneuronal network model. J. Neurosci. 1996;16:6402–6413. doi: 10.1523/JNEUROSCI.16-20-06402.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams GV, Castner SA. Under the curve: critical issues for elucidating D1 receptor function in working memory. Neuroscience. 2006;139:263–276. doi: 10.1016/j.neuroscience.2005.09.028. [DOI] [PubMed] [Google Scholar]
- Zhou FM, Hablitz JJ. Dopamine modulation of membrane and synaptic properties of interneurons in rat cerebral cortex. J. Neurophysiol. 1999;81:967–976. doi: 10.1152/jn.1999.81.3.967. [DOI] [PubMed] [Google Scholar]