Analysis of Regional Cerebral Blood Flow Data to Discriminate Among Alzheimer's Disease, Frontotemporal Dementia, and Elderly Controls: Multi-Block Barycentric Discriminant (Mubada) Methodology

Hervé Abdi; Lynne J Williams; Derek Beaton; Mette T Posamentier; Thomas S Harris; Anjali Krishnan; Michael D Devous, Sr

doi:10.3233/JAD-2012-112111

. Author manuscript; available in PMC: 2013 Jul 29.

Published in final edited form as: J Alzheimers Dis. 2012;31(0 3):S189–S201. doi: 10.3233/JAD-2012-112111

Analysis of Regional Cerebral Blood Flow Data to Discriminate Among Alzheimer's Disease, Frontotemporal Dementia, and Elderly Controls: Multi-Block Barycentric Discriminant (Mubada) Methodology

Hervé Abdi ^1,³, Lynne J Williams ², Derek Beaton ¹, Mette T Posamentier ¹, Thomas S Harris ³, Anjali Krishnan ⁴, Michael D Devous Sr ^1,³

PMCID: PMC3725397 NIHMSID: NIHMS459880 PMID: 22785390

Abstract

We present a generalization of mean-centered-partial-least-squares-correlation called multiblock-barycentric-discriminant-analysis (MUBADA) that integrates multiple regions of interest (ROIs) to analyze functional brain images of cerebral blood flow or metabolism obtained with SPECT or PET. To illustrate MUBABDA we analyzed data from a group of 104 participants comprising Alzheimer's disease (AD) patients, fronto-temporal dementia (FTD) patients, and elderly normal (EN) controls. Brain images were analyzed via 28 ROIs (59,845 voxels) selected for clinical relevance. This is a discriminant analysis (DA) question with several blocks (one per ROI) and with more variables than observations, a configuration that precludes using standard DA. MUBADA revealed two factors explaining 74% and 26% of the total variance: Factor 1 isolated FTD, and Factor 2 isolated AD. A MUBADA random effects model correctly classified 64% (chance = 33%) of “new” participants (p < .0001). MUBADA identified ROIs that best discriminated groups: ROIs separating FTD were bilateral inferior, middle frontal, left inferior and middle temporal gyri, while ROIs separating AD were bilateral thalamus, inferior parietal gyrus, inferior temporal gyrus, left precuneus, middle frontal, and middle temporal gyri. MUBADA classified participants at levels comparable to standard methods (i.e., SVM, PCA-LDA, and PLS-DA) but provided information (e.g., discriminative ROIs and voxels) not easily accessible to these methods.

Keywords: MUBADA, BADA, discriminant analysis, multiblock analysis, PLS methods, partial least squares correlation, neuroimaging, SPECT, PET, dementia

Introduction

Neuroimaging data are intrinsically multivariate, and so would be natural domains of application for multivariate data analysis [1]. Unfortunately, neuroimaging data often have far more variables than participants, a configuration that violates the assumptions of most multivariate methods. Also, we often test hypotheses that involve specific regions of interest (ROIs). This leads to a problem of clinical and theoretical importance for imaging, behavior, and neuroscience: How to predict group membership with large data sets that are structured into coherent blocks of variables?

To answer this question we extended mean centered partial least squares correlation (MC-PLSC)—a well-known and well-used method in neuroimaging (see [2, 3] for reviews). This new method called multiblock barycentric discriminant analysis (MUBADA) was used to analyze regional cerebral blood flow (rCBF) data derived from single-photon emission computerized tomography (SPECT) studies of participants with neurodegenerative disorders and healthy controls. MUBADA has been designed specifically for SPECT and for positron-emission tomography (PET) data, where there are typically one or very few observations per participant and where each voxel represents a parametric value such as rCBF or regional cerebral glucose metabolism. MUBDADA however can also be used for any type of data suited for MC-PLSC when the goal is to predict group membership from a large number of variables structured into blocks.

Specifically, we wanted to predict the clinical group of the participants based on their SPECT scans which, themselves, are organized into “blocks” of variables or “subtables” that represent specific ROIs. This is a discriminant analysis problem, but to integrate and evaluate the contribution of these different blocks requires a more sophisticated version of discriminant analysis. Moreover, standard discriminant analysis cannot handle data sets with more variables than observations (see [4] for potential palliatives). For MUBADA, the data are organized such that one row is one observation (i.e., one participant) and one column is one variable (i.e., one voxel) and at the intersection of a row and a column is the activity of this column or voxel for this row or participant (see Figure 1). In addition, voxels are grouped into blocks of voxels and each block constitutes an ROI (one voxel belongs to only one ROI).

Overview of the Method

Barycentric discriminant analysis (BADA)—the foundations of MUBADA—generalizes and integrates MC-PLSC and discriminant analysis (DA). Like DA, BADA is performed when measurements made on some observations are combined to assign these or new observations to a-priori defined groups. Like MC-PLSC, BADA is performed when the goal of the analysis is to find the variables responsible for group separation. Unlike DA, BADA can be performed when the predictor variables are multi-collinear (and in particular when the number of variables exceed the number of observations) and does not rely on parametric assumptions (such as normality or homoscedasticity). Unlike MC-PLSC, BADA adds an explicit prediction component to the analysis and evaluates the quality of the prediction with cross-validation methods.

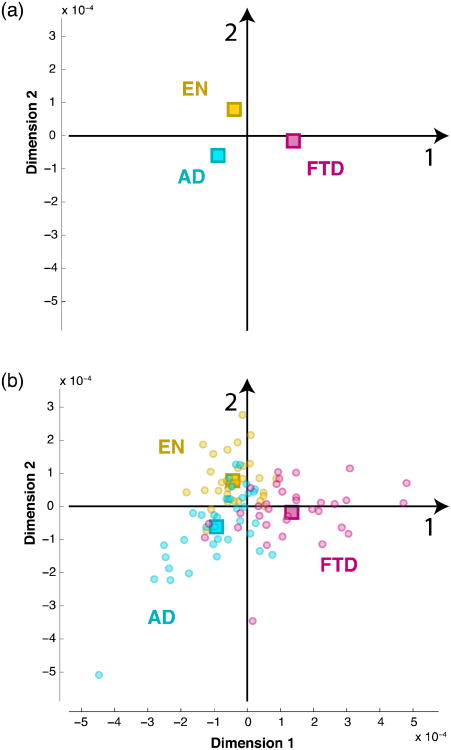
Actually, BADA refers to a class of methods, which all rely on the same principle: each group of interest is represented by the barycenter of its observations (i.e., the weighted average; also called the center of gravity of the observations of a group), and a generalized principal component analysis (GPCA) is performed on the group-by-variable matrix. This analysis gives a set of discriminant factor scores for the groups and a set of loadings for the variables (voxels). The original observations are then projected onto the group factor space, and this provides a set of factor scores for the observations. The distances of each observation to each of the groups are computed from their factor scores and each observation is assigned to the closest group. The results of this analysis can be visualized by using the factor scores to plot the group barycenters as points on a map (see Figures 1 and 2a). The original observations can also be plotted on this map as points and the distances between points on the map best approximate the distances computed from the factor scores (see Figures 1 and 2b). A convenient representation of the dispersion of the observations of a group around their barycenter can be obtained by fitting an ellipsoid—called a tolerance ellipsoid—or a convex hull, that encompasses a specific proportion of the observations closest to the barycenter (typically 95%, see Figures 1 and 3a). Tolerance ellipsoids and convex hulls are typically centered on the barycenter of their groups.

*(a)* Projection of the barycenters on the GPCA space; *(b)* Projection of the observations as supplementary elements. EN = Elderly Normal, AD = Alzheimer's Disease, FTD = Fronto-Temporal Dementia.

*(a)* Tolerance intervals, *(b)* Prediction intervals, and *(c)* Confidence intervals.

The comparison between the a-priori and a-posteriori group assignments is used to assess the quality of the discriminant procedure. The model is built with a subset of the observations (called the training set), and its predictive performance is evaluated with a different set (called the testing set). A specific case of this approach is the “leave-one-out” technique in which each observation is used in turn as the testing set, while the rest of the observations play the role of the training set. This scheme has the advantage of providing an approximately unbiased estimate of the generalization performance of the model [5]. The distinction between training and testing sets mirrors the familiar distinction between fixed and random effects in analysis of variance. In a manner analogous to the tolerance ellipsoids or convex hulls, the results of the leave-one-out can also be visualized by projecting the predicted observations on the discriminant space and then representing the dispersion of the predicted observations by fitting an ellipsoid—called a prediction ellipsoid—or a convex hull, that encompasses a specific proportion of the predicted observations closest to the barycenter (typically 95%, see Figures 1 and 3b). Prediction ellipsoids and convex hulls are not required to be centered on the barycenters of their groups, but tend to be for large samples (as is the case here, cf. Figures 3a and 3b).

The stability of the discriminant model can be assessed by a resampling strategy such as the bootstrap [5, 6]. In this procedure, multiple sets of observations are generated by sampling with replacement from the original set of observations, and new group barycenters are computed, which are then projected onto the discriminant factor space. For convenience, the confidence interval of a barycenter can be represented graphically as a confidence ellipsoid that encompasses a given proportion (e.g., 95%) of the bootstrapped barycenters (see Figures 1 and 3c).

In summary, BADA is a generalized principal component analysis (GPCA) performed on the group barycenters. GPCA encompasses most multivariate techniques [7-10] and for each specific type of GPCA, there is a corresponding version of BADA. For example, when the GPCA is correspondence analysis, this gives the most well known version of BADA: discriminant correspondence analysis [8, 11-13]. When BADA is used with quantitative data, it analyzes the same matrix of group mean activation values as MC-PLSC and therefore will generate the same results. BADA will, however, also provide a predictive model that can be evaluated by cross-validation methods. Because BADA is based on GPCA, it can also handle data tables comprised of blocks and analyze them in a way comparable to multiple factor analysis or STATIS [14-17]. This last step of projecting part of the data onto the common factor space corresponds to the multiblock extension of BADA and therefore defines MUBADA. In addition, with MUBADA, the specific contribution of each block to the overall discrimination can be evaluated and represented as a graph and factor scores for the groups and observations each ROI can be also computed (and the average of these factor scores gives back the BADA factor scores). Figure 1 shows a sketch of the steps in MUBADA, a detailed pictorial and a formal presentation are given in the Appendix.

Methods

We used MUBADA to assign SPECT neuroimaging data from 104 participants to three a-priori groups: (1) Alzheimer's Disease patients (AD, N = 37, 57% female, 63.0 ± 11.5 years), (2) Fronto-Temporal Dementia patients (FTD, N = 33, 39% female, 64.8 ± 7.3 years), and (3) Elderly Normal controls (EN, N = 34, 47% female, 58.4±12.0 years). The AD participants were generally somewhat younger than typical AD patients and were chosen so that there was no meaningful age difference compared to the FTD group. As with the AD participants, EN participants were chosen to best match the age and gender of the FTD group. All participants were recruited in accordance with the guidelines set by the Institutional Review Board at the University of Texas Southwestern Medical Center. Participants with FTD and AD were recruited from the longitudinal cohorts of the UT Southwestern Alzheimer's Disease Center (ADC). AD participants received a diagnosis of possible or probable AD according to the NINDS/ADRD criteria [18] with a Clinical Dementia Rating (CDR) summary score of 1.0. FTD participants were all diagnosed with behavioral variant FTD in accordance with the Neary criteria ([19]) and were required to have an MMSE of greater than 15. Healthy elderly normal controls (EN) were also recruited from the ADC normal control cohort. Participants with FTD and AD had cognitive impairment in the mild to moderate range.

Image acquisition and pre-processing

For each participant, we collected a resting state (eyes open, ears unplugged, dimly lit room, quiet background) 3-dimensional SPECT rCBF image. An intravenous line was placed in an antecubital vein and after 10 min 20 mCi of the SPECT rCBF tracer ^99mTc HMPAO (GE Healthcare, Princeton, New Jersey) was administered over 30 sec and followed by a 10 ml saline flush over 30 sec. For tracer administration participants sat in a dimly lit room with eyes open and ears unoccluded (only background noise from air conditioning and machine cooling fans provided auditory stimuli). SPECT scans were obtained 90 min following ^99mTc HMPAO administration to allow time for tracer activity to clear from blood and non-brain tissues. Images were obtained on a PRISM 3000S 3-headed SPECT camera (Picker International, Cleveland, OH) using ultra-high-resolution fan-beam collimators (reconstructed resolution of 6.5mm) in a 128 × 128 matrix in three-degree increments. Reconstructed images were smoothed with a 6th-order Butterworth three-dimensional filter, and attenuation corrected using a Chang first-order method with ellipse size adjusted for each slice (voxels in reconstructed images are 1.9mm³).

SPECT images were resliced to 2mm³ voxels. After acquisition, the scans were smoothed with an 8mm Gaussian kernel using SPM2 [21] and normalized to whole brain counts (to correct for individual differences in global cerebral blood flow) as follows. Whole brain counts were determined in the SPECT image by simple thresholding, wherein “brain voxels” are identified as voxels with greater than 10% of the median count density for all voxels. Counts for voxels which survive this threshold are then averaged, and the original count density in each voxel is then divided by this average count density to obtain the normalized value used for subsequent calculations. This process ensures that the mean voxel value of each scan is equal to one (and eliminates voxels that are external to the cortical mantle). These images represent the brain as a set of voxels whose numerical value gives relative rCBF (to global CBF).

The SPECT images were then co-registered to the Montréal Neurological Institute (MNI) space using the MNI T1 MRI template ([20].we used the MNI T1 template because it allowed us to subsequently extract the ROIs directly from the MNI template). Each 3-dimensional image comprises a total of 95 × 79 × 69 = 517,845 voxels. From each scan we then extracted a subset of 59,845 voxels comprising 14 ROIs per hemisphere (total of 28 ROIs, see Table 1), identified using the automatic labeling atlas in MRIcro [22]. The ROIs were chosen a-priori because of their clinical relevance and potential for discriminating between the clinical groups. Each ROI was considered as a block of voxels, and therefore, the data analysis problem can be seen as a discriminant analysis with multiple blocks (one per ROI). The goal of the analysis was to assign observations to their clinical group and to evaluate the specific contribution of the ROIs. Prior to subsequent analysis, each scan (which now consists of 59,845 voxels extracted from the original set of 517,845 voxels) was normalized such that the sum of squares of all its voxel values was equal to one. This normalization ensured that the voxels of each scan now have the same (i.e., within subject) variance and that differences between scans are not due to overall differences in activation. In addition, the mean scan of all participants was subtracted from all scans prior to the analysis.

Table 1. Regions of interest for the analyses.

Frontal	Temporal	Parietal	Other

Inferior Middle Gyrus rectus	Inferior Middle Superior	Inferior Middle Superior Precuneus	Thalamus Parahippocampal Hippocampus Amygdala

Open in a new tab

Results

Results are organized as in the methods sections, describing our findings based on each step in MUBADA.

Factor scores and supplementary elements

Figure 2a shows the projections of the barycenters on the GPCA space and Figure 2b shows the projections of the observations as supplementary elements in the GPCA space. The analysis provides two dimensions that explained, respectively, 74% and 26% of the total variance (with associated eigenvalues equal to λ₁ = 9.6 × 10^–9 and λ₂ = 3.4 × 10^–9). Factor 1 separates FTD from the other groups, while Factor 2 separates AD from the other groups (in particular EN).

Training and testing sets

The confusion matrix for the whole set is shown in Table 2a. The corresponding values for the sensitivity and specificity of the discrimination between pairs of categories are shown in Table 2b. The fixed effect model (training set) showed good, but not perfect, performance and correctly classified 78 out of 104 participants (75%, chance = 33%, p < .0001 by binomial test). As expected, the AD and EN groups were well separated with 50 out of 66 participants being correctly classified (76%). Of the 26 participants who were miss-classified, fewer EN participants (N = 3) were assigned to the AD group than the inverse (N = 13). The model exhibits good generalization as the random effect model (testing set) correctly classified 67 out of 104 or 64% of “new” participants (chance = 33%, p < .0001 by binomial test).

Table 2. Table 2a: Fixed and random effect confusion matrices for MUBADA.

	Fixed Effects Model				Random Effects Model

	Actual Class				Actual Class

	EN	AD	FTD		EN	AD	FTD
EN (N=34)	28	13	1	EN (N=34)	24	14	5
AD (N=37)	3	23	5	AD (N=37)	5	20	5
FTD (N=33)	3	1	27	FTD (N=33)	5	3	23

Table 2b: Specificity and Sensitivity for the fixed and random effect confusion matrices for MUBADA
	Fixed Effects Model				Random Effects Model

	Actual Class				Actual Class

	EN	AD	FTD		EN	AD	FTD
EN	-	64%/90%	96%/90%	EN	-	59%/83%	82%/83%
AD	90%/64%	-	84%/96%	AD	83%/59%	-	82%/87%
FTD	90%/96%	96%/84%	-	FTD	83%/82%	87%/82%	-

Open in a new tab

Quality of prediction and group separation

Explained inertia and confidence intervals

The quality of the assignment of the participants to their groups is good (R² = .38, p < .0001 by permutation test). This interpretation is supported by the tolerance interval (an ellipse that includes 95% of the observations; see Figure 3a) and the prediction interval (an ellipse that includes 95% of the predicted observations; see Figure 3b), and by the confusion matrices for the fixed and random effect models (Table 2). In addition, the confidence intervals revealed that group separation was very reliable (see Figure 3c), and that the AD and FTD groups showed more variability than the EN group.

Finding the important regions of interest

The structures that contribute to the discrimination between groups are shown in Figure 4 (separate plots for right and left hemispheres). Referring to Figure 2, the first and second dimensions appear to isolate FTD. On the first dimension, the FTD group is separated from the other groups, and opposed to AD and EN. The ROIs that contribute most to this separation (have the greatest weights on Dimension 1 in Figure 4) are bilateral inferior and middle frontal gyri, and left inferior and middle temporal gyri.

ROI contribution to group discrimination: *(a)* right hemisphere and *(b)* left hemisphere partial contributions of the ROIs to the discriminant factors. Axes represent increasing factor weight. Circle diameters are proportional to the ROI's contribution to the total variance.

Again referring to Figure 2, the second dimension isolates the AD group. ROIs with large contributions in this dimension (have the greatest weights on Dimension 2 in Figure 4) include bilateral thalamus, inferior parietal, inferior temporal gyri, and left precuneus, middle frontal, and middle temporal gyri, as well as right superior temporal, middle temporal, precuneus, and middle frontal ROIs.

Comparison with other pattern recognition classification methods

MUBADA is part of the family of pattern classifiers (also often called multivariate pattern analysis, MVPA, see [1]) that has become of increasing importance in neuroimaging (see, e.g., [1], and [23] for reviews of recent trends). As we have already mentioned, MUBADA can be considered as a generalization of MC-PLSC that adds prediction and multiblock components. Among the current pattern classifiers used for predicting group membership in neuroimaging, three are used extensively: support vector machines [24], partial least squares regression discriminant analysis (PLS-DA, [25, 26, 27, 28]), and principal component analysis followed by linear discriminant analysis on the subset of “generalizable” components (PCA-LDA, see e.g., [24] for an example with PET data). None of these methods incorporates a multiblock component and therefore we could only compare these techniques and MUBADA on the basis of their classification performance. Canonical STATIS ([15]) is the only method that could incorporate ROIs but requires that all ROIs are full rank matrices, a requirement that precludes its use for the present (and in general SPECT or PET data set). Just like for MUBADA (see Table 2), we computed confusion matrices for fixed and random effects. Recall that, fixed effects reflect the performance reached on the training set but do not indicate the level of performance that can be expected for new observations (equal to 75% for MUBADA). Random effects indicate the level of performance to be expected for new observations (equal to 64% for MUBADA).

SVM is a popular tool in neuroimaging ([24], [29]); we implemented this technique with WEKA ([30]), which is an ubiquitous software that implements SVMs (and many other data mining and statistical techniques). For the SVM, we left all parameters as default except that we changed the kernel type to linear learning and set normalization to true (which normalizes values in each row to a min of 0 and max of 1). We built the SVM model with no training and no cross-validation to find the classification accuracy of the fixed effects model (Table 3, left, which is 100%). For the random effects model we used a k-fold cross-validation scheme and set k = N. This procedure implements the same leave-one-out scheme as MUBADA. The random effects classification of the SVM model then drops to 67% (Table 3, right), a value comparable to MUBADA.

Table 3. Fixed and random effect confusion matrices for linear support vector machine (SVM).

	Fixed Effects Model				Random Effects Model

	Actual Class				Actual Class

	EN	AD	FTD		EN	AD	FTD
EN (N=34)	34	0	0	EN (N=34)	24	8	5
AD (N=37)	0	37	0	AD (N=37)	6	25	7
FTD (N=33)	0	0	33	FTD (N=33)	4	4	21

Open in a new tab

The second technique is a linear discriminant analysis computed on the regularized factor space obtained from a PCA of the participants-by-voxels matrix. We implemented PCA-LDA with 1) our own PCA and PRESS code (available online, see [31]) in Matlab® (R2009a, Mathworks, Inc., Natick, MA) and 2) Matlab's “classify” function (which performs LDA). PRESS revealed that four factors should be used. The fixed-effects model shows only a 66% classification for fixed effects (Table 4, left). To compute the random effects model, we wrote an in-house Matlab script to execute a leave-one-out by 1) performing PCA on N – 1 observations with the left out observation projected as supplementary and 2) using the “classify” function to predict the left out observation. The random effects model maintains nearly the same prediction level as the fixed effects model at 65% (Table 4, right).

Table 4.

Fixed and random effect confusion matrices for PCA+LDA (4 factors).

	Fixed Effects Model				Random Effects Model

	Actual Class				Actual Class

	EN	AD	FTD		EN	AD	FTD
EN (N=34)	26	12	5	EN (N=34)	26	13	7
AD (N=37)	6	20	5	AD (N=37)	5	19	3
FTD (N=33)	2	5	23	FTD (N=33)	3	5	23

Open in a new tab

Finally, we performed a partial least squares regression discriminant analysis (PLS-DA) with a dummy coded predictor matrix with our own code (available online, see [25]). We also chose to use 4 factors, just as in the PCA-LDA approach. The fixed effects model shows an 89% correct classification (Table 5, left). For the random effects model, the leave-one-out technique showed that the random effects classification reduced to 63% (Table 5, right).

Table 5. Fixed and random effect confusion matrices for PLS-DA (4 factors).

	Fixed Effects Model				Random Effects Model

	Actual Class				Actual Class

	EN	AD	FTD		EN	AD	FTD
EN (N=34)	33	1	4	EN (N=34)	28	11	5
AD (N=37)	1	34	3	AD (N=37)	4	19	9
FTD (N=33)	0	2	26	FTD (N=33)	2	7	19

Open in a new tab

In short, these three, very common, linear classifiers show no better performance for random effects classification than one another or—and more importantly— than MUBADA. By contrast with these methods however, MUBADA provides more information because 1) it can handle multiblock data and 2) it is also computationally more efficient (particularly for the cross-validation component).

Discussion

In general, our approach performed well when challenged with a-priori groups not normally easy to separate. AD and FTD were well separated from each other and from EN. It is also encouraging that the ROIs contributing to these separations are, mostly, those expected to do so. For example, as expected (see, e.g., [32, 33]), FTD is separated from the other groups by a difference in rCBF activation in bilateral inferior and middle frontal gyri. Also contributing to this separation are left middle and inferior temporal gyri, which support normal language function [34].

Similarly, the AD group is characterized by rCBF abnormalities in the posterior cortical association areas (i.e., left precuneus and bilateral inferior parietal and inferior temporal gyri), which are known to be involved in the onset of the disease [33] and whose metabolism is in general abnormal when AD patients are compared to normal elderly controls [32]. Involvement of the frontal areas is observed in well-established AD [35]. Though thalamus is not commonly identified as functionally impaired in AD, it is among key subcortical structures engaged in cholinergic neurotransmission, and loss of thalamic cholinergic neurons is observed in AD [36]. Further, recent structural imaging studies have focused on degeneration of this critical deep gray matter region. For example, de Jong et al [37] performed morphometric studies from high resolution T1-weighted MRI in 69 probable AD subjects. In addition to finding the typical association between hippocampal atrophy and cognitive decline in AD, thalamic volume was significantly reduced and the decrease in volume correlated linearly with impaired global cognitive performance. Thus our finding of bilateral thalamus abnormality separating AD from EN and FTD is not unreasonable.

While it could be possible to simply restrict our analyses to ROIs already known to be involved in these neurodegenerative disorders, the purpose of this effort was to explore methods for the analysis of complex neuroimaging data sets. Thus the dataset from these participants served as a test case. However, it is important to note that without any a-priori assumptions about what regions would be relevant, MUBADA correctly identified those ROIs most often associated with AD and FTD. Further, as seen in Figure 4, the relative contributions of various ROIs are a normal output of this approach: An insight that typical analyses of small sets of ROIs would not provide. Finally, it is also noteworthy that new ROIs were identified that bear further study (e.g., thalamus) in terms of their role in discriminating groups (in particular, FTD from AD).

There are certainly limitations to the generalizability of our findings. For example, variations in data acquisition techniques across sites are problematic for functional neuroimaging data, and perhaps our single-site data represent a “best-case scenario.” Similarly, SPECT rCBF data do not have the same spatial resolution as PET FDG images, or the same signal-to-noise ratio for lesion detection. Thus data derived from PET studies might perform even better. In addition, mixed pathologies plague all studies of neurodegenerative disorders, and even in the context of cohorts evaluated by an NIH-funded Alzheimer's Disease Center diagnostic heterogeneity is unavoidable short of autopsy-confirmed diagnoses. Thus our finding should be considered carefully in the context of the sample explored. In addition to these limitations, the results we obtained depend also upon pre-processing choices. For example, we did not explicitly report the effects of the type of smoothing used (while we do not present these results here, we found that changing the level of smoothing had little effect on the results) nor the effect of normalizing the scans prior to the analysis (we found that this normalization had a small but real effect). We did not explore the effect of the type of spatial normalization used (i.e., MNI vs other schemes), but we suspect that it is likely to have an effect. To completely explore the effect of these choices on classifier performance remains an important question that should be addressed by further work.

Block normalization and relationship with other approaches

Blocks (ROIs) in MUBADA are simply considered as sets of variables. Therefore, the influence of a given block (ROI) depends, in part, upon its number of variables (voxels) as well as its factorial structure because a block with a large first eigenvalue will have a large influence on the first factor of the whole table. By contrast, a block with a small first eigenvalue will have a small effect on the first factor of the whole table. In order to eliminate such discrepancies, the multiple factor analysis approach [14, 16, 17, 38] normalizes each block by dividing each element of a block by its first singular value, an alternate approach STATIS finds normalization weights that will optimize the between block (ROI) similarity (see [17], for a comprehensive review). Fortunately, for BADA, all normalization schemes can be performed on the blocks of the original data matrix, but their effects are easier to analyze if they are performed on the barycentric matrix. We plan to explore the effects of these normalizations schemes in further work but, for the sake of simplicity, we have decided not to implement any of these normalization schemes in the present work.

Though not part of this work, it is noteworthy that MUBADA can straightforwardly handle multi-modal data in addition to ROIs. For, example, if we had collected bio-markers and behavioral data for all our participants, we could have integrated these two data sets in the analysis by treating them as two virtual ROIs. Similarly, MUBADA could directly be used for analyzing multimodal brain imaging data (e.g., SPECT/fMRI, or SPECT/PET)—an approach that has recently been recommended as one of the next step to follow in brain imaging applied to the study of Alzheimer disease [42. In brief, MUBADA reaches the same level as other pattern classifiers, but is superior to these classifiers in its ability to handle large data sets, to preserve voxels information, to compute statistical estimates by cross-validation, and in its unique ability to handle multiple ROIs and multi-modal information.

Conclusion

MUBADA seems well suited to analyze functional neuroimaging data such as SPECT because it can handle very large data sets (with more variables than observations) that are structured in ROIs or in multiple data tables. It is versatile enough to be used also in cases where multiple scans are obtained on several participants (e.g., as in fMRI [1, 43]). Also, because it can incorporate inferential components, it complements other popular approaches such as partial least squares [2, 3], which are widely used to analyze neuroimaging data. In our data, MUBADA separated AD and FTD groups from the EN group based on contributions from ROIs known to be involved in the relevant neuropathology of the dementias.

Acknowledgments

The authors wish to thank the investigators who participated in the original studies from which these data were taken, including Drs. Roger Rosenberg, Frederick Bonte, Ramon Diaz-Arrastia, Myron Weiner, and Kyle Womack. The original technical assistance of J. Kelly Payne in these studies is also greatly appreciated. This work was supported in part by NIH/NIA grant 5P30AG-12300.

Appendix

Formal Presentation of Mubada

Notations

The original data matrix is an N observations by J variables matrix denoted X. Prior to the analysis, the matrix X can be pre-processed (1) by centering (i.e., subtracting the column mean from each column), (2) by transforming each column into a Z-score, or (3) by normalizing each row so that the sum of its elements or the sum of its squared elements is equal to one (which is the normalization used here). The observations (rows) in X are partitioned into I a-priori groups of interest with N_i being the number of observations of the ith group (and so Σ N_i = N). The variables (columns) of matrix X can be arranged in K a-priori blocks (or sub-tables). The number of columns of the kth block are denoted J_k (and therefore Σ J_k = J). So, the matrix X can be decomposed into I by K blocks as (see Figure 5, for an illustration):

x = {\overset{\begin{matrix} 1 & \dots & k & \dots & K \end{matrix}}{\begin{matrix} 1 \\ ⋮ \\ i \\ ⋮ \\ I \end{matrix} [\begin{matrix} x_{1, 1} & \dots & x_{1, k} & \dots & x_{1, K} \\ ⋮ & ⋱ & ⋮ & ⋱ & ⋮ \\ x_{i, 1} & \dots & x_{i, k} & \dots & x_{i, K} \\ ⋮ & ⋱ & ⋮ & ⋱ & ⋮ \\ x_{I, 1} & \dots & x_{I, k} & \dots & x_{I, K} \end{matrix}]}}_{.}

(1)

Notations for the groups (rows)

We denote by Y the N by I design (a.k.a., dummy) matrix for the groups describing the rows of X: y_n,i = 1 if row n belongs to group i, y_n,i = 0 otherwise. We denote by m the N by 1 vector of masses for the rows of X and by M the N by N diagonal matrix whose diagonal elements are the elements of m (i.e., using the diag operator which transforms a vector into a diagonal matrix, we have M = diag{m}). Masses are positive numbers and it is convenient (but not necessary) to have the sum of the masses equal to one. The default value for the mass of each observation is in general equal to $\overset{1}{} / \underset{N}{}$ . We denote by b the I by 1 vector of masses for the groups describing the rows of X and by B the I by I diagonal matrix whose diagonal elements are the elements of b.

Notations for the blocks (columns)

We denote by Z the J by K design matrix for the blocks from the columns of X: z_j,k = 1 if column j belongs to block k; z_j,k = 0 otherwise. We denote by w the J by 1 vector of weights for the columns of X and by W the J by J diagonal matrix whose diagonal elements are the elements of w. We denote by c the K by 1 vector of weights for the blocks of X and by C the K by K diagonal matrix whose diagonal elements are the elements of c. The default value for the weight of each variable is $\overset{1}{} / \underset{J}{}$ , a more general case requires only W to be positive definite (i.e., in order to include non-diagonal weight matrices).

BADA

The first step of BADA is to compute the barycenter of each of the I groups comprising the rows. The barycenter of a group is the weighted average of the rows in which the weights are the masses re-scaled such that the sum of the weights for one group is equal to one. Specifically, the I by J matrix of barycenters, denoted R, is computed as

R = {(diag {Y^{T} M 1})}^{- 1} Y^{T} MX

(2)

where 1 is a N by 1 vector of 1s and the diagonal matrix (diag{Y^TM1})⁻¹ rescales the masses of the rows such that their sum is equal to one for each group (see Figure 6 for an illustration)

Computing the R matrix of the group barycenters (i.e., means) of the groups of participants.

Masses and weights

The type of preprocessing, the choice of the matrix of masses for the groups (B), and the matrix of weights for the variables (W) is crucial because these choices determine the type of GPCA used. For example, discriminant correspondence analysis is obtained by transforming the rows of R into relative frequencies, and by using the relative frequencies of the barycenters as the masses of the rows and the inverse of the column frequencies as the weights of the variables. The choice of weight matrix W is equivalent to defining a generalized Euclidean distance between J-dimensional vectors (see [39]). Specifically, if x_n and x_n′ are two J-dimensional vectors, the generalized Euclidean squared distance between these two vectors is

d_{w}^{2} (X_{n}, X_{n'}) = {(X_{n} - X_{n'})}^{T} W (X_{n} - X_{n'}) .

(3)

For the data in this study, each voxel was given an equal weight of $\overset{1}{} / \underset{J}{}$ and each observation was given an equal mass of $\overset{1}{} / \underset{N}{}$ (and therefore each group was given a mass of $\overset{N_{1}}{} / \underset{J}{}$ ).

GPCA of the barycenter matrix

The analysis is implemented by performing a generalized singular value decomposition of matrix R[7, 10, 31, 38, 40], which is expressed as:

R = P Δ Q^{T} with P^{T} BP = Q^{T} WQ = I

(4)

where Δ is the L by L diagonal matrix of the singular values (with L being the number of non-zero singular values), and P (respectively Q) being the I by L (respectively J by L) matrix of the left (respectively right) generalized singular vectors of R.

Factor scores

The I by L matrix of factor scores for the groups is obtained as:

F = P Δ = RWQ .

(5)

The variance of the columns of F is given by the square of the corresponding singular values (i.e., the “eigenvalues” denoted λ) and is stored in the diagonal matrix Λ. This can be shown by combining Equations 4 and 5 to give:

F^{T} BF = Δ P^{T} BP Δ = Δ^{2} = Λ .

(6)

These factor scores are the projections of the groups on the GPCA space (see Figure 7 for an illustration).

Computing the PCA (i.e., singular value decomposition) of R provides factors scores for participants (and loadings for the voxels).

Supplementary elements

The N rows of matrix X can be projected (as “supplementary” or “illustrative” elements) onto the space defined by the factor scores of the barycenters. Note that the matrix WQ from Equation 5 is a projection matrix (see Figure 8 for an illustration). Therefore, the N by L matrix H of the factor scores for the rows of X can be computed as

H = XWQ .

(7)

These projections are barycentric, because the weighted average of the factor scores of the rows of a group gives the factors scores of that group. This is shown by first computing the barycenters of the row factor scores as (cf. Equation 2) as:

H = {(diag {YM 1})}^{- 1} YMH

(8)

and then plugging in Equation 7 and developing. Taking this into account, Equation 8 gives

H = {(diag {YM 1})}^{- 1} YMXWQ = RWQ = F .

(9)

Loadings

The loadings describe the variables of the barycentric data matrix and are used to identify the variables important for the separation between the groups. As for standard PCA, there are several ways of defining the loadings. The loadings can be defined as the correlation between the columns of matrix R and the factor scores. They can also be defined as the matrix Q or (as we do in our case) as:

G = Q Δ .

(10)

Quality of the prediction

The performance, or quality, of the prediction of a discriminant analysis is assessed by predicting the group membership of the observations and by comparing the predicted group membership with the actual group membership. The pattern of correct and incorrect classifications can be stored in a confusion matrix in which the columns represent the actual groups and the rows represent the predicted groups. At the intersection of a row and a column is the number of observations from the column group assigned to the row group.

The performance of the model can be assessed for the observations used to compute the groups: these observations constitute the training set. The true performance of the model, however, needs to be evaluated with observations not used to compute the model: these observations constitute the testing set.

Training set

The observations in the training set are used to compute the barycenters of the groups. In order to assign an observation to a group, the first step is to compute the distance between this observation and all I groups. Then, the observation is assigned to the closest group. Several possible distances can be chosen, but a natural choice is the Euclidean distance computed in the factor space. If we denote by h_n the vector of factor scores for the nth observation, and by f_i the vector of factor scores for the ith group, then the squared Euclidean distance between the nth observation and the ith group is computed as:

d^{2} (h_{n}, f_{i}) = {(h_{n} - f_{i})}^{T} (h_{n}, f_{i}) .

(11)

Obviously, other distances are possible, but the Euclidean distance has the advantage of being “directly read” on the map.

Tolerance intervals

The quality of the group assignment of the actual observations can be displayed using tolerance intervals. A tolerance interval encompasses a given proportion of a sample. When displayed in two dimensions, these intervals have the shape of an ellipse and are called tolerance ellipsoids.

For BADA, a group tolerance ellipsoid is plotted on the group factor score map. This ellipsoid is obtained by fitting an ellipse that includes a given percentage (e.g., 95%) of the observations. Tolerance ellipsoids are centered on their groups and the overlap of the tolerance ellipsoids of two groups reflects the proportion of misclassifications between these two groups. (see Figure 9 for an illustration)

Drawing ellipsoid that comprises 95% of the participants' factor scores provides *tolerance* ellipsoids.

Testing set

The observations of the testing set are not used to compute the barycenters but are used only to evaluate the quality of the assignment of new observations to groups. A variation of this process is the “leave-one-out” approach: each observation is taken out from the data set, in turn, and is then projected onto the factor space of the remaining observations in order to predict its group membership. For the estimation to be unbiased, the left-out o(x00303)bservation should not be used in any way in the analysis. In particular, if the data matrix is preprocessed, the left-out observation should not be used in the preprocessing. So, for example, if the columns of the data matrix are transformed into Z-scores, the left-out observation should not be used to compute the means and standard deviations of the columns of the matrix to be analyzed. However, these means and standard deviations will be used to compute the Z-score for the left-out observation.

The assignment of a new observation to a group follows the same procedure as for an observation from the training set: the observation is projected onto the group factor scores, and it is assigned to the closest group. Specifically, we denote by X_−n the data matrix without the nth observation and by x_n the 1 by J row vector representing the nth observation. If X_−n is preprocessed (e.g., centered and normalized), the pre-processing parameters will be estimated without x_n (e.g., the mean and standard deviation of X_−n is computed without x_n) and x_n will be pre-processed with the parameters estimated for X_−n (e.g., x_n will be centered and normalized using the means and standard deviations of the columns of X_−n). Then the matrix of barycenters R_−n is computed and its generalized eigendecomposition is obtained as (cf. Equation 4):

R_{- n} = P_{- n} Δ_{- n} Q with P_{- n}^{T} W_{- n} P_{- n} = Q_{- n}^{T} B_{- n} Q_{- n} = I

(12)

(with B_−n and W_−n being the mass and weight matrices for R_−n). The matrix of factor scores denoted F_−n is obtained as (cf. Equation 5)

F_{- n} = P_{- n} Δ_{n} = R_{n} W_{- n} Q_{- n} .

(13)

The projection of the nth observation, considered as the “testing observation” is denoted h_n and it is obtained as (cf. Equation 7)

h_{n} = x_{n} W_{- n} Q_{- n} .

(14)

Distances between this nth observation and the I groups can be computed with the factor scores (cf. Equation 11). The observation is then assigned to the closest group.

Prediction intervals

In order to display the quality of the prediction for new observations we use prediction intervals. A “leave-one-out” is used to predict each observation from the other observation. To compute prediction intervals, we first project the left-out observations onto the original complete factor space, in our case using a two-step procedure. First, the observation is projected onto its training set space and is reconstructed from its projections. Then, the reconstituted observation, denoted x_n, is projected onto the full factor score solution. A left-out observation is reconstituted from its factor scores as (cf. Equations 4 and 14):

\tilde{x} = h_{n} Q_{- n}^{T} .

(15)

The projection of the left-one-out observation is denoted and is obtained by projecting x_n as a supplementary element in the original solution. Specifically, ĥ_n is computed as:

\begin{matrix} {\hat{h}}_{n} = {\tilde{x}}_{n} WQ (cf . Equation 4) \\ = {\tilde{h}}_{n} Q_{- n}^{T} WQ (cf . Equation 14) \\ = x_{n} W_{- n} Q_{- n} Q_{- n}^{T} WQ (cf . Equation 13) . \end{matrix}

(16)

Prediction ellipsoids are not necessarily centered on their groups (the distance between the center of the ellipse and the group represents the estimation bias). The overlap of two predictions intervals directly reflects the proportion of misclassifications for the “new” observations.

Quality of the group separation

Explained inertia (R²) and permutation test

In order to evaluate the quality of the discriminant model, we used a coefficient inspired by the coefficient of correlation. Because BADA is a barycentric technique, the total inertia (i.e., the “variance”) of the observations to the grand barycenter (the barycenter of all groups) can be decomposed into two additive quantities: (1) the inertia of the observations relative to the barycenter of their own group, and (2) the inertia of the group barycenters to the grand barycenter.

Specifically, if we denote by f̄ the vector of the coordinates of the grand barycenter (i.e., each component of this vector is the average of the corresponding components of the barycenters), the total inertia, denoted ℑ_Total, is computed as the sum of the squared distances of the observations to the grand barycenter:

ℑ_{Total} = \sum_{n}^{N} m_{n} d^{2} (h_{n}, \bar{f}) = \sum_{n}^{N} m_{m} d^{2} {(h_{n} - \bar{f})}^{T} (h_{n} - \bar{f}) .

(17)

The inertia of the observations relative to the barycenter of their own group is abbreviated as the “inertia within.” It is denoted ℑ_Within and computed as:

ℑ_{Within} = \sum_{i}^{I} \sum_{n in group i} m_{n} d^{2} (h_{n}, f) = \sum_{i}^{I} \sum_{n in group i} m_{n} d^{2} {(h_{n} - f)}^{T} (h_{n} - f) .

(18)

The inertia of the barycenters to the grand barycenter is abbreviated as the “inertia between.” It is denoted ℑ_Between and computed as:

ℑ_{Between} = \sum_{n}^{N} b_{i} \times d^{2} (f_{i}, \bar{f}) = \sum_{n}^{N} b_{i} \times d^{2} {(f_{i} - \bar{f})}^{T} (f_{i} - \bar{f}) .

(19)

So the additive decomposition of the inertia can be expressed as

ℑ_{Total} = ℑ_{Within} + ℑ_{Between} .

(20)

This decomposition is similar to the familiar decomposition of the sum of squares in the analysis of variance, suggesting that the intensity of the discriminant model can be tested by the ratio of between inertia and the total inertia. This ratio is denoted R² and it is computed as:

R^{2} = \frac{ℑ_{Between}}{ℑ_{Total}} = \frac{ℑ_{Between}}{ℑ_{Within} + ℑ_{Between}} .

(21)

The R² ratio takes values between 0 and 1, the closer to one the better the model. The significance of R² can be assessed by permutation tests, and confidence intervals can be computed using resampling techniques such as the Bootstrap method (see [31]).

Confidence intervals

The stability of the position of the groups can be displayed using confidence intervals, which reflect the variability of a population parameter or its estimate. In two dimensions, these intervals become confidence ellipsoids. The problem of estimating the variability of the position of the groups cannot, in general, be solved analytically and cross-validation techniques need to be used. Specifically, the variability of the position of the groups is estimated by generating bootstrapped samples from the sample of observations. A bootstrapped sample is obtained by sampling with replacement from the observations. The “bootstrapped barycenters” obtained from these samples are then projected onto the discriminant factor space and, finally, an ellipse is plotted such that it comprises a given percentage (e.g., 95%) of these bootstrapped barycenters (see Figure 10 for an illustration). When the confidence intervals of two groups do not overlap, these two groups are “significantly different” at the corresponding alpha level (e.g., α = .05, see [41]).

Fitting ellipsoids that comprises 95% of the bootstrapped means provides *confidence* ellipsoids.

MUBADA

In a multiblock analysis, the blocks can be analyzed by projecting the groups and the observations for each block. As was the case for the groups, these projections are barycentric because the barycenter of the all the blocks gives the coordinates of the whole table.

Partial projection

Each block can be projected in the common solution. The procedure starts by rewriting Equation 4 (see Figure 11 for an illustration):

Projecting an ROI onto the groups factor space provides a *partial factor score* for this ROIs (note the mean of the ROIs' partial scores is equal to the group factor scores).

R = P Δ Q^{T} = P Δ {[Q_{1}, \dots, Q_{k}, \dots, Q_{k}]}^{T},

(22)

where Q_k is the kth block (comprising the J_k columns of Q corresponding to the J_k columns of the kth block). Then, to get the projection for the kth block, Equation 5 is rewritten as:

F_{k} = {KX}_{k} W_{k} Q_{k}

(23)

(where W_k is the weight matrix for the J_k columns of the kth block).

Equation 19 can also be used to project supplementary rows corresponding to a specific block. Specifically, if $x_{sup, k}^{T}$ is a 1 by J_k row vector of a supplementary element to be projected according to the kth block, its factor scores are computed as:

f_{sup, k} = K x_{sup, k} W_{k} Q_{k}

(24)

(Note that x_sup,k is to have been pre-processed as X_k; for example if X_k has been transformed into Z-scores, x_sup,k will be transformed into a Z-score using the mean and standard deviation computed from X_k).

Inertia of a block

Recall from Equation 6 that, for a given dimension, the variance of the factor scores of all the J columns of matrix R is equal to the eigenvalue of this dimension. Because each block comprises a set of columns, the contribution of a block to a dimension can be expressed as the sum of this dimension squared factor scores of the columns of this block (see Figure 12 for an illustration). The inertia for the kth table and the ith dimension is computed as:

Summing all the contribution of the voxels of a given ROI provides the inertia (i.e., variance) explained by this ROI. The inertia explained by all the ROIs can be plotted as 2D maps.

ℑ_{ℓ, k} = \sum_{j \in jk} W_{j} f_{ℓ, j}^{2} .

(25)

Note that the sum of the inertia of the blocks for a given dimension gives back the eigenvalue (i.e., the inertia) of this dimension:

λ_{ℓ} = \sum_{k} ℑ_{ℓ, k} .

(26)

Also the sum of the all the partial inertias gives back the total inertia.

Finding the important ROIs

The structures that contribute to the discrimination between the classes are identified from their partial contributions to the inertia (see Equation 25).

Footnotes

The authors declare that no conflict of interest exists.

Author Note: Matlab and R programs implementing MUBADA and masks (in analyze format) will be made available for download from the first author's home page at http://www.utdallas.edu/∼herve

References

1.O'Toole AJ, Jiang F, Abdi H, Pénard N, Dunlop JP, Parent MA. Theoretical, statistical, and practical perspectives on pattern-based classification approaches to the analysis of functional neuroimaging data. J Cogn Neurosci. 2007;19:1735–1752. doi: 10.1162/jocn.2007.19.11.1735. [DOI] [PubMed] [Google Scholar]
2.Krishnan A, Williams LJ, McIntosh AR, Abdi H. Partial Least Squares (PLS) Methods for Neuroimaging: A Tutorial and Review. NeuroImage. 2011;56:455–475. doi: 10.1016/j.neuroimage.2010.07.034. [DOI] [PubMed] [Google Scholar]
3.McIntosh AR, Lobaugh NJ. Partial least square analysis of neuroimaging data: applications and advances. NeuroImage. 2004;23:5250–5263. doi: 10.1016/j.neuroimage.2004.07.020. [DOI] [PubMed] [Google Scholar]
4.Dudoit S, Fridlyand J, Speed T. Comparison of discrimination methods for the classification of tumors using gene expression data. J Am Stat Assoc. 2002;97:77–87. [Google Scholar]
5.Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. 2nd. New York: Springer Verlag; 2008. [Google Scholar]
6.Efron B, Tibshirani R. An introduction to the bootstrap. New York: Chapman & Hall; 1993. [Google Scholar]
7.Abdi H. Singular Value Decomposition (SVD) and Generalized Singular Value Decomposition (GSVD) In: Salkind NJ, editor. Encyclopedia of measurement and statistics. Vol. 2007. Thousand Oaks: Sage; pp. 907–912. [Google Scholar]
8.Abdi H. Encyclopedia of measurement and statistics. Vol. 2007. Thousand Oaks: Sage; Discriminant Correspondence Analysis (DCA) pp. 280–284. [Google Scholar]
9.Gittins R. Canonical analysis: A review with applications in ecology. New York: Springer Verlag; 1980. [Google Scholar]
10.Greenacre M. Theory and applications of correspondence analysis. London: Academic Press; 1984. [Google Scholar]
11.Perriére G, Thioulouse J. Use of Correspondence Discriminant Analysis to predict the subcellular location of bacterial proteins. Comput Methods Programs Biomed. 2003;70:99–105. doi: 10.1016/s0169-2607(02)00011-1. [DOI] [PubMed] [Google Scholar]
12.Saporta G, Niang N. Correspondence analysis and classification. In: Greenacre M, Blasius J, editors. Multiple correspondence analysis and related methods. Boca Raton: Chapman & Hall/CRC; 2006. pp. 371–392. [Google Scholar]
13.Williams L, Abdi H, French R, Orange J. A tutorial on Multi-Block Discriminant Correspondence Analysis (MUDICA): A new method for analyzing discourse data from clinical populations. J Speech Lang Hear Res. 2010;53:1372–1393. doi: 10.1044/1092-4388(2010/08-0141). [DOI] [PubMed] [Google Scholar]
14.Abdi H, Valentin D. Multiple factor analysis. In: Salkind N, editor. Encyclopedia of measurement and statistics. Thousand Oaks: Sage; 2007. pp. 657–663. [Google Scholar]
15.Abdi H, Valentin D. STATIS. In: Salkind N, editor. Encyclopedia of measurement and statistics. Vol. 2007. Thousand Oaks: Sage; pp. 284–290. [Google Scholar]
16.Escofier B, Pagès J. Multiple factor analysis. Computational Statistics & Data Analysis. 1990;18:121–140. [Google Scholar]
17.Abdi H, Williams LJ, Valentin D, Bennani-Dosse M. STATIS and DISTATIS: Optimum multi-table principal component analysis and three way metric multidimensional scaling. Wiley Interdisciplinary Reviews: Computational Statistics. 2012;4:124–167. [Google Scholar]
18.McKhann G, Drachman D, Folstein M, et al. Clinical diagnosis of Alzheimer's disease: Report of the NINDS-ADRDA work group under the auspices of the Department of Health and Human Services Task Force of Alzheimer's disease. Neurology. 1984;34:939–944. doi: 10.1212/wnl.34.7.939. [DOI] [PubMed] [Google Scholar]
19.Neary D, Snowden JS, Gustafson L, Passant U, Stuss D, Black S, et al. Frontotemporal lobar degeneration: a consensus on clinical diagnostic criteria. Neurology. 1998:1546–54. doi: 10.1212/wnl.51.6.1546. [DOI] [PubMed] [Google Scholar]
20.Evans A, Collins D, Mills S, Brown E, Kelly R, Peters T. 3D statistical neuroanatomical models from 305 MRI volumes; Proceedings of the IEEE Nuclear Science Symposium and Medical Imaging Conference; London. 1993; MTP Press; 1993. pp. 1813–1817. [Google Scholar]
21.Friston K, Holmes A, Worsley K, Poline J, Frith C, Frackowiak R. Statistical parametric maps in functional imaging: a general linear approach. Hum Brain Mapp. 1995;2:189–210. [Google Scholar]
22.Rorden C. MRIcro (Version 1.37, Build 4) 2003 [Computer software[. Retrieved October 14. [Google Scholar]
23.Connolly AC, Gobbini MI, Haxby JV. Three virtues of similarity- based multivariate pattern analysis: an example from the human object vision pathway. In: Kriegeskorte N, Kreiman G, editors. Visual population codes: toward a common multivariate framework for cell recording and functional imaging. Cambridge, MA: MIT; 2012. [Google Scholar]
24.Pereira F, Mitchell T, Botvinick M. Machine learning classifiers and fMRI: A tutorial overview. NeuroImage. 2009;45(1, Supplement 1):S199–S209. doi: 10.1016/j.neuroimage.2008.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
25.Abdi H. Partial least square regression, projection on latent structure regression, PLS-Regression. Wiley Interdisciplinary Reviews: Computational Statistics. 2010;2:97–106. [Google Scholar]
26.Silverman D, Devous M., Sr . PET and SPECT Imaging in Evaluating Alzheimer's Disease and Related Dementias. In: Ell P, Gambhir S, editors. Nuclear Medicine in Clinical Diagnosis and Treatment. 3rd. London: Churchill Livingstone; 2004. pp. 1435–1448. [Google Scholar]
27.Stühler E, Platsch G, Weih M, Kornhuber J, Kuwert T, Merhof D. Multiple Discriminant Analysis of SPECT Data for Alzheimer's Disease, Frontotemporal Dementia and Asymptomatic Controls; IEEE Medical Imaging Conference (IEEE MIC); 2011; p. MIC22. [Google Scholar]
28.Stühler E, Merhof D. Principal Component Analysis Applied to SPECT and PET Data of Dementia Patients –A Review. In: Sanguansat Parinya., editor. Principal Component Analysis: Multidisciplinary Applications. Rijeka, Croatia: InTech; 2012. pp. 167–186. [Google Scholar]
29.Mur M, Bandettini PA, Kriegeskorte N. Revealing representational content with pattern-information fMRI--an introductory guide. Soc Cogn Affect Neurosci. 2009;4:101–109. doi: 10.1093/scan/nsn044. [DOI] [PMC free article] [PubMed] [Google Scholar]
30.Hall M, Frank E, Holmes G, Pfahringer B, Reutemann P, Witten IH. The WEKA data mining software. ACM SIGKDD Explorations Newsletter. 2009;11:10. [Google Scholar]
31.Abdi H, Williams LJ. Principal component analysis. Wiley Interdisciplinary Reviews: Computational Statistics. 2010;2:433–459. [Google Scholar]
32.Jagust W. Positron emission tomography and magnetic resonance imaging in the diagnosis and prediction of dementia. Alzheimer's Dement. 2006;2:36–42. doi: 10.1016/j.jalz.2005.11.002. [DOI] [PubMed] [Google Scholar]
33.Santens P, De Bleecker J, Goethals P, Strijckmans K, Lemahieu I, Sledgers G, Dierckx R, De Reuck J. Differential regional cerebral uptake of (18)F-fluoro- 2-deoxy-D-glucose in Alzheimer's disease and frontotemporal dementia at initial diagnosis. Eur Neurol. 2001;45:19–27. doi: 10.1159/000052084. [DOI] [PubMed] [Google Scholar]
34.Binder J, Frost J, Hammeke T, Bellgowan PSF, Springer JA, Kaufman JN, Possing ET. Human temporal lobe activation by speech and nonspeech sounds. Cereb Cortex. 2000;10:512–528. doi: 10.1093/cercor/10.5.512. [DOI] [PubMed] [Google Scholar]
35.Weiner M, Wighton-Benn W, Risser R, Svetlik D, Tintner R, Hom J, Rosenburg RN, Bonte FJ. Xenon-133 SPECT-determined regional cerebral blood flow in Alzheimer's disease: what is typical? J Neuropsychiatry Clin Neurosci. 1993;5:415–418. doi: 10.1176/jnp.5.4.415. [DOI] [PubMed] [Google Scholar]
36.Braak H, Braak E. Alzheimer's disease affects limbic nuclei of the thalamus. Acta Neuropathologica. 1991;81:261–268. doi: 10.1007/BF00305867. [DOI] [PubMed] [Google Scholar]
37.De Jong LW, van der Hiele K, Veer IM, Houwing JJ, Westendorp RGJ, Bollen ELEM, de Bruin PW, Middelkoop HAM, van Buchem MA, van der Grond J. Strongly Reduced Volumes of Putamen and Thalamus in Alzheimer's Disease: An MRI Study. Brain. 2008;131:3277–3285. doi: 10.1093/brain/awn278. [DOI] [PMC free article] [PubMed] [Google Scholar]
38.Escoufier Y. L'analyse conjointe de plusieurs matrices de données [Joint analysis of multiple data matrices] In: Jolivet M, editor. Biométrie et Temps. Vol. 1980. Paris: Société Française de Biométrie; pp. 59–76. [Google Scholar]
39.Abdi H. Distance. In: Salkind N, editor. Encyclopedia of measurement and statistics. Thousand Oaks: Sage; 2007. pp. 270–275. [Google Scholar]
40.Takane Y. Relationships among various kinds of eigenvalue and singular value decompositions. In: Yanai H, Okada A, Shigemasu K, Kano Y, Meulman, editors. New developments in psychometrics. Tokyo: Springer Verlag; 2002. pp. 45–56. [Google Scholar]
41.Abdi H, Dunlop JP, Williams LJ. How to compute reliability estimates and display confidence and tolerance intervals for pattern classifiers using the Bootstrap and 3-way multidimensional scaling (DISTATIS) NeuroImage. 2009;45:89–95. doi: 10.1016/j.neuroimage.2008.11.008. [DOI] [PubMed] [Google Scholar]
42.Reiman EM, Jagust WJ. Brain imaging in the study of Alzheimer's disease. NeuroImage. 2012;61:505–516. doi: 10.1016/j.neuroimage.2011.11.075. [DOI] [PMC free article] [PubMed] [Google Scholar]
43.Abdi H, Williams LJ, Connolly AC, Gobbini MI, Dunlop JP, Haxby JV. Multiple Subject Barycentric Discriminant Analysis (MUSUBADA): How to assign scans to categories without using spatial normalization. Computational and Mathematical Methods in Medicine 2012. 2012:1–15. doi: 10.1155/2012/634165. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R1] 1.O'Toole AJ, Jiang F, Abdi H, Pénard N, Dunlop JP, Parent MA. Theoretical, statistical, and practical perspectives on pattern-based classification approaches to the analysis of functional neuroimaging data. J Cogn Neurosci. 2007;19:1735–1752. doi: 10.1162/jocn.2007.19.11.1735. [DOI] [PubMed] [Google Scholar]

[R2] 2.Krishnan A, Williams LJ, McIntosh AR, Abdi H. Partial Least Squares (PLS) Methods for Neuroimaging: A Tutorial and Review. NeuroImage. 2011;56:455–475. doi: 10.1016/j.neuroimage.2010.07.034. [DOI] [PubMed] [Google Scholar]

[R3] 3.McIntosh AR, Lobaugh NJ. Partial least square analysis of neuroimaging data: applications and advances. NeuroImage. 2004;23:5250–5263. doi: 10.1016/j.neuroimage.2004.07.020. [DOI] [PubMed] [Google Scholar]

[R4] 4.Dudoit S, Fridlyand J, Speed T. Comparison of discrimination methods for the classification of tumors using gene expression data. J Am Stat Assoc. 2002;97:77–87. [Google Scholar]

[R5] 5.Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. 2nd. New York: Springer Verlag; 2008. [Google Scholar]

[R6] 6.Efron B, Tibshirani R. An introduction to the bootstrap. New York: Chapman & Hall; 1993. [Google Scholar]

[R7] 7.Abdi H. Singular Value Decomposition (SVD) and Generalized Singular Value Decomposition (GSVD) In: Salkind NJ, editor. Encyclopedia of measurement and statistics. Vol. 2007. Thousand Oaks: Sage; pp. 907–912. [Google Scholar]

[R8] 8.Abdi H. Encyclopedia of measurement and statistics. Vol. 2007. Thousand Oaks: Sage; Discriminant Correspondence Analysis (DCA) pp. 280–284. [Google Scholar]

[R9] 9.Gittins R. Canonical analysis: A review with applications in ecology. New York: Springer Verlag; 1980. [Google Scholar]

[R10] 10.Greenacre M. Theory and applications of correspondence analysis. London: Academic Press; 1984. [Google Scholar]

[R11] 11.Perriére G, Thioulouse J. Use of Correspondence Discriminant Analysis to predict the subcellular location of bacterial proteins. Comput Methods Programs Biomed. 2003;70:99–105. doi: 10.1016/s0169-2607(02)00011-1. [DOI] [PubMed] [Google Scholar]

[R12] 12.Saporta G, Niang N. Correspondence analysis and classification. In: Greenacre M, Blasius J, editors. Multiple correspondence analysis and related methods. Boca Raton: Chapman & Hall/CRC; 2006. pp. 371–392. [Google Scholar]

[R13] 13.Williams L, Abdi H, French R, Orange J. A tutorial on Multi-Block Discriminant Correspondence Analysis (MUDICA): A new method for analyzing discourse data from clinical populations. J Speech Lang Hear Res. 2010;53:1372–1393. doi: 10.1044/1092-4388(2010/08-0141). [DOI] [PubMed] [Google Scholar]

[R14] 14.Abdi H, Valentin D. Multiple factor analysis. In: Salkind N, editor. Encyclopedia of measurement and statistics. Thousand Oaks: Sage; 2007. pp. 657–663. [Google Scholar]

[R15] 15.Abdi H, Valentin D. STATIS. In: Salkind N, editor. Encyclopedia of measurement and statistics. Vol. 2007. Thousand Oaks: Sage; pp. 284–290. [Google Scholar]

[R16] 16.Escofier B, Pagès J. Multiple factor analysis. Computational Statistics & Data Analysis. 1990;18:121–140. [Google Scholar]

[R17] 17.Abdi H, Williams LJ, Valentin D, Bennani-Dosse M. STATIS and DISTATIS: Optimum multi-table principal component analysis and three way metric multidimensional scaling. Wiley Interdisciplinary Reviews: Computational Statistics. 2012;4:124–167. [Google Scholar]

[R18] 18.McKhann G, Drachman D, Folstein M, et al. Clinical diagnosis of Alzheimer's disease: Report of the NINDS-ADRDA work group under the auspices of the Department of Health and Human Services Task Force of Alzheimer's disease. Neurology. 1984;34:939–944. doi: 10.1212/wnl.34.7.939. [DOI] [PubMed] [Google Scholar]

[R19] 19.Neary D, Snowden JS, Gustafson L, Passant U, Stuss D, Black S, et al. Frontotemporal lobar degeneration: a consensus on clinical diagnostic criteria. Neurology. 1998:1546–54. doi: 10.1212/wnl.51.6.1546. [DOI] [PubMed] [Google Scholar]

[R20] 20.Evans A, Collins D, Mills S, Brown E, Kelly R, Peters T. 3D statistical neuroanatomical models from 305 MRI volumes; Proceedings of the IEEE Nuclear Science Symposium and Medical Imaging Conference; London. 1993; MTP Press; 1993. pp. 1813–1817. [Google Scholar]

[R21] 21.Friston K, Holmes A, Worsley K, Poline J, Frith C, Frackowiak R. Statistical parametric maps in functional imaging: a general linear approach. Hum Brain Mapp. 1995;2:189–210. [Google Scholar]

[R22] 22.Rorden C. MRIcro (Version 1.37, Build 4) 2003 [Computer software[. Retrieved October 14. [Google Scholar]

[R23] 23.Connolly AC, Gobbini MI, Haxby JV. Three virtues of similarity- based multivariate pattern analysis: an example from the human object vision pathway. In: Kriegeskorte N, Kreiman G, editors. Visual population codes: toward a common multivariate framework for cell recording and functional imaging. Cambridge, MA: MIT; 2012. [Google Scholar]

[R24] 24.Pereira F, Mitchell T, Botvinick M. Machine learning classifiers and fMRI: A tutorial overview. NeuroImage. 2009;45(1, Supplement 1):S199–S209. doi: 10.1016/j.neuroimage.2008.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R25] 25.Abdi H. Partial least square regression, projection on latent structure regression, PLS-Regression. Wiley Interdisciplinary Reviews: Computational Statistics. 2010;2:97–106. [Google Scholar]

[R26] 26.Silverman D, Devous M., Sr . PET and SPECT Imaging in Evaluating Alzheimer's Disease and Related Dementias. In: Ell P, Gambhir S, editors. Nuclear Medicine in Clinical Diagnosis and Treatment. 3rd. London: Churchill Livingstone; 2004. pp. 1435–1448. [Google Scholar]

[R27] 27.Stühler E, Platsch G, Weih M, Kornhuber J, Kuwert T, Merhof D. Multiple Discriminant Analysis of SPECT Data for Alzheimer's Disease, Frontotemporal Dementia and Asymptomatic Controls; IEEE Medical Imaging Conference (IEEE MIC); 2011; p. MIC22. [Google Scholar]

[R28] 28.Stühler E, Merhof D. Principal Component Analysis Applied to SPECT and PET Data of Dementia Patients –A Review. In: Sanguansat Parinya., editor. Principal Component Analysis: Multidisciplinary Applications. Rijeka, Croatia: InTech; 2012. pp. 167–186. [Google Scholar]

[R29] 29.Mur M, Bandettini PA, Kriegeskorte N. Revealing representational content with pattern-information fMRI--an introductory guide. Soc Cogn Affect Neurosci. 2009;4:101–109. doi: 10.1093/scan/nsn044. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R30] 30.Hall M, Frank E, Holmes G, Pfahringer B, Reutemann P, Witten IH. The WEKA data mining software. ACM SIGKDD Explorations Newsletter. 2009;11:10. [Google Scholar]

[R31] 31.Abdi H, Williams LJ. Principal component analysis. Wiley Interdisciplinary Reviews: Computational Statistics. 2010;2:433–459. [Google Scholar]

[R32] 32.Jagust W. Positron emission tomography and magnetic resonance imaging in the diagnosis and prediction of dementia. Alzheimer's Dement. 2006;2:36–42. doi: 10.1016/j.jalz.2005.11.002. [DOI] [PubMed] [Google Scholar]

[R33] 33.Santens P, De Bleecker J, Goethals P, Strijckmans K, Lemahieu I, Sledgers G, Dierckx R, De Reuck J. Differential regional cerebral uptake of (18)F-fluoro- 2-deoxy-D-glucose in Alzheimer's disease and frontotemporal dementia at initial diagnosis. Eur Neurol. 2001;45:19–27. doi: 10.1159/000052084. [DOI] [PubMed] [Google Scholar]

[R34] 34.Binder J, Frost J, Hammeke T, Bellgowan PSF, Springer JA, Kaufman JN, Possing ET. Human temporal lobe activation by speech and nonspeech sounds. Cereb Cortex. 2000;10:512–528. doi: 10.1093/cercor/10.5.512. [DOI] [PubMed] [Google Scholar]

[R35] 35.Weiner M, Wighton-Benn W, Risser R, Svetlik D, Tintner R, Hom J, Rosenburg RN, Bonte FJ. Xenon-133 SPECT-determined regional cerebral blood flow in Alzheimer's disease: what is typical? J Neuropsychiatry Clin Neurosci. 1993;5:415–418. doi: 10.1176/jnp.5.4.415. [DOI] [PubMed] [Google Scholar]

[R36] 36.Braak H, Braak E. Alzheimer's disease affects limbic nuclei of the thalamus. Acta Neuropathologica. 1991;81:261–268. doi: 10.1007/BF00305867. [DOI] [PubMed] [Google Scholar]

[R37] 37.De Jong LW, van der Hiele K, Veer IM, Houwing JJ, Westendorp RGJ, Bollen ELEM, de Bruin PW, Middelkoop HAM, van Buchem MA, van der Grond J. Strongly Reduced Volumes of Putamen and Thalamus in Alzheimer's Disease: An MRI Study. Brain. 2008;131:3277–3285. doi: 10.1093/brain/awn278. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R38] 38.Escoufier Y. L'analyse conjointe de plusieurs matrices de données [Joint analysis of multiple data matrices] In: Jolivet M, editor. Biométrie et Temps. Vol. 1980. Paris: Société Française de Biométrie; pp. 59–76. [Google Scholar]

[R39] 39.Abdi H. Distance. In: Salkind N, editor. Encyclopedia of measurement and statistics. Thousand Oaks: Sage; 2007. pp. 270–275. [Google Scholar]

[R40] 40.Takane Y. Relationships among various kinds of eigenvalue and singular value decompositions. In: Yanai H, Okada A, Shigemasu K, Kano Y, Meulman, editors. New developments in psychometrics. Tokyo: Springer Verlag; 2002. pp. 45–56. [Google Scholar]

[R41] 41.Abdi H, Dunlop JP, Williams LJ. How to compute reliability estimates and display confidence and tolerance intervals for pattern classifiers using the Bootstrap and 3-way multidimensional scaling (DISTATIS) NeuroImage. 2009;45:89–95. doi: 10.1016/j.neuroimage.2008.11.008. [DOI] [PubMed] [Google Scholar]

[R42] 42.Reiman EM, Jagust WJ. Brain imaging in the study of Alzheimer's disease. NeuroImage. 2012;61:505–516. doi: 10.1016/j.neuroimage.2011.11.075. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R43] 43.Abdi H, Williams LJ, Connolly AC, Gobbini MI, Dunlop JP, Haxby JV. Multiple Subject Barycentric Discriminant Analysis (MUSUBADA): How to assign scans to categories without using spatial normalization. Computational and Mathematical Methods in Medicine 2012. 2012:1–15. doi: 10.1155/2012/634165. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Analysis of Regional Cerebral Blood Flow Data to Discriminate Among Alzheimer's Disease, Frontotemporal Dementia, and Elderly Controls: Multi-Block Barycentric Discriminant (Mubada) Methodology

Hervé Abdi

Lynne J Williams

Derek Beaton

Mette T Posamentier

Thomas S Harris

Anjali Krishnan

Michael D Devous Sr

Abstract

Introduction

Figure 1.

Overview of the Method

Figure 2.

Figure 3.

Methods

Image acquisition and pre-processing

Table 1. Regions of interest for the analyses.

Results

Factor scores and supplementary elements

Training and testing sets

Table 2. Table 2a: Fixed and random effect confusion matrices for MUBADA.

Quality of prediction and group separation

Explained inertia and confidence intervals

Finding the important regions of interest

Figure 4.

Comparison with other pattern recognition classification methods

Table 3. Fixed and random effect confusion matrices for linear support vector machine (SVM).

Table 4.

Table 5. Fixed and random effect confusion matrices for PLS-DA (4 factors).

Discussion

Block normalization and relationship with other approaches

Conclusion

Acknowledgments

Appendix

Formal Presentation of Mubada

Notations

Figure 5. The X matrix with participants nested in clinical groups and voxels nested in ROIs.

Notations for the groups (rows)

Notations for the blocks (columns)

BADA

Figure 6.

Masses and weights

GPCA of the barycenter matrix

Factor scores

Figure 7.

Supplementary elements

Figure 8. The projections of a participant (as a supplementary element) in the group factor score space provides a factor scores for this participant.

Loadings

Quality of the prediction

Training set

Tolerance intervals

Figure 9.

Testing set

Prediction intervals

Quality of the group separation

Explained inertia (R2) and permutation test

Confidence intervals

Figure 10.

MUBADA

Partial projection

Figure 11.

Inertia of a block

Figure 12.

Finding the important ROIs

Footnotes

References

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases

Explained inertia (R²) and permutation test