Abstract
Multicomponent-driven equilibrium single-component observation of T1 and T2 offers a new approach to multiple component relaxation time and myelin water analysis. The method derives two-component relaxation information from spoiled and fully balanced steady-state (SPGR and bSSFP) imaging data acquired over multiple flip angles. Although these steady-state imaging techniques afford rapid acquisition times and high signal-to-noise ratio efficiency, they are also sensitive to main (B0) and transmit (B1) magnetic field inhomogeneities. These effects alter the measured signal from their theoretical values and lead to substantive errors in the derived myelin volume fraction estimates. Here, we incorporate correction techniques to mitigate these effects. DESPOT1-HIFI is used to first calibrate the transmitted flip angles; and B0 affects are removed through the inclusion of an additional parameter in the multicomponent-driven equilibrium single-component observation of T1 and T2 fitting, coupled with the acquisition of multiple phase-cycled bSSFP data. The performance of these correction techniques was evaluated using numerical simulations, demonstrating effective removal of B0 and B1-induced errors in the derived myelin fraction relaxation parameters. The approach was also successfully demonstrated in vivo, with near artifact-free whole-brain, high spatial resolution (1.7 mm × 1.7 mm × 1.7 mm isotropic voxels) myelin water fraction maps acquired in a clinically feasible 16 min.
Keywords: multicomponent relaxation, T1, T2, quantitative magnetic resonance imaging, human brain imaging, steady-state imaging
Multicomponent analysis of longitudinal and transverse (T1 and T2) relaxation data provides information reflecting discrete subvoxel anatomical microstructure. Interrogation of multiecho T2 data in human brain parenchyma, e.g., has consistently revealed the presence of slow and fast relaxing species with T2 < 50 msec and T2 > 80 msec, respectively (1–4). Through investigations of the relative magnitudes of these components in grey and white matter, their variation in disease, and comparison with histological analysis (1–7), these species are broadly attributed to the water trapped within the myelin bilayer and to the less restricted intracellular and extracellular water, respectively.
Conventionally, investigation of these microanatomical water pools is performed using the T2 spin-echo-based approach of Whittal et al. (4). This technique, uses a Poon–Henkelman multiple spin-echo imaging sequence (8) to acquire data over a range of echo times, provides discrete or continuous distribution estimates of each water compartment’s T2 relaxation time and relative volume fraction. Quantitative estimates of the fast relaxing component’s volume fraction corresponds strongly with histologically derived myelin content estimates (5–7), thus providing a noninvasive means of assessing this biologically important parameter.
Multicomponent-driven equilibrium single-pulse observation of T1 and T2 (mcDESPOT) (9) is an extension of the DESPOT1 and DESPOT2 T1 and T2 mapping techniques (10,11) and is a clinically feasible alternative to SE-based multicomponent relaxation analysis approaches. The method combines spoiled and fully balanced steady-state imaging data (SPGR and bSSFP, respectively), acquired over a range of flip angles (α) and with constant repetition time (TR), to derive the free-water T1 and T2 (T1,F, T2,F); myelin-associated water T1 and T2 (T1,M, T2,M); relative myelin and free-water volume fractions (fM and fF); and the myelin and free-water proton residence times (τM and τF).
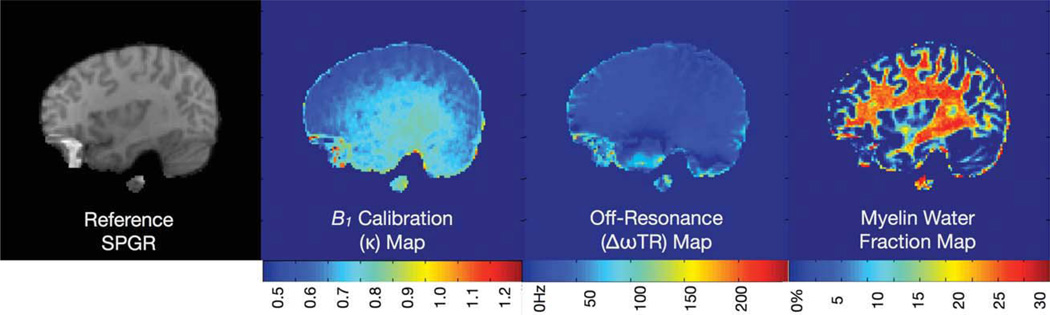
Although these rapid and signal-to-noise efficient (SNR per unit scan time) three-dimensional (3D) imaging techniques enable whole-brain acquisitions with rapid scan times, SPGR and bSSFP are sensitive to main and transmit magnetic field (B0 and B1, respectively) inhomogeneity. These effects alter the measured SPGR and bSSFP signals from their theoretically predicted values (10, 12) and lead to substantive errors in the derived multicomponent parameters. Flip angle (B1) errors occur from tissue dielectric effects. In addition, if a volume selective pulse is applied alongside a slab-selection gradient, the gaussian or Sinc envelopes of typical radiofrequency (RF) excitation pulses will yield a nonuniform flip across the volume in the slab-select direction. The severity of this profile will depend on the specific attributes of the RF pulse [including duration and time-bandwidth (BW) product]. Main magnetic field (B0) inhomogeneity, and off-resonance effects (phase precession of the transverse magnetization), observed in regions with steep susceptibility-induced gradients, such as near the sinuses, brainstem, or inner ear, and presented as areas of signal void in the bSSFP data (13). The affect of flip angle and off-resonance errors on the derived myelin fraction estimates is shown in Fig. 1 and clearly limits the research and diagnostic potential of the technique.
FIG. 1.
Example illustrations of the affects of B0 and B1 inhomogeneity on mcDESPOT derived myelin volume fraction maps.
In this work, the aim was to mitigate the affect of B0 and B1 inhomogeneity through the incorporation of the DESPOT1-HIFI B1 mapping/flip angle calibration technique (14); and the inclusion of off-resonance modeling in the bSSFP signal coupled with the acquisition of bSSFP data with two or more RF phase-cycling patterns (13). The theoretical performance of these calibration techniques was first demonstrated through numerical simulations, which revealed substantial improvement in parameter estimate accuracy (less than 5% absolute error) even with substantial B0 and B1 inhomogeneity. The utility of the method was then established in vivo, demonstrating substantial artifact reduction in the derived multiparameter maps.
MATERIALS AND METHODS
General mcDESPOT Theory and Modeling the Two-Component SPGR and bSSFP Signal
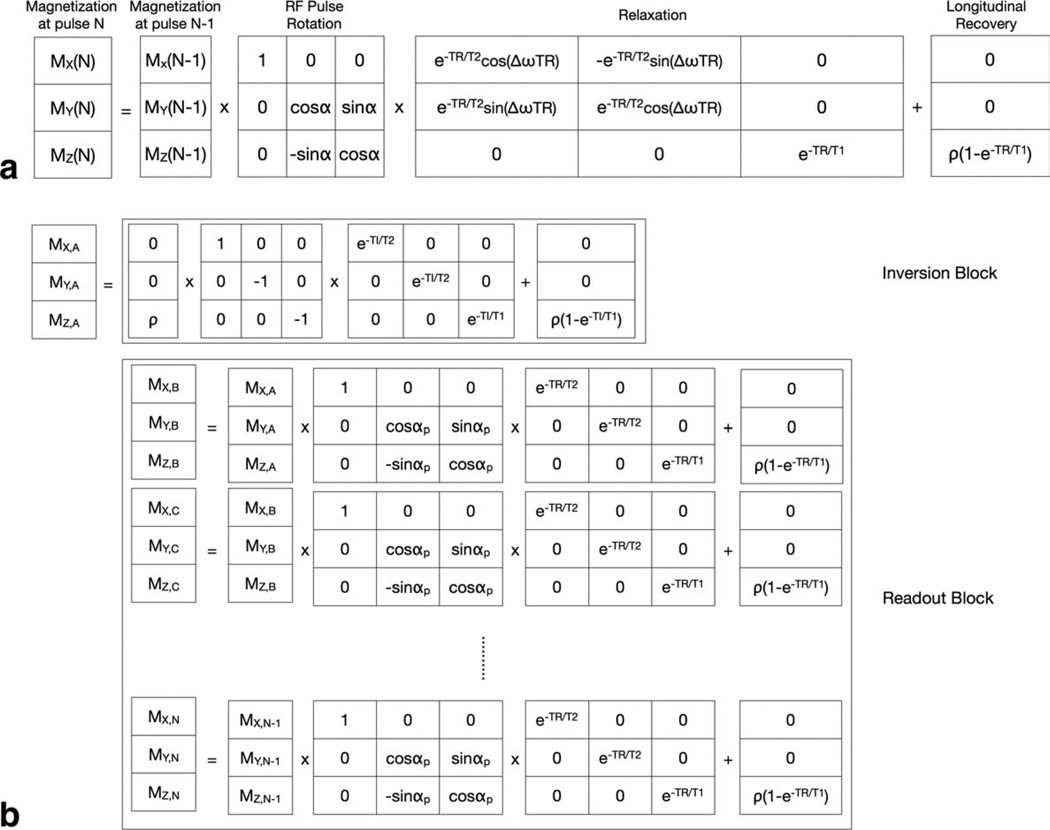
Solutions to the general Bloch-McConnell magnetization expressions (15) may be derived for any pulse sequence using discrete-time formalism, where the pulse sequence is modeled as a series of matrix expressions acting upon the magnetization vector. For example, the two-component bSSFP signal may be modeled as repeated RF pulse, relaxation, and longitudinal recovery “blocks” as shown in Fig. 2. The steady-state signal is determined through iterative evaluation of these blocks until the transverse magnetization components reach a constant value.
FIG. 2.
Illustrations of the discrete-time matrix solution for the magnetization in an MR pulse sequence. In general, a sequence can be described by rotation, relaxation and recovery operations applied against the magnetization vector (a). This approach may be expanded to include intricate pulse sequences, such as IR-SPGR (b) consisting of an initial inversion pulse and inversion time delay, following be a series of low flip angle readout pulses separated by TR.
In the case of some pulse sequences a closed form solution for the magnetization and signal can also be found by equating the magnetization immediately before and following an RF pulse, relaxation, and longitudinal recovery block and solving symbolically. The closed form expressions for the two component SPGR and bSSFP magnetization evaluated in this manner are presented in Appendix A and comprise 11 free parameters, including: the free-water T1 and T2 (T1,F, T2,F); the myelin-associated water T1 and T2 (T1,M, T2,M); the relative myelin and free-water volume fractions (fM and fF); the myelin and free-water proton residence times (τM and τF); the myelin and free water off-resonance (with respect to the central water peak) values (δωM, δωF); and a factor related to the total equilibrium longitudinal magnetization and containing additional factors including scanner amplifier gains, RF coil receive biases, etc. (ρ).
The total number of free-parameters in these models may be reduced to six through four steps/assumptions: (1) normalizing all data with respect to the mean (thereby eliminating ρ); (2) Assuming both water pools are on-resonance (i.e., δωM = δωF = 0); (3) assuming only two water pools (fM + fF = 1); and (4) assuming the water pools are in exchange equilibrium (fM/τM = fF/τF). Presuming correct knowledge of the flip angle (α), Eqs. (A5) and (A6), can be fit to acquired SPGR and bSSFP data to derive estimates of T1,M, T2,M, T1,F, T2,F, τM, and fM. However, errors are introduced into these estimates when a deviates from the prescribed nominal value, and when the transverse phase precession (δωM and δωF) is nonzero. To correct for these effects, we propose to calibrate α using the DESPOT1-HIFI B1 mapping approach (14), and account for off-resonance affects by including an additional term, δω, where δω = δωM = δωF, in the multiparameter fitting; coupled with acquisition of bSSFP data with more than one phase-cycling pattern.
DESPOT1-HIFI and Modeling the Two-Component Inversion-Prepared-SPGR Signal
As described in (14), DESPOT1-HIFI involves the combined acquisition of multiangle SPGR data and at least one inversion-prepared (IR)-SPGR image. From this data, and assuming single-component T1 relaxation, ρ, T1 and the transmitted flip angle may be calculated. Here, the transmitted flip angle (αT) is related to the actual “prescribed” value as αT = καP, where κ is the spatially varying B1 “calibration” field and includes tissue dielectric and RF pulse profile effects.
Two potential limitations of the DESPOT1-HIFI method may, however, prevent its use alongside mcDESPOT. The first is the assumed linear relationship between the prescribed and transmitted flip angle values (αT = καP). In the presence of the frequency variations associated with slab-select gradient applied concomitant with the RF pulse, this linear relationship may be valid for a large flip angle range, or at all locations throughout the excited volume. The second is the single-component T1 assumption in DESPOT1-HIFI. It is unclear if estimates of κ made under this assumption will be correct in multicomponent systems. In answer to this second point, if the exchange rate between the water pools is fast with respect to T1 (i.e., the system is in the fast exchange regime), as is generally assumed, the longitudinal relaxation should be faithfully characterized by a single relaxation rate. In these systems, DESPOT1-HIFI should yield correct estimates of κ despite its simplified model.
Numerical simulations were performed to assess each of these limitations. To examine the linear flip angle relationship, a Bloch simulation was performed to evaluate the magnetization across a 14 cm imaging volume (using the same method as described in Ref. 16). T1 and T2 were set to 800 and 65 msec, respectively, for the simulation. The 800 µsec linear phase SLR RF pulse and gradient waveforms used for the in vivo imaging (discussed below) were used for the simulation. Simulation were performed separately for prescribed flip angle values of {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, and 70}°. For each simulation, the transmitted flip angle and κ were determined at 256 points across the slab select direction. The percentage change between κ at 2° and 70°, for each of the 256 points, was then determined. Under ideal conditions of perfect linearity, the percent change should be zero.
To assess the accuracy of DESPOT1-HIFI κ estimates derived from two-component data, numerical simulations using theoretical data generated with two-component variants of the SPGR and IR-SPGR signal models were performed. Like the SPGR and bSSFP signals above, the two-component IR-SPGR signal may be modeled using an iterative discrete-time solution to the Bloch-McConnell expressions. The model comprises repeated “blocks” representing the inversion pulse; inversion time (TI) delay with T1 and T2 relaxation; and a train of NRF readout pulses separated by TR (Fig. 2b). The transverse components are set to zero before each RF pulse to model ideal spoiling. These blocks are iteratively evaluated until the longitudinal magnetization following the inversion pulse, TI delay, and first readout pulse reach equilibrium (generally five iterations), and this value is taken as the IR-SPGR signal.
For each simulation, a numerical phantom with T1,M = 465 msec, T1,F = 970 msec, T2,M = 15 msec, T2,F = 86 msec, τM = 150 msec, and variable fM was used for data generation, and consisted of 65,000 realizations with complex gaussian-distributed (0 mean, variable SD) noise added to the theoretical values. Accuracy was defined as the absolute percent difference between the mean of the 65,000 estimates and the “true” κ value, and precision was evaluated as the estimate mean divided by the SD.
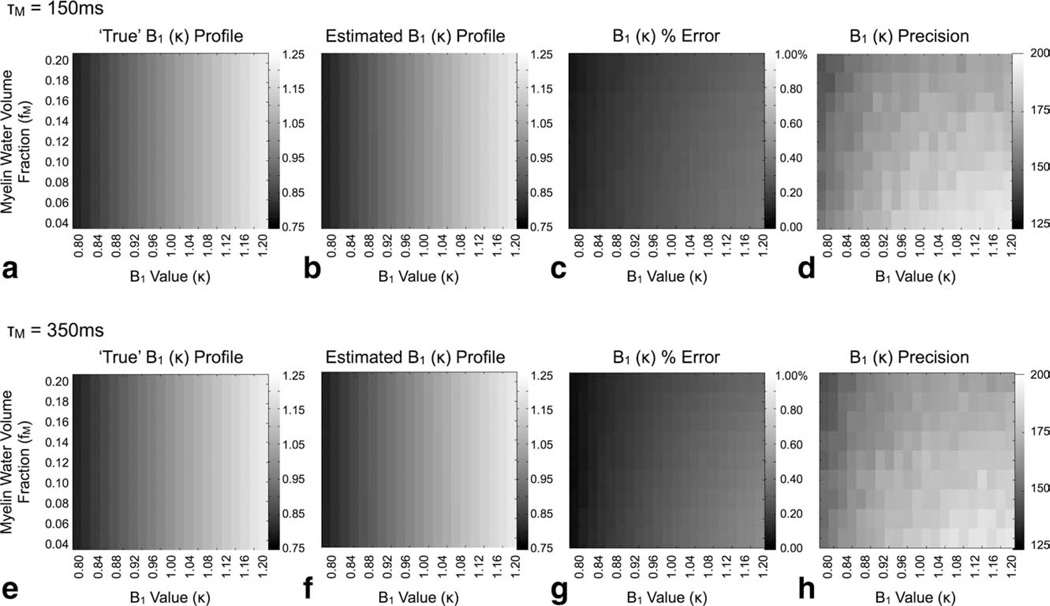
DESPOT1-HIFI data were generated using the following parameters: SPGR: TR = 5.4 msec, αP = {2, 4, 6, 8, 10, 12, 14, 16, and 18}°; IR-SPGR: TR = 5.4 msec, TI = 450 msec, αP = 5°, NRF = 64, as fM was varied from 0.04 to 0.2 in increments of 0.02; as κ was varied from 0.8 to 1.2 in increments of 0.02; and for τM values of 150 and 350 msec. For each fM, κ and τM combination, 65,000 estimates of κ were evaluated.
Building on this first simulation, the accuracy and precision of subsequently derived multicomponent mcDESPOT parameters (T1,F, T2,F, T1,M T2,M, τM and fM, with δω = 0) was investigated. Two-component SPGR, IR-SPGR, and bSSFP data were generated as fM was varied from 0.04 to 0.2 in increments of 0.02; and for κ values of 0.8, 1.00, and 1.20. Modeled “acquisition” parameters were: SPGR: TR = 5.4 msec, αP = {2, 4, 6, 8, 10, 12, 14, 16, and 18}°; IR-SPGR: TR = 5.4 msec, TI = 450 msec, αP = 5°, NRF = 64; bSSFP: TR = 3.5 msec, αP = {8, 16, 24, 32, 40, 48, 56, 64, 72}°. For the analysis κ was first estimated from the IR-SPGR and SPGR data and then used in the multicomponent model fitting. As above, 65,000 estimates of κ, T1,F, T2,F, T1,M, T2,M, τM and fM were evaluated at each fM and κ combination. For comparison, the simulation was also performed with κ set to one (i.e., no assumed B1 inhomogeneity). The nonlinear mcDESPOT fitting was performed using the stochastic region contraction approach described in Appendix B and illustrated in Fig. 3. As effects of B0 inhomogeneity were not included in the simulation, only a six-parameter fit for T1,F, T2,F, T1,M, T2,M, τM, and fM was performed.
FIG. 3.
Graphical illustration of the stochastic region contraction fitting routine used to fit the two-component SPGR and bSSFP signal models to the acquired multiple flip angle imaging data.
Accounting for Off-Resonance Affects of RF Phase-Cycling on bSSFP
The general two-component expression for the bSSFP signal is presented in Eq. (A5) with off-resonance effects denoted by (σRF + δω). To account for B0 inhomogeneity and off-resonance we assume, as a first approximation, that within each imaging voxel the free water and myelin associated water share similar off-resonance characteristics, i.e., δω = δωM = δωF. This additional parameter may then be included in the nonlinear fitting (Appendix B) to model these effects.
For some values of δω, however, the resultant bSSFP signal will be very near zero for all values of α. To ensure sufficient data for robust fitting, bSSFP may be acquired with two or more phase-cycling patterns. Phase-cycling refers to incrementing the phase increment applied to each pulse along the RF pulse train [denoted by σRF in Eq. A3)]. Adjusting σRF shifts the spatial location of the signal null (13), thus ensuring at least one set of bSSFP data will have nonzero signal.
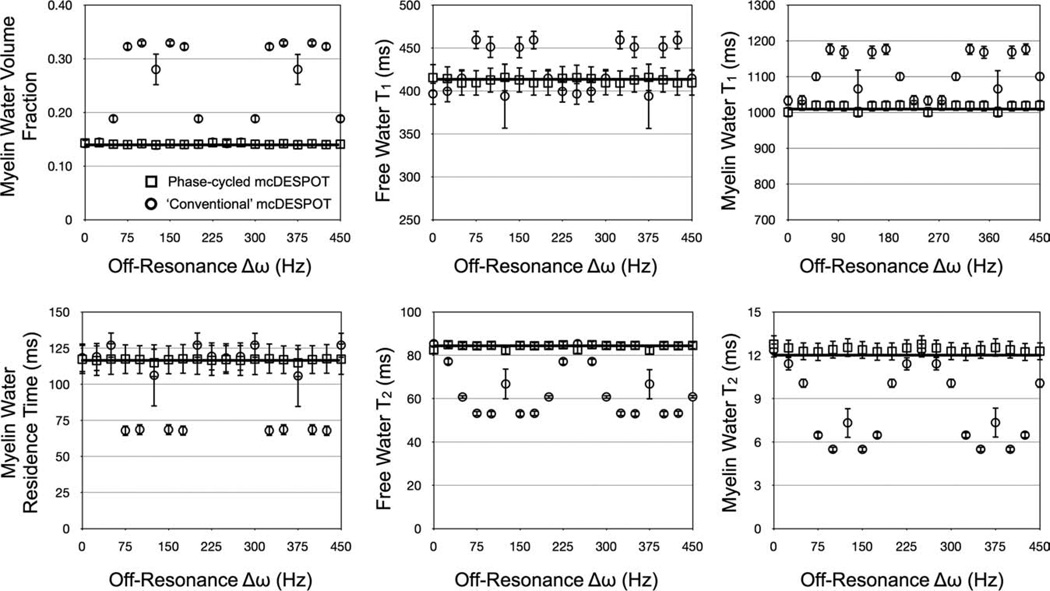
The accuracy and robustness of this phase-cycling approach was first examined through numerical simulations. Using the previously detailed numerical phantom (with fM = 0.14) two-component SPGR and bSSFP data were generated while δω was varied from 0 to 450 Hz in increments of 25 Hz. Parameters used for the SPGR data were: TR = 5.4 msec and α = {2, 4, 6, 8, 10, 12, 14, 16, and 18}°; and for the bSSFP data: TR = 3.5 msec, α = {8, 16, 24, 32, 40, 48, 56, 64, and 72}° and phase-cycling increments of ωrF = 0° and π°. Sixty-five thousand T1,M, T1,F, T2,M, T2,F, fM, τM and δω estimates were calculated for each value of δω. For comparison, 65,000 estimates of T1,M, T1,F, T2,M, T2,F, fM, and |M were calculated using a six-parameter fit with δω = 0 using only the σRF = π° data. The accuracy and precision of each derived parameter were calculated at each δω increment and compared between the corrected and noncorrected methods. For this and the following simulation, no B1 error was assumed.
Accuracy and precision of the approach were next evaluated over a range of myelin water volume fraction and off-resonance conditions. Theoretical data were generated for fM from 0.02 to 0.20 (in increments of 0.04) and 800 from 0 to 450 Hz (in increments of 50 Hz). Sixty-five thousand T1,M, T1,f, T2,M, T2,F, fM, τM and δω estimates were calculated for each fM and δω combination and the accuracy and precision examined. Estimates were also calculated assuming δω = 0 and using only the σRF = π° data for comparison.
Putting It All Together—In Vivo Imaging
Building on the numerical simulations, a series of in vivo human brain imaging experiments were performed to evaluate the combined DESPOT1-HIFI + phase-cycled bSSFP mcDESPOT approach. All imaging experiments were performed on a GE Signa Excite 1.5 T HDx scanner with an eight-channel receive-only head array RF coil. Informed consent was obtained from each healthy volunteer before scanning and the study was performed with ethics approval from the host institute.
SPGR, IR-SPGR, and phase-cycled bSSFP data were acquired of four healthy volunteers, 28–42 years of age. A common 22 cm × 22 cm × 14 cm sagittal field-of-view (FOV), 128 × 128 × 80 acquisition matrix (with 0.75 partial Fourier acquisition), and the following sequence-specific acquisition parameters were used:
SPGR: TE/TR = 2.3 msec/5.4 msec, α = {2, 4, 6, 8, 10, 12, 14, 16, and 18}°, and receiver BW = ±19.23 kHz; IR-SPGR: TE/TR/TI/Tr = 2.3 msec/5.4 msec/350 msec/566 msec, α = 5°, BW = ±19.23 kHz; bSSFP: TE/TR = 1.8 msec/3.5 msec, α = {8, 16, 24, 32, 40, 48, 56, 64, and 72}°, σRF = 0° and π°, and receiver BW = ±50 kHz.
To achieve the various low-angle readout flip angles, the B1 amplitude was scaled with duration held constant (800 µsec). The same RF pulse profile was used for all acquisitions, save the adiabatic IR-SPGR inversion pulse.
To exemplify the RF pulse profile effects, data were also acquired in the coronal orientation using the same acquisition parameters. Acquisition time per volunteer was ~16 min for each orientation (32 min in total). Including participant preparation, localizer scans, and participant removal, the entire protocol was ~40 min in length.
Alongside the 1.5 T data acquisitions, a proof-of-concept acquisition was also performed at 3 T. A 22 cm × 22 cm × 16 cm sagittal FOV, 128 × 128 × 92 acquisition matrix (with 0.6 partial Fourier acquisition) and sequence-specific acquisition parameters of:
SPGR: TE/TR = 2.1 msec/4.8 msec, α = {2, 4, 6, 8, 10, 12, 14, 16, and 18}°, and receiver BW = ±31.25 kHz; IR-SPGR: TE/TR/TI/Tr = 2.1 msec/4.3 msec/450 msec/656 msec, α = 5°, BW = ±31.25 kHz; bSSFP: TE/TR = 1.8 msec/3.6 msec, α = {6, 12, 18, 24, 30, 36, 42, 48, and 56}°, σRF = 0° and π°, and receiver BW = ±62.5 kHz. Total protocol (preparation, localizer scans, and removal) time for this acquisition was less than 20 min.
To minimize pulse profile effects, Dowell and Tofts (17) have suggested simply turning off the slab select gradient during the RF pulse. A limitation of this approach, however, is that it is restricted to applications in which the field of view covers the entire object of interest to avoid aliasing. Thus, imaging of the spinal cord or non-sagittal whole-brain acquisitions is problematic without the use of surface RF receiver coils. To investigate the utility of this approach, 3 T data were acquired of a healthy volunteer as described above with and without the slab-seclect gradient and rewinders turned on.
A potential pitfall of complex models is “over-fitting” the data, i.e., extracting information from models not supported by the data. To avoid this, one can use any number of parsimony metrics or statistical tests to justify the use of more complex models. Using the acquired 3 T data, we compared the conventional single-component DESPOT1 and DESPOT2 fits with the more complex two component mcDESPOT fit. Residuals to the single- and two-component fits were calculated and then compared using the Bayesian information criterion (BIC), (18) to determine which model was better supported by the data. The BIC compares the magnitude of the residuals while penalizing for the number of estimated parameters.
Following data acquisition, each volunteer’s data was linearly coregistered (19) and nonbrain signal was removed from each image (20). Three sets of mcDESPOT multicomponent parameter maps were calculated for each of the four volunteers: (1) No B0 or B1 correction, using only the SPGR and bSSFP (σRF = π°) data; (2) B0 correction, but no B1 correction; and (3) both B0 and B1 correction. After calculation of the maps, the coronal and sagitally oriented data were coregistered and mean frontal white matter T1,M, T1,F, T2M, T2,F, fM, and τM were compared. Calculation time for the fully corrected whole brain maps was ~9 h on an eight-core (2.8 GHz) MacPro with in-house C code.
RESULTS
Simulation Results
To confirm the linear relationship between the prescribed and transmitted flip angles (αT = καP) across the excited volume over the range of flip angles used, a Bloch simulation was performed examining this relationship for flip angles between 2° and 70°. Results of this simulation are shown in Fig. 4. Figure 4a – c contains results of the simulated pulse profiles for 2°, 10°, and 20° flip angles. Figure 4d contains the calculated κ values for each flip angle across the excited slab. Figures 4e and 4f are plots of the percent difference between κ calculated at 2° and 70° and 2° and 50°, respectively. Results show that while ideal linearity is not achieved across the full flip angle range, the deviation from linearity is small and occurs at flip angles greater than 50°. Between 2° and 70°, the maximum percent difference in κ was under 4%, and between 2° and 50°, the maximum percent difference was less than 0.6% toward the periphery of the volume.
FIG. 4.
a–c: Numerical simulation of RF profiles for 2°, 10°, and 20° flip angles. d: Numerical evaluation of ratio of the transmitted : prescribed flip angle (α). Absolute percent difference in κ between the 2° and 70° flip angle profiles (b); and between the 2° and 50° flip angle profiles (c). Though perfect linearity is not seen across the full flip angle range, a maximum percent difference of 3.7% is noted between 2° and 70°. Less than 0.6% difference is observed between 2° and 50°, which encompasses 75% of the acquired mcDESPOT data at 1.5 T and 92% of the data at 3 T. Thus, the assumption of linearity across all flip angles is supported. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]
Results of our investigation of the accuracy of DESPOT1-HIFI κ estimates derived from two-relaxation component data assuming a single-component T1 model are shown in Fig. 5. For both residence times investigated (150 and 350 msec) the method provides accurate κ estimates, with less than 1% error, over the full range of κ and fM investigated despite assuming a simplified T1 relaxation model.
FIG. 5.
Simulation results showing the accuracy (percent error) and precision of calculated flip angle calibration factors (κ) using the DESPOT1-HIFI approach with two-relaxation component SPGR and IR-SPGR data. For both exchange times investigated, the method shows high B1 accuracy despite assuming single-component relaxation. The grayscale values in (a), (b), (e), and (f) correspond to the B1 value at each point in the 2D grid.
The accuracy of subsequent multicomponent estimates calculated with and without the DESPOT1-HIFI κ values is shown in Fig. 6. Incorrect knowledge of the transmitted flip angle results in substantial deviations in each of T1,M, T1,F, T2,M, T2,F, fM, and τM. This result appears to differ from a prior investigation, which showed little influence of B1 influence in mcDESPOT [9]. Further examination revealed a nonlinear response of fM in the presence of flip angle errors. For 0.9 < κ <1.1, little effect is noted in the fM estimates. For κ outside this range, however, the inaccuracy of the fM estimates increases rapidly. In comparison, calibration of the transmitted flip angles using DESPOT1-HIFI results in substantial improvement in mcDESPOT parameter accuracy across the full range of myelin volume fraction investigated.
FIG. 6.
Simulation results comparing non-B1 corrected (square markers) and B1 corrected (circle markers) mcDESPOT estimates for different cases of B1 (κ) error and myelin volume fraction values. The substantial deviation from theoretical truth (denoted by the line) observed in the noncorrected estimates is markedly improved with B1 correction.
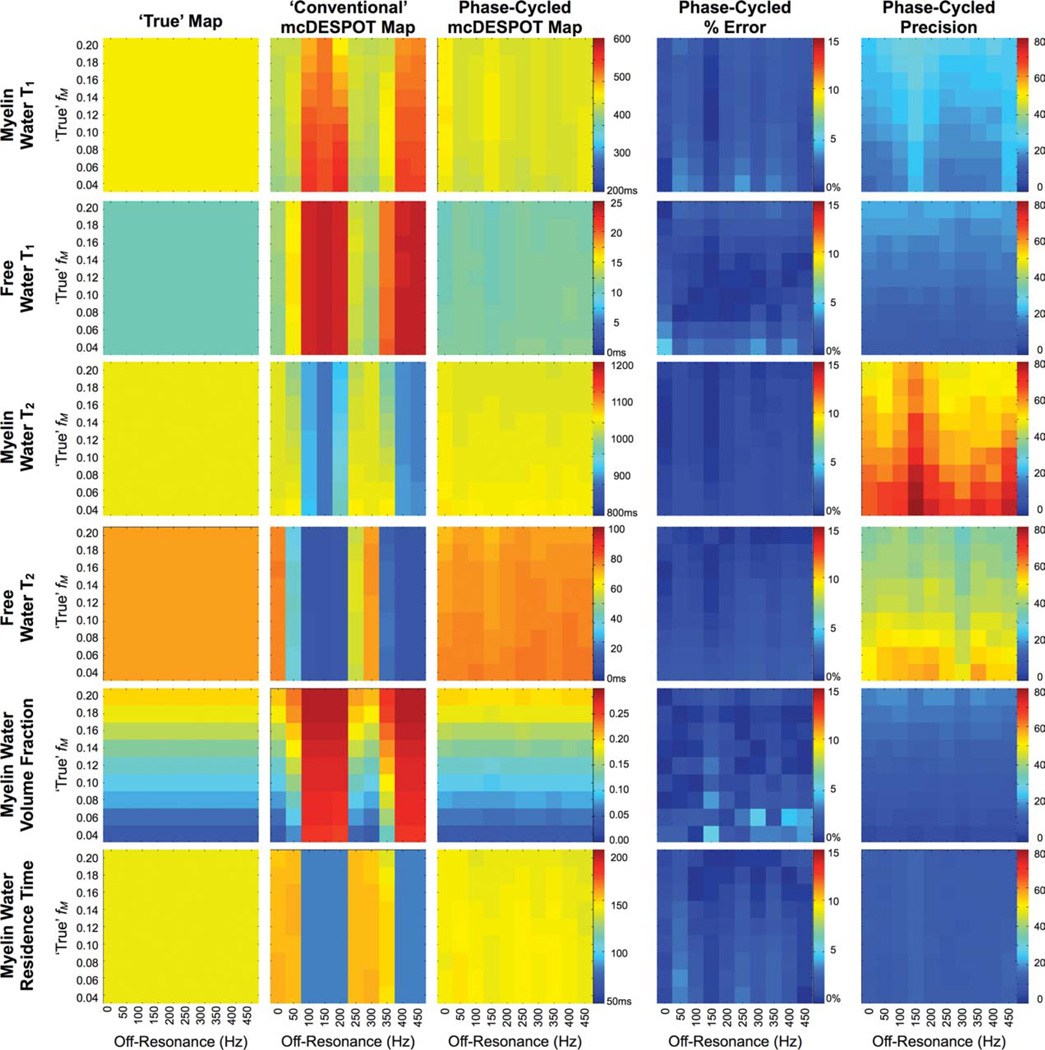
Results of the RF phase-cycling simulations are shown in Figs. 7 and 8, which show corrected and uncorrected T1,M, T1,F, T2,M, T2,F, fM, and tM estimates over a range of myelin water volume fraction and off-resonance values. The sensitivity of mcDESPOT to off-resonance is visually demonstrated in Figs. 7 and 8. The uncorrected estimates show significant deviation from the true theoretical values at even subtle δω. The inclusion of off-resonance modeling significantly improves the accuracy of the derived parameter estimates, with less than 5% absolute error observed in each of the parameters across the investigated myelin fraction and off-resonance values.
FIG. 7.
Simulation results exploring B0 and off-resonance affects on derived mcDESPOT parameters. Uncorrected estimates (circles markers) show significant deviation from theoretical truth (denoted by the line). This error is substantially reduced with the inclusion of off-resonance modeling (square markers), which are approximately independent of off-resonance value.
FIG. 8.
Simulation results of the accuracy and precision of off-resonance corrected myelin water volume fraction estimates. Error in the derived estimates was less than 5%.
In Vivo Imaging Results
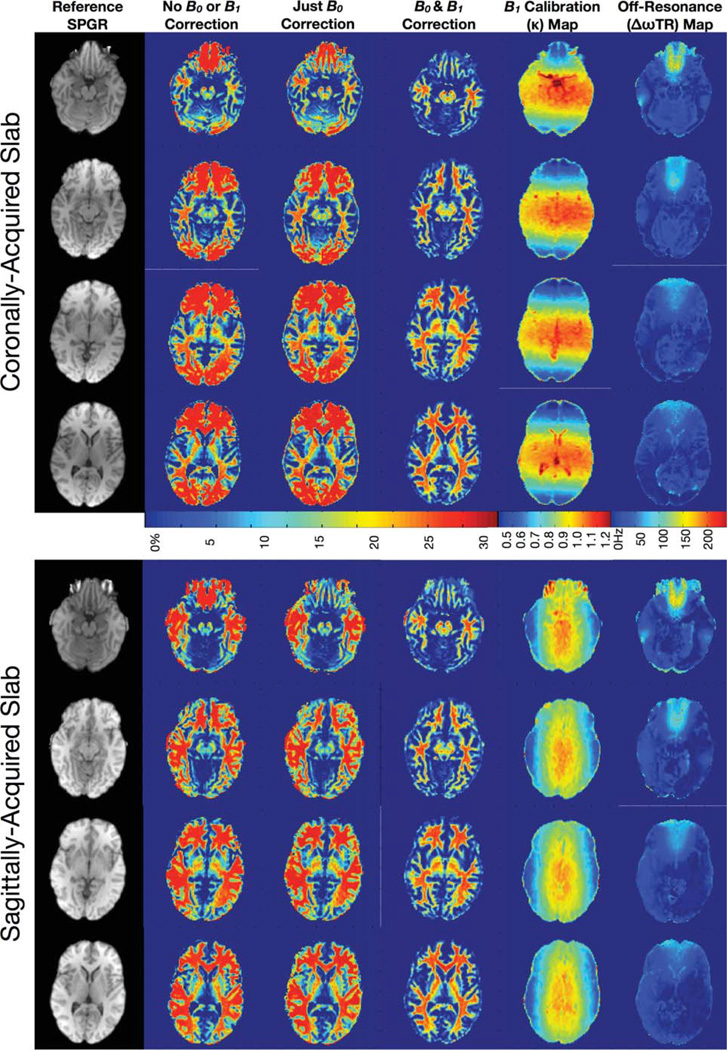
Representative imaging results are shown in Figures 9– 12. Figure 9 contains comparative sagittal and coronally acquired myelin water volume fraction’s maps, reformatted as axial slices at approximately the same level, calculated without B0 and B1 correction; with only B0 correction; and with both B0 and B1 correction. These data clearly demonstrate the influence of flip angle and off-resonance errors in the derived maps. Errors related to flip angle inhomogeneity are greatest along the slab-select direction at the edges of excited volume and correspond to the profile of the RF pulse. Errors resulting from off-resonance conditions are maximal near the sinuses, inner ear, and brain stems.
FIG. 9.
Representative axially reformatted slices through the myelin water fraction map volumes calculated without any correction; with only B0 correction; and with B0 and B1 correction, along with the corresponding calculated B0 map and B1 calibration map and an example reference T1-weighted SPGR image.
FIG. 12.
Example axially reformatted myelin water fraction, myelin and free water T1, myelin and free water T2, myelin residence time, and B0 and B1 calibration maps derived from 3 T data. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]
Figure 10 displays maps of each of the six mcDESPOT parameters (T1,M, T1,F, T2,M, T2,F, fM, and τM) calculated without B0 or B1 correction; with only B0 correction; and with both B0 and B1 correction. As observed in Fig. 8, these data exemplify the B0 and B1-related errors in each of the multicomponent parameters and demonstrate the corrective ability of the presented flip angle and off-resonance modeling techniques. In general, it is noted that flip angle errors appear to predominately affect the T1 measures, whereas off-resonance principally influence the T2 measures. However, both have significant influence on the derived myelin water fraction estimates.
FIG. 10.
Axially reformatted through each of the mcDESPOT parameter maps calculated without any correction; with only B0 correction; and with B0 and B1 correction. As shown in the simulations, both B0 and B1 inhomogeneity result in widespread error in each of the multicomponent parameters. These areas of artifact are significantly improved in the corrected images.
In Fig. 11, we show axially reformatted images through the uncorrected; B0 only; and fully B0 and B1 corrected myelin water volume fractions maps at different levels throughout the brain. Again, these images demonstrate not only the severity of artifact in the uncorrected maps but also their effective removal and elimination when B0 and B1 are modeled and appropriately accounted for.
FIG. 11.
Example axially reformatted T1-weighted SPGR, calculated myelin water fraction, B0 and B1 calibration maps from a single volunteer’s data at different levels through the brain volume. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]
As noted throughout the numerical simulations, areas of off-resonance translate into over-estimations of myelin water fraction. Similarly, incorrect knowledge of the transmitted flip angle, such as at the edges of the excited volume, also translate into myelin water fraction over-estimation. A comparison of mean myelin water fraction values obtained from frontal white matter is shown in Table 1 and supports the qualitative results observed in Figs. 8–11. Averaging the corrected results from both orientation acquisitions across all four volunteers, mean frontal region white matter values were: T1,M = 387 ± 26 msec, T1,F = 946 ± 53 msec, T2,M = 10.4 ± 3.2 msec, T2,F = 108 ± 12 msec, fM = 0.232 ± 0.0017, and τM = 98 ± 26 msec. No significant difference was noted between the values derived from the sagittal or coronally acquired data. These values compare favorably with previously reported values at 1.5 T of T1,M = 350–460 msec, T1,F = 970 msec, T2,M = 10–55 msec, T2,F = > 55 msec, and fM = 0.12–0.32, respectively (12,13).
Table 1.
Mean Myelin Volume Fraction Values (SD Shown in Brackets) Obtained from Right Frontal (WM) in Each of the Volunteers
| Frontal WM—coronally acquired |
Frontal WM—sagittally acquired |
|||||
|---|---|---|---|---|---|---|
| Volunteer | Uncorrected | B0 only | B0 +B1 | Uncorrected | B0 Only | B0 +B1 |
| 1 | 26.1 (0.3) | 26.5 (0.4) | 23.2 (0.2) | 24.8 (0.5) | 25.9 (0.6) | 23.1 (0.4) |
| 2 | 25.1 (0.7) | 25.3 (1.1) | 23.6 (0.8) | 26.0 (0.3) | 26.4 (0.4) | 23.3 (0.7) |
| 3 | 27.6 (1.2) | 26.5 (0.3) | 22.9 (0.5) | 25.4 (0.8) | 26.2 (0.4) | 22.8 (0.3) |
| 4 | 26.3 (0.8) | 27.5 (1.2) | 23.0 (0.5) | 25.7 (0.4) | 26.1 (0.7) | 23.1 (0.7) |
As proof-of-concept, demonstration of the technique at the higher 3 T field strength is shown in Fig. 12. As with the results shown previously at 1.5 T, the inclusion of B1 and B0 modeling removes these effects from the calculated mcDESPOT parameter maps.
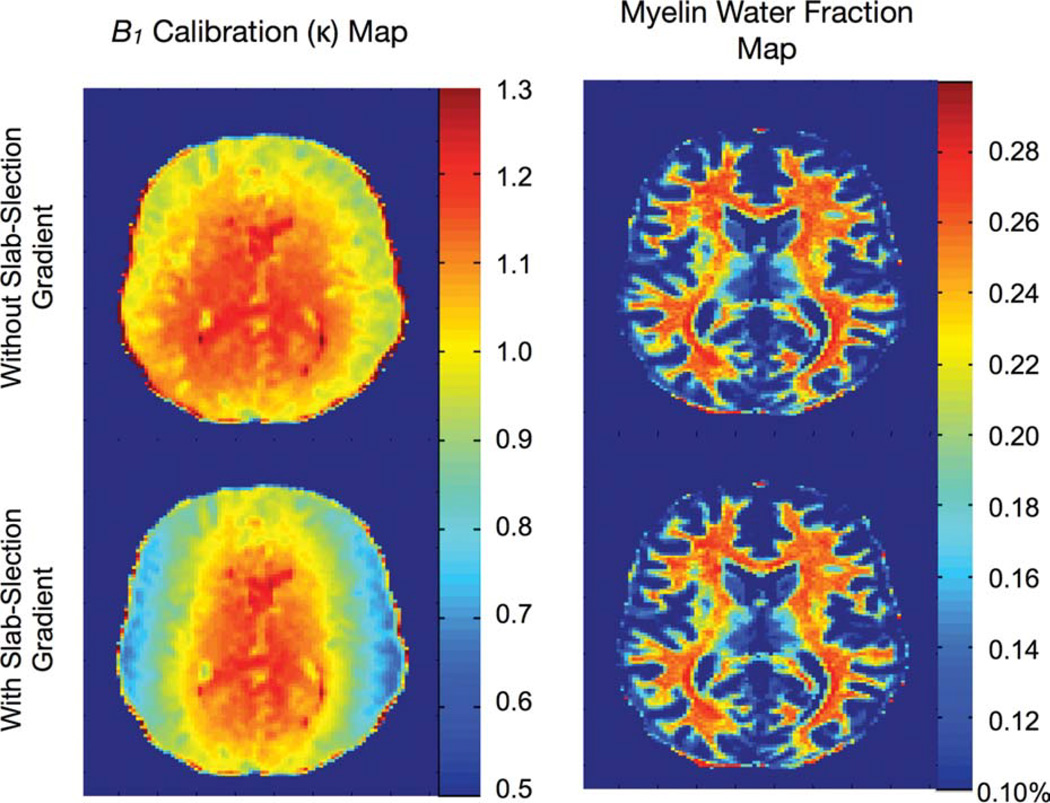
As has been suggested previously, one approach to eliminate pulse profile affects is to eliminate the slab-selection gradient. Results of similar acquisitions with and without the slab-selection gradient are shown in Fig. 13 and show similar results regardless of the presence or absence of the gradient. This lends further credence to our simulation findings, which showed only a slight deviation in the linear relationship between the prescribed and transmitted flip angles even in the presence of off-resonance effects associated with the slab-selection gradient.
FIG. 13.
Comparison of 3 T results obtained with and without the slab-select gradient turned on during RF excitation. Removal of the gradient eliminates the RF slab-profile effects from the B1 field maps; however, no obvious difference is noted in the derived myelin fraction maps. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]
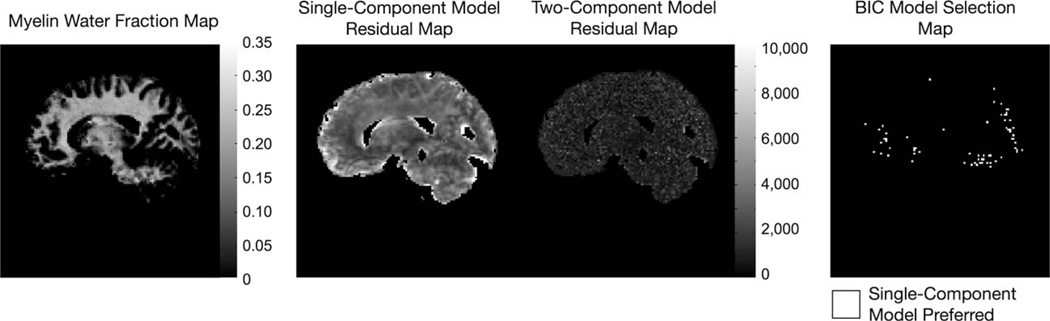
Finally, results of the single- and two-component residuals and BIC analysis are shown in Fig. 14. Despite the complexity of the two component mcDESPOT model, this analysis shows the mcDESPOT model is justified by the data throughout the majority of the image.
FIG. 14.
Analysis of residuals and model selection. To illustrate the improved fit, and justify the more complex two-component fit, cumulative residuals to the single-component T1 and T2 fits, as well as two-component mcDESPOT residuals are shown alongside a myelin fraction image derived from 3 T mcDESPOT data. In the BIC model selection map, white voxels correspond to those in which the single-component model is preferred. The BIC parsimony metric shows the two component model is preferred across the majority of voxels.
DISCUSSION
The two primary sources of error associated with the mcDESPOT multicomponent relaxation method are off-resonance affects related to main B0 field inhomogeneities in the bSSFP data, and inaccurate knowledge of the transmitted flip angle. As a result, utility of the method at higher imaging field strengths (i.e., 3 T and above) or in combination with asymmetric (surface) RF coils has been limited. As data presented herein attest, these affects cause significant errors in the derived multicomponent parameters.
In this work, we have introduced a combination of techniques to correct for these effects. The DESPOT1-HIFI B1 mapping method was used to first calibrate the transmitted flip angles, and phase-cycled bSSFP data, coupled with off-resonance modeling, were used to remove B0 inhomogeneity-induced artifacts and errors. Despite the added acquisition and computational complexity, success of the approach was shown using numerical simulations, demonstrating high accuracy and precision, as well as through in vivo imaging experiments, showing a dramatic improvement in image quality and removal of B0 and B1-related artifacts. Although alternative B0 and B1 mapping techniques exist, the methods utilized herein were chosen based on their close similarity and compatibility to the mcDESPOT technique. For example, the SPGR data acquired, as part of a mcDESPOT experiment, is the same as required for DESPOT1-HIFI, thus requiring only the additional acquisition of an IR-SPGR image. Similarly, mcDESPOT already incorporates bSSFP data and, thus, requires only an additional acquisition with a different RF phase-cycling pattern. A complete whole-brain mcDESPOT+ experiment (mcDESPOT + DESPOT1-HIFI + RF phase-cycling) requires approximately 16 min with reasonable spatial resolution, i.e. 1.7 × 1.7 × 1.7 mm3 isotropically resolved voxels, at 1.5 T. It is presumed that at increased field strength, the use of parallel imaging will facilitate either reduced acquisition times, or improved spatial resolution.
A persistent finding in mcDESPOT-derived parameters has been a bias toward larger myelin volume fraction estimates relative to spin-echo-based T2-MCR estimates (4,5,11). Results presented herein suggest that this bias may be partially, though not wholly, attributed to B0 and/or B1 field variations throughout the brain volume. As demonstrated in the in vivo results (Figs. 8–10), over-estimation of the transmitted flip angle (particularly near the edges of the excited slab volume) and under-estimation of the off-resonance term (near the sinuses, brainstem or inner-ear) result in significant over-estimations in the derived myelin volume fraction. However, even when these affects are cleanly removed, the estimated myelin volume fraction remains greater than spin-echo-based measures. The source of this remaining bias remains unknown and under investigation. Leading contenders include an unresolved third component, corresponding to the intra-axonal water with intermediary T1 and T2 values (21), or as-yet accounted for magnetization transfer (22). Additional work, however, is required to determine the contribution of these potential signal sources to the measured values.
In modeling the B0 effects, we assumed equal off-resonance in the free and myelin-associated water pools. Recent work, investigating the off-resonance profile of the bSSFP signal (i.e., the bSSFP signal plotted against the RF pulse phase), has suggested this may be an oversimplified assumption and that these pools may different in resonant frequency by 10–30 Hz depending on the local fiber orientation (with respect to the main B0 field) (23). Although the exact mechanism for this frequency dispersion remains under investigation, it may also bear partial responsibility for the increased myelin water fractions observed with mcDESPOT. Although the method proposed allows us to fit for each water pool’s off-resonance value independently, bSSFP data with more than two RF phase-cycling patterns will be required to do so robustly, substantially increasing acquisition time and limiting the practical utility of the technique.
The success of the approach demonstrated herein at 1.5 T suggests the method may be directly translated to higher field strengths (i.e., 3 T and above), or used with asymmetric surface RF coils. The improved SNR anticipated at 3 T may be used to reduce acquisition times and/or improve spatial resolution, lending the method to more detailed investigations of myelin fraction, such as within the cortex or in small structures such as the optic nerve; or in challenging patient populations who are unable to remain still for long periods (young children and elder dementia patients). A potential concern at 3 T, however, is increased specific absorption rate (SAR). bSSFP can accurately characterized as a “SAR-intensive” sequence, with high-RF energy deposition per unit time. SAR issues become a particular concern at high-flip angles and limit the useable flip angle range in bSSFP acquisitions. However, T1 also increases with field strength. For constant TR, increased T1 shifts the peak of the bSSFP vs. flip angle curve toward lower angles and, therefore, the maximum flip angle required for mcDESPOT becomes smaller. Although a full optimization is beyond the scope of this work, simulations have shown mcDESPOT should provide reproducible myelin water fraction estimates at 3 T with a maximum bSSFP flip angle between 50° and 60°. Indeed, as demonstrated herein is a high-quality myelin fraction map acquired at 3 T. In our experience, 60° flip angles can be safely achieved with bSSFP in the majority of volunteers and patient populations. To further alleviate SAR concerns, the RF pulse may be lengthened or the time-BW product lowered.
CONCLUSIONS
mcDESPOT is a rapid and SNR efficient technique for multicomponent relaxation analysis. However, as originally implemented, the technique suffered from main and transmit magnetic field induced errors. In this work, we have reported on effective approaches for correcting these artifacts using previously described B0 and B1 mapping methods. Inclusion of these methods provides substantial improvement in image quality and artifact reduction while maintaining a clinically feasible 16-min exam time for whole-brain acquisitions.
Acknowledgments
Grant sponsor: Medical Research Council (MRC, UK) CDA Fellowship;
Grant number: G0800298
APPENDIX A
Closed-Form Solutions for the Two-Component SPGR and bSSFP Steady-State Signal
As presented in (24), the general expression describing the two-component bSSFP magnetization is given by
| [A1] |
where MbSSFP is a vector containing the x, y and z magnetization components,
| [A2] |
TM denotes the transpose of the matrix, I is the 6 × 6 identity matrix, R(α) is a rotation matrix defining the RF pulse with excitation flip angle α, AbSSFP is a matrix containing T1 and T2 relaxation, exchange, off-resonance effects (δω) with respect to the central water peak, and the phase of the applied RF pulse, σRF,
| [A3] |
C is related to the equilibrium longitudinal magnetization,
| [A4] |
and ρ is a term proportional to the proton spin density including extraneous effects such as RF amplifier gains, receive RF coil sensitivities, etc. The measured bSSFP signal (SbSSFP) is the quadrature summation of the transverse components of MbSSFP,
| [A5] |
The two-component SPGR signal represents a simplified form of Eqn. [A5], including only the longitudinal magnetization components (25),
| [A6] |
where
| [A7] |
and
| [A8] |
APPENDIX B
Nonlinear Fitting of the Two-Component SPGR and bSSFP Signal Models to Acquired Data
To fit Eqs. (A7) and (A8) to the multiple flip angle SPGR and bSSFP data, a stochastic region contraction approach (26) is used. As illustrated in Fig. 3, this approach begins by defining the expected search-space extents, e.g., 100 msec ≤ T1,M, T1,F ≤ 2500 msec; 1 msec ≤ T2,M, T2,F ≤ 150 msec; 0.0 ≤ fM ≤ 0.45; and 25 ≤ τM < 500 msec (and 0.0 ≤ δω ≤ 1/TR). Because of the periodic nature of the (σRF + δω) in Eq. (A3), we can limit the range of δω investigated to 0 ≤ δω ≤ 1/TR, i.e., δω =δω + 2 repeating with a frequency of 1/TR. N1 samples of T1,M, T1,f, T2,M, T2,F, fM, and τM (and δω) are then randomly chosen from these uniform distributions and for each combination, the theoretical SPGR and bSSFP signal curves generated, normalized (with respect to the mean value), and the sum-of-squares residuals are calculated. To calculate the residuals, the acquired SPGR data is normalized with respect to the mean signal intensity; and each acquired bSSFP dataset is also normalized with respect to their respective means. The theoretical SPGR and bSSFP are likewise normalized. The cumulative sum-of-squares are then calculated across all data-points.
The N1 combinations are then rank sorted by increasing residual and from the top N2 combinations, the minimum and maximum sampled value of each parameter is determined. These values are then used to update the extents of search-space and the sampling process repeated. In this way, the search-space slowly contracts to the globally optimum solution. The algorithm continues until the difference between the minimum and maximum value of each parameter falls below a predefined threshold (Td) or some number (NT) of iterations are performed and the top solution upon termination is taken as the solution. Throughout this work, we use N1 = 5000, N2 = 50, Td = 0.5% and NT = 8. These parameters have been arrived at through an ad hoc optimization study.
REFERENCES
- 1.Kroeker RM, Henkelman RM. Analysis of biological NMR Relaxation data with continuous distributions of relaxation times. J Magn Reson. 1986;69:218–235. [Google Scholar]
- 2.Menon RS, Rusinko MS, Allen PS. Multiexponential proton relaxation in model cellular systems. Magn Reson Med. 1991;20:196–213. doi: 10.1002/mrm.1910200204. [DOI] [PubMed] [Google Scholar]
- 3.Cheng KH. In Vivo tissue characterization of human brain by chisquares parameter maps: multiparameter proton T2-relaxation analysis. Magn Reson Imag. 1994;12:1099–1109. doi: 10.1016/0730-725x(94)91242-o. [DOI] [PubMed] [Google Scholar]
- 4.Whittal KP, MacKay AL, Graeb DA, Nugent RA, Li DK, Paty DW. In vivo measurement of T2 distributions and water contents in normal human brain. Magn Reson Med. 1997;37:34–43. doi: 10.1002/mrm.1910370107. [DOI] [PubMed] [Google Scholar]
- 5.MacKay A, Laule C, Vavsour I, Bjarnason T, Kolling S, Madler B. Insights into brain microstructure from the T2 distribution. Magn Reson Imag. 2006;24:515–525. doi: 10.1016/j.mri.2005.12.037. [DOI] [PubMed] [Google Scholar]
- 6.Laule C, Leung E, Lis DK, Traboulsee AL, Paty DW, MacKay AL, Moore GR. Myelin water imaging in multiple sclerosis: quantitative correlations with histopathology. Mult Scler. 2006;12:747–753. doi: 10.1177/1352458506070928. [DOI] [PubMed] [Google Scholar]
- 7.Webb S, Munro CA, Midha R, Stanisz GJ. Is multicomponent T2 a good measure of myelin content in peripheral nerve? Magn Reson Med. 2003;49:638–645. doi: 10.1002/mrm.10411. [DOI] [PubMed] [Google Scholar]
- 8.Poon CS, Henkelman RM. Pratical T2 quantitatiion for clinical applications. J Magn Reson Imaging. 1992;2:541–553. doi: 10.1002/jmri.1880020512. [DOI] [PubMed] [Google Scholar]
- 9.Deoni SCL, Rutt BK, Arun T, Pierpaoli C, Jones DK. Gleaning multi-component T1 and T2 information from steady-state imaging data. Magn Reson Med. 2008;60:1372–1387. doi: 10.1002/mrm.21704. [DOI] [PubMed] [Google Scholar]
- 10.Christensen KA, Grand DM, Schulman EM, Walling C. Optimal determination of relaxation times of Fourier transform nuclear magnetic resonance. Determination of spin-lattice relaxation times in chemically polarized species. J Phys Chem. 1974;78:1971–1977. [Google Scholar]
- 11.Deoni SCL, Rutt BK, Peters TM. Rapid combined T1 and T2 mapping with gradient recalled acquisition in the steady-state. Magn Reson Med. 2003;46:515–526. doi: 10.1002/mrm.10407. [DOI] [PubMed] [Google Scholar]
- 12.Freeman R, Hill HDW. Phase and intensity anomalies in Fourier transform NMR. J Magn Reson. 1971;4:366–383. [Google Scholar]
- 13.Zur Y, Wood ML, Neuringer LJ. Motion-insensitive, steady-state free precession imaging. Magn Reson Med. 1990;16:444–459. doi: 10.1002/mrm.1910160311. [DOI] [PubMed] [Google Scholar]
- 14.Deoni SCL. High-resolution T1 mapping of the brain at 3 T with driven equilibrium single pulse observation of T1 with high-speed incorporation of RF field inhomogeneities (DESPOT1-HIFI) J Magn Reson Imaging. 2007;26:1106–1111. doi: 10.1002/jmri.21130. [DOI] [PubMed] [Google Scholar]
- 15.McConnell HM. Relaxation rates by nuclear magnetic resonance. J Chem Phys. 958;28:430–431. [Google Scholar]
- 16.Parker GJM, Barker GJ, Tofts Accurate multi-slice gradient echo T1 measurement in the presence of non-ideal rf pulse shape and RF field inhomogeneity. Magn Reson Med. 2001;45:838–845. doi: 10.1002/mrm.1112. [DOI] [PubMed] [Google Scholar]
- 17.Dowell NG, Tofts PS. Fast, accurate, and precise mapping of the RF field in vivo using the 180 degree signal null. Magn Reson Med. 2007;58:622–630. doi: 10.1002/mrm.21368. [DOI] [PubMed] [Google Scholar]
- 18.Schwarz GE. Estimating the dimension of a model. Ann Stat. 1978;6:461–464. [Google Scholar]
- 19.Jenkinson M, Bannister PR, Brady JM. Improved optimization for the robust and fast linear registration and motion correction of brain images. Neuroimage. 2002;17:825–841. doi: 10.1016/s1053-8119(02)91132-8. [DOI] [PubMed] [Google Scholar]
- 20.Smith SM. Fast robust automated brain extraction. Hum Brain Mapp. 2002;17:143–155. doi: 10.1002/hbm.10062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lancaster JL, Andrews T, Hardies J, Dodd S, Fox PT. Three-pool model of white matter. J Magn Reson Imag. 2003;17:1–10. doi: 10.1002/jmri.10230. [DOI] [PubMed] [Google Scholar]
- 22.Gloor M, Scheffler K, Bieri O. Quantitative magnetization transfer using balanced SSFP. Magn Reson Med. 2008;60:691–700. doi: 10.1002/mrm.21705. [DOI] [PubMed] [Google Scholar]
- 23.Miller KL, Jezzard P. Balanced SSFP Profile Asymmetries Detect Small Frequency Shifts in White Matter. Proceedings of 17th Meeting of the ISMRM Hawaii. 2009:258. [Google Scholar]
- 24.Deoni SCL, Rutt BK, Jones DK. Investigating exchange and multicomponent relaxation in fully-balanced steady-state free precession imaging. J Magn Reson Imaging. 2008;27:1421–1429. doi: 10.1002/jmri.21079. [DOI] [PubMed] [Google Scholar]
- 25.Spencer RGS, Fishbein KW. Measurement of spin-lattice relaxation times and concentrations in systems with chemical exchange using the one-pulse sequence: breakdown of the Ernst model for partial saturation in nuclear magnetic resonance spectrscopy. J Magn Reson. 2000;142:120–135. doi: 10.1006/jmre.1999.1925. [DOI] [PubMed] [Google Scholar]
- 26.Berger MF, Silverman HF. Microphone array optimization by stochastic region contraction. IEEE Trans Signal Process. 1991;39:2377–2386. [Google Scholar]