Abstract
The interactions between proteins, DNA, and RNA in living cells constitute molecular networks that govern various cellular functions. To investigate the global dynamical properties and stabilities of such networks, we studied the cell-cycle regulatory network of the budding yeast. With the use of a simple dynamical model, it was demonstrated that the cell-cycle network is extremely stable and robust for its function. The biological stationary state, the G1 state, is a global attractor of the dynamics. The biological pathway, the cell-cycle sequence of protein states, is a globally attracting trajectory of the dynamics. These properties are largely preserved with respect to small perturbations to the network. These results suggest that cellular regulatory networks are robustly designed for their functions.
Despite the complex environment in and outside of the cell, various cellular functions are carried out reliably by the underlying biomolecular networks. How is the stability of a cell state achieved? How can a biological pathway take the cell from one state to another reliably? Evolution must have played a crucial role in the selection of the architectures of these networks for them to have such a remarkable property. Much attention has recently been focused on the “topological” properties of large-scale networks (1–5). It was argued that a power-law distribution of connectivity, which is apparent for some bionetworks (2, 4), is more tolerable against random failure (1). Here we address this question from a dynamic systems point of view. We study the network regulating the cell cycle of the budding yeast, investigating its global dynamical property and stability. We find that the stationary states of the cell, or states at the checkpoints in general, correspond to global attractors of the dynamics: almost all initial protein states flow to these biological stationary states. Furthermore, the biological pathway of the cell-cycle sequence, which is a particular trajectory in the state space, is a globally stable and attracting trajectory of the dynamics. These dynamic properties, arising from the underlying network connection, are also robust against small perturbations to the network. They are directly responsible for the robustness of the cellular process.
The Yeast Cell-Cycle Network
The cell-cycle process, by which one cell grows and divides into two daughter cells, is a vital biological process the regulation of which is highly conserved among the eukaryotes (6). The process consists of four phases: G1 (in which the cell grows and, under appropriate conditions, commits to division), S (in which the DNA is synthesized and chromosomes replicated), G2 (a “gap” between S and M), and M (in which chromosomes are separated and the cell is divided into two). After the M phase, the cell enters the G1 phase, hence completing a “cycle.” The process has been studied in great detail in the budding yeast Saccharomyces cerevisiae, a single-cell model eukaryotic organism (see supporting information, which is published on the PNAS web site, for references). There are ≈800 genes involved in the cell-cycle process of the budding yeast (7). However, the number of key regulators that are responsible for the control and regulation of this complex process is much smaller. Based on extensive literature studies, we have constructed a network of key regulators that are known so far, as shown in Fig. 1A (for details, see supporting information).
Fig. 1.
(A) The cell-cycle network of the budding yeast. (B) Simplified cell-cycle network with only one checkpoint “cell size.”
There are four classes of members in this regulatory network: cyclins (Cln1, -2, and -3 and Clb1, -2, -5, and -6, which bind to the kinase Cdc28); the inhibitors, degraders, and competitors of the cyclin/Cdc28 complexes (Sic1, Cdh1, Cdc20, Cdc14); transcription factors (SBF, MBF, Mcm1/SFF, Swi5); and checkpoints (the cell size, the DNA replication and damage, and the spindle assembly). Green arrows in Fig. 1 represent positive regulations. For example, under rich nutrient conditions and when the cell grows large enough, the Cln3/Cdc28 will be “activated”, which in turn activates (by phosphorylation) a pair of transcription factor groups, SBF and MBF, which transcriptionally activate the genes of the cyclins Cln1 and -2 and Clb5 and -6, respectively. Red arrows in Fig. 1 represent “deactivation” (inhibition, repression, or degradation). For example, the protein Sic1 can bind to the Clb/Cdc28 complex to inhibit its function, Clb1 and -2 phosphorylates Swi5 to prevent its entry into the nucleus, whereas Cdh1 targets Clb1 and -2 for degradation. The cell-cycle sequence starts when the cell commits to division by activating Cln3 (the START). The subsequent activity of Clb5 drives the cell into the S phase. The entry into and exit from the M phase is controlled by the activation and degradation of Clb2. After the M phase, the cell comes back to the stationary G1 phase, waiting for the signal for another round of division. Thus the cell-cycle process starts with the “excitation” from the stationary G1 state by the “cell-size” signal and evolves back to the stationary G1 state through a well defined sequence of states.
The Model and Dynamic Properties
In principle, the arrows in the network have very different time scales of action, and a dynamic model would involve various binding constants and rates (8, 9). However, because in the cell-cycle network much of the biology seems to be reflected in the on–off characteristics of the network components and we are mainly concerned here with the overall dynamic properties and the stability of the network, we use a simplified dynamics on the network, which treats the nodes and arrows as logic-like operations.¶ Thus, in the model, each node i has only two states, Si = 1 and Si = 0, representing the active and the inactive state of the protein, respectively. The protein states in the next time step are determined by the protein states in the present time step via the following rule:
 |
[1] |
where aij = ag for a green arrow from protein j to protein i and aij = ar for a red arrow from j to i. We first focus on the case where all of the other checkpoints are always off, except that of the cell size. That is, the cell size checkpoint will act as a start signal, whereas other checkpoints will always let the “traffic” pass when it come to it. We therefore arrive at a slightly simplified network shown in Fig. 1B, with 11 nodes (plus a signal node). We have also added “self-degradation” (yellow loops) to those nodes that are not negatively regulated by others. [This is a simplification for the actual degradation processes. See supporting information for details.] The degradation is modeled as a time-delayed interaction: if a protein with a self yellow arrow is active at time t (Si(t) = 1) and if its total input is zero from t + 1 to t = t + td, it will be degraded at t = t + td, i.e., Si(t + td) = 0. The results presented below were obtained with ag = –ar = 1 and td = 1. As will be discussed later, the overall dynamic properties of the network are not very sensitive to the choice of these parameters.
Fixed Points. We use the dynamic model described above to study the time evolution of the protein states. First, we study the attractors of the network dynamics by starting from each of the 211 = 2,048 initial states in the 11-node network of Fig. 1B. We find that all of the initial states eventually flow into one of the seven stationary states (fixed points) shown in Table 1. Among the seven fixed points, there is one big fixed point attracting 1,764 or ≈86% protein states. Remarkably, this super stable state is the biological G1 stationary state. The advantage for a cell's stationary state to be a big attractor of the network is obvious: the stability of the cell state is guaranteed. Under normal conditions, the cell will be sitting at this fixed point, waiting for the signal for another round of division.
Table 1. The fixed points of the cell-cycle network.
| Basin size | Cln3 | MBF | SBF | Cln1,2 | Cdh1 | Swi5 | Cdc20 | Clb5,6 | Sic1 | Clb1,2 | Mcm1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1,764 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 151 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 109 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 7 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
Each fixed point is represented in a row. The first column is the size of the basin of attraction for the fixed point; the other 11 columns show the protein states of the fixed point. The protein states of the biggest fixed point correspond to that of the G1 stationary state.
Biological Pathway. Next, we start the cell-cycle process by “exciting” the G1 stationary state with the cell size signal, and observe that the system goes back to the G1 stationary state. The temporal evolution of the protein states, presented in Table 2, indeed follows the cell-cycle sequence, going from the excited G1 state (the START) to the S phase, the G2 phase, the M phase, and finally to the stationary G1 state. This is the biological trajectory or pathway of the cell-cycle network.
Table 2.
Temporal evolution of protein states for the simplified cell-cycle network of Fig. 1B
| Time | Cln3 | MBF | SBF | Cln1,2 | Cdh1 | Swi5 | Cdc14 | Clb5,6 | Sic1 | Clb1,2 | Mcm1/SFF | Phase |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | START |
| 2 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | G1 |
| 3 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | G1 |
| 4 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | G1 |
| 5 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | S |
| 6 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | G2 |
| 7 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | M |
| 8 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | M |
| 9 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | M |
| 10 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | M |
| 11 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | M |
| 12 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | G1 |
| 13 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | Stationary G1 |
The right column indicates the cell-cycle phases. Note that the number of time steps in each phase do not reflect its actual duration.
To investigate the dynamical stability of this biological pathway, we study the dynamic trajectories of all 1,764 protein states that will flow to the G1 fixed point. In Fig. 2, each of these protein states is represented by a dot, with the arrows between them indicating dynamic flows from one state to another. The biological pathway is colored in blue and so is the node representing the G1 stationary state. We see that the dynamic flow of the protein states is convergent onto the biological pathway, making the pathway an attracting trajectory of the dynamics. With such a topological structure of the phase diagram of protein states, the cell-cycle pathway is a very stable trajectory; it is very unlikely for a sequence of events, starting at the beginning (or at any other point) of the cell-cycle process, to deviate from the cell-cycle pathway. Interestingly, the topology of the converging trajectories shown in Fig. 2 is reminiscent of the converging kinetic pathways in protein folding where a protein sequence is facing the challenge of finding the unique native state among a huge number of conformations (10–12).
Fig. 2.
Dynamical trajectories of the 1,764 protein states (green nodes) flowing to the G1 fixed point (blue node). Arrows between states indicate the direction of dynamic flow from one state to another. The cell-cycle sequence is colored blue. The size of a node and the thickness of an arrow are proportional to the logarithm of the traffic flow passing through them.
Comparison with Random Networks. To investigate how likely a big fixed point and a converging pathway can arise by chance, we study an ensemble of random networks (13, 14) that have the same numbers of nodes and links in each color as in the cell-cycle network. We find that random networks typically have more attractors (fixed points and limit cycles), with the average number being 14.28. The sizes of the basins of attraction in the random networks have a power-law distribution, as shown in Fig. 3A. The probability for a random network to have an attractor of a basin size B equal to or larger than that of the cell-cycle network (B ≥ 1764) is 10.34%.
Fig. 3.
Comparison with random networks. (A) Attractor size distribution of random networks. (B) w-value distributions for the cell-cycle network and for random networks. Ten thousand random networks were used to generate the statistics. (C) Schematic illustration of the definition of wn. The number next to an arrow indicates the total traffic through the arrow. The number next to a node is the wn of the node.
To quantify the “convergence” of trajectories, we define a quantity wn (n = 1, 2,..., 2,048) for each of the 2,048 network states that measures the overlap of its trajectory with all other trajectories (Fig. 3C). Denote Tj,k the total traffic flow through the arrow Aj,k that takes state j to k in one time step, i.e., Tj,k is the total number of trajectories starting from all network states that pass through Aj,k. If the trajectory from state n to its attractor has Ln steps Lso that it consists Ln arrows Ak–1,k, k = 1, 2,..., Ln, 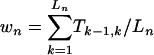 . The overall overlap of all trajectories in a network can be measured by W =〈wn〉, where the average is over all network states. The normalized histogram of wn for all network states is shown in Fig. 3B for both the cell-cycle and the random networks. Without any significant overlap or convergence of trajectories and with a much shorter transient times to attractors, the random networks have their w distribution peaked at small w's, with an average W = 124. However, for the cell-cycle network, the distribution is peaked at very large numbers (W = 743), indicating significant convergence of trajectories. The probability for a random network to have a W ≥ 743 is 0.25%.
. The overall overlap of all trajectories in a network can be measured by W =〈wn〉, where the average is over all network states. The normalized histogram of wn for all network states is shown in Fig. 3B for both the cell-cycle and the random networks. Without any significant overlap or convergence of trajectories and with a much shorter transient times to attractors, the random networks have their w distribution peaked at small w's, with an average W = 124. However, for the cell-cycle network, the distribution is peaked at very large numbers (W = 743), indicating significant convergence of trajectories. The probability for a random network to have a W ≥ 743 is 0.25%.
Network Perturbations. We see that the cell-cycle network has two distinct dynamic properties compared with random networks: it has a super fixed point and it has a converging pathway. What effects would perturbations of the network have on these properties? We perturbed a network by deleting an interaction arrow, adding a green or red arrow between nodes that are not linked by an arrow, or switch a green arrow to red and vice versa. The relative change in the size B of the basin of attraction for the biggest attractor, ΔB/B were then measured as a result of the perturbation. The distributions of ΔB/B are plotted in Fig. 4 for each kind of perturbation, respectively, along with those obtained from the ensemble of random networks. We observe that only a very small fraction of perturbations will eliminate the fixed point completely (ΔB/B = 1). For most perturbations, the relative changes of the basin size are small. A similar behavior in the changes of quantity W as results of the perturbations was also seen. Interestingly, this high “homeostatic stability” (13) is also evident in the ensemble of random networks of the same size (Fig. 4). In fact, we found that for random networks with the dynamic rule of Eq. 1 the homeostatic stability increases monotonically with the average number of arrows per node k (Y.L. and C.T., unpublished work), which is very different from the random Boolean network where a “chaotic” phase with low homeostatic stability is seen for k > kc (13). Recent studies suggest that either a scale-free Boolean network (15) or a genetic network with minimal frustration (16) would also lead to a more stable phase.
Fig. 4.
The histogram of the relative changes of the size of the basin of attraction for the biggest fixed point with respect to network perturbations. Shown are 34 line deletions (A), 174 line additions (B); 29 red–green switchings (C); and the average of A–C (D). One thousand random networks were used to generate statistics.
To examine the effects of these perturbations on the biological pathway itself, for each perturbed cell-cycle network we start at the START state and follow its time evolution. We found that under perturbation a significant fraction of the trajectories reach the G1 stationary state and the cell-cycle sequence is by far the most probable trajectory (Fig. 5).
Fig. 5.
Trajectories of the perturbed cell-cycle network starting from the START. The trajectories from each kind of perturbations (34 from arrow deletions, 174 from arrow additions, and 29 from red–green switchings) are first superimposed on top of each other to form three groups. The three groups are then superimposed on top of each other with equal weights. The width of an arrow and the size of a node are proportional to the logarithm of the number of shared trajectories. The biological pathway is colored blue. The percentages of the perturbed networks that still evolve to the G1 state from START are 41.2%, 57.4%, and 64.7% for arrow-deletion, arrow addition, and color-switching, respectively.
Other Dynamical Rules. We found that the results are insensitive to the values of the weights ag and ar in Eq. 1 and to the protein lifetime td, as long as –ar ≥ ag and td > 0. For example, with ar =–10, ag = 1, and td = 4, there exist the same seven fixed points. The G1 fixed point attracts 90% of all protein states and W = 907. The network is somewhat more robust against perturbation (see supporting information). Preliminary results with differential equations replacing the simple discrete dynamic rule support the overall conclusions (unpublished data).
Other Checkpoints. We also studied the cases in which one of the other checkpoints, instead of the “cell size,” will act as the stop–go signal. We found that, in all cases, there exists a big fixed point that corresponds to the biological state waiting at the checkpoint and the biopathway is a converging trajectory. The studies were done on the full network (Fig. 1 A), keeping only one checkpoint at a time. The basin size B of the big fixed point and the convergence measure W of the biopathway for each checkpoint are, respectively, B = 99.4% and W = 4,257 (InterS), B = 89.8% and W = 3,821 (Spindle Assembly), B = 99.8% and W = 4,925 (DNA Damage). For comparison, the corresponding values for the Cell-Size checkpoint with the full network are B = 90.8% and W = 6,757 (see supporting information).
Discussion
We have demonstrated that the yeast cell-cycle network is robustly designed. The biological states at the checkpoints are big attractors and the biopathway is an attracting trajectory. These robust dynamical properties are also seen in the life cycle network of the budding yeast (unpublished data), suggesting that they may be common features of regulatory networks. The cell-cycle network is rather stable against perturbations. Note that the network we studied (Fig. 1A) is only a skeleton of a larger cell-cycle network with many “redundant” components and interactions (e.g., any member of the G1 cyclins can, to a large extend, perform the functions of other members). Thus, we expect the complete network to be even more stable against perturbations.
The idea that aspects of biological systems can be modeled as dynamic systems and biological states can be interpreted as attractors has a long history, with examples in neural networks (17, 18), immune systems (19, 20), genetic networks (21, 13), cell regulatory network (22), and ecosystems (23). Our study on an actual yeast cellular network lends support to this idea. Furthermore, our results suggest that not only do biological states correspond to big fixed points but the biological pathways are also robust.
Functional robustness has been found in other biological networks, e.g., in the chemotaxis of E. coli (in the response to external stimuli) (24) and in the gene network setting up the segment polarity in insects development (with respect to parameter changes) (25, 26). It has also been found at the single molecular level, in the mutational and thermodynamic stability of proteins (27). In some sense, biological systems have to be robust to function in complex (and very noisy) environments. More robust could also mean more evolvable, and thus more likely to survive; a robust “module” is easier to be modified, adapted, added-on, and combined with others for new functions and new environments (28). Indeed, robustness may provide us with a handle to understand the profound driving force of evolution.
Supplementary Material
Acknowledgments
We thank Hamid Bolouri, Terry Hwa, Stuart Kauffman, Hao Li, Albert Libchaber, Leihan Tang, and Saeed Tavazioe for helpful discussions. The networks and dynamic trajectories are drawn with pajek (http://vlado.fmf.uni-lj.si/pub/networks/pajek). This work was partly supported by the National Key Basic Research Project of China (No. 2003CB715900). T.L. and Y.L. acknowledge the support from the Jun Zheng foundation.
This paper was submitted directly (Track II) to the PNAS office.
Footnotes
Making the time constants of all arrows the same could have disastrous consequences in network dynamics. However, we are saved for this particular network because of its intrinsic sequential nature. We have tested the dynamics with varied time scales of action (phosphorylation and transcriptional activation) for different arrows and obtained similar results.
References
- 1.Albert, R., Jeong, H. & Barabási, A.-L. (2000) Nature 406, 378–382. [DOI] [PubMed] [Google Scholar]
- 2.Jeong, H., Tombor, B., Albert, R., Oltval, Z. N. & Barabási, A.-L. (2000) Nature 407, 651–654. [DOI] [PubMed] [Google Scholar]
- 3.Jeong, H., Mason, S., Barabási, A.-L. & Oltvai, Z. N. (2001) Nature 411, 41–42. [DOI] [PubMed] [Google Scholar]
- 4.Maslov, S. & Sneppen, K. (2002) Science 296, 910–913. [DOI] [PubMed] [Google Scholar]
- 5.Milo, R., Shen-Orr, S., Itzkovitz, S., Kashtan, N., Chklovskii, D. & Alon, U. (2002) Science 298, 824–827. [DOI] [PubMed] [Google Scholar]
- 6.Murray, A. & Hunt, T. (1993) The Cell Cycle (Oxford Univ. Press, New York).
- 7.Spellman, P. T., Sherlock, G., Zhang, M. Q., Iyer, V. R., Anders, K., Eisen, M. B., Brown, P. O., Botstein, D. & Futcher, B. (1998) Mol. Biol. Cell 9, 3273–3297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chen, K., Csikasz-Nagy, A., Gyorffy, B., Val, J., Novak, B. & Tyson, J. J. (2000) Mol. Biol. Cell 11, 369–391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tyson, J. J., Chen, K. & Novak, B. (2001) Nat. Rev. Mol. Cell Biol. 2, 908–916. [DOI] [PubMed] [Google Scholar]
- 10.Wolynes, P. G., Onuchic, J. N. & Thirumalai, D. (1995) Science 267, 1619–1620. [DOI] [PubMed] [Google Scholar]
- 11.Onuchic, J. N., Luthey-Schulten, Z. & Wolynes, P. G. (1997) Annu. Rev. Phys. Chem. 48, 545–600. [DOI] [PubMed] [Google Scholar]
- 12.Dill, K. A. & Chan, H. S. (1997) Nat. Struct. Biol. 4, 10–19. [DOI] [PubMed] [Google Scholar]
- 13.Kauffman, S. A. (1993) The Origins of Order (Oxford Univ. Press, New York).
- 14.Aldana-Gonzalez, M., Coppersmith, S. & Kadanoff, L. P. (2003) in Perspectives and Problems in Nonlinear Science, eds. Kaplan, E., Marsden, J. E. & Sreenivasan, K. R. (Springer, New York), pp 23–89.
- 15.Aldana, M. (2003) Physica D 185, 45–66. [Google Scholar]
- 16.Sasai, M. & Wolynes, P. G. (2003) Proc. Natl. Acad. Sci. USA 100, 2374–2379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.McCulloch, W. S. & Pitts, W. (1943) Bull. Math. Biophys. 5, 99–115. [DOI] [PubMed] [Google Scholar]
- 18.Hopfield, J. J. (1982) Proc. Natl. Acad. Sci. USA 79, 2554–2558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Jerne, N. K. (1974) Ann. Immunol. 125C, 373–389. [PubMed] [Google Scholar]
- 20.Parisi, G. (1990) Proc. Natl. Acad. Sci. USA 87, 429–433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kauffman, S. A. (1969) J. Theor. Biol. 22, 437–467. [DOI] [PubMed] [Google Scholar]
- 22.Huang, S. & Ingber, D. E. (2000) Exp. Cell Res. 261, 91–103. [DOI] [PubMed] [Google Scholar]
- 23.May, R. M. (1974) Science 186, 645–647. [DOI] [PubMed] [Google Scholar]
- 24.Alon, U., Surette, M. G., Barkai, N. & Leibler, S. (1999) Nature 397, 168–171. [DOI] [PubMed] [Google Scholar]
- 25.von Dassow, G., Meir, E., Munro, E. M. & Odell, G. M. (2000) Nature 406, 189–192. [DOI] [PubMed] [Google Scholar]
- 26.Albert, R. & Othmer, H. G. (2003) J. Theor. Biol. 223, 1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Li, H., Helling, R., Tang, C. & Wingreen, N. (1996) Science 273, 666–669. [DOI] [PubMed] [Google Scholar]
- 28.Kirschner, M. & Gerhart, J. (1998) Proc. Natl. Acad. Sci. USA 95, 8420–8427. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.







