Abstract
Recent technological advances coupled with large sample sets have uncovered many factors underlying the genetic basis of traits and the predisposition to complex disease, but much is left to discover. A common thread to most genetic investigations is familial relationships. Close relatives can be identified from family records, and more distant relatives can be inferred from large panels of genetic markers. Unfortunately these empirical estimates can be noisy, especially regarding distant relatives. We propose a new method for denoising genetically—inferred relationship matrices by exploiting the underlying structure due to hierarchical groupings of correlated individuals. The approach, which we call Treelet Covariance Smoothing, employs a multiscale decomposition of covariance matrices to improve estimates of pairwise relationships. On both simulated and real data, we show that smoothing leads to better estimates of the relatedness amongst distantly related individuals. We illustrate our method with a large genome-wide association study and estimate the “heritability” of body mass index quite accurately. Traditionally heritability, defined as the fraction of the total trait variance attributable to additive genetic effects, is estimated from samples of closely related individuals using random effects models. We show that by using smoothed relationship matrices we can estimate heritability using population-based samples. Finally, while our methods have been developed for refining genetic relationship matrices and improving estimates of heritability, they have much broader potential application in statistics. Most notably, for error-in-variables random effects models and settings that require regularization of matrices with block or hierarchical structure.
Key words and phrases: Covariance estimation, cryptic relatedness, genome-wide association, heritability, kinship
Introduction
In the past decade tremendous progress has been made toward understanding the genetic basis of disease. This challenging endeavor has given rise to numerous study designs with a vast arsenal of statistical machinery. A common theme, however, is the pivotal role played by familial relationships. Traditionally relationships are encoded in pedigrees of known relatives [Thompson (1974, 1975), Boehnke and Cox (1997), Epstein, Duren and Boehnke (2000), McPeek and Sun (2000)], but for more distantly related individuals, pedigree information can sometimes be erroneous or difficult to obtain. Relatedness can also be calculated from large panels of genetic markers [Milligan (2003), Albers et al. (2008), Anderson and Weir (2007), Browning (2008), Browning and Browning (2010), Purcell et al. (2007), Day-Williams et al. (2011), Yang et al. (2010a)]. While this approach has greatly expanded the scope of inference for relationships, empirical estimates are noisy, especially regarding distant relatives.
The search for a disease gene begins with finding unusual sharing of genetic material among individuals who share a trait (phenotype). Linkage analysis involves the study of joint inheritance of genetic material and phenotypes within relatives [Hopper and Mathews (1982), Almasy and Blangero (1998)]. Typically, these studies are restricted to relatives within a pedigree, but more recently the approach has been extended to samples of people who are more distantly related and without known pedigree structure [Day-Williams et al. (2011)]. Alternatively, genetic associations can be discovered from population samples, which are usually based on case–control studies. In these studies the sample is assumed to be unrelated, but the presence of distant relatives (i.e., cryptic relatedness) can reduce power or generate spurious associations [Lander and Schork (1994), Astle and Balding (2009)]. Numerous methods have been proposed to deal with familial structure in genetic association studies [Choi, Wijsman and Weir (2009), Bravo et al. (2009), Thornton and McPeek (2010), Kang et al. (2010)], all of which require an estimate of family relationships among individuals within the study.
Relationships are also critical for quantitative genetics. A common problem for quantitative genetics is to estimate the fraction of variance of a continuous trait, such as height, due to genetic variation amongst individuals in a population. This feature, known as heritability, delineates the relative contributions of genetic and nongenetic factors to the total phenotypic variance in a population. Heritability is a fundamental concept in genetic epidemiology and disease mapping. Using a variety of close relatives, the heritability of quantitative and qualitative traits can be estimated directly [Fisher (1918), Devlin, Daniels and Roeder (1997)]. With complex pedigrees, applying the same principles, heritability can be estimated using random effects models [Henderson (1950)]. Heritability of height, weight, IQ and many other quantitative traits have been investigated for nearly a century and continue to generate interest [Deary et al. (2012)].
Interest in the genetic basis of disease is high because greater understanding of disease etiology will in principle lead to better treatments. Large population-based samples are enhancing our ability to identify DNA variants affecting risk for disease and it has become the standard to search for genetic variants associated with common disease using genome-wide association studies (GWAS). Thousands of associations for common diseases/phenotypes have already been validated [Visscher et al. (2012)]. Nevertheless, even in the most successful cases, such as Inflammatory Bowel Disease studied in McGovern et al. (2010) and Imielinski et al. (2009), discoveries account for only a fraction of the heritability.
Given the relatively limited discoveries thus far, a reasonable question is whether the heritability of a trait estimated from relatives truly does trace to genetic variation. Yang et al. (2010a) offer a novel approach to genetic analysis that shows that indeed much of it does. They propose to analyze population samples, rather than pedigrees, for the heritability of the trait. To do so they first estimate the correlation between all pairs of individuals in the population sample using a dense set of common genetic variants, such as those typically used for a GWAS. They then take this matrix and relate it to the covariance matrix of phenotypes for these subjects to derive an estimate of heritability. Thus, in their application, where essentially all relatives are removed from the sample, heritability refers to the proportion of variance in the trait explained by the measured genetic markers. They provide a fascinating example of how this approach works in the case of human height and they and others applied these techniques to many other traits [reviewed by Visscher et al. (2012)].
The work of Yang et al. (2010a) inspired us to consider applying a related approach to answer a different question. Could estimates of relatedness obtained from a population sample be improved by using smoothing techniques on the variance–covariance matrix? If so, population samples could be used to estimate heritability—in the traditional sense—without requiring close relatives. This approach has application to phenotypes for which extended pedigrees are difficult to obtain. For instance, there is controversy in the literature concerning the heritability of autism, which is typically estimated from twin studies [Hallmayer et al. (2011)]. Smoothing techniques could also be used to estimate relatedness in samples of distantly related individuals for many other genetic analyses. For example, a version of linkage analysis could be applied to distant relatives.
We propose Treelet Covariance Smoothing—a novel method for smoothing and multiscale decomposition of covariance matrices—as a means to improving estimates of relationships. Treelets were first introduced in Lee and Nadler (2007) and Lee, Nadler and Wasserman (2008) as a multi-scale basis that extends wavelets to unordered data. The method is fully adaptive. It returns orthonormal basis functions supported on nested clusters in a hierarchical tree. Unlike other hierarchical methods, the basis and the tree structure are computed simultaneously, and both reflect the internal structure of the data.
In this work, we extend the original treelet framework for smoothing of one-dimensional signals to smoothing and denoising of variance–covariance matrices with hierarchical block structure and unstructured noise. Smoothing is achieved by a nonlinear approximation scheme in which one discards small elements in a multi-scale matrix decomposition. The basic idea is that if the data have underlying structure in the form of groupings of correlated variables, then we can enforce sparsity by first transforming the data into a treelet representation by a series of rotations of pairs of correlated variables, and then thresholding covariances. We refer to this new regularization approach for covariance matrices with groupings on multiple scales as Treelet Covariance Smoothing (TCS).
We apply TCS to genetically inferred relationship matrices, with the goal of improving estimates of pairwise relationships from large pedigrees and population-based samples. On both simulated and real data, we show that TCS leads to better estimates of the relatedness between individuals. Using these estimates allows us to estimate the heritability from population-based samples provided they include some distantly related individuals, a property that is almost inevitable in practice. Finally, we discuss how estimating heritability is simply a case of variance component estimation for an error-in-variables random effects model. Therefore, our method can be applied to a whole family of more general models of similar structure.
Models
GWAS panels
The human genome contains many millions of single nucleotide polymorphisms (SNPs) and other genetic variation distributed across the genome. In a GWAS it is now typical to measure a panel of at least 500,000 SNPs from each subject. SNPs typically have only two forms or alleles within a population. Whichever allele is less frequent is called the minor allele. The genotype of an individual at a SNP can then be coded as 0, 1 or 2 depending on the number of minor alleles the individual has at that SNP. Alleles at SNPs in close physical proximity are often highly correlated (i.e., in linkage disequilibrium). When multiple SNPs are in linkage disequilibrium, we say one of these SNPs “tags,” or represents, the others. Although estimates vary, well-designed panels of 500,000 SNPs do not tag all of the common SNPs in the genome and they tag very few of the SNPs with rare minor alleles [Yang et al. (2010a)]. Nevertheless, GWAS provide considerable information about familial relationships.
Estimating genetic relationships
The relatedness between a pair of individuals is defined by the frequency by which they share alleles identical by descent (IBD). Formally, two alleles are considered IBD if they descended from a common ancestor without an intermediate mutation. Within a pedigree relatives share very recent common ancestors, hence, many alleles are IBD. For a more detailed exposition of genetic relationships, see Astle and Balding (2009).
The quantity of interest in this investigation is the Additive Genetic Relationship which is defined as the expected proportion of alleles IBD for a pair of individuals. For individuals i and j we use Aij to denote this quantity, which is more familiar when viewed as the degree of relationship, where Rij = −log2(Aij). For example, for siblings, first cousins and second cousins, who are 1st, 3rd and 5th degree relatives, A is 1/2, 1/8 and 1/32, respectively. Within a noninbred pedigree A can be computed using a recursive algorithm [Thompson (1986)]. For example, if individual i has parents k and l, then Aij = Aji = 1/2(Ajk + Ajl).
For distantly related individuals, detailed pedigree information is not often available; however, with GWAS data one can calculate genome-average relatedness directly [Astle and Balding (2009)]. Even with complete information regarding IBD status of the chromosomes, the fraction of genetic material shared by relatives will differ slightly from the expectation calculated from the pedigree due to the stochastic nature of the meiotic process [Weir, Anderson and Hepler (2006)]. For the purpose of genetic investigations, one could argue that genome-average relatedness is a truer measure of relatedness. For example, while two distantly related individuals are expected to share a small fraction of their genetic material, if they do not inherit anything from their common ancestor, it seems appropriate to consider them unrelated.
Under many population genetic models Aij can also be interpreted as a correlation coefficient. Let zik denote the scaled minor allele count for individual i at SNP k: , where is the minor allele count and pk is the minor allele frequency. For individuals i and j at genetic variant k, it follows from our model that
| (1) |
Exploiting this feature leads to a method of moments estimate of A from a panel of m genetic markers. To see this, let zk denote a column vector of observed scaled allele counts for all individuals at the kth SNP, then let
| (2) |
where Z = (z1, …, zm). The Genome-wide Complex Trait Analysis (GCTA) software from Yang et al. (2010b) computes this estimator.
The method of moments estimator is unbiased if the population allele frequencies are known [Milligan (2003)]. In practice, the pk’s are estimated from the sample data. A criticism of this estimator is that some off-diagonal elements are negative, which does not conform to the interpretation of Aij as a probability. Viewed as a correlation coefficient, however, negative quantities suggest the pair of individuals share fewer alleles than expected given the allele frequencies. Alternatively, maximum likelihood estimators of A have been developed [Thompson (1975), Milligan (2003)], but these estimators are quite computationally intensive for GWAS panels. Hence, while method of moments estimators are typically less precise than maximum likelihood estimators, they are more commonly used when a large SNP panel is available.
Estimating heritability
By definition, the heritability of a quantitative trait (y) such as height is determined by the additive effect of many genes and genetic variants (g), each of small effect (i.e., the polygenic model). For individuals i = 1, …, n, suppose that the genetic effects are explained by J causal SNPs, and we can express the genetic effect as
| (3) |
where uj is the additive random effect of the j th causal variant, weighted by the scaled number zij of minor alleles at this variant. Let g = (g1, …, gn)t be the vector of random effects corresponding to the additive genetic effects for individuals i = 1, …, n. For u = (u1, …, uJ)t and Zc = [zij], we write g = Zcu. Define G as the variance–covariance matrix of g. Assuming , it follows that
| (4) |
where .
In the traditional model for quantitative traits a continuous phenotype y is modeled as
| (5) |
where e = (e1, …, en)t is the vector of residual effects, and y = (y1, …, yn)t is the vector of phenotypes. In matrix notation, y = 1μ + g + e. The residuals are assumed to be independent with variance–covariance equal to and the random effects and residual error are assumed to be normally distributed. Consequently,
| (6) |
The heritability of the phenotype y is defined as
This quantity is more accurately known as the additive or narrow-sense heritability, in contrast to the broad-sense heritability, which includes nonadditive genetic effects such as gene–gene interactions. Our inferences will be confined to narrowsense heritability.
If the causal SNPs (or good tag SNPs) and the phenotype were directly measured, then one could estimate h2 based on equation (5) and the implied random effects model using maximum likelihood (REML) [Searle, Casella and McCulloch (1992)]. Notationally, Zc is an n × J matrix that picks out J columns of the full SNP panel Z. In practice, Zc is not known. Few of the causal SNPs are known for any phenotype, and many causal SNPs will be missing from Z (i.e., not tagged by any measured SNPs).
How then is h2 estimated in practice? Assuming various subsets of individuals in the sample are related with relationship matrix A (defined previously), heritability can be estimated without any knowledge of causal genetic variants that constitute g. From equation (1) and the polygenic model it follows that as J gets large. This inspires an alternative random effects model which has long been utilized in population genetics:
| (7) |
Historically, A has been derived from known pedigree structure. However, provided some subsets of the individuals in the sample are related (even distantly), one can estimate A from genetic markers using either method of moments or maximum likelihood estimation techniques. This approach has been applied frequently in quantitative genetics, especially in breeding studies [Lynch and Ritland (1999), Eding et al. (2001), Visscher et al. (2006), Hayes and Goddard (2008)]. We conjecture that by using TCS, we can improve estimates of A and obtain better estimates of heritability without knowledge of causal variants.
Alternatively, if the sample is completely unrelated, then substituting the result of equation (2) for (6) does not lead to an estimate of h2 unless all of the causal SNPs have been recorded. Instead this approach estimates , the proportion of the variance in phenotype explained by the SNP panel [Yang et al. (2010a)]. In this setting, TCS will not improve estimates of .
Methods
Treelet covariance smoothing (TCS)
The genetic relationship matrix A is a measure of the additive covariance structure that exists between individuals due to a common genetic background. We estimate the relationship matrix using genotyped SNPs, but this estimate is usually noisy. Hence, we propose a method for improving upon this estimate using treelets.
Treelets simultaneously return a hierarchical tree and orthonormal basis functions supported on nested clusters in the tree—both reflect the underlying structure of the data. Here we extend the original treelet framework [Lee and Nadler (2007), Lee, Nadler and Wasserman (2008)] for smoothing one-dimensional signals and functions, to a new means of smoothing and denoising variance–covariance matrices with hierarchical block structure and unstructured noise. The main idea is to first move to a different basis representation through a series of local transformations, and then impose sparsity by thresholding the transformed covariance matrix. We refer to the approach as Treelet Covariance Smoothing (TCS). The general setup is as follows. [See Appendix in Lee, Nadler and Wasserman (2008) for details on how to compute the treelet transformation. The treelet algorithm, as well as its implementation, is available in R on CRAN as the treelet library.]
Let z be a random vector in ℝN with variance–covariance matrix Σ. In our context, z represents the scaled minor allele counts for a set of N individuals at any SNP, and the covariance Σ = A, the additive genetic relationship matrix of the N individuals [equation (1)]. Now at each level of the treelet algorithm, we have an orthonormal multiscale basis. Let {v1, …, vN} denote the basis at the top of the tree [corresponding to level ℓ = N − 1 if using the notation in Lee, Nadler and Wasserman (2008)]. We write
| (8) |
where ci = 〈z, vi〉 represent the orthogonal projections onto local basis vectors on different scales. It follows that the covariance of z can be written in terms of a multi-scale matrix decomposition
| (9) |
where γi,i = Var(ci) and γi,j = Cov(ci, cj). The first term in equation (9) describes the diagonally symmetric block structure of the variance–covariance matrix. These blocks are organized in a hierarchical tree. The second term describes a more complex structure, including off-diagonal rectangular blocks, which are also hierarchically related to each other in a multi-scale matrix decomposition.
In practice, the covariance Σ is unknown, and both the covariance matrix and the treelet basis need to be estimated from data. For relationship matrices, one can, for example, derive an estimate Σ̂ = Â from marker data using method of moments or maximum likelihood methods. Denote the treelet basis derived from Σ̂ by {v̂1, …, v̂N}, and write
where and .
Let T(Σ̂) be the covariance estimate after a treelet transformation, that is, after applying a full set of N − 1 Jacobi rotations of pairs of correlated variables. A calculation shows that
| (10) |
where ci ≡ 〈z, vi〉 and cj ≡ 〈z, vj 〉. This suggests2 a smoothed estimate of the covariance by thresholding:
| (11) |
with the thresholding function
| (12) |
where λ is a smoothing parameter.
To summarize and in matrix short-hand notation, the smoothed genetic relationship matrix is given by
| (13) |
where B = (v̂1, …, v̂N) and T(Â), respectively, denote the treelet basis and the covariance matrix at the top of the tree, and fλ corresponds to element-wise thresholding [equation (12)]. Note that to compute B we only need to know the Jacobi rotations at each level of the tree, more precisely, the treelet basis, B = J(1) · J(2) ····· J(N−1), where the Jacobi rotation matrix J(ℓ) is the rotation matrix at level ℓ. The covariance estimate after a treelet transformation and before smoothing is Σ̂ℓ ≡ T(Â) = Bt ÂB.
Choosing a smoothing parameter
The goal is to choose a threshold (λ) that reduces noise in the estimated relationships. Traditional cross-validation is not an option because we cannot predict Aij without including persons i and j. Alternatively, we have an abundance of genetic information from which to estimate Â. We propose a SNP subsampling procedure to estimate the tuning parameter.
We begin by breaking the genome into independent training and test sets by randomly placing half the chromosomes into each set. To improve the efficiency of our estimate of A, we utilize a “blackout window” of length b to avoid sampling SNPs that are highly correlated. This b can be considered either in terms of physical location along the chromosome or the number of SNPs between any two SNPs in question. From the set of training chromosomes, select a relatively large sample of M independent SNPs to get a reliable estimate of Â. We train our algorithm by smoothing  using TCS to get Ã(λ), for all λ ∈ Λ, where Λ is a grid of reasonable threshold values.
Once we have Ã(λ), for a given λ, we subsample L SNP sets of size k from the test set of chromosomes. Here, k ≪ M and the SNPs within each of the L subsampled sets follow our defined blackout window, b. Then, for all l = 1, …, L, estimate the relationship matrix, Âl, based on the subset of SNPs. We then compare our smoothed relationship matrix, Ã(λ), from the training chromosomes to each of the L nonsmoothed relationship matrices, Âl, via a weighted risk function:
| (14) |
where wij is a weight associated with each element in A. Clearly, the optimal tuning parameter is λ̂ = argminλ∈Λ H(λ).
The reason for introducing the weighting scheme is because many subjects are nearly unrelated. Thus, we aim to upweight the loss function so that the preponderance of near-zero elements in the off-diagonal do not overwhelm the loss function. We suggest using the learned hierarchical tree to get the weights. More specifically, wij = |[T(Â)]ij|, corresponding to the absolute value of the correlations between the final groupings of individuals after N − 1 rotations [equation (10)]. Also, we set wii = 0 because we are not interested in estimating inbreeding coefficients. It should be noted that this is a rather general weighting method. Other schemes may be more appropriate if there is a priori information suggesting the importance of particular relationships.
Results
Simulations
To produce realistic simulations, we started with the phased genomes (haplotypes) of individuals from the HapMap 3 database3, selecting two populations with European ancestry (CEU and TSI). Utilizing the small sample of available haplotypes, our first objective was to generate a large sample of haplotypes, representative of those that might be sampled from unrelated founders of a population. The challenge was to keep intact the realistic haplotype structure for a human population, including linkage disequilibrium (LD), without generating unusual sharing between the founders. To accomplish this goal, we took the HapMap data on CEU and Tuscan samples, which were phased quite accurately into haplotypes, as the initial sample of chromosomes from which to generate founders. Now each founder haplotype was created by sampling pieces of chromosomes (or haplotypes) from the initial sample. To do so, the number of recombination spots per chromosome was determined using an overall recombination of θ = 10−6 per Mb, which is 100 times the normal rate of recombination for humans. The actual location of the recombination spots were then determined using the recombination map provided by HapMap, a procedure that successfully keeps intact the LD structure of the chromosome. From this pool of generated haplotype pairs, chromosomes were randomly assigned to each of the 39 founders in each of 100 families. These founder chromosomes were then dropped through a seven generation pedigree; see Figure 1 for the pedigree of a single family used for simulations. At each generation the chromosomes underwent recombination with an overall rate of θ = 10−8 at locations determined by HapMap’s recombination map. Within each pedigree, the genotype information of twenty individuals was collected (colored yellow). We then sampled ten individuals of varying relatedness from this group with a random sampling strategy that favored individuals of distant relatedness within the pedigree. The highest pairwise relatedness within a family is 0.125, corresponding to R = 3, and the lowest is < 0.001. Individuals from different families are unrelated. Each simulation produced a total of 1000 individuals made up of 100 ten-member families of varying levels of relatedness. Finally, the entire process was repeated fifty times.
Fig. 1.
Pedigree of a single family used for simulations. Genomes were dropped through the entire pedigree and ten individuals were sampled from the twenty possible highlighted individuals. Individuals 35–39 are unrelated to everyone else in the pedigree.
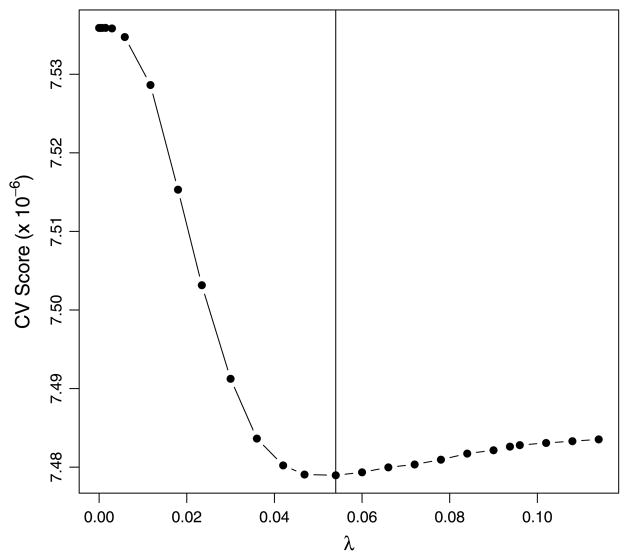
Because we know the pedigree structure, we can compare the unsmoothed estimate  to à found via TCS. Here, we use the GCTA software [Yang et al. (2010b)] to estimate  using 100,000 randomly chosen SNPs with MAF > 0.05. The optimal level of smoothing (λ̂) is chosen via the subsampling scheme described previously using M = 5000, b = 10, k = 50, L = 50 and repeating everything ten times. Here, b is in terms of number of SNPs. We choose λ̂ by examining a plot of H(λ) across a grid of λ values. The optimal smoothing parameter is the one that minimizes the risk function, H. For one such simulation sample we can see from Figure 2 that λ̂ ≈ 0.051.
Fig. 2.
Cross-validation plot showing the weighted risk function at varying levels of the thresholding parameter, λ. The optimal λ is the point where the H(λ) (CV Score) is minimized.
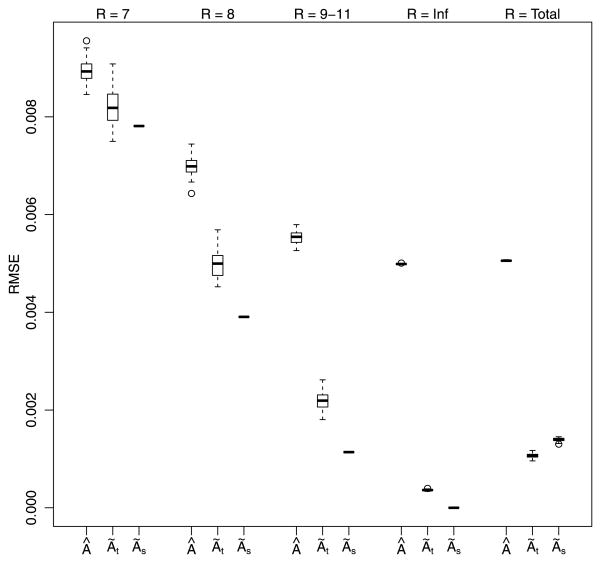
The question then becomes, does TCS improve estimates of relatedness? Figures 3 and 4 display boxplots comparing the root mean square error (RMSE) of  to à at varying levels of known pairwise relationship values. For a full comparison, we have included two smoothing methods: TCS, as previously described, as well as “simple thresholding,” wherein the elements of  are directly thresholded. [The latter approach is a degenerate case of TCS models, at level ℓ = 0, for which the basis is the Dirac basis, i.e., vi = v̂i = δi for i = 1,…, N in equations (8)–(13).] Moving from left to right in the figures, the true degree of relatedness increases from R = 4, …, 11, to no relatedness. Over the entire matrix of estimates, the RMSE is 0.0055, 0.0015 and 0.0019 for the unsmoothed (Â), TCS (Ãt) and simple thresholding (Ãs) methods respectively, demonstrating an overall advantage of TCS. As with many shrinkage methods, TCS introduces a slight bias that is reflected in a higher RMSE for closely related individuals. Consequently, TCS has a larger RMSE than the unsmoothed estimate for smaller values of R. Where TCS gains a notable advantage over the unsmoothed estimate is in differentiating between more distantly related individuals and noise. From Figures 3 and 5 we can see that simple thresholding incurs a substantially larger RMSE for closer relationships because it thresholds too aggressively. For R = 4, 70% of the pairs are zeroed out, and for R > 4 virtually all pairs are zeroed out. Naturally, this method has the smallest RMSE for the sample of unrelated pairs because thresholding zeros out all of these entries. Notably, TCS does almost as well in this setting. A direct comparison of RMSE does not fully reflect the true loss incurred in practice. In most genetic studies close relatives are often recorded in pedigrees and, hence, estimates are not required. Alternatively, considering distant relatives to be unrelated leads to a substantial loss for estimating heritability and most other genetic applications.
Fig. 3.
Boxplots of RMSE for unsmoothed (Â) along with smoothed using TCS (Ãt) and simple thresholding (Ãs) at increasing degrees of relatedness (R = 4, 5, 6; see header). Here, TCS is better than simple thresholding as the latter method thresholds too aggressively.
Fig. 4.
Boxplots of RMSE for unsmoothed (Â) along with smoothed using TCS (Ãt) and simple thresholding (Ãs) at increasing degrees of relatedness (R = 7, 8, 9–11). Also included is the comparison of RMSE values for unrelated pairs (R = Inf) and average RMSE for the entire relationship matrix (R = Total). We see that both thresholding methods remove noise, but TCS works better than simple thresholding overall.
Fig. 5.
Barplots of the percentage of relationships that are equal to 0 for no smoothing (A), smoothing using TCS (T) and simple thresholding (S). The three cases are compared at increasing degrees of relatedness (R = 3, …, 11). Any value below ε = 10−5 is considered to be 0.
Heritability in health ABC study
Body Mass Index (BMI) is one of several traits measured as part of the study entitled “Whole Genome Association Study of Visceral Adiposity” as part of the Health Aging and Body Composition (Health ABC) Study. These data are archived in the Database for Genotypes and Phenotypes (dbGaP)4. We restrict our attention to those 1644 individuals with self-reported European ancestry. To control for confounding, prior to analysis, we adjust BMI scores by regressing out age, gender and collection site. Our objective is to estimate heritability of BMI from this population sample. Published heritability estimates range from as low as 0.05 to as high as 0.90 [Allison et al. (1996)]; however, based on estimates derived from known pedigrees, the heritability of BMI is estimated to be approximately 50–75% [Kangas-Kontio et al. (2010), Zabaneh et al. (2009)].
From the full sample of SNPs (Illumina 1M platform) we remove those with missingness greater than 0.1% and MAF < 0.01. From these we select a subpanel of 90,000 SNPs, chosen to be nearly evenly spaced. Based on these SNPs, we calculated the relationship matrix Â, and find that the individuals are predominately unrelated. The most highly related pair appear to be third degree relatives, such as first cousins. And more than half of the pairs appear to be more distantly related than 10th degree relatives.
To estimate the heritability in this setting, we input the smoothed relationship matrix in equation (11) into the REML algorithm. The required smoothing parameter λ is selected in two ways: (i) minimizing the loss function in equation (14) via the subsampling approach; and (ii) using a profile likelihood approach. With both techniques, we get estimates of the heritability that are very close to what is found in the literature.
For a range of smoothing parameters, 0 ≤ λ ≤ 0.40, we calculate the smoothed relationship matrix, Ãλ, and plug this value into the REML model to obtain a profile likelihood (Figure 6). Also plotted in this figure is , the heritability that maximizes REML as a function of λ (or minimizes—2 times the log-likelihood). Without smoothing (λ = 0), which is not shown in the plot, ĥ2 = 0.23. Smoothing the relationship matrix results in an increasing estimate of the heritability which stabilizes at about 70%. Further smoothing beyond the range displayed leads to a numerically unstable optimization problem and diminished likelihood. Using the profile likelihood approach, λ is chosen to be the point at which REML is maximized. This method results in an estimate of λ̂ = 0.20 corresponding to ĥ2 = 0.71. Smoothing using our SNP subsampling scheme results in λ̂ = 0.18 and ĥ2 = 0.72.
Fig. 6.
Estimating heritability in the Health ABC data set. Solid curve is the estimated heritability at increasing values of the smoothing parameter λ. The dashed curve is ∝ −2 log(
 ), where,
), where,
 is the maximum profile likelihood obtained from the REML algorithm. The solid vertical line is the optimally chosen threshold value using our subsampling scheme. The dashed vertical line represents the optimally chosen threshold value when minimizing the likelihood profile. A: For BMI, h2 = 0.72 when using subsampling to choose an optimal smoothing parameter (λ̂ = 0.18). Similarly, h2 = 0.71 when using the profile likelihood plot (λ̂ = 0.20). With no smoothing (λ = 0), h2 = 0.23. This is not shown on the plot. B: For AVFD, h2 = 0.29 when using our subsampling approach to choose an optimal smoothing parameter. However, h2 = 0.36 when using the profile likelihood plot (λ̂ = 0.09). These are compared to h2 = 0.11, the heritability when there is no smoothing (not shown).
is the maximum profile likelihood obtained from the REML algorithm. The solid vertical line is the optimally chosen threshold value using our subsampling scheme. The dashed vertical line represents the optimally chosen threshold value when minimizing the likelihood profile. A: For BMI, h2 = 0.72 when using subsampling to choose an optimal smoothing parameter (λ̂ = 0.18). Similarly, h2 = 0.71 when using the profile likelihood plot (λ̂ = 0.20). With no smoothing (λ = 0), h2 = 0.23. This is not shown on the plot. B: For AVFD, h2 = 0.29 when using our subsampling approach to choose an optimal smoothing parameter. However, h2 = 0.36 when using the profile likelihood plot (λ̂ = 0.09). These are compared to h2 = 0.11, the heritability when there is no smoothing (not shown).
For comparison, we have repeated the above experiments with an orthogonal basis computed by principal component analysis (PCA) in lieu of a treelet basis. Such an approach does not improve the estimates of family relationships or heritability. When noise is present, PCA is unable to uncover the underlying sparse structure of the relationship matrix. In fact, the results with PCA are identical to those without smoothing (with the profile likelihood peaking when the tuning parameter is set to 0).
Another trait that was measured in this study is the Abdomen Visceral Fat Density (AVFD). As was the case with BMI, we restricted our attention to individuals of European descent and regressed out age, sex and collection site. According to the literature, the heritability of AVFD should be between 45–70% [Katzmarzyk, Perusse and Bouchard (1999)]. According to Figure 6, one can see that using the smoothing parameter based on our subsampling scheme (λ̂ = 0.18) we get ĥ2 = 0.29. On the other hand, exploiting the profile likelihood plot results in λ̂ = 0.09 and ĥ2 = 0.36. When no smoothing was used (not shown in figure), λ̂ = 0.11. Thus, both methods for choosing the smoothing parameter used in TCS resulted in estimates of the heritability that are closer to what is established in the literature than without smoothing.
It is notable that ĥ2 for both traits increased toward the established estimate of heritability regardless of how we estimate the optimal smoothing parameter, because only a small fraction of the genome was sampled by the SNP panel. Thus, our results underscore the fact that the quantitative trait model given in equation (5) does not require measurement of the causal SNPs that constitute equation (3). What is required is a good estimate of A based on relatives.
Our analysis of BMI and AVFD illustrates the difference between estimates of heritability in the traditional sense and estimates of , the heritability attributable to the SNPs in the panel. From equations (6) and (7) it is clear that heritability derived from the classic quantitative traits model can distinguish between variance explained by relatives and variance explained by causal SNPs only if either (i) all causal SNPs are excluded, or (ii) all relatives are excluded. Because a large number of undiscovered SNPs scattered across the genome are likely to be causal, and large samples invariably contain distantly related individuals, some ambiguity will always be present.
Clearly, the 90,000 SNPs in our panel do not explain a substantial fraction of the variation in BMI and yet we obtain an accurate estimate of heritability using TCS. The increase in estimated heritability of BMI from 23% to 72% suggests that smoothing improves the estimate of A and that a substantial fraction of the correlation in BMI in our sample is due to genetic relatedness. In a similar study with a larger population sample Yang et al. (2011) estimated of BMI at 17% when using the full SNP panel, but excluding all detectable relatives. Assuming relatives were successfully removed, they conclude that approximately 17% of the variability in BMI is explained by common variants included or tagged by the SNP panel.
Discussion
Recently, there has been an upsurge of papers on sparse covariance matrix estimation; see Bickel and Levina (2008), Cai and Liu (2011) and the references within. Most of this research concerns the problem of estimating population covariance matrices from samples of multivariate data in the “large p–small n” regime using banding or thresholding techniques in the original coordinate system. Our setting is slightly different with a more complex data structure: We want to improve estimates of a large covariance matrix (A) in which we expect a hierarchical block structure due to clustering of distantly related individuals. A noisy estimate of covariance is obtained from a large sample of SNPs, each of which contains very little information. This matrix is interpreted as the additive genetic relationship matrix and it can be used to infer degree of relationship between pairs of individuals.
We propose a new method, which we call treelet covariance smoothing (TCS), for regularizing real symmetric matrices with hierarchical block structure and unstructured noise. We show how a subsampling strategy applied to SNPs can be used to choose the tuning parameter for the smoothing procedure. For simulated data, we show that TCS does indeed improve estimates of family relationships. As an application we show how TCS can be used to estimate heritability of quantitative traits from a genome-wide sample of SNPs by smoothing relationships estimated from those SNPs. We then apply TCS to the problem of estimating the heritability of body mass index (BMI) and abdomen visceral fat density (AVFD) in the Health ABC data set. In particular, BMI heritability is usually quoted to be at least 0.50, but an estimate based on a noisy estimate of A yields a much lower value of 0.23. By denoising the estimated relationship matrix with treelets, we increase the estimated heritability of BMI from 0.23 to 0.72. AVFD heritability analysis produces similar results. Thus, a careful examination of heritability estimates using more distant relatives demonstrates that one may substantially improve relationship estimates using TCS.
Other covariance regularization schemes exist in the literature, but systematic comparison is beyond the scope of this work. Direct application of regularization methods for a sample covariance matrix ( ) is sometimes further complicated if we do not have direct access to the multivariate data matrix Zc. Cai and Liu (2011), for example, describe a state-of-the-art adaptive thresholding method for heteroscedastic problems that requires an estimate of the variability of the entries of a sample covariance matrix. To our knowledge, TCS is the only principled approach to regularization of general similarity matrices with block structure on multiple scales. In addition, the computed basis vectors themselves contain information of the internal structure of the data—a topic that we will explore in a separate paper with applications to complex extended pedigrees. One can also easily modify the TCS algorithm so that positive semi-definiteness is always guaranteed.
Our results are relevant to a recent area of burgeoning interest in genetics, namely, the estimation of heritability from population samples [Yang et al. (2010a)]. However, our purpose is to estimate heritability, as traditionally defined, rather than to determine the fraction of variation explained by measured SNPs. We expect that the TCS-refined genetic relationships will find wide application to other problems in genetics, such as population-based linkage analysis [Day-Williams et al. (2011)], along with linear mixed models for testing association [Kang et al. (2010)].
Furthermore, TCS can be applied to a whole family of mixed effects “error-in-variables” models of the form
| (15) |
where y ∈ ℝn is a vector of response variables; β ∈ ℝp is a vector of fixed effects; u ∈ ℝq represents random effects; and e ∈ ℝn is a vector of residual errors. In the general case, we assume that there are c random effects, where each random effect originates from a specific distribution with zero mean and unknown variance. In vector-matrix notation,
where ui is a qi × 1 vector whose elements are the levels of the ith random factor, q = q1 + ··· + qc, and Zi is an n × qi matrix of regressors for the ith random factor. Assuming
 (u) =
(u) =
 (e) = 0 and
(e) = 0 and
where
, yields
 [y] = Wβ and
[y] = Wβ and
where the variance components and E are unknown and to be estimated. Now consider an error-in-variables scenario in which the matrix W of regressors of fixed effects is known, but we only have noisy estimates of some or all of the positive semi-definite (p.s.d.) matrices associated with the random effects. If these matrices have block structure and the noise is unstructured, then one could potentially improve estimates of variance components by first applying TCS. In our application, for example, we looked at a special case where we first estimate the p.s.d. matrix in an additive polygenic model using marker-based data, and then use a denoised estimate of to estimate the variance components, and in a random effects model where and .
In summary, we have introduced a new method, called Treelet Covariance Smoothing (TCS), that regularizes a relationship matrix estimated from a large panel of genetic markers. In the context of a GWAS study a huge number of SNPs are measured, each of which provides information about the relationship between individuals in the sample. We proposed a SNP subsampling procedure that exploits this rich source of information to choose a tuning parameter for the algorithm. We illustrated one instance of the utility of such estimates by substituting the resulting smoothed relationship matrix into a random effects model to estimate the heritability of body mass index. While others have used genetically inferred estimates of relatedness from samples of close relatives to estimate heritability, we believe this is the first time such estimates have been applied to population-based samples when the goal is to estimate heritability in the traditional sense.
Acknowledgments
We would like to thank Daniel Weeks, Nadine Melhem and Cosma Shalizi for comments on the manuscript, Elizabeth Thompson for guidance in designing the simulations, and Evan Klei for assistance with the simulations.
Footnotes
Supported by National Institute of Mental Health Grants MH057881 and MH097849, ONR Grant N0014-08-1-0673 and NSF Grant DMS0943577. Funding support for the CIDR Visceral Adiposity Study (Study accession number: phs000169.v1.p1) was provided through the Division of Aging Biology and the Division of Geriatrics and Clinical Gerontology, NIA. The CIDR Visceral Adiposity Study includes a genome-wide association study funded as part of the Division of Aging Biology and the Division of Geriatrics and Clinical Gerontology, NIA. Assistance with phenotype harmonization and genotype cleaning, as well as with general study coordination, was provided by Health ABC Study Investigators.
The special case ci ≡ 〈z, δi〉 and cj ≡ 〈z, δj〉, where δi denotes the Kronecker delta function, corresponds to simple thresholding of the original covariance estimate. Here we consider more general groupings of correlated variables on different scales.
References
- Albers CA, Stankovich J, Thomson R, Bahlo M, Kappen HJ. Multipoint approximations of identity-by-descent probabilities for accurate linkage analysis of distantly related individuals. Am J Hum Genet. 2008;82:607–622. doi: 10.1016/j.ajhg.2007.12.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allison D, Kaprio J, Korkeila M, Koskenvuo M, Neale M, Hayakawa K, et al. The heritability of body mass index among an international sample of monozygotic twins reared apart. International Journal of Obesity. 1996;20:501–506. [PubMed] [Google Scholar]
- Almasy L, Blangero J. Multipoint quantitative-trait linkage analysis in general pedigrees. Am J Hum Genet. 1998;62:1198–1211. doi: 10.1086/301844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson AD, Weir BS. A maximum likelihood method for estimation of pairwise relatedness in structured populations. Genetics. 2007;176:421–420. doi: 10.1534/genetics.106.063149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Astle W, Balding DJ. Population structure and cryptic relatedness in genetic association studies. Statist Sci. 2009;24:451–471. [Google Scholar]
- Bickel PJ, Levina E. Regularized estimation of large covariance matrices. Ann Statist. 2008;36:199–227. [Google Scholar]
- Boehnke M, Cox NJ. Accurate inference of relationships in sib-pair linkage studies. Am J Hum Genet. 1997;61:423–429. doi: 10.1086/514862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bravo HC, Lee KE, Klein BEK, Klein R, Iyengar SK, Wahba G. Examining the relative influence of familial, genetic, and environmental covariate information in flexible risk models. Proc Natl Acad Sci USA. 2009;106:8128. doi: 10.1073/pnas.0902906106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Browning SR. Estimation of pairwise identity by descent from dense genetic marker data in a population sample of haplotypes. Genetics. 2008;178:2123. doi: 10.1534/genetics.107.084624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Browning SR, Browning BL. High-resolution detection of identity by descent in unrelated individuals. Am J Hum Genet. 2010;86:526–539. doi: 10.1016/j.ajhg.2010.02.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai T, Liu W. Adaptive thresholding for sparse covariance matrix estimation. J Amer Statist Assoc. 2011;106:672–684. [Google Scholar]
- Choi Y, Wijsman EM, Weir BS. Case-control association testing in the presence of unknown relationships. Genet Epidemiol. 2009;33:668–678. doi: 10.1002/gepi.20418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Day-Williams AG, Blangero J, Dyer TD, Lange K, Sobel EM. Linkage analysis without defined pedigrees. Genet Epidemiol. 2011;35:360–370. doi: 10.1002/gepi.20584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deary IJ, Yang J, Davies G, Harris SE, Tenesa A, Liewald D, Luciano M, Lopez LM, Gow AJ, Corley J, et al. Genetic contributions to stability and change in intelligence from childhood to old age. Nature. 2012;482:212–215. doi: 10.1038/nature10781. [DOI] [PubMed] [Google Scholar]
- Devlin B, Daniels M, Roeder K. The heritability of IQ. Nature. 1997;388:468–471. doi: 10.1038/41319. [DOI] [PubMed] [Google Scholar]
- Eding H, et al. Marker-based estimates of between and within population kinships for the conservation of genetic diversity. Journal of Animal Breeding and Genetics. 2001;118:141–159. [Google Scholar]
- Epstein MP, Duren WL, Boehnke M. Improved inference of relationship for pairs of individuals. Am J Hum Genet. 2000;67:1219–1231. doi: 10.1016/s0002-9297(07)62952-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher RA. The correlation between relatives on the supposition of Mendelian inheritance. Transactions of the Royal Society of Edinburgh. 1918;52:399–433. [Google Scholar]
- Hallmayer J, Cleveland S, Torres A, Phillips J, Cohen B, Torigoe T, Miller J, Fedele A, Collins J, Smith K, Lotspeich L, Croen LA, Ozonoff S, Lajonchere C, Grether JK, Risch N. Genetic heritability and shared environmental factors among twin pairs with autism. Arch Gen Psychiatry. 2011;68:1095–1102. doi: 10.1001/archgenpsychiatry.2011.76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayes BJ, Goddard ME. Technical note: Prediction of breeding values using marker-derived relationship matrices. J Anim Sci. 2008;86:2089–2092. doi: 10.2527/jas.2007-0733. [DOI] [PubMed] [Google Scholar]
- Henderson CR. Estimation of genetic parameters. Biometrics. 1950;6:186–187. [Google Scholar]
- Hopper JL, Mathews JD. Extensions to multivariate normal models for pedigree analysis. Ann Hum Genet. 1982;46:373–383. doi: 10.1111/j.1469-1809.1982.tb01588.x. [DOI] [PubMed] [Google Scholar]
- Imielinski M, Baldassano RN, Griffiths A, Russell RK, Annese V, Dubinsky M, Kugathasan S, Bradfield JP, Walters TD, Sleiman P, et al. Common variants at five new loci associated with early-onset inflammatory bowel disease. Nature Genetics. 2009;41:1335–1340. doi: 10.1038/ng.489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang HM, Sul JH, Zaitlen NA, Kong S, Freimer NB, Sabatti C, Eskin E, et al. Variance component model to account for sample structure in genome-wide association studies. Nature Genetics. 2010;42:348–354. doi: 10.1038/ng.548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kangas-Kontio T, Huotari A, Ruotsalainen H, Herzig K-H, Tamminen M, Ala-Korpela M, Savolainen MJ, Kakko S. Genetic and environmental determinants of total and high-molecular weight adiponectin in families with low HDL-cholesterol and early onset coronary heart disease. Atherosclerosis. 2010;210:479–485. doi: 10.1016/j.atherosclerosis.2009.12.022. [DOI] [PubMed] [Google Scholar]
- Katzmarzyk P, Perusse L, Bouchard C. Genetics of abdominal vesceral fat levels. American Journal of Human Biology. 1999;11:225–235. doi: 10.1002/(SICI)1520-6300(1999)11:2<225::AID-AJHB10>3.0.CO;2-J. [DOI] [PubMed] [Google Scholar]
- Lander ES, Schork NJ. Genetic dissection of complex traits. Science. 1994;265:2037–2048. doi: 10.1126/science.8091226. [DOI] [PubMed] [Google Scholar]
- Lee AB, Nadler B. Treelets—a tool for dimensionality reduction and multi-scale analysis of unstructured data. In. In: Meila M, Shen X, editors. JMLR WCP; Proceedings of the Eleventh International Conference on Artificial Intelligence and Statistics; 2007. pp. 259–266. [Google Scholar]
- Lee AB, Nadler B, Wasserman L. Treelets—an adaptive multi-scale basis for sparse unordered data. Ann Appl Stat. 2008;2:435–471. doi: 10.1214/07-AOAS137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M, Ritland K. Estimation of pairwise relatedness with molecular markers. Genetics. 1999;152:1753–1766. doi: 10.1093/genetics/152.4.1753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGovern DPB, Gardet A, Törkvist L, Goyette P, Essers J, Taylor KD, Neale BM, Ong RTH, Lagacé C, Li C, et al. Genome-wide association identifies multiple ulcerative colitis susceptibility loci. Nature Genetics. 2010;42:332–337. doi: 10.1038/ng.549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McPeek MS, Sun L. Statistical tests for detection of misspecified relationships by use of genome-screen data. The American Journal of Human Genetics. 2000;66:1076–1094. doi: 10.1086/302800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milligan BG. Maximum-likelihood estimation of relatedness. Genetics. 2003;163:1153–1167. doi: 10.1093/genetics/163.3.1153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MAR, Bender D, Maller J, Sklar P, De Bakker PIW, Daly MJ, et al. PLINK: A tool set for whole-genome association and population-based linkage analyses. The American Journal of Human Genetics. 2007;81:559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Searle SR, Casella G, McCulloch CE. Variance Components. Wiley; New York: 1992. [Google Scholar]
- Thompson EA. Gene identities and multiple relationships. Biometrics. 1974;30:667–680. [PubMed] [Google Scholar]
- Thompson EA. The estimation of pairwise relationships. Ann Human Genetics. 1975;39:173–188. doi: 10.1111/j.1469-1809.1975.tb00120.x. [DOI] [PubMed] [Google Scholar]
- Thompson EA. Pedigree Analysis in Human Genetics. Johns Hopkins Univ. Press; Baltimore, MD: 1986. [Google Scholar]
- Thornton T, McPeek MS. ROADTRIPS: Case-control association testing with partially or completely unknown population and pedigree structure. Am J Hum Genet. 2010;86:172–184. doi: 10.1016/j.ajhg.2010.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visscher PM, Medland SE, Ferreira MAR, Morley KI, Zhu G, Cornes BK, Montgomery GW, Martin NG. Assumption-free estimation of heritability from genome-wide identity-by-descent sharing between full siblings. PLoS Genet. 2006;2:e41. doi: 10.1371/journal.pgen.0020041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visscher PM, Brown MA, McCarthy MI, Yang J. Five years of GWAS discovery. Am J Hum Genet. 2012;90:7–24. doi: 10.1016/j.ajhg.2011.11.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weir BS, Anderson AD, Hepler AB. Genetic relatedness analysis: Modern data and new challenges. Nat Rev Genet. 2006;7:771–780. doi: 10.1038/nrg1960. [DOI] [PubMed] [Google Scholar]
- Yang J, Benyamin B, McEvoy BP, Gordon S, Henders AK, Nyholt DR, Madden PA, Heath AC, Martin NG, Montgomery GW, et al. Common SNPs explain a large proportion of the heritability for human height. Nature Genetics. 2010a;42:565–569. doi: 10.1038/ng.608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J, Lee SH, Goddard ME, Visscher PM. GCTA: A tool for genome-wide complex trait analysis. The American Journal of Human Genetics. 2010b;88:76–82. doi: 10.1016/j.ajhg.2010.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J, Manolio TA, Pasquale LR, Boerwinkle E, Caporaso N, Cunningham JM, De Andrade M, Feenstra B, Feingold E, Hayes MG, et al. Genome partitioning of genetic variation for complex traits using common SNPs. Nature Genetics. 2011;43:519–525. doi: 10.1038/ng.823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zabaneh D, Chambers JC, Elliott P, Scott J, Balding DJ, Kooner JS. Heritability and genetic correlations of insulin resistance and component phenotypes in Asian Indian families using a multivariate analysis. Diabetologia. 2009;52:2585–2589. doi: 10.1007/s00125-009-1504-7. [DOI] [PubMed] [Google Scholar]