Kinetic isotope effects significantly influence intracellular metabolite 13C labeling patterns and flux determination

Thomas M Wasylenko; Gregory Stephanopoulos

doi:10.1002/biot.201200276

. Author manuscript; available in PMC: 2014 Jun 4.

Published in final edited form as: Biotechnol J. 2013 Aug 5;8(9):1080–1089. doi: 10.1002/biot.201200276

Kinetic isotope effects significantly influence intracellular metabolite ¹³C labeling patterns and flux determination

Thomas M Wasylenko ¹, Gregory Stephanopoulos ¹

PMCID: PMC4045492 NIHMSID: NIHMS582384 PMID: 23828762

Abstract

Rigorous mathematical modeling of carbon-labeling experiments allows estimation of fluxes through the pathways of central carbon metabolism, yielding powerful information for basic scientific studies as well as for a wide range of applications. However, the mathematical models that have been developed for flux determination from ¹³C labeling data have commonly neglected the influence of kinetic isotope effects on the distribution of ¹³C label in intracellular metabolites, as these effects have often been assumed to be inconsequential. We have used measurements of the ¹³C isotope effects on the pyruvate dehydrogenase enzyme from the literature to model isotopic fractionation at the pyruvate node and quantify the modeling errors expected to result from the assumption that isotope effects are negligible. We show that under some conditions kinetic isotope effects have a significant impact on the ¹³C labeling patterns of intracellular metabolites, and the errors associated with neglecting isotope effects in ¹³C-metabolic flux analysis models can be comparable in size to measurement errors associated with GC–MS. Thus, kinetic isotope effects must be considered in any rigorous assessment of errors in ¹³C labeling data, goodness-of-fit between model and data, confidence intervals of estimated metabolic fluxes, and statistical significance of differences between estimated metabolic flux distributions.

Keywords: Isotope Effects, Isotopomer Modeling, Metabolic Engineering, Metabolic Flux Analysis, Modeling errors

1 Introduction

Cells assimilate carbon, energy, and reducing power for growth and other essential processes through the reactions of central carbon metabolism. The magnitudes of the fluxes through these central metabolic reactions are tightly controlled, and represent the functional output of transcriptional, translational, and post-translational regulatory processes [1, 2]. Consequently, in microbial systems knowledge of the distribution of metabolic fluxes in different strains or under different conditions has proven to be extremely powerful in basic physiological studies [3, 4].

Moreover, experimentally determined metabolic flux distributions can be informative in biotechnological applications, for instance in understanding the genetic manipulations and metabolic rearrangements that might lead to increased production of a desired compound [5] or how metabolism changes over the course of a fermentation [6]. In recent years, methods for metabolic flux estimation have begun to be applied in more complex plant systems [7, 8], and in mammalian systems elucidation of metabolic fluxes has provided insight into the proliferating phenotype of cancer cells [9] and identified a novel target for antiviral therapies [10].

Determination of intracellular metabolic fluxes is experimentally challenging. Direct measurement of these metabolic fluxes is impossible so that mathematical models are required to estimate the intracellular flux distribution from other directly measurable quantities [11]. In the metabolite balancing approach, measured rates of consumption and production of extracellular metabolites (referred to as “extracellular flux measurements”), known stoichiometry of intracellular reactions, and a pseudo- steady state assumption on intracellular metabolite concentrations are used to construct a mass balance constraint for each metabolite in the metabolic network [12]. However, in most systems of interest the number of unknown fluxes to be estimated exceeds the number of metabolites for which a mass balance equation can be written so that the resulting system of linear equations is underdetermined and an infinite number of solutions for the metabolic flux distribution exist. Additional constraints can be obtained through the application of isotopic tracers, substrates which are selectively “labeled” with rare, stable isotopes. The most commonly used stable isotope label is ¹³C, and so we will focus on ¹³C-labeling experiments in this contribution.

The ¹³C atoms from the tracer may be incorporated into any of the carbon atom positions of an intracellular metabolite. For a metabolite with n carbons in its backbone, there are 2ⁿ possible carbon labeling patterns, each of which corresponds to a different combination of ¹²C and ¹³C atoms at the various carbon atom positions. These 2ⁿ species are referred to as the “isotopic isomers,” or “isotopomers,” of the metabolite. For each metabolite, the set of 2ⁿ mole fractions describing the fraction of the total metabolite pool with each possible ¹³C labeling pattern is referred to as the “isotopomer distribution” of that metabolite. If an appropriate choice is made for the tracer, these isotopomer distributions will be functions of the intracellular metabolic fluxes, so that information about metabolite labeling patterns can be used to add constraints to the stoichiometric models described above. Such information can in principle be obtained using ¹H nuclear magnetic resonance (NMR) [13], ¹³C NMR [11, 14, 15], or mass spectroscopy (MS) [16, 17], although in practice MS has become the technology of choice for determination of ¹³C labeling patterns because its sensitivity and precision greatly exceed those of NMR [18, 19]. The supplementation of a stoichiometric model with additional constraints derived from measured isotopic labeling patterns typically yields a system that is significantly overdetermined, allowing for determination of a unique flux solution.

Over the past 20 years, rigorous quantitative methods have been developed for the estimation of the metabolic fluxes through central carbon metabolism using such stoichiometric models augmented with ¹³C labeling data [11, 13, 20–24]. Flux estimation is achieved through an iterative procedure in which a putative metabolic flux distribution is generated and the ¹³C label distributions in intracellular metabolites that would result from this flux distribution are predicted. The putative metabolic fluxes are refined until the predicted ¹³C metabolite labeling data match as closely as possible the ¹³C labeling data obtained from experiment. The metabolic flux distribution that minimizes the lack-of-fit between simulated and measured ¹³C metabolite labeling data is considered to be the best estimate for the true intracellular metabolic fluxes.

The key step in these flux estimation algorithms is the prediction of the ¹³C labeling state that will result from a putative flux distribution. This typically involves the solution of a large set of isotopomer balance equations, or a similar set of equations with equivalent information content [22, 25]. However, these isotopomer balance equations implicitly assume the absence of isotope effects on the rates of the enzyme-catalyzed reactions of central carbon metabolism. That is, these equations inherently assume that the enzymes involved in central carbon metabolism will turn over all isotopomers of their substrate metabolites at the same rate. There is in fact a large body of literature showing that isotope effects do occur in central carbon metabolism. For instance it is well-known that plants assimilating inorganic carbon preferentially assimilate ¹²C over ¹³C, and that the extent of the discrimination against ¹³C depends on whether carbon is assimilated through Rubisco or PEP carboxylase [26, 27]. More generally, ¹³C atoms form stronger bonds than ¹²C atoms so that the presence of ¹³C atoms in a metabolite is expected to slow the rate of its enzymatic conversion [16, 28]. Nonetheless in ¹³C-metabolic flux analysis (MFA) it has commonly been assumed, either explicitly [16, 20, 29] or implicitly, that such carbon isotope effects are negligible in the prediction of the ¹³C labeling states of intracellular metabolites. To our knowledge, the validity of this assumption has never been investigated quantitatively. Although Christensen and Nielsen [16] concluded that isotope effects were unlikely to significantly affect ¹³C labeling patterns of intracellular metabolites, using gas chromatography–combustion-isotope ratio mass spec-trometry (GC–C-IRMS) Heinzle et al. have shown that isotope effects do significantly influence ¹³C labeling data in specialized ¹³C-MFA experiments at low ¹³C enrichments, and that correction for these isotope effects is necessary for flux estimation in these systems [28, 30]. In this contribution, we sought to quantify the error that could result from neglecting carbon isotope effects in traditional ¹³CMFA experiments, with standard levels of ¹³C enrichment and conventional MS measurements used to obtain ¹³C labeling data for flux estimation. As a case study, we investigated the potential for kinetic isotope effects to cause isotopic fractionation at the pyruvate node.

2 Modeling isotopic fractionation at the pyruvate node

It has been known for more than 50 years that lipids and the carboxyl group of leucine, both of which are derived from acetyl-CoA, are generally depleted in the ¹³C isotope relative to other biomass constituents [31, 32]. Monson and Hayes [33] used indirect evidence from measurement of positional ¹³C enrichment in lipids to conclude that this depletion of ¹³C was a result of an isotope effect on the reaction catalyzed by pyruvate dehydrogenase (PDH), and the isotope effects associated with PDH enzymes from Escherichia coli and Saccharomyces cerevisiae have been characterized by Melzer and Schmidt [34]. How ever, the influence that these isotope effects will have on metabolite isotopomer distributions is difficult to predict, as isotopic fractionation due to isotope effects will depend on the metabolic flux distribution and the kinetic state of the system [35, 36]. We performed simulations to investigate the potential consequences of isotope effects at the pyruvate node in ¹³C-MFA labeling experiments.

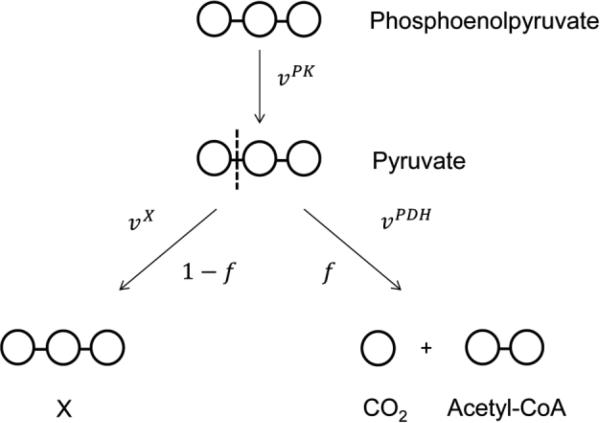
To model the influence of isotope effects at the pyruvate branch point on intracellular metabolite isotopomer distributions, we constructed a simplified model of the pyruvate node (Fig. 1). Pyruvate is produced from phosphoenolpyruvate in the reaction catalyzed by pyruvate kinase (PK). We assume that this reaction is effectively irreversible, and the flux through PK is denoted v^PK. We further assume that all reactions other than the PDH reaction that consume pyruvate can be lumped into a single reaction forming a metabolite X, as in [33]. These reactions that form metabolite X could include anaplerotic reactions, amino acid biosynthesis (e.g. synthesis of ala-nine), or production of byproducts such as lactate. We further assumed that the reaction converting pyruvate to X is irreversible and has no significant isotope effects. The latter assumption is justified by the fact that reactions in which carbon–carbon bonds are broken (such as the PDH reaction) are generally expected to have much larger ¹³C isotope effects than reactions in which all carbon–carbon bonds are left intact (such as production of lactate or ala-nine from pyruvate). The flux through the reaction converting pyruvate to metabolite X is denoted v^X. Finally, for simplicity we assumed that acetyl-CoA is synthesized exclusively from pyruvate through PDH. This reaction is assumed to be irreversible, and the flux from pyruvate to acetyl-CoA is denoted v^PDH.

The pyruvate node model system. We assume that pyruvate is produced through pyruvate kinase (PK) and consumed through one of two reactions. In the pyruvate dehydrogenase (PDH) reaction, the bond between C₁ and C₂ of pyruvate is broken (represented by the dashed line), yielding one molecule of CO₂ and one acetyl-CoA two-carbon unit. This reaction is subject to isotope effects, as measured by Melzer and Schmidt (see text). In the other reaction, pyruvate is converted to a metabolite X. In this reaction all carbon–carbon bonds in pyruvate remain intact, so we assume the isotope effects on this reaction are small relative to those on the PDH reaction. The ratio of the flux through PDH to the flux through PK is equal to f, while the ratio of the flux to metabolite X to the flux through PK is equal to 1 – f. Circles represent the carbon atoms of each metabolite.

Here we define some nomenclature that will be used in the following discussion. The positional isotopomers of pyruvate will be denoted ijk, where the binary variables i, j, and k represent the labeling states at C₁, C₂, and C₃ of pyruvate, respectively. These variables take on values i, j, k = 0 if the carbon at the respective position in the pyruvate molecule is ¹²C and i, j, k = 1 if the carbon is ¹³C. So for instance the isotopomer 001 has ¹²C atoms at C₁ and C₂ and a ¹³C atom at C₃. The ¹³C labeling state of pyruvate can be described by a set of eight isotopomer mole fractions $y_{i j k}^{P}$ , where $y_{i j k}^{P}$ is equal to the mole fraction of the total pyruvate pool with the labeling pattern ijk. The labeling state of the two-carbon unit of acetyl-CoA will similarly be represented by four isotopomer mole fractions $y_{i j k}^{A}$ .

At steady state, a mass balance on pyruvate dictates that the rate of pyruvate production must equal the rate of pyruvate consumption:

v^{PK} = v^{X} + v^{PDH}

(1)

Similarly, a mass balance can be written for each of the isotopomers of pyruvate:

v_{i j k}^{PK} = v_{i j k}^{X} + v_{i j k}^{PDH}

(2)

where $v_{i j k}^{PK}$ is the rate at which pyruvate isotopomer ijk is produced through PK and $v_{i j k}^{X}$ and $v_{i j k}^{PDH}$ are the rates at which pyruvate isotopomer ijk is metabolized to metabolite X and acetyl-CoA, respectively. We define f to be the ratio of the flux through PDH to the flux through PK (Fig. 1):

f \equiv \frac{v^{PDH}}{v^{PK}}

(3)

and the variables f_ijk are defined analogously for each of the isotopomers of pyruvate:

f_{i j k} \equiv \frac{v_{i j k}^{PDH}}{v_{i j k}^{PK}}

(4)

The total flux of pyruvate through PDH must equal the sum of the fluxes of each of the pyruvate isotopomers:

v^{PDH} = \sum v_{i j k}^{PDH}

(5)

Using the definition of f_ijk, this can be rewritten as:

v^{PDH} = \sum v_{i j k}^{PK} f_{i j k}

(6)

which is equivalent to:

f = \sum {\tilde{v}}_{i j k}^{PK} f_{i j k}

(7)

where we have introduced the “isotopomer flux fraction” ${\tilde{v}}_{i j k}^{PK}$ :

{\tilde{v}}_{i j k}^{PK} \equiv \frac{v_{i j k}^{PK}}{v^{PK}}

(8)

The isotopomer flux fraction ${\tilde{v}}_{i j k}^{PK}$ is equal to the fraction of the total flux through PK that produces the pyruvate isotopomer ijk. We note that although under the typical assumption that isotope effects are negligible the isotopomer flux fractions are equal to the pyruvate isotopomer mole fractions $y_{i j k}^{P}$ , in the case where isotope effects are present this is not the case; the $y_{i j k}^{P}$ will deviate from the ${\tilde{v}}_{i j k}^{PK}$ and Eq. (7) must be written as a flux fraction-weighted average rather than as a mole fraction-weighted average.

In order to quantify the effects of isotopic fractionation at the pyruvate branch point, we sought to determine the f_ijk. In the idealized case (without isotope effects),

f_{i j k}^{ideal} = f, \forall i, j, k

(9)

i.e. the f_ijk are independent of i, j, and k. However, when isotope effects are present this will not be the case.

The split ratio at any branch point can be viewed as the ratio of two effective rate constants. In the model system described above, there are two competing reactions which consume pyruvate:

\begin{matrix} Pyr & \to AcCoA + {CO}_{2} \\ Pyr & \to X \end{matrix}

We assume the fluxes of these reactions can be approximated by Eqs. (10) and (11), respectively:

v^{PDH} = k^{PDH} [Pyr]

(10)

v^{X} = k^{X} [Pyr]

(11)

where k^PDH is the effective rate constant for the PDH reaction, k^X is the effective rate constant for the reaction forming metabolite X, and [Pyr] is the intracellular concentration of pyruvate. Substituting Eq. (1) into Eq. (3), f can be expressed as:

f = \frac{v^{PDH}}{v^{PDH} + v^{X}}

(12)

Substituting the expressions from Eqs. (10) and (11) into (12), we have:

f = \frac{k^{PDH}}{k^{PDH} + k^{X}}

(13)

so that f is expressed as a ratio of rate constants. The f_ijk can similarly be expressed as ratios of rate constants:

f_{i j k} = \frac{k_{i j k}^{PDH}}{k_{i j k}^{PDH} + k^{X}}

(14)

where $k_{i j k}^{PDH}$ is the rate constant for the PDH reaction with the pyruvate isotopomer ijk as the substrate. k^X is constant for all isotopomers of pyruvate since we have assumed the isotope effects on this reaction are negligible. The $k_{i j k}^{PDH}$ can be expressed relative to $k_{000}^{PDH}$ (which can be fixed to equal one). We define a set of β_ijk, which are equal to the ratios $k_{i j k}^{PDH} ∕ k_{000}^{PDH}$ so that the rate constants can be expressed as:

k_{i j k}^{PDH} = β_{i j k} k_{000}^{PDH}

(15)

The β_ijk for singly labeled isotopomers of pyruvate can be determined directly from the data of Melzer and Schmidt, who have measured the isotope effects on C₁, C₂, and C₃ of pyruvate. These are denoted α₁, α₂, and α₃, respectively:

\begin{matrix} α_{1} = & \frac{k_{000}^{A}}{k_{100}^{A}} \\ α_{2} = & \frac{k_{000}^{A}}{k_{010}^{A}} \\ α_{3} = & \frac{k_{000}^{A}}{k_{001}^{A}} \end{matrix}

(16)

Melzer and Schmidt [34] have determined these parameters to be α₁ = 1.0093 for E. coli and 1.0238 for S. cere -visiae, α₂ = 1.0213 for E. coli and 1.0254 for S. cerevisiae, and α₃ = 1.0031 for the enzymes of both organisms.

The rates of reaction for isotopomers with multiple ¹³C atoms were not measured by Melzer and Schmidt. Thus the rate constants for these isotopomers must be approximated from the rate constants for the singly labeled isotopomers. We investigated two different cases in which the β_ijk are defined by the following two equations:

β_{i j k} = (i \frac{1}{α_{1}} + (1 - i)) (j \frac{1}{α_{2}} + (1 - j)) (k \frac{1}{α_{3}} + (1 - k))

(17)

β_{i j k} = \min [(i \frac{1}{α_{1}} + (1 - i)), (j \frac{1}{α_{2}} + (1 - j)), (k \frac{1}{α_{3}} + (1 - k))]

(18)

Equation (17) assumes that the isotope effects are roughly additive. Each β_ijk is equal to the product of the isotope effect contributions of the three individual carbon atoms of pyruvate, where the isotope effect contribution of each individual carbon atom is equal to one (if the carbon is ¹²C) or the reciprocal (multiplicative inverse) of its respective α-value (if the carbon is ¹³C). The result is that multiply labeled isotopomers will have rate constants that reflect the product of the isotope effects on each of their labeled atoms. Equation (18) assumes that the isotope effects are not additive and that the ¹³C atom with the largest isotope effect will dominate the kinetics. In this case, each β_ijk is equal to the minimum of the individual carbon atom contributions, where the individual carbon atom contributions are the same as above. Thus multiply labeled isotopomers will not have rate constants that are smaller than those of the singly labeled isotopomers. This latter case will represent a lower bound on the error that can be expected to result from neglecting isotope effects in the enzymatic reactions of central carbon metabolism.

Under the assumptions listed above, the fractionation of isotopes at the pyruvate node (and therefore the error associated with neglecting isotope effects) will depend solely on f and the isotopomer flux fractions ${\tilde{v}}_{i j k}^{PK}$ . To determine realistic values for the ${\tilde{v}}_{i j k}^{PK}$ , we performed simulations based on a flux distribution similar to the one estimated in [6] using five commonly used glucose tracer mixtures and glucose labeled to natural abundance as the substrates. For simplicity, we assumed that isotope effects in the metabolism of glucose to pyruvate were negligible. Under this assumption, the ${\tilde{v}}_{i j k}^{PK}$ are equal to the $y_{i j k}^{P}$ obtained from simulation of the normal isotopomer balance equations. The selected tracers were 1-¹³C-glucose (commonly used to estimate flux through the oxidative pentose phosphate pathway [37–39]), 1,2-¹³C₂-glucose (determined to be the optimal tracer for a mammalian cell network in [40]), 3,4-¹³C₂-glucose (determined to be optimal for resolution of pyruvate carboxylase flux in [41]), 20% U-¹³C -glucose [37–39], and 75% 1-¹³C-glucose+25% U-¹³C₆-glucose (the tracer mixture used in the original study [6]). The isotopomer flux fractions resulting from application of these tracers and natural abundance glucose given the flux distribution in [6] and neglecting isotope effects in the metabolism of glucose to pyruvate are summarized in Table1.

Table 1.

Predicted isotopomer flux fractions

Isotopomer flux fractions	Tracers
Isotopomer flux fractions	NA	1	1,2	3,4	20%U	75%1 + 25%U
${\tilde{v}}_{000}^{PK}$	0.968	0.706	0.606	0.132	0.754	0.518
${\tilde{v}}_{001}^{PK}$	0.011	0.243	0.069	0.005	0.019	0.187
${\tilde{v}}_{010}^{PK}$	0.011	0.021	0.015	0.043	0.013	0.016
${\tilde{v}}_{011}^{PK}$	1.2E–04	0.006	0.228	0.001	0.018	0.027
${\tilde{v}}_{100}^{PK}$	0.011	0.017	0.017	0.755	0.029	0.031
${\tilde{v}}_{101}^{PK}$	1.2E–04	0.005	0.039	0.009	0.002	0.008
${\tilde{v}}_{110}^{PK}$	1.2E–04	0.002	0.012	0.052	0.008	0.011
${\tilde{v}}_{111}^{PK}$	1.3E–06	5.0E–04	0.013	0.002	0.157	0.202

Open in a new tab

The isotopomer flux fractions ${\tilde{v}}_{i j k}^{PK}$ are predicted for each of the five glucose tracer mixtures listed in the text and for glucose labeled to natural abundance. NA, natural abundance glucose; 1 = 1-¹³C-glucose; 1,2 = 1,2-¹³C₂-glucose; 3,4 = 3,4-¹³C₂-glucose; 20%U = 20% U-¹³C₆-glucose; 75%1 + 25%U = 75% 1-¹³C-glucose + 25% U-¹³C₆-glucose.

For a given value of f, the isotopomer distribution of the two-carbon unit in acetyl-CoA, $y_{i j}^{A}$ , can be predicted for a specified tracer and the associated isotopomer flux fractions ${\tilde{v}}_{i j k}^{PK}$ in the following way: the choice of the organism determines the values of α₁, α₂, and α₃. The β_ijk are then computed using either Eq. (17) or (18), depending on whether isotope effects are assumed to be additive or not. The rate constants $k_{i j k}^{PDH}$ are computed using Eq. (15) (with $k_{000}^{PDH}$ fixed equal to one – the results are independent of the value of $k_{000}^{PDH}$ ) and substituted into Eq. (14). Equations (14) and (7) then yield nine equations with nine unknowns (k^X and f_ijk), which can be solved using a nonlinear equation solver (we used the Matlab function fsolve.m). Assuming there are no isotope effects on the reactions downstream of acetyl-CoA that significantly affect its labeling pattern, the isotopomer distribution of acetyl-CoA will then be given by:

\begin{matrix} y_{00}^{A^{isotope}} = & \frac{f_{000} {\tilde{v}}_{000}^{PK} + f_{100} {\tilde{v}}_{100}^{PK}}{f} \\ y_{01}^{A^{isotope}} = & \frac{f_{001} {\tilde{v}}_{001}^{PK} + f_{101} {\tilde{v}}_{101}^{PK}}{f} \\ y_{10}^{A^{isotope}} = & \frac{f_{010} {\tilde{v}}_{010}^{PK} + f_{110} {\tilde{v}}_{110}^{PK}}{f} \\ y_{11}^{A^{isotope}} = & \frac{f_{011} {\tilde{v}}_{011}^{PK} + f_{111} {\tilde{v}}_{111}^{PK}}{f} \end{matrix}

(19)

In the idealized case (neglecting isotope effects), using Eq. (9) this can be simplified to:

\begin{matrix} y_{00}^{A^{ideal}} = & {\tilde{v}}_{000}^{PK} + {\tilde{v}}_{100}^{PK} \\ y_{01}^{A^{ideal}} = & {\tilde{v}}_{001}^{PK} + {\tilde{v}}_{101}^{PK} \\ y_{10}^{A^{ideal}} = & {\tilde{v}}_{010}^{PK} + {\tilde{v}}_{110}^{PK} \\ y_{11}^{A^{ideal}} = & {\tilde{v}}_{011}^{PK} + {\tilde{v}}_{111}^{PK} \end{matrix}

(20)

Predicted isotopomer flux fractions As mentioned above, ¹³C labeling data are often obtained from MS, which resolves isotopomers by molecular mass. Consequently, isotopomers with the same number of ¹³C atoms cannot be differentiated and are lumped into a single “mass isotopomer,” which is simply a set of all the isotopomers of a metabolite with a particular mass (or equivalently, a particular number of ¹³C atoms). For a metabolite with n carbons and a mass M when all of the carbon atoms are ¹²C, MS will yield a set of n + 1 mass isotopomer mole fractions, where the ith mole fraction is equal to the mole fraction of the total metabolite pool with mass M + i (i = 0, 1, 2, n). This set of mole fractions is referred to as the “mass isotopomer distribution” (MID) of the metabolite. The mole fraction of each mass isotopomer is equal to sum of the mole fractions of its constituent isotopomers; for instance the M + 2 mole fraction of the pyruvate MID will be equal to the sum $y_{011}^{P} + y_{101}^{P} + y_{110}^{P}$ . The set of MIDs obtained from MS (for as many metabolites as can be detected and accurately quantitated) makes up the ¹³C labeling dataset used in the flux estimation algorithms described above. In order to estimate the error in MS ¹³C labeling data that could result from neglecting isotope effects, we converted both the $y_{i j}^{A^{ideal}}$ and $y_{i j}^{A^{isotope}}$ isotopomer distributions into MIDs:

\begin{matrix} y_{0}^{A} = & y_{00}^{A} \\ y_{1}^{A} = & y_{01}^{A} + y_{10}^{A} \\ y_{2}^{A} = & y_{11}^{A} \end{matrix}

(21)

where y^A_i is equal to the mole fraction of the M + i mass isotopomer in the MID of the acetyl-CoA two-carbon unit. These equations hold for both the idealized case and the case with isotope effects included. The errors associated with the assumption that isotope effects are negligible can be estimated to be the difference between $y_{i j}^{A^{ideal}}$ (the MID mole fractions expected to be obtained from a simulation which neglects isotope effects) and $y_{i j}^{A^{isotope}}$ (the MID mole fractions expected to be obtained from a ¹³C labeling experiment):

\begin{matrix} y_{0}^{A^{error}} = y_{0}^{A^{ideal}} - y_{0}^{A^{isotope}} \\ y_{1}^{A^{error}} = y_{1}^{A^{ideal}} - y_{1}^{A^{isotope}} \\ y_{2}^{A^{error}} = y_{2}^{A^{ideal}} - y_{2}^{A^{isotope}} \end{matrix}

(22)

3 Results

We computed the $y_{i}^{A^{error}}$ as functions of f for each of the five glucose tracers listed above and for glucose labeled to natural abundance using the α_i values measured by Melzer and Schmidt [34] for both the E. coli and S. cerevisiae PDH enzymes. Two typical results for the E. coli PDH enzyme assuming additivity of isotopes effects are shown in Fig.2.

Typical results for errors associated with neglecting isotope effects as a function of f. The predicted modeling errors associated with neglecting isotope effects on the *E. coli* PDH enzyme (assuming additivity of isotope effects for multiply labeled isotopomers of pyruvate) with (A) natural abundance glucose and (B) 20% U-¹³C₆-glucose substrates are plotted as a function of the ratio of flux through PDH to flux through PK, f. The errors for each of the three mass isotopomer mole fractions of the acetyl-CoA two-carbon unit MID are shown.

It can be seen that the magnitude of the error is maximum when f is small and decreases linearly as f increases, approaching zero as f approaches unity. This is a well-known result [33, 36]. There is zero error associated with isotope effects when f = 1 because isotopic fractionation can only occur at a branch point in the metabolic network [35]. When metabolism is at steady state, if one enzyme discriminates against an isotopomer of its substrate metabolite then there must be another enzyme in the cell that turns over a disproportionately high fraction of that isotopomer due to conservation of mass. For instance, in the model system investigated above PDH discriminates against the heavy isotopomers of pyruvate and consequently the enzyme forming metabolite X will metabolize a disproportionately high fraction of these heavy isotopomers. If the conversion of the PDH reaction is 100%, the PDH enzyme must turn over all isotopomers of pyruvate completely and so there can be no discrimination against any of the pyruvate isotopomers at steady state.

Under the assumption of additive isotope effects, the error associated with the E. coli PDH enzyme with glucose labeled to natural abundance as the substrate approach- es 0.025 mol% as f approaches zero (Fig.2). An identical result (to the nearest thousandth of a mole percent) is obtained if isotope effects are assumed to be non-additive (data not shown); because metabolism of glucose labeled to natural abundance produces very few multiply labeled isotopomers, the predicted errors with this substrate are relatively insensitive to the assumption on additivity of isotope effects. The predicted maximum error of 0.025 mol% is in good agreement with the results of Monson and Hayes, who predicted acetyl-CoA would be depleted in ¹³C relative to pyruvate by approximately 23 per mille for small f (see Fig. 4 of [33]). When the ¹³C enrichment in glucose is increased by introduction of ¹³C-labeled tracers, the errors in MID measurements associated with neglecting isotope effects increase. The results with 20% U-¹³C₆-glucose as the tracer indicate that these errors can approach 0.5 mol% for the E. coli PDH enzyme for small f.

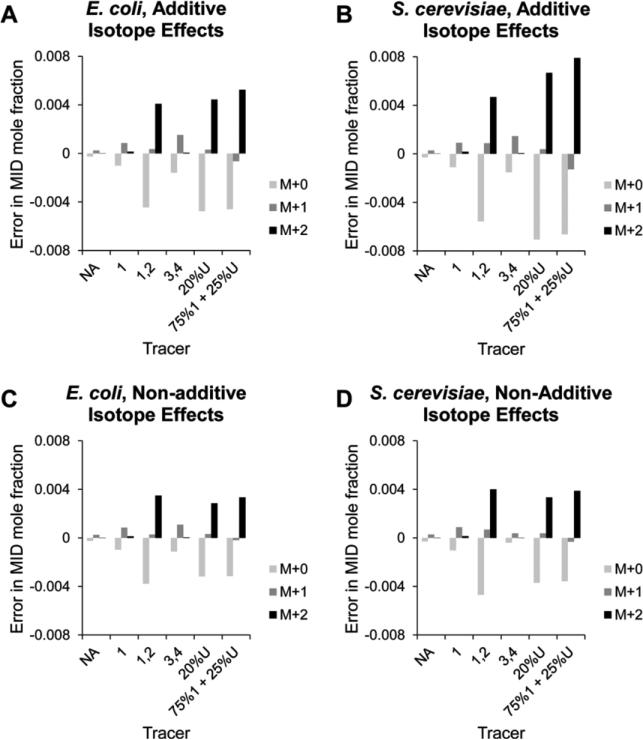
In order to investigate the effect of the organism (E. coli vs. S. cerevisiae), the glucose tracer, and the assumption on the additivity of isotope effects for multiply labeled isotopomers of pyruvate (Eqs. 17 and 18), we visualized the error in each case with f fixed to a value of 1% (Fig.3). This represents something of a “worst case scenario” since the errors are maximum for small values of f. The errors associated with isotope effects are predicted to be larger in S. cerevisiae than in E.coli, which is expected since the α₁ and α₂ values measured by Melzer and Schmidt were greater for the S. cerevisiae PDH. The expected errors with a 1-¹³C-glucose tracer are relatively small because metabolism of this tracer yields pyruvate primarily labeled at C₃, which does not participate in the bond that is broken in the PDH reaction and consequently has a relatively small isotope effect. The expected errors with a 3,4-¹³C₂-glucose tracer are also relatively minor. At first this may seem surprising since metabolism of this tracer yields pyruvate primarily labeled at C₁, and there is a significant isotope effect on this carbon. However, the set of isotopomer flux fractions that result from application of this tracer is dominated by a single isotopomer (the isotopomer with labeling pattern 100). In fact, in this case 85% of the flux to pyruvate produces the isotopomers with the labeling patterns 100, 010, or 110, and the unlabeled isotopomer 000 accounts for only approximately 13% of the total flux to pyruvate. The small flux producing the unlabeled isotopomer, which is the isotopomer turned over at the highest rate by PDH, mitigates the effects of isotopic discrimination so that the errors associated with neglecting isotope effects are smaller than might be expected. The applications of the tracers 1,2-¹³C₂-glucose, 20% U-¹³C₆-glucose, and 75% 1-¹³C-glucose + 25% U-¹³C₆-glucose result in the highest expected errors. Metabolism of each of these tracers results in an unlabeled (000) isotopomer flux fraction >50% and significant flux fractions for isotopomers labeled at one or both of the carbons with large isotope effects. Consequently, with these tracers neglecting isotope effects is expected to result in relatively large errors.

Expected errors associated with isotope effects at low values of f. The predicted modeling errors associated with neglecting isotope effects at a fixed value of f = 0.01 for different combinations of organism, tracer, and assumption on the additivity of isotope effects for multiply labeled isotopomers of pyruvate. (A) Predicted errors for each glucose substrate are plotted for the cases of *E. coli* assuming additive isotope effects, (B) *S. cerevisiae* assuming additive isotope effects, (C) *E. coli* assuming non-additive isotope effects, and (D) *S. cerevisiae* assuming non-additive isotope effects. NA, natural abundance glucose; 1 = 1-¹³C-glucose; 1,2 = 1,2-¹³C -glucose; 3,4 = 3,4-¹³C₂-glucose; 20%U = 20% U-¹³C₆-glucose; 75%1 + 25%U = 75% 1-¹³C-glucose + 25% U-¹³C₆-glucose.

It can be seen from Fig.3 that, under the assumption that isotope effects are additive, the errors associated with isotope effects can exceed 0.5 mol% and can even approach 0.8 mol%. Antoniewicz et al. have shown that MIDs of amino acids labeled to natural abundance can be measured to an accuracy of 0.4 mol% and with a precision of 0.2 mol% using gas chromatography (GC) coupled to MS [42]. Thus, in some cases the errors associated with isotope effects may exceed the measurement errors associated with the GC/MS instrument and could in fact be the dominant source of error in the modeling of GC/MS MID data for flux estimation. Even in the case where isotope effects are assumed to be completely non-additive, the errors associated with isotopic discrimination can approach the 0.4 mol% upper bound for error in GC/MS data which was given in [42].

4 Discussion

It was noted above that the errors in Fig. 3 represent something of a “worst-case scenario.” Because the magnitudes of the errors associated with neglecting isotope effects decrease as f increases, in systems in which the majority of pyruvate is metabolized through PDH the actual errors will be significantly smaller. For these systems, the ratio of the actual error to the error shown in Fig 3 will be approximately equal to 1–f, since the magnitude of the error decreases linearly as f increases and is equal to zero when f equals unity. However in many cases the errors associated with isotope effects will be significant. For instance, a recent ¹³C-MFA study in the A549 cancer cell line revealed that in these cells the majority of pyruvate was metabolized to lactate so that in this system f was only approximately 10% [40]. Thus the errors associated with the acetyl-CoA two-carbon unit MID in ¹³C-MFA studies in cancer cells may approach the errors shown in Fig. 3.

Moreover, the dependence of reaction kinetics on ¹³C-labeling is not unique to the PDH enzyme. In fact, for enzymes catalyzing carbon–carbon bond-breaking reactions, significant isotope effects appear to be the norm rather than the exception. Gleixner and Schmidt [43] observed an isotope effect of 1.6% on C₃ of fructose-1,6-bisphosphate (FBP) for FBP aldolase from rabbit muscle (although the isotope effect on C₄ was negligible), and Hermes et al. [44] determined the isotope effect on C₄ of malate to be approximately 3% for malic enzyme from chicken liver. Significant isotope effects have also been observed for the enzymes of the oxidative pentose phosphate pathway. Hermes et al. [44] determined the isotope effect on C₁ of glucose-6-phosphate (G6P) to be 1.65% for the G6P dehydrogenase from Leuconostoc mesenteroides, while the isotope effect on C₁ of 6-phosphogluconate (6PG) has been estimated to be anywhere from 0.59 to 2.25% for 6PG dehydrogenases from various sources [45–47]. The results for 6PG dehydrogenase (and the results for the PDH enzymes of E. coli and S. cerevisiae discussed above) reveal that the isotope effect on a single chemical reaction can vary significantly across different enzymes and different organisms. In fact, the isotope effect associated with a single enzyme can in some cases be highly condition-dependent – Grissom and Cleland measured the isotope effect on C₆ of isocitrate for NADP-dependent isocitrate dehydrogenase over a range of pH values and found that the isotope effect varied from 0.3% (pH 7.0) to 2.76% (pH 4.1) [48]. The presence of significant isotope effects in the kinetics of such a large number of the enzymes of central carbon metabolism and the variation in the magnitudes of these effects across different organisms and under different conditions makes it difficult to predict the impact that isotopic discrimination will have on the ¹³C labeling patterns of intracellular metabolites. However, given the preceding analysis (in which we neglected isotope effects in all reactions upstream and downstream of PDH for simplicity) and the ubiquity of enzymes with kinetics subject to isotope effects in the various pathways of central metabolism, it seems likely that isotope effects will exert significant influence on the distribution of ¹³C label in metabolic systems.

Rigorous interpretation of ¹³C-MFA results requires an accurate assessment of the measurement errors in the ¹³C labeling data. Knowledge of the measurement errors is necessary to conduct goodness-of-fit tests, which quantify how well a set of labeling data fit a metabolic model, and to compute confidence intervals for the estimated fluxes, which is necessary to determine if differences in estimated fluxes in different strains or under different conditions are statistically significant [23, 29, 49]. Failure to account for any significant source of error in a ¹³C-MFA can potentially lead to underestimation of the errors associated with labeling data. This can result in a biased estimated metabolic flux distribution, failure of a chi-square test for goodness-of-fit even with a complete model metabolic network, and overly optimistic estimation of the confidence intervals for the computed fluxes. To-date, the most common methods for determining the magnitude of the error in MS data have been measurement of MIDs of metabolites labeled to natural abundance (for which the MIDs are theoretically independent of the flux distribution and can be computed from the well-known natural abundances of heavy isotopes) [17, 42, 50], calculation of standard deviations from replicate samples (which is really a measure of precision, not accuracy) [5, 50], and comparison of labeling data for metabolites which should in principle have identical labeling patterns (i.e. comparison of redundant data) [24]. None of these methods are capable of quantifying the errors associated with neglecting isotope effects in central carbon metabolism. These errors are structural in nature and can only be quantified by modeling the impact of isotope effects on the distribution of ¹³C atoms in intracellular metabolites, which at present seems to be a challenging task. We further note that as long as the isotopomer balance equations used for prediction of the labeling state associated with a flux distribution neglect isotope effects, the errors associated with isotope effects place a bound on the accuracy that can be achieved in modeling ¹³C labeling data. No matter how accurate the measurement technique, the errors will never be smaller than those associated with the assumption that isotope effects are negligible.

In this contribution, we have modeled isotopic fractionation at the pyruvate node to quantitatively assess the potential modeling errors associated with kinetic isotope effects. We have also proposed a framework that can be used to estimate modeling errors associated with isotope effects at other branch points in metabolism. Our results show that under some conditions the modeling errors associated with isotope effects are significant and will be comparable in size to the measurements errors associated with GC–MS. The quantification of these errors will facilitate accurate interpretation of the results of future ¹³C-MFA studies.

Acknowledgments

We acknowledge support from United States Department of Energy grant DE-SC0008744. T.M.W. is supported by the MIT/NIGMS Biotechnology Training Program.

Abbreviations

CoA: coenzyme A
GC: gas chromatography
MFA: meta bolic flux analysis
MID: mass isotopomer distribution
MS: mass spectrometry
PDH: pyruvate dehydrogenase
PK: pyruvate kinase

Footnotes

The authors declare no conflict of interest.

References

1.Nielsen J. It is all about metabolic fluxes. J. Bacteriol. 2003;185:7031–7035. doi: 10.1128/JB.185.24.7031-7035.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
2.Sauer U. Metabolic networks in motion: 13C-based flux analysis. Mol. Syst. Biol. 2006;2:62. doi: 10.1038/msb4100109. [DOI] [PMC free article] [PubMed] [Google Scholar]
3.Gombert AK, dos Santos MM, Christensen B, Nielsen J. Network identification and flux quantification in the central metabolism of Saccharomyces cerevisiae under different conditions of glucose repression. J. Bacteriol. 2001;183:1441–1451. doi: 10.1128/JB.183.4.1441-1451.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
4.Fischer E, Sauer U. Large-scale in vivo flux analysis shows rigidity and suboptimal performance of Bacillus subtilis metabolism. Nat. Genet. 2005;37:636–640. doi: 10.1038/ng1555. [DOI] [PubMed] [Google Scholar]
5.Wittmann C, Heinzle E. Genealogy profiling through strain improvement by using metabolic network analysis: Metabolic flux genealogy of several generations of lysine-producing corynebacteria. Appl. Environ. Microbiol. 2002;68:5843–5859. doi: 10.1128/AEM.68.12.5843-5859.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
6.Antoniewicz MR, Kraynie DF, Laffend LA, González-Lergier J, et al. Metabolic flux analysis in a nonstationary system: Fed-batch fermentation of a high yielding strain of E. coli producing 1,3-propanediol. Metab. Eng. 2007;9:277–292. doi: 10.1016/j.ymben.2007.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
7.Schwender J. Metabolic flux analysis as a tool in metabolic engineering of plants. Curr. Opin. Biotechnol. 2008;19:131–137. doi: 10.1016/j.copbio.2008.02.006. [DOI] [PubMed] [Google Scholar]
8.Allen DK, Libourel IGL, Shachar-Hill Y. Metabolic flux analysis in plants: Coping with complexity. Plant Cell Environ. 2009;32:1241–1257. doi: 10.1111/j.1365-3040.2009.01992.x. [DOI] [PubMed] [Google Scholar]
9.Keibler MA, Fendt SM, Stephanopoulos G. Expanding the concepts and tools of metabolic engineering to elucidate cancer metabolism. Biotechnol. Prog. 2012;28:1409–1418. doi: 10.1002/btpr.1629. [DOI] [PMC free article] [PubMed] [Google Scholar]
10.Munger J, Bennett BD, Parikh A, Feng XJ, et al. Systems-level metabolic flux profiling identifies fatty acid synthesis as a target for antiviral therapy. Nat. Biotechnol. 2008;26:1179–1186. doi: 10.1038/nbt.1500. [DOI] [PMC free article] [PubMed] [Google Scholar]
11.Schmidt K, Nielsen J, Villadsen J. Quantitative analysis of metabolic fluxes in Escherichia coli, using two-dimensional NMR spectroscopy and complete isotopomer models. J. Biotechnol. 1999;71:175–189. doi: 10.1016/s0168-1656(99)00021-8. [DOI] [PubMed] [Google Scholar]
12.Vallino JJ, Stephanopoulos G. Metabolic flux distributions in Corynebacterium glutamicum during growth and lysine overproduction. Biotechnol. Bioeng. 1993;41:633–646. doi: 10.1002/bit.260410606. [DOI] [PubMed] [Google Scholar]
13.Marx A, de Graaf AA, Wiechert W, Eggeling L, Sahm H. Determination of the fluxes in the central metabolism of Corynebacterium glutamicum by nuclear magnetic resonance spectroscopy combined with metabolite balancing. Biotechnol. Bioeng. 1996;49:111–129. doi: 10.1002/(SICI)1097-0290(19960120)49:2<111::AID-BIT1>3.0.CO;2-T. [DOI] [PubMed] [Google Scholar]
14.Szyperski T. Biosynthetically directed fractional 13C-labeling of proteinogenic amino acids. An efficient analytical tool to investigate intermediary metabolism. Eur. J. Biochem. 1995;232:433–448. doi: 10.1111/j.1432-1033.1995.tb20829.x. [DOI] [PubMed] [Google Scholar]
15.Sauer U, Hatzimanikatis V, Bailey JE, Hochuli M, et al. Metabolic fluxes in riboflavin-producing Bacillus subtilis. Nat. Biotechnol. 1997;15:448–452. doi: 10.1038/nbt0597-448. [DOI] [PubMed] [Google Scholar]
16.Christensen B, Nielsen J. Isotopomer analysis using GC–MS. Metab. Eng. 1999;1:282–290. doi: 10.1006/mben.1999.0117. [DOI] [PubMed] [Google Scholar]
17.Dauner M, Sauer U. GC–MS analysis of amino acids rapidly provides rich information for isotopomer balancing. Biotechnol. Prog. 2000;16:642–649. doi: 10.1021/bp000058h. [DOI] [PubMed] [Google Scholar]
18.Wittmann C, Heinzle E. Mass spectrometry for metabolic flux analysis. Biotechnol. Bioeng. 1999;62:739–750. doi: 10.1002/(sici)1097-0290(19990320)62:6<739::aid-bit13>3.0.co;2-e. [DOI] [PubMed] [Google Scholar]
19.Christensen B, Gombert AK, Nielsen J. Analysis of flux estimates based on (13)C-labelling experiments. Eur. J. Biochem. 2002;269:2795–2800. doi: 10.1046/j.1432-1033.2002.02959.x. [DOI] [PubMed] [Google Scholar]
20.Wiechert W, de Graaf AA. Bidirectional reaction steps in metabolic networks: I. Modeling and simulation of carbon isotope labeling experiments. Biotechnol. Bioeng. 1997;55:101–117. doi: 10.1002/(SICI)1097-0290(19970705)55:1<101::AID-BIT12>3.0.CO;2-P. [DOI] [PubMed] [Google Scholar]
21.Wiechert W, Siefke C, de Graaf AA, Marx A. Bidirectional reaction steps in metabolic networks: II. Flux estimation and statistical analysis. Biotechnol. Bioeng. 1997;55:118–135. doi: 10.1002/(SICI)1097-0290(19970705)55:1<118::AID-BIT13>3.0.CO;2-I. [DOI] [PubMed] [Google Scholar]
22.Wiechert W, Möllney M, Isermann N, Wurzel M, de Graaf AA. Bidirectional reaction steps in metabolic networks: III. Explicit solution and analysis of isotopomer labeling systems. Biotechnol. Bioeng. 1999;66:69–85. [PubMed] [Google Scholar]
23.Möllney M, Wiechert W, Kownatzki D, de Graaf AA. Bidirectional reaction steps in metabolic networks: IV. Optimal design of isotopomer labeling experiments. Biotechnol. Bioeng. 1999;66:86–103. doi: 10.1002/(sici)1097-0290(1999)66:2<86::aid-bit2>3.0.co;2-a. [DOI] [PubMed] [Google Scholar]
24.Schmidt K, Nørregaard LC, Pedersen B, Meissner AJ, et al. Quantification of intracellular metabolic fluxes from fractional enrichment and 13C–13C coupling constraints on the isotopomer distribution in labeled biomass components. Metab. Eng. 1999;1:166–179. doi: 10.1006/mben.1999.0114. [DOI] [PubMed] [Google Scholar]
25.Antoniewicz MR, Kelleher JK, Stephanopoulos G. Elementary metabolite units (EMU): A novel framework for modeling isotopic distributions. Metab. Eng. 2007;9:68–86. doi: 10.1016/j.ymben.2006.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
26.Whelan T, Sackett WM, Benedict CR. Carbon isotope discrimination in a plant possessing the C4 dicarboxylic acid pathway. Biochem. Biophys. Res. Commun. 1970;41:1205–1210. doi: 10.1016/0006-291x(70)90214-7. [DOI] [PubMed] [Google Scholar]
27.Whelan T, Sackett WM, Benedict CR. Enzymatic fractionation of carbon isotopes by phosphoenolpyruvate carboxylase from c(4) plants. Plant Physiol. 1973;51:1051–1054. doi: 10.1104/pp.51.6.1051. [DOI] [PMC free article] [PubMed] [Google Scholar]
28.Heinzle E, Yuan Y, Kumar S, Wittmann C, et al. Analysis of 13C labeling enrichment in microbial culture applying metabolic tracer experiments using gas chromatography–combustion-isotope ratio mass spectrometry. Anal. Biochem. 2008;380:202–210. doi: 10.1016/j.ab.2008.05.039. [DOI] [PubMed] [Google Scholar]
29.van Winden W, Verheijen P, Heijnen S. Possible pitfalls of flux calculations based on (13)C-labeling. Metab. Eng. 2001;3:151–162. doi: 10.1006/mben.2000.0174. [DOI] [PubMed] [Google Scholar]
30.Yuan Y, Yang TH, Heinzle E. 13C metabolic flux analysis for larger scale cultivation using gas chromatography–combustion-isotope ratio mass spectrometry. Metab. Eng. 2010;12:392–400. doi: 10.1016/j.ymben.2010.02.001. [DOI] [PubMed] [Google Scholar]
31.Abelson PH, Hoering TC. Carbon isotope fractionation in formation of amino acids by photosynthetic organisms. Proc. Natl. Acad. Sci. USA. 1961;47:623–632. doi: 10.1073/pnas.47.5.623. [DOI] [PMC free article] [PubMed] [Google Scholar]
32.Park R, Epstein S. Metabolic fractionation of C13 & C12 in plants. Plant Physiol. 1961;36:133–138. doi: 10.1104/pp.36.2.133. [DOI] [PMC free article] [PubMed] [Google Scholar]
33.Monson KD, Hayes JM. Carbon isotopic fractionation in the biosynthesis of bacterial fatty acids. Ozonolysis of unsaturated fatty acids as a means of determining the intramolecular distribution of carbon isotopes. Geochim. Cosmochim. Acta. 1982;46:139–149. [Google Scholar]
34.Melzer E, Schmidt HL. Carbon isotope effects on the pyruvate dehydrogenase reaction and their importance for relative carbon-13 depletion in lipids. J. Biol. Chem. 1987;262:8159–8164. [PubMed] [Google Scholar]
35.Schmidt HL. Fundamentals and systematics of the non-statistical distributions of isotopes in natural compounds. Naturwissenschaften. 2003;90:537–552. doi: 10.1007/s00114-003-0485-5. [DOI] [PubMed] [Google Scholar]
36.DeNiro MJ, Epstein S. Mechanism of carbon isotope fractionation associated with lipid synthesis. Science. 1977;197:261–263. doi: 10.1126/science.327543. [DOI] [PubMed] [Google Scholar]
37.Fischer E, Sauer U. Metabolic flux profiling of Escherichia coli mutants in central carbon metabolism using GC–MS. Eur. J. Bio-chem. 2003;270:880–891. doi: 10.1046/j.1432-1033.2003.03448.x. [DOI] [PubMed] [Google Scholar]
38.Blank LM, Kuepfer L, Sauer U. Large-scale 13C-flux analysis reveals mechanistic principles of metabolic network robustness to null mutations in yeast. Genome Biol. 2005;6:R49. doi: 10.1186/gb-2005-6-6-r49. [DOI] [PMC free article] [PubMed] [Google Scholar]
39.Fendt SM, Sauer U. Transcriptional regulation of respiration in yeast metabolizing differently repressive carbon substrates. BMC Syst. Biol. 2010;4:12. doi: 10.1186/1752-0509-4-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
40.Metallo CM, Walther JL, Stephanopoulos G. Evaluation of 13C isotopic tracers for metabolic flux analysis in mammalian cells. J. Biotechnol. 2009;144:167–174. doi: 10.1016/j.jbiotec.2009.07.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
41.Crown SB, Ahn WS, Antoniewicz MR. Rational design of 13C-labeling experiments for metabolic flux analysis in mammalian cells. BMC Syst. Biol. 2012;6:43. doi: 10.1186/1752-0509-6-43. [DOI] [PMC free article] [PubMed] [Google Scholar]
42.Antoniewicz MR, Kelleher JK, Stephanopoulos G. Accurate assessment of amino acid mass isotopomer distributions for metabolic flux analysis. Anal. Chem. 2007;79:7554–7559. doi: 10.1021/ac0708893. [DOI] [PubMed] [Google Scholar]
43.Gleixner G, Schmidt HL. Carbon isotope effects on the fructose-1,6-bisphosphate aldolase reaction, origin for non-statistical 13C distributions in carbohydrates. J. Biol. Chem. 1997;272:5382–5387. doi: 10.1074/jbc.272.9.5382. [DOI] [PubMed] [Google Scholar]
44.Hermes JD, Roeske CA, O'Leary MH, Cleland WW. Use of multiple isotope effects to determine enzyme mechanisms and intrinsic isotope effects. Malic enzyme and glucose-6-phosphate dehydrogenase. Biochemistry. 1982;21:5106–5114. doi: 10.1021/bi00263a040. [DOI] [PubMed] [Google Scholar]
45.Rendina AR, Hermes JD, Cleland WW. Use of multiple isotope effects to study the mechanism of 6-phosphogluconate dehydrogenase. Biochemistry. 1984;23:6257–6262. doi: 10.1021/bi00320a056. [DOI] [PubMed] [Google Scholar]
46.Hwang CC, Cook PF. Multiple isotope effects as a probe of proton and hydride transfer in the 6-phosphogluconate dehydrogenase reaction. Biochemistry. 1998;37:15698–15702. doi: 10.1021/bi981288w. [DOI] [PubMed] [Google Scholar]
47.Hwang CC, Berdis AJ, Karsten WE, Cleland WW, Cook PF. Oxidative decarboxylation of 6-phosphogluconate by 6-phosphogluconate dehydrogenase proceeds by a stepwise mechanism with NADP and APADP as oxidants. Biochemistry. 1998;37:12596–12602. doi: 10.1021/bi980611s. [DOI] [PubMed] [Google Scholar]
48.Grissom CB, Cleland WW. Isotope effect studies of the chemical mechanism of pig heart NADP isocitrate dehydrogenase. Biochemistry. 1988;27:2934–2943. doi: 10.1021/bi00408a040. [DOI] [PubMed] [Google Scholar]
49.Antoniewicz MR, Kelleher JK, Stephanopoulos G. Determination of confidence intervals of metabolic fluxes estimated from stable isotope measurements. Metab. Eng. 2006;8:324–337. doi: 10.1016/j.ymben.2006.01.004. [DOI] [PubMed] [Google Scholar]
50.van Winden WA, van Dam JC, Ras C, Kleijn RJ, et al. Metabolic-flux analysis of Saccharomyces cerevisiae CEN.PK113-7D based on mass isotopomer measurements of (13)C-labeled primary metabolites. FEMS Yeast Res. 2005;5:559–568. doi: 10.1016/j.femsyr.2004.10.007. [DOI] [PubMed] [Google Scholar]

[R1] 1.Nielsen J. It is all about metabolic fluxes. J. Bacteriol. 2003;185:7031–7035. doi: 10.1128/JB.185.24.7031-7035.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R2] 2.Sauer U. Metabolic networks in motion: 13C-based flux analysis. Mol. Syst. Biol. 2006;2:62. doi: 10.1038/msb4100109. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R3] 3.Gombert AK, dos Santos MM, Christensen B, Nielsen J. Network identification and flux quantification in the central metabolism of Saccharomyces cerevisiae under different conditions of glucose repression. J. Bacteriol. 2001;183:1441–1451. doi: 10.1128/JB.183.4.1441-1451.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R4] 4.Fischer E, Sauer U. Large-scale in vivo flux analysis shows rigidity and suboptimal performance of Bacillus subtilis metabolism. Nat. Genet. 2005;37:636–640. doi: 10.1038/ng1555. [DOI] [PubMed] [Google Scholar]

[R5] 5.Wittmann C, Heinzle E. Genealogy profiling through strain improvement by using metabolic network analysis: Metabolic flux genealogy of several generations of lysine-producing corynebacteria. Appl. Environ. Microbiol. 2002;68:5843–5859. doi: 10.1128/AEM.68.12.5843-5859.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R6] 6.Antoniewicz MR, Kraynie DF, Laffend LA, González-Lergier J, et al. Metabolic flux analysis in a nonstationary system: Fed-batch fermentation of a high yielding strain of E. coli producing 1,3-propanediol. Metab. Eng. 2007;9:277–292. doi: 10.1016/j.ymben.2007.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R7] 7.Schwender J. Metabolic flux analysis as a tool in metabolic engineering of plants. Curr. Opin. Biotechnol. 2008;19:131–137. doi: 10.1016/j.copbio.2008.02.006. [DOI] [PubMed] [Google Scholar]

[R8] 8.Allen DK, Libourel IGL, Shachar-Hill Y. Metabolic flux analysis in plants: Coping with complexity. Plant Cell Environ. 2009;32:1241–1257. doi: 10.1111/j.1365-3040.2009.01992.x. [DOI] [PubMed] [Google Scholar]

[R9] 9.Keibler MA, Fendt SM, Stephanopoulos G. Expanding the concepts and tools of metabolic engineering to elucidate cancer metabolism. Biotechnol. Prog. 2012;28:1409–1418. doi: 10.1002/btpr.1629. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R10] 10.Munger J, Bennett BD, Parikh A, Feng XJ, et al. Systems-level metabolic flux profiling identifies fatty acid synthesis as a target for antiviral therapy. Nat. Biotechnol. 2008;26:1179–1186. doi: 10.1038/nbt.1500. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R11] 11.Schmidt K, Nielsen J, Villadsen J. Quantitative analysis of metabolic fluxes in Escherichia coli, using two-dimensional NMR spectroscopy and complete isotopomer models. J. Biotechnol. 1999;71:175–189. doi: 10.1016/s0168-1656(99)00021-8. [DOI] [PubMed] [Google Scholar]

[R12] 12.Vallino JJ, Stephanopoulos G. Metabolic flux distributions in Corynebacterium glutamicum during growth and lysine overproduction. Biotechnol. Bioeng. 1993;41:633–646. doi: 10.1002/bit.260410606. [DOI] [PubMed] [Google Scholar]

[R13] 13.Marx A, de Graaf AA, Wiechert W, Eggeling L, Sahm H. Determination of the fluxes in the central metabolism of Corynebacterium glutamicum by nuclear magnetic resonance spectroscopy combined with metabolite balancing. Biotechnol. Bioeng. 1996;49:111–129. doi: 10.1002/(SICI)1097-0290(19960120)49:2<111::AID-BIT1>3.0.CO;2-T. [DOI] [PubMed] [Google Scholar]

[R14] 14.Szyperski T. Biosynthetically directed fractional 13C-labeling of proteinogenic amino acids. An efficient analytical tool to investigate intermediary metabolism. Eur. J. Biochem. 1995;232:433–448. doi: 10.1111/j.1432-1033.1995.tb20829.x. [DOI] [PubMed] [Google Scholar]

[R15] 15.Sauer U, Hatzimanikatis V, Bailey JE, Hochuli M, et al. Metabolic fluxes in riboflavin-producing Bacillus subtilis. Nat. Biotechnol. 1997;15:448–452. doi: 10.1038/nbt0597-448. [DOI] [PubMed] [Google Scholar]

[R16] 16.Christensen B, Nielsen J. Isotopomer analysis using GC–MS. Metab. Eng. 1999;1:282–290. doi: 10.1006/mben.1999.0117. [DOI] [PubMed] [Google Scholar]

[R17] 17.Dauner M, Sauer U. GC–MS analysis of amino acids rapidly provides rich information for isotopomer balancing. Biotechnol. Prog. 2000;16:642–649. doi: 10.1021/bp000058h. [DOI] [PubMed] [Google Scholar]

[R18] 18.Wittmann C, Heinzle E. Mass spectrometry for metabolic flux analysis. Biotechnol. Bioeng. 1999;62:739–750. doi: 10.1002/(sici)1097-0290(19990320)62:6<739::aid-bit13>3.0.co;2-e. [DOI] [PubMed] [Google Scholar]

[R19] 19.Christensen B, Gombert AK, Nielsen J. Analysis of flux estimates based on (13)C-labelling experiments. Eur. J. Biochem. 2002;269:2795–2800. doi: 10.1046/j.1432-1033.2002.02959.x. [DOI] [PubMed] [Google Scholar]

[R20] 20.Wiechert W, de Graaf AA. Bidirectional reaction steps in metabolic networks: I. Modeling and simulation of carbon isotope labeling experiments. Biotechnol. Bioeng. 1997;55:101–117. doi: 10.1002/(SICI)1097-0290(19970705)55:1<101::AID-BIT12>3.0.CO;2-P. [DOI] [PubMed] [Google Scholar]

[R21] 21.Wiechert W, Siefke C, de Graaf AA, Marx A. Bidirectional reaction steps in metabolic networks: II. Flux estimation and statistical analysis. Biotechnol. Bioeng. 1997;55:118–135. doi: 10.1002/(SICI)1097-0290(19970705)55:1<118::AID-BIT13>3.0.CO;2-I. [DOI] [PubMed] [Google Scholar]

[R22] 22.Wiechert W, Möllney M, Isermann N, Wurzel M, de Graaf AA. Bidirectional reaction steps in metabolic networks: III. Explicit solution and analysis of isotopomer labeling systems. Biotechnol. Bioeng. 1999;66:69–85. [PubMed] [Google Scholar]

[R23] 23.Möllney M, Wiechert W, Kownatzki D, de Graaf AA. Bidirectional reaction steps in metabolic networks: IV. Optimal design of isotopomer labeling experiments. Biotechnol. Bioeng. 1999;66:86–103. doi: 10.1002/(sici)1097-0290(1999)66:2<86::aid-bit2>3.0.co;2-a. [DOI] [PubMed] [Google Scholar]

[R24] 24.Schmidt K, Nørregaard LC, Pedersen B, Meissner AJ, et al. Quantification of intracellular metabolic fluxes from fractional enrichment and 13C–13C coupling constraints on the isotopomer distribution in labeled biomass components. Metab. Eng. 1999;1:166–179. doi: 10.1006/mben.1999.0114. [DOI] [PubMed] [Google Scholar]

[R25] 25.Antoniewicz MR, Kelleher JK, Stephanopoulos G. Elementary metabolite units (EMU): A novel framework for modeling isotopic distributions. Metab. Eng. 2007;9:68–86. doi: 10.1016/j.ymben.2006.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R26] 26.Whelan T, Sackett WM, Benedict CR. Carbon isotope discrimination in a plant possessing the C4 dicarboxylic acid pathway. Biochem. Biophys. Res. Commun. 1970;41:1205–1210. doi: 10.1016/0006-291x(70)90214-7. [DOI] [PubMed] [Google Scholar]

[R27] 27.Whelan T, Sackett WM, Benedict CR. Enzymatic fractionation of carbon isotopes by phosphoenolpyruvate carboxylase from c(4) plants. Plant Physiol. 1973;51:1051–1054. doi: 10.1104/pp.51.6.1051. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R28] 28.Heinzle E, Yuan Y, Kumar S, Wittmann C, et al. Analysis of 13C labeling enrichment in microbial culture applying metabolic tracer experiments using gas chromatography–combustion-isotope ratio mass spectrometry. Anal. Biochem. 2008;380:202–210. doi: 10.1016/j.ab.2008.05.039. [DOI] [PubMed] [Google Scholar]

[R29] 29.van Winden W, Verheijen P, Heijnen S. Possible pitfalls of flux calculations based on (13)C-labeling. Metab. Eng. 2001;3:151–162. doi: 10.1006/mben.2000.0174. [DOI] [PubMed] [Google Scholar]

[R30] 30.Yuan Y, Yang TH, Heinzle E. 13C metabolic flux analysis for larger scale cultivation using gas chromatography–combustion-isotope ratio mass spectrometry. Metab. Eng. 2010;12:392–400. doi: 10.1016/j.ymben.2010.02.001. [DOI] [PubMed] [Google Scholar]

[R31] 31.Abelson PH, Hoering TC. Carbon isotope fractionation in formation of amino acids by photosynthetic organisms. Proc. Natl. Acad. Sci. USA. 1961;47:623–632. doi: 10.1073/pnas.47.5.623. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R32] 32.Park R, Epstein S. Metabolic fractionation of C13 & C12 in plants. Plant Physiol. 1961;36:133–138. doi: 10.1104/pp.36.2.133. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R33] 33.Monson KD, Hayes JM. Carbon isotopic fractionation in the biosynthesis of bacterial fatty acids. Ozonolysis of unsaturated fatty acids as a means of determining the intramolecular distribution of carbon isotopes. Geochim. Cosmochim. Acta. 1982;46:139–149. [Google Scholar]

[R34] 34.Melzer E, Schmidt HL. Carbon isotope effects on the pyruvate dehydrogenase reaction and their importance for relative carbon-13 depletion in lipids. J. Biol. Chem. 1987;262:8159–8164. [PubMed] [Google Scholar]

[R35] 35.Schmidt HL. Fundamentals and systematics of the non-statistical distributions of isotopes in natural compounds. Naturwissenschaften. 2003;90:537–552. doi: 10.1007/s00114-003-0485-5. [DOI] [PubMed] [Google Scholar]

[R36] 36.DeNiro MJ, Epstein S. Mechanism of carbon isotope fractionation associated with lipid synthesis. Science. 1977;197:261–263. doi: 10.1126/science.327543. [DOI] [PubMed] [Google Scholar]

[R37] 37.Fischer E, Sauer U. Metabolic flux profiling of Escherichia coli mutants in central carbon metabolism using GC–MS. Eur. J. Bio-chem. 2003;270:880–891. doi: 10.1046/j.1432-1033.2003.03448.x. [DOI] [PubMed] [Google Scholar]

[R38] 38.Blank LM, Kuepfer L, Sauer U. Large-scale 13C-flux analysis reveals mechanistic principles of metabolic network robustness to null mutations in yeast. Genome Biol. 2005;6:R49. doi: 10.1186/gb-2005-6-6-r49. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R39] 39.Fendt SM, Sauer U. Transcriptional regulation of respiration in yeast metabolizing differently repressive carbon substrates. BMC Syst. Biol. 2010;4:12. doi: 10.1186/1752-0509-4-12. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R40] 40.Metallo CM, Walther JL, Stephanopoulos G. Evaluation of 13C isotopic tracers for metabolic flux analysis in mammalian cells. J. Biotechnol. 2009;144:167–174. doi: 10.1016/j.jbiotec.2009.07.010. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R41] 41.Crown SB, Ahn WS, Antoniewicz MR. Rational design of 13C-labeling experiments for metabolic flux analysis in mammalian cells. BMC Syst. Biol. 2012;6:43. doi: 10.1186/1752-0509-6-43. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R42] 42.Antoniewicz MR, Kelleher JK, Stephanopoulos G. Accurate assessment of amino acid mass isotopomer distributions for metabolic flux analysis. Anal. Chem. 2007;79:7554–7559. doi: 10.1021/ac0708893. [DOI] [PubMed] [Google Scholar]

[R43] 43.Gleixner G, Schmidt HL. Carbon isotope effects on the fructose-1,6-bisphosphate aldolase reaction, origin for non-statistical 13C distributions in carbohydrates. J. Biol. Chem. 1997;272:5382–5387. doi: 10.1074/jbc.272.9.5382. [DOI] [PubMed] [Google Scholar]

[R44] 44.Hermes JD, Roeske CA, O'Leary MH, Cleland WW. Use of multiple isotope effects to determine enzyme mechanisms and intrinsic isotope effects. Malic enzyme and glucose-6-phosphate dehydrogenase. Biochemistry. 1982;21:5106–5114. doi: 10.1021/bi00263a040. [DOI] [PubMed] [Google Scholar]

[R45] 45.Rendina AR, Hermes JD, Cleland WW. Use of multiple isotope effects to study the mechanism of 6-phosphogluconate dehydrogenase. Biochemistry. 1984;23:6257–6262. doi: 10.1021/bi00320a056. [DOI] [PubMed] [Google Scholar]

[R46] 46.Hwang CC, Cook PF. Multiple isotope effects as a probe of proton and hydride transfer in the 6-phosphogluconate dehydrogenase reaction. Biochemistry. 1998;37:15698–15702. doi: 10.1021/bi981288w. [DOI] [PubMed] [Google Scholar]

[R47] 47.Hwang CC, Berdis AJ, Karsten WE, Cleland WW, Cook PF. Oxidative decarboxylation of 6-phosphogluconate by 6-phosphogluconate dehydrogenase proceeds by a stepwise mechanism with NADP and APADP as oxidants. Biochemistry. 1998;37:12596–12602. doi: 10.1021/bi980611s. [DOI] [PubMed] [Google Scholar]

[R48] 48.Grissom CB, Cleland WW. Isotope effect studies of the chemical mechanism of pig heart NADP isocitrate dehydrogenase. Biochemistry. 1988;27:2934–2943. doi: 10.1021/bi00408a040. [DOI] [PubMed] [Google Scholar]

[R49] 49.Antoniewicz MR, Kelleher JK, Stephanopoulos G. Determination of confidence intervals of metabolic fluxes estimated from stable isotope measurements. Metab. Eng. 2006;8:324–337. doi: 10.1016/j.ymben.2006.01.004. [DOI] [PubMed] [Google Scholar]

[R50] 50.van Winden WA, van Dam JC, Ras C, Kleijn RJ, et al. Metabolic-flux analysis of Saccharomyces cerevisiae CEN.PK113-7D based on mass isotopomer measurements of (13)C-labeled primary metabolites. FEMS Yeast Res. 2005;5:559–568. doi: 10.1016/j.femsyr.2004.10.007. [DOI] [PubMed] [Google Scholar]

PERMALINK

Kinetic isotope effects significantly influence intracellular metabolite ¹³C labeling patterns and flux determination

Thomas M Wasylenko

Gregory Stephanopoulos

Abstract

1 Introduction

2 Modeling isotopic fractionation at the pyruvate node

Figure 1.

Table 1.

3 Results

Figure 2.

Figure 3.

4 Discussion

Acknowledgments

Abbreviations

Footnotes

References

ACTIONS

PERMALINK

RESOURCES

Cite

Add to Collections

PERMALINK

Kinetic isotope effects significantly influence intracellular metabolite 13C labeling patterns and flux determination

Thomas M Wasylenko

Gregory Stephanopoulos

Abstract

1 Introduction

2 Modeling isotopic fractionation at the pyruvate node

Figure 1.

Table 1.

3 Results

Figure 2.

Figure 3.

4 Discussion

Acknowledgments

Abbreviations

Footnotes

References

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases

Kinetic isotope effects significantly influence intracellular metabolite ¹³C labeling patterns and flux determination