Abstract
The firing rate of individual neurons depends on the firing frequency of their distributed synaptic inputs, with linear and non-linear relations subserving different computational functions. This paper explores the relationship between the degree of synchrony among excitatory synapses and the linearity of the response using detailed compartmental models of cortical pyramidal cells. Synchronous input resulted in a linear input/output releationship, while asynchronous stimulation yielded sub- and supra-proportional outputs at low and high frequencies, respectively. The dependence of input/output linearity on synchrony was sigmoidal and considerably robust with respect to dendritic location, stimulus irregularity, and alteration of active and synaptic properties. Moreover, synchrony affected firing rate differently at lower and higher input frequencies. A reduced integrate-and-fire model suggested a mechanism explaining these results based on spatio-temporal integration, with fundamental implications relating synchrony to memory encoding.
Keywords: compartmental models, pyramidal cells, spiking frequency, integration
1. Introduction
A key aspect of neuronal computation consists of the integration of thousands of synaptic signals on the dendrites into a spiking pattern in the axon. Since the activity of each synapse in turn derives from the firing output of the afferent cell, neuronal integration can be expressed in terms of the output firing frequency as a function of the mean input synaptic frequency. If such input/output (I/O) relationship is linear, or proportional, the neuron works as an information relay, possibly amplifying or reducing the firing rate throughout the whole frequency range. If the I/O relationship is not proportional (e.g. sigmoidal, or logarithmic), the neuron can perform operations of pattern completion or discrimination depending on the input frequency (Guzowski et al., 2004; Leutgeb et al., 2004). In the typical non-linear I/O relation, as the rate of synaptic excitation increases, the neuron remains silent until a critical threshold is reached. Additional increase of input frequency results in a sharp rise of the output frequency up to a saturation level (Gerstner and Kistler, 2002). Further increases of input frequency do not significantly alter this output plateau. Both proportional and non-proportional I/O integration modes have been observed in the nervous system (Cash and Yuste, 1999; Polsky et al., 2004; Liang, 2006), highlighting the ability to perform different computational functions.
Network synchrony is also known to occur in the central nervous system at variable levels. Neural synchronization has been proposed to underlie sensory integration or “binding” in the visual system (Singer and Gray, 1995), and has been similarly investigated in the sensorimotor cortex (Fetz et al., 2000), olfactory system (Laurent et al., 1996), and hippocampus Harris et al., 2003), with a variety of putative mechanisms and functions (Ritz and Sejnowski, 1997). The balance between synchronous and asynchronous activity also plays an important role in several pathological conditions, most noticeably seizure-related (Netoff and Schiff, 2002; Dominguez et al., 2005). Cortical synchrony also changes with different phases of rhythmic oscillations (Buzsaki and Draguhn, 2004), which have been associated with distinct stages of memory encoding and retrieval in the hippocampus (Wallenstein et al., 1998). At the same time, converging evidence points to proportional and non-proportional input/output relationships as substrates of alternative modes of hippocampal information processing (Lee et al., 2004; Vazdarjanova and Guzowski, 2004). Thus, the effect of afferent synchrony on the proportionality of the I/O relationship can be an important coding principle in the network mechanisms underlying learning and memory.
It is experimentally challenging to measure synchrony accurately from large neuronal assemblies (Buzsaki, 2004; Guevara et al., 2005). The question as to how synchronous inputs act differently on a target neuron, however, has been explored computationally in several seminal studies. Most notably, Bernander et al. (1994) investigated the role of synaptic synchronization as a function of the number of inputs and the threshold to trigger an action potential in neocortical cells. Their findings were consistent with a balanced influence of the low-pass filter nature of dendritic membranes and the refractory period of voltage-dependent channels. Softky and Koch (1993) employed both simplified integrate-and-fire models and more detailed, anatomically and biophysically realistic simulations to explore the potential mechanisms underlying the discharge patterns recorded from the visual cortex of awake monkeys. They concluded that temporal integration over distributed synaptic inputs implies regular firing, and fast active conductances or strong synchronization are necessary to match the experimental degree of firing variability.
Other studies used somatic injections of current patterns mimicking integrated synaptic barrages to examine the effect of synchrony on the output temporal variability (Stevens and Zador, 1998) and vice versa (Reyes, 2003). Nevertheless, systematically controlling synaptic synchronization over thousands of inputs on an individual neuron far exceeds current experimental techniques.
In our own simulations, we observed that fully synchrounous and asynchronous stimuli tended to elicit linear and logarithmic response curves, respectively (Li and Ascoli, 2006). However, this relation remains unexplored in more realistic conditions of intermediate and variable network synchronization. In order to investigate the effects of afferent synchrony on the neuronal I/O relationship quantitatively, we employed computational modeling of membrane biophysics using compartmental simulations of anatomically detailed hippocampal pyramidal cells. Different patterns of excitation through one thousand synaptic inputs distributed on the dendritic trees elicited a broad span of axonal firing frequencies, corresponding to input/output relationships ranging from highly proportional to considerably non-proportional. Synchronization systematically lowered the threshold and reduced the gain of the response. This effect depended on the method of synchronization, but was robust with respect to several stimulation details and model parameters. These features have potential implications regarding the computational function of network synchrony. We further validated the generality of these findings and explore the possible mechanisms by using a simplified integrate-and-fire model.
2. Methods
The computational model of the hippocampal pyramidal neuron was the same as previously reported (Li and Ascoli, 2006). In particular, eight three-dimensional reconstructions of rat CA1 pyramidal cells (Ishizuka et al., 1995), freely available at http://NeuroMorpho.Org (Ascoli, 2006), were imported into the NEURON (v.5.7) simulation environment (Hines and Carnevale, 2001). The model scripts are publicly posted on ModelDB (http://senselab.yale.med.edu). Membrane and synaptic properties were distributed without modification (Li and Ascoli, 2006), and are thus only briefly described here.
Passive parameters and the density of the sodium and delayed rectifier potassium conductances were uniform, with the exception of the somatic compartments, in which INa was doubled. The slow potassium and non-specific hyperpolarizing cation conductances were distributed non-uniformly in the soma, axon, and dendrites. In particular, their densities increased linearly with the distance from the soma along the main apical trunk. In most simulations, the same linear increase extended to the whole dendritic arborization, including basal, oblique, and distal tuft (“Type I” in Li and Ascoli, 2006). In a variation of the model (“Type C” in Li and Ascoli, 2006), these conductances only increased in the main apical trunk, but were kept constant in all other dendritic compartments, at the value of the corresponding point of attachment on the main trunk (or soma for the basal trees). A subset of simulations were based on a completely different model (Poirazi et al., 2003), which includes calcium conductances and a more comprehensive set of active channels. The corresponding NEURON scripts were also obtained from ModelDB and employed as previously described (Li and Ascoli, 2006).
In most simulations, 1000 excitatory synapses were randomly distributed within the first two thirds of the apical dendrites, corresponding to the stratum radiatum. When noted, synapses were located in the basal dendrites, corresponding to the stratum oriens. These dendritic regions receive excitatory input from the Schaffer collaterals originating in CA3 and the associational fibers from other CA1 neurons, respectively (Witter and Amaral, 2004). Synaptic kinetics were constant and corresponded in most simulations to the characteristics of AMPA channels. Synaptic conductances were increased quadratically with the distance from the soma, so to evoke a constant somatic EPSP upon stimulation of the main apical trunk. In the standard Type I model the same function was used throughout the dendritic trees, while in the Type C model the synaptic conductances were kept constant outside of the main apical trunk (Li and Ascoli, 2006). Synaptic stimuli were generally delivered at regular intervals dictated by the input frequency. When noted as “irregular”, stimuli were temporally spread according to a Poisson distribution with the average interval corresponding to the input frequency. In a subset of simulations, slow synaptic conductances mimicking NMDA-like receptors were also included (Poirazi et al., 2003; Li and Ascoli, 2006), with contributions of NMDA and AMPA currents in each synapse distributed according to a 4:1 ratio (Wei et al., 2000).
In fully asynchronous stimulation, each synapse was connected to an independent presynaptic neuron (implemented as a NetStim function in NEURON). The opposite extreme of fully synchronous configuration was obtained by simultaneously activating all synapses in locked phase (with one and the same NetStim call). We used two methods to create intermediate synchrony levels, even grouping and dominant recruiting. In the grouping method (Fig. 1C), the 1000 synapses are divided in equal groups that are asynchronous among themselves, but with synchronous synapses within each group. The grouping value signifies the size of the group, i.e. grouping of 1 and 1000 correspond to fully asynchronous and synchronous modes, while grouping of k entails 1000/k asynchronous groups (separate NetStim calls) of k synchronous synapses each.
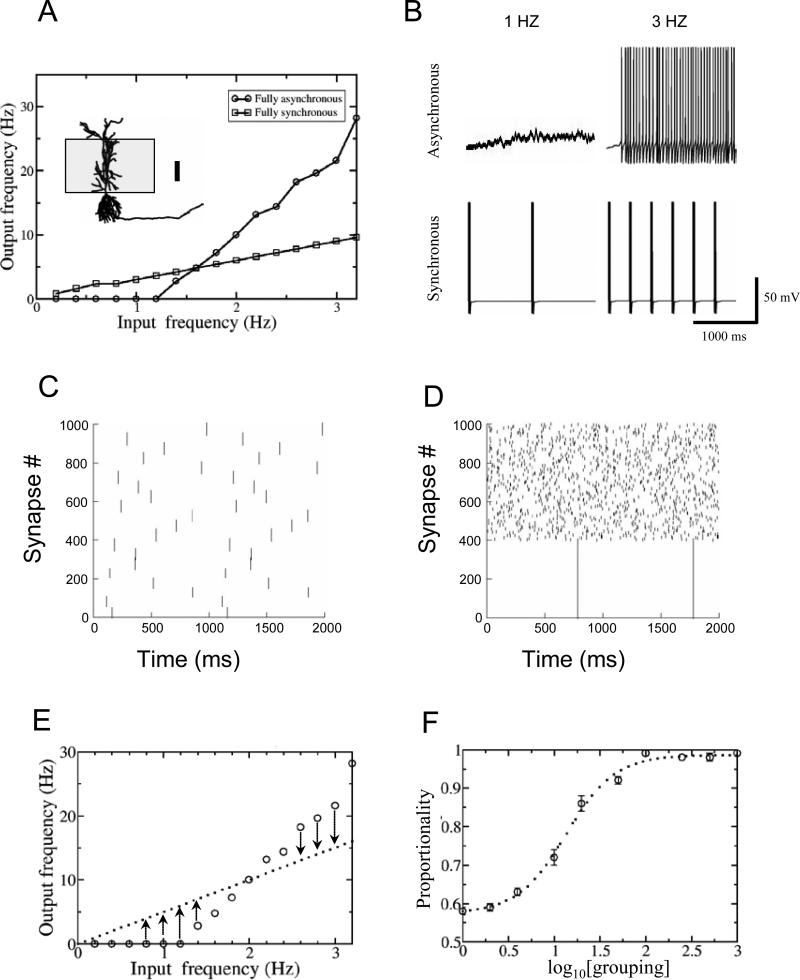
Fig. 1.
A) Input-output relation of one neuron with fully synchronous or asynchronous inputs. Inset: neuronal morphology and the synaptic distribution area on the apical tree (scale bar: 100 μm). B) Axonal voltage recordings with asynchronous and synchronous inputs at two representative frequencies. C) Raster plots showing 1000 synapses activated with the grouping synchronization method at the value of 50 (i.e., 20 groups of 50 synapses each). D) Recruiting method with recruiting value of 400. E) Proportionality is expressed as a function of the deviation of the output firing rate from the linear regression (through the origin) of the input frequency (see Methods). F) Increase of I/O proportionality with the grouping value (apical stimulation, Type I model). Mean and standard error over 8 cells fitted by a sigmoidal function (see Table 1 for formula and parameter values).
In the recruiting method (Fig. 1D) a variable number of synapses is synchronized in one and the same master group, while all others remain independent. Recruiting values of 1 and 1000 again correspond to fully asynchronous and synchronous modes, while recruiting of k entails one group of k synchronous synapses and 1000-k asynchronous individuals (1001-k NetStim calls). In both grouping and recruiting methods the selection of synapses within the dendrite is random, i.e. with no spatial clustering bias. Synaptic cross-correlation (Reyes, 2003) was measured at zero lag to compare the synchronization resulting from the same grouping and recruiting values.
The following method was used to characterize the proportionality of the input/output relationship at different levels of synaptic synchrony. The I/O functions in the fully synchronous and asynchronous conditions intersect at a unique input frequency (e.g. Fig. 1A), which typically varies on a neuron-by-neuron basis. Input frequencies were evenly selected along a range corresponding to twice the cross-over value, so to yield an equal number of points (generally 8) on either side. The resulting activity rates (typically up to ~3 Hz) are consistent with experimental observations (Barnes et al., 1990), which demonstrate considerably sparser firing in the hippocampus compared to other brain regions. The scatter of points relating input and output frequencies for a given level of synchrony was fitted with a line passing through the origin (Fig 1E). The absolute deviations of all data point from the linear regression, each normalized by the corresponding fitted value, were averaged. Proportionality was defined as the complement to unity of this average, and ranged between 0 and 1 (1 being the perfectly proportional relationship): Proportionality = 1-(Σ|d-f|/f)/n, where d and f represent the measured and fitted output frequencies, respectively, and the sum is taken over all n input frequencies.
Each cell was divided into isopotential compartments shorter than one tenth of the space constant at 100 Hz. Each compartment was further divided in three to ensure numerical convergence (Lazarewicz et al., 2002). All simulations were run with variable time step on a 1.7 GHz Athlon under Linux (Red Hat 7.3). Finally, a single-compartment integrate-and-fire model was built with the same number of input synapses, a threshold of 50 active inputs, and an integration window of 20 ms. The bin size of 20 ms was found empirically among round values, but is consistent with the upper bound given by the time constant (28 ms). The threshold number of (50) synaptic inputs corresponded to the optimal model value (see e.g. Figure 2D), and is consistent with experimental estimates (Barnes et al., 1990) considering that synaptic background is included in this count. Fitting and statistical analyses were carried out with the freeware software Grace (http://plasma-gate.weizmann.ac.il/Grace).
Fig. 2.
Effect of synaptic synchrony on I/O (apical synapses, regular stimulation). A) Amount of synchronization (measured by synaptic cross-correlation) as a function of grouping and recruiting values. B) Proportionality with intermediate levels of grouping and recruiting (Type I model) replotted versus synchrony values obtained from Fig. 2A. C) Representative single-neuron data relating output firing rate to synchrony: output frequency vs. grouping at various synaptic input levels. D) Data from panel C normalized to unity at grouping value of 50. E) Output frequency vs. recruiting at various synaptic input levels. F) Data from E normalized to unity at recruiting value of 800.
3. Results
In the basic simulation setup, 1000 excitatory synapses randomly distributed on the apical dendrites of CA1 pyramidal cells (Fig. 1A inset) were activated at various frequencies and synchrony levels. Consistently with recent reports (Li and Ascoli, 2006), the dependence of output firing frequency on the stimulus rate was essentially a linear function through the origin when all synapses were activated synchronously, while the input/output relationship was considerably non-proportional in the fully asynchronous mode (Fig. 1A). In particular, at low input frequencies synchronous stimuli elicited a stronger response than asynchronous ones, but the inequality was reversed at higher input rates. This situation is illustrated by representative output voltage traces corresponding to two synchronous and asynchronous excitation frequencies (Fig. 1B). In the asynchronous mode, the response transitions from quiescence to intense spiking, whereas a more moderate change is observed with full synchrony. Note that output frequencies upon synchronous stimulation, resulting from bursts of spikes, are averaged over multiple cells and are not necessarily reflected by individual neuronal traces.
In order to quantify the proportionality of the I/O relationship at intermediate levels of synchrony (Fig. 1C, D), we computed the deviation of the output firing rate from the linear regression (through the origin) of the input frequency (Fig. 1E), as described in the Methods. Proportionality, or “linearity”, followed a sigmoidal trend when plotted against a logarithmic grouping axis, with similar behavior if irregular excitation patterns were used instead of constant inter-stimulus intervals. The variability across different neuronal reconstructions was extremely small, and the average over eight neurons was well fitted by an analytical function (Fig. 1F). The results remained almost identical when switching the distributions of active and synaptic conductances from Type I to Type C (see Methods) and/or when moving the synaptic location from the apical to the basal trees (Table 1).
Table 1.
Parameters of the best fitting sigmoid function y=A+B/[1+10(C-xD)] relating the 8-neuron average of proportionality (y) to the logarithm of grouping or recruiting (x) with different models, (Type C and Type I), synaptic distributions (apical and basal dendrites), and stimulus patterns (regular and irregular). No statistically significant differences are found within a given synchronization method.
| Parameter → Model ↓ | A | B | C | D |
|---|---|---|---|---|
| Apical, Grouping Type C, Regular | 0.57 | 0.42 | 1.84 | 1.63 |
| Apical, Grouping Type I, Regular | 0.56 | 0.43 | 1.80 | 1.58 |
| Basal, Grouping Type C, Regular | 0.59 | 0.40 | 1.27 | 1.30 |
| Basal, Grouping Type I, Regular | 0.58 | 0.40 | 1.85 | 1.71 |
| Apical, Grouping Type I, Irregular | 0.60 | 0.38 | 1.79 | 1.60 |
| Apical, Recruiting Type C, Regular | 0.48 | 0.83 | 2.96 | 1.08 |
| Apical, Recruiting Type I, Regular | 0.49 | 0.83 | 2.96 | 1.07 |
Using the dominant synaptic recruiting protocol to increase synchrony (see Methods and Fig. 1C, D) also gradually linearized the I/O relationship. Similarly to the grouping method, recruiting results changed only minimally among neurons and model types, and with respect to synaptic location and stimulus regularity (not shown). However, the dependence of I/O proportionality on recruiting differed from that on grouping (Table 1). In order to carry out a quantitative comparison, the amount of synchronization was computed as function of both grouping and recruiting by measuring synaptic input cross-correlation. Synchrony was linearly dependent on grouping but sub-linearly on recruiting (Fig. 2A). As shown in Fig. 2B, a greater amount of synchrony was typically necessary with dominant recruiting than with even grouping to achieve the same level of I/O proportionality. In particular, synaptic grouping attained full proportionality with 10% synchrony, compared to 35% with the recruiting method.
The effect of synchrony on neuronal response was further investigated as a function of both grouping and recruiting. At low input frequencies, the dependence of output firing rate on grouping was bell-shaped with a clear maximum for most neurons around a grouping value of 50 (Fig. 2C). At higher input frequencies, the output firing rate tended to decrease across the whole range of grouping values. The transition is particularly clear when normalizing data at the value corresponding to the optimal low-frequency grouping value (Fig. 2D). The effect of recruiting on output firing also switched with synaptic frequency. At low input frequencies, the output firing rate increased to a plateau, whereas at high input frequencies it decreased with recruiting (Fig. 2E). As a consequence, there was one input frequency at which the output firing rate was essentially independent of recruiting value. This effect is highlighted by normalizing data to the high-recruiting plateau values (Fig. 2F). The input frequency that made firing rate constant with respect to recruiting was the same at which a clear output frequency maximum and optimal grouping value disappeared (~1.8 Hz). On a neuron-by-neuron basis, this frequency corresponded to the cross-over value between proportional and non-proportional I/O curves in response to fully synchronous and asynchronous stimulation (Fig. 1A).
The optimal grouping value at low input frequencies could be interpreted as a firing threshold for the neuron. Spatial summation of synaptic inputs progressively increases with synchrony up to the threshold. Any further increase in synaptic synchrony beyond this point reduces the opportunity for temporal summation. In order to test this simple mechanism, we built a reduced integrate-and-fire model consisting of a single compartment receiving the same 1000 synapses. Both theory (Gerstner and Kistler, 2002) and experiments under physiological conditions (Shadlen and Newsome, 1994) set an upper limit to the temporal integration window in the passive membrane time constant. In our multi-compartment Type I and Type C models this parameter (computed from the passive properties, which are the same for all the eight cells) is 28 ms, in good agreement with empirical data for hippocampal pyramidal cells (Li and Ascoli, 2006). Therefore we chose a value of 20 ms as the temporal summation window in the reduced integrate-and-fire model. In other words, we directly computed output frequency as the number of 20 ms time bins with at least 50 active synaptic inputs in a 1 s period.
This simple framework nicely reproduced the firing rate trends as a function of grouping at various input frequencies (similar to Fig. 2D). The main features of the dependence of output firing rate on recruiting were also captured, namely the increase at low input frequencies, decrease at high frequencies, and the plateau reached with the recruitment of 400 or more synapses (similar to Fig. 2F). Moreover, the behavior of the integrate-and-fire model also reflected the effect of synchrony on proportionality, with the greater efficiency of even grouping compared to dominant recruiting in linearizing the I/O relationship (similar to Fig. 2B).
Finally, we checked the robustness of the main distinction between the effects of synchronous and asynchronous excitation on the I/O relationship in light of known dendritic non-linearities in CA1 pyramidal neurons and over a broader stimulus range (not shown). In particular, slower NMDA and calcium conductances can contribute substantially to post-synaptic response. In one additional set of simulations, synaptic response was modeled with an excess of NMDA-like conductance relative to the faster AMPA contribution (Wei et al., 2000). Moreover, a further suite of simulations was based on an alternative model of CA1 pyramidal cell biophysics, which included calcium and a more comprehensive collection of active channels (Poirazi et al., 2003). The results obtained with the main model were essentially unchanged by the adoption of this altered compendium of membrane properties and were qualitatively consistent with the addition of NMDA currents in both the fully asynchronous and synchronous cases (Li and Ascoli, 2006). These sets of simulations were also extended to a higher input frequency, confirming the non-proportional, saturating I/O relation in response to asynchronous stimuli as opposed to the proportional, non-saturating response to synchronous excitation. In particular, the data points for all three models were better fitted by logarithmic than by linear functions in the asynchronous case, while the opposed relation held in the synchronous case (Li and Ascoli, 2006).
4. Discussion
A major distinction of our results from previous investigations consists of the detailed analysis of how the input/output relation gradually shifts from non-proportional to proportional as the synchrony of the stimulation increases. In particular, we show that this sigmoidal dependence is quantitatively robust with respect to dendritic and synaptic conductances as well as to synaptic regularity and location (Fig. 1F and Table 1), but clearly varies with the mechanism of synchronization (grouping vs. recruiting: Fig. 2A,B). Additional novel findings include the existence of a “resonant” intermediate grouping synchrony that maximizes output rate (Fig. 2C) and of a “cross-over” input frequency at which output rate is independent of recruiting synchrony (Fig. 2F).
With asynchronous stimulation, the input-output function is flatter than a proportional response (a line through the origin) at low excitation levels, but steeper at high excitation levels. When all stimuli are synchronized, the input-output function is fully proportional. The intersection point between the linear and non-linear I/O relationships occurs at a transition frequency above which output firing rate decreases with synchrony. Below this input frequency, output firing rate increases with dominant recruiting of synapses and reaches a maximum at an optimal level of even grouping. Noticeably, the size of individual assemblies in vivo varies broadly, encompassing the entire range used in this study (Eytan and Marom, 2006).
That even an integrate-and-fire model qualitatively reproduced the main features of the dependence of output frequency on synaptic rate and synchrony suggests an intuitive mechanistic explanation based on spatio-temporal integration and a firing threshold. Over a large number of synapses, synchronous inputs guarantee suprathreshold summation, but also imply lack of output between successive stimuli. This deterministic response results in a flatter I/O curve than in the asynchronous case, whereas a higher level of synaptic activity is required to reach threshold, but a steeper rate of increase (up to saturation) is ensured by the uniform temporal distribution of the inputs. This simple framework also directly accounts for the coincidence of the crossover point between the proportional and non-proportional I/O relations and the critical input frequency described above. This coincidence is due to the sub-proportional (flatter) and supra-proportional (steeper) responses to lower and higher asynchronous stimuli. At the cross-over point, the asynchronous response is essentially proportional and corresponds to the output in the synchronous case. The constant output frequency at all intermediate levels of synchrony is a direct extension of the two extremes.
In the rodent hippocampus, network synchrony decreases by an order of magnitude during theta rhythms (Harris et al., 2003), when the animal is engaged in active exploration, involving both encoding and retrieval of spatial and episodic memories (Wallenstein et al., 1998). These two functions might occur in separate phases of each theta oscillation, namely information encoding during the trough and retrieval during the peak (Hasselmo, 2005). Our findings offer an elegant cellular mechanism for such separation. The theta trough corresponds to reduced firing and thus low input frequency for individual cells. In the asynchronous activity characterizing theta, this implies a regime of sub-linear integration, which is consistently with a function of pattern completion (Guzowski et al., 2004). Conversely, the theta peak, corresponding to higher input frequencies, is linked by our results to a supra-linear response of pyramidal cells, a condition sufficient and necessary for pattern discrimination (Treves, 2004). A key aspect of sub- and supra-linear regimes is the slower or faster growth than the proportional response (line through the origin), as in the asynchronous curves.Thus, pattern completion and separation, entailing the distinct encoding and retrieval elements of memory processing, could be subserved at the single-cell level by the non-linear input/output relationship resulting from asynchronous excitation.
Highly synchronous activity is characteristic of the irregular, large amplitude oscillations observed during non-theta behavioral states, such as grooming, rest, and non-REM sleep. It has long been noted that these “sharp waves” are ideally suited to underlie long term potentiation (Buzsaki, 1989), providing an exquisite mechanism for memory consolidation if the firing probability of each neuron is proportional to its recent activity (Samsonovich and Ascoli, 2005). Thus, the I/O relationship resulting from synchronous excitation could provide a cellular correlate for both spatial and episodic learning. Moreover, while we only considered absolute synchronization (i.e., zero-lag synaptic cross-correlation), temporal phase-locking can also change gradually, implying an added dimension of control (Svirskis and Rinzel, 2000). In particular, ~10ms lags could be functionally significant, because of the AMPA time constant. An important element of neuronal complexity missing in our simulations is synaptic inhibition. This omission is apparent upon comparison of the input and output frequency ranges, which differ by an order of magnitude (Fig. 1A).
The simultaneous use of somatic and dendritic recording and multisite glutamate uncaging has recently shown that dendritic integration in CA1 pyramidal cells is linear in response to asynchronous or spatially distributed synaptic excitation (Gasparini and Magee, 2006). Conversely, temporally and spatially converging synaptic activity is integrated non-linearly by the dendrite on which the synapses are clustered, resulting in a precisely timed somatic action potential. On the surface such results may appear to contradict our findings. However, these observations involve the subthreshold-to-single-spike regime of neuronal activity, and relate to the fundamental non-linearity (all-or-none-behavior) of action potentials. In contrast, our excitation range, corresponding to a realistic but experimentally unapproachable number of inputs, reflects the “steady-state” activity measured by average firing frequency (Li and Ascoli, 2006). Moreover, the constraint of synaptic clustering necessary for non-linearity in the above study constitutes an opposite condition to our spatial distribution of synapses throughout the dendritic tree, implying an additional layer of local computation (Migliore et al., 2005).
Interestingly, feedforward excitation in vitro increases network synchrony in successive neuronal layers (Reyes, 2003). Our results predict a gradual reduction of threshold and gain of response as activity progresses in these architectures. When suitable experimental data become available for a direct comparison, our simulations could be extended to the more natural condition of nonuniform input frequencies across synapses. In addition, synchrony in vivo is likely to reflect a combination of dominant synaptic recruiting and even grouping. The ability of the computational approach to separately analyze these “pure” synchronization modes uncovered their different capacity to linearize the I/O relation while suggesting a general and fundamental link between network synchrony and neuronal response.
Acknowledgements
The authors are indebted to Drs. Julia Berzhanskaya and Paul So for their insightful feedback on an earlier version of this manuscript. This project was supported by NIH R01 grants NS39600 jointly funded by NINDS, NIMH, and NSF under the Human Brain Project, and AG025633 as part of the NSF/NIH Collaborative Research in Computational Neuroscience program.
References
- Ascoli GA. Mobilizing the base of neuroscience data: the case of neuronal morphologies. Nat Rev Neurosci. 2006;7:318–24. doi: 10.1038/nrn1885. [DOI] [PubMed] [Google Scholar]
- Barnes CA, McNaughton BL, Mizumori SJ, Leonard BW, Lin LH. Comparison of spatial and temporal characteristics of neuronal activity in sequential stages of hippocampal processing. Prog Brain Res. 1990;83:287–300. doi: 10.1016/s0079-6123(08)61257-1. [DOI] [PubMed] [Google Scholar]
- Bernander O, Koch C, Usher M. The effects of synchronized inputs at the single neuron level. Neural Comput. 1994;6:622–41. [Google Scholar]
- Buzsaki G. Two-stage model of memory trace formation: a role for “noisy” brain states. Neuroscience. 1989;31:551–70. doi: 10.1016/0306-4522(89)90423-5. [DOI] [PubMed] [Google Scholar]
- Buzsaki G. Large-scale recording of neuronal ensembles. Nat Neurosci. 2004;7:446–51. doi: 10.1038/nn1233. [DOI] [PubMed] [Google Scholar]
- Buzsaki G, Draguhn A. Neuronal oscillations in cortical networks. Science. 2004;304:1926–9. doi: 10.1126/science.1099745. [DOI] [PubMed] [Google Scholar]
- Cash S, Yuste R. Linear summation of excitatory inputs by CA1 pyramidal neurons. Neuron. 1999;22:383–94. doi: 10.1016/s0896-6273(00)81098-3. [DOI] [PubMed] [Google Scholar]
- Dominguez LG, Wennberg RA, Gaetz W, Cheyne D, Snead OC, 3rd, Perez Velazquez JL. Enhanced synchrony in epileptiform activity? Local versus distant phase synchronization in generalized seizures. J Neurosci. 2005;25:8077–84. doi: 10.1523/JNEUROSCI.1046-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eytan D, Marom S. Dynamics and effective topology underlying synchronization in networks of cortical neurons. J Neurosci. 2006;26:8465–76. doi: 10.1523/JNEUROSCI.1627-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fetz EE, Chen D, Murthy VN, Matsumura M. Synaptic interactions mediating synchrony and oscillations in primate sensorimotor cortex. J Physiol Paris. 2000;94:323–31. doi: 10.1016/s0928-4257(00)01089-5. [DOI] [PubMed] [Google Scholar]
- Gasparini S, Magee JC. State-dependent dendritic computation in hippocampal CA1 pyramidal neurons. J Neurosci. 2006;26:2088–100. doi: 10.1523/JNEUROSCI.4428-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerstner W, Kistler WM. Spiking Neuron Models. Cambridge Univ. Press.; 2002. [Google Scholar]
- Guevara R, Velazquez JL, Nenadovic V, Wennberg R, Senjanovic G, Dominguez LG. Phase synchronization measurements using electroencephalographic recordings: what can we really say about neuronal synchrony? Neuroinformatics. 2005;3:301–14. doi: 10.1385/NI:3:4:301. [DOI] [PubMed] [Google Scholar]
- Guzowski JF, Knierim JJ, Moser EI. Ensemble dynamics of hippocampal regions CA3 and CA1. Neuron. 2004;44:581–4. doi: 10.1016/j.neuron.2004.11.003. [DOI] [PubMed] [Google Scholar]
- Harris KD, Csicsvari J, Hirase H, Dragoi G, Buzsaki G. Organization of cell assemblies in the hippocampus. Nature. 2003;424:552–6. doi: 10.1038/nature01834. [DOI] [PubMed] [Google Scholar]
- Hasselmo ME. What is the function of hippocampal theta rhythm? Linking behavioral data to phasic properties of field potential and unit recording data. Hippocampus. 2005;15:936–49. doi: 10.1002/hipo.20116. [DOI] [PubMed] [Google Scholar]
- Hines ML, Carnevale NT. NEURON: a tool for neuroscientists. Neuroscientist. 2001;7:123–35. doi: 10.1177/107385840100700207. [DOI] [PubMed] [Google Scholar]
- Ishizuka N, Cowan WM, Amaral DG. A quantitative analysis of the dendritic organization of pyramidal cells in the rat hippocampus. J Comp Neurol. 1995;362:17–45. doi: 10.1002/cne.903620103. [DOI] [PubMed] [Google Scholar]
- Laurent G, Wehr M, Davidowitz H. Temporal representations of odors in an olfactory network. J Neurosci. 1996;16:3837–47. doi: 10.1523/JNEUROSCI.16-12-03837.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazarewicz MT, Boer-Iwema S, Ascoli GA. Practical aspects in anatomically accurate simulations of neuronal electrophysiology. In: Ascoli GA, editor. Computational Neuroanatomy: Principles and Methods. Humana Press; Totowa, NJ: 2002. pp. 127–148. [Google Scholar]
- Lee I, Yoganarasimha D, Rao G, Knierim JJ. Comparison of population coherence of place cells in hippocampal subfields CA1 and CA3. Nature. 2004;430:456–9. doi: 10.1038/nature02739. [DOI] [PubMed] [Google Scholar]
- Leutgeb S, Leutgeb JK, Treves A, Moser MB, Moser EI. Distinct ensemble codes in hippocampal areas CA3 and CA1. Science. 2004;305:1295–8. doi: 10.1126/science.1100265. [DOI] [PubMed] [Google Scholar]
- Li X, Ascoli GA. Computational simulation of the input-output relationship in hippocampal pyramidal cells. J Comput Neurosci. 2006;21:191–209. doi: 10.1007/s10827-006-8797-z. [DOI] [PubMed] [Google Scholar]
- Liang CW. One dendritic arbor, two modes of integration. J Neurosci. 2006;26(25):6664–5. doi: 10.1523/JNEUROSCI.1548-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Migliore M, Ferrante M, Ascoli GA. Signal propagation in oblique dendrites of CA1 pyramidal cells. J Neurophysiol. 2005;94:4145–55. doi: 10.1152/jn.00521.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Netoff TI, Schiff SJ. Decreased neuronal synchronization during experimental seizures. J Neurosci. 2002;22:7297–307. doi: 10.1523/JNEUROSCI.22-16-07297.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poirazi P, Brannon T, Mel BW. Arithmetic of subthreshold synaptic summation in a model CA1 pyramidal cell. Neuron. 2003;37:977–87. doi: 10.1016/s0896-6273(03)00148-x. [DOI] [PubMed] [Google Scholar]
- Polsky A, Mel BW, Schiller J. Computational subunits in thin dendrites of pyramidal cells. Nat Neurosci. 2004;7:621–7. doi: 10.1038/nn1253. [DOI] [PubMed] [Google Scholar]
- Reyes AD. Synchrony-dependent propagation of firing rate in iteratively constructed networks in vitro. Nat Neurosci. 2003;6:593–9. doi: 10.1038/nn1056. [DOI] [PubMed] [Google Scholar]
- Ritz R, Sejnowski TJ. Synchronous oscillatory activity in sensory systems: new vistas on mechanisms. Curr Opin Neurobiol. 1997;7:536–46. doi: 10.1016/s0959-4388(97)80034-7. [DOI] [PubMed] [Google Scholar]
- Samsonovich AV, Ascoli GA. A simple neural network model of the hippocampus suggesting its pathfinding role in episodic memory retrieval. Learn Mem. 2005;12:193–208. doi: 10.1101/lm.85205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadlen MN, Newsome WT. Noise, neural codes and cortical organization. Curr Opin Neurobiol. 1994;4:569–79. doi: 10.1016/0959-4388(94)90059-0. [DOI] [PubMed] [Google Scholar]
- Singer W, Gray CM. Visual feature integration and the temporal correlation hypothesis. Annu Rev Neurosci. 1995;18:555–86. doi: 10.1146/annurev.ne.18.030195.003011. [DOI] [PubMed] [Google Scholar]
- Softky WR, Koch C. The highly irregular firing of cortical cells is inconsistent with temporal integratrion of random EPSPs. J Neurosci. 1993;13:334–350. doi: 10.1523/JNEUROSCI.13-01-00334.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stevens CF, Zador AM. Input synchrony and the irregular firing of cortical neurons. Nat Neurosci. 1998;1:210–217. doi: 10.1038/659. [DOI] [PubMed] [Google Scholar]
- Svirskis G, Rinzel J. Influence of temporal correlation of synaptic input on the rate and variability of firing in neurons. Biophys J. 2000;79:629–37. doi: 10.1016/S0006-3495(00)76321-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Treves A. Learning to predict through adaptation. Neuroinformatics. 2004;2:361–6. doi: 10.1385/NI:2:3:361. [DOI] [PubMed] [Google Scholar]
- Vazdarjanova A, Guzowski JF. Differences in hippocampal neuronal population responses to modifications of an environmental context: evidence for distinct, yet complementary, functions of CA3 and CA1 ensembles. J Neurosci. 2004;24:6489–96. doi: 10.1523/JNEUROSCI.0350-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallenstein GV, Eichenbaum H, Hasselmo ME. The hippocampus as an associator of discontiguous events. Trends Neurosci. 1998;21:317–23. doi: 10.1016/s0166-2236(97)01220-4. [DOI] [PubMed] [Google Scholar]
- Wei F, Xu ZC, Qu Z, Milbrandt J, Zhuo M. Role of EGR1 in hippocampal synaptic enhancement induced by tetanic stimulation and amputation. J Cell Biol. 2000;149:1325–34. doi: 10.1083/jcb.149.7.1325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Witter MP, Amaral DG. Hippocampal Formation. In: Paxinos G, editor. The Rat Nervous System 3rd ed. Academic Press; 2004. pp. 635–704. [Google Scholar]