Abstract
There is growing body of research devoted to designing imaging-based biomarkers that identify Alzheimer’s disease (AD) in its prodromal stage using statistical machine learning methods. Recently several authors investigated how clinical trials for AD can be made more efficient (i.e., smaller sample size) using predictive measures from such classification methods. In this paper, we explain why predictive measures given by such SVM type objectives may be less than ideal for use in the setting described above. We give a solution based on a novel deep learning model, randomized denoising autoencoders (rDA), which regresses on training labels y while also accounting for the variance, a property which is very useful for clinical trial design. Our results give strong improvements in sample size estimates over strategies based on multi-kernel learning. Also, rDA predictions appear to more accurately correlate to stages of disease. Separately, our formulation empirically shows how deep architectures can be applied in the large d, small n regime — the default situation in medical imaging. This result is of independent interest.
1 Introduction
Alzheimer’s disease (AD) affects over 20 million people worldwide, and in the last decade, efforts to identify biomarkers for AD have intensified. There is now broad consensus that the disease pathology manifests in the brain images years before the onset of AD. Various groups have adapted sophisticated machine learning methods, to learn patterns of pathology by classifying healthy controls from AD subjects. The success of these methods (which obtain over 90% accuracy [16]) has led to attempts at more fine grained classification tasks, such as separating controls from Mild Cognitively impaired (MCI) subjects and even identifying which MCI subjects will go on to develop AD [14,7]. Even in this difficult setting, multiple current methods have reported over 75% accuracy. While accurate classifiers are certainly desirable, one may ask if they address a real practical need — if no treatments for AD are currently available, is AD diagnosis meaningful? To this end, [9,6] showed the utility of statistical learning methods beyond diagnosis/prognosis; they can in fact be leveraged for designing efficient clinical trials for AD. The basic strategy here uses imaging data from two time points (i.e., TBM data or hippocampus volume change), and derives a machine learning based biomarker. Based on this measure, the top one–third quantile subjects may be selected to be included in the trial. Using this “enriched” cohort, the drug effect can then be detected with higher statistical power with far fewer subjects, making the trial more cost effective and far easier to setup/conduct.
In this work, we ask if machine learning models can play a more fundamental role. Consider a trial where participants are randomly assigned to treatment (intervened) and placebo (non-intervened) groups, and the goal is to quantify any drug effect. Traditionally, this effect is quantified based on a “primary” outcome, like cognitive measure or brain atrophy. If the distributions of this outcome for the two groups are statistically different, we conclude that the drug is effective. When the effects are subtle, the number of subjects required to see statistically meaningful differences can be huge, making the trial infeasible. Instead, one may derive a “customized outcome” (i.e., a continuous predictor) from a statistical machine learning model. Here, the system assigns predictions based on probabilities of class membership (no enrichment is used). If these customized predictions are statistically separated (classification is a special case), it directly implies that potential improvements in power and the efficiency of the trial are possible. This paper is focused on designing specialized learning architectures towards this final objective. In principle, any machine learning method should be appropriate for the above task. But it turns out that high statistical power in these experiments is not merely a function of the classification accuracy of the model, rather the conditional entropy of the outputs (prediction variables) from the classifier at test time. An increase in classifier accuracy does not directly reduce the variance in the predictor (from the learnt estimator). Therefore, SVM type methods are applicable, but significant improvements are possible by deriving a learning model with the concurrent goals of classifying the stages of dementia as well as ensuring small conditional entropy of the outcomes.
Our contributions
We achieve these goals by proposing a novel learning model based on deep learning. Deep architectures are non-parametric learning models [1,3] that have received much interest in machine learning and computer vision recently. Although powerful, it is well known that they require very large amounts of unsupervised data, which is infeasible in neuroimaging, where the dimensionality d of the data is always much larger than the number of instances (n). A naïve use of off-the-shelf deep learning models on neuroimaging data expectedly yields poor performance. In the last few months, however, independent of our work, deep learning methods have been used successfully in structural and functional neuroimaging [12,5,10]. To get around the difficulty highlighted above, [12] uses a region of interest approach whereas [5,10] sub-samples each data instance to increase n. Our work provides a mechanism where no such adjustments are necessary. The key contributions of this paper include (a) Scalable deep architecture(s) for learning problems in neuroimaging where number of data instances is much smaller than the data dimensionality (i.e., our models permit whole–brain analysis) and (b) An imaging derived continuous measure with smaller variance that leads to efficient AD clinical trials with moderate sample sizes (and based only on one time–point data).
2 Model
2.1 Stacked Denoising Autoencoders (SDA)
We motivate our formulation by highlighting the difficulty in using stacked denoising autoencoders (SDA) [1,3] directly in the n ≪ d regime. An autoencoder is a single layer neural network that learns robust distributed representations of the input data. A denoising autoencoder (DA) constructs these representations by stochastically corrupting the inputs. Denoting the d dimensional inputs by , a DA outputs hi = σ(Wxi+p) (σ is a point–wise sigmoid) by minimizing the loss ℒ(․) between the input and its reconstruction x̂i = σ(WThi + q) as,
| (1) |
where γ(․) is the point–wise stochastic corruption [1]. A stacked denoising autoencoder (SDA) greedily concatenates L(> 1) DAs, i.e., lth layer outputs are the un–corrupted inputs for (l + 1)th layer,
| (2) |
where θ denotes the full set of stochastic gradient (SG) learning parameters (corruption rate, learning rate, hidden layer length). The transformations serve as a warm–start for supervised tuning where one compares the output of the Lth layer to . This greedy layer–wise unsupervised training followed by supervised fitting is central to most deep architectures [3,1].
Recall that SG learning is expected to converge to a local minimum only in the asymptotic setting (of large n). Hence, the warm–start described above is only reliable when large amounts of unsupervised data are available, which is the case in computer vision but not in neuroimaging. Otherwise, the network overfits whenever d is much larger than n. In neuroimaging, d is generally on the order of millions (number of voxels) and n < 1000. Hence, traditional SDAs cannot be directly used (they will generalize poorly). Recent work uses deep architectures in neuroimaging either by reducing d (using anatomical ROIs or feature selective) or increased n (splitting a data instance using sets of 2D slices) [12,5,10]. Nonetheless, frameworks to perform whole–brain analysis (the de-facto input when SVMs are used for brain image classification) will yield improvements by exploiting 3D local neighborhood dependencies directly.
2.2 Randomized Denoising Autoencoders (rDA)
In Section 1, we motivated the task of concurrently optimizing two goals. Our system should be able to capture differences across different dementia stages (i.e., controls, MCI, AD) while at the same time keeping intra-stage prediction variance as small as possible. In other words, we seek to decrease the prediction variance at no cost of approximation bias. Although, these seem like competing requirements, it turns out that this behavior is exactly what is offered by ensemble learning [2]. Recall that Ensembles are bootstrap randomizations around sets of weak learners which reduce the prediction variance in expectation. So, properly incorporating an ensemble approach within a deep architecture should yield the behavior we expect. We can generate the ensembles for a given learner in multiple ways [2] — a randomization over the number of features and/or data instances. Here, we already have n ≪ d, so randomization over n is infeasible. Instead, we distribute/randomize over the dimensions d where each weak learner will correspond to a SDA. This randomization allows a single SDA weak learner to process pathologically correlated voxels across 3D local neighborhoods while still operating on the whole-brain image. Unlike the SVM objective which has a global optimum, SDAs can only converge to a local optimum via SG [1].We compensate for this by including a second level of randomization that samples sets of hyperparameters from a given hyper–parameter space. This basic structure drives the performance of our randomized denoising autoencoder (rDA).
Let 𝒱 = {1, ⋯, d} denote the indices of dimensions/voxels, and τ (υ), a distribution over υ ∈ 𝒱. In the simplest case, this can be a uniform distribution. We generate a bootstrap sample of B “blocks” where each block corresponds to input data along sb dimensions/voxels (length of the block, fixed a priori). The mapping between voxels and blocks is given by τ (υ). Note that blocks may not be mutually exclusive (a voxel may belong to multiple blocks). Each block will be presented to T weak learners. Each of these weak learners correspond to a unique θt ∈ Θ for t = 1, …, T where Θ is the given hyper–parameter space. This means that each sample from the hyper-parameter space yields a weak learner. Our weak learner module is a L-layered stacked denoising autoencoder (SDA). The overall rDA architecture is an ensemble of B × T SDAs. Alg. 2.2 summarizes the block–wise training of rDA. Given training data as , we first learn the transformations . Denoting the Lth layer outputs by , the weighted regression pooling gives
| (3) |
where U are the regression coefficients and λ is the regularization constant. z is the known weight vector on B × T estimated Lth layer outputs. [[·]] denotes column–wise concatenation. The prediction for a new test input x is
| (4) |
The simplest choice for the block–wise sampler τ (υ) (i.e., at b = 1) assigns uniform probability over all dimensions/voxels. However, we can assign large weights on local neighborhoods which are more sensitive to dementia progression, if desired. Since d is large, we modify τ (υ) after each iteration (Reweigh step in Alg. 2.2) to prevent starvation of the previously unsampled dimensions. We can also setup τ (·) based on entropy or the result of a hypothesis test. Each weak learner output is an estimate of y. Recall that SG learning is sensitive to the choice of hyper–parameters θt, particularly, the number of epochs and gradient learning rate influences the range and variance of these estimates [1,3]. Hence, randomization over θt mitigates this dependency by averaging over T such estimates for each block (i.e., set of dimensions/voxels). We can pool the block estimates via various means – average, using a ridge regression or other sophisticated schemes. But since SDAs are already capable of learning complex concepts [1], we use a simple linear combination with ℓ2-loss providing minimum mean squared error. This addresses our goal of reducing the stochastic error of final predictions. Observe that rDA extends easily to multi–modal inputs by first constructing individual blocks for each modality and pooling across all modalities.
Algorithm.
rDA Blocks training
| Input: θt ~ Θ, 𝒱, B, sB, L, T, | |
|
Output:
| |
| for b = 1, …, B do | |
| Ib ~ τ (𝒱) | |
| for t = 1, …, T do | |
| end for | |
| τ (𝒱) ← Reweigh (τ (𝒱), Ib) | |
| end for |
The sigmoid non–linearity ensures that rDA outputs are in ∈ [0, 1]. By labeling healthy controls as 1 and AD subjects as 0, we can then project the dementia scale to [0, 1]. The pooled outputs, referred to as rDA measure (rDAm), are then imaging–derived continuous predictors. We can then compute the sample sizes using rDAm as a customized outcome [11]. Denoting the mean change of rDA for placebo and treatment groups by μp and μt respectively, the number of subjects per arm is given by 2(Zα/2+Z1−β)2σ2/(μp−μt)2 where 1−β is the desired power at significance level α. Using a conversion rate of ρ ∈ [0, 1] from MCI to AD, and inducing a drug effect of η (i.e., the treatment decreases the mean change by a fraction η), the sample size expression then simplifies to 2c2(Zα/2+Z1−β)2/(ηρ)2 where c = σ/μ is the coefficient of variation. Since we only use one time–point data, the proportion ρ is set based on information from previously reported studies [13] Since rDA is an ensemble designed to reduce the prediction variance (and hence c), we hope to see much smaller sample sizes compared to others.
3 Evaluations
3.1 Data and Setup
We used Amyloid, FDG–PET and MRI data at baseline for 447 subjects (210 male, 237 female) from ADNI2 (Alzheimer’s Disease Neuroimaging Initiative). 131 were healthy (CN), 92 were demented (AD), 120 and 104 had early and late MCI (EMCI and LMCI) respectively. The labeling of EMCI and LMCI (done by ADNI) is based on the cognitive status of each subject. Of the 224 MCIs, 100 had maternal family history (FH) of AD, 52 had paternal and 23 had both. Pre-processing included extracting grey matter in normalized space, and correcting PET for average intensities in ponsvermis (FDG) and cerebellum (Amyloid). We train rDA on ADs (labeled 0) and CNs (labeled 1) alone, and test on MCIs. We use a multi-modal (MKL) ε–support vector regression (εMKm) as the baseline learning model [7]. Firstly, we evaluate if rDAm differentiates EMCI from LMCI. Additionally, we evaluated parental family history as a contributing risk factor. Since rDAm is a continuous marker, its correlations with CSF levels –τ, pτ, Aβ, τ/Aβ and pτ/Aβ (τ: τ-protein, pτ: phospho τ-protein, Aβ: Amyloid-β, are the cerebrospinal fluid protein levels, and very sensitive biomarkers of AD) are also assessed to verify if it is meaningful. We then estimate sample sizes using MCI to AD conversion rate of 37.7% [13]. rDA hyper-parameters in our experiments are L = 2, B = 1000 and T = 9, with uniform weighting (i.e., ).
3.2 Results and Discussion
Table 1(a) and (b) show that rDAm is highly sensitive to EMCI vs. LMCI and the influence of FH. Although the baseline εMKm picks up these group differences, rDAm has much higher delineation power. In particular, the p–values for rDAm for FH positive vs. negative case are an order of magnitude smaller than that of εMKm. These show that rDAm is at least as good as a current state-of-the-art machine learning derived measures. Table 2 shows that rDAm has significant correlation (higher than εMKm in all but two cases) to CSF levels, which are proven biomarkers for MCI to AD progression [15]. Note that a negative correlation with say τ implies that rDAm decreases and the subject gets demented as τ increases. Specifically, higher correlations (with p ≤ 0.01) with pτ and pτ/Aβ suggest that rDAm is a useful continuous predictor. In most cases, these significance levels increase as more modalities are combined.
Table 1.
Performance of rDAm vs. εMKm in delineating MCI sub–groups. A : Amyloid, F : FDG and T : T1GM. Each cell shows the ANOVA p–value and corresponding F–statistic.
| Model | Amyloid | FDG | T1GM | A+F | A+T | F+T | A+F+T |
|---|---|---|---|---|---|---|---|
| (a) Early versus Late MCI | |||||||
| MKL | < .001, 20.5 | < .001, 16.8 | < .001, 16.5 | < .001, 16.4 | < .001, 20.4 | ≪ .001, 23.6 | ≪ .001, 27.9 |
| rDA | ≪ .001, 22.1 | .001, 9.7 | < .001, 20.0 | < .001, 19.5 | ≪ .001, 24.1 | ≪ .001, 21.2 | ≪ .001, 27.6 |
| (b) Family History Positive versus Negative | |||||||
| MKL | 0.04, 4.3 | 0.007, 7.5 | 0.02, 5.3 | 0.007, 7.3 | 0.009, 6.8 | 0.01, 6.6 | 0.004, 8.3 |
| rDAm | 0.03, 4.7 | < .001, 11.8 | < .001, 11.2 | 0.009, 6.8 | < .001, 12.4 | < .001, 13.2 | < .001, 13.3 |
Table 2.
Correlation of CSF levels to rDAm vs. εSm. Note that Amyloid is used as reference modality here. Each cell represents the Spearman correlation p–value and the coefficient for the corresponding marker.
| CSF | Marker | Amyloid | A+F | A+T | A+F+T | ||||
|---|---|---|---|---|---|---|---|---|---|
| τ | εMKm | 0.01 | −0.24 | 0.04 | −0.20 | 0.14 | −0.15 | 0.15 | −0.15 |
| rDAm | 0.002 | −0.31 | 0.01 | −0.25 | 0.09 | −0.17 | 0.11 | −0.16 | |
| pτ | εMKm | < 0.001 | −0.40 | < 0.001 | −0.37 | 0.01 | −0.27 | 0.008 | −0.28 |
| rDAm | < 0.001 | −0.39 | < 0.001 | −0.36 | 0.008 | −0.27 | 0.009 | −0.28 | |
| Aβ | εMKm | 0.01 | 0.24 | 0.09 | 0.17 | 0.29 | 0.11 | 0.38 | 0.09 |
| rDAm | 0.03 | 0.22 | 0.03 | 0.23 | 0.44 | 0.08 | 0.37 | 0.09 | |
| τ/Aβ | εMKm | 0.004 | −0.29 | 0.01 | −0.27 | 0.15 | −0.15 | 0.14 | −0.15 |
| rDAm | < 0.001 | −0.35 | 0.007 | −0.28 | 0.08 | −0.18 | 0.11 | −0.16 | |
| pτ/Aβ | εMKm | 0.001 | −0.41 | 0.001 | −0.37 | 0.01 | −0.25 | 0.01 | −0.25 |
| rDAm | < 0.001 | −0.42 | < 0.001 | −0.37 | 0.01 | −0.26 | 0.01 | −0.26 | |
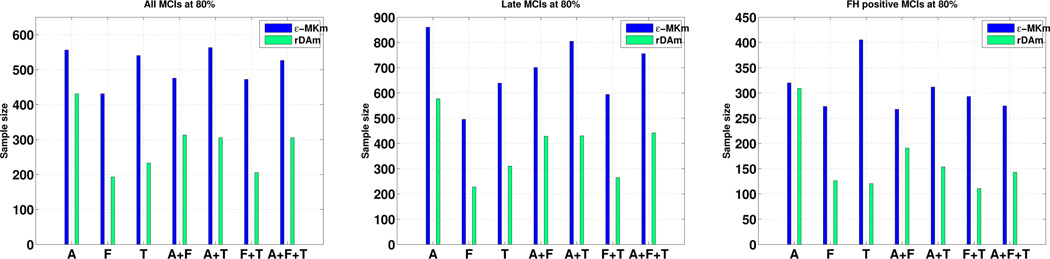
Table 3 shows that the coefficient of variation (CV) of rDAm for three different populations of interest – all MCIs, LMCIs and MCIs with positive FH. Observe that rDAm’s CV is smaller than that of εMKm for all three populations, and all possible combinations of modalities – making it a better candidate to be used as a prediction measure. Also, the CVs for MCIs with positive FH are smaller than that of late MCIs. This also suggests that a significant number of late MCIs currently have only a mild dementia in terms of rDAm. Fig. 1 shows the estimates on the same three populations of interest as above at 80% power (Refer to the supplement for more plots). Following Table 3, it should be straight forward to expect smaller sample estimates for rDAm compared to εMKm, which is exactly the case as shown in Fig. 1. Particularly, FDG and MRI gave smaller estimates than that of Amyloid following their smaller CV, reflecting that ~ 30% of healthy elderly have positive Amyloid scans. FH positive MCIs (last plot in Fig. 1) lead to much smaller sizes compared to using all MCIs and late MCIs. To get a sense of the improvement with respect to non–imaging based markers, we compared the best estimate (over all modalities) of εMKm and rDAm with that of MMSE and CSF levels in Table 4. At 80% power, the best estimates across CSF markers was 973 and 975 (for τ and τ/Aβ respectively) compared to that of 193 using rDAm – more than 5–fold decrease. It should be noted that all these estimates use only “single time–point” data combined with known conversion rates, in contrast to direct longitudinal measurement [8,4]. Hence, the sizes using MMSE and CSF are as high as 1500, indicating that estimates on the order of two hundred (that of rDAm) are highly significant. Overall, the results show that imaging–derived markers lead to much smaller trials than cognitive scores and/or CSF levels.
Table 3.
CV of rDAm vs. εMKm.
| Modality | Marker | MCIs | LMCIs | FHMCIs |
|---|---|---|---|---|
| Amyloid | εMKm | 0.56 | 0.70 | 0.42 |
| rDAm | 0.49 | 0.57 | 0.41 | |
| FDG | εMKm | 0.49 | 0.53 | 0.39 |
| rDAm | 0.33 | 0.36 | 0.26 | |
| T1MRI | εMKm | 0.55 | 0.60 | 0.48 |
| rDAm | 0.36 | 0.42 | 0.26 | |
| A+F | εMKm | 0.52 | 0.63 | 0.39 |
| rDAm | 0.42 | 0.49 | 0.33 | |
| A+T | εMKm | 0.56 | 0.67 | 0.42 |
| rDAm | 0.41 | 0.49 | 0.29 | |
| F+T | εMKm | 0.51 | 0.58 | 0.41 |
| rDAm | 0.34 | 0.38 | 0.25 | |
| A+F+T | εMKm | 0.54 | 0.65 | 0.39 |
| rDAm | 0.41 | 0.50 | 0.28 | |
Fig. 1.
Sample estimates per arm for rDAm vs. εMKm using all MCIs, LMCIs and FH positive MCIs respectively, at 80% power and 0.05 significance level. Conversion rate is 37.7%, and the induced drug effect is 0.25. Refer to supplement for 85% and 90% plots. εMKm is blue and rDAm is green.
Table 4.
Best rDAm and εMKm sample estimates perm arm (from Fig. 1) vs. MMSE and CSF levels.
| Power | MMSE | τ | pτ | Aβ | τ/Aβ | pτ/Aβ | εMKm | rDAm |
|---|---|---|---|---|---|---|---|---|
| 80% | > 2500 | 973 | 1447 | > 2500 | 975 | > 2000 | 431 | 193 |
| 85% | > 2500 | 1117 | > 1500 | > 2500 | 1120 | > 2500 | 495 | 221 |
| 90% | > 2500 | 1303 | > 1500 | > 2500 | 1306 | > 2500 | 577 | 258 |
4 Conclusions
We propose a novel deep learning architecture, randomized denoising autoencoders, that scales to very large dimensions and learns from a small number of instances. We construct a continuous predictor based on rDA and show that not only does it have high correspondence with other markers of AD, but also leads to efficient clinical trials with much smaller sample estimates.
Supplementary Material
Acknowledgments
This work was supported in part by NIH R01 AG040396; NSF CAREER award 1252725; Wisconsin Partnership proposal; UW ADRC P50 AG033514; UW ICTR 1UL1RR025011 and a VA Merit review grant I01CX000165. The contents do not represent views of the Dept. of Veterans Affairs or the US Government.
References
- 1.Bengio Y. Learning deep architectures for AI. Foundations and Trends in Machine Learning. 2009;2:1–127. [Google Scholar]
- 2.Dietterich TG. Machine-learning research. AI magazine. 1997;18(4):97–136. [Google Scholar]
- 3.Erhan D, Bengio Y, Courville A, Manzagol PA, Vincent P, Bengio S. Why does unsupervised pre-training help deep learning? JMLR. 2010;11:625–660. [Google Scholar]
- 4.Grill JD, Di L, Lu PH, Lee C, Ringman J, Apostolova LG, et al. Estimating sample sizes for predementia Alzheimer’s trials based on the Alzheimer’s Disease Neuroimaging Initiative. Neurobiology of aging. 2013;34:62–72. doi: 10.1016/j.neurobiolaging.2012.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gupta A, Ayhan M, Maida A. Natural image bases to represent neuroimaging data; Proceedings of the 30th ICML; 2013. pp. 987–994. [Google Scholar]
- 6.Hinrichs C, Dowling N, Johnson S, Singh V. Mkl-based sample enrichment and customized outcomes enable smaller ad clinical trials. In: Langs G, Rish I, Grosse-Wentrup M, Murphy B, editors. MLINI, LNCS. Vol. 7263. Berlin Heidelberg: Springer; 2012. pp. 124–131. [Google Scholar]
- 7.Hinrichs C, Singh V, Xu G, Johnson SC. Predictive markers for AD in a multi-modality framework: an analysis of MCI progression in the ADNI population. Neuroimage. 2011;55:574–589. doi: 10.1016/j.neuroimage.2010.10.081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Holland D, McEvoy LK, Dale AM. Unbiased comparison of sample size estimates from longitudinal structural measures in ADNI. Human brain mapping. 2012;33(11):2586–2602. doi: 10.1002/hbm.21386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kohannim O, Hua X, Hibar DP, Lee S, Chou YY, Toga AW, Jack CR, Jr, Weiner MW, Thompson PM. Boosting power for clinical trials using classifiers based on multiple biomarkers. Neurobiology of aging. 2010;31:1429–1442. doi: 10.1016/j.neurobiolaging.2010.04.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Plis SM, Hjelm DR, Salakhutdinov R, Calhoun VD. Deep learning for neuroimaging: a validation study. arXiv preprint arXiv:1312.5847. 2013 doi: 10.3389/fnins.2014.00229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sakpal TV. Sample size estimation in clinical trial. Perspectives in clinical research. 2010;1(2):67–69. [PMC free article] [PubMed] [Google Scholar]
- 12.Suk HI, Shen D. Deep learning-based feature representation for ad/mci classification. In: Mori K, Sakuma I, Sato Y, Barillot C, Navab N, editors. MICCAI, LNCS. Vol. 8150. Berlin Heidelberg: Springer; 2013. pp. 583–590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Tatsuoka C, Tseng H, Jaeger J, Varadi F, Smith MA, Yamada T, et al. Modeling the heterogeneity in risk of progression to Alzheimer’s disease across cognitive profiles in mild cognitive impairment. Alzheimers Res Ther. 2013;5:14. doi: 10.1186/alzrt168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Teipel SJ, Born C, Ewers M, Bokde AL, Reiser MF, Möller HJ, Hampel H. Multivariate deformation-based analysis of brain atrophy to predict Alzheimer’s disease in mild cognitive impairment. Neuroimage. 2007;38:13–24. doi: 10.1016/j.neuroimage.2007.07.008. [DOI] [PubMed] [Google Scholar]
- 15.Vemuri P, Wiste H, et al. MRI and CSF biomarkers in normal, MCI, and AD subjects predicting future clinical change. Neurology. 2009;73(4):294–301. doi: 10.1212/WNL.0b013e3181af79fb. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zhang D, Wang Y, Zhou L, et al. Multimodal classification of Alzheimer’s disease and mild cognitive impairment. Neuroimage. 2011;55(3):856–867. doi: 10.1016/j.neuroimage.2011.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.