Abstract
Visualization and mapping of function on the cortical surface is difficult because of its sulcal and gyral convolutions. Methods to unfold and flatten the cortical surface for visualization and measurement have been described in the literature. This makes visualization and measurement possible, but comparison across multiple subjects is still difficult because of the lack of a standard mapping technique. In this paper, we describe two methods that map each hemisphere of the cortex to a portion of a sphere in a standard way. To quantify how accurately the geometric features of the cortex – i.e., sulci and gyri – are mapped into the same location, sulcal alignment across multiple brains is analyzed, and probabilistic maps for different sulcal regions are generated to be used in automatic labelling of segmented sulcal regions.
Keywords: Brain, Cortex, MRI, Mapping, Flattening, Conformal mapping, Partially flattened maps, Mean curvature, Sulci labelling
1. Introduction
Understanding the relationship between the structure and function of the human brain cortex is a primary goal in human brain mapping. Visualization and localization of function on the cortical surface, however, is difficult because of the extensive sulcal and gyral convolutions and their variability between individuals. Cortical unfolding procedures expose the buried folds of cortical gray matter, to reveal the entire structure of part or all of the cortex on a flat, convex, or radial surface (Carman et al., 1995; Drury et al., 1996; Wandell et al., 1996; Hurdal et al., 1999; Angenent et al., 1999; Fischl et al., 1999; Timsari and Leahy, 2000; Tosun and Prince, 2001; Grossmann et al., 2002). Preservation of the metric details – i.e., creation of approximately isometric maps – of the 3D surface has been a major goal in flattening (Fischl et al., 1999; Carman et al., 1995; Drury et al., 1996; Timsari and Leahy, 2000; Grossmann et al., 2002). With these maps, visual assessment and measurements of geometric relationships – e.g., distances, angles, areas – are similar to the original surface. Because it is impossible to generate an exact isometric map from the convoluted cortical surface, several mapping approaches use “cuts” in the surface, which are generally made manually (Fischl et al., 1999). This makes it difficult to establish a “standard” coordinate system for cortical mapping because the shape of the final map is dependent on the cut that is made.
A more recent goal in cortical unfolding is to create maps that are in a standardized coordinate system, in the sense that they put known anatomical features – e.g., sulci and gyri – at the same coordinates in the mapped space (MacDonald et al., 2000; Thompson et al., 2000; Gu et al., 2003). Some methods enforce manually identified corresponding features to correspond on the computed maps (Thompson et al., 2000; Gu et al., 2003). Others derive correspondence by maintaining strict point correspondences between parametric models that are initialized and deformed in similar fashion throughout the surface estimation process (MacDonald et al., 2000).
Our long-term goal is to derive a standardized cortical map that does not require strict point correspondences throughout the estimation process and does not require manually identified landmarks. In this paper, we present a first step in this direction. Our approach combines parametric relaxation, iterated closest point registration, and conformal mapping. While no single one of these steps is new by itself, the specific implementation and combination of the methods is unique, and we also provide an extensive validation of the performance of the algorithm in providing automatic labelling of specific sulci: central, cingulate, superior frontal, and parieto-occipital.
2. Background
The visualization and mapping methods we present in this paper start with a triangle mesh representation of the human brain cortex. Overall, the general approach we use in finding such surfaces from magnetic resonance (MR) image data is described in (Xu et al., 1999), although several improvements have been incorporated, as described in (Xu et al., 2000) and (Han et al., 2001a, 2002, 2003b). In this section, we briefly describe our approach.
The cortical surface extraction starts with a three-dimensional T1-weighted SPGR volumetric axial magnetic resonance (MR) data set (Wang and Rieder, 1990). Our MR images are obtained from the Baltimore longitudinal study of aging (BLSA) (Resnick et al., 2000). A given data set comprises a volumetric SPGR series acquired axially on a GE Signa 1.5 Tesla scanner with the following parameters: TE=5, TR=35, FOV=24, flip angle=45°, slice thickness=1.5, gap=0, matrix=256×256, NEX=1. The native voxel size is 0.9375 mm×0.9375 mm×1.5 mm. The first processing step is to remove the cerebellum, extracranial tissue, and brain stem (at the level of the diencephalon) from the image data. The image volume is then resampled to obtain isotropic voxels each having size 0.9375 mm×0.9375 mm×0.9375 mm using cubic B-spline interpolation in order to make subsequent processing less sensitive to orientation.
The next step in processing this “skull-stripped” MR volume is to apply fuzzy segmentation (Pham and Prince, 1999; Pham, 2001), yielding three membership function image volumes representing the fractions of white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF) within each image voxel. The WM membership function is then processed using an algorithm that fills the ventricles and subcortical GM structures such as the putamen and the caudate nucleus with white matter (Han et al., 2001a). When an isosurface algorithm is applied to the resulting volume, the largest resulting triangle mesh surface is a close approximation to the GM/WM interface within each hemisphere, and it connects the two hemispheres across the corpus callosum at the top and through the brainstem at the bottom. (The WM filling procedure prevents the surface from traveling into the ventricles and sub-cortical gray matter.)
Although an isosurface of filled WM membership as shown in Figs. 1(a) and (b) is a good approximation to the GM/WM interface, it invariably has the wrong topology, typically having numerous handles, like those of a coffee cup, due to noise and artifacts. Since, in this paper, we are primarily concerned with mapping the cortical surface to a sphere, such topological defects are unacceptable. Therefore, a further processing of this filled WM membership function is conducted in order to obtain a topologically correct initial estimate of the cortical surface. We use a graph-based topology correction algorithm described in (Han et al., 2002) in order to further modify the WM membership function so that an isosurface algorithm produces a GM/WM estimate having the correct topology. Figs. 1(c) and (d) show two views of a topologically correct GM/WM interface.
Fig. 1.
Isosurface of filled WM membership (a) top view; (b) bottom view. Topologically correct cortical surfaces: (c) GM/WM interface top view; (d) GM/WM interface bottom view; (e) central surface top view; and (f) central surface bottom view.
Although the GM/WM interface (with correct topology) can potentially be used in surface mapping studies, we prefer to use a central surface representation. A central cortical surface lies halfway between the GM/WM and GM/CSF surfaces of the cortex. As a single surface, the central surface best represents the true geometry of the cortex itself, which is actually a thick sheet, and we have shown experimentally that it is the most reproducibly estimated among the three surfaces (GM/WM, central, and GM/CSF) (submitted to NeuroImage with a preliminary description in (Han et al., 2001b). We find the central surface using a topology-preserving geometric deformable surface model followed by an isosurface algorithm (Han et al., 2001b, 2003a,b). Figs. 1(e) and (f) show two views of a topologically correct central surface and Fig. 2 shows the contours of the same surface superposed on (skull-stripped) MR image cross sections (axial, coronal and sagittal views). It should be noted that each reconstructed central surface is a triangle mesh comprising approximately 300,000 vertices. These surfaces are the starting point for cortical unfolding, visualization and mapping, as described in the following section.
Fig. 2.

An estimated central surface displayed as contours intersecting skull-stripped MR image cross sections: (a) axial, (b) coronal and (c) sagittal.
3. Methods
Cortical unfolding procedures generally start from a triangle mesh representation of the cortical surface, as described in the preceding section. The simplest way to establish spherical coordinates on one of these surfaces is to iteratively deform the vertices of the triangle mesh until the surface is convex, at which point it can be projected to a sphere (Fischl et al., 1999; Sereno et al., 1996; Timsari and Leahy, 2000). This approach is at the heart of several published spherical mapping methods, and has the advantages of providing fine control over the full metric properties of the resulting map and producing very uniform triangle meshes. It does, however, have several difficulties. First, it is computationally intensive, particularly if the relaxed surface that projects to the sphere is expected to closely resemble a sphere. Second, although techniques can be used to encourage quasi-isometry of the resulting maps, it is not clear how to automatically encourage key anatomical features, such as gyri and sulci, to map to the same locations on the sphere from subject to subject. Third, there is considerable arbitrariness in the stopping criterion and origin at the point when the convex surface is mapped to the sphere.
Another way to establish spherical coordinates on a cortical surface is using conformal mapping (Angenent et al., 1999), which maps the convoluted brain surface to the complex plane (or sphere) while preserving relative angles, local shape, and connectivity of the triangulated surface. The conformal mapping approach, which is a direct mathematical mapping from the initial cortical surface to the sphere (see below), also has difficulties. Most notably, conformal mapping methods are very sensitive to the precise details of the triangle mesh representation of the cortical surface. Alternate triangulations that are equally valid in representing the surface can yield considerably different conformal maps, putting sulci and gyri in drastically different positions on the sphere – positions that cannot be aligned by a simple rotation of one map relative to another on the sphere. Furthermore, the precise details of the conformal mapping algorithm – most notably, the selection of the “north pole” – will yield considerably different maps even from the same triangle mesh.
The hypothesis we are testing in this paper is that a combination of the two mapping methods, which will utilize the advantageous properties of these two general approaches, will yield an overall map that will put sulci and gyri in the same locations on the sphere across subjects. The idea is to allow the initial cortical surface to partially relax, yielding a partially flattened surface, and then use conformal mapping from this partially flattened surface to yield a map on the sphere. In principle, the relaxation operator used in a surface inflation algorithm will yield a more regular triangle mesh surface that is simpler than the original cortical surface so that the conformal map will be less sensitive to the particular details of the surface mesh.
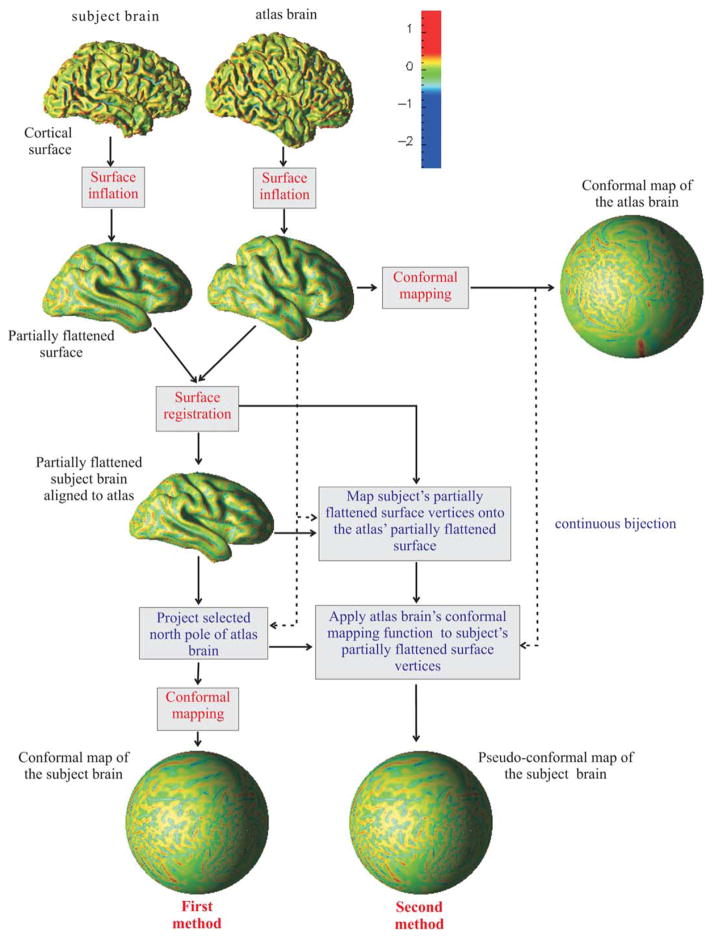
A remaining key question is whether it will be better to apply individual conformal maps, ones arising from the individual partially flattened maps, or to apply a single conformal map arising from an atlas brain and mathematically mapped to each individual brain. We have developed and compared these two methods, both of which are described within the block diagram of Fig. 3. Both methods start with a partial flattening of both a subject and an atlas brain using surface inflation, and they both end up on the sphere using conformal mapping. The specific conformal map that is used, however, is derived differently in the two methods. We now describe our implementation of each of the core algorithms comprising both of these methods – surface inflation and conformal mapping – followed by a description of the steps in Fig. 3 that link them together into unique, individual methods for cortical mapping.
Fig. 3.
Summary of proposed mapping methods. (Mean curvature of the original cortical surface is displayed.)
3.1. Surface inflation
Surface inflation has been previously utilized for visualization purposes (Fischl et al., 1999; Sereno et al., 1996). In our work, surface inflation is used as an initial step, prior to conformal mapping. By using surface inflation prior to conformal mapping, we markedly reduce the dependency on local mesh structure during conformal mapping. To obtain a more regular mesh structure, the surface mesh is smoothed using a relaxation operator (Drury et al., 1996; Timsari and Leahy, 2000); specifically, the vertices are iteratively repositioned according to
| (1) |
where Vi is the position of the ith vertex, t is the iteration number, λ∈[0,1] is a smoothing parameter, and V̄i is the average vertex position, defined as follows. Let Ni be the set of all triangles that contains vertex Vi, and let Cj and Bj be the center and area, respectively, of triangle j. Then
| (2) |
Surface inflation is a parametric surface deformation method. Our goal is to stop relaxation at the point of a partially flattened surface that should be comparable across individuals. Accordingly, we must define a stopping criterion based on the geometry of the desired final surface. The relaxation operator defined in Eqs. (1) and (2) smooths the initial surface, and mean curvature is one of the geometric features to quantify the amount of smoothing. During relaxation, however, the surface decreases in size. A global measure that quantifies the global shape of the surface and allows comparison between cortical surfaces from different individuals should be scale invariant to capture information about the shape of the surface. Our stopping criterion is based on the L2 norm of mean curvature, ||H||2 (Smith et al., 2000), which is defined as
| (3) |
where H is the mean curvature. This is a global measure of extrinsic geometry, and is minimum for a sphere.
The measure ||H||2 is approximated by discrete differential geometry operators (Meyer et al., 2002). Let κ̄i = Hini be the mean curvature normal at vertex Vi, where Hi is the mean curvature, and ni is the surface normal. The mean curvature normal κ̄i can be expressed as
| (4) |
where αij and γij are the two angles opposite to the edge in the two triangles sharing the edge (Vi,Vj), as shown in Fig. 4(a), and AVi is the surface area of the 1-ring neighborhood (Ni) of vertex Vi with piecewise linear boundaries crossing the triangle edges at their midpoints with right angle, as illustrated in Fig. 4(b).
Fig. 4.

(a) Angles opposite to the edge (Vi,Vj); (b) 1-ring neighborhood (Ni) of vertex Vi.
We stop the relaxation when ||H||2 ≤ β for a pre-selected β. The left column of Fig. 5 shows an initial cortical surface and several stages during relaxation corresponding to stopping criteria of β=3.25, β=2.5 and β=2.0. The corresponding distributions of triangle angles in the meshes are shown to the right of the figures. A regular mesh should have angles more nearly equal to 60°, which is apparently approximately satisfied by all three partially flattened maps. In order to preserve the most prominent anatomical details representing the major sulci, we have selected β=3.25 as a stopping criterion in this paper [which corresponds to Fig. 5(b)]. In future work, we expect to optimize this selection rather than using this arbitrary choice.
Fig. 5.
Surface inflation: (a) Original cortical surface, (b) ||H||2 ≤ 3.25, (c) ||H||2 ≤ 2.5 and (d) ||H||2 ≤ 2.0.
3.2. Conformal mapping
Angenent et al. (1999) proposed a way to construct a conformal flattening equivalence as the solution of a second-order elliptic partial differential equation on the 3D surface to be flattened. Solution of this partial differential equation represents an analytic procedure to map a cortical surface to the complex plane; for triangulated surfaces, a numerical procedure involving a finite element approximation can be used. We have implemented and augmented this basic approach in order to make the resulting maps more standard and have minimum metric distortion (Tosun and Prince, 2001), as we now describe.
The left and right cortical hemispheres are identified by defining a cut around the corpus callosum, as shown in Fig. 6(a) (the red path). This is done automatically using knowledge of the locations of the anterior and posterior commissures (the AC and PC points), which are previously identified for Talairach registration (Talairach and Tournoux, 1988). The line through the AC and PC points is aligned with a vertical line parallel to the y-axis (points from the tip of the patient’s nose to the back of his/her head) during resampling of the MR image volume to obtain isotropic voxels. This line defines the location of the “mid-sagittal” vertical plane. The vertices of triangles cut by the mid-sagittal plane form the hemispherical cut path around the corpus callosum. A fixed north pole is required for conformal mapping using the method of (Angenent et al., 1999). The north pole point is chosen automatically on the top of the corpus callosum, in a triangle adjacent to the hemispherical cut path and equidistant to the AC and PC points, as shown in Fig. 6(a) (yellow point). The entire surface (both hemispheres) are then mapped to the complex plane using the technique described in (Angenent et al., 1999). Fig. 6(b) shows the resulting locations of the triangle mesh vertices on the complex plane. The vertices coinciding with the hemispherical cut path are shown in red. The north pole point is mapped to the point at infinity of the extended complex plane.
Fig. 6.

(a) Hemispherical cut path colored by red on the original surface with the north pole point marked by yellow, (b) the original flat map and (c) the spherical map (scaled for display purposes). Hemispherical cut path (red); left cortical hemisphere (blue); right cortical hemisphere (green); North pole point (yellow).
Points on the complex plane can be mapped onto the unit sphere surface using the inverse stereographic projection, given by
| (5) |
where w2=u2+v2, and u and v represent the real and imaginary coordinates of a point in the complex plane. This transformation yields points on the unit sphere (with the north pole removed). A simple way to picture this operation is to imagine a unit sphere sitting on the complex plane with its south pole on the origin and its north pole pointing straight up, out of the plane, as illustrated by Fig. 7. All points are mapped to the sphere by connecting the point itself to the north pole of the sphere with a line segment, and the point where the line segment intersects the sphere surface is the mapped point. The north pole of the unit sphere is identified with the point at infinity of the extended complex plane, for completeness. The inverse stereographic projection is conformal, so the combined process yields a conformal map from the cortex to the sphere.
Fig. 7.

Illustration of the inverse stereographic projection.
Although it is possible to directly map the points on the complex plane produced by Angenent’s method to the sphere using inverse stereographic projection, it is also possible to take advantage of certain remaining flexibilities in the steps leading up to the inverse stereographic projection and in the projection process itself to yield more standard maps with smaller metric distortion and consistent orientation. Furthermore, we can move the sphere to which we map in order to yield separate hemispherical maps of the cortical hemispheres, each of which can be conformal to a partial sphere, yet having even smaller metric distortion than the complete spherical map. These steps are important in the production of a standard map that puts sulci and gyri from different brains into similar positions on the spherical or hemispherical maps. We will refer to either the spherical map or the hemispherical map as the final map when such generality is permitted in the following discussion.
Our spherical map is designed to map each hemisphere of the brain to one half of the sphere such that the hemispherical cut maps to a great circle, as shown in Fig. 6(c). It is also designed to be consistently oriented and appropriately scaled. By “consistently oriented”, we mean that the anterior part of the brain corresponds to the upper (positive y) part of the sphere and the posterior part of the brain corresponds to the lower (negative y) part of the sphere. Also, the left hemisphere should correspond to the left (negative x) part of the sphere and the right hemisphere should correspond to the right (positive x) part of the sphere. The map is also designed to distribute the points on the sphere such that the area distortion between the original cortical surface and the final map is minimized.
Two steps are required in order to map the hemispherical cut path to a great circle in the center of the unit sphere. First, we must define a south pole point on the brain along the hemispherical cut path, which will correspond to the south pole of the sphere. The south pole point is defined as the point on the hemispherical cut path with the maximum geodesic distance (cf. Rettmann et al., 2002) from the north pole point. All points on the complex plane are then translated so that the south pole point maps to the complex origin. Second, the points on the complex plane must be rotated such that the points to which the hemispherical cut path maps are oriented along the imaginary axis and anterior corresponds to the positive imaginary axis. This step guarantees that the anterior/ posterior orientation is correct. If necessary, in order to obtain the appropriate left/right orientation, the points on the complex plane are then reflected left-to-right to make the right hemisphere map to the half-plane corresponding to the positive real numbers. The distribution of the points on the sphere can be modified by uniformly scaling the magnitude of the points on the complex plane, leading to different stereographic projections. The one with the minimum area distortion with respect to the original surface (which is described below) will be the final map on the spherical surface.
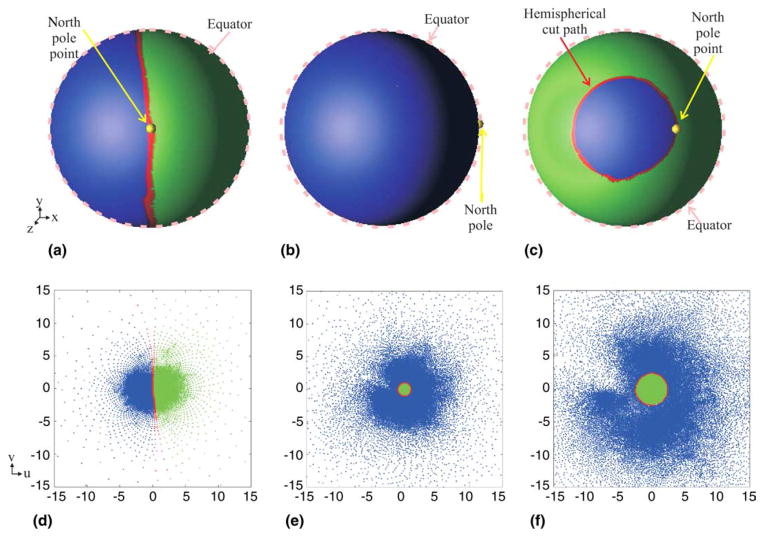
Imagine rotating the unit sphere 90° about the y-axis so that the hemispherical cut path will be mapped to the equator of the unit sphere instead of a great circle through its equator, as illustrated in Figs. 8(a) and (b). This rotation facilitates a unified presentation of both spherical mapping and hemispherical mapping, in which the points on the hemispherical cut path fall on a horizontal circle within the sphere that is not necessarily the equator, as shown in Fig. 8(c). Defining θ as the angle off the z-axis, then this circle is defined by the angle any point on the circle makes with the z-axis, and the center of the circle is defined by the point (0,0,cosθ). For the spherical map, θ=90°, while in a hemispherical map, 0<θ<90°. With reference to Fig. 7, it is not hard to see that the radius of the hemispherical cut path in the complex plane should be r = 2sinθ/(1−cosθ) (centered at the origin), as shown in Figs. 8(e) and (f).
Fig. 8.
(a) The original spherical map, (b) the spherical map after 90° rotation about the y-axis, (c) one of the hemispherical maps, and (d)–(f) the corresponding maps on the complex plane. Hemispherical cut path (red); left cortical hemisphere (blue); right cortical hemisphere (green); north pole point (yellow).
In a hemispherical map, the circumference of the circle to which the hemispherical cut maps is smaller than that on a spherical map. Also, one hemisphere of the cortex occupies a larger portion of the sphere than the other. It is intuitively clear that cortical distances will be better represented on a hemispherical map of the brain hemisphere that maps to the large portion of the sphere. It is logical that the area distortion would be smaller on this map as well. Accordingly, this larger map yields a hemispherical map for a given brain hemisphere, and the second hemispherical map can be computed by rotating the sphere 180° around the y-axis.
These steps, except the left-to-right reflection, can be undertaken using a single transformation in the complex plane called the Möbius transformation (Needham, 2000). A Möbius transformation is a linear fractional function M given by
where {a,b,c,d} are the coefficients of the Möbius transformation, ad−bc ≠0, {a, b, c, d} ∈
 , and {z, z′} ∈
, and {z, z′} ∈
 , where
, where
 is defined as the complex plane. The transformation is analytic on
is defined as the complex plane. The transformation is analytic on
 \ {−d/c} and is one-to-one and conformal there. The transformation can be extended to the entire extended complex plane (Riemann sphere)
\ {−d/c} and is one-to-one and conformal there. The transformation can be extended to the entire extended complex plane (Riemann sphere)
 ∪ {∞} by defining
∪ {∞} by defining
Every Möbius transformation defines a one-to-one conformal mapping of a Riemann sphere to itself, and the composition of a conformal flattening with a Möbius transformation is still conformal. A Möbius transformation maps extended circles onto extended circles which is determined by three points and ∞ can be one of these points. Accordingly, it is completely determined by its values at three distinct points. The required translation, rotation and scaling can be used to select these three points, and the points they will be mapped to determine the a, b, c and d coefficients of the Möbius transformation we are interested in.
Consider the following particular Möbius transformation:
| (6) |
where {r} ∈ ℝ and {ρ, s} ∈
 are the coefficients of the Möbius transformation, where ℝ is the set of real numbers. Eq. (6) performs a translation, rotation and scaling using the term ρ(z−s) (transforming Fig. 6(b) into Fig. 8(d), for example). Next, the unit sphere is rotated and scaled using the mapping r(z+1)/(z−1) (i.e., mapping the vertical line (on the imaginary axis) in Fig. 8(d) to a circle of radius r on the complex plane in Fig. 8(f)). With reference to Figs. 6 and 8, the relationship between the coefficients of the proposed Möbius transformation in Eq. (6) and the translation, rotation and scaling steps explained above are as follows: the coefficient s is determined by the required translation, the phase of (complex number) ρ is determined by the rotation, and the modulus of ρ and r are determined by the scaling required to minimize the area distortion by properly distributing the points on the unit sphere surface.
are the coefficients of the Möbius transformation, where ℝ is the set of real numbers. Eq. (6) performs a translation, rotation and scaling using the term ρ(z−s) (transforming Fig. 6(b) into Fig. 8(d), for example). Next, the unit sphere is rotated and scaled using the mapping r(z+1)/(z−1) (i.e., mapping the vertical line (on the imaginary axis) in Fig. 8(d) to a circle of radius r on the complex plane in Fig. 8(f)). With reference to Figs. 6 and 8, the relationship between the coefficients of the proposed Möbius transformation in Eq. (6) and the translation, rotation and scaling steps explained above are as follows: the coefficient s is determined by the required translation, the phase of (complex number) ρ is determined by the rotation, and the modulus of ρ and r are determined by the scaling required to minimize the area distortion by properly distributing the points on the unit sphere surface.
We defined a measure of area distortion of the final map to be
| (7) |
where T is the number of triangles in the mesh, Bi is the area of the ith triangle on the cortical surface, B is the total surface area on the cortical surface, Si(|ρ|) is the area of the ith triangle on the sphere, which depends on the modulus of the scale factor ρ, and S(r) is the total surface area of the final map as a function of r,
The measure of area distortion D(r,|ρ|) is minimized within the group of Möbius transformations,
for a given s ∈
 , using the conjugate gradient algorithm. r=2 yields a spherical map, where optimization on both hemispheres is carried out simultaneously. For hemispherical maps, separate optimization is carried out on the left and right cortical hemispheres. Based on our analysis of the relative area distortion between the final maps and the original cortical surfaces for fifteen human brains reported in (Tosun and Prince, 2001), the optimum conical angle of the spherical cap removed out of a total of 360° for both the left and right cortical hemispheres is 64° – i.e., θ=32°. The final maps on the spherical surface with segmented sulci (Rettmann et al., 2002) are shown in Fig. 9. Area distortion is substantially smaller and more uniform over the hemispherical maps as compared to the spherical map (Tosun and Prince, 2001).
, using the conjugate gradient algorithm. r=2 yields a spherical map, where optimization on both hemispheres is carried out simultaneously. For hemispherical maps, separate optimization is carried out on the left and right cortical hemispheres. Based on our analysis of the relative area distortion between the final maps and the original cortical surfaces for fifteen human brains reported in (Tosun and Prince, 2001), the optimum conical angle of the spherical cap removed out of a total of 360° for both the left and right cortical hemispheres is 64° – i.e., θ=32°. The final maps on the spherical surface with segmented sulci (Rettmann et al., 2002) are shown in Fig. 9. Area distortion is substantially smaller and more uniform over the hemispherical maps as compared to the spherical map (Tosun and Prince, 2001).
Fig. 9.

Cortical unfolding: (a) cortical surface with segmented sulci, (b) spherical map and (c) hemispherical maps.
3.3. Surface registration
Conformal mapping can be applied at any stage to map a surface to a sphere or hemisphere. Since triangle regularity of the meshes is quite good after surface inflation, the conformal mapping is less sensitive to its initial conditions. But it is still necessary to pick a “north pole” for the conformal mapping of a surface so that it corresponds to a common position across all brains – these north poles will map to the same point on the sphere.
To choose a good common north pole, we have selected one brain out of our database of 35 brains to be an “atlas brain”. All other partially flattened surfaces are registered to the partially flattened surface of our atlas brain using a modified iterated closest point (ICP) (Besl and McKay, 1992) algorithm. The north pole of the atlas brain, selected at the top of the hemispherical cut path is then projected to the subject brain and used as the subject’s north pole for conformal mapping. The surface registration provides not only a north pole point with a common position across all brains, but also standardizes the way the conformal coordinates are set up on the surfaces (see (Angenent et al., 1999)). Furthermore, registering the partially flattened surfaces of the atlas and the subject brains instead of their original surfaces permits the construction of the second spherical mapping method outlined in Fig. 3, and makes the method more consistent and stable than using the original surfaces which are highly variable and detailed compared to the partially flattened surfaces.
We use a modification of ICP to align a given partially flattened surface to the atlas’ partially flattened surface. ICP is an iterative method for registering two point sets. Given two surfaces V and W represented by the point sets in V and in W – mesh vertices connected by triangular surface elements – the ICP algorithm computes the rigid body transformation that aligns the point sets.
Ordinarily, ICP ignores the fact that V and W are surfaces when creating correspondences. Instead, it finds a mapping
 (i) that gives the closest vertex
(i) that gives the closest vertex
 ∈ W corresponding to the vertex vi∈V, forming the correspondence pair (vi,
∈ W corresponding to the vertex vi∈V, forming the correspondence pair (vi,
 ). At each iteration, ICP first finds the closest point correspondences between the point sets, and then finds the rigid body transformation
). At each iteration, ICP first finds the closest point correspondences between the point sets, and then finds the rigid body transformation
 (·) of points in W that minimizes the average distance of the corresponding points, given by
(·) of points in W that minimizes the average distance of the corresponding points, given by
| (8) |
where ||·||2 gives the length of a vector. These steps are repeated until convergence.
Our modification to ICP acknowledges the fact that V and W are triangulated surfaces rather than simple point sets. This means that the closest point to vi∈V on W may not be a vertex, but may instead be a point on a triangular element defined by the vertices in W, as illustrated in Fig. 10. In our modification to ICP, correspondence pairs are identified by projection operators
 (·) (onto V) and
(·) (onto V) and
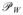 (·) (onto W). In particular, we identify the closest point to vi∈V on the surface W by the projection
(·) (onto W). In particular, we identify the closest point to vi∈V on the surface W by the projection
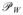 (vi), and similarly, the closest point to wj∈W on the surface V is given by
(vi), and similarly, the closest point to wj∈W on the surface V is given by
 (wj). This identification yields the correspondence pairs (vi,
(wj). This identification yields the correspondence pairs (vi,
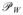 (vi)), i=1,…,N and (wj,
(vi)), i=1,…,N and (wj,
 (wj)), j=1,…,M. In order to reduce possible directional bias, we define the modified ICP objective function in a bilateral fashion, as follows:
(wj)), j=1,…,M. In order to reduce possible directional bias, we define the modified ICP objective function in a bilateral fashion, as follows:
| (9) |
Fig. 10.

Illustration of the modified ICP “correspondence pairs”.
The fact that W is being moved under a rigid body transformation is reflected in this expression by the use of the rigid body transformation operator
 (·).
(·).
To provide quantitative comparison on the matching quality of ICP and the modified ICP algorithms, we defined two distance measures from one surface to the other. The first distance function “W-distance” is defined on the mesh nodes
of the surface W, as the distance between correspondence pairs (wj,
 (wj)), j=1,…,M. In an analogous fashion, the second distance function “V-distance” is defined on the mesh nodes
of the surface V, as the distance between correspondence pairs (vj,
(wj)), j=1,…,M. In an analogous fashion, the second distance function “V-distance” is defined on the mesh nodes
of the surface V, as the distance between correspondence pairs (vj,
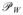 (vi)), i=1,…,N. W-distance and V-distance measures are illustrated in Fig. 10.
(vi)), i=1,…,N. W-distance and V-distance measures are illustrated in Fig. 10.
In order to assess the matching quality of the surface registration algorithms, each of the 34 subjects’ surfaces is registered to the surface of our atlas brain twice, once using the ICP algorithm and once using the modified ICP algorithm. The W-distances from the registered surfaces to the atlas surface and V-distances from the atlas surface to the registered surfaces are measured. For each subject, the modified ICP yields a combined distance (incorporating both W-distance and V-distance) with smaller mean and standard deviation over the mesh vertices, compared with those of the ICP algorithm. In Table 1, the range and the average of the means and standard deviations over 34 subjects are reported. Smaller mean values and significant decrease in the standard deviation support the claim that our modifications to the ICP algorithm improve the matching quality of the rigid body transformation.
Table 1.
Combined distance (incorporating both W-distance and V-distance) in mm
| Mean | SD | |
|---|---|---|
| ICP | ||
| Range | 1.61–2.34 | 1.28–2.36 |
| Average | 1.89 | 1.66 |
| Modified ICP | ||
| Range | 1.54–1.77 | 1.14–1.45 |
| Average | 1.62 | 1.24 |
3.4. Spherical mapping
The preceding alignment procedure automatically yields a common north pole and conformal coordinates so that a given partially flattened surface can generate its own conformal map to the sphere or hemisphere using the method described in Section 3.2. It is guaranteed that the orientation of the mapped surface is correct and that its area distortion relative to the original surface is minimized (within the group of Möbius transformations).
The first method we describe (see the block diagram shown in Fig. 3) starts with the iterative surface inflation stopped at the stage of a partially flattened map. Then, the partially flattened surface is aligned with the atlas’ partially flattened surface and the atlas’ north pole point is projected to the subject’s partially flattened surface. The maps on the spherical surface are then generated using the conformal mapping algorithm. There is no expectation, of course, that the total map will be conformal or isometric to the original cortical surface.
The second method (again, see the block diagram in Fig. 3) is readily developed using the single optimized conformal map of the atlas brain’s partially flattened surface. Since each subject’s partially flattened surface is registered to the atlas, and all surfaces have very similar overall shape due to the mean curvature stopping criterion, it is possible to map all subject’s partially flattened surface vertices to the atlas’ partially flattened surface. Then, since the atlas’ conformal map is a continuous bijection defined on the entire surface of its triangle mesh, all these points are readily mapped to the sphere (or hemisphere) using the atlas map, which is a pseudo-conformal map. In this way, to the extent that regions – e.g., sulci and gyri – are well-aligned on the partially flattened surfaces, they are guaranteed to be well-aligned on the spherical maps. This method proves to be quite reliable compared to the first method, as we demonstrate in the next section.
4. Results and discussion
In this section, we evaluate how common brain features map to similar locations on the sphere under the described mapping methods. We start by analyzing the locations to which four sulci are mapped in 30 brains. We then demonstrate the power of a simple sulcal labelling technique on five brains given the probabilistic map created from the 30 training brains.
4.1. Probabilistic maps
We randomly picked 30 brain surfaces from our database of 35 surfaces. Four sulcal regions, defined as the buried cortex surrounding the sulcal spaces, were automatically segmented (Rettmann et al., 2002) and manually labelled on all 35 brains. These sulcal regions are the central sulcus (cs), superior frontal (sf), cingulate sulcus (cn) and parieto-occipital sulcus (po) on both the left and right cortical hemispheres. The reason we select these sulci is that they could be consistently labelled across three scans of the same subject (Rettmann, 2003). These sulci are colored on the left hemisphere of one cortical surface in Fig. 11.
Fig. 11.
The location of the sulcal regions labelled on (a) the lateral surface and (b) the medial surface illustrated on one cortical surface.
Let HSr denote the reference hemisphere to which all brains are mapped. (This hemisphere is parameterized by the particular conformal map of the atlas brain, which is just one of the 30 brains picked randomly.) To see where the four sulci map to on HSr, we generated four probabilistic maps Ii:HSr→[0,1] for i=cs, sf, cn and po. For each sulcal region, Ii is initialized to zero, and for each vertex of HSr, the value of the probabilistic map is incremented by 1 for each training brain, if the corresponding point on the hemispherical map of that brain has the same sulcal label. Then Ii is divided by 30 to normalize its values to the range [0,1]. This gives a probabilistic map comprising an estimated conditional probability of the location of a sulcal region for each of four sulcal regions.
Two probabilistic maps were generated, one for the map I(1) created using individual conformal maps (first method), and one for the map I(2) created by using only the atlas conformal map (second method). Fig. 12 shows the probabilistic maps for i=cs, sf, cn, po for both the left and right cortical hemispheres. The maximum values of the probabilistic maps and are given in Table 2. The table reveals a lack of good sulcal alignment for Method 1, the individual conformal maps method.
Fig. 12.
Probabilistic maps on the atlas’ partially flattened surface (a,c) and pseudo-conformal map (b,d) for both left (a,b) and right (c,d) cortical hemispheres (color map: dark blue(0) – dark red(1)).
Table 2.
Maximum of probabilistic maps
| Mapping | cs | sf | cn | po |
|---|---|---|---|---|
| Left cortical hemisphere | ||||
| I(1) | 0.72 | 0.74 | 0.88 | 0.72 |
| I(2) | 0.97 | 0.90 | 0.97 | 1.00 |
| Right cortical hemisphere | ||||
| I(1) | 0.61 | 0.61 | 0.94 | 0.78 |
| I(2) | 0.97 | 0.90 | 1.00 | 0.97 |
4.2. Automatic sulcal labelling
Here, we examine the performance of a simple automated sulcal labelling technique using the probabilistic maps derived in the previous section. Let Ii be one of the probabilistic maps derived in the previous section using the 30 training set surfaces. Now consider one the five remaining test surfaces, each of which is mapped to a hemisphere using either the first or second method. For each segmented sulcal region on the test surface, the maximum of each probabilistic map is calculated. If the maximum is larger than 0.5, then the label of that probabilistic map is assigned to the entire sulcal region.
Fig. 13(a) shows a mapped sulcal segmentation. The correct manual labels for the four sulcal regions under consideration are given (for the left hemisphere) in Fig. 13(b). Fig. 13(c) shows the result of the automated labelling technique.
Fig. 13.

Pseudo-conformal map of test brain: (a) sulcal segmentation, (b) manually labelled sulcal regions, (c) automatically labelled sulcal regions using I(2). Color map for (b) and (c): left cs (blue), left sf (green), left cn (pink) and left po (red).
To evaluate the effectiveness of this labelling technique, and hence the spherical mapping technique, two types of labelling errors are defined: probability of detection and probability of false alarm . Probability of detection is defined as the percentage area of the manually labelled region that is correctly labelled by our automatic labelling method. Probability of false alarm is defined as the percentage area of the automatically labelled region that is not manually labelled. The probabilities of detection and false alarm averaged for the five test brains are reported in Table 3. Higher values and lower show that our second method yields a better standardized coordinate system. The probability of detection in the range between 0.83–1.00 is quite good in comparison to other methods in the literature (cf. Behnke et al., 2003).
Table 3.
Automatic labelling errors
| Errors | cs | sf | cn | po |
|---|---|---|---|---|
| Left cortical hemisphere | ||||
| by | 0.93 | 0.81 | 0.83 | 0.90 |
| by | 0.34 | 0.23 | 0.04 | 0.17 |
| by | 1.00 | 0.86 | 0.91 | 0.98 |
| by | 0.02 | 0.23 | 0.03 | 0.17 |
| Right cortical hemisphere | ||||
| by | 1.00 | 0.94 | 0.89 | 0.92 |
| by | 0.32 | 0.22 | 0.08 | 0.37 |
| by | 1.00 | 1.00 | 1.00 | 1.00 |
| by | 0.00 | 0.17 | 0.09 | 0.33 |
4.3. Quality of isometry
In this work, our aim is to develop a standard, automatic mapping technique that makes comparison across multiple brains possible. Although moderate distortion of distance can be achieved in spherical mapping techniques, it is a well known fact (Carmo, 1976) that a cortical surface and a spherical surface are not developable – i.e., there is no isomorphism between a cortical surface and a sphere since a cortical surface has spatially varying Gaussian curvature unlike a sphere’s constant Gaussian curvature.
To quantify the degree of isometry between a cortical surface and its final mapped surface, a random reference vertex X and a set of N random vertices are picked on the given cortical surface. Then the minimal geodesic distance from X to each Yi on the original surface and on the final map is calculated by the fast marching algorithm on the triangle mesh (cf. Rettmann et al., 2002), and denoted by do(i) and df(i), respectively. To avoid possible errors due to distance normalization required for comparison, the pairwise ratio of geodesic distances is used instead of absolute geodesic distance. Let the pairwise ratio of geodesic distances be organized as a lower triangular matrix T, Tij=do(i)/ do(j), and the pairwise ratio of geodesic distances be organized as a lower triangular matrix T*, . A similarity measure between T and T* is defined by E:
| (10) |
similar to the “stress” measure proposed by (Sammon, 1969; Schwartz et al., 1989) to quantify the error in the “multidimensional” scaling problem. To eliminate the dependency of measure E on the reference point selection, for each of 35 subjects, E is measured 100 times using 100 different reference points X, and point sets of size N=5000. The analysis of variance (ANOVA) technique (Scheffe, 1959; Crow et al., 1990) is used to decide whether different reference point selections have a significant effect on measure E for a fixed value of N=5000, and to estimate these effects.
Statistics over 35 subjects are reported in Table 4. The reference point selection factor failed to reach significance (Pr(>F) >0.1) for any combination of original surfaces and final maps analyzed in this experiment. The overall mean stress value on the conformal mapping and pseudo-conformal is between 0.044 and 0.070 which are comparable with the errors reported in (Sammon, 1969). Note that a lower value of E indicates a better level of isometry. As expected, a better level of isometry is achieved in the hemispherical maps as compared to the spherical maps. For partially flattened surfaces, the mean stress value is 0.013 which is comparable to the stress value about 0.010 achieved by the cortical surface flattening method proposed in (Schwartz et al., 1989). The reason for the better isometry level of the partially flattened surfaces is due to the geometric features – i.e., deep sulcal regions – preserved on these maps that the spherical maps lack.
Table 4.
Quality of isometry: overall mean and standard deviation of measure E, and ANOVA results
| Original surface | Final map | Mean | SD | ANOVA
|
|
|---|---|---|---|---|---|
| F value | Pr(>F) | ||||
| Cortex | Partially flattened | 0.013 | 0.006 | 1.174 | 0.118 |
| Cortex | Spherical map (first method) | 0.068 | 0.018 | 1.218 | 0.075a |
| Cortex | Left hemispherical map (first method) | 0.051 | 0.018 | 0.944 | 0.637 |
| Cortex | Right hemispherical map (first method) | 0.044 | 0.017 | 0.975 | 0.550 |
| Cortex | Spherical map (second method) | 0.070 | 0.014 | 1.039 | 0.378 |
| Cortex | Left hemispherical map (second method) | 0.046 | 0.016 | 1.049 | 0.353 |
| Cortex | Right hemispherical map (second method) | 0.042 | 0.014 | 0.986 | 0.520 |
Significance at the 95% confidence level.
5. Discussion and summary
We have developed a standard mapping technique that automatically produces mappings with good sulcal alignment across multiple brains. Our method depends only on the geometry of the cortical surface. One of the primary goals of the proposed coordinate system is to reduce the spatial uncertainty associated with the location of a given anatomical or functional area. The first method proposed establishes the fact that conformal mapping results from different brains are not stable, even in ideal circumstances when the individual brains are regularized and smoothed. The instability of these individual conformal maps results in poor sulcal alignment across subjects.
This conclusion sets up the construction of the second proposed method, which utilizes the simplicity of the partially flattened surfaces and the bijection property of the atlas’ conformal map that can be readily interpolated once the subject’s surface is aligned with the atlas’ surface. This method results in a good sulcal alignment across multiple subjects. In future work, we plan to incorporate additional cortical features (i.e., geodesic depth) and to explore the effect that the value of β has on the sulcal alignment across multiple brains. The major anatomical features of the cortex, such as the central sulcus and sylvian fissure are clearly visible on the partially flattened surfaces, while the secondary and tertiary foldings are largely absent depending on the pre-selected β value. An extended analysis on the folding pattern of the partially flattened surfaces, and its effects on the surface registration could be used to yield further improvements in establishing spherical coordinate systems on a cortical hemisphere and on automatic labelling of sulcal regions. In future work, in addition to these primary sulci, the performance analysis of the proposed mapping methods on the secondary foldings should be performed.
Acknowledgments
We thank Dr. Susan Resnick and Dr. Dzung Pham for access to and guidance in the use of the BLSA data. This work was supported by the NIH/NINDS under Grant R01NS37747.
Footnotes
Expanded version of work presented at the Medical Image Computing and Computer-Assisted Intervention – MICCAI 2003, Montréal, Québec, Canada.
Contributor Information
Duygu Tosun, Email: dtosun@jhu.edu.
Maryam E. Rettmann, Email: rettmann@nih.gov.
Jerry L. Prince, Email: prince@jhu.edu.
References
- Angenent S, Haker S, Tannenbaum A, Kikinis R. On the Laplace–Beltrami operator and brain surface flattening. IEEE Trans Med Imag. 1999;18 (8):700–711. doi: 10.1109/42.796283. [DOI] [PubMed] [Google Scholar]
- Behnke KJ, Rettmann ME, Pham DL, Shen D, Davatzikos C, Resnick SM, Prince JL. Automatic classification of sulcal regions of the human brain cortex using pattern recognition. Proc SPIE: Med Imag. 2003;5032:1499–1510. [Google Scholar]
- Besl PJ, McKay ND. A method for registration of 3D shapes. IEEE Trans Pattern Anal Machine Intell. 1992;14 (2):239–255. [Google Scholar]
- Carman GJ, Drury HA, van Essen DC. Computational methods for reconstructing and unfolding the cerebral cortex. Cerebral Cortex. 1995;5 (6):506–517. doi: 10.1093/cercor/5.6.506. [DOI] [PubMed] [Google Scholar]
- Carmo MPD. Differential Geometry of Curves and Surfaces. Prentice Hall College Div; 1976. [Google Scholar]
- Crow EL, Davis FA, Maxfield MW. Statistics Manual. Dover; New York: 1990. [Google Scholar]
- Drury HA, Essen DCV, Anderson CH, Lee WC, Coogan TA, Lewis JW. Computerized mapping of the cerebral cortex: a multiresolution flattening method and a surface-based coordinate system. J Cogn Neuro. 1996;8 (1):1–28. doi: 10.1162/jocn.1996.8.1.1. [DOI] [PubMed] [Google Scholar]
- Fischl B, Sereno MI, Dale AM. Cortical surface-based analysis II: Inflation, flattening, and a surface-based coordinate system. NeuroImage. 1999;9 (2):195–207. doi: 10.1006/nimg.1998.0396. [DOI] [PubMed] [Google Scholar]
- Grossmann R, Kiryati N, Kimmel R. Computational surface flattening: a voxel-based approach. IEEE Trans Pattern Anal Machine Intell. 2002;24 (April):441–443. [Google Scholar]
- Gu X, Wang Y, Chan TF, Thompson PM, Yau ST. Information Processing in Medical Imaging. Ambleside, UK: 2003. Jul, Genus zero surface conformal mapping and its application to brain surface mapping; pp. 172–184. [DOI] [PubMed] [Google Scholar]
- Han X, Xu C, Rettmann ME, Prince JL. Automatic segmentation editing for cortical surface reconstruction. Proc SPIE Med Imag. 2001a;4322 (Feb):194–203. [Google Scholar]
- Han X, Xu C, Tosun D, Prince JL. Cortical surface reconstruction using a topology preserving geometric deformable model. Proceedings of the 5th IEEE Workshop on Mathematical Methods in Biomedical Image Analysis (MMBIA2001); Kauai, Hawaii. Dec, 2001b. pp. 213–220. [Google Scholar]
- Han X, Xu C, Braga-Neto U, Prince JL. Topology correction in brain cortex segmentation using a multiscale, graph-based algorithm. IEEE Trans Med Imag. 2002;21:109–121. doi: 10.1109/42.993130. [DOI] [PubMed] [Google Scholar]
- Han X, Xu C, Prince JL. Geometric Level Set Methods in Imaging, Vision and Graphics. Springer; Berlin: 2003a. Topology preserving geometric deformable models and brain reconstruction; p. 152b. [Google Scholar]
- Han X, Xu C, Prince JL. A topology preserving level set method for geometric deformable models. IEEE Trans Pattern Anal Machine Intell. 2003b;25:755–768. [Google Scholar]
- Hurdal MK, Bowers PL, Stephenson K, Sumners DWL, Rehm K, Schaper K, Rottenberg DA. Lecture Notes in Computer Science. Vol. 1679. Springer; 1999. Quasi-conformally flat mapping the human cerebellum; pp. 279–286. [Google Scholar]
- MacDonald D, Kabani N, Avis D, Evans A. Automated 3D extraction of inner and outer surfaces of cerebral cortex from MRI. NeuroImage. 2000;12 (3):340–356. doi: 10.1006/nimg.1999.0534. [DOI] [PubMed] [Google Scholar]
- Meyer M, Desbrun M, Schroder P, Barr AH. Discrete differential geometry operators for triangulated 2-manifolds. VisMath’02 Proceedings 2002 [Google Scholar]
- Needham T. Visual Complex Analysis. Clarendon Press; New York: 2000. [Google Scholar]
- Pham DL. Robust fuzzy segmentation of magnetic resonance images. Proceedings of the Fourteenth IEEE Symposium on Computer-Based Medical Systems (CBMS2001); 2001. pp. 127–131. [Google Scholar]
- Pham DL, Prince JL. Adaptive fuzzy segmentation of magnetic resonance images. IEEE Trans Med Imag. 1999;18 (9):737–752. doi: 10.1109/42.802752. [DOI] [PubMed] [Google Scholar]
- Resnick SM, Goldszal AF, Davatzikos C, Golski S, Kraut MA, Metter EJ, Bryan RN, Zonderman AB. One-year age changes in MRI brain volumes in older adults. Cerebral Cortex. 2000;10 (5):464–472. doi: 10.1093/cercor/10.5.464. [DOI] [PubMed] [Google Scholar]
- Rettmann ME. PhD thesis. Johns Hopkins University; Baltimore, MD 21218, USA: 2003. Analysis of regional cortical geometry using automated sulcal segmentation from a surface model of the human cerebral cortex. [Google Scholar]
- Rettmann ME, Han X, Xu C, Prince JL. Automated sulcal segmentation using watersheds on the cortical surface. NeuroImage. 2002;15 (February):329–344. doi: 10.1006/nimg.2001.0975. [DOI] [PubMed] [Google Scholar]
- Sammon JW. A nonlinear mapping for data structure analysis. IEEE Trans Comput. 1969;18 (5):401–409. [Google Scholar]
- Scheffe H. The Analysis of Variance. Wiley; New York: 1959. [Google Scholar]
- Schwartz EL, Shaw A, Wolfson E. A numerical solution to the generalized mapmaker’ problem: flattening nonconvex polyhedral surfaces. IEEE Trans Pattern Anal Machine Intell. 1989;11 (9):1005–1008. [Google Scholar]
- Sereno JI, Dale AM, Liu A, Tootell RBH. A surface-based coordinate system for a canonical cortex. Proceedings of the 2nd International Conference on Human Brain Mapping, NeuroImage. 1996;3(3):S252. [Google Scholar]
- Smith AC, Batchelor PG, Hill DLG, Dean AF, Cox T, Hawkes DJ. The shape of the developing foetal cortex from MR images. Proceedings of the Medical Image Understanding and Analysis (MIUA2000).2000. [Google Scholar]
- Talairach J, Tournoux P. 3-Dimensional Proportional System: An Approach to Cerebral Imaging. Thieme Medical Publisher Inc; Stuttgart, New York: 1988. Co-planar Stereotaxic Atlas of the Human Brain. [Google Scholar]
- Thompson PM, Woods RP, Mega MSW, Toga A. Human Brain Mapping. Vol. 9. San Antonio, TX, USA: 2000. Mathematical/computational challenges in creating deformable and probabilistic atlases of the human brain; pp. 81–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Timsari B, Leahy R. Optimization method for creating semi-isometric flat maps of the cerebral cortex. Proceedings of the SPIE Conference on Medical Imaging: Image Processing; 2000. pp. 698–708. [Google Scholar]
- Tosun D, Prince JL. Hemispherical map for the human brain cortex. Proc of SPIE Med Imag. 2001;4322:290–300. [Google Scholar]
- Wandell B, Engel S, Hel-Or H. Creating images of the flattened cortical sheet. Invest Opth Vis Sci. 1996;36:S612. [Google Scholar]
- Wang HZ, Rieder SJ. A spoiling sequence for suppression of residual transverse magnetization. Magn Reson Med. 1990;15 (2):175–191. doi: 10.1002/mrm.1910150202. [DOI] [PubMed] [Google Scholar]
- Xu C, Han X, Prince JL. Improving cortical surface reconstruction accuracy using an anatomically consistent gray matter representation. Proceedings of the 6th International Conference on Functional Mapping of the Human Brain; June; 2000. p. S581. [Google Scholar]
- Xu C, Pham DL, Rettmann ME, Yu DN, Prince JL. Reconstruction of the human cerebral cortex from magnetic resonance images. IEEE Trans Med Imag. 1999;18 (6):467–480. doi: 10.1109/42.781013. [DOI] [PubMed] [Google Scholar]