Sparsely populated folding intermediates of the Fyn SH3 domain: Matching native-centric essential dynamics and experiment

Methods

Native-Centric Topological Modeling. Dynamics trajectories of a model Fyn SH3 molecule were computed with a topological modeling program published by Kaya and Chan (14). All parameter values were taken from their work. No desolvation barrier was included in the present potential energy function.

The model is coarse-grained, specifying protein conformation entirely by the positions of the C^α atoms. Motion and energetics are simulated by using Langevin dynamics with a native-centric potential energy function. Local energy terms are based on distances, angles, and dihedrals between adjacent C^α atoms in the protein chain. Native-like nonlocal contacts between residues are subject to a 10–12 Lennard-Jones potential, whereas nonnative nonlocal interactions are repulsive. Minima in all energy terms are positioned to match distances, angles, and dihedrals observed in a native reference structure of the protein, and native contacts between residues are identified by using this structure. In this work, an x-ray crystal structure [PDB ID code 1SHF (27), chain B] served as the reference, and 145 native contacts were obtained by using the csu program (28).

Two versions of the modeling program were used. One records a histogram containing the value of the potential energy function at every time step for use in simulated calorimetry. A second version calculates a separate potential energy for each residue by assigning an equal portion of each interaction energy to each of the involved residues. The energy of each residue is averaged over blocks (periods) of 400 simulation steps and recorded at the end of each averaging period for use in a covariance analysis. The Cartesian coordinates of each residue's C^α atom are similarly averaged and recorded in parallel to the energy data for use in a structural analysis of intermediates.

Each simulation is 200 million time steps in length and runs in ∼36 h on a 1.7-GHz AMD processor (Advanced Micro Devices, Sunnyvale, CA). Data from the first million steps is discarded to allow for equilibration. The simulation's energy autocorrelation time was measured to be 5,200 ± 1,500 steps over a wide range of Langevin dynamics temperatures. The energy-scaling factor ε (as defined in ref. 14) was the same for all kinetic simulations.

Separation of Data from the Folded and Unfolded States. Prior to covariance analysis, simulation data were separated into subsets, depending on the state (folded or unfolded) of the model protein by using the following procedure: First, average state energies, E_folded < E_unfolded, are extracted from potential energy data by numerically minimizing

where E(t) is the model's overall potential energy measured during sampling period t, N_samp is the number of sampling periods, and the min function returns the lesser of its arguments. Second, the data are scanned for folding transitions, which are identified when the overall potential energy subsequently crosses thresholds at E = E_folded and E = E_unfolded. Data collected during transitions are discarded, and sampling periods between transitions are assigned to the appropriate data subset.

Intermediate Structural Ensembles. Ensembles of structures representative of the endpoints of energy-fluctuation modes from the covariance analysis were collected as described in Theoretical Considerations. Each ensemble constitutes 1% of the structures observed during the relevant simulation trajectory. The structures were aligned by using a best-fit rotation (29), taking a selected element of secondary structure as a reference point. A subset of 50 structures with approximately the same mean and standard deviation in each particle coordinate as the full ensemble was then selected by using a Monte Carlo procedure. These 50 structures were plotted to visually represent intermediate states. A detailed description of this procedure is included in the supporting information, which is published on the PNAS web site.

Simulated Calorimetry. The thermodynamic folding cooperativity of the native-centric Fyn SH3 model was tested with a multiple-histogram simulated calorimetry method (30), because we found that single-simulation histogram techniques (31, 32) were not adequate for the present model. Here, a model protein's density of states as a function of energy, n(E), is determined approximately from histograms of potential energy values observed during multiple simulations run at N_temp different temperatures. The data are combined according to

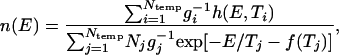[1]

where h(E, T_i) is the number of conformations with energy E observed during a simulation at temperature T_i (energy histogram), N_i = ∑_E h(E, T_i), f(T_i) is the free energy at temperature T_i, and the Boltzmann constant k_B has been set equal to 1. The factor g_i = 1 + 2τ_{ac, i}, where τ_{ac, i} is the energy autocorrelation time at temperature T_i, is included to account for the fact that successive samples from a simulation are not fully independent. To obtain τ_{ac, i}, an exponential decay is fit to the simulation's energy autocorrelation function: 〈E_tE_t+τ〉 ∼ exp(–τ/τ_ac). When folding transitions are present in a data set, the autocorrelation function must be fit to a sum of two exponentials to separate τ_{ac, i} from the slower folding correlation time. The free energies are defined by exp[f(T_i)] = ∑_E n(E) exp(–E/T_i) and can be determined by iteration between this equation and Eq. 1 (30).

This n(E) is then used to evaluate the protein's heat capacity as a function of temperature, C_P(T), which can be interpreted as the results of a calorimetry experiment. After a baseline subtraction (11), the C_P(T) curve is analyzed to determine the calorimetric enthalpy of folding, ΔH_cal = ∫ C_P(T)dT, and the van't Hoff enthalpy of folding, 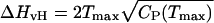, where T_max is the temperature at which C_P(T) is maximal. The ratio of these enthalpies, κ = ΔH_vH/ΔH_cal, is a measure of the cooperativity of the protein's folding transition; κ ≈ 1 is consistent with a two-state folding model. (Note that as defined in ref. 11.)

Results and Discussion

Theoretical Considerations. Covariance analysis, also known as essential dynamics or principal component analysis, identifies correlations between multiple fluctuating variables in sampled numerical data (33). It is routinely applied to atomic coordinate data from molecular dynamics simulations to find favored modes of conformational fluctuation (34) and to native-centric modeling of the dynamics of the folded state (35–37). We have attempted a similar analysis of C^α coordinate trajectory data from our native-centric Fyn SH3 domain model (which is described in Methods) by using an algorithm from the literature (33, 34). Before covariance analysis, data must be processed to remove overall translations and rotations of the model protein, which strongly interfere with the identification of coordinated internal motions. However, the present investigation of the folding/unfolding transition requires the consideration of highly disordered conformations. Their presence precludes a straightforward removal of overall rotations and consequently makes it difficult to gain insight through coordinate-based principal component analysis.

This difficulty led us to a different approach. Here, covariance analysis is applied in the energy regime rather than the coordinate regime. In the analysis below, we use the technique to treat site-resolved energy trajectory data from the Fyn SH3 model. Motions irrelevant to folding cannot interfere with such an analysis because they do not change the model's energy. The simulation produces energy data of the form , where N_res is the number of residues in the protein, e_i(t) is the energy of residue i measured during sampling period t, ê_i is a unit vector for the energy of residue i, and t = 1,..., N_samp, where N_samp is the number of sampling periods. Variations in residue energies during the simulation cause fluctuations in the displacement of 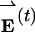from its average position. According to García's derivation (33), the object of covariance analysis is to determine the most probable direction of this displacement by finding the unit vector v̂ that maximizes

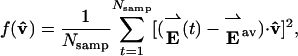[2]

where 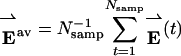. This expression can be simplified to f(v̂) = (Cv̂)·v̂ where C is the residue energy covariance matrix:

[3]

In the supporting information we show that f(v̂) is maximal for vectors v̂ that satisfy Cv̂ = λv̂, i.e., for eigenvectors of the covariance matrix. Because C is symmetric, it will always be possible to find N_res orthonormal eigenvectors v̂₁,v̂₂,..., v̂_Nres with corresponding eigenvalues λ₁, λ₂,..., λ_Nres. Note that f(v̂_n) = λ_n for these vectors, so that by Eq. 2, eigenvalue λ_n gives the mean square projection of 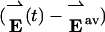along eigenvector v̂_n. The eigenvalues will therefore always be positive. We sort the eigenvectors in order of decreasing eigenvalue, so that f(v̂₁) is the global maximum of f(v̂) and f(v̂₂),..., f(v̂_Nres) are lesser maxima of decreasing significance.

The eigenvectors and eigenvalues contain valuable data on the model protein's exploration of conformational space. Each v̂_n describes a mode of energy fluctuation favored by the model protein to an extent indicated by λ_n. This energy fluctuation must be driven by some fluctuation in the protein's conformation, the nature of which can be examined when the eigenvector is expressed in the basis of residue energies: . Each component v_n,i of v̂_n reveals how the conformational fluctuation affects a different residue in the model protein. The magnitude of v_n,i indicates how strongly the fluctuation affects the potential energy of residue i, and the relative signs of v_n,i and v_n,j indicate whether the fluctuation leads to a correlated or anticorrelated change in the energies of residues i and j. All covariance analysis results presented here were tested for convergence by using a procedure described in supporting information.

Although analysis of the eigenvectors efficiently identifies the model protein's dominant modes of conformational fluctuation, it is preferable to consider coordinate data when drawing conclusions about structure. We therefore wish to relate the covariance analysis results to coordinate data recorded in parallel to the energy data. Energy data 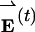can be transformed from the residue energy basis {ê_i} to a basis of eigenvectors {v̂_n} by using the same unitary transformation U that diagonalizes C (see supporting information). Thus, , where is the projection of the model protein's energy along eigenvector v̂_n during sampling period t. Extremal points on the ε_n(t) trajectory correspond to maximal conformational excursions associated with mode v̂_n. By retrieving coordinate data from those 1% of sampling periods t with the greatest values of ε_n(t) we can collect an ensemble of structures characteristic of one endpoint of the fluctuation. The other endpoint can be characterized by selecting periods for which ε_n(t) is smallest. The structures are then aligned relative to some element of the model protein's secondary structure, and a representative subset is selected for display and analysis. A detailed description of this procedure is presented in supporting information.

Covariance Analysis Identifies Transient Protein-Folding Intermediates. Site-resolved energy data were recorded during a single simulation of the native-centric Fyn SH3 model near its folding midpoint temperature. Fig. 1 shows typical data for a small portion of the trajectory. The model's overall potential energy (Fig. 1 A) exhibits only two stable states, folded and unfolded, and each of the 145 observed transitions between these states is rapid. The potential energy of each residue in the model protein similarly shows two distinct states, and abrupt transitions between folded and unfolded occur synchronously for all residues. Despite the concerted nature of the transitions, significant variations in energetics exist between different sites. Some residues in the hydrophobic core (e.g., residue 38, Fig. 1B) exhibit large energy fluctuations while the protein is unfolded, with energies briefly reaching average values for the folded configuration. The fluctuations of several core residues seem to be correlated (e.g., the residues in strand β3), suggesting a cooperative process. Likewise, residues in the N- and C-terminal strands (e.g., residue 5, Fig. 1C) undergo large, coordinated energy fluctuations while the protein is folded.

Covariance analysis was used to quantitatively characterize correlations in the site-resolved energy data. Because the model is native-centric, any major energy change must involve the formation or dissolution of native-like structure. The analysis, therefore, identifies cooperative, multiresidue interactions related to folding. The energy fluctuations of many residues change significantly in character when the protein folds or unfolds, so the data were divided into folded and unfolded subsets comprising 96,184,400 and 97,263,600 simulation steps, respectively (240,461 and 243,159 sampling periods), with separate covariance analyses performed on each.

Covariance analysis of the unfolded energy trajectory identified a transient intermediate on the protein's folding pathway. The most significant energy fluctuation mode found by the analysis, v̂₁, accounts for 22% of the unfolded protein's mean square energy fluctuations (i.e., , where λ_i is an energy eigenvalue of the covariance matrix defined in Eq. 3). The components of v̂₁ (Fig. 2 A) indicate that the fluctuation is mostly localized in strands β2, β3, and β4 and the distal loop. This is especially clear when the components are mapped onto a 3D structure of Fyn SH3 (Fig. 2B). The mode apparently involves the cooperative formation of the three central strands into a core of native-like structure in an otherwise unfolded protein. Strand β3 makes the greatest contribution to the structure, whereas β2 and β4 are less strongly involved. The data also indicate that the RT loop is weakly involved at the point where it contacts β4.

As described in the preceding section, it is possible to obtain a structural representation of the endpoints of conformational fluctuations associated with a given mode v̂_n by selecting structures that correspond to energy extrema in ε_n(t). Fig. 3A shows an ensemble of 50 structures representing the minimum ε₁(t) endpoint of the v̂₁ mode from the trajectory of the unfolded state. These structures correspond, therefore, to the lowest energy states along the folding excursion characterized by v̂₁. Strands β2, β3, and β4 and the loops connecting them form a well defined native-like sheet structure, as would be expected from the eigenvalue components (Fig. 2 A and B). The ensemble of Fig. 3A includes structures from 1% of the unfolded trajectory data (961,600 simulation steps, 2,404 sampling periods; see supplemental information). The ensemble establishes that strands β2–β4 must frequently come together to form local native-like structure while the protein is unfolded, producing a partially structured intermediate on the protein's folding pathway.

A separate covariance analysis of the energy data subset corresponding to the folded state has revealed a transient intermediate on the protein's unfolding pathway. Mode v̂₁, accounting for 32% of the folded protein's mean square energy fluctuations, has the components shown in Fig. 2 C and D. This mode affects strand β1, strand β5 (especially residue 55, though eigenvector components are elevated throughout the strand), and that portion of strand β2 that contacts β1 in the native structure. A picture emerges in which strands β1 and β5 frequently dissociate from the rest of the β-sheet while the protein as a whole remains folded, forming a transient unfolding intermediate. The presence of the intermediate is confirmed by an ensemble of structures collected from the simulation data corresponding to maximum ε₁(t) values from the trajectory of the folded protein (Fig. 3B). In these structures, which comprise 1% of the folded trajectory (corresponding to 972,400 simulation steps or 2,431 sampling periods), strands β1 and β5 are disordered but the core strands remain intact.

Energy fluctuation modes beyond v̂₁ were investigated in both the folded and unfolded covariance analysis results. From the analysis of data derived from the unfolded protein, mode v̂₂, which accounts for 13% of the mean square energy fluctuations in the unfolded state, shows an energy anticorrelation between residues in the core of the protein and residues in the RT loop. The anticorrelation is a consequence of the protein's two-state nature; these regions cannot both assume their native conformations without a folding transition, so a balance in their energies is observed. Modes beyond v̂₂ for the unfolded data and beyond v̂₁ for the folded data each account for only a small fraction of the model protein's mean square energy fluctuations and cannot be interpreted easily in terms of conformational fluctuations.

Comparison to Experimental Measurements. It is illuminating to compare the findings described above with the results of our recent relaxation dispersion NMR spectroscopy study of the folding of a pair of Fyn SH3 point mutants (G48M and G48V), which are less stable than the wild-type protein but have a significantly greater folding rate. For both mutants, a low population folding intermediate was detected in equilibrium with the folded and unfolded states (21). A comparison of chemical shifts measured for the intermediate, folded, and unfolded states established that strands β2, β3, and β4 and the distal loop connecting β3 and β4 are reasonably well structured in the intermediates of both the G48M and G48V mutants, with significantly less structure in other regions of the protein. The formation of structure in the central strands of one of the intermediates is illustrated in Fig. 2E in which Δ_exp values for the G48V mutant are plotted vs. residue number. The value of Δ_exp(i) = [δ_F(i) – δ_I(i)]/[δ_F(i) – δ_U(i)], where δ_k(i) is the ¹⁵N chemical shift of residue i in state k [k = folded (F), intermediate (I), or unfolded (U)], provides a measure of the extent to which amide site i in the protein is folded in the I state. Values of Δ_exp(i) close to zero indicate native-like structure at this position, whereas values close to unity are consistent with an unfolded-like conformation (21). The Δ_exp(i) values are plotted on the structure of the folded state of the Fyn SH3 domain in Fig. 2F. Comparing Fig. 2 B and F, a very significant correlation clearly exists between the folding intermediate identified by simulation in our simplified Fyn SH3 model and by experiment.

Our results also have interesting similarities to those of protein-engineering studies of several homologous SH3 domains, in which folding transition states were characterized by using Φ-values from kinetic studies of mutants. Northey et al. (22) identified in the Fyn SH3 domain a “core folding nucleus” of residues in strands β2, β3, and β4 that are important for transition-state stabilization. Multiple residues in the distal β-hairpin (comprising strands β3 and β4 and the distal loop) and one in strand β2 are strongly implicated in the transition state for src SH3 (23). Residues in the distal β-hairpin are also highly structured in the transition state for the α-spectrin SH3 domain (24). Another study concluded that formation of the distal loop in α-spectrin SH3 in an obligatory step in forming the transition state, because it is necessary to bring together strands β3 and β4 (25). With the exception of certain transition-state features that are not conserved among these homologous proteins [i.e., structuring of the C-terminal residues in the RT loop in src SH3 (23) and of the 3₁₀ helix in α-spectrin SH3 (24)], a strong correlation is observed between experiment and our simulation results.

The nature of the model's unfolding intermediate (Fig. 3B) is also consistent with previous experimental results. In a study on the src SH3 domain it was found that creating a disulfide crosslink between strands β1 and β5 greatly decreases the protein's unfolding rate, which indicates that dissociation of the N- and C-terminal strands is an early step on the unfolding pathway (26).

Comparison with the Two-State Model of Protein Folding. The folding behavior of Fyn SH3 (38) and its homologs src SH3 (39) and spectrin SH3 (40) have previously been characterized as consistent with the two-state model of protein folding. In general, evidence of two-state folding is drawn from measurements that do not resolve multiple sites within a protein molecule; these include data from calorimetry, CD spectroscopy, and fluorescence emission spectroscopy (41). With this in mind we have investigated the folding of our native-centric Fyn SH3 model with simulated calorimetry techniques.

A simulated calorimetry method (see Methods and ref. 30) was applied to data from 15 Fyn SH3 simulations run at a wide range of temperatures and the heat capacity of the model domain was calculated as a function of temperature, C_P(T) (Fig. 4). The resulting heat-capacity profile has a single sharp peak and κ = 0.987 (the calorimetric two-state criterion is κ ≈ 1), indicating that the thermodynamic folding behavior of the model is well described by a two-state model by conventional standards (42).

It is interesting to consider the covariance analysis results in light of this finding. The folding and unfolding intermediates that we have observed are consistent with two-state folding because they do not accumulate. Indeed, in-depth theoretical analyses have shown that the usual calorimetric two-state criterion does not imply that conformations with intermediate energies are nonexistent and that the criterion, in fact, allows for a minute population of such conformations (11, 15, 43), although it does imply that such a population cannot be large (4, 11, 44). Nevertheless, the sparsely populated intermediates revealed in the present model study expose subtleties in the folding mechanism that a simple two-state picture would not lead us to consider. Similar observations have been made in site-resolved experimental studies of protein folding, including our NMR study of fast-folding Fyn SH3 mutants (21), in which intermediates on the order of 1% of the total population of protein molecules in solution were observed. These results emphasize that experimental measures that do not probe multiple sites within a molecule can mislead us toward an oversimplified view of the folding reaction.

Conclusion

In summary, we have identified folding and unfolding intermediates in a native-centric computational model of the Fyn SH3 domain. The folding intermediate, observed while the protein as a whole was unfolded, is a partially structured state formed by association of the protein's three central β-strands. It is strikingly similar to Fyn SH3 folding intermediates recently characterized by relaxation dispersion NMR methods (21) and to folding transition states elucidated in point mutagenesis studies of several homologous SH3 domains (22–25). The unfolding intermediate is a partially unstructured state formed when the two terminal β-strands dissociate from the folded domain; structures of this sort are also inferred from experiment (26). Because our model is native-centric, to a significant degree, the experimentally observed intermediates are a consequence of native-like interactions (10–14). The present investigation complements recent simulation studies on homologous SH3 domains (13, 45–48). Our finding of sparsely populated intermediates, indicating early formation of the central β-sheet during the folding process, is in general agreement with previous simulation results (45–47). The present approach is limited in that it uses only a reduced chain representation, solvation (13, 14, 45, 48, 49) is not explicitly treated, and aspects of kinetic cooperativity (15) are yet to be addressed. Nonetheless, the simplicity of our model allows for broad conformational sampling and energy covariance and thermodynamic analyses over many cycles of reversible folding/unfolding transitions, which are currently difficult to achieve in higher-resolution models. The model's folding/unfolding behavior was found to display apparent two-state thermodynamics; techniques such as calorimetry or CD that measure only global parameters would, therefore, give no information about the presence of intermediates along the folding trajectory. This emphasizes the importance of methods (both computational and experimental) that can provide information on a per-residue basis to supplement the more traditional approaches that have been used to study protein-folding dynamics.

Supplementary Material